Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Glass structure as a driver of polaronic conductivity in phosphate glasses containing MoO3 and WO3†
Sanja
Renka
a,
Radha D.
Banhatti
b,
Grégory
Tricot
c,
Petr
Kalenda
d,
Luka
Pavić
 a,
Petr
Mošner
d,
Ladislav
Koudelka
d and
Ana
Šantić
a,
Petr
Mošner
d,
Ladislav
Koudelka
d and
Ana
Šantić
 *a
*a
aDivision of Materials Chemistry, Ruđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia. E-mail: asantic@irb.hr
bGisela Tech. Assz., Konrad-Adenauer-Ring 51, 69214 Eppelheim, Germany
cLASIRE UMR-CNRS 8516, Université de Lille, Sciences et Technologies, Villeneuve d’Ascq F-59655, Lille, France
dDepartment of General and Inorganic Chemistry, Faculty of Chemical Technology, University of Pardubice, 53210 Pardubice, Czech Republic
First published on 2nd June 2023
Abstract
Glasses containing transition metal (TM) oxides exhibit polaronic conductivity which, according to a well-accepted view, depends on the overall amount of TMO and the fraction of reduced TM ions. In this study we show that in phosphate glasses containing WO3 and MoO3, polaronic conductivity is entirely governed by the structural features of the glass network and cannot be correlated with these parameters. Tungsten glasses are found to exhibit six orders of magnitude higher conductivity than their molybdenum counterparts despite a significantly lower fraction of W5+ ions and the compositional change of DC conductivity is non-monotonic in both glass systems. We relate the former effect to the tendency of WO6 units to aggregate by forming W–O–W–O–W bonds which facilitate polaronic transport, in contrast to MoO6 and MoO4 units which are prone to incorporate into a phosphate network uniformly thus failing to provide such fast conduction pathways. More interestingly, we show that the latter effect originates from the manner in which tungstate or molybdate units are mutually linked within the phosphate network: if they form chains with a sufficient number of flexible terminal oxygen bonds (lower TMO content) polaronic transport is facilitated whereas if they connect three-dimensionally, causing a reduction in the number of terminal oxygens (higher TMO content), conductivity is hindered. A detailed analysis of frequency-dependent conductivity and permittivity using the MIGRATION concept helps us understand the structural features that influence conductivity in these glasses and points out the importance of network connectivity in the propagation of polarons on long-range and localized scales.
1. Introduction
Interest in electronically conducting oxide glasses was initiated more than 60 years ago by an investigation by Denton et al. on the glass-forming characteristics and electrical properties of vanadate glasses.1 Since then, many other oxide glass systems have been found to exhibit electronic conduction and studies on the mechanism of electronic transport in these materials have been reported extensively. Generally, electronic conduction is a characteristic of oxide glasses containing transition metal (TM) oxides such as V2O5, WO3, MoO3 and Fe2O3.2–5 In these glasses, TM ions are present in more than one oxidation state and the conduction arises by the transfer of electrons from TM ions in a low oxidation state to the ones in a high oxidation state. In this process, the transferred electron becomes self-trapped in the potential well formed by the displacement of the surrounding atoms and, together with the atomic displacements that produce the well, forms a quasiparticle called a polaron. Accordingly, conductivity in glasses containing TM oxides is polaronic by nature and follows the small polaron hopping theory.3 It has been widely accepted that the main factors that influence polaronic conductivity in oxide glasses are the amount of TM oxides, the fraction of TM ions in different oxidation states and the distance between TM ions.5–9 While the amount of transition metal oxides is a matter of choice of stoichiometry and related glass-forming ability, the fraction of TM ions in different oxidation states depends on many parameters, including preparation conditions such as the melting time, temperature and atmosphere, types of raw materials, concentration of TM oxides and presence of other substances in the batch.10–12Among various families of polaronic oxide glasses, phosphate glasses containing WO3 and MoO3 are especially attractive due to their wide glass-forming composition range and desirable physiochemical properties. Incorporation of MoO3 and WO3 into the phosphate glass increases the electrical conductivity and improves the mechanical properties and chemical resistance against atmospheric moisture as well as thermal stability against devitrification.12 These properties make them important in various domains of applications including optical, photochromic and electrochromic to those related to gas sensors and solid state batteries.12,13
The first systematic study of the electrical transport in binary phosphate glasses containing WO3 and MoO3 was reported by Mansingh et al.14–17 The authors investigated glasses within a relatively narrow composition range, from 60 to 85 mol% of MoO315 and 67 to 80 mol% of WO3,16 and proposed small polaron hopping as the conduction mechanism in both glass systems. Furthermore, Murawski et al.5 re-examined the DC conductivity reported by Mansingh et al. in the framework of Mott's theory2 and proposed that in WO3–P2O5 glasses hopping of small polarons exhibits an adiabatic character. On the other hand, MoO3–P2O5 glasses were reported to show non-adiabatic small polaron hopping5 in which an electron may not always follow the lattice motions and miss many coincident events before making a hop. In a number of studies that followed, the focus was placed on the effects of addition of alkali oxides or additional TM oxides on electrical transport in molybdenum- and tungsten-phosphate glasses whilst polaronic conduction in simple binary MoO3–P2O5 and WO3–P2O5 glass systems was investigated only sporadically.18–21 In our recent studies22,23 on electrical transport in alkali/silver–zinc–phosphate glasses containing WO3 and MoO3, we have showed that a significantly higher conductivity of the 60WO3–40P2O5 (in mol%) glass in comparison to that of the 60MoO3–40P2O5 (in mol%) analogue is related to a high tendency of clustering of tungstate units in the phosphate network which provides easy conducting pathways for polaron transport. In the 60WO3–40P2O5 glass, high conductivity was achieved despite a low fraction of W5+/Wtot (< 2%) indicating that the glass structure plays a pivotal role in the transport of polarons.
Through this work, we aim to gain deep insights into the dynamics of polarons in these materials by a detailed structural and electrical characterization of binary xMoO3-(100−x)P2O5 and xWO3-(100−x)P2O5 glasses in a wider range of composition, x = 49–81 mol%, using various experimental methods (Raman, 31P MAS-NMR, ESR and impedance spectroscopies) and numerical modelling of electrical conductivity and permittivity spectra using the MIGRATION concept.24 The results reported in this work prove that the glass structure is a key factor for polaronic conductivity in these glasses. In particular, the structure can facilitate or hinder the transport of polarons depending on the manner in which the tungstate or molybdate units are linked. These findings deepen our understanding of the nature of polaron transport in binary oxide glasses and open possibilities for engineering desired compositions of highly electronically conducting tungsten- and molybdenum-phosphate materials.
2. Experimental and computational procedures
2.1 Experimental
Two binary glass series xWO3-(100−x)P2O5 and xMoO3-(100−x)P2O5, x = 49–81 mol%, were prepared by melt-quenching technique from reagent grade chemicals H3PO4 (85.0%, PENTA), WO3 (99.9%, Sigma-Aldrich) and MoO3 (99.9% Sigma-Aldrich) in batches of 25 g. Homogenized starting mixtures were slowly calcined up to 600 °C and held at that temperature for 2 hours in order to remove water. The reaction mixtures were then melted at 1300–1450 °C under ambient air, in an alumina crucible, after which the melts were transferred to a graphite mould preheated at T < Tg. Obtained dark blue glasses were cooled to room temperature and their amorphous character was checked by X-ray diffraction analysis. The exact glass composition was determined using an energy dispersive X-ray analyzer (EDS) by analyzing the surface and cross-section of the prepared samples. The glasses in this work were labelled according to their composition, for example, W-50 corresponds to the 50WO3–50P2O5 (mol%) glass composition.The glass density, ρ, was determined using a helium gas pycnometer AccuPyc II 1340, while the glass transition temperature, Tg, was measured on bulk samples using a thermomechanical analyzer TMA 402 F3 (Netzsch). Measurements were carried out under an inert atmosphere of N2 at a heating rate of 5 °C min−1. From the obtained dilatometric curves, Tg was determined from the change in the slope of elongation vs. temperature.
The electron spin resonance (ESR) spectra of the samples were recorded at ambient temperature at an X-band (∼9.5 GHz) using a spectrometer ESR 221 Magnettech. A microwave power of 10 mW, sufficiently below the saturation power, was used. The obtained ESR spectra were double integrated and experimental parameters were used to obtain comparable areas of all spectra. Using Mn2+ as a standard, the spin concentration was determined for all samples and the ratio of Mo5+/Motot and W5+/Wtot was calculated.
The Raman spectra of glasses were recorded in the range of 1500–200 cm−1 on glassy bulk samples at room temperature using a DXR Raman spectrometer Thermo Scientific with a 532 nm solid-state (Nd:YAG) diode pumped laser. The complex shape of the Raman spectra was analysed using the least square fitting procedure assuming the Gaussian shape for all bands. The position and intensity of each component band were determined from the deconvoluted Raman spectra. To find the optimal fit, a minimum number of bands corresponding to the number of distinct features observed in the Raman spectra such as resolved maximum and well detectable shoulders was used. The structural units in the phosphate network were classified according to their connectivity by Qn notation where n represents the number of bridging oxygen atoms per PO4 tetrahedron (n = 0–3).
31P MAS-NMR experiments were performed at 162.9 MHz using a 9.4 T AVANCE II Bruker spectrometer equipped with a 4-mm probehead operating at 12.5 kHz. Each spectrum was collected with a pulse length of 1.5 μs (corresponding to a π/6 flip angle), 8–16 transients and a recycle delay of 5–15 s allowing for quantitative measurements.
Impedance spectroscopy was used for measuring the conductivity spectra of glasses. The glass samples were prepared as ∼1 mm thick discs and gold electrodes (6 mm in diameter) were sputtered on both sides of the samples using a sputter coater SC7620. Complex impedance was measured using an impedance analyzer (Novocontrol Alpha-AN Dielectric Spectrometer) in wide frequency (0.01 Hz–1 MHz) and temperature (from −90 °C to 240 °C) ranges. The temperature was controlled to an accuracy of ±0.2 °C.
2.2. Numerical modelling of the conductivity and permittivity spectra
The modelling of the conductivity and permittivity spectra was performed using the MIGRATION concept (an acronym for MIsmatch Generated Relaxation for the Accommodation and Transport of IONs),24,25 which was developed for describing ion dynamics in disordered structures such as ionic glasses, fragile melts and salt-in-polymer electrolytes. This model is based on a simple picture of understanding the success of the forward hop of a central ion, made at t = 0 to an adjacent suitable site, in terms of a time-correlation factor, W(t). Since such a hop induces a dipole moment, g(t), and a corresponding dipole field in its neighborhood, the multi-particle relaxation of the neighborhood triggers the correlated forward–backward hops of the central ion. Thus, the success (through a single attempt or repeated attempts) of the hop of the central ion over time is dependent on its elementary hopping rate as well as on the strength of the dipole moment and decay of the dipole field, which in turn depends on the effective number of ions, N(t), in the neighborhood still responding to the dipole field.Recently, we have shown that both the model leitmotif and its formulation can be used to describe the conductivity spectra and hence understand the charge transport in polaronic glasses as well,9 since the polarisation field caused by the hopping polaron is to first order a dipole field. Furthermore, as per the small polaron theory, since the electron is at all times relaxed in the potential well of its lattice distortion (resulting in an induced dipole moment) it can respond rapidly to the induced dipole field, provided it finds transition ions of the correct oxidation state in its immediate neighbourhood.
A detailed formulation of the model can also be found in ref. 9. Here, it suffices to state in brief the essential fact that the time correlation factor W(t) is calculated by solving two coupled rate equations defining the time-dependent decay of both W(t) and g(t), and a related third equation describing the decay of the dipole field, and these equations are formulated using three model parameters. These equations are
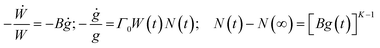 | (1) |
What makes modelling experimental spectra using the MIGRATION concept unique is that it yields quantitative information which can be correlated to factors influencing the charge carrier dynamics. For example, one can calculate the spatial extent of the localised diffusion of the charge carrier,26 a material property of the glass. Since, as stated above, the local glass structure is especially relevant for understanding charge transport in polaronic glasses, a systematic modelling of conductivity and permittivity isotherms for a wide range of compositions of polaronic glasses has been performed for the very first time using the MIGRATION concept, to ascertain how important is the role played by the glass network structure in facilitating charge transport in any given series of glasses and for a given glass composition,26 and to help deepen our understanding of the fundamental features of polaronic transport in binary oxide glasses.
3. Results and discussion
3.1. Glass composition, thermal properties and oxidation states of molybdenum and tungsten ions
All glasses from both series, xWO3-(100−x)P2O5 and xMoO3-(100−x)P2O5, x = 49–81 mol%, were found to be fully amorphous, except the W-81 glass where traces of crystallization were detected. The glass composition determined by EDS analysis and selected physical parameters of the samples are reported in Table 1. The EDS analysis shows that glass samples contain very small amounts of Al (<0.8 wt%) due to a slight dissolution of Al2O3 crucibles during melting, see Section S2 of the ESI.† However, such small amounts are not expected to have any influence on the structural and physical properties of glasses. From Table 1, it can be seen that the addition of MoO3 and WO3 to phosphate glasses results in a steady increase of the glass density, ρ, but causes non-monotonic changes in the glass transition temperature (Tg). While a linear increase in ρ is related to the replacement of phosphate ions with heavier molybdenum/tungsten ones, the non-linear trend of Tg reflects the changes in the cross-link density and strength of the chemical bonds with the incorporation of molybdate/tungstate units. The initial increase in Tg from 495 °C to 585 °C with an increasing MoO3 content from 49 to 57 mol% is associated with the higher cross-link density between the molybdate and phosphate units. However, with further MoO3 addition, Tg decreases as a result of depolymerization of the phosphate glass network, see Section 3.2.1., and the effect of the replacement of stronger P–O bonds (599 kJ mol−1) with weaker Mo–O bonds (502 kJ mol−1) that reduces the mean bond strength in the glass structure.27–29 Unlike in the MoO3 series, the differences in Tg values in the WO3 series are much smaller and vary within a span of 100 °C. These variations result from the competing effect of the replacement of the P–O bonds by the stronger W–O bonds (720 kJ mol−1)27–29 and a decrease in the cross-link density due to the depolymerization of the phosphate network and the clustering of WO6 octahedra, see Section 3.2.1. Since the former effect dominates the latter, Tg of WO3 containing glasses shows a slight increase over the entire range of compositions. For the same reason, tungsten glasses exhibit higher Tg values (662–760 °C) and hence form a more thermally stable glass network in comparison to the molybdenum glasses (Tg = 382–585 °C).| MoO3 | P2O5 | Mo5+/Motot (%) | ||||
|---|---|---|---|---|---|---|
| Mo-49 | 49 | 51 | 3.9 | 3.02 | 495 | 26.5 |
| Mo-57 | 57 | 43 | 4.5 | 3.17 | 585 | 22.8 |
| Mo-61 | 61 | 39 | 4.8 | 3.24 | 505 | 15.5 |
| Mo-70 | 70 | 30 | 6.0 | 3.32 | 431 | 3.4 |
| Mo-80 | 80 | 20 | 8.5 | 3.57 | 382 | 0.5 |
The dominant oxidation states of TM ions in these glasses are Mo6+ and W6+, with some small fractions of Mo5+ and W5+ ions, see Table 1 and Section 3 of the ESI.† The fractions of W5+/Wtot (%) were found to be very low and approximately constant (0.2–1.9%) for all samples. On the other hand, in the molybdenum series, the Mo5+/Motot ratio decreases from 26.5% in the Mo-49 glass to 0.5% in the Mo-80 glass showing the strongest decrease from the Mo-61 sample to the Mo-70 sample. The higher values of Mo5+/Motot originate from the stronger reduction tendency of molybdenum in comparison with tungsten ions in the melting process.12
3.2. Network structure in WO3–P2O5 and MoO3–P2O5 glasses
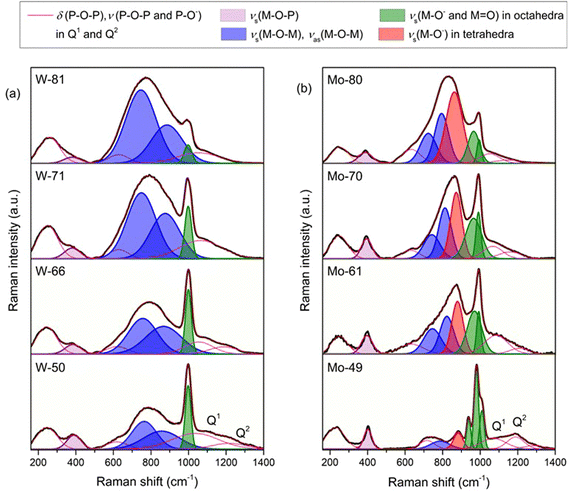
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and W–O− bonds in WO6 octahedra, see Fig. 1(a).27,30 These spectra also contain broad, less intense bands in the 750–880 cm−1 region, associated with the symmetrical and asymmetrical W–O stretching vibrations within W–O–W bonds.27,30 With the increase in the WO3 content, the intensity of the bands related to the vibrations of bridging oxygen in W–O–W bonds gradually increases, and for glasses with ≥71 mol% WO3, these bands overpower the band associated with the vibrations of terminal oxygens. This indicates that WO6 octahedra have a strong tendency to mutually interconnect and form a three-dimensional structural network. This is also supported by the fact that the band at ≈400 cm−1, related to the stretching vibrations of P–O–W bonds,22,23,27 decreases with the addition of WO3 denoting a reduction in interconnectivity between WO6 octahedra and phosphate units. Although the bands related to the phosphate units are of much smaller intensity and are greatly overlapped by the strong metal-oxygen bands, some conclusions can be drawn on their presence. That is, for glasses containing ≤66 mol% of WO3, the relatively weak bands at ≈1080 cm−1 and ≈1210 cm−1 reveal that pyrophosphate (Q1) and metaphosphate (Q2) units are present in the glass network.23 With an increasing WO3 content above 66 mol%, only the band at ≈1080 cm−1 related to pyrophosphate units remains present indicating the complete depolymerization of metaphosphate chains. Here, it should be noted that the vibrations associated with the isolated orthophosphate (Q0) units are completely covered by those of the tungsten-oxygen bands, so their presence is impossible to identify from the Raman spectra.
O and W–O− bonds in WO6 octahedra, see Fig. 1(a).27,30 These spectra also contain broad, less intense bands in the 750–880 cm−1 region, associated with the symmetrical and asymmetrical W–O stretching vibrations within W–O–W bonds.27,30 With the increase in the WO3 content, the intensity of the bands related to the vibrations of bridging oxygen in W–O–W bonds gradually increases, and for glasses with ≥71 mol% WO3, these bands overpower the band associated with the vibrations of terminal oxygens. This indicates that WO6 octahedra have a strong tendency to mutually interconnect and form a three-dimensional structural network. This is also supported by the fact that the band at ≈400 cm−1, related to the stretching vibrations of P–O–W bonds,22,23,27 decreases with the addition of WO3 denoting a reduction in interconnectivity between WO6 octahedra and phosphate units. Although the bands related to the phosphate units are of much smaller intensity and are greatly overlapped by the strong metal-oxygen bands, some conclusions can be drawn on their presence. That is, for glasses containing ≤66 mol% of WO3, the relatively weak bands at ≈1080 cm−1 and ≈1210 cm−1 reveal that pyrophosphate (Q1) and metaphosphate (Q2) units are present in the glass network.23 With an increasing WO3 content above 66 mol%, only the band at ≈1080 cm−1 related to pyrophosphate units remains present indicating the complete depolymerization of metaphosphate chains. Here, it should be noted that the vibrations associated with the isolated orthophosphate (Q0) units are completely covered by those of the tungsten-oxygen bands, so their presence is impossible to identify from the Raman spectra.
The evolution of the Raman spectra of phosphate glasses with the addition of MoO3 shows somewhat different changes in the glass network, see Fig. 1(b). The most intense band at 980 cm−1 accompanied by a band at 939 cm−1 and a shoulder at 1012 cm−1 in the spectrum of the Mo-49 glass is ascribed to the stretching vibrations of terminal Mo–O− and Mo![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds in MoO6 octahedra.28,31 However, in this spectrum, there is an additional band at 883 cm−1 which is related to the stretching vibration of Mo–O− bonds in MoO4 tetrahedra.28,31 With an increasing MoO3 content, the intensity of νs(Mo–O−) in MoO4 tetrahedra increases while that of νs(Mo–O−) in octahedra decreases indicating the change in the coordination of molybdenum ions from six to four. Also, by comparing the spectra of both glass series, there is an obvious difference in the intensity of stretching bands of TM–O–TM and TM–O–P bonds. First, in tungsten containing glasses, ν(W–O–W) bands are strong throughout the whole series, whereas in MoO3–P2O5 glasses, ν(Mo–O–Mo) bands are not so pronounced and their intensity does not increase so drastically. Second, the Raman band that corresponds to the stretching vibration of Mo–O–P bonds at ≈400 cm−1 is more pronounced than the equivalent band of W–O–P bonds and retains intensity throughout the glass series. These differences indicate that while in tungsten containing glasses WO6 units mostly interconnect mutually, in molybdenum glasses molybdate units are more prone to associate with phosphate ones, thus forming a uniform phosphate–molybdate glass network.
O bonds in MoO6 octahedra.28,31 However, in this spectrum, there is an additional band at 883 cm−1 which is related to the stretching vibration of Mo–O− bonds in MoO4 tetrahedra.28,31 With an increasing MoO3 content, the intensity of νs(Mo–O−) in MoO4 tetrahedra increases while that of νs(Mo–O−) in octahedra decreases indicating the change in the coordination of molybdenum ions from six to four. Also, by comparing the spectra of both glass series, there is an obvious difference in the intensity of stretching bands of TM–O–TM and TM–O–P bonds. First, in tungsten containing glasses, ν(W–O–W) bands are strong throughout the whole series, whereas in MoO3–P2O5 glasses, ν(Mo–O–Mo) bands are not so pronounced and their intensity does not increase so drastically. Second, the Raman band that corresponds to the stretching vibration of Mo–O–P bonds at ≈400 cm−1 is more pronounced than the equivalent band of W–O–P bonds and retains intensity throughout the glass series. These differences indicate that while in tungsten containing glasses WO6 units mostly interconnect mutually, in molybdenum glasses molybdate units are more prone to associate with phosphate ones, thus forming a uniform phosphate–molybdate glass network.
However, along with the differences, there are also some similarities between the two glass series. In both systems, the increase in WO3 and MoO3 contents causes the depolymerization of metaphosphate chains and consequently the increase in the fraction of pyrophosphate units. But even more important is the fact that the Raman spectra of glasses containing less than 70 mol% of both WO3 and MoO3 (lower bright yellow panels in Fig. 1) are dominated by intense vibrations of terminal oxygen bonds, whereas for glasses with ≥70 mol% of WO3 and MoO3 (upper panels in Fig. 1) the bands related to bridging oxygens in W–O–W and Mo–O–Mo bonds prevail. The ratio between the terminal and bridging oxygen bonds will be shown to have surprisingly important implications for polaronic transport which is reported in the next sections.
3.3. Polaronic transport in WO3–P2O5 and MoO3–P2O5 glasses
In the theory proposed by Austin and Mott,3,15 the conduction process in TM oxide glasses occurs by phonon-assisted hopping of small polarons between nearest localized states. In this model, the temperature dependence of DC conductivity is given by the following expression:
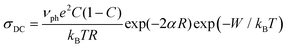 | (2) |
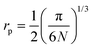 , are also reported in Table 2. The values of the rate of the wave function decay, α, and the polaron radius, rp, are in good agreement with similar polaron conducting glasses.4,15,16,18
, are also reported in Table 2. The values of the rate of the wave function decay, α, and the polaron radius, rp, are in good agreement with similar polaron conducting glasses.4,15,16,18
| Glass | σ DC/(Ω cm)−1 at 303 K | W (eV) | N (cm−3) × 1021 | R (Å) = N−1/3 | r p (Å) | exp(−2αR) | α (Å−1) |
|---|---|---|---|---|---|---|---|
| W-50 | 8.53 × 10−8 | 0.36 | 6.48 | 5.36 | 2.16 | 4.63 × 10−4 | 0.72 |
| W-61 | 1.66 × 10−6 | 0.33 | 8.49 | 4.90 | 1.98 | 4.40 × 10−3 | 0.55 |
| W-66 | 2.40 × 10−5 | 0.28 | 9.38 | 4.74 | 1.91 | 7.96 × 10−4 | 0.75 |
| W-71 | 7.74 × 10−7 | 0.35 | 10.4 | 4.58 | 1.85 | 1.41 × 10−3 | 0.72 |
| W-81 | 8.04 × 10−10 | 0.53 | 12.9 | 4.26 | 1.72 | 1.18 × 10−3 | 0.79 |
| Mo-49 | 1.94 × 10−13 | 0.67 | 6.24 | 5.43 | 2.19 | 1.28 × 10−5 | 1.04 |
| Mo-57 | 2.13 × 10−12 | 0.62 | 7.60 | 5.09 | 2.05 | 1.41 × 10−5 | 1.10 |
| Mo-61 | 4.96 × 10−10 | 0.49 | 8.31 | 4.94 | 1.99 | 4.08 × 10−5 | 1.02 |
| Mo-70 | 9.84 × 10−12 | 0.55 | 9.76 | 4.68 | 1.89 | 7.35 × 10−5 | 1.02 |
| Mo-80 | 1.02 × 10−11 | 0.62 | 10.2 | 4.37 | 1.76 | 9.76 × 10−4 | 0.79 |
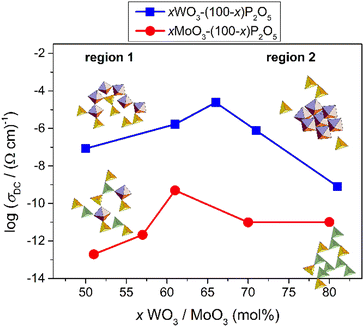
In order to explain the observed conductivity trends, several parameters need to be discussed. According to the classical understanding of the polaronic transport in oxide glasses, one of the most important factors for conductivity is the fraction of reduced TM ions (TM5+/TMtot). The increase of this fraction usually causes an increase in polaronic conductivity due to the increase in the number of TM5+–TM6+ ion pairs through which the electron transfer occurs. Our results, however, contradict this hypothesis. For one, the fraction of W5+/Wtot is ≤1.9% throughout the entire series but the DC conductivity varies largely. On the other hand, with the addition of MoO3 from 49% to 61%, the Mo5+/Motot ratio decreases while the DC conductivity simultaneously increases, see Table 1. Even if we take into account the increase in the MoO3 content and calculate the number density of Mo5+ ions we see that this value changes from ≈1.7 × 1021 cm−3 to ≈1.3 × 1021 cm−3 as the amount of MoO3 increases to 61%, which, again, cannot explain the observed increase in conductivity. Secondly, if we compare the two glass systems, tungsten glasses exhibit significantly higher DC conductivity than their molybdenum counterparts despite a significantly lower W5+/Wtot ratio. This difference is especially pronounced at the lowest TMO content of about 50–60 mol%, where the greatest difference between W5+/Wtot and Mo5+/Motot is observed. A similar difference in conductivity between these two glass systems was reported in previous studies; however, therein, glasses were investigated in a relatively narrow range of compositions.4,6,23 For instance, Sayer and Mansingh4 reported approximately five orders of magnitude higher electrical conductivity of 50WO3–50P2O5 than that of the 50MoO3–50P2O5 glass and our recent study23 showed a similar conductivity difference for 60WO3–40P2O5 (4.26 × 10−6 (Ω cm)−1) and 60MoO3–40P2O5 (2.76 × 10−11 (Ω cm)−1) glasses. In these studies, the higher electrical conductivity of tungsten glasses in comparison to molybdenum analogues was ascribed to the clustering of tungstate units that ease the polaronic transport; i.e. the higher number of facilitating W–O–W bonds in comparison to the higher number of inhibiting Mo–O–P bonds in molybdenum glasses. In our present study, we show that the higher conductivity of tungsten glasses is evident throughout the wide compositional range, x(TMO) ranging from 50 to 80 mol%, and that, indeed, this difference can be related to the glass structure. In fact, as per the analysis in Section 3.2.1., it emerges that all tungsten containing glasses are characterized by a high tendency of WO6 units to mutually connect and form W–O–W–O–W bonds that gradually start to dominate the glass network as the amount of WO3 increases. On the other hand, in the molybdenum glasses, MoO6 octahedra and MoO4 tetrahedra are interconnected with the phosphate units forming a mixed phosphate–molybdate glass network. From this, it is reasonable to assume that the network composed of tungstate clusters provides more conductive pathways for polarons via W–O–W bonds than the mixed phosphate–molybdate network with preferred Mo–O–P bonding. Therefore, the increase in the polaronic conductivity of glasses containing up to 66 mol% of WO3 and 61 mol% of MoO3 (marked as region I in Fig. 4), as well as the difference between the two series, is directly related to the increase in the number of W–O–W and Mo–O–Mo bonds with increasing TMO, as well as a generally higher fraction of W–O–W bonds in comparison to Mo–O–Mo bonds (see Fig. 1).
However, although the formation of the fast polaron transport pathways via bridging TM–O–TM bonds explains well the trends up to the conductivity maximum, it fails to explain the decrease in conductivity with the further addition of both oxides. In particular, it is interesting to observe that the decrease in conductivity is especially strong in tungsten glasses for which the formation of W–O–W bonds is extremely favored. Again, this result is in disagreement with the general idea that clustering of TM units has a facilitating effect on polaron transport. So, the main question to be answered is, what is the cause of the observed decrease in conductivity at high amounts of WO3 and MoO3? From the Raman spectra shown in Fig. 1(a), we observe that above 66 mol% of WO3, WO6 octahedra form a three-dimensional network by consuming oxygen atoms for linking and hence causing a strong decrease in the number of terminal oxygen bonds (see upper panels in Fig. 1). Such formation of WO6 clusters with a small number of terminal oxygens results in a rigid tungstate network which seems to be unfavorable for the structural rearrangement involved in polaron formation and hence its conductivity. This is especially evident in the W-81 glass for which the polaronic conductivity shows the strongest decrease along with the strongest decrease in the intensity of the Raman band corresponding to the terminal oxygen atoms, compare Fig. 1(a) and 4. This further indicates that the key factor that governs the polaronic transport in these glasses is the way in which the tungstate units interconnect, or more precisely the interplay between the number of bridging and terminal oxygen bonds which defines the flexibility of the tungstate network. Accordingly, when the former bonds start to overpower the latter, the network becomes rigid and the conductivity gets hindered. A similar finding on the importance of the flexibility of the bonds involved in polaronic transport was recently reported for crystalline V2O5.34 Based on the DFT+U calculations, the authors showed that the least favourable polaron migration pathway is through the stiff 3-coordinated oxygen atom connected between vanadium centres that results in a distorted transition state structure with high energy. In contrast, bridging V–O–V bonds appear to be favorable for polaron migration even though their hopping distance is quite large. The reason for this is the higher flexibility of bridging oxygen atoms which causes a less constrained transition state structure and a lower transition state energy. Furthermore, our most recent study on binary V2O5–P2O5 glasses exhibits an almost linear increase in the polaronic conductivity, even up to 90 mol% of V2O5, followed by a gradual increase in the intensity of bridging V–O–V bonds but with the retained high intensity of terminal V–O bonds over the entire compositional range.35 These findings support our conclusion that for fast polaron transport it is crucial to have TM–O–TM bonding; however, once the clustering of TM units starts to occur three-dimensional with a significant loss of flexible terminal oxygen bonds, polaronic transport gets hampered.
Similar correlations can also be made for molybdenum glasses in which the polaronic conductivity drops above 61 mol% of MoO3 (see region II in Fig. 4). In this system too, the Raman spectra show that the three-dimensional networking of molybdenum units takes place above 61 mol% of MoO3 and eventually rigid oxygen bonds dominate causing a decrease in polaronic conductivity. However, here, the decrease, while significant for Mo-70, does not decrease further for Mo-80. The network connectivity offered by MoO4 tetrahedra vis-a-vis the significant loss of flexible terminal oxygen bonds has an obvious role in this implying that the coordination of TM ions, i.e. octahedral vs. tetrahedral, also plays a role in the ease of charge conduction in these glasses. In the next step, we aim to shed some light on these trends with our analysis of the conductivity and permittivity spectra using the MIGRATION concept.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (σs(ωs)) vs. log(ωs), where
(σs(ωs)) vs. log(ωs), where 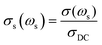 , with
, with 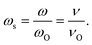 Using σDC determined from the experiment, the suitable model spectrum is chosen on shifting the experimental isotherm on the scaled x-axis by log(vo), which is defined as the onset frequency of conductivity dispersion for that temperature, such that the shape and form of the experimental isotherm match that of the model isotherm. Here, the crucial model parameter describing the shape of the isotherm around the onset of conductivity dispersion is K. Normally for ionic glasses, B can be chosen arbitrarily large and N(∞) can be set to zero for this step. However, in polaronic glasses, as in mixed former ionic glasses,36 rather a small value of B is needed to describe the shape of the permittivity isotherm, and a non-zero value of N(∞) is additionally needed to model the gradual onset of conductivity dispersion at lower frequencies of the isotherm. The model permittivity spectrum is plotted as εs(ωs) vs. log(ωs), and is defined as
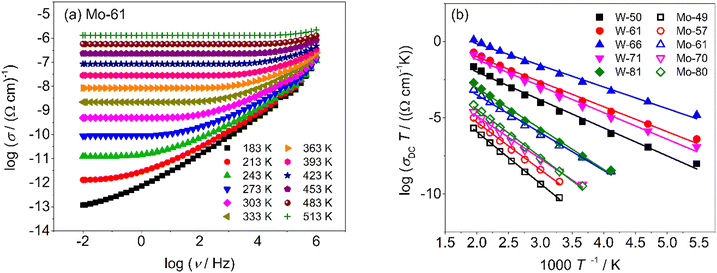
Using σDC determined from the experiment, the suitable model spectrum is chosen on shifting the experimental isotherm on the scaled x-axis by log(vo), which is defined as the onset frequency of conductivity dispersion for that temperature, such that the shape and form of the experimental isotherm match that of the model isotherm. Here, the crucial model parameter describing the shape of the isotherm around the onset of conductivity dispersion is K. Normally for ionic glasses, B can be chosen arbitrarily large and N(∞) can be set to zero for this step. However, in polaronic glasses, as in mixed former ionic glasses,36 rather a small value of B is needed to describe the shape of the permittivity isotherm, and a non-zero value of N(∞) is additionally needed to model the gradual onset of conductivity dispersion at lower frequencies of the isotherm. The model permittivity spectrum is plotted as εs(ωs) vs. log(ωs), and is defined as 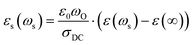 . In polaronic glasses, the scaled permittivity isotherm exhibits a reasonably well-defined low-frequency plateau, εs(0). Note that ε(∞) is the permittivity due to faster electronic relaxation processes and is not related to the slower relaxation processes connected with polaronic hopping. In Fig. 5, we plot conductivity and permittivity isotherms in the scaled representation for W-66 and Mo-61 glasses, superimposed on the model curves that best describe the experimental spectra. The experimental conductivity spectra of the Mo-61 glass are shown in Fig. 3a, whereas its permittivity spectra as well as the conductivity and permittivity spectra of the W-66 glass are shown in Fig. S1 of the ESI.†
. In polaronic glasses, the scaled permittivity isotherm exhibits a reasonably well-defined low-frequency plateau, εs(0). Note that ε(∞) is the permittivity due to faster electronic relaxation processes and is not related to the slower relaxation processes connected with polaronic hopping. In Fig. 5, we plot conductivity and permittivity isotherms in the scaled representation for W-66 and Mo-61 glasses, superimposed on the model curves that best describe the experimental spectra. The experimental conductivity spectra of the Mo-61 glass are shown in Fig. 3a, whereas its permittivity spectra as well as the conductivity and permittivity spectra of the W-66 glass are shown in Fig. S1 of the ESI.†
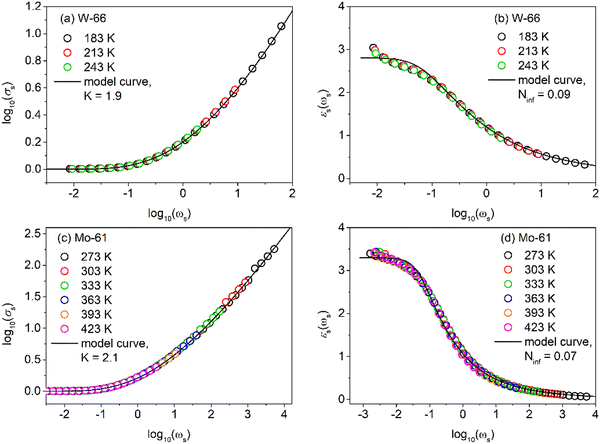 | ||
| Fig. 5 Scaled experimental (a and c) conductivity and (b and d) permittivity spectra of W-66 and Mo-61 glasses superimposed on corresponding model curves with B = 12. | ||
In Table 3, we present the parameters of the model spectra used for modelling the conductivity and permittivity spectra of glasses from the xWO3-(100−x)P2O5 and xMoO3-(100−x)P2O5 series. To recall, the W-81 glass was excluded from analysis due to partial crystallization, and Mo-49 due to the lack of a good permittivity plateau in experimental isotherms. In considering the observed changes in the parameter K, two comments are in order. Firstly, the variation in K shows a neat inverse correlation to DC conductivity for both systems. Secondly, the absolute values of K for glasses containing WO3 are lower (K = 1.9 and 2.0) than those for glasses containing MoO3 (K = 2.1 and 2.2) which is in agreement with the trends exhibited for the values of DC conductivity in these glasses, see Fig. 4. From the body of spectra which have been so far modelled using the MIGRATION concept, it has been found that for the majority of the single-alkali ionic glasses be it borate, silicate or phosphate glasses or in mixed glass formers systems, the parameter K has a value of 2.0.25,26,36 In ionic glasses, values of K > 2.0 could be correlated to either a lower connectivity of conductivity pathways or a lower number density of the charge carriers.37–39 On the other hand, for polaronic iron phosphate-based glasses, the value of K was found to be 1.9, indicating an earlier onset of long-range charge transport in contrast to ionic glasses.9 It is to be noted that although the K parameter has been found to have values from 1 to 3 in the spectra of materials modelled so far, a difference of 0.1 on either side of K = 2.0 is significant. Thus, one of the factors responsible for a much higher value of σDC in the W-66 glass as compared to that of Mo-61, see Fig. 4, is the ease of the transport of polarons in the former. Also, it is important to note that although the value for the two glasses W-61 and W-66 is K =1.9 as in the polaronic iron phosphate glasses,9 the factors responsible for it are different. In the latter systems, the fraction of the reduced iron ions is correlated directly to σDC, see Fig. 8 in ref. 9, while the phosphate glass network structure remains very similar. This is not true for phosphate glasses containing tungsten and molybdenum oxides studied here. In our current study, it is evident that the polaron conductivity is driven by the structural features of the glass such as the network connectivity of different structural units (see Fig. 1 and discussions following it) and is not correlated to the TM5+ fraction. Therefore, we infer that an increase from K = 2.1 for Mo-61 glasses to K = 2.2 for all other MoO3 contents is indicative of lesser available pathways for the polaron transport in the glass network in the latter samples. On the other hand, the value of K decreasing from 2.0 for W-50 and W-71 glasses to 1.9 for W-61 and W-66 samples suggests that the network connectivity is less important than the faster local relaxations which implies shallow potential wells and hence faster polaronic transport. Indeed, from the structural results based on the analysis of Raman and 31P MAS-NMR spectra, we can infer that one main advantage of the clustering of tungstate units is that they could allow for fast local relaxations. And a larger value of σDC as well as this small value of K = 1.9 allows us to put forth a picture of tissue connectivity, where the polaron transport within the nodules composed of two-dimensionally connected tungsten units is fast and there is a conducting pathway to the next cluster.
| Glass | K | B | N(∞) | ε s (0) | 〈rloc2(∞)〉0.5 in Å |
|---|---|---|---|---|---|
| W-50 | 2.0 | 12 | 0.12 | 2.67 | 1.47 ± 0.06 |
| W-61 | 1.9 | 12 | 0.09 | 2.81 | 1.27 ± 0.05 |
| W-66 | 1.9 | 12 | 0.11 | 2.66 | 1.21 ± 0.03 |
| W-71 | 2.0 | 12 | 0.02 | 4.31 | 1.53 ± 0.02 |
| Mo-57 | 2.2 | 12 | 0.02 | 5.25 | 2.08 ± 0.07 |
| Mo-61 | 2.1 | 12 | 0.08 | 3.15 | 1.11 ± 0.03 |
| Mo-70 | 2.2 | 12 | 0.13 | 2.73 | 1.06 ± 0.05 |
| Mo-80 | 2.2 | 12 | 0.10 | 3.03 | 0.92 ± 0.03 |
In the right-hand side panels of Fig. 5, we present the scaled permittivity spectra of W-66 and Mo-61 samples with the corresponding master spectrum (the similar representation of the modelled scaled permittivity spectrum for other glasses is shown in Fig. S2 of the ESI†). Here, a suitable value of the parameter, N(∞), helps us to find the plateau value of εs(0). The value of B could be ascertained by modelling the permittivity spectrum and is found to be rather small, implying that for the lowest measured temperature, conductivity dispersion cannot be more than 5.2 decades on the logarithmic scale. This further implies that, for instance, for the Mo-61 glass at the lowest temperature (namely 183 K), the high-frequency conductivity plateau would lie just close to a few MHz. This result in itself is sensational, since polaronic glasses have not been measured at higher frequencies and, based on this inference from modelling, it could imply that any further dispersion one would observe in conductivity at higher frequencies may not correspond to processes contributing to translational charge transport, but rather to localized relaxation processes of the oxide network. We also observe that B = 12 fits the permittivity spectrum of the highly conductive W-66 glass, although even at 183 K, due to the higher value of DC conductivity, the tail of ε(∞) attaining a zero value is not yet observed in the experimental frequency range. A perusal of Table 3 reveals that the value of εs(0) changes from 5.25 to 2.73 for the glasses containing MoO3 while it is around 2.7–2.8 for glasses containing WO3, except for W-71.
In Table 3, we additionally quantify the length scale of the localized polaronic hops, 〈rloc2(∞)〉0.5 for each composition using the relationship (3):
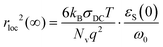 | (3) |
In considering the parameters in Table 3, it is interesting to note that in these glasses despite a steady increase in N as a function of the TM oxide content, see Table 2, all dynamic values of polaron transport, parameter K, 〈rloc2(∞)〉0.5 and εs(0) mirror each other. This confirms the inferences from a detailed structural analysis that the dynamics of polaron transport in these glasses is guided by the interconnectivity of structural units and hence the formation of conduction pathways for the polarons. Two features that are worthy of comments are (i) for the glasses containing MoO3, there is a strong decrease of εs(0), which is also reflected in the trend shown by 〈rloc2(∞)〉0.5 and (ii) an increase in εs(0) for the W-71 glass in the series containing WO3. We recall that the Mo-57 glass exhibits the lowest conductivity among the four compositions that could be modelled for this series. As discussed earlier, the number of Mo–O–Mo bonds increases with the increase in the MoO3 content which explains the ease of polaron conductivity due to better network connectivity. In contrast, for the W-71 glass, the absence of terminal oxygen bonds means the three-dimensional networking of WO6 octahedra and hence increased charge stored in W–O–W–O–W bridges in clusters, which is reflected both by an increase in εs(0), as well as in parameter K and 〈rloc2(∞)〉0.5.
One last feature worth mentioning is that unlike in the mixed glass former glasses with ions as charge carriers,36 where 〈rloc2(∞)〉0.5 features the same compositional dependence as σDC; here, the typical polaronic hopping length is inversely correlated with σDC, compare Fig. 3 and Table 3, similarly as in polaronic iron phosphate glasses.9,40 This brings to focus the fact that polaronic conductivity has distinctive features that distinguish them from ionic charge carriers. As it is the transport of charge that propagates in the form of polaronic hops, whereas in ionic glasses, there is a spatial propagation of the charged species. Correspondingly, the value of 〈rloc2(∞)〉0.5 is a physical quantity there, whereas it is a characterization of the spatial extent of the local dipolar disturbance field in polaronic glasses.
4. Conclusions
This study reports on the nature of polaronic conductivity in binary phosphate glasses containing WO3 and MoO3 in a wide compositional rage: xWO3-(100−x)P2O5 and xMoO3-(100−x)P2O5, x = 49–81 mol%. The results show that the parameters of the polaronic transport cannot be correlated to the fraction of reduced tungsten and molybdenum ions and the overall amount of WO3 and MoO3, which are the factors that are generally acknowledged to have the most important role in electrical processes in glasses. In contrast, our detailed structural and electrical studies using Raman, 31P MAS-NMR, ESR and impedance spectroscopies, as well as numerical modelling of the conductivity and permittivity spectra using the MIGRATION concept revealed that the polaronic conductivity in these glasses is entirely governed by the structural characteristics of the glass network. Firstly, a significantly higher conductivity (nearly six orders of magnitude) of glasses containing WO3 in comparison to their MoO3 counterparts results from the high tendency of WO6 units to aggregate by forming W–O–W–O–W bridges which act as easy conduction pathways. Molybdenum units, MoO4 and MoO6, on the other hand, tend to uniformly incorporate into the phosphate network by forming P–O–Mo bonds that hinder the ease of polaron hops. Secondly, the non-monotonic trend of polaronic conductivity as a function of glass composition, showing maxima at 61 mol% of MoO3 and 66 mol% of WO3, indicates that the key factor that governs the polaronic transport in these glasses is the manner in which the tungstate and molybdenum units interconnect mutually. While the two-dimensional interconnection of these units has a positive effect on the dynamics of polarons by providing fast conduction pathways, the three-dimensional linking negatively affects the polaron transport due to a decrease in the number of terminal TM–O bonds which are important for the formation and transport of polarons. To state it simply, the clustering of transition metal units in oxide glasses does not facilitate the polaronic conductivity per se; it is the manner in which these units are connected that governs the conduction process.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Croatian Science Foundation, POLAR-ION-GLASS project IP-2018-01-5425. P. M. and L. K. are grateful for the financial support from the project no. 18-01976S of the Grant Agency of the Czech Republic.References
- E. P. Denton, H. Rawson and J. E. Stanworth, Nature, 1945, 173, 1030–1032 CrossRef.
- N. F. Mott, J. Non-Cryst. Solids, 1968, 1, 1–17 CrossRef CAS.
- I. G. Austin and N. F. Mott, Adv. Phys., 1969, 18(71), 41–102 CrossRef CAS.
- M. Sayer and A. Mansingh, Phys. Rev. B: Solid State, 1972, 6(12), 4629–4643 CrossRef CAS.
- L. Murawski, C. H. Chung and J. D. Mackenzie, J. Non-Cryst. Solids, 1979, 32, 91–104 CrossRef CAS.
- N. Chopra, V. Gupta, A. Mansingh and G. K. Chadha, Philos. Mag. B, 1997, 75, 249–259 CrossRef CAS.
- C. H. Chung and J. D. Mackenzie, J. Non-Cryst. Solids, 1980, 42, 357–370 CrossRef CAS.
- A. Šantić and A. Moguš-Milanković, Croat. Chem. Acta, 2012, 85(3), 245–254 CrossRef.
- A. Šantić, R. D. Banhatti, L. Pavić, H. Ertap, M. Yüksek, M. Karabulut and A. Moguš-Milanković, Phys. Chem. Chem. Phys., 2017, 19, 3999–4009 RSC.
- X. Fang, C. S. Ray, A. Moguš-Milanković and D. E. Day, J. Non-Cryst. Solids, 2001, 283, 162–172 CrossRef CAS.
- C. Mercier, G. Palavit, L. Montagne and C. Follet-Houttemane, C. R. Chimie, 2002, 5, 693–703 CrossRef CAS.
- G. Poirier, F. S. Ottoboni, F. C. Cassanjes, A. Remonte, Y. Messaddeq and S. J. L. Ribeiro, J. Phys. Chem. B, 2008, 112, 4481–4487 CrossRef CAS PubMed.
- M. Ataalla, A. S. Afify, M. Hassan, M. Abdallah, M. Milanova, H. Y. Aboul-Enein and A. Mohamed, J. Non-Cryst. Solids, 2018, 491, 43–54 CrossRef CAS.
- A. Mansingh, J. K. Vaid and R. P. Tandon, J. Phys. C: Solids State Phys., 1976, 9, 1809–1817 CrossRef CAS.
- A. Mansingh, J. K. Vaid and R. P. Tandon, J. Phys. C: Solids State Phys., 1977, 10, 4061–4066 CrossRef CAS.
- A. Mansingh, A. Dhawan, R. P. Tandon and J. K. Vaid, J. Non-Cryst. Solids, 1978, 27, 309–318 CrossRef CAS.
- A. Mansingh, R. P. Tandon and J. K. Vaid, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21(10), 4829–4839 CrossRef CAS.
- M. H. Hekmat-Shoar, C. A. Hogarth and G. R. Moridi, J. Mater. Sci., 1985, 20, 889–894 CrossRef CAS.
- A. M. Al-Shukri, G. D. Khattak and M. A. Salim, J. Mater. Sci., 2000, 35, 123–126 CrossRef CAS.
- S. V. Pershina, S. N. Shkerin and A. S. Tolkacheva, Int. J. Energy Res., 2019, 1–7 Search PubMed.
- S. V. Pershina, Russ. J. Appl. Chem., 2019, 92(4), 482–489 CrossRef CAS.
- J. Nikolić, L. Pavić, A. Šantić, P. Mošner, L. Koudelka, D. Pajić and A. Moguš-Milanković, J. Am. Ceram. Soc., 2018, 101, 1221–1235 CrossRef.
- L. Pavić, A. Šantić, J. Nikolić, P. Mošner, L. Koudelka, D. Pajić and A. Moguš-Milanković, Electrochim. Acta, 2018, 276, 434–445 CrossRef.
- K. Funke and R. D. Banhatti, Solid State Ionics, 2004, 169, 1–8 CrossRef CAS.
- K. Funke and R. D. Banhatti, Solid State Ionics, 2006, 177, 1551–1557 CrossRef CAS.
- R. D. Banhatti, C. Cramer, D. Zielniok, A. H. Jean Robertson and M. D. Ingram, Z. Phys. Chemie, 2009, 223, 1201–1215 CrossRef CAS.
- L. Koudelka, J. Šubčík, P. Mošner, L. Montagne and L. Delevoye, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol. B, 2012, 53(3), 79–85 CAS.
- J. Šubčík, L. Koudelka, P. Mošner, L. Montagne, G. Tricot, L. Delevoye and I. Gregora, J. Non-Cryst. Solids, 2010, 256, 2509–2516 CrossRef.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, Florida, 2009, pp. 9–68 Search PubMed.
- C. Y. Kim and R. A. Condrate, J. Phys. Chem. Solids, 1984, 45, 1213–1218 CrossRef CAS.
- S. H. Santagneli, C. C. de Araujo, W. Strojek, H. Eckert, G. Poirier, S. J. L. Ribeiro and Y. Messaddeq, J. Phys. Chem. B, 2007, 111, 10109–10117 CrossRef CAS PubMed.
- M. Lahaye, B. Doumert, B. Revel, K. Ben Tayeb, H. Vezin and G. Tricot, J. Phys. Chem. C, 2015, 119, 17288–17297 CrossRef CAS.
- V. N. Bogomolov and D. N. Mirlin, Phys. Stat. Solidi B, 1968, 27, 443–453 CrossRef CAS.
- P. Watthaisong, S. Jungthawan, P. Hirunsit and S. Suthirakun, RSC Adv., 2019, 9, 19483–19494 RSC.
- M. Razum, L. Pavić, D. Pajić, J. Pisk, T. Čižmar and A. Šantić, Novel insights into the mechanism of polaronic conduction in binary V2O5-P2O5 glasses, in preparation.
- K. Sklepić, R. D. Banhatti, G. Tricot, P. Mošner, L. Koudelka and A. Moguš-Milanković, J. Phys. Chem. C, 2017, 121, 17641–17657 CrossRef.
- R. D. Banhatti and K. Funke, Solid State Ionics, 2004, 175, 661–663 CrossRef CAS.
- C. Cramer, S. Brückner, Y. Gao and K. Funke, Phys. Chem. Chem. Phys., 2002, 4, 3214–3218 RSC.
- K. Funke, R. D. Banhatti, S. Brückner, C. Cramer, C. Krieger, A. Mandanici, C. Martiny and I. Ross, Phys. Chem. Chem. Phys., 2002, 4, 3155–3167 RSC.
- L. Pavić, S. Fazinić, H. Ertap, M. Karabulut, A. Moguš-Milanković and A. Šantić, Materials, 2020, 13(2505), 1–15 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc00954h |
| This journal is © The Royal Society of Chemistry 2023 |