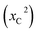Open Access Article
Open Access ArticleExtensive rainfall data analysis: event separation from continuous record, fitting of theoretical distributions, and event-based trend detection†
Aniekan E.
Essien
 *,
Yiping
Guo
*,
Yiping
Guo
 and
Sarah E.
Dickson-Anderson
and
Sarah E.
Dickson-Anderson

Department of Civil Engineering, Mcmaster University, Hamilton, Ontario L8S 4L7, Canada. E-mail: essiena@mcmaster.ca
First published on 4th April 2023
Abstract
The impact of climate change on the environment, particularly water resources, can never be over-emphasized. Therefore, it is imperative to continuously study and understand climate data, especially on a regional scale. This paper used the sites in the four nations' capitals in the United Kingdom as the study areas with extensive rainfall data collected from a total of six weather stations. The article is the first study conducted on extensive hourly rainfall data observed at selected weather stations in the four nations of the UK for exponentiality testing of their rainfall characteristics before carrying out a comprehensive comparative analysis of their distribution parameters and conducting event-based trend analysis to investigate the potential impact of climate change on the regional rainfall characteristics. Several earlier studies have considered separating continuous rainfall data into individual rainfall events as the most challenging and time-consuming aspect of rainfall data analysis. Therefore, first, this paper provided a step-by-step guide on rainfall event separation, especially for data with missing values, before conducting frequency analysis to test the exponentiality of rainfall event characteristics using large samples. The results from the study indicated that the rainfall event characteristics observed at the weather stations in the four nations of the UK were both exponentially and gammally distributed. The comparative analysis of the distribution parameters demonstrated that the observed rainfall data have heterogeneous spatial distributions. The event-based trend analysis showed an upward trend in the number of extreme rainfall events and the number of rainfall events per year in the observed data. However, there was no correlation between temperature and the rainfall characteristics, although, in a global context, a correlation is suggested.
Environmental significanceRainfall is the principal element controlling the regional hydrologic cycle and water resource availability. Therefore, effective water resources systems planning and management require a good understanding of rainfall event characteristics and distributions. Frequency analysis is essential to finding suitable models that could predict several natural processes. This study demonstrated that the observed rainfall event characteristics in the UK fit well to an exponential distribution model. In addition, for the first time using an event-based approach on rainfall data observed at selected weather stations in the four nations of the UK, the paper assessed the potential factors that influenced the distributions of rainfall event characteristics. The findings obtained from this study would be useful for environmental engineers, agriculturists, climatologists, and environmental policymakers and regulators. |
1 Introduction
The amount of weather events and their distributions worldwide or at a regional scale is an essential aspect affecting several environmental, social, and economic systems. For example, extreme rainfall events, interevent times (dry periods), and extreme temperatures can lead to flooding or drought, causing disturbances to the earlier mentioned systems. To contextualize this, in the UK, the Meteorological Office, otherwise known as the Met Office, through several studies, projected prolonged precipitation events during winter and more extended dry periods during summer.1 In 2022, the Met Office declared the temperature of 40.3 °C at Coningsby, Lincolnshire, to be the highest temperature ever recorded in the UK,2 and July 2022 was verified as the driest month since 1935.3 This resulted in drought being declared in some parts of the UK in August 2022.4 Another study by Essien et al., using data from the UK, summarised that traffic flow characteristics (i.e., speed, volume, and density) correlate with rainfall event volume variations.5 Therefore, one could say that it is critical to continuously study and understand the UK climate data (rainfall event characteristics and temperature) and their distributions as well as the potential impacts of climate change on their distributions.The limitation in understanding rainfall characteristics and distributions may minimize water engineers' effective design of stormwater management facilities. Another aspect the limitation can impact is the provision of additional knowledge to water policymakers in ensuring that effective policies are put forward for optimal regulatory practises and institutional framework regarding agricultural activities, roads and drainage construction, water allocation and networking in urban and rural areas. Hence, many researchers have continually used statistical analysis to express the frequency of rainfall event characteristics and their probability of occurrences by fitting probability distributions to a set of historical precipitation data.
Rainfall and temperature data are important elements in understanding water balance on a global scale, as well as studying and understanding the complexity of human-water systems (social hydrology).6 However, rainfall patterns may vary from region to region, and in some cases, they may differ from one weather station to another in the same region. On the other hand, as supported by many studies, homogeneity in terms of theoretical distribution can be found. For example, studies by Hassini and Guo, Adams and Papa, and Shamsudin et al. fitted rainfall event characteristics to exponential distributions with observed data from the US, Canada, and Malaysia, respectively.7–9 Moreover, based on the reports from several studies, one could conclude that exponential distribution is one of the most widely used theoretical distributions for rainfall data.10–13
Consequently, collecting, analyzing, interpreting, and understanding rainfall data is an essential component of interest for scientists, engineers, regulators, and agriculturists. However, within all these rationales associated with the importance of rainfall data to the aforementioned professionals, transforming and interpreting extensive rainfall event characteristics in terms of future probabilities of occurrence may be considered one of the challenging tasks.14 Although several papers have discussed procedures for separating continuous rainfall data into individual events,7,15 to the authors' knowledge, no published study has provided a comprehensive step-by-step guide for separating individual events from extensive continuous historical rainfall data, especially for rainfall data with gaps or missing values, like those received by the authors from the Met Office. Moreover, in the case of the study areas, testing the exponentiality and comparing the distribution parameters of large samples of rainfall event characteristics extracted from 55 year-hourly rainfall data as well as conducting an event-based trend analysis to investigate the potential impacts of climate change on the rainfall events are unprecedented and topical. Therefore, this paper aims to: (1) provide a comprehensive step-by-step guide for the separation of extensive continuous rainfall data into individual rainfall events and conduct frequency analyses of the characteristics of separated rainfall events, (2) demonstrate the goodness-of-fit of theoretical distributions to the rainfall event characteristics of the different regions of UK and conducting a comparative analysis, and (3) conduct event-based trend analysis on rainfall event characteristics and temperatures to assess the potential impacts of climate change on them.
2 Methodology
2.1 Area of study and sources of climate data
The United Kingdom is the area of study for this paper. This region was selected because, unlike other regions, such as the US and Canada, where extensive studies have been conducted and the goodness-of-fit of exponential distributions to large samples' of rainfall event characteristics were verified already, no study has yet been conducted using extensive rainfall data observed at the selected weather stations in the four nations of the UK (one extensive rainfall series per location in each nation). Moreover, a better understanding of rainfall event characteristics of the UK is useful for climate change adaptation and stormwater management. Another reason for choosing the UK as the area of study is because the UK is considered by many historians as the place of origin of the industrial revolution; hence, it is imperative to assess the impact of climate change on the human-water systems for this region.16 The UK comprises four nations, England, Scotland, Wales, and Northern Ireland (Fig. 1). The basic characteristics of the four nations used in this study, including area and population, are presented in Table 1.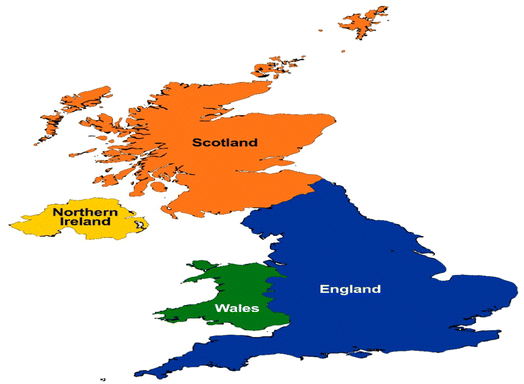 | ||
| Fig. 1 Map showing the location of the study areas.17 | ||
| Country name | Area (km2) | Population | Density (persons per km2) |
|---|---|---|---|
| England | 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
56,286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
432 |
| Scotland | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 903 903 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463 463![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
70 |
| Wales | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 736 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 879 879 |
152 |
| Northern Ireland | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793 793 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893 893![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667 667 |
136 |
Extensive hourly rainfall and monthly average temperature data were obtained for a total of six stations located in the capital cities of England, Scotland, Wales, and Northern Ireland. These capital cities are London, Edinburgh, Cardiff, and Belfast. These stations were chosen because they provided the longest and most consistent data. The data were requested and received via email directly from the UK Met Office. For the purpose of this study and clarity of presentation, the names of the nations where the data was recorded were used only as the possessive adjective of the selected weather stations. Table 2 shows the geographical information of the selected stations. The number of years of the climate data extracted for each station is 55. The average percentage coverage of the hourly rainfall data recorded at these stations was 99%, i.e., only 1% data is missing. The winter months were removed from the data. This is because urban stormwater management is the main intended application of the results of this analysis, and urban stormwater management facilities are all designed based on rainfall statistics of non-winter months. However, if snowfall or the temperature of the whole year is also of interest, the winter months may also be included.
| Weather station name | Station location identifier (NGR) | Latitude | Longitude | Altitude (m) | City | Country |
|---|---|---|---|---|---|---|
| Heathrow | 5077E 1767N | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48N 48N |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45W 45W |
35 | London | England |
| Turnhouse | 3159E 6739N | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95N 95N |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35W 35W |
35 | Edinburgh | Scotland |
| Gogarbank | 3161E 6714N | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 93N 93N |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34W 34W |
57 | ||
| Rhoose | 3066E 1677N | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40N 40N |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34W 34W |
65 | Cardiff | Wales |
| St Athan | 2999E 1684N | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40N 40N |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44W 44W |
49 | ||
| Aldergrove | 3146E 3810N | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66N 66N |
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22W 22W |
63 | Belfast | Northern Ireland |
2.2 Separation of continuous rainfall data into individual events
The following steps were followed to separate the continuous hourly rainfall series into individual rainfall events:Step 1: calculate the percentage of total missing data in the data set. If the percentage of the total missing data is >1%, the data set may be considered unsuitable for use in this study. This resulted in the final choice of the six stations listed in Table 2. In addition, one could also check if the missing data are concentrated in one specific year.
Step 2: assess and delete years with too many missing data or too large data gaps. It was found that not many weather stations have data covering over 50 years without any data gaps. In some countries, meteorological stations with over 50 years of complete hourly data do not exist. In the UK, even the best stations have some data gaps (B. Duncan, Met Office, personal communication, April 1st, 2022). Therefore, it is necessary to delete those years where too many data are missing. For this study, this was achieved by selecting the most consistent 55 year data from the entire data set with 99% average coverage.
Step 3: change all the rainfall depths recorded as “trace” to 0.0 mm. This is because according to the Met Office of UK, “trace” was recorded if either of the following applies (B. Duncan, Met Office, personal communication, July 7th, 2021):
(a) “The measured fall is less than 0.05 mm, and the observer knows that the water in the gauge is not the result of water draining from the sides of the can after the previous measurement.”
(b) “The gauge contains no water, but the observer knows that some rain or other precipitation has fallen since the previous observation.”
Step 4: delete the rainfall data for the winter months.
Step 5: separate the continuous rainfall series into individual rainfall events according to the following procedure:
(a) Determine a suitable interevent time definition (IETD).
(b) Delete the first rainfall event or interevent time at the beginning and end of every year. This is necessary because the winter month was deleted for every year.
(c) If a year's record starts with an interevent time (dry period) less than the selected IETD and then it is followed by a rainfall event, the interevent time must be deleted and not counted as a complete dry period. This first rainfall event following the first interevent time must also be deleted and not counted as a complete rainfall event. This is because it is unsure if there were rainfalls immediately before that first dry period, so the exact length of this first dry period is unknown, and the first rainfall event may also contain rainfalls falling before the start of the record.
(d) Delete rainfall events and their corresponding durations as well as interevent time starting with n/a. “n/a” stands for missing data or data gap. This could have resulted from several factors, such as equipment failure, staff absence, operational failures, or other technical difficulties (B. Duncan, Met Office, personal communication, July 15th, 2021).
(e) Delete rainfall events and the corresponding durations as well as interevent times ending with n/a.
(f) Delete rainfall events and the corresponding durations as well as interevent dry periods having n/a in the middle of them.
Points (d) through (f) needs to be followed because having n/a before, in between, or at the end of a rainfall event or interevent dry period is an indication that the actual volume of the rainfall event and its corresponding duration or the exact interevent time are unknown.
Step 6: after separating continuous rainfall series into individual rainfall events, if applicable, which may be subject to the purpose of study, remove rainfall events with volumes less than a pre-selected minimum rainfall volume threshold. This is necessary because small rainfall events may not generate any runoff, and some of them may have resulted from measurement errors.20
To apply the volume threshold, the following rules were executed:
(a) Delete all the rainfall events less than the selected rainfall event volume threshold and add their corresponding durations to the preceding interevent time. This preceding interevent time is combined with the succeeding interevent time to form a new interevent time.
(b) If there are more than one consecutive rainfall events that are less than the rainfall event volume threshold, add all corresponding rainfall event durations to the total interevent time and form a new interevent time.
(c) It should be noted that the total number of rainfall events and their corresponding durations may not equal the total number of interevent times. When applying the volume threshold, the total number of rainfall events and their corresponding durations may be less than the total number of interevent times.
Step 7: based on samples obtained from the above-described rainfall event separation procedures, carry out frequency analysis for the three rainfall event characteristics, i.e., rainfall event volume (v), rainfall event duration (t), and interevent time (b).
2.3 Frequency analysis and goodness-of-fit testing
Frequency analysis is required to understand better how frequently different magnitudes of rainfall events occur and how frequently different lengths of interevent times occur. Usually, hydrologic data of at least 30 years are considered long enough for these purposes.21 To conduct a frequency analysis for the separated rainfall event characteristics, the number of classes must first be chosen. Eqn (1) below may be used to determine the suitable number of classes (NC).22| NC = [1 + (3.3 × log10(n))] × 2 | (1) |
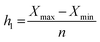 | (2) |
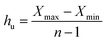 | (3) |
The selected class width must be greater than hl and less than hu. The selected class width should also be of equal width whenever it is possible. Some other points considered in this paper for the determination of the number of classes and class widths included: (1) the width within each class should be mutually exclusive,26 and (2) avoid using open-ended classes at the lower and upper bound.26
Goodness-of-fit (GOF) test is conducted to examine how close the observed data follow a specific type of theoretical distribution. The chi-square test was used in this study because it considers the relative performance of all the different parts of a distribution.27 The value of the chi-squared test statistic (χ2) is determined using eqn (4).7
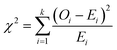 | (4) |
| Ei = n[F(xi+1) − F(xi)] | (5) |
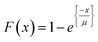 | (6) |
The parameter μ and values of x are positive real quantities, where μ is the sample mean used to calculate the distribution parameter.
Earlier studies (e.g., Adams et al., Balistrocchi et al., Guo and Adams, etc.) have found that rainfall event volume v, duration t, and interevent time b may follow the following exponential distributions for many different locations:8,29,30
| fV(v) = ζe−ζv, v ≥ 0 | (7) |
| fT(t) = λe−λt, t ≥ 0 | (8) |
| fB(b) = ψe−ψb, b ≥ 0 | (9) |
Goodness-of-fit (GOF) test will be conducted using these exponential distributions as the theoretical distributions. In addition, for comparison purposes, the gamma distribution will also be used as the theoretical distributions for v, t, and b. The probability density function f(x) of a gamma distribution is depicted in eqn (10):31
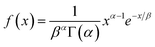 | (10) |
2.4 Trend analysis
The frightening nature of the potential impacts of climate change on rainfall distribution is one of the rationales behind the trend analysis conducted in this study. This is because minor variations in climate could result in extreme rainfall event volumes and/or interevent times. The trend analysis considered are summarised below, and all the rainfall event volumes, without vt, were considered for the trend analysis. Simple linear regression (SLR), as depicted in eqn (11),32 was used for the trend analyses.| Y = a + mx | (11) |
The trend analyses conducted in this study include:
(a) Trend analysis on the annual total number of rainfall events.
(b) Trend analysis of the total number of rainfall events at or greater than a given threshold.
(c) Trend analysis of the annual total rainfall volumes and annual average rainfall event volumes.
2.5 Maximum annual average intensity
Maximum annual average rainfall intensities observed at the selected weather stations in the four nations were calculated and compared to obtain an initial general sense of the intensity of rainfalls in the four nations. To determine the maximum annual average intensity for the four nations, first, the annual average intensity was calculated as shown in eqn (12).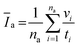 | (12) |
2.6 Correlation analysis
In this analysis, the emphasis was to investigate the impacts of regional temperature variations on rainfall event characteristics (v and b) in the UK. This was conducted by plotting the average temperatures and the number of rainfall events with characteristics greater than a specific threshold against their corresponding demi-decade-represented years. The demi-decade presented in this study is considered a period of consecutive 5 years between the selected continuous data.3 Results and discussion
3.1 Data transformation
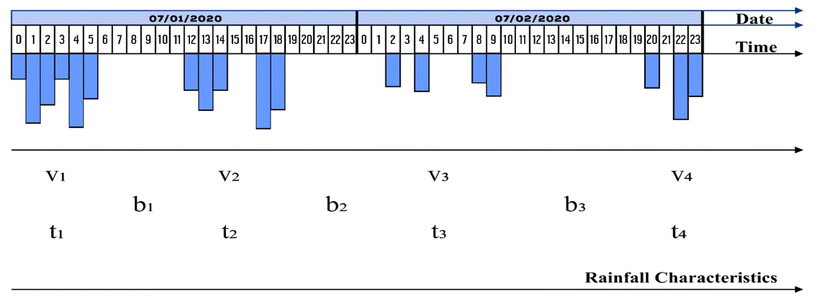
Hourly rainfall data received from the UK Met Office cover 1949–2019 for the station in England and 1960–2019 for Scotland, Wales, and Northern Ireland. For Scotland and Wales, data from two weather stations in the same area were combined into one extensive hourly rainfall data series (Table 2). The authors found that this is acceptable, as the study by Gregory et al. reported strong correlations in rainfall patterns for locations in the same region.36 The selected weather stations for the four UK nations had consistent 55 year data after deleting years with too many missing data. Hourly rainfall values stated as “trace” were changed to 0.0, as stated in step 3 in Section 2.2. The winter months were removed from the record, which the Met Office defines as December 1 to February 28 (or 29 in a leap year).37 Interevent time definition (IETD) is the minimum number of dry hours between two consecutive rainfall events. To qualify as an individual rainfall event, there must be fewer than IETD consecutive dry hours during the rainfall hours, as shown in Fig. 2. It is recommended to use 6–12 hours as the IETD for urban stormwater management to ensure that runoff generated from consecutive rainfall events will have enough time to separate from each other.7 However, IETDs may be increased up to 30 hours for large catchments. The study conducted by Hydroscience, Inc. in 1979 indicated that IETD for rainfall data could be between 3 and 30 hours.38 For small urban catchments, the selected IETD was 6 hours (Fig. 2).After selecting an IETD of 6 hours, the data from the selected weather stations for the four nations were separated into individual events. The first event (either the rainfall event and its corresponding duration or interevent time) at the beginning of March was deleted every year. The same was performed for the last event or interevent time at the end of November. More detailed rules as described in points (c) to (f) of step 5 in Section 2.2 were followed in identifying rainfall events and interevent times. The volume threshold (vt) for this study was set at 1 mm. Therefore, any rainfall events less than 1 mm were removed. This is supported by studies conducted by Benestad and Benestad et al. as they observed that rainfall data appeared to be better exponentially distributed when its event volume threshold is set at 1 mm.39–41 Introducing the volume threshold on the initially separated events will result in adding their corresponding durations to the preceding interevent times; for easier comprehension, this procedure is demonstrated in Fig. 3.
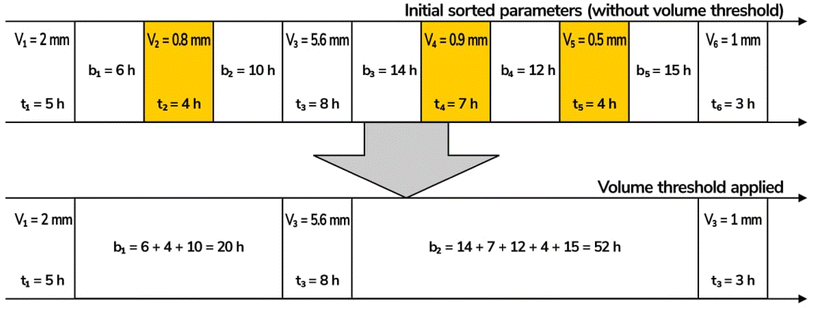 | ||
| Fig. 3 Demonstration of how rainfall events with v < 1 mm are removed and how the affected interevent times are modified. | ||
3.2 Frequency analysis and goodness-of-fit tests
The frequency analysis and chi-square GOF conducted for the exponential distributions (fitted using the method of moment) followed strictly the methodology described in Section 2. The study's hypothesis was tested using a level of significance of 5%. Therefore, a p-value ≥ 5% will result in a failure to reject the null hypothesis. The exact p-values were computed using the statistical software R.The p-values of the GOF tests with the null hypothesis of the theoretical distributions for the observed data recorded at the selected weather stations in the UK all approached 1, and their calculated chi-square values 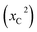 and chi-square critical values (Cv) are shown in Table 3. Fig. S1.1a–c, S1.2a–c, S1.3a–c, and S1.4a–c (ESI†) show the graphical comparisons of the observed frequency distributions and fitted exponential distributions for the rainfall data observed in the weather station in England, Scotland, Wales, and Northern Ireland, respectively, after applying the volume threshold (vt) of 1 mm. Both the infographic comparison and the aforementioned results of the chi-square GOF tests suggest that exponential distributions fit well the rainfall data observed at the selected weather stations in the four nations of the UK.
and chi-square critical values (Cv) are shown in Table 3. Fig. S1.1a–c, S1.2a–c, S1.3a–c, and S1.4a–c (ESI†) show the graphical comparisons of the observed frequency distributions and fitted exponential distributions for the rainfall data observed in the weather station in England, Scotland, Wales, and Northern Ireland, respectively, after applying the volume threshold (vt) of 1 mm. Both the infographic comparison and the aforementioned results of the chi-square GOF tests suggest that exponential distributions fit well the rainfall data observed at the selected weather stations in the four nations of the UK.
| Country name | Weather station name | Distribution parameters (with vt) | (exponential) | (gamma) | C v (exponential and gamma) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ζ (mm−1) | λ (hr−1) | Ψ (hr−1) | θ | Ṽ aat (mm) | v | t | b | v | t | b | v | t | b | ||
| England | Heathrow | 0.158 | 0.110 | 0.012 | 71 | 450 | 0.06 | 0.05 | 0.57 | 0.03 | 0.01 | 0.02 | 37.65 | 37.65 | 37.65 |
| Scotland | Turnhouse and Gogarbank | 0.165 | 0.095 | 0.015 | 82 | 500 | 0.48 | 0.12 | 0.15 | 0.04 | 0.05 | 0.03 | 38.89 | 38.89 | 38.89 |
| Wales | Rhoose and St Athan | 0.134 | 0.094 | 0.017 | 90 | 666 | 0.05 | 0.08 | 1.80 | 0.01 | 0.02 | 0.03 | 38.89 | 38.89 | 38.89 |
| Northern Ireland | Aldergrove | 0.171 | 0.095 | 0.019 | 103 | 603 | 0.22 | 0.14 | 0.71 | 0.06 | 0.04 | 0.03 | 38.89 | 38.89 | 38.89 |
3.3 Comparative analysis of rainfall event characteristics
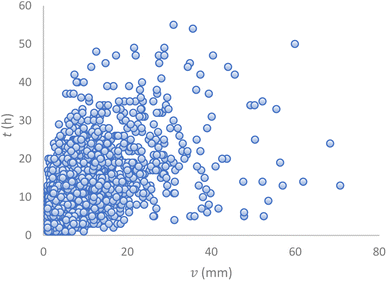
To verify the previously mentioned statement that exponential distribution is one of the most widely used theoretical distributions for rainfall data and was found to fit well observed frequency distributions, the authors compared the goodness of fit of the rainfall event characteristics of the UK to the gamma distribution. Gamma distribution was chosen, as the study by Gregory et al. indicated that the UK daily precipitations in most regions tend to be gamma distributed.36 Moreover, Stagge et al. recommended gamma distribution as a default distribution for European rainfall data.42 Looking at Fig. S1.1a–c, S1.2a–c, S1.3a–c, and S1.4a–c (ESI†), which show the visual comparison of the observed frequency, exponential modeling, and gamma modeling of the rainfall event characteristics (v, t, and b) with vt ≥ 1 mm for the station in England, Scotland, Wales, and Northern Ireland, respectively, and the lower values of the chi-square test statistic from gamma modelling, demonstrated that the UK rainfall event characteristics were better gammally distributed than exponentially. Therefore, this supports the study by Gregory et al. and Stagge et al.36,42 However, exponential distribution is still preferred because compared to all other theoretical distributions for variables with finite mean and positive values, exponential distribution has the largest entropy.43 Using a distribution with the largest entropy ensures that all possible and extreme cases will be included. Moreover, the exponential distribution model is highly mathematically tractable, resulting in many closed-form analytical equations which can be used to directly quantify many physical quantities of interest.44 One interesting trend noticed for the rainfall event characteristics with respect to the observed frequency recorded at the selected weather stations in the four nations of the UK is the overestimation of most frequencies for v and t and the underestimation of most frequencies for b by exponential model. On the other hand, most frequencies for v, t, and b were overestimated by the gamma model except for the t frequencies for the station in England, which were underestimated.Meteorological processes involved in the generation of rainfalls make it obvious that v and b as well as t and b are statistically independent.12 However, this may not be so between t and v. Therefore, a correlation analysis was conducted to quantify the dependence between t and v for the observed data recorded at the selected weather stations in the four nations. The correlation coefficients between t and v for the station in England, Scotland, Wales, and Northern Ireland were found to be 0.57, 0.66, 0.66, and 0.61, respectively. In addition, the linear correlations between t and v in the observed data were found to be statistically significant (the null hypothesis that there is no meaningful relationship between t and v was rejected because the p-values were all lower than 0.05). However, the scatter plots conducted for the observed data recorded at the selected weather stations in four nations showed that t and v are weakly correlated and treating them as linearly correlated random variables may result in inaccuracies too. An example of the scatter plots between t and v is shown in Fig. 4. Consequently, for practical purposes, t and v may be treated as statistically independent. This assumption is supported by a study conducted by Guo and Guo, where the authors stated that treating t and v as statistically independent may not result in significant losses of accuracy.45
After it was found that the observed rainfall event characteristics (v, t, and b) fit well to exponential distributions, a comparison of the values of the distribution parameters was conducted. The values of the distribution parameters for rainfall characteristics are shown in Table 3. The exponential distribution parameters ζ, λ, and ψ were calculated as the inverse of the average values of the rainfall event characteristics. Table 3 also reports the values for θ and Ṽaat, where θ is the annual average number of rainfall events and Ṽaat is the average annual total rainfall volume.
The average annual total rainfall volumes for the station in Wales, Northern Ireland, Scotland, and England are 666 mm, 603 mm, 500 mm, and 450 mm, respectively. The results shown in Table 3 also align well with the results obtained by Gregory et al. using daily and monthly data spanning the period from 1931 to 1989 for the four nations of the UK to investigate the spatial heterogeneity of rainfall characteristics. The authors concluded that rainfall events are inhomogeneous between the station in England, Scotland, Wales, and Northern Ireland.46
3.4 Trend analysis
The event-based trend analysis conducted in this section is based on the knowledge that several factors could be used to assess and evaluate the impact of global warming on the environment, especially water resources. However, due to rainfall distribution being an important aspect of the climate, trend analysis of the extensive historical climate data was considered to assess the local climatology for the locations where the observed rainfall data were collected in the four nations of the UK. Similar event-based analysis were conducted by Jun et al. and Dallet et al. for data observed in Seoul, Korea and Eastern Italian Alps, respectively. However, both studies focussed only on the trends of extreme rainfall events.47,48As rainfall intensity is one of the essential elements affected by climate change, the maximum annual average rainfall intensity was calculated for the observed data recorded at the weather stations in the four nations (eqn (12)). The maximum annual average rainfall intensities for the period of 55 years were summarised as follows: 0.79 > 0.65 > 0.63 > 0.52 (mm h−1) for the station in England, Northern Ireland, Scotland, and Wales, respectively. Following the trend, it was noticed that the station in England, seconded by the station in Northern Ireland and followed by the station in Scotland, has the highest annual maximum average rainfall. The high maximum annual average rainfall intensities recorded in Northern Ireland's station and Scotland's station could simply be a result of the warmed moist westerly winds from the Atlantic weather systems that the western part of the UK is likely prone to in the form of frontal rainfall.49 However, England's station topping the four locations may have resulted from the impact of local climatology due to increasing urbanization and industrial activities.
Fig. 5 shows the year-by-year changes in the annual total number of rainfall events over the 55 year period for the observed data recorded at the selected weather stations in the four nations. Visually, Fig. 5 demonstrates a positive increasing trend for the observed data recorded at the selected stations in the four nations. To further understand how the increasing number of rainfall events for the 55 year period were distributed, the rainfall rates were classified into different categories shown in Table 4. For this study, rainfall events greater than 4 mm h−1 were classed as extreme rainfall events, which is supported by the study conducted by Deumlich and Gericke on the trend analysis of heavy rainfall days in Germany.50
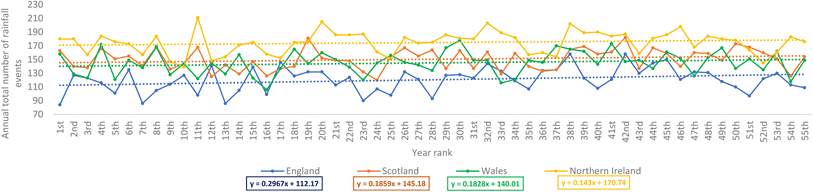 | ||
| Fig. 5 Annual total number of rainfall events for the observed data recorded at the selected weather stations in the four nations for the 55 year period. Note: as a result of the missing years in the rainfall data recorded in the selected weather stations in the four nations of the UK, the ranking was used instead of the year so as to be able to plot the event-based rainfall events on the same axis for the UK's four nations' stations. The 55 year historical rainfall data recorded at the selected weather stations in the four nations were ranked in ascending order. This is shown in S2 (ESI†). | ||
| Category | Rate of rainfall |
|---|---|
| Moderate rain | >0.5 mm h−1, but <4.0 mm h−1 |
| Heavy rain | >4 mm h−1, but <8 mm h−1 |
| Very heavy rain | >8 mm h−1 |
Fig. 6 shows how the annual total number of rainfall events greater than 1 mm changes in the 55 year period. This analysis was considered as the vt used on the observed data fitted to the theoretical distributions was 1 mm (Section 3.1). Moreover, rainfall events >1 mm may promote a better washout effect on atmospheric particulate pollution, such as nanoplastics and microplastics.53 This annual total counted and summed all the rainfall events greater than 1 mm in each continuous year. The results indicated an increasing trend for the observed data recorded at the selected stations in the four nations. The increasing trend in the number of rainfall events greater than 1 mm for Scotland's station and Wales' station as shown in Fig. 6, was also supported by Fig. 7, which shows the annual average rainfall event volume changed over the 55 year period. However, it is observed that the annual average rainfall event volumes for the station in England and Northern Ireland have a decreasing trend. Nevertheless, this relatively aligned with the results in Fig. 6 as their degrees of steepness in the increasing trend of rainfall events >1 mm were the lowest compared to the other two nations' stations.
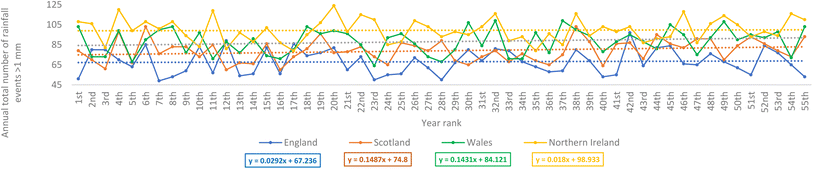 | ||
| Fig. 6 Annual total number of rainfall events greater than 1 mm for the observed data recorded at the selected weather stations in the four nations for the 55 year period. | ||
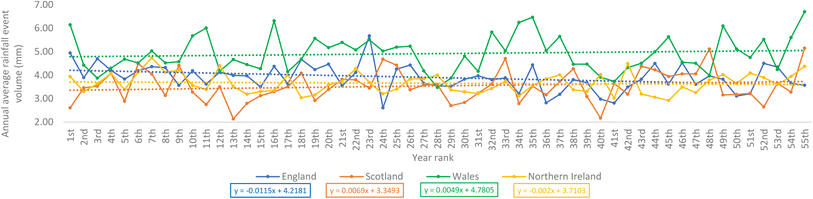 | ||
| Fig. 7 Annual average rainfall event volume changed over the 55 year period for the observed data recorded at the selected stations in the four nations. | ||
In addition, it was interesting to notice that even if the trend indicated that the number of rainfall events that result in rainfall volume >1 mm was increasing across the nations (Fig. 6), Fig. 8 clearly demonstrates that England's station has recorded a negative trend in the number of moderate rainfall events over the 55 year period. Moderate rainfall events contribute the vast majority of the annual total rainfall volumes. This finding, with additional information or results from more weather stations, may have significant implications as it may be related to or be used to explain the causes of the drought currently experienced in some parts of the UK, of which England constitutes a large part. The fitted linear decreasing line for the station in England in Fig. 8 seems to suggest that the current drought in a city like London may be an inevitable result of a long-term decreasing trend. Wales' station, although it recorded a positive trend, had a lower steepness when compared to its rate of change in the number of rainfall events that resulted in volumes greater than 1 mm (Fig. 6). Fig. 9 shows the annual total rainfall volume for the observed data recorded at the selected weather stations in the four nations over the 55 year period. England's station's negative trend shown in this figure strongly aligns with the drought currently experienced in the London areas. However, positive trends were recorded for the other three nations' stations.
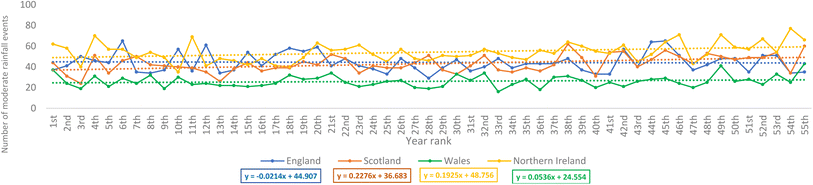 | ||
| Fig. 8 Annual total number of moderate rainfall events for the 55 year period rainfall data recorded at the selected stations in the four nations. | ||
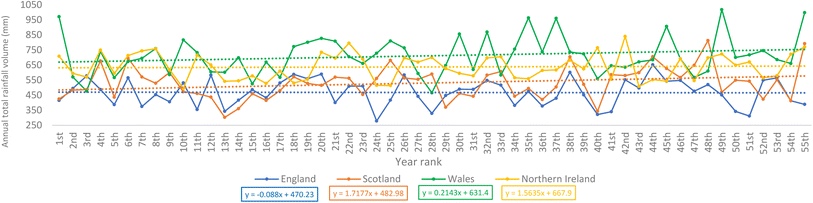 | ||
| Fig. 9 Annual total rainfall volumes recorded at the selected station in the four nations for the 55 year period. | ||
In addition, the event-based results shown in Fig. 5–8, with additional information and rainfall data from more stations, may be used to answer some of the typical questions often asked about UK's rainfall conditions (otherwise called “The Great British rain paradox”).54 For example, if it seems like it rains so often in the UK, why are some parts of the UK currently experiencing drought? Using the data observed in the stations to suggest the answer to this question, based on Fig. 5, the increase in the annual number of rainfall events does mean that these rainfall events provide the required volume of water enough for groundwater recharge. This is because, as reported by Jin et al. in their study on the Chinese Loess Plateau, it took an accumulated rainfall volume of 9 mm to trigger a response in the soil moisture at a depth of 10 cm in grassland sites.55 However, in Fig. 10, it was interesting to notice that there were more extreme rainfall events observed in Wales' station within the first 10 year period and between the 30th and 40th year period. Extreme rainfall events are key pollutant carriers, such as microplastics (MPs). For example, a study by Forrest et al. noticed that the concentration of MPs doubled in an urban river during extreme rainfall events.56 Therefore, the upward trends in the number of extreme rainfall events observed in the stations in the four nations of the UK, as shown in Fig. 10, would be valuable data to consider for these locations if one is researching emerging pollutants such as MPs.
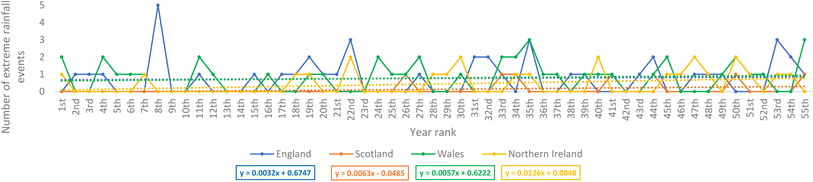 | ||
| Fig. 10 Annual total number of extreme rainfall events for the 55 year rainfall data recorded at selected weather stations in the four nations. | ||
The surface energy budget and planetary boundary layer affect the formation of rainfalls,57 and the earth's surface temperature is highly influenced by the surface energy balance.58Fig. 11 shows a photo shared by the American Space Agency (NASA) posted by Dan Holley, a BBC weather presenter and meteorologist, online to demonstrate the impact of the increasing temperature on the rate of dryness of the UK land surfaces over the period of 12 months.59 Although many considered the photos to be shocking, most importantly, this shows the potential negative impacts of the increasing surface temperature and extensive interevent times as demonstrated in Fig. S1.1c, S1.2c, S1.3c and S1.4c (ESI†). In addition, the figure shows that what may be considered as slight changes in rainfall conditions could trigger devastating environmental impacts. Consequently, the analysis of the corresponding temperatures for the 55 year period was conducted to establish the trend and the relationship between the observed air temperature and rainfall event characteristics.
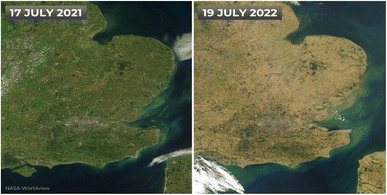 | ||
| Fig. 11 Satellite image shared by NASA demonstrating the UK's dryness rate over one year.60 | ||
Fig. S3.1 and S3.4 (ESI†) show the trends of the demi-decade-averaged (5-yearly average) temperature and demi-decade total number of extreme rainfall events observed at the selected weather stations in the four nations. The graphical presentations provide visual comparisons of the relationship between demi-decade-averaged temperature and demi-decade total number of extreme rainfall events. The results demonstrate that the linear trend for both variables was positive, indicating that the number of extreme rainfall events increased as temperature increased. This may be considered an expected result as a warmer atmosphere holds more moisture and, therefore, more easily gives rise to extreme rainfall events when it is over-saturated. In addition, the results show that the positive trend of the demi-decade total number of extreme rainfall events observed at the stations in Scotland and Northern Ireland changed at a faster rate over the 55 year period than that of England and Wales. This may be due to the aforementioned warmed moist westerly winds from the Atlantic weather systems in addition to the impacts of the regional climate change.
According to Trenberth and Shea, temperature and precipitation records should not be analyzed without considering the existence of covariability between them.61 Therefore, Table 5 shows the results for the test of the relationship between the demi-decade-averaged temperature and demi-decade total number of extreme rainfall events under the null hypothesis that there is no correlation between them at a significance level of 0.05. The results indicated a non-statistical significance, i.e., no significant linear relationships existed between the two variables for observed data recorded at the selected weather stations in the four nations. This may be a result of the sample size used in this study, as in a large spatiotemporal context, there might be a correlation between the trends of increasing rainfall and increasing temperature. This is indeed demonstrated by a recent study conducted by Benestad et al.; the study suggested that the spatial range of precipitation features can be influenced by the average temperature of the planet.62
| Nations | p values | Correlation coefficients |
|---|---|---|
| England | 0.90 | 0.044 |
| Scotland | 0.08 | 0.551 |
| Wales | 0.20 | 0.422 |
| Northern Ireland | 0.18 | 0.438 |
The UK Environmental Agency predicted that rainfall during summer might decrease by up to 15% by the 2050s,63 thereby resulting in increased interevent times. More generally, climate change may lead to more increase in drought risks within the UK due to the increasingly hotter and drier summers (with reduced moderate rainfall events).63 Fig. S3.5–S3.8 (ESI†) show the trend plots of the demi-decade-averaged temperature and demi-decade total number of interevent times greater than its individual nation station's average interevent time (INSAIT). There were variations between observed average interevent times (INSAIT). The results in descending order were as follows: 48 > 36 > 30 h for the station in England, Scotland/Wales, and Northern Ireland, respectively. England's station recorded the longest INSAIT. In addition, England station's positive trend (S3.5 (ESI†)) in the demi-decade total number of interevent times > INSAIT has a steepness (0.61) greater than that of Scotland's station (0.15).
Table 6 shows the results for the correlation test under the null hypothesis that there is no correlation between the demi-decade-averaged temperature and the demi-decade total number of interevent times > INSAIT at 0.05 level of significance. Based on the results, there was no observed significant relationship between the two variables. These results were similar to the one reported in Table 5 but did not directly align with the result reported by the University of Leicester, which indicated that the dryness in England has a direct relationship with its land surface temperatures.64 Moreover, air temperature differs from land surface temperature, although they influence each other.64
| Nations | p values | Correlation coefficients |
|---|---|---|
| England | 0.54 | 0.208 |
| Scotland | 0.60 | 0.180 |
| Wales | 0.40 | 0.281 |
| Northern Ireland | 0.66 | 0.153 |
4 Conclusions
This study tested the exponentiality of rainfall event characteristics sampled from extensive continuous rainfall data recorded at selected stations in the four nations of the UK. The step-by-step procedure for separating continuous historical rainfall data into individual events was extensively discussed. Two-parameter distribution model was also used to see if it fits better the large samples of rainfall event characteristics. A comparative analysis was conducted to examine the goodness-of-fit of the two distribution models. The variation of the distribution parameter values at different stations was examined. Event-based trend analysis was also conducted.The results presented in this study demonstrated that observed rainfall event characteristics at the stations in England, Scotland, Wales, and Northern Ireland can be treated as both exponentially and gammally distributed. The comparative analysis of the distribution parameters reinforced earlier findings about how rainfall conditions change over the UK topography (Section 2.1). The comparative analysis of the best fit distribution indicated that the best fit distribution for the observed data recorded at the selected stations in the four nations of the UK is the gamma distribution, but the exponential distribution was the preferred model because it possesses the largest entropy. Moreover, as per the graphical comparison, the differences in fitness between the exponential and gamma distributions were insignificant. Therefore, the results for both distributions support the existing literature that rainfall event characteristics are likely to follow the exponential distribution and that gamma distribution may provide a better fit for rainfall events in most European countries. In addition, it was noticed that the exponential distribution model underestimated most of the occurrence frequencies, while the gamma distribution model overestimated most of them.
The magnitudes of climatic variabilities expressed based on individual rainfall events were identified in the event-based trend analysis of the data observed at the selected weather stations in the four nations. This served as an indicator of how climate change has impacted and how it could further impact these nations on a regional scale. Although the number of rainfall events increased in all the data recorded in the UK over the 55 year period, moderate rainfall events, which could be said to provide adequate rainfall intensity for aquifer recharge, showed a negative trend in England's station (Fig. 8). The trends of the demi-decade-averaged temperatures and demi-decade total number of extreme rainfall events observed were all positive. However, only the station in England and Scotland showed a positive trend in the demi-decade total number of interevent times > INSAIT. Furthermore, there was no observed linear relationship between the demi-decade-averaged temperatures and demi-decade total number of extreme events as well as the demi-decade-averaged temperatures and demi-decade total number of interevent times > INSAIT. Nevertheless, in a global context, there is a suggestion of a correlation between them.
The overall results obtained from this study are essential for climate policy initiatives and stormwater managers, especially the estimated distribution parameter values and event-based trend analysis findings. Using the exponential distributions with the known parameter values, the percentages of rainfall events with volumes less than or greater than a specified threshold can be easily determined, so are interevent times. The comprehensive guidance provided for the separation of continuous rainfall data with missing values into individual rainfall events can be used by others for other locations. The simple trend analysis conducted based on these separated individual rainfall events is first of its kind for the selected locations in the four nations of the UK and may be utilized for other locations.
Conflicts of interest
There are no conflicts of interest.Acknowledgements
The climate data were provided directly by the UK Met Office, and the authors would like to say thank you, especially to Duncan Ball, Met Office Information Specialist, for the technical support during the provision of the historical climate data and their kind responses to all the authors' queries.References
- Met Office, UK and Global Extreme Events – Drought, https://www.metoffice.gov.uk/research/climate/understanding-climate/uk-and-global-extreme-events-drought, accessed 12 August 2022 Search PubMed.
- Met Office, Record High Temperatures Verified, https://www.metoffice.gov.uk/about-us/press-office/news/weather-and-climate/2022/record-high-temperatures-verified, accessed 13 August 2022 Search PubMed.
- Met Office, Driest July in England Since 1935, https://www.metoffice.gov.uk/about-us/press-office/news/weather-and-climate/2022/driest-july-in-england-since-1935, accessed 13 August 2022 Search PubMed.
- UK Government, Environment Agency Chairs National Drought Group as Parts of Country Move into Drought, https://www.gov.uk/government/news/environment-agency-chairs-national-drought-group-as-parts-of-country-move-into-drought, accessed 13 August 2022 Search PubMed.
- A. Essien, I. Petrounias, P. Sampaio and S. Sampaio, in Database and Expert Systems Applications: 28th International Conference, DEXA, Springer, Cham, Regensburg, 2018, vol. 11030 LNCS, pp. 399–407 Search PubMed.
- A. E. Essien, K. White and M. Mohammadi, Interrelationship study of the impacts of hydraulic fracturing on the environment and socioeconomic activities: a novel approach to finding sustainable solutions, Environ. Sci. Adv., 2022, 1, 305–319 Search PubMed.
- S. Hassini and Y. Guo, Exponentiality, test procedures for large samples of rainfall event characteristics, J. Hydrol. Eng., 2016, 21, 04016003 CrossRef.
- B. J. Adams and F. Papa, Urban Stormwater Management Planning with Analytical Probabilistic Models, John Wiley, New York, 2000 Search PubMed.
- S. Shamsudin, S. Dan’azumi, A. Aris and Z. Yusop, Optimum combination of pond volume and outlet capacity of a stormwater detention pond using particle swarm optimization, Urban Water J., 2014, 11, 127–136 CrossRef.
- C. D. D. Howard, Theory of storage and treatment-plant overflows, J. Environ. Eng. Div., 1976, 102, 709–722 CrossRef.
- P. S. Eagleson, Climate, soil, and vegetation: 2. The distribution of annual precipitation derived from observed storm sequences, Water Resour. Res., 1978, 14, 713–721 CrossRef.
- B. J. Adams, H. G. Fraser, C. D. D. Howard and M. Sami Hanafy, Meteorological data analysis for drainage system design, J. Environ. Eng., 1986, 112, 827–848 CrossRef.
- P. S. Eagleson, Dynamics of flood frequency, Water Resour. Res., 1972, 8, 878–898 CrossRef.
- V. Kumar, Shanu and Jahangeer, Statistical distribution of rainfall in Uttarakhand, India, Appl. Water Sci., 2017, 7, 4765–4776 CrossRef.
- F. Marra, M. Borga and E. Morin, A unified framework for extreme subdaily precipitation frequency analyses based on ordinary events, Geophys. Res. Lett., 2020, 47, e2020GL090209 CrossRef.
- Met Office, UK Regional Climates, https://www.metoffice.gov.uk/research/climate/maps-and-data/regional-climates/index, accessed 22 July 2022 Search PubMed.
- Government of the Netherlands, Which Countries Make Up the United Kingdom?, https://www.government.nl/topics/brexit/question-and-answer/which-countries-make-up-the-united-kingdom, accessed 22 July 2022 Search PubMed.
- Office for National Statistics (ONS), Population Estimates for the UK, England and Wales, Scotland and Northern Ireland, Provisional, https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationestimates/bulletins/annualmidyearpopulationestimates/mid2019#toc, accessed 22 July 2022 Search PubMed.
- UK Government, Offshore Energy SEA 4: Appendix 1 Environmental Baseline, https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/1061601/Appendix_1g_-_Population___human_health.pdf, accessed 23 July 2022 Search PubMed.
- B. Bacchi, M. Balistrocchi and G. Grossi, Proposal of a semi-probabilistic approach for storage facility design, Urban Water J., 2008, 5, 195–208 CrossRef.
- H. Li, J. Sun, H. Zhang, J. Zhang, K. Jung, J. Kim, Y. Xuan, X. Wang and F. Li, What large sample size is sufficient for hydrologic frequency analysis?-A rational argument for a 30-year hydrologic sample size in water resources management, Water, 2018, 10, 430 CrossRef.
- H. A. Sturges, The choice of a class interval, J. Am. Stat. Assoc., 1926, 21, 65–66 CrossRef.
- D. W. Scott, Sturges' rule, Wiley Interdiscip. Rev. Comput. Stat., 2009, 1, 303–306 CrossRef.
- A. Kumar Biswas and A. Biswas, The Choice of Bins of a Histogram: A Kolmogorov Distance-Based Approach, Hal Open Science Search PubMed.
- M. P. Wand, Data-based choice of histogram bin width (Corr: 1999, 53, 174), Am. Stat., 1997, 51, 59–64 Search PubMed.
- S. Manikandan, Frequency distribution, J. Pharmacol. Pharmacother., 2011, 2, 54–56 CrossRef CAS PubMed.
- M. C. Acreman and M. G. Acreman, A simple stochastic model of hourly rainfall for Farnborough, England, Hydrol. Sci. J., 2009, 35, 119–148 CrossRef.
- W. Viessman and G. L. Lewis, Introduction to Hydrology, Pearson Education, India, 2003 Search PubMed.
- M. Balistrocchi, G. Grossi and B. Bacchi, An analytical probabilistic model of the quality efficiency of a sewer tank, Water Resour. Res., 2009, 45, 12420 CrossRef.
- Y. Guo and B. J. Adams, Hydrologic analysis of urban catchments with event-based probabilistic models: 1. Runoff volume, Water Resour. Res., 1998, 34, 3421–3431 CrossRef.
- H. C. S. Thom, A note on the gamma distribution, Mon. Weather Rev., 1958, 86, 117–122 Search PubMed.
- G. Fu, F. H. Chiew, H. Zheng, D. E. Robertson, N. J. Potter, J. Teng, D. A. Post, S. P. Charles and L. Zhang, Statistical analysis of attributions of climatic characteristics to nonstationary rainfall-streamflow relationship, J. Hydrol., 2021, 603, 127017 CrossRef.
- United States Environmental Protection Agency, Nonpoint Source Monitoring: TechNOTES, https://www.epa.gov/nps/nonpoint-source-monitoring-technotes, accessed 28 October 2022 Search PubMed.
- X. Li, W. Wong, E. L. Lamoureux and T. Y. Wong, Are linear regression techniques appropriate for analysis when the dependent (outcome) variable is not normally distributed?, Invest. Ophthalmol. Visual Sci., 2012, 53, 3082–3083 CrossRef PubMed.
- N. Subash and A. K. Sikka, Trend analysis of rainfall and temperature and its relationship over India, Theor. Appl. Climatol., 2014, 117, 449–463 CrossRef.
- J. M. Gregory, T. M. L. Wigley and P. D. Jones, Application of Markov models to area-average daily precipitation series and interannual variability in seasonal totals, Clim. Dyn., 1993, 8, 299–310 CrossRef.
- The Met Office, When Does Winter Start?, https://www.metoffice.gov.uk/weather/learn-about/weather/seasons/winter/when-does-winter-start, accessed 6 August 2021 Search PubMed.
- E. D. Driscoll, D. M. D. Toro and R. V. Thomann, A statistical method for the assessment of urban stormwater, in Environmental Protection Agency, Water Planning Division, Nonpoint Sources Branch, Washington, 1979 Search PubMed.
- R. E. Benestad, D. Nychka and L. O. Mearns, Specification of Wet-Day Daily Rainfall Quantiles from the Mean Value, New pub: Stockholm uni Press, DOI:10.3402/TELLUSA.V64I0.14981.
- R. E. Benestad, K. M. Parding, H. B. Erlandsen and A. Mezghani, A simple equation to study changes in rainfall statistics, Environ. Res. Lett., 2019, 14, 084017 CrossRef CAS.
- R. E. Benestad, J. Lutz, A. V. Dyrrdal, J. E. Haugen, K. M. Parding and A. Dobler, Testing a simple formula for calculating approximate intensity-duration-frequency curves, Environ. Res. Lett., 2021, 16, 044009 CrossRef.
- J. H. Stagge, L. M. Tallaksen, L. Gudmundsson, A. F. van Loon and K. Stahl, Candidate distributions for climatological drought indices (SPI and SPEI), Int. J. Climatol., 2015, 35, 4027–4040 CrossRef.
- D. Koutsoyiannis, Uncertainty, entropy, scaling and hydrological stochastics. 1. Marginal distributional properties of hydrological processes and state scaling, Hydrol. Sci. J., 2005, 381–404 Search PubMed.
- R. R. Inman, Empirical evaluation of exponential and independence assumptions in queueing models of manufacturing systems, Prod. Oper. Manage., 1999, 8, 409–432 CrossRef.
- R. Guo and Y. Guo, Analytical equations for use in the planning of infiltration facilities, J. Sustainable Water Built Environ., 2018, 4, 06018001 CrossRef.
- J. M. Gregory, P. D. Jones and T. M. L. Wigley, Precipitation in Britain: an analysis of area-average data updated to 1989, Int. J. Climatol., 1991, 11, 331–345 CrossRef.
- C. Jun, X. Qin, Y. K. Tung and C. de Michele, On the statistical analysis of rainstorm events between historical (1777–1907) and modern (1961–2010) periods in Seoul, Korea, Int. J. Climatol., 2020, 40, 2078–2090 CrossRef.
- E. Dallan, M. Borga, M. Zaramella and F. Marra, Enhanced summer convection explains observed trends in extreme subdaily precipitation in the eastern italian alps, Geophys. Res. Lett., 2022, 49, e2021GL096727 CrossRef.
- Met Office, How Much Does it Rain in the UK?, https://www.metoffice.gov.uk/weather/learn-about/weather/types-of-weather/rain/how-much-does-it-rain-in-the-uk, accessed 21 August 2022 Search PubMed.
- D. Deumlich and A. Gericke, Frequency trend analysis of heavy rainfall days for germany, Water, 2020, 12, 1950 CrossRef.
- U.S. Geological Survey (USGS), Rainfall Calculator, Metric-How Much Water Falls During a Storm?, https://water.usgs.gov/edu/activity-howmuchrain-metric.html, accessed 9 October 2022 Search PubMed.
- B. Dale and N. Stylianou, What Will Climate Change look Like Near Me?, https://www.bbc.co.uk/news/resources/idt-d6338d9f-8789-4bc2-b6d7-3691c0e7d138, accessed 9 October 2022 Search PubMed.
- L. C. Guo, Y. Zhang, H. Lin, W. Zeng, T. Liu, J. Xiao, S. Rutherford, J. You and W. Ma, The washout effects of rainfall on atmospheric particulate pollution in two Chinese cities, Environ. Pollut., 2016, 215, 195–202 CrossRef CAS PubMed.
- Cambridge Water, The Great British Rain Paradox, https://www.cambridge-water.co.uk/news/the-great-british-rain-paradox, accessed 26 October 2022 Search PubMed.
- Z. Jin, L. Guo, H. Lin, Y. Wang, Y. Yu, G. Chu and J. Zhang, Soil moisture response to rainfall on the Chinese Loess Plateau after a long-term vegetation rehabilitation, Hydrol. Processes, 2018, 32, 1738–1754 CrossRef.
- S. A. Forrest, D. McMahon, W. A. Adams and J. C. Vermaire, Change in microplastic concentration during various temporal events downstream of a combined sewage overflow and in an urban stormwater creek, Front. Water, 2022, 4, 128 Search PubMed.
- Y. Zhang, J. A. Smith, L. Luo, Z. Wang and M. L. Baeck, Urbanization and rainfall variability in the Beijing metropolitan region, J. Hydrometeorol., 2014, 15, 2219–2235 CrossRef.
- D. L. Hartmann, Global Physical Climatology, Academic Press, San Diego, 1994 Search PubMed.
- K. Feethan, Scorched Earth Britain: NASA Images Show How Parched and Brown Country is Due to Heatwave, https://www.dailymail.co.uk/news/article-11041505/Scorched-earth-Britain-NASA-images-parched-brown-country-heatwave.html, accessed 23 October 2022 Search PubMed.
- J. Peat, Crazy NASA Photos Show How Parched and Burnt the UK is, https://www.thelondoneconomic.com/news/crazy-nasa-photos-show-how-parched-and-burnt-the-uk-is-330358/, accessed 15 October 2022 Search PubMed.
- K. E. Trenberth and D. J. Shea, Relationships between precipitation and surface temperature, Geophys. Res. Lett., 2005, 32, 1–4 CrossRef.
- R. E. Benestad, C. Lussana Id, J. Lutz Id, A. Dobler, O. Landgrenid, J. E. Haugenid, A. Mezghaniid, B. Casatiid and K. M. Pardingid, Global hydro-climatological indicators and changes in the global hydrological cycle and rainfall patterns, PLoS Clim., 2022, 1, e0000029 CrossRef.
- Environment Agency, Lack of Water Presents ‘Existential’ Threat, Says Environment Agency Chief, https://www.gov.uk/government/news/lack-of-water-presents-existential-threat-says-environment-agency-chief, accessed 20 October 2022 Search PubMed.
- University of Leicester, Space Images Confirm England's Drought Areas Correlate With High Land Surface Temperatures, https://le.ac.uk/news/2022/august/space-drought-images, accessed 20 October 2022 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2va00294a |
| This journal is © The Royal Society of Chemistry 2023 |