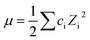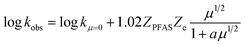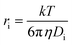Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Linear perfluoroalkyl carboxylate reduction dynamics with solvated electrons from ferrocyanide and sulfite†
William A.
Maza
 *,
James A.
Ridenour
*,
James A.
Ridenour
 ,
Brian L.
Chaloux
,
Brian L.
Chaloux
 ,
Albert
Epshteyn
,
Albert
Epshteyn
 and
Jeffrey C.
Owrutsky
and
Jeffrey C.
Owrutsky

Chemistry Division, US Naval Research Laboratory, Washington, D.C., 20375, USA. E-mail: william.maza@nrl.navy.mil
First published on 10th October 2023
Abstract
The initial reduction dynamics of perfluoroalkyl substances (PFASs) by the hydrated electron, eaq−, is a topic of great interest and importance due to the pervasive environmental presence of PFAS in soil and waters and the need to remediate the contamination. Understanding how PFAS behaves in water, including the potential effect of aggregation on the apparent PFAS reduction rate constant (kPFAS) is, therefore, of paramount importance. In this publication we re-examine the proposition that submicellar aggregation decreases the apparent kPFAS for sodium perfluorocarboxylates of varying chain lengths (NaPFxA, x = number of carbons in the PFAS backbone, ranging from 4 to 8) using transient absorption spectroscopy. We compare the dynamics for eaq− quenching by NaPFxA in aqueous solutions of ferrocyanide, Fe(CN)64−, and sulfite, SO32−. The results demonstrate that the apparent rate constant depends on the choice of eaq− precursor. We demonstrate that the ionic strength of the solution and the counterion of the PFxA salt both affect the measured rate constant of PFAS reduction by eaq−. The results presented here help to better understand PFAS degradation by advanced reduction processes.
Environmental significanceAdvanced reduction processes (ARP) have proven to be quite effective at the destruction of PFAS and other contaminants in tainted waters. However, the processes underlying the reduction of PFAS by hydrated electrons (formed by the UV-excitation of appropriate ions capable of carrying out ARP, like sulfite) are still poorly understood; particularly, the early processes related to the initial reduction of PFAS. Until now, studies utilizing fast spectroscopic techniques like nanosecond transient absorption spectroscopy to elucidate the dynamics between the hydrated electron and PFAS have used ferrocyanide instead of sulfite as the electron donor for a variety of reasons with the assumption that the electron precursor has little effect on the reaction between the hydrated electron and PFAS. In this study we demonstrate that this assumption may not hold true and explore ionic strength effects, as well as counterion effects, to try to pinpoint the factors that make the fast reaction occurring in solutions of ferrocyanide and sulfite so vastly different. We argue that perfluoroalkyl carboxylates (PFxA) tend to aggregate in water at concentrations well below the critical micelle concentration. Furthermore, the concentration of sulfite needed to effectively carry out ARP for practical degradation of contaminated waters shifts the PFxA equilibrium towards aggregation. The implication is that the [PFxA] used in typical degradation studies found in the literature are primarily in some aggregated state. Therefore, the degradation models proposed thus far require revision to include the aggregation of PFxA and the role of aggregation in modulating reactivity with hydrated electrons. |
Introduction
Groundwater contamination by poly- and perfluoroalkyl substances (PFAS), such as perfluorooctanoic acid (PFOA in the literature, PF8A here), has garnered significant attention due to their potential adverse health effects.1 Historically, PFASs were used as particularly effective components in firefighting foams,2 however their ubiquitous use now extends beyond fire suppression3 for their exceptional thermal and electrochemical stability arising from the strength of the C–F bond (e.g. ∼127 kcal mol−1, 5.5 eV for C2F6).4 Not coincidentally, decontamination efforts aimed at removing PFAS from the environment have proven challenging due to these same chemical properties.5UV-irradiation of solutions containing sulfite (SO32−) under alkaline conditions (pH > 8) efficiently degrades PFAS by producing hydrated electrons, eaq−, that are photodetached from SO32−.6–8 This process has become the prototype of so-called ‘Advanced Reduction Processes’ (ARP) for high energy reductive decontamination of tainted waters. The large standard reduction potential (−2.9 V)9 of the eaq− is nearly iso-energetic to the potentiometric biases required for the defluorination reaction of many perfluoroalkanes (e.g.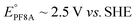 and
and 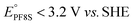 ).10–14 However, most of the work reporting on the fast reaction dynamics of the reduction of PF8A by eaq− has been done in solutions of ferrocyanide (Fe(CN)64−) rather than SO32−.15–18
).10–14 However, most of the work reporting on the fast reaction dynamics of the reduction of PF8A by eaq− has been done in solutions of ferrocyanide (Fe(CN)64−) rather than SO32−.15–18
Fe(CN)64− is a well-studied precursor for generating solvated electrons via photodetachment.19–23 It is an attractive alternative to SO32− for modelling the behaviour of eaq− quenching by PFAS, particularly in the absence of Brønsted acids. Unlike SO32− (pKb = 6.8), Fe(CN)64− is aprotic at pH > 4.3 and has a 100-fold larger molar extinction coefficient (ε) at the 254 nm excitation wavelength (SO32−ε254nm ∼ 50 M−1 cm−1; Fe(CN)64−ε254nm ∼ 5000 M−1 cm−1).24–28 Ferrocyanide also has a high photodetachment quantum yield, even in the near UV.23 In particular, the quantum yield of eaq− formation (Φe) from Fe(CN)64− approaches unity as the excitation wavelength decreases (SO32−Φe ∼ 0.1 at 254 nm excitation, pH 8; Fe(CN)64−Φe ∼ 0.65 at 254 nm excitation, pH 8).28
SO32− and Fe(CN)64− are not unique in their ability to undergo photoinduced ionization to produce eaq−. Other photochemically active anions also produce eaq− and have been used in ARP for the degradation of PFAS. Examples include ethylenediaminetetraacetate (EDTA4−),29 ionic indole derivatives,30 as well as iodide (I−) solutions that produce eaq− in both the absence and presence of SO32−.31–34
We previously reported that the apparent rate constant measured for eaq− quenching by PF8A can be underestimated at high concentrations (above ∼1 mM) due to surfactant aggregation18 including micellization above ∼30 mM. Aggregation of PF8A results in a decrease of the monomeric quencher concentration and appears to reduce the apparent eaq− quenching rate constants.18
As mentioned above, the majority of transient studies probing PFAS reduction dynamics by the eaq− have been carried out in solutions of Fe(CN)64− due to the reasons already outlined. This assumes that the initial reduction of PFAS by eaq− is independent of the source of the eaq−. However, this assumption omits other factors that could potentially modulate eaq− reactivity with PFAS. Due to the differences in the photophysical properties of the various electron donors and the solution conditions required to optimize the degradation of contaminants by ARP, it is imperative to characterize the reduction dynamics of PFAS in each case. In this report, we challenge the supposition that the dynamics of ARP are independent of the eaq− donor, find clear differences between processes carried out in solution of Fe(CN)64−versus SO32−, and present evidence that suggest that these differences are due to differences in the aggregation state of the PFAS induced by the respective solution conditions. The evidence presented here suggests that these differences are, in part, due to ionic strength effects that affect not only the apparent quenching rate constants resulting from well-known screening affects, but also promote submicellar aggregation of PFAS at low concentrations. In addition to the transient absorption studies used to characterize the quenching rate constants, concentration-dependent UV-visible absorption spectra were measured and provide corroborating evidence of aggregation.
Experimental
All chemicals were used as received without further purification. Sodium sulfite (Na2SO3, 98%) was obtained from Alfa Aesar. Potassium ferrocyanide trihydrate was obtained from Sigma Aldrich and Alfa Aesar at different levels of purity (>99.95%, >99.5%, and >98.5%). Sodium perfluorooctanoate (NaPF8A, 95%) was obtained from Strem. Sodium perfluoroheptanoate (NaPF7A, 95%) and sodium perfluoropentanoate (NaPF5A, 95%) were obtained from Matrix Scientific. Sodium perfluorohexanoate (NaPF6A, 95%) and sodium perfluorobutanoate (NaPF4A, 95%) were obtained from Combi-Blocks, Inc.Sample preparation
Stock solutions of Na2SO3 and K4Fe(CN)6 were freshly prepared before each analysis. Samples used for transient absorption experiments were prepared in a standard 1 cm pathlength quartz cuvette and consisted of either 10 mM Na2SO3 or 40 μM K4Fe(CN)6 in 40 mM borate buffer15 (pH ∼ 10) by the appropriate dilution of the stock solutions. Dissolved O2 was removed by sparging with N2 and samples were kept de-aerated by maintaining a dynamic headspace of N2. Stock solutions of NaPFxA, where x is the number of carbons comprising the perfluoroalkyl backbone, were prepared at a concentration of either 80 mM or 500 mM.UV-visible absorption
Steady-state UV-visible absorption spectra were obtained using a PerkinElmer Lambda 1050 UV-vis spectrometer. Spectra were collected between 190 nm and 400 nm either in neat water or aqueous 1 M NaCl solutions. No K4Fe(CN)6 or Na2SO3 were added in these experiments. Aliquots of the NaPFxA stock solutions were added to 2 mL neat water or 1 M NaCl and the absorbance at 230 nm was monitored.Nanosecond transient absorption
Nanosecond transient absorption (nsTA) measurements were performed on an Edinburgh LP980K where the pump and probe were quasi-collinear. Samples were irradiated with a 254 nm laser pulse (pulse width < 7 ns) using an Ekspla NT340B optical parametric oscillator. Each transient shown represents the average of at least 5 shots. Sample solutions were continuously stirred at 800 rpm using a Quantum Northwest Luma 40 thermostatted cuvette sample holder while maintaining a dynamic headspace of N2 during the acquisition of the eaq− lifetimes. All transient data obtained were analyzed using OriginPro software.Ionic strength correction
The observed decay rates obtained from monoexponential fits of the kinetic traces were corrected for the ionic strength (μ) of the solution,where ci is the concentration of ion i and Zi is the charge of the ion, with each addition of PFAS according to35–38
where kobs is the observed eaq− decay rate, kμ=0 is the eaq− decay rate at zero μ, ZPFAS and Ze are the charge on the PFAS and eaq−, respectively, and a is a parameter related to the contact distance (r) between the interacting species; if r < 3 Å a = 1, whereas a = 3 for r > 3 Å.38,39 The contact distance r between PFAS and eaq− is estimated as the sum of their hydrodynamic radii. The radii have been estimated from their diffusion coefficients, Di, according to
The diffusion coefficient for eaq− is reported to be 2.5 × 10−5 cm2 s−1 (r = 1.5 Å),40 and determined by us for PF8A to be 4 × 10−6 cm2 s−1 (r = 4 Å) using 19F DOSY NMR (see ESI, Fig. S1 and S2†). We, therefore, chose a = 3 to correct the observed decay rates (Fig. S3†).
Results and discussion
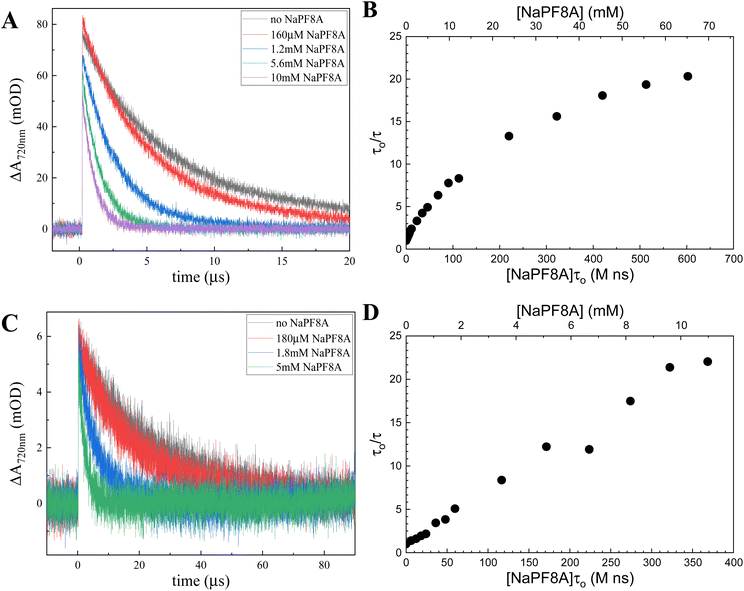
Irradiation of aqueous solutions containing either Na2SO3 or K4Fe(CN)6 with a 254 nm, <7 ns pulse produces a positive absorption on the microsecond timescale at 720 nm, which corresponds to the formation and decay of the eaq−.41–43 In 40 mM borax (pH ∼ 10), the lifetimes obtained for the eaq− produced from a 10 mM solution of Na2SO3 or a 40 μM solution of K4Fe(CN)6 in the absence of NaPFxA (τo) are 28 ± 6 μs and 11 ± 3 μs (Fig. 1), respectively.eaq− quenching by NaPF8A in Fe(CN)64− and SO32−
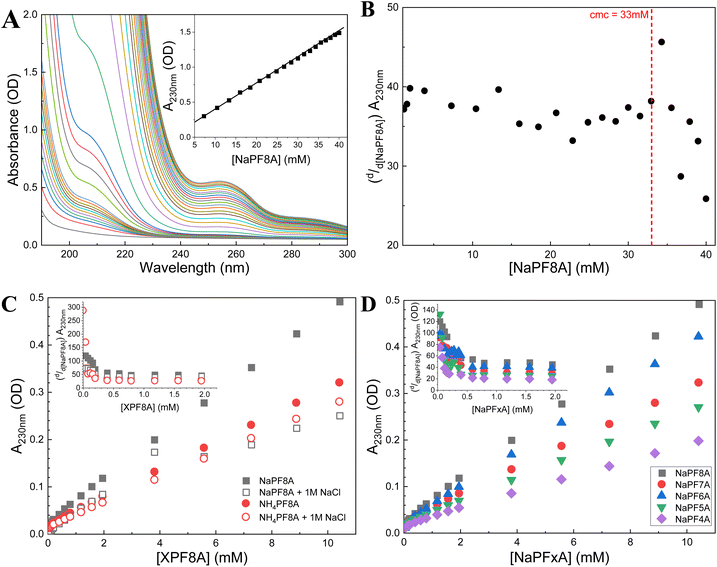
NaPF8A was added stepwise to aqueous borate solutions containing either 40 μM Fe(CN)64− or 10 mM SO32− and the transient decays at 720 nm were recorded upon excitation at 254 nm to probe the interaction of eaq− with NaPF8A. The transients obtained at 720 nm with each addition of NaPF8A were fit to a monoexponential decay function. In the presence of NaPF8A, an increase in the eaq− decay rate was noted in solutions of both SO32− and Fe(CN)64− (Fig. 1). The apparent bimolecular rate constant, kNaPF8A, for the initial interaction of NaPF8A and the eaq− was determined from the decrease in the eaq− lifetime with increased [NaPF8A]. The rate expression corresponding to the diffusional quenching of eaq− by NaPF8A monomers resulting in the reduction of NaPF8A according to reaction 1, | (1) |
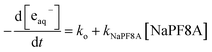 | (2) |
 | (3) |
In Fe(CN)64−, the eaq− decay rate depends linearly on [NaPF8A] for [NaPF8A] < 1 mM with a kNaPF8A of ∼3.3 × 108 M−1 s−1. However, the eaq− decay rate becomes nonlinear for [NaPF8A] > 1 mM. These results are consistent with our previous results,18 which we attributed to the submicellar aggregation of NaPF8A. We will note that others have reported on the propensity of PF8A to form premicellar aggregates. For example, Sarmiento, et al.44,45 invoked this process to explain changes in the partial molar volume in aqueous solutions of LiPF8A at submicellar concentrations.
Szajdzinska-Pietek and Gebicki46 reported radiolysis data that also exhibited two distinct linear regimes in the dependence of the eaq− decay rate as a function of the concentration of ammonium perfluorooctanoate, NH4PF8A, in water at [NH4PF8A] between 5 mM and 40 mM. In their work, they reported a discontinuity that occurs near the critical micelle concentration (∼30 mM).
We previously developed a kinetic model for the eaq− decay rate dependence on [NaPF8A]18 that included eaq− quenching terms by both NaPF8A monomers according to reaction 4 and aggregates assuming that the only configuration of the aggregates are dimers according to reaction 5.
 | (4) |
 | (5) |
The fits reported were restricted to [NaPF8A] < 2 mM to isolate the dynamic concentration range in which monomers and dimers are presumed to dominate the population of NaPF8A. Although adequate fits of the data < 1 mM NaPF8A were obtained using the model, it was stressed that the PF8A aggregation is likely complex and involves a wide range of aggregation states. We, therefore, will refrain from invoking the dimerization model here and, instead, report kNaPF8A based on linear fits over regions in which the concentration dependence is nearly linear (e.g. [NaPF8A] < 1 mM, 1 mM < [NaPF8A] < 10 mM, and [NaPF8A] > 10 mM). From this point on, [NaPF8A] refers to the total concentration of NaPF8A rather than distinguishing between monomers and aggregates; as a result, the reported kNaPF8A are likely lower than the actual values for the bimolecular rate constants.
A linear fit of the data in 40 mM borate at [NaPF8A] < 1 mM yields a kNaPF8A = (2.0 ± 0.9) × 108 M−1 s−1, which is approximately a factor of 3 smaller, but on the same order of magnitude as the result previously reported at concentrations below 200 μM in neat water, (7.1 ± 0.6) × 108 M−1 s−1.17 The reaction conditions here differ from those of our previous reports due to the presence of borate, which buffered the sample solutions at pH 10. Repeating the experiment where aliquots of NaPF8A were added to a solution of Fe(CN)64− in neat water (Fig. S3B†) yields a kNaPF8A = (5.5 ± 1.6) × 108 M−1 s−1 at [NaPF8A] < 1 mM, which is in excellent agreement with our previous results.17,18 The reason for the near 3-fold decrease in kNaPF8A in borate is not readily apparent and outside the scope of this study.
Linear fits at 1 mM < [NaPF8A] < 10 mM yield a kNaPF8A of (5.9 ± 2.0) × 107 M−1 s−1, which is in agreement with previous results reported by us18 and by Szajdzinska-Pietek and Gebicki46 (e.g., 5.1 × 107 M−1 s−1) for [NH4PF8A] < 30 mM, but still about five times greater than the (1.7 ± 0.5) × 107 M−1 s−1 value reported by Huang, et al.16 Linear fits of the data at [NaPF8A] > 10 mM yield a kNaPF8A of (2.4 ± 0.7) × 107 M−1 s−1, which is within experimental error of the aforementioned results reported by Huang et al.16 and in good agreement with the 1.3 × 107 M−1 s−1 value reported by Szajdzinska-Pietek and Gebicki46 for [NH4PF8A] > 30 mM, above its critical micelle concentration, CMC.
The reduction of PFxA by eaq− is believed to proceed by one of three mechanisms: the associative (reaction 6), concerted dissociative (reaction 7), or stepwise dissociative mechanism (reaction 8). Due to experimental limitations, the dominant mechanism driving PFAS reduction and defluorination has yet to be positively identified. As such, a good deal of theoretical work has been dedicated to disentangling these fast initial reactions.12,47–51
| RCF2COO− + eaq− → RCF2(COO−)− | (6) |
| RCF2COO− + eaq− → RC˙FCOO− + F− | (7) |
| RCF2COO− + eaq− → [R(CF2)−COO−] | (8a) |
| [R(CF2)−COO−] → RC˙FCOO− + F− | (8b) |
Daily and Minakata48 used density functional theory to calculate the one electron reduction potentials corresponding to reactions 6–8 for PF4A, PF6A, and PF8A among other organic compounds. From the theoretical reduction potentials the authors then calculated the predicted rate constants for reduction and found that for PF8A the associative and concerted dissociative mechanisms are expected to proceed with a rate constant of 5.8 × 108 M−1 s−1 and 1.7 × 107 M−1 s−1, respectively. These predicted values are in excellent agreement with our results in neat aqueous solutions of Fe(CN)64− at [NaPF8A] < 1 mM and >10 mM, respectively, and in very good agreement with solutions of Fe(CN)64− in borax (Table 1) in the same concentration ranges.
| 40 μM Fe(CN)64− | k NaPFxA (M−1 s−1) | Literature | Ref. | ||
|---|---|---|---|---|---|
| [NaPFxA] < 1 mM | 1 mM < [NaPFxA] < 10 mM | [NaPFxA] > 10 mM | [NaPFxA] > 5 mM | ||
| NaPF8A | (2.0 ± 0.9) × 108 | (5.9 ± 2.0) × 107 | (2.4 ± 0.7) × 107 | (1.7 ± 0.5) × 107 | 16 |
| NaPF7A | (7.7 ± 2.0) × 107 | (2.5 ± 0.4) × 107 | (1.9 ± 0.4) × 107 | ||
| NaPF6A | (9.8 ± 2.0) × 107 | (3.3 ± 0.3) × 107 | (2.4 ± 0.3) × 107 | ||
| NaPF5A | (6.7 ± 1.6) × 107 | (1.5 ± 0.3) × 107 | (1.3 ± 0.1) × 107 | ||
| NaPF4A | (1.0 ± 0.2) × 107 | (3.7 ± 0.2) × 107 | (2.5 ± 0.3) × 107 | (7.1 ± 0.3) × 106, (1.3 ± 0.1) × 107 | 15 and 16 |
| 10 mM SO32− | k NaPFxA (M−1 s−1) |
|---|---|
| NaPF8A | (5.6 ± 0.2) × 107 |
| NaPF7A | (2.0 ± 0.1) × 107 |
| NaPF6A | (2.9 ± 0.2) × 107 |
| NaPF5A | (1.0 ± 0.1) × 107 |
| NaPF4A | (2.0 ± 0.2) × 107 |
We note that a recent study has disputed the nonlinearity observed by us for eaq− quenching in solutions of Fe(CN)64− at PFAS concentrations < 1 mM.15 In order to verify that our observed trend is not due to impurities in our commercially obtained K4Fe(CN)6, we performed the same experiment where aliquots of NaPF8A were incrementally added to aqueous solutions (in the absence of borate) of K4Fe(CN)6 obtained from two different suppliers and three different degrees of purity. We found the trend and results, particularly at [NaPF8A] < 1 mM, to be virtually indistinguishable between the three data sets (Fig. S3B†).
Interestingly, the interactions between eaq− and NaPF8A are quite different in 10 mM SO32− solutions compared to Fe(CN)64− over similar [NaPF8A]. Upon addition of NaPF8A to 10 mM SO32−, negligible eaq− lifetime quenching was observed below 200 μM. At [NaPF8A] > 200 μM, however, the eaq− decay rate increases linearly with [NaPF8A] up to 10 mM and has a kNaPF8A of (5.6 ± 0.2) × 107 M−1 s−1, which correlates well with the values obtained here for the kNaPF8A in 1 mM < [NaPF8A] < 10 mM solutions of Fe(CN)64−. A nonlinear dependence of the eaq− decay rate on [NaPF8A] is also observed in solutions of 1 mM KI (Fig. S4†) in neat water; however, the dependence of the eaq− decay rate on [NaPF8A] becomes increasing linear when the concentration of KI is increased. The kNaPF8A between 1 mM < [NaPF8A] < 10 mM was also observed to decrease from 5.9 × 107 M−1 s−1 in 1 mM KI to 3.5 × 107 M−1 s−1 in 10 mM KI. Moreover, a significant difference in the kNaPF8A obtained between 1 mM < [NaPF8A] < 10 mM was noted when comparing results in 10 mM KI and 80 μM indole to 40 μM Fe(CN)64− and 10 mM SO32−.
Effect of NaPF8A on the absorption spectrum of eaq−
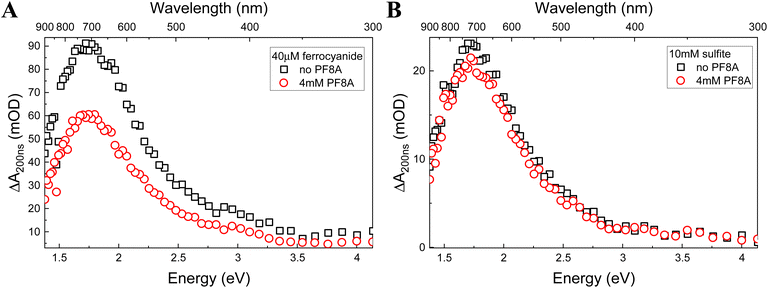
We recorded the eaq− spectrum in Fe(CN)64− and SO32− solutions both with and without 4 mM NaPF8A (Fig. 2). The eaq− spectrum is unaffected by the presence of NaPF8A suggesting that the solvent properties are unperturbed. It is known that the transition energy of eaq− depends on the solvent and is, therefore, sensitive to the differences in its local environment.52–54 These differences manifest in a shift of the wavelength of the eaq− absorption maximum. For example, excitation of aqueous Triton tx-165 at concentrations above its CMC results in the formation of two distinct populations of eaq− evidenced by the presence of two absorption maxima located at 720 nm and 630 nm that respectively correspond to eaq− in water and in the less polar micellar interior.54 Here, the eaq− displays an absorption maximum at 719 nm and 717 nm in solutions of Fe(CN)64− and SO32−, respectively, in the absence of NaPF8A. In the presence of 4 mM NaPF8A, no shifts were observed for the eaq− absorption maxima in solutions of Fe(CN)64− and SO32− suggesting that perturbations to the physicochemical properties of the solvent are negligible up to 4 mM NaPF8A.Salt effect on the NaPF8A reduction rate constant
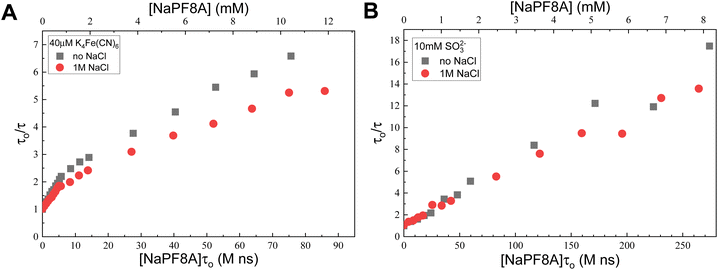
Increased salt concentration and ionic strength are known to promote aggregation and lower CMC values.55,56 To determine the effect of ionic strength on the measured rates constants, we incrementally added aliquots of NaPF8A into solutions of Fe(CN)64− and SO32− containing 1 M NaCl (Fig. 3). In solutions of Fe(CN)64−, the presence of 1 M NaCl results in a more pronounced deviation from a linear dependence of the eaq− decay rate with [NaPF8A] and the kNaPF8A values at [NaPF8A] < 1 mM and 1 mM < [NaPF8A] < 10 mM are (1.3 ± 0.3) × 108 M−1 s−1 and (4.1 ± 0.5) × 107 M−1 s−1, respectively. The kNaPF8A obtained at [NaPF8A] < 1 mM in the absence and presence of 1 M NaCl are found to agree within experimental error. However, at 1 mM < [NaPF8A] < 10 mM, addition of NaCl induces a nearly two-fold decrease in the kNaPF8A. Interestingly, the addition of 1 M NaCl to solutions of SO32− resulted in a nearly negligible decrease in kNaPF8A to (4.2 ± 0.8) × 107 M−1 s−1 (Fig. 3).There is less of an effect from adding NaCl to the 10 mM SO32− because it has a higher initial ionic strength than that of the 40 μM Fe(CN)64− so the former is less susceptible to additional increases in the ionic strength. Increasing the NaCl concentration promotes NaPF8A aggregation but the effect is reduced in sulfite solution because the ionic strength is already high. This interpretation is corroborated by the trend observed in varying concentrations of KI with NaPF8A (Fig. S4†) in which the non-linearity of the data decreases with increasing [KI] and, as a result, the solution ionic strength (vide supra). The results obtained at high [NaCl] lend further support to this proposal. As noted earlier, the critical micelle concentration is known to decrease with increasing ionic strength.55,56 Analogously, we believe that the interactions between PFAS monomers increase with increasing ionic strength shifting the equilibrium from monomers to aggregates.
Effect of PF8A counterion on eaq− quenching
Counterions are known to affect surfactant aggregation.57,58 For example, Lunkenheimer, et al. demonstrated a decrease in the CMC of various PF8A salts following the series Li+ > Na+ > K+ > NH4+ > Rb+ > Cs+.57,58 We, therefore, investigated whether there were differences between Na+ and NH4+ cations on the eaq− quenching behavior of PF8A in Fe(CN)64− and SO32− solutions. Results of NH4PF8A and NaPF8A quenching using Fe(CN)64− and SO32− as precursor are shown in Fig. 4. In Fe(CN)64− solutions the dependence of the eaq− decay rate was lower for NaPF8A than for NH4PF8A at 1 mM < [XPF8A] < 10 mM which is consistent with more aggregation in the former. We found that the kXPF8A (where X is either Na+ or NH4+) was 3–4 times greater for NH4PF8A, (2.0 ± 0.1) × 108 M−1 s−1 than for NaPF8A, (5.9 ± 0.2) × 107 M−1 s−1. We believe the difference in the kXPF8A observed between Na+ and NH4+ are related to differences in the interaction strength between the carboxylate head group of PF8A and the counter ion. We should note that the radius of hydration differ between Na+ and NH4+ which may also contribute to the differences in the observed trends;58 however, the nature of the contribution is uncertain at this time. Interestingly, in solutions of Fe(CN)64− the dependence of the eaq− decay rate on [NH4PF8A] displays a larger deviation from linearity in the presence of 1 M NaCl (Fig. S5†) likely due to cation exchange in excess Na+. In solutions of SO32−, we found that the kXPF8A was similarly larger by a factor of 3–4 for NH4PF8A, (1.8 ± 0.1) × 108 M−1 s−1 compared to NaPF8A, (5.6 ± 0.2) × 107 M−1 s−1.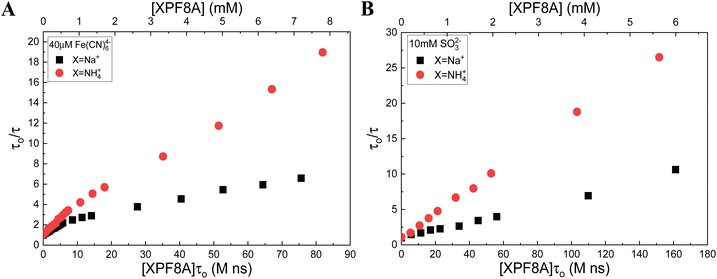 | ||
| Fig. 4 Modified Stern–Volmer plots of the eaq− lifetime dependence on the [NaPF8A] (black) and [NH4PF8A] (red) in 40 mM borate solutions of (A) 40 μM Fe(CN)64− and (B) 10 mM SO32−. | ||
eaq− quenching by NaPFxA
In addition to NaPF8A, we also examined NaPFxAs of other chain lengths, where x corresponds to the number of carbons comprising the PFAS backbone (x = 8, 7, 6, 5, and 4). In each case we found a nonlinear dependence of the eaq− decay rate on [NaPFxA] in Fe(CN)64− solutions (Fig. 5). Although the data are nonlinear in Fe(CN)64−, suggesting aggregation with increasing [NaPFxA] in all cases, we will direct our attention to the kNaPFxA at 1 mM < [NaPFxA] < 10 mM for comparison to the data obtained in SO32−. In both Fe(CN)64− and SO32− a general decreasing trend is observed for the kNaPFxA in the range 1 mM < [NaPFxA] < 10 mM with decreasing chain length, which is in good agreement with the trend that has been reported in the literature for the initial reduction of PFxA.16 We will note that although the kNaPF8A obtained by us in Fe(CN)64− (6.6 × 107 M−1 s−1) and SO32− (5.6 × 107 M−1 s−1) at [NaPF8A] > 1 mM are 3–4 times greater than the 1.7 × 107 M−1 s−1 value reported by Huang, et al.16 they are in very good agreement with the 5.1 × 107 M−1 s−1 value reported by Szajdzinska-Pietek and Gebicki46 in the concentration range of 5 mM < [NH4PF8A] < 30 mM. We have previously18 pointed out that the rate constant reported by Huang, et al.16 is in very good agreement with the 1.3 × 107 M−1 s−1 rate constant reported by Szajdzinska-Pietek and Gebicki46 at [NH4PF8A] above the CMC ∼ 30 mM.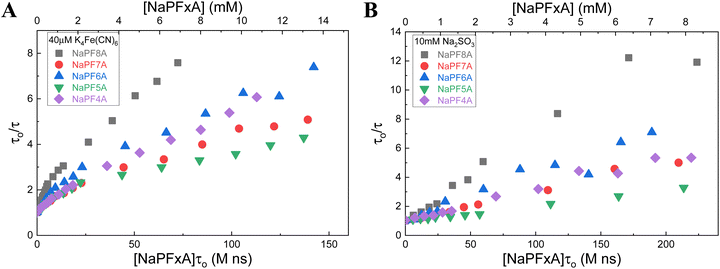 | ||
| Fig. 5 Modified Stern–Volmer plots of the eaq− lifetime dependence on the [NaPFxA] in 40 mM borate solutions of (A) 40 μM Fe(CN)64− and (B) 10 mM SO32−. | ||
Steady-state absorption spectrum of NaPFxA
A number of experimental techniques have traditionally been used to monitor aggregation in solution, particularly vis-à-vis surfactant aggregation and micelle formation, including surface tensiometry, conductivity, steady-state absorbance and fluorescence spectroscopy. In the case of absorbance and fluorescence spectroscopy, due to the low molar extinction and fluorescence quantum yields of many surfactant molecules, surfactant aggregation is typically estimated with the help of solvatochromic reporters or hydrophobic chromophores that preferentially partition within the hydrophobic core of micelles. However, despite the low molar extinction of many surfactants, we believe that deviations from linearity of the absorbance of the surfactants in water may be observed and would be indicative of aggregation (Fig. S6†).59As a demonstration that surfactant absorption can be used to identify aggregation, steady-state spectra were measured for aqueous solutions with increasing amounts of NaPFxA up to 40 mM. At low concentrations of NaPF8A (<100 μM), the spectrum obtained is relatively featureless at wavelengths > 200 nm (Fig. 6). A shoulder centered at ∼210 nm emerges at ∼100 μM NaPF8A and increases in prominence with increasing [NaPF8A]. At [NaPF8A] > 2 mM, another shoulder is observed centered at ∼255 nm; at much higher concentrations another feature is observed at ∼288 nm. A small deviation from linearity in the steady-state absorption is observed between 5 mM and 40 mM (as shown in the inset of Fig. 6). The first derivative plot of the absorbance at 230 nm with respect to the [NaPF8A] displays an inflection point between 30 mM and 38 mM; this is consistent with the reported CMC values between 33 mM and 36 mM for NaPF8A.60–66 When adding NH4PF8A to neat water up to 10 mM, we observed only a feature at 210 nm up to 10 mM.
 | ||
| Fig. 6 (A) Steady-state absorbance of aqueous solutions (in the absence of borate, Fe(CN)64−, and SO32−) at concentrations of NaPF8A increasing from 40 μM to 40 mM. (B) First derivative of the steady-state absorbance at 230 nm as a function of the concentration of NaPF8A between 5 mM and 40 mM. The dotted red line is the CMC value reported for NaPF8A in ref. 60. (C) Steady-state absorbance at 230 nm as a function of the concentration of NaPF8A (black) and NH4PF8A (red) up to 10 mM; the inset shows the first-derivative of the same data between 0 mM and 2 mM. (D) Steady-state absorbance at 230 nm as a function of the concentration of NaPF8A (black), NaPF7A (red), NaPF6A (blue), NaPF5A (green), and NaPF4A (purple) up to 10 mM; the inset shows the first-derivative of the same data between 0 mM and 2 mM. | ||
Results similar to those for NaPF8A were observed for other NaPFxAs up to 10 mM. In all cases, a prominent inflection point in the steady-state absorbance data of aqueous NaPFxA solutions was observed at [NaPFxA] < 0.5 mM, well below the respective CMCs, which we attribute to the formation of pre-micellar aggregates (vide infra).18,44,45 It is interesting that this inflection feature occurs at nearly the same concentration for each NaPFxA when the CMCs are very much chain length dependent and vary in magnitude by a considerable amount suggesting that premicellar aggregation is less influenced by the chain length and dominated by some other property.60,66 It is also noteworthy that, although absent in the transient absorption data in solutions of SO32−, deviations from linearity in the observed eaq− decay rates as a function of [NaPFxA] in solutions of Fe(CN)64− occur at nearly the same concentrations lending more weight to the argument that the trends observed in the transient absorption data in solutions of Fe(CN)64− are due to aggregation effects. We believe that the latter is not coincidental and that the physical process inducing the nonlinearity in the steady-state absorbance is the same process that underly the trend in the transient absorption data in solutions of Fe(CN)64−; namely, submicellar aggregation of NaPFxA.
Conclusions
Although the biomolecular rate constants for the quenching of the eaq− by PFAS were previously assumed to not depend on the identity of the eaq− photodetachment precursor, in actuality the measurement of the reaction kinetics are complicated by several factors. Here, nanosecond transient absorption spectroscopy was used to measure apparent rate constants, kNaPFxA, for NaPFxA quenching of the eaq− with ferrocyanide and sulfite precursors in water. The results herein demonstrated that ionic strength and cation identity effects carry significant ramifications for PFAS reactivity with the eaq− due to their influence on submicellar surfactant aggregation.We found that the kNaPF8A for eaq− quenching by NaPFxA is not constant over the quencher concentration range for ferrocyanide. Additional studies were carried out to demonstrate the aggregation of NaPFxA, even below the CMC. Ionic strength is known to not only influence the measured rate constants for eaq− due to electrostatic screening, which we accounted for, but it can also influence aggregation, as shown here. The results of other measurements further corroborate our interpretation that aggregation explains the anomalous, concentration-dependent rate constant values. The eaq− decay rate was also found to vary when the PFxA counterion was changed in a manner consistent with aggregation. Steady-state UV-visible spectra of NaPFxA without ferrocyanide or sulfite (or borate) deviate significantly from the Beer–Lambert law well below their CMC, which is yet another indication of submicellar aggregation of PFxA. The results here reinforce our previous interpretation that PFxA exhibit strong aggregation tendencies, which should be taken into account to get accurate rate constants when measuring solvated electron quenching kinetics.
Author contributions
WAM: conceptualization, methodology, investigation, formal analysis, writing – original draft. JAR: investigation, formal analysis, writing – review & editing. BLC: investigation, formal analysis, writing – review & editing. AE: supervision, writing – review & editing. JCO: supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the Office of Naval Research through the U.S. Naval Research Laboratory (N0001422WX00033).References
- Y. Li, T. Fletcher, D. Mucs, K. Scott, C. H. Lindh, P. Tallving and K. Jakobsson, Occup. Environ. Med., 2018, 75, 46–51 CrossRef PubMed.
- X. C. Hu, D. Q. Andrews, A. B. Lindstrom, T. A. Bruton, L. A. Schaider, P. Grandjean, R. Lohmann, C. C. Carignan, A. Blum, S. A. Balan, C. P. Higgins and E. M. Sunderland, Environ. Sci. Technol. Lett., 2016, 3, 344–350 CrossRef CAS PubMed.
- G. F. Peaslee, J. T. Wilkinson, S. R. McGuinness, M. Tighe, N. Caterisano, S. Lee, A. Gonzales, M. Roddy, S. Mills and K. Mitchell, Environ. Sci. Technol. Lett., 2020, 7, 594–599 CrossRef CAS.
- C. D. Vecitis, H. Park, J. Cheng, B. T. Mader and M. R. Hoffmann, Front. Environ. Sci. Eng., 2009, 3, 129–151 CrossRef CAS.
- B. Ji, P. Y. Kang, T. Wei and Y. Q. Zhao, Chemosphere, 2020, 250, 126316 CrossRef CAS PubMed.
- Y. R. Gu, T. Z. Liu, H. J. Wang, H. L. Han and W. Y. Dong, Sci. Total Environ., 2017, 607, 541–548 CrossRef PubMed.
- Y. R. Gu, W. Y. Dong, C. Luo and T. Z. Liu, Environ. Sci. Technol., 2016, 50, 10554–10561 CrossRef CAS PubMed.
- Y. R. Gu, T. Z. Liu, Q. Zhang and W. Y. Dong, Chem. Eng. J., 2017, 326, 1125–1133 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 3477–3489 CrossRef CAS.
- J. A. Marsella, A. G. Gilicinski, A. M. Coughlin and G. P. Pez, J. Org. Chem., 1992, 57, 2856–2860 CrossRef CAS.
- A. A. Pud, G. S. Shapoval, V. P. Kukhar, O. E. Mikulina and L. L. Gervits, Electrochim. Acta, 1995, 40, 1157–1164 CrossRef CAS.
- D. J. Van Hoomissen and S. Vyas, Environ. Sci. Technol. Lett., 2019, 6, 365–371 CrossRef CAS.
- B. Guan, J. Zhi, X. Zhang, T. Murakami and A. Fujishima, Electrochem. Commun., 2007, 9, 2817–2821 CrossRef CAS.
- V. Ochoa-Herrera, R. Sierra-Alvarez, A. Somogyi, N. E. Jacobsen, V. H. Wysocki and J. A. Field, Environ. Sci. Technol., 2008, 42, 3260–3264 CrossRef CAS PubMed.
- C. K. Amador, D. J. Van Hoomissen, J. Q. Liu, T. J. Strathmann and S. Vyas, Chemosphere, 2023, 311, 136918–136926 CrossRef CAS PubMed.
- L. Huang, W. B. Dong and H. Q. Hou, Chem. Phys. Lett., 2007, 436, 124–128 CrossRef CAS.
- W. A. Maza, V. M. Breslin, J. C. Owrutsky, B. B. Pate and A. Epshteyn, Environ. Sci. Technol. Lett., 2021, 8, 525–530 CrossRef CAS.
- W. A. Maza, B. D. Etz, T. C. Schutt, B. L. Chaloux, V. M. Breslin, B. B. Pate, M. K. Shukla, J. C. Owrutsky and A. Epshteyn, Environ. Sci. Technol. Lett., 2022, 9, 226–232 CrossRef CAS.
- P. Airey and F. S. Dainton, Proc. R. Soc. London, Ser. A, 1966, 291, 340–352 CAS.
- M. Shirom and G. Stein, J. Chem. Phys., 1971, 55, 3372–3378 CrossRef CAS.
- M. Shirom and M. Tomkiewi, J. Chem. Phys., 1972, 56, 2731–2736 CrossRef CAS.
- G. Stein, Isr. J. Chem., 1970, 8, 691–697 CrossRef CAS.
- G. M. Sando and J. C. Owrutsky, J. Phys. Chem. B, 2006, 110, 9586–9592 CrossRef CAS PubMed.
- W. A. Maza, V. M. Breslin, N. T. Plymale, P. A. DeSario, A. Epshteyn, J. C. Owrutsky and B. B. Pate, Photochem. Photobiol. Sci., 2019, 18, 1526–1532 CrossRef CAS PubMed.
- A. E. Martell and R. M. Smith, Critical Stability Constants, Plenum Press, New York, N.Y., 1974 Search PubMed.
- E. Hayon, A. Treinin and J. Wilf, J. Am. Chem. Soc., 1972, 94, 47–57 CrossRef CAS.
- L. Dogliotti and E. Hayon, J. Phys. Chem., 1968, 72, 1800–1807 CrossRef CAS.
- M. C. Sauer, R. A. Crowell and I. A. Shkrob, J. Phys. Chem. A, 2004, 108, 5490–5502 CrossRef CAS.
- P. F. Gu, C. J. Zhang, Z. Y. Sun, H. Z. Zhang, Q. Zhou, S. J. Lin, J. Y. Rong and M. R. Hoffmann, Chem. Eng. J., 2020, 379, 122338 CrossRef CAS.
- Z. H. Chen, Y. Teng, N. Mi, X. Jin, D. S. Yang, C. Wang, B. Wu, H. Q. Ren, G. X. Zeng and C. Gu, Environ. Sci. Technol., 2021, 55, 3996–4006 CrossRef CAS PubMed.
- H. Park, C. D. Vecitis, J. Cheng, N. F. Dalleska, B. T. Mader and M. R. Hoffmann, Photochem. Photobiol. Sci., 2011, 10, 1945–1953 CrossRef CAS PubMed.
- H. Park, C. D. Vecitis, J. Cheng, W. Choi, B. T. Mader and M. R. Hoffmann, J. Phys. Chem. A, 2009, 113, 690–696 CrossRef CAS PubMed.
- Y. Qu, C. J. Zhang, F. Li, J. Chen and Q. Zhou, Water Res., 2010, 44, 2939–2947 CrossRef CAS PubMed.
- K. E. Yu, X. C. Li, L. W. Chen, J. Y. Fang, H. L. Chen, Q. B. Li, N. P. Chi and J. Ma, Water Res., 2018, 129, 357–364 CrossRef CAS PubMed.
- J. Rabani, in Solvated Electron, ed. R. F. Gould, American Chemical Society, Washington, D.C., 1965, vol. 50, ch. 17, p. 242 Search PubMed.
- M. Matheson, in Solvated Electron, ed. R. F. Gould, American Chemical Society, Washington, D.C., 1965, vol. 50, ch. 5, p. 45 Search PubMed.
- S. R. Logan, Trans. Faraday Soc., 1967, 63, 3004–3008 RSC.
- G. Czapski and H. A. Schwarz, J. Phys. Chem., 1962, 66, 471–474 CrossRef.
- S. Gordon, E. J. Hart, M. S. Matheson, J. Rabani and J. K. Thomas, J. Am. Chem. Soc., 1963, 85, 1375–1377 CrossRef CAS.
- M. Anbar, in Solvated Electron, ed. R. F. Gould, American Chemical Society, Washington, D.C., 1965, vol. 50, ch. 6, p. 55 Search PubMed.
- G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513–886 CrossRef CAS.
- L. M. Dorfman, F. Jou and R. Wageman, Ber. Bunsen-Ges., 1971, 75, 681–685 CrossRef CAS.
- E. J. Hart, B. Michael and K. H. Schmidt, J. Phys. Chem., 1971, 75, 2798–2805 CrossRef CAS.
- E. Blanco, P. Messina, J. M. Ruso, G. Prieto and F. Sarmiento, Mol. Phys., 2005, 103, 3271–3281 CrossRef.
- A. Gonzalez-Perez, J. M. Ruso, G. Prieto and F. Sarmiento, J. Surfactants Deterg., 2004, 7, 387–395 CrossRef CAS.
- E. Szajdzinska-Pietek and J. L. Gebicki, Res. Chem. Intermed., 2000, 26, 897–912 CrossRef CAS.
- M. J. Bentel, Y. Yu, L. Xu, Z. Li, B. M. Wong, Y. Men and J. Liu, Environ. Sci. Technol., 2019, 53, 3718–3728 CrossRef CAS PubMed.
- R. Daily and D. Minakata, Environ. Sci.: Water Res. Technol., 2022, 8, 543–574 RSC.
- S. Biswas, S. S. R. K. C. Yamijala and B. M. Wong, Environ. Sci. Technol., 2022, 56, 8167–8175 CrossRef CAS PubMed.
- S. Biswas and B. M. Wong, ACS EST Engg., 2023 DOI:10.1021/acsestengg.3c00216.
- S. S. R. K. C. Yamijala, R. Shinde and B. M. Wong, Phys. Chem. Chem. Phys., 2020, 22, 6804–6808 RSC.
- L. M. Dorfman, F. Jou and R. Wageman, Ber. Bunsen-Ges., 1971, 75, 681–685 CrossRef CAS.
- E. J. Hart and J. W. Boag, J. Am. Chem. Soc., 1962, 84, 4090–4095 CrossRef CAS.
- H. Ghosh, D. Palit, A. Sapre, K. RamaRao and J. Mittal, Chem. Phys. Lett., 1993, 203, 5–11 CrossRef CAS.
- L. Ambrosone and R. Ragone, J. Colloid Interface Sci., 1998, 205, 454–458 CrossRef CAS PubMed.
- P. Palladino and R. Ragone, Langmuir, 2011, 27, 14065–14070 CrossRef CAS PubMed.
- K. Lunkenheimer, K. Geggel and D. Prescher, Langmuir, 2017, 33, 10216–10224 CrossRef CAS PubMed.
- K. Lunkenheimer, D. Prescher and K. Geggel, Langmuir, 2022, 38, 891–902 CrossRef CAS PubMed.
- X. Cui, S. Mao, M. Liu, H. Yuan and Y. Du, Langmuir, 2008, 24, 10771–10775 CrossRef CAS PubMed.
- H. Kunieda and K. Shinoda, J. Phys. Chem., 1976, 80, 2468–2470 CrossRef CAS.
- N. Muller and H. Simsohn, J. Phys. Chem., 1971, 75, 942–945 CrossRef CAS.
- H. Nakayama, Bull. Chem. Soc. Jpn., 1967, 40, 1592–1595 CrossRef CAS.
- K. Shinoda, M. Hato and T. Hayashi, J. Phys. Chem., 1972, 76, 909–914 CrossRef CAS.
- K. Shinoda and K. Katsura, J. Phys. Chem., 1964, 68, 1568–1569 CrossRef CAS.
- J. L. Lopez-Fontan, F. Sarmiento and P. C. Schulz, Colloid Polym. Sci., 2005, 283, 862–871 CrossRef CAS.
- K. Shinoda, M. Hato and T. Hayashi, J. Phys. Chem., 1972, 76, 909–914 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2279639 contains the supplementary crystallographic data for the crystal structure of NaPF8A in Fig. S7 in the supplemental. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3va00223c |
| This journal is © The Royal Society of Chemistry 2023 |