Machine learning assisted binary alloy catalyst design for the electroreduction of CO₂ to C₂ products

Abstract

The carbon dioxide reduction reaction (CO₂RR) has become one of the most important catalytic reactions due to its potential impact on global emissions. Among the many products this reaction yields, C₂ products are the most valuable due to their potential use as hydrocarbon fuels. For the efficient conversion of CO₂ into C₂ products, however, further work needs to be done on understanding the reaction pathway mechanisms and ideal catalytic surfaces. Herein, we gain insight into the C₂ pathway through a combination of Density Functional Theory (DFT) and machine learning (ML) by studying the adsorption of *COCOH on eight different types of Cu-based binary alloy catalysts (BAC) and subsequently discover the ideal BAC surfaces through configurational space exploration. 8 different ML models were evaluated with descriptors for elemental period, group, electronegativity, and the number of unpaired d orbital electrons. The top performing models could successfully predict the adsorption energy of *COCOH on Cu-based BACs to within 0.095 eV mean absolute error (MAE). The most accurate models found Cu/Ag and Cu/Au BACs with 2–3 atom nanoislands on the surface and high Ag/Au density subsurfaces had the most favorable reaction energy pathway which corresponds with the weakest *COCOH adsorption energies.

---

1. Introduction

For the past decade, climate change has been a major topic for scientific research. Global-scale environmental degradation has proven to have severe impacts on human health, wildlife and ecosystems.^1,2 This has prompted large amounts of research into the carbon dioxide reduction reaction (CO₂RR) in an attempt to reverse the catastrophic damage our environment has incurred. One promising pathway to this goal that has recently emerged is the conversion of CO₂ into energy rich hydrocarbons for use as a renewable fuel.^3–6 This pathway is attractive because it not only offers an economic replacement for traditional fossil fuels, but also provides a potential pathway to sustainable energy sources.^5–7

There are still hurdles before a sustainable energy architecture can be realistically implemented. The stable nature of CO₂ under ambient conditions makes the decomposition of CO₂ into C and O₂ require 395 kJ mol⁻¹ of energy which is very costly and current methods yield mixed products such as HCOOH, CO, CH₃OH, C₂H₄,C₂H₅OH and CH₄ due to the multistep nature of the CO₂RR.^8–11 Regardless, the products consisting of two or more carbons (C₂₊ products) deserve more attention because they can more readily be used as reactants for fuel production and polymerization.¹²

Both experimental and computational studies suggest C₂₊ products start with two carbons simultaneously bonding to the catalytic surface (bidentate).¹⁴ In particular, the Cu(100) facet has been shown to be highly favorable for this dimerization due to its low onset potential in non-acidic environments.¹⁴ For the bidentate CO₂RR pathway to win over auxiliary monodentate reactions, a close to ideal electrocatalyst will have to be used.¹³ Although Cu(100) is known to be the best monometal for the dimerized CO hydrogenation pathway to C₂₊ products, few studies have tried pushing this CO₂RR pathway further through elemental additions and *COCOH adsorbate studies.¹⁴ Among the many families of electrocatalysts, transition metals are commonly studied because of their unique electronic structure and active electrons in metallic bonds.^15,16 With the addition of a second metal, the ligand effect and ensemble effect are introduced.^17,18 The influence of one can hardly be separated from the other since the extra atom changes the electronic structure and surface ensemble at the same time.¹⁹ Nonetheless, studies find the ensemble effect contributes significantly more than the ligand effect in the improvement of reactivity and selectivity.^17–19 In the current research landscape, binary alloy catalysts (BACs) have been studied for single carbon products by generating databases of various intermediates (CO, CHO, COH) along with stoichiometric optimizations but no work has been done on elucidating the link between *COCOH adsorption, a key intermediate in the pathway towards C₂₊ products and high performing BACs.^20,21

In this paper, we report on the design of BACs through the curation of a 1600 datapoint DFT generated dataset to train machine learning (ML) models on. With the trained model which best understands the complex intermingled influences of the bidentate adsorption pathway for the CO₂RR, adsorption energy (E_ads) predictions were made on 8000 random BAC structures. The reliability and generalizability of the ML models were tested on tertiary alloy catalysts (TACs) to propose new complex catalysts. The top performing BAC candidates were further studied to elucidate factors correlating E_{ads *COCOH} to favorable reaction energy pathway surfaces.

2. Methods

2.1. DFT calculations

All adsorption energy DFT calculations were performed using Quantum Espresso (QE) with the Perdew–Burke–Ernzerhof (PBE) type ultrasoft pseudopotential (USPP).^22,23 The Cu(100) surface consisting of 4 layers of (3 × 4) Cu atoms (48 atoms in total) and 10 Å of vacuum, was calculated with a kinetic energy for wavefunction cutoff of 57 Ry, charge density cutoff of 326 Ry and Gamma-centered 2 × 2 × 1 k-points mesh. The k-points mesh was chosen based on a convergence test which determined a Gamma-centered 2 × 2 × 1 mesh to be the most computationally efficient and accurate parameter for high throughput E_ads calculations (Fig. S1, ESI†). The convergence criteria was set to under 10⁻⁶ Ry. The Cu(100) surface was chosen for its activity, favored C₂ pathway for the CO₂RR and loose packing order of the surface. During geometry optimization, only the adsorbate (*COCOH) and top 2 layers were allowed to be freely relaxed, while the bottom 2 layers were fixed. The intention of fixing the lower layers was to simulate the bulk versus surface morphology of a BAC where the surface atoms were afforded greater degrees of freedom to relax compared to the bulk layer.²⁴ The exact adsorption energy of *COCOH can be defined as:

E_{ads, *COCOH} = E_{*COCOH/Cu alloy} – E_{Cu alloy} – E_*COCOH (1)

where E_{*COCOH/Cu alloy} is the total energy of an adsorbed *COCOH molecule on the Cu alloy surface; E_{Cu alloy} is the energy of Cu alloy slab; E_*COCOH is the energy of the isolated adsorbate *COCOH molecule.²⁵ Since the *COCOH is highly unstable in vacuum, the energy of E_*COCOH is not obtainable and was substituted as the vacuum energy of substituent molecules shown in eqn (2):^26,27

E_{ads, *COCOH} = E_{*COCOH/Cu alloy} – E_{Cu alloy} – [2*E_CO/vacuum – (1/2)*E_H2/vacuum] (2)

where E_CO/vacuum is the total energy of CO molecule in vacuum and E_H2/vacuum is the energy of a H₂ molecule in vacuum to ultimately calculate *COCOH adsorption energies.^28–31 When comparing the E_ads of *COCOH on pure Cu(100) calculated by other computational groups against this works method, the importance of adsorbate orientation becomes evident. There was a ∼0.8 eV difference in E_ads between monodentate and bidentate adsorption geometries (Fig. S2, ESI†).³² Literature reference for *COCOH adsorption is limited but the references available calculated the E_ads of *COCOH on Cu(100) through the typical slab model method with a monodentate *COCOH orientation (eqn (3)). This method was not used in order to specifically study the bidentate CO dimerization route towards *COCOH products.³²

E_{ads, *COCOH} = E_{*COCOH/Cu alloy} – E_{Cu alloy} – E_{*COCOH/vacuum} (3)

Additional charge density difference and Bader charge analysis calculations were performed on specific Os datapoints which exhibited special geometric configurations. These calculations were performed using the Vienna Ab initio Simulation Package (VASP) with a 4 × 4 × 1 k-points mesh and same pseudopotentials as the Quantum Espresso calculations. Bader charge analysis calculations were performed using the Henkelman group's publicly available scripts.

The models of Cu-based alloys were constructed by randomly changing the 13 Cu atoms nearest to the adsorbate into another metal element at 4 positions in the top layer and 9 positions in the second top layer with a 20% possibility (visualization shown in Fig. S3, ESI†). One of eight noble metals (Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) was selected to replace the Cu atoms at these 13 positions to generate the 1600 datapoint dataset. The Cu alloys investigated in the study were not given adsorbate migration or synthesis feasibility considerations. Datapoints were only removed if the adsorbate was unstable on the adsorption site.

To test the generalizability of the ML models, 3 tertiary alloy structures underwent the same *COCOH E_ads calculations as the BAC database. Since the atomic substitutions in the lattice were minimal compared to the overall system size, lattice parameter re-calculations were not performed and assumed to be the same as the BACs.

To draw a stronger correlation between *COCOH adsorption energies and BAC surfaces, reaction energy calculations were performed following the dimerized *CO hydrogenation route towards *COCOH. A weak, moderate, and strong E_ads BAC was randomly selected for free energy calculations done through VASP. The same k-points and potentials used in the charge density difference and Bader charge simulations were used for the reaction energy calculations.

2.2. Machine learning architecture and feature engineering

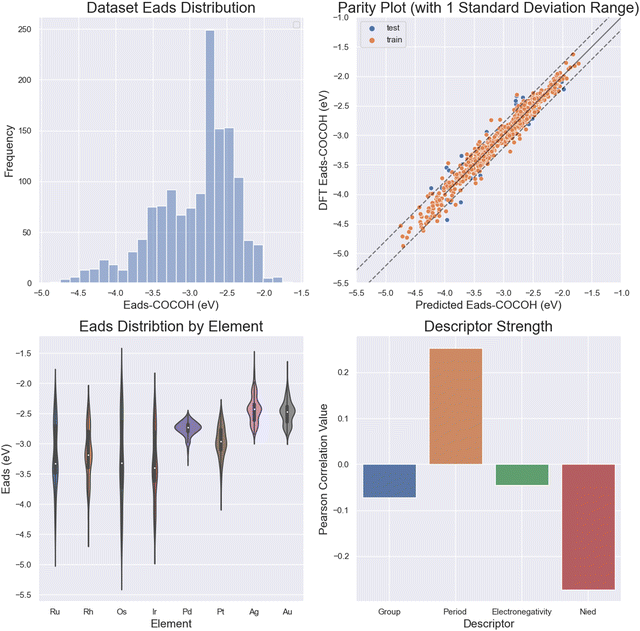
The target value predicted by the ML models was adsorption energy of *COCOH in eV. In order to accurately predict this label using a set of descriptors suitable for random datapoint generation, the selection of descriptors had to be purely chemical.^33–35 The reason DFT calculated descriptors could not be used is because the configurational space exploration required the random generation of datapoints with minimal computational cost. Thus, the group, period, electronegativity and unpaired d orbital electrons (N_ied) of the 13 nearest neighbor elements were selected. The addition of the novel d orbital electron descriptor improved MAE performance by 0.02–0.04 eV MAE and was shown to have the strongest correlation to E_ads of the 4 descriptors used. This was likely due to the deeper comprehension the ML models could derive on the ligand and ensemble effects in metal systems.^36–38

Based on previous ML publications for catalyst design, the following 8 popular regression models were evaluated for performance: linear regression (LR), kernel ridge regression (KRR), Gaussian kernel-based support vector machine (SVM), gradient boosted regression (GBR), decision tree (DT), random forest (RF), extra tree regression (E_tree), and neural network (NN).^33,39,40 The training, validation and test sets were split 80%/10%/10% using sklearn's train_test_split package. The performance and accuracy of the models in predicting the adsorption energies of the testing sets were evaluated using the mean absolute error (MAE) and root-mean-square error (RMSE) in eV between the predicted energies and true energies (Fig. S4, ESI†). Initial model exploration was conducted using scikit-learn and all machine learning prediction and configurational space exploration was done using TensorFlow 2.0 Keras API.^41,42 The best-performing models were a multilayer perceptron NN, extra tree, and random forest regressor which obtained accuracies on the scale of ∼0.095 ± 0.04 eV MAE. For all reported test set MAE values, the reported value was the average of 5 dataset shuffle and retrains. Feature importance analysis was performed based on the average correlation between a given descriptor and E_ads for each of the 13 atom locations.

The NN had 3 hidden layers with a total of 8204 trainable parameters. The models optimal MAE values were obtained with an Adam optimizer (learning rate = 0.01), dynamic learning rate callback, and mean-squared-error (MSE) loss function to minimize outlier inaccuracy. The model was trained for 3000 epochs and the lowest validation MAE model weights were then returned for future optimization. Each layer used a relu activation function aside for the final layer which utilized a linear activation function. The size of the NN was chosen through a parametric sweep of different NN architectures ranging from 1–4 hidden layers with 8–64 nodes each. The top performing models underwent hyperparameter optimization for later use in the optimization studies.

The Extra tree regressor used for fitting the dataset had no limit to the tree depth, a minimum of 2 samples to split a node, 100 trees, and was optimized for mean squared error. The random forest model used the same hyperparameters as the extra tree regressor.

For each model, the descriptor representation of each datapoint starts as a 2D array where each of the 13 rows represented one of the 13 nearest neighbor atoms and each of the 4 columns represented the corresponding atoms elemental descriptors. The order of the columns was group, period, electronegativity then N_ied. The 13 × 4 2D array would lastly be flattened into a 52 element vector for model training and prediction. This architecture allowed for rapid generation of random datapoints and extrapolation to newer material systems not apart of the original training set such as 3 element tertiary alloys.

To benchmark the descriptor based NN models against top performing graph based models, the Atomistic Line Graph Neural Network (ALIGNN) developed by K. Choudhary was trained on the dataset.⁴³ Default hyperparameters were utilized and all geometric structures were converted into VASP readable POSCARs for training.

2.3. Configurational space exploration for the discovery of optimal adsorption surfaces

Borrowing from the Monte Carlo idea of random sampling, this study obtained adsorption energy predictions of catalyst surfaces without extra DFT calculations through the use of a NN. 1000 random BAC's for each of the 8 element combinations were generated with the same method as the initial 1600 datapoint dataset. The 8000 newly generated surface predicted E_ads values are compiled in Fig. S5 (ESI†). This approach allowed the ML model to identify the ideal elements for BAC CO₂RR bidentate pathway.^16,19 The adsorption energy distribution for the predictions dataset resembled a normal distribution far more than the DFT calculated dataset due to the difference in sample size (<200 vs. 1000). Additionally, each binary alloy possessed a large peak at −2.8 eV which is a statistical artifact originating from the randomly generated structures of pure Cu possessing 0 atom substitutions.

Because the models were capable of performing E_ads predictions from descriptor based input structures without any DFT data required, the models generalizability and transferability were evaluated through an extrapolation study to 3 element tertiary alloys. The same random sampling method was used but for each randomly generated structure, 2 sequential random element substitutions would be performed instead of 1. 3 TACs predicted to have weak, moderate and strong E_ads were compared against DFT calculated E_ads values to gain a quantitative measurement of the NNs generalizability.

3. Results and discussion

3.1. Bidentate adsorption

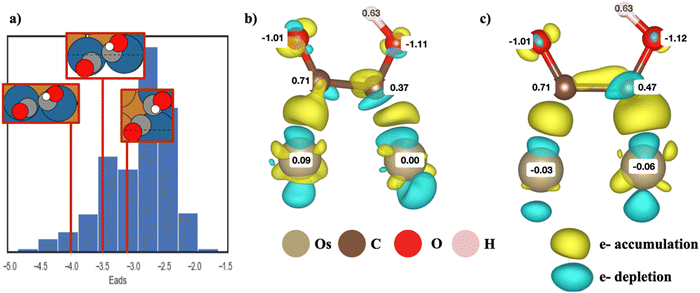
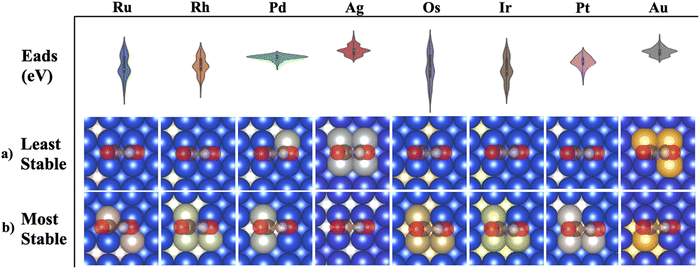
As shown in eqn (2), to obtain the adsorption energies of *COCOH on the Cu-based BAC, the energy of isolated adsorbate *COCOH (E_*COCOH), energy of gaseous H₂ (E_H2/vacuum) and energy of gaseous CO (E_CO/vacuum) were calculated. The resulting E_{ads, *COCOH} was within the range of −1.62 eV to −4.87 eV. A unique geometry arising from energy minimization occurred for the Cu/Ir, Cu/Os, Cu/Rh, Cu/Ru binary alloys (Fig. 1a). The *COCOH molecule has a 30–45 degree rotation between the CO bonds along the C–C axis. The exact angle between the dimers varied from datapoint to datapoint however there were 2 clear trends that emerged. Firstly, this geometric rotation only occurred when two non Cu atoms were adjacent to each other, directly below the *COCOH adsorbate and surrounded by mostly Cu. This is likely because the bidentate adsorption sites were ideal for C but not O and thus the bonds were rotated to obtain electron orbital stabilization from neighboring Cu atoms. Notably, the adsorption site atoms were the elements with the largest numbers of unpaired d orbital electrons, suggesting this non-planar geometry may be linked to the ensemble effect.

Fig. 1 (a) Top down view of unique *COCOH adsorption conformations on Cu/Os BACs relative to the adsorption energies, (b) charge density difference and Bader charge values of a non-planar *COCOH adsorbate, (c) charge density difference and Bader charge values of a typical planar *COCOH adsorbate.

Bader charge analysis and electron density differences revealed a unique electron depletion occurring on the C attached to OH compared to typical *COCOH geometries (Fig. 1b and c). Additionally, the substrate atoms directly below the adsorbate possessed more positive Bader charges as opposed to typical geometries which accumulated electron charge. The largest difference in Bader charges was observed on the C atom attached to OH which was 0.1 electrons less than typical geometry conformations. This electron accumulation was present for the majority of non-planar *COCOH adsorbates regardless of E_ads (Fig. S6, ESI†). The Adsorption energy of these sites varied significantly across the entire datasets E_ads range and the configurational space exploration considered these specific substrates as some of the more stable BACs possible for Ru, Rh, Ir, Os. When comparing the Bader charge difference of 3 non-planar *COCOH adsorbates to a planar *COCOH adsorbate, the non Cu atoms directly below the *COCOH molecule are observed to have the most significant positive charge difference (Fig. S7, ESI†). This charge is likely taken away from the C atom attached to OH, contributing to the non-planar conformation.

The distribution of E_ads for the different elements varied greatly and showed a strong correlation to the N_ied of the element Cu was combined with (Fig. 2).

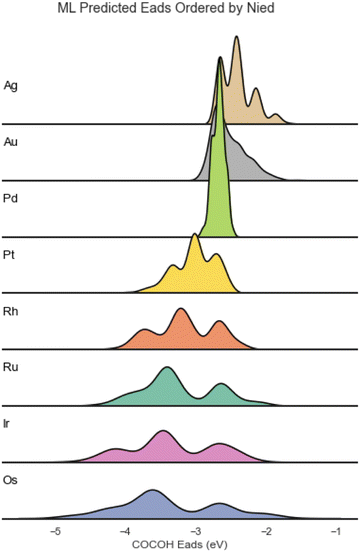Fig. 2 Adsorption energy distribution of the ML predicted BACs ordered from lowest N_ied count (top) to highest N_ied count (bottom).

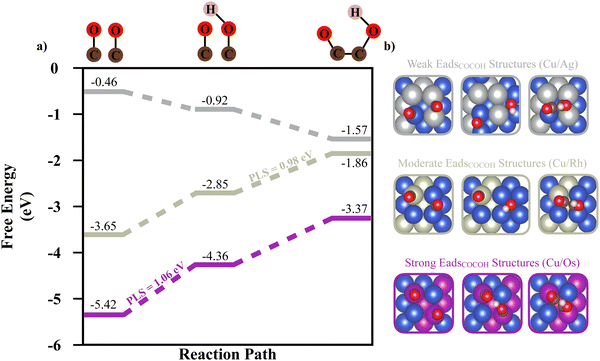
To link the adsorption energy of *COCOH to catalytic performance, reaction energy calculations conducted on 3 BAC systems composed of Cu/Ag, Cu/Rh, Cu/Os BAC with weak, moderate, and strong ML predicted E_ads values were studied. The strong correlation between unpaired d orbital electrons of the alloyed element and adsorption energy is also inversely present for reaction energy (Fig. 3a). Although the stronger adsorption energy BACs (such as Cu/Os) observe much less intermediate migration potentially leading to higher surface coverage and simultaneous adsorbate conversion, the potential limiting step (PLS) between dimerized CO adsorbates and dimerized CO/COH adsorbates is the largest of the 3 types of systems (1.06 eV) (Fig. 3a and b). The second largest PLS was observed in the moderate E_ads structure between the dimerized CO/COH to *COCOH step (0.98 eV). For the strong and moderate *COCOH E_ads structures, free energy calculations indicate dimerized CO is the most stable adsorbate intermediate whereas the weak E_ads structure becomes more stable as the C₂₊ reaction progressed towards *COCOH. This suggests the weak E_ads structures are optimal for dimerized CO conversion to *COCOH (Fig. 3a). This type of ideal reaction surface is likely related to the large migration both CO adsorbates undergo for hydrogenation and ultimately bidentate bonding. The hydrogenation of CO for the weak E_ads structure migrates toward a hollow site before ultimately forming bidentate *COCOH without requiring significant energy or re-arrangement.

Fig. 3 (a) Free energy along the dimerized CO hydrogenation reaction pathway towards *COCOH with the potential limiting step indicated. The grey pathway corresponds to a randomly sampled weak *COCOH E_ads BAC (Cu/Ag), the metallic grey pathway is the moderate *COCOH E_ads BAC (Cu/Rh) and the purple pathway is the strong *COCOH E_ads BAC (Cu/Os). (b) The adsorbate migration associated with each step of the reaction pathway shown in (a).

3.2. Machine learning prediction of E_ads

The multilayer perceptron NN showed great accuracy when tasked with predicting the adsorption energy of *COCOH across a wide range of values (0.095 eV MAE) (Fig. 4a and b). The ML models also gained the majority of its insight from the number of unpaired d orbital electrons (Os, Ir, Ru, Rh) (Fig. 4c). The strong influence of the unpaired d orbital electron count is best demonstrated by performing a descriptor correlation to E_ads. By taking the average correlation between each descriptor for each of the 13 atoms, it is revealed that N_ied had the largest correlation followed by period, group and electronegativity (Fig. 4d).

Fig. 4 (a) Adsorption energy distribution of the entire *COCOH dataset, (b) parity plot with dotted lines outlining 1 standard deviation error, (c) adsorption energy distribution by element Cu is alloyed with, (d) Pearson correlation value of each descriptor averaged across all 13 nearest atoms to the adsorbate.

Due to the outstanding accuracy of the NN and its ability to accurately predict outliers, this model can be considered an alternative option to predict BAC adsorption energies that is magnitudes cheaper and faster from a computational perspective than DFT. This model can also be applied with minimal preparation on other systems, serving as a more universal and explorative tool in early stage catalyst design than simulations or experimentation for BAC materials.³³

When compared against the ALIGNN model, the descriptor based NN performed comparably. The ALIGNN model obtained an MAE of 0.06 eV MAE. This improvement likely came from the model consideration of adsorbate bond angles and interatomic distance descriptors embedded in the graph neural networks edges. The ∼0.04 eV difference suggests the descriptor based NN successfully captured the majority of catalytic dynamics which can be derived from the material systems chemical properties. Although the ALIGNN model yielded a more accurate prediction, this model was ultimately not used because of graph neural networks incapability to perform this works exhaustive compositional space exploration. Since graph neural networks consider atomic distances, the inputs require information gained from DFT minimized structures which makes random datapoint generation exponentially more costly than the descriptor based array method detailed in Section 2.3.

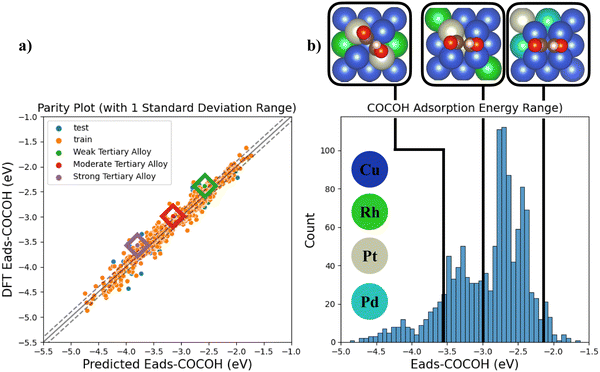
Since the descriptor based NN was shown to capture the majority of the chemical factors influencing E_ads-*COCOH with high data efficiency (Fig. S8, ESI†), 3 additional TACs were simulated and compared against the NNs E_ads prediction (Fig. 5a). The 3 sample points were chosen randomly from 3 ranges of adsorption energies (weak, moderate, strong E_ads) to quantify the models ability to extrapolate to more complex systems across the entire range of *COCOH adsorption energies. The absolute error (in eV) for the predicted adsorption energies compared to DFT values was 0.18, 0.15 and 0.22 eV for the weak, moderate and strong adsorption energy TACs. The weak TAC possessed 2 Pd substitutions and 2 Pt substitutions whereas the moderate and strong TACs possessed 2 Rh and 2 Pt substitutions (Fig. 5b). For each structure, the model showed a consistent small bias towards over-estimating *COCOH stability but can still be considered highly transferable due to the low error associated with each prediction. The models transferability is further highlighted by the strong E_ads TACs geometric configuration. The majority of the training dataset had the *COCOH adsorbate resting on dual bridge sites but with the strong E_ads TAC, the adsorbate rotated towards dual top site adsorptions. Although this rotation resulted in the highest absolute error, the difference between this error and the models test set MAE is ∼0.1 eV which is acceptably small considering the molecular rotation the adsorbate underwent.

Fig. 5 (a) Parity Plot of all BAC test points and the 3 tertiary alloy systems (b) DFT calculated *COCOH E_ads distribution with the 3 tertiary alloy systems visualized at their respective DFT calculate E_ads values.

3.3. Optimal machine learning predicted surfaces

Au and Ag possessed the weakest adsorption surfaces on average and were the only alloys to have an average adsorption above −2.55 eV in addition to having some of the smallest ranges of adsorption energies (Table 1). For the bidentate pathway, these elements are likely the best candidates according to the reaction pathway shown in Fig. 3b. According to L. Ou, the co adsorption of COCO* and H* on Cu(100) is −4.12 eV and the E_ads of *COCOH on Cu(100) is −3.85 eV.³² To favor the formation of *COCOH over co-adsorption, it is likely necessary to have a BAC with weaker CO E_ads so that the endergonic step of hydrogenating dimerized CO does not slow reaction kinetics. For the 5 BACs with lower N_ied counts, the mean *COCOH adsorption energies ranged from (−2.67 eV) – (−3.15 eV) with similar ranges and possessed a correlation to the amount of unpaired d orbital electrons the alloyed element possessed, making them strong BAC candidates for optimal *COCOH formation. For the 3 elements which possessed the most stable E_ads structures and highest N_ied counts (Os, Ir, Ru), the substitution locations which resulted in the most negative adsorption energy predictions were almost identical (Fig. 6a). The maximized surfaces all possessed 2–3 atom nano-islands on the surface beneath *COCOH with a large amount of subsurface alloyed elements. This suggests that the adsorption of *COCOH onto a highly stable BACs is likely influenced by high energy valence electron interactions of the subsurface atoms donating to the top site surface atoms in order to produce favorable bidentate adsorption configurations for *COCOH molecules. For the other moderate-high N_ied count BACs, the most stable E_ads configurations were similar. The lowest N_ied count BACs (Cu/Au and Cu/Ag) had inverse influences on *COCOH stability. For these BACs, the most stable configurations arose with minimal surface islands and a smaller amount of subsurface substitutions (Fig. 6b). The least stable configurations out of all BACs came from large nano-islands of Ag/Au, suggesting these elements may be suitable additives if the objective is to destabilize the adsorption of *COCOH and facilitate conversion of dimerized CO towards *COCOH.

Table 1 ML prediction statistics and relation to unpaired d orbital electrons

Element	Mean (eV)	Range (eV)	Most stable datapoint (eV)	Number of unpaired d orbital electrons
Ru	−3.23	2.55	−4.50	3
Rh	−3.15	1.99	−4.27	2
Ag	−2.40	1.09	−2.72	0
Au	−2.52	1.45	−2.98	0
Ir	−3.33	2.79	−4.84	3
Os	−3.38	3.52	−4.98	4
Pd	−2.67	0.54	−2.97	0
Pt	−3.01	1.55	−4.02	1

---

Fig. 6 (a) ML predicted surface compositions for lowest possible predicted adsorption energy. Blue atoms are Cu, other atoms are labeled above the composition (b) ML predicted surface compositions for highest possible predicted adsorption energy. Blue atoms are Cu, other atoms are labeled above the composition.

4. Conclusions

In the current work, a machine learning configurational space exploration framework was discussed for the bidentate electrocatalytic CO₂RR on Cu based BACs. Using DFT, the adsorption energies of *COCOH on 1600 randomly configured Cu-based SAA surfaces were calculated to use as a dataset for supervised ML models. 8 regression models with 80/10/10 train/val/test splits with 3 chemical descriptors and 1 quantum descriptor were evaluated. Analysis and interpretation of the top performing NN predicted structures provided 3 key findings:

1. Cu/Au and Cu/Ag alloys have the weakest adsorption energy on average for *COCOH and the best reaction energy pathway for C₂₊ products. Although Au/Ag are costly, it is possible to maximize catalytic efficiency of the BACs by synthesizing nano-islands of the metal on the surface.

2. Metals with high counts of unpaired d orbital electrons are the most stable surfaces for *COCOH with moderate PLS values for the bidentate CO₂RR pathway. The strongest adsorption surfaces came from Ru/Ir/Os BACs with 2-3 atom nano-islands directly beneath the adsorbate with high densities of substitutions on the subsurfaces.

3. There is a clear correlation with N_ied and E_{ads *COCOH}. The relation between N_ied and reaction energy steps is inversely related to E_{ads *COCOH} and the top performing BACs possessed the lowest amounts of unpaired d orbital electrons which resulted in unique surfaces where *COCOH was more energetically favorable than dimerized CO.

This work provided the first ever ML informed look into BAC design for optimal *COCOH adsorption energies. Having the current work as a major step towards the effective conversion of CO₂ into hydrocarbon fuels, additional studies are still necessary. Future efforts should be directed towards studying the top performing BACs (Cu/Au, Cu/Ag) in addition to the more complex TACs studied in this work. This future direction will provide insight into reducing the material cost of bidentate electrocatalysts along with understanding the role subsurface alloying plays in improving electrocatalytic performance.

Author contributions

C. V. Singh, G. Chen, A. Xu, Z. Lu conceived, designed and simulated the quantum espresso dataset. Z. Gariepy performed all data anlytics, machine learning, DFT VASP anaylsis. Z. Gariepy, Z. W. Chen and C. V. Singh wrote the paper. All authors discussed and revised the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support from the Nature Science and Engineer Research Council of Canada (NSERC), University of Toronto and National Research Council (NRC). We also acknowledge Compute Ontario and Compute Canada for providing computing resources at the SciNet, CalculQuebec.

References

1. G.-R. Walther, et al., Ecological responses to recent climate change, Nature, 2002, 416, 389–395,  DOI:10.1038/416389a.
2. J. Melillo et al. Government Review Draft Third NCA Front Matter. U.S Global Change Research Program: US Government; 2013. 10p. Report No.: 3.
3. A. Firoozabadi and P. C. Myint, Prospects for subsurface CO₂ sequestration, AIChE J., 2010, 56(6), 1398–1405,  DOI:10.1002/aic.12287.
4. S. C. Frerich, Biopolymer foaming with supercritical CO²⁻-Thermodynamics, foaming behaviour and mechanical characteristics, J. Supercrit. Fluids, 2015, 96, 349–358,  DOI:10.1016/j.supflu.2014.09.043.
5. C. Graves, S. D. Ebbesen, M. Mogensen and K. S. Lackner, Sustainable hydrocarbon fuels by recycling CO₂ and H₂O with renewable or nuclear energy, Renewable Sustainable Energy Rev., 2011, 15(1), 1–23,  DOI:10.1016/j.rser.2010.07.014.
6. O. S. Bushuyev, et al., What Should We Make with CO₂ and How Can We Make It?, Joule, 2018, 2(5), 825–832,  DOI:10.1016/j.joule.2017.09.003.
7. J. Fernández-González, M. Rumayor, A. Domínguez-Ramos and Á. Irabien, CO₂ electroreduction: Sustainability analysis of the renewable synthetic natural gas, Int. J. Greenhouse Gas Control, 2022, 114,  DOI:10.1016/j.ijggc.2021.103549.
8. J. Ager and A. Lapkin, Chemical storage of renewable energy, Science, 2018, 360(6390), 706–707,  DOI:10.1126/science.aat1983.
9. X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Understanding trends in electrochemical carbon dioxide reduction rates, Nat. Commun., 2017, 8,  DOI:10.1038/ncomms15438.
10. A. Woldu, et al., Electrochemical CO₂ reduction (CO₂RR) to multi-carbon products over copper-based catalysts, Coord. Chem. Rev., 2021, 454,  DOI:10.1016/j.ccr.2021.214340.
11. C. Wang, C. Zhu, M. Zhang, Y. Geng and Z. Su, Copper Dimer Anchored in g-CN Monolayer as an Efficient Electrocatalyst for CO₂ Reduction Reaction: A Computational Study, Adv. Theory Simul., 2020, 3(12) DOI:10.1002/adts.202000218.
12. A. J. Garza, A. T. Bell and M. Head-Gordon, Mechanism of CO₂ Reduction at Copper Surfaces: Pathways to C₂ Products, ACS Catal., 2018, 8(2), 1490–1499,  DOI:10.1021/acscatal.7b03477.
13. W. Ma, X. He, W. Wang, S. Xie, Q. Zhang and Y. Wang, Electrocatalytic reduction of CO₂ and CO to multi-carbon compounds over Cu-based catalysts, Chem. Soc. Rev., 2021, 50, 12897–12914,  10.1039/D1CS00535A Available from.
14. J. H. Montoya, C. Shi, K. Chan and J. K. Nørskov, Theoretical insights into a CO dimerization mechanism in CO₂ electroreduction, J. Phys. Chem. Lett., 2015, 6(11), 2032–2037,  DOI:10.1021/acs.jpclett.5b00722.
15. B. Hammer and J. B. K. Norskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343(3), 211–220,  DOI:10.1016/0039-6028(96)80007-0.
16. J. Greeley, J. K. Nørskov and M. Mavrikakis, Electronic structure and catalysis on metal surfaces, Annu. Rev. Phys. Chem., 2002, 53, 319–348,  DOI:10.1146/annurev.physchem.53.100301.131630.
17. F. Gao and D. W. Goodman, Pd–Au bimetallic catalysts: Understanding alloy effects from planar models and (supported) nanoparticles, Chem. Soc. Rev., 2012, 41(24), 8009–8020,  10.1039/c2cs35160a.
18. F. R. Lucci, T. J. Lawton, A. Pronschinske and E. C. H. Sykes, Atomic scale surface structure of Pt/Cu(111) surface alloys, J. Phys. Chem. C, 2014, 118(6), 3015–3022,  DOI:10.1021/jp405254z.
19. P. Liu and J. K. Nørskov, Ligand and ensemble effects in adsorption on alloy surfaces, Phys. Chem. Chem. Phys., 2001, 3(17), 3814–3818,  10.1039/b103525h..
20. M. Zhong, et al., Accelerated discovery of CO₂ electrocatalysts using active machine learning, Nature, 2020, 581(7807), 178–183,  DOI:10.1038/s41586-020-2242-8.
21. M. Xing, Y. Zhang, S. Li, H. He and S. Sun, Prediction of Carbon Dioxide Reduction Catalyst Using Machine Learning with a Few-Feature Model: WLEDZ, J. Phys. Chem. C, 2022, 126(40), 17025–17035,  DOI:10.1021/acs.jpcc.2c02161.
22. P. Giannozzi, J. Phys.: Condens. Matter, 2009, 21, 395502.
23. M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange–correlation functional, J. Chem. Phys., 1999, 110(11), 5029–5036,  DOI:10.1063/1.478401.
24. Y. F. Zhukovskii, et al., Bulk and surface properties of metallic aluminium: DFT simulations, Comput. Model. Simul. Eng., 2002, 6(1), 7–28 Available from.
25. S. Hanselman, M. T. M. Koper and F. Calle-Vallejo, Computational Comparison of Late Transition Metal (100) Surfaces for the Electrocatalytic Reduction of CO to C2 Species, ACS Energy Lett., 2018, 3(5), 1062–1067,  DOI:10.1021/acsenergylett.8b00326.
26. X. Zhi, Y. Jiao, Y. Zheng, A. Vasileff and S. Z. Qiao, Selectivity roadmap for electrochemical CO₂ reduction on copper-based alloy catalysts, Nano Energy, 2020, 71,  DOI:10.1016/j.nanoen.2020.104601.
27. L. Ou, Z. He, H. Yang and Y. Chen, Theoretical Insights into Potential-Dependent C-C Bond Formation Mechanisms during CO₂ Electroreduction into C₂ Products on Cu(100) at Simulated Electrochemical Interfaces, ACS Omega, 2021, 6(28), 17839–17847,  DOI:10.1021/acsomega.1c01062.
28. X. Song, H. Zhang, Y. Yang, B. Zang., M. Zuo, X. Cao, J. Sun, C. Lin, X. Li and Z. Jiang, Bifunctional Nitrogen and Cobalt Codoped Hollow Carbon for Electrochemical Syngas Production, Adv. Sci., 2018, 5(7) DOI:10.1002/advs.201800177.
29. Q. Zhao, J. M. P. Martirez and E. A. Carter, Revisiting Understanding of Electrochemical CO₂ Reduction on Cu(111): Competing Proton-Coupled Electron Transfer Reaction Mechanisms Revealed by Embedded Correlated Wavefunction Theory, J. Am. Chem. Soc., 2021, 143(16), 6152–6164,  DOI:10.1021/jacs.1c00880.
30. C. Shi, H. A. Hansen, A. C. Lausche and J. K. Nørskov, Trends in electrochemical CO₂ reduction activity for open and close-packed metal surfaces, Phys. Chem. Chem. Phys., 2014, 16(10), 4720–4727,  10.1039/c3cp54822h.
31. Q. Wu, et al., A CO₂ adsorption dominated carbon defect-based electrocatalyst for efficient carbon dioxide reduction, J. Mater. Chem. A, 2020, 8(3), 1205–1211,  10.1039/c9ta11473d.
32. L. Ou, W. Long, Y. Chen and J. Jin, New reduction mechanism of CO dimer by hydrogenation to C₂H₄ on a Cu(100) surface: theoretical insight into the kinetics of the elementary steps, RSC Adv., 2015, 5(117), 96281–96289,  10.1039/c5ra15905a.
33. Z. Lu, Z. W. Chen and C. V. Singh, Neural Network-Assisted Development of High-Entropy Alloy Catalysts: Decoupling Ligand and Coordination Effects, Matter, 2020, 3(4), 1318–1333,  DOI:10.1016/j.matt.2020.07.029.
34. T. Toyao, K. Suzuki, S. Kikuchi, S. Takakusagi, K. I. Shimizu and I. Takigawa, Toward Effective Utilization of Methane: Machine Learning Prediction of Adsorption Energies on Metal Alloys, J. Phys. Chem. C, 2018, 122(15), 8315–8326,  DOI:10.1021/acs.jpcc.7b12670.
35. Z. W. Chen, Z. Lu, L. X. Chen, M. Jiang, D. Chen and C. V. Singh, Machine-learning-accelerated discovery of single-atom catalysts based on bidirectional activation mechanism, Chem Catal., 2021, 1(1), 183–195,  DOI:10.1016/j.checat.2021.03.003.
36. S. Back, J. Yoon, N. Tian, W. Zhong, K. Tran and Z. W. Ulissi, Convolutional Neural Network of Atomic Surface Structures to Predict Binding Energies for High-Throughput Screening of Catalysts, J. Phys. Chem. Lett., 2019, 10(15), 4401–4408,  DOI:10.1021/acs.jpclett.9b01428.
37. A. J. Chowdhury, W. Yang, K. E. Abdelfatah, M. Zare, A. Heyden and G. A. Terejanu, A Multiple Filter Based Neural Network Approach to the Extrapolation of Adsorption Energies on Metal Surfaces for Catalysis Applications, J. Chem. Theory Comput., 2020, 16(2), 1105–1114,  DOI:10.1021/acs.jctc.9b00986.
38. Z. Lu, S. Yadav and C. V. Singh, Predicting aggregation energy for single atom bimetallic catalysts on clean and O* adsorbed surfaces through machine learning models, Catal. Sci. Technol., 2020, 10(1), 86–98,  10.1039/c9cy02070e.
39. A. J. Chowdhury, W. Yang, E. Walker, O. Mamun, A. Heyden and G. A. Terejanu, Prediction of Adsorption Energies for Chemical Species on Metal Catalyst Surfaces Using Machine Learning, J. Phys. Chem. C, 2018, 122(49), 28142–28150,  DOI:10.1021/acs.jpcc.8b09284.
40. S. Nayak, S. Bhattacharjee, J. H. Choi and S. C. Lee, Machine Learning and Scaling Laws for Prediction of Accurate Adsorption Energy, J. Phys. Chem., 2020, 124(1), 247–254,  DOI:10.1021/acs.jpca.9b07569.
41. Martin Abadi, P. Barham, J. Chen, Z. Chen, A. Davis and J. Dean, et al. Tensorflow: A system for large-scale machine learning, Symposium on Operating Systems Design and Implementation, 2016, 265–283.
42. F. Pedrogosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 2825–2830.
43. K. Choudhary and B. Decost, Atomistic Line Graph Neural Network for Improved Materials Property Predictions, npj Comput. Mater., 2021, 7, 185,  DOI:10.1038/s41524-021-00650-1.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ya00316c

---