Open Access Article
Open Access ArticleOn the concept of metal–hydrogen peroxide batteries: improvement over metal–air batteries?†
Kai S.
Exner
 abc
abc
aUniversity Duisburg-Essen, Faculty of Chemistry, Theoretical Inorganic Chemistry, Universitätsstraße 5, 45141, Essen, Germany. E-mail: kai.exner@uni-due.de
bCluster of Excellence RESOLV, 44801, Bochum, Germany
cCenter for Nanointegration (CENIDE) Duisburg-Essen, 47057, Duisburg, Germany
First published on 14th February 2023
Abstract
While metal–air batteries (MABs) are considered to outperform lithium-ion batteries for energy-storage applications, the sluggish bifunctional oxygen electrocatalysis at the cathode of MABs still represents a major bottleneck that severely limits efficiency. Recently, it was motivated by means of electronic structure calculations to replace the oxygen redox chemistry at the cathode of MABs by the redox chemistry of peroxide, considering that the latter is governed by kinetically facile two-electron processes. Herein, two different concepts of rechargeable metal–hydrogen peroxide batteries are investigated, consisting of either the peroxide reduction (PRR) and peroxide formation (PFR) reactions or the two-electron oxygen reduction (ORR) and two-electron oxygen evolution (OER) reactions at the cathode. Applying a dedicated thermodynamic framework in the spirit of the descriptor Gmax(U), a potential-dependent activity measure that factors overpotential and kinetic effects into the evaluation of adsorption free energies, generalized volcano plots for the PRR, PFR, two-electron ORR, and two-electron OER as well as their competing side reactions are derived. It is illustrated that for the PFR/PRR, selectivity can be steered toward the desired product without loss in activity whereas for the two-electron ORR/OER, a trade-off between activity and selectivity is encountered. The derived volcano models in this contribution may aid the search for potential material motifs for the PFR/PRR and the two-electron ORR/OER by calculations in the framework of electronic structure theory.
1 Introduction
Metal–air batteries (MABs) are discussed as a promising concept for energy storage with the aptitude to replace lithium-ion batteries (LIBs) in the long run thanks to their higher energy density.1–4 The application of MABs is still in its infancy and severe performance losses are encountered though, which are majorly related to oxygen reduction (ORR) and oxygen evolution (OER) taking place during discharge and charge at the cathode of this device, respectively.5,6| 4e− ORR: O2 + 4H+ + 4e− → 2H2O, U0 = 1.23 V vs. reversible hydrogen electrode (RHE) | (1) |
| 4e− OER: 2H2O → O2 + 4H+ + 4e−, U0 = 1.23 V vs. RHE | (2) |
Both the ORR and OER are kinetically restrained since significant overpotentials of several hundred millivolts are required to obtain current densities on the order of mA cm−2.7 The reason for the sluggish kinetics on a molecular level is traced to a scaling relation between the *OOH and *OH intermediates in the reaction mechanisms of the ORR and OER.8–10
As is evident from Fig. 1, rechargeable MABs suffer from a huge potential window between the ORR and OER, which can be quantified by experimental cyclic voltammetry referring to the so-called bifunctional index (BI).11 So far, it appears to be a formidable task to obtain enhanced bifunctional performance in oxygen electrocatalysis. Even if advanced materials with two different active sites for the ORR and OER have been synthesized,12 hitherto, the BI could not be reduced below 0.60 V, and this value is still above the theoretical limit despite scaling relations.13–15
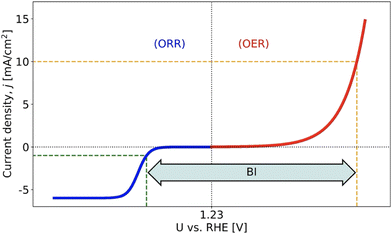 | ||
| Fig. 1 Scheme to illustrate the bifunctional index (BI) of the oxygen electrocatalysis, which can be assessed by the difference in electrode potentials between jOER = 10 mA cm−2 and jORR = −1 mA cm−2. Experimentally, BI values larger than 0.60 V refer to the state-of-the-art, causing severe performance losses for metal–air batteries. Figure reproduced from the work of Razzaq et al.,15 Copyright 2022, The Authors. | ||
A promising opportunity to overcome large BI values refers to the redox chemistry of hydrogen peroxide (H2O2), as discussed by Siahrostami from the perspective of theory in a recent article.16 The main idea is that the redox processes involving hydrogen peroxide consist only of two proton–electron transfer steps, thus resulting in smaller overpotentials compared to the four-electron bifunctional oxygen electrocatalysis.17,18 While the reduction of the potential window for rechargeable MABs is desirable, the introduction of H2O2 in these devices is accompanied by a selectivity challenge, considering that the redox chemistry of the two-electron peroxide processes is thermodynamically unfavored compared to the ORR and OER. Two different situations are conceivable for the notion of rechargeable metal–hydrogen peroxide batteries:
(a) Peroxide reduction (PRR) and peroxide formation (PFR) reactions:
| 2e− PRR: H2O2 + 2H+ + 2e− → 2H2O, U0 = 1.76 V vs. RHE (discharge) | (3) |
| 2e− PFR: 2H2O → H2O2 + 2H+ + 2e−, U0 = 1.76 V vs. RHE (charge) | (4) |
(b) Two-electron ORR and two-electron OER:
| 2e− ORR: O2 + 2H+ + 2e− → H2O2, U0 = 0.70 V vs. RHE (discharge) | (5) |
| 2e− OER: H2O2 → O2 + 2H+ + 2e−, U0 = 0.70 V vs. RHE (charge) | (6) |
In the present work, the two different scenarios of metal–hydrogen peroxide batteries are evaluated by means of volcano analyses and are critically compared to the bifunctional oxygen electrocatalysis of MABs. A particular focus is set on the selectivity aspect of the competing peroxide and oxygen redox chemistry by identifying the optimum binding strength referring to the descriptor ΔG1 = ΔG(*OH) for the two different battery concepts. Please note that the present article does not discuss the anode of MABs or metal–hydrogen peroxide batteries where intercalation processes occur, but rather the focus is on the cathode to spur new conceptual ideas aiming to overcome the long-standing issues with MABs.
2 Method
The presented modeling approach relies on an in-house methodology that connects the adsorption free energies of the intermediate species in the electrocatalytic processes of eqn (1)–(6) to electrocatalytic activity by the descriptor Gmax(η),19,20 in the following denoted as Gmax(U), where U indicates the applied electrode potential on the RHE scale. The following three reaction intermediates are considered in the approach: *OOH, *O, and *OH.21–23The pathways of the oxygen and hydrogen peroxide electrocatalysis are thoroughly evaluated by making use of an extended set of reaction mechanisms.24–27 For the 4e− ORR, the mononuclear, electrochemical *OOH dissociation, and chemical *OOH dissociation mechanisms are accounted for as these pathways have been shown to govern the volcano curve of the ORR.28,29 The 4e− OER is described by the mononuclear and *OO⋯OO* recombination mechanisms, as recently reported by Binninger et al.,30 emphasizing that the *OO⋯OO* recombination mechanism is energetically favored over the mononuclear description at the volcano apex.31 For the PRR, PFR, 2e− ORR, and 2e− OER a single mechanism with one intermediate is taken into account, following previous theoretical works on the same topic.32–35 The elementary steps of all mechanistic pathways are summarized in the ESI,† Section S1.
The free-energy changes of the elementary steps are analyzed by a rigorous thermodynamic framework in that they are related to two descriptors, namely the adsorption free energy of the *OH intermediate, ΔG1, and the scaling-relation intercept, SRI, between the *OH and *OOH adsorbates.28,29,31 This procedure is exemplary demonstrated for the mononuclear OER mechanism in the following:
| M + H2O → M–OH + H+ + e− ΔG1 | (7) |
| M–OH → M–O + H+ + e− ΔG2 | (8) |
| M–O + H2O → M–OOH + H+ + e− ΔG3 | (9) |
| M–OOH → M + O2(g) + H+ + e− ΔG4 | (10) |
The four OER free-energy changes of eqn (7)–(10) meet the criterion of eqn (11):
| ΔG1 + ΔG2 + ΔG3 + ΔG4 = +4.92 eV @U = 0 V vs. RHE | (11) |
Therefore, the free energies of the reaction intermediates can be expressed by eqn (12)–(16):
| GM(U) = 0 | (12) |
| GM–OH(U) = ΔG1 − 1 × e × U | (13) |
| GM–O(U) = ΔG1 + ΔG2 − 2 × e × U | (14) |
| GM–OOH(U) = ΔG1 + ΔG2 + ΔG3 − 3 × e × U | (15) |
| GM+O2(U) = + 4.92 eV − 4 × e × U | (16) |
By considering the scaling relations of eqn (17) and (18),
| ΔG2 + ΔG3 = SRI | (17) |
| ΔG2 = 2 × ΔG1 | (18) |
We obtain for the energetics of the intermediate states:
| GM(U) = 0 | (19) |
| GM–OH(U) = ΔG1 − 1 × e × U | (20) |
| GM–O(U) = 3 × ΔG1 − 2 × e × U | (21) |
| GM–OOH(U) = ΔG1 + SRI − 3 × e × U | (22) |
| GM+O2(U) = +4.92 eV − 4 × e × U | (23) |
Eqn (19)–(23) indicate that the energetics of the reaction intermediates depend on the free-energy change ΔG1 and the applied electrode potential, U, if the SRI is fixed in the analysis. Different SRI values, ranging from 2.8 eV to 3.2 eV in agreement with the recent literature,36–38 are considered in this approach. For the free-energy change ΔG1, a basis set is defined by referring to the work by Rossmeisl and coworkers, indicating that basically all relevant materials to the oxygen electrocatalysis are within ΔG1 = [−0.50, 2.50] eV.39 Therefore, this free-energy regime with a step size of 0.01 eV is used to compile a volcano curve at a predefined applied electrode potential that is related to the respective equilibrium potential of the peroxide redox processes (cf.eqn (3)–(6)). The thermodynamic treatment for all mechanistic pathways of the ORR, OER, PRR, PFR, two-electron ORR, and two-electron OER is given in Section S2 of the ESI.†
The descriptor Gmax(U) is assessed as an activity measure in the volcano curves to comprehend the electrocatalytic activity by means of the reaction intermediates.19,20 Please note that the determination of the electrocatalytic activity by Gmax(U) goes far beyond the conventionally applied limiting potential analysis, UL, because overpotential and kinetic effects are qualitatively included in the evaluation of Gmax(U) whereas this statement does not hold true for the descriptor UL. Further implications of the descriptor Gmax(U) are discussed in a recent perspective article by the author.40 The concept of Gmax(U) relies on a free-energy span model41,42 by extracting the largest free-energy difference between the intermediate states at a given target electrode potential. Eqn (24) illustrates that for the mononuclear OER mechanism, nine free-energy spans are conceivable:
| GM–OH(U) − GM(U); GM–O(U) − GM(U); GM–OOH(U) − GM(U); GM–O(U) − GM–OH(U); GM–OOH(U) − GM–OH(U); GM+O2(U) − GM–OH(U); GM–OOH(U) − GM–O(U); GM+O2(U) − GM–O(U); GM+O2(U) − GM–OOH(U) | (24) |
The largest free-energy difference among the set of available spans governs the activity measure Gmax(U):
| Gmax(U) = max{GM–OH(U) − GM(U); GM–O(U) − GM(U); GM–OOH(U) − GM(U); GM–O(U) − GM–OH(U); GM–OOH(U) − GM–OH(U); GM+O2(U) − GM–OH(U); GM–OOH(U) − GM–O(U); GM+O2(U) − GM–O(U); GM+O2(U) − GM–OOH(U)} | (25) |
The free-energy spans for the mechanistic pathways of the ORR, OER, PRR, PFR, two-electron ORR, and two-electron OER, which culminate in the determination of Gmax(U), are summarized in Section S3 of the ESI.†
Based on the above summary, the volcano curves discussed in the next section can be reproduced. Yet, I would like to point out a few caveats of the presented approach:
(i) While the scaling relation between the *OH and *OOH intermediates is robust and well accepted, the *OH vs. *O scaling is much less pronounced.9,39,43 Therefore, in Section S4 of the ESI,† a sensitivity analysis of the *OH vs. *O scaling relation is provided, indicating that the main results of this study are not prone to change when the energetics of the *O and *OH intermediates are altered to a reasonable extent.
(ii) Volcano curves are constructed at the equilibrium potential of the peroxide redox processes, that is, U = 1.76 V vs. RHE or U = 0.70 V vs. RHE. Electrocatalytic turnover, however, can only be obtained if sufficiently large cathodic or anodic overpotentials are applied. This implies that the cathodic PRR is operative at U < 1.76 V vs. RHE whereas the anodic PFR occurs for U > 1.76 V vs. RHE. Similarly, the 2e− ORR and 2e− OER commence for U < 0.70 V vs. RHE and U > 0.70 V vs. RHE, respectively. Given that the descriptor Gmax(U) is a potential-dependent activity measure, the presented analysis can also be conducted for non-equilibrium conditions, in contrast to the conventionally applied descriptor UL. In Section S5 of the ESI,† potential-dependent volcano plots in the approximation of Gmax(U) are compiled, indicating that the main conclusions of this study remains unchanged even if non-equilibrium conditions are considered.
(iii) The performance of electrode materials in MABs majorly depends on the chosen electrolyte solution, given that besides aqueous alkaline solutions also aprotic solvents are discussed in the literature.44,45 We do not model electrolyte effects explicitly, emphasizing that the contemplation of different solvents goes far beyond the scope of the present study. The chosen input parameters for the volcano models (SRI and basis set of ΔG1) are based on electronic structure calculations in the density functional theory approximation, using either gas phase or implicit solvation schemes.39 These computational tools are best referred to the case of aqueous MABs, indicating that the obtained results cannot be directly transferred to aprotic solvents.
3 Results and discussion
3.1 PRR and PFR
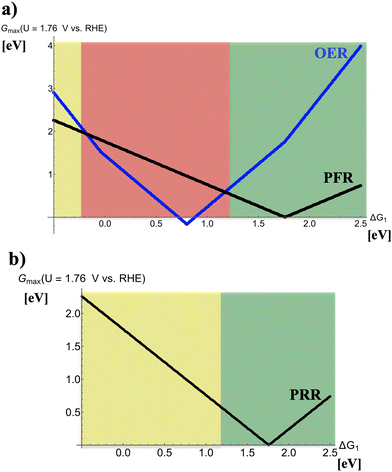
Fig. 2 depicts volcano curves for the PRR and PFR at U = 1.76 V vs. RHE. While panel (a) indicates the anodic process during charge of the device, thereby recalling that the PFR is accompanied by the (unwanted) 4e− OER, panel (b) refers to the PRR during discharge. Three different regions are marked in Fig. 2a by dissimilar colors:(i) −0.5 eV < ΔG1 < −0.25 eV (yellow): the volcano curve reveals that the electrocatalytic activity for the PFR exceeds that of the OER, indicating that the selectivity is in favor of forming H2O2. However, electrode materials at the left leg of the volcano are not reasonably active, implying the need for large overpotentials to sustain peroxide formation at reasonable rates. Therefore, this free-energy regime of the descriptor ΔG1 is reconciled with mediocre electrocatalysts for this process.
(ii) −0.25 eV < ΔG1 < 1.25 eV (red): the OER volcano curve reaches its apex, corresponding to the highest electrocatalytic activity, at ΔG1 = 0.8 eV, and the electrocatalytic activity of the OER excels that of the PFR in the entire range. The strong competition of the OER causing low selectivity toward the PFR implies that electrocatalysts in this regime of the volcano curve are not suitable for selective peroxide formation.
(iii) 1.25 eV < ΔG1 < 2.50 eV (green): this free-energy regime of the descriptor ΔG1 is reconciled with optimum performance since the PFR volcano apex is located therein (ΔG1 = 1.76 eV), and the selectivity is on the side of the PFR.
On the contrary, the PRR during discharge (cf.Fig. 2b) is not impeded by any detrimental side reaction so that one can only distinguish between optimum or mediocre electrocatalysts for ΔG1 > 1.25 eV and ΔG1 < 1.25 eV, respectively.
While Siahrostami discussed in her recent work the notion of a rechargeable metal–hydrogen peroxide battery based on the PFR and PRR while neglecting the accompanied selectivity challenge,16 in the next section we translate the presented approach to the two-electron ORR and two-electron OER in the context of a rechargeable metal–hydrogen peroxide battery.
3.2 Two-electron ORR and two-electron OER
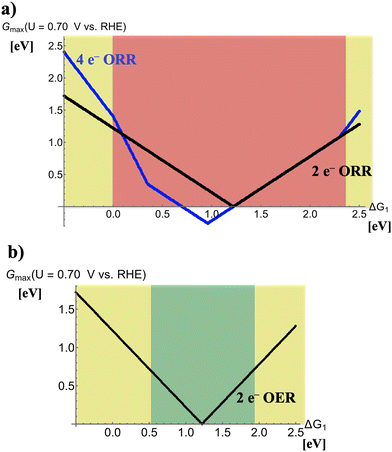
Fig. 3 illustrates volcano plots for the two-electron ORR and two-electron OER at U = 0.70 V vs. RHE. Like Fig. 2, different regions in both panels are marked by various colors to quantify the performance of electrocatalysts in dependence of the descriptor ΔG1.The selectivity problem of the four-electron and two-electron ORR during discharge in Fig. 3a indicates that there is a trade-off between activity and selectivity for peroxide formation. This unfortunate situation is related to the fact that the apexes of the volcano plots for the four-electron and two-electron ORR are close, but in the regime of high peroxide activity the selectivity is in favor of water formation referring to the four-electron process (0 eV < ΔG1 < 2.4 eV). Therefore, only at the volcano legs for strong (ΔG1 < 0 eV) or weak (ΔG1 > 2.4 eV) bonding of the *OH adsorbate, selectivity toward the desired product peroxide is observed. This fact is ultimately related to the difference in the volcano slopes of the four-electron and two-electron ORR, as discussed in more detail in a recent article.29
In Fig. 3b, the two-electron OER during charge is characterized by a single volcano curve since no side reaction is encountered under these potential conditions. As such, optimum performance is met for electrocatalysts in the free-energy regime of 0.55 eV < ΔG1 < 1.95 eV as materials in this range reveal high activity for the oxidation of peroxide to gaseous oxygen. At the volcano legs for strong (ΔG1 < 0.55 eV) or weak (ΔG1 > 1.95 eV) binding of the *OH adsorbate, the modest electrocatalytic activity requires enhanced overpotentials to obtain sufficient turnover.
3.3 Comparison
In the following, the results for the two different concepts of metal–hydrogen peroxide batteries are critically discussed. The motivation to introduce the peroxide redox chemistry into rechargeable batteries is related to the significant performance loss of MABs as the bifunctional oxygen electrocatalysis requires large overpotentials during discharge and charge both (cf.Fig. 1). Without any ado, it can be concluded that the necessitated overpotential for metal–hydrogen peroxide batteries is smaller when inspecting the elementary processes at the cathode only, recalling that the peroxide redox chemistry consists of kinetically facile two-electron processes (cf.eqn (3)–(6)). The major drawback, though, refers to the accompanied selectivity challenge when making use of the peroxide redox chemistry since the equilibrium potentials of these processes interfere with the OER and ORR.The PRR and PFR, discussed in Section 3.1, are operative under high-potential conditions due to its equilibrium potential of 1.76 V vs. RHE. While the four-electron OER competes with the two-electron PFR under anodic conditions (charge), it is possible to steer activity and selectivity toward the desired product (cf. green-highlighted regime in Fig. 2a). On the contrary, the two-electron ORR and two-electron OER, discussed in Section 3.2, reveal smaller equilibrium potential of 0.70 V vs. RHE, and the selectivity challenge is encountered between the two-electron and four-electron ORR under cathodic conditions (discharge). However, this selectivity issue is accompanied by a trade-off between activity and selectivity since high selectivity toward the desired product causes low intrinsic activity (cf. yellow-highlighted regime in Fig. 3a).
The difference in the selectivity for the two concepts of metal–hydrogen peroxide batteries impacts the desired electrocatalyst properties. For the PRR and PFR, a single site electrocatalyst is called for since optimum performance for both processes is observed in the same free-energy regime of the descriptor ΔG1 (cf.Fig. 2). On the contrary, a dual site electrocatalyst is needed for the two-electron ORR and two-electron OER since either excessive strong or weak bonding of *OH or a medium binding strength of *OH is required for optimum performance (cf.Fig. 3), respectively.
The different equilibrium potentials of the redox couples can be related to the stability aspect of electrocatalysts in these devices. The reaction conditions for the PRR and PFR are harsh due to their large equilibrium potential of 1.76 V vs. RHE, which can accelerate the degradation of electrode materials during operation.46–48 While this statement particularly holds true for acidic electrolytes, even for alkaline solutions as met in rechargeable batteries, these anodic potentials, which are in a similar order of magnitude than that of electrolyzers, are critical. Here, the two-electron ORR and two-electron OER are advantageous since decomposition processes may not be a limiting factor in the potential range of 0.70 V vs. RHE.
Another difference manifests relating to the need for air cathodes. Conventional MABs contain an air cathode due to gaseous oxygen as a reactant in the ORR. Also, for the two-electron ORR and two-electron OER, an air cathode is needed since gaseous oxygen serves as the reactant during discharge. On the contrary, the PRR and PFR do not require an air cathode since peroxide is encountered with the reactant during discharge. Even if air cathodes based on the concept of gas diffusion electrodes are firmly established,49,50 it can be seen as an advantage if no gas diffusion electrode is needed since the elementary steps at the complex triple phase boundary may limit the reaction rate compared to the simpler solid/liquid interface.
Finally, it should be noted that, in contrast to conventional MABs where the formation of peroxide corresponds to an unwanted side reaction, peroxide is the major reactant within the concept of metal–hydrogen peroxide batteries. While this may cause safety concerns due to its toxic and hazardous nature, it should be emphasized that it is yet eco-friendly since peroxide decomposes into oxygen and hydrogen. Besides, peroxide has already been used since the 1990s for battery applications, following the works of Licht or Wei and coworkers.51,52
Fig. 4 summarizes the discussion on rechargeable metal–hydrogen peroxide batteries compared to MABs. While it appears that the PRR and PFR excel over the two-electron ORR and two-electron OER, the stability aspect should not be underrated, considering that for industrial applications stability is often even more important than activity. Therefore, I do not want to make a statement as to which of these two concepts is superior, but rather to conclude that rechargeable metal–hydrogen peroxide batteries as an alternative to MABs deserve further attention in future experimental and theoretical studies.
Though, a few caveats of rechargeable metal–hydrogen peroxide batteries need to be mentioned. First, the concentration of hydrogen peroxide is of importance for the electrocatalytic processes at the cathode. While in the present modeling approach the activity of peroxide is assumed to be unity, it is still a challenge to model concentration dependency of electrocatalytic reactions by first-principles or descriptor-based approaches.53 Thus, I need to point out that the derived guidelines may be prone to alter if the peroxide concentrations deviate strongly from the assumed activity of unity. Another issue relates to the corrosion among hydrogen peroxide and binders or separator, making it a challenge to build a full peroxide battery. Also, self-discharge of the full cell through hydrogen peroxide decomposition is another detrimental side effect, which is a hindrance for the large-scale implementation of rechargeable metal–hydrogen peroxide batteries.54 Despite these shortcomings, recent experimental studies have indicated that peroxide batteries show higher energy density and better cycling stability than conventional metal–air batteries, and that near-surface solvent engineering can steer selectivity toward the two-electron processes rather the four-electron OER and ORR.55 Therefore, the dedicated combination of experimental and theoretical studies may foster further progression to overcome the accompanied challenges of rechargeable metal–hydrogen peroxide batteries.
4 Conclusions
Metal–air batteries (MABs) are a promising concept for energy storage, yet their application is still restricted because of the sluggish bifunctional oxygen electrocatalysis at the cathode (cf.Fig. 1), consisting of the oxygen reduction (ORR) and oxygen evolution (OER) reactions during discharge and charge, respectively. In a recent article motivated by electronic structure calculations, Siahrostami suggested to include the redox chemistry of hydrogen peroxide (H2O2) into MABs, giving rise to rechargeable metal–hydrogen peroxide batteries. Herein, two different models of metal–hydrogen peroxide batteries are discussed: on the one hand, the peroxide reduction (PRR) and peroxide formation (PFR) reactions operating at elevated electrode potentials (U0 = 1.76 V vs. RHE), and on the other hand, the two-electron ORR and two-electron OER operating at moderate electrode potentials (U0 = 0.70 V vs. RHE).To study these two scenarios of metal–hydrogen peroxide batteries, we apply an in-house approach by compiling volcano plots based on a rigorous thermodynamic treatment of the reaction intermediates’ free energies. Please note that the focus of the present contribution is not on the investigation of a certain material class for these electrocatalytic processes, but rather volcano curves are used to comprehend general trends and the requirements of electrocatalysts for the PRR and PFR or the two-electron ORR and two-electron OER. Emphasis is set on the selectivity aspect, recalling that the PFR and two-electron ORR compete with the four-electron OER and four-electron ORR under the reaction conditions, respectively. It is illustrated that for the PFR, selectivity can be steered toward the desired product without loss of activity (cf.Fig. 2a) whereas for the two-electron ORR, a trade-off between activity and selectivity is encountered (cf.Fig. 3a). Taking the volcano curves for the reverse reactions into account (cf.Fig. 2b–3b), it arises that a single site or a dual electrocatalyst are required for the PFR/PRR and two-electron ORR/OER, respectively.
The insight gained from the volcano analyses is discussed in Section 3.3 to aid the understanding of metal–hydrogen peroxide batteries in the framework of activity, selectivity, and catalyst stability (cf.Fig. 4). While the comparison between the PRR and PFR and two-electron ORR and two-electron OER suggests that the first concept may excel over the latter, it is emphasized that the stability aspect for the PRR and PFR is critical due to the harsh anodic operating potentials. It is key to identify stable electrode coatings that can withstand these reaction conditions without catalyst decomposition, and additionally suitable materials need to reveal selectivity toward the PFR rather than toward the competing four-electron OER.
All conclusions rendered based on the investigated volcano models hold true for the cathode whereas the intercalation chemistry at the anode of MABs or metal–hydrogen peroxide batteries is not explicitly addressed herein. It can therefore not be inferred in an unbiased fashion whether rechargeable metal–hydrogen peroxide batteries can overcome the long-standing issues with MABs, but it can be stated that the general idea of rechargeable metal–hydrogen peroxide batteries is worthy of further investigations. Materials design for the electrocatalytic reactions at the cathode of these devices has been largely driven by electronic structure calculations in recent years, and the derived volcano plots in this contribution, which go far beyond the conventional approach in terms of the limiting potential analysis, can aid the search for suitable material motifs for experimental investigations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
KSE acknowledges funding by the Ministry of Culture and Science of the Federal State of North Rhine-Westphalia (NRW Return Grant). KSE is associated with the CRC/TRR247: “Heterogeneous Oxidation Catalysis in the Liquid Phase” (Project number 388390466-TRR 247), the RESOLV Cluster of Excellence, funded by the Deutsche Forschungsgemeinschaft under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV, and the Center for Nanointegration (CENIDE). This article is based upon the work from COST Action 18234, supported by COST (European Cooperation in Science and Technology).References
- A. R. Armstrong and P. G. Bruce, Synthesis of layered LiMnO2 as an electrode for rechargeable lithium batteries, Nature, 1996, 381, 499–500 CrossRef CAS
.
- J. S. Lee, S. T. Kim, R. Cao, N. S. Choi, M. Liu, K. T. Lee and J. Cho, Metal-air batteries with high energy density: Li-Air versus Zn-Air, Adv. Energy Mater., 2011, 1, 34–50 CrossRef CAS
.
- J. Janek and W. G. Zeier, A solid future for battery development, Nat. Energy, 2016, 1, 16141 CrossRef
.
- J. W. Choi and D. Aurbach, Promise and reality of post-lithium-ion batteries with high energy densities, Nat. Rev. Mater., 2016, 1, 16013 CrossRef CAS
.
- Y. Gorlin and T. F. Jaramillo, A Bifunctional nonprecious metal catalyst for oxygen reduction and water oxidation, J. Am. Chem. Soc., 2010, 132, 13612–13614 CrossRef CAS PubMed
.
- Z.-F. Huang, J. Wang, Y. Peng, C.-Y. Jung, A. Fisher and X. Wang, Design of efficient bifunctional oxygen reduction/evolution electrocatalyst: Recent advances and perspectives, Adv. Energy Mater., 2017, 7, 1700544 CrossRef
.
- S. Hou, R. M. Kluge, R. W. Haid, E. L. Gubanova, S. A. Watzele, A. S. Bandarenka and B. Garlyyev, A Review on Experimental Identification of Active Sites in Model Bifunctional Electrocatalytic Systems for Oxygen Reduction and Evolution Reactions, ChemElectroChem, 2021, 8, 3433–3456 CrossRef CAS
.
- M. T. M. Koper, Thermodynamic Theory of Multi-Electron Transfer Reactions: Implications for Electrocatalysis, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS
.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS
.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Universality in Oxygen Reduction Electrocatalysis on Metal Surfaces, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS
.
- J. Masa, W. Xia, I. Sinev, A. Zhao, Z. Sun, S. Grützke, P. Weide, M. Muhler and W. Schuhmann, MnxOy/NC and CoxOy/NC nanoparticles embedded in a nitrogen-doped carbon matrix for high- performance bifunctional oxygen electrodes, Angew. Chem., Int. Ed., 2014, 53, 8508–8512 CrossRef CAS PubMed
.
- M. Retuerto, F. Calle-Vallejo, L. Pascual, G. Lumbeeck, M. T. Fernandez-Diaz, M. Croft, J. Gopalakrishnan, M. A. Peña, J. Hadermann, M. Greenblatt and S. Rojas, La1.5Sr0.5NiMn0.5Ru0.5O6 double perovskite with enhanced ORR/OER bifunctional catalytic activity, ACS Appl. Mater. Interfaces, 2019, 11, 21454–21464 CrossRef CAS PubMed
.
- S. S. Shinde, C. H. Lee, J.-Y. Jung, N. K. Wagh, S.-H. Kim, D.-H. Kim, C. Lin, S. U. Lee and J.-H. Lee, Unveiling dual-linkage 3D hexaiminobenzene metal–organic frameworks towards long-lasting advanced reversible Zn–air batteries, Energy Environ. Sci., 2019, 12, 727–738 RSC
.
- M. J. Kolb and F. Calle-Vallejo, The bifunctional volcano plot: Thermodynamic limits for single-atom catalysts for oxygen reduction and evolution, J. Mater. Chem. A, 2022, 10, 5937–5941 RSC
.
- S. Razzaq and K. S. Exner, Method to Determine the Bifunctional Index for the Oxygen Electrocatalysis from Theory, ChemElectroChem, 2022, 9, e202101603 CrossRef CAS
.
- S. Siahrostami, Rechargeable Metal–Hydrogen Peroxide Battery, A Solution to Improve the Metal–Air Battery Performance, ACS Energy Lett., 2022, 7, 2717–2724 CrossRef CAS
.
- S. Anantharaj and S. Noda, Dos and don’ts in screening water splitting electrocatalysts, Energy Adv., 2022, 1, 511–523 RSC
.
- Z. Manappadan and K. Selvaraj, Multi-functional O2–H2 electrochemistry by an abundant mineral: a novel and sustainable alternative for noble metals in electrolyzers and metal–air batteries, Energy Adv., 2022, 1, 886–899 RSC
.
- K. S. Exner, A Universal Descriptor for the Screening of Electrode Materials for Multiple-Electron Processes: Beyond the Thermodynamic Overpotential, ACS Catal., 2020, 10, 12607–12617 CrossRef CAS
.
- K. S. Exner, Why approximating electrocatalytic activity by a single free-energy change is insufficient, Electrochim. Acta, 2021, 375, 137975 CrossRef CAS
.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, Electrolysis of Water on Oxide Surfaces, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS
.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Unifying the 2e− and 4e− Reduction of Oxygen on Metal Surfaces, J. Phys. Chem. Lett., 2012, 3, 2948–2951 CrossRef CAS PubMed
.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Understanding Catalytic Activity Trends in the Oxygen Reduction Reaction, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed
.
- J. A. Keith, G. Jerkiewicz and T. Jacob, Theoretical Investigations of the Oxygen Reduction Reaction on Pt(111), Chem. Phys. Chem., 2010, 11, 2779–2794 CrossRef CAS PubMed
.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Introducing structural sensitivity into adsorption-energy scaling relations by means of coordination numbers, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed
.
- J. Huang, A. Malek, J. Zhang and M. J. Eikerling, Non-monotonic Surface Charging Behavior of Platinum: A Paradigm Change, J. Phys. Chem. C, 2016, 120, 13587–13595 CrossRef CAS
.
- J. Huang, J. Zhang and M. Eikerling, Unifying theoretical framework for deciphering the oxygen reduction reaction on platinum, Phys. Chem. Chem. Phys., 2018, 20, 11776–11786 RSC
.
- K. S. Rapid Exner, Screening of Mechanistic Pathways for Oxygen-Reduction Catalysts, ChemCatChem, 2022, e202201222 Search PubMed
.
- K. S. Exner, Steering Selectivity in the Four-Electron and Two-Electron Oxygen-Reduction Reactions: On the Importance of the Volcano Slope, ACS Phys. Chem. Au, 2023 DOI:10.1021/acsphyschemau.2c00054
.
- T. Binninger and M. L. Doublet, The Ir–OOOO–Ir transition state and the mechanism of the oxygen evolution reaction on IrO2(110), Energy Environ. Sci., 2022, 15, 2519–2528 RSC
.
- K. S. Exner, Implications of the M-OO⋯OO-M recombination mechanism on materials screening and the oxygen evolution reaction, J. Phys. Energy, 2023, 5, 014008 CrossRef
.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeisl, Enabling Direct H2O2 Production through Rational Electrocatalyst Design, Nat. Mater., 2013, 12, 1137 CrossRef CAS PubMed
.
- V. Viswanathan, H. A. Hansen and J. K. Nørskov, Selective Electrochemical Generation of Hydrogen Peroxide from Water Oxidation, J. Phys. Chem. Lett., 2015, 6, 4224–4228 CrossRef CAS PubMed
.
- S. Siahrostami, G.-L. Li, V. Viswanathan and J. K. Nørskov, One- or Two-Electron Water Oxidation, Hydroxyl Radical, or H2O2 Evolution, J. Phys. Chem. Lett., 2017, 8, 1157–1160 CrossRef CAS PubMed
.
- S. Siahrostami, S. J. Villegas, A. H. Bagherzadeh Mostaghimi, S. Back, A. B. Farimani, H. Wang, K. A. Persson and J. Montoya, A Review on Challenges and Successes in Atomic-Scale Design of Catalysts for Electrochemical Synthesis of Hydrogen Peroxide, ACS Catal., 2020, 10, 7495–7511 CrossRef CAS
.
- V. Viswanathan and H. A. Hansen, Unifying solution and surface electrochemistry: limitations and opportunities in surface electrocatalysis, Top. Catal., 2014, 57, 215–221 CrossRef CAS
.
- H. B. Tao, J. Zhang, J. Chen, L. Zhang, Y. Xu, J. G. Chen and B. Liu, Revealing Energetics of Surface Oxygen Redox from Kinetic Fingerprint in Oxygen Electrocatalysis, J. Am. Chem. Soc., 2019, 141, 13803 CrossRef CAS PubMed
.
- K. S. Exner, Design Criteria for Oxygen Evolution Electrocatalysts from First Principles: Introduction of a Unifying Material-Screening Approach, ACS Appl. Energy Mater., 2019, 2, 7991–8001 CrossRef CAS
.
- S. Divanis, T. Kutlusoy, I. M. I. Boye, I. C. Man and J. Rossmeisl, Oxygen evolution reaction: a perspective on a decade of atomic scale simulations, Chem. Sci., 2020, 11, 2943–2950 RSC
.
- S. Razzaq and K. S. Exner, Materials Screening by the Descriptor Gmax(η): The Free-Energy Span Model in Electrocatalysis, ACS Catal., 2023, 13, 1740–1758 CrossRef CAS PubMed
.
- S. Kozuch and S. Shaik, How to conceptualize catalytic cycles? The Energetic Span Model, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed
.
- S. Kozuch, A refinement of everyday thinking: the energetic span model for kinetic assessment of catalytic cycles, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 795–815 CAS
.
- M. Busch, N. B. Halck, U. U. Kramm, S. Siahrostami, P. Krtil and J. Rossmeisl, Beyond the top of the volcano? – A unified approachto electrocatalytic oxygen reduction and oxygen evolution, Nano Energy, 2016, 29, 126–135 CrossRef CAS
.
- D. Wang, X. Mu, P. He and H. Zhou, Materials for advanced Li-O2 batteries: Explorations, challenges and prospects, Mater. Today, 2019, 26, 87–99 CrossRef CAS
.
- X. Zou, Q. Lu, K. Liao and Z. Shao, Towards practically accessible aprotic Li-air batteries: Progress and challenges related to oxygen-permeable membranes and cathodes, Energy Storage Mater., 2022, 45, 869–902 CrossRef
.
- F.-Y. Chen, Z.-Y. Wu, Z. Adler and H. Wang, Stability challenges of electrocatalytic oxygen evolution reaction: From mechanistic understanding to reactor design, Joule, 2021, 5, 1704–1731 CrossRef CAS
.
- H. Over, Fundamental Studies of Planar Single-Crystalline Oxide Model Electrodes (RuO2, IrO2) for Acidic Water Splitting, ACS Catal., 2021, 11, 8848–8871 CrossRef CAS
.
- M. Wohlgemuth, M. L. Weber, L. Heymann, C. Baeumer and F. Gunkel, Activity-Stability Relationships in Oxide Electrocatalysts for Water Electrolysis, Front. Chem., 2022, 10, 913919 Search PubMed
.
- M. Inaba, A. W. Jensen, G. W. Sievers, M. Escudero-Escribano, A. Zana and M. Arenz, Benchmarking high surface area electrocatalysts in a gas diffusion electrode: measurement of oxygen reduction activities under realistic conditions, Energy Environ. Sci., 2018, 11, 988–994 RSC
.
- H. Rabiee, L. Ge, X. Zhang, S. Hu, M. Li and Z. Yuan, Gas diffusion electrodes (GDEs) for electrochemical reduction of carbon dioxide, carbon monoxide, and dinitrogen to value-added products: a review, Energy Environ. Sci., 2021, 14, 1959–2008 RSC
.
- C. Marsh and S. Licht, A Novel Aqueous Dual-Channel Aluminum-Hydrogen Peroxide Battery, J. Electrochem. Soc., 1994, 141, 61–63 CrossRef
.
- L. Xu, J. Liu, P. Chen, Z. Wang, D. Tang, X. Liu, F. Meng and X. Wei, High-Power Aqueous Zn-H2O2 Batteries for Multiple Applications, Cell Rep. Phys. Sci., 2020, 1, 100027 CrossRef
.
- K. Doblhoff-Dier and M. T. M. Koper, Modeling the Gouy–Chapman Diffuse Capacitance with Attractive Ion–Surface Interaction, J. Phys. Chem. C, 2021, 125, 16664–16673 CrossRef CAS
.
- M. A. Riaz and Y. Chen, Electrodes and electrocatalysts for electrochemical hydrogen peroxide sensors: a review of design strategies, Nanoscale Horiz., 2022, 7, 463–479 RSC
.
- W. Sun, F. Wang, B. Zhang, M. Zhang, V. Küpers, X. Ji, C. Theile, P. Bieker, K. Xu, C. Wang and M. Winter, A rechargeable zinc-air battery based on zinc peroxide chemistry, Science, 2021, 371, 46–51 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Reaction mechanisms. Thermodynamic theory of the elementary steps. Free-energy spans relating to the descriptor Gmax(U). Sensitivity analysis of the scaling relation. Potential dependence of volcano curves. See DOI: https://doi.org/10.1039/d3ya00002h |
| This journal is © The Royal Society of Chemistry 2023 |