Open Access Article
Open Access ArticleAssessing alkyl side chain effects on electron transport properties of Y6-derived non-fullerene acceptors†
Daniele
Padula
 *a,
Alessandro
Landi
*a,
Alessandro
Landi
 *b and
Giacomo
Prampolini
*b and
Giacomo
Prampolini
 *c
*c
aDipartimento di Biotecnologie, Chimica e Farmacia, Università di Siena, Via A. Moro 2, 53100 Siena, Italy. E-mail: daniele.padula@unisi.it
bDipartimento di Chimica e Biologia Adolfo Zambelli, Università di Salerno, Via Giovanni Paolo II, I-84084 Fisciano (SA), Italy. E-mail: alelandi1@unisa.it
cIstituto di Chimica dei Composti OrganoMetallici (ICCOM-CNR), Area della Ricerca, Via G. Moruzzi 1, 56124 Pisa, Italy. E-mail: giacomo.prampolini@pi.iccom.cnr.it
First published on 20th July 2023
Abstract
Recent advances in non-fullerene acceptors (NFAs) have significantly increased the efficiency of organic photovoltaics, reaching approximately 20% in single junction solar cells. These advancements are attributed to the introduction of the promising L8-R series, derived from the high-performance NFA known as Y6. To gain a deeper insight about such efficiency improvement, here we computationally characterise Y6 and its derivatives, focusing on the supramolecular structure of the resulting aggregates and their electron transfer properties. The applied computational protocol indicates an evident relationship between different side chains and the electronic features of the NFA supramolecular architectures, and provides a possible rationale for their impact on photovoltaic device efficiency. Using density functional theory and experimental crystal structures, we show that shorter and branched alkyl side chains on L8-R derivatives improve electron transfer integrals and charge mobilities compared to Y6. This improvement is attributed to differences in crystal packing. The effect of thermal fluctuations on the performance of the NFA aggregate is instead investigated through molecular dynamics simulations with quantum-mechanically derived force fields. Results indicate that, despite a minimal impact on electron transport capabilities due to dynamic disorder, the various substitution patterns significantly influence the supramolecular arrangement of the aromatic cores. The validation of the presented computational protocol, which integrates in a multi-level procedure accurate charge transfer rates computed on reliable morphologies obtained through classical molecular dynamics with refined force fields, paves the way towards a bottom-up modelling of donor/acceptor interfaces with polymeric donors, where the accurate description of structural and electronic disorder is key to reach a computationally-driven identification of higher performing components for organic photovoltaics.
1. Introduction
In recent years, among promising types of solar cells, organic photovoltaics (OPVs) have attracted significant attention, mainly because of their low cost, lightweight, and flexibility.1–3 Organic materials used in OPVs are typically composed of conjugated polymers or small molecules, which can be finely tuned to absorb specific light wavelengths.The major challenge in OPVs is achieving high power conversion efficiency (PCE, η), a critical point for commercialisation.1 After 2012, the efficiency of OPV cells reached a plateau around 10–12%, a level of performance unchallenged until very recently,2,4,5 when researchers introduced a small-molecule non-fullerene acceptor (NFA) called Y6, which enabled OPV cells to achieve efficiencies exceeding 15%.6 Since then, Y6 has become a key component of many high-efficiency OPV cells,7–13 typically in combination with polymeric donors but also with small molecules.14 Following its discovery, Y6 garnered significant attention and both theoretical and experimental studies have been devoted to rationalise and even further improve its exceptional features.15–21
From a theoretical point of view, researchers traced back Y6 excellent charge and exciton transport properties to its strong delocalisation capability, which results in a reduced chance of recombination.15–17 On the experimental side, while it is debated whether Y6 alone could lead to photocurrent and hence function as a photovoltaic material without a heterojunction,21 several derivatives were proposed, including a systematic study for a set of NFAs with branched alkyl side-chains (see Fig. 1) employed in heterojunctions with a polymeric donor (PM6).18 Indeed, chemical substitution of different side chains decorating the Y6 core led to unparalleled efficiencies in solar cells, with better performances registered for the Y6 derivative with shorter branched side chains, which showed efficiencies up to 18.3%.20
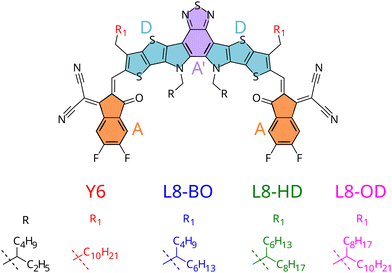 | ||
| Fig. 1 Structure of small-molecule acceptors with varying side-chains and moieties constituting the A–D–A′–D–A architecture highlighted. | ||
Such encouraging results seem to suggest that different crystal packing induced by the modification of Y6's alkyl pendants might be the cause of such significant improvement of charge and exciton transport. As a matter of fact, differences in alkyl side chains (of both acceptor and donor components) are known to impact the performance of the resulting OPV devices,22–29 being pivotal to modulate both cristallinity30 and solubility in organic solvents.31 This, in turn, is a central point to improve the processability of the device. For instance, beside enabling solution printing,32 it affects the miscibility between components, increasing the chance of charge transfer from the donor to the acceptor, without amplifying the recombination processes that could alter charge migration.33,34
To gain deeper insight onto the mechanisms connecting chemical substitution patterns with device performances, in this work we study the set of L8-R NFAs experimentally investigated in ref. 20, focusing on the possible differences induced by the varied alkyl chains on the crystal packing and its consequent electronic behaviour. In this respect, it should be stressed that such differences are indirect effects, because alkyl side chains are not expected to affect the electronic structure of the π-conjugated core to a significant extent. The ability to predict such features is in fact critical to shift the paradigm from a trial-and-error, experimentally-driven research to a rational design based on theoretical predictions.35 Yet, the effect of side chains on OPV performance is not easily predictable: although one can speculate that in similar supra-molecular architectures π-conjugated cores substituted with longer alkyl chains possibly experience stronger effects from an increased number of low frequency vibrations,36 there are cases where side chains of intermediate length resulted in more efficient devices,29 or where longer side chains induce extended planarity in the π-conjugated core, resulting in a performance increase.37
To accomplish the challenging task of an in silico design of efficiently substituted NFAs, three main goals need to be achieved: (i) a prediction of morphology (or crystal structure) of the components38–42 (ii) a prediction of electronic properties of the aggregate in its morphology (iii) a prediction of the morphological and electronic interaction between components. In previous work, some of us have shown how point (iii) could be approached studying donor/acceptor blends based on small molecules.17 Here we instead focus on point (ii), and apply our computational protocols to the set of L8-R NFAs experimentally employed in ref. 20. By investigating their aggregation and morphology, we aim at giving a rationale on the impact of the resulting supramolecular structures on the predicted charge and exciton transport properties. In particular, on the one hand we will exploit the specific chemical structure of the considered NFAs (which all share the same core but differ for their alkyl pendants, see Fig. 1) and the homogeneous composition of the simulated NFA aggregates, to simplify the comparison among the considered compounds and clarify the relationship between the different structures and the computed electronic properties. On the other hand, it should be noticed that a positive performance of the computational protocols here proposed for simpler homogeneous systems would pave the way to future investigations on binary or ternary blends, as for instance explicitly including polymeric donors.
2. Methods
2.1 Electronic calculations on the crystal structure
The crystal structures for L8-BO, L8-HD, and L8-OD were retrieved from the Cambridge Structural Database (CSD),43 as reported in the work with their experimental characterisation.20 Conversely, the Y6 crystal was taken from the supporting information of ref. 44, which was chosen because other crystal structures available for Y6 have incomplete or even missing alkyl side chains.15,45All four structures were employed to compute the transfer integrals between frontier orbitals as
Jij = 〈ϕi|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) |ϕj〉, |ϕj〉, | (1) |
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) is the Fock operator of the dimer.46–50 The absolute sign of transfer integrals was assigned following the approach reported in ref. 51, i.e. based on the sign of the LUMO coefficients of the p atomic orbitals with respect to molecular geometry, for a reference atom in the π-conjugated moiety of each monomer involved in the interaction.
is the Fock operator of the dimer.46–50 The absolute sign of transfer integrals was assigned following the approach reported in ref. 51, i.e. based on the sign of the LUMO coefficients of the p atomic orbitals with respect to molecular geometry, for a reference atom in the π-conjugated moiety of each monomer involved in the interaction.
Together with additional geometry optimisation and frequency calculations (which we carried out on the π-conjugated core only, assuming a similar behaviour for the four NFAs), transfer integral values allow to evaluate electron transfer rates according to Fermi's Golden Rule (FGR),
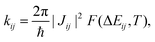 | (2) |
Unless otherwise stated, all electronic calculations were carried out with the Gaussian16 software,56 within the Density Functional Theory (DFT) framework, making use of the B3LYP functional and the popular 6-31G* basis set, accounting for dispersion through the Grimme D3 correction scheme.57 We chose FGR to evaluate the rates because of its improvements with respect to the widely used classical Marcus theory, since it allows taking into account tunneling effects and frequency changes between initial and final electronic states, including the whole sets of normal modes in the computation,52,53,55,58,59 leading to extremely reliable rates of radiative and non-radiative electronic transitions.54,59–61
Predicted electron transfer rates were used to estimate the drift mobility of electrons μ according to Einstein–Smoluchowski's relation
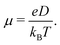 | (3) |
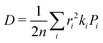 | (4) |
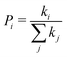 is the probability of the hop along the i-th pathway, and the summation runs over all the charge transfer pathways.
is the probability of the hop along the i-th pathway, and the summation runs over all the charge transfer pathways.
It should be noted that eqn (4) implies the adoption of a hopping transport mechanism, whose applicability to organic crystals where J ≈ λ is highly debated.62–66 However, both theoretical estimations67 and experimental measurements68 of mobility carried out at different temperatures show that the hopping model is adequate for the evaluation of charge mobility, at least at room temperature, in particular when quantum mechanical effects are included in the rates,58,59,69 such as in the case of the FGR used here.
Additionally, notwithstanding other popular protocols employed in the prediction of charge mobilities, such as the transient localisation theory, are generally valid for any molecular crystal, they have been usually used for perfect crystals showing herringbone structures.70 Finally, we also highlight that eqn (4) is valid only for isotropic systems,71 thus it is not entirely compatible with classical MD simulations (vide infra).
2.2 Computational protocols for dynamic disorder
Dynamic disorder originates from the fact that aggregates of organic molecules are held together by weak van der Waals interactions. Although this feature enables applications that are not possible with other types of substrates, it is at the origin of strong modulations of transfer integrals by low frequency vibrations induced by thermal energy. This modulation results in localisation of charge carriers and thus hinders transport. Yet, it is a difficult feature to limit due to its nature, although some strategies based on identifying “killer modes”, electrostatic interactions, and reduced overlap between nearest neighbours have been suggested,36,72–74 despite this latter inevitably leads to lower transfer integrals. To the best of our knowledge, there are essentially two ways of estimating dynamic disorder: (i) through the evaluation of transfer integrals gradients with respect to vibrations,50,72–77 (ii) computing transfer integrals along an MD trajectory.78–80The first strategy has the clear advantage of precisely identifying the lattice or molecular vibrations directly responsible for large modulations of transfer integrals, but as a downside it assumes the harmonic approximation, which is valid only for small displacements from the equilibrium geometry. This is an unlikely event for low frequency modes, which usually show a rather flat potential energy profile, often characterised by several local minima. The second strategy instead relies on retrieving the large modulations of transfer integrals from the spectral density obtained by Fourier Transforming the autocorrelation function of the time series to a frequency domain description. As such, no direct assignment of vibrations is possible, although anharmonicity is accounted for.
While in future work we plan to compare the two strategies, in this work we resort to the classical MD approach. The main drawback of MD based protocols is the possibly poor description of the potential energy surface provided by general purpose force fields (FFs). A possible route to overcome this lack consists in resorting to highly accurate quantum mechanically derived force fields (QMD-FFs), which can be specifically tailored for the molecules under study. Indeed, the benefits of adopting such accurate description have been recently demonstrated in the domain of spectroscopic and electronic properties of organic semiconductors.81,82 Furthermore, the importance of the QMD-FF specialised description for organic aggregates was also recently assessed through simulations of the self-assembly of similar small organic molecules into orientationally ordered liquid crystal phases,83–85 where the phase transition is modulated by a delicate interplay of intramolecular flexibility and intermolecular interactions.
2.3 QMD-FF parameterisation and MD simulations
Thanks to a previous parameterisation, specifically carried out by some of us for the intramolecular degrees of freedom of the Y6 core,17 only two other tasks need to be achieved for building the QMD-FFs purposely tailored on the L8-R displayed in Fig. 1: (i) join the representation of the core with that of chains of the appropriate length and shape, (ii) obtain a QMD-FF description of intermolecular interactions. According to the previous overview on dynamic disorder, both these descriptions should contribute to it significantly, and thus it is desirable to have a reliable set of FF parameters for both the intra- and the inter-molecular contributions (see also Section S1.2 in the ESI†). Concerning point (i), alkyl side chains intramolecular terms were parameterised following the Joyce procedure,86,87 with QM reference data (Hessian, relaxed scans) obtained at B3LYP-D3/6-31G(d) level. The final QMD-FFs were eventually obtained by merging the core and chain topologies as detailed in Section S1.2 of the ESI.† To achieve task (ii), we resorted to the QMD-FF transferability scheme recently proposed by some of us for organic molecules composed by aromatic cores and flexible alkyl chains.83 Concretely, to reduce the computational burden, we transferred the Lennard-Jones (LJ) terms for the alkyl chains from the OPLS force field,89 but we refined against QM descriptors the intermolecular parameters of the aromatic moieties, following the Picky procedure,84,90,91 based on iteratively converging the QMD-FF parameters by fitting interaction energies of dimers extracted from MD trajectories of random aggregates.In fact, as detailed in Section S2 in the ESI,† the OPLS general-purpose FF does not reproduce well the quantum chemical interaction potential energy surface computed at DFT level, yielding an average error larger than 10 kJ mol−1. Even limiting to the most probable configurations, hence comparing selected interaction energy profiles (see Fig. S3 and S4, ESI†), minima are significantly shifted, and the relative stability of different molecular arrangements is not correctly described.
This poor description of intermolecular interactions could in principle significantly affect packing, and consequently transfer integrals. For these reason, we first fitted all atomic point charges, according to the RESP procedure,92 to the B3LYP-D3/6-31G* electrostatic potential of the entire molecule, and thereafter parameterised the intermolecular Lennard-Jones terms of the aromatic core following the Picky procedure as detailed in the ESI.† In summary, the QMD-FF parameterisation of the intra- and inter-molecular terms were respectively carried out with the Joyce93 and Picky94 packages. Additionally, to separately analyse the impact of point (i) and (ii) to the description of dynamic disorder through MD simulation, two other FFs were assembled for each considered molecule, according to the procedures summarised in Table 1 and detailed in Section S1.2 of the ESI.†
| Fragment | Parameters | ||
|---|---|---|---|
| π intramolecular | OPLS | Joyce | Joyce |
| π intermolecular | OPLS | OPLS | Picky |
| Alkyl intramolecular | OPLS | Joyce | Joyce |
| Alkyl intermolecular | OPLS | OPLS | OPLS |
| Label | OPLS | Hyb-FF | QMD-FF |
3. Results and discussion
3.1 Charge transfer pathways in the crystal
The first step of our study consisted in characterising unique charge transfer pathways in the crystal.17,95 This was achieved by identifying all non-equivalent homodimers formed by a given molecule with its nearest neighbours. The L8-R crystals all share a similar pattern (see Fig. 2): each molecule is surrounded by three neighbours approximately lying in the (a,c) plane, giving rise to three non-equivalent charge transfer pathways. Each pathway is described by an electron transfer integral Ji: J1 and J3 both originate from π-stacking interactions between two side acceptor groups A (reported in orange in Fig. 1) of two different monomers. The difference is in the relative orientation of the two monomers, which are parallel in J1 and antiparallel in J3. J2 instead shows a bigger overlap between the involved monomers oriented in an antiparallel arrangement, and originates from two π-stacking interactions between the side acceptor moiety of one monomer, and one of the two central donor moieties of the other monomer.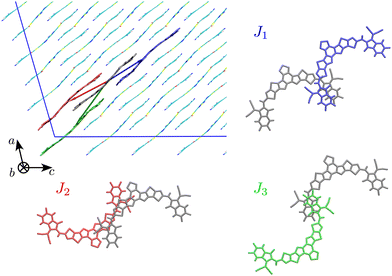 | ||
| Fig. 2 Unique charge transfer pathways and associated transfer integrals J identified in the crystal structure of L8-BO (L8-HD and L8-OD displays the same pathways). Side chains omitted for clarity. | ||
The Y6 crystal is instead different from the ones of the L8 series, although the same three charge transfer pathways can be identified. Table 2 reports a characterisation of the charge transfer pathways computed for the investigated crystals, resulting in a good agreement with electron transfer integrals and rates computed on crystal geometries and aggregates of Y6 by others.15,96 From the data reported in Table 2 we already see a trend of electron mobility that parallels the one of PCE in the corresponding heterojunctions with PM6: shorter and branched side chains lead to higher electron mobilities. The difference in the mobility between the species under study is easily rationalisable by looking at the transfer integral values of the interacting pairs. Indeed, we can see that J2 and J3, the transfer integrals for the pairs with the highest distance r (i.e. the ones which most influence the diffusion coefficient) are significantly higher for L8-BO and this has a trivial impact on the final mobility.
| NFA | Path | r/Å | J/meV | k/s−1 | μ/cm2 V−1 s−1 |
|---|---|---|---|---|---|
| Y6 | J 1 | 9.4 | −59 | 3.75 × 1013 | 1.88 |
| J 2 | 18.5 | 18 | 3.49 × 1012 | ||
| J 3 | 14.0 | −15 | 2.46 × 1012 | ||
| L8-BO | J 1 | 13.8 | −4 | 1.70 × 1011 | 8.11 |
| J 2 | 18.8 | 45 | 2.23 × 1013 | ||
| J 3 | 13.8 | −82 | 7.32 × 1013 | ||
| L8-HD | J 1 | 12.2 | 5 | 3.06 × 1011 | 2.13 |
| J 2 | 18.9 | 22 | 5.01 × 1012 | ||
| J 3 | 13.7 | −43 | 1.98 × 1013 | ||
| L8-OD | J 1 | 12.7 | −18 | 3.39 × 1012 | 2.02 |
| J 2 | 18.5 | 17 | 3.06 × 1012 | ||
| J 3 | 12.8 | 46 | 2.29 × 1013 | ||
These results seem to indicate that one of the reasons of the better performance of L8-BO with respect to the related NFAs can be the different transport properties in the microcrystalline acceptor domains that form in the donor/acceptor blend in the solar cell. Of course, this hypothesis has to be confirmed through accurate studies of the blends, a task we are currently working on and that we plan to report in forthcoming work. This explanation is in agreement with qualitative analyses based on visual inspection of the L8-R crystal structures, suggesting L8-BO superiority due to multiple charge transport channels, as well as with experimental data of electron mobilities in the blend.2,20 However, it is well known that transfer integrals are not the only parameter affecting transport. In fact, as discussed in the previous section, a crucial role is also played by dynamic disorder,72 whose main contribution is given by electron–phonon coupling. To evaluate this effect and the relative role of transfer integrals and dynamic disorder in ultimately determining the experimentally observed trend, we resorted to classical MD simulations.
3.2 QMD-FFs validation
For the L8-BO crystal, the performances of the three force fields models of increasing accuracy, reported in Table 1, were evaluated through the comparison of selected properties computed along the resulting MD trajectories, namely cell parameters, volume, density, and second rank order parameter P2;97–99 radial distribution functions (RDFs) between centres of mass of the rings constituting the π-conjugated core of the molecules; thermodynamic stability.In Table 3 we report the results obtained with MD simulations carried out at 150 K, i.e. the temperature at which the experimental crystal structure characterisation was performed. Further computational characterisation at 100 K and 293 K is available in the ESI.† On the one hand, as far as the structural parameters of the unit cell are concerned, crystallographic axes and angles seem not to vary much and negligible differences arise among the benchmarked FFs, all three yielding values in rather good agreement with the experimental measures, with errors ranging from less than 1% to ≈7%. On the other hand, density and volume are known to be observables more sensitive to intermolecular interactions, hence reflecting in the better agreement with experimental values registered for a complete reparameterisation (QMD-FF). Interestingly, partially refining the general purpose (OPLS) FF in its intra-molecular term (Hyb-FF) also leads toward a more realistic density. This further confirms that the overall description of the aggregate is regulated by a delicate interplay between internal flexibility and intermolecular interactions. Finally, the order of the crystal expressed in terms of the second rank order parameter P2 directed either along the largest or the smallest eigenvector of the Saupe ordering matrix (see Section S3 in the ESI†) is comparable with all FFs employed.
| Property | Expt.20 | QMD-FF | Hyb-FF | OPLS |
|---|---|---|---|---|
| a/Å | 27.704 | 28.46 ± 0.05 | 28.04 ± 0.03 | 27.30 ± 0.08 |
| b/Å | 20.855 | 21.05 ± 0.02 | 21.43 ± 0.03 | 20.50 ± 0.03 |
| c/Å | 28.363 | 26.24 ± 0.07 | 26.54 ± 0.01 | 28.8 ± 0.1 |
| α/° | 90.0 | 90.0 | 90.0 | 90.0 |
| β/° | 105.949 | 106.95 ± 0.02 | 106.584 ± 0.009 | 104.99 ± 0.06 |
| γ/° | 90.0 | 90.0 | 90.0 | 90.0 |
| V/Å3 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 ± 8 721 ± 8 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 ± 13 950 ± 13 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149 ± 13 149 ± 13 |
| ρ/kg m−3 | 1248 | 1254 ± 1 | 1235 ± 1 | 1217 ± 1 |
| P ‖core2 | 0.942 ± 0.001 | 0.942 ± 0.001 | 0.952 ± 0.002 | |
| P ‖core4 | 0.813 ± 0.003 | 0.815 ± 0.003 | 0.845 ± 0.005 | |
| P ⊥core2 | −0.500 | −0.500 | −0.495 | |
| P ⊥core4 | 0.374 | 0.374 | 0.364 ± 0.001 |
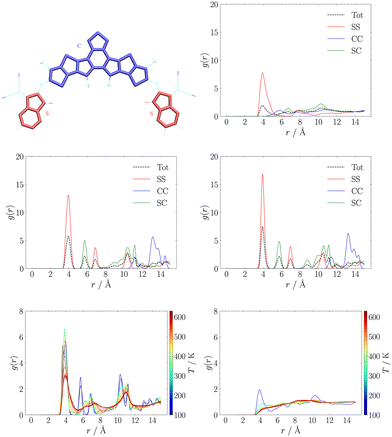
Another popular way to analyse supramolecular architectures is through radial distribution functions (RDFs). In our case we partitioned the π-conjugated core in three subsystems constituted by the central D–A′–D moiety (labelled as C), and the side A moieties (labelled as S). We used this partition to compute RDFs between the centres of mass of any pair of C or S moieties. These results are reported for MD trajectories at 150 K in the central panel of Fig. 3. While in the RDFs obtained with either QMD-FF and Hyb-FF we observe essentially the same comb-like profile, typical of highly ordered aggregates such as crystals, for OPLS we obtain a much broader and less structured profile, suggesting the formation of a less ordered aggregate that can be easily disrupted.
In particular, we highlight how each peak in the RDFs obtained with refined FFs is associated to a specific intermolecular interaction: we assign the first peak at r ≈ 4 Å to π-stacking interactions between S moieties belonging to different molecules (those seen in J1 and J3 couplings, see Fig. 2), while the second peak at r ≈ 6 Å is due to interactions between S and C moieties (those in J2 couplings, see Fig. 2), and all other peaks can be assigned easily. Conversely, in the RDF obtained with the general purpose FF, only the first peak is assignable, while at longer distances there are several overlapping contributions, diagnostic of a less structured and stable aggregate. To confirm this finding, the thermodynamic stability of the resulting NFA aggregates was first investigated through comparison of crystal parameters obtained from simulations at room temperature (the operational condition of solar cells), whose results are reported in Table S1 in the ESI.† Thereafter, heating simulation sequences (see Section S1.3.1 in the ESI†) were carried out in the 100–600 K range, and the resulting RDFs at different temperatures are displayed in the bottom panel of Fig. 3.
We notice that the general purpose description starts deviating significantly from the ordered behaviour of a crystal at an early stage of the heating sequence: the peak at r ≈ 4 Å is significantly reduced already at about room temperature, and completely lost above T ≈ 400 K, providing RDFs reminiscent of isotropic aggregates. On the contrary, the RDF peak broadening, induced by the increasing, temperature-driven disorder, is significantly slower for the QMD-FF and longer simulations are needed to observe a net transition to an isotropic phase.
Although a quantitative determination of transition temperatures would require much more extensive simulations,83,85 beyond the scope of the present work, as a general trend it appears that either partial (Hyb-FF) or total (QMD-FF) reparameterisation allow for a more accurate and reliable description of the crystal.79,100 More importantly, a general purpose representation provides a description of the aggregate in poor agreement with real-world experiments, both quantitatively (with an estimated L8-BO melting temperature TOPLSm < 530 K that badly compares with experiments yielding Tm ≈ 593 K) and qualitatively, since the crystal completely loses its order within few nanoseconds (see Fig. S11 in the ESI†), upon heating, while phase transitions for organic molecules of comparable size require significantly longer simulations.83,85
In conclusion, all the above discussed validation tests agree in indicating that at least a partial refinement of general purpose descriptions is required to achieve reliable results.79,100 Besides the intermolecular parameterisation, which directly impacts the relative arrangements of neighbouring NFA units and hence the charge transport properties of the resulting aggregate, it should be stressed that important differences were found also as a consequence of the sole intramolecular re-parameterisation. In this respect, the effect of the refinement of the QMD intra-molecular parameters is twofold. On the one hand, the accurate fitting of the flexible chain dihedrals rules the conformational dynamics within the chain, in turn affecting the supramolecular structure. On the other hand, a reliable representation of valence bonds and angles, based on higher level QM data, is beneficial to the successive electronic calculations carried out along the classical trajectories, allowing to overcome the so-called “potential energy surface mismatch” problem.101–103
3.3 Electron mobility along MD trajectories
The validation of the here proposed QMD-FFs to reliably account for NFA aggregate structure, allows us to confidently exploit MD simulations to estimate the impact of deviation from a perfect crystalline structure on charge mobility. Following the procedure described in the Section 2 (see eqn (1)–(3), we first computed electron transfer integrals along MD trajectory. In Table 4, we report the average value for each transfer integral over the whole MD trajectory and its standard deviation. Interestingly, while transfer integral values corresponding to the same charge transfer paths are significantly different among the various derivatives and their average values range between 0 and −78 meV, their relative oscillations (σ) are more similar, in any case within 12 and 36 meV. This suggests that the varied performances registered along the L8 series are probably more influenced by the differences in J, rather than by its fluctuations, an evidence supporting our choice to employ FGR for our analyses. Besides varying among the considered NFAs, a comparison with the values reported in Table 2 reveals that the transfer integrals also show significant deviations with respect to the perfect crystalline arrangement.| NFA | J 1 ± σ/meV | J 2 ± σ/meV | J 3 ± σ/meV |
|---|---|---|---|
| Y6 | −42 ± 30 | 34 ± 20 | 0 ± 0 |
| L8-BO | −7 ± 15 | −78 ± 25 | 50 ± 19 |
| L8-HD | 25 ± 21 | −58 ± 31 | 15 ± 16 |
| L8-OD | 35 ± 36 | −44 ± 24 | 7 ± 12 |
Such marked variation with respect to the static crystals can be traced back mainly to two factors (see Fig. 4):104 a change in the intermolecular π distances between the interacting molecules due to a displacement perpendicular to the aromatic planes (Fig. 4, bottom left panel) and a relative slide between the molecular planes (Fig. 4, upper panels) or rotation (Fig. 4, bottom right panel) around the plan normal axis.
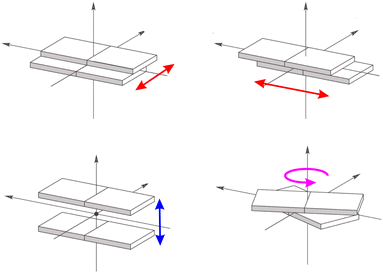 | ||
| Fig. 4 Lateral (red arrows) and vertical (blue arrow) relative displacements of two molecular planes. In magenta the relative rotation of the molecular planes. | ||
Before addressing a deeper discussion on the role played by such kind of supramolecular displacements on dynamic disorder, it is appropriate to again verify the FF reliability in their description. Fig. S3 and S4 in the ESI† show the remarkably increased agreement with respect to higher level DFT descriptions gained with the QMD re-parameterisation of the intermolecular FF terms. Interestingly, such test also reveals different shapes for the FF interaction energy curves computed varying either the stacking distance or the angle between the aromatic planes, the former being characterised by a rather steep and well defined minimum, while the latter presents a more flat profile. This in turn reflects on the distributions of dimer arrangements populated along the MD trajectories, where the intermolecular distance is essentially unaltered with respect to the value found in the crystal, hence suggesting that the main cause for the different transfer integrals values can be related to a relative slide or rotation, which are favourable to maximise π-stacking interactions without altering the distance between the aromatic planes.
Indeed, for such large conjugated molecules, the molecular orbitals (which determine the transfer integral values, see eqn (1)) show a complex nodal structure (see Fig. S18 in the ESI†) so that even a slight shift in their relative position and overlap can have a strong impact on the interaction among the aromatic cores. In this respect it should be stressed that, for a reliable sampling of such displaced dimer arrangements, it is of the foremost importance to rely on refined QMD-FFs, able to entail the QM accuracy in the description of complex π–π interaction energy surfaces.91,105
The difference in the transfer integrals with respect to the perfect crystal case is expected to translate in different charge mobility values. As a first estimation, we have computed the diffusion coefficient following eqn (4), by considering all the neighbouring couples in the MD system. We remark that this approach, although not rigorous because it is applicable only to isotropic systems, represents an estimation of the results from a stochastic charge hopping simulation (e.g. via kinetic Monte Carlo),3,71 and it is accurate enough to allow us to rationalise the observed experimental trend.
Indeed, inspection of Table 5 shows that the average mobility evaluated along the MD trajectory is slightly higher than the one evaluated for the perfect crystal structure. Nevertheless, the trend (L8-BO > L8-HD > L8-OD > Y6) is preserved. This trend seems to suggest that L8-R derivatives have better transport properties than the parent material and that shorter and branched side chains lead to enhanced charge mobility. As a consequence, devices built exploiting such derivatives are expected to yield enhanced efficiencies. After optimising the NFA, researchers further investigated the effect of blend morphology by studying ternary solar cells,106 where a new auxiliary donor designed based on the Y6 core was added.107 This led to unprecedented efficiencies of ≈19.3% in single-junction cells. However, it is not guaranteed that separate optimisation of the components can lead to the best results, as their synergy must also be considered.108,109
| Y6 | L8-BO | L8-HD | L8-OD | |
|---|---|---|---|---|
| Crystal | 1.88 | 8.11 | 2.13 | 2.02 |
| MD | 3.92 | 9.18 | 5.60 | 4.67 |
4. Conclusions
This work reports a detailed computational characterisation of a recently introduced NFA acceptor, Y6, and its three derivatives (L8-R) differing for the alkyl side chains, and aims at rationalising the impact of such chemical substitution on the performance of these NFAs in OPV devices. To this end, key properties as electron transfer rates and charge mobilities were computed at QM level on both the experimental crystal structures, and exploiting classical MD simulations of the aggregate in the proper thermodynamic conditions to account for the role of thermal fluctuations.Concerning the latter calculations, the thorough set of MD runs and analyses of the resulting trajectories indicates that a reparameterisation of force fields for classical molecular dynamics based on quantum chemical reference data leads to much more realistic description of aggregates of organic semiconductors with respect to general purpose parameters.
Turning to the predicted properties, charge mobilities computed in single crystal and along the MD trajectory show that, in agreement with previously reported experiments, L8-R NFAs show enhanced electron transport capabilities with respect to the parent Y6 compound, with a clear trend showing that shorter and branched chains lead to the best performance. This is due to an increase in electron transfer integrals, which results from the altered crystal packing induced by the alkyl side chains.
This work is a necessary first step towards studying the performance of the NFA under study in binary or ternary blends with polymeric donors,20,106 where the importance of structural disorder on the electronic properties of these substrates110 calls for the adoption of accurate descriptions of both structural flexibility of all involved species, and supramolecular interaction patterns among all components of the blend. The good agreement between our analyses and the available experimental data for the investigated aggregates strongly supports the extension of the present protocols to multi-component systems, a work currently in progress in our group.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. P. gratefully acknowledges funding from the Italian Ministry of University and Research (MUR, Rita Levi Montalcini grant PGR18PJMBW) and Università di Siena (F-CUR research support contribution), and computational resources kindly provided by CINECA (ISCRA C HP10CA066O and HP10CJR0ZF) and Università di Siena (hpc@dbcf). G. P. thanks the financial support from ICSC – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU – PNRR, Missione 4 Componente 2 Investimento 1.4.References
- K. Leo, Nat. Rev. Mater., 2016, 1, 16056 CrossRef CAS.
- G. Zhang, F. R. Lin, F. Qi, T. Heumüller, A. Distler, H.-J. Egelhaaf, N. Li, P. C. Y. Chow, C. J. Brabec, A. K.-Y. Jen and H.-L. Yip, Chem. Rev., 2022, 122, 14180–14274 CrossRef CAS.
- A. Landi, A. Landi, A. Velardo and A. Peluso, ACS Appl. Energy Mater., 2022, 5, 10815–10824 CrossRef CAS.
- A. Kuzmich, D. Padula, H. Ma and A. Troisi, Energy Environ. Sci., 2017, 10, 395–401 RSC.
- H. Wang, J. Cao, J. Yu, Z. Zhang, R. Geng, L. Yang and W. Tang, J. Mater. Chem. A, 2019, 7, 4313–4333 RSC.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H.-L. Yip, T.-K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1140–1151 CrossRef CAS.
- J. Yuan and Y. Zou, Org. Electron., 2022, 102, 106436 CrossRef CAS.
- B. Lu, J. Wang, Z. Zhang, J. Wang, X. Yuan, Y. Ding, Y. Wang and Y. Yao, Nano Select, 2021, 2, 2029–2039 CrossRef CAS.
- C. He, Z. Chen, T. Wang, Z. Shen, Y. Li, J. Zhou, J. Yu, H. Fang, Y. Li, S. Li, X. Lu, W. Ma, F. Gao, Z. Xie, V. Coropceanu, H. Zhu, J.-L. Bredas, L. Zuo and H. Chen, Nat. Commun., 2022, 13, 2598 CrossRef CAS PubMed.
- Y. Zhang, Y. Ji, Y. Zhang, W. Zhang, H. Bai, M. Du, H. Wu, Q. Guo and E. Zhou, Adv. Funct. Mater., 2022, 32, 2205115 CrossRef CAS.
- Z.-C. Wen, H. Yin and X.-T. Hao, Surf. Interfaces, 2021, 23, 100921 CrossRef CAS.
- Q. Guo, Q. Guo, Y. Geng, A. Tang, M. Zhang, M. Du, X. Sun and E. Zhou, Mater. Chem. Front., 2021, 5, 3257–3280 RSC.
- J. Hofinger, C. Putz, F. Mayr, K. Gugujonovic, D. Wielend and M. C. Scharber, Mater. Adv., 2021, 2, 4291–4302 RSC.
- R. Zhou, Z. Jiang, C. Yang, J. Yu, J. Feng, M. A. Adil, D. Deng, W. Zou, J. Zhang, K. Lu, W. Ma, F. Gao and Z. Wei, Nat. Commun., 2019, 10, 5393 CrossRef.
- G. Zhang, X.-K. Chen, J. Xiao, P. C. Y. Chow, M. Ren, G. Kupgan, X. Jiao, C. C. S. Chan, X. Du, R. Xia, Z. Chen, J. Yuan, Y. Zhang, S. Zhang, Y. Liu, Y. Zou, H. Yan, K. S. Wong, V. Coropceanu, N. Li, C. J. Brabec, J.-L. Bredas, H.-L. Yip and Y. Cao, Nat. Commun., 2020, 11, 3943 CrossRef CAS PubMed.
- S. Giannini, W.-T. Peng, L. Cupellini, D. Padula, A. Carof and J. Blumberger, Nat. Commun., 2022, 13, 2755 CrossRef CAS.
- A. Landi and D. Padula, J. Mater. Chem. A, 2021, 9, 24849–24856 RSC.
- Q. Lv, C. An, T. Zhang, P. Zhou and J. Hou, Polymer, 2021, 218, 123475 CrossRef CAS.
- Y. Yang, ACS Nano, 2021, 15, 18679–18682 CrossRef CAS.
- C. Li, J. Zhou, J. Song, J. Xu, H. Zhang, X. Zhang, J. Guo, L. Zhu, D. Wei, G. Han, J. Min, Y. Zhang, Z. Xie, Y. Yi, H. Yan, F. Gao, F. Liu and Y. Sun, Nat. Energy, 2021, 6, 605–613 CrossRef CAS.
- M. B. Price, P. A. Hume, A. Ilina, I. Wagner, R. R. Tamming, K. E. Thorn, W. Jiao, A. Goldingay, P. J. Conaghan, G. Lakhwani, N. J. L. K. Davis, Y. Wang, P. Xue, H. Lu, K. Chen, X. Zhan and J. M. Hodgkiss, Nat. Commun., 2022, 13, 2827 CrossRef CAS PubMed.
- Y. Yang, Z.-G. Zhang, H. Bin, S. Chen, L. Gao, L. Xue, C. Yang and Y. Li, J. Am. Chem. Soc., 2016, 138, 15011–15018 CrossRef CAS.
- V. Savikhin, M. Babics, M. Neophytou, S. Liu, S. D. Oosterhout, H. Yan, X. Gu, P. M. Beaujuge and M. F. Toney, Chem. Mater., 2018, 30, 7872–7884 CrossRef CAS.
- J. Zhu, G. Cai, P. Xue, B. Jia, C. Zhang, X. Lu, Z. Li and X. Zhan, Energy Fuels, 2021, 35, 19055–19060 CrossRef CAS.
- M. H. Choi, K. W. Song, D. K. Moon and J. R. Haw, J. Ind. Eng. Chem., 2015, 29, 120–128 CrossRef CAS.
- G. H. L. Heintges, P. J. Leenaers and R. A. J. Janssen, J. Mater. Chem. A, 2017, 5, 13748–13756 RSC.
- M. Saito, S. Ogawa and I. Osaka, ChemSusChem, 2021, 14, 5032–5041 CrossRef CAS PubMed.
- C. Han, H. Jiang, P. Wang, L. Yu, J. Wang, J. Han, W. Shen, N. Zheng, S. Wen, Y. Li and X. Bao, Mater. Chem. Front., 2021, 5, 3050–3060 RSC.
- L. Ye, K. Weng, J. Xu, X. Du, S. Chandrabose, K. Chen, J. Zhou, G. Han, S. Tan, Z. Xie, Y. Yi, N. Li, F. Liu, J. M. Hodgkiss, C. J. Brabec and Y. Sun, Nat. Commun., 2020, 11, 6005 CrossRef CAS.
- Y. Wu, X. Kang, S. Zhang, X. Liang, D. Zhu, C. Yang, X. Qu, S. Wen and X. Bao, J. Mater. Chem. C, 2022, 10, 6754–6761 RSC.
- T. Lee, C. E. Song, S. K. Lee, W. S. Shin and E. Lim, ACS Omega, 2021, 6, 4562–4573 CrossRef CAS PubMed.
- L. Sun, K. Fukuda and T. Someya, npj Flex. Electron., 2022, 6, 89 CrossRef.
- J. Guo, K. Hu, B. Qiu, J. Zhang, D. Yang, L. Zhou, S. Li, L. Meng, Z. Zhang and Y. Li, ACS Appl. Mater. Interfaces, 2021, 13, 36033–36043 CrossRef CAS.
- Y. Wang, Q. Fan, Y. Wang, J. Fang, Q. Liu, L. Zhu, J. Qiu, X. Guo, F. Liu, W. Su and M. Zhang, Chin. J. Chem., 2021, 39, 2147–2153 CrossRef CAS.
- Y. Cui, P. Zhu, X. Liao and Y. Chen, J. Mater. Chem. C, 2020, 8, 15920–15939 RSC.
- G. Schweicher, G. DAvino, M. T. Ruggiero, D. J. Harkin, K. Broch, D. Venkateshvaran, G. Liu, A. Richard, C. Ruzié, J. Armstrong, A. R. Kennedy, K. Shankland, K. Takimiya, Y. H. Geerts, J. A. Zeitler, S. Fratini and H. Sirringhaus, Adv. Mater., 2019, 31, 1902407 CrossRef CAS PubMed.
- X. Li, H. Huang, I. Angunawela, J. Zhou, J. Du, A. Liebman-Pelaez, C. Zhu, Z. Zhang, L. Meng, Z. Xie, H. Ade and Y. Li, Adv. Funct. Mater., 2019, 30, 1906855 CrossRef.
- S. L. Price, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC.
- Q. Zhu and S. Hattori, J. Mater. Res., 2022, 38, 19–36 CrossRef.
- A. Mattei, R. S. Hong, H. Dietrich, D. Firaha, J. Helfferich, Y. M. Liu, K. Sasikumar, N. S. Abraham, R. M. Bhardwaj, M. A. Neumann and A. Y. Sheikh, J. Chem. Theory Comput., 2022, 18, 5725–5738 CrossRef CAS PubMed.
- R. Nikhar and K. Szalewicz, Nat. Commun., 2022, 13, 3095 CrossRef CAS PubMed.
- D. H. Bowskill, I. J. Sugden, S. Konstantinopoulos, C. S. Adjiman and C. C. Pantelides, Annu. Rev. Chem. Biomol. Eng., 2021, 12, 593–623 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Cryst. B, 2016, 72, 171–179 CrossRef CAS.
- W. Zhu, A. P. Spencer, S. Mukherjee, J. M. Alzola, V. K. Sangwan, S. H. Amsterdam, S. M. Swick, L. O. Jones, M. C. Heiber, A. A. Herzing, G. Li, C. L. Stern, D. M. DeLongchamp, K. L. Kohlstedt, M. C. Hersam, G. C. Schatz, M. R. Wasielewski, L. X. Chen, A. Facchetti and T. J. Marks, J. Am. Chem. Soc., 2020, 142, 14532–14547 CrossRef CAS PubMed.
- C. Xiao, C. Li, F. Liu, L. Zhang and W. Li, J. Mater. Chem. C, 2020, 8, 5370–5374 RSC.
- A. Troisi and G. Orlandi, Chem. Phys. Lett., 2001, 344, 509–518 CrossRef CAS.
- A. Landi and D. Padula, J. Mater. Chem. C, 2022, 10, 10699–10707 RSC.
- A. Landi, A. Troisi and A. Peluso, J. Mater. Chem. C, 2019, 7, 9665–9670 RSC.
- A. Landi, A. Capobianco and A. Peluso, J. Phys. Chem. Lett., 2020, 11, 7769–7775 CrossRef CAS.
- T. Nematiaram, D. Padula, A. Landi and A. Troisi, Adv. Funct. Mater., 2020, 30, 2001906 CrossRef CAS.
- C.-I. Wang, M. K. E. Braza, G. C. Claudio, R. B. Nellas and C.-P. Hsu, J. Phys. Chem. A, 2019, 123, 7792–7802 CrossRef CAS.
- R. Kubo and Y. Toyozawa, Prog. Theor. Phys., 1955, 13, 160–182 CrossRef.
- M. Lax, J. Chem. Phys., 1952, 20, 1752–1760 CrossRef CAS.
- A. Landi, R. Borrelli, A. Capobianco, A. Velardo and A. Peluso, J. Chem. Theory Comput., 2018, 14, 1594–1601 CrossRef CAS PubMed.
- R. Borrelli and A. Peluso, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 542–559 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Landi, R. Borrelli, A. Capobianco, A. Velardo and A. Peluso, J. Phys. Chem. C, 2018, 122, 25849–25857 CrossRef CAS.
- L. Wang, G. Nan, X. Yang, Q. Peng, Q. Li and Z. Shuai, Chem. Soc. Rev., 2010, 39, 423–434 RSC.
- A. Landi, J. Phys. Chem. C, 2019, 123, 18804–18812 CrossRef CAS.
- A. Velardo, R. Borrelli, A. Capobianco, A. Landi and A. Peluso, J. Phys. Chem. C, 2019, 123, 14173–14179 CrossRef CAS.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- F. Ortmann, K. S. Radke, A. Günther, D. Kasemann, K. Leo and G. Cuniberti, Adv. Funct. Mater., 2014, 25, 1933–1954 CrossRef.
- S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 3843 CrossRef PubMed.
- A. Troisi and G. Orlandi, Phys. Rev. Lett., 2006, 96, 086601 CrossRef.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347 RSC.
- F. Ortmann, F. Bechstedt and K. Hannewald, Phys. Status Solidi B, 2011, 248, 511–525 CrossRef CAS.
- O. D. Jurchescu, J. Baas and T. T. M. Palstra, Appl. Phys. Lett., 2004, 84, 3061–3063 CrossRef CAS.
- G. Nan, X. Yang, L. Wang, Z. Shuai and Y. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115203 CrossRef.
- T. Nematiaram, S. Ciuchi, X. Xie, S. Fratini and A. Troisi, J. Phys. Chem. C, 2019, 123, 6989–6997 CrossRef CAS.
- W.-Q. Deng and W. A. Goddard, J. Phys. Chem. B, 2004, 108, 8614–8621 CrossRef CAS.
- T. Nematiaram and A. Troisi, Mater. Horiz., 2020, 7, 2922–2928 RSC.
- A. Y. Sosorev, O. D. Parashchuk, N. V. Tukachev, D. R. Maslennikov, D. I. Dominskiy, O. V. Borshchev, M. S. Polinskaya, M. S. Skorotetcky, O. G. Kharlanov and D. Y. Paraschuk, Phys. Chem. Chem. Phys., 2021, 23, 15485–15491 RSC.
- M. A. Dettmann, L. S. R. Cavalcante, C. A. Magdaleno and A. J. Moulé, Adv. Funct. Mater., 2023, 2213370 CrossRef CAS.
- X. Xie, A. Santana-Bonilla and A. Troisi, J. Chem. Theory Comput., 2018, 14, 3752–3762 CrossRef CAS PubMed.
- A. Landi and A. Troisi, J. Phys. Chem. C, 2018, 122, 18336–18345 CrossRef CAS.
- Z. J. Knepp and L. A. Fredin, J. Phys. Chem. A, 2022, 126, 3265–3272 CrossRef CAS.
- A. Troisi and G. Orlandi, J. Phys. Chem. A, 2006, 110, 4065–4070 CrossRef CAS PubMed.
- J. Nelson, J. J. Kwiatkowski, J. Kirkpatrick and J. M. Frost, Acc. Chem. Res., 2009, 42, 1768–1778 CrossRef CAS.
- J. Elsner, S. Giannini and J. Blumberger, J. Phys. Chem. Lett., 2021, 12, 5857–5863 CrossRef CAS.
- J. Cerezo, D. Aranda, F. J. A. Ferrer, G. Prampolini and F. Santoro, J. Chem. Theory Comput., 2019, 16, 1215–1231 CrossRef.
- A. Segalina, J. Cerezo, G. Prampolini, F. Santoro and M. Pastore, J. Chem. Theory Comput., 2020, 16, 7061–7077 CrossRef CAS.
- L. G. da Silveira, P. R. Livotto, D. Padula, J. G. Vilhena and G. Prampolini, J. Chem. Theory Comput., 2022, 18, 6905–6919 CrossRef.
- J. G. Vilhena, L. Greff da Silveira, P. R. Livotto, I. Cacelli and G. Prampolini, J. Chem. Theory Comput., 2021, 17, 4449–4464 CrossRef CAS.
- G. Prampolini, L. G. da Silveira, J. G. Vilhena and P. R. Livotto, J. Phys. Chem. Lett., 2021, 13, 243–250 CrossRef PubMed.
- I. Cacelli and G. Prampolini, J. Chem. Theory Comput., 2007, 3, 1803–1817 CrossRef CAS.
- J. Cerezo, G. Prampolini and I. Cacelli, Theor. Chem. Acc., 2018, 137, 80 Search PubMed.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- I. Cacelli, A. Cimoli, P. R. Livotto and G. Prampolini, J. Comput. Chem., 2012, 33, 1055 CrossRef CAS PubMed.
- G. Prampolini, P. R. Livotto and I. Cacelli, J. Chem. Theory Comput., 2015, 11, 5182–5196 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- I. Cacelli, J. Cerezo, N. De Mitri and G. Prampolini,Joyce2.10, a Fortran 77 code for intra-molecular force field parameterization, available free of charge at http://www.iccom.cnr.it/en/joyce-2/, last consulted May 2022, 2019 Search PubMed.
- G. Prampolini, A. Cimoli and I. Cacelli, Picky3.0, a Fortran 77 code for inter-molecular force field parameterization, available free of athttps://www.iccom.cnr.it/en/picky-en/, last consulted May 2022, 2020.
- G. Ricci, S. Canola, Y. Dai, D. Fazzi and F. Negri, Molecules, 2021, 26, 4119 CrossRef CAS PubMed.
- G. Kupgan, X. Chen and J. Brédas, Mater. Today Adv., 2021, 11, 100154 CrossRef CAS.
- P. G. deGennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, Oxford, 2nd edn, 1993 Search PubMed.
- C. Zannoni, Liq. Cryst., 2018, 45, 1880–1893 CrossRef CAS.
- M. P. Allen, Mol. Phys., 2019, 117, 2391–2417 CrossRef CAS.
- K. Do, M. K. Ravva, T. Wang and J.-L. Brédas, Chem. Mater., 2016, 29, 346–354 CrossRef.
- A. M. Rosnik and C. Curutchet, J. Chem. Theory Comput., 2015, 11, 5826–5837 CrossRef CAS.
- D. Padula, S. Jurinovich, L. DiBari and B. Mennucci, Chem. - Eur. J., 2016, 22, 17011–17019 CrossRef CAS PubMed.
- D. Padula, M. H. Lee, K. Claridge and A. Troisi, J. Phys. Chem. B, 2017, 121, 10026–10035 CrossRef CAS.
- D. A. da Silva Filho, E. G. Kim and J. L. Brédas, Adv. Mater., 2005, 17, 1072–1076 CrossRef CAS.
- L. Greff Da Silveira, M. Jacobs, G. Prampolini, P. R. Livotto and I. Cacelli, J. Chem. Theory Comput., 2018, 14, 4884–4900 CrossRef CAS.
- L. Zhu, M. Zhang, J. Xu, C. Li, J. Yan, G. Zhou, W. Zhong, T. Hao, J. Song, X. Xue, Z. Zhou, R. Zeng, H. Zhu, C.-C. Chen, R. C. I. MacKenzie, Y. Zou, J. Nelson, Y. Zhang, Y. Sun and F. Liu, Nat. Mater., 2022, 21, 656–663 CrossRef CAS.
- Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, Sci. Bull., 2020, 65, 272–275 CrossRef CAS.
- D. Padula and A. Troisi, Adv. Energy Mater., 2019, 9, 1902463 CrossRef CAS.
- D. Padula, J. D. Simpson and A. Troisi, Mater. Horiz., 2019, 6, 343–349 RSC.
- E. Palacino-González and T. L. C. Jansen, J. Phys. Chem. C, 2023, 127(14), 6793–6801 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational details, interaction energy curves, further structural and electronic characterisation along MD simulations. See DOI: https://doi.org/10.1039/d3ya00149k |
| This journal is © The Royal Society of Chemistry 2023 |