On the water transport mechanism through the microporous layers of operando polymer electrolyte fuel cells probed directly by X-ray tomographic microscopy

Abstract

Product water transport via the microporous layer (MPL) and gas diffusion layer (GDL) substrate during polymer electrolyte fuel cell (PEFC) operation was directly and quantitatively observed by X-ray tomographic microscopy (XTM). The liquid water distribution in two types of MPLs with different pore size distributions (PSDs) was characterized as a function of the inlet gas relative humidity (RH) and current density under humid operating conditions at 45 °C. During the first minute of PEFC operation, liquid water mainly accumulated at the catalyst layer (CL)/MPL interface and in the GDL substrate close to the flow fields. Furthermore, under all tested conditions, saturation in the MPL was low (<25%), whereas under the rib, the saturation in the GDL was up to ca. 70%. Based on these XTM results, it is confirmed that in the high porosity MPLs, vapor transport was non-negligible even at high humidity conditions. Therefore, on top of the widely discussed MPL pore size and its distribution, it is proposed that the lower thermal conductivity from the high porosity of MPLs can also be a main cause of promoted vapor transport, reducing water saturation near the CL.

---

1. Introduction

Hydrogen-fueled polymer electrolyte fuel cells (PEFCs) efficiently convert hydrogen into electricity. When coupled with green hydrogen, this technology can play an important part in a sustainable energy infrastructure in the (near) future.^1,2 High power density and wide-range applicability (applicable to hydrogen fueled electric cars, trucks, trains or even aircraft) are major characteristics of PEFCs.

Still, achieving a more efficient use of the fuel or higher power density is essential when manufacturing competitive and cost-effective fuel cell technology for demanding mobility applications. Nowadays, high-performance PEFCs have “two-layer”-structure gas diffusion layers (GDLs)—namely, a carbon fiber porous substrate (for example, carbon paper) with a microporous layer (MPL) at the interface toward the catalyst layer. The goal of this arrangement is to achieve efficient water management and improve the performance especially at humid conditions.^3–11 Microporous layers (MPLs) are conventionally composed of carbon and/or graphite nanoparticles as the conductive materials, which are modified and bound by fluoropolymer binders (such as PTFE and FEP) to give the MPLs net hydrophobic surface properties.¹² While the pore size distribution (PSD) of the GDL substrates is typically in the range of 5–80 μm,^13–17 MPLs’ modal pore size is generally much smaller—smaller than 1 μm.^18–20

Until now, several hypotheses have been formulated to explain the PEFC performance improvement by MPLs based on either modeling results or PEFC performance characterizations. For instance, MPLs are said to bring about a reduction of the water saturation in the GDL substrate due to constricted number of water breakthrough points from the catalyst layer (CL).^9,21–24 This hypothesis is similar to the concept that the capillary pressure gradient from the MPL to the GDL substrate leads to a “wicking” effect that assists liquid water removal generated from the CL.^10,12 Moreover, the hydrophobic, nanoscale pores of the MPLs have been proposed to prevent water accumulation in the GDL near the catalyst layer.^9,20,25–28 The small hydrophobic pores constituting a capillary barrier that facilitates water back diffusion from the cathode to the anode.^4,29–33 While this effect is said to improve membrane hydration, it could also, in theory, result in higher CL saturation, leading to reduced turnover frequencies of the catalyst due to hindered reactant mass transport. In recent years, there have been studies which argued that MPLs introduce a layer of lower thermal conductivity,³⁴ locally increasing the temperature of the catalyst layer during operation, thereby promoting vapor transport.^35,36

In fact, observations and explanations for MPL functions in various literature often appear fragmented and lack a completely consistent picture, leading to conflicting results.^8,21,37–40 One notable example is that there is not yet a unified design for MPL morphology, regarding the introduction of cracks. Both cracked MPLs^{37,38,41–44} and crack-free MPLs^45–47 can be seen promoted in the literature and are widely accepted by the market. Similarly, there are also various different ways of attuning MPL porosity and its pore size distribution (PSD) that all somehow showed improved performance, despite noticeable differences in their design among one another.^{8,37,39,48–50}

It seems clear that although performance testing and modeling can verify some functions of the MPL, there is a noticeable gap between understanding proposed mechanisms and confirming their actual effects. Direct observations of water transport within this specific layer can help elucidate the reasons why MPL promote performance, and are therefore essential. Yet they remain scarce. This is at least partly due to the difficulties arising from the small MPL pore size and their low thickness (many of them <50 μm).⁵¹

Over the past decade, X-ray imaging methods are gaining insights to water distributions in operando PEFC diffusion and even catalyst layers,⁵²e.g. by radiography^{3,28,43,53–58} and X-ray tomographic microscopy (XTM).^3,56,59–62 Both methods are compatible with operando fuel cell investigations as they are not intrusive. For MPL characterization, often radiography is used.^{53,57,58,63–67} However, radiography can be highly sensitive to sample orientation, and the boundaries between interfacial regions (CL/MPL/GDL substrate) are not always straightforward to distinguish clearly based on the radiographs. The boundary surfaces are often not perfectly smooth and can undergo movement during PEFC operation.^63,68 X-ray tomographic microscopy thus has advantages over radiography in the respect that it allows distinguishing the interfacial regions more accurately by the three-dimensional (3D) information it provides.

In this work, we quantitatively investigate the liquid water quantity distribution across the MPL and GDL substrate using X-ray tomographic microscopy (XTM), starting from a dry state and with a focus on the MPLs. Synchrotron radiation enables fast operando imaging, so the evolution of the water distribution during the first minute can be characterized, and allows for insight into the water transport mechanisms through the MPLs. Here, two types of in-house made highly porous hydrophobic MPLs (ca. 80% porosity)—one carbon black and one fiber based—are used as they improve PEFC performance under humid operating conditions.^37,65

2. Experimental section

2.1 PEFC components and XTM analyzing zones

A small PEFC suitable for X-ray tomographic imaging with an active area of 0.16 cm² (4.5 mm × 3.6 mm) and double flow channel configuration was used for operando liquid water characterization (Fig. 1). The design of this tomo-cell was described in detail by Eller et al.⁶⁹

Fig. 1 (a) X-ray tomographic through-plane image slice showing the components of the PEFC with Freudenberg H14 GDLs and VGCF MPL coating; (b) enlarged image under the channel region illustrating the different zones (CL, CL/MPL, MPL, MPL/GDL, GDL, GDL/Channel and Channel) of the PEFC for measurements (cathode). Dashed lines indicate that the zone boundaries are not always clear-cut.

For this study, two types of gas diffusion layers based on the same Freudenberg H14 substrates (hydrophobically treated) but different in house-made MPLs were used, namely the vacuum-grown carbon fiber (VGCF) MPL and the acetylene black (Denka) Li100 MPL. The H14 GDL substrate was evaluated to have an average of 66% bulk porosity, based on the binary segmentation of its tomographic images, (for detailed methodology, see Chen et al. (2022)⁵¹). The manufacturing processes and properties of both MPL materials were described by Simon et al. (2019)³⁷ and (2017),³⁹ respectively. The two MPLs were prepared with the same additives and PTFE content (20 wt%). Both MPLs had similar porosity (79% for Li100 MPL and 83% for VGCF MPL) but distinctly different pore size distributions (PSD): the Li100 MPL had a pore size distribution between ca. 30 nm and ca. 10 μm and a modal pore size of 67 nm; whereas the VGCF MPL had a pore size distribution between ca. 300 nm and ca. 4 μm, with modal pore size of 722 nm.^37,39 The uncompressed MPL thickness was measured by tomographic images to be 43 ± 4 μm and 50 ± 4 μm for Li100 and VGCF MPL, respectively. The total uncompressed thickness of the GDL including the MPL was 162 ± 4 μm for Li100 and 179 ± 4 μm for VGCF GDL. The thickness measurement error was derived from the assumption that judgments of MPL and GDL thickness involve ±1 voxel edge length of uncertainty at the upper boundary and the lower boundary each (between which the thickness is determined). This translated to ca. ±1.4 voxel-equivalent thickness assessment error, namely, ±4 μm.

The membrane electrode assembly (MEA) consisted of a catalyst coated membrane (CCM, Gore® Primea® A510.1/M815.15/C510.4); having a 15 μm thick membrane with anode/cathode Pt loadings of 0.1/0.4 mg cm⁻². The active area of 4.5 mm × 3.6 mm was shaped by laser ablation of the surrounding catalyst layer. The CCM was sandwiched between two identical gas diffusion layers, either with VGCF or Li100 MPL coating. In the PEFC assembly, the MEA was compressed by using thickness-adapted FEP gaskets to tune the GDL thickness (including the MPL) to ca. 80% of its original thickness (132 ± 3–144 ± 3 μm after compression) under the rib regions. The PEFC configuration and different characterization zones (CL, CL/MPL, MPL, MPL/GDL, GDL, GDL/Channel and Channel) are illustrated in Fig. 1. For additional drawings of the PEFC for tomography experiments, the reader is referred to Xu et al. (2022).⁷⁰

2.2 Operando PEFC XTM at the swiss light source (SLS)

All operando X-ray tomographic microscopy (XTM) imaging was conducted at the TOMCAT (X02DA) beamline of the Swiss Light Source (SLS) at Paul Scherrer Institut (PSI). A monoenergetic X-ray beam of 16 keV (Δ E/E ≅ 2–3%) was used to exploit the quantitative linear attenuation coefficients of a monochromatic beam. This beam energy was chosen to improve the transmission of X-ray beam through the platinum-based catalyst layer while maintaining the image contrast for the carbon and liquid water phases. The GigaFRoST camera⁷¹ coupled with an Optic Peter macroscope (magnification of 4.0×)⁷² resulted in a voxel edge length of 2.75 μm. The scintillator used was a LuAG:Ce screen with a thickness of 150 μm. The detector field of view was 2016 pixels × 1500 pixels. For X-ray tomography, 800 projections were taken for a sample rotation of 180°, and the exposure time for each projection was 1 ms. This resulted in an acquisition time of 0.8 s per tomographic scan.

Prior to XTM characterization, PEFCs were conditioned in the lab for ten hours at ca. 26 °C with H₂/Air supply at 100 mL min⁻¹ and 100% relative humidity (RH) for both anode and cathode. The conditioning protocol started with operating at constant voltage at 0.6 V for 45 min, followed by 0.95 V for 10 min and 0.85 V for 5 min; the protocol was repeated for a total of ten times.

To characterize the influences of relative humidity and current density on water distribution in the GDL/MPL, three current densities (0.5, 1.0, 1.5 A cm⁻²) were tested. At each current density, three relative humidity (RH) conditions for the feed gases (90%, 100% and 110%, corresponding to gas dew points of 43 °C, 45 °C and 47 °C) were tested (same humidity for the anode and cathode gas). This constituted nine conditions for each GDL/MPL material in total. The cell temperature was 45 °C for all conditions; anode and cathode gas feed was H₂/air at 200 mL min⁻¹.

For the operando X-ray tomographic imaging, first, the cell was dried at 45 °C by flushing it with nitrogen at 50% RH, 200 mL min⁻¹ flow rate. The cell was considered to be dry without excessive membrane shrinking when the high frequency resistance (HFR) measurement exceeded 0.40 Ω. With an active catalyst layer area of 0.16 cm², this translated to an area resistance of >0.064 Ω cm². Drying protocols for XTM cells were always a compromise between drying of the cell properly and achieving minimal membrane shrinking. Both membrane shrinking during drying protocol (may result in local irreversible structural changes at the CL/MPL interfaces) and membrane swelling during operation made the subtraction-based image evaluation challenging (see chapter 2.4), in particular for the MPL phase. There was no reliable method to verify the degree of dryness in the MPL as a result of the drying protocol, but it is noteworthy that any water remained in the MPL would be reflected in the tomographic image error estimation step (chapter 2.5), and interpreted as uncertainty (discussions are given below). Therefore, remaining wetness (if present) should have not invalidated the signal interpretation as long as the tomographic image error was taken into account.

After the nitrogen drying, the cell was flushed with H₂/Air with the target RH with 200 mL min⁻¹ for 30 s before the target current (density) was drawn. Just one second before the current was switched on, a tomographic scan was taken and it is referred to as the “dry scan”; from then on, seven operando “wet scans” were taken at the 1st, 3rd, 5th, 10th, 15th, 30th and 60th second of cell operation at the targeted constant current density. The study was limited to eight scans per condition, distributed over the first 60 s to avoid radiation damage bias and to allow for measuring nine conditions (three current densities at three different humidities of feed gases) for two different materials in the limited beam time of 24 h. Note that the “dry scan” was acquired after gases at the designated operation RH (90%, 100% or 110%) were flushed through the cell for 30 s. The dry scan and its following seven wet scans together were referred to as a “dynamic scan series”. Such dynamic scan series were done for each of the nine PEFC operating conditions.

2.3 PEFC radiation heating and damage

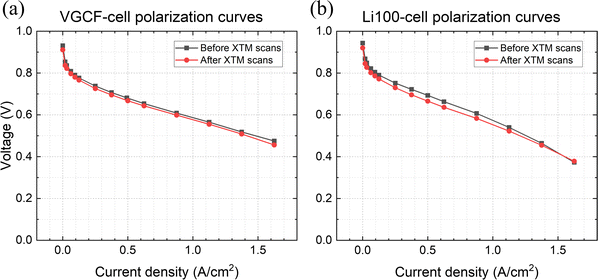
The radiation heating effects for the PEFC set-up used here have been analyzed for the 13.5 keV monochromatic beam of the TOMCAT beamline at SLS by Eller and Büchi (2014).⁷³ The beam intensity of the 16 keV beam used in the present experiments (7.9 × 10¹¹ photons s⁻¹ mm⁻²) was slightly higher than 13.5 keV (6.0 × 10¹¹ photons s⁻¹ mm⁻²). However, the lower absorption at 16 keV made it likely that the two effects compensated each other. Therefore, we assumed a similar radiation induced heating power to the cells at 13.5 keV (Eller and Büchi (2014)⁷³) and 16 keV. The electrochemical energy conversion heating power was approximately 275 mW cm⁻² (HHV) for 0.5 A cm⁻² (∼0.7 V) and ca. 1125 mW cm⁻² at 1.5 A cm⁻² (∼0.5 V). So, using the heating power values Eller and Büchi (2014) derived for 13.5 keV, the heating power of the beam added to maximally 4% heat for the low current density and 1% heat for the high current density. We therefore think the X-ray heating effect was negligible.

The radiation damage is another concern, this can be directly be assessed by polarization curves. The data for the VGCF- and Li100-cells before and after XTM scanning of all nine conditions are shown in Fig. 2. During X-ray tomographic imaging, the whole catalyst active area is was fully exposed to the X-ray beam irradiation. This ensured that the influence or damage from the radiation was easily detectable.

Fig. 2 Polarization curves of (a) VGCF-cell and (b) Li100-cell before X-ray exposure and after all nine tomographic scans; during polarization curve acquisition, cell temperature: 45 °C, H₂/air flow rate: 200/200 mL min⁻¹, relative humidity (RH) of H₂/air: 100%/100%.

The polarization curves of the VGCF- and Li100-cells showed the expected trends, which were previously shown by Simon et al.^37,39 Both cells performed similarly in the kinetic and ohmic regime (low and intermediate current densities), while the VGCF-cell outperformed the Li100-cell under mass transport limited conditions (high current densities, e.g. >1.5 A cm⁻²). It was previously shown that the performance improvement of the VGCF MPL at wet conditions (high RH, high pressure) correlated with a reduced oxygen transport resistance.^37,39 Since both operando cells showed little change in polarization curves before and after XTM characterization, the degradation of the cell due to X-ray irradiation was judged to be minor. Due to this stability in electrochemical performance, all scans for all conditions were considered to be valid for water volume fraction estimation and transport mechanism characterizations.

2.4 Image processing workflows

The reconstructed absorption-contrast tomograms are 32-bit⁷⁴ where each voxel's grayscale value (GSV) is proportional to the linear attenuation coefficient of the materials in that voxel. The product water's liquid volume fraction (LVF) distribution can be obtained by subtracting the dry scan image from the wet scans (scans taken during PEFC operation). The resultant images (referred to as “difference images”) have GSV proportional to the volume of liquid water in each voxel, because water is supposed to be the only material phase that changed in amount during PEFC operation.

Prior to image subtraction, the selected dry state images and the wet images of the cathode regions under the rib and channels (defined in Fig. 1a, measurement volume) were aligned separately using 3DSlicer (version 4.11) with the in-built rigid registration and affine registration functions (with default registration parameters).⁷⁵ Dry images that resulted in the least negative LVF peaks were selected to be the reference because LVF cannot be negative. Note that such selection of dry images was allowed because the dry state structures were treated as equivalent, and the tomographic image error can still be captured by the error estimation (see 2.5) to some extent. The dry scan was the fixed image and the wet scans were the moving images. The alignment was done for regions below channels and below ribs separately to mitigate the adverse impact from inhomogeneous membrane swelling on image evaluation. This practice resulted in better-aligned image stacks and reduced error from misalignment.

The obtained difference images were divided by a constant normalization factor, which is the average GSV of pure liquid water phase measured in the difference images (sampled from water droplets in the channels of VGCF-cell at the 110% RH operation condition). This procedure rendered the liquid volume fraction (LVF) of water across the entire tomographic image stacks based on the proportionality of GSV and linear attenuation coefficient. The normalization factor was measured to be 2.88 × 10⁻⁴ and was used to evaluate all images. To reduce the image noise, the images were subsequently filtered (two-dimensional) with ImageJ filtering function, “mean filter” (two-dimension), with a radius of 6 pixels. To obtain color-coded LVF distribution maps, ImageJ LUT “Physics” was applied to the mean-filtered images.

To obtain LVF profiles under the channel and under the rib, average LVF values were calculated for each LVF image under the respective channel/rib region at each through-plane position (illustrated Fig. 1b). The measured average LVF was plotted against the through-plane position.

2.5 Tomographic image error estimation (from imaging artifacts and misalignment)

Due to the low transmission of X-ray beams through the catalyst layer (CL), there are artificial features in the vicinity of the CL, sometimes referred to as “catalyst shining” in PEFC tomographic images. Catalyst shining is likely a result of photon starvation and has been a major obstacle to characterizing liquid water in the MPLs, because MPLs are generally thin (20–100 μm) and close to the CL. This means that the grayscale values (GSVs) of a significant volume of the MPL may be altered by catalyst shining. Nevertheless, catalyst shining can be compensated or largely nullified in cases where there is minimal membrane swelling and where the image alignment quality is good (Fig. S1, ESI†). These requirements are not always fulfilled for operando imaging, where errors can emerge from local inhomogeneous membrane swelling (causing image misalignment) and from local structure changes due to repeated cell drying, humidifying and operation.

To estimate the error involving all non-random error sources, we assume that the degree of structural differences and membrane movement among dry scans taken at different RH conditions and different times across all nine conditions would be comparable to that among the dry scans and wet scans (operando scans).

With this premise, the nine dry scans (taken at different RH conditions or different moments) were aligned against one another using 3DSlicer with the same default registration parameters mentioned before (rigid registration followed by affine registration), and image subtraction was subsequently carried out. This resulted in 72 difference images, whose average grayscale values (GSVs) with respect to the through-plane distance reflected the error (mainly from image misalignment and membrane swelling) and were used to model the emerging error during operando scans. Plotting the averaged normalized GSVs of the dry–dry difference images against the through-plane distance, with the origin at the CL position and the direction toward the flow fields, 70–72 “error curves” modeling the non-random error from local structural change were obtained. The range across which 80% of all error curves span was arbitrarily determined to be the estimated non-random error range for dynamic scan series because the authors believe that the (CL and MPL) structural differences within one dynamic scan series would not be larger than the dry–dry scan differences captured across all nine dry scans at different RH conditions.

The high frequency resistance (HFR) of the cell at the time of recording the dry scan (one second before applying current) and different RH conditions is provided in Fig. S2 (ESI†). It is shown that minor differences occurred between the same dew point/humidity conditions, whereas the expected differences were observed across different humidity conditions. This shows the good repeatability of the protocol before scanning and points toward validity of the error evaluation. The error is not dominated by macroscopic cell parameters but is indeed imaging-based.

The abovementioned procedure was done for the regions under the channel and under the rib separately, and was also done for the VGCF- and Li100-cells separately. The error obtained is plotted as orange shading in the LVF profiles in Fig. 3, 4, 6 and 7. It should be noted that the error estimation done this way would also include the error caused by any wetness in different PEFC layers, in case the cell drying protocol (2.2) was not sufficient to remove all water from the diffusion layers.

Fig. 3 Average liquid volume fraction (LVF) of product water in the CL, MPL and GDL of the operando VGCF-cell with 90% RH feed gases; LVF profiles are given at indicated times after the start of constant current operation with the estimated non-random error plotted as orange shade at (a) and (b) 0.5 A cm⁻² & 1.5 A cm⁻² under the channel, (c) and (d) 0.5 A cm⁻² & 1.5 A cm⁻² under the rib.

Fig. 4 Average liquid volume fraction (LVF) of product water in CL, MPL and GDL of the operando VGCF-cell with 110% RH feed gases; LVF profiles are given at indicated times after the start of constant current operation are given with estimated non-random error plotted as orange shade at (a) and (b) 0.5 A cm⁻² & 1.5 A cm⁻² under the channel, (c) and (d) 0.5 A cm⁻² 1.5 A cm⁻² under the rib.

It is worth mentioning that the error at the catalyst layer may be relatively poorly modeled. Since the images were cropped near this layer before carrying out image alignment, some part of the CL may have been cropped out during alignment, resulting in a poorer estimation of error. Consequently, the water LVF in the CL is not discussed here.

2.6 Influence of tomographic image noise on the discernability of liquid volume fraction (LVF)

In addition to tomography artifacts, image noise also alters the values of image voxels and adds uncertainty to the voxel-based LVF evaluation. Assuming that the tomographic image noise is approximately Gaussian-distributed, the error from tomographic image noise can be obtained by measuring large numbers of the voxel GSVs of a certain, constant materials phase (e.g. air, water). This allows to assess the confidence when we interpret the local LVF of an image. With homogeneous, Gaussian-distributed noise over the LVF image region of interest, the probability that two regions with the same physical LVF (i.e., actual LVF in the MPLs) would have different imaged LVF (LVF measured by tomography) separated by ≥2.8σ, is <0.05 (derived from the probability density function of Gaussian distribution). This provides a limit and also a guideline to LVF image interpretation: LVF images are to be interpreted in probabilistic manners, and to obtain discernability of LVF among any two regions, one can either reduce image noise at the image acquisition steps (higher photon flux per voxel volume or higher image contrast), or compare the averaged LVF of larger areas, i.e., conduct voxel averaging that effectively reduce σ. When the voxel averaging method is used, the relationship between the measured 2.8σ uncertainty with respect to the number of voxels sampled is given in Fig. S9 (ESI†). More details on discernability can be found in Chen et al.⁵¹

3. Results

The effect of current density and feed gas RH on water distribution in the MPL and GDL substrates at the cathode was probed by analyzing the water volume (fraction) distribution using X-ray tomographic microscopy. The PEFCs were operated at low temperature (45 °C) with feed gas relative humidity (RH) values between 90% and 110%. According to literature, this relatively lower cell temperature should promote liquid transport within the MPL.^25,76,77 We are interested in the first minute of PEFC operation to gain insight to potential water transport mechanisms, which are easier to understand when starting from a dry porous material.

The liquid water evolution in different zones of the membrane electrode assembly (MEA)—namely, at CL/MPL interface, MPL, MPL/GDL interface and GDL (substrate)—was characterized by the average liquid volume fraction (LVF) of product water in the through-plane direction. The CL is close to the image boundary and is prone to error during alignment procedure (in some images, the CL region is cropped out during image alignment). As a result, the LVF in the CL is not discussed. Results for two different MEAs with different high porosity MPLs are presented—one based on vapor-grown carbon fibers (VGCF) and one on acetylene black (Li100), at both 90% and 110% RH, and both 0.5 and 1.5 A cm⁻².

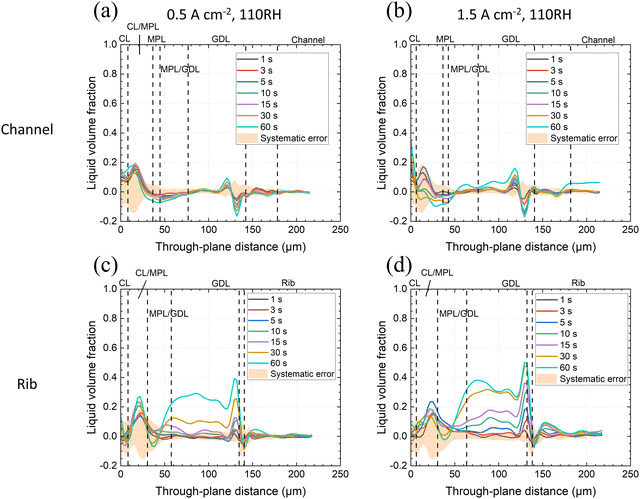
3.1 VGCF-cell operando water distribution – LVF profiles and LVF maps

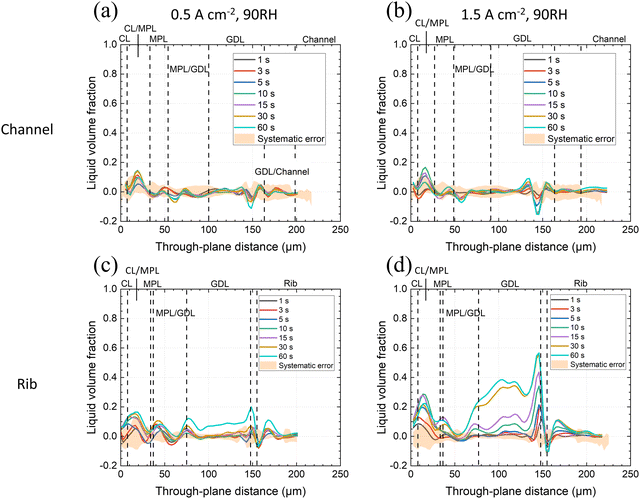
The VGCF MPL has a high porosity (83% when uncompressed). Its pore size distribution is between ca. 300 nm and ca. 4 μm where the modal pore size is 722 nm (Section 2.1) and a noticeable portion of the MPL pores are >1 μm.³⁷ Additionally, the VGCF MPL has coarsely distributed larger, ellipsoidal pores that can be 40–50 μm wide in the in-plane direction (Fig. S3, ESI†). The uncompressed MPL thickness was ca. 50 ± 4 μm as measured under the channels. However, under the rib, the MPL was compressed to ca. 28 ± 4 μm. This is a 44 ± 9% compression, higher than the overall 22 ± 2% compression of the GDL (including MPL). As a result, the MPL porosity under the channel will be 83% but under the rib ca. 70 ± 5% (assuming the solid part remained the same in volume).

Operando LVF profiles across zones of the MEA at the cathode at 45 °C, 90% RH and current densities of 0.5 and 1.5 A cm⁻² are given in Fig. 3 for the first minute of operation when starting from a dry MEA. The through-plane position originates from the CL-plane and directs toward the flow field (channels and ribs). Liquid volume fraction profiles were analyzed separately for the cathode's rib and channel domains.

Under the channel, at 90% RH, there was no liquid water observed, neither in the MPL nor in the GDL substrate regardless of the current density for the first minute operation (Fig. 3a and b). The LVF peaks at the CL/MPL interface were close to the estimated non-random error. The origin of the negative peak appearing in most LVF profiles at through-plane distance ca. 150 μm (close to the GDL/flow field interface) was not clear. We suspect that this was a result of edge enhancement at the GDL/rib interfaces, whose intensity varied depending on how much water existed on the rib surface—although, to determine the definite cause, further inspections need to be made. The CL/MPL interface was sometimes thicker than the (pure) MPL domain thickness because of the slight waviness of these layers.

In contrast, under the rib, liquid water accumulation in the GDL was observed after 60 seconds of operation at 0.5 A cm⁻² (Fig. 3c). Whereas at 1.5 A cm⁻² (Fig. 3d), liquid water was first seen condensed at the surface of the rib (through-plane position 150 μm) already after only 3–5 s of cell operation, and further filled up all the surface of the rib (Fig. S4, ESI†). Within the GDL pores, water accumulation was observed at the 10th second of operation, and starting from the same time water could be seen at the CL/MPL interface, and LVF kept growing during PEFC operation. There was consistently less water in the MPL zone and almost no water at the MPL/GDL interface (Fig. 3d). It seemed obvious that for 90% RH condition, water removal from the catalyst layer by vapor transport was prominent. Therefore, no significant LVF signals were observed at the CL/MPL boundary and the diffusion layers, except for the 1.5 A cm⁻² current density under the rib, where the longer diffusion path and/or lower local temperature (due to underlying rib structure) led to a noticeable LVF. The positive LVF signal in the rib solid part (through-plane distance >160 μm in Fig. 3c and d) was of unknown origin, as there should not exist any water inside the solid ribs. It is suspected that the signal was also a result of interfacial edge-enhancement artifact of the water accumulation under the ribs, related to the negative peaks at through-plane distance ca. 150–160 μm, as previously proposed.

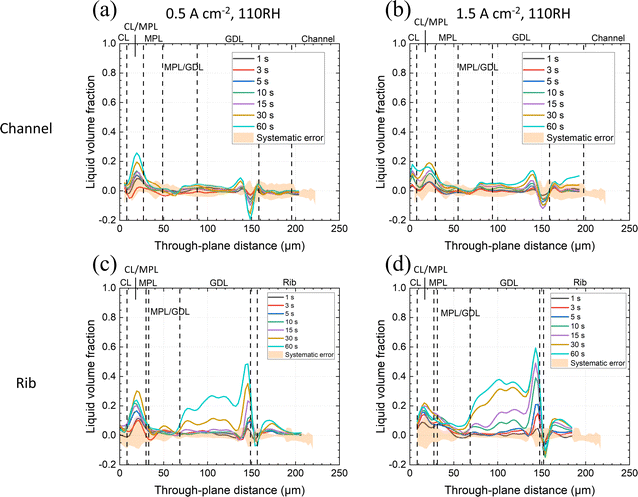
The results for the VGCF-cell with enhanced, 110% RH are given in Fig. 4.

The higher RH led to an increase of liquid water accumulation, markedly at the CL/MPL interface and in the substrate of the rib region (Fig. 4). At 1.5 A cm⁻², also in the MPL under the rib (at a through-plane distance of ca. 30 μm) there was an increased liquid water volume fraction observed (Fig. 4d). It is inferred that at the higher RH condition, water removal by vapor transport was less efficient, and therefore condensation and liquid transport occurred at both current densities (0.5 and 1.5 A cm⁻²), regardless of the rib/channel region. Again, since the CL is close to the image boundary and is prone to error, the LVF in this layer is not discussed.

Judging from Fig. 3 and 4, the relative humidity of gas and the local temperature gradient from the CL to the flow field seemed to determine the water transport via MPL. During operation, CL temperature increases locally^78,79 and the thermal gradient is proposed to be further accentuated in the presence of MPLs by their low heat conductivity^35,80,81 (especially for the materials with high porosity,^34,82 like the ones used here), resulting in promoted vapor transport via the MPL.^36,83 (This was observed for VGCF-cell at 90% RH, Fig. 3). However, when the relative humidity in the channel increased to 110% RH, the reduced vapor transport capability led to increased accumulation of liquid water at the CL/MPL interface (compared to the absence of water in Fig. 3a–c) and combined vapor/liquid transport. At higher water generation rates (1.5 A cm⁻²), the accumulation of water further took place in the bulk of the VGCL MPL, especially under the rib (Fig. 4d), indicating the increase of liquid transport. Note that it can occur, that the magnitude of measured LVF did not always increase with time progression. For example, at the CL/MPL interface in Fig. 4b–d (through-plane distance ca. 20 μm), the LVF at 60 s is lower than at 30 s. This may have been a result of higher error at that interface.

Despite the fact that water accumulation in the MPL was observed at the highest current density condition (1.5 A cm⁻²), there was less water in the MPL than at the CL/MPL interface in general. Water predominately accumulated in the CL/MPL mixed zone and in the GDL substrate, instead of in the MPL. The higher LVF of water at the CL/MPL interface of the VGCF-cell under the channel, compared to in the MPL, was also clearly seen from the distribution maps of product water in Fig. 5 for the high humidity and high current density condition. This observation coincides with the findings of Lee et al. (2015),⁶⁷ who reported that the MPL generally reduces the amount of liquid water, regardless of the MPL thickness.

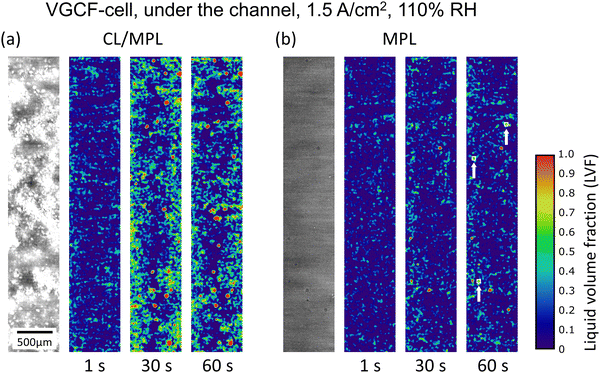Fig. 5 Liquid water distribution under the channel: (a) at the CL/MPL interface (through-plane position ca. 17 μm in Fig. 4(b)), and (b) in the MPL (through-plane position 39 μm) of the VGCF-cell operated at 1.5 A cm⁻² and 110% RH; from left to right: dry state tomographic image, product water LVF distribution maps at 1, 30 and 60 s PEFC operation time; white boxes indicated with arrows in the rightmost map show 50 μm × 50 μm areas, where LVF of >21% represent a 95% probability of real water).

The LVF maps in Fig. 5 confirm the tendency of water accumulation at the CL/MPL interface. At the CL/MPL interface (Fig. 5a), most of the about 25 larger pores were filled with water (red circular dots) after 30 s PEFC operation, and the pattern of water distribution remained similar further to 60 s. When the images in Fig. 5 are considered not to be severely influenced by image artifacts, LVF can be judged by the discernability criterion (details in chapter 2.6 and Fig. S9, ESI†). In many mesoporous regions in the 30 s and 60 s images in Fig. 5a, the LVF between 0.5 and 0.7 (green and yellow color), exceeded the discernability criterion (for a 50 μm × 50 μm area region, >21% LVF represents a >95% probability that liquid water existed in those mesopores).

In the MPL bulk (Fig. 5b, 22 μm further away from the CL/MPL interface shown in Fig. 5a), there was much less liquid water, and only 5–6 larger pores were filled (red circular dots). There was also considerably less water in the MPL mesopores (e.g., the two squared regions, marked by arrows exceeding the discernability criterion for 50 μm × 50 μm). No water was detected in most of other mesoporous regions. The clear observation of water in the large pores, together with the discernability criterion that allows us to distinguish water from random noise (in the absence of image artifacts), demonstrated that the LVF profile peak of Fig. 4b at the CL/MPL interface was real and not just an imaging error. For the water distribution maps at all scanned times for this condition, the reader is referred to the ESI† (Fig. S5).

Overall, it can be stated that in the MPL, vapor transport seemed to be the predominant mechanism of transport at low RH and/or low current density, while a mixed water transport mode (vapor/liquid) took place for high RH and high current density.

3.2 Li100-cell operando water distribution – LVF profiles and LVF maps

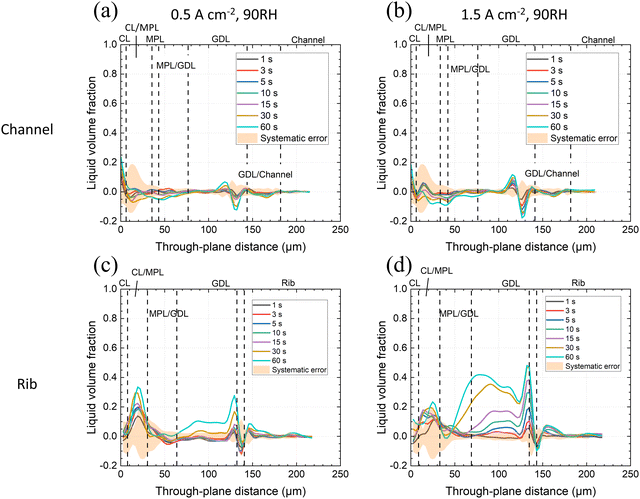
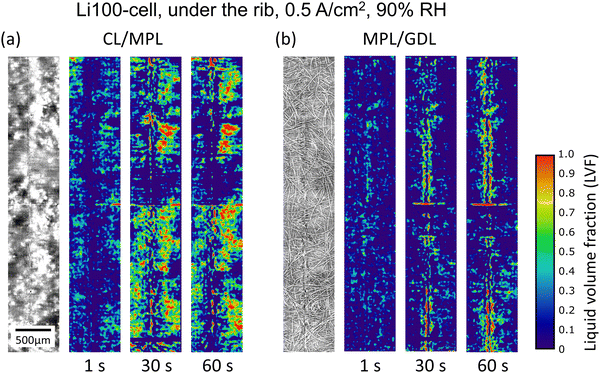
The Li100-cell's MPL has similarly high porosity (79% when uncompressed) as the VGCF MPL (83%). However, based on carbon black powder, at its modal pore size (67 nm) is an order of magnitude lower and it has a PSD between ca. 30 nm to ca. 10 μm (Section 2.1). Unlike VGCF, the Li100 MPL does not have larger pores that can serve as structural references during image alignment. As a result, there was a larger error from local misalignment and uncompensated catalyst shining at the CL/MPL interface and in the MPL, resulting in a wider error range. The average MPL thickness was ca. 43 ± 4 μm as measured under the channels. However, under the rib, the thickness was compressed to ca. 25 ± 4 μm (see Fig. S6, ESI†). Together with the slight waviness of the CCM, this low MPL thickness made no separate MPL phase observable, unlike that for VGCF in Fig. 5. The MPL rib-thickness resulted in a 42 ± 10% compression of the MPL, which was more than the 20 ± 3% compression of the overall GDL (including MPL). Consequently, while the MPL under the channel had an estimated porosity of ca. 79%, under the rib, the porosity dropped to 64 ± 7%.

Operando LVF profiles across the zones of the MEA at 45 °C, 90% RH, for 0.5 and 1.5 A cm⁻² current density, are presented in Fig. 6.

Fig. 6 Average liquid volume fraction (LVF) of product water in CL, MPL and GDL of the operando Li100-cell with 90% RH feed gases; LVF profiles at are given at indicated times after the start of constant current operation are given with estimated non-random error plotted as orange shade at (a) and (b) 0.5 A cm⁻² & 1.5 A cm⁻² under the channel, (c) and (d) 0.5 A cm⁻² & 1.5 A cm⁻² under the rib.

Similar to the VGCF-cell, for the Li100-cell, no significant amount of water was observed under the channels when operated at 90% RH over the entire range of the porous layers (Fig. 6a and b), regardless of the current density.

In contrast to the VGCF-cell, under the rib, there was an LVF peak at the CL/MPL interface at 0.5 A cm⁻² (the peak values became significant at the 30th and 60th second of operation). Water was also seen in the GDL at the same time (Fig. 6c). However, this slightly larger peak compared to the VGCF-cell might have been outweighed by the larger error of the Li100-cell. Note that under the rib, the low MPL thickness made no separate MPL phase visible. The CL/MPL interface was followed directly by the MPL/GDL interface.

In the GDL substrate, similar to the case with the VGCF-cell, water first appeared on the surface of the rib, as indicated by the LVF peak at a through-plane position of ca. 130 μm (Fig. 6c) (see also Fig. S7, ESI†). The saturation in the GDL pores increased both in the middle region of the GDL substrate and on the surface of the rib. The effect of higher current density resulted in a much earlier onset of water condensation on the rib surface, already after 3 s of PEFC operation, as well as an increased amount of liquid water within the GDL (Fig. 6d).

Overall, at 90% RH condition for the first minute of operation, there was no water in the MPL zone at the channel. But under the rib, supposedly due to the lower local temperature, liquid water could be observed at the MPL/GDL interface and in the GDL substrate (Fig. 6c and d). The reason why the LVF was larger at 0.5 A cm⁻², CL/MPL interface compared to 1.5 A cm⁻² is unclear. It could either be due to lower waste heat at low current density or image error.

The results for Li100-cell operation at 110% RH are given in Fig. 7.

Fig. 7 Average liquid volume fraction (LVF) of product water in CL, MPL and GDL of the operando Li100-cell with 110% RH feed gases; LVF profiles are given at indicated times after the start of constant current operation are given with estimated non-random error plotted as orange shade at (a) and (b) 0.5 A cm⁻² & 1.5 A cm⁻² under the channel, (c) and (d) 0.5 A cm⁻² & 1.5 A cm⁻² under the rib.

Different from the VGCF-cell, for the Li100-cell under the channel, the higher RH did not promote any water accumulation at the CL/MPL interface and in the MPL that was significant enough to be detected within the first minute of operation (Fig. 7a and b).

Under the Li100-cell rib, water was observed at the CL/MPL interface, though less prominent than for VGCF, as shown in Fig. 7c. It is therefore judged that overall, the Li100 MPL suppressed liquid water occurrence within the MPL better than VGCF (Fig. 4c, d and 7c, d). It is suggested that the smaller (hydrophobic) pores of Li100 MPL constituted a strong capillary barrier that prevented a significant quantity of liquid water from residing stably within the MPL.

Common for both MPL materials, there was more liquid water at the CL/MPL interface than in the MPL and at the MPL/GDL interface. For the Li100-cell, this was also verified by the LVF distribution maps in Fig. 8 showing the rib region at 0.5 A cm⁻², 90% RH at the first, 30th and the 60th second of operation.

Fig. 8 Liquid water distribution under the rib: (a) at the CL/MPL interface and (b) at the MPL/GDL interface of the Li100-cell operated at 0.5 A cm⁻², 90% RH; from left to right: dry state tomographic image, product water LVF distribution maps at 1, 30 and 60 s PEFC operation time. The Li-100 LVF distribution maps are more susceptible to artifacts (horizontal lines) than the VGCF ones, due to more difficult registration.

Despite being influenced by image artifacts, the LVF distribution maps of the CL/MPL interface under the rib indicated an increase of liquid water signals from the 1 s to the 30 s. From there the pattern of signals seemed to stabilize (Fig. 8a). The LVF determined for the Li100-cell rib had more artificial features and a larger error compared to the results for the VGCF-cell (Fig. 5). The error stemmed from misalignment, uncompensated catalyst shining, and ring artifacts, as judged by the exceedingly high and low LVF regions measured locally across the maps (e.g., the red regions showing LVF ≥1.0 in Fig. 8a) and the vertical stripe features in Fig. 8b. These errors occurred presumably because the Li100 MPL lacked resolvable features for very accurate image alignment to be achieved. Catalyst shining was thus not well compensated. LVF interpretation was therefore qualitative and based on image comparison at different operation times rather than absolute LVF readings. The discernability criterion for interpreting LVF in noisy images is not advised to be applied here due to the prominent image artifacts. The LVF evaluation error from image misalignment in in-plane and through-plane directions is briefly discussed in Fig. S8 (ESI†).

4. Discussion

4.1 General observations and interpretations

Although no major difference in the average LVF at each layer is observed between the two cells with VGCF and Li100 MPLs for different operating conditions, overall, it is clear that these MPLs remarkably reduce liquid water occurrence in the GDL part next to the CL when compared to a study with a similar GDL substrate (Freudenberg H23) without an MPL. The study of Xu et al.⁸⁴ showed that liquid water accumulates first in the GDL near the CL. With the presence of the VGCF and Li100 MPLs, at the beginning of current production (<15 s), the majority of liquid water first condensed on the surface of the rib. It is hypothesized that both Li100 and VGCF MPLs, having high porosity exhibit low thermal conductivity, thereby facilitating vapor transport and reducing liquid water occurrence in the GDL near the CL.

At longer operation times (>15 s) particularly under the rib, high liquid water fractions are observed in the GDL. Based on the present analyses, it is difficult to decide whether these LVFs occur due to condensation or capillary transport, most probably a combination of both.⁷⁰ The LVFs in the GDL are slightly different for VGCF and Li100, as discussed in Section 4.2.

In this study, the water LVFs are only discussed for the cathode. With the molar fraction of hydrogen gas being five times that of oxygen in the cathode and an about 8-fold diffusion coefficient, it is expected that the mass transport limitation will predominantly manifest itself in the cathode. If of interest, the LVF distribution in the anode needs to be investigated in future studies.

4.2 Comparison of VGCF- and Li100-cells

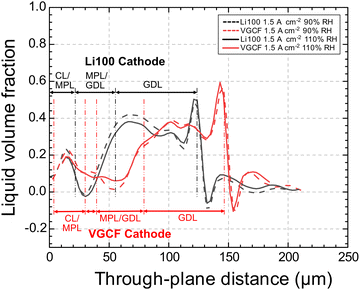
The water distribution in the cells with the two different MPLs shows both similarities and differences. The general liquid volume fraction in the MPL and GDL substrate, such as between current densities, gas humidity and channel/rib locations, shows similar behavior. However, at high current densities (Fig. 1), the VGCF-cell outperforms the Li-100 cell. The hypothesis for this difference in cell performance is thus likely based on different water distributions in the GDL.^37,39 During the current experiment, it is observed that the Li100-cell shows higher LVF in the GDL substrate near the MPL (Fig. 9), which has been previously shown to lead to lower performance. In Fig. 9, while the overall LVF difference of the two cells in the GDL substrate region (through-plane distance 80–110 μm) is not significant, liquid water in the Li100-cell substrate accumulates closer to the GDL/MPL interface (compare the two peaks marked by black arrows) than in the VGCF-cell (compare the two peaks marked by the red arrows).

Fig. 9 LVF comparison of the Li100- and VGCF-cells at 1.5 A cm⁻² current density under the rib at 60 s for the RH = 90% and 110% conditions. The LVF profiles are aligned at the CL/MPL interface, and the respective domains (CL/MPL, MPL/GDL and GDL) for cells with both are specified with dashed red or black lines. Note that the thickness of the GDLs of the two cells is different, by ca. 17 μm (when uncompressed).

Csoklich et al.⁸⁵ reported that the overall saturation may not be the only performance determining factor, but water present in the GDL in the vicinity of the catalyst layer has the potential to reduce the cell performance more significantly than water present farther from this interface.

As the GDL substrate is identical, the nature of the difference in LVF in the GDL between the cells with the two different MPLs must come from the differences in MPL pore structure. For example, Nagai et al.²¹ have described that MPLs containing large pores can change and reduce the LFV in the GDL substrate. This leads to the hypothesis that the large pores in VCGF have a similar effect, creating more defined injection points into the GDL substrate, thus directing the LVF away from the MPL/GDL interface.

Upon closer look, though, it may be noticed in Fig. 9, that the cathode GDLs of the VGCF-cell and Li100-cell differ in thickness by ca. 17 μm. This raises the question of whether the water distribution analysis based on the PSD mentioned previously may be generalized for VGCF- and Li100-cells. Firstly, in assembling the cells, the GDLs were not selected by its thickness. Natural thickness variation intrinsic to the GDL materials should thus exist. Of the 17 μm thickness difference, ca. 7 μm is contributed by MPL thickness difference and only ca. 10 μm by the GDL substrate (see the Experimental section, 2.1). Given that the H14 substrate is reported to be 140 μm thick and measured to be ca. 124 μm, 10 μm difference translates to ca. 7–8% thickness variation, which we find to be reasonably intrinsic to a GDL substrate material.

Indeed, to further compare the LVF at every through-plane position, future work can be done where the natural thickness variation among GDL samples is intentionally eliminated. For the current study of water transport mechanisms through MPLs, however, such natural thickness variation in cathode GDL thickness should be minor and should not affect the observed phenomena relevant to the water transport mechanisms.

5. Conclusion

The influence of MPLs and water volume fraction in MPLs on water transport mechanism in the cathode of PEFCs has been investigated by X-ray tomographic microscopy (XTM). The liquid water distribution in the MPLs and GDL substrates was determined under operando conditions. In the MPL, the water content is derived from the grayscale change without resolving the pore structure. The influence of two types of MPLs (VGCF, modal pore size of 722 nm, and Li100, modal pore size of 67 nm) was inferred from the dynamic evolution of the liquid volume fractions in the cathode part of the MEA (without the CL) at different RH and current densities, for the first minute of operation starting from dry conditions.

The results show that in the channel sections of the MPL/GDL, there was generally little or no liquid water observed, except for the conditions with high current density and high RH. However, liquid water was observed for all conditions in the MPL/GDL rib sections. Notably, the liquid water preferentially accumulated at the CL/MPL interface and in the GDL bulk, but not in the MPL. The first appearance of water, just a few seconds after current initiation, occurred as condensed droplets on the rib surface. It typically took 15–30 s of operation time for a liquid volume fraction to be observed throughout the GDL.

In the MPL (away from the CL/MPL interface), little to no liquid water emerged for lower RH and lower current density conditions, regardless of the MPL type (VGCF or Li100). Only under high RH and high current density conditions, liquid water was clearly observed in the MPL under the rib. However, the LVF in the MPL during the first minute of operation is always <15%. This means that the saturation level in the MPL, even considering the compression-induced lower porosity under the ribs, stayed constantly below 25%.

In contrast, in the GDL, for high current density conditions (1.5 A cm⁻²), a water volume fraction in the GDL substrate of up to 40% is observed under the rib after 60 seconds of cell operation. Since the average bulk porosity of the Freudenberg H14 substrate under the rib was measured (by XTM) to be ca. 57%, this translated to up to ca. 70% saturation in the GDL, much higher than in the MPL. The MPL was confirmed to effectively keep the saturation level low next to the CL.

When comparing the two cells with Li100 and VGCF MPLs, the overall saturation in the GDL substrates was similar at all conditions, regardless of the MPL materials used. Similarly, for both cells, the vapor condensation on the rib surface at the first few seconds of operation was prominent. This serves as evidence that water traveled through the two MPLs largely in vapor phase at the beginning of operation. Only in the region under the rib, where the diffusion paths towards the channels are longer and the local heat removal is enhanced, liquid water in the MPL was observed.

The difference in steady state performance at higher current densities (especially >1.5 A cm⁻²) and wet conditions between the different MPLs, as described by Simon et al.,^37,39 might be explained by the different location of water accumulation in the GDL substrate. In the VGCF cell at 1.5 A cm⁻², when approaching steady state conditions (at 60 s), the water appeared to accumulate farther inside the GDL (away from the CL/MPL interface), while the water in the GDL of the Li100-cell accumulated closer to the CL/MPL interface. A water location closer to the CL/MPL interface more strongly limits the oxygen supply to the CL. Further study with stricter control of GDL thickness is suggested to confirm this observation.

Comparing the present results to studies using similar GDLs without an MPL at comparable operating conditions, the main difference in water transport mode becomes clear: the introduction of the Li100 and VGCF MPLs efficiently suppressed the liquid water formation at the CL/GDL interface. Most remarkably, it caused the water accumulation site to shift from close to the CL (the case without an MPL, see Xu et al.⁸⁴) to close to the flow fields, and significantly promoted vapor condensation even at saturated RH conditions. The small, hydrophobic pores of the MPL alone may not explain the promotion of vapor transport in both VGCF- and Li100-cells. However, consider that MPL porosity has a strong influence on thermal conductivity properties of the MPLs, which in turn further has a considerate influence on the temperature gradient of the MEA during operation, the introduction of high porosity MPLs likely altered the transport mechanism by introducing a material layer of particularly lower thermal conductivity. A brief application of the model proposed by Andisheh-Tadbir et al. using simplistic assumptions showed that increasing the porosity of MPLs from 60% to 80% may result in significantly reduced thermal conductivity, depending on the PSD of the MPLs.³⁴ Note that the temperature-gradient-induced vapor transport mechanism has also been suggested by Thomas et al. (2014) and Hatzell et al. (2011) as well, using Sigracet SGL materials.^36,86

Since a low saturation level in the vicinity of catalyst layers and high effective diffusivity of gas diffusion layers tend to be beneficial for reducing oxygen transport resistance during PEFC operation, it is suggested that for PEFCs operated under highly humid conditions, the MPLs could be designed with a larger pore size distribution like the VGCF MPL, with high porosity and low thermal conductivity to prevent flooding at the vicinity of the catalyst layer. Incidentally, due to the fact that liquid water saturation is generally lower in the MPL than in the GDL substrate, it may be beneficial to increase the thickness of highly porous MPLs to reduce the overall diffusion layer saturation. However, it is known that thicker MPLs may also promote membrane dry out. Therefore, optimal MPL structural parameters such as thermal conductivity, PSD, porosity and thickness should be simultaneously considered when improving MPL designs. Due to the direct influence of MPL properties on the water management, it is likely that optimal MPL designs may vary depending on specific operating conditions.

The X-ray tomographic microscopy (XTM) results presented here provide information about the transient liquid water distribution in the MPL and in the GDL substrate. From there, the water transport mechanism through the porous layers—and especially through the microporous layer—is derived for the given set of materials and operating conditions. For a more general picture of the influence of the water transport mode in MPLs on water management in the entire GDL, further work will be necessary. The voxel-based evaluation of X-ray absorption contrast imaging methodology used here is suitable for MPL analysis.

In the future work, the method can be refined with more sophisticated image analysis, such as registration of featureless/moving MPL, and can be combined with segmentation-based data of water clusters in the GDL substrate and their possible connections to the water in the MPL. Additionally, as contact angle, gas permeability and water breakthrough pressure also take part in influencing the two-phase flow in the MPLs as well as the PEFC performance, performing analyses on these properties with a wider selection of different MPLs can finally lead to a more comprehensive understanding of the role of MPL in water transport, required for materials and PEFC performance optimization.

Author contributions

Yen-Chun Chen: data curation, formal analysis, methodology, visualization, writing – original draft. Tim Dörenkamp: investigation, software, writing – review & editing. Christoph Csoklich: investigation, software. Anne Berger: resources, writing – review & editing. Federica Marone: resources, data curation, software, writing – review & editing. Jens Eller: resources, writing – review & editing. Thomas J. Schmidt: supervision, funding acquisition, writing – review & editing. Felix N. Büchi: conceptualization, supervision, funding acquisition, project administration, writing – original draft, Writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge funding from the Swiss National Science Foundation under the Sinergia funding scheme (project grant number 180335). The authors acknowledge the help from Thomas Gloor (PSI) for his assistance with the maintenance and instruction for the fuel cell test benches. Furthermore, the help and support at the TOMCAT beamline of the Swiss Light Source of Matthieu Dessiex, Cesar Weber, Kinanti Aliyah and Arnaud Schuller is gratefully acknowledged. We appreciate the insightful discussions with Prof. Dr Hubert Gasteiger from Technical University of Munich (TUM). We acknowledge the Paul Scherrer Institut, Villigen, Switzerland for provision of the synchrotron radiation beamtime at the TOMCAT beamline of the SLS.

References

1. EERE. Hydrogen and Fuel Cell Technologies Office Multi-Year Research, Development, and Demonstration Plan. EERE Publication and Product Library, Washington, D.C. (United States) March 16, 2012.  DOI:10.2172/1219578.
2. M. J. O’Malley, M. B. Anwar, S. Heinen, T. Kober, J. McCalley, M. McPherson, M. Muratori, A. Orths, M. Ruth, T. J. Schmidt and A. Tuohy, Multicarrier Energy Systems: Shaping Our Energy Future, Proc. IEEE, 2020, 108(9), 1437–1456,  DOI:10.1109/JPROC.2020.2992251.
3. H. Liu, M. G. George, R. Zeis, M. Messerschmidt, J. Scholta and A. Bazylak, The Impacts of Microporous Layer Degradation on Liquid Water Distributions in Polymer Electrolyte Membrane Fuel Cells Using Synchrotron Imaging, ECS Trans., 2017, 80(8), 155–164,  DOI:10.1149/08008.0155ecst.
4. N. Holmström, J. Ihonen, A. Lundblad and G. Lindbergh, The Influence of the Gas Diffusion Layer on Water Management in Polymer Electrolyte Fuel Cells, Fuel Cells, 2007, 7(4), 306–313,  DOI:10.1002/fuce.200700003.
5. Z. Qi and A. Kaufman, Improvement of Water Management by a Microporous Sublayer for PEM Fuel Cells, J. Power Sources, 2002, 109(1), 38–46,  DOI:10.1016/S0378-7753(02)00058-7.
6. H. K. Atiyeh, E. Halliop, J. Pharoah, K. Karan, A. Phoenix and B. Peppley, Experimental Investigation of the Role of a Microporous Layer on the Water Transport and Performance of a PEM Fuel Cell, J. Power Sources, 2007, 170(1), 111–121,  DOI:10.1016/j.jpowsour.2007.04.016.
7. J. Chen, T. Matsuura and M. Hori, Novel Gas Diffusion Layer with Water Management Function for PEMFC, J. Power Sources, 2004, 131(1–2), 155–161,  DOI:10.1016/j.jpowsour.2004.01.007.
8. R. Lin, L. Chen, T. Zheng, S. Tang, X. Yu, M. Dong and Z. Hao, Interfacial Water Management of Gradient Microporous Layer for Self-Humidifying Proton Exchange Membrane Fuel Cells, Int. J. Heat Mass Transfer, 2021, 175, 121340,  DOI:10.1016/j.ijheatmasstransfer.2021.121340.
9. J. H. Nam, K.-J. Lee, G.-S. Hwang, C.-J. Kim and M. Kaviany, Microporous Layer for Water Morphology Control in PEMFC, Int. J. Heat Mass Transfer, 2009, 52(11–12), 2779–2791,  DOI:10.1016/j.ijheatmasstransfer.2009.01.002.
10. J. H. Nam and M. Kaviany, Effective Diffusivity and Water-Saturation Distribution in Single- and Two-Layer PEMFC Diffusion Medium, Int. J. Heat Mass Transfer, 2003, 46(24), 4595–4611,  DOI:10.1016/S0017-9310(03)00305-3.
11. T. Kim, S. Lee and H. Park, A Study of Water Transport as a Function of the Micro-Porous Layer Arrangement in PEMFCs, Int. J. Hydrogen Energy, 2010, 35(16), 8631–8643,  DOI:10.1016/j.ijhydene.2010.05.123.
12. M. F. Mathias, J. Roth, J. Fleming and W. Lehnert, Diffusion Media Materials and Characterisation. in Handbook of Fuel Cells, ed. W. Vielstich, A. Lamm, H. A. Gasteiger and H. Yokokawa, John Wiley & Sons, Ltd, Chichester, UK, 2010, p. f303046.  DOI:10.1002/9780470974001.f303046.
13. G. Lin, S. Liu, G. Qu, Y. Song, T. Li, F. Liu and Y. Hu, Effect of Pore Size Distribution in the Gas Diffusion Layer Adjusted by Composite Carbon Black on Fuel Cell Performance, Int. J. Energy Res., 2021, 45(5), 7689–7702,  DOI:10.1002/er.6350.
14. H. Wang, G. Yang, S. Li, Q. Shen, J. Liao, Z. Jiang, G. Zhang, H. Zhang and F. Su, Effect of Binder and Compression on the Transport Parameters of a Multilayer Gas Diffusion Layer, Energy Fuels, 2021, 35(18), 15058–15073,  DOI:10.1021/acs.energyfuels.1c01598.
15. I. V. Zenyuk, D. Y. Parkinson, L. G. Connolly and A. Z. Weber, Gas-Diffusion-Layer Structural Properties under Compression via X-Ray Tomography, J. Power Sources, 2016, 328, 364–376,  DOI:10.1016/j.jpowsour.2016.08.020.
16. A. El-kharouf, T. J. Mason, D. J. L. Brett and B. G. Pollet, Ex-Situ Characterisation of Gas Diffusion Layers for Proton Exchange Membrane Fuel Cells, J. Power Sources, 2012, 218, 393–404,  DOI:10.1016/j.jpowsour.2012.06.099.
17. J. Lobato, P. Cañizares, M. A. Rodrigo, C. Ruiz-López and J. J. Linares, Influence of the Teflon Loading in the Gas Diffusion Layer of PBI-Based PEM Fuel Cells, J. Appl. Electrochem., 2008, 38(6), 793–802,  DOI:10.1007/s10800-008-9512-8.
18. Y. Yang, X. Zhou, B. Li and C. Zhang, Recent Progress of the Gas Diffusion Layer in Proton Exchange Membrane Fuel Cells: Material and Structure Designs of Microporous Layer, Int. J. Hydrogen Energy, 2021, 46(5), 4259–4282,  DOI:10.1016/j.ijhydene.2020.10.185.
19. H. Ostadi, P. Rama, Y. Liu, R. Chen, X. X. Zhang and K. Jiang, 3D Reconstruction of a Gas Diffusion Layer and a Microporous Layer, J. Membr. Sci., 2010, 351(1–2), 69–74,  DOI:10.1016/j.memsci.2010.01.031.
20. J. Zhou, S. Shukla, A. Putz and M. Secanell, Analysis of the Role of the Microporous Layer in Improving Polymer Electrolyte Fuel Cell Performance, Electrochim. Acta, 2018, 268, 366–382,  DOI:10.1016/j.electacta.2018.02.100.
21. Y. Nagai, J. Eller, T. Hatanaka, S. Yamaguchi, S. Kato, A. Kato, F. Marone, H. Xu and F. N. Büchi, Improving Water Management in Fuel Cells through Microporous Layer Modifications: Fast Operando Tomographic Imaging of Liquid Water, J. Power Sources, 2019, 435(March), 226809,  DOI:10.1016/j.jpowsour.2019.226809.
22. Z. Lu, M. M. Daino, C. Rath and S. G. Kandlikar, Water Management Studies in PEM Fuel Cells, Part III: Dynamic Breakthrough and Intermittent Drainage Characteristics from GDLs with and without MPLs, Int. J. Hydrogen Energy, 2010, 35(9), 4222–4233,  DOI:10.1016/j.ijhydene.2010.01.012.
23. J. T. Gostick, M. A. Ioannidis, M. W. Fowler and M. D. Pritzker, On the Role of the Microporous Layer in PEMFC Operation, Electrochem. Commun., 2009, 11(3), 576–579,  DOI:10.1016/j.elecom.2008.12.053.
24. D. Niblett, A. Mularczyk, V. Niasar, J. Eller and S. Holmes, Two-Phase Flow Dynamics in a Gas Diffusion Layer – Gas Channel – Microporous Layer System, J. Power Sources, 2020, 471, 228427,  DOI:10.1016/j.jpowsour.2020.228427.
25. J. P. Owejan, J. E. Owejan, W. Gu, T. A. Trabold, T. W. Tighe and M. F. Mathias, Water Transport Mechanisms in PEMFC Gas Diffusion Layers, J. Electrochem. Soc., 2010, 157(10), B1456–B1456,  DOI:10.1149/1.3468615.
26. Y. Tabe, Y. Aoyama, K. Kadowaki, K. Suzuki and T. Chikahisa, Impact of Micro-Porous Layer on Liquid Water Distribution at the Catalyst Layer Interface and Cell Performance in a Polymer Electrolyte Membrane Fuel Cell, J. Power Sources, 2015, 287, 422–430,  DOI:10.1016/j.jpowsour.2015.04.095.
27. G. Lin and T. V. Nguyen, A Two-Dimensional Two-Phase Model of a PEM Fuel Cell, J. Electrochem. Soc., 2006, 153(2), A372,  DOI:10.1149/1.2142267.
28. P. Deevanhxay, T. Sasabe, S. Tsushima and S. Hirai, Effect of Liquid Water Distribution in Gas Diffusion Media with and without Microporous Layer on PEM Fuel Cell Performance, Electrochem. Commun., 2013, 34, 239–241,  DOI:10.1016/j.elecom.2013.07.001.
29. M. Blanco and D. P. Wilkinson, Investigation of the Effect of Microporous Layers on Water Management in a Proton Exchange Membrane Fuel Cell Using Novel Diagnostic Methods, Int. J. Hydrogen Energy, 2014, 39(29), 16390–16404,  DOI:10.1016/j.ijhydene.2014.07.147.
30. A. Z. Weber and J. Newman, Effects of Microporous Layers in Polymer Electrolyte Fuel Cells, J. Electrochem. Soc., 2005, 152(4), A677–A677,  DOI:10.1149/1.1861194.
31. U. Pasaogullari, C.-Y. Wang and K. S. Chen, Two-Phase Transport in Polymer Electrolyte Fuel Cells with Bilayer Cathode Gas Diffusion Media, J. Electrochem. Soc., 2005, 152(8), A1574,  DOI:10.1149/1.1938067.
32. D. Spernjak, A. K. Prasad and S. G. Advani, Experimental Investigation of Liquid Water Formation and Transport in a Transparent Single-Serpentine PEM Fuel Cell, J. Power Sources, 2007, 170(2), 334–344,  DOI:10.1016/j.jpowsour.2007.04.020.
33. X. Wang and T. V. Nguyen, Modeling the Effects of the Cathode Micro-Porous Layer on the Performance of a PEM Fuel Cell, ECS Trans., 2019, 16(2), 3–12,  DOI:10.1149/1.2981838.
34. M. Andisheh-Tadbir, E. Kjeang and M. Bahrami, Thermal Conductivity of Microporous Layers: Analytical Modeling and Experimental Validation, J. Power Sources, 2015, 296, 344–351,  DOI:10.1016/j.jpowsour.2015.07.054.
35. R. Bock, A. D. Shum, X. Xiao, H. Karoliussen, F. Seland, I. V. Zenyuk and O. S. Burheim, Thermal Conductivity and Compaction of GDL-MPL Interfacial Composite Material, J. Electrochem. Soc., 2018, 165(7), F514–F525,  DOI:10.1149/2.0751807jes.
36. A. Thomas, G. Maranzana, S. Didierjean, J. Dillet and O. Lottin, Thermal and Water Transfer in PEMFCs: Investigating the Role of the Microporous Layer, Int. J. Hydrogen Energy, 2014, 39(6), 2649–2658,  DOI:10.1016/j.ijhydene.2013.11.105.
37. C. Simon, J. Endres, B. Nefzger-Loders, F. Wilhelm and H. A. Gasteiger, Interaction of Pore Size and Hydrophobicity/Hydrophilicity for Improved Oxygen and Water Transport through Microporous Layers, J. Electrochem. Soc., 2019, 14.
38. M. N. Islam, U. Shrivastava, M. Atwa, X. Li, V. Birss and K. Karan, Highly Ordered Nanoporous Carbon Scaffold with Controllable Wettability as the Microporous Layer for Fuel Cells, ACS Appl. Mater. Interfaces, 2020, 12(35), 39215–39226,  DOI:10.1021/acsami.0c10755.
39. C. Simon, D. Kartouzian, D. Müller, F. Wilhelm and H. A. Gasteiger, Impact of Microporous Layer Pore Properties on Liquid Water Transport in PEM Fuel Cells: Carbon Black Type and Perforation, J. Electrochem. Soc., 2017, 164(14), F1697–F1711,  DOI:10.1149/2.1321714jes.
40. T. Tanuma, M. Kawamoto and S. Kinoshita, Effect of Properties of Hydrophilic Microporous Layer (MPL) on PEFC Performance, J. Electrochem. Soc., 2017, 164(6), F499–F503,  DOI:10.1149/2.0371706jes.
41. S. G. Kandlikar, M. L. Garofalo and Z. Lu, Water Management in A PEMFC: Water Transport Mechanism and Material Degradation in Gas Diffusion Layers, Fuel Cells, 2011,(No. 6), 814–823,  DOI:10.1002/fuce.201000172.
42. S. Hasanpour, M. Hoorfar and A. B. Phillion, Characterization of Transport Phenomena in Porous Transport Layers Using X-Ray Microtomography, J. Power Sources, 2017, 353, 221–229,  DOI:10.1016/j.jpowsour.2017.03.153.
43. T. Sasabe, P. Deevanhxay, S. Tsushima and S. Hirai, Soft X-Ray Visualization of the Liquid Water Transport within the Cracks of Micro Porous Layer in PEMFC, Electrochem. Commun., 2011, 13(6), 638–641,  DOI:10.1016/j.elecom.2011.03.033.
44. X. Zhang, Y. Gao, H. Ostadi, K. Jiang and R. Chen, Modelling Water Intrusion and Oxygen Diffusion in a Reconstructed Microporous Layer of PEM Fuel Cells, Int. J. Hydrogen Energy, 2014, 39(30), 17222–17230,  DOI:10.1016/j.ijhydene.2014.08.027.
45. J. H. Chun, D. H. Jo, S. G. Kim, S. H. Park, C. H. Lee and S. H. Kim, Improvement of the Mechanical Durability of Micro Porous Layer in a Proton Exchange Membrane Fuel Cell by Elimination of Surface Cracks, Renew. Energy, 2012, 48, 35–41,  DOI:10.1016/j.renene.2012.04.011.
46. M. Wang, S. Medina, J. R. Pfeilsticker, S. Pylypenko, M. Ulsh and S. A. Mauger, Impact of Microporous Layer Roughness on Gas-Diffusion-Electrode-Based Polymer Electrolyte Membrane Fuel Cell Performance, ACS Appl. Energy Mater., 2019, 2(11), 7757–7761,  DOI:10.1021/acsaem.9b01871.
47. J. Shi, Z. Zhan, D. Zhang, Y. Yu, X. Yang, L. He and M. Pan, Effects of Cracks on the Mass Transfer of Polymer Electrolyte Membrane Fuel Cell with High Performance Membrane Electrode Assembly, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2021, 36(3), 318–330,  DOI:10.1007/s11595-021-2412-z.
48. H. Tang, S. Wang, M. Pan and R. Yuan, Porosity-Graded Micro-Porous Layers for Polymer Electrolyte Membrane Fuel Cells, J. Power Sources, 2007, 166(1), 41–46,  DOI:10.1016/j.jpowsour.2007.01.021.
49. L. Chen, R. Lin, S. Tang, D. Zhong and Z. Hao, Structural Design of Gas Diffusion Layer for Proton Exchange Membrane Fuel Cell at Varying Humidification, J. Power Sources, 2020, 467, 228355,  DOI:10.1016/j.jpowsour.2020.228355.
50. A. Mohseninia, D. Kartouzian, R. Schlumberger, H. Markötter, F. Wilhelm, J. Scholta and I. Manke, Enhanced Water Management in PEMFCs: Perforated Catalyst Layer and Microporous Layers, ChemSusChem, 2020, 13(11), 2931–2934,  DOI:10.1002/cssc.202000542.
51. Y.-C. Chen, C. Karageorgiou, J. Eller, T. J. Schmidt and F. N. Büchi, Determination of the Porosity and Its Heterogeneity of Fuel Cell Microporous Layers by X-Ray Tomographic Microscopy, J. Power Sources, 2022, 539, 231612,  DOI:10.1016/j.jpowsour.2022.231612.
52. P. Deevanhxay, T. Sasabe, S. Tsushima and S. Hirai, In Situ Diagnostic of Liquid Water Distribution in Cathode Catalyst Layer in an Operating PEMFC by High-Resolution Soft X-Ray Radiography, Electrochem. Commun., 2012, 22, 33–36,  DOI:10.1016/j.elecom.2012.05.028.
53. H. Naito, K. Ishikawa, T. Sasabe, S. Hirai and T. Tanuma, Investigation of Effects of Hydrophilic Micro-Porous Layer on Liquid Water Behavior by X-Ray Imaging, J. Power Sources, 2021, 507, 230285,  DOI:10.1016/j.jpowsour.2021.230285.
54. F. Akitomo, T. Sasabe, T. Yoshida, H. Naito, K. Kawamura and S. Hirai, Investigation of Effects of High Temperature and Pressure on a Polymer Electrolyte Fuel Cell with Polarization Analysis and X-Ray Imaging of Liquid Water, J. Power Sources, 2019, 431(April), 205–209,  DOI:10.1016/j.jpowsour.2019.04.115.
55. A. Kato, S. Kato, S. Yamaguchi, T. Suzuki and Y. Nagai, Mechanistic Insights into Water Transport in Polymer Electrolyte Fuel Cells with a Variation of Cell Temperature and Relative Humidity of Inlet Gas Elucidated by Operando Synchrotron X-Ray Radiography, J. Power Sources, 2022, 521, 230951,  DOI:10.1016/j.jpowsour.2021.230951.
56. S. Kato, S. Yamaguchi, W. Yoshimune, Y. Matsuoka, A. Kato, Y. Nagai and T. Suzuki, Ex Situ Visualization of the Wet Domain in the Microporous Layer in a Polymer Electrolyte Fuel Cell by X-Ray Computed Tomography under Water Vapor Supply, Electrochem. Commun., 2020, 111(December 2019), 106644,  DOI:10.1016/j.elecom.2019.106644.
57. J. Lee, J. Hinebaugh and A. Bazylak, Synchrotron X-Ray Radiographic Investigations of Liquid Water Transport Behavior in a PEMFC with MPL-Coated GDLs, J. Power Sources, 2013, 227, 123–130,  DOI:10.1016/j.jpowsour.2012.11.006.
58. P. Deevanhxay, T. Sasabe, S. Tsushima and S. Hirai, Observation of Dynamic Liquid Water Transport in the Microporous Layer and Gas Diffusion Layer of an Operating PEM Fuel Cell by High-Resolution Soft X-Ray Radiography, J. Power Sources, 2013, 230, 38–43,  DOI:10.1016/j.jpowsour.2012.11.140.
59. S. S. Alrwashdeh, I. Manke, H. Markötter, M. Klages, M. Göbel, J. Haußmann, J. Scholta and J. Banhart, In Operando Quantification of Three-Dimensional Water Distribution in Nanoporous Carbon-Based Layers in Polymer Electrolyte Membrane Fuel Cells, ACS Nano, 2017, 11(6), 5944–5949,  DOI:10.1021/acsnano.7b01720.
60. T. Sugahara, T. Sasabe, H. Naito, M. Kodama and S. Hirai, 3D Visualization of Liquid Water Penetration from MPL to Substrate Layer in PEFC Using In-Situ X-Ray Tomographic Microscopy, ECS Trans., 2021, 104(8), 93–99,  DOI:10.1149/10408.0093ecst.
61. S. J. Normile, D. C. Sabarirajan, O. Calzada, V. De Andrade, X. Xiao, P. Mandal, D. Y. Parkinson, A. Serov, P. Atanassov and I. V. Zenyuk, Direct Observations of Liquid Water Formation at Nano- and Micro-Scale in Platinum Group Metal-Free Electrodes by Operando X-Ray Computed Tomography, Mater. Today Energy, 2018, 9, 187–197,  DOI:10.1016/j.mtener.2018.05.011.
62. S. Prass, S. Hasanpour, P. K. Sow, A. B. Phillion and W. Mérida, Microscale X-Ray Tomographic Investigation of the Interfacial Morphology between the Catalyst and Micro Porous Layers in Proton Exchange Membrane Fuel Cells, J. Power Sources, 2016, 319, 82–89,  DOI:10.1016/j.jpowsour.2016.04.031.
63. S. Chevalier, N. Ge, M. G. George, J. Lee, R. Banerjee, H. Liu, P. Shrestha, D. Muirhead, J. Hinebaugh, Y. Tabuchi, T. Kotaka and A. Bazylak, Synchrotron X-Ray Radiography as a Highly Precise and Accurate Method for Measuring the Spatial Distribution of Liquid Water in Operating Polymer Electrolyte Membrane Fuel Cells, J. Electrochem. Soc., 2017, 164(2), F107–F114,  DOI:10.1149/2.0041702jes.
64. S. S. Alrwashdeh, H. Markötter, J. Hauβmann, A. Hilger, M. Klages, B. R. Müller, A. Kupsch, H. Riesemeier, J. Scholta and I. Manke, Investigation of Water Transport in Newly Developed Micro Porous Layers for Polymer Electrolyte Membrane Fuel Cells, Appl. Microsc., 2017, 47(3), 101–104,  DOI:10.9729/AM.2017.47.3.101.
65. P. Antonacci, S. Chevalier, J. Lee, N. Ge, J. Hinebaugh, R. Yip, Y. Tabuchi, T. Kotaka and A. Bazylak, Balancing Mass Transport Resistance and Membrane Resistance When Tailoring Microporous Layer Thickness for Polymer Electrolyte Membrane Fuel Cells Operating at High Current Densities, Electrochim. Acta, 2016, 188, 888–897,  DOI:10.1016/j.electacta.2015.11.115.
66. S.-G. Kim and S.-J. Lee, A Review on Experimental Evaluation of Water Management in a Polymer Electrolyte Fuel Cell Using X-Ray Imaging Technique, J. Power Sources, 2013, 230, 101–108,  DOI:10.1016/j.jpowsour.2012.12.030.
67. J. Lee, R. Yip, P. Antonacci, N. Ge, T. Kotaka, Y. Tabuchi and A. Bazylak, Synchrotron Investigation of Microporous Layer Thickness on Liquid Water Distribution in a PEM Fuel Cell, J. Electrochem. Soc., 2015, 162(7), F669–F676,  DOI:10.1149/2.0221507jes.
68. N. Ge, S. Chevalier, J. Hinebaugh, R. Yip, J. Lee, P. Antonacci, T. Kotaka, Y. Tabuchi and A. Bazylak, Calibrating the X-Ray Attenuation of Liquid Water and Correcting Sample Movement Artefacts during in Operando Synchrotron X-Ray Radiographic Imaging of Polymer Electrolyte Membrane Fuel Cells, J. Synchrotron Radiat., 2016, 23(2), 590–599,  DOI:10.1107/S1600577515023899.
69. J. Eller, J. Roth, F. Marone, M. Stampanoni and F. N. Büchi, Operando Properties of Gas Diffusion Layers: Saturation and Liquid Permeability, J. Electrochem. Soc., 2017, 164(2), F115–F126,  DOI:10.1149/2.0881702jes.
70. H. Xu, M. Bührer, F. Marone, T. J. Schmidt, F. N. Büchi and J. Eller, Effects of Gas Diffusion Layer Substrates on PEFC Water Management: Part II. In Situ Liquid Water Removal via Evaporation, J. Electrochem. Soc., 2022, 169(10), 104503,  DOI:10.1149/1945-7111/ac94a2.
71. R. Mokso, C. M. Schlepütz, G. Theidel, H. Billich, E. Schmid, T. Celcer, G. Mikuljan, L. Sala, F. Marone, N. Schlumpf and M. Stampanoni, GigaFRoST: The Gigabit Fast Readout System for Tomography, J. Synchrotron Radiat., 2017, 24(6), 1250–1259,  DOI:10.1107/S1600577517013522.
72. M. Bührer, M. Stampanoni, X. Rochet, F. Büchi, J. Eller and F. Marone, High-Numerical-Aperture Macroscope Optics for Time-Resolved Experiments, J. Synchrotron Radiat., 2019, 26(4), 1161–1172,  DOI:10.1107/S1600577519004119.
73. J. Eller and F. N. Büchi, Polymer Electrolyte Fuel Cell Performance Degradation at Different Synchrotron Beam Intensities, J. Synchrotron Radiat., 2014, 21(1), 82–88,  DOI:10.1107/S1600577513025162.
74. F. Marone, A. Studer, H. Billich, L. Sala and M. Stampanoni, Towards On-the-Fly Data Post-Processing for Real-Time Tomographic Imaging at TOMCAT, Adv. Struct. Chem. Imaging, 2017, 3(1), 1,  DOI:10.1186/s40679-016-0035-9.
75. A. Fedorov, R. Beichel, J. Kalpathy-Cramer, J. Finet, J.-C. Fillion-Robin, S. Pujol, C. Bauer, D. Jennings, F. Fennessy, M. Sonka, J. Buatti, S. Aylward, J. V. Miller, S. Pieper and R. Kikinis, 3D Slicer as an Image Computing Platform for the Quantitative Imaging Network, Magn. Reson. Imaging, 2012, 30(9), 1323–1341,  DOI:10.1016/j.mri.2012.05.001.
76. Y. Aoyama, K. Suzuki, Y. Tabe and T. Chikahisa, Observation of Water Transport in the Micro-Porous Layer of a Polymer Electrolyte Fuel Cell with a Freezing Method and Cryo-Scanning Electron Microscope, Electrochem. Commun., 2014, 41, 72–75,  DOI:10.1016/j.elecom.2013.12.029.
77. Y. Aoyama, K. Suzuki, Y. Tabe, T. Chikahisa and T. Tanuma, Water Transport and PEFC Performance with Different Interface Structure between Micro-Porous Layer and Catalyst Layer, J. Electrochem. Soc., 2016, 163(5), F359–F366,  DOI:10.1149/2.0451605jes.
78. C.-Y. Jung, H.-S. Shim, S.-M. Koo, S.-H. Lee and S.-C. Yi, Investigations of the Temperature Distribution in Proton Exchange Membrane Fuel Cells, Appl. Energy, 2012, 93, 733–741,  DOI:10.1016/j.apenergy.2011.08.035.
79. S.-K. Lee, K. Ito, T. Ohshima, S. Noda and K. Sasaki, In Situ Measurement of Temperature Distribution across a Proton Exchange Membrane Fuel Cell, Electrochem. Solid-State Lett., 2009, 12(9), B126,  DOI:10.1149/1.3152331.
80. H. Sadeghifar, N. Djilali and M. Bahrami, Effect of PTFE on Thermal Conductivity of Gas Diffusion Layers of PEM Fuel Cells, in ASME 2013 11th International Conference on Fuel Cell Science, Engineering and Technology, American Society of Mechanical Engineers, Minneapolis, Minnesota, USA, 2013, p. V001T01A003 DOI:10.1115/FuelCell2013-18070.
81. O. S. Burheim, H. Su, S. Pasupathi, J. G. Pharoah and B. G. Pollet, Thermal Conductivity and Temperature Profiles of the Micro Porous Layers Used for the Polymer Electrolyte Membrane Fuel Cell, Int. J. Hydrogen Energy, 2013, 38(20), 8437–8447,  DOI:10.1016/j.ijhydene.2013.04.140.
82. N. Zamel, J. Becker and A. Wiegmann, Estimating the Thermal Conductivity and Diffusion Coefficient of the Microporous Layer of Polymer Electrolyte Membrane Fuel Cells, J. Power Sources, 2012, 207, 70–80,  DOI:10.1016/j.jpowsour.2012.02.003.
83. A. Thomas, G. Maranzana, S. Didierjean, J. Dillet and O. Lottin, Measurements of Electrode Temperatures, Heat and Water Fluxes in PEMFCs: Conclusions about Transfer Mechanisms, J. Electrochem. Soc., 2013, 160(2), F191–F204,  DOI:10.1149/2.006303jes.
84. H. Xu, M. Bührer, F. Marone, T. J. Schmidt, F. N. Büchi and J. Eller, Effects of Gas Diffusion Layer Substrates on PEFC Water Management: Part I. Operando Liquid Water Saturation and Gas Diffusion Properties, J. Electrochem. Soc., 2021, 168(7), 074505,  DOI:10.1149/1945-7111/ac1035.
85. C. Csoklich, H. Xu, F. Marone, T. J. Schmidt and F. N. Büchi, Laser Structured Gas Diffusion Layers for Improved Water Transport and Fuel Cell Performance, ACS Appl. Energy Mater., 2021, 4(11), 12808–12818,  DOI:10.1021/acsaem.1c02454.
86. M. C. Hatzell, A. Turhan, S. Kim, D. S. Hussey, D. L. Jacobson and M. M. Mench, Quantification of Temperature Driven Flow in a Polymer Electrolyte Fuel Cell Using High-Resolution Neutron Radiography, J. Electrochem. Soc., 2011, 158(6), B717–B726,  DOI:10.1149/1.3577597.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00189j

---