Open Access Article
Open Access ArticlePressure dependence of ionic conductivity in site disordered lithium superionic argyrodite Li6PS5Br†
Vasiliki
Faka
a,
Matthias T.
Agne
a,
Paul
Till
a,
Tim
Bernges
a,
Marcel
Sadowski
 c,
Ajay
Gautam
a,
Karsten
Albe
c,
Ajay
Gautam
a,
Karsten
Albe
 c and
Wolfgang G.
Zeier
c and
Wolfgang G.
Zeier
 *ab
*ab
aInstitute of Inorganic and Analytical Chemistry, University of Münster, Corrensstraße 28/30, 48149 Münster, Germany. E-mail: wzeier@uni-muenster.de
bInstitut für Energie-und Klimaforschung (IEK), IEK-12: Helmholtz-Institut Münster, Forschungszentrum Jülich, 48149 Münster, Germany
cDepartment of Materials Science, Technical University of Darmstadt, Otto-Berndt-Strasse 3, D-64287 Darmstadt, Germany
First published on 2nd October 2023
Abstract
The understanding of transport in Li+ solid ionic conductors is critical for the development of solid-state batteries. The influence of activation volumes on ion transport in solid electrolytes has recently garnered renewed research interest, due to the need to control the ion dynamics that influence the ionic conductivity in solid electrolytes. Microscopic activation volumes are believed to correspond to the volume change in the atomic structure of a material that occurs during an ion jump and can be determined thermodynamically from pressure dependent conductivity measurements. However, it remains unknown if and how this external pressure can affect the structure and transport properties of Li+ solid electrolytes. The lithium argyrodites Li6PS5Br have shown high ionic conductivities, influenced by their Br−/S2− site disorder, which is associated with more spatially diffuse lithium-ion distributions. Herein, impedance spectra were acquired over a pressure range of 0.1 GPa to 1.5 GPa and revealed the activation volumes for Li+ migration. Specifically, activation volumes for Li+ migration increase with increasing degrees of Br−/S2− site disorder in Li6PS5Br and with more spatially distributed lithium-ions. Furthermore, estimations of the corresponding migration volumes, which are thought to be a constant of the diffusing mobile ion in the structure are here found to change significantly among different Br−/S2− site disorders. These observations motivate further investigations on how the thermodynamic activation volume in superionic Li+ conductors may provide novel insights to the influences of structure on ion transport in fast ionic conductors.
1. Introduction
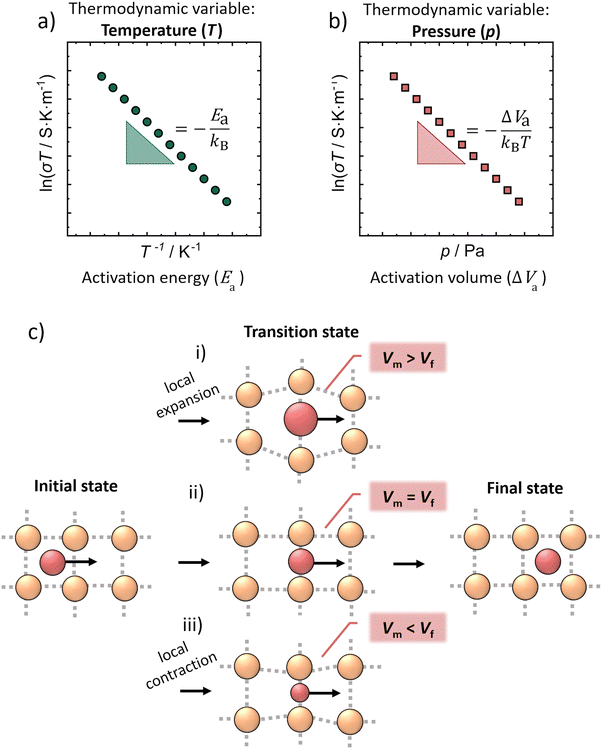
Inorganic solid ion conductors with high ionic conductivities have the potential for application in solid-state batteries (SSBs), which are investigated as a next-generation energy storage technology.1,2 The aim of the solid-state electrolytes is to replace the conventional liquid electrolytes;3,4 as the performance of the lithium-ion batteries will eventually approach a limit. The high ionic conductivity of lithium thiophosphates combined with their low mechanical moduli are the reasons why sulfide-based composites play a dominant role in the development of SSBs for room-temperature operation.5 Among them, lithium ion conducting argyrodites Li6PS5X (X = Cl, Br, I) have been extensively studied and have attracted considerable attention due to their high ionic conductivity, their electrochemical stability and processability.6–8 The conductivity of Li6PS5Br can be controlled synthetically, as demonstrated by Gautam et al., who showed that different Br−/S2− site disorders (and thus different ionic conductivities) can be obtained through quenching Li6PS5Br from different annealing temperatures.9 The disorder is considered to introduce charge inhomogeneity into the anionic sublattice – the higher the disorder, the larger the charge inhomogeneity – resulting in a more diffuse (or spread out) lithium ion density across the different crystallographic Li+ sites.10 The changes in charge inhomogeneity result from the change of the average anionic charge in the center of the Li+ cages and have been shown to lead to different Li+–Li+ jump distances. The easier Li+ jumps due to the shorter Li+–Li+ distance and the more diffuse distribution of Li+ are thought to be the two main reasons why the ionic conductivity in Li6PS5Br is increased with higher disorder.9While the temperature dependence of the ionic conductivity is well understood in the Li6PS5X argyrodites,11,12 the relation between applied pressure and the ionic transport properties was yet not investigated. Pressure, as another thermodynamic variable can affect ion dynamics and with that alter the ionic conductivity of solids.13 In addition, solid state batteries are studied under constant pressure, therefore, knowing the effect of pressure on the solid electrolytes is important and the understanding of the pressure-transport properties is crucial. The pressure dependence of ionic conductivity can be defined by a characteristic activation volume for ion transport (Fig. 1b), the activation volume ΔVa which is analogous to the activation energy Ea of Arrhenius transport with temperature (Fig. 1a).14–16
The activation energy has been extensively studied in the last decade compared to the activation volume. This may be partially due to the need to optimize temperature operation for energy applications. In addition, a variable-pressure impedance spectroscopy setup is more challenging to be built, since the requirements of the simultaneous control of pressure and temperature and the in situ densification of the sample need to be satisfied.17 Therefore, the activation volume of Li+ solid electrolytes still remains a poorly explored area and the fundamental influence of external pressure on ionic conductivity and their correlations have not been properly analyzed yet.
The activation volume ΔVa as a thermodynamic quantity is defined as the variation of the change in Gibbs free energy ΔG with pressure p (at constant temperature T), as:
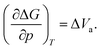 | (1) |
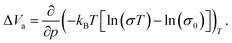 | (2) |
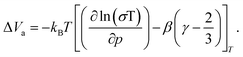 | (3) |
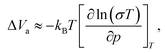 | (4) |
Although the activation volume is a thermodynamic quantity, it is often discussed in terms of a microscopic picture as a local volume change associated with ion transport. Here, it should be noted that there are two common perspectives of how the local volume change can be described:
(1) The activation volume can be viewed as the total (net) volume change when the jumping atom is transferred from the ground position (or equilibrium position) to the transition state (or saddle point).19–21
(2) In contrast, the activation volume may be considered as the local volume change at the saddle point, namely to be a measure of the degree to which the lattice must expand as the mobile ion passes through the transport bottleneck.22–24 In this case, ΔVa is defined as the difference between the volume an ion needs at the transition site during ion migration (Vm) and the already available free crystallographic volume (Vf) in the structure at the same site,21,22,25,26 explicitly
| ΔVa = Vm − Vf. | (5) |
In general, the value of the activation volume strongly depends on the material, the migrating ion and the composition.27 Depending on the size of the mobile ion in the same structure, for instance in β-alumina22 (Fig. 1c), there are three different possibilities for the motion of ions in the structure, which result in three different values of activation volume. The interpretation of the activation volume in β-alumina follows eqn (5), leading to the possibility of positive, negative and zero values of activation volume as schematically demonstrated in Fig. 1c. More specifically, the activation volume for Na+ migration is found to be zero (Fig. 1c-ii), leading to the interpretation that the Na+ can be transferred easily through the planes in β-alumina. When larger alkali ions (K+) are inserted into the structure, the activation volume becomes positive (Fig. 1c-i), because the alumina planes need to be expanded to allow this migration (Vm > Vf). However, in Li-β-Al2O3, the activation volume is found to be negative (Fig. 1c-iii) because the Li+ is attracted by the planes, which need to be contracted to allow the Li+ migration (Vm < Vf).22
So far, activation volumes have not been widely studied in superionic materials, and especially not for high-performance solid conductors which aim for application in solid-state batteries.17 Some studies of activation volumes have investigated the effects of chemical substitution,25,26 general changes in the composition,22,28 the effect of doping26 and the impact of different synthetic approaches on the structure of the studied material.17 Mezaki et al., studied the influence of Ca2+ addition in LiBH4 which results in a decrease of ΔVa, attributed to the contribution of defect formation due to the large amount of vacancies introduced by Ca2+ substitution.26 Ingram et al., studied ΔVa in doped AgPO3 glassy electrolytes and found that ΔVa has a strong coupling with the activation energy, Ea, which suggests that the free volume plays a dominant role in conductivity enhancement.29 Famprikis et al., studied ΔVa in Na3PS4 prepared in two different synthetic routes (high temperature annealing and ball milling synthesis) and found that the synthesis procedure has an important role on ΔVa.17 In this case, we may question the assumption that in superionic conductors, the free energy of defect formation, ΔGd ≈ 0, as synthesis has shown to have a strong influence on the defects in this class of materials.30 It is important that activation volumes should be related to a specific structure and migration mechanism.17 Positive activation volumes have been reported for polymers,19 inorganic compounds,25 and ionic conductors.13,19 Activation volumes have also been measured for a variety of ion-conducting glasses, in which the pressure is found to reduce the number of free ions capable of moving in a glass.24,28,29 Negative activation volumes have been reported for Ag+ conductors (β-AgI and γ-AgI) and are thought to be related to their negative thermal expansion coefficient.16 Zeolites also have negative ΔVa as a result of the interaction between the mobile cations and the anion framework. In general, the origin of negative activation volumes is related to the complex interaction between defects or impurities and ionic migration.22,31
Nevertheless, often the influence of chemical composition and structural changes on the activation volumes cannot be deconvoluted. Therefore, in this study, we use pressure-dependent measurements to investigate the activation volumes for four different (10%, 18%, 28% and 34%) Br−/S2− site disordered Li6PS5Br compounds. Here, the chemical composition remains constant, and hence only the structural changes due to disorder and the application of pressure affect the transport and no convolution with the chemical composition will exist. We report larger activation volumes with increasing Br−/S2− site disorder and decreasing unit cell volumes, which motivates us to search how the activation volume for Li+ migration is correlated to the structure of Li6PS5Br. By considering the known lithium diffusion mechanism for lithium argyrodites, we estimate the available crystallographic volumes (Vf) in Li6PS5Br for ion jumps and calculate the migration volume for Li+. As a result, we find that – contrary to expectation – the migration volume Vm of Li6PS5Br is not constant within different Br−/S2− site disorders. This finding is unexpected in the current microscopic understanding of activation volume, which suggests the local volume change at the saddle point and brings us to the question of how activation volume data should be interpreted in solid electrolytes. Nevertheless, pressure is found to be an effective variable for probing fundamental influences of ion transport in Li+ superionic conductors.
2. Experimental
2.1 Synthesis of Br−/S2− site disordered Li6PS5Br
All synthesis steps of Li6PS5Br were carried out under an inert Ar atmosphere (O2 < 0.5 ppm and H2O < 1 ppm). Lithium sulfide (Li2S, Alfa-Aesar, 99.9%), phosphorous pentasulfide (P4S10, Merck, 99%) and lithium bromide (LiBr, ultradry, Alfa-Aesar, 99.99%) were mixed in the appropriate stoichiometric ratio and hand-ground in an agate mortar. For the ball-milling synthesis, the obtained composition was inserted in a 80 mL zirconia ball milling cup with 5 mm diameter milling media (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio of milling media to precursor) and was milled for a total of 150 cycles with intermediate cooling time (10 min milling time and 10 min resting time). During the 150 cycles of milling, the milling set was opened twice to remove caked powders from the walls of the milling cups. The obtained powder was pressed into a 1 cm diameter pellet and filled into carbon-coated quartz ampoules. The ampoules were preheated at 1073 K for 2 hours under dynamic vacuum, to remove any traces of H2O. Then, the ampoules were sealed under vacuum and transferred into a tube furnace that was already preheated at 823 K. The ampoules were annealed for 30 minutes and left to cool down with a cooling rate of 4 K h−1, which results in low (10%) Br−/S2− site disorder. An optimization in the synthesis procedure can be found elsewhere,32 shown that this process results in a material with high crystallinity. To prepare four different disorders, the material was hand-ground again, pressed into pellets and loaded into carbon-coated ampoules. Then, the ampoules were inserted into a tube furnace that was already equilibrated at 623 K, 673 K and 723 K, respectively. The reactions were performed for 2 hours and then the ampoules were quenched into liquid N2 to stabilize the disorders occurred from the different annealing temperatures.
1 mass ratio of milling media to precursor) and was milled for a total of 150 cycles with intermediate cooling time (10 min milling time and 10 min resting time). During the 150 cycles of milling, the milling set was opened twice to remove caked powders from the walls of the milling cups. The obtained powder was pressed into a 1 cm diameter pellet and filled into carbon-coated quartz ampoules. The ampoules were preheated at 1073 K for 2 hours under dynamic vacuum, to remove any traces of H2O. Then, the ampoules were sealed under vacuum and transferred into a tube furnace that was already preheated at 823 K. The ampoules were annealed for 30 minutes and left to cool down with a cooling rate of 4 K h−1, which results in low (10%) Br−/S2− site disorder. An optimization in the synthesis procedure can be found elsewhere,32 shown that this process results in a material with high crystallinity. To prepare four different disorders, the material was hand-ground again, pressed into pellets and loaded into carbon-coated ampoules. Then, the ampoules were inserted into a tube furnace that was already equilibrated at 623 K, 673 K and 723 K, respectively. The reactions were performed for 2 hours and then the ampoules were quenched into liquid N2 to stabilize the disorders occurred from the different annealing temperatures.
2.2 Neutron powder diffraction and Rietveld analysis
High-resolution neutron powder diffraction data were collected at the Heinz Maier–Leibnitz Zentrum (research reactor FRM II, Garching b. München Germany) using the high-resolution diffractometer SPODI operating with monochromatic neutrons (wavelength of λ = 1.54820(2) Å). Approximately 2.5 g of each material was filled into a 10 mm diameter cylindrical vanadium container (wall thickness 150 μm) under argon atmosphere and then sealed using an indium wire to prevent air exposure during the measurement. Reference measurement data of an empty can was also collected for background correction. Rietveld refinements were performed using the TOPAS-Academic V6 software package. The structural information obtained from the neutron diffraction refinement of Li6PS5Br from Minafra et al.10 and the structural information of the Br−/S2− site disordered samples was obtained from Gautam et al.92.3 Potentiostatic electrochemical impedance spectroscopy (PEIS)
AC impedance spectroscopy was used to determine the electrical conductivities using an SP-150 impedance analyzer (Bio-Logic Science instruments Ltd). The measurements were performed at room temperature (298 K) with an equilibration time of 2 hours, utilizing a sinusoidal excitation voltage signal at frequencies of 1 MHz to 100 mHz with an amplitude of 150 mV.2.4 Pressure dependent measurements
The CompreDrive setup (rhd instruments) was used for the pressure-dependent experiments and 100 mg of Li6PS5Br were loaded into the 6C CompreCell (6 mm inner diameter). The pressure was applied uniaxially and was kept constant with a high accuracy (0.5%). A heating mantle was used externally from the CompreCell which kept the temperature constant at 298 K throughout the entire measurement, controlled via a Presto A40 thermostat (Julabo).The material was initially pressed at 370 MPa for 5 minutes (to ensure better contact between the steel electrodes and the material) and then for each measurement a pressure range from 0.1 GPa to 1.5 GPa (with a step of 0.05 GPa) was used upon compression and decompression of the material. The resulting impedance spectra were evaluated with RelaxIS 3 software (rhd instruments). The uncertainties of the conductivity are calculated from triplicate measurements. The activation volumes were calculated from the logarithm of the ionic conductivity during the decompression step from 1.5 GPa to 0.8 GPa, where the needed linear behavior is observed and the pellet is already fully densified (Fig. S12, ESI†).33
2.5 AIMD simulations
Ab initio molecular dynamics (AIMD) simulations have been performed in the NVT ensemble using the Vienna ab initio simulation package (VASP)34–36 with projector-augmented pseudopotentials37,38 and the Perdew–Burke–Ernzerhof (PBE)39 exchange–correlation functional. The energy cut-off for the plane wave basis set was taken as the highest default value of 499 eV and only the gamma-point was treated. Temperatures of 700 K, 800 K and 900 K were used and the time step was set to 1 fs. The utilized models were constructed as a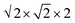 supercell of the conventional cubic unit cell (16 formula units, 208 atoms). Br−/S2− site disorder of 12.5% and 25% were introduced. For both disorders, four different models with differently distributed Br−/S2− ions were considered. The cell vectors of these models were uniformly rescaled with the smallest model size of 14.037 × 14.037 × 19.851 Å3 and the largest model size of 14.691 × 14 × 691 × 20.777 Å3. Data for energy–volume curves were obtained from AIMD simulations, which allows to sample over realistic Li distributions. To this end, we first allowed for 1 ps of equilibration, which was checked to suffice for the given system and setting. Next, the average free energy EAIMD was computed over approximately 5 ps, and the data was fitted with the Birch–Murnaghan equation of state40,41 to obtain the bulk modulus. The atomic trajectories were further used to compute the average volume of the T2 sites.
supercell of the conventional cubic unit cell (16 formula units, 208 atoms). Br−/S2− site disorder of 12.5% and 25% were introduced. For both disorders, four different models with differently distributed Br−/S2− ions were considered. The cell vectors of these models were uniformly rescaled with the smallest model size of 14.037 × 14.037 × 19.851 Å3 and the largest model size of 14.691 × 14 × 691 × 20.777 Å3. Data for energy–volume curves were obtained from AIMD simulations, which allows to sample over realistic Li distributions. To this end, we first allowed for 1 ps of equilibration, which was checked to suffice for the given system and setting. Next, the average free energy EAIMD was computed over approximately 5 ps, and the data was fitted with the Birch–Murnaghan equation of state40,41 to obtain the bulk modulus. The atomic trajectories were further used to compute the average volume of the T2 sites.
3. Results and discussion
3.1 Influence of the synthesis on the structure
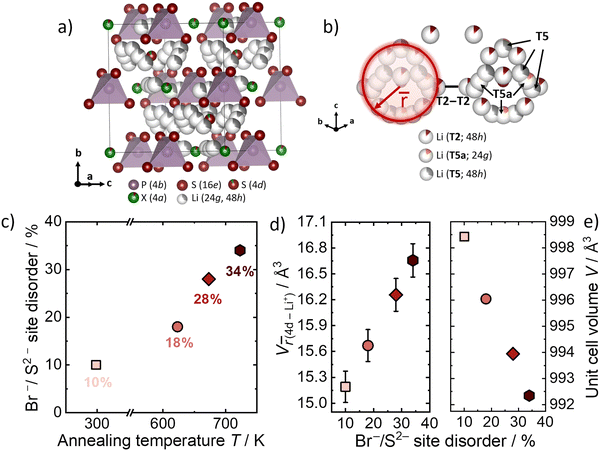
Li6PS5Br with different Br−/S2− site disorder have already been synthesized and analyzed in the previous work of Gautam et al.9 The influence of the Br−/S2− site disorder into the lithium substructure was studied by using Rietveld refinement against neutron data that can be found in Fig. S1–S4 (ESI†). All other structural parameters and further analysis can be found in the previous work.9 The crystal structure of Li6PS5Br can be seen in Fig. 2a. The quenching in liquid N2 from different annealing temperatures results in different Br−/S2− site disorders in Li6PS5Br (Fig. 2c). Higher annealing temperature results in higher Br−/S2− site disorder. The Br−/S2− site disorder is the critical factor which affects the unit cell volume and the lithium substructure (Fig. 2d and e). Higher Br−/S2− site disorder leads to a more homogeneous charge distribution of lithium ions through the structure, which results in the shrinkage of the unit cell due to electrostatic interactions (Fig. 2e).9 The shortest distance between the Li+ and the anion at the center of the cage (Wyckoff 4d position), designated as average distance is describing the changes in the Li+ occupancy and positions (Fig. 2b). The average distance between the three different Li+ sites away from the center anion at Wyckoff 4d, weighted by the number of Li+ ions located on the specific sites within one cage has been calculated and is referred to![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) .9,10 The increase of the site disorder leads to a decrease in the average charge on 4d as the divalent sulfide is replaced by the monovalent bromide and as a consequence
.9,10 The increase of the site disorder leads to a decrease in the average charge on 4d as the divalent sulfide is replaced by the monovalent bromide and as a consequence ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) increases. The volume V
increases. The volume V![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (4d-Li+) is introduced here, to relate possible changes between the volume that the radial distribution
(4d-Li+) is introduced here, to relate possible changes between the volume that the radial distribution ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (4d-Li+) occupies within the various site disorders (Fig. 2d). The values of V
(4d-Li+) occupies within the various site disorders (Fig. 2d). The values of V![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (4d-Li+) were calculated by using
(4d-Li+) were calculated by using ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (4d-Li+) as the radius, weighted by the number of Li+ ions and their occupancies located on specific sites (T5, T5a, T2) within one cage. It is observed in Fig. 2d, that the volume V
(4d-Li+) as the radius, weighted by the number of Li+ ions and their occupancies located on specific sites (T5, T5a, T2) within one cage. It is observed in Fig. 2d, that the volume V![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (4d-Li+) is increasing upon increasing disorder. The volume V
(4d-Li+) is increasing upon increasing disorder. The volume V![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (4d-Li+) captures the changes in the lithium-ion substructure with varying site disorders and will be related to the activation volumes in the next part of the results.
(4d-Li+) captures the changes in the lithium-ion substructure with varying site disorders and will be related to the activation volumes in the next part of the results.
3.2 Evolution of ionic conductivity under applied pressure
The influence of external pressure applied on the Br−/S2− site disordered Li6PS5Br compounds is probed by potentiostatic electrochemical impedance spectroscopy at constant room temperature (298 K). Fig. 3a shows a representative Nyquist plot of the 28% Br−/S2− site disordered Li6PS5Br upon decompression (at representative pressures), in the applied pressure range from 1.5 GPa to 0.1 GPa. The lines represent the obtained fit to the data, according to the depicted equivalent circuit. The grey-shaped data points represent the data that were not included in the fitting process after evaluating the data quality using the Kramers–Kronig analysis. The impedance data were fit with an equivalent circuit consisting of a resistor in series with a constant phase element (CPE) that represents the low frequency tail resulting from the blocking electrode setup. While generally, a semicircle in the Nyquist plot is expected for processes related to in-grain conduction of ions (that can be fitted by a CPE/resistor element), here only a simple resistor describes the corresponding resistance contribution. This is because the semicircle is shifted to higher frequencies, outside the measurement range, given the high ionic conductivity (low resistance) of the investigated materials.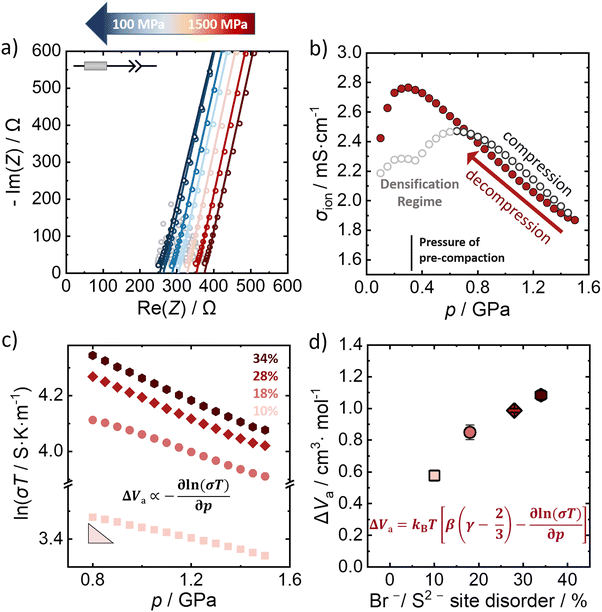 | ||
| Fig. 3 Determination of activation volumes from pressure dependence of ionic conductivity. (a) Representative Nyquist plots of 28% Br−/S2− site disordered Li6PS5Br upon decompression. (b) The corresponding change of ionic conductivity upon compression and decompression for a pressure range from 0.1 GPa to 1.5 GPa. (c) The relationship between the logarithm of ionic conductivity with the pressure upon decompression for all the Br−/S2− site disordered lithium argyrodites. (d) Activation volumes for all disorders calculated according to the extended equation (eqn 3) using the slope obtained from a linear regression of the data shown in panel c with β = 1/23 GPa−1 and γ = 1.7, as determined computationally. Uncertainties of the values reflect the standard deviations obtained by triplicate measurements. | ||
The impedance data for the 10%, 18% and 34% Br−/S2− site disorders under decompression can be found in the ESI† (Fig. S5–S7, ESI†), as well as the evolution of the ionic conductivity under applied pressure (Fig. S8–S10, ESI†). The material was pre-compacted to 370 MPa to ensure a better contact between the sample and the steel electrodes prior to the measurements. When pressure is applied on Li6PS5Br, an initial increase in ionic conductivity is observed as the consolidation of the pellet takes place.42 During the initial increase of the external applied pressure, the gaps between particles are filled and particle–particle contact is enhanced during the pellet formation33,43 (Fig. 3b). The pressure range up to approximately 0.7 GPa is considered to be the densification regime of the material, where the density increases to the theoretical density at 0.7 GPa. Because of the pre-compaction procedure there is a feature in the ionic conductivity data during densification at 370 MPa, which is absent when the material is not pre-compacted before the measurement (Fig. S11, ESI†). For pressures higher than 1.0 GPa, the powder is fully consolidated with a relative density of 99% (Fig. S12, ESI†) and applying more pressure primarily acts to compress the atomic structure. In this regime, there is an approximately linear relationship between the pressure and the ionic conductivity up to the maximum applied pressure of 1.5 GPa. Since the material is already fully densified, the linear relation is observed over a larger pressure range during decompression. Considering the impact on ionic conductivity we find that the pressure change of ∼1.0 GPa has a change in ionic conductivity of ∼1.0 mS cm−1. The change in the ionic conductivity with the application of pressure is similar to the change from compositional/disorder effects,44 and statistically significant.
The linearity of the ionic conductivity with applied pressure about decompression is characterized by the activation volume (ΔVa). The activation volumes are related to the slope of ln(σT) vs. p according to eqn (3). Here, the approximately linear region of the decompression data was utilized (1.5 GPa to 0.8 GPa) to evaluate the slopes needed to calculate ΔVa for each of the different site disorders (Fig. 3c). The slope of the decompression curve was found to be reproducible within 10%. This is shown in Fig. S13 (ESI†) representing the values of ln(σT) with p and their uncertainties extracted from triplicate measurements for each disorder. The activation volumes were also calculated using the simplified equation (eqn (4)) and the errors are also in a range of 10% (Fig. S14, ESI†), with the values of the simplified equation about 10% lower than those calculated using eqn (4). For the calculation of the activation volumes including the Grüneisen parameter γ and the compressibility β (Fig. 3d), the β and γ values were extracted from the Burch-Murnaghan fit of the energy – volume relation (Fig. S15, ESI†) obtained by the ab initio molecular dynamics simulations at three different temperatures (700 K, 800 K and 900 K). Specifically, the bulk modulus B = 23 ± 3 GPa was calculated by averaging the bulk moduli found for the three different temperatures (700 K, 800 K, 900 K) for all the disorders. Any differences in the bulk moduli between different disorders is within the uncertainty of the simulations, so we used a constant value of β = 1/B for all ΔVa calculations. The reported bulk modulus B = 29 GPa45 is comparable with the one found herein. The pressure derivative of the bulk modulus can be utilized to estimate the value of the Grüneisen parameter, determined here to be approximately γ = 1.7. Notably, this value is comparable to the one obtained from the phonon pressure model,46 where the reported bulk and shear moduli from the literature were utilizied,45 resulting in γ = 2, (see eqn (S14) and (S15) in the ESI†). Hence, for the purposes of this study, the values of B = 23 ± 3 GPa and γ = 1.7, calculated by the ab initio molecular dynamics simulations, are employed for the calculation of ΔVa.
3.3 Influence of Br−/S2− site disorder on the activation volumes
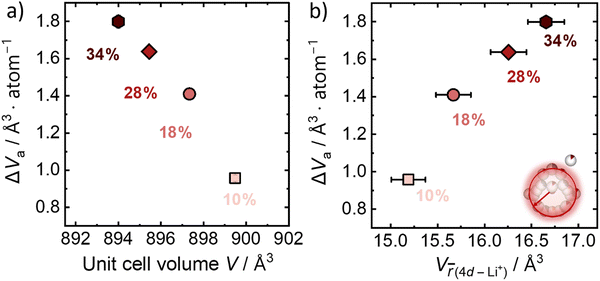
The activation volume for Li+ conduction seems to be influenced by the Br−/S2− site disorder in the Li6PS5Br, as it increases monotonically from 0.96 Å3 atom−1 (0.58 cm3 mol−1) for 10% Br−/S2− site disorder to 1.80 Å atom−1 (1.08 cm3 mol−1) for the 34% Br−/S2− site disorder (Fig. 4a), as calculated using eqn (3). Activation volumes are typically reported in the literature in units of cm3 mol−1, in this work they are given in units of Å atom−1 to directly compare them with crystallographic volumes.When comparing the activation volume to the unit cell volume (Fig. 4a), we arrive at the seemingly intuitive result that structures with more available volume per mobile ion have ionic conductivities that are less sensitive to changes in pressure. In other words, having more free volume in the unit cell provides a buffer to any changes in volume due to changes in pressure. At the same time, there is an opposite correlation of the activation volume with the volume occupied by the Li+ cage substructure (Fig. 4b), suggesting that the more spatially distributed Li+ and the shorter distances, which are responsible for the inter-cage jumps, the more volume is needed for the Li+ mobile ion to jump between sites. In other words, a weaker bonding environment10 for the lithium ion within the cage results in higher values of activation volume. Importantly, this analysis shows that larger crystallographic volumes (Vf) may not always relate to lower activation volumes, as is suggested by eqn (5) depending on which crystallographic volume is used. These considerations motivate the need for further study of the microscopic origins of activation volume.
3.4 Migration volume for Li+
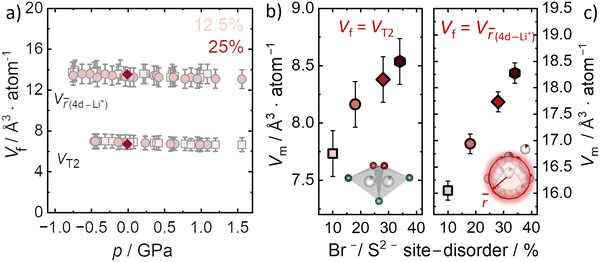
Here, we specifically consider the two main factors related to the high ionic conductivity in Li6PS5Br as they pertain to the microscopic activation volume according to eqn (5). It is known that Li+ jumps between T2–T2 sites are responsible for long-range Li+ transport, while the diffuse distribution of Li+ in the cages is also linked to better Li+ mobility.9 Both factors contribute to the continuous three-dimensional diffusion pathway of inter-cage transport through the argyrodite structure.10 Thus, for our analysis of migration volumes we separately utilize the T2 tetrahedral volume and Li+ cage volume to designate the nominal free volume Vf in the structure. Because activation volume has units of Å atom−1, the crystallographic volumes are also normalized by the respective number of atoms contained within them. To investigate the effect of pressure on the T2 tetrahedral volumes, ab initio molecular dynamics simulations are employed for the 12.5% and 25% Br−/S2− site disorder (Fig. 5a). The T2 volumes are found to be approximately constant within uncertainty across the applied pressure range (−0.5 GPa to 1.5 GPa). The computationally determined T2 volumes (Vf = 7.2 ± 0.8 Å3 atom−1) are in excellent agreement, within the uncertainty, with those obtained experimentally for all Br−/S2− site disorders (Vf = 6.8 ± 0.2 Å3 atom−1) indicating that neither disorder nor pressure significantly affect the T2 volume. Thus, we use the experimental value to estimate the migration volumes Vm for the four different disorders (Fig. 5b) according to eqn (5). This calculation suggests that the migration volume Vm increases with increasing disorder (Fig. 5b), which is unexpected since Vm is expected to be constant for a given mobile ion passing through nominally the same structural bottleneck (taken here to be the T2–T2 jump). This analysis suggests that the T2–T2 jump may not dominate the pressure dependence of ionic conductivity, which is itself unexpected since this jump dominates the long-range Li+ transport relevant to impedance measurements. Nevertheless, it is possible that another crystallographic volume should be considered as Vf.The other logical microscopic choice for Vf should be related to the lithium cage sub-structure, where the volume can be determined from the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) distance. Given that the size of the Li+ cages centered around the 4d site changes as a function of Br−/S2− disorder, quantified by the
distance. Given that the size of the Li+ cages centered around the 4d site changes as a function of Br−/S2− disorder, quantified by the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) distance, we also consider that the free volume Vf may be represented by this structural parameter. In this case, we calculate the migration volume Vm, by using the volume per atom defined by the
distance, we also consider that the free volume Vf may be represented by this structural parameter. In this case, we calculate the migration volume Vm, by using the volume per atom defined by the ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) distance between the Li+ and the Wyckoff 4d position, as the crystallographic volume Vf. However, because the size of the Li+ cage increases with disorder, as does the activation volume, the net result is also an increase in Vm (Fig. 5c).
distance between the Li+ and the Wyckoff 4d position, as the crystallographic volume Vf. However, because the size of the Li+ cage increases with disorder, as does the activation volume, the net result is also an increase in Vm (Fig. 5c).
Thus, the two crystallographic volumes most pertinent to Li+ transport (T2 and Li+ cage substructure) both suggest that Vm increases with increasing disorder. Furthermore, the relative increase of Vm with disorder is similar in both cases. According to eqn (5), the interpretation of this result is that the space Li+ occupies at the transition state is not constant among these materials, even though the T2 site geometry is unchanged among the different Br−/S2− site disorders and, if anything, there is more free volume in the Li+ cages with increased Br−/S2− site disorder. If the microscopic interpretation of the activation volume being a change in the transition state volume is correct, then the migration volume for a given mobile ion (here Li+) is supposed to be constant and we would expect to find the same migration volumes among the different disorders for the Li+ migration in Li6PS5Br. One possible explanation for the different and increasing migration volumes in Li6PS5Br is that eqn (3) cannot be applied in highly defective superionic conductors. However, as a thermodynamic relationship this seems highly unlikely, although the possibility of a non-zero ΔGd should be generally considered.
Another possible reason is that using the free volume of the transition state is an incomplete description of the relevant microscopic volume change when the jumping ion is transferred from the ground position (or equilibrium position) to the transition state (or saddle point).20 In the end, it may very well be that a thermodynamic relationship that carries the unit of a volume may not be directly related to a real crystallographic volume (change). Nevertheless, these findings suggest that it is important to carefully consider how to interpret the pressure dependence of ionic conductivity, both thermodynamically and microscopically, and motivates us to further investigate and rationalize the thermodynamic activation volume and its potential correlation to structural factors in ion transport.
4. Conclusion
In this work, we have studied the influence of applied pressure on Br−/S2− site disordered Li6PS5Br argyrodite and found that, after initial consolidation, the ionic conductivity decreases with increasing applied pressure. The magnitude of this effect is quantified by the thermodynamic activation volume, which increases monotonically with site disorder. When the activation volumes are related to microscopic structural descriptors, i.e., the Li+ tetrahedral volume and the Li+ cage substructure, however, an unexpected result is obtained. Namely, the migration volume changes by approximately 10–15%, even though the mobile ion (Li+) is the same, suggesting that the Li+ volume at the transition site is not constant. Thus, this work motivates the use of pressure-dependent measurements to further investigate microscopic influences on ion transport in Br−/S2− disordered argyrodites.Even if ΔVa – as a real thermodynamic quantity – does not relate to a specific microscopic volume, characterizing the thermodynamic activation volume in other superionic Li+ conductors may provide novel insights to the influences of atomic structure and bonding on fast ionic transport.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was supported by the Deutsche Forschungsgemeinschaft (DFG) under grant number ZE 1010/12-1. M. T. A. acknowledges the Alexander von Humboldt Foundation for financial support through a Postdoctoral Fellowship. The authors gratefully acknowledge the computing time provided to them at the NHR Center NHR4CES at TU Darmstadt (project number p0020377). This is funded by the Federal Ministry of Education and Research, and the state governments participating on the basis of the resolutions of the GWK for national high performance computing at universities (https://www.nhr-verein.de/unsere-partner). We further acknowledge funding by the Bundesministerium für Bildung und Forschung (BMBF project FestBatt 03XP0435C). This research used resources at the high-resolution diffractometer SPODI and monochromatic neutron source, operated by the Heinz Maier-Leibnitz Zentrum, Technische Universität München, 85748 Garching, Germany.References
- J. Janek and W. G. Zeier, A Solid Future for Battery Development, Nat. Energy, 2016, 1(9), 16141, DOI:10.1038/nenergy.2016.141.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Materials Design of Ionic Conductors for Solid State Batteries, Prog. Energy, 2020, 2(2), 022001, DOI:10.1088/2516-1083/ab73dd.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Design Principles for Solid-State Lithium Superionic Conductors, Nat. Mater., 2015, 14(10), 1026–1031, DOI:10.1038/nmat4369.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction, Chem. Rev., 2016, 116(1), 140–162, DOI:10.1021/acs.chemrev.5b00563.
- J. Janek and W. G. Zeier, Challenges in Speeding up Solid-State Battery Development, Nat. Energy, 2023, 8(March), 230–240, DOI:10.1038/s41560-023-01208-9.
- H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Li6PS5X: A Class of Crystalline Li-Rich Solids With an Unusually High Li+ Mobility, Angew. Chem., Int. Ed., 2008, 47(4), 755–758, DOI:10.1002/anie.200703900.
- S. Boulineau, M. Courty, J.-M. Tarascon and V. Viallet, Mechanochemical Synthesis of Li-Argyrodite Li6PS5X (X = Cl, Br, I) as Sulfur-Based Solid Electrolytes for All Solid State Batteries Application, Solid State Ionics, 2012, 221, 1–5, DOI:10.1016/j.ssi.2012.06.008.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, Influence of Lattice Polarizability on the Ionic Conductivity in the Lithium Superionic Argyrodites Li6PS5X (X = Cl, Br, I), J. Am. Chem. Soc., 2017, 139(31), 10909–10918, DOI:10.1021/jacs.7b06327.
- A. Gautam, M. Sadowski, M. Ghidiu, N. Minafra, A. Senyshyn, K. Albe and W. G. Zeier, Engineering the Site-Disorder and Lithium Distribution in the Lithium Superionic Argyrodite Li6PS5Br, Adv. Energy Mater., 2021, 11(5), 2003369, DOI:10.1002/aenm.202003369.
- N. Minafra, M. A. Kraft, T. Bernges, C. Li, R. Schlem, B. J. Morgan and W. G. Zeier, Local Charge Inhomogeneity and Lithium Distribution in the Superionic Argyrodites Li6PS5Br (X = Cl, Br, I), Inorg. Chem., 2020, 59(15), 11009–11019, DOI:10.1021/acs.inorgchem.0c01504.
- S.-T. Kong, H.-J. Deiseroth, C. Reiner, Ö. Gün, E. Neumann, C. Ritter and D. Zahn, Lithium Argyrodites with Phosphorus and Arsenic: Order and Disorder of Lithium Atoms, Crystal Chemistry, and Phase Transitions, Chem. – Eur. J., 2010, 16(7), 2198–2206, DOI:10.1002/chem.200902470.
- R. P. Rao, N. Sharma, V. K. Peterson and S. Adams, Formation and Conductivity Studies of Lithium Argyrodite Solid Electrolytes Using In-Situ Neutron Diffraction, Solid State Ionics, 2013, 230(C), 72–76, DOI:10.1016/j.ssi.2012.09.014.
- H. Wang, M. Yu, Y. Wang, Z. Feng, Y. Wang, X. Lü, J. Zhu, Y. Ren and C. Liang, In-Situ Investigation of Pressure Effect on Structural Evolution and Conductivity of Na3SbS4 Superionic Conductor, J. Power Sources, 2018, 401(May), 111–116, DOI:10.1016/j.jpowsour.2018.05.037.
- N. Nachtrieb and G. Handler, A Relaxed Vacancy Model for Diffusion in Crystalline Metals, Acta Metall., 1954, 2(6), 797–802, DOI:10.1016/0001-6160(54)90031-0.
- O. D. Sherby, J. L. Robbins and A. Goldberg, Calculation of Activation Volumes for Self-Diffusion and Creep at High Temperature, J. Appl. Phys., 1970, 41(10), 3961–3968, DOI:10.1063/1.1658396.
- H. Hoshino and M. Shimoji, The Effect of the Hydrostatic Pressure on the Electrical Conductivity of Silver Iodide, J. Phys. Chem. Solids, 1972, 33(12), 2303–2309, DOI:10.1016/S0022-3697(72)80305-6.
- T. Famprikis, Ö. U. Kudu, J. A. Dawson, P. Canepa, F. Fauth, E. Suard, M. Zbiri, D. Dambournet, O. J. Borkiewicz, H. Bouyanfif, S. P. Emge, S. Cretu, J.-N. Chotard, C. P. Grey, W. G. Zeier, M. S. Islam and C. Masquelier, Under Pressure: Mechanochemical Effects on Structure and Ion Conduction in the Sodium-Ion Solid Electrolyte Na3PS4, J. Am. Chem. Soc., 2020, 142(43), 18422–18436, DOI:10.1021/jacs.0c06668.
- B.-E. Mellander and D. Lazarus, Electrical Conductivity and Activation Volume for α-Li2SO4, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31(10), 6801–6803, DOI:10.1103/PhysRevB.31.6801.
- J. J. Fontanella, Pressure and Temperature Variation of the Electrical Conductivity of Poly(Propylene Glycol) Containing LiCF3SO3, J. Chem. Phys., 1999, 111(15), 7103–7109, DOI:10.1063/1.480002.
- H. Mehrer, Diffusion in Solids, Springer Series in Solid-State Sciences, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, vol. 155. DOI:10.1007/978-3-540-71488-0.
- D. N. Bose, G. Parthasarathy, D. Mazumdar and E. S. R. Gopal, Resistivity Maxima in Lithium Fast-Ion Conductors at High Pressure, Phys. Rev. Lett., 1984, 53(14), 1368–1371, DOI:10.1103/PhysRevLett.53.1368.
- R. H. Radzilowski and J. T. Kummer, The Hydrostatic Pressure Dependence of the Ionic Conductivity of β-Aluminas, J. Electrochem. Soc., 1971, 118(5), 714, DOI:10.1149/1.2408152.
- D. N. Yoon and D. Lazarus, Pressure Dependence of Ionic Conductivity in KCl, NaCl, KBr, and NaBr, Phys. Rev. B: Solid State, 1972, 5(12), 4935–4945, DOI:10.1103/PhysRevB.5.4935.
- M. D. Ingram, C. T. Imrie, I. Konidakis and S. Voss, Significance of Activation Volumes for Cation Transport in Glassy Electrolytes, Phys. Chem. Chem. Phys., 2004, 6(13), 3659–3662, 10.1039/B314879C.
- Y. Inaguma, J. Yu, Y. Shan, M. Itoh and T. Nakamuraa, The Effect of the Hydrostatic Pressure on the Ionic Conductivity in a Perovskite Lanthanum Lithium Titanate, J. Electrochem. Soc., 1995, 142(1), L8–L11, DOI:10.1149/1.2043988.
- T. Mezaki, Y. Kuronuma, I. Oikawa, A. Kamegawa and H. Takamura, Li-Ion Conductivity and Phase Stability of Ca-Doped LiBH4 under High Pressure, Inorg. Chem., 2016, 55(20), 10484–10489, DOI:10.1021/acs.inorgchem.6b01678.
- P. Žguns and B. Yildiz, Strain Sensitivity of Li-Ion Conductuctivity in β-Li3PS4 Solid Electrolyte, PRX Energy, 2022, 1(2), 023003, DOI:10.1103/PRXEnergy.1.023003.
- M. D. Ingram, C. T. Imrie and I. Konidakis, Activation Volumes and Site Relaxation in Mixed Alkali Glasses, J. Non. Cryst. Solids, 2006, 352(30–31), 3200–3209, DOI:10.1016/j.jnoncrysol.2006.05.009.
- M. Ingram, Effects of Pressure on the Ionic Conductivity of AgI–AgPO3 and KI–AgPO3 Glasses, Solid State Ionics, 1998, 105(1–4), 103–107, DOI:10.1016/S0167-2738(97)00455-4.
- T. Krauskopf, S. P. Culver and W. G. Zeier, Local Tetragonal Structure of the Cubic Superionic Conductor Na3PS4, Inorg. Chem., 2018, 57(8), 4739–4744, DOI:10.1021/acs.inorgchem.8b00458.
- M. D. Rutter, R. A. Secco and Y. Huang, Ionic Conduction in Hydrated Zeolite Li-, Na- and K-A at High Pressures, Chem. Phys. Lett., 2000, 331(2–4), 189–195, DOI:10.1016/S0009-2614(00)01191-X.
- A. Gautam, M. Sadowski, N. Prinz, H. Eickhoff, N. Minafra, M. Ghidiu, S. P. Culver, K. Albe, T. F. Fässler, M. Zobel and W. G. Zeier, Rapid Crystallization and Kinetic Freezing of Site-Disorder in the Lithium Superionic Argyrodite Li 6 PS 5 Br, Chem. Mater., 2019, 31(24), 10178–10185, DOI:10.1021/acs.chemmater.9b03852.
- T. Bernges, T. Böger, O. Maus, P. S. Till, M. T. Agne and W. G. Zeier, Scaling Relations for Ionic and Thermal Transport in the Na + Ionic Conductor Na 3 PS 4. ACS, Mater. Lett., 2022, 4(12), 2491–2498, DOI:10.1021/acsmaterialslett.2c00846.
- G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269, DOI:10.1103/PhysRevB.49.14251.
- G. Kresse, Ab Initio Molecular Dynamics for Liquid Metals, J. Non. Cryst. Solids, 1995, 192–193, 222–229, DOI:10.1016/0022-3093(95)00355-X.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- F. D. Murnaghan, The Compressibility of Media under Extreme Pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244–247, DOI:10.1073/pnas.30.9.244.
- F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71(11), 809–824, DOI:10.1103/PhysRev.71.809.
- C. Schneider, C. P. Schmidt, A. Neumann, M. Clausnitzer, M. Sadowski, S. Harm, C. Meier, T. Danner, K. Albe, A. Latz, W. A. Wall and B. V. Lotsch, Effect of Particle Size and Pressure on the Transport Properties of the Fast Ion Conductor t-Li7SiPS8, Adv. Energy Mater., 2023, 13, 2203873, DOI:10.1002/aenm.202203873.
- M. Kodama, S. Komiyama, A. Ohashi, N. Horikawa, K. Kawamura and S. Hirai, High-Pressure in Situ X-Ray Computed Tomography and Numerical Simulation of Sulfide Solid Electrolyte, J. Power Sources, 2020, 462(February), 228160, DOI:10.1016/j.jpowsour.2020.228160.
- A. Gautam, M. Ghidiu, E. Suard, M. A. Kraft and W. G. Zeier, On the Lithium Distribution in Halide Superionic Argyrodites by Halide Incorporation in Li7−xPS6−xClX, ACS Appl. Energy Mater., 2021, 4(7), 7309–7315, DOI:10.1021/acsaem.1c01417.
- Z. Deng, Z. Wang, I.-H. Chu, J. Luo and S. P. Ong, Elastic Properties of Alkali Superionic Conductor Electrolytes from First Principles Calculations, J. Electrochem. Soc., 2016, 163(2), A67–A74, DOI:10.1149/2.0061602jes.
- M. T. Agne, S. Anand and G. J. Snyder, Inherent Anharmonicity of Harmonic Solids, Research, 2022, 2022, DOI:10.34133/2022/9786705.
Footnote |
| † Electronic supplementary information (ESI) available: The discussion on the derivation of the activation volume is presented. For all the (10%, 18%, 28%, 34%) Br−/S2− site disordered Li6PS5Br there are plots of the neutron diffraction data with the corresponding Rietveld refinements, Nyquist plots at three different pressures, pressure-dependent ionic conductivity measurements, Heckel plots upon compression, graphs of the triplicate measurements of the ionic conductivity vs. pressure and the formulas used for the calculation of the Grüneisen parameter γ. See DOI: https://doi.org/10.1039/d3ya00424d |
| This journal is © The Royal Society of Chemistry 2023 |