Open Access Article
Open Access ArticleIon parking in native mass spectrometry†
Nicolas J.
Pizzala
,
Jay S.
Bhanot
,
Ian J.
Carrick
,
Eric T.
Dziekonski
 and
Scott A.
McLuckey
and
Scott A.
McLuckey
 *
*
Department of Chemistry, Purdue University, West Lafayette, Indiana 47907-2084, USA. E-mail: mcluckey@purdue.edu
First published on 11th April 2024
Abstract
A forced, damped harmonic oscillator model for gas-phase ion parking using single-frequency resonance excitation is described and applied to high-mass ions of relevance to native mass spectrometry. Experimental data are provided to illustrate key findings revealed by the modelling. These include: (i) ion secular frequency spacings between adjacent charge states of a given protein are essentially constant and decrease with the mass of the protein (ii) the mechanism for ion parking of high mass ions is the separation of the ion clouds of the oppositely-charged ions with much less influence from an increase in the relative ion velocity due to resonance excitation, (iii) the size of the parked ion cloud ultimately limits ion parking at high m/z ratio, and (iv) the extent of ion parking of off-target ions is highly sensitive to the bath gas pressure in the ion trap. The model is applied to ions of 17 kDa, 467 kDa, and 2 MDa while experimental data are also provided for ions of horse skeletal muscle myoglobin (≈17 kDa) and β-galactosidase (≈467 kDa). The model predicts and data show that it is possible to effect ion parking on a 17 kDa protein to the 1+ charge state under trapping conditions that are readily accessible with commercially available ion traps. It is also possible to park β-galactosidase efficiently to a roughly equivalent m/z ratio (i.e., the 26+ charge state) under the same trapping conditions. However, as charge states decrease, analyte ion cloud sizes become too large to allow for efficient ion trapping. The model allows for a semi-quantitative prediction of ion trapping performance as a function of ion trapping, resonance excitation, and pressure conditions.
Introduction
Electrospray ionization (ESI)1 has been among the most impactful developments in mass spectrometry (MS) in the past five decades by virtue of the wide range of important applications that it has enabled. The ability to generate ions directly from solution provides means for producing ions from polar non-volatile molecules that greatly facilitates the coupling of condensed-phase separations, such as liquid chromatography2 and capillary electrophoresis,3 with MS as well as a soft ionization approach for many classes of polymers,4 including biopolymers,5 and complexes derived therefrom.6,7 A hallmark of ESI is its tendency to generate multiply-charged ions from molecules with multiple polar sites. The multiple-charging phenomenon has profound implications for MS and tandem MS (MS/MS). For example, multiple-charging reduces mass-to-charge (m/z) ratios, which reduces the upper m/z requirement for the mass analyzer, allows for higher mass resolution measurements for analyzers that provide better resolution at low m/z (e.g., Fourier transform ion cyclotron resonance (FTICR)8 and Orbitrap™9 mass analyzers), and improves detection efficiency both for approaches based on image current measurements, such as the FTICR and Orbitrap™, and for approaches that rely on electron multiplication.10 The multiple-charging phenomenon also affects the kinetic stability of the molecule-ion as well as the favored dissociation channels such that tandem mass spectra, and the structural information derived therefrom, are charge-state dependent.11 These consequences of multiple charging generally facilitate the determination of the masses and primary structures of analyte ions and can motivate the use of conditions that maximize the charge state.12,13 Furthermore, under appropriate conditions, charge state distributions can reveal conformational states in solution.14,15The multiple-charging phenomenon associated with ESI can also present measurement challenges. For example, it introduces ambiguity in determining mass from the measurement of m/z due to the fact that both mass and charge are, a priori, unknown. For this reason, charge state determination is an essential element in many applications of ESI MS(/MS). A variety of approaches have been developed to determine the charge states of ions generated via ESI. It was shown early in the application of ESI to proteins that the presence of two or more ions from the same molecule with known differences in mass and charge allows for the determination of ion charge via the solution of a set of simultaneous equations.16 Several algorithms have since been described that can be used to automatically determine the mass of an analyte from the most probable charge state distribution.17,18 A variety of approaches have been used to reduce charge states to facilitate their resolution so that they can be identified. Many involve altering solution conditions, such as the use of additives, to shift charge state distributions to lower values.19,20 The exposure of electrospray droplets to acids or bases has been shown to be effective in reducing charge states21–23 and the use of gas-phase ion/molecule reactions for charge state reduction has been described.24–26 The most robust means for charge reduction in the gas phase is via ion/ion reactions either prior to sampling ions into a mass spectrometer27–29 or within the mass spectrometer.30,31 Ion/ion reactions are capable of reducing charge states to arbitrarily low values32,33 and have been demonstrated to be useful in addressing the charge-state overlap problem associated with mixture analysis34 and determining the charge of the product ion.35 A more direct approach for determining the charge state of a specific ion is to determine the m/z spacings between isotope peaks,36 provided the resolution of the analyzer is sufficient and there is minimal overlap between signals from ions of different mass and charge but similar m/z ratio. An alternative approach is to measure the absolute charge of an individual ion in concert with the measurement of its m/z ratio, as is accomplished with charge detection MS37–39 and individual ion MS.40
ESI also generally gives rise to a distribution of charge states, which spreads the analytical signal among a variety of peaks. This can limit dynamic range in MS/MS experiments and can complicate mixture analysis when charge state distributions overlap in m/z-space. It has been demonstrated that it is possible to selectively inhibit ion/ion reaction rates in electrodynamic ion traps to allow for ions distributed across a range of charge states to be largely concentrated into a narrower range of charge states in techniques referred to as ion parking,41 parallel ion parking,42 or valet ion parking,43 depending upon the application. Ion parking techniques have been demonstrated, for example, to be useful for concentrating ion signals into a single charge state for subsequent MS/MS,44–48 for quantitation of biotherapeutic proteins,49 and for inhibiting sequential reactions in electron transfer dissociation studies.50,51 To date, ion parking has not been applied to ions of relatively high m/z values (e.g., >m/z 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). Ions generated under conditions amenable to the preservation of specific bio-complexes (i.e., under conditions used in the field of native MS52–56) are often of relatively high m/z ratios.57 In this work, we describe and employ a general first-order model for ion parking in an electrodynamic quadrupole ion trap using a single supplementary dipolar frequency to inhibit the ion/ion reaction rate of a selected charge state of an analyte of interest. Given the practical limitations associated with electrodynamic ion traps (e.g., the amplitudes of radio-frequency (RF) voltages that can be applied to the ion trap electrodes) this model allows for the prediction of the limits of performance of ion parking as the mass of the analyte ion increases and is therefore highly relevant to ion parking in native MS. We illustrate predictions arising from the model with experimental data using ions derived from apo-myoglobin (mass ≈ 17 kDa), to represent protein ions of relatively low m/z ratio, and ions derived from the β-galactosidase tetramer (mass ≈ 467 kDa), to represent ions relevant to native MS. Ions of 2 MDa are also modelled to illustrate ion parking performance that might be anticipated for species higher in mass than generally encountered in most native MS studies.
000). Ions generated under conditions amenable to the preservation of specific bio-complexes (i.e., under conditions used in the field of native MS52–56) are often of relatively high m/z ratios.57 In this work, we describe and employ a general first-order model for ion parking in an electrodynamic quadrupole ion trap using a single supplementary dipolar frequency to inhibit the ion/ion reaction rate of a selected charge state of an analyte of interest. Given the practical limitations associated with electrodynamic ion traps (e.g., the amplitudes of radio-frequency (RF) voltages that can be applied to the ion trap electrodes) this model allows for the prediction of the limits of performance of ion parking as the mass of the analyte ion increases and is therefore highly relevant to ion parking in native MS. We illustrate predictions arising from the model with experimental data using ions derived from apo-myoglobin (mass ≈ 17 kDa), to represent protein ions of relatively low m/z ratio, and ions derived from the β-galactosidase tetramer (mass ≈ 467 kDa), to represent ions relevant to native MS. Ions of 2 MDa are also modelled to illustrate ion parking performance that might be anticipated for species higher in mass than generally encountered in most native MS studies.
Experimental section
Materials
Lyophilized β-galactosidase powder, purchased from Sigma Aldrich (St Louis, MO, U.S.A.), was dissolved in HPLC-grade water purchased from Fisher Scientific (Pittsburgh, PA), and underwent buffer exchange with 150 mM ammonium acetate from Sigma Aldrich (St Louis, MO, U.S.A). The solution was then washed via centrifugation (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g min−1, 10 minutes) eight times with 150 μM ammonium acetate in a Vivaspin® 10 kDa MWCO spin column from Vivaproducts (Littleton, MA, U.S.A.). The washed solution was diluted in 150 mM ammonium acetate to a final β-galactosidase concentration of 5 μM. Horse skeletal muscle myoglobin was purchased from Sigma Aldrich and washed 3 times in a 3 kDa MWCO filter from Amicon® and diluted to a final concentration of 5 μM in ultrapure water with 5% acetic acid by total volume. 1H,1H-Pentadecafluoro-1-octonal (PFO) was purchased from Sigma Aldrich. A 1 mg mL−1 methanolic PFO stock solution was diluted to 100 μM in a 47.5/47.5/5 methanol/water/ 28–30% ammonium hydroxide solution. Proton-bound dimers, which served as proton transfer reagents, are readily generated using nano-electrospray in the negative mode at m/z 799 for PFO.
000 g min−1, 10 minutes) eight times with 150 μM ammonium acetate in a Vivaspin® 10 kDa MWCO spin column from Vivaproducts (Littleton, MA, U.S.A.). The washed solution was diluted in 150 mM ammonium acetate to a final β-galactosidase concentration of 5 μM. Horse skeletal muscle myoglobin was purchased from Sigma Aldrich and washed 3 times in a 3 kDa MWCO filter from Amicon® and diluted to a final concentration of 5 μM in ultrapure water with 5% acetic acid by total volume. 1H,1H-Pentadecafluoro-1-octonal (PFO) was purchased from Sigma Aldrich. A 1 mg mL−1 methanolic PFO stock solution was diluted to 100 μM in a 47.5/47.5/5 methanol/water/ 28–30% ammonium hydroxide solution. Proton-bound dimers, which served as proton transfer reagents, are readily generated using nano-electrospray in the negative mode at m/z 799 for PFO.
Instrumentation
All experiments were performed on a modified 5600 triple quadrupole/time-of-flight mass spectrometer (Sciex, Concord, ON, Canada).58 The instrument schematic is provided in Fig. S1.† A two-emitter59 nanoelectrospray (nESI) set-up enabled the generation of reagent cations and anions that were transferred alternately to the collision cell (q2) and mutually stored. One of the emitters was used in the positive ion mode to generate analyte cations while another emitter was used to generate singly-charged anions for ion/ion reactions. Mutual storage of cations and anions was enabled by application of a 298 kHz waveform at 2 V on the aperture plates at the entrance (IQ2) and exit (IQ3) of the linear ion trap/collision cell (q2) (Fig. S1†). The q2 collision cell (inscribed radius = 4.17 mm) was driven by a 1.8432 MHz power supply with capabilities for auxiliary dipolar AC, for ion acceleration in the radial dimension, to be superimposed across an opposing set of rods. The collision cell is equipped with “linear accelerator” (LINAC) electrodes to enable the imposition of an axial DC gradient to encourage ions to move to the ion trap exit.60Ions were parked by application of a single frequency AC in resonance with the fundamental secular frequency of the ion to be parked (see below). This frequency was calculated using the m/z of the ion along with the trapping and operation conditions of the quadrupole.
Results and discussion
The ion parking experiment involves the mutual storage of multiply-charged analyte ions with (usually) singly-charged reagent ions of opposite polarity allowing for sequential charge reduction reactions (usually via proton transfer). Trapping conditions must therefore be maintained that allow for the mutual storage of the reagent ions along with the charged-reduced analyte ions that can be far larger in m/z ratio. Even if the reagent ions are of relatively high m/z, the highest achievable low m/z cut-off (LMCO) of the quadrupole array used as the reaction vessel for the ion/ion reaction will ultimately limit how well ion parking can work at high m/z. In the following discussion, the principles of ion parking using a selective form of ion acceleration, referred to as ‘resonance excitation’,61,62 are discussed with emphasis on high m/z ions relevant to a native MS experiment using the parameters available with a commercially available quadrupole array (i.e., r0 = 4.17 mm, Ω/2π = 1.8432 MHz, VRF,max = 2469.15 V0-p for a LMCO of m/z 450) and charge states of ions of mass = 17 kDa, 467 kDa, and 2 MDa. A general model has been developed for ion parking using resonance excitation in order to anticipate limits of performance. A full description of the model along with its development and underlying assumptions is provided in ESI.† Selected equations relevant to the model are included in the main text along with plots that illustrate key aspects to understanding ion parking of high mass ions.Frequency spacing between charge states
From the standpoint of parking a selected charge state from all others for a given protein, the secular frequency spacing between adjacent charge states is relevant. The difference in the fundamental secular frequencies of adjacent charge states in the absence of a quadrupolar DC field can be estimated by: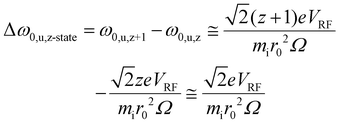 | (1) |
| Δf0,u,z-state = Δω0,u,z-state/2π | (2) |
The masses of the ions in adjacent charge states are not strictly equal, as they differ by the mass of the species responsible for the charge difference (usually a proton). However, this mass difference is negligible relative to the mass of a high mass complex. Fig. S2† shows a plot of Δf0,u,z-state (eqn (1) and (2)) versus mass for r0 = 0.00417 m; VRF = 2469.15 V0-p and Ω/2π = 1.8432 MHz (these values lead to a LMCO of m/z 450), which illustrates the fact that the frequency difference between adjacent charge states decreases with the mass of the ion.
Mechanisms of ion parking
The following part of the discussion describes how trapping parameters and m/z values of the ions relate to the mechanism of ion parking using resonance excitation. The basis for ion parking is the selective inhibition of an ion/ion reaction rate, RI–I, given by:| RI–I = kc[cations][anions] | (3) |
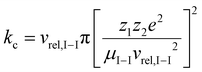 | (4) |
The average kinetic energy of an ion undergoing resonance excitation includes both its initial thermal kinetic energy and the additional kinetic energy resulting from acceleration by the dipolar oscillatory field. While the latter is determined by several variables, the maximum kinetic energy, KEmax, is limited by the product of the ion charge and the pseudopotential well-depth, Du:65,66
| KEmax ≅ zeDu | (5) |
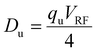 | (6) |
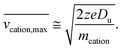 | (7) |
The above relationship can be used for an estimate of the relative ion velocities and the average velocity of the reagent anion (see ESI eqn (15)†) to estimate the maximum relative velocity, vrel,I–I,max, for each analyte charge state that can be achieved via resonance excitation for a given set of trapping conditions:
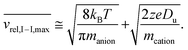 | (8) |
The ratio of the ion/ion reaction rate constants with and without resonance excitation can then be estimated by:
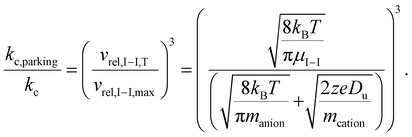 | (9) |
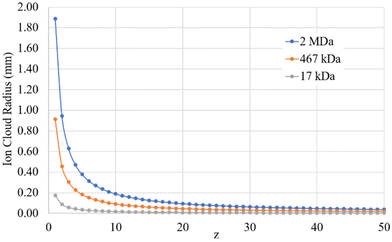
Given the inverse cubed relationship between the rate constant and relative velocity in relation (4), it is necessary to increase the relative velocity by a factor of 2.15 in order to reduce the ion/ion rate constant by a factor of ten. Fig. 1 provides plots of  vs. z for cations of 17 kDa, 467 kDa, and 2 MDa in reaction with a singly-charged anion of 799 Da (LMCO = m/z 450). The kc,parking values are obtained at KEmax for the cation whereas kc values are determined from thermal energy cations. These curves represent the maximum extent to which an ion/ion reaction rate constant can be diminished via manipulation of the velocity of the cation. The plot shows that it is possible to inhibit reaction rates to below 0.1 of the rate for an unparked ion on the basis of increased cation velocity for all charge states of a protein of 17 kDa. In the case of an analyte ion of 467 kDa, charge states of 6+ and below cannot be accelerated to a sufficiently high velocity to lead to a 10-fold decrease in reaction rate without first being ejected from the ion trap. In the case of a 2 MDa analyte, the charge state cut-off for reducing the reaction rate by a factor of 10 is roughly 30+. Note that this analysis does not account for the finite size of the cation cloud (see below), which would lead to significant ion ejection for ions that approach the average maximum cation velocity for each of the respective charge states. Hence, the charge states at which ion ejection would preclude an ion parking experiment would likely be somewhat higher for the larger cations included here.
vs. z for cations of 17 kDa, 467 kDa, and 2 MDa in reaction with a singly-charged anion of 799 Da (LMCO = m/z 450). The kc,parking values are obtained at KEmax for the cation whereas kc values are determined from thermal energy cations. These curves represent the maximum extent to which an ion/ion reaction rate constant can be diminished via manipulation of the velocity of the cation. The plot shows that it is possible to inhibit reaction rates to below 0.1 of the rate for an unparked ion on the basis of increased cation velocity for all charge states of a protein of 17 kDa. In the case of an analyte ion of 467 kDa, charge states of 6+ and below cannot be accelerated to a sufficiently high velocity to lead to a 10-fold decrease in reaction rate without first being ejected from the ion trap. In the case of a 2 MDa analyte, the charge state cut-off for reducing the reaction rate by a factor of 10 is roughly 30+. Note that this analysis does not account for the finite size of the cation cloud (see below), which would lead to significant ion ejection for ions that approach the average maximum cation velocity for each of the respective charge states. Hence, the charge states at which ion ejection would preclude an ion parking experiment would likely be somewhat higher for the larger cations included here.
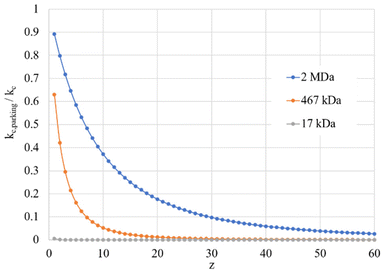 | ||
| Fig. 1 Plots of the ratio of rate constants with (kc,parking)/without (kc) resonance excitation of the analyte ion at the KEmax value (eqn (9)) for each charge-state as a function of z for analytes of 17 kDa, 467 kDa, and 2 MDa. | ||
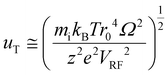 | (10) |
When uT approaches r0, the stored ion cloud begins to undergo ion evaporation as the high energy tail of the ion kinetic energy distribution exceeds Du. Fig. 2 shows plots of uT at 300 K (LMCO = m/z 450) as a function of z for analytes of 17 kDa, 467 kDa, and 2 MDa.
The ion cloud sizes of the anions and cations in an ion parking experiment are relevant in establishing the extent to which they can be separated under resonance excitation conditions. If it is assumed that the ion cloud under resonance excitation conditions moves coherently and that the clouds of oppositely charged ions are of sufficiently low densities that they have minimal influence over each other's size, the amplitude of the ion cloud oscillation, AAC, must exceed the sum of the radii of the cation and anion clouds for complete separation of the ion clouds:
| AAC > uT,cation + uT,anion. | (11) |
When the sum of the AAC and uT,cation approaches r0, resonance excitation will result in cation loss as the cation cloud begins to contact the rods. Hence, AAC must be less than the difference between r0 and uT,cation, i.e.:
| AAC < r0 − uT,cation. | (12) |
For perspective, the uT,anion for the reagent anion used in this study (m/z 799), as estimated viaeqn (10), is 3.8 × 10−5 m at a LMCO of m/z 450 and 1.7 × 10−4 m at a LMCO of m/z 100 whereas for singly-charged β-galactosidase (mass ≈ 467 kDa), the uT,cation values are 9.1 × 10−4 m and 4.1 × 10−3 m at LMCO values of m/z 450 and m/z 100, respectively. (Note that LMCO is the m/z for which the q-value is 0.908 (see eqn (S5)†) and is directly proportional to VRF.) These values indicate that the anion cloud size is well within 1 mm over the range of trapping conditions that might be used with the present linear ion trap. However, at a LMCO of m/z 100, the ion cloud for a 300 K population of β-galactosidase is estimated to fill the inscribed area of the quadrupole array. Rapid ion evaporation would be expected in this case and ion parking would obviously not be possible. At a LMCO of m/z 450, however, the model suggests that there would be enough room in the LIT to allow for ion cloud separation. That is, the maximum AAC that can be used without ion ejection (from eqn (12)) is 3.26 mm (4.17–0.91 mm) and the minimum AAC required for complete ion cloud separation (eqn (11)) is 0.95 mm (0.91 mm + 0.04 mm).
The preceding discussion suggests that ion parking can be effected with very high mass ions primarily by reducing ion cloud overlap via resonance excitation even when increasing the relative cation velocity is marginally effective. (Note that Fig. 1 suggests a maximum reduction of kc for 1+ of β-galactosidase, 467 kDa, of 37% on the basis of the increase in relative velocity.) However, at very low q-values/well-depths, the cloud size of the high mass ion ultimately limits the extent to which ion clouds can be separated.
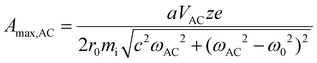 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71,72), VAC is the p–p amplitude of the dipolar AC applied to opposing rods, and c is the term to account for damping resulting from collisions with a bath gas. Many ion trap modelling papers73 base the determination of collision frequency on polarization theory and usually use the familiar Langevin formalism. A convenient consequence of the use of the polarization model is that the collision rate constant is velocity independent, which leads to a constant damping factor. However, the Langevin ion-induced dipole model assumes the ion to be a point-charge, which is most appropriate for relatively small ions. However, the sizes of the ions encountered in native MS generally have cross-sections much larger than those determined via the Langevin formalism. We therefore have used a combined hard-sphere + ion-induced dipole model for determining the collision frequency and assume an elastic model for momentum transfer. The damping term, c, is determined from:
71,72), VAC is the p–p amplitude of the dipolar AC applied to opposing rods, and c is the term to account for damping resulting from collisions with a bath gas. Many ion trap modelling papers73 base the determination of collision frequency on polarization theory and usually use the familiar Langevin formalism. A convenient consequence of the use of the polarization model is that the collision rate constant is velocity independent, which leads to a constant damping factor. However, the Langevin ion-induced dipole model assumes the ion to be a point-charge, which is most appropriate for relatively small ions. However, the sizes of the ions encountered in native MS generally have cross-sections much larger than those determined via the Langevin formalism. We therefore have used a combined hard-sphere + ion-induced dipole model for determining the collision frequency and assume an elastic model for momentum transfer. The damping term, c, is determined from: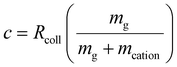 | (14) |
| Rcoll = ngσh-svrel,I–M + ngσLvrel,I–M | (15) |
| Rcoll = ngσh-svrel,I–M + ngkL | (16) |
The hard-sphere collision rate, on the other hand, is dependent on vrel,I–M. For a given charge state of an ion under fixed trapping conditions, the maximum relative velocity, vrel,I–M,max, is limited by zeDu, in analogy with the vrel,I–I,max discussed above (eqn (5)). A similar relationship can be used to approximate this value using the mass of the bath gas in place of the mass of the anion:
 | (17) |
Fig. S3† shows plots of 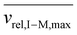 versus z for cations of mass 17 kDa, 467 kDa, and 2 MDa at LMCO = m/z 450. These plots show an intercept of
versus z for cations of mass 17 kDa, 467 kDa, and 2 MDa at LMCO = m/z 450. These plots show an intercept of 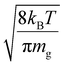 and a slope of
and a slope of 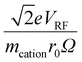 , which reflects the lower sensitivity of the relative velocity to cation acceleration as the mass of the cation increases.
, which reflects the lower sensitivity of the relative velocity to cation acceleration as the mass of the cation increases.
The value of c (i.e., the damping factor) is dependent on vrel,I–M, which depends on the amplitude of the resonance excitation voltage. For a given analyte ion, the range of c values, cmin to cmax, can be estimated by determining cmin in the absence of resonance excitation, as estimated by:
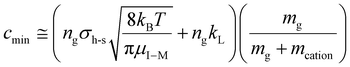 | (18) |
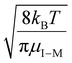 , for vrel,I–M,T, the minimum relative velocity, and determining cmax at the maximum extent of resonance excitation prior to ejection from the ion trap, as reflected by
, for vrel,I–M,T, the minimum relative velocity, and determining cmax at the maximum extent of resonance excitation prior to ejection from the ion trap, as reflected by 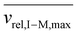 :
: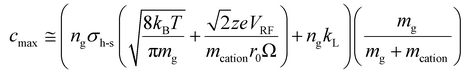 | (19) |
Fig. S4† provides plots of cmin and cmax as a function of z for ions of mass 467 kDa (Fig. S4a†) and 17 kDa (Fig. S4b†) at four nitrogen bath gas pressures (viz., 1, 5, 10, and 15 mTorr). There is a linear dependence of both cmin and cmax upon z, although the slopes differ. In the case of cmin, the Langevin cross-section (see ESI eqn (33)†), increases linearly with z whereas in the case of cmax, the Langevin cross-section and 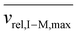 (see eqn (17)) both increase linearly with z resulting in a larger slope. The difference between cmin and cmax decreases as the mass of the cation increases (compare Fig. S4a with Fig. S4b†) due to the fact that vrel,I–M is less sensitive to resonance excitation as the mass of the cation increases. Note that the c values are also linearly related to the bath gas number density, ng, which has a significant impact on the charge-state resolution single-frequency ion parking (see below).
(see eqn (17)) both increase linearly with z resulting in a larger slope. The difference between cmin and cmax decreases as the mass of the cation increases (compare Fig. S4a with Fig. S4b†) due to the fact that vrel,I–M is less sensitive to resonance excitation as the mass of the cation increases. Note that the c values are also linearly related to the bath gas number density, ng, which has a significant impact on the charge-state resolution single-frequency ion parking (see below).
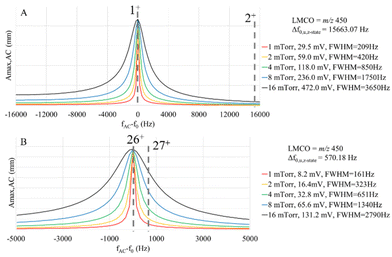
The actual c-value in a given ion parking experiment is expected to fall within the range bounded by cmin and cmax, as the former estimates the c-value in the absence of resonance excitation and the latter estimates the c-value at the maximum oscillatory amplitude of the center of the analyte ion cloud prior to ion ejection. For the simulations shown below, we use the cmax value, which tends to overestimate the damping factor and, as a result, tends to underestimate the maximum oscillatory amplitude under resonance excitation conditions, Amax,AC, as predicted by eqn (13). For a given ion and a fixed set of ion storage conditions, the main experimental variables available to the analyst to optimize a parking experiment are VAC, excitation frequency, and bath gas pressure. The bath gas pressure is an important variable via its role in determining c. Fig. 3 compares plots of Amax,ACversus the difference between the excitation frequency, fAC, and the ion fundamental secular frequency, f0, i.e. (fAC − f0), at five different bath gas pressures for a 1+ ion of 17 kDa and σh-s = 15 nm2 (as estimated from a range of reported cross-sections for apomyoglobin74) (Fig. 3a) and a 26+ ion of 467 kDa and σh-s = 165 nm2 (as estimated from reported values for several charge states of β-galactosidase75) (Fig. 3b). These ions were selected because they have similar m/z ratios but different masses, charges, and σh-s values. For each plot, the VAC is adjusted to give the same on-resonance Amax,AC for the condition in which Amax,AC = uT,cation + uT,anion. This VAC values represent the minimum resonance excitation amplitude required for separation of the cation and anion clouds at the relevant pressure. The plots, therefore, show the extent of off-resonance power absorption under equivalent parking conditions (i.e., the same extent of ion cloud separation). The widths of the absorbance profiles (FWHM in Hz) for the two ions are similar at the same pressure. The frequency spacings between adjacent charge states, however, are dramatically different (15.7 kHz for the 17 kDa ions versus 570 Hz for the 467 kDa ions) as the spacing is inversely related to ion mass (eqn (1), converted to units of Hz). Hence, the likelihood for off-target ion parking increases with the mass of the ion.
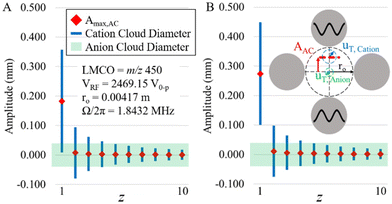
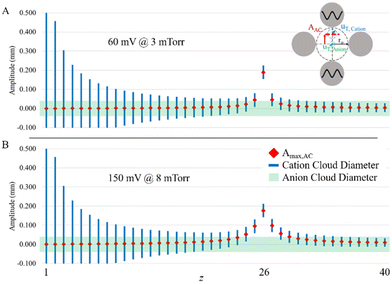
The plots of Fig. 3 do not strictly indicate off-resonance power absorption by off-target charge states because the z-state and c-value of an off-target charge state differ from those of the target charge state. The oscillatory amplitudes of off-target charge states due to power absorption from the applied frequency in resonance with the target charge state can be determined from eqn (13) using the z- and c-values of the off-target ions and their difference in secular frequency from that of the target ion. In order to evaluate the potential for significant parking of adjacent charge states, it is instructive to plot both the sizes of the ion clouds, as reflected by 2uT,cation and 2uT,anion (see eqn (10)), as well as the oscillatory amplitude due to resonance excitation of the parked ion and off-resonance excitation at nearby charge-states. Such a plot for parking the 1+ charge state of a 17 kDa protein using resonance excitation at 200 mV (A) and 300 mV (B) is shown in Fig. 4. The maximum amplitude of oscillation of the cation cloud, indicated as a red diamond, does not exceed the size of the anion cloud, the diameter of which is indicated by the green shaded box, for any charge state except that of the 1+ ion that is undergoing resonance excitation for both resonance excitation amplitudes. The model would therefore predict that it is possible to park the +1 ion without any significant off-target ion parking of the 2+ (or any higher z-state) ion. However, given that the 1+ cation cloud, the diameter of which is shown by the blue lines, does not fully separate from the anion cloud (note the overlap in cation and anion clouds) in Fig. 4A suggests that 200 mV is not sufficient to park the 1+ ion with optimal efficiency. At 300 mV, on the other hand, the 1+ cation ion cloud fully separates from the anion cloud at the maximum oscillatory amplitude (Fig. 4B). Hence, ion parking would be expected to be relatively efficient at 300 mV.
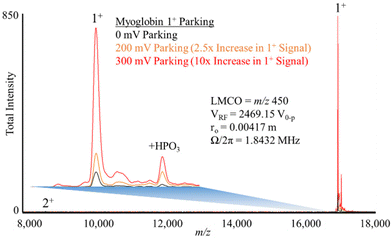
Fig. 5 shows experimental ion parking data for the 1+ apo-myoglobin ion under conditions in which virtually no 2+ ions (m/z 8475) remain in the absence of parking. In order for all of the 2+ ions to react, a large majority of the ions must be neutralized.76 When 200 mV dipolar waveform at 15.66 kHz, the secular frequency of the 1+ ion, was used to park the 1+ charge state, a roughly 2.5-fold increase in the 1+ ion signal was observed whereas a 300 mV, 15.66 kHz resonance excitation waveform signal was used to ion park the 1+ charge state, a roughly 10-fold increase in signal, relative to no parking, was observed. At 100 mV, no significant increase in the 1+ signal was observed and at amplitudes greater than 300 mV, little to no further increase in the 1+ signal was noted (data not shown). These experimental results are in qualitative agreement with the simulation in that at least some ion parking is observed at 200 mV whereas the maximum observed extent of ion parking was noted at 300 mV. Note that at least some reaction rate reduction might be expected to take place due to the increase in the relative velocity of the reactant ions (see Fig. 1), although KEmax is not reached at either 200 or 300 mV. Note also that there is no evidence for off-target ion parking of the 2+ charge state under either set of ion parking conditions, which is also consistent with the model (Fig. 4).
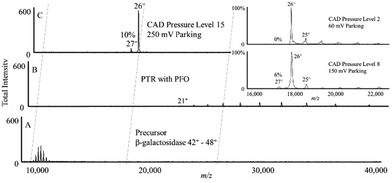
The simulations of Fig. 3 clearly show broadened absorption profiles at high pressures but the frequency spacing between adjacent charge states for the 17 kDa protein is sufficiently high that little off-target ion parking would be expected. However, with the much smaller frequency spacing between adjacent charge states for the 467 kDa protein, the extent of off-target ion parking is expected to be increasingly likely over the pressure range modelled in Fig. 3. Fig. 6 illustrates an ion parking experiment for the 26+ charge state of β-galactosidase with the pre-ion/ion reaction mass spectrum (A), a post-ion/ion reaction spectrum without parking (B), and a spectrum resulting from ion parking of the 26+ charge state (C). Roughly 90% of the summed intensities of the pre-ion/ion reaction charge states appears in the 26+ charge state after parking. The pressure in q2 is adjustable via software control (CAD pressure level) but is not read directly. A CAD pressure level of 6 is estimated to be roughly 4 mTorr.77 The results in Fig. 6 were collected at a CAD pressure level of 15. The inset shows the parked region at CAD pressure levels of 2 and 8, respectively. At CAD pressure level 2, it is possible to park the 26+ ion using a 60 mV amplitude with very little evidence for off-target parking of the 27+ ion. Some ‘leakage’ to lower charge states is observed, as expected since reactions can occur as the oppositely-charged ion clouds pass through one another. At CAD pressure level 8, however, a higher amplitude is required for parking (150 mV, in this case) which leads to evidence of off-target parking of the 27+ charge state. The data collected at CAD pressure level 15 shows the highest degree of off-target parking of the 27+ ion.
Fig. 7 shows results of the model for parking the 26+ charge state of β-galactosidase at pressures of 3 and 8 mTorr. While there is uncertainty regarding the pressures associated with the CAD pressure levels, the simulation shows that at a q2 pressure of 3 mTorr and 60 mV resonance excitation, it is possible to completely remove the oppositely-charged ion clouds at the maximum cation oscillatory amplitude while significant overlap remains for the 27+ ion. However, for a similar maximum oscillatory amplitude for the 26+ ion at 8 mTorr, a resonance excitation amplitude of 150 mV is required, which leads to separation of the 27+ ion from the anion cloud at maximum oscillatory amplitude. Hence, a degree of off-target ion parking might be expected.
Conclusions
In this report, we introduce a qualitative forced-damped harmonic oscillator model for gas-phase ion parking using single-frequency dipolar resonance excitation and apply it to ions with masses and charges relevant to native mass spectrometry using trapping conditions accessible with a commercially available linear quadrupole ion trap. A number of conclusions can be drawn from the model as well as experiments conducted to evaluate the model. Notable points include:• Ion parking can occur due to the effect of an increase in ion/ion relative velocity, which affects the rate constant, and/or by separation of ion clouds, which affects ion/ion overlap. As the mass of the analyte ion increases, the effect of resonance excitation on relative velocity decreases due to the fact that it is increasingly difficult to increase relative velocity by accelerating the heavy particle. Hence, for high-mass ions often encountered in native mass spectrometry, ion parking due to decreasing the rate constant may not be effective, particularly at low charge states (see Fig. 2).
• Ion cloud separation due to resonance excitation can still give rise to effective ion parking even when the rate constant is not significantly altered by ion acceleration. Ion cloud separation reduces the effective concentrations of the reactant ions.
• The oscillatory amplitude of the parked ion must be sufficiently high to give rise to partial or full separation of the positive and negative ion clouds but low enough to avoid collisions with the electrodes. As the radius of the analyte ion cloud increases, the window of amplitudes between the minimum needed for parking and the maximum before neutralization at the electrodes becomes increasingly narrow as the ion m/z increases. Hence, ion cloud size is the factor that ultimately limits ion parking at high mass.
• The ability to park a selected charge state without affecting nearby charge states is determined both by the frequency spacing between charge states and the line shape of the power absorption profile (i.e., the oscillatory amplitude as a function of excitation frequency). The frequency spacing between charge states in the charge state distribution of a given species is essentially constant under a fixed set of storage conditions and decreases with the mass of the species. Hence, frequency spacings between adjacent charge states decrease as the analyte mass increases.
• The power absorption profile for an ion undergoing resonance excitation is broadened by collisional damping in the ion trap. Hence, for a given ion of fixed mass and charge, the collision cross-section and pressure in the trap (as well as the mass of the background gas) have a significant effect on the resolution with which a selected charge state can be parked without also reducing the reaction rates of nearby charge states.
While the model described here makes a number of simplifying assumptions, it predicts experimental behavior semi-quantitatively and can be useful in anticipating optimal conditions from establishing an ion parking experiment for ions of relevance to native mass spectrometry given the accessible experimental conditions in the ion trap. It also points to strategies involving changes to ion storage conditions, such as the use of lower drive frequencies and lower pressures, that can lead to smaller cloud sizes and lower off-target power absorption.
Author contributions
N. J. P. and J. S. B.: writing the original draft, investigation, visualization. I. J. C.: investigation, validation. E. T. D.: methodology, writing – review and editing. S. A. M.: writing original draft, review and editing, conceptualization, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the National Institute of General Medical Sciences under Grant GM R37-45372. The authors acknowledge SCIEX, and particularly Mr Frank Londry, for modifying the instrument to enable the ion/ion reaction experiments, and Dr James Hager, also of SCIEX, for helpful discussions.References
- J. B. Fenn, M. Mann, C. K. Meng, S. F. Wong and C. M. Whitehouse, Electrospray Ionization for Mass Spectrometry of Large Biomolecules, Science, 1989, 246(4926), 64–71 CrossRef CAS PubMed.
- W. M. A. Niessen, “Liquid Chromatography Mass Spectrometry”, Taylor & Francis, Boca Raton, FL, 3rd edn, 2006, ISBN: 10:0-8247-4082-3 Search PubMed.
- P. Schmitt-Kopplin and M. Frommberger, Capillary electrophoresis-mass spectrometry: 15 years of developments and applications, Electrophoresis, 2003, 24, 3837–3867 CrossRef CAS PubMed.
- K. De Bruycker, A. Welle, S. Hirth, S. J. Blanksby and C. Barner-Kowollik, Mass spectrometry as a tool to advance polymer science, Nat. Rev. Chem., 2020, 4, 257–268 CrossRef PubMed.
- G. R. D. Prabhu, E. R. Williams, M. Wilm and P. L. Urban, Mass spectrometry using electrospray ionization, Nat. Rev. Methods Primers, 2023, 3, 23 CrossRef CAS.
- J. A. Loo, Electrospray ionization mass spectrometry: a technology for studying non-covalent macromolecular complexes, Int. J. Mass Spectrom., 2000, 200, 175–186 CrossRef CAS.
- J. A. Loo, Studying noncovalent protein complexes by electrospray ionization mass spectrometry, Mass Spectrom. Rev., 1997, 16, 1–23 CrossRef CAS PubMed.
- A. G. Marshall, C. L. Hendrickson and G. S. Jackson, Fourier transform ion cyclotron resonance mass spectrometry: A primer, Mass Spectrom. Rev., 1998, 17, 1–35 CrossRef CAS PubMed.
- A. Makarov, Electrostatic Axially Harmonic Orbital Trapping: A High-Performance Technique of Mass Analysis, Anal. Chem., 2000, 72, 1156–1162 CrossRef CAS PubMed.
- G. Westmacott, W. Ens and K. G. Standing, Secondary ion and electron yield measurements for surfaces bombarded with large molecular ions, Nucl. Instrum. Methods Phys. Res., Sect. B, 1996, 108, 282–289 CrossRef CAS.
- G. E. Reid, J. Wu, P. A. Chrisman, J. M. Wells and S. A. McLuckey, Charge State Dependent Sequence Analysis of Protonated Ubiquitin Ions via Ion Trap Tandem Mass Spectrometry, Anal. Chem., 2001, 73, 3274–3281 CrossRef CAS.
- A. T. Iavarone and E. R. Williams, Mechanism of Charging and Supercharging Molecules in Electrospray Ionization, J. Am. Chem. Soc., 2003, 125, 2319–2327 CrossRef CAS PubMed.
- D. A. Abaye, I. A. Agbo and B. V. Nielsen, Current perspectives on supercharging reagents in electrospray ionization mass spectrometry, RSC Adv., 2021, 11, 20355–20369 RSC.
- A. Dobo and I. A. Kaltashov, Detection of multiple protein conformational ensembles in solution via deconvolution of charge state distributions in ESI MS, Anal. Chem., 2001, 73, 4763–4773 CrossRef CAS PubMed.
- R. Grandori, Origin of the conformation dependence of protein charge-state distributions in electrospray ionization mass spectrometry, J. Mass Spectrom., 2003, 38, 11–15 CrossRef CAS.
- M. Mann, C. K. Meng and J. B. Fenn, Interpreting Mass Spectra of Multiply Charged Ions, Anal. Chem., 1989, 61, 1702–1708 CrossRef CAS.
- H. Zheng, P. C. Ojha, S. McClean, N. D. Black, J. G. Hughes and S. Shaw, Heuristic charge assignment for deconvolution of electrospray mass spectra, Rapid Commun. Mass Spectrom., 2003, 17, 429–436 CrossRef CAS.
- M. T. Marty, A. J. Baldwin, E. G. Marklund, G. K. A. Hochberg, J. L. P. Benesch and C. V. Robinson, Bayesian Deconvolution of Mass and Ion Mobility Spectra: From Binary Interactions to Polydisperse Ensembles, Anal. Chem., 2015, 87, 4370–4376 CrossRef CAS PubMed.
- M. I. Catalina, R. H. H. van den Heuvel, E. van Duijn and A. J. R. Heck, Decharging of globular proteins and protein complexes in electrospray, Chemistry, 2005, 11, 960–968 CrossRef CAS PubMed.
- T. E. Walker, A. Laganowsky and D. H. Russell, Surface Activity of Amines Provides Evidence for the Combined ESI Mechanism of Charge Reduction for Protein Complexes, Anal. Chem., 2002, 94, 10824–10831 CrossRef PubMed.
- J. T. S. Hopper, K. Sokratous and N. J. Oldham, Charge state and adduct reduction in electrospray ionization-mass spectrometry using solvent vapor exposure, Anal. Biochem., 2012, 421, 788–790 CrossRef CAS PubMed.
- A. Kharlamova, B. M. Prentice, T.-Y. Huang and S. A. McLuckey, Electrospray Droplet Exposure to Gaseous Acids for the Manipulation of Protein Charge State Distributions, Anal. Chem., 2010, 82, 7422–7429 CrossRef CAS PubMed.
- A. Kharlamova and S. A. McLuckey, Negative Electrospray Droplet Exposure to Gaseous Bases for the Manipulation of Protein Charge State Distributions, Anal. Chem., 2011, 83, 431–439 CrossRef CAS PubMed.
- S. A. McLuckey, G. J. Van Berkel and G. L. Glish, Reactions of Dimethylamine with Multiply Charged Ions of Cytochrome c, J. Am. Chem. Soc., 1990, 112, 5668–5670 CrossRef CAS.
- S. A. McLuckey, G. L. Glish and G. L. Van Berkel, Charge, Determination of Product Ions Formed from Collision-Induced Dissociation of Multiply Protonated Molecules via Ion/Molecule Reactions, Anal. Chem., 1991, 63, 1971–1978 CrossRef CAS PubMed.
- R. R. O. Loo and R. D. Smith, Proton transfer reactions of multiply charged peptide and protein cations and anions, J. Mass Spectrom., 1995, 30, 339–347 CrossRef.
- R. R. O. Loo, H. R. Udseth and R. D. Smith, A New Approach for the Study of Gas-Phase Ion-Ion Reactions Using Electrospray Ionization, J. Am. Soc. Mass Spectrom., 1992, 3, 695–705 CrossRef CAS.
- S. L. Kaufman, J. W. Skogen, F. D. Dorman, F. Zarrin and K. C. Lewis, Macromolecule analysis based on electrophoretic mobility in air: globular proteins, Anal. Chem., 1996, 68, 1895–1904 CrossRef CAS PubMed.
- M. Scalf, M. S. Westphall, J. Krause, S. L. Kaufman and L. M. Smith, Controlling charge states of large ions, Science, 1999, 283, 194–197 CrossRef CAS PubMed.
- J. L. Stephenson and S. A. McLuckey, Ion/Ion Reactions in the Gas Phase: Proton Transfer Reactions Involving Multiply-Charged Proteins, J. Am. Chem. Soc., 1996, 118, 7390–7397 CrossRef CAS.
- D. L. Foreman and S. A. McLuckey, Recent Developments in Gas-Phase Ion/ion Reactions for Analytical Mass Spectrometry, Anal. Chem., 2020, 92, 252–266 CrossRef CAS PubMed.
- S. A. McLuckey and J. L. Stephenson, Ion/Ion Chemistry of High-Mass Multiply Charged Ions, Mass Spectrom. Rev., 1998, 17, 369–407 CrossRef CAS.
- S. J. Pitteri and S. A. McLuckey, Recent Developments in the Ion/Ion Chemistry of High-Mass Multiply Charged Ions, Mass Spectrom. Rev., 2005, 24, 931–958 CrossRef CAS PubMed.
- J. L. Stephenson Jr., S. A. McLuckey, G. E. Reid, J. M. Wells and J. L. Bundy, The Detection and Identification of Intact Proteins from Complex Mixtures using Ion/Ion Chemistry: Current Status and Future Implications, Curr. Opin. Biotechnol., 2002, 13, 57–64 CrossRef PubMed.
- J. L. Stephenson Jr. and S. A. McLuckey, Simplification of Product Ion Spectra Derived from Multiply-Charged Parent Ions via Ion/Ion Chemistry, Anal. Chem., 1998, 70, 3533–3544 CrossRef CAS PubMed.
- K. D. Henry and F. W. McLafferty, Electrospray ionization with Fourier-transform mass spectrometry- Charge state assignment from resolved isotopic peaks, Org. Mass Spectrom., 1990, 25, 490–492 CrossRef CAS.
- J. C. Schultz, C. A. Hack and W. H. Benner, Mass Determination of Megadalton-DNA Electrospray Ions Using Charge Detection Mass Spectrometry, J. Am. Soc. Mass Spectrom., 1998, 9, 305–313 CrossRef CAS PubMed.
- C. C. Harper, A. G. Elliott, L. M. Oltrogge, D. F. Savage and E. R. Williams, Multiplexed Charge Detection Mass Spectrometry for High-Throughput Single Ion Analysis of Large Molecules, Anal. Chem., 2019, 91, 7458–7465 CrossRef CAS PubMed.
- M. F. Jarrold, Applications of Charge Detection Mass Spectrometry in Molecular Biology and Biotechnology, Chem. Rev., 2022, 122, 7415–7441 CrossRef CAS PubMed.
- J. O. Kafader, R. D. Melani, K. R. Durbin, B. Ikwuagwu, B. P. Early, R. T. Fellers, S. C. Beu, V. Zabrouskov, A. A. Makarov, J. T. Maze, D. L. Shinholt, P. F. Yip, D. Tullman-Ercek, M. W. Senko, P. D. Compton and N. L. Kelleher, Multiplexed mass spectrometry of individual ions improves measurement of proteoforms and their complexes, Nat. Methods, 2020, 17, 391–394 CrossRef CAS PubMed.
- S. A. McLuckey, G. E. Reid and J. M. Wells, Ion Parking during Ion/Ion Reactions in Electrodynamic Ion Traps, Anal. Chem., 2002, 74(2), 336–346 CrossRef CAS PubMed.
- P. A. Chrisman, S. J. Pitteri and S. A. McLuckey, Parallel Ion Parking of Protein Mixtures, Anal. Chem., 2006, 78, 310–316 CrossRef CAS PubMed.
- D. J. Foreman, J. S. Bhanot, K. W. Lee and S. A. McLuckey, Valet Parking for Protein Ion Charge State Concentration: Ion/Molecule Reactions in Linear Ion Traps, Anal. Chem., 2020, 92, 5419–5425 CrossRef CAS PubMed.
- G. E. Reid, H. Shang, J. M. Hogan, G. U. Lee and S. A. McLuckey, Gas-Phase Concentration, Purification, and Identification of Whole Proteins from Complex Mixtures, J. Am. Chem. Soc., 2002, 124, 7353–7362 CrossRef CAS PubMed.
- S. A. Ugrin, A. M. English, J. E. P. Syka, D. L. Bai, L. C. Anderson, J. Shabanowitz and D. F. Hunt, Ion-Ion Proton Transfer and Parallel Ion Parking for the Analysis of Mixtures of Intact Proteins on a Modified Orbitrap Mass Analyzer, J. Am. Soc. Mass Spectrom., 2019, 30(10), 2163–2173 CrossRef CAS PubMed.
- C. R. Weisbrod, L. C. Anderson, C. L. Hendrickson, L. V. Schaffer, M. R. Shortreed, L. M. Smith, J. Shabanowitz and D. F. Hunt, Advanced Strategies for Proton-Transfer Reactions Coupled with Parallel Ion Parking on a 21 T FT-ICR MS for Intact Protein Analysis, Anal. Chem., 2021, 93(26), 9119–9128 CrossRef CAS PubMed.
- D. D. Holden, W. M. McGee and J. S. Brodbelt, Integration of Ultraviolet Photodissociation with Proton Transfer Reactions and Ion Parking for Analysis of Intact Proteins, Anal. Chem., 2016, 88(1), 1008–1016 CrossRef CAS PubMed.
- Y. Lin, A. M. Agarwal, L. C. Anderson and A. G. Marshall, Discovery of a biomarker for β-Thalassemia by HPLC-MS and improvement from Proton Transfer Reaction – Parallel Ion Parking, J. Mass Spectrom. Adv. Clin. Lab, 2023, 28, 20–26 CrossRef CAS PubMed.
- J. L. Campbell and J. C. Y. Le Blanc, “Targeted ion parking for the quantitation of biotherapeutic proteins: Concepts and preliminary data”, J. Am. Soc. Mass Spectrom., 2010, 21, 2011–2022 CrossRef CAS PubMed.
- P. A. Chrisman, S. J. Pitteri and S. A. McLuckey, Parallel Ion Parking: Improving Conversion of Parents to First-Generation Products in Electron Transfer Dissociation, Anal. Chem., 2005, 77, 3411–3414 CrossRef CAS PubMed.
- E. M. Duselis, M. C. Panepinto, J. E. P. Syka, C. Mullen, R. A. D'Ippolito, A. M. English, S. A. Igrin, J. Shabanowitz and D. F. Hunt, Improved Sequence Analysis of Intact Proteins by Parallel Ion Parking during Electron Transfer Dissocation, Anal. Chem., 2021, 93, 15728–15735 CrossRef CAS PubMed.
- A. C. Leney and A. J. R. Heck, Native Mass Spectrometry: What is in the Name?, J. Am. Soc. Mass Spectrom., 2017, 28, 5–13 CrossRef CAS PubMed.
- A. A. Rostom and C. V. Robinson, Detection of the Intact GroEL Chaperonin Assembly by Mass Spectrometry, J. Am. Chem. Soc., 1999, 121, 4718–4719 CrossRef CAS.
- A. A. Rostom, P. Fucini, D. R. Benjamin, R. Juenemann, K. H. Nierhaus, F. U. Hartl, C. M. Dobson and C. V. Robinson, Detection and selective dissociation of intact ribosomes in a mass spectrometer, Proc. Natl. Acad. Sci., 2000, 97, 5185–5190 CrossRef CAS PubMed.
- H. Hernández and C. V. Robinson, Determining the stoichiometry and interactions of macromolecular assemblies from mass spectrometry, Nat. Protoc., 2007, 2, 715–726 CrossRef PubMed.
- J. Snijder, R. J. Rose, D. Veesler, J. E. Johnson and A. J. R. Heck, Studying 18 MDa Virus Assemblies with Native Mass Spectrometry, Angew. Chem., Int. Ed., 2013, 52, 4020–4023 CrossRef CAS.
- A. J. R. Heck, Native mass spectrometry: a bridge between interactomics and structural biology, Nat. Methods, 2008, 5, 927 CrossRef CAS.
- J. S. Bhanot, K. C. Fabijanczuk, A. M. Abdillahi, H.-C. Chao, N. J. Pizzala, F. A. Londry, E. T. Dziekonski, J. W. Hager and S. A. McLuckey, Adaptation and Operation of a Quadrupole/Time-of-Flight Tandem Mass Spectrometer for High Mass Ion/Ion Reaction Studies, Int. J. Mass Spectrom., 2022, 478, 116874 CrossRef CAS PubMed.
- Y. Xia, X. Liang and S. A. McLuckey, Pulsed Dual Electrospray Ionization for Ion/Ion Reactions, J. Am. Soc. Mass Spectrom., 2005, 16, 1750–1756 CrossRef CAS PubMed.
- A. Loboda, A. Krutchinsky, O. Loboda, J. McNabb, V. Spicer, W. Ens and K. Standing, Novel LINAC II electrode geometry for creating an axial field in a multipole ion guide, Eur. J. Mass Spectrom., 2000, 6, 531–536 CrossRef CAS.
- J. E. Fulford, D. Nhu-Hoa, R. J. Hughes, R. E. March, R. F. Bonner and G. J. Wong, Radio-frequency mass selective excitation and resonant ejection of ions in a three-dimensional quadrupole ion trap, J. Vac. Sci. Technol., 1980, 17, 829–835 CrossRef CAS.
- R. E. March and J. F. J. Todd, Quadrupole Ion Trap Mass Spectrometry, John Wiley & Sons, Hoboken, 2nd edn, 2005, ch.3, ISBN: 13 978-0-471-48888-0 Search PubMed.
- P. B. Grosshans, C. M. Ostrander and C. A. Walla, Method and Apparatus to Control Charge Neutralization Reactions in Ion Traps, U.S. Patent, 6570151, 2003 Search PubMed.
- S. A. McLuckey, J. L. Stephenson and K. G. Asano, Ion/Ion Proton-Transfer Kinetics: Implications for Analysis of Ions Derived from Electrospray of Protein Mixtures, Anal. Chem., 1998, 70(6), 1198–1202 CrossRef CAS PubMed.
- R. F. Wuerker, H. Shelton and R. V. Langmuir, Electrodynamic Containment of Charged Particles, J. Appl. Phys., 1959, 30, 342–349 CrossRef.
- F. G. Major and H. G. Dehmelt, Exchange-Collision Technique for the rf Spectroscopy of Stored Ions, Phys. Rev., 1968, 170, 91–107 CrossRef CAS.
- D. J. Douglas, A. J. Frank and D. Mao, Linear ion traps in mass spectrometry, Mass Spectrom. Rev., 2005, 24, 1–29 CrossRef CAS PubMed.
- D. Trypogeorgos and C. J. Foot, Co-trapping different species in ion traps using multiple radio frequencies, Phys. Rev. A, 2016, 94, 023609 CrossRef.
- C. J. Foot, D. Trypogeorgos, D. E. Bentine, A. Gardner and M. Keller, Two-frequency operation of a Paul trap to optimize confinement of two species of ions, Int. J. Mass Spectrom., 2018, 430, 117–125 CrossRef CAS.
- W. Xu, W. J. Chappell and Z. Ouyang, Modeling of ion transient response to dipolar AC excitation in a quadrupole ion trap, Int. J. Mass Spectrom., 2011, 308, 49–55 CrossRef CAS.
- D. J. Douglas and N. V. Konenkov, Mass Selectivity of Dipolar Resonant Excitation in a Linear Quadrupole Ion Trap, Rapid Commun. Mass Spectrom., 2014, 28(5), 430–438, DOI:10.1002/rcm.6795.
- A. L. Michaud, A. J. Frank, C. Ding, X. Zhao and D. J. Douglas, Ion Excitation in a Linear Quadrupole Ion Trap with an Added Octopole Field, J. Am. Soc. Mass Spectrom., 2005, 16(6), 835–849, DOI:10.1016/j.jasms.2005.02.006.
- D. E. Goeringer, W. B. Whitten, J. M. Ramsey, S. A. McLuckey and G. L. Glish, Theory of High Mass Resolution Achieved via Resonance Ejection in the Quadrupole Ion Trap, Anal. Chem., 1992, 64, 1434–1439 CrossRef CAS.
- Y.-L. Chen, B. A. Collings and D. J. Douglas, Collision Cross Sections of Myoglobin and Cytochrome c Ions with Ne, Ar, and Kr, J. Am. Soc. Mass Spectrom., 1997, 8, 681–687 CrossRef CAS.
- S. J. Allen, A. M. Schwartz and M. F. Bush, Effects of polarity on the structures and charge states of native-like proteins and protein complexes in the gas phase, Anal. Chem., 2013, 85, 12055–11206 CrossRef CAS PubMed.
- J. L. Stephenson, G. J. Van Berkel and S. A. McLuckey, Ion/ion Proton Transfer Reactions of Bio-ions Involving Non-Covalent Interactions: Holomyoglobin, J. Am. Soc. Mass Spectrom., 1997, 8, 637–644 CrossRef CAS.
- C. Markert, M. Thinius, L. Lehmann, C. Heintz, F. Stappert, W. Wissdorf, H. Kersten, T. Benter, B. S. Schneider and T. R. Covey, Observation of charged droplets from electrospray ionization (ESI) plumes in API mass spectrometers, Anal. Bioanal. Chem., 2021, 413, 5587–5600 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4an00242c |
| This journal is © The Royal Society of Chemistry 2024 |