Label-free impedimetric analysis of microplastics dispersed in aqueous media polluted by Pb²⁺ ions

Abstract

The rapid differentiation between polluted and unpolluted microplastics (MPs) is critical for tracking their presence in the environment and underpinning their potential risks to humans. However, the quantitative analysis of polluted microplastics on the field is limited by the lack of rapid methods that do not need optical analysis nor their capture onto sophisticated electrochemical sensor platforms. Herein, a simple analytical approach for MPs dispersed in aqueous media leveraging electrochemical impedance spectroscopy (EIS) analysis on screen-printed sensors is presented. This method is demonstrated by the EIS-based analysis of two standards of microplastics beads (MPs), one of polystyrene (PS) and one of polystyrene carboxylated (PS-COOH), when exposed to aqueous solutions containing Pb²⁺ ions. The adsorption of Pb²⁺ ions on the MPs was quantitatively determined by voltammetric analysis. EIS permitted to rapidly (about 2 minutes) differentiate clean MPs from the Pb²⁺ polluted ones. These results could constitute a first-step towards the realization of a portable impedimetric sensor for the quantification of microplastics polluted by metal ions in aqueous solutions.

---

Introduction

Plastic waste in the ocean is predicted to reach 29 million tonnes in 2029. This continuous diffusion of plastic waste in the aquatic environment and their effects have become among the main subjects of study of the worldwide scientific community.¹ Due to the degradation environmental phenomena of different type of plastic polymers, their morphological characteristics are highly variable, as well as the size of their particles that can reach the micro and nanometre ranges (MPs, NPs). Indeed, MPs can be considered as small plastic debris whose sizes is less than 5 mm (0.20 in) in length, according to the European Chemicals Agency.² They can be further classified as primary MPs if their size is equal or below 5 mm or secondary MPs if they are produced by the fragmentation of larger plastic products. Both types are recognized to persist in the environment at high levels, particularly in aquatic and marine ecosystems, where they cause water pollution.³ The MPs toxicity stems from their intrinsic effect upon oxidative stress, presence of thermal stabilizers and UV stabilizers and, remarkably given their ability to act as substrates that are able to adsorb toxic substances which are in the environment. The third aspect is particularly important, as both NPs and MPs can adsorb a great variety of toxic chemicals (toxic metal ions, organic pollutants like dyes or antibiotics) from the surrounding seawater and transfer them to marine organisms.⁴

In order to quantify the amount of adsorbed toxic pollutant, it is important to understand the pollutants adsorption mechanism on the MPs surface and the main factors governing it. Among them, a remarkable effect is played by the presence of surfactants causing typically hydrophobic MPs to become more hydrophilic, that might enhance the adsorption of hydrophilic pollutants by electrostatic interactions. Indeed, literature reports have demonstrated that surfactant increased MPs adsorption of lead,⁵ antibiotics⁶ and other organic pollutants.⁷ Such synergic surfactant-MPs effect can results in increased toxicity, as observed in Daphnia magna model organisms⁸ or even affect surface roughness of seawater waves.⁹

To this aim, it becomes fundamental to develop rapid MPs detection and quantification methods in aquatic systems.^10,11 Some specific methods for microplastics analysis have been developed, underpinning different analytical approaches. The most relevant analytical methodologies include Fourier transform infrared spectroscopy,¹² Nile red staining,¹³ Raman spectroscopy,¹⁴ gas chromatography/mass spectroscopy,¹² some of them are also implemented as portable sensor devices.¹⁵ Electroanalytical methods are also intensively studied,¹¹ in particular dielectrophoresis¹⁶ and impedance spectroscopy¹⁷ permitting rapid analysis within microfluidic devices.

In particular, electrochemical impedance spectroscopy (EIS) could represent a suitable approach, since it allows for the analysis of the kinetic and mechanistic processes of electrochemical systems, resulting in chemical and biological sensors.¹⁸ Our group has shown the ability to determine the size and speed of oil dispersed in water by impedance measurements in a lab-on-chip microfluidics system.¹⁹ EIS allows the electrical analysis of single cells, enabling the differentiation between living organism to MPs and the chemical identification of MPs, as already shown in the pivotal article by Colson and coworkers.¹⁷ This approach has been recently extended to other electrochemical sensor platforms, resulting in the determination of polystyrene MPs at different particle size ranges.²⁰ Screen printed sensors have also been used for capturing microplastics by microrobots and impedance detection,²¹ allowing the rapid detection of microplastic in both experimental and environmental samples.

All these approaches can accurately detect microplastics with good sensitivity and selectivity, showing good potential for fast screening of many types of standard polymers. EIS typically enables the quantification of MPs by a faradaic signal transduction on the working electrode which is, however, not able to distinguish virgin vs. polluted MPs.²¹ To bridge such gap, this work shows the analysis of two standards of MPs beads, one of polystyrene (PS) and one of carboxylated polystyrene (PS-COOH), which adsorb Pb²⁺ ions on their surfaces. The two standards of MPs contained traces of the anionic surfactant sodium dodecyl sulphate (SDS). The two different types of standard MPs used in this study (PS and PS-COOH MPs) have been chosen to explore the possible different adsorption ability under two significantly different experimental conditions, supposing that smaller and carboxy-terminated PSs might be able to adsorb a higher amount of Pb²⁺ ions. The PS-COOH MPs might in principle represent a model system for testing Pb²⁺ ions adsorption onto surface oxidated and smaller sized MPs, originated from larger PS MPs. The adsorption of lead ions was quantified by voltammetric measurements and the adsorption isotherms of lead ions on the MPs were determined. EIS of few μL of MPs dispersion in ultrapure water allows for a rapid (about 2 minutes), electrochemical mediator-free, sensitive detection of the MPs. “Clean” MPs were rapidly differentiated from the polluted ones as a result of their different electrochemical properties. SEM, EDS, ζ potential and FT-IR characterizations were conducted on the MPs exposed to Pb²⁺ ions, adding further knowledge on the effect of Pb²⁺ ions exposure, corroborating the findings obtained by EIS. Additional adsorption experiments of Pb²⁺ ions were conducted with MPs of polystyrene “surfactant free” prepared from pellets of the polymer (PS*) to take into account the effect of surfactant on the adsorption of the toxic metal ion.

Experimental

Materials

The standard MPs suspensions used in this article were PS (Thermo Fisher Scientific, 10% w/v, 0.37 μm particle diameter) and PS-COOH (Polysciences, Inc., 2.6% w/v, 0.19 μm particle diameter). Both standard MPs suspensions contain trace of the surfactant sodium dodecyl sulphate (SDS). Polystyrene MPs were also obtained from pellets of the polymer (Sigma-Aldrich) solubilized in CHCl₃ (VWR, HiPerSolv CHROMANORM® R for HPLC). All the aqueous solutions/dispersions were obtained using CO₂-free ultrapure water (ρ ≥ 18 MΩ cm⁻¹). The aqueous solutions containing Pb²⁺ ions were prepared by dissolving in water the appropriate quantities of the Pb(NO₃)₂ salt (Sigma-Aldrich, purity equal to 99.999%). The ionic strength of the solutions was brought to the desired value using NaNO₃ salt (Sigma-Aldrich, purity of 99.0%) as the ionic medium. The pH of the Pb²⁺ aqueous solutions was adjusted with diluted solutions of HNO₃ and NaOH, prepared from standard solutions of NaOH 0.5 M (Sigma-Aldrich) and HNO₃ 1 M (Sigma-Aldrich). The calibration of the potentiometric cell used to perform the pH measurements of the aqueous solutions was carried out using buffer solutions at three different pH (7.00 ± 0.02; 4.01 ± 0.02 and 9.21 ± 0.02) (METTLER TOLED InLab® Solutions). The calibration of the voltammetric cells, subsequently used for the quantitative analysis of the Pb²⁺ ions, was carried out using a standard solution of Pb²⁺ 1000 ± 2 mg L⁻¹ in HNO₃ 2% (Sigma-Aldrich). SDS (Sigma-Aldrich with purity grade ≥ 98%) has been added to some MPs suspensions to facilitate the dispersion of microplastics in water or to evaluate the effect of surfactant on the toxic metal ion adsorption.

Preparation of polystyrene MPs from pellets

Polystyrene MPs were also prepared from pellets of the polymer with the aim of having MPs particles without surfactant (PS*). To this end, 4.6 g of pellets were dissolved in 230 mL of CHCl₃. The mixture was stirred on a magnetic stirrer at room temperature until complete dissolution. Then, the mixture was transferred into different Petri dishes which were covered with filter paper. After solvent evaporation, the polystyrene membranes were peeled from the Petri dishes, cut into small pieces and shredded with a grinder. A microscope-mounted digital camera (Digitus-DA-70351) was used to capture an optical image of PS* sample, which was analysed by ImageJ software (Fig. S5†) in order to estimate the size of PS*.

Voltammetric determination of Pb²⁺ ions

The concentration of Pb²⁺ ions in aqueous solutions used in metal ion adsorption experiments was determined by differential pulse anodic stripping voltammetry (DP-ASV) using a voltammetric system (663 VA Stand-Metrohm) combined with a potentiostat (AUTOLAB, Utrecht, Netherlands), coupled to the interface (IME 663) for the management of the mercury electrode, and managed by the NOVA v. 1.10 software. The voltammetric cell used consisted of three electrodes: a Multi Mode Electrode Pro-Metrohm working electrode used in “Static Mercury Drop Electrode (SMDE)” mode, a graphite auxiliary electrode and a double-junction Ag/AgCl/KCl reference electrode (3 mol L⁻¹). The cell parameters were the following: deposition potential (V): −0.55 V, deposition time: 1 s, balance time: 10 s, potential range: −0.55–0.20 V, scan speed 0.01 V s⁻¹, potential step 5 mV, modulation amplitude 50 mV, modulation time 0.01 s, time interval: 0.5 s. The calibration curve for the Pb²⁺ ion was constructed in the concentration range 0–15 mg L⁻¹ with aqueous solution containing the ionic medium NaNO₃ 0.1 mol L⁻¹ at pH = 5.

Electrochemical impedance spectroscopy (EIS)

EIS measurements were carried out to quantify the MPs concentration in aqueous solutions and to evaluate the effect of surfactant on impedance measurements. To this aim, a miniaturized serigraphic electrochemical sensor with three screen-printed electrodes on a polyester substrate (ItalSens Carbon SPE, PalmSens) was employed. The sensor was connected to a potentiostat (AUTOLAB, Utrecht, Netherlands) interfaced to a computer through the NOVA 2.1.5 software. The sensor consisted of the following electrodes: a graphite working electrode (3 mm in diameter), an Ag pseudo-reference electrode and a graphite auxiliary electrode. The experimental conditions were the following: frequency range 500 kHz–0.1 Hz, ten frequencies per decade, 10 mV frequency amplitude, sinusoidal wave type and scan duration time equal to 212 s.

Fourier-transform infrared (FTIR), ζ potential measurements and SEM-EDX experiments

FTIR spectra were recorded using a single beam FTIR spectrometer (FT/IR-4X, Jasco Corp.) coupled with the ATR-PRO4X (ZnSe prism) single reflection accessory with an angle of incidence of 45° and contact area with diameter of 2.5 mm. The scan range was set to 500–7000 cm⁻¹, with an accumulation of 60 and a wavenumber resolution of 2 cm⁻¹.

Further experiments aimed at analysing the interaction of MPs with the Pb²⁺ ion were carried out through ζ potential measurements with the Zetasizer Nano ZS instrument (Malvern Instruments, Worcestershire, United Kingdom) exploiting the “M3-PALS” technique. Several suspensions of PS and PS-COOH 0.001% w/v were prepared and each of these was placed in contact with 10 mL of solutions containing a variable concentration of Pb²⁺ ions (2–20 mg L⁻¹) in NaNO₃ 0.1 mol L⁻¹ at pH = 5.0. All prepared suspensions were shaken for 24 h and thereafter, on each of them the ζ potential was measured.

SEM-EDX measurements to analyse the two MPs before and after the adsorption of Pb²⁺ ions were carried out by means of a scanning electron microscope with field emission gun (FEG-SEM) model Tescan Mira-3 (TESCAN, Brno, Czech Republic), operated at 30 keV energy and 3 nA electron beam current, equipped with an energy dispersive X-ray spectroscopy (EDX) detector (Oxford Xplore 30, United Kingdom). Samples of MPs with adsorbed Pb²⁺ were obtained by washing several times with ultrapure water. Afterwards, they were left to dry overnight at 313.15 K in an oven (Thermo Electron Corporation, Waltham, Massachusetts, United States). The measurements were carried out to analyse the differences features of MPs between PS and PS-COOH pre and post Pb²⁺ ion adsorption. Two suspensions that did not contain the Pb²⁺ ions were prepared under the same treatment and the same experimental conditions (NaNO₃ 0.1 mol L⁻¹, at pH = 5.0 and T = 298.15 K) as those containing the metal ion (stirring for 24 h, centrifugation, washing and drying in the oven).

Pb²⁺ adsorption isotherms determination

The adsorption isotherms of Pb²⁺ ions onto PS and PS-COOH MPs were studied by determining the concentration of the metal ion in solution by DP-ASV analysis. Suspensions containing 10–150 mg of PS MPs and different concentrations of Pb²⁺ ions (c_Pb²⁺ = 1–15 mg L⁻¹) at pH = 5.0 and in NaNO₃ 0.1 mol L⁻¹ at the final 7.1–8.5 mL volume range were prepared. Similarly, suspensions of PS-COOH containing different amounts of PS-COOH (0.4–2.6 mg) and Pb²⁺ ions (c_Pb²⁺ = 10 mg L⁻¹) at pH = 5.0 and NaNO₃ 0.1 mol L⁻¹ were prepared at the final volume in the range 7.03–8.00 mL. All the prepared suspensions were vortexed for 24 hours using an orbital mixer (model M201-OR, MPM Instruments, Bernareggio, Italy) and then centrifuged for 45 minutes at 9000 rpm (Thermo Electron Corporation's IEC CL31). The supernatants were recovered and analysed by DP-ASV.

The effect of surfactant (present in traces in both the standards of PS and PS-COOH MPs used in this study) on the Pb²⁺ adsorption was evaluated carrying out additional isotherm experiments with the MPs of polystyrene surfactant free (PS*). Different amounts of PS* MPs (40–400 mg) were placed in Erlenmeyer flasks with 30 mL of Pb²⁺ aqueous solution (c_Pb²⁺ = 2–15 mg L⁻¹) containing NaNO₃ 0.1 mol L⁻¹, at pH = 5.0 and T = 298.15 K. The suspensions were stirred by an orbital shaker for 48 h and then filtered with 0.45 μm filters. The supernatants were collected for the subsequent Pb²⁺ determination. The experiment was replicated with Pb²⁺ solutions, at the same experimental conditions, containing the surfactant SDS 0.1 mmol L⁻¹.

EIS measurements

Several suspensions of PS and PS-COOH MPs at different concentration were prepared (ranging from 0.001 to 0.2% w/v for PS-COOH and from 0.01 to 0.2% w/v for PS) by dispersing the appropriate volume of standard suspension in 10 mL ultrapure water. EIS measurements were conducted on the prepared suspensions to quantify the concentration of MPs dispersed in water. Other EIS measurements were carried out on the MPs suspensions recovered from the samples used for DP-ASV experiments to investigate the electrochemical differences between clean and Pb²⁺ adsorbed MPs. To this aim, 5 mg of the deposited MPs were recovered and dispersed in 10 mL of distilled water. To ensure better dispersion, 3 drops (each of 140 μL) of SDS (0.01% w/v) were added to the 10 mL initial suspension and left to agitate for 45 minutes. An aliquot of 0.15 mL of each prepared suspension was used to perform the EIS analysis.

Results and discussion

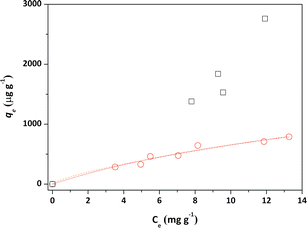
Initially, the adsorption properties of the PS and PS-COOH MPs were evaluated by preparing MPs–Pb²⁺ ion suspensions at different c_MPs/c_Pb²⁺ ratios. Differential Pulse Anodic Stripping Voltammetry measurements were carried out to measure the Pb²⁺ ions adsorbed by the two MPs at the equilibrium, similarly to our previous studies.^22,23 The q_evs. c_e data of both MPs are reported in Fig. 1. The calculated q_e values did not allow to obtain experimental data suitable for modelling study of the PS-COOH MPs. Differently, in the case of PS MPs, the acquired experimental data were processed with the non-linear forms of Langmuir (eqn (1)) and Freundlich (eqn (2)) isotherm equations whose parameters values are reported in Table 1 together with their experimental errors and the values of the statistical parameter R² of the fits. Both MPs have an adsorbent capacity towards the Pb²⁺ ions up to a few thousand of μg g⁻¹ in the analysed lead concentration range. In particular, the maximum adsorption ability of PS MPs calculated by Langmuir equation was 2100 μg g⁻¹. The presence of carboxyl groups in the MPs of PS-COOH makes the adsorbent capacity of this microplastic slightly higher than that of PS MPs with the highest q_e value of 2760 μg g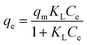⁻¹.

q_e = K_FC_e^1/n (2)

Fig. 1 Adsorption isotherms of Pb²⁺ ions onto PS (red circles) and PS-COOH MPs (black squares) in aqueous solutions containing NaNO₃ 0.1 mol L⁻¹, at pH = 5.0 and T = 298.15 K. The experimental data were fitted with Langmuir isotherm models (continuous line) and Freundlich (dotted line), isotherm models.

Table 1 Freundlich and Langmuir isotherm parameters for the Pb²⁺ adsorption onto PS MPs in aqueous solution containing NaNO₃ 0.1 mol L⁻¹, at pH = 5.0 and T = 298.15 K

Langmuir
q m	K L	R ^2
a μg g^−1. b L mg^−1. c L^1/n g^−1 μg mg^−1/n.
2100 ± 600	0.05 ± 0.02	0.9679

---

Freundlich
K F	n	R ^2
120 ± 20	1.4 ± 0.2	0.9637

---

The calculated q_e values well agree with data reported in previous literature reports (see Table S1†).

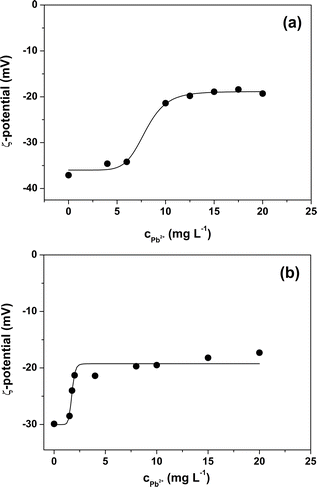
From the ζ potential characterization of the two MPs (Fig. 2) it can be seen that suspensions that do not contain Pb²⁺ ions have a negative value of ζ. The negative surface charge is likely due to the presence of anionic surfactant in the standard MPs beads suspensions used in the experiments. Indeed, SDS surfactant is added in trace amounts by the manufacturers of the two MPs suspensions as a stabilizer in order to avoid aggregation or sedimentation. Both types of MPs, in the absence of Pb²⁺ ions, have values of ζ approx. −30 mV and this means that the two suspensions can be classified as stable suspensions.²⁴ As the concentration of Pb²⁺ ions increases, the absolute value of the ζ potential of the suspensions decreases. Electrostatic interactions between the Pb²⁺ ions and the two MPs reduce their surface charge. As a result, an increase in the adsorbed Pb²⁺ ions leads to a decrease in net surface charges and thus to a lower absolute value of the ζ potential. The decrease in the absolute value of ζ potential with increasing concentration of Pb²⁺ in solution does not follow a linear relationship but reaches a plateau. This point corresponds to the achievement of the saturation of the surface of the two types of MPs particles. Interestingly, the saturation phenomenon occurs for both MPs with a relatively small increment of the ζ potential which is calculated as the difference between the absolute value of the saturation potential ζ and the absolute value of the ζ potential immediately preceding saturation. The relatively small increase in ζ indicates that the amount of Pb²⁺ ions required to saturate the surface of the two MPs is also small and therefore, in agreement with the results obtained from the adsorption experiments, the adsorption capacity of PS and PS-COOH is to be considered rather low. Finally, the graphs obtained from these experiments show that the ζ potential value at which saturation is reached remains negative for both PS and PS-COOH particles. This suggests that the stoichiometry of interaction between metal ions and negative surface charges is different from the ratio of 1 : 1.

Fig. 2 Analysis of the ζ potential of (a) PS and (b) PS-COOH MPs as a function of c_Pb²⁺.

The important role of surfactant traces in the Pb²⁺ uptake onto both the MPs emerged from ζ potential measurements have been further investigated carrying out additional Pb²⁺ adsorption isotherm experiments with PS* MPs (surfactant free MPs, see previous section) in aqueous solutions containing NaNO₃ 0.1 mol L⁻¹, at pH = 5.0, with and without the addition of SDS 0.1 mmol L⁻¹. The q_evs. c_e values and the parameters values of Langmuir and Freundlich isotherm models are reported in Fig. S4 and Table S5 of ESI,† respectively. The maximum adsorption capacity of PS* increases when the Pb²⁺ solution contains the surfactant (q_m = 535 and 198 μg g⁻¹ in presence and in the absence of SDS 0.1 mmol L⁻¹, respectively) confirming the fundamental role of SDS. The q_m value of PS* MPs lower than that of PS MPs can be attributed to the lowest surface area of PS* MPs. Indeed, the PS* MPs particle size of 0.2–1.5 mm, estimated from micrograph analysis (see Fig. S5 of ESI†), is three orders of magnitude higher than that of PS MPs beads (0.37 μm).

Going back to the investigation on the two standard MPs beads, Fig. 3 shows the SEM images of PS and PS-COOH MPs, obtained at magnifications of 60 000×. From the SEM images, there is no difference in the morphology of PS and PS-COOH particles pre- (Fig. 3a and d) and post (Fig. 3b, c, e and f) the adsorption process of Pb²⁺ ions. The average particle size measured by the SEM images is in the range 360–370 nm for PS particles and 160–170 nm for PS-COOH particles, in accord to the data provided by the manufacturers. After adsorption of Pb²⁺ ions, particle sizes show no significant morphological change in either case. However, the presence of traces of the metal ion on the surfaces of the particles of the two types of MPs after Pb²⁺ adsorption was confirmed by the acquisition of the EDS spectra reported in Fig. S1.† The spectral region related to transitions to the electron shell “L” with energies ranging from 10 to 15 keV show that the Pb²⁺ ion is present on the surface of the particles of both types of MPs.

Fig. 3 SEM images of PS MPs pre- (a) and after Pb²⁺ absorption q_e = 480 μg g⁻¹ (b) and q_e = 780 μg g⁻¹ (c). SEM images of PS-COOH MPs pre- (d) and after Pb²⁺ absorption q_e = 420 μg g⁻¹ (e) and q_e = 1380 μg g⁻¹ (f).

In fact, in both the case of PS and PS-COOH, the peaks due to the electronic transition's characteristic of the Pb element are found. The same figure reports both the spectra of PS and PS-COOH MPs before and after adsorption of Pb²⁺ at different values of q_e. It should be emphasized that the intensity of the peaks related to the electronic transitions of the Pb, in both spectra, is particularly low. A semi-quantitative analysis of the elements present on the surface of the MPs spectra has been carried out from the area of all the peaks of the EDS spectra, the results of which are reported in Table 2. It can be observed that the two MPs are able to adsorb only traces amounts of Pb²⁺ ion. This is again in agreement with the adsorption experiments carried out by voltammetric measurements.

Table 2 Semiquantitative determination of the elements on MPs of PS and PS-COOH

MPs sample (qe)^a	Pb^b (wt%)
a μg g^−1. b σ = 0.01.
PS (0)	0.01
PS (480)	0.02
PS (780)	0.03
PS-COOH (0)	0.01
PS-COOH (420)	0.03
PS-COOH (1380)	0.04

---

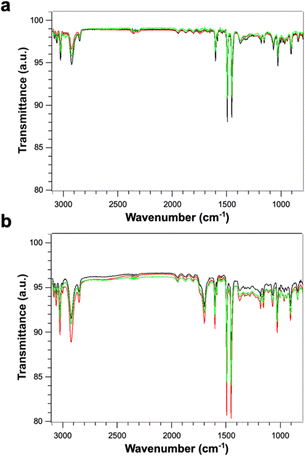
Fig. 4 shows the FTIR spectra of PS (Fig. 4a) and PS-COOH (Fig. 4b) PS MPs. The two samples display an identical peak pattern which is characteristic of polystyrene.^25,26 Briefly, the absorption peaks at the wavenumbers of 3082, 3060 and 3026 cm⁻¹ are due to aromatic C–H stretching vibration absorption; the absorption bands at 2923 and 2848 cm⁻¹ can be ascribed to the asymmetric and symmetric stretching vibrations of methylene groups –CH₂; the three absorption peaks at the wavenumbers of 1601, 1493 and 1452 cm⁻¹ are due to aromatic C=C stretching vibration absorption; the absorption peaks at the wavenumbers of 757 and 697 cm⁻¹ correspond to C–H out-of-plane bending vibration absorption. As expected, the carboxylated microspheres show an additional peak at 1700 cm⁻¹ which is characteristic of the C=O bond on the carboxyl group.²⁷ The absence of significative effects due to the Pb²⁺ ion adsorption on the FT-IR spectra can be attributed to low amount of absorbed Pb.

Fig. 4 (a) FT-IR spectra of PS MPs pre- (black line) and post-adsorption of Pb²⁺ ions at q_e = 480 μg g⁻¹ (red line) and q_e = 780 μg g⁻¹ (green line). (b) FT-IR spectra of PS-COOH pre- (black line) and post-adsorption of Pb²⁺ ions at q_e = 420 μg g⁻¹ (red line) and q_e = 1380 μg g⁻¹ (green line).

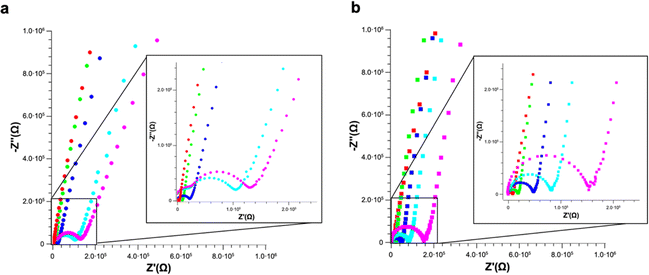
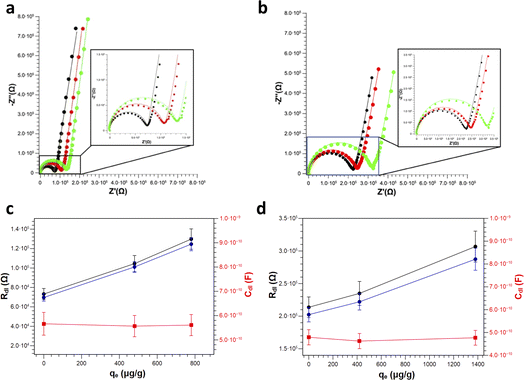
EIS measurements were carried out on PS and PS-COOH suspensions in ultrapure water. The Nyquist plots reported in Fig. 5 clearly show that for both samples, PS (Fig. 5a) or PS-COOH MPs (Fig. 5b). It is evident that the higher is the concentration of the PS or PS-COOH MPs, the lower is the total impedance of the suspension. This might seem counterintuitive given the hydrophobicity of PS, however the negative charges on the surface of PS and PS-COOH particles are mainly ascribed to the presence of the SDS surfactant, that increases the hydrophilicity of the MPs.^5,6 The ions transport in ultrapure water includes parallel contributions due to the double-layer capacitance and electrode–water interface, taking into account capacitive reactance phenomena at high frequencies.²⁸ The Nyquist plot for ultrapure water (reported in Fig. S2†) shows a small semicircle at high frequencies due to the graphite/water interface, which can be described by a contact resistance (R_c) and two constant phase elements (CPE), all these elements are ascribed to capacitive reactance. Differently, the larger semicircle in the intermediate-frequency region is due to the electron transfer through the electrolytes/graphite interface. In this process, the double layer resistance (R_dl) in series and the Warburg impedance (W) modelling the electrolyte diffusion process are in parallel with the double-layer capacitance (C_dl). The fitting parameters are reported in Table S2.† MPs dispersed in water lead to one semicircle in the Nyquist plot, whose width is inversely dependent on the concentration of PS/PS-COOH MPs. This observation can be explained by considering an equivalent circuit model in which SDS forms a capacitance double layer around the MPs, resulting in an EIS of the suspensions modelled as a modified equivalent Randles circuit similar to one reported by Véliz et al.,²⁹ in which the impedance spectrum is a dielectric dispersion of the MPs double layer.³⁰

Fig. 5 (a) Nyquist plots of PS dispersed in water at different concentrations: 0.67% w/v (red circles); 0.2% w/v (green circles); 0.1% w/v (blue circles); 0.02% w/v (cyan circles); 0.01% w/v (magenta circles); (b) Nyquist plots of PS-COOH dispersed in water at different concentrations: 0.052% w/v (red squares); 0.026% w/v (green squares); 0.0104% w/v (blue squares); 0.005% w/v (cyan squares); 0.0026% w/v (magenta squares).

The charged MPs dramatically change the electrical behaviour of ultrapure water. Notably, PS MPs Nyquist spectra can be fitted by using the same equivalent circuit used for ultrapure water, especially at low MPs concentrations. However, the higher is the concentration of PS MPs, the smaller become the semicircle radii eventually merging into a single one, which in turn simplifies the model circuit. Differently, in the case of PS-COOH MPs, only one semicircle is observed even at low concentrations. This might be due to the higher amount of SDS counterions and/or the surface charges of the PS-COOH MPs. In this regard, SDS molecules are described to determine a capacitive reactance in accord with previous results.^31–34 Accordingly, it is possible to introduce a CPE³⁵ (CPE1) in the equivalent circuit in series with the double layer resistance (R_dl) and the Warburg impedance (W) modelling the electrolyte diffusion process in parallel with the double-layer capacitance (C_dl), as reported in the model circuit (herein defined as circuit 1) in Fig. 6. Similarly, the Warburg impedance used for the fit also does not show significant differences that can be of interest for the analysis. These results are in accord with Vidal et al.³⁶ who found that C_dl values do not change upon MPs adsorption on the working electrode, given that the electrode surface cannot be covered by the MPs layer and, as a consequence, it does not become an insulator. Differently, the R_dl value is inversely dependent on the MPs concentration for both PS and PS-COOH MPs, in accord with the increase in the SDS counterion concentration in the suspension.³⁴ As an alternative, a slightly modified version of the model circuit (herein defined as circuit 2) described by Urso et al.²¹ is also used (Fig. S3†). This has the double-layer capacitance of the working electrode described by a CPE is in parallel with the double layer resistance at the electrolyte/electrode interface (R_dl) and a second CPE. As the concentration of MPs dispersed decreases, the R_dl value increases, as evident by the size decrease of the semicircle in the Nyquist plot by increasing the MPs concentration. Differently, the pseudo-capacitance values remain almost unaffected, as the capacitive changes of the double layer are not related to the MPs migration to the working electrode. The fitting parameters for PS MPs and PS-COOH MPs using circuit 1 are reported in Table S3.†

Fig. 6 Linear response of 1/R_dlvs. microplastic concentration using circuit 1 for (a) PS and (b) PS-COOH MPs. The inset shows the equivalent circuit used for fitting the data of the Nyquist plots of PS and PS-COOH MPs dispersions in water.

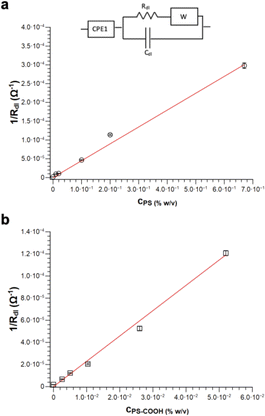
It is possible to obtain a linear response of the inverse of the double layer resistance at the electrolyte/electrode interface (1/R_dl) for both circuit 1 and circuit 2, as a function of both PS MPs (Fig. 6a) and PS-COOH MPs (Fig. 6b). From these results a quantification of the MPs in the suspension, along with a determination of the Limit of Detection (LOD), calculated as 3.3S_y/S, where S_y is the standard deviation of the response of the curve and S is the slope of the calibration curve. The two circuit models provide almost the same linear quantitative response as a function of the MPs concentration. For PS MPs, circuit 1 (R² = 0.9874) gives LOD equal to 0.073% w/v, circuit 2 (R² = 0.9858) provides an LOD equal to 0.077% w/v. For PS-COOH MPs, circuit 1 (R² = 0.9926) gives LOD equal to 0.059% w/v, circuit 2 (R² = 0.9944) provides a LOD equal to 0.051% w/v. The two circuits provide fitting parameters which are, in both cases, statistically equivalent. However, circuit 2 does not provide a good fit of the EIS spectrum at the low frequency region, which is instead well fitted by using the circuit 1 and it also lacks in providing reliable values for CPE2 in parallel to the R_dl. This results in the lack of convergence for the fit of circuit 2, that can be explained by considering that circuit 1 includes the Warburg impedance, modelling the diffusion at low frequency. Even if not able to provide convergence, circuit 2 still permits to provide R_dl values in accord to the ones of circuit 1, given that such circuit element is fitted at the region at high frequencies. As a result, the EIS spectra of polluted PS were fitted by using circuit 1.

The herein described method allows discriminating the presence or absence of MPs. Indeed, the R_dl value of the sample without MPs (which is the larger semicircle observed in the spectrum in Fig. S2†) is significantly higher (540 kOhm) than the one obtained in the presence of the MPs (110 kOhm) at the lowest investigated PS MPs concentration (0.01% w/v). The quantification of MPs is obtained in the absence of absorbed Pb²⁺, as the inverse of the R_dl value is found to be directly proportional to their concentration, as shown in Fig. 6. Notably, these measurements are carried out by diluting the MPs standards from the stock solution in DI water, in a way the EIS detects the SDS layer on the MPs surface. Indeed, the higher the MPs concentration, the higher is the SDS surfactant concentration and, as a result, the lower is the R_dl value obtained from the equivalent circuit.

Finally, clean vs. Pb²⁺ polluted PS (Fig. 7a) and PS-COOH (Fig. 7b) MPs at 0.05% w/v were analysed by EIS to test their different responses. From the Nyquist plots, it is again possible to extract the R_dl and the C_dl values in all cases by fitting the experimental data with circuit 1. Intriguingly, for both PS (Fig. 7c) and PS-COOH (Fig. 7d) MPs, R_dl show a significant increase at increasing q_e values, whereas C_dl remain almost unaffected. This trend confirms that the R_dl is the most suitable parameter for the analysis of the MPs and the prompt differentiation between clean and polluted MPs. The higher R_dl values of PS-COOH vs. PS in the absence of Pb²⁺ adsorbed well agrees with the lower absolute value of the ζ potential of the former vs. the latter (Fig. 2). The fitting parameters are reported in Table S4.† These experimental observations also permit to state that the increase in R_dl as the value of q_e can be ascribed to the adsorption of the Pb²⁺ ion on the surface of the microparticles which mainly occurs through an electrostatic interaction between the negative charges present on the surface of MPs and the positive charges of the metal ion. As a result, the adsorption of Pb²⁺ ions causes a decrease of the charges available for migration at the interface of the working electrode, which results in an increase in R_dl. Differently, the C_dl values are not affected by Pb²⁺ adsorption, since this does not lead to their adsorption at the working electrode even if their ζ potential becomes less negative. The EIS results well agree with the ζ potential values, from which the adsorption of Pb²⁺ ions on the surface of the MPs caused a decrease in the surface charge in accord with the decrease of the ζ potential values. However, whereas metal ions adsorption on MPs is studied in depth,^37–39 the effect of surfactant is typically overlooked or simply not considered in detail.^40,41 Importantly, the monodisperse MPs standards used in this work are prepared by emulsion polymerization method, in which surfactant molecules are used to obtain mono-dispersed polystyrene (PS) beads at sub-micrometer scale.⁴² Differently from MPs originated from fragmentation, the monodisperse MPs produced at these scales can be more easily dispersed in aqueous media given the presence of the surfactant molecules which increase their colloidal stability, leading to higher toxicity since they are more prone to be transported inside cells and living organisms. As reported by the producer, traces of surfactants are typically present in the MPs suspension or in the MPs dry pellet. For these reasons, the role of the surfactant molecules cannot be ignored in the resulting adsorption of Pb²⁺ ions from the MPs but must be considered for elucidating the mechanism of Pb²⁺ adsorption in these experimental conditions. However, from these experiments, the presence of surfactant, even in trace amounts, substantially modifies the surface charge of particles and this also has repercussions on the interaction of the MPs and the metal ion. In fact, Huang and collaborators demonstrated that the adsorbent capacities of biodegradable polylactate microplastics in the presence of SDS ([SDS] < c.m.c.) in comparisons of the Pb²⁺ ion increase significantly compared to those in the absence of surfactant.⁴³

Fig. 7 EIS-based differentiation of PS and PSCOOH MPs pre- and post-adsorption of Pb²⁺ ions. (a) Nyquist plots of PS MPs dispersed in water pre- (black dots) and post-Pb²⁺ ions adsorption at two different q_e values, namely 480 μg g⁻¹ (red dots) and 780 μg g⁻¹ (green dots). (b) Nyquist plots of PS-COOH MPs dispersed in water pre- (black dots) and post-Pb²⁺ adsorption at two different q_e values, namely 420 μg g⁻¹ (red dots) and 1380 μg g⁻¹ (green dots). For both panels, the lines represent the fit to the experimental data by using circuit 1. (c) R_dl (black dots for circuit 1, blued dots for circuit 2) and C_dl (red squares) values as a function of q_e values for PS MPs. (d) R_dl (black dots for circuit 1, blued dots for circuit 2) and C_dl (red squares) values as a function of q_e values for PS-COOH MPs.

In light of the results of Pb²⁺ adsorption obtained with MPs produced by fragmentation, it is clear that the obtained q_e values of PS and PS-COOH are more similar to the q_e obtained from fragmentated MPs in the presence of SDS surfactant. These experimental results permit to state that SDS molecules at the interface between the MPs and the aqueous phase are able to stabilize the dispersion given the electrostatic repulsion between the negatively charged sulphate groups. Pb²⁺ ions can be electrostatically adsorbed by the negative groups at the surface of the MPs. According to the Langmuir model, the Pb²⁺ ions adsorbed forms a monolayer on the MPs surface covered by surfactant. These experimental observations well agree with computational studies⁴⁴ in which the negatively charged headgroups of the SDS preassembled micelles are able to trap Pb²⁺ ions due to electrostatic interactions modelled by particle mesh Ewald method.⁴⁵

The analytical features of the method are compared with previously published reports and summarized in Table 3. Differently from other reports, this work offers a simple, label-free and direct approach for quantification of MPs, also permitting to differentiate the presence of Pb²⁺ ions adsorbed at water/MP interface thanks to the quantification of the R_dl value obtained by fitting to a model circuit.

Table 3 Important factors (type of MPs, presence of adsorbed pollutants, electrochemical mediator, differentiation between MPs and biological systems, quantification range, LOD) in our approach (first row) vs. other recently EIS-based analytical methods for MPs. N. R.: value not reported

MPs and/or biological systems analysed	Adsorption of pollutants on the MPs	Presence of an electrochemical mediator	Differentiation between different MPs (and/or biological systems)	Quantification range	LOD	Ref.
PS (0.37 μm particle diameter) and PS-COOH (0.19 μm particle diameter)	Yes, Pb^2+ ions measured by differential-pulse voltammetry	No	Differentiation between clean and Pb^2+ polluted MPs by label-free EIS	Investigated range for PS: 0.67–0.01% w/v; investigated range for PS-COOH: 0.052–0.0026% w/v	LOD for PS: 0.073% w/v; LOD for PS-COOH: 0.059% w/v	This work
Polyethylene (PE) MPs in 6 size ranges (212–250, 300–355, 425–500, 500–600, 600–710, and 850–1000 μm) vs. 8 biological samples	No	No	Differentiation by using k-nearest neighbours algorithm of MPs and biological samples using Z change at 1.1 MHz and 10 kHz frequencies	N. R.	N. R.	Colson et al.^17
PS-COOH nanoplastics (50 nm size)	No	Yes, Fe(CN)6^4−/3− as the redox probe	Capture by MXene-derived oxide microrobots	∼10^6 and 10^14 MPs mL^−1	N. R.	Urso et al.^21
PS (0.1, 0.5, and 10 μm diameter) and expanded PS MPs	Yes, bisphenol A measured by differential-pulse voltammetry	Capacitive and faradaic detection (using ferrocene-methanol probe)	Blocking of the charge transfer of ferrocene-methanol through chronoamperometry and EIS	MPs detection in the linear range from 0.005 pM to 0.500 pM	N. R.	Vidal. et al.^36
PS MPs (0.08–20 μm size)	No	Yes, Fe(CN)6^4−/3− as the redox probe	EIS data processed by component analysis and singular value decomposition	Z′′ vs. lg Cps (concentration range 0.01–25 mg L^−1); Z′ vs. lg Dps (particle size range 0.08–20 μm)	N. R.	Du et al.^20
PE and PS MPs (20 μm and 150 μm diameter)	No	No	k-Nearest neighbour model identification of microplastic material in question, by using self-normalized ratio between two characteristic frequencies of 7 MHz and 8.9 MHz	N. R.	N. R.	Ching et al.^46
Polypropylene (PP) and polyolefin particles (2–4 mm diameter) with different organic pollutants (1.0%, 3.0%, 5.0%) or water salinity (0.5%, 1.0%, 3.5%)	No	No	EIS data treated by support vector machines to classify different MPs materials and particle sizes	N. R.	N. R.	Meiler et al.^47
Polyethylene terephthalate (PET) MPs at different sizes (0.5–4 mm)	No	No	Analysis of the MPs pollution in water that leverages an electronic tongue and machine learning under different experimental conditions (water + MPs + living organisms and organic and inorganic matter)	N. R.	N. R.	Sarmiento et al.^48
PS MPs (diameter 2 μm, 3 μm, 5 μm) and PMMA MPs (diameter 8 μm) together with phytoplankton samples	No	No	Dual frequency impedance (particle size @ 1 MHz; electrical composition @ 500 MHz) on-chip differentiation between microplastics and four plankton species at dimensions <10 μm	100 particles per μL	N. R.	Butement et al.^49
PS MPs (0.5 μm; 1 μm; 3 μm, 6 μm). The surfaces of the 1 μm and 3 μm large particles were carboxy-modified	No	No	The signal phase at of 4.4 MHz and 11 MHz frequencies indicate MPs dispersed in water	MPs detection at the concentration values: 0.05%, 0.10%, and 0.20% expressed as solid particle percentage (g mL^−1)	N. R.	Aghel et al.^50
			The carboxy-modified MPs have different value of the signal phase with respect to the pristine ones

---

Notably, other methods in the literature employ complex post-measurements tools, such as Principal Component Analysis and Support Vector Machines⁴⁷ to extract analytical information from the EIS data, as usually the differences measured from the different samples are not immediately evident to a common user of electroanalytical methods. This work shows that it is possible to leverage EIS performing a dielectric spectroscopy of the double layer around the MPs, obtaining analytical information without complex data treatment. Such method enables a label-free non-faradic quantification method of MPs and the classification as virgin or Pb²⁺ polluted, whilst also providing a fundamental understanding of the critical role of surfactants in the mechanism of Pb²⁺ absorption on their surface.

The method shown in this study is simpler in comparison to other studies carried out on sensors, such as the one from Urso and collaborators²¹ in which electrochemical reports are used. Indeed, they found a similar increase in the charge transfer resistance (R_ct) value of a faradaic process using Fe(CN)₆^4−/3− as the redox probe following adsorption of PS-COOH MPs (negatively charged). Such increase was justified with the decrease in charges available at the interface following the interaction between MPs and the material deposited on the electrode. Differently, this work shows the possibility to detect MPs in the absence of the redox probe, relying on the analysis of the different double layer charge on the MPs as consequence of the presence of SDS surfactant and of the adsorption of Pb²⁺ ions, so resulting in data which could also be employed as EIS-derived fingerprints for MPs differentiation in terms of chemical composition and surface charge. The analytical method shown in this work provides a rapid assay for MPs quantification and differentiate clean vs. polluted MPs. Future experiments will investigate upon the possibility to explore the non-faradaic EIS transduction sensor by monitoring the double-layer capacitance (C_dl)⁵¹ resulting in the possibility to study the effect of MP size and shape on the EIS based response and also determine the pollutants that can be adsorbed by the MPs by sensors based on voltammetry.⁵² In particular, after functionalization of the working electrode surface, the same sensor used for EIS determination of MPs could be employed for the simultaneous analysis of toxic metals.⁵³

Conclusions

This study is a preliminary investigation reporting on an easy label-free EIS-based approach to study PS and PS-COOH MPs suspensions in ultrapure water and differentiate clean vs. Pb²⁺ ion polluted MPs. The EIS quantification of MPs results from the perturbation of the pseudo double layer formed by SDS surfactant at the interface between the MPs and water resulting from the adsorption of Pb²⁺ ions. The analysis is obtained from the MPs dispersed in ultrapure water without any electrochemical reporter or any support electrolyte apart from the SDS counterions. The value of R_dl is chosen for MPs quantification purposes and is found to be dependent to the Pb²⁺ ions adsorbed at the MPs surface, this being confirmed by ζ potential values of the MP_S and the DP-ASV Pb²⁺ quantification post Pb²⁺ ion adsorption. In this preliminary study, the two types of MPs result in different R_dl values, which are in accord to the ζ potential values. This could be a promising feature of the herein proposed method, which will be investigated in future studies to fully ascertain the possibility to differentiate MPs based on their chemical composition, size or other geometrical features. At this stage of the research, it is reasonable to assume that both surfactant presence and surface area affect the adsorbent capacity as was highlighted by comparing polystyrene from standard with others obtained from pellet fragmentation. Finally, the herein reported method requires a simple post-analysis data treatment, based on conventional EIS circuit model fitting to obtain the R_dl values. However, it is also possible to extract the data simply by reading the R_dl value from the Nyquist plot without performing a fit.

As a consequence, it could be applied to low-resource world settings or portable sensors to use on the field, given the simplicity, low-cost and efficiency of the detection. Indeed, the sensors used in this study could extract EIS data using a smartphone and send the data to the laboratory. The further development of the analytical method shown in this work would permit to promptly identify areas which are a potential source of plastic pollution. Such information could allow to better shape future policies for mitigating plastic originated pollution, and to implement suitable remediation strategies for reducing potential hazards to humans.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

DL: data acquisition, data processing, analysis and curating, writing of original draft; SC: data acquisition, data processing, analysis and curating; NM: data acquisition, data processing, analysis and curating; GP: data acquisition, data processing, analysis and curating; BP: methodology, resources, writing – review and editing; GL: resources, funding acquisition, writing – review and editing; GA: conceptual design, writing – review and editing; conceptual design, analytical strategy, selection of samples, data acquisition, data processing, analysis and curating, writing of original draft; AP: resources, funding acquisition, writing – review and editing, conceptual design, analytical strategy, selection of samples, writing of original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support of the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.4 – call for tender No. 3138 of 16 December 2021, rectified by Decree No. 3175 of 18 December 2021 of Italian Ministry of University and Research funded by the European Union – NextGenerationEU; Project code CN_00000033, Concession Decree No. 1034 of 17 June 2022 adopted by the Italian Ministry of University and Research, CUP B73C22000790001, Project title “National Biodiversity Future Center – NBFC”. They also acknowledge the support of the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.3 – funded by the European Union – NextGenerationEU and SiciliAn MicronanOTecH Research And Innovation CEnter “SAMOTHRACE” (MUR, PNRR-M4C2, ECS_00000022), spoke 3 – Università degli Studi di Palermo “S2-COMMs – Micro and Nanotechnologies for Smart & Sustainable Communities”.

Notes and references

1. Z. Yuan, R. Nag and E. Cummins, Sci. Total Environ., 2022, 823, 153730.
2. J. P. G. L. Frias and R. Nash, Mar. Pollut. Bull., 2019, 138, 145–147.
3. M. A. Browne, Sources and Pathways of Microplastics to Habitats, Marine Anthropogenic Litter, ed. M. Bergmann, L. Gutow and M. Klages, Springer International Publishing, Cham, 2015, ch. 9, pp. 229–244.
4. A. Menéndez-Pedriza and L. Jaumot, Toxics, 2020, 8, 1–40.
5. M. Shen, B. Song, G. Zeng, Y. Zhang, F. Teng and C. Zhou, Chem. Eng. J., 2021, 405, 126989.
6. X. Xue, S. Hong, R. Cheng, H. Li, L. Qiu and C. Fang, Chemosphere, 2022, 307, 136195.
7. Y. Xia, J.-J. Zhou, Y.-Y. Gong, Z.-J. Li and E. Y. Zeng, Environ. Pollut., 2020, 265, 115061.
8. M. Renzi, E. Grazioli and A. Blašković, Bull. Environ. Contam. Toxicol., 2019, 103, 367–373.
9. Y. Sun, T. Bakker, C. Ruf and Y. Pan, Sci. Rep., 2023, 13, 1–18.
10. V. Kumar, M. Umesh, P. Chakraborty, P. Sharma, S. Sarojini, T. Basheer, K. Kaur, R. Pasrija and D. Barcelo, TrAC, Trends Anal. Chem., 2024, 170, 117392.
11. M. Mosquera-Ortega, L. de Sousa, S. Susmel, E. Cortón and F. Figueredo, Anal. Methods, 2023, 15, 5978–5999.
12. Y. Picó and D. Barceló, TrAC, Trends Anal. Chem., 2020, 130, 115964.
13. G. Sancataldo, G. Avellone and V. Vetri, Environ. Sci.: Processes Impacts, 2020, 22, 2266–2275.
14. C. F. Araujo, M. M. Nolasco, A. M. P. Ribeiro and P. J. A. Ribeiro-Claro, Water Res., 2018, 142, 426–440.
15. M. G. Blevins, H. L. Allen, B. C. Colson, A. M. Cook, A. Z. Greenbaum, S. S. Hemami, J. Hollmann, E. Kim, A. A. Larocca, K. A. Markoski, P. Miraglia, V. L. Mott, W. M. Robberson, J. A. Santos, M. M. Sprachman, P. Swierk, S. Tate, M. F. Witinski, L. B. Kratchman and A. P. M. Michel, Sensors, 2021, 21, 1–27.
16. Y. Wu, Y. Ren, Y. Tao, L. Hou and H. Jiang, Anal. Chem., 2018, 90, 11461–11469.
17. B. C. Colson and A. P. M. Michel, ACS Sens., 2021, 6, 238–244.
18. A. C. Lazanas and M. I. Prodromidis, ACS Meas. Sci. Au, 2023, 3, 162–193.
19. G. Arrabito, V. Errico, A. De Ninno, F. Cavaleri, V. Ferrara, B. Pignataro and F. Caselli, Langmuir, 2019, 35, 4936–4945.
20. H. Du, G. Chen and J. Wang, Sci. Total Environ., 2023, 862, 160873.
21. M. Urso, M. Ussia, F. Novotný and M. Pumera, Nat. Commun., 2022, 13, 1–14.
22. S. Cataldo, A. Gianguzza, D. Milea, N. Muratore and A. Pettignano, Int. J. Biol. Macromol., 2016, 92, 769–778.
23. S. Anselmo, S. Cataldo, T. Avola, G. Sancataldo, M. C. D'Oca, T. Fiore, N. Muratore, M. Scopelliti, A. Pettignano and V. Vetri, J. Colloid Interface Sci., 2022, 610, 347–358.
24. Annual Book of ASTM Standards: End Use Products ASTM Standard Vol.15.07–1999–Revision issued annually Annual book of ASTM standards, ed. R. F. Allen, ASTM, 1999.
25. D. Olmos, E. V Martín and J. González-Benito, Phys. Chem. Chem. Phys., 2014, 16, 24339–24349.
26. J. Fang, Y. Xuan and Q. Li, Sci. China: Technol. Sci., 2010, 53, 3088–3093.
27. B. Zhang, J. Lu, X. Liu, H. Jin, G. He and X. Guo, Int. J. Polym. Sci., 2018, 8702597.
28. S. Xiaoping, P. Spitzer and U. Sudmeier, Accredit. Qual. Assur., 2007, 12, 351–355.
29. B. Véliz, A. Orpella, M. Dominguez and S. Bermejo, Mater. Chem. Phys., 2020, 243, 122620.
30. C. Grosse and A. V. Delgado, Curr. Opin. Colloid Interface Sci., 2010, 15, 145–159.
31. S. Wang and K. Zhao, Colloid Polym. Sci., 2017, 295, 2133–2140.
32. J. M. G. Neto, H. N. Da Cunha, J. M. M. Neto and G. F. L. Ferreira, J. Sol-Gel Sci. Technol., 2006, 38, 191–195.
33. M. Abe and K. Ogino, J. Colloid Interface Sci., 1981, 80, 58–66.
34. H. P. De Oliveira and C. P. De Melo, J. Phys. Chem. B, 2011, 115, 6903–6908.
35. S. Holm, T. Holm and Ø. G. Martinsen, PLoS One, 2021, 16, 1–12.
36. J. C. Vidal, J. Midón, A. B. Vidal, D. Ciomaga and F. Laborda, Microchim. Acta, 2023, 190, 1–10.
37. S. Liu, J. Huang, W. Zhang, L. Shi, K. Yi, H. Yu, C. Zhang, S. Li and J. Li, J. Environ. Manage., 2022, 302, 113995.
38. N. Khalid, M. Aqeel, A. Noman, S. M. Khan and N. Akhter, Environ. Pollut., 2021, 290, 118104.
39. L. Gao, D. Fu, J. Zhao, W. Wu, Z. Wang, Y. Su and L. Peng, Mar. Pollut. Bull., 2021, 169, 112480.
40. Y. Sun, J. Yuan, T. Zhou, Y. Zhao, F. Yu and J. Ma, Environ. Pollut., 2020, 265, 114864.
41. M. Lang, X. Yu, J. Liu, T. Xia, T. Wang, H. Jia and X. Guo, Sci. Total Environ., 2020, 722, 137762.
42. T. Al Najjar, N. K. Allam and E. N. El Sawy, Nanoscale Adv., 2021, 3, 5626–5635.
43. W. Huang, J. Deng, J. Liang and X. Xia, Chem. Eng. J., 2023, 460, 141838.
44. M. d. A. Pacheco-Blas and L. Vicente, Colloids Surf., A, 2019, 578, 123613.
45. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
46. C. T. S. Ching, P. Y. Lee, N. Van Hieu, H. H. Chou, F. Y. D. Yao, S. Y. Cheng, Y. K. Lin and T. L. Phan, Biotechnol. Bioprocess Eng., 2023, 28, 459–466.
47. V. Meiler, J. Pfeiffer, L. Bifano, C. Kandlbinder-Paret and G. Fischerauer, IEEE Sens. J., 2023, 23, 4863–4872.
48. J. Sarmiento, M. Anaya and D. Tibaduiza, Int. J. Distrib. Sens. Netw., 2024, 2024, 5298635.
49. J. T. Butement, X. Wang, F. Siracusa, E. Miller, K. Pabortsava, M. Mowlem, D. Spencer and H. Morgan, ACS Sens., 2024 DOI:10.1021/acssensors.4c01353.
50. M. Aghel, S. Fardindoost, N. Tasnim and M. Hoorfar, Environments, 2024, 11, 96.
51. J. Muñoz, R. Montes and M. Baeza, TrAC, Trends Anal. Chem., 2017, 97, 201–215.
52. T. Hu, Q. Lai, W. Fan, Y. Zhang and Z. Liu, Sensors, 2023, 23, 4125.
53. I. Palchetti, S. Laschi and M. Mascini, Anal. Chim. Acta, 2005, 530, 61–67.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ay01324g

---