Rethinking polyiodides: the role of electron-deficient multicenter bonds

Abstract

Despite a bicentennial history, the interest in polyiodides and related systems still flourishes. The chemical puzzle provided by the intricate nature of chemical bonding in these polyanions remains challenging these days. The advent of the halogen bond and the spreading interest in supramolecular interactions of halogen-based systems promoted further recent interest. Research in the area of materials, where local bonding details eventually result in desired macroscopic properties, provided a further boost. Herein, we illustrate the consequences of contemplating a different bonding scheme for polyiodides, one making explicit use of electron-deficient multicenter bonds (EDMBs), an emerging concept in this area. We present a reinterpretation of polyiodide bonding using a revised approach to the Lewis dot formulas, leading to a clearer pen-and-paper understanding of their bonding. The model is general and can be applied to other related problems (here polyiodonium cations, and other homo- and hetero-polyhalides). Our alternative narrative has a few interesting consequences on several traditional and currently hot topics, including the nature of basic building blocks for polyiodides, hypervalency vs. hypercoordination, the distinction between covalent bonds and supramolecular interactions, and the nature of secondary and halogen bonds.

---

Introduction

Polyiodides have long^1,2 been a classic among scientifically challenging systems for chemists and physicists alike. Structural chemistry and geometrical possibilities displayed by polyiodides are particularly rich.^3,4 To such a richness subtends complexity: even the simplest of polyiodides, I⁻₃, was immediately recognized as an anion defying the octet rule. The apparent violation of the octet rule has led to a mainstream explanation of polyiodides as hypervalent species and has played a pivotal role in the understanding of, and/or constitutes a prime example of, three-center–four-electron (3c–4e) bonds, also known as electron-rich multicenter bonds (ERMBs).^5–7

On the other hand, polyiodides with a larger number of atoms in the chain than I⁻₃ also possess an interesting alternation in terms of bond lengths, with many I⋯I bonds(?)/contacts(?)/interactions(?)⁸ that fall in an intermediate region between single covalent (2c–2e bonds, like in I₂) bonds and supramolecular interactions, which are, nevertheless, strongly directional.^3,4 For this very reason, polyiodides have been a prime crucible for the elaboration of novel concepts, in general, in inorganic, physical, and also supramolecular chemistry. In the latter realm, namely, secondary bonds^9,10 and halogen bonds¹¹ (and actually further models in between)^12–14 are here of special relevance. To this end, polyiodides have been generally approached with a reductionist mindset, dismantling superior species in terms of complexes of the I₂, I⁻, and I⁻₃ reassuring basic building blocks, often via an I⋯I experimental distance-based approach to differentiate them in covalently-, secondary-/halogen-, and non-bonded fragments.^3,15–17

This is, in a nutshell, the summary of the first two centuries of the history of polyiodides. What is now prompting us to rethink the whole matter are three recent facts: (i) supramolecular interaction models, old (secondary bonds) and new (halogen bonds), have been criticized on both experimental and theoretical grounds (see discussion herein and in ref. 8 and 18 for an overview); (ii) the need and possibility of coherently rebuilding a view of related supramolecular interactions were advanced and contact points were highlighted;^4,8,18,19 and (iii) an apparently innocent-yet-revolutionary statement recently made: linear multicenter bonds on more than 3 atoms must be of the electron-deficient type (i.e. 2c–1e electron-deficient multicenter bonds, or EDMBs), even for electron-rich elements, such as I, with plenty (7) of valence electrons.^20–23

Herein, we start from the contributions of Manjón and coworkers on the nature of bonding in chain-type systems, present in pnictogens and chalcogens,^20,22 as well as in halides,²³ and work our way to re-understand polyiodide bonding and geometries. These same observations – to different extents, stemming from different backgrounds, and reaching a variety of conclusions – are simultaneously emerging in very recent works of several research groups around the world, especially for halogen-related systems.^24–27

In the following sections, we will briefly attempt to re-explain polyiodides using a revisited version of Lewis dot formulas. On these grounds, we will then re-discuss and re-think current models for polyiodides and iodine–iodine bonds and interactions.

Polyiodides re-explained: a simple electron disposition exercise

Arguably, the single key concept in chemistry is the covalent bond. This is accompanied by the importance of electronic doublets, forming part of either bonding electron pairs (BEPs) or non-bonding lone electron pairs (LEPs). Rationalization and prediction of bonding and geometry in molecules are – still these days – dominated by Lewis dot formulas.²⁸ Drawing most molecules according to the Lewis formalism leads to easily predicting their atomic connectivity and valence electron distribution, thus evidencing the bond multiplicities and the number of LEPs present on each atom. From there, the well-known VSEPR theory²⁹ allows us to derive local molecular geometry, granting an easy visualization of the three-dimensional structure of molecules.

Although this approach does not have the full and stringent predicting power of quantum mechanical calculations, it allows us to arrive at almost correct bond multiplicities and geometries (actual deviations from ideal VSEPR angles are generally rather small and can also be foreseen and approximately quantified within a VSEPR framework). This has significantly contributed to the relevance of the Lewis dot formulas, which, as a matter of fact, still constitute a fundamental topic in any general chemistry teaching course.

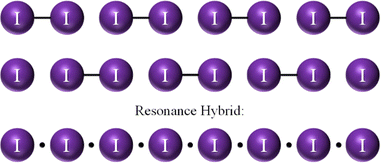
Pervaded by single covalent (2c–2e) bonds and used to drawing full bonds (–) between atoms, a chemist, when asked to draw bonds for an infinite linear iodine chain, I_∞, would likely draw pairs of diiodine molecules (Fig. 1 top).

Fig. 1 Conceivable bonds in an infinite linear iodine chain, I_∞. Top and mid graphs show alternated single covalent (2c–2e) bonds and “no bonds” along the chain. The bottom resonance hybrid is the solution now proved correct: extended 2c–1e EDMBs.

A slightly more careful thinking would have a chemist state that there are two possible alternate chains and that the two should resonate (Fig. 1 top and center). Uneven resonance (possibly brought about by crystal surroundings) about covalent and 3c–4e bonds was already envisaged by Hach and Rundle to explain the odd bonding alternation in polyiodides.³⁰

Returning to I_∞, the resonance between alternated 2c–2e bonds and “no bonds” would indeed be a 2c–1e EDMB (Fig. 1 bottom). As a concept, EDMBs, especially in the finite case, are not new, nor poorly understood, having led to a Nobel Prize for the explanation of boron hydrides, also known as boranes, in terms of 3c–2e bonds (i.e. two interacting 2c–1e bonds).³¹ There is nothing special about the 2c–1e EDMB extended to infinite, except for the considerable cultural shock of having to admit EDMBs as a “natural” type of bond in such chains, even for (valence) electron-rich elements, such as pnictogens, chalcogens, and halogens.^20,22,23 In this sense, beyond an initial sense of scandal, the proposition and formal demonstration of the presence of EDMBs in infinite linear chains along one, two, and three dimensions, including the one-dimensional infinite linear iodine chain, as advanced by Manjón and coworkers,^20,22,23 stand out as a Columbus’ egg.

We will show how it is possible to predict stability, bending, and bond alternation in linear (i.e. not branched) chain polyiodides of all main series (I⁻_n, I²⁻_n, I³⁻_n) with a simple pen-and-paper approach based on the following broad concepts: (i) Lewis dot formulas; (ii) the octet rule; (iii) the VSEPR theory; and (iv) the single covalent 2c–2e bond, the 3c–4e bond (ERMB, with the notion they cannot extend beyond 3 atoms)^20,22,23 and the extended 2c–1e bond (EDMB, with the notion they are the standard bond for I_∞, the finite charge being irrelevant in the infinite chain limit).²³

The exercise we are going to make for polyiodides is untrivial with standard Lewis formulas using only electronic doublets (BEPs and LEPs), much like it is not possible to achieve a satisfying picture of molecules like B₂H₆ without considering the 3c–2e EDMB (the finite version of the extended or infinite 2c–1e EDMB of I_∞). To that end, we will refer to the I_∞ limit as the situation in which each I atom is surrounded by 3 LEPs and is involved in an infinite 2c–1e EDMB (Fig. 1 bottom, cf. ref. 23).

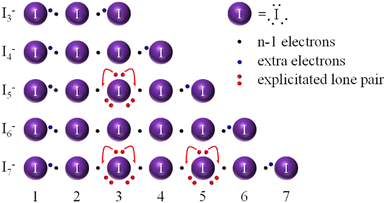
To start with, we have to stress that the electron distribution done until now in chemistry for I_∞ has to be reconsidered. Instead of immediately placing a BEP among any two I atoms in I_∞ and then deriving the number of LEPs around each atom, as for general Lewis formulas writing rules, we will first take into account the linear geometry of the molecule and, according to the VSEPR rules, ascribe six electrons to 3 LEPs to each iodine atom (the 3 LEPs located in the plane perpendicular to the linear chain, thus forming a trigonal bipyramidal geometry for each iodine atom) and then populate the I–I bonds with the remaining electrons.²³ The same procedure is followed for any linear chain, irrespective of the charge (x⁻) of the I^x−_n chain. Instead of drawing full bonds, we will first place one single electron binding each I atom to its neighbours, as per the I_∞ limit solution. Any extra electron is then used to complete the octet for the peripheral atoms, as for the standard Lewis formulas writing. In the general case of an I^x−_n chain, n + x electrons are placed in n − 1 bonds in a simple electron disposition exercise. As said, after ascribing 3 LEPs per iodine atom, we start by placing one electron binding each iodine atom to its neighbours; this means that for n atoms, we need to distribute n − 1 electrons in n − 1 bonds in this way. In the following (cf.Fig. 2), these are called “black” electrons. For the generic I^x−_n chain, we will be left with x + 1 further electrons to be distributed along the chain. These “extra” electrons are called “blue” electrons (cf.Fig. 2). Graphs obtained according to the above rules for the I⁻_n series are presented in Fig. 2.

Fig. 2 Revised Lewis dot formulas for polyiodides of the I⁻_n series.

Since the case of I₂ is trivial and has been commented on in ref. 23, it will not be further discussed.

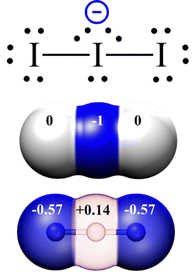
Therefore, we will start discussing the linear I⁻₃ system. In fact, the I⁻₃ drawing shown in Fig. 2 (4 electrons in the chain for 2 bonds) is already revealing. The use of LEPs and full bonds only (Fig. 3, top) leads to a central atom surrounded by 5 electron pairs. This makes the central I atom hypervalent and bearing, using the standard textbook definition of formal charge (in brief, the difference between valence electrons of the neutral atom and the electrons assigned to it in the Lewis formula assuming BEP are heterolytically divided between bonded atoms), and has a formal charge of −1. It is well known that the formal charge of −1 on the central atom is not mirrored by calculated atomic charges on the I⁻₃ anion, where the negative charge is equally distributed on the lateral atoms instead:²³ this mismatch between drawn (Fig. 3 top and middle) and real (Fig. 3 bottom, data from ref. 32) distributions of charge (read: electrons) already invites to a reflection about the quality of the picture generated by standard Lewis formulas in the special case of polyiodides.

Fig. 3 Hypervalent and formally charge-bearing central atom in the “doublets-only” classical Lewis formalism. Top: Hypervalent Lewis formula with formal charge; middle: Graphic depiction of the formal charge distribution; bottom: Actual Bader's atomic charges according to ref. 32 (color code: red positive, blue negative, transparency (in %) used to represent non-integer charges).

We notice that clues about the actual electronic distribution are also found experimentally in I⁻₃ coordination modes when this anion acts as a ligand for a metal cation, with end-on coordination (i.e. via the terminal I atom) favoured over side-on coordination (i.e. via the central I atom), as shown by Rogachev and Hoffmann³³ (see also the LAQSUV crystal structure and ref. 34 for recently found rare species resembling a transition state between the two possibilities, closely looking like the in silico “sliding” intermediate discussed in ref. 33).

Equivalent pictures of related 3c–4e systems are instead obtained using improvements to the original Rundle–Pimentel model.^5,30 Beyond mere inclusion of the s,p orbital mixing (see later),³⁵ the resonance VB model proposed by Coulson,³⁶ which opens to the inclusion of the ionic resonant structure (e.g. I–I I⁻ ↔ I⁻ I⁺ I⁻ ↔ I⁻ I–I), helps in arriving at a correct picture. Modern and finer VB methods (e.g. breathing-orbital VB)³⁷ have led to the establishment of charge-shift bonds,^38,39 for those species where the covalent-ionic resonance is so important that it becomes the major reason for stability. Model systems showing ERMBs, such as XeF₂,⁴⁰ SF_n (n = 1, 2, 4), PF₅ and ClF₃, have been clearly discussed to be related to the presence of charge-shift bonds.⁴¹ The I⁻₃ anion complies with the criteria for the hypervalency (see later) formulated in a charge-shift bond perspective (essentially low ionization potential for the central atom, electronegative and LEP-bearing substituents).⁴¹ Lastly, using Slater's cheap yet tremendously effective trick, a strict similarity of I⁻₃ and FHF⁻ can be invoked.⁶ In the bifluoride anion case, it is arguably easier to see how the charge rests on the atoms at the periphery and how H must avoid exceeding a valence electron count of 2 (8 in the case of the central I of I⁻₃).

So on the one hand, there is plenty of evidence that the simple I⁻₃ Lewis formula is unable predict the correct electronic distribution, while, on the other hand, advanced computational methods, admittedly due to their high level,⁴¹ tend to lose the immediacy of the description, which we are here trying to safeguard instead.

The electron-by-electron approach, we have previously commented, suggests drawing the I⁻₃ anion as 2 I·I 2c–1e bonds and then adding the 2 extra electrons. The picture shown in Fig. 2 is similar to the standard one (Fig. 3), although upon adding the last two “blue” electrons one is forced to mind that the external atoms need one electron each to complete the octet while the central one formally has already an 8-electron count. This invites the placing of such electrons as not completely shared with the central atom. This picture finds support in the MO picture of the I⁻₃ anion (the two electrons populate a non-bonding orbital, Fig. 4) and the actual charge distribution of the anion (Fig. 3), with most of the negative charge located on the external atoms rather than on the central one. The picture is also in keeping with the charge-shift bond description, as discussed earlier.⁴⁰ This simple example highlights how electrons can be paired (I⁻₃ anion and polyiodides are generally diamagnetic), without implying an integer bond order (bonds in I⁻₃ are longer than in I₂). In this way, the central iodine of the I⁻₃ anion is hypercoordinated but does not violate the octet rule (for sure not achieving a 10-electron count). In other words, the central atom can be considered to have an 8 + 2 electron environment, with 8 electrons in the first electronic shell and 2 additional electrons in the second electronic shell (at a longer distance than the first one), thus resolving the issue of hypervalency. The location of electrons in two different electronic shells that we propose matches with a recent work that has introduced the penetration index (interatomic distance description), where different kinds of interactions/bonds between two atoms show a different interpenetration of their different electronic spheres (the valence and the van der Waals spheres).⁴² In the case of the I⁻₃ anion, the central atom would have 8 electrons in the valence sphere and 2 electrons in the van der Waals sphere or crust (the region of space between the covalent and the van der Waals radii of a given element). Therefore, no violation of the octet rule occurs for the central atom in the I⁻₃ anion since there are no more than 8 electrons in the valence sphere. This reasoning applies in general to all 3c–4e bonds; therefore, there is no hypervalency but simple hypercoordination.^20,22

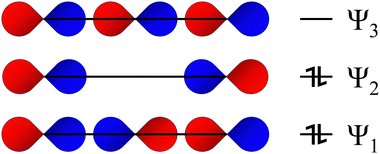Fig. 4 Qualitative Rundle–Pimentel MO picture of the I⁻₃ anion showing the 3c–4e bond (ERMB). The extra pair of electrons beyond the bonding pair goes into Ψ₂, a non-bonding level, where they are predominantly located on the terminal iodine atoms. Reproduced from ref. 18 with permission from RSC, copyright 2024. Despite the Rundle–Pimentel model for the ERMB being superior to the expanded octet rule, the unsuitability of this simple model and the need for a more complex one to explain many features of ERMBs has been addressed in ref. 40 and 41, where the relationship between ERMB and charge-shift bonding has been clearly shown.

It is interesting to note that it has been suggested that the shift of the excess electronic charge toward the external atoms in molecules with 3c–4e bonds is a mechanism of the central atom to avoid violating the octet rule.⁴³ Some similar arguments to justify the lack of violation of the octet rule are also found in the related ref. 24. Furthermore, the actual distribution of atomic charges fully supports this picture.

According to the aforementioned rules, the linear I⁻₄ system (5 electrons in the chain for 3 bonds) would be built by using 3 electrons in 3 I·I 2c–1e bonds and adding 2 more at the periphery of the molecule as in the standard Lewis formulas writing. This creates the situation of 2 weakly bound I₂ molecules by a single I·I 2c–1e bond. It is also to be noted that in even membered linear I_n chains, there are n/2 bonding MOs and n/2 antibonding MOs, so that I⁻₄, unlike I⁻₃ or I⁻₅ (see below), starts populating an antibonding level (an unfavourable situation from the energetic point of view). Moreover, the ERMB cannot be formed over more than 3 centers^20,21,23 and bending (occurring in the I⁻₅ system explained later) cannot improve global bond order along the chain in the I⁻₄ anion. Moreover, we have to stress that the 2c–1e bond is a kind of multicenter bond (the minimum set for the EDMB is the 3c–2e bond), so there is a lack of a second 2c–1e bond in the I⁻₄ anion, which further supports the lack of experimental evidence of this unit. Lastly, as for other odd-electron species, radicals are in general high-energy species, of overall rare occurrence with respect to even-electron species. As a matter of fact, the I⁻₄ anion has not been experimentally observed to our knowledge.³

Let us now discuss the linear I⁻₅ case (6 electrons in the chain for 4 bonds). This example allows us to highlight the reason for the bending of polyiodides and focus on the bond distance alternation. The classical picture of the anion is shown in Fig. 5 top. According to the aforementioned rules for electron distribution, the linear I⁻₅ chain shown in Fig. 2 would result in using 4 electrons in 4 I–I bonds and adding 2 more at the two peripheral bonds of the molecule as in the standard Lewis formulas writing. This would result in two external I₂ molecules being weakly bonded to a central I atom via two 2c–1e bonds (i.e. a 3c–2e bond). If the MO picture shown in Fig. 4 (for three centers) is updated and applied to five centers, the aforementioned electronic configuration would allow us to populate completely 3 of the 5 MO levels; i.e. the two bonding orbitals and the non-bonding orbital, so it is not so unfavorable as the I⁻₄ case.

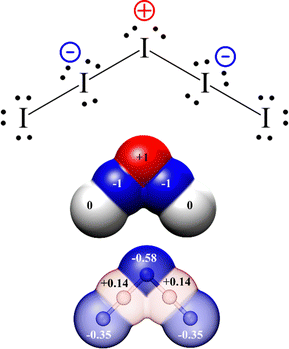Fig. 5 Top. Traditional Lewis formula for the I⁻₅ anion. Atoms at positions 2 and 4 result in hypervalent and formally negative charge bearing. Central atom (atom 3) results formally electron-deficient and positively charged. Bond length alternation is not manifested as all bonding electronic doublets are equal. Middle: Graphic depiction of formal charge distribution. Bottom: Actual Bader's atomic charges according to ref. 32 (colour code: red positive, blue negative, transparency (in %) has been used to represent non-integer charges).

In the linear I⁻₅ chain, ERMBs cannot be formed since there is a deficiency of electrons²¹ that leads to the presence of two 2c–1e bonds, i.e. EDMBs.²³ However, the bending of the chain around the central atom as shown in Fig. 2 can improve the stability of the system. The central atom might employ one of its LEPs to restore 3c–4e bonds around atoms 2 and 4, improving the number of bonding electrons in the chain. By doing so, it reduces its LEP count, and finds itself surrounded by 4 domains of electrons instead of 5: VSEPR theory easily allows local chain bending to be justified. Thus, by doing so, the bending around the central atom is introduced and explained. Such electron displacement has to be carefully made though, in close analogy to I⁻₃, in order to avoid exceeding the 8 electrons count for atoms 2 and 4. Consequently, we can state that hypercoordination rather than hypervalency is a feature of 3c–4e bonds.^18–20 The uneven sharing of bonding electrons in 3c–4e bonds, required by the octet rule as already explained for I⁻₃, brings experimentally observed I⁻₅ anions to be V- or L-shaped. In the V-shaped pentaiodide, the experimental bond distances are as follows: 2.78(9) Å (external 1–2 and 4–5 bonds) and 3.1(1) Å (internal 2–3 and 3–4).²⁶ In this way, the linear 1–2–3 and 3–4–5 chains can be seen as perturbed 3c–4e bonds with short and long bonds. While the short external (1–2 and 4–5) bonds can be considered closer to 2c–2e bonds, the long internal (2–3 and 3–4) bonds can be considered as intermediate between 3c–4e and 2c–1e bonds.

L-shaped pentaiodides, traditionally pictured as an [I⁻₃·I₂] complex, are just cases where one of the two resonant limit structures for the V-shaped anion (i.e. the 3c–4e system on the left or right side of atom 3) is favoured over the other (e.g. by packing forces in the crystal). The bond distances in L-shaped I⁻₅ were quantified as follows: formal I₂ fragment 2.8(1) Å, formal I⁻₃ fragment 3.0(1) Å, and bridging bond 3.1(2) Å.²⁶ Still, in comparison to the unbent chain (2.84 Å and 3.40 Å, Scheme 1 ref. 23, clearly showing 2c–2e and 2c–1e bond lengths), the bending process overall shortens bond lengths along the chain, and thus bond orders improve, formally reaching an 8-electron count for 4 bonds. The noticeable stability of the angular I⁻₅ anion (V- or L-shaped) is perhaps to be ascribed to its nature as two fused 3c–4e systems, as also noted in ref. 24, a situation only possible for exactly 5 atoms. The necessity for bond length alternation emerges naturally from our depiction. In any case, the dot model helps to see that bonds cannot be equal and to foresee which will be the long ones (i.e. those that achieve a formal 2-electron count due to the bending process).

A bolder take on the matter (one that is related to the secondary bonding section) could be addressing the matter from a Bent's rule perspective: LEPs are better stabilized by s-type orbitals (or s character in hybrid orbitals).⁴⁴ Linear polyiodine/polyiodide chains are widely pictured as combinations of 5p orbitals. Thus, in a sense, LEP sharing and chain bending increase the s-character in iodine bonding orbitals instead. “Shared” LEP is not much so. The concept has also been stated for 3c–4e systems by saying that the s,p orbital mixing would give non-bonding levels a slight antibonding character.³⁵ Although connected with the discussion of ERMB bonds (and the improvements made through the years from the Rundle–Pimentel^5,30 model to the VB model with charge-shift bond contribution)^38–41 rather than to EDMB, this aspect represents a valid point to account for bond alternation in polyiodides.

Finally, it must be noted that, in terms of atomic charges, our model clearly shows how linear I⁻₅ molecule is supposed to have atomic positions 1 and 5 with a valence electron count shifted towards 8, else atoms 2 and 4 would significantly violate the octet rule (in a similar situation to the I⁻₃ case). The bending process in I⁻₅ can be read as a formal electron donation from atom 3 towards atoms 2 and 4. It should be noted, as commented, that the ability of atoms 2 and 4 to accept such electrons is again limited due to octet rule concerns. Overall, our dot graph suggests positions 1, 3, and 5 as those bearing most of the negative charge. This finds confirmation in in silico data of both linear and bent I⁻₅ anions.^32,45 Notice how this picture (Fig. 5 bottom) is significantly different from that obtained from the standard Lewis formula (Fig. 5 middle).

Regarding the linear I⁻₆ molecule (7 electrons in the chain for 5 bonds), this system has similarities with the linear I⁻₄ molecule (5 electrons in the chain for 3 bonds). I⁻₄ has a single I·I bond, which could not be helped by bending (a 2-electron process), whereas I⁻₆ has 3 I·I bonds, thus, like in I⁻₄, there is a lack of another I·I bond, and there is no possible symmetric bending to stabilize the system. Moreover, any possible bending process would have 4 iodine atoms in a row connected by 2 electrons each: as ERMB cannot extend beyond a 3-atom system,^20–22 there is little to do to resolve the I⁻₆ anion instability. As a matter of fact, I⁻₆ has not been experimentally observed to our knowledge.³

The case of the linear I⁻₇ molecule (8 electrons in the chain for 6 bonds) is also interesting (Fig. 2). Here, the reasoning for the linear molecule is similar to that of the linear I⁻₅ molecule. In fact, a similar situation to I⁻₅ is envisaged, only with the requirement of bending around two atomic positions (atoms 3 and 5), in a Z-like fashion, thus reaching formally 12 electrons for 6 bonds. Octet concerns arise due to the bending process for atoms 2 and 6, while atom 4 finds itself in a linear 3-atomic moiety, 3–4–5, which is in an I⁻₃-like situation. Thus, the interpretation of the I⁻₇ molecule as an I₂–I₃–I₂ formal complex emerges naturally, together with expected (and experimentally found) average bond lengths (2.7(3) Å – bonds 1–2 and 6–7, 3.2(1) Å – bonds 2–3 and 5–6, and 2.9(2) Å – bonds 3–4 and 4–5 – CSD data on 19 deposited crystal structures, cf. ESI†).⁴⁶ Therefore, the Z-like bent I⁻₇ molecule can be seen again as 3 merged 3c–4e systems fused for 2 atoms (3 and 5), although the electron sharing becomes more and more uneven, a feature already observed for I⁻₅ with respect to I⁻₃. Proposed graphs help show how the existence of longer bonds in polyiodides, like those within the formal I₂ and formal I⁻₃ fragments, arises naturally as per a necessary compromise between donating electrons from LEPs to 2c–1e bonds and violating the octet rule for some involved atoms. Thus, both bond modulation and bond lengths beyond the Coppens threshold (3.30 Å)¹⁷ appear to be justified. The complete dismissal of such long bonds as non-covalent interactions requires reconsideration in the light of the EDMB model.^20,22 Structural arguments in support of this view were previously raised²⁶ and find here a conceptual framework.

The reasoning we have just demonstrated up to here could be extended to longer polyiodides, yet with I⁻₇, we already have the onset of structural isomers, i.e. branched species, like pyramidal I⁻₇, which can be considered as 3 fused 3c–4e systems with a single atom acting as the pyramid vertex and three branches of two atoms, so that all branches are characterized by linear 3c–4e bonds. One may thus expect I⁻₉ to be the next logically stable polyiodide in the series, although its rare reports only saw it as a branched rather than a linear species. If it were assumed as linear, our reasoning suggests that bending would occur at atoms 3, 5, and 7, i.e. the existence of the anion as a formal series of 4 fused 3c–4e systems held together by weaker (intermediate between 2c–2e and 2c–1e) bonds. It should be noticed that increasing the number of formally fused 3c–4e systems (e.g. moving from I⁻₅ to I⁻₇) already results in significant lengthening of the longest bond in the chain, meaning that an anion of formula I⁻₉ (much like I⁻₇) would likely propend for branched geometries instead.

These and other complex systems with more I atoms are beyond the scope of the present discussion. The reason is manyfold. First, for what concerns further infinite chains (e.g. the zigzag one), they were recently addressed.²³ Second, charge and odd/even number of I atoms suffice to have a global reference MO picture of linear polyiodides (see later): such is not the case for branched or cyclic structures, which would require dedicated individual attention. Third, the more complex the polyiodide, the more subtle the bond/interaction issue, i.e. if it should or should not be described as a molecule (a theme which is instead developed later in dedicated sections). Lastly, this contribution is intended as an original look back to existing literature and cannot aspire to solve all open questions. In this sense, we mention having personally encountered differences in bonding, even with analogous ligands, in transitioning from 11- to 18-membered (supramolecular, some would say) polyiodide rings.³⁴ Still, lacking the conceptual framework here provided, we limited ourselves to observation and description. In due time, provided the view herein presented is accepted, we might tackle more complex species in which iodine atoms are involved.

In conclusion, it is thus observed how I⁻_n stable anion series should be of the I⁻_2n+1 type, being bent molecules preferred over linear ones for molecules containing more than 3 centers; i.e. beyond I⁻₃. This does not stem from the formal necessity of polyiodides to derive from I₂ and I⁻ building blocks, but rather from the fact that anions of the I⁻_2n+1 series have an even number of bonding electrons to be distributed among an even number of bonds along the chain. This is required by the 3c–4e bonding per se in I⁻₃ or stems from a partial donation of some LEPs into EDMBs in bent polyiodides, ultimately leading to 2n electrons distributed in n bonds. Chains of odd electron counts, I⁻_2n polyiodides, do not have access to such a stabilization process and are not encountered in nature.

The arguments provided in the previous paragraphs can be easily extended to the I²⁻_n and I³⁻_n series, so that bonding electrons must always be an even number. For the I²⁻_n series, even-numbered polyiodides (I_2n+2²⁻) are stable according to the above even/odd number of bonding electrons in the chain, whereas for the I³⁻_n series, the odd-numbered polyiodides (I_2n+3³⁻) are favored. Notably, the simplest experimentally encountered polyiodides of 2− and 3− charge are I²⁻₄, I²⁻₈ (even number of I atoms, even number of chain electrons), and I³⁻₇ (odd number of I atoms, even number of chain electrons).³

The above even/odd arguments regarding the existence or non-existence of molecules of the I²⁻_n and I³⁻_n series, are also supported by the energetic arguments that we have already discussed for the I⁻_n series. Even-numbered I_n chains have n/2 bonding and n/2 antibonding MOs, while odd-numbered chains have (n − 1)/2 bonding, 1 non-bonding, and (n − 1)/2 antibonding MOs.⁴⁵ Thus, I_2n+2²⁻ and I_2n+3³⁻ series do begin to populate antibonding orbitals, reducing their intrinsic stability. In particular, anions of the I_2n+2²⁻ series fill 2n/2 bonding orbitals and 1 antibonding orbital, while anions of the I_2n+3³⁻ series fill 2n − 1 bonding orbitals, 1 non-bonding orbital, and 1 antibonding orbital. In other words, any polyiodide of superior charge would need to put extra electrons in antibonding levels. The energetic instability caused by the population of antibonding orbitals allows an explanation as to why no polyiodides with higher charge are generally experimentally encountered.³

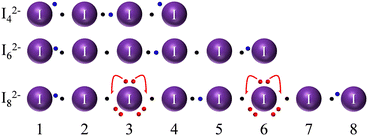
We have to notice that even the simplest of the I_2n+2²⁻ and I_2n+3³⁻ anions (I²⁻₄) was predicted to be unstable.⁴⁵ Still, its instability with respect to the formal I₂ and I⁻ components is not marked: even scholars who predicted the anion to be unstable stated that it could be possible for crystal packing and further supramolecular interactions to stabilize the anion.⁴⁵ In fact, higher level calculations, a quarter of a century later, have validated I²⁻₄ as a stable adduct.⁴⁷ Interestingly, I²⁻₄, I²⁻₈ and even I³⁻₇ have been experimentally observed in the solid state, often in situations in which ligand/anion shape/size stereo-electronic complementarity was deliberately sought (supramolecular caging of polyiodides type studies, cf. dedicated section in ref. 4). A discussion of our suggested Lewis dot graphs for some of these poly-charged anions (Fig. 6) is instructive and is briefly presented later.

Fig. 6 Revised Lewis dot formulas for polyiodides of the I_2n+2²⁻ series.

When drawing linear I²⁻₄, it is instructive to stop at the I₄ neutral chain, in consideration of the fact that extra electrons occupy an antibonding orbital. Note that a full EDMB is only possible in extended systems or, equivalently, that bond alternation is more significant in shorter chains. This results in the obvious instability of a neutral I₄ chain towards 2 fundamentally not bonded I₂ molecules (cf.Fig. 1). The addition of two further electrons to the I₄ system (in order to produce the I²⁻₄ dianion) allows for stabilization of the system at the price of increased electrostatic repulsion. I²⁻₄ dianion is generally depicted as 2 external I⁻ ions weakly interacting with a central I₂ molecule. Beyond electrostatics, the reason for bond alternation can be found in concerns about the octet rule for atoms 2 and 3: maintaining 2c–2e bonds on both sides would mean having more than 8 electrons in the valence sphere. In that sense, a careful reader could object that atoms 2 and 3 of the I²⁻₄ anion must exceed the 8-electron count (more than atom 2 of the I⁻₃ case); a clever answer would be that exceeding the octet rule comes at the price of stability and that those same extra electrons, as far as MO is concerned, start filling antibonding orbitals, as preventively stated earlier. This further argument supports the view of chains of p bonding orbitals, rather than d orbitals involvement. Despite the above facts pointing to the limited stability of this anion, the linear I²⁻₄ anion has enough stability to be sometimes isolated in the solid phase thanks to packing forces.

Experimental bond lengths for the I²⁻₄ anion are easily understood and justified within this context (3.3(1) Å – bonds 1–2 and 3–4, and 2.811(5) Å – bond 2–3 – CSD data on 30 deposited crystal structures cf. ESI†).⁴⁶ These experimental results sustain the idea of a residual covalency even for the long bond that separates formal I⁻ and formal I₂ fragments, advocating for a [I·I₂·I]²⁻ picture rather than from a mere electrostatic explanation of the bond lengths. Note that the external 1–2 and 3–4 bonds with 3.3 Å are in the region of 2c–1e bonds, as suggested by Fig. 8 to be later discussed. This is not surprising since the linear I²⁻₄ anion is not found isolated in nature but in the solid phase linked to other ligands. These ligands can receive charge from the linear I²⁻₄ anion thus reducing the charge of the external bonds of the I²⁻₄ anion, as has been already found in “end-on” bonded linear I⁻₃ anions to different ligands.³³

As a further argument, it is tempting to consider I²⁻₄ also as a resonance hybrid between [I⁻₃·I⁻] and [I⁻·I⁻₃] situations (in agreement with the fact that ERMB cannot extend beyond 3 centers). In such a resonance hybrid, the 2–3 bond remains short in both limit formulas, and the 1–2 and 3–4 bonds must be longer, as experimentally observed.

For the neutral I₆ chain, the argument of instability towards 3 I₂ molecules also applies, as for the neutral I₄ chain. The I²⁻₆ dianion (Fig. 6 center) is instead a special case and, despite correct (even) chain electron count, it is the most experimentally elusive anion of the I²⁻_2n series.⁴⁸ Although it might seem that the anion can form a chain with 2n electrons distributed in n bonds, as our model easily shows, the cause of instability is to be found in the impossibility of the ERMB to extend beyond 3 centers, making I²⁻₆ unstable towards 2 I⁻₃ anions (understood as a formal displacement of the central black/blue electron pair in Fig. 6 to reinforce bonds 2–3 and 4–5, leading to two independent I⁻₃ units with their corresponding 3c–4e bonds).

The case of the I²⁻₈ chain (bottom of Fig. 6) is again effective in illustrating the bending stabilization mechanism (around atoms 3 and 6) and the limited ability of atoms contributing with electrons of their LEPs to provide bonding electrons for chain stabilization (avoiding a severe violation of the octet rule by neighbour atoms). Again, our simple sketch allows us to forecast and rationalize the existence of this species as a weak [I₃·I₂·I₃]²⁻ formal complex and to adequately predict the experimentally encountered bond alternation (2.8(2), 3.0(1), 3.4(1) Å for formal I₂, I⁻₃ and I₂⋯I₃ bonds).²⁶ Long bonds are, again, those whose shortening will lead to a significant violation of the octet rule.

The case of the linear I³⁻₇ chain (Fig. 7) is similar to that of the I²⁻₈ chain, with the chain needing to bend around its central atom to achieve 2n electrons for n bonds. Its detailed discussion would not add much to the above-exposed arguments. The impossibility of forming ERMBs of more than 3 centers results in the formation of a weak [I·I₂·I·I₂·I]³⁻ formal complex as shown in the bottom of Fig. 7.

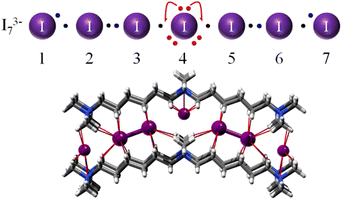Fig. 7 I³⁻₇ Lewis dot graph and the (symmetrical) anion found in the PEKKEX crystal structure.⁴⁹ I–I interatomic distances are 3.388 (1–2 and 6–7), 2.813 (2–3 and 5–6) and 3.427 Å (3–4 and 4–5). Adapted from ref. 4 with permission from RSC, copyright 2021.

Adding more electrons to a polyiodide (i.e. further increasing its charge via a reduction process) will result in filling more antibonding orbitals (reducing overall bond order), and thus reducing the stability of the resulting species. Still, it is instructive to notice here that, among the cases critically evaluated by Svensson and Kloo in their 2003 review,³ a potential I⁴⁻₁₆ survives, featuring two formal I²⁻₈ units connected by a long bond (3.45 Å).⁵⁰ Therefore, the possibility of encountering superior polyiodides with higher charge cannot be entirely ruled out since, when the number of atoms in the chain increases, also the number of bonding levels increases. In other words, much like in an infinite chain (finite charge is irrelevant),²³ very large chains (n = 16 in this case) could be able to stabilize higher charges. Although not likely to be frequent, we cannot rule out that further high-charge linear chain polyiodides could be observed (in which case, our arguments allow us to predict their geometries).

In conclusion, we have shown how the introduction of EDMBs in electron-rich atoms and the impossibility of having ERMBs longer than 3 centers (otherwise a violation of the octet rule would occur), together with well-known and fully established broad chemical concepts, such as those of the VSEPR theory, provides a comprehensive picture of linear chain polyiodides, which, in our opinion, never appeared so clear and accessible in the past. The huge number of literature studies discussing bonding features and/or presenting high-end calculations even for simple polyiodides supports our claims of increased clarity.

Within an octet-rule framework, this new view can predict: (i) stable and unstable linear polyiodides; (ii) where and why they are bent; (iii) bond alternation; (iv) correct qualitative charge distribution, and (v) finer modulation of bond lengths. These appear as significant advantages over the standard Lewis dot formulas. All of the above with the simplicity and elegance of a pen-and-paper electron disposition exercise in which a revised version of Lewis dot formulas is formulated.

A few consequences

Encouraged revision of polyiodide formal building blocks

In light of the above arguments, we would also like to suggest a revision of commonly accepted formal building blocks for polyiodides, traditionally I₂, I⁻₃ and I⁻ fragments.³ In a sense, the inclusion of I⁻ has always been somewhat problematic. I⁻ is a fragment which, if strongly representative, would imply that the I^x−_n chain, i.e. the molecule/anion is broken somewhere or almost so, in such a way that it would not be a molecule. We advocate here for the following alternative: polyiodides are made of I₂, I⁻₃ and I·I fragments, as discussed earlier, i.e. they are made of covalent- (2c–2e), electron-rich multicenter- (3c–4e), and electron-deficient multicenter-like bonds (2c–1e). There are no changes in terms of expected spectral features; typical Raman bands are as follows: 2c–2e bond of I₂, 170–180 cm⁻¹; 3c–4e bond of I⁻₃, 110 cm⁻¹; bands in the region of 140–180 cm⁻¹ are diagnostic of superior polyiodides (presenting 2c–1e bonds), and correspond to weakened covalent bonds.¹⁶ I⁻₅ is likely the better characterized superior polyiodide: in its linear form, it is characterized by a 150 cm⁻¹ Raman band,⁵¹ while in solution (DMSO), it is possible to follow its transition from V-shaped (170 cm⁻¹) to its L-shaped forms (165 cm⁻¹) upon interaction with a ligand.⁵² Still, this very simple change of view suggests the inclusion of long I·I 2c–1e EDMBs within a picture of normality for these systems and provides a theoretical framework (easily accessible via pen-and-paper means) to rationalize them. This is important as it reduces the sense that polyiodides are formed by simple building blocks “glued” together by mysterious forces, and rather passes the idea that we have a good general model for them. In other words, the model herein presented is in good – arguably better – keeping with experimentally observed spectral features. Bond length variability seems to mostly arise from the compromise that needs to be made in maintaining a formal count of 2n electrons for n bonds, like in any typically covalent setting, without exceeding the octet rule significantly for any atom.

An implicit message is that polyiodides, and in reality all molecules, are concerned with their total energy, rather than (see later) with mere intrinsic hierarchy, or energy, of individual bonds. An all 2c–2e bond chain, although individual bonds are more stable than alternatives, would lead to severe and expensive (energy-wise) octet rule violations:²³ such appears the driving force for the coexistence of covalent bonds, ERMBs, and EDMBs in these systems, which leads to observed bond length alternation. The impossibility of extending 3c–4e ERMBs over more than 3 centers creates, under a valence bond (VB) setting, preferred resonant formulas, also contributing to bond length alternation. The view of chains of covalent bonds, ERMBs, and EDMBs also resolves some issues connected with the interpretation of the Raman spectra of polyiodides, which were reduced to I₂ and I⁻₃ fragments eventually perturbed (note that long I·I 2c–1e bonds will lead to vibrational modes below 100 cm⁻¹ as corresponds to longer bonds and with less electronic charge than 3c–4e bonds).¹⁶ The nature of the invoked perturbation appears now much clearer and changes in bond force constants for the three possible bond types are both expected and rationalized.

Hypervalent or hypercoordinated?

The above reasoning is also in line with avoiding the violation of the octet rule, or almost so, for polyiodides; thus, it is against the picture of triiodide featuring 10 electrons at its central atom, and in agreement with the criticism of a classical hybridization model assuming the important role of d orbitals in 3c–4e systems. Such an argument has been reviewed elsewhere,¹⁹ finding one of its first critics in Pauling,⁵³ and the development of this very theme led to fundamental contributions by Pimentel,⁵ Rundle,⁵⁴ Hoffmann,^55,56 among others, to establish the 3c–4e ERMB model. The point was further explored, and quantitative data finally provided to show that d orbital involvement gives a minor contribution to total binding energies, as revisited in the charge-shift bond-related literature.^40,41

At this point, besides what is conveniently taught in general chemistry courses, it is about time we start recognizing I⁻₃ and polyiodides in general as hypercoordinated species rather than hypervalent ones. We had commented on this point previously.^18,20,23

Covalent or supramolecular?

We previously commented how, instead of showing different intra- and inter-molecular distances,⁵⁷ the different I–I distances in polyiodides show a relatively smooth transition from covalency towards what has been dubbed secondary or halogen bonds.²⁶ The “no man's land” in between covalent and supramolecular forces,⁴ generating a peak of confusion in the assignment of experimental data centered around 3.3–3.4 Å, can now be properly explained.

If we adopt Pauling's formula for calculating bond order from bond length data (d = d₀ – c log(n)),⁵³ we can clearly show how the longest bonds in each polyiodide show a smooth transition to lower and lower bond orders (Fig. 8 top). Such a transition mirrors the tailing of I–I “covalent” experimental distances towards the “supramolecular” distance range (Fig. 8 bottom).

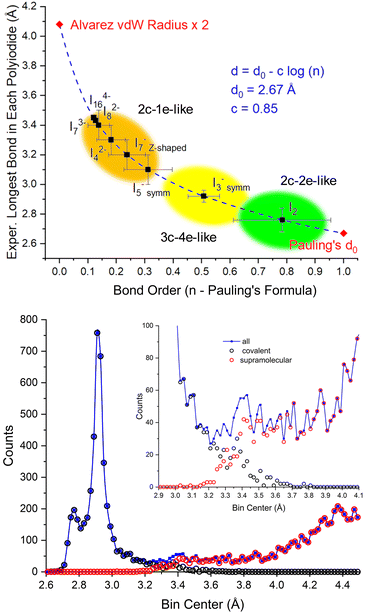Fig. 8 Top: Experimental longest bond distance in each polyiodide vs. bond order according to Pauling's formula (Pauling's d₀ = 2.67 Å (ref. 53) and two times Alvarez's vdW radii = 2.04 Å (ref. 57) are reported as limits). Bottom: Experimental distribution of I–I distances and their respective assignments as inter- or intra-molecular interactions in the CSD database. Partially reproduced from ref. 26, with permission from RSC, copyright 2022. Covalency fades into supramolecular interactions as per an S_N2-type coordinate.

Intriguingly, I²⁻₈ and higher charge polyiodides (I³⁻₇ and I⁴⁻₁₆ bond length variability not reported since the number of observations is insufficient) start accumulating in a similar spot with a bond order of about 0.1. In any case, this is a qualitative bond order view of the Lewis dot formula considerations made earlier. In other words, polyiodides showing bonds in the 3.3–3.4 Å range show Pauling bond orders > 0.2. As a reference, 3.40 Å is also the 2c–1e bond distance calculated for the longest bond of the linear I⁻₅ chain.²³ Thus, the view of polyiodides as a mixture of (modulated) 2c–2e-like, 3c–4e-like and the now included 2c–1e-like multicenter bonds, it conceptually resolves the “no man's land”⁴ regions of bond lengths that are experimentally observed between intra- and inter-molecular bonds. This proposed scheme also suggests the revision of the 3.30 Å sharp cutoff distance for covalency,¹⁷ as we previously advocated based on interatomic distances,²⁶ and has been also recently questioned in periodates.²⁷

In conclusion, calculations using Pauling's formula clearly suggest that the bond length increases as we go from the 2c–2e bond to the 3c–4e bond and further to the 2c–1e type of bond; i.e. as the number of electrons shared (ES) between two atoms decreases. This result is in agreement with the decrease of the calculated ES values between two atoms (obtained from the quantum theory of atoms in molecules)⁵⁸ when we go from the covalent bond (ES ≈ 2) to the ERMB (2 > ES > 1.4) and further to the EDMB (ES < 1.4).^20,22,23

This sort of continuum between different kinds of bonds (electron distribution description) matches what is seen under the lens of the recently introduced penetration index (interatomic distance description),⁴² which allows the differentiation between different kinds of interaction/bonds between any two atoms depending on the different interpenetration of their valence and so-called van der Waals spheres. Mentioning such a holistic descriptor conveniently introduces the theme of the next section.

Neither secondary, nor halogen bonds, nor necessarily holes: onto the need for a new model for supramolecular interactions

Some of us tried to humbly tackle the raising nomenclature issue in the near past, when the concern was still mostly circumscribed to the halogen bond and there was still room for manoeuvre.⁴ The old school secondary bond model seemed to hold better than the more modern halogen bond model. Naming efforts continued at the community level regardless.⁵⁹ A more pressing critique, not just to the halogen bond concept, but to the whole group-by-group nomenclature, was recently presented, raising several conceptual and historical arguments against it.¹⁸ Intervention by IUPAC was suggested.

It is impossible to accommodate here the whole reasoning. The bare-bones underlying misconception in halogen (and related) bonds lies in the oversimplistic nucleophile–electrophile reading of the σ-hole bond model for intermediate interactions between covalent bonds and mere van der Waals contacts.⁶⁰ This oversimplification: (i) prevents the appreciation of a subtending reaction coordinate (generally an S_N2 one);^18,43,61,62 (ii) does not allow for the categorization of interactions featuring fractional bond orders; (iii) creates counterintuitive interactions; and (iv) ultimately aspires to reduce the whole matter to static σ-holes. Moreover, a lack of attention to part of the last century's discussion on the matter, notably ideas related to secondary bonds, and the unclear relationship with Lewis acid and base alternative nomenclature, was highlighted.¹⁸ Fragmentation of interactions steered by the same basic mechanism into countless names is also potentially detrimental to effective communication.^18,63

As the present contribution was being prepared, a recent perspective paper by Taylor, criticizing the group-by-group nomenclature of supramolecular interactions, also appeared.⁸ In line with us, Taylor strongly opposes, on both similar and diverse conceptual grounds, both proliferation and usage of the group-by-group nomenclature of supramolecular interactions, further demonstrating the urgency of addressing this issue by IUPAC. As a relevant point for debate, which he also wisely left up for discussion in the community, Taylor propends for σ-, π- (eventually p-) hole interactions naming. This “hole” nomenclature is not chosen here for three main reasons: (1) it arguably carries strong descriptive power in terms of interaction geometries, but not necessarily in terms of electronic distribution, which is the key point of the present discussion; (2) the case of multicenter bonds was addressed by Taylor suggesting “peri-covalent” or “peri-hypervalent” names, stating that further naming attention to this specific “subtype” of interactions might indeed be needed (and we do agree); (3) among “bonded” (whatever we mean by the term) iodine atoms of an arbitrarily large chain, there are no holes in-between atoms. Notice that it is undeniable that hole interactions and multicenter bonds are conceptually linked.^{8,18–20,22,23} We hope that the relevant arguments exposed herein, which favour a (possibly equivalent) covalent, ERMB and EDMB description, i.e. – regardless of names – a description that directly conveys electronic distribution rather than interaction geometry, will also be taken into due account as the community tries to agree on a satisfactory naming scheme.

Interestingly, very recent publications related to the present study, also envisaging the possibility of 2c–1e bonds in polyiodides, decided to adopt a general picture of σ-hole/secondary bonding (rather than halogen bonding).^20,22,24,27 We did the same stating we would shortly return on the matter.²³ In particular, we notice here two main facts. First, the failure of all attempts to reduce polyiodide complexity to mere electrostatics was demonstrated in seminal studies of the 1960s.^64,65 It does not really matter if we call them in the old-fashioned way of “nucleophilic bumps and electrophilic hollows” or in the new-wave “σ-lumps and σ-holes”: the “static” σ-hole picture will hardly work for these soft systems since electron reorganisation is inherent to the formation of multicenter bonds, either EDMBs or ERMBs, whose formation mechanism comprises up to three stages.^20,22,66

Second, the choice of secondary bonding terminology, rather than halogen bonding, is interesting, as one can see how the nomenclature issue has become pressing for such systems and needs immediate attention. While we do agree that secondary bonding carries a superior generality (in terms of applicability to the periodic table) in comparison to the halogen bond, we still feel that secondary bond terminology is ultimately out of place here.

Notice that there are both theoretical and practical arguments against ascribing long bonds in polyiodides to the category/model of secondary bonds. On the theoretical side, “secondary Lewis acid–base interactions”⁹ were traditionally intended to be a sort of second-sphere or close-shell interactions. After all primary (i.e. valency) needs have been satisfied, molecules/ions retain some sort of interaction hotspots, although much weaker than those belonging to the valence shell,^9,10 and that can be considered to be located at the van der Waals crusts.⁴² The situation of polyiodides is at odds with this original view, as the long bonds in polyiodides, especially if admitting the participation of 2c–1e EDMBs, still are contributed by the primary/valence sphere; i.e. it could be catalogued as share–shell interactions as well as in ERMBs.⁶⁶ Therefore, the categorization of multicenter bonds and even asymmetric multicenter bonds as secondary bonds does not really apply, as it was already pointed out by Espinosa et al. when discussing stage II in the formation of ERMBs, such as those in FHF⁻ anion.⁶⁶

Even if Alcock's rules framework is used,¹⁰ it is expected that secondary bonds are formed collinearly and opposite to the central atom's substituent. This view would force one to imagine that, choosing any I atom along an arbitrarily large polyiodide chain, one side of the chain is a substituent and the opposite side is an incoming external interacting moiety. There is the same degree of arbitrariness in this procedure as there is in picturing which is the I₂ molecule and which is the I⁻ anion in a perfectly symmetrical I⁻₃ species, which overall is the same pitfall of the group-by-group nomenclature when it demands that a nucleophile and electrophile should be identified (it might not be apparent in the I⁻₃ example, but symmetry can be easily broken, also nomenclature-wise, e.g. by considering a Ch⋯I⋯I, Ch = chalcogen, as done in ref. 18). On the practical side, Alcock's rules,¹⁰ although fully functioning, had a clear pragmatic inspiration and lacked the conceptual and quantum mechanical depth that we can finally give to these concepts nowadays, as correctly stated in ref. 24.

As a result, long I–I bonds in polyiodides cannot be reduced to secondary bonds as they involve valence electrons, thus being in truth, despite reduced bond order, primary bonds for what the secondary bond model is concerned. This empirical model, established well before Nobel recognition of supramolecular chemistry itself,⁶⁷ served us well in the last 50 years, but it should not surprise that is now in need of revision.

According to the above arguments, we are left now with two unsatisfactory models. On the one hand, the halogen bond recommendation,⁶⁰ that does not cover situations like those encountered in polyiodides and that has possibly overlooked older studies and alternative concepts,¹⁸ and on the other hand, the secondary bond concept, dominated by an old, if not outdated, empirical framework.

Given the contingency (see above), and the fact that the present contribution and a number of recent studies open interesting perspectives on the relevance of 2c–1e bonds in electron-rich systems,^{20,22–25,27} we are, once again,^4,18 advocating for a global overhaul of present views on related supramolecular interactions. Furthermore, there is an emerging feature due to the consideration of the EDMB model,^20,22,23 the recent criticism of group-by-group naming,^8,18 the reaction coordinate reasoning, and the revised Lewis dot formulas presented earlier.

As shown in ref. 18 (and references therein), the halogen bond lies on an S_N2/Walden's inversion coordinate, which has, as its middle point, a 3c–4e system centered on the halogen itself. In other words, using resonant formulas, the general halogen bond between an X–R molecule and a Y moiety can be pictured as: [Y: X–R ↔ Y⋯X⋯R ↔ Y–X :R], where : denotes a LEP, – denotes the covalent bond, and ⋯ denotes the 3c–4e bond. Stated in words, the halogen bond can be thought of as arising from resonance between the LEP of the Y moiety and a covalently bonded fragment (X–R). Note that the formal equivalence of a 3c–4e bonding view and a n → σ* charge transfer was noted by Chen and Hoffmann.⁵⁶ This resonance is well explained by a model that combines the possible VB configurations and takes into account the charge-shift bond.^40,41 As shown in the opening, 2c–1e EDMB arises instead from the resonance between a bonded and a non-bonded situation, like the one encountered in an infinite linear I_∞ chain (Fig. 1). Therefore, it can be concluded that 3c–4e multicenter bonds are fundamentally different from 2c–1e multicenter bonds (although they share partial bond order and strong directionality). In particular, we have shown that the halogen bond formally belongs to the first category (3c–4e) and demonstrated that long bonds in polyiodides formally belong to the second one (2c–1e). Consequently, the two bonding situations are not at all equal. Fig. 8 top provides a further visual aid to see the differences between ERMBs and EDMBs. So that, as we already stated on different grounds,^4,18 the very concept of halogen bond ironically does not apply to long bonds in polyhalides, prime systems for its conceptual and historical development. This further element, again, calls for revision of our way of depicting relevant supramolecular interactions.

In summary, considering the criticism of the halogen bond/σ-hole picture on the one side, the slow obsolescence of secondary bond notions on the other side, and the newfound understanding of the topic, it seems that the time is about ripe for piecing back together the whole supramolecular puzzle by coherently reworking all these notions into a single comprehensive view.

Extension of the Lewis electron-counting model

The pen-and-paper method we propose in this work is not limited to anions nor to iodine-based species. As a demonstration, we will consider here the case in point of the polyiodonium I₅⁺ cation, which results from eliminating two electrons from the I⁻₅ molecule (blue extra ones in Fig. 2). This leads to the scheme depicted in Fig. 9, in which a chain containing four 2c–1e bonds is obtained. Much like the impossibility of having ERMBs in molecules longer than 3 centers, this linear configuration of EDMBs is also not stable since the octet rule would be satisfied for the internal atoms (2, 3, and 4) but not for the external ones (there is a lack of one electron for each of the external atoms 1 and 5 of the chain). This chain could formally restore a 2-electron-per-bond situation by bending at atoms 2 and 4. In this way, atoms 1 and 5 can fully accept a further electron (achieving 8 electron count), while the central atom (atom 3) cannot: this explains bond length alternation (longer internal bonds than external bonds) in the I₅⁺ cation. Atomic experimental coordinates from the IZUXOS⁶⁸ crystal structure correspond exactly to our conclusions. The stability and geometries of polyiodionium cations could be thus estimated with this approach. As our Lewis dot model uses the infinite linear I_∞ chain (any finite charge is irrelevant), its conclusions, as demonstrated in the case of the I₅⁺ cation, remain valid whatever the charge.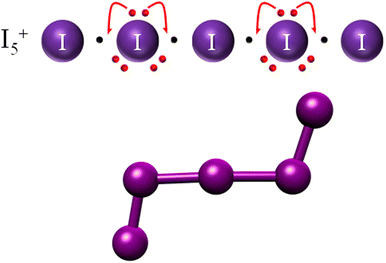

Fig. 9 Lewis dot model and expected bending in the I₅⁺ cation and a depiction of I₅⁺ experimental geometry as observed in the IZUXOS crystal structure.⁶⁸

Concerning the extension of our reasoning to non-iodine-containing systems, the easiest ones to examine are clearly other systems with 7-valence electrons, such as the rest of the halogens. Accordingly, we searched the CSD⁴⁶ for polyhalides, excluding iodine atoms. It turns out, of course, that general odd/even, charge/electron count, and bending sites, are all congruent with what we have previously proposed for polyiodides (Table 1).

Table 1 Overview of relevant non-iodine-containing unbranched polyhalides. Geometries, distance alternation (for the different atoms, in bold), and positioning of less electronegative atoms in heteropolyhalides are all congruent with the dot model presented above for polyiodides. Details about CSD datasets are reported in the ESI

	Hits	Counts	Angle^a (°)	Distances^a (Å)
a Numbers in bold refer to atomic positions indexes; figures in parenthesis indicate the standard deviation on measured quantities. b In the case of trihalides we report the difference (Δ) of the two bond lengths.
Trihalides
F–F–F^−	0
Cl–Cl–Cl^−	9	9	178.2 ± 0.7	Δ 0.2 ± 0.2^b
Br–Br–Br^−	274	345	178 ± 2	Δ 0.07 ± 0.09^b
Others	12	8 Cl–Br–Cl^−
		2 Cl–Br–Br^−
		1 F–Cl–F^−
		1 F–Br–F^−
Tetrahalides
Br4^2−	3	3	2 176(3)	1–2 3.00(5)
			3 176(3)	2–3 2.41(2)
				3–4 3.00(5)
Pentahalides
Br5^−	6	6	2 176(3)	1–2 2.389(7)
			3 97(9)	2–3 2.79(8)
			4 177(1)	3–4 2.70(5)
				4–5 2.41(2)
Cl-Br-Cl-Br-Cl^−	3	3	2 177.1(7)	1–2 2.24(4)
			3 104(11)	2–3 2.60(7)
			4 175.2(4)	3–4 2.60(3)
				4–5 2.25(2)
Hexalides
None
Heptahalides
None
Octahalides
Cl8^2−	1	1	Bent on atoms 3 and 6	Bond alternation as for I^2−8
Br8^2−	2	2	Bent on atoms 3 and 6	Bond alternation as for I^2−8

---

Another interesting fact is observed. We have already commented that atomic charges as seen from our dot model are not the same as those predicted by Lewis formulas using only electronic doublets (Fig. 3 and 4). We have also shown how our simple dot scheme better responds to calculated atomic charges/electron distribution. Experimentally, whenever we are in the presence of a heteropolyhalide, the positions we draw as surrounded by fewer electrons are those that are actually occupied by the least electronegative element (atom 2 for a trihalide, atoms 2 and 4 for a pentahalide, etc…). This is not a new observation. We mention here specifically a contribution by Linn and Hall in 1993.³² They predicted the same molecular geometries using other concepts like VSEPR, dative bonds, and σ-holes, i.e. with electrons still localized/belonging to certain specific atoms (see the above section): such a picture could not possibly account for 2c–1e bonds. Incidentally, the interesting mix of concepts calls again for the systematization of these interactions. For what concerns the notions of positioning of less electronegative atoms in heteropolyhalide chains, although Lin and Hall correctly demonstrated the point, they needed to calculate first the Bader's atomic charges⁶⁹ for each investigated system. Alternatively, our way of drawing the Lewis dot formulas in this work offers an immediate qualitative description of the localization of atomic charges, which allows for a correct interpretation with a pen-and-paper approach, making understanding the matter much easier.

Conclusions

As said in the Introduction, the nature of chemical bonding in polyiodides and related systems is currently a hot topic. In this work, we have played an apparently innocent electron disposition game for polyiodides in which the consideration of the VSEPR (geometry) and Lewis–Langmuir (octet) rules lead in a natural way to simple covalent (2c–2e) bonds, electron-rich multicenter (3c–4e) bonds, and electron-deficient multicenter (2c–1e) bonds. The consideration of these three types of bonds leads to a fresh outlook on polyiodides and some interesting considerations:

(1) Some aspects confirm previous views, namely hypervalency vs. hypercoordination issue, which is nevertheless still challenged due to the first-year undergraduate simplistic orbital hybridization view.

(2) Some concepts are restated and reappreciated under a new light, one which makes them more accessible: chain bond alternation and bending in polyhalides, and, in the case of heteropolyhalides systems, the positioning of less electronegative atoms.

(3) Some arguments challenge basic knowledge, inviting us to rethink the building blocks for polyiodides, revisit the “no-man's” land in-between covalent and non-covalent forces, and reestablish a coherent and comprehensive nomenclature for such interactions.

Finally – with full respect to the results of high-end calculations – when it comes to understanding a matter, there is arguably nothing better than being able to work it out by oneself in front of a plain piece of paper.

As a closing, anticipation, and a measure of the quality of the present discussion, we leave here a quote by Galileo Galilei: “True conclusions have thousands of favorable re-encounters that confirm them”.⁷⁰ This seems to be the case for the concept of electron-deficient multicenter bonds in electron-rich systems, here applied to the understanding of chemical bonding and geometries of polyiodides and previously used to understand the chemical bonding and geometries (hypercoordination) of phase change materials, pnictogens, chalcogens,^20,22,23 and periodates.²⁷

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication is financed by the Spanish Ministerio de Ciencia e Innovación and the Agencia Estatal de Investigación MCIN/AEI/10.13039/501100011033 as part of the project MALTA Consolider Team network (RED2022-134388-T), and I+D+i project PID2022-138076NB-C42 (co-financed by EU FEDER funds) and by project PROMETEO CIPROM/2021/075 (GREENMAT) financed by Generalitat Valenciana. This study also forms part of the Advanced Materials program supported by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1) and by Generalitat Valenciana through project MFA/2022/025 (ARCANGEL).

Notes and references

1. J. L. Gay-Lussac, Mémoire sur l’iode, 1815.
2. H. Davy, Philos. Trans. R. Soc. London, 1814, 104, 74–93.
3. P. H. Svensson and L. Kloo, Chem. Rev., 2003, 103, 1649–1684.
4. M. Savastano, Dalton Trans., 2021, 50, 1142–1165.
5. G. C. Pimentel, J. Chem. Phys., 1951, 19, 446–448.
6. J. C. Slater, Acta Crystallogr., 1959, 12, 197–200.
7. R. C. L. M. Slater, Acta Crystallogr., 1959, 12, 187–196.
8. R. Taylor, Cryst. Growth Des., 2024, 24, 4003–4012.
9. H. A. Bent, Chem. Rev., 1968, 68, 587–648.
10. N. W. Alcock, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1972, vol. 15, pp. 1–58.
11. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
12. P. Walden, Ber. Dtsch. Chem. Ges., 1896, 29, 133–138.
13. A. R. Olson, J. Chem. Phys., 1933, 1, 418–423.
14. R. S. Mulliken, J. Phys. Chem., 1952, 56, 801–822.
15. L. Kloo, J. Rosdahl and P. H. Svensson, Eur. J. Inorg. Chem., 2002, 1203–1209.
16. P. Deplano, J. R. Ferraro, M. L. Mercuri and E. F. Trogu, Coord. Chem. Rev., 1999, 188, 71–95.
17. P. Coppens, in Extended Linear Chain Compounds, ed. J. S. Miller, Springer US, Boston, MA, 1982, vol. 1, pp. 333–356.
18. M. Savastano, Dalton Trans., 2024, 53, 1373–1392.
19. R. H. Crabtree, Chem. Soc. Rev., 2017, 46, 1720–1729.
20. H. H. Osman, A. Otero-de-la-Roza, P. Rodríguez-Hernández, A. Muñoz and F. J. Manjón, Metavalent multicenter bonding in pnictogens and chalcogens: nature and mechanism of formation, ChemRxiv, 2023 DOI:10.26434/chemrxiv-2023-pv66p-v2.
21. J. C. Golden, V. Ho and V. Lubchenko, J. Chem. Phys., 2017, 146, 174502.
22. H. H. Osman, A. Otero-de-la-Roza, A. Munoz, P. Rodríguez-Hernandez and F. J. Manjón, J. Mater. Chem. C, 2024, 12, 10447–10474.
23. F. J. Manjón, H. H. Osman, M. Savastano and Á. Vegas, Materials, 2024, 17, 2840.
24. J. Hempelmann, P. C. Müller, L. Reitz and R. Dronskowski, Inorg. Chem., 2023, 62, 20162–20171.
25. Y. Yin, A. Aslandukova, N. Jena, F. Trybel, I. A. Abrikosov, B. Winkler, S. Khandarkhaeva, T. Fedotenko, E. Bykova, D. Laniel, M. Bykov, A. Aslandukov, F. I. Akbar, K. Glazyrin, G. Garbarino, C. Giacobbe, E. L. Bright, Z. Jia, L. Dubrovinsky and N. Dubrovinskaia, JACS Au, 2023, 3, 1634–1641.
26. M. Savastano, C. Bazzicalupi and A. Bianchi, Dalton Trans., 2022, 51, 10728–10739.
27. D. Errandonea, H. H. H. Osman, R. Turnbull, D. Diaz-Anichtchenko, A. Liang, J. Sanchez-Martin, C. Popescu, D. Jiang, H. Song, Y. Wang and F. J. Manjón, Mater. Today Adv., 2024, 22, 100495.
28. G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785.
29. R. J. Gillespie, Coord. Chem. Rev., 2008, 252, 1315–1327.
30. R. J. Hach and R. E. Rundle, J. Am. Chem. Soc., 1951, 73, 4321–4324.
31. W. N. Lipscomb, Science, 1977, 196, 1047–1055.
32. Z. Lin and M. B. Hall, Polyhedron, 1993, 12, 1499–1504.
33. A. Y. Rogachev and R. Hoffmann, Inorg. Chem., 2013, 52, 7161–7171.
34. Á. Martínez-Camarena, M. Savastano, S. Blasco, E. Delgado-Pinar, C. Giorgi, A. Bianchi, E. García-España and C. Bazzicalupi, Inorg. Chem., 2022, 61(1), 368–383.
35. M. L. Munzarová and R. Hoffmann, J. Am. Chem. Soc., 2002, 124, 4787–4795.
36. C. A. Coulson, J. Chem. Soc., 1964, 1442–1454.
37. P. C. Hiberty and S. Shaik, Theor. Chem. Acc., 2002, 108, 255–272.
38. S. Shaik, D. Danovich, B. Silvi, D. L. Lauvergnat and P. C. Hiberty, Chem. - Eur. J., 2005, 11, 6358–6371.
39. S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, Nat. Chem., 2009, 1, 443–449.
40. B. Braïda and P. C. Hiberty, Nat. Chem., 2013, 5, 417–422.
41. B. Braida, T. Ribeyre and P. C. Hiberty, Chem. - Eur. J., 2014, 20, 9643–9649.
42. J. Echeverría and S. Alvarez, Chem. Sci., 2023, 14, 11647–11688.
43. S. J. Grabowski, Phys. Chem. Chem. Phys., 2017, 19, 29742–29759.
44. H. A. Bent, Chem. Rev., 1961, 61, 275–311.
45. L. J. Sæthre, O. Gropen, J. Sletten, T. Pedersen, L. B. Zinner, F. Lehrich, C. J. Nielsen, D. L. Powell and M. Trætteberg, Acta Chem. Scand., 1988, 42a, 16–26.
46. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
47. G. Manca, A. Ienco and C. Mealli, Cryst. Growth Des., 2012, 12, 1762–1771.
48. M. Van Megen and G. J. Reiss, Inorganics, 2013, 1, 3–13.
49. J. Lin, J. Martí-Rujas, P. Metrangolo, T. Pilati, S. Radice, G. Resnati and G. Terraneo, Cryst. Growth Des., 2012, 12, 5757–5762.
50. F. H. Herbstein and M. Kapon, J. Chem. Soc., Chem. Commun., 1975, 677–678.
51. A. A. Tonkikh, D. V. Rybkovskiy and E. D. Obraztsova, J. Phys. Chem. C, 2023, 127, 3005–3012.
52. M. Savastano, C. Bazzicalupi, C. Gellini and A. Bianchi, Crystals, 2020, 10, 387.
53. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, 1960.
54. R. E. Rundle, J. Am. Chem. Soc., 1963, 85, 112–113.
55. R. Hoffmann, J. M. Howell and E. L. Muetterties, J. Am. Chem. Soc., 1972, 94, 3047–3058.
56. M. M. L. Chen and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 1647–1653.
57. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
58. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, New York, 1994.
59. Project Details: Categorizing Chalcogen, Pnictogen, and Tetrel Bonds, and Other Interactions Involving Groups 14–16 Elements, https://iupac.org/project/, (accessed July 1, 2023).
60. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
61. S. J. Grabowski, Molecules, 2021, 26, 4939.
62. S. J. Grabowski, Science, 2022, 4, 17.
63. S. J. Grabowski and W. A. Sokalski, Chem. Phys. Chem., 2017, 18, 1569–1577.
64. E. H. Wiebenga, E. E. Havinga and K. H. Boswijk, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeleus and A. G. Sharpe, Academic Press, 1961, vol. 3, pp. 133–169.
65. E. H. Wiebenga and D. Kracht, Inorg. Chem., 1969, 8, 738–746.
66. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
67. The Nobel Prize in Chemistry 1987, https://www.nobelprize.org/prizes/chemistry/1987/summary/, (accessed July 29, 2020).
68. P. Bertocco, C. Bolli, J. Derendorf, C. Jenne, A. Klein and K. Stirnat, Chem. - Eur. J., 2016, 22, 16032–16036.
69. R. F. W. Bader, P. J. MacDougall and C. D. H. Lau, J. Am. Chem. Soc., 1984, 106, 1594–1605.
70. G. Galilei, Dialogo Sopra i Due Massimi Sistemi del Mondo, 1632.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the CSD dataset for polyiodide bond length. See DOI: https://doi.org/10.1039/d4cc02832e

---