Open Access Article
Open Access ArticleSynthesis and characterization of tetrapodal nickel complexes with adaptable ligand binding geometries†
Hsien-Liang
Cho
a,
Kelly L.
Gullett
b and
Alison R.
Fout
 *a
*a
aDepartment of Chemistry, Texas A&M University, College Station, Texas 77843, USA. E-mail: fout@tamu.edu
bSchool of Chemical Sciences, University of Illinois at Urbana-Champaign, 600 S. Mathews Ave., Urbana, Illinois 61801, USA
First published on 4th September 2024
Abstract
This study explores the versatile binding properties of a tetrapodal ligand framework with nickel, demonstrating significant ligand fluxionality through the interconversions of several complexes. Kinetic studies using UV-vis and NMR techniques underscore the pivotal role of solvent coordination in initiating these dynamic processes. A unique reverse-dative Ni → Ag interaction provides another approach in modifying nickel's geometry.
Nickel is a biologically crucial transition metal in bacteria, playing an essential function in enzymatic anaerobic metabolism.1 Several nickel-dependent enzymes, including [NiFe]-carbon monoxide dehydrogenases (Ni-CODHs)2,3 and [NiFe]-hydrogenases ([NiFe]-H2ases),4 are integral for bacterial adaptation to anoxic environments. The adaptability of nickel as a catalytic centre enables the accommodation of diverse binding geometries for various metabolic processes. A notable example is nickel superoxide dismutase (Ni-SOD), which changes reversibly between square planar and square pyramidal geometry upon oxidation.5
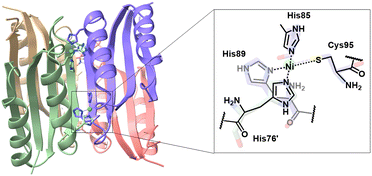
Without altering oxidation states, nickel also exhibits a unique coordination change between octahedral and square planar geometry in biological systems. In E. coli, the NikR homotetramer features a C-terminal metal-binding domain (MBD) and two N-terminal DNA-binding domains (DBD). NikR acts as a transcriptional factor, modulating high nickel concentrations to prevent toxicity.6,7 Its function is highly conformational-dependent. The high-affinity nickel site has a square-planar geometry, ligated by His-87, His-89, and Cys-95 residues from one monomer, and His-76 from another (Fig. 1).8 Upon interaction to the DNA operator, the nickel centre shifts to a six-coordinate geometry, suppressing transcription of the nik operon and inhibiting nickel transport.9–11 Recent studies have focused on protein-DNA interactions and conformational changes during DNA binding. The Ni(II)-bound protein was found to induce an α-helix disorder-to-order transition, allosterically activating DNA binding.12–14 The DBD then adopts a cis conformation stabilized by potassium, to recognize and bind the operon.10,12,15,16 NikR's response to various metals have been studied, showing that despite Cu(II) having similar binding geometry and higher affinity, NikR remains nickel-selective due to increased DNA binding affinity in the presence of excess nickel.17–19 Solomon and coworkers demonstrated that the electronic structures of metal–protein complexes influence the geometry of the metal site and thus protein conformation.20
While extensive research has focused on the NikR-DNA interaction and its regulatory mechanisms, the initiation of geometry and coordination changes at the nickel binding site remains elusive. Understanding how the initiation occurs might provide valuable insight to the relationship between conformation changes and ligand rearrangements in NikR or other nickel-containing enzymes. To model the dynamic nickel binding, we sought to harness a tetrapodal ligand21 that offers multiple coordination sites for potential 4, 5, and 6 coordination-modes to mimic the nickel binding behaviours observed in NikR processes. Herein, we characterized a series of tetrapodal nickel complexes and unravelled the binding transformation between square-planar to octahedral geometry upon protonation of the ligand arms. Additionally, we report a study of the initial rates of the geometry changes using time-resolved UV-vis spectroscopy to observe the disappearance of square-planar nickel species in various solvents and temperatures. By recognizing solvent coordination as the rate-limiting step, a better understanding of the reaction mechanism has been achieved.
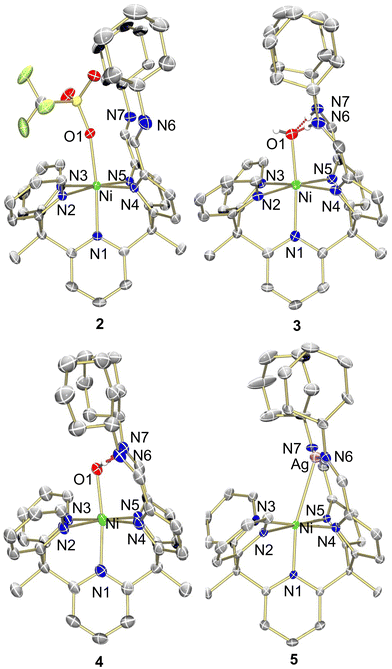 | ||
| Fig. 2 Molecular structure of 2–5 shown with 50% probability ellipsoids. For clarity, solvents, outer sphere anions, and selected hydrogens are omitted. | ||
In our study, we aimed to optimize the synthesis of nickel complexes featuring a tetrapodal ligand (Py2Py(piCy) = 2,2′,2′-methylbis-pyridyl-6-(2,2′,2′-methylbis-5-cyclohexyliminopyrr-ol)-pyridine). This method initially involved the deprotonation of the ligand platform followed by the addition of Ni(OTf)2. We hypothesized that upon deprotonation of the pyrroles, the stronger ligand-field afforded by the anionic nitrogens would enhance metalation efficiency due to the poor solubility of Ni(OTf)2. The reaction's progress was indicated by a color change from pink to orange, concomitant with the dissolution of Ni(OTf)2. The mixture was stirred overnight to ensure completion, and after appropriate workup the desired product, Py3(piCy)2Ni (compound 1), was isolated as an orange powder (Scheme 1).
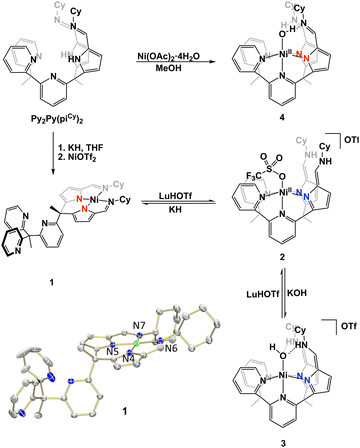 | ||
| Scheme 1 Complexation of Py2Py(piCy)2 and interconversion between nickel complexes to form complexes 1–4. | ||
Characterization of 1 was performed using 1H NMR spectroscopy. The singlet integrating to 2 at 6.94 ppm corresponded to the two imine protons within the secondary coordination sphere and was suggestive of a square pyramidal coordination geometry at nickel (Fig. S1, ESI†). The IR spectrum was inconsistent with this coordination geometry as the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching frequency for the pyrrole-imines was significantly shifted at 1573 cm−1 from typical C
N stretching frequency for the pyrrole-imines was significantly shifted at 1573 cm−1 from typical C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretches in this system.21–24 X-ray crystallography revealed that 1 adopted a square planar binding mode – binding solely through the pyrrole-imine arms and not engaging with any of the ligand pyridine moieties (Fig. 2, see Table S1, ESI† for structural parameters). The blue-shift in the IR spectrum could then be attributed to the unique binding mode of the ligand to form a square planar nickel complex.
N stretches in this system.21–24 X-ray crystallography revealed that 1 adopted a square planar binding mode – binding solely through the pyrrole-imine arms and not engaging with any of the ligand pyridine moieties (Fig. 2, see Table S1, ESI† for structural parameters). The blue-shift in the IR spectrum could then be attributed to the unique binding mode of the ligand to form a square planar nickel complex.
To obtain a nickel complex that was bound in the pocket to both pyridine and pyrrole fragments of the ligand we strategically protonated the imine nitrogen of the ligand in complex 1. By inducing ligand tautomerization from the pyrrole-imine (pi) to azafulvene-amine (afa) linkages we hypothesized that the weaker ligand field may facilitate coordination to both the pyridines and now azafulvene moieties of the ligand scaffold. The addition of lutidinium triflate to 1 in an acetonitrile and benzene mixture overnight resulted in a gradual colour change from orange to a slightly brown–yellow colour. Analysis of the new product, Py2Py(afaCy)NiOTf2 (2), via IR spectroscopy revealed the characteristic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretches at 1631 cm−1, consistent with the azafulvene-amine (afa) tautomeric form of the ligand. Additionally, features at 3209 and 3282 cm−1 were assigned to N–H stretches of the amines. 1H NMR spectroscopy also revealed a paramagnetic Ni species and the magnetic data was consistent with two unpaired electrons (Fig. S3, ESI†). Single crystals suitable for X-ray analysis confirmed the octahedral geometry of nickel with three pyridines, and two azafulvene arms and a triflate bound to nickel (Fig. 2). Both of the amine arms extended away from the nickel centre and one of them participated in hydrogen bonding interactions with an outersphere triflate anion. Selected bond angles and distances for 2 are summarized in Table S1 (ESI†).
N stretches at 1631 cm−1, consistent with the azafulvene-amine (afa) tautomeric form of the ligand. Additionally, features at 3209 and 3282 cm−1 were assigned to N–H stretches of the amines. 1H NMR spectroscopy also revealed a paramagnetic Ni species and the magnetic data was consistent with two unpaired electrons (Fig. S3, ESI†). Single crystals suitable for X-ray analysis confirmed the octahedral geometry of nickel with three pyridines, and two azafulvene arms and a triflate bound to nickel (Fig. 2). Both of the amine arms extended away from the nickel centre and one of them participated in hydrogen bonding interactions with an outersphere triflate anion. Selected bond angles and distances for 2 are summarized in Table S1 (ESI†).
To explore the reactivity of 2, the reaction with KOH was investigated, as an OH-bound nickel complex exhibiting hydrogen bonding between the axial oxygen and NH in the secondary coordination sphere was of interest. The addition of 1.5 equivalents of KOH to 2 in acetonitrile did not result in a colour change but improved solubility of the resultant solid in dichloromethane and acetonitrile. When compared to 2 this indicated a reaction and formation of a new product. The desired Ni–OH complex, [Py2Py(afaCy)2NiOH]OTf (3-OTf), was isolated and characterized via IR spectroscopy, which displayed a single C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch at 1663 cm−1, indicative of the afa tautomeric form of the ligand. Interestingly, the IR spectrum in the 3100–3500 cm−1 range appeared nearly featureless. No N–H or O–H stretches were observed and this lack of stretching frequencies likely arises from the confinement of vibrations due to the hydrogen bonding between the oxygen and nitrogen protons within the secondary coordination sphere. Despite numerous attempts complex 3-OTf could not be crystallized. Anion exchange of 3-OTf with NaPF6 afforded a new product, [Py2Py(afaCy)2NiOH]PF6 (3-PF6) as ascertained by a new resonance in the 19F NMR spectrum (Fig. S6, ESI†). Single crystals of 3-PF6 were grown via layer diffusion of hexane to dichloromethane. The resulting crystal structure confirmed the presence of a nickel(II)-hydroxide complex, characterized by a Ni–O bond length of 2.046(4) Å and hydrogen bonding network at the secondary coordination sphere with the bond lengths of 1.786(3) Å and 1.745(3) Å.
N stretch at 1663 cm−1, indicative of the afa tautomeric form of the ligand. Interestingly, the IR spectrum in the 3100–3500 cm−1 range appeared nearly featureless. No N–H or O–H stretches were observed and this lack of stretching frequencies likely arises from the confinement of vibrations due to the hydrogen bonding between the oxygen and nitrogen protons within the secondary coordination sphere. Despite numerous attempts complex 3-OTf could not be crystallized. Anion exchange of 3-OTf with NaPF6 afforded a new product, [Py2Py(afaCy)2NiOH]PF6 (3-PF6) as ascertained by a new resonance in the 19F NMR spectrum (Fig. S6, ESI†). Single crystals of 3-PF6 were grown via layer diffusion of hexane to dichloromethane. The resulting crystal structure confirmed the presence of a nickel(II)-hydroxide complex, characterized by a Ni–O bond length of 2.046(4) Å and hydrogen bonding network at the secondary coordination sphere with the bond lengths of 1.786(3) Å and 1.745(3) Å.
A variety of metalation strategies were sought with different nickel sources. The addition of 1 equiv. of Ni(OAc)2·4H2O to Py2Py(PiCy)2 in methanol at ambient conditions caused an immediate colour change from light yellow to brown. Given the colour change, we hypothesized that the Ni(II) hydroxide complex was formed. This was further corroborated by the paramagnetic features in the 1H NMR spectrum. However, upon crystallization via hexane layer diffusion into DCM, instead a new product was isolated, Py2Py(piCy)2NiOH2 (4). The crystal structure lacked the expected outer-sphere counteranion observed in complex 3 and the slightly elongated Ni–O bond distance was suggestive of a water-bound nickel complex. The presence of two anionic ligand arms for charge balance was further confirmed by IR spectroscopy, displaying a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch at 1618 cm−1 corresponding to pyrrole-imine (pi) tautomer. Additionally, the shorter pyrrole–nickel bonds was consistent with those observed in our previously published water-bound iron complexes.21 Formation of 4 likely arises from acetate acting as a weak base, deprotonating one of the NH residues and forming an unstable mixed-arm nickel hydroxide complex, Py2Py(afaCy)(piCy)NiOH. The proton transfer from the afa tautomer to the hydroxide ion stabilizes the relatively robust aqua complex 4, which readily crystallized (Fig. S12, ESI†).
N stretch at 1618 cm−1 corresponding to pyrrole-imine (pi) tautomer. Additionally, the shorter pyrrole–nickel bonds was consistent with those observed in our previously published water-bound iron complexes.21 Formation of 4 likely arises from acetate acting as a weak base, deprotonating one of the NH residues and forming an unstable mixed-arm nickel hydroxide complex, Py2Py(afaCy)(piCy)NiOH. The proton transfer from the afa tautomer to the hydroxide ion stabilizes the relatively robust aqua complex 4, which readily crystallized (Fig. S12, ESI†).
The use of external acid and/or base to readily convert between complexes 1, 2, and 3 was monitored by 1H NMR spectroscopy. Compound 3 could be readily converted back to 2 by the addition of lutidinium triflate, leading to the formation of a tentatively assigned nickel-aqua species, where the axial-bound water molecule could be removed by MgSO4. Additionally, we explored the synthesis of 1 by adding KH to 2. Upon deprotonation of the NH proton in the secondary coordination sphere, ligand tautomerization resulted in formation of the pi tautomer and altered ligation at nickel to subsequently form complex 1. Similar to the biological system, NikR undergoes geometry change without changing nickel oxidation state, complexes 1 and 2 readily change from square planar to octahedral at Ni(II), respectively. This ability to readily interconvert between 1 and 2 demonstrates that dynamic ligand binding can be finely tuned through the donor ability of the ligand framework. A stronger, anionic ligand field effectively splits the energy gap of the d-orbitals, favouring the square planar geometry whereas, a weaker, neutral ligand field promotes octahedral coordination.
To gain a better understanding of the ligand fluxionality, we sought to monitor the reaction through time-resolved UV-visible spectroscopy. By tracking the disappearance of a distinctive d–d transition only observable in the square-planar nickel complex 1 at 428 nm (see ESI†), the transformation rate was determined under pseudo-first-order conditions while using an excess of lutidinium triflate. To ensure complete dissolution of both nickel complexes and the excess acid, a mixed solvent of benzene and acetonitrile was applied, and the reaction was followed over the initial 2.5 hours at room temperature, with each UV-vis spectra recorded every 3–5 minutes. The rate constant (k) was calculated by plotting the natural logarithm of the absorbance ratio against time. Surprisingly, the resulting kinetics revealed a zero-order rate dependence on acid concentration (Fig. S18, ESI†). Even with significantly excess acid, the rate remained nearly constant, suggesting that the rate-determining step is independent of imine protonation at the ligand.
Given the lack of influence of acid on the rate, we sought to understand the effects of solvent on the transformation of 1 to 2. Interestingly, the rate of formation of 2 was significantly altered when different solvents were incorporated. Faster rates were observed in the presence of a more-coordinating solvent like acetonitrile; a less-coordinating solvent like tetrahydrofuran (THF) led to a one-order-of-magnitude slower rate. To further understand the role of acetonitrile, various compositions of benzene to acetonitrile solvent mixtures were explored (Fig. S30, ESI†). By graphing the initial rates against the ratio of acetonitrile, we found a first-order dependence on acetonitrile concentration, implying that an acetonitrile molecule is involved in the rate-determining step. By comparison, reactions rarely occur in a non-coordinating solvent such as dichloromethane (DCM). The activation parameters for the transition state were extracted using the Eyring and Arrhenius equations (ΔH‡ = 13.46 kcal mol−1, ΔS‡ = −21.24 J K−1 mol−1, and Ea = 13.96 kcal mol−1) (Fig. S24, ESI†). Due to the significant influence of solvent on the rate of the reaction, we proposed the rate-limiting step is acetonitrile coordination to nickel, which is consistent with the negative entropy observed.
To further interrogate the mechanism 1H NMR spectroscopy was used to see if ligand protonation/tautomerization could be observed in acetonitrile solutions. If protonation is prior to acetonitrile coordination, lutidinium triflate may either protonate one of the ligand arms or the tripyridine site, which should be seen in the 1H NMR spectrum. Nevertheless, the crude 1H NMR spectrum after the first 15 min of reaction of 1 with acid did not show a significant 1H NMR peak shift in the pyridine and imine regions, suggesting that the ground state in the overall transformation is 1 rather than protonated 1 (Fig. S31, ESI†). Therefore, we hypothesize that the reaction pathway, where acetonitrile first coordinates to the nickel centre, followed by the protonation and tautomerization of the ligand is more likely (Scheme S1, ESI†).
Given the fluxionality of the ligand we were curious if oxidation of complex 1 would result in an octahedral binding mode at nickel with the nickel being pushed into the pocket of the ligand scaffold. Oxidation of complex 1 with AgOTf resulted in an immediate colour change from orange to red but with no noticeable Ag0 being formed. The anticipated paramagnetic Ni(III) species was not observed by 1H NMR spectroscopy and instead, a new diamagnetic red species, [Py3(piCy)2Ni(Ag)]OTf, 5, was obtained. Surprisingly, structural analysis using X-ray crystallography unveiled an in-pocket nickel centre engaged in binding to the pyridine and pyrrole nitrogens while the imine nitrogens were bound to silver. An unexpected interaction between Ni and Ag completed the coordination sphere at nickel with a bond distance of 2.8665(7) Å. Not only is this uncommon Ni–Ag bond of interest, the resulting diamagnetic 1H NMR spectrum of an octahedral Ni(II) complex also remained a question. This observation therefore prompted us to investigate the unique orbital interaction between nickel and silver, which afforded an overall diamagnetic complex.
Figueroa and co-workers have shown that metal-only Lewis pairs (MOLPs) formed from zero-valent group 10 transition metals with Lewis acidic Tl(I) centres, contain a reverse-dative M → Tl interaction. Further they have isolated a Pd/Pt–Ag complex where the Ag behaved as a Lewis acid upon addition of AgOTf to the Pd or Pt bis-isocyanides complexes.25 In addition, Gabbaï and co-workers observed the binding enhancement of the ligand trans to the Z-type ligand which manifests in a shortening of the ipso atom metal bond length.26,27 This similar push–pull effect can be seen in the crystal structure of 5 where the apical pyridine nitrogen bond length was significantly shortened. A comparison of the Ni–N bond distances to previous synthesized octahedral nickel complexes revealed that the Ni–N1 bond distance in 5 of 2.041(3) Å was the shortest Ni–N bond, even shorter than that of the anionically pyrrole Ni–Npyr bonds of 2.049(3) and 2.060(3) Å in 5 (see Table S1, ESI†).
The shortened Npy–Ni bond may compensate for the electron deficient nickel as the nickel provides two electrons to the Lewis acidic Ag, which stabilizes the empty p-orbital of the silver atom (Fig. S32, ESI†). Because the bond distance suggests a nickel–silver interaction with silver pulling electron density away from the nickel, the nickel needs more electron density which can only be compensated by the axial pyridine in the ligand framework. The similar concept can be better explained by a push–pull interaction where the pyridine lone pair, the dz2 orbital of nickel, and the pz-orbital of silver are aligned and engage in the overall orbital interactions. This would result in a Ni–Ag interaction and a shortening of the Ni–Npy bond which was observed in the crystal structure of 5. It is these donor–acceptor interactions that allow for the isolation of a diamagnetic Ni(II) species which is consistent with the 1H NMR spectrum. Although oxidation at nickel did not occur upon reaction of 1 with AgOTf the resultant complex 5 demonstrates the adaptability of this ligand scaffold to both binding of nickel and other Lewis acids.
In summary, we have successfully demonstrated the versatile binding of the tetrapodal ligand framework with nickel. The ligand fluxionality was best demonstrated between the interconversions of complexes 1, 2, and 3. The UV-vis and NMR kinetic studies highlight the significance of solvents, where solvent coordination is proposed to initiate the dynamic processes. Together these results may provide some mechanistic insight into the dynamic behaviour of metalloenzymes where the binding of water could facilitate coordination mode changes. The addition of silver triflate to 1, showcased a reverse-dative Ni → Ag interaction, displaying an unusual way to change the geometry of nickel.
This work was supported by the U. S. Department of Energy, Office of Sciences, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and biosciences Division under award number DOE DE-SC0025026. K. L. G. is thankful for a Robert C. & Carolyn J. Springborn Fellowship. H. L. C. is thankful for a HEEP Fellowship from Texas A&M University.
Data availability
The dataset supporting this article have been uploaded as part of the ESI.†Conflicts of interest
There are no conflicts to declare.References
- M. Alfano and C. Cavazza, Protein Sci., 2020, 29, 1071–1089 CrossRef CAS PubMed.
- M. Can, et al., Chem. Rev., 2014, 114, 4149–4174 CrossRef CAS PubMed.
- Y. Kung and C. L. Drennan, Curr. Opin. Chem. Biol., 2011, 15, 276–283 CrossRef CAS PubMed.
- H. Ogata, et al., J. Biochem., 2016, 160, 251–258 CrossRef CAS PubMed.
- D. P. Barondeau, et al., Biochemistry, 2004, 43, 8038–8047 CrossRef CAS PubMed.
- K. D. Pina, et al., J. Bacteriol., 1999, 181, 670–674 CrossRef PubMed.
- L. Macomber and R. P. Hausinger, Metallomics, 2011, 3, 1153–1162 CrossRef CAS PubMed.
- E. R. Schreiter, et al., Nat. Struct. Mol. Biol., 2003, 10, 794–799 CrossRef CAS PubMed.
- P. E. Carrington, et al., Nat. Struct. Biol., 2003, 10, 126–130 CrossRef CAS PubMed.
- S. C. Wang, et al., J. Am. Chem. Soc., 2010, 132, 1506–1507 CrossRef CAS PubMed.
- C. M. Phillips, et al., Biochemistry, 2010, 49, 7830–7838 CrossRef CAS PubMed.
- E. R. Schreiter, et al., Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13676–13681 CrossRef CAS PubMed.
- K. A. Baksh and D. B. Zamble, J. Biol. Chem., 2020, 295, 1673–1684 CrossRef CAS PubMed.
- K. A. Baksh, et al., J. Biol. Chem., 2021, 296, 100069 CrossRef CAS PubMed.
- C. M. Phillips, et al., J. Am. Chem. Soc., 2009, 131, 10220–10228 CrossRef CAS PubMed.
- S. Krecisz, et al., Biochemistry, 2012, 51, 7873–7879 CrossRef CAS PubMed.
- C. M. Phillips, et al., Biochemistry, 2008, 47, 1938–1946 CrossRef CAS PubMed.
- S. L. Bloom and D. B. Zamble, Biochemistry, 2004, 43, 10029–10038 CrossRef CAS PubMed.
- S. C. Wang, et al., Biochemistry, 2004, 43, 10018–10028 CrossRef CAS PubMed.
- Y. Ha, et al., Biochemistry, 2019, 58, 3585–3591 CrossRef CAS PubMed.
- M. J. Drummond, et al., J. Am. Chem. Soc., 2019, 141, 6639–6650 CrossRef CAS PubMed.
- E. M. Matson, et al., Inorg. Chem., 2014, 53, 4450–4458 CrossRef CAS PubMed.
- E. M. Matson, et al., J. Am. Chem. Soc., 2014, 136, 17398–17401 CrossRef CAS PubMed.
- Z. Gordon, et al., Inorg. Chem., 2017, 56, 4852–4863 CrossRef CAS PubMed.
- B. R. Barnett and J. S. Figueroa, Chem. Commun., 2016, 52, 13829–13839 RSC.
- J. S. Jones and F. P. Gabbaï, Acc. Chem. Res., 2016, 49, 857–867 CrossRef CAS PubMed.
- D. You, et al., J. Am. Chem. Soc., 2018, 140, 9644–9651 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2366270–2366274. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc03186e |
| This journal is © The Royal Society of Chemistry 2024 |