Atomic-scale investigation on the electronic states in a one-dimensional π–d conjugated metal–organic framework

Abstract

Enhanced electronic coupling gives rise to many intriguing properties in π–d conjugated metal–organic frameworks (CMOFs). By low-temperature scanning tunneling microscopy and density functional theory calculation, we investigate the electronic coupling in one-dimensional (1D) π–d conjugated FeQDI polymers. Our experiments have resolved the bulk and end states stemming from Fe atoms in different coordination environments and their spatial extension due to π–d conjugation. By fitting the band structure by Wannier functions in an energy range of −0.5 eV to 0 eV, the Fe–Fe, QDI–QDI and Fe–QDI hopping integrals are determined to be 15 meV, 121 meV and 24 meV, respectively. Our work provides experimental and theoretical insights into the electronic coupling in 1D CMOFs.

---

Conjugated metal–organic frameworks (CMOFs) are a family of MOFs in which the transition metal atoms are chelated by conjugated organic ligands at bidentate groups, enabling fully π–d conjugation over the framework.^1–5 The enhanced electronic coupling between the π orbital of the organic ligand and the d orbital of the metal atom leads to many intriguing properties, such as high electrical conductivity,^6,7 superconductivity,^8,9 elevated electrocatalytic activity,^10,11 high capacity^12–14 and ferromagnetism,^15,16 and is the basis for the band formation in CMOF.^17,18 In this context, it is of practical significance to reveal the electronic coupling between organic ligands and transition metal atoms in CMOFs. On the other side, in conventional MOFs,¹⁹ the electronic and magnetic properties of coordinated metal atoms are mostly determined by their coordination environments.^20,21 However, in CMOFs, the impact of π–d conjugation on the local electronic state of coordinated metal atoms is yet to be clarified.

The development in the on-surface synthesis of CMOFs under ultra-high vacuum conditions has inspired scanning tunneling microscopy (STM) studies on their electronic states, magnetic properties, and even topological states at the atomic scale.^4,22–31 In these studies, 2HQDI (2,5-diamino-1,4-benzoquinonediimine) molecules exhibit remarkable feasibility to form various 1D MQDI CMOFs with M = Cr, Fe, Co and Ni,³² and their magnetic anisotropy, conductance and band dispersion have been studied by STM and angle-resolved photoemission spectroscopy.^33–35 With reduced dimensionality,³⁶ the MQDI also provides us a practical system to study the electronic coupling between organic ligands and transition metal atoms.

Here by low-temperature STM, we perform atomic scale investigation on the electronic states of FeQDI polymers on Au(111) substrate. We have resolved a bulk state stemming from inner Fe atoms coordinated in four-fold bis(diimino)-Fe motifs, and an end state given by the end Fe atom in a two-fold diimino-Fe motif. Interestingly, the spatial extension of the end state suggests an impact length of 1 unit cell (∼7.7 Å), which exemplifies the influence of π–d conjugation on the local electronic states in CMOF. We reveal the electronic coupling in FeQDI by extracting the hopping integrals between different components in FeQDI from band structure calculation, in which the structural relaxation of FeQDI upon adsorption has been taken into consideration. The evolution of the bulk and end states near the end is further simulated by a tight-binding model.

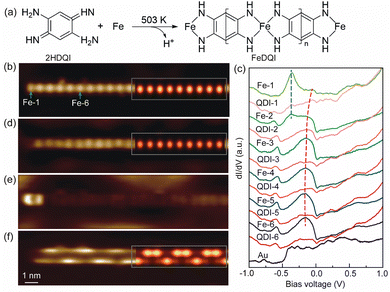
The 1D FeQDI polymers were synthesized on Au(111) substrate by sequentially depositing Fe atoms with the substrate held at room temperature and 2HQDI molecules with the substrate held at 503 K (see Methods in ESI†). As shown in Fig. 1(a), the 2HQDI molecules undergo dehydrogenation reaction upon deposition and form 1D CMOF with Fe atoms. The FeQDI polymers extend mainly along the 〈11̄0〉 directions of the Au(111) substrate, and the length of the polymers may exceed 100 nm (Fig. S1(a), ESI†). Fig. 1(b) shows the zoomed-in STM image of a FeQDI polymer, in which the bright and dim spots are Fe atoms and QDI molecules, respectively. The FeQDI polymer shows a period of d₀ = 0.77 ± 0.02 nm (Fig. S1(b) and (c), ESI†), in agreement with the previous report.³²

Fig. 1 (a) Schematic illustration of the on-surface synthesis of the FeQDI polymer from 2HQDI molecules and Fe atoms. (b) Zoomed-in STM image of an FeQDI polymer scanned at −0.60 V and 100 pA. (c) dI/dV–V spectra measured at the centers of Fe atoms and QDI molecules along the polymer in (a). The curves are vertically shifted for clarity. The end and bulk state are indicated by blue and red dashed lines, respectively. A spectrum measured on the Au(111) surface is also shown for reference. (d)–(f) dI/dV maps of the same area as (a) scanned at −0.18 V, −0.36 V and −0.60 V, respectively. The DFT simulated STM image and LDOS maps are superposed on (b), (d) and (f).

As illustrated in Fig. 1(a), in the interior of the FeQDI polymer each Fe atom is coordinated to two QDI molecules through a four-fold bis(diimino)-Fe motif, while at the end of the polymer the Fe atom is coordinated to only one QDI molecule through a two-fold diimino-Fe motif. To reveal the electronic states associated with Fe atoms in different coordination environments, we measured site-dependent differential conductance (dI/dV–V) spectra along the polymer in Fig. 1(b). The dI/dV–V spectra measured at the centers of different Fe and QDI molecules are compared in Fig. 1(c).

From Fe-6 to Fe-3 in Fig. 1(c) (Fe-n labels the nth Fe atom counted from the end to the interior of the polymer), the Fe atoms exhibit similar electronic states, a broad peak at −0.15 V and a weak state at −0.60 V. The inner QDI molecules QDI-6 to QDI-3 in Fig. 1(c) show a similar electronic state at −0.60 V, but weakened electronic state around −0.15 V. From Fe-3 to Fe-1, the intensity of the −0.15 V and −0.60 V states gradually decreases, and the −0.15 V state shifts to −0.05 V, which appears as a shoulder in the dI/dV−V spectra of Fe-1. As shown in the dI/dV map in Fig. 1(d), the −0.15 V state is distributed at the inner Fe atoms with similar intensity, but gets decreased at the end Fe atom. According to its spatial distribution, the −0.15 V state is assigned as a bulk state of FeQDI polymer, stemming from orbital hybridization in bis(diimino)-Fe coordination motifs.

In Fig. 1(c), the outermost two Fe atoms show an electronic state at −0.36 V, as marked by the blue dashed line. As shown in Fig. 1(e), this −0.36 V state shows maximal intensity at the end Fe, and extends further to the neighbouring Fe atom (Fe-2). We attribute the −0.36 V state to the orbital hybridization in the two-fold diimino-Fe motif. Since this state is observed at the end the of FeQDI polymer, it is denoted as the end state hereafter.

Notably, both the bulk and end states evolve near the end of the polymer: the bulk state extends to the end Fe atom with decreased intensity and shifts to a higher energy. The end state extends to the second Fe atom from the end. This is in sharp contrast to the non-conjugated MOF, where the local electronic state of coordinated metal atoms is determined by their coordination environment,²¹ and no spatial extension has been observed.

The spatial extension of the bulk and end states can be attributed to π–d conjugation in the framework: since the bulk/end state is given by the π–d hybridization in the bis(diimino)-Fe/diimino-Fe coordination motif, the hybridized electronic state gets delocalized due to the presence of delocalized π electrons in the polymer. In our experiment, the end state extends to the Fe-2 but gets neglectable on Fe-3, and the bulk state extends to the end Fe atom at a higher energy, suggesting an impact length of 1 unit cell (∼7.7 Å) of the π–d conjugation in FeQDI. Such evolution of the bulk and end states has been observed at both ends of the FeQDI polymer (Fig. S2, ESI†). As discussed later, this evolution is simulated using a tight-binding model by enhanced hopping integrals between the outermost three Fe atoms.

As shown in Fig. 1(c), there is a −0.60 V state in both Fe atoms and QDI molecules. This −0.60 V state is distributed at the two sides along the polymer, and shows intensity modulations at both sides (Fig. 1(f)). Note that the intensity modulation is asymmetric, that is, the intensity maximum at one side is opposite to the intensity minimum at the other side. A detailed inspection of the dI/dV map indicates that the intensity modulation has a period of ∼3d₀ (Fig. S3, ESI†).

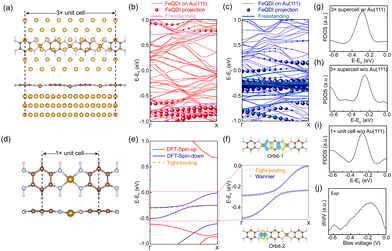
To reveal the adsorption geometry and electronic structures of the FeQDI polymer, we performed first-principles calculations (see Methods in ESI†). Fig. 2(a) shows the DFT optimized adsorption structure of the FeQDI polymer on the Au(111) substrate. The FeQDI polymer extends along the [11̄0] direction of the Au(111) substrate, and each 3 FeQDI unit fits 8 Au atoms in this direction, amounting to a 3× supercell of 3d₀ ≈ 8a₀ ≈ 2.31 nm (a₀ = 0.288 nm is the lattice constant of the Au(111) surface). As shown by the side view in the lower panel of Fig. 2(a), the QDI molecules take a planer adsorption geometry on the Au(111) substrate, and the Fe atoms have an adsorption height 0.02 Å lower than the QDI molecular plane. The Fe–N bond length is calculated to be 1.90 Å, which is in good agreement with previous reports²³. The charge transfer between FeQDI and the Au(111) substrate is calculated to be 0.74 e per 3× supercell (Fig. S4 in ESI†).

Fig. 2 (a) Top (upper panel) and side (lower panel) views of the DFT optimized adsorption structure of the FeQDI 3× supercell on the Au(111) substrate. In the top view only the first layer Au atoms are shown for clarify. (b) Spin-up and (c) spin-down bands of the FeQDI 3× supercell on the Au(111) substrate and their projections on the band structure of the freestanding FeQDI 3× supercell without a substrate. (d) Freestanding FeQDI 1× unit cell adapted from the adsorption geometry in (a) by considering the averaged Fe displacement from the molecular plane. (e) DFT calculated spin-polarized band structure (red and blue solid lines) and TB calculated band structure (orange dashed line) of the freestanding FeQDI 1× unit cell. (f) Wannier function fitting to the bands in (e) in an energy range of −0.5 eV to 0 eV. (g)–(i) PDOS of Fe in FeQDI calculated by different methods, from top to bottom: FeQDI 3× supercell with Au(111) substrate, FeQDI 3× supercell without Au(111) substrate, FeQDI 1× unit cell without Au(111) substrate. (j) A dI/dV–V spectrum measured at an inner Fe atom.

Fig. 2(b) and (c) show the spin-polarized bands of the FeQDI 3× supercell on the Au(111) substrate and their projections on the band structure of the freestanding FeQDI 3× supercell. The calculated projected density of states (PDOS) of the Fe atom (Fig. 2(g)) reproduces the experimentally measured −0.15 V state (Fig. 2(j)). Our DFT calculations indicate that the −0.15 V state is mainly contributed by the hybridization between Fe 3d_x²−y² and N 2p_z orbitals, and the −0.60 V state is given by the N 2p_z and C 2p_z orbitals of the QDI molecule (Fig. S5, ESI†).

The DFT simulated local density of states (LDOS) map at −0.18 V is superposed on Fig. 1(d), which reproduces the main features of the experimental images, and supports the assignment of bright dots as Fe atoms in Fig. 1(b).

The intensity modulation of the −0.60 V state can be well explained by the interfacial interaction between QDI molecules and the Au(111) substrate, in which the arrangements of gold atoms below the two sides of the QDI molecules are different (see the top panel of Fig. 2(a)). Consequently, the intensity modulation shows a period equal to the length of the supercell, 2.31 nm. The DFT simulated LDOS map at −0.60 V (Fig. 1(f)) captures the experimentally observed asymmetric modulation at the two sides, as well as the modulation period. In our experiment, the orientation of the FeQDI polymer may vary from the [11̄0] direction of the Au(111) substrate. In that situation, the modulation period varies from 2.31 nm or even gets diminished (Fig. S6, ESI†).

By fixing the FeQDI adsorption geometry and removing the Au(111) substrate, we obtained the freestanding FeQDI 3× supercell without Au(111) substrate. The band structure of FeQDI on Au(111) can be represented by the freestanding FeQDI 3× supercell that considers the Fe displacement from the QDI molecular plane (solid lines in Fig. 2(b) and (c)). To evaluate the electronic coupling between different components in FeQDI, we then extract the geometry of the FeQDI 1× unit cell from the 3× supercell by considering the averaged Fe displacement from the QDI molecular plane, as shown in Fig. 2(d). The spin-polarized band structure of the FeQDI 1× unit cell is plotted in Fig. 2(e). The two bands in the energy window from −0.5 eV to 0 eV, which contribute the electronic state at −0.15 V, are fitted by two Wannier orbitals using VASP and Wannier90³⁷ (Fig. 2(f)). The spatial distribution of the two Wannier orbitals is plotted in Fig. 2(f), with orbital-1 mainly contributed by the p_z orbital of the QDI molecule and orbital-2 by Fe 3d_x²−y² (Fig. S5, ESI†). By using the tight-binding Hamiltonian constructed with Wannier90, we can extract the hopping integrals between and within these two Wannier orbitals, i.e. the Fe–Fe, QDI–QDI and Fe–QDI hopping integrals, which are determined to be 15 meV, 121 meV and 24 meV, respectively. These values provide estimations of the hopping integrals between different components in the FeQDI polymer. Fig. 2(h) and (i) show the calculated PDOS of Fe from the FeQDI 3× supercell and from 1× unit cell, which reproduce the −0.15 V state measured by experiment (Fig. 2(j)).

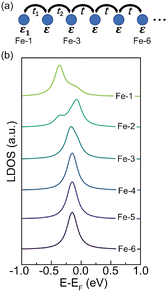
Since the bulk and end state are mainly distributed on Fe atoms, we employ a tight-binding (TB) model

H(k) = ε + 2t cos k

to simulate the evolution of the bulk and end state near the end of the FeQDI polymer, where t is the hopping integral between two nearest Fe atoms, and ε is the on-site energy of the Fe atom. As depicted in Fig. 3(a), the inner part of the semi-infinite chain t is fixed at 15 meV, which is adopted from the Wannier fitting, and ε is set to −0.15 eV, which is determined by the measured bulk state (Fig. 1(c)). Near the end, we set t₁ (t₂) as the hopping integral between Fe-1 and Fe-2 (Fe-2 and Fe-3) and ε₁ as the on-site energy on Fe-1. As plotted in Fig. 3(b), the shifting of the −0.15 V bulk state to a higher energy at the end, the emergence of the −0.36 V end state, and the double-peak feature at Fe-2 can be well reproduced with t₁ = 107 meV, t₂ = 53 meV and ε₁ = −0.31 eV.

Fig. 3 (a) Schematic representation of a semi-infinite tight binding model with varied hopping integrals (t₁, t₂) and on-site energy (ε₁) at the end. (b) From top to bottom, calculated LDOS of Fe-1 to Fe-6 atoms with t₁ = 107 meV, t₂ = 53 meV and ε₁ = −0.31 eV.

We have tested different combinations of t₁, t₂ and ε₁, but the experimental results can only be simulated with enhanced t₁ and t₂ and reduced ε₁ at the end (see Fig. S7 for details, ESI†). The reduced ε₁ can be ascribed to the two-fold diimino-Fe coordination motif at the end. The enhanced hopping integral near the end of FeQDI may be explained by a shortened Fe–Fe distance, as suggested by our model calculation (Fig. S8 in ESI†).

The DFT calculation indicates that the 3× supercell on Au(111) has a ferromagnetic ground state, with the magnetic moment of 2.35μ_B on each Fe atom (Fig. S9, ESI†). In the experiment, the STS of the end Fe atom shows a dip feature near the Fermi level, which can be fitted by a Fano function, but no obvious magnetic signal was discerned on the inner Fe atoms (Fig. S10, ESI†).

In conclusion, we have examined the electronic coupling in 1D CMOF by investigating the electronic states in the FeQDI polymer at the atomic scale. We have resolved the electronic states given by Fe atoms in different coordination environments and their spatial extension due to π–d conjugation. We have extracted the hopping integrals between different components of FeQDI from band structure calculation, and simulated the evolution of the bulk and end states using a tight-binding model. Our work provides experimental and theoretical insights into the electronic coupling in 1D metal–organic frameworks with π–d conjugation.

Weihua Wang and Zhengfei Wang supervised the project. Nuoyu Su, Weiliang Zhong, Guangyao Miao and Weihua Wang performed the STM experiments. Nuoyu Su, Jiandong Guo and Weihua Wang analyzed the experimental data. Tingfeng Zhang and Zhengfei Wang carried out theoretical calculations. All authors discussed the results and commented on the manuscript.

This work was supported by the National Natural Science Foundation of China (No. 12374198, 12174369, 11974402), “Strategic Priority Research Program (B)” of the Chinese Academy of Sciences (No. XDB33000000), Innovation Program for Quantum Science and Technology (No. 2021ZD0302800) and Fundamental Research Funds for the Central Universities.

Data availability

The data supporting this article have been included as a part of the ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Notes and references

1. T. Chen, J.-H. Dou, L. Yang, C. Sun and N. J. Libretto, et al. , J. Am. Chem. Soc., 2020, 142(28), 12367–12373.
2. L. S. Xie, G. Skorupskii and M. Dinca, Chem. Rev., 2020, 120(16), 8536–8580.
3. S. Shang, C. Du, Y. Liu, M. Liu and X. Wang, et al. , Nat. Commun., 2022, 13(1), 7599.
4. J. Liu and N. Lin, ChemPlusChem, 2022, e202200359.
5. J. Liu, G. Xing and L. Chen, Acc. Chem. Res., 2024, 8979–8987.
6. X. Huang, P. Sheng, Z. Tu, F. Zhang and J. Wang, et al. , Nat. Commun., 2015, 6(1), 7408.
7. D. Sheberla, L. Sun, M. A. Blood-Forsythe, S. L. Er and C. R. Wade, et al. , J. Am. Chem. Soc., 2014, 136(25), 8859–8862.
8. X. Zhang, Y. Zhou, B. Cui, M. Zhao and F. Liu, Nano Lett., 2017, 17(10), 6166–6170.
9. X. Huang, S. Zhang, L. Liu, L. Yu and G. Chen, et al. , Angew. Chem., 2018, 130(1), 152–156.
10. Y. Ni, L. Lin, Y. Shang, L. Luo and L. Wang, et al. , Angew. Chem., Int. Ed., 2021, 60(31), 16937–16941.
11. L. Lin, Q. Zhang, Y. Ni, L. Shang and X. Zhang, et al. , Chem, 2022, 8(7), 1822–1854.
12. G. Cai, P. Cui, W. Shi, S. Morris and S. N. Lou, et al. , Adv. Sci., 2020, 7(20), 1903109.
13. M. Majumder, M. S. Santosh, R. Viswanatha, A. K. Thakur and D. P. Dubal, et al. , Energy Storage Mater., 2021, 37, 396–416.
14. Z. Sang, J. Liu, X. Zhang, L. Yin and F. Hou, et al. , ACS Nano, 2023, 17(3), 3077–3087.
15. R. Dong, Z. Zhang, D. C. Tranca, S. Zhou and M. Wang, et al. , Nat. Commun., 2018, 9(1), 2637.
16. S. Feng, H. Duan, H. Tan, F. Hu and C. Liu, et al. , Nat. Commun., 2023, 14(1), 7063.
17. Z. Wang, N. Su and F. Liu, Nano Lett., 2013, 13(6), 2842–2845.
18. W. Jiang, X. Ni and F. Liu, Acc. Chem. Res., 2021, 54(2), 416–426.
19. L. Dong, Z. A. Gao and N. Lin, Prog. Surf. Sci., 2016, 91(3), 101–135.
20. B. Liu, H. Fu, J. Guan, B. Shao and S. Meng, et al. , ACS Nano, 2017, 11(11), 11402–11408.
21. B. Li, X. Zhao, J. Guo, X. Shi and W. Wang, J. Phys. Chem. C, 2022, 126(15), 6662–6667.
22. C.-H. Hsu, J. Liu, F.-C. Chuang, R. Zhang and B. Xia, et al. , Nanoscale, 2019, 11(3), 878–881.
23. Z. A. Gao, Y. Gao, M. Hua, J. Liu and L. Huang, et al. , J. Phys. Chem. C, 2020, 124(49), 27017–27023.
24. J. Liu, Y. Gao, T. Wang, Q. Xue and M. Hua, et al. , ACS Nano, 2020, 14(9), 11283–11293.
25. M. Hua, B. Xia, M. Wang, E. Li and J. Liu, et al. , J. Phys. Chem. Lett., 2021, 12(15), 3733–3739.
26. W. Zhong, T. Zhang, D. Chen, N. Su and G. Miao, et al. , Small, 2023, 19(21), 2207877.
27. T. Hu, W. Zhong, T. Zhang, W. Wang and Z. Wang, Nat. Commun., 2023, 14(1), 7092.
28. J. Liu, M. Abel and N. Lin, J. Phys. Chem. Lett., 2022, 13(5), 1356–1365.
29. B. Mallada, P. BlonSki, R. Langer, P. Jelinek and M. Otyepka, et al. , ACS Appl. Mater. Interfaces, 2021, 13(27), 32393–32401.
30. P. Tin, M. J. Jenkins, J. Xing, N. Caci and Z. Gai, et al. , Nat. Commun., 2023, 14(1), 5454.
31. H. Denawi, M. Koudia, R. Hayn, O. Siri and M. Abel, J. Phys. Chem. C, 2018, 122(26), 15033–15040.
32. V. M. Santhini, C. Wäckerlin, A. Cahlík, M. Ondráček and S. Pascal, et al. , Angew. Chem., 2021, 133(1), 443–449.
33. C. WäCkerlin, A. Cahlik, J. Goikoetxea, O. Stetsovych and D. Medvedeva, et al. , ACS Nano, 2022, 16(10), 16402–16413.
34. F. Frezza, F. Schiller, A. Cahlík, J. E. Ortega and J. V. Barth, et al. , Nanoscale, 2023, 15(5), 2285–2291.
35. A. CahliK, M. Ondracek, C. Wackerlin, A. P. Sole and O. Siri, et al. , ACS Nano, 2024, 18(13), 9576–9583.
36. J. Hu, T. W. Odom and C. M. Lieber, Acc. Chem. Res., 1999, 32(5), 435–445.
37. A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee and I. Souza, et al. , Comput. Phys. Commun., 2014, 185(8), 2309–2310.

---

Footnotes

† Electronic supplementary information (ESI) available: Methods, and additional experimental and calculation results. See DOI: https://doi.org/10.1039/d4cc03758h

‡ Nuoyu Su and Tingfeng Zhang contributed equally to this work.

---