Solvent-assisted mechanochemical crystallization of the metal-free perovskite solid solution (H₂dabco, H₂hmta)NH₄(BF₄)₃

Abstract

All-proportional solid solutions of the metal-free perovskite (H₂dabco_1−y, H₂hmta_y)(NH₄)(BF₄)₃ ((d,h)-BF₄) were crystallized via a mechanochemical method. Their molecular dynamics depend on the ratio y with a compositional boundary at y = 0.43, where H₂dabco²⁺ was deduced to be at a dynamic disorder state, even below phase transition temperature to a plastic crystalline phase seen at y = 0.

---

Perovskite-type oxides in functional materials such as ferroelectrics and piezoelectrics are often found in solid solution.^1,2 This is because their chemical and physical properties can be finely controlled by a combination and ratio of metal ions. A solid solution with different structural symmetries also exhibits unique physical properties related to structural instability at the compositional boundary of components, known as a morphotropic phase boundary, such as lead zirconate titanate.^3–5

In 2002, the third type of ABX₃ perovskite structures was reported, followed by traditional fully inorganic perovskites and organic–inorganic hybrid perovskites.⁶ Both A-sites and B-sites are occupied by molecular ions instead of metals, in what are known as metal-free molecular perovskites. In 2018, ferroelectricity was realized using non-centrosymmetric organic molecules at the A-site.⁷ Successive reports have described the properties of these materials, including visible luminescence with high fluorescence quantum yields, and X-ray detection.^8–12 These materials have advantageous qualities with respect to reduced effects on humans and the environment more broadly.

Spontaneous polarization of perovskites is often caused by distortion of the {BX₆} octahedron. Unlike metal-containing systems however, whose distortion usually originates from metal ions via the pseudo-Jahn–Teller effect, the {(NH₄)X₆} octahedron in metal-free perovskites does not have a mechanism for spontaneous polarization. Both polarization and dielectric properties are affected by the characteristics of the interaction, steric hindrances, symmetry, and orientation of the A-site molecule.

We have investigated solid solutions of A-site molecules with different characteristics: hexamethylenetetramine (hmta) and 1,4-diazabicyclo[2.2.2]octane (dabco). In the perovskite structure, non-centrosymmetric (H₂hmta)(NH₄)Br₃ (h-Br)¹³ was mixed with centrosymmetric (H₂dabco)(NH₄)Br₃ (d-Br), resulting in the solid solution (H₂dabco, H₂hmta)(NH₄)Br₃ ((d,h)-Br). Unlike d-Br, which underwent a first-order type phase transition to a plastic crystalline (PC) phase at 327 K,⁷ a second-order type transition with Debye-type dielectric relaxation at approximately 200 K was observed for (d,h)-Br. It was considered that H₂hmta²⁺ induced structural fluctuations in the lattice that activate the thermal motion of surrounding H₂dabco²⁺.¹⁴ However, the solid solution was crystallized from an aqueous solution, and hmta was only miscible below a few mol% due to hydrolysis in the acidified aqueous solution.

Mechanochemical methods^15–22 are techniques for reacting components via mechanical processes such as compression and shearing. This can facilitate products and reactions that differ from those associated with solution-based synthesis.^15–17 Metal-free perovskites have been crystallized via mechanochemical methods.¹⁸ Additionally, mechanochemical methods have been used to achieve solid solutions of species that are difficult to mix in solution or the liquid phase.^19–22

The present study investigated the use of mechanochemical methods to crystallize solid solutions of the metal-free perovskite crystals between (H₂hmta)(NH₄)(BF₄)₃ (h-BF₄) and (H₂dabco)(NH₄)(BF₄)₃ (d-BF₄). The phase transition of d-BF₄ was reported by Fu et al.,^23,24 which undergoes phase transitions from the ordered phase of space group Pa3̄ (phase III) to the PC phase (phase II; Fm3̄c) at 333 K, losing the orientational order of H₂dabco²⁺. The hmta analogue h-BF₄ was newly crystallized in the current study and underwent a transition to phase II at 390 K from a tetragonal phase (phase IV; I4₁/a).‡ We successfully crystallized ((d,h)-BF₄) with a wide range of compositions, and the compositional dependence of phase transition behaviour was investigated.

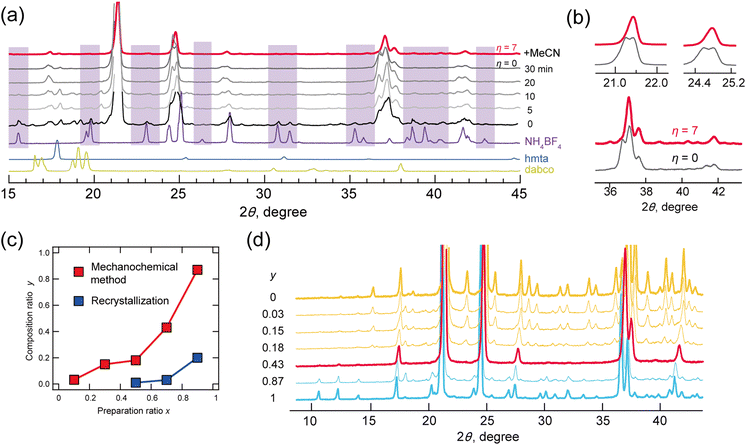
The powder X-ray diffraction (P-XRD) patterns of a mixture of dabco (5.0 mmol), hmta (5.0 mmol), NH₄BF₄ (7.5 mmol), and an aqueous solution of HBF₄ (20.0 mmol) after grinding for 0, 5, 10, 20 and 30 minutes are shown in Fig. 1a. At t = 0, diffraction peaks by the perovskite structure were observed in those of NH₄BF₄. With grinding the mixture, the diffraction peaks by NH₄BF₄ disappeared at t > 20, indicating that NH₄BF₄ was converted to a perovskite structure. Some diffraction peaks were split however, indicating low structural purity. Mechanochemical synthesis often proceeds via the addition of a solvent,^{20,21,25–27} where methods can be classified with parameter η as neat (η = 0), liquid-assisted grinding (η = 0–2 μL mg⁻¹), slurrying (η = 2–12 μL mg⁻¹), and solution (η > 12).¹⁷ Parameter η is defined by eqn (1), where V is the amount of solvent (μL) and m is the reactant weight (mg):

η = V/m (1)

Fig. 1 (a) Time evolution of the P-XRD patterns of solids mixed after grinding for 0, 5, 10, 20 and 30 minutes, and P-XRD pattern of the solid solution prepared by grinding with the addition of acetonitrile for 30 min (black). (b) Extended graph of the P-XRD patterns of η = 0 and 7. (c) Plots of the mixing ratio x and composition ratio y for mechanochemical (red) and recrystallization (blue) methods. (d) P-XRD patterns of solid solution prepared via mechanochemical methods at variable y.

In the present study, split diffraction patterns at η = 0 were improved at η = 7 via the addition of acetonitrile (red line; Fig. 1a and b). Mechanochemical reactions at η = 7 with acetonitrile were then performed with various mixing ratios (0.1, 0.3, 0.5, 0.7 and 0.9) for hmta (10x mmol), dabco (10–10x mmol), NH₄BF₄ (10–5x mmol) and HBF₄ (20 mmol). For comparison, the corresponding crystallizations were also performed by dissolving the compounds in water.

The compositions y (dabco; hmta = 1 − y:y) in solid solutions were plotted for mechanochemical methods (red) and recrystallization from water (blue) (Fig. 1c). These y values determined by peak area in liquid chromatography–mass spectrometry and elemental analysis were relatively concordant (calibration in Fig. S3-1 (ESI†) and experimental results in Tables S3 and S4-1, ESI†). In all cases, the y values obtained via mechanochemical methods were higher than those obtained via recrystallization. This is accounted for by hydrolysis of hmta by an acid. Respective ratios y for mixing ratios x of 0.1, 0.3, 0.5, 0.7, and 0.9 were 0.03, 0.15, 0.18, 0.43 and 0.87. Solid solutions crystallized via mechanochemical methods were all-proportional solid solutions.

Fig. 1d shows the P-XRD patterns of solid solutions prepared via mechanochemical methods, measured at room temperature. The diffraction patterns of lower hmta contents, y = 0.03, 0.15 and 0.18 (indicated by yellow lines in Fig. 1d), corresponded to that of static phase d-BF₄ (space group Pa3̄, phase III). At y = 0.43, the diffraction pattern (indicated by a red line) differed from those of d-BF₄ and h-BF₄ above 93 K (Fig. S4-1, ESI†). This corresponds well with that of their PC phase (phase II; comparisons are shown in Fig. S4-1, ESI†). At y = 0.87, the diffraction pattern was consistent with that of the static phase of h-BF₄ (phase IV). These experimental results indicated the compositional phase transition between d-BF₄ and h-BF₄, where an anomaly phase (phase V) appeared at their boundary y = 0.43.

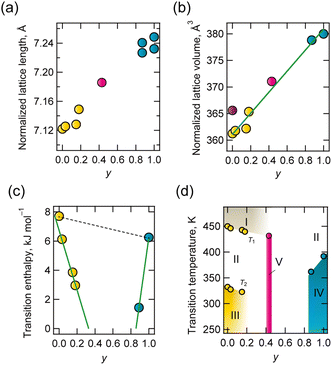
The lattice parameters of solid solutions were evaluated, and the composition dependence of lattice length and volume normalized for the ABX₃ composition is shown in Fig. 2a and b. The lattice dimensions were linearly associated with composition. This is a typical relationship in all-proportional solid solutions, known as Vegard's law.

Fig. 2 Component dependence of (a) normalized lattice length, (b) normalized lattice volume (purple circle represents values at phase II of d-BF4), (c) transition enthalpy to phase II from phase III (yellow) or phase IV (blue) and (d) phase diagram.

The respective transition temperatures of d-BF₄ and h-BF₄ to the PC phase were 332 K and 392 K. Differences in intermolecular interactions and the high symmetry of hmta contribute to higher transition temperatures. Solid state hmta melted at 536 K without a transition to the PC phase, even though dabco transitioned to the PC phase at 351 K before melting (434 K). This is considered to be because highly symmetric hmta has a lower entropy change with respect to transition.²⁸ The results of differential thermal analysis (DTA) and differential scanning calorimetry (DSC) are summarized in Table S4-2 and Fig. S4-2, Fig. S4-3 (ESI†). Thermal anomaly, which indicates a transition to phase II (transition temperature T₂), was observed except for the case y = 0.43. At approximately 450 K (transition temperature T₁), thermal anomaly was also observed for y = 0, 0.03, 0.15, 0.18 and 0.43 in the DTA chart. This is considered to represent disordering of BF₄⁻ (phase I). The phase transition enthalpy against y is shown in Fig. 2c, and a phase diagram is shown in Fig. 2d. Transition enthalpies and temperature decreased toward y = 0.43, at which point the thermal anomaly disappeared in both DSC and DTA.

At the transition from ordered phase III or IV to disordered phase II, the compositional average of enthalpy change, ΔH(y), is represented by

ΔH(y) = (1 − y)ΔH (d-BF₄) + yΔH (h-BF₄) (2)

with ΔH (d-BF₄) being 7.71 kJ mol⁻¹ and ΔH (h-BF₄) being 6.11 kJ mol⁻¹. This model assumes that H₂hmta²⁺ and H₂dabco²⁺ behave independently at phase transitions. However, experimental values do not follow this model (dotted line in Fig. 2c), indicating that H₂hmta²⁺ and H₂dabco²⁺ are randomly distributed in the solid state, and the thermal motion of each is correlated. We consider that the structural correlation may be due to a structural relationship between the A-site molecule and {NH₄(BF₄)₆} octahedron.

Lattice length and volume were consistent with the compositional average, but their phase transition behaviours were not. In addition, the compositional boundary was observed at y = 0.43, where (i) the diffraction pattern was consistent with that of the PC phase of cubic Fm3̄c above 223 K, but (ii) the thermal anomaly identical to a first-order-type phase transition disappeared. The unit cell volume normalised for composition was 371 ų for y = 0.43 at room temperature, which is larger than the 367 ų of phase II of d-BF₄, but smaller than the 395 ų of h-BF₄. H₂dabco²⁺ molecules at y = 0.43 are thus considered to be in enough space to exhibit rotational disorder, but hmtaH₂²⁺ is not. One possible structure proposed at y = 0.43 at approximately room temperature is a mixture of static (random) orientational disorder of H₂hmta²⁺ and dynamic disorder of H₂dabco²⁺. Solid-state ¹³C-NMR (nuclear magnetic resonance; Fig. S4-9, ESI†) was characterized for y = 0.43, d-BF₄ and h-BF₄ at 300 K, and the results are summarized in Table S4-1 (ESI†). Peaks for dabco and hmta at y = 0.43 were sharper than those associated with d-BF₄ and h-BF₄. This implies that A-site molecules at y = 0.43 are in higher structural symmetry. This is consistent with our structural model.

The dynamics of molecular motion were investigated via temperature variable complex permittivity measurements. Solid solution (d,h)-BF₄ (y = 0.03, 0.15, 0.18, 0.43 and 0.87) exhibited identical frequency and temperature dispersion at 100–300 K (Fig. S4-4 to S4-8, ESI†) due to Debye-type electric dipole relaxation. The corresponding anomaly was not observed for d-BF₄, but was observed for h-BF₄ in different temperature ranges above 300 K. A plot of activation energy and temperature at 0.01 Hz estimated from the Arrhenius relationship is shown in Fig. 3a. These values were less dependent on composition at 0.3–0.4 eV and ∼130 K respectively, indicating that the dipole relaxations have the same origin. In contrast, ε₁, ε₂ and D (≡ε₂/ε₁) values depend strongly on y. D values at 1 MHz at different y points are shown in Fig. 3b. Peak top temperature did not depend on y, but the peak was largest at y = 0.43. We consider that this dipole relaxation originated from the thermal motion of the H₂dabco²⁺ and/or {NH₄(BF₄)₆} octahedron, whose static order melt point is approximately 140 K.

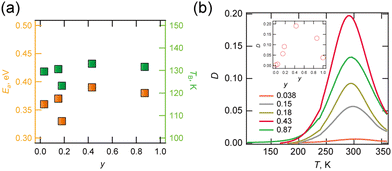Fig. 3 (a) Plot of activation energy E_a and temperature T_B estimated for f = 0.01 Hz via Arrhenius plotting and (b) plot of D against T at variable y (inset: plot of D at 300 K with y).

In summary, mechanical methods crystallized all-proportional solid solutions of d-BF₄ and h-BF₄. Even though lattice dimensions were proportional to y, the thermodynamic values of phase transition were not. As y increased, unit cell volume exceeded that of PC phase d-BF₄, and the compositional boundary appeared at y = 0.43, where highly symmetric cubic-type diffraction was observed above 223 K. We considered the structural mode of the boundary to be a random mixture of thermally dynamic H₂dabco²⁺ and orientationally disordered H₂hmta²⁺. Phase transition temperature and molecular dynamics strongly depend on the ratio of the two, clearly indicating that solid metal-free perovskite solution is advanced and effective for tuning physical properties, as are traditional perovskites, where mechanical crystallization is a useful technique for all-proportional solid solution. We think that band tuning for optoelectronic properties is also possible because A-site molecules contributed to the electronic state (band gap) of the crystal.²⁹

The authors acknowledge the extensive contribution of Structural Sciences from Leading-Edge Materials to Cultural and Archaeological Works, Yamaguchi University. They also express their gratitude to Mr Matsuoka, Institute of Systems Biology and Radioisotope Analysis, Yamaguchi University, for his valuable advice and support with the analysis of liquid chromatography–mass spectrometry conducted using a Thermo Fisher Orbitrap Exploris 120. The authors acknowledge the financial support from the cooperative research program of the Network Joint Research Centre for Materials and Devices of Japan.

Data availability

Crystallographic data for the structures reported in this article have been deposited at the Cambridge Crystallographic Data Centre under deposition numbers CCDC 2347881 and 2347882. Copies of the data can be obtained free of charge viahttps://www.ccdc.cam.ac.uk/structures/. All other relevant data generated and analysed during this study, which include analytical, spectroscopic, crystallographic, thermal and dielectric data, are included in this article and its ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. I. Grinberg, D. V. West, M. Torres, G. Gou, D. M. Stein, L. Wu, G. Chen, E. M. Gallo, A. R. Akbashev, P. K. Davies, J. E. Spanier and A. M. Rappe, Nature, 2013, 503, 509–512.
2. X. Hou and J. Yu, J. Am. Ceram. Soc., 2013, 96, 2218–2224.
3. B. Jaffe, R. S. Roth and S. Marzullo, J. Appl. Phys., 1954, 25, 809–810.
4. Z. H. Liu, A. R. Paterson, H. Wu, P. Gao, W. Ren and Z. G. Ye, J. Mater. Chem. C, 2017, 5, 3916–3923.
5. W. Q. Liao, D. Zhao, Y. Y. Tang, Y. Zhang, P. F. Li, P. P. Shi, X. G. Chen, Y. M. You and R. G. Xiong, Science, 2019, 363, 1206–1210.
6. C. A. Bremner, M. Simpson and W. T. A. Harrison, J. Am. Chem. Soc., 2002, 124, 10960–10961.
7. H. Y. Ye, Y. Y. Tang, P. F. Li, W. Q. Liao, J. X. Gao, X. N. Hua, H. Cai, P. P. Shi, Y. M. You and R. G. Xiong, Science, 2018, 361, 151–155.
8. X. Song, Q. Li, J. Han, C. Ma, Z. Xu, H. Li, P. Wang, Z. Yang, Q. Cui, L. Gao, Z. Quan, S. F. Liu and K. Zhao, Adv. Mater., 2021, 33, e2102190.
9. H. S. Wu, B. T. Murti, J. Singh, P. K. Yang and M. L. Tsai, Adv. Sci., 2022, 9, 2104703.
10. X. Song, G. Hodes, K. Zhao and S. F. Liu, Adv. Energy Mater., 2021, 11, 2003331.
11. Z. Z. Li, G. Q. Peng, Z. H. Li, Y. K. Xu, T. Wang, H. X. Wang, Z. T. Liu, G. Wang, L. M. Ding and Z. W. Jin, Angew. Chem., Int. Ed., 2023, 62, e202218349.
12. X. Song, T. Li, H. Li, S. Lin, J. Yin and K. Zhao, Sci. China Mater., 2024, 67, 1348–1355.
13. H. Morita, R. Tsunashima, S. Nishihara, K. Inoue, Y. Omura, Y. Suzuki, J. Kawamata, N. Hoshino and T. Akutagawa, Angew. Chem., Int. Ed., 2019, 58, 9184–9187.
14. H. Morita, R. Tsunashima, S. Nishihara and T. Akutagawa, CrystEngComm, 2020, 22, 2279–2282.
15. T. Seo, N. Toyoshima, K. Kubota and H. Ito, J. Am. Chem. Soc., 2021, 143, 6165–6175.
16. G. W. Wang, K. Komatsu, Y. Murata and M. Shiro, Nature, 1997, 387, 583–586.
17. T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., 2020, 132, 1030–1041.
18. F. Lyu, Z. Chen, R. Shi, J. Yu and B. L. Lin, J. Solid State Chem., 2021, 304, 122548.
19. A. Karmakar, A. M. Askar, G. M. Bernard, V. V. Terskikh, M. Ha, S. Patel, K. Shankar and V. K. Michaelis, Chem. Mater., 2018, 30, 2309–2321.
20. M. Lusi, I. J. Vitorica-Yrezabal and M. J. Zaworotko, Cryst. Growth Des., 2015, 15, 4098–4103.
21. E. Batisai, M. Lusi, T. Jacobs and L. J. Barbour, Chem. Commun., 2012, 48, 12171–12173.
22. R. Tsunashima, CrystEngComm, 2022, 24, 1309–1318.
23. G. Z. Liu, J. Zhang and L.-Y. Wang, Synth. React. Inorg., Met.-Org., Nano-Met. Chem., 2011, 41, 1091–1094.
24. L. L. Chu, T. Zhang, W. Y. Zhang, P. P. Shi, J. X. Gao, Q. Ye and D. W. Fu, J. Phys. Chem. Lett., 2020, 11, 1668–1674.
25. E. Schur, E. Nauha, M. Lusi and J. Bernstein, Chemistry, 2015, 21, 1735–1742.
26. B. Saikia, A. Seidel-Morgenstern and H. Lorenz, Cryst. Growth Des., 2021, 21, 5854–5861.
27. D. Braga, L. Maini and F. Grepioni, Chem. Soc. Rev., 2013, 42, 7638–7648.
28. L. N. Becka and D. W. J. Cruickshank, Proc. R. Soc. London, Ser. A, 1963, 273, 435–454.
29. J. Bie, D. B. Yang, M. G. Ju, Q. Pan, Y. M. You, W. Fa, X. C. Zeng and S. Chen,, JACS Au, 2021, 1, 475–483.

---

Footnotes

† Electronic supplementary information (ESI) available: Method, FT-IR spectra, TG-DTA, LC-MS, DSC, powder X-ray diffraction, complex permittivity, and solid-state ¹³C-NMR. CCDC 2347881 and 2347882. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc04010d

‡ h-BF₄ was isolated as colourless block single crystals from mixed aqueous hmta and HBF₄ solution (Fig. S2-1, ESI†). Details on the crystallization procedure and characterization are included in the ESI.† In temperature-variable single crystal X-ray diffraction studies (Table S1 and Fig. S2-3, S2-4, ESI†) and thermal DTA (Fig. S2-5, ESI†) and DSC (Fig. S2-6, ESI†) analyses, a phase transition from the space group I4₁/a (ordered phase) to Fm3̄c (PC disordered phase), where the A-site molecule was disordered but the orientation of BF₄⁻ was frozen, was observed at 392 K. In temperature and frequency dependence measurements of complex permittivity, Debye-type relaxation was observed above 300 K (Fig. S2-7, ESI†). The activation energy for dipole relaxation was estimated to be 0.78 eV based on an Arrhenius plot (Fig. S2-8, ESI†). We consider that this originates from the thermal disorder of H₂hmta²⁺ toward a transition to the PC phase.

---