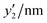Machine-learning-assisted prediction of the size of microgels prepared by aqueous precipitation polymerization

Abstract

The size of soft colloids (microgels) is essential; however, control over their size has typically been established empirically. Herein, we report a linear-regression model that can predict microgel size using a machine learning method, sparse modeling for small data, which enables the determination of the synthesis conditions for target-sized microgels.

---

Hydrogel nano/microparticles (nanogels/microgels) are hydrophilic or amphiphilic colloids that are highly swollen by water and are dispersed stably in aqueous solution.¹ Due to their fascinating properties related to their softness and stimuli-responsiveness, their use in various applications, including controlled uptake/release of functional molecules,² as particulate stabilizers for interfaces,³ and as soft colloidal crystals/glasses/gels,⁴ has been proposed.

Among the methods for producing microgels, aqueous free radical precipitation polymerization is an excellent strategy for forming microgels of uniform size under environmentally friendly and cost-effective experimental conditions.^1a,5 It is widely accepted that the monomers for these polymers are water soluble, but that upon growing, the polymers become insoluble in water, which results in the formation of nuclei for the growth of microgels; these nuclei then grow until they acquire sufficient colloidal stability.^2a,5c To date, tremendous efforts have been devoted to revealing the detailed mechanism of precipitation polymerization,^1a,5b,c,6 which would allow the size of simple microgels (e.g., a monomer and crosslinker) obtained by precipitation polymerization to be controlled.⁷ However, copolymerization with various functional monomers to add further functionality to simple microgels is usually required, complicating the reaction and hence the prediction of the microgel size. In addition, various parameters including polymerization temperature and stirring conditions affect the size of the resultant microgel. Thus, in many cases, the microgel size in precipitation polymerizations has been controlled using a trial-and-error approach for each parameter based on the experience and intuition of professional researcher(s). If the size of functional microgels could be predicted, the development of applications that require precise control of the microgel size, such as targeted drug delivery and the formation of colloidal crystals composed of different microgels, would be accelerated.

Against this background, we found that machine learning (ML) is an effective way to predict the size of microgels prepared by aqueous free radical precipitation polymerization (Fig. 1). ML has been widely applied to the optimization of processes and the exploration of materials, such as controlled synthesis of nanosheet materials and discovery of new organic active materials for energy-related applications.⁸ However, in conventional experimental approaches, it can be difficult to collect a sufficiently large dataset to train and construct the corresponding predictors. Our group has developed a technique, which is called sparse modelling for small data (SpM-S), that combines ML and chemical insight.⁹ This method provides straightforward, interpretable, and generalizable models using datasets that are small compared to other ML algorithms. Here, SpM-S is applied to predict the size of microgels.

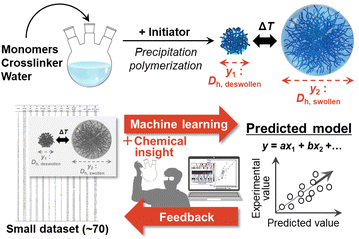Fig. 1 Schematic illustration of the machine-learning-assisted prediction of the microgel size developed in this study.

In this study, four previously reported¹⁰ and 66 newly synthesized microgels were used to prepare the training dataset. The polymerization conditions were varied randomly (Table S1, ESI†). The hydrodynamic diameter (D_h) determined by dynamic light scattering (DLS) was employed as the size parameter for all 70 microgels (i.e., the objective variable; y₁: deswollen microgels; y₂: swollen microgels), since it is difficult to measure the size of microgels by means of microscopy techniques, given that the microgels are highly deformed on the solid substrates (Table S1, ESI†).¹¹ Prior to the DLS measurements, the size uniformity was examined using scanning electron microscopy (SEM) in order to confirm the validity of calculating D_h using the Stokes–Einstein equation (Fig. 2(b)–(d) and Fig. S1–S3, ESI†). The microgels were clearly uniform in size with no secondary or individual particles, indicating that the determined D_h values are reliable. The D_h values in this study were measured at pH = 3, where the carboxyl groups in the microgels are protonated.^10,12 In many cases, the obtained time-correlation functions were unreliable for highly swollen microgels with a D_h > 5 μm, and thus, these data were not used for this investigation (Table S1, ESI†). All time-correlation functions used for determining D_h are summarized in Fig. 2(c) and (d) as well as Fig. S2 and S3 (ESI†).

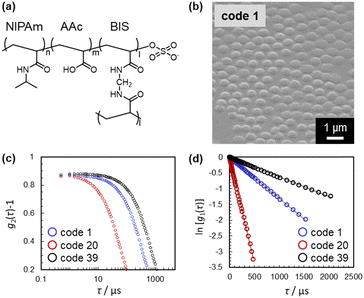Fig. 2 (a) Chemical structure of the microgels. (b)–(d) Representative (b) SEM image, (c) time-correlation function of the scattering intensity, g₂(τ) − 1, and (d) calculated time-correlation function of the scattering electric field, ln[g₁(τ)], of selected microgels. All SEM images and time-correlation functions for all microgels used in this study are summarized in Fig. S1 and S2 (ESI†).

Then, ten experimental parameters and conditions, including concentration, stirring speed, and solution temperature, were set as the explanatory variables (x_n) based on our chemical insight (Table 1). Here, N-isopropyl acrylamide (denoted as NIPAm, x₁/mM) and crosslinker N,N′-methylenebis(acrylamide) (BIS, x₂/mM) were chosen as the chemical constituents of the microgels (Fig. 2(a)). In order to add functionality to the microgels, acrylic acid (AAc, x₃/mM) was selected as a model comonomer (Fig. 2(a)). Additionally, other explanatory variables that we thought would be likely to affect the microgel size, based on our empirical experience, were chosen (x_n: n = 4–10) (Table 1): total monomer concentration used for the polymerization (x₄/mM), concentration of the anionic surfactant sodium dodecyl sulfate (SDS) (x₅/mM), concentration of sodium chloride (NaCl) (x₆/mM), concentration of the water-soluble anionic initiator potassium persulfate (KPS) (x₇/mM), amount of water (x₈/mL), stirring speed (x₉/rpm), and polymerization temperature T (x₁₀/°C).

Table 1 List of explanatory variables (x_n: n = 1–10)

No.	Explanatory variables, xn	Unit
1	N-isopropyl acrylamide (NIPAm) concentration	mM
2	N,N′-methylenebis(acrylamide) (BIS) concentration	mM
3	Acrylic acid (AAc) concentration	mM
4	Monomer concentration	mM
5	Anionic surfactant (sodium dodecyl sulfate (SDS)) concentration	mM
6	Inorganic salt (sodium chloride (NaCl)) concentration	mM
7	Aqueous anionic initiator (potassium persulfate (KPS)) concentration	mM
8	Water	mL
9	Stirring speed	rpm
10	T	°C

---

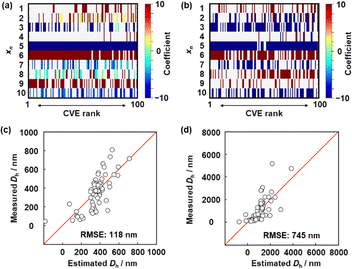
Next, the descriptors of the size of the deswollen (y₁) and swollen (y₂) microgels were extracted using SpM-S (Fig. 3). The detailed procedure is described in the ESI.† The potential descriptors were visualized in the weight diagram of the exhaustive search for linear regression (ES-LiR) (Fig. 3(a) and (b)).⁹ Here, multiple linear-regression models were prepared for all possible combinations of x_n (n = 1–10) to study the contribution of each x_n exhaustively, for a total of 2¹⁰ − 1 (=1023) patterns. After sorting the models in ascending order of cross-validation error (CVE), the coefficients of each x_n were visualized using a color scale in the weight diagram. Positive and negative coefficients are depicted using warm and cool colors, respectively (Fig. 3(a) and (b)). The more densely filled bars represent x_n that are used in the models more frequently. In the present work, we selected the descriptors three steps. The potential descriptors were visually extracted from the weight diagram based on the intensity and density of the horizontal color bars (Fig. 3a and b). Then, the selection was carried out based on our chemical insight. The descriptors were finally fixed based on the prediction accuracy with adding and removing a couple of x_n.

Fig. 3 Sparse modeling for small data (SpM-S) for the construction of the prediction model. (a) and (b) Weight diagrams representing the coefficients of each x_n in the constructed models in ascending order of the smallest 100 CVE values: (a) y₁ and (b) y₂. (c) and (d) Relationship between the estimated and measured hydrodynamic diameters; (c) y₁ and (d) y₂.

The detailed processes of the variable selection for y₁ and y₂ were described in the ESI† (Fig. S4 and S5, ESI†). The prediction model for y₁ was constructed using these six descriptors (eqn (1)); the root-mean-squared error (RMSE) was 118 nm (Fig. 3c). In eqn (1), each x_n was converted to the normalized frequency distribution (mean 0, standard deviation 1). The weight of each descriptor is represented by the coefficients.

y₁ = −91.7x₅ + 57.4x₆ − 2.3x₇ − 7.4x₁₀ + 33.1x₁ + 38.1x₉ + 356.2 (1)

The y₂ predictor was constructed using these six descriptors (eqn (2)) with a RMSE of 745 nm (Fig. 3d).

y₂ = −17.2x₂ − 341.1x₅ + 435.7x₆ − 252.3x₇ − 96.1x₁₀ − 189.6x₃ + 1107.4 (2)

The descriptors in the models are partially consistent with our experience and chemical insight as experimental scientists. The anionic surfactant SDS (x₅) is known to decrease the size of both the deswollen and swollen microgels (y₁ and y₂) during the aqueous precipitation polymerization of pNIPAm-based microgels.^7a,13 In contrast, the size (y₁ and y₂) increases with increasing ionic strength (here, the concentration of NaCl (x₆)) during polymerization.¹⁴ These findings are described by eqn (1) and (2), which provide interpretable quantitative models that are consistent with previous considerations. Although the contribution of each individual factor has been studied previously, an overall quantitative model that considers a combination of these factors has not yet been achieved.

Furthermore, although a systematic investigation of the effect of the KPS concentration (x₇) has not yet been reported, based on eqn (1) and (2), it is plausible that increasing the concentration of the water-soluble initiator KPS during the polymerization decreases y₁ and y₂. Regarding the polymerization temperature (x₁₀), it has been reported that temperature-programmed syntheses in which the precipitation polymerization was started at a low temperature (ca. 40 °C) and then ramped up to ca. 70 °C drastically increased the size of the resulting microgels.^7b,c,15 Different from the temperature-programmed method, in the precipitation polymerization, the polymerization temperature was kept constant, and increasing the polymerization temperature (x₁₀) decreased y₁ and y₂.

Finally, the preparation conditions for functional microgels with a desired size were predicted using the developed prediction model. As it is mainly microgels in the swollen state that play a crucial role, a swollen-microgel size (y₂) of 500 nm was targeted. For the prediction experiments, we fixed the values of several of the polymerization conditions (x_n), i.e., the concentration of AAc (x₃ = 4.5 mM) and BIS (x₂ = 0.75 mM, 1.50 mM, or 9.00 mM). Appropriate values for the other parameters that are included in eqn (2) under these conditions were calculated. For the parameters that are not included in eqn (2), representative values were chosen based on our experience as professional researchers: x₄ = 150 mM, x₈ = 100 mL, and x₉ = 250 rpm. The resultant microgels all showed a size of ca. 500 nm in the swollen state regardless of the degree of crosslinking (the measured actual size of targeted microgels 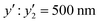at x₂ = 0.75 mM, 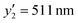at x₂ = 1.50 mM, and 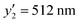at x₂ = 9.00 mM) (Table 2 and Fig. S6, ESI†). The cross validation was carried out with the addition of these new data to the original training dataset (Fig. S7, ESI†). These results demonstrate that the developed prediction method is highly reliable.

Table 2 Polymerization conditions and resulting size of the microgels

BIS concentration	Other parameters included in eqn (2)					Target y2 = 500 nm
x 2/mM	x 1/mM	x 5/mM	x 6/mM	x 7/mM	x 10/°C
0.75	144.75	0.50	0	3.37	70	500
1.50	144.00	0.45	0	3.38	70	511
9.00	163.50	0.10	0	2.91	80	512

---

It should be noted that eqn (1) and (2) have the potential to be further developed by adding datasets including different parameters, such as other functional comonomers, which are crucial for the development of novel microgels for new applications.^12,16 Based on our previous reports,^9,17 it is also likely that in addition to size, other important properties (or functions) of microgels, such as e.g., softness, can be predicted. Thus, our results represent an important first step toward a reliable method to predict microgel characteristics, which is crucial for accelerating the development of microgel science and technology.

The size of microgels prepared by aqueous free radical precipitation polymerization has been predicted using the SpM-S method to construct a prediction model using parameters that were chosen based on the authors’ experience. The size of microgels in both the deswollen and swollen state was quantitatively described by the prediction model, and the model was used successfully to determine the experimental conditions for synthesizing complicated microgels of a target size (here: 500 nm). Our findings showcase the utility of the development of machine learning with small datasets for controlling the size of colloidal particles, which is important for achieving desired functionality in applications where the size is crucial, such as drug-delivery systems and colloidal assemblies with more complex ordering. In addition, SpM-S can be applied to other small data if we can prepare a similar dataset based on the experimental results, as shown in Table S1 (ESI†).^9a

D. S., H. M. and Y. O. wrote the draft of the manuscript. D. S. and Y. O. modified the manuscript. H. M., Y. S., and R. N. synthesized the microgels and contributed to microgel characterization. R. S., Y. I. and Y. O. constructed the prediction model using machine learning on small data. D. S., Y. O., H. M., and R. S. discussed the entire paper. D. S. and Y. O. designed and supervised the overall study.

D. S. and Y. O. gratefully acknowledge a Grant-in-Aid for Scientific Research (B) (24K01550) from the Japan Society for the Promotion of Science (JSPS). D. S. gratefully acknowledges a CREST grant-in-aid (JPMJCR21L2) from the Japan Science and Technology Agency (JST). The authors thank Takuma Kureha, Nahomi Matsuki, Emi Arai, and Miyuki Kuwano for assistance with the DLS measurements.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33; (b) F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140; (c) D. Suzuki, K. Horigome, T. Kureha, S. Matsui and T. Watanabe, Polym. J., 2017, 49, 695–702; (d) M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255; (e) Y. Nishizawa, K. Honda and D. Suzuki, Chem. Lett., 2021, 50, 1226–1235; (f) D. Suzuki, Langmuir, 2023, 39, 7525–7529; (g) Y. Gerelli, F. Camerin, S. Bochenek, M. M. Schmidt, A. Maestro, W. Richtering, E. Zaccarelli and A. Scotti, Soft Matter, 2024, 20, 3653–3665.
2. (a) S. Nayak and L. A. Lyon, Angew. Chem., Int. Ed., 2005, 44, 7686–7708; (b) Y. Hoshino, K. Imamura, M. Yue, G. Inoue and Y. Miura, J. Am. Chem. Soc., 2012, 134, 18177–18180; (c) T. Kureha, Y. Nishizawa and D. Suzuki, ACS Omega, 2017, 2, 7686–7694; (d) T. Kureha and D. Suzuki, Langmuir, 2018, 34, 837–846; (e) S. Matsui, K. Hosho, H. Minato, T. Uchihashi and D. Suzuki, Chem. Commun., 2019, 55, 10064–10067.
3. (a) T. Ngai, S. H. Behrens and H. Auweter, Chem. Commun., 2005, 331–333; (b) S. Fujii, E. S. Read, B. P. Binks and S. P. Armes, Adv. Mater., 2005, 17, 1014–1018; (c) D. Suzuki, S. Tsuji and H. Kawaguchi, J. Am. Chem. Soc., 2007, 129, 8088–8089; (d) W. Richtering, Langmuir, 2012, 28, 17218–17229; (e) V. Schmitt and V. Ravaine, Curr. Opin. Colloid Interface Sci., 2013, 18, 532–541; (f) T. Watanabe, M. Takizawa, H. Jiang, T. Ngai and D. Suzuki, Chem. Commun., 2019, 55, 5990–5993; (g) Y. Nishizawa, T. Watanabe, T. Noguchi, M. Takizawa, C. Song, K. Murata, H. Minato and D. Suzuki, Chem. Commun., 2022, 58, 12927–12930.
4. (a) T. Hellweg, C. D. Dewhurst, E. Brückner, K. Kratz and W. Eimer, Colloid Polym. Sci., 2000, 278, 972–978; (b) L. A. Lyon, J. D. Debord, S. B. Debord, C. D. Jones, J. G. McGrath and M. J. Serpe, J. Phys. Chem. B, 2004, 108, 19099–19108; (c) D. Suzuki, J. G. McGrath, H. Kawaguchi and L. A. Lyon, J. Phys. Chem. C, 2007, 111, 5667–5672; (d) J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu, D. R. Reichman and D. A. Weitz, Nature, 2009, 462, 83–86; (e) D. Suzuki, T. Yamagata, K. Horigome, K. Shibata, A. Tsuchida and T. Okubo, Colloid Polym. Sci., 2012, 290, 107–117; (f) S. Minami, D. Suzuki and K. Urayama, Curr. Opin. Colloid Interface Sci., 2019, 43, 113–124.
5. (a) R. H. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247–256; (b) A. Pich and W. Richtering, Chemical Design of Responsive Microgels, Springer-Verlag, Berlin, Heidelberg, 2010, 1–37; (c) Y. Nishizawa, H. Minato, T. Inui, T. Uchihashi and D. Suzuki, Langmuir, 2021, 37, 151–159.
6. (a) W. McPhee, K. C. Tam and R. Pelton, J. Colloid Int. Sci., 1993, 156, 24–30; (b) F. Meunier, A. Elaïssari and C. Pichot, Polym. Adv. Technol., 1995, 6, 489–496; (c) D. Duracher, A. Elaïssari and C. Pichot, J. Polym. Sci., Part A: Polym. Chem., 1999, 37, 1823–1837; (d) Z. Dai and T. Ngai, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 2995–3003; (e) S. Wellert, A. Radulescu, A. Carl, R. von Klitzing and K. Gawlitza, Macromolecules, 2015, 48, 4901–4909; (f) O. L. J. Virtanen, M. Brugnoni, M. Kather, A. Pich and W. Richtering, Polym. Chem., 2016, 7, 5123–5131.
7. (a) K. C. Tam, S. Ragaram and R. H. Pelton, Langmuir, 1994, 10, 418–422; (b) Z. Meng, M. H. Smith and L. A. Lyon, Colloid Polym. Sci., 2009, 287, 277–285; (c) H. Minato, M. Murai, T. Watanabe, S. Matsui, M. Takizawa, T. Kureha and D. Suzuki, Chem. Commun., 2018, 54, 932–935.
8. (a) S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201; (b) K. T. Butler, J. M. Frost, J. M. Skelton, K. L. Svane and A. Walsh, Chem. Soc. Rev., 2016, 45, 6138–6146; (c) A. Aspuru-Guzik, Digital Discovery, 2022, 1, 6–7.
9. (a) Y. Oaki and Y. Igarashi, Bull. Chem. Soc. Jpn., 2021, 94, 2410–2422; (b) H. Tobita, Y. Namiuchi, T. Komura, H. Imai, K. Obinata, M. Okada, Y. Igarashi and Y. Oaki, Energy Adv., 2023, 2, 1014–1021; (c) Y. Haraguchi, Y. Igarashi, H. Imai and Y. Oaki, Digital Discovery, 2022, 1, 26–34; (d) R. Mizuguchi, Y. Igarashi, H. Imai and Y. Oaki, Nanoscale, 2021, 13, 3853–3859.
10. H. Minato, M. Takizawa, S. Hiroshige and D. Suzuki, Langmuir, 2019, 35, 10412–10423.
11. (a) K. Horigome and D. Suzuki, Langmuir, 2012, 28, 12962–12970; (b) K. Horigome, T. Ueki and D. Suzuki, Polym. J., 2016, 48, 273–279.
12. T. Kureha, D. Aoki, S. Hiroshige, K. Iijima, D. Aoki, T. Takata and D. Suzuki, Angew. Chem., Int. Ed., 2017, 56, 15393–15396.
13. (a) D. Suzuki, T. Yamagata, K. Horigome, K. Shibata, A. Tsuchida and T. Okubo, Colloid Polym. Sci., 2012, 290, 107–117; (b) Y. Nishizawa, T. Inui, R. Namioka, T. Uchihashi, T. Watanabe and D. Suzuki, Langmuir, 2022, 38, 16084–16093; (c) Y. Nishizawa, H. Yokoi, T. Uchihashi and D. Suzuki, Soft Matter, 2023, 19, 5068–5075.
14. (a) D. Suzuki and R. Yoshida, Polym. J., 2010, 42, 501–508; (b) D. Suzuki and K. Horigome, Langmuir, 2011, 27, 12368–12374; (c) D. Suzuki and K. Horigome, J. Phys. Chem. B, 2013, 117, 9073–9082; (d) T. Kawamoto, H. Minato and D. Suzuki, Soft Matter, 2024, 20, 5836–5847.
15. (a) Z. Li, M.-H. Kwok and T. Ngai, Macromol. Rapid Commun., 2012, 33, 419–425; (b) M.-H. Kwok, Z. Li and T. Ngai, Langmuir, 2013, 29, 9581–9591.
16. (a) T. Hoare and R. Pelton, Macromolecules, 2004, 37, 2544–2550; (b) D. Suzuki and H. Kawaguchi, Langmuir, 2005, 21, 8175–8179; (c) S. Nayak, D. Gan, M. J. Serpe and L. A. Lyon, Small, 2005, 1, 416–421; (d) D. Suzuki, H. Taniguchi and R. Yoshida, J. Am. Chem. Soc., 2009, 131, 12058–12059; (e) M. Keerl, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2009, 131, 3093–3097; (f) A. C. Brown, S. E. Stabenfeldt, B. Ahn, R. T. Hannan, K. S. Dhada, E. S. Herman, V. Stefanelli, N. Guzzetta, A. Alexeev, W. A. Lam, L. A. Lyon and T. H. Barker, Nat. Mater., 2014, 13, 1108–1114; (g) T. Kureha and D. Suzuki, Langmuir, 2018, 34, 837–846; (h) T. Watanabe, Y. Nishizawa, H. Minato, C. Song, K. Murata and D. Suzuki, Angew. Chem., Int. Ed., 2020, 59, 8849–8853; (i) F. Grabowski, V. S. Petrovskii, F. Fink, D. E. Demco, S. Herres-Pawlis, I. I. Potemkin and A. Pich, Adv. Sci., 2022, 9, 2204853.
17. (a) G. Nakada, Y. Igarashi, H. Imai and Y. Oaki, Adv. Theory Simul., 2019, 2, 1800180; (b) H. Numazawa, Y. Igarashi, K. Sato, H. Imai and Y. Oaki, Adv. Theory Simul., 2019, 2, 1900130; (c) K. Noda, Y. Igarashi, H. Imai and Y. Oaki, Adv. Theory Simul., 2020, 3, 2000084; (d) K. Noda, Y. Igarashi, H. Imai and Y. Oaki, Chem. Commun., 2021, 57, 5921–5924; (e) Y. Haraguchi, Y. Igarashi, H. Imai and Y. Oaki, Adv. Theory Simul., 2021, 4, 2100158; (f) K. Sakano, Y. Igarashi, H. Imai, S. Miyakawa, T. Saito, Y. Takayanagi, K. Nishiyama and Y. Oaki, ACS Appl. Energy Mater., 2022, 5, 2074–2082; (g) T. Komura, K. Sakano, Y. Igarashi, H. Numazawa, H. Imai and Y. Oaki, ACS Appl. Energy Mater., 2022, 5, 8990–8998.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc04386c

---