Flow-gel approach enables rapid extraction of pure magnesium phase from seawater

Abstract

Current methods for separating critical materials from feedstock solutions remain chemistry- and energy-intensive. We demonstrate the rapid extraction of a pure magnesium phase from seawater via precipitation with sodium hydroxide in a flow-gel device. Our approach is scalable, suitable for high-throughput extraction, and does not rely on specialty chemicals.

---

Advancing to a sustainable and green economy will require a reliable supply of critical materials, whose sourcing is currently beset by environmental and ethical challenges. These materials include rare earth, transition, and other metals, essential for various technologies, ranging from renewable energy devices and batteries to consumer electronics and semiconductors.¹ Accordingly, the National Academies of the United States of America have highlighted the need for new chemical separation technologies to mitigate these supply chain concerns.²

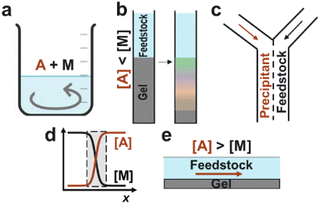
One solution to this problem involves re-imagining precipitation, which is a cornerstone technique in the chemical separations industry. Traditionally, the feedstock solution is directly mixed with a precipitating agent, which yields insoluble products that are then separated from the feedstock stream (Fig. 1a). However, since many target ions have comparable solubilities and chemical properties, this process often results in a crude mixture of multiple precipitates that require further purification steps.

Fig. 1 Schematics of precipitation-based separation methods. (a) Bulk mixing of the precipitating agent (A) and feedstock (M) solutions, (b) precipitation chromatography and (c) laminar co-flow separations, (d) steep concentration gradients at liquid–liquid interface, (e) proposed flow-gel method for rapid separations.

Recently, we reported two methods for precipitation-based separations that show significant improvement in extracting specific elements compared to bulk mixing. The first method is “precipitation chromatography”, wherein a feedstock solution is placed in a column on top of a gel loaded with precipitant (Fig. 1b).³ As the metal ions diffuse into the gel, the fastest-forming product consumes the precipitating agent, delaying the nucleation of the competing ions. The result is a spatial unfolding of the various precipitates along the length of the column – even for target ions that have comparable solubilities. In the laminar co-flow method,⁴ the feedstock and precipitant solutions flow side by side in a microfluidic device, creating a liquid–liquid interface where precipitation occurs (Fig. 1c). Although multiple components are supersaturated at this interface, only the fastest-forming product begins to precipitate and locally depletes the precipitating agent, thus achieving separations. Using these two methods, we have demonstrated the recovery of magnesium from seawater, manganese from battery cathodes, and neodymium from magnet solutions.^3–5

The common feature between the laminar co-flow and solution-gel methods is that the separation efficiency is enhanced by the coupling of ion transport and precipitation kinetics.^6–9 Rather than precipitating all supersaturated species in a mixed reactor, these methods create local conditions wherein the interplay between crystallization, diffusion, and reactant depletion can achieve separations beyond predictions based on solubility constants. Moreover, these methods do not require specialty membranes, ligands, or solvents. Instead, they rely on simple commodity chemicals such as sodium hydroxide (NaOH) as the precipitating agent. However, two main challenges need to be addressed: (1) Can the solid products be recovered efficiently from either the gel or microfluidic device? (2) Can the process be scaled up to high capacity and throughput?

In this work, we developed an alternative “flow-gel” method that addresses these challenges and enables the rapid recovery of target ions from multicomponent solutions. Our rationale was to reproduce the unique condition of sharp concentration gradients at the liquid–liquid interface (Fig. 1d), without the need for co-laminar flow in a microfluidic device. In the proposed approach, the feedstock solution is delivered on top of a thin gel layer loaded with a high concentration of the precipitating agent (Fig. 1e). Since the total ion concentration in the gel layer is larger than that in the feedstock, the ion flux was primarily from the gel into the feedstock solution. We anticipated that the precipitates would form mainly in the flowing solution, such that the particles could be collected downstream.

To validate this hypothesis, we attempted to extract magnesium from seawater using the flow-gel method. Magnesium (Mg) is designated by the U.S. Department of Energy (DOE) as a critical material¹⁰ due to its supply chain risk and importance for a variety of products, including magnesia-based cements,¹¹ biodegradable implants,¹² batteries,¹³ and alloys.¹⁴ Accordingly, there is increasing attention to sourcing Mg from seawater brines, but promising technologies remain at the laboratory scale.¹⁵ Recently, we reported the extraction of >99 at% pure Mg(OH)₂ product from seawater using the laminar co-flow method; an improvement from 88–95 at% purity obtained by direct bulk mixing.

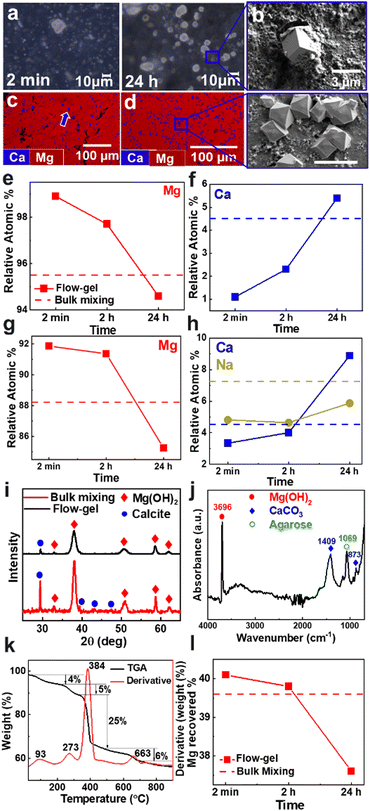
In the first set of experiments, we placed a synthetic seawater solution on top of an agarose gel layer loaded with 1 M NaOH in a Petri dish. The seawater solution contained typical concentrations of 10 902 mg L⁻¹ sodium, 1297 mg L⁻¹ magnesium, 392 mg L⁻¹ potassium, 386 mg L⁻¹ calcium, and 8 mg L⁻¹ strontium ions.¹⁶ In two separate batches, the Petri dishes were either kept under static conditions or continuously shaken using an orbital shaker (see ESI† for details, Fig. S1). In all experiments, a white precipitate began to form near the solution-gel interface within a few seconds. The precipitate consisted of a thick layer of agglomerated small particles and few large crystals of 1–10 μm in size (Fig. 2a). After 24 h, the large crystals became more prominent and adopted euhedral shapes, as evident by scanning electron microscopy (SEM) imaging (Fig. 2b).

Fig. 2 Magnesium extraction from model seawater. (a) Optical and (b) SEM imaging of products of flow-gel method. (c) and (d) EDS maps of precipitates collected at 24 h using (c) flow-gel and (d) bulk mixing methods. Inset in (d) shows calcite crystals (3 μm scale bar). (e) and (f) EDS and (g) and (h) ICP-OES analyses showing Ca, Mg, and Na at% in the precipitates and comparison with bulk mixing (dashed lines). (i) XRD patterns of the precipitates collected at 24 h using flow-gel (black) and bulk mixing (red). (j) FT-IR spectra and (k) TGA curves of the precipitate obtained after 2 min, (l) % Mg recovered from the precipitates.

To evaluate the chemical composition of the precipitates, we performed energy dispersive X-ray spectroscopy (EDS) mapping (Fig. 2c). The smaller particles that agglomerate into a thick coating consisted primarily of a magnesium phase. In contrast, the larger euhedral crystals consisted mostly of a calcium phase, with only trace inclusions of magnesium. Similar particle morphologies were observed by direct bulk mixing of the seawater with 1 M NaOH in a 1 : 1 volume ratio, which produced more of the Ca-rich product (Fig. 2d). In addition to mapping the spatial distribution, we compared the relative composition of Mg and Ca in the various products (Fig. 2e and f and Fig. S2, ESI†). Using the flow-gel method, the precipitate consisted of 98.9 at% magnesium and 1.1 at% calcium after 2 min. The Mg content decreased to 97.7 at% after 2 h and 94.6 at% after 24 h. Meanwhile, the Ca content increased to 5.4 at%. By comparison, the products from bulk mixing had a relative composition of 95.5 at% Mg and 4.5 at% Ca; slightly improved from our previous study using bulk mixing but showing a less pure product compared to the rapid flow-gel method.

These results were further validated by inductively coupled plasma optical emission spectroscopy (ICP–OES) measurements (Fig. 2g and h and Fig. S2, ESI†). We observed higher purity products in the flow-gel method after 2 min and 2 h compared to bulk mixing. Notably, the ICP-OES data showed an appreciable amount of sodium; 4.8 at% at 2 min increasing to 5.9 at% at 24 h. By comparison, bulk mixing resulted in an even higher inclusion of 7.3 at% sodium.

Furthermore, the crystallographic nature of the products was determined using powder X-ray diffraction (XRD) measurements (Fig. 2i). The diffraction patterns showed that Mg(OH)₂ – specifically brucite – is the most dominant phase, as evident by the largest intensity [011] reflection at 38.1°.¹⁷ We also detected the minor presence of CaCO₃, identified by the calcite [104] reflection at 29.4°.¹⁸ Notice that the precipitates obtained by bulk mixing showed more intense calcite peaks compared to the flow-gel products, consistent with the earlier EDS and ICP-OES analyses. We also measured infrared (IR) spectra to confirm the precipitate chemistry (Fig. 2j and Fig. S3, ESI†). The most intense absorption band at 3696 cm⁻¹ corresponds to the hydroxyl (O–H) stretching vibrations of brucite Mg(OH)₂.¹⁹ The small broad band in the 3500–3200 cm⁻¹ range is attributed to hydroxyl stretching, indicating the presence of adsorbed water.¹⁹ The 1409 cm⁻¹ vibration is characteristic of the asymmetric CO₃²⁻ stretching band of the crystalline CaCO₃ phase.²⁰ Similarly, the 873 cm⁻¹ peak corresponds to the out-of-plane bending vibrations of the carbonate ions.²¹ The 1069 cm⁻¹ absorption peak of the C–O stretching suggests the presence of agarose inclusions in the precipitate.²²

We then used thermogravimetric analysis (TGA) to characterize the various components of the precipitate. Fig. 2k plots the weight changes during the heating process, which showed four key stages of product decomposition. The initial stage was a 4% weight loss around 93 °C due to the evaporation of residual adsorbed water at the precipitate surface. The second weight loss was 5% with a peak at 273 °C, indicating the removal of potential agarose inclusions.²³ The largest weight loss of about 25% occurred around 384 °C, corresponding to the decomposition of brucite Mg(OH)₂ into its end product MgO by releasing water molecules.²⁴ Finally, a 6% weight loss occurred around 663 °C, which is ascribed to the decomposition of CaCO₃ to CaO by the removal of carbon dioxide.²⁵ Additional TGA measurements on the precipitates collected at different time points showed similar results (Fig. S4, ESI†).

Furthermore, we quantified the recovery rate based on the total magnesium present in the original feedstock solution. Based on the TGA results, we assumed that the product included 5 wt% agarose and 4 wt% water. We also assumed that Ca existed exclusively as CaCO₃ and Mg as Mg(OH)₂. Fig. 2l shows that a reaction time of 2 min was sufficient to extract 40.1% of the total Mg, which decreased slightly after 5 and 30 min, reaching 37.6% after 24 h since some particles became entrapped in the gel over longer timescales (Fig. S8, ESI†). These recovery rates were on par with bulk mixing, which yielded a 39.6% recovery rate. Note that using [NaOH] = 0.1 M also resulted in a high-purity Mg product, but the crystals tended to grow in the gel, thus reducing the recovery rates (Fig. S8, ESI†).

In the next set of experiments, we implemented the flow-gel method by 3D-printing a prototype device to test the extraction of magnesium from seawater (see ESI† for details, Fig. S7). The device had an inlet for flowing the seawater feedstock via a syringe pump and an outlet where the outflow and the as-formed solid products could be recovered (Fig. 3a). The bottom of the device was coated with an agarose layer loaded with 1 M NaOH. A total volume of 35 mL of the gel was used, which resulted in a gel layer thickness of approximately 10 mm. As an initial attempt, a flow rate of 1 mL min⁻¹ was tested, but the particles grew to large sizes and sank into the gel, thus complicating their recovery.

Fig. 3 Flow-gel device (a) schematics of the high-throughput prototype, (b) snapshots showing precipitate formation within 1 min, (c) EDS maps of precipitate obtained at a flow rate of 30 mL min⁻¹.

Accordingly, we increased the flow rate to 30 mL min⁻¹, drastically reducing the residence time and rapidly processing 35 mL in less than 1 min (Fig. 3b). This was also facilitated by placing the device at a ∼10° angle to allow easier recovery of the precipitates, yielding 15.7 mg of the product in <1 min., with a relative atomic composition of 97.9 at% Mg and 2.1 at% Ca as confirmed by the EDS analysis (Fig. 3c). These values correspond to a recovery rate of 12.5% of the total Mg in the feedstock in a single pass through the device without additional optimization.

Beyond these benchmarking experiments, we anticipate that multiple parameters can be optimized to enhance the flow-gel separation process. These include the device's dimensions and shape, flow rate, gel thickness, and concentration of the precipitant. For example, the particles were accumulating near the narrow outlet channel, indicating that changing the device shape can increase the efficiency of product recovery.

To gain physical insights into the coupling between transport and precipitation reactions, we developed a simple model considering precipitation, advection, and diffusion under steady-state conditions (see ESI†). We assume that (i) the precipitation only takes place at the top of the gel interface (z = L) where a cationic reactant A (Mg²⁺) supplied by advection meets an anionic reactant B (OH⁻) supplied by diffusion throughout the gel and (ii) a concentration of B (C_B) at the bottom of the gel (z = 0) is maintained as a constant C_B0. Both assumptions allow us to develop a 1D reaction-diffusion-advection model by using a flux boundary condition for B at z = L, via a flux balance such that 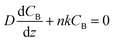, where D is the ion diffusivity, n is a molar ratio of B to A for precipitation (e.g., n = 2 for Mg²⁺⋯OH⁻), and k is a parameter (in a unit of length per time) representing advection and/or precipitation that will “remove” B at the gel interface. As such, k can be used to evaluate the relative importance of advection and precipitation in the process. Solving the 1D steady-state diffusion equation in z direction with the two boundary conditions yields:

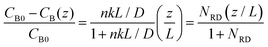where L denotes the thickness of the gel. Here, N_RD (= nkL/D) represents the relative timescale of advection/precipitation to diffusion. The two limiting cases are (1) N_RD ≫ 1 indicating an immediate consumption of B and diffusion as the rate-determining step and (2) N_RD ≪ 1 indicating advection/precipitation as a rate-determining step.

This simple model can be extended to the case of two competing reactants A₁ (Mg²⁺) and A₂ (Ca²⁺) in the feedstock. Following a similar scaling argument implies that N¹_RD ≫ 1 and N²_RD ≪ 1 is the condition to achieve separation of A₁ from the feedstock using the flow-gel approach, which can be optimized by tuning gel thickness, flow rate, and concentration, regardless of the details of the feedstock chemistry.

While the flow-gel method can be further optimized, we anticipate multiple advantages, namely improved separation efficiency, capacity, throughput, and product recovery:

(1) Higher separation efficiency compared to bulk mixing, on par with the laminar co-flow method.

(2) Feasibility of recovering the solid products downstream with a high yield.

(3) Significant increase in capacity and throughput of processing feedstock solutions.

(4) Significant decrease in the amount of hydrogel required compared to precipitation chromatography, since the gel serves as a reservoir of the precipitating agent rather than the reaction medium.

(5) Ability to separate ions from more dilute feedstocks compared to seawater using higher ion concentrations in the gel, which promotes ion flux into the feedstock.

Perhaps the main advantage of the flow-gel method is that it does not require specialty chemicals that are highly specific and difficult to scale-up. Instead, separations are facilitated by transport-precipitation coupling with simple chemicals already used in industrial separations. Future work should explore the applicability and optimization of this method to enable the recovery of critical materials from diverse feedstocks, including geothermal brines, electronic waste, produced water, and other sources where the target ion is more dilute than the competitor precipitating ions. The challenge is that the separation efficiency in the flow-gel method is predicated on differences in precipitation kinetics – beyond simply the relative solubility of the competing products – which are difficult to predict a priori.

The initial experiments were supported by the Open Call Initiative, under the Laboratory Directed Research and Development (LDRD) Program at Pacific Northwest National Laboratory (PNNL). The systematic experimental study, flow-gel device development, and model/scaling analysis were supported by the Laboratory Directed Research and Development (LDRD) program at PNNL, under the Non-Equilibrium Transport Driven Separations Initiative (NETS). PNNL is a multi-program national laboratory operated for the U.S. Department of Energy (DOE) by Battelle Memorial Institute under Contract No. DE-AC05-76RLO 1830.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

References

1. Minerals, Critical Minerals, and the U.S. Economy, 2008.
2. National Academies of Sciences, Engineering, and Medicine, A Research Agenda for Transforming Separation Science, National Academies Press, Washington, DC, 2019 DOI:10.17226/25421.
3. Q. Wang and E. Nakouzi, Environ. Sci. Technol. Lett., 2023, 10, 1188–1194.
4. Q. Wang, E. Nakouzi, E. A. Ryan and C. V. Subban, Environ. Sci. Technol. Lett., 2022, 9, 645–649.
5. Q. Wang and C. V. Subban, RSC Sustainability, 2024, 2, 1400–1407.
6. E. Tóth-Szeles, B. Bohner, Á. Tóth and D. Horváth, Cryst. Growth Des., 2017, 17, 5000–5005.
7. P. Papp, Á. Tóth and D. Horváth, Chem. Eng. Sci., 2022, 261, 117955.
8. X. Chen, M. Yang, S. Zheng, F. Temprano-Coleto, Q. Dong, G. Cheng, N. Yao, H. A. Stone, L. Hu and Z. J. Ren, Nat. Water, 2023, 1, 808–817.
9. E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, e1601144.
10. J. D. Applegate, 2022 Final List of Critical Minerals, 2022.
11. S. A. Walling and J. L. Provis, Chem. Rev., 2016, 116, 4170–4204.
12. S. Sankaranarayanan and M. Gupta, Mater. Today: Proc., 2021, 39, 311–316.
13. R. Deivanayagam, B. J. Ingram and R. Shahbazian-Yassar, Energy Storage Mater., 2019, 21, 136–153.
14. J. Zhang, J. Miao, N. Balasubramani, D. H. Cho, T. Avey, C.-Y. Chang and A. A. Luo, J. Magnesium Alloys, 2023, 11, 3867–3895.
15. D. Fontana, F. Forte, M. Pietrantonio, S. Pucciarmati and C. Marcoaldi, Environ. Dev., Sustainability, 2023, 25, 13733–13754.
16. M. Atkinson and C. Bingman, J. Aquaric. Aquat. Sci., 1997, 8, 39–43.
17. A. van Veelen, R. Copping, G. T. W. Law, A. J. Smith, J. R. Bargar, J. Rogers, D. K. Shuh and R. A. Wogelius, Mineral. Mag., 2012, 76, 3095–3104.
18. S. S. Al-Jaroudi, A. Ul-Hamid, A.-R. I. Mohammed and S. Saner, Powder Technol., 2007, 175, 115–121.
19. R. L. Frost and J. T. Kloprogge, Spectrochim. Acta, Part A, 1999, 55, 2195–2205.
20. J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Nanoscale, 2011, 3, 265–271.
21. D. Chakrabarty and S. Mahapatra, J. Mater. Chem., 1999, 9, 2953–2957.
22. A. Badri, S. Razak, W. I. Nawawi, N. Sabani, M. N. Norizan and A. Abul Shukor, Polym. Bull., 2023, 80, 9437–9450.
23. Q.-Q. Ouyang, Z. Hu, S.-D. Li, W.-Y. Quan, L.-L. Wen, Z.-M. Yang and P.-W. Li, Food Chem., 2018, 264, 277–283.
24. C. Liu, T. Liu and D. Wang, J. Therm. Anal. Calorim., 2018, 134, 2339–2347.
25. T. Siva, S. Muralidharan, S. Sathiyanarayanan, E. Manikandan and M. Jayachandran, J. Inorg. Organomet. Polym. Mater., 2017, 27, 770–778.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental results on notes on the reaction rate analysis. See DOI: https://doi.org/10.1039/d4cc04711g

---