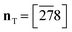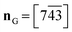A score and nine years of irbesartan

Abstract

Irbesartan is a non-peptide antagonist of the angiotensin-II-AT1 receptor and is used for the treatment of hypertension. Here, the history, achievements and open questions related to irbesartan are examined. Tautomery of the tetrazole moiety leads to two desmotropes, A and B. Roughly ten dozen data collections on single crystals at various temperatures, from X-rays and neutrons, are presented, deposited and interpreted; new structures are described and a detailed evolution of the thermal expansion is achieved. Disorder of the n-butyl-chains is observed in A and B. The trigonal desmotrope A builds its structure incorporating a hydrate channel upon nucleation. The hydrophobic nature of the n-butyl-chains induces the growth of a flat crown of chains in a meta-stable phase, disappearing after the thermally activated creation of a gauche conformer that distorts this wreath to a more prolate shape. This irreversible, conformational transition leads, henceforth, to a different evolution of lattice parameters and thermal expansion; the water inclusion explains the strained, imperfect crystallites, complex solubilities, a capricious packing coefficient and slow growth. In the triclinic desmotrope B, the all-trans → gauche disorder in the n-butyl-chain leads to random, diffuse changes in the structure between 265 and 165 K. As confirmed by calorimetry and thermal expansion, these subtle, local re-arrangements do not affect the space group and trigger a reversible, first-order phase transition at 208 K. The neutron study brings desirable clarity regarding the geometry of the tetrazole and its hydrogen, and precious reference values for the weak interactions. Focussing on the tetrazole and the n-butyl-chains, we propose an alternative interpretation of the ¹⁵N NMR spectra, published more than two decades earlier.

---

1 Historical review

The non-peptide angiotensin-II-AT1 receptor-antagonist irbesartan, 2-butyl-3-{[2′-(1-H-tetrazol-5-yl)biphenyl-4-yl]methyl}-1,3-diazaspiro[4,4]non-1-en-4-one, 1, is a godsend for people suffering from high blood pressure. First investigated in 1992 by Cazaubon et al.¹ and Bernhart et al.,² and initially marketed as Aprovel by Sanofi in 1997, it remained at the centre of efforts to raise the yield or avoid costly purification methods and expensive or dangerous solvents.^3–5 The structural ingredients required for such an antagonist were recently revealed in a spectacular femtosecond free-electron-laser experiment,⁶ namely (i) aromatic segments, (ii) acidic moieties on the tetrazole, (iii) aliphatic chains and (iv) hydroxyls (or halogens).

The usefulness of 1 is by no means limited to hypertension, but permeates other, unexpected areas of research as well. Thus, 1 has been reported to alter the gel → liquid crystal transformation in bilayer membranes, such as those of dipalmitoylphosphatidylcholine, by fine-tuning the amphipathic interactions in order to facilitate its diffusion to the receptor site.⁷ And 1,2-Dimyristoyl-sn-glycero-3-phosphoglycerol presents a mysterious phase between the gel and the fluid state; this can be triggered by an ionic strength inferior to 100 mM and pH > 6 or by adding losartan to the system. 1 might modify the viscosity η of the particularly viscous vesicular phase and tailor the delivery of encapsulated drugs.⁸ Another thread of research is devoted to improving the solubility of 1 by incorporating it into β-cyclodextrins and thereby optimising galenic properties.⁹ Another application concerns the use of 1 : 1 mixtures of amorphous atorvastatin and 1, which present improved intrinsic dissolution rates and aging properties.¹⁰ The antihypertensive effect of 1 is nowadays exploited to lower intraocular pressure by means of eye-drops containing 1 encapsulated in nano-particles of γ-cyclodextrin and tyloxapol.¹¹

Owing to the presence of the tetrazole moiety (Tet, Fig. 1), 1 exhibits a tautomeric equilibrium in solution (which Alkorta et al.¹² refer to as water-assisted proton exchange). This phenomenon is responsible for the wide and unresolved Tet-proton signal in solution.

Fig. 1 The structural formula of irbesartan, 1, with empirical formula C₂₅H₂₈N₆O, of which both desmotropes, 1-A (1H) and 1-B (2H), are shown. Abbreviations: Cp for cyclopentyl (turquoise), Imi for imidazole (blue), Tet for tetrazole (blue) and n.b.c. for the n-butyl-chain (green).

Bezard & El-Hajji¹³ substituted the Tet-hydrogen in solution with a methyl group and isolated the two isomers corresponding to the two tautomers. They confirmed, via¹³C solution NMR, the substantial difference in the chemical shifts of 154.7 (1-A) and of 165.4 (1-B) ppm for the carbon C5 of the Tet-ring, which was pointed out¹⁴ for the ¹³C solid-state (SS) NMR of the two desmotropes.

Quite complex acid–base equilibria of 1 in water have been reported,¹⁵ and an irreversible chemical reduction of 1 in water/methanol (7 : 3).¹⁶ Both processes are said to depend on the pH, and might likely also influence the dynamics of the N–H⋯N1N hydrogen bond.

Because of the rapid dynamical equilibrium in solution, it is, in general, challenging to separate these tautomers as two stable, solid forms. Although it was possible to obtain the desmotropes¹⁷1-A and 1-B for 1, this is a rather rare event. Indeed, there are few pharmaceutical compounds in the literature for which structures containing pure tautomeric isomers have been characterised; we can mention sulfasalazine^18,19 and omeprazole.^20–22 Later, the structures of other salts and/or hydrates of 1 were determined in which the Tet-cycle was either in the 1H form^23,24 or in the 2H form.²⁵

Both desmotropes of 1 were also thoroughly investigated via¹H and ¹³C solution-NMR, ¹³C and ¹⁵N solid-state CP-MAS NMR, vibrational spectroscopy²⁶ and growth studies (with additives).²⁷ The Tet is the most intriguing moiety in 1, not only for its bioisosterism,²⁸ but also because of its subtle electronic structure, which is challenging to model even via quantum chemical computation.²⁹

FTIR revealed that the low-energy region of 1 mainly contains internal deformation and torsion modes of the cyclopentyl (Cp) and n-butyl chain (n.b.c., Fig. 1) and that phonons play a very minor role indeed. The vibrations in the mid-IR range were considered difficult to assign because of spectral congestion,³⁰ until ref. 31 pointed out helpful vibrations capable of distinguishing the desmotropes; moreover, it was noticed that there was a structural or chemical instability of 1-B in a moist environment above room temperature. For the ¹⁵N NMR spectra of 1-B, a rather intricate model of correlated proton-hopping and Tet-flipping was proposed;¹⁴ the prohibitive cost (211.5 kJ mol⁻¹) of such a proton transfer was then estimated.¹² These authors also estimated the energies of hydrogen bonds in neutral N_Tet–H⋯N_Imi (imidazole, Fig. 1) and in the zwitter-ion N_Tet–H⋯N_imidazolium and concluded that both were possible and that the preference depended on the dielectric constants of the medium. A comprehensive study³² on the influence of solvent and acidity on the crystallisation of 1 is summarised in Tables S12 and S13 in the ESI.‡ By computations at the B3LYP/6-311++G** level, Franca et al.²⁶ obtained an accurate assignment of the ¹⁵N chemical shifts observed in 1. In a recent, multi-nuclear SS NMR study, Skotnicki & Hodgkinson³³ found that a 1-A → 1-B conversion is possible in the molten phase, leading, above T_g in the glass phase, to the presence of both desmotropes with rapid movement of the n.b.c. and a large-scale motion of the aromatic moieties.

The crystal structure of a columnar, triclinic crystal of 1-B, determined at room temperature,³⁴ contained two disordered conformers of the n.b.c., namely an all-trans (TT) and a gauche (G⁺T) one. We shall show here that this disorder is temperature-dependant and a source of interesting thermal phenomena.

Crystallisation of 1-A being difficult at best, the first structural characterisation of the fibrous crystallites of 1-A was obtained in 1999 from high-resolution synchrotron powder diffraction (carried out on beam-line BM16 at the ESRF under the direction of Professor Michel Anne, Fig. S16‡), in particular the trigonal unit cell and the space group R3̄.

The crystallisation and the growth of 1-A were investigated in depth.^35–37 These authors established that the growth of the prism faces of 1-A proceeded as regular over- and intergrowths and that the (hk0) faces were atomically rough. They also investigated the influence of solvents on the growth speeds of certain faces and computed the attachment energies. We present a summary of the habits, zones and growth properties of 1 in sections A.1.1, A.1.2, A.1.4 and A.2.2 (Fig. S18) in the ESI.‡

A very thin prism from these earlier experiments³⁵ was studied using synchrotron radiation at the ESRF (beam-line ID11) in 1999 and yielded the first rough structure of 1, containing the coordinates of an ordered model, but no standard uncertainties, nor confidence factors, not to mention any experimental conditions or CCDC number. This approximate model was used³⁰ for a terahertz spectroscopic study; later, Schenk-Joß et al.³⁸ obtained a quite convincing model, the refinement of which has now culminated in the deposition of the structure of 1-A in the Cambridge Structural Database.³⁹

We had already established³⁸ the presence of water in the channels of 1-A; using state-of-the-art equipment we shall present here deeper insight into the fine details of the structure, such as the molecular disorder and the positioning of the 1-H Tet-hydrogen. We have collected, at various temperatures, new X-ray and neutron diffraction data for both desmotropes, and carried out DSC experiments (Fig. S35‡) at low temperature for 1.

Their interpretation provides the thermal evolution of the structures, accurate geometries of the active Tet-moieties, and a thorough analysis of the static and dynamic disorders of the n.b.c., hinted at for 1-B³⁴ and altogether novel for 1-A. These disorders are temperature-dependant and furnish further insight into hitherto unknown phase transitions in this system.

2 Experiments

2.1 Crystal growth

Numerous attempts at growing crystals of 1 were carried out, starting from microcrystalline powders dissolved in various mixtures of solvents. Even the naked eye could tell that in certain crystallisations there appeared two different concomitant habits. Indeed, some single crystals of 1 grow to a stubby habit, of which the longest edge can reach more than one millimeter (1-B), whereas others develop a notoriously fibrous habit with an aspect ratio of 70 or more (1-A). The growth of this elongated, trigonal prism is very slow (its thickness reaches hardly 5 to 6 microns) and the growth of the rhombohedron is clearly fastest, as suggested by simple Bravais–Friedel–Donnay–Harker (BFDH) theory.^40–42 In the luckiest case, our results are as good as Taulelle et al.'s,^36,37 and quite beautiful faces could be obtained, as shown in Fig. S18‡ (see also the SEM photograph (Fig. 4 in ref. 37)). The most promising single crystals of 1-A were obtained via diffusion of ethanol into water. Various methods of crystallisation of 1 are compiled in Table S12,‡ amongst which is the one we used: heating a suspension of 1 in acidic water to 85 °C affords well-defined beautiful single crystals of the desmotrope 1-B (Fig. S3–S6, S12 and S13‡).

2.2 Data collections

A drop of mother liquor containing two crystals of 1-A was scooped up, placed on a glass slide, analysed on a stereo-microscope and immediately mounted in the cold stream (133 K) on a Bruker-Nonius KCCD diffractometer equipped with Mo radiation. The results of the crystals were similar and we report one of them only (AM1 in Table S9‡). Others were then kept – for subsequent data collections – in sealed tubes over several years, either in their mother liquor or in Paratone oil (see ESI-A-2‡).

Two crystals of 1-B were measured: B1 at 125 K (B11), at 231 K (B12) and at 293 K (B13) using X-rays (see Table S6‡), and crystal N3 at 125 K (N32) and at 293 K (N31) using neutrons at the ILL in Grenoble. Later, four more crystals of this same batch, kept in a refrigerator, gave rise to more series of data collections (see ESI-A-1‡).

3 Desmotropy

3.1 Molecular duality

In view of the disperse earlier atom numberings, we decided to break free from any prior constraint and re-define it according to IUCR-standards (see Fig. 1, S1, S7, S17, S21 and S24‡).

In 1-A (see Section A.2‡), 1 adopts a flattish (thickness ∼ 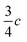) shape (Fig. S2a‡) and presents the hydrogen atom, H1, on the Tet ring at the position adjacent to carbon atom C5 (Fig. 1 or S17‡). In the T-shaped 1-B (Fig. S2b‡) atom H2 is found on the nitrogen opposite to carbon C5 (Fig. 1 and S1‡).

In the following discussion and according to common knowledge, we shall be using normalised bond lengths and angles wherever they are appropriate (e.g., 1.089 Å for C–H). Owing to the large dispersion of the N–H distances in the literature (e.g., Troyanov et al.⁴³ found values between 1.007(13) and 1.043(12) Å at 80 K and even 1.14(5) Å at room temperature for (NH₄)H₅(PO₄)), we finally decided to retain our freely refined values of this bond in the analyses and discussions, especially those from neutron data.

The distances d(N–H) are, from X-ray analysis, 0.96(3) Å at 114 K in 1-A, and 1.00(2) Å at 100 K in 1-B (even a nice 1.12(2) Å at 125 K from neutron analysis). Moreover, in both desmotropes, the Tet-hydrogen participates in a strong hydrogen bond towards the unsubstituted nitrogen of the Imi-ring of the closest neighbour (Table 2). The intermolecular nitrogen–nitrogen distance between Tet and Imi, associated with the hydrogen bonds, is near-identical in both forms: 2.739(3) Å in 1-A (at 114 K), 2.7292(18) Å in 1-B (at 100 K) and 2.730(9) Å (at 125 K from data collection N32).

The n.b.c. is disordered in both desmotropes. For 1-B, Böcskei et al.³⁴ had already determined a TT/G⁺T-ratio of 0.659(12) : 0.341(12) at 293 K; we analyse this over an extended range between 360 and 90 K (Fig. 7 left). For 1-A we establish, for the first time, an intricate static and dynamic ordering process of the n.b.c. between 360 and 90 K.

The Cp in 1-A (Fig. S23 or S24‡) adopts a unique envelope conformation at all studied temperatures, atoms C6N,…,C9N defining the plane 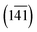and atom C5N lying about 0.52 Å off this plane. The mean planes of the Imi and the Cp are roughly perpendicular (85°), and intramolecular C–H⋯O and, possibly, C–H⋯N hydrogen bonds might stabilise the Cp in the Cp + Imi moiety.

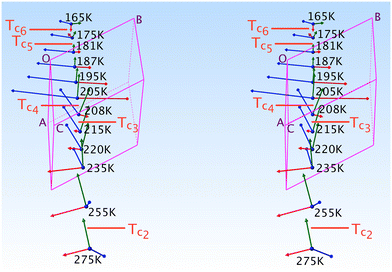
Although the Cp in 1-B is disordered, the same intramolecular interactions as in 1-A are also active here and the Cp/Imi planes are even more perpendicular to each other (88.6°). Below 165 K, we observe one envelope conformation of the Cp of which plane (213) contains all the atoms, but with C7N lying 0.62 Å above the plane (Fig. S7‡); however, above T > 165 K, a second envelope (same plane, but with the out-of-plane atom C8N) is generated by a dynamical process (Fig. 7 right and S41‡), seemingly correlated to the dynamics of the n.b.c.

The Tet-geometries resulting from our refinements are graphically summarised in Fig. S58 and S61.‡ They all lie well within the ballpark of those found in the CCDC structures, shown in the Fig. S59 and S62.‡ The computations (in the gas-phase), based on rather large basis sets and high levels of theory, shown in Fig. S57 and S60,‡ have also reached a convincing correspondence (e.g., Δ_dist < 0.015 Å (ref. 44)). Therefore, the intermolecular interactions (crystal effect) appear weak in these crystals. Note that more elaborate computations do not necessarily lie closer to observations. The observed bond lengths and angles in 1 are very similar at all temperatures between 90 and 360 K. This seems to indicate an absence of significant libration up to quite high temperatures. At the lowest temperature, the atomic displacement parameters (ADPs) of the Tet are quite isotropic, but at about 200 K, a component perpendicular to this ring begins to develop. It is fair to say that the molecules do not vary beyond expected libration below the glass transition.¹⁰ Not even the indices of the planes π_Imi and π_Tet vary a lot, and neither do their dihedral angles.

In 1-A, at T = 90 K, the plane 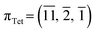very nearly (12.6°) lies in the [001] zone, and the main dihedral angles⁶ (explained in Fig. S30‡) τ₀, τ₁ and τ₂ are 33.5, 49.9 and 39.9°, respectively. These hardly vary in the temperature range.

In 1-B, π_Tet = (459̄) is a good description of this plane throughout the temperature range, and π_Imi = (043̄), at 90 K, changes only a little to (098̄), at 360 K. The dihedral angles τ₀, τ₁ and τ₂ are 40.9, 30.9 and 55.0° at 90 K; note that τ₁ undergoes a discontinuous change by roughly 2.5° between 195 and 215 K. Even this conspicuous geometrical change succeeds in hiding in a superposition of the structures.

The endocyclic distances and angles of the Tet in 1-A are remarkably similar between 90 and 365 K; the differences in the distances observed are less than 0.015 Å, and those in the angles are lower than 0.5°. At 114 K, the N–N–N bond angles in the Tet are quite regular, i.e., 106.61(13) (N1–N2–N3) to 110.75(13) (N2–N3–N4), and so are the bond lengths: the “double” ones are 1.296(2) and 1.324(2) Å, and the “single” ones lie between 1.340(2) and 1.361(2) Å. They lie close to Balabin's²⁹ values and confirm the classical picture with double bonds between N2–N3 and C5–N4 (see Fig. S60‡).

In 1-B, the endocyclic angle at N2, the carrier atom of H2, varies little between 360 and 90 K (0.023 Å), and is clearly bigger than those around the other ring atoms, namely 113.89(9)° at 90 K. A naive χ² test comparing the computed and observed distances is worse for 1-B than 1-A. The differences between “double” and “single” N–N bonds become blurred and only N4–C5 is prominent (1.3584(15) Å), and the spread of the endocyclic angles becomes wider. Yet, it is the Tet in 1-B that presents the higher aromaticity-index.⁴⁵ It appears that in 1-A, the steric effects near the carbon C5 oppose the electronic effects due to the position of the hydrogen, while these effects add up in 1-B and lead to a less symmetric geometry of the Tet (Fig. S58‡).

Should we be disappointed with the performance of the high-level computations for the Tet in 1-B? Many of the complex features of 1-B are still awaiting an entirely satisfactory explanation. Some of them are clearly related to the intriguing hybridisation of the Tet ring, e.g., the surprising shortness of the N2–N3 bond (1.3124(18) Å) and its strength (intrinsic bond strength index (IBSI)⁴⁶) at room temperature in 1-B. We believe that Pauling's resonance structures and their modern computational implementations⁴⁷ might lead the way to progress in these questions, especially when paying particular attention to the influence of aromatic electron-donating substituents as in 1.⁴⁸ In ESI Section A.1.5‡ we present some qualitative hints on how to explain these features (Fig. S15‡).

Indeed, the analysis by resonance shows that the geometry of the Tet in 1-A can be explained by the left two resonance structures in Fig. S15,‡ but that three such structures are required for obtaining a satisfactory description for the Tet in 1-B, in particular those with charges or double excitations (Fig. S15‡). This model will also be helpful for explaining the 2D exchange spectroscopy (EXSY) ¹⁵N SS-observations (section 3).

In Imi, the endocyclic distances and angles are remarkably similar in both desmotropes, yet the molecular conformations in 1 are clearly different in the two forms (Fig. S2‡). In both desmotropes, at high temperature (i.e., above T_g), the ADP-surfaces have become quite prolate for all Imi and Tet atoms. In 1-B the biggest displacement of all the Tet-atoms lies normal to π_Tet, and that of the Imi-atoms lie parallel to 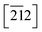. In 1-A this displacement also lies normal to π_Tet for the Tet-atoms, but that of the Imi-atoms lie within π_Imi = (321̄).

3.2 Structural dichotomy

The position of the hydrogen on the Tet has decisive consequences in the solid state. Indeed, in 1-A (Fig. 2 and S53‡) the N1–H1⋯N1N hydrogen bond pulls the Tet to an orientation almost perpendicular to the plane of the dimer; in 1-B the hydrogen bond and the Tet lie approximately within said plane (Fig. 3 and S55‡).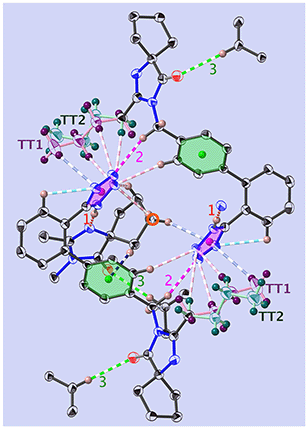

Fig. 2 View of the dimer in 1-A, at T = 130 K and along [001]. Shown are the principal interactions (see Tables 1 and S8‡) and the centre of inversion (red circle): N–H⋯N (red, u₁), C–H⋯O (green, u₃), C–H⋯N (pink, u₂), C–H⋯π (blue) and intramolecular bonds are turquoise. COG0 (pink) is the centre of gravity of the tetrazole, and COG1 (green) is that of the phenyl C1B,…,C6B. The all-trans n.b.c. TT1 is purple, and TT2 is blue-green (more complete figure in Fig. S64‡).

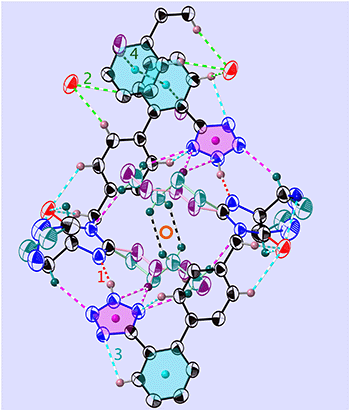Fig. 3 View of the folded dimer (or “madeleine”) in 1-B, at T = 255 K and in the molecular plane (213̄). Shown are the main interactions (see Tables 2 and S15‡) and the centre of inversion (red circle): N–H⋯N (red, v₁), C–H⋯O (green, v₂), C–H⋯N (turquoise, v₃), and C–H⋯π (dark green, v₄). COG0 (pink) is the centre of gravity of the tetrazole and COG1 (turquoise) is that of the phenyl C1P,…,C6P. The all-trans n.b.c. TT is purple and the GT one is blue-green (more complete figure in Fig. S65‡).

But, we shall show below that there is a unifying structural entity, too: the disordered n.b.c. groups are the main driving forces for the thermal phenomena within a large temperature range. The thermal evolution of their occupation numbers is shown, for 1-A, in Fig. S36‡ and for 1-B, in Fig. 7 left.

3.2.1 1-A. The interactions in 1-A suggest the following, hypothetical growth scenario, which, of course, needs confirmation. Its trigonal crystalline edifice (and its nucleation) is triggered and determined by the strong hydrogen bond u₁ (Table 1) which firmly connects two molecules swimming in the solvent. Then u₂ teams up with u₁ to make the nucleus grow bigger. After this, the only notable C–H⋯O interaction, u₃, joins forces and initiates the lateral growth of the crystal (Fig. S31‡), connecting three such dimers into one coil of the characteristic rod (elica) of this desmotrope, thereby creating the screw rotations 3₁ and 3₂. These hydrogen bonds (periodic bond chain (PBC)^49,50) also naturally explain the habit of 1-A (see ESI Section A.3‡).

Table 1 Normalised [to d(C–H) = 1.089 Å, except d(N1–H1), which was refined to 0.977(17) Å] hydrogen bonds (Å, °) in 1-A at T = 90 K (fuller version in Table S14‡)

u	D–H⋯A	H⋯A	Symmetry operation	∠DHA
1	N1–H1⋯N1N	1.758(17)	⅓ − x + y, ⅔ − x, −⅓ + z	176.1(17)
2	C1M–H1MA⋯N3	2.434(2)	1 − x, 1 − y, 1 − z	157.7
3	C6P–H6P⋯O1N	2.499	⅔ − y, ⅓ + x − y, −⅓ + z	170.1

---

The effect of this dominating hydrogen bond u₁ causes a spiral arrangement of left-handed molecules around the screw axis 3₂ at 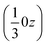. But other right-handed molecules circulate in the mother liquor as well, and these assemble in a second column around 3₁ at 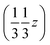(Fig. S54‡). The two rotations are of opposite sign, and therefore related by a centre of inversion at 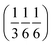(Fig. S53 and S64‡); they are anchored to each other by means of u₂ and define a dimer we refer to as open. Because of the ternary symmetry, this happens six times and in such a way, the [001]-channel comes to lie at (00z).

We may thus describe the structure of the desmotrope 1-A as a collection of columns, of rod-group p3₁11, with alternately right-handed molecules at 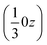, 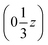and 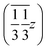, and left-handed molecules at 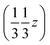, 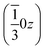and 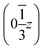. Each six closest such columns generate a threefold roto-inversion axis at (000), 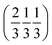and 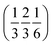, thus enclosing [001]-channels (Fig. S32‡), and defining in the van der Waals picture a bore of about 5 Å.

Most of the interactions participate in the build-up of “bagels” (open dimers); note especially the clear attraction of the n.b.c. TT1 (Fig. 2 and S64‡) with the plane of the Tet by the two C–H⋯N, u₇ and u₈, and one C–H⋯π, u₁₇. Two other such interactions, u₄ and u₁₅, fix the Cp with respect to the COG0 and COG1.

Each molecule of 1-A has four nearest neighbours. These four neighbouring molecules establish fourteen interactions (cut-off 2.9 Å) with the Tet of the central molecule: quite strong hydrogen bonds u₁, u₂ and u₃, a C–H⋯π interaction C9N–H9NA⋯COG1, or u₄, and twelve weak interactions C–H⋯N, one of which (u₁₈) is intramolecular (Table S14 and Fig. S64‡).

The interactions most important for the structural cohesion are compiled in Table S14‡ and graphically represented in Fig. S20, S22 and S30.‡ In Fig. 2 and the Table 1, we did not show a plethora of further C–H⋯π and C–H⋯H–X dihydrogen bond⁵¹ interactions, so as not to overload the already dense representation.

While most of the atoms in 1-A undergo little, if any, change beyond the usual thermal expansion, the behaviour of the n.b.c. is different. Indeed, depending on the temperature and crystal history, we have identified up to three different conformers (Fig. S19, S20 and S47‡).

Since the n.b.c. groups extend towards the [001] channels, they are exposed to little steric hindrance and have, therefore, no reason not to adopt the stablest TT conformation (statistical disorder between chains TT1 and TT2). It is only at temperatures above 293 K that a substantial increase of the dynamical disorder between the major TT and a G⁺T-conformer sets in. The corresponding occupation numbers will cause different conversion rates during the next cooling cycle.

Indeed, upon lowering the temperature towards 95 K, the occupation numbers of the conformers became quite different from those of the first heating cycle. It is tempting to correlate the temperature range of this growing conversion with the β-process in a thermally stimulated current (TSC)-spectroscopic study.⁵²

In the final stages of the refinement of crystal A1 (ESI Section A.2.2.3,‡ CCDC-number 1999410), difference maps revealed the presence of residual density of up to 0.85 e A⁻³ in the channels mentioned above. Our refinements then led, painstakingly, to the hitherto unknown realisation that these residuals corresponded to partial oxygen atoms from water molecules, in particular in crystals freshly fished out of their mother liquors. Based on the AM1 data, this finding was presented at IUCr-22 in Madrid,³⁸ and later⁵³ corroborated by ¹³C-NMR SS-spectra.

The main identified maxima lie in the neighbourhood (roughly 2.4 Å away) of the methyl groups of the minority TT2 n.b.c. As reported in ESI Section A.2.2.4,‡ (CCDC-number 2268210), crystal A1 did furnish a rather satisfactory description of the partial water molecules (imposing only a mild ISOR restraint). Indeed, we found seven partial oxygen atoms (Fig. S28‡), the site occupancy factors (s.o.f.s) of which added up to 1.2 waters per molecule of 1, pleasantly close to the value of 1.0 afforded by Spek's SQUEEZE algorithm. Unsurprisingly, the water content of the air-dried crystals is lower; density maps from crystal A2 (ESI Section A.2.2.2,‡ CCDC-number 1999411) indicate that the channels do not contain any residual density larger than 0.18 e A⁻³, corresponding to 0.3 waters. This water is not bound very tightly to the channel walls and leaves the crystals, not eagerly, but readily, when out of the mother liquor.

3.2.2 1-B. The N_Tet–H⋯N_Imi hydrogen bond v₁ (Table 2), is, by far, the strongest interaction in 1-B, estimated at ∼44 kJ mol⁻¹, stronger than an analogous bond involving a hydroxy group.²⁸

Table 2 Normalised [to d(C–H) = 1.089 Å, except d(N2–H2) which was refined to 0.99(2) Å] hydrogen bonds (Å, °) in 1-B at T = 215 K. COG1 is the centre of gravity of the phenyl C1P,…,C6P (fuller version in Table S15‡)

v	D–H⋯A	H⋯A	Symmetry operation	∠DHA
1	N2–H2⋯N1N	1.766(2)	−x, 1 − y, 1 − z	169(2)
2	C6P–H6P⋯O1N	2.333	1 − x, 2 − y, 2 − z	145.0
3	C3P–H3P⋯N4	2.488	x, y, z	97.84
4	C3TT–H3TA⋯COG1	2.499(1)	1 − x, 1 − y, 1 − z	162.53(1)

---

Again, the n.b.c. groups are disordered, but here between a TT and a G⁺T conformer, which coexist within the same restricted volume and can dynamically convert into each other. Fig. 3 shows that the n.b.c. groups participate in various C_methyl–H⋯N hydrogen bonds (see Table S15‡). Between 210 K and 205 K, these bonds shorten by 0.1 Å. This shortening could be connected to the slowing-down of the 3-site-hop of the methyl group of the energetically favoured G⁺T-conformers. A direct consequence of this would be that the TT-conformer becomes rarer and rarer. Another manifestation of the transformation is the change, by 1.83°, of the dihedral angle between the planes of the Tet and its adjacent phenyl ring, τ₁.⁶

The phenyl C1P,…,C6P and its image under inversion at 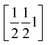, C1P′,…,C6P′, establish a π⋯π interaction (see Fig. S65 and Table S15‡). The distance of their centres of gravity (COG1) is 3.813(1) Å and their projections lie 0.39 Å apart along the vector b. This distance seems well accepted for a benzene–benzene style interaction according to Tsuzuki et al.⁵⁴ and Sakaki et al.,⁵⁵ with an estimated interaction energy of 2.05 kJ mol⁻¹.

The hydrogen H5B establishes a C–H⋯π interaction with the COG0 of the Tet ring (Table S15‡). Indeed, the normalised H⋯COG0 distance of 2.592(7) Å lies well in the range of [2.44…3.02] Å adopted by Ran & Wong⁵⁶ or that determined by Nayak et al.,⁵⁷ namely [2.56…2.84] Å.

The C–H⋯O/N hydrogen bonds we drew in Fig. 3 conform with the ranges determined by Brovarets et al.⁵⁸ in an exhaustive ab initio study. These interactions are partially compiled in Table 2 and more details are given in Table S15 and Fig. S14.‡

An inversion generates the pair of hydrogen bonds v₁ and −v₁ which, in turn, define a non-polar madeleine§ or closed-dimer structure, the orientations of which may be described by (538̄) planes. These dimers may already be formed in solution and the growth then consists in packing the madeleines in a compact way. The dimer (Fig. 3) is further stabilised by an intramolecular hydrogen bond, v₃ = [314], between the Tet and its phenyl (Table 2), and quite some more C–H⋯O1N interactions. In opposition to the dimers of 1-A, the n.b.c. groups are folded here and the oxygen atoms lie on the hull of the madeleines for further contact. This would explain the stability of the crust of the madeleines, which can be superimposed at all temperatures.

Since the interactions v₁, v₃ and others (Table S15‡) lie quite precisely in the plane (101̄), and since even v₂ presents a noteworthy component in this plane, we can image the growth to proceed in this plane (Fig. S63‡). This is a reasonable hypothesis, since the interactions mentioned above are amongst the strongest ones, v₁ being the dominant one (Table 2). Growth in the plane (101̄) is, therefore, much more likely than perpendicular to it; this is thus a case of layer-wise growth (ESI Section A.1.4‡).

But interactions perpendicular to (101̄) do exist, the π–π interactions (COG1–COG1 in Table S15‡) being one example, and for this reason one observes growth along a* as well.

A useful image of the solid-state structure is furnished by a cash box; indeed the dimers are stacked along the a*-axis like the coins in said box (Fig. S38‡). The structure is then completed by juxtaposing such columns in the “b, c” plane in a way resembling a tenon–mortise joint. But none of these interactions are clearly perpendicular to (101̄), and they are, in general, truly weak. We suspect that (100) might be a good cleavage plane, as opposed to (101̄) and (111), which are bad ones. The n.b.c. groups define the heart of the dimer and the O1N atom on the Imi lies at the border of the dimers, forming hydrogen bonds v₂ (Table 2 and Fig. 3) and v₉ (Table S15 and Fig. S65‡). These are the only marginally strong intermolecular interactions and one would therefore expect quite isotropic and small growth velocities. The very existence of columnar and tabular habits growing from the same mother liquor³⁵ had already indicated that the nucleation and growth of crystal 1-B are a rather delicate matter, and one would therefore expect quite isotropic habits owing to the comparable growth velocities. Along a*, the outside of the dimers offers nothing but van der Waals and C–H⋯π interactions.

In other words: the structure of 1-B owes its cohesion to a plethora of diverse weakest interactions entangled in a 3D network capable of the subtlest variations.

3.3 Thermal investigations

3.3.1 In 1-A. The thermal evolution of the lattice parameters, and the eigenvectors of the tensor of thermal expansion, α, are essentially determined by two factors: (1) the statistical (Fig. S26‡) and dynamical (Fig. S47‡) disorder of the n.b.c., and (2) the amount of water in the [001]-channels.

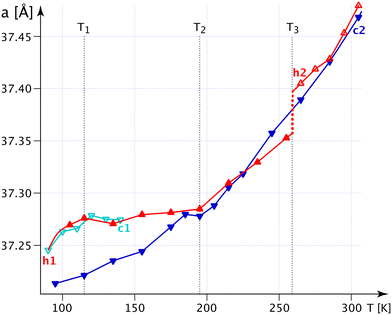
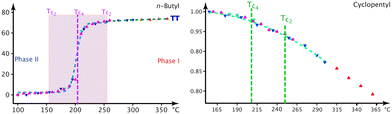
The bulges of the [001]-channels are filled with water at the time of crystallisation (see CCDC-number 1999410), and these filled bulges force the n.b.c. to adopt the flattest possible configuration. Thence, the lattice parameter a reaches its biggest value, and c, mutatis mutandis, its smallest one. The water is not very tightly bound and will – with time and temperature – leave the crystals; but the channels will not crumble spectacularly with less or no water, not before a substantial increase in the G⁺T-conformer above T₃ (Fig. 4) anyway. The fraction of the G⁺T-conformers keeps increasing up to 365 K, where it reaches ∼0.2. At a certain percentage of these conformers, the wreath of n.b.c. will become more prolate along c and narrower along a and change the behaviour of the system henceforth. The discontinuity of the lattice parameter a at T₃ and the different decrease in the occupation number of the chain TT2 upon decreasing the temperature indicate an irreversible process. We shall refer to the as-grown phase as I′ and to that thermally activated above T₃ as I. For the refinement of the n.b.c., some mild DFIX (1.54, σ = 0.03), DANG (2.54, σ = 0.04) and SIMU (σ = 0.005) restraints had to be used.

Fig. 4 The thermal evolution of the lattice parameter a in 1-A obtained from 42 DCs on A5K. c1 means the first (140 → 90 K) and c2 the second cooling (365 → 95 K), and h1 the first (95 → 255 K) and h2 the second heating (265 → 365 K). T₁, T₂ and T₃ = 260 K are characteristic temperatures referred to in the text.

Fig. S20‡ shows the crucial C4T1–H4TB⋯COG0 interaction (Table S14‡), which becomes shorter and stronger with decreasing temperature; indeed, more and more of the turquoise chains are converted into mauve ones. Therefore, the forces along c partly disappear and the crystal becomes softer along c, but, correspondingly, the forces in the “a, b” plane are reinforced and the structure becomes more rigid, thus reducing α₁₁.

The most spectacular observations in the thermal expansion in 1-A are caused by relatively tiny, and possibly also very slow, changes in the structure. These will be discussed in more detail in an upcoming study.

3.3.2 In 1-B. By scrutinising the structures and lattice parameters obtained from the early data collections B11, N31 and N32,³⁸ it had already been concluded that (i) the disorder (TT → GT) of the n.b.c. had locked-in at T = 125 K, and it was suspected that (ii) the principal thermal expansion coefficients presented a rather different functional form. In order to obtain more precise information on these issues, we conducted fifty more data collections, using copper radiation from a rotating-anode micro-source, at temperatures between T = 365 and 90 K. These demonstrated (Fig. 7 left) that the TT-conformer gradually disappears in a huge temperature interval of almost 100 K, passing through a 50 : 50 ratio at T_c4 = 208 K, where a clear discontinuity of the lattice parameters is observed.

In Fig. 5, we present the thermal evolution of the lattice parameters of 1-B obtained via X-ray diffraction from several crystalline and powdery samples. Upon lowering the temperature from 365 to 100 K, we observe discontinuities in most lattice parameters at T_c4 = 208 K. This thermal behaviour turned out to be reversible.

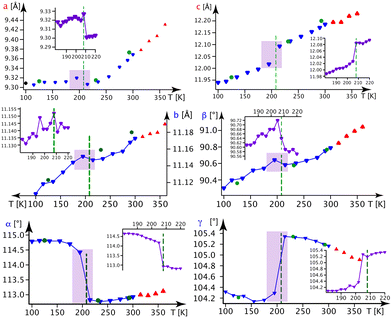Fig. 5 Lattice parameters in 1-B as a function of the temperature. Blue ▼s refer to the BD series, red ▲s to the BH series and violet ▼s to the BN series (the series BD, BH and BN are defined in section A.1. of the ESI‡). Green ●s refer to measurements on crystal B1 and black ◆s stem from a powder refinement using synchrotron data (the insets show a finer temperature evolution around the phase transition as indicated by the violet rectangle).

Here we shall discuss the evolution (Fig. 6) of the tripods of eigenvectors (largest norm in blue, medium in green and smallest in red) of the expansion tensor α in relation to the thermal ordering (conversion) of the n.b.c. moiety.

Fig. 6 The tripods of eigenvectors of the α-tensor of 1-B as a function of the temperature. Each blue dot corresponds to a data collection at the indicated temperature. The indices i near the red lines stand for the ith critical temperature.

Between 208 and 205 K, a domain corresponding to an equipopulation of the TT and G⁺T chains, we observe an abrupt re-orientation of the α-tripod, which is linked to a significant thermal event such as a first-order transition.

Above and below this clear thermal anomaly, subtle changes in the α-tripod and α-surfaces can be related to minor changes in the n.b.c. All these epiphenomenogical changes will be discussed in more detail in a follow-up publication, of which we can nevertheless present the main conclusions:

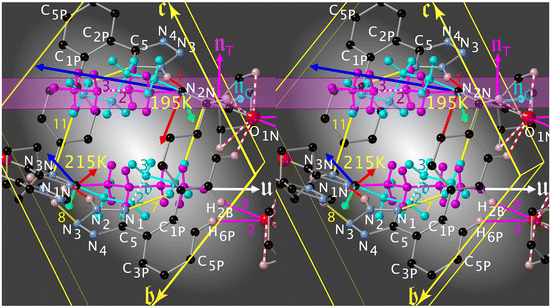
The red norm remains small (order of magnitude 10 MK⁻¹ at T = 300 K) above T_c4 and its eigenvector lies roughly along v₂; such a small thermal expansion in this direction hints at v₂ being the “strongest” interaction in this system. At T_c4, the red eigenvector suddenly inverts its direction (i.e., parallel to the vector d = r_C3GT − r_C2GT and quite perpendicular to π_Imi in Fig. 8) and enters a regime of negative thermal expansion with an eigenvalue of −150 MK⁻¹. Its norm gradually decreases down to T_c6, where its eigenvector reaches its final orientation of [331̄].

The green eigenvector presents quite normal values between 365 and 100 K; it lies approximately along [201̄] (v₈, Table S15‡). This hydrogen bond behaves quite normally and does not seem to be too affected by the conversion of the n.b.c. (it links atoms of the crusts of the madeleines).

The blue eigenvector lies roughly in the plane (1̄20) between 365 K and T_c4. It rotates around the red eigenvector from 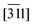to [1̄28] and suddenly jumps to [011] at T_c4. This change in orientation and huge eigenvalue of +316.3 MK⁻¹ (even for an organic compound) can also be rationalised: the n.b.c. groups slightly shorten during the TT → GT conversion; since the blue eigenvector lies roughly (Δ = 23°) parallel to the director u of the TT-chain (Fig. 8), it seems logical to associate this huge eigenvalue with an equally substantial smoothness in this direction.

We cannot help but conclude that the forces in 1-B cannot be coerced into a synthesis of – even numerous – classical interactions. Even ab initio kinds of computations are hampered by the various dynamical processes happening and changing at various temperatures. Nevertheless, they would furnish a valuable confirmation of some of the hypotheses advanced in this paper.

3.4 Phase transition in 1-B

The following picture of the phase transition at T_c4 = 208 K in 1-B has emerged from the interpretation of calorimetry (Fig. S35‡), thermal expansion (Fig. 6), the thermal evolution of the lattice parameters (Fig. 5) and the modelling of the chain dynamics via single crystal diffraction.

Our refinements show that at T = 360 K there are about 3/4 TT- and 1/4 G⁺T-chains. Upon cooling to liquid-nitrogen temperature, we observe: (1) the fraction of TT-conformers decreases to zero in phase II (Fig. 7) between T_c2 = 265 K and T_c6 = 165 K, (2) the thermal evolution of the lattice parameters (Fig. 5) reveals a thermotropic first-order phase transition at T_c4 = 208 K and (3) the freezing-in of a conformational disorder of the Cp ring occurs in phase I, right above T_c4. The preponderance of the G⁺T-conformer at low temperature (unlike in n-alkanes) can be understood via the attachment of the n.b.c. at the Imi^59,60 and the shrinking of their housing.

Fig. 7 Occupation numbers of the indicated moieties of 1-B as a function of the temperature. Blue ▼s stem from crystal K1, mauve ▲s from crystal K2, turquoise ▼s from crystal K3 and red ▲s from crystal K4. The reversibility of the transition is quite beautifully confirmed and the external standard uncertainty seems low. The very-extended nature of the OD processes is demonstrated.

The behaviour of the lattice parameters and the s.o.f.s of the n.b.c. upon re-heating seems very reversible (Fig. S51‡). We shall show below that the transition is first-order and isosymmetric involving two thermal regimes, one essentially cooperative and one decidedly chaotic and amorphous.

The G⁺T-conformer has lower energy in 1-B at low temperature and there is hardly any doubt that the conformers do inter-convert at higher temperature. Tóbiás et al.⁶¹ found conversion rates between 0.022 and 2400 ns⁻¹. Molecular dynamics (MD) computations also estimated that the activation energies for the conversions of the conformers are not symmetrical.^61,62 We conjecture that they also show a different temperature-dependence, and even depend on the location in the crystal. Indeed, no trace of diffuse scattering is observed, so we assume that this conversion of conformers is a local, non-collective phenomenon.

The extended domain of the TT → GT conversion makes us conclude that this is a chaotic process. It may then happen that, at a random location in the crystal, a TT-conformer remains trapped or blocked and therefore creates a local structure that is energetically different from the bulk. If E_T→G has become large enough, the frustrated TT-conformer may stay in its state even during the phase transition at T_c4. The crystal might therefore be in a rather inhomogeneous state around T_c4, in the sense that between different locations in the crystal there will exist a residual stress affecting the conversion rate of the n.b.c. Therefore, the conversion might not happen at the same temperature for all locations in the crystal. This state could be described by the space group P1, or even as partly amorphous.

This stress will reach a critical value at T_c4, such as to induce a cooperative release of the accumulated strain in a sudden deformation of the cell within a narrow temperature interval (this corresponds to the mauve, dashed line in Fig. S35a‡). But almost half the n.b.c. groups are still in the wrong conformation and in need of conversion. This conversion will take place, but at different temperatures, since they are all locally different; this process appears as the turquoise tail in Fig. S35a.‡ Upon warming up – or upon successive heating and cooling – these processes will be repeated within an even larger range of temperatures and the effects will be so minor that one cannot observe them any more.

4 Summary of hopes, achievements and caveats

We have discussed and deposited a number of structures of 1, in particular the still missing desmotrope 1-A. The tautomery of 1 in solution can be resolved, upon crystallisation in certain solvents, into (concomitant) desmotropes, of which the most conspicuous difference lies in their crystal packing. In 1-B, madeleines around a centre of inversion of the space group P1̄ are formed and then packed to a compact structure by growth of (101̄)-layers. In 1-A, p3₁-rods of 1 are built up, which are then laterally completed into a crystalline edifice in which one finds hexagonal channels along the threefold roto-inversion-axis. A [001]-channel is defined by six disordered n.b.c. groups pointing towards its centre; these channels are not homogeneous, but resemble a chain of sausages, of which the n.b.c. groups define the links, and the phenyls and tetrazoles the sausages. The bore is 5.5 Å at the links and 9.5 Å at the sausages.

We have shown that a crystal of 1-A – taken directly out of its mother liquor – does contain a variable quantity of water, not very firmly attached to the walls of the hexagonal channels near the n.b.c. In industrial batches of 1, it was shown, by ¹³C-NMR SS-spectra, that the methyl signal appeared as a doublet, of which the ratio is reproducible and constant for each of several factories, but as a singlet in carefully dried samples. Based on these observations, Chandrappa⁵³ finally formulated a relation between the water content and the quotient of the doublet intensities. Interestingly, this doublet had already arisen in Bauer et al.'s¹⁴ study of 1-A (but not in 1-B, which can be seen as a confirmation of the absence of water), but had not been further discussed; the presence of water in 1-A has also been conjectured from the shape of the baseline in terahertz spectroscopy.³⁰

The noteworthy interactions with neighbouring molecules of 1-A are compiled in Tables 1 and S14‡ and those of 1-B in Tables 2 and S15.‡ The strongest interaction in 1, N–H⋯N, behaves as a classical PBC in 1-A. This dominant force induces growth of long and thin prisms by linking molecules into endless helices around a 3₁ axis; such columns are then laterally connected by weaker hydrogen bonds to build up a 3D crystal edifice. The anisotropy of the forces leads to anisotropic growth velocities, attachment energies and corresponding habits. But in 1-B, hydrogen bond v₁ links only two molecules to a madeleine, which is then incorporated into a (101̄)-layer by the next strongest “PBCs” and the growth proceeds layer-wise. This eventually leads to a quite isometric columnar or tabular habit. The aggregation in various solvents remains an open and challenging issue, quite reminiscent of the phenomenon of inverse solubility, ref. 35 and 63's observation, and even the zwitter-ion character of 1 in relation to the pH of the mother liquor.

Void spaces for the two desmotropic structures (both at low temperature, no water) were visualized in Mercury with a probe radius of 1.2 Å and an approximate grid spacing of 0.7 Å. Unsurprisingly, a clear difference was found: no void in 1-B, but one of 11.75% of the total cell volume in 1-A. This discrepancy is also reflected in the packing coefficients (0.63 for 1-A, 0.75 for 1-B). The presence of these channels in 1-A entails a clear difference in the densities of the two polymorphs: 1.10 g cm⁻³ for 1-A versus 1.36 g cm⁻³ for 1-B; such a difference is quite uncommon between polymorphs, be they tautomers or not.

The n.b.c. groups are disordered in both desmotropes. In 1-A, one observes two TT-conformers between T₃ and 90 K; the population of one of them gets smaller and smaller with decreasing temperature. Although the methyl groups of the chains define the walls of the [001]-channels, they are hardly constrained and adopt TT conformations. The situation resembles the gas-phase of n-alkanes, in which the TT-conformer has lowest energy; a G⁺T-conformer begins to reach sizeable concentrations in 1-A at T₃ with increasing temperature.

In Fig. S20‡ we show the competition between statistical and dynamic disorder in 1-A: the TT1 (mauve) conformer is roughly perpendicular to π_Imi and more stable at low temperatures, whereas the TT2 (turquoise) one is more parallel to this plane. The occupation numbers vary between 90 K and T₃ and present a negative correlation; the turquoise occupation number reduces to 0.03(4) at liquid-nitrogen temperature.

After this statistical disorder has reached equiproportion at T₃, a new dynamical equilibrium between the three disordered conformers is adjusted (Fig. S20, S24 and S47‡). The G⁺T-conformer (green) has its zig-zag plane also quite perpendicular to π_Imi, and its occupation number increases up to 365 K, where it approaches 0.16 (turquoise, 0.42; mauve, 0.42).

In 1-B, the TT-conformer (mauve) lies in the plane of π_Imi and the G⁺T-conformer (turquoise) nearly perpendicular to it (Fig. 8). These two conformers are bound to coexist in a limited cylindrical space and the disorder is clearly dynamical here. Surprisingly, it is the unexpected^59,60 G⁺T-conformer that has the lowest energy and highest occupation number at low temperature. The fraction of TT to G⁺T-conformers is 3 : 1 above T_c2, 1 : 1 at T_c4 and 0 : 1 below T_c6.

Fig. 8 The triggering of the I → II transition for desmotrope 1-B, i.e., a rotation, by , of the turquoise C2CT–C3CT bond around vector u. Two α-tripods, centred at atoms C2N, at 215 and 195 K are shown. The white vector is parallel to the director of the TT-chain (mauve), and the turquoise vector d = [461̄] to atoms C2 and C3 of the GT-chain (turquoise). The mauve zig-zag plane is π_TT = (056̄), Δ = 1.04° and its normal vector is . The normal of π_GT is . The norms of the α-eigenvectors (tripod: red, green and blue) are not necessarily drawn to scale.

The endocyclic distances and angles of the Tet in 1 clearly lie in the ranges found by a search in the CSD (Version 5.42 (November 2020) + 2 updates): 169 compounds for 1H and 30 for 2H (Fig. S59 and S62‡). The same holds true for quite a few quantum-chemical computations (e.g., 5-azido-1H-tetrazole⁶⁴ for 1H and 5-(fluorodinitromethyl)-2H-tetrazole⁶⁵ for 2H). The question of the aromaticity has been answered in the comprehensive quantum-chemical analysis by Sadlej-Sosnowska,⁴⁵ who found that 2H is more aromatic than 1H. It remains quite challenging, however, to explain the deviations from an ideal geometry in terms of simple concepts, such as the number of repulsions of the lone pairs (two in 1-A, one in 1-B), bonding strain, ionic contributions to bonds or steric factors. It is also fair to say that many questions around Tet are far from settled.^44,66

The bond lengths are reminiscent of the classical “single” and “double” bond picture: in 1-A and many 1-H derivatives, the N2–N3 bond was found to be shortest and expresses, as expected, a diene character. In 1-B, surprisingly, the bond N3–N4 is not the shortest one, but rather it is the “single” bond N2–N3; and these distances indicate a more conjugated nature (see computations^45,66 and Fig. S57 and S60‡). The asymmetric HNN-angles around N2 in 1-B, or N1 in 1-A, are explained by the influence of the N–H⋯N1N hydrogen bonds; a nice coplanarity between N2–H2⋯N1N and π_Tet is observed in 1-B (Δ = 0.0025, 0.0744 Å).

Since we found a dynamical disorder of the n.b.c. in both polymorphs, compounded by one of the Cps in 1-B, it appears a valid idea to analyse the ¹⁵N spectra by means of these disorders. In 1-A, the mean zig-zag planes of the n.b.c. lie quite parallel to and stacked with the planes π_Tet (the channel walls), their methyl groups defining the narrowest bore (the links) of the channel point. It is always the TT1 conformer establishing at least three stable contacts with the Tet (Fig. S53‡), thus offering an explanation for the stable and narrow NMR signals at room temperature. Contrariwise, at the same temperature, in 1-B these zig-zag planes are not stacked with π_Tet, but rather juxtaposed laterally, thus offering a maximum of dynamical interactions between the Tet and the G⁺T-conformer, in particular via C4GT–H4GB⋯N1 (v₇, Table S15‡).

These ordering processes call for a more curious look at Bauer et al.'s¹⁴ observation on the thermal evolution, between room temperature and 253 K, of the ¹⁵N NMR signals of the Tet in 1-B; in particular, they report a correlation between the nitrogens in the pair (N1,N4) and in the pair (N2,N3). In their model, the latter correlation requires the dissociation of the rather strong N2–H2⋯N1N hydrogen bond, as well as a perfect 180° flip of the Tet followed by its re-protonation. Our results contradict the proposed model, indeed:

(i) The packing index of 1-B (0.75) seems inappropriate for 180°-flips, for which Dale et al.⁶⁷ reported a value of 0.645 and a timescale of 1 ms for N-salicylideneaniline. Such a “loose” structure appears more apt at accommodating the unwieldy disorder-movement of a pyridine, for which the weak C–H⋯N interaction provides a pivot. Gauto et al.⁶⁸ emphasise the importance of void volumes and coordinated movements of surrounding residues in the water-rich ubiquitin; they report timescales between 15 ns for the flips of PHE4 and 1 for those of PHE45.

(ii) The asymmetry of the Tet in 1 with respect to a perfect 180°-flip around the bond C2P–C5 (Fig. S58‡) and the quasi-isotropy of the ADPs of its constituting atoms are incompatible with such a motion.

(iii) No evidence for any proton delocalisation was found in 1-B during our neutron refinements.

All these points shed reasonable doubt on the ring-flipping model at least and allow us to suggest an alternative “non-flipping” explanation for the NMR observations. A realistic model should mainly be compatible with two features:

(i) the thermal evolution of the line-widths of the ¹⁵N NMR SS-spectra in 1-B, and

(ii) the correlations observed in the 2D-EXSY experiment at 253 K in 1-B.

Thence the broad lines in 1-B might be explained by: the wide distribution of chemical environments, the thermal evolution of the timescales of the disordered moieties, the more or less complete averaging of the various coupling tensors, and changes in the charge distribution within the nitrogens of the Tet. The thermal processes established in this work (Cp and n.b.c. surrounding the Tet) and the suggested resonance structures of the Tet (Fig. S15,‡ Scheme 8 in ref. 69 or ref. 66) provide a convincing and more likely way of improving the resolution of the ¹⁵N spectra. Indeed:

(i) they can induce a correlation in the pair (N1,N4) by modifying the charges of these atoms; moreover, the positive partial charge on N1 will strengthen the hydrogen bond v₇;

(ii) they can generate a weaker correlation in the pair (N2,N3); indeed the N⋯H⋯N bond fluctuations may induce a partial positive charge on the N atom of the N–H bond;

(iii) they can explain several typical features of the NNN- and NNH-bending frequencies observed.³¹

Note that our arguments do not require any flip after deprotonation (as proposed in ref. 14), nor a partial rotation without deprotonation (as proposed in ref. 12) in their base-promoted SS proton-transfer model. In their exhaustive study, Bauer et al.¹⁴ had already noticed both Cp and aliphatic disorders. But the lack of details of their dynamics and of EXSY-spectra at several temperatures hindered them from including these disorders in their model.

5 Conclusions

For 1-B, the combination of refinements, calorimetry, thermal expansion and evolution of lattice parameters led to the identification of a thermotropic, isosymmetric first-order phase transition and an intertwined, progressive inversion of the chain populations, covering almost a hundred degrees. Indeed, the hardly correlated reduction of the average amplitude of the molecular vibrations and the changing conversion rates of the two conformers build up a residual stress in the structure, which is then released at T_c4 = 208 K in a first-order transition.

For 1-A, similar experiments and evaluations revealed a meta-stable phase built up during crystal growth at room temperature owing to the presence of water in the [001]-channels. This phase is surprisingly long-lived and only disappears under a dynamical disordering of one TT-conformer at T₃. This disordering causes, in turn, a deformation of the wreath of n.b.c.; this new phase presents a quite different thermal evolution and never returns to the original phase. Bigger solvent molecules might possibly lead to a different behaviour.

We shall not try to end the controversy as to whether the presence of these traces of water excludes 1 from the realm of genuine tautomeric polymorphs. It is noteworthy that the existence and the impact of these kind of structures (i.e., desolvated solvates, dehydrated hydrates), which are capable of evolution with time and which play a role in the pharmaceutical world (e.g., zolpidem), did not meet with great interest in the influential journals dedicated to polymorphism of molecular crystals.^70,71 Since the Tet ring in irbesartan shows a distinct hybridisation in 1-A and 1-B, we can still classify 1 as a rare example of desmotropism.⁷²

The therapeutic usefulness and effectiveness of 1 were established a score and nine years ago. But solid irbesartan has still been awaiting the elucidation of some of its complex thermal features. We have shown 1 to be driven by a plethora of weakest interactions (most of them related to the disordering of the n.b.c.) generating varied and complex responses, such as its nucleation, phase transitions, and slow and diffuse thermal processes. More ambitiously, we have begun to interpret the build up of macroscopically observable phenomena from the interplay of weakest interactions and tiny structural changes. Attached to this work, the deposition of structures of 1-A and 1-B (see section A.1. in the ESI‡) at temperatures between 90 and 365 K will doubtless open the field for even finer analyses and a deeper understanding of the underlying processes.

Author contributions

P. O. defined the project, grew crystals, determined structures of the desmotropes, and supervised the progress of the research. M. E.-H. initiated and followed the project. F. F. collected and determined the X-ray crystal structures. M.-H. L. conducted and interpreted the neutron experiment. J. K. grew crystals of the 1-A desmotrope. D. G. performed the DSC experiments. P. O. wrote the original draft and M. B. and K. S. analysed the thermal behaviour, performed the necessary computations, and reviewed and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Beatrice Frey from the Departement für Chemie, Biochemie und Pharmazie der Universität Bern for the revealing DSC measurements of irbesartan. Thanks are also due to Mrs Audrey Gillet for help with crystallisation during her masters work at Sanofi-Aventis in Montpellier.

Notes and references

1. C. Cazaubon, J. Gougat, F. Bousquet, P. Guiraudou, R. Gayraud, C. Lacour, A. Roccon, G. Galindo, G. Barthelemy, B. Gautret, C. Bernhart, P. Perreaut, J.-C. Breliere, G. Le Fur and D. Nisato, J. Pharmacol. Exp. Ther., 1993, 265(2), 826–834.
2. C. A. Bernhart, P. M. Perreaut, B. P. Ferrari, Y. A. Muneaux, J.-L. A. Assens, J. Clément, F. Haudricourt, C. F. Muneaux, J. E. Taillades, M.-A. Vignal, J. Gougat, P. R. Guiraudou, C. A. Lacour, A. Roccon, C. F. Cazaubon, J.-C. Brelière, G. Le Fur and D. Nisato, J. Med. Chem., 1993, 36, 3371–3380.
3. S. Rádl, J. Stach, J. Havlíček, M. Tkadlecová and L. Plaček, Acta Chim. Slov., 2009, 56, 559–565.
4. S. N. Rao and K. S. Babu, Org. Commun., 2011, 4(4), 105–111.
5. J. Pandya, J. Verdia and N. Joshi, Afinidad, 2014, LXXI, 234–238.
6. T. F. Kellici, D. Ntountaniotis, E. Kritsi, M. Zervou, P. Zoumpoulakis, C. Potamitis, S. Durdagi, R. E. Salmas, G. Ergun, E. Godkemir, M. Halabalaki, I. P. Gerothanassis, G. Liapakis, A. Tzakos and T. Mavromoustakos, Curr. Med. Chem., 2016, 23, 36–59.
7. P. Zoumpoulakis, I. Daliani, M. Zervou, I. Kyrikou, E. Siapi, G. Lamprinidis, E. Mikros and T. Mavromoustakos, Chem. Phys. Lipids, 2003, 125, 13–25.
8. L. R. Winther, The Phase Transition of DMPG and its Dependence on pH, 2008.
9. A. S. Liossi, D. Ntountaniotis, T. F. Kellici, M. V. Chatziathanasiadou, G. Megariotis, M. Mania, J. Becker-Baldus, M. Kriechbaum, A. Krajnc, E. Christodoulou, C. Glaubitz, M. Rappolt, H. Amenitsch, G. Mali, D. N. Theodorou, G. Valsami, M. Pitsikalis, H. Iatrou, A. G. Tzakos and T. Mavromoustakos, Biochim. Biophys. Acta, Gen. Subj., 2017, 1859, 1089–1098.
10. M. Skotnicki, B. Jadach, A. Skotnicka, B. Milanowski, L. Tajber, M. Pyda and J. Kujawski, Pharmaceutics, 2021, 13, 118.
11. P. Jansook, C. Muankaew, E. Stefánsson and T. Loftsson, Pharm. Dev. Technol., 2015, 20, 626–632.
12. I. Alkorta, I. Rozas and J. Elguero, J. Chem. Soc., Perkin Trans. 2, 1998, 2671–2675.
13. J.-P. Bezard and M. El-Hajji, Personal communication, 1998.
14. M. Bauer, R. K. Harris, R. C. Rao, D. C. Apperley and C. A. Rodger, J. Chem. Soc., Perkin Trans. 2, 1998, 475–481.
15. P. Tosco, B. Rolando, R. Fruttero, Y. Henchoz, S. Martel, P.-A. Carrupt and A. Gasco, Helv. Chim. Acta, 2008, 91, 468–482.
16. B. Bozal, B. Doǧan-Topal, B. Uslu, S. A. Özkan and H. Y. Aboul-Enein, Anal. Lett., 2009, 42, 2322–2338.
17. J. Elguero, Cryst. Growth Des., 2011, 11, 4731–4738.
18. L. A. Filip, M. R. Caira, S. I. Fǎrcaş and M. T. Bojiţǎ, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 435–436.
19. A. J. Blake, X. Lin, M. Schröder, C. Wilson and R.-X. Yuan, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2004, 60, o226–o228.
20. P. M. Bhatt and G. R. Desiraju, Chem. Commun., 2007, 2057–2059.
21. N. E. Eltayeb, S. G. Teoh, C. K. Quah, H.-K. Fun and R. Adnan, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o1613–o1614.
22. M. K. Mishra, U. Ramamurty and G. R. Desiraju, J. Am. Chem. Soc., 2015, 137, 1794–1797.
23. G. Bartolucci, B. Bruni, M. Di Vaira and V. Giannellini, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, o1529–o1531.
24. L. Wang, L.-N. Zhou, Y. Bao and J.-K. Wang, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, o4933.
25. D. Stepanovs, in Material Science and Applied Chemistry: Scientific Journal of Riga Technical University. Vol. 27: Materials of the 8th Paul Walden Symposium on Organic Chemistry, 2013, p. 99.
26. C. A. Franca, S. B. Etcheverry, R. P. Diez and P. A. M. Williams, J. Raman Spectrosc., 2009, 40, 1296–1300.
27. E. Garcia, C. Hoff and S. Veesler, J. Cryst. Growth, 2002, 237–239, 2233–2239.
28. F. H. Allen, C. R. Groom, J. W. Liebeschuetz, D. A. Bardwell, T. S. G. Olsson and P. A. Wood, J. Chem. Inf. Model., 2012, 52, 857–866.
29. R. M. Balabin, J. Chem. Phys., 2009, 131, 154307.
30. S. P. Delaney, D. Pan, M. Galella, S. X. Yin and T. M. Korter, Cryst. Growth Des., 2012, 12, 5017–5024.
31. A. M. Araya-Sibaja, C. E. M. de Campos, C. Fandaruff, J. R. Vega-Baudrit, T. Guillén-Girón, M. Navarro-Hoyos and S. L. Cuffini, J. Pharm. Anal., 2019, 9, 339–346.
32. A. M. Araya-Sibaja, M. Urgellés, F. Vásquez-Castro, F. Vargas-Huertas, J. R. Vega-Baudrit, T. Gullén-Girón, M. Navarro-Hoyos and S. L. Cuffini, RSC Adv., 2019, 9, 5244–5250.
33. M. Skotnicki and P. Hodgkinson, Solid State Nucl. Magn. Reson., 2022, 118, 101783.
34. Z. Böcskei, K. Simon, R. Rao, A. Caron, C. A. Rodger and M. Bauer, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1998, 54, 808–810.
35. E. Garcia, PhD thesis, Université d'Aix-Marseille III, Aix-en-Provence, Marseille, 2000.
36. P. Taulelle, J. P. Astier, C. Hoff, G. Pépe and S. Veesler, Chem. Eng. Technol., 2006, 29, 239–246.
37. P. Taulelle, G. Sitja, G. Pépe, E. Garcia, C. Hoff and S. Veesler, Cryst. Growth Des., 2009, 9, 4706–4709.
38. K. Schenk-Joß, M. Bonin, P. Ochsenbein, J. Kieffer, M. El-Hajji, M.-H. Lemée-Cailleau and S. Mason, Acta Crystallogr., Sect. A: Found. Crystallogr., 2011, 67, C569.
39. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
40. A. Bravais, Études cristallographiques, Gauthier-Villars, Paris, 1866.
41. G. Friedel, Bull. Soc. Fr. Mineral., 1907, 30, 326–455.
42. J. D. H. Donnay and D. Harker, Am. Mineral., 1937, 22, 446–467.
43. S. I. Troyanov, E. V. Kosterina, A. Loose, M. Reehuis and E. Kemnitz, Z. Kristallogr., 2003, 218, 470–474.
44. V. G. Kiselev, P. B. Cheblakov and N. P. Gritsan, J. Phys. Chem. A, 2011, 115, 1743–1753.
45. N. Sadlej-Sosnowska, J. Org. Chem., 2001, 66, 8737–8743.
46. J. Klein, H. Khartabil, J.-C. Boisson, J. Contreras-Garcia, J.-P. Piquemal and E. Hénon, J. Phys. Chem. A, 2020, 124, 1850–1860.
47. E. D. Glendening and F. Weinhold, Molecules, 2021, 26(14), 4110.
48. W. P. Oziminski and T. M. Krygowski, Tetrahedron, 2011, 67, 6316–6321.
49. P. Hartman and W. G. Perdok, Acta Crystallogr., 1955, 8, 49–52.
50. P. Hartman and W. G. Perdok, Acta Crystallogr., 1955, 8, 521–524.
51. R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980.
52. N. Boutonnet-Fagegaltier, J. Menegotto, A. Lamure, H. Duplaa, A. Caron, C. Lacabanne and M. Bauer, J. Pharm. Sci., 2002, 91, 1548–1560.
53. R. K. Chandrappa, MSc thesis, Université de Versailles, Saint-Quentin-en-Yvelines, 2011.
54. S. Tsuzuki, T. Uchimaru, K. Matsumura, M. Mikami and K. Tanabe, Chem. Phys. Lett., 2000, 319, 547–554.
55. S. Sakaki, K. Kato, T. Miyazaki, Y. Musashi, K. Ohkubo, H. Ihara and C. Hirayama, J. Chem. Soc., Faraday Trans., 1993, 89, 659–664.
56. J. Ran and M. W. Wong, J. Phys. Chem. A, 2006, 110, 9702–9709.
57. S. K. Nayak, R. Sathishkumar and T. N. G. Row, CrystEngComm, 2010, 12, 3112–3118.
58. O. O. Brovarets, Y. P. Yurenko and D. M. Hovorun, J. Biomol. Struct. Dyn., 2014, 32, 993–1022.
59. J. Seelig, Q. Rev. Biophys., 1977, 10(3), 353–418.
60. P. P. Wanjari, A. V. Sangwai and H. S. Ashbaugh, Phys. Chem. Chem. Phys., 2012, 14, 2702–2709.
61. R. Tóbiás, A. G. Császár, L. Gyevi-Nagy and G. Tasi, J. Comput. Chem., 2018, 39, 424–437.
62. K. P. Travis and D. J. Searles, J. Chem. Phys., 2006, 125, 164501.
63. J. M. Kadro, K. Nonomura, D. Gachet, M. Grätzel and A. Hagfeldt, Sci. Rep., 2015, 5, 11654.
64. S. Khan and A. Reshak, Int. J. Electrochem. Sci., 2013, 8, 9459.
65. R. Haiges and K. O. Christe, Dalton Trans., 2015, 44, 10166–10176.
66. R. E. Trifonow and V. A. Ostrovskii, Russ. J. Org. Chem., 2006, 42, 1585–1605.
67. B. L. Dale, N. R. Halcovitch, M. J. G. Peach and J. M. Griffin, Magn. Reson. Chem., 2019, 57, 230–242.
68. D. F. Gauto, O. O. Lebedenko, L. M. Becker, I. Ayala, R. Lichtenecker, N. R. Skrynnikov and P. Schanda, bioRxiv, 2022, preprint,  DOI:10.1101/2022.07.07.499110.
69. H. Szatylowicz, O. A. Stasyuk and T. M. Krygowski, Advances in Heterocyclic Chemistry, Elsevier Inc., 2015, vol. 116, pp. 137–192.
70. G. R. Desiraju, Cryst. Growth Des., 2008, 8, 3–5.
71. J. Bernstein, Cryst. Growth Des., 2011, 11, 632–650.
72. A. J. Cruz-Cabeza and C. R. Groom, CrystEngComm, 2011, 13, 93–98.

---

Footnotes

† May our synthesis keep Professor Bertrand Castro's passion, creativity and legacy alive.

‡ Electronic supplementary information (ESI) available. CCDC 1999410–1999413, 2266410 and 2268210. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ce01172k

§ A madeleine is a cupcake created – according to one legend – by Madeleine Paulmier of Commercy in France in 1755. These scallop-shaped cupcakes (about 3 by 2 by 1 in) play a certain role in French culture: to dip one's Madeleine is synonymous to a convivial discussion at coffee time, and the author Marcel Proust made it trigger a narrator's childhood memories in “À la recherche du temps perdu”. Obviously, we do not make reference to the blood-drenched “Cimetière de la Madeleine”, on which many hundreds of noblemen, ladies and commoners were laid to rest after having met Doctor Guillotin's greedily efficient ax.

---