Structure and electrical properties of Cu, Bi and Mn co-doped K0.5Na0.5NbO3 single crystals grown by the seed-free solid state crystal growth method
Abstract
K0.5Na0.5NbO3 (KNN) crystals have great application prospects due to their excellent piezoelectric properties, high Curie temperature, and environmental friendliness. Currently, KNN crystals grown by the seed-free solid-state crystal growth (SFSSCG) method exhibit relatively high dielectric loss. In order to reduce their dielectric loss, Cu, Bi and Mn co-doped KNN lead-free piezoelectric single crystals were prepared by the SFSSCG method. The effects of the CuO doping content on the structure and electrical properties of (1 − x)(0.996KNN–0.004BiMnO3)–xCuO crystals were systematically studied. The results show that an appropriate doping amount of CuO is beneficial for the growth of the crystals and the improvement of electrical properties. When the diameter of the billets is 40 mm, the maximum crystal size of 25 × 21 × 2 mm3 is obtained. All crystals have a typical perovskite structure almost with a single orthorhombic phase and are very compact almost without holes. The minimum average domain width of 276 nm is obtained for the crystal at x = 0.005. The KNN crystals exhibit normal ferroelectric characteristics and a space-charge-limited-conduction (SCLC) mechanism. The introduction of Cu2+ ions reduces the dielectric loss of the crystal and increases its piezoelectric and dielectric properties. The Cu, Bi and Mn co-doped KNN crystals achieve excellent comprehensive properties: d33 = 314 pC N−1, Pr = 29.9 μC cm−2, Ec = 10.1 kV cm−1, 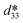 = 869 pm V−1, Qm = 56.8, Kt = 0.38, tan δ = 0.013 and TC = 409 °C. This provides a route to improve the electrical properties of KNN-based crystals.
= 869 pm V−1, Qm = 56.8, Kt = 0.38, tan δ = 0.013 and TC = 409 °C. This provides a route to improve the electrical properties of KNN-based crystals.



 Please wait while we load your content...
Please wait while we load your content...