 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Melting of aqueous NaCl solutions in porous materials: shifted phase transition distribution (SIDI) approach for determining NMR cryoporometry pore size distributions†
Sarah E.
Mailhiot
 *a,
Katja
Tolkkinen
*a,
Katja
Tolkkinen
 a,
Henning
Henschel
a,
Henning
Henschel
 b,
Jiří
Mareš
b,
Jiří
Mareš
 a,
Matti
Hanni
a,
Matti
Hanni
 cde,
Miika T.
Nieminen
cde,
Miika T.
Nieminen
 cde and
Ville-Veikko
Telkki
cde and
Ville-Veikko
Telkki
 *a
*a
aNMR Research Unit, University of Oulu, Oulu, Finland. E-mail: sarahmailhiot@gmail.com; ville-veikko.telkki@oulu.fi
bDepartment of Medicinal Chemistry, Uppsala University, Uppsala, Sweden
cResearch Unit of Health Sciences and Technology, University of Oulu, Oulu, Finland
dDepartment of Diagnostic Radiology, Oulu University Hospital, Oulu, Finland
eMedical Research Center Oulu, University of Oulu and Oulu University Hospital, Oulu, Finland
First published on 27th December 2023
Abstract
Nuclear magnetic resonance cryoporometry (NMRC) and differential scanning calorimetry thermoporometry (DSC-TPM) are powerful methods for measuring mesopore size distributions. The methods are based on the fact that, according to the Gibbs–Thomson equation, the melting point depression of a liquid confined to a pore is inversely proportional to the pore size. However, aqueous salt solutions, which inherently exist in a broad range of biological porous materials as well as technological applications such as electrolytes, do not melt at a single temperature. This causes artefacts in the pore size distributions extracted by traditional Gibbs–Thomson analysis of NMRC and DSC-TPM data. Bulk aqueous NaCl solutions are known to have a broad distribution of melting points between the eutectic and pure water phase transition points (252–273 K). Here, we hypothesize that, when aqueous NaCl solution (saline) is confined to a small pore, the whole melting point distribution is shifted toward lower temperatures by the value predicted by the Gibbs–Thomson equation. We show that this so-called shifted phase transition distribution (SIDI) approach removes the artefacts arising from the traditional Gibbs–Thomson analysis and gives correct pore size distributions for saline saturated mesoporous silica gel and controlled pore materials analyzed by NMR cryoporometry. Furthermore, we demonstrate that the method can be used for determining pore sizes in collagen–chondroitin sulphate hydrogels resembling the composition of the extracellular matrix of articular cartilage. It is straightforward to apply the SIDI analysis for DSC-TMP data as well.
1. Introduction
Mesoporous materials and their associated pore structures are of interest to several fields of science and technology. They have pores ranging from 2 to 50 nm in diameter and are of high interest with over 4000 publications related to the topic each year.1–3 Mesoporous materials have applications in areas such as catalysis,4,5 electronics,6–8 construction materials,9–11 medicine12–14 and energy storage.15 Due to an increasing use of mesoporous materials, there is a need for reliable characterization methods capable of measuring their pore size distributions.Gas adsorption and desorption16–18 as well as mercury intrusion porosimetry (MIP)19,20 are the most popular methods for measuring pore size distributions of mesoporous materials. However, neither method can be applied to wet samples. One alternative method is thermoporometry (TPM).21 TPM is a calorimetric method that utilizes differential scanning calorimetry (DSC) for the observation of solid–liquid phase transitions in pores which can be applied to wet samples.2,3,12,21–24 Another means for detecting the distribution of phase transitions is Nuclear Magnetic Resonance Cryoporometry (NMRC).25–27 DSC-TPM and NMRC methods are based on the fact that liquid confined in a small pore melt at a lower temperature than free liquid. The melting point depression ΔT is mathematically related to the pore size through the Gibbs–Thomson equation
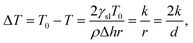 | (1) |
Due to their versality, DSC-TPM and NMRC have found lots of applications for measuring the pore size distributions in a range of hydrated solid porous media,9,10,28,35–40 gels14,24,31,41,42 and biological samples including wood,43–45 skin,22 articular cartilage12 and collagen fibres.46 However, despite the advantages of the methods for measuring wet samples, they have not been widely applied to biological samples because the use of a pure probe liquid is required. This limits their use because many biological samples need to be stored in a salt solution to prevent swelling. Bulk aqueous NaCl solution does not have a single freezing or melting temperature. Instead, it has a broad melting point distribution between the melting point of pure water (273 K) and eutectic phase transition temperature (252 K).47 Therefore, it is not possible to assume that a single lowered melting point temperature is associated with a single pore size like in the traditional Gibbs–Thomson equation-based pore size analysis. It has been experimentally verified that replacing pure water by a salt solution shifts the pore size distribution obtained by NMRC towards smaller pore sizes.48 Similar issue may be encountered in technological applications such as freezing and melting studies of aqueous electrolytes confined within mesopores.49
Recently, there has been some efforts to evaluate how the phase transitions in salt solutions can be exploited in DSC-TPM. Burba et al. observed that confined aqueous NaCl solutions have dominant melting points that are lower than those of pure water confined within the same porous silica host, and the magnitude of the melting point depression increases with increasing salt concentration.50 Furthermore, they developed an extended Gibbs–Thomson equation for the melting of the ice phase in dilute NaCl solutions in porous materials. Similarly, Malfait et al. introduced an extended version of Gibbs–Thomson equation for the melting of aqueous solutions of glycerol confined in porous material.51 These rigorous equations provide theoretical framework to understand the melting behaviour of the pore-confined solutions with different concentrations, however their use in practical applications is not straightforward. The depression of the eutectic phase transition has previously been observed in several salt solutions in porous media. Meissner et al.52 showed that there is a systematic decrease in the eutectic phase transition temperature with decreasing pore size and increasing salt concentration for a series of aqueous salt systems in silica materials, indicating that the eutectic phase transition depression could be used for determining pore sizes by DSC-TPM. Majda et al.12 exploited the eutectic melting point depression for determining the pore size distribution in bovine cartilage saturated in saline (0.9 wt% of NaCl in water) by DSC. The resulting pore size distributions included a single peak at the lower edge of detection, at about 6 nm, with a tail over a range of pore sizes up to 200 nm. However, also these methods rely on an assumption of a single phase transition temperature, which is not strictly correct for salty solutions, and therefore they may produce artefacts in pore size distributions, especially for the systems including several pore sizes. Furthermore, the amount of saline freezing/melting in the eutectic phase transition is only about 3% of the total amount of saline, and therefore the methods relying on the eutectic phase transitions are rather insensitive. Depression of both dominant and eutectic phase transition temperatures of NaCl solution in porous structure is explained by the larger fraction of pore volume occupied by salt hydrates.50,52 In pore-confined NaCl solutions, the Na+ ions strive to position along the pore walls.49 In addition, during freezing, salts have a habit of crystallizing in form of hydrates, which makes them occupy larger space. This changes the surface to volume ratio of the pore wall which the solution experiences, leading to lowered melting points.
In this study, we propose a novel method for determining pore size distributions, which does not assume a single phase transition temperature of saline in a pore. Instead, we assume that, for saline confined to a pore, the whole melting point curve of bulk saline is shifted towards lower temperatures, and the shift is inversely proportional to pore size according to the Gibbs–Thomson equation. This is a reasonable assumption, because, as described above, both dominant and eutectic phase transition temperatures have been shown to be lowered in a small pore size.50,52 This so-called shifted phase transition distribution (SIDI) method is tested by studying melting of saline in mesoporous silica gels and control pore glasses as well as hydrogels mimicking extracellular matrix of articular cartilage using NMRC. We show that the method results in pore size distributions which are in good agreement with the known pore sizes, and the distributions do not include artificial peaks, which are present in the distributions obtained by assuming a single dominant or eutectic phase transition point in a pore. Furthermore, the sensitivity of the method is significantly higher than that of the method relying on the observation of depressed eutectic phase transition temperature. The SIDI method is applicable for analysing DSC-TPM data as well.
2. Materials and methods
2.1. Materials
Porous materials saturated with saline (0.9 wt% NaCl in H2O) were investigated by NMRC. The porous materials included three silica gels (SG, Merck, Darmstadt, Germany) with mean pore diameters of 4, 5, and 10 nm and particle sizes of 63–200 μm, and one controlled pore glass (CPG, CPG Inc, Lincoln Park, New Jersey) with mean pore diameter of 8.1 nm and particle sizes of 125–177 μm, respectively. The sizes were given by the manufacturers. The samples are referred to as SG 4 nm, SG 6 nm, SG 10 nm and CPG 8.1 nm, respectively. The samples were placed in a 5 mm NMR tube with a layer of bulk saline above the particles, which was partially inside the NMR detection region and used as an internal standard. For comparison, a bulk saline sample including 0.9 wt% NaCl in water without any porous material was also analysed.Four hydrogel samples were prepared with varying collagen type II and chondroitin sulphate (CS) content in phosphate buffered saline (PBS): 20 mg g−1 of collagen type II with 10 mg g−1 of CS, and 40 mg g−1 of collagen type II with 0, 10 mg g−1 or 20 mg g−1 of CS. Collagen solution (rat tail, ∼6 mg mL−1 in 0.01 M acetic acid, Merck KGaA, Darmstadt, Germany), 5 mL and 10 mL for final collagen concentrations of 20 mg g−1 and 40 mg g−1, respectively, was added to a sample tube together with 0.15 mL 10× PBS. Stock solution of CS (50–80 mg mL−1 CS powder from bovine trachea, Merck KGaA, Darmstadt, Germany in double distilled water) corresponding to the desired final CS concentration was added to the collagen solution and the mixture was diluted with double distilled water to give a total volume of 6 and 11 mL, respectively. Samples were thoroughly mixed, and pH adjusted to basic (pH: 8–9) using 1 M sodium hydroxide (NaOH) and 0.5 M hydrochloric acid (HCl). Sample tubes were placed for 45–60 min in a water bath at 37 °C to solidify the mixture into a gel. If samples did not solidify during this time, the pH adjustment and incubation steps were repeated. The solid was removed from the sample tubes, transferred into a plastic cell culture dish, and dried at 40 °C in a laminar flow oven until the mass of each sample was reduced to 1.50 ± 0.03 g in order to achieve final collagen contractions higher than the concentration of the commercially obtained solution. Finally, these samples were also placed in 5 mm NMR tubes.
2.2. NMRC measurements
1H NMRC experiments were performed using a Bruker Avance III 500 MHz spectrometer equipped with a 10 mm BBO probe and liquid nitrogen evaporator for sample cooling. NMR signal intensity was acquired as a function of temperature using the CPMG pulse sequence.33 In the analysis of the NMRC data, the intensity of the first CPMG echo was used. The CPMG was run with a 200 μs echo time and 5000 echoes for a total detection time of 1 second. The whole CPMG trace was collected to assure the quality of the experiments and to evaluate whether the echo time was suitable for filtering the solid signal. Relaxation delay was 3.5 s and 64 scans were acquired. The CPMG experiment time was 4 min 49 seconds. In the measurements of the silica gels and the controlled pore glass, the temperature was varied from 185 to 293 K by 1.15 K steps for a total of 95 steps, and in the measurements of the hydrogels, from 185 to 191.2 K by 1.8 K steps for total of 60 steps. Average heating rate was about 0.13 K min−1. At the beginning of the experiment, the sample was kept at 185 K for 3 h to ensure the sample reached equilibrium. The total experiment time of the whole temperature series was 17 h.2.3. Data analysis
The data analysis included fitting of eqn (9) (the SIDI signal curve) with the experimental NMRC signal intensities measured as a function of temperature. Sums of least squares were minimized using Solver in Excel. The Excel files can be found from ESI.† In the fitting, the melting point distribution was assumed to be a sum of two or three Gaussian functions (eqn (12), N = 2 or 3), from which one corresponds to melting of bulk saline. The melting point distributions were converted into pore size distributions by using eqn (11). For comparison, NMRC signal intensities were also converted into pore size distributions by the standard Gibbs–Thomson analysis using eqn (8). An alternative Python based code for the SIDI analysis (sidiPackage) is given in the ESI.†3. Results and discussion
3.1. Freezing and melting of bulk saline
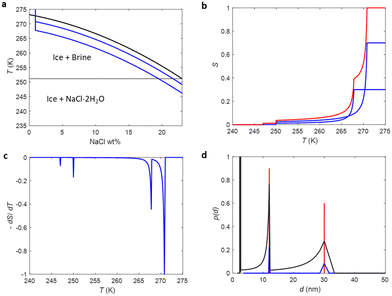
The phase diagram of NaCl and water binary system is shown in Fig. 1a.53,54 According to the diagram, saline, 0.9 wt% of NaCl in water, starts to freeze when the sample is cooled below 272.8 K. A small portion of liquid turns into ice, and NaCl is squeezed out from the ice phase, increasing the NaCl concentration in the remaining liquid (brine) phase and therefore decreasing its freezing point. As illustrated in Fig. 1e, the relative amount of ice increases with decreasing temperature, and, at the same time, the NaCl concentration of the residual liquid brine increases. At the eutectic phase transition temperature (252 K), remaining high NaCl concentration (23 wt%) brine solidifies.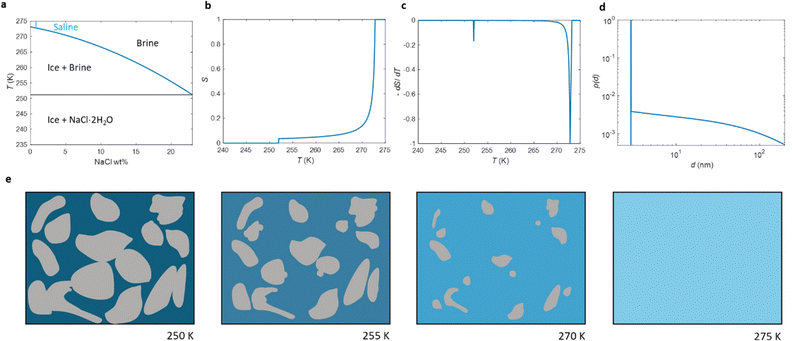 | ||
| Fig. 1 (a) Phase diagram of NaCl and water binary system. The light blue vertical line represents the saline including 0.9 wt% NaCl. (b) Theoretical (eqn (7)) NMRC signal intensity of bulk saline as a function of temperature. The intensity is proportional to the amount of liquid water in unfrozen brine. (c) Negation of the derivative of the theoretical NMRC signal intensity as a function of temperature, which is equivalent to the heat curve observed in DSC-TPM. The peaks corresponding to the dominant and eutectic phase transition are visible around 272.8 and 252 K. The derivative is non-zero over the whole region in between of those temperatures. (d) Pore size distribution obtained by analyzing the theoretical bulk saline NMRC melting curves using the Gibbs–Thomson equation (eqn (1), T0 = 272.8 K). Note the logarithmic scale on the vertical axis. The distribution includes an artificial peak around 3 nm due to eutectic melting point as well as non-zero values at higher pore sizes due to continuous melting of saline between the eutectic and dominant melting points. (e) Schematics of freezing and melting of saline. Light blue represents liquid saline/brine (saline refers to 0.9% NaCl solution, brine to higher salt concentration), gray ice and dark blue solidified brine. At 275 K, whole saline sample is in liquid state. Below 272.8 K, saline starts to freeze, and small ice crystals are visible at 270 K. During freezing, NaCl is squeezed out from ice, increasing NaCl concentration in liquid brine (illustrated by darker blue color). The amount of ice and size of ice crystals increases with decreasing temperature.47 Below the eutectic phase transition point (252 K), remaining high NaCl concentration (about 23 wt%) brine is solidified. | ||
According to ref. 53 and 54, the freezing/melting temperature of brine as a function of NaCl mass fraction wNaCl (wt%) is
| T = b1wNaCl2 + b2wNaCl + T0, | (2) |
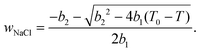 | (3) |
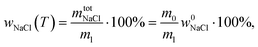 | (4) |
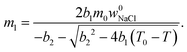 | (5) |
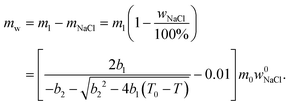 | (6) |
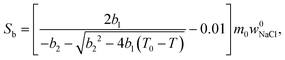 | (7) |
Relative NMRC signal as a function of temperature (eqn (7)) is plotted in Fig. 1b. At the lowest temperatures, signal is zero, as there is only NaCl·2H2O and ice. At the eutectic melting point (252 K), there is a sudden increase in the intensity from 0 to about 0.03, i.e., eutectic melting corresponds to about 3% of the maximum amplitude. Thereafter, the signal increases slowly with increasing temperature. Before 272.8 K, there is a sharp increase in signal intensity due to dominant melting transition of saline.
An alternative way for visualizing the melting point distribution is to plot the derivative of the NMRC signal, dS/dT, as a function of temperature, or alternatively −dS/dT, because the latter function is analogous to the heat flow graphs of endothermic melting transitions obtained in DSC TMP experiments. The theoretical −dS/dT curve represented in Fig. 1c show a major phase transition around 272.8 K and a minor phase transition corresponding to eutectic melting point at 252 K. The derivative is non-zero over the whole region in between these points.
3.2. Melting of saline in porous materials
In conventional NMRC and DSC-TMP analysis, porous materials are saturated with a single component probe liquid, such as water,28 acetonitrile30 or cyclohexane,32 which freeze or melt in a single temperature. The freezing or melting point of the liquid in a small pore is lower than that of bulk liquid, and typically freezing occurs at lower temperatures than melting. This phenomenon of different freezing and melting temperatures of liquid in pores is called freezing-melting hysteresis. Hysteresis originates from the nucleation barriers and pore blocking effects which are present only during freezing.35 Here, only the melting transitions are discussed.According to the Gibbs–Thomson equation (eqn (1)), the melting point depression is inversely proportional to the pore size. The NMRC signal intensity, being proportional to the amount of unfrozen probe liquid, reveals the distribution of melting points in the sample. Consequently, the NMRC signal intensity can be converted into pore size distribution using the following equation:26
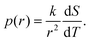 | (8) |
In DCS-TMP, heat flow graphs reveal the melting point distribution, and pore size distribution is calculated by an equation analogous to eqn (8).
Because binary liquids, such as aqueous solutions of NaCl, do not freeze or melt at a single temperature, conventional pore size distribution analysis by the Gibbs–Thomson equation results in artefacts. For example, when the theoretical NMRC signal curve of bulk saline shown in Fig. 1b is converted into pore size distribution by eqn (8) using k = 30 K nm, which is a typical value determined for water,26 the distributions shown in Fig. 1d include a sharp peak around d = 3 nm arising from the eutectic transition as well as a broad distribution of pores above that due to continuous melting of brine between the eutectic and dominant phase transition temperatures (252–272.8 K), although the bulk saline includes no pores. Therefore, different a kind of analysis is needed.
As explained in Introduction, according to ref. 12, 50 and 52 both eutectic and dominant phase transitions of binary solutions of water and salts are lowered, when the solutions are confined to a small pore, allowing, in principle, estimation of pore sizes by means of the Gibbs–Thomson equation. However, if the melting point depression of the dominant transition is used in the determination of pore size distribution, artificial peaks due to eutectic phase transition as well as the distribution of melting points in between the eutectic and dominant phase transition temperatures are observed, leading to a biased picture about the porous structures. In principle, determination of pore size distribution based on depression of eutectic phase transition would be less prone for artefacts, as the derivative of the signal above the eutectic phase transition point is small (see Fig. 1b and c). However, this approach suffers from low sensitivity, as the signal corresponding to the eutectic phase transition is only about 3% of the maximum signal.
Here, we propose an alternative way for extracting pore size distribution from NMRC signal and DSC-TMP heat flow graphs of binary solutions of water and salts confined to porous materials. As both eutectic and dominant melting point depressions are known to be inversely proportional to pore size, we hypothesize that, for saline confined to a small pore, the whole melting point curve (eqn (2)) is shifted towards lower temperatures by the amount indicated by the Gibbs–Thomson equation (eqn (1)), as illustrated in Fig. 2a. The proposed phase diagram has a close resemblance with the experimentally observed phase diagrams of H2O–CaCl2 binary solution in bulk and KSKG silica gel.56 Consequently, the NMRC signal intensity function of saline in a small pore has the same shape as bulk saline (eqn (7)), but it is shifted towards lower temperatures. In the general case, in which the sample includes pores with different sizes, NMRC signal is an integral of the NMRC signal distributions corresponding to the bulk saline (eqn (7)) shifted by the melting point depression ΔT indicated by the Gibbs–Thomson equation (eqn (1)) and weighted by the melting point distribution corresponding to the pore size distribution:
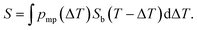 | (9) |
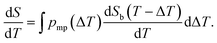 | (10) |
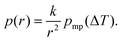 | (11) |
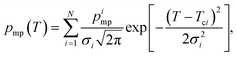 | (12) |
 | ||
| Fig. 2 (a) Phase diagram of NaCl and water binary system. The diagram is identical to Fig. 1a but complemented with the hypothesized concentration curves of saline confined to small pores with two different pore sizes, in which the concentration curves of bulk saline are shifted by 2 and 5 K (blue lines). (b) Theoretical NMRC signal of a saline saturated sample including the two different pore sizes (d = 30 and 12 nm, relative pore volumes 0.7 and 0.3, respectively), calculated by eqn (9). The signals of each component are represented by blue lines and their sum by red solid line. (c) Corresponding derivative plot. (d) Pore size distributions obtained by the conventional Gibbs–Thomson analysis (eqn (8)) using the dominant (272.8 K, black line) and eutectic (252 K, blue line) melting point depression as well as the SIDI analysis proposed in this article (red line). In the analysis, k was assumed to be 30 nm K. | ||
Fig. 2b shows a theoretical NMRC signal curve of a sample including pores with two different sizes saturated by saline calculated by eqn (9). In the calculations, ΔT values associated with the bigger and smaller pores were assumed to be 2 and 5 K and relative pore volumes are 0.7 and 0.3, respectively. The curves corresponding to individual pores are drawn by blue lines and their sum by red line. Corresponding derivative curves, calculated by eqn (10), are shown in Fig. 2c. The derivative curves show two major peaks around 270 and 267 K associated with the depressed dominant phase transition temperatures in the big and small pores, respectively. Furthermore, there are two smaller peaks around 248 and 245 K related to the lowered eutectic phase transition points in the big and small pores, respectively. The pore size distribution calculated by converting the melting point distribution obtained by fitting eqn (9) with the signal intensity curve is shown in Fig. 2d (red curve; k was assumed to be 30 nm K).26 It reveals that the sizes of the small and big pores are 12 and 30 nm, respectively. For comparison, pore size distributions obtained by the conventional Gibbs–Thomson analysis based on the dominant (black curve) and eutectic (blue curve) transition are shown in Fig. 2d as well. The former includes two artificial peaks associated with the eutectic phase transition around 2–3 nm, and the true peaks are also significantly broadened and partially overlapping due to broad dominant transition temperature range. The distribution corresponding to the eutectic phase transition does not include the artificial peaks. However, the true peaks are broadened, and sensitivity lowered as only about 3% of water molecules contribute signal. Consequently, this theoretical example demonstrates well the potential of the proposed SIDI method for improving the reliability and quality of the NMRC and DSC TMP pore size distributions.
3.3. Pore size distributions of mesoporous materials
To test how the SIDI analysis works in practice, three silica gel (SG) and one controlled pore glass (CPG) mesoporous materials saturated with saline were analysed by 1H NMRC. NMRC signal curves of the porous materials measured as a function of temperature from 185 to 293 K are shown in Fig. 3a (solid lines). For the comparison, the signal curve of the bulk saline sample is shown as well. The experimental saline signal curve is qualitatively similar to the theoretical curve shown in Fig. 1b. However, the experimental curve is smoothened both around the eutectic and dominant phase transition points, most probably due to experimental factors such as small temperature gradients in the sample and imperfect equilibrium due to the finite (8 min K−1) temperature stabilization delays.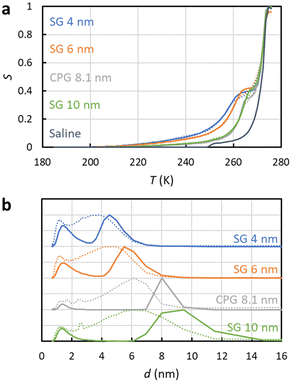 | ||
| Fig. 3 (a) Experimental 1H NMRC signal curves (solid lines) of the mesoporous silica gel (SG) and controlled pore glass (CPG) materials saturated with saline (0.9 wt% NaCl in water). For the comparison, corresponding curve of the bulk saline sample is shown as well. The dotted lines show the fits of eqn (9) with the experimental data (the SIDI approach). (b) Pore size distributions obtained by the SIDI (solid lines) and conventional (dotted lines) approaches. | ||
Above 270 K, the curves of the porous materials follow roughly the curve of the bulk saline, as this region is associated with the dominant melting transition of bulk saline on top and in between the 63–200 μm particles. The knees around 260–270 K arise from lowered dominant melting transitions of saline confined to mesopores. The knees shift to lower temperatures with decreasing nominal pore size in agreement with the Gibbs–Thomson equation. Signal intensities at the lowest temperature in the region of 200–240 K are also inversely proportional to the pore size, indicating that also the eutectic melting point shifts to lower temperatures with decreasing pore size.
Fits of the theoretical SIDI signal curve (eqn (9)) with the experimental data are shown by dotted lines in Fig. 3a. The experimental signal curve of the bulk saline was used as Sb(T − ΔT) in eqn (9), because the bulk saline and porous materials experiments were expected to have similar experimental imperfections due to the temperature gradients, heating rates etc. The melting point distribution pmp(T) was assumed to be a sum of three Gaussian functions (N = 3 in eqn (12)). One component is associated with the bulk transition above 270 K and another with the mesopore transition between 260 and 270 K. Furthermore, good fits require an additional low temperature (230–245 K) transition component corresponding to smaller pores or non-frozen surface layer (see below).
The SIDI pore size distributions calculated by eqn (11) are shown in Fig. 3b (solid lines). The positions of the dominant peaks are in good agreement with the nominal pore sizes. The centres of the SG 6 nm and CPG 8.1 nm peaks are almost perfectly located on the nominal pore sizes. On the other hand, the centres of the SG 4 nm and SG 10 nm are shifted to slightly above and below the nominal pore size, respectively. This may reflect small inaccuracy of the method or nominal pore sizes given by manufacturers; in fact, our earlier NMC analysis of the same porous materials using acetonitrile as a probe liquid resulted in similar deviations from the nominal pore sizes.58 The CPG 8.1 nm peak is narrower than the SG peaks because the CPG material is known to have narrower pore size distributions than the SG materials.58
The pore size distributions also include a minor component below 2 nm, which has been observed also in the NMRC of silica materials using acetonitrile as a probe liquid.59 It may arise from saline in micropores, or it may be an artefact arising from the non-frozen surface layer.59
For comparison, pore size distributions obtained by the conventional Gibbs–Thomson analysis using eqn (8) are shown by dotted lines in Fig. 3b. As expected, the distributions are much broader than the SIDI distributions due to the artefacts caused by the broad melting point distribution of salty solutions. There is a broad major peak ranging from 1 nm to slightly above the nominal pore size, and the distribution extends much beyond that toward larger pore sizes due to the spread bulk transition. The mean pore size is much below the nominal pore size. There is a small bump around 2.6 nm associated with the eutectic phase transition point of the bulk saline on top and in between the particles in the pore size distributions of CPG 8.1 nm and SG 100 nm. Overall, the SIDI distributions are in much better agreement with the known pore size distributions of the materials than the distributions obtained by the conventional Gibbs–Thomson analysis.
3.4. Pore size distributions of collagen and chondroitin sulphate hydrogels
The SIDI analysis method was also tested for analysing pore sizes in hydrogels composed of varying concentrations of collagen type II and chondroitin sulphate. The collagen and chondroitin sulphate gels are models for the extracellular matrix (ECM) of articular cartilage, which is the tissue that covers the end of articulating joints. The ECM of cartilage is primarily composed of collagen type II, proteoglycans, and water (including NaCl). Collagen is a rope like protein responsible for forming the fibril network. The collagen–collagen covalent crosslinks create the collagen network. Proteoglycans are hydrophilic macromolecules composed of negatively charged glycosaminoglycans (GAGs) covalently bonded to a protein core. Chondroitin sulphate is the most common GAG in cartilage. Proteoglycans exist in the intrafibrillar space created by collagen–collagen crosslinks. Water exists within the matrix formed by the proteins and comprises about 60–80% of the tissue mass.60–62The pore size distribution of cartilage is difficult to determine as it must contain buffer solution, such as PBS, and the pore size may change under pressure and other mechanical stress. An additional constraint is that the pore size distributions in polymer gels are not well defined. To address these limitations, the effective pore size of cartilage has been measured using indirect methods such as estimating the pore size based on the transport of molecules with varying diameters63–67 and hydraulic permeability methods.61 The downside of these measurements is that they require the introduction of tracer molecules which interact with the sample or require the use of high pressures which may alter the structure of the sample. The cartilage ECM have been estimated to have pore sizes of 2–6 nm in the inter-GAG spacing62,68–72 and 10–100 nm in the inter-collagen fibril spacing.46
NMRC signal curves of the hydrogel samples including 20–40 mg g−1 of collagen type II, 0–20 mg g−1 of chondroitin sulphate and PBS are shown Fig. 4a. The signal intensities are non-zero below the eutectic melting point of bulk PBS in the region of 230–250 K, and they are higher than the intensity of the bulk PBS sample in the region of 250–270 K due to the porosity of the gel. The pore size distributions extracted by the SIDI method include a peak ranging from about 2 to 6 nm, which is in a good agreement with the pore sizes of the inter-GAG spacing determined by the indirect methods. As the pore sizes are well above the 1 nm peak of the SG and CPG samples, which may be an artefact arising from the non-frozen surface layer, we expect that the pore size distributions reflect true pore structures of the gels. The distributions obtained by the conventional approach include an artificial broad shoulder extending to about 40 nm due to the melting point distribution of the bulk PBS in the gels, again emphasizing the importance of the SIDI analysis.
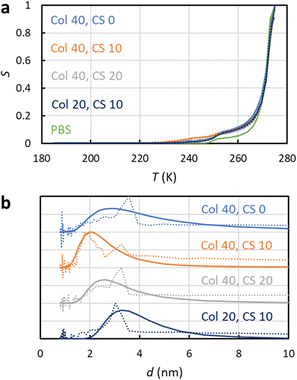 | ||
| Fig. 4 (a) Experimental 1H NMRC signal curves (solid lines) of collagen and chondroitin sulphate hydrogels. The amounts of collagen (Col) and chondroitin sulphate (CS) in the unit of mg g−1 are indicated in the figure. For the comparison, corresponding curve of the bulk phosphate buffered saline (PBS) sample is shown as well. The dotted lines show the fits of eqn (9) with the experimental data (the SIDI approach). (b) Pore size distributions obtained by the SIDI (solid lines) and conventional (dotted lines) approaches. | ||
4. Conclusions
A novel method for analysing NMR cryoporometry (NMRC) and differential scanning calorimetry (DSC) thermoporometry (TPM) data of porous materials saturated with water and NaCl binary solutions was introduced. The approach is based on the hypothesis that, in a small pore, the whole melting point distribution curve of bulk saline is shifted to lower temperatures by the value predicted by the Gibbs–Thomson equation. Theoretical analysis shows that the proposed shifted phase transition distribution (SIDI) approach removes artefacts existing in the pore size distributions obtained by the conventional Gibbs–Thomson analysis assuming a single phase transition temperature in a pore. The SIDI approach takes into account the eutectic phase transition at 252 K as well as a broad distribution of phase transitions between 252 and 273 K for bulk saline. The method was experimentally tested by measuring NMRC data of mesoporous silica gel and controlled pore glass materials saturated with saline. The SIDI pore size distributions were in good agreement with known pore size distributions of the materials, while the conventional Gibbs–Thomson analysis gave significantly biased pore size distributions. Furthermore, the method was applied for characterization of pore size distributions of hydrogels resembling the composition of articular cartilage, and the resulting pore sizes (2–6 nm) were in good agreement with the inter-GAG spacing determined by other methods. The SIDI method has a broad range of potential applications in the analysis of biological and technological electrolytes.Author contributions
S. Mailhiot was responsible for conceptualization, methodology, validation, investigation, resources, and writing – original draft. K. Tolkkinen was responsible for conceptualization, methodology, validation, investigation, and writing – review and editing. H. Henschel, M. T. Nieminen and M. Hanni were responsible for planning and preparing the hydrogel sample, and writing – review and editing. J. Mares was responsible for making the Python SIDI analysis code, and writing – review and editing. V.-V. Telkki was responsible for conceptualization, supervision, resources, and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the European Research Council (ERC) under Horizon 2020 (H2020/2018-2022/ERC grant agreement no. 772110), Marie Sklodowska-Curie Actions (grant no. 896824), Research Council of Finland (grant no. 321701 and 340099), and Kvantum institute (University of Oulu). The authors thank Olli-Pekka Aro for gel preparation. Part of the work was carried out with the support of the Centre for Material Analysis, University of Oulu, Finland.References
- U. Ciesla and F. Schüth, Ordered mesoporous materials, Microporous Mesoporous Mater., 1999, 27, 131–149 CrossRef CAS.
- J. Riikonen, J. Salonen and V.-P. Lehto, Utilising thermoporometry to obtain new insights into nanostructured materials, J. Therm. Anal. Calorim., 2011, 105, 811–821 CrossRef CAS.
- J. Riikonen, J. Salonen and V.-P. Lehto, Utilising thermoporometry to obtain new insights into nanostructured materials, J. Therm. Anal. Calorim., 2011, 105, 823–830 CrossRef CAS.
- A. Taguchi and F. Schüth, Ordered mesoporous materials in catalysis, Microporous Mesoporous Mater., 2005, 77, 1–45 CrossRef CAS.
- P. S. Shinde, P. S. Suryawanshi, K. K. Patil, V. M. Belekar, S. A. Sankpal, S. D. Delekar and S. A. Jadhav, A Brief Overview of Recent Progress in Porous Silica as Catalyst Supports, J. Compos. Sci., 2021, 5, 75 CrossRef CAS.
- V. Parkhutik, Porous silicon—mechanisms of growth and applications, Solid-State Electron., 1999, 43, 1121–1141 CrossRef CAS.
- Y. Qu, L. Liao, Y. Li, H. Zhang, Y. Huang and X. Duan, Electrically Conductive and Optically Active Porous Silicon Nanowires, Nano Lett., 2009, 9, 4539–4543 CrossRef CAS PubMed.
- F. Vaca Chávez and M. Schönhoff, Pore size distributions in polyelectrolyte multilayers determined by nuclear magnetic resonance cryoporometry, J. Chem. Phys., 2007, 126, 104705 CrossRef PubMed.
- J. Li, S. Mailhiot, H. Sreenivasan, A. M. Kantola, M. Illikainen, E. Adesanya, L. Kriskova, V.-V. Telkki and P. Kinnunen, Curing process and pore structure of metakaolin-based geopolymers: Liquid-state 1H NMR investigation, Cem. Concr. Res., 2021, 143, 106394 CrossRef CAS.
- M. A. Javed, S. Komulainen, H. Daigle, B. Zhang, J. Vaara, B. Zhou and V.-V. Telkki, Determination of pore structures and dynamics of fluids in hydrated cements and natural shales by various 1H and 129Xe NMR methods, Microporous Mesoporous Mater., 2019, 281, 66–74 CrossRef CAS.
- Y. Zhao, L. Peng, S. Liu, B. Cao, Y. Sun and B. Hou, Pore structure characterization of shales using synchrotron SAXS and NMR cryoporometry, Mar. Pet. Geol., 2019, 102, 116–125 CrossRef.
- D. Majda, A. Bhattarai, J. Riikonen, B. D. Napruszewska, M. Zimowska, A. Michalik-Zym, J. Töyräs and V. P. Lehto, New approach for determining cartilage pore size distribution: NaCl-thermoporometry, Microporous Mesoporous Mater., 2017, 241, 238–245 CrossRef CAS.
- A. Jane, R. Dronov, A. Hodges and N. H. Voelcker, Porous silicon biosensors on the advance, Trends Biotechnol., 2009, 27, 230–239 CrossRef CAS PubMed.
- N. Buchtová, A. D’Orlando, P. Judeinstein, O. Chauvet, P. Weiss and J. Le Bideau, Water dynamics in silanized hydroxypropyl methylcellulose based hydrogels designed for tissue engineering, Carbohydr. Polym., 2018, 202, 404–408 CrossRef PubMed.
- W. Li, J. Liu and D. Zhao, Mesoporous materials for energy conversion and storage devices, Nat. Rev. Mater., 2016, 1, 16023 CrossRef CAS.
- K. Sing, The use of nitrogen adsorption for the characterisation of porous materials, Colloids Surf., A, 2001, 187–188, 3–9 CrossRef CAS.
- S. Brunauer, P. H. Emmett and E. Teller, Adsorption of Gases in Multimolecular Layers, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- E. P. Barrett, L. G. Joyner and P. P. Halenda, The Determination of Pore Volume and Area Distributions in Porous Substances. I. Computations from Nitrogen Isotherms, J. Am. Chem. Soc., 1951, 73, 373–380 CrossRef CAS.
- J. Van Brakel, S. Modrý and M. Svatá, Mercury porosimetry: state of the art, Powder Technol., 1981, 29, 1–12 CrossRef CAS.
- B. Bafarawa, A. Nepryahin, L. Ji, E. M. Holt, J. Wang and S. P. Rigby, Combining mercury thermoporometry with integrated gas sorption and mercury porosimetry to improve accuracy of pore-size distributions for disordered solids, J. Colloid Interface Sci., 2014, 426, 72–79 CrossRef CAS PubMed.
- M. Brun, A. Lallemand, J.-F. Quinson and C. Eyraud, A new method for the simultaneous determination of the size and shape of pores: the thermoporometry, Thermochim. Acta, 1977, 21, 59–88 CrossRef CAS.
- N. N. Fathima, M. P. Kumar, J. R. Rao and B. U. Nair, A DSC investigation on the changes in pore structure of skin during leather processing, Thermochim. Acta, 2010, 501, 98–102 CrossRef CAS.
- M. R. Landry, Thermoporometry by differential scanning calorimetry: experimental considerations and applications, Thermochim. Acta, 2005, 433, 27–50 CrossRef CAS.
- K. Ishikiriyama and M. Todoki, Pore Size Distribution Measurements of Silica Gels by Means of Differential Scanning Calorimetry, J. Colloid Interface Sci., 1995, 171, 103–111 CrossRef CAS.
- J. H. Strange, M. Rahman and E. G. Smith, Characterization of porous solids by NMR, Phys. Rev. Lett., 1993, 71, 3589–3591 CrossRef CAS PubMed.
- O. V. Petrov and I. Furó, NMR cryoporometry: Principles, applications and potential, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 54, 97–122 CrossRef CAS.
- J. Mitchell, J. Webber and J. Strange, Nuclear magnetic resonance cryoporometry, Phys. Rep., 2008, 461, 1–36 CrossRef CAS.
- A. Schreiber, I. Ketelsen and G. H. Findenegg, Melting and freezing of water in ordered mesoporous silica materials, Phys. Chem. Chem. Phys., 2001, 3, 1185–1195 RSC.
- N. Billamboz, J.-M. Nedelec, M. Grivet and M. Baba, Cross-Linking of Polyolefins: A Study by Thermoporosimetry with Benzene Derivatives as Swelling Solvents, ChemPhysChem., 2005, 6, 1126–1132 CrossRef CAS PubMed.
- M. Wulff, Pore size determination by thermoporometry using acetonitrile, Thermochim. Acta, 2004, 419, 291–294 CrossRef CAS.
- J.-M. Nedelec, J.-P. E. Grolier and M. Baba, Thermoporosimetry: A powerful tool to study the cross-linking in gels networks, J. Sol-Gel Sci. Technol., 2006, 40, 191–200 CrossRef CAS.
- Y. Kharbanda, M. Urbańczyk, O. Laitinen, K. Kling, S. Pallaspuro, S. Komulainen, H. Liimatainen and V.-V. Telkki, Comprehensive NMR Analysis of Pore Structures in Superabsorbing Cellulose Nanofiber Aerogels, J. Phys. Chem. C, 2019, 123, 30986–30995 CrossRef CAS PubMed.
- S. Meiboom and D. Gill, Modified Spin-Echo Method for Measuring Nuclear Relaxation Times, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS.
- R. M. E. Valckenborg, L. Pel and K. Kopinga, Combined NMR cryoporometry and relaxometry, J. Phys. D: Appl. Phys., 2002, 35, 249–256 CrossRef CAS.
- O. Petrov and I. Furó, A study of freezing–melting hysteresis of water in different porous materials. Part I: Porous silica glasses, Microporous Mesoporous Mater., 2011, 138, 221–227 CrossRef CAS.
- C. Faivre, D. Bellet and G. Dolino, Phase transitions of fluids confined in porous silicon: A differential calorimetry investigation, Eur. Phys. J. B, 1999, 7, 19–36 CrossRef CAS.
- O. V. Petrov and I. Furó, A joint use of melting and freezing data in NMR cryoporometry, Microporous Mesoporous Mater., 2010, 136, 83–91 CrossRef CAS.
- A. M. Kjeldsen and M. R. Geiker, On the interpretation of low temperature calorimetry data, Mater. Struct., 2007, 41, 213–224 CrossRef.
- D. Kondrashova and R. Valiullin, Improving structural analysis of disordered mesoporous materials using NMR cryoporometry, Microporous Mesoporous Mater., 2013, 178, 15–19 CrossRef CAS.
- H. R. N. B. Enninful, D. Schneider, B. Rudolph, A. Meyer, S. Mascotto and R. Valiullin, Nuclear Magnetic Resonance Cryoporometry Study of Solid–Liquid Equilibria in Interconnected Spherical Nanocages, J. Phys. Chem. C, 2021, 125, 26916–26926 CrossRef CAS.
- M. Baba, J.-M. Nedelec, J. Lacoste, J.-L. Gardette and M. Morel, Crosslinking of elastomers resulting from ageing: use of thermoporosimetry to characterise the polymeric network with n-heptane as condensate, Polym. Degrad. Stab., 2003, 80, 305–313 CrossRef CAS.
- M. Baba, J.-L. Gardette and J. Lacoste, Crosslinking on ageing of elastomers II. Comparison of solvent freezing point depression and conventional crosslinking evaluation, Polym. Degrad. Stab., 1999, 65, 415–420 CrossRef CAS.
- W. J. Grigsby, H. Kroese and E. A. Dunningham, Characterisation of pore size distributions in variously dried Pinus radiata: analysis by thermoporosimetry, Wood Sci. Technol., 2013, 47, 737–747 CrossRef CAS.
- P. M. Kekkonen, A. Ylisassi and V.-V. Telkki, Absorption of Water in Thermally Modified Pine Wood As Studied by Nuclear Magnetic Resonance, J. Phys. Chem. C, 2014, 118, 2146–2153 CrossRef CAS.
- C. Cai, M. A. Javed, S. Komulainen, V.-V. Telkki, A. Haapala and H. Heräjärvi, Effect of natural weathering on water absorption and pore size distribution in thermally modified wood determined by nuclear magnetic resonance, Cellulose, 2020, 27, 4235–4247 CrossRef CAS.
- N. N. Fathima, M. Baias, B. Blumich and T. Ramasami, Structure and dynamics of water in native and tanned collagen fibers: Effect of crosslinking, Int. J. Biol. Macromol., 2010, 47, 590–596 CrossRef CAS PubMed.
- B. Han, R. V. Devireddy and J. C. Bischof, Advances in Bioengineering, ASMEDC, 2002, pp. 67–75 Search PubMed.
- M. Fleury, T. Gimmi and M. Mazurek, Porewater Content, Pore Structure and Water Mobility in Clays and Shales from NMR Methods, Clays Clay Miner., 2022, 70, 417–437 CrossRef CAS.
- P. E. Videla, J. Sala, J. Martí, E. Guàrdia and D. Laria, Aqueous electrolytes confined within functionalized silica nanopores, J. Chem. Phys., 2011, 135, 104503 CrossRef PubMed.
- C. M. Burba and J. Janzen, Confinement effects on the phase transition temperature of aqueous NaCl solutions: The extended Gibbs–Thomson equation, Thermochim. Acta, 2015, 615, 81–87 CrossRef CAS.
- B. Malfait, A. Pouessel, A. Jani and D. Morineau, Extension and Limits of Cryoscopy for Nanoconfined Solutions, J. Phys. Chem. Lett., 2020, 11, 5763–5769 CrossRef CAS PubMed.
- J. Meissner, A. Prause and G. H. Findenegg, Secondary Confinement of Water Observed in Eutectic Melting of Aqueous Salt Systems in Nanopores, J. Phys. Chem. Lett., 2016, 7, 1816–1820 CrossRef CAS PubMed.
- X. Ge and X. Wang, Calculations of Freezing Point Depression, Boiling Point Elevation, Vapor Pressure and Enthalpies of Vaporization of Electrolyte Solutions by a Modified Three-Characteristic Parameter Correlation Model, J. Solution Chem., 2009, 38, 1097–1117 CrossRef CAS.
- V. Gekas, C. Gonzalez, A. Sereno, A. Chiralt and P. Fito, Mass transfer properties of osmotic solutions. I. Water activity and osmotic pressure, Int. J. Food Prop., 1998, 1, 95–112 CrossRef CAS.
- A. Abragam and L. C. Hebel, The Principles of Nuclear Magnetism, Am. J. Phys., 1961, 29, 860–861 CrossRef.
- Y. I. Aristov, G. Di Marco, M. M. Tokarev and V. N. Parmon, Selective water sorbents for multiple applications, 3. CaCl2 solution confined in micro- and mesoporous silica gels: Pore size effect on the “solidification-melting” diagram, React. Kinet. Catal. Lett., 1997, 61, 147–154 CrossRef CAS.
- R. Schmidt, E. W. Hansen, M. Stoecker, D. Akporiaye and O. H. Ellestad, Pore Size Determination of MCM-51 Mesoporous Materials by means of 1H NMR Spectroscopy, N2 adsorption, and HREM. A Preliminary Study, J. Am. Chem. Soc., 1995, 117, 4049–4056 CrossRef CAS.
- V.-V. Telkki, J. Lounila and J. Jokisaari, Determination of Pore Sizes and Volumes of Porous Materials by 129 Xe NMR of Xenon Gas Dissolved in a Medium, J. Phys. Chem. B, 2005, 109, 24343–24351 CrossRef CAS PubMed.
- D. W. Aksnes, K. Førland and L. Kimtys, Pore size distribution in mesoporous materials as studied by 1H NMR, Phys. Chem. Chem. Phys., 2001, 3, 3203–3207 RSC.
- A. J. Sophia Fox, A. Bedi and S. A. Rodeo, The Basic Science of Articular Cartilage: Structure, Composition, and Function, Sports Health: A Multidiscip. Approach, 2009, 1, 461–468 CrossRef PubMed.
- V. C. Mow, M. H. Holmes and W. Michael Lai, Fluid transport and mechanical properties of articular cartilage: A review, J. Biomech., 1984, 17, 377–394 CrossRef CAS PubMed.
- V. C. Mow, A. Ratcliffe and A. Robin Poole, Cartilage and diarthrodial joints as paradigms for hierarchical materials and structures, Biomaterials, 1992, 13, 67–97 CrossRef CAS PubMed.
- C. D. DiDomenico, M. Lintz and L. J. Bonassar, Molecular transport in articular cartilage—what have we learned from the past 50 years?, Nat. Rev. Rheumatol., 2018, 14, 393–403 CrossRef CAS PubMed.
- A. G. Ogston, The spaces in a uniform random suspension of fibres, Trans. Faraday Soc., 1958, 54, 1754 RSC.
- D. S. Clague and R. J. Phillips, Hindered diffusion of spherical macromolecules through dilute fibrous media, Phys. Fluids, 1996, 8, 1720–1731 CrossRef CAS.
- B. Amsden, Solute Diffusion within Hydrogels. Mechanisms and Models, Macromolecules, 1998, 31, 8382–8395 CrossRef CAS.
- E. M. Renkin, Filtration, diffusion, and molecular sieving through porous cellulose membranes, J. Gen. Physiol., 1954, 38, 225–243 CAS.
- L. Ng, A. J. Grodzinsky, P. Patwari, J. Sandy, A. Plaas and C. Ortiz, Individual cartilage aggrecan macromolecules and their constituent glycosaminoglycans visualized via atomic force microscopy, J. Struct. Biol., 2003, 143, 242–257 CrossRef CAS PubMed.
- A. Maroudas, Biophysical chemistry of cartilaginous tissues with special reference to solute and fluid transport1, Biorheology, 1975, 12, 233–248 CAS.
- A. Maroudas and P. Bullough, Permeability of Articular Cartilage, Nature, 1968, 219, 1260–1261 CrossRef CAS PubMed.
- C. W. McCutchen, The frictional properties of animal joints, Wear, 1962, 5, 1–17 CrossRef.
- C. Weiss, L. Rosenberg and A. J. Helfet, An Ultrastructural Study of Normal Young Adult Human Articular Cartilage, J. Bone Jt. Surg., 1968, 50, 663–674 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04029a |
| This journal is © the Owner Societies 2024 |
