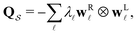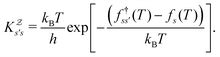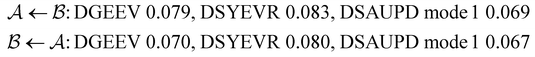Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analysis and interpretation of first passage time distributions featuring rare events†
Esmae J.
Woods
 ab and
David J.
Wales
ab and
David J.
Wales
 *b
*b
aCavendish Laboratory, Department of Physics, University of Cambridge, Cambridge CB3 0HE, UK
bYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: dw34@cam.ac.uk
First published on 22nd November 2023
Abstract
In this contribution we consider theory and associated computational tools to treat the kinetics associated with competing pathways on multifunnel energy landscapes. Multifunnel landscapes are associated with molecular switches and multifunctional materials, and are expected to exhibit multiple relaxation time scales and associated thermodynamic signatures in the heat capacity. Our focus here is on the first passage time distribution, which is encoded in a kinetic transition network containing all the locally stable states and the pathways between them. This network can be renormalised to reduce the dimensionality, while exactly conserving the mean first passage time and approximately conserving the full distribution. The structure of the reduced network can be visualised using disconnectivity graphs. We show how features in the first passage time distribution can be associated with specific kinetic traps, and how the appearance of competing relaxation time scales depends on the starting conditions. The theory is tested for two model landscapes and applied to an atomic cluster and a disordered peptide. Our most important contribution is probably the reconstruction of the full distribution for long time scales, where numerical problems prevent direct calculations. Here we combine accurate treatment of the mean first passage time with the reliable part of the distribution corresponding to faster time scales. Hence we now have a fundamental understanding of both thermodynamic and kinetic signatures of multifunnel landscapes.
I. Introduction
Molecules or condensed phases that support alternative competing metastable states may exhibit a variety of characteristic time scales and kinetics corresponding to different pathways. This information is encoded in the first passage time distribution for transitions between selected starting configurations (sources) and product states (sinks). The mean first passage time (MFPT) is the average over this first passage time (FPT) distribution, and a rate constant corresponding to the reciprocal of the MFPT is often reported. However, the full FPT distribution contains far more information,1–5 and we have recently shown how it reports on the organisation of the underlying energy landscape, in terms of kinetic traps and multiple relaxation time scales.6 We showed that the MFPT can also be used to survey the structure of the landscape, if it can be obtained as a function of the observation time scale. Hence it is particularly important to establish what a given experiment is actually measuring when comparing to calculations, especially for the multifunnel landscapes7–9 that we expect to correspond to multifunctional molecules or materials.In principle, we know how to calculate the full FPT distribution given a kinetic transition network of local minima and the transition states that connect them. Here, we assume that such a network has already been obtained using rare events techniques, either based on explicit dynamics10–18 or geometry optimisation in the discrete path sampling approach.19,20 If all the rates associated with transitions in the network are available, then we can set up a master equation for the global kinetics.21
The MFPT can be calculated deterministically using the graph transformation22–26 (GT) approach, which is numerically robust. Computation of the FPT either requires eigendecomposition of a transition matrix, or direct simulations based on kinetic Monte Carlo (kMC) methods.27–29 The dimensionality of the networks obtained in discrete path sampling typically contain between 104 and 106 local minima, which can be too large for eigendecomposition. However, we have shown that graph transformation can produce a renormalised network of amenable size where the FPT distribution is preserved, so long as key minima are retained.30 This partial graph transformation procedure forms the basis of all the calculations for larger networks in the present report.
Extracting the full FPT is problematical for systems that feature long time scales because the corresponding transition network is ill-conditioned. The linear algebra approaches that underpin eigendecomposition then break down because of numerical issues,24 while standard kMC methods encounter multiple recrossings (‘flickering’3,31) and require unfeasibly long trajectories. Kinetic path sampling (kPS),3,32 addresses the flickering problem using graph transformation to analyse escape from subnetworks, but requires a careful description of the metastable sets of nodes,31 which may itself be a difficult problem in practice.33–35 Here we focus instead on schemes to overcome the numerical problems of eigendecomposition.
We begin with a summary of the theory in Section II, starting from the underlying master equation. Next, we investigate the FPT itself in more detail, and show that peaks in the FPT may be associated with particular local minima in the landscape, providing an assignment for the specific relaxation modes (Section IIIA). This assignment uses the right eigenvector of the transition matrix. The left eigenvector allows us to scan the number of peaks in the FPT for all the possible sources, diagnosing starting conditions that would highlight alternative relaxation time scales (Section IIIB). We test this framework using a model landscape that features four distinct time scales, and show how the MFPT as a function of the observation time scale displays features that correspond to peaks in the FPT. The peak assignments are verified using direct kinetic Monte Carlo simulations, which are feasible in this test case if the temperature is not too low.
We then describe partial graph transformation for producing a renormalised network that approximately preserves the FPT with suitable dimensionality for eigendecomposition (Section IV). The renormalised network can be visualised using free energy disconnectivity graphs,36–39 which provide direct insight into the structure of the landscape and the competing relaxation time scales. The free energies are defined to reproduce the stationary distribution of the renormalised landscape30 and the transition rates between the states that are retained. Results are presented for a double-funnel37,40,41 atomic cluster.
The last two sections describe strategies for calculating the full FPT in cases where eigendecomposition breaks down. We first consider fitting individual peaks using results that cover a temperature range where the eigenvalues and eigenvectors are reliable (Section V). This approach is used to help validate an alternative hybrid scheme in Section VI. The hybrid approach combines the strengths of eigendecomposition and graph transformation, using eigenvalues and eigenvectors at the shorter time scale end of the spectrum, which remain accurate even when the results for slow relaxations are incorrect. Assuming that there is one missing slow relaxation, we can use the accurate MFPT obtained from graph transformation to deduce the missing part of the FPT.
The hybrid approach appears to be particularly powerful, and enables us to present results for the atomic cluster benchmark over 40 orders of magnitude. In particular, we can probe temperatures that cover the key change in morphology from icosahedral to close-packing.
II. First passage time distributions
In this section we summarise key results from previous work. Details of all the derivations can be found elsewhere.26,30,42 Our results are all based on analysis of a kinetic transition network43–45 using discrete state Markov chains. In particular, we focus on databases of local minima and the transition states that connect them on a molecular potential energy surface, which we obtain from discrete path sampling.19,20 However, appropriate networks can be obtained using alternative rare events methodology, including methods based on explicit dynamics.10,13,14,17,18 The corresponding kinetics are expressed in terms of interconversion rates between minima directly connected by a transition state, which gives a linear master equation:21,46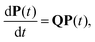 | (1) |
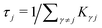 is the mean waiting time associated with a transition from state j.
is the mean waiting time associated with a transition from state j.
We denote the product states by the set 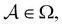 and partition Ω as
and partition Ω as 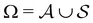 with
with 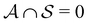 . We may also specify initial states,
. We may also specify initial states,  as a subset of
as a subset of  . The first passage time distribution to
. The first passage time distribution to  can be treated by setting all escape rates from
can be treated by setting all escape rates from  to zero and considering the substochastic matrix
to zero and considering the substochastic matrix 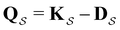 for the subset of the full transition matrix Q containing the interstate transition rates within
for the subset of the full transition matrix Q containing the interstate transition rates within 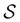 .
. 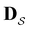 is the corresponding subset of D including the escape rates to
is the corresponding subset of D including the escape rates to 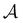 . The kinetics up to absorption are unchanged, so we analyse the master equation
. The kinetics up to absorption are unchanged, so we analyse the master equation
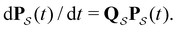 | (2) |
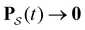 as t → ∞ because all trajectories are eventually absorbed in
as t → ∞ because all trajectories are eventually absorbed in 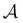 for a connected network.
for a connected network.
For a reversible Markov process eigendecomposition gives
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and wR
and wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are the left and right eigenvectors and ⊗ is the diadic (outer) product; wL
are the left and right eigenvectors and ⊗ is the diadic (outer) product; wL![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is a row vector. The eigenvalues of
is a row vector. The eigenvalues of 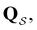 −λ
−λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) < 0, are real and negative for a reversible Markov process on a connected network. For a non-reversible process a Jordan normal form might be required. Using the representation in eqn (3) in the formal solution of eqn (2) enables us to write the probability distribution for the
< 0, are real and negative for a reversible Markov process on a connected network. For a non-reversible process a Jordan normal form might be required. Using the representation in eqn (3) in the formal solution of eqn (2) enables us to write the probability distribution for the 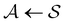 first passage time θ as
first passage time θ as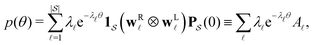 | (3) |
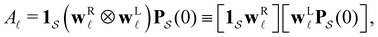 a product of dot products. Here,
a product of dot products. Here, 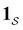 is a row vector of ones and
is a row vector of ones and 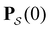 is the initial occupation probability in
is the initial occupation probability in  . The corresponding probability distribution for y = ln
. The corresponding probability distribution for y = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,
θ, 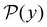 , is
, is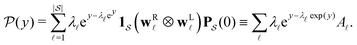 | (4) |
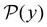 are normalised distributions, and
are normalised distributions, and  .
.
Moments of the p(t) distribution can be calculated from eqn (3); in particular, the mean first passage time (MFPT) is
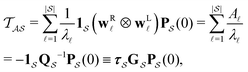 | (5) |
 is defined as
is defined as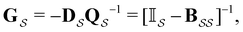 | (6) |
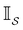 the identity matrix and
the identity matrix and 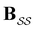 the branching matrix for
the branching matrix for 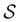 .
. 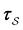 is the vector of waiting times for states in
is the vector of waiting times for states in  .
.
Our previous investigation showed how kinetic traps in the energy landscape produce signatures in the MFPT as a function of the observation timescale, tobs. Integrating θp(θ) up to tobs and including the corresponding normalisation z(tobs) gives:6
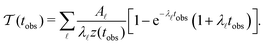 | (7) |
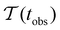 when the slowest relaxation timescales are well separated, and the steps occur at values that correspond to
when the slowest relaxation timescales are well separated, and the steps occur at values that correspond to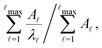 | (8) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) max, ordering the eigenmodes from the fastest to the slowest relaxation. The steps in
max, ordering the eigenmodes from the fastest to the slowest relaxation. The steps in 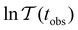 will occur at successive values of ln
will occur at successive values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ−1
λ−1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , and hence match the peak positions in
, and hence match the peak positions in 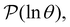 if
if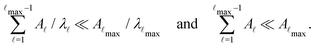 | (9) |
III. Features of the 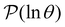 distribution
distribution
We focus on networks that exhibit a clear separation of timescales for the slowest relaxations, which correspond to physical systems that exhibit rare events. The observation time scale of an experiment that interrogates the kinetics determines which processes will be resolved.6 Systems with a hierarchy of slow relaxations are expected for multifunnel energy landscapes, and the corresponding time scales report on the kinetic traps and hence the organisation of the landscape. The 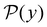 probability distribution, written in terms of y = ln
probability distribution, written in terms of y = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, highlights these features,3,31 because the individual terms in the sum over eigenvalues exhibit a maximum at ln
θ, highlights these features,3,31 because the individual terms in the sum over eigenvalues exhibit a maximum at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ−1
λ−1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , independent of the initial distribution
, independent of the initial distribution 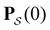 . When the eigenvalues are well separated in magnitude, we find that peaks in
. When the eigenvalues are well separated in magnitude, we find that peaks in 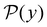 correspond closely to the maxima that arise for individual terms in the sum, as illustrated below.
correspond closely to the maxima that arise for individual terms in the sum, as illustrated below.
A. Assignment of first passage time features to local minima from the right eigenvector
From the mean first passage time expression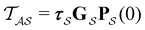 we find that the time spent in state s′ for trajectories starting in state s is
we find that the time spent in state s′ for trajectories starting in state s is 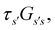 where we replace the
where we replace the 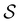 subscript with the specific components for
subscript with the specific components for 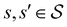 for the vector and matrix components. If all the waiting times are set to zero aside from τs′, and Pα(0) = δαs, then
for the vector and matrix components. If all the waiting times are set to zero aside from τs′, and Pα(0) = δαs, then 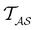 becomes the time spent in state s′. If τs′ is set to one we see that the number of visits to state s′ is Gs′s, which is known as the dynamical activity.47,48 The time spent in s′ can also be obtained in terms of the s′ components of the right eigenvectors,
becomes the time spent in state s′. If τs′ is set to one we see that the number of visits to state s′ is Gs′s, which is known as the dynamical activity.47,48 The time spent in s′ can also be obtained in terms of the s′ components of the right eigenvectors, 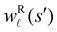 from the occupation probability Ps′(t):
from the occupation probability Ps′(t):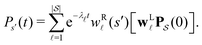 | (10) |
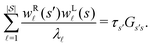 | (11) |
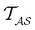 from mode
from mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is wR
is wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (β)/wR
(β)/wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (α), independent of the initial distribution. We therefore investigate the components wR
(α), independent of the initial distribution. We therefore investigate the components wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (s′) to associate peaks in
(s′) to associate peaks in 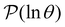 with states that correspond to different kinetic traps.
with states that correspond to different kinetic traps.
The individual terms in the sum over eigenmodes that defines 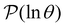 each have a maximum at y = ln
each have a maximum at y = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ−1
λ−1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , where the peak height is A
, where the peak height is A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /e, and the curvature (second derivative) is −A
/e, and the curvature (second derivative) is −A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /e. Each term can be approximated quite well as λ
/e. Each term can be approximated quite well as λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) A
A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[y − λ
exp[y − λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) exp(y)] ≈ A
exp(y)] ≈ A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(y + ln
exp[−(y + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ
λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )2/2]/e, where the Gaussian has an integrated peak area about 8% less than the correct value.
)2/2]/e, where the Gaussian has an integrated peak area about 8% less than the correct value.
For well separated time scales the positions and peak heights in 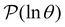 correspond closely to the values for the individual terms. Since
correspond closely to the values for the individual terms. Since 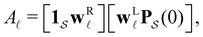 the peak height contains a factor that is the sum of right eigenvector components, wR
the peak height contains a factor that is the sum of right eigenvector components, wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (s′), with a second factor that depends on the overlap of wL
(s′), with a second factor that depends on the overlap of wL![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and the initial probability distribution.
and the initial probability distribution.
Hence the relative values of wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (s′) are related to the time spent in state s′, while the sum modulates the peak height in
(s′) are related to the time spent in state s′, while the sum modulates the peak height in 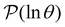 at ln
at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ ln
θ ≈ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ−1
λ−1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The components wR
. The components wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (s′) are not themselves observables, and they can have different signs. However, we find that the relative magnitudes do indeed correlate with the time spent in particular states when we break down the number of visits to each state for the different peaks.
(s′) are not themselves observables, and they can have different signs. However, we find that the relative magnitudes do indeed correlate with the time spent in particular states when we break down the number of visits to each state for the different peaks.
To illustrate this correspondence we return to a model landscape that features four distinct relaxation time scales.6 The disconnectivity graph36,37 is shown in Fig. 1. The energy and all other quantities are measured in reduced units for this example. At a temperature T = 1.5 the longest kinetic Monte Carlo (kMC) trajectories do not exceed 1010 steps for a standard rejection-free27–29 scheme. For comparison with the eigendecomposition results 105 kMC trajectories were run, which is sufficient to converge the first passage time distribution. The number of visits to each local minimum was retained for each trajectory, providing a breakdown of the peaks in 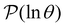 .
.
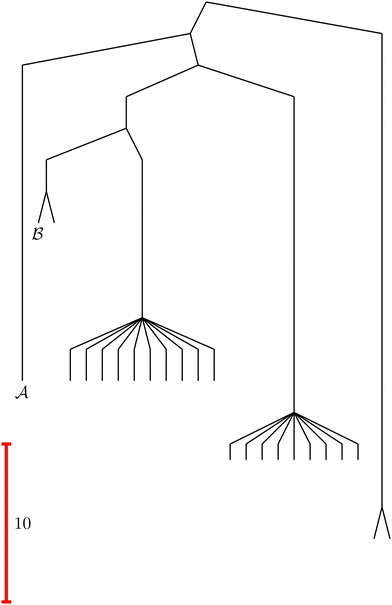 | ||
Fig. 1 Disconnectivity graph36,37 for a model energy landscape that features multiple kinetic traps.6 The scale bar corresponds to ten energy units and the local minima 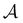 (sink) and (sink) and 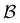 (source) are marked. (source) are marked. | ||
Fig. 2 presents the mean first passage time as a function of the observation time scale, 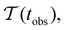 calculated from eqn (7). The arrows in this figure correspond to the predicted plateau values from eqn (8), which correspond to time scales that progressively access deeper kinetic traps in the landscape as tobs increases. This figure also shows
calculated from eqn (7). The arrows in this figure correspond to the predicted plateau values from eqn (8), which correspond to time scales that progressively access deeper kinetic traps in the landscape as tobs increases. This figure also shows 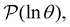 with the time scales corresponding to ln
with the time scales corresponding to ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ−1
λ−1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and the plateau values for
and the plateau values for 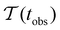 both marked. The steps in
both marked. The steps in  match the peak positions closely, except for the slowest relaxation. For this landscape A
match the peak positions closely, except for the slowest relaxation. For this landscape A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is essentially zero for all the modes except the slowest four, which correspond to A
is essentially zero for all the modes except the slowest four, which correspond to A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /λ
/λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values of 5.2, 2.0 × 106, 3.9 × 108, and 3.2 × 109, respectively.
values of 5.2, 2.0 × 106, 3.9 × 108, and 3.2 × 109, respectively.
 | ||
Fig. 2 Results for the model landscape illustrated in Fig. 1 at T = 1.5, left: mean first passage time  as a function of the observation time scale cutoff, tobs, calculated from the analytical eigendecomposition formulation in eqn (7). The red arrows mark the position of steps in as a function of the observation time scale cutoff, tobs, calculated from the analytical eigendecomposition formulation in eqn (7). The red arrows mark the position of steps in 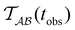 predicted from eqn (8). Right: The probability distribution predicted from eqn (8). Right: The probability distribution 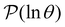 . The blue arrows correspond to the four longest time scales defined by ln . The blue arrows correspond to the four longest time scales defined by ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ−1 λ−1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for eigenvalues of the Markov transition matrix for eigenvalues of the Markov transition matrix 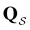 . The red arrows correspond to the same times as for the steps in . The red arrows correspond to the same times as for the steps in 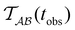 . . | ||
The number of visits to the four sets of minima in Fig. 1 that constitute kinetic traps for relaxation to 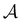 can be separated by assigning each of the 105 kMC trajectories to one of the four peaks in
can be separated by assigning each of the 105 kMC trajectories to one of the four peaks in  shown in Fig. 2. The results of this decomposition are shown in Fig. 3. We find that the four peaks can indeed be assigned to trajectories that access the traps in order of increasing depth. The longest trajectories for the peak centred at ln
shown in Fig. 2. The results of this decomposition are shown in Fig. 3. We find that the four peaks can indeed be assigned to trajectories that access the traps in order of increasing depth. The longest trajectories for the peak centred at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 24 visit the deepest trap; the trajectories corresponding to the peak centred at ln
θ = 24 visit the deepest trap; the trajectories corresponding to the peak centred at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 20 visit all the traps except the deepest, etc.
θ = 20 visit all the traps except the deepest, etc.
 | ||
Fig. 3 Breakdown of kinetic Monte Carlo results for visits to the four sets of minima that constitute kinetic traps for relaxation to  in the landscape illustrated in Fig. 1. The four panels (a)–(d) are the visit statistics for kMC trajectories with first passage times corresponding to the four peaks in in the landscape illustrated in Fig. 1. The four panels (a)–(d) are the visit statistics for kMC trajectories with first passage times corresponding to the four peaks in 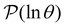 shown in Fig. 2, with (a) corresponding to the longest time scale, and (d) the fastest. Each panel contains separate histograms for the number of visits to the four traps, coloured orange, green, blue and red, which correspond to the four sets of minima from left to right and from highest to lowest energy in Fig. 1, starting with the two states that include the source shown in Fig. 2, with (a) corresponding to the longest time scale, and (d) the fastest. Each panel contains separate histograms for the number of visits to the four traps, coloured orange, green, blue and red, which correspond to the four sets of minima from left to right and from highest to lowest energy in Fig. 1, starting with the two states that include the source 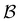 . . | ||
Having verified the peak assignment we can now compare this breakdown with the components of wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (s′) for the four eigenmodes associated with the four peaks. The objective is to determine whether the peaks could be assigned to local minima, s′, by inspecting the relative values of wR
(s′) for the four eigenmodes associated with the four peaks. The objective is to determine whether the peaks could be assigned to local minima, s′, by inspecting the relative values of wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (s′), instead of performing kMC runs, which become computationally unfeasible as the temperature decreases and the relaxation time scales increase exponentially. For this analysis we scale the components of wR
(s′), instead of performing kMC runs, which become computationally unfeasible as the temperature decreases and the relaxation time scales increase exponentially. For this analysis we scale the components of wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) so that the largest value is 100. If we start from the slowest relaxation we find that a systematic assignment scheme appears to emerge. For this slowest mode the components for the two states in the deepest trap in Fig. 1 are 100, and the next largest magnitude component is less than 1. Moving to the
so that the largest value is 100. If we start from the slowest relaxation we find that a systematic assignment scheme appears to emerge. For this slowest mode the components for the two states in the deepest trap in Fig. 1 are 100, and the next largest magnitude component is less than 1. Moving to the 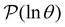 peak at ln
peak at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 20, we find components of 100 for the nine states in the next deepest trap, values of −55 for the two minima we have just associated with the slowest relaxation, and a next largest value of 2.3. We therefore assign the third peak in
θ = 20, we find components of 100 for the nine states in the next deepest trap, values of −55 for the two minima we have just associated with the slowest relaxation, and a next largest value of 2.3. We therefore assign the third peak in 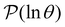 to the minima in the third trap.
to the minima in the third trap.
For the second peak at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 16, the ten minima in the second set of trap states have wR
θ = 16, the ten minima in the second set of trap states have wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) coefficients of 100, and the values for the states assigned to the third and fourth peaks are −70 and −21, respectively. Finally, for the small peak at ln
coefficients of 100, and the values for the states assigned to the third and fourth peaks are −70 and −21, respectively. Finally, for the small peak at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 5, it is the source state
θ = 5, it is the source state 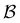 that has the maximum component of 100 (with 97 for the partner minimum, which is only connected to
that has the maximum component of 100 (with 97 for the partner minimum, which is only connected to 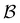 ), while the next largest magnitude is −21 for states assigned to the second peak.
), while the next largest magnitude is −21 for states assigned to the second peak.
Hence it appears that we can assign the peaks to states using the largest components of wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . For the example considered here, the next largest components in magnitude for wR
. For the example considered here, the next largest components in magnitude for wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) have the opposite sign, and correspond to the states assigned to relaxation mode
have the opposite sign, and correspond to the states assigned to relaxation mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1, ordering the relaxation times from fastest to slowest. If the terms in the sum that contribute to
+ 1, ordering the relaxation times from fastest to slowest. If the terms in the sum that contribute to 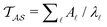 can be treated separately, then the peak height at ln
can be treated separately, then the peak height at ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ−1
λ−1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for
for 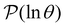 depends on the sum
depends on the sum 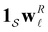 . The components of wR
. The components of wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) can take opposite signs, but our results suggest that the states making the largest contribution correspond to the kinetic trap that determines the time scale in question.
can take opposite signs, but our results suggest that the states making the largest contribution correspond to the kinetic trap that determines the time scale in question.
B. Predicting first passage time peaks for different initial conditions from the left eigenvector
The number of peaks that can be distinguished in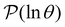 depends on the initial conditions. Each amplitude A
depends on the initial conditions. Each amplitude A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) depends on the product
depends on the product 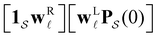 . The right eigenvector contribution was used above to guide assignment of relaxation modes to local minima. For a single source s we have Pα(0) = δαs and
. The right eigenvector contribution was used above to guide assignment of relaxation modes to local minima. For a single source s we have Pα(0) = δαs and 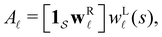 so all the source dependence is contained in the left eigenvector.
so all the source dependence is contained in the left eigenvector.
Having performed an eigendecomposition we can evaluate all the A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for each source state and identify the eigenmodes that make a significant contribution to the sum that determines
for each source state and identify the eigenmodes that make a significant contribution to the sum that determines 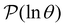 . Restricting the sum to terms above a given threshold provides an efficient calculation of the distribution (and its moments) for each source state, since the number of terms required is usually small. The number of peaks in
. Restricting the sum to terms above a given threshold provides an efficient calculation of the distribution (and its moments) for each source state, since the number of terms required is usually small. The number of peaks in 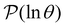 above a chosen cutoff height can be counted during the calculation of each distribution, thus identifying sources that produce interesting structure.
above a chosen cutoff height can be counted during the calculation of each distribution, thus identifying sources that produce interesting structure.
Fig. 4 illustrates first passage time distributions to 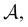 starting from a selected minimum in each of the four sets constituting kinetic traps. As the system is initialised in progressively deeper traps, the number of peaks decreases, and when a peak disappears its probability amplitude is transferred to the next fastest peak. For example, when the source is changed from
starting from a selected minimum in each of the four sets constituting kinetic traps. As the system is initialised in progressively deeper traps, the number of peaks decreases, and when a peak disappears its probability amplitude is transferred to the next fastest peak. For example, when the source is changed from 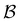 to a minimum in the next set of states to the right in Fig. 1, the small peak around ln
to a minimum in the next set of states to the right in Fig. 1, the small peak around ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 5 disappears, and the amplitude of the peak around ln
θ = 5 disappears, and the amplitude of the peak around ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 16 increases slightly.
θ = 16 increases slightly.
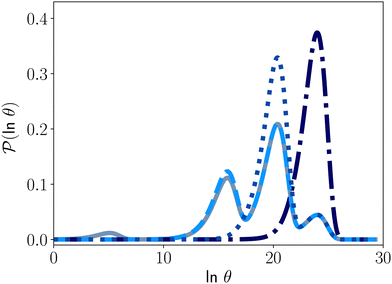 | ||
Fig. 4 First passage time distributions to  starting from selected individual minima in the four different kinetic traps in Fig. 1 from left to right: the shallowest trap containing starting from selected individual minima in the four different kinetic traps in Fig. 1 from left to right: the shallowest trap containing  (solid grey), the second trap (dashed light blue), the third trap (dotted blue), and the deepest trap (dashdot dark blue). The contribution of each eigenvalue to the first passage time distribution depends on the initial condition of the network. (solid grey), the second trap (dashed light blue), the third trap (dotted blue), and the deepest trap (dashdot dark blue). The contribution of each eigenvalue to the first passage time distribution depends on the initial condition of the network. | ||
IV. Graph transformation as a network reduction tool
The eigendecomposition approach described in Section II is a powerful tool for kinetic analysis,42,49,50 and we note that an analogous framework has been employed in milestoning calculations.4,5 Unfortunately, in systems featuring rare events and a large separation of timescales for the slowest relaxation modes, severe metastability makes the Markov matrix highly ill-conditioned, and linear algebra approaches break down because of finite numerical precision.24,42,51–54 Additionally, some networks are too large for full eigendecomposition to be tractable on a feasible time scale. Some further discussion of these issues can be found in ref. 30. However, the graph transformation approach22–24,26,55–57 enables us to calculate the mean first passage time accurately in a deterministic procedure. States are successively removed singly, or in groups, and the branching probabilities and waiting times are renormalised as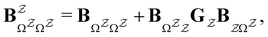 | (12) |
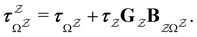 | (13) |
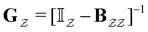 is the Green's matrix for
is the Green's matrix for 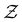 , and
, and 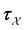 is the row vector of waiting times for states in
is the row vector of waiting times for states in 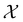 .
.
The mean first passage time is certainly important, providing a phenomenological rate constant via the reciprocal. However, it cannot report on multiple relaxation time scales,6 which we associate with energy landscapes featuring multiple funnels and potentially multifunctional systems.7–9 Instead, the rate constant calculated in this way is likely to be dominated by the slowest relaxation process, which might lie beyond the experimental time scale. Enhanced kinetic Monte Carlo schemes, such as Monte Carlo with absorbing Markov chains (MCAMC)58,59 and kinetic path sampling,3,32,60 can provide the full first passage time distribution. However, they require a definition of metastable macrostates, and become computationally expensive when these states are large. Instead, we have recently introduced the partial graph transformation approach (pGT),30 and we showed how judicious choice of the set of removed states 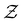 can yield a reduced network that retains the full first passage time distribution quite well.
can yield a reduced network that retains the full first passage time distribution quite well.
The equilibrium occupation probability distribution for a pGT network Ω where nodes in set 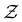 have been removed,
have been removed, 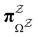 , can be obtained by applying the balance condition.30 The result is
, can be obtained by applying the balance condition.30 The result is
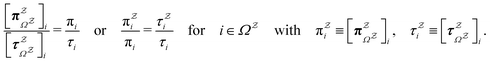 | (14) |
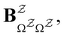 and waiting times,
and waiting times, 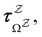 can be used to define free energies for the retained minima, fs(T), and the transition states that connect them,
can be used to define free energies for the retained minima, fs(T), and the transition states that connect them, 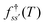 as
as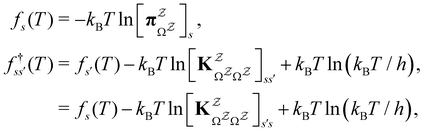 | (15) |
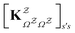 in
in  is
is  or
or 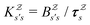 with
with 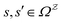 . The rate constants in the reduced network define a master equation for the retained states
. The rate constants in the reduced network define a master equation for the retained states 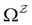 . Hence
. Hence 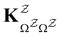 corresponds to the equilibrium occupation probabilities
corresponds to the equilibrium occupation probabilities 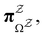 and the effective free energies fs(T) are defined to reproduce these relative probabilities. Similarly, the free energies of the transition states reproduce
and the effective free energies fs(T) are defined to reproduce these relative probabilities. Similarly, the free energies of the transition states reproduce 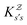 :
:We can therefore obtain a free energy disconnectivity graph for the reduced network, corresponding to the thermodynamic and kinetic properties of
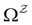 . This approach has recently been applied to translate rates from a quantum master equation and provide new insight into polaritonic rate suppression.61
. This approach has recently been applied to translate rates from a quantum master equation and provide new insight into polaritonic rate suppression.61
The first passage time (FPT) results presented in our previous contribution6 employed minimal subsets of much larger kinetic transition networks to demonstrate how multifunnelled landscapes with traps produce multiple features in 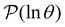 . Here, we tackle the full database using the partial graph transformation approach, without using community definitions.
. Here, we tackle the full database using the partial graph transformation approach, without using community definitions.
A. Partial graph transformation
Our previous analysis of partial graph transformation for a model landscape, focused on reproducing FPT distributions between metastable communities. We showed that the first passage time distribution was preserved very well if only boundary states between communities and the lowest minima in each community were retained.30 However, in order to reproduce accurate first passage time distributions between global minima of metastable communities (with one source and one sink), it is actually sufficient to just keep the global minima of each trap (see ESI†). Whatever the source and sink of interest, if we retain the global minimum of each trap in the network, alongside the source(s) and sink(s), pGT preserves the long time behaviour of the first passage time distribution. In fact, it is more challenging to preserve the short time peaks.We have now found better ways to determine which states to retain with pGT, in order to properly preserve the full FPT distribution. Various possibilities were considered, and we will focus on the most successful approaches for brevity. The minimal starting information required is the identity of the source and sink states and the minima at the bottom of competing funnels in the landscape.
We first show how the simple model landscape shown in Fig. 1 can be reduced. We must retain at least one state from each kinetic trap, and the source and sinks 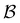 and
and 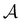 . However, we cannot arbitrarily choose which state to keep, because when a state is removed via GT, the waiting time for all the neighbouring states increases. This effect can increase the time taken to traverse a short-time path as states are removed. For example, the path corresponding to the shortest time peak in Fig. 2 corresponds to the direct transition
. However, we cannot arbitrarily choose which state to keep, because when a state is removed via GT, the waiting time for all the neighbouring states increases. This effect can increase the time taken to traverse a short-time path as states are removed. For example, the path corresponding to the shortest time peak in Fig. 2 corresponds to the direct transition 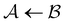 . To protect this path from the effects of GT, we must keep all the neighbours of
. To protect this path from the effects of GT, we must keep all the neighbours of 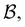 otherwise the waiting time to leave
otherwise the waiting time to leave  increases, and the shortest time peak shifts to longer times. For this simple landscape, we retain
increases, and the shortest time peak shifts to longer times. For this simple landscape, we retain  and all of its neighbours, which explicitly includes
and all of its neighbours, which explicitly includes  and at least one state from each kinetic trap. Visualisations of the resulting network are shown in Fig. 5, alongside the first passage time distributions generated from the full and pGT reduced networks, which are essentially identical.
and at least one state from each kinetic trap. Visualisations of the resulting network are shown in Fig. 5, alongside the first passage time distributions generated from the full and pGT reduced networks, which are essentially identical.
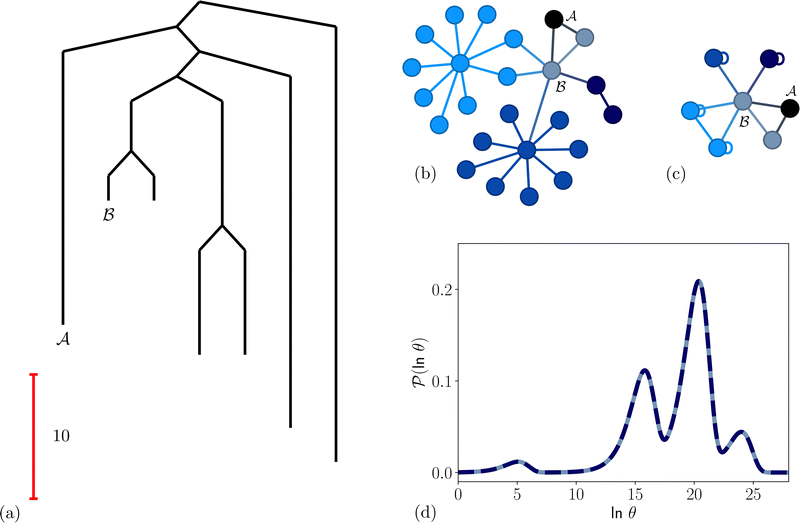 | ||
Fig. 5 Partial graph transformation of the model landscape shown in Fig. 1. We retain state 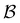 and all its neighbours, which explicitly includes the sink and all its neighbours, which explicitly includes the sink 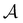 , and at least one state from each kinetic trap. (a) Disconnectivity graph for the reduced network, computed as described in Section IV. (b) and (c) Network visualisations showing connections between states, using Gephi,65 for the full and reduced networks, respectively. As states are removed their neighbours gain self-transitions. The colour scheme is the same as in Fig. 4. (d) The first passage time distributions for , and at least one state from each kinetic trap. (a) Disconnectivity graph for the reduced network, computed as described in Section IV. (b) and (c) Network visualisations showing connections between states, using Gephi,65 for the full and reduced networks, respectively. As states are removed their neighbours gain self-transitions. The colour scheme is the same as in Fig. 4. (d) The first passage time distributions for 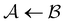 for the full (solid grey) and the reduced (dashed dark blue) network are essentially identical. for the full (solid grey) and the reduced (dashed dark blue) network are essentially identical. | ||
To extend this process to larger, more complicated networks, we perform Dijkstra's shortest path algorithm62 for all pairs of states within the sources and sinks list, using edge weights equal to the branching probabilities in the original network, −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bij.63,64 This analysis is equivalent to finding the path that makes the largest contribution to the rate constant when intervening minima are placed in steady state, in other words, the fastest path in the steady state regime.19 Using a straightforward depth-first algorithm we then calculate the minimum number of steps (via transition states) for every minimum to the minima in the fastest paths, with separate lists for the number of steps to the path endpoints, and to the full path. To study the convergence of the FPT as more minima are retained, states can be systematically added for an increasing number of steps (see the ESI,† for figures illustrating convergence).
Bij.63,64 This analysis is equivalent to finding the path that makes the largest contribution to the rate constant when intervening minima are placed in steady state, in other words, the fastest path in the steady state regime.19 Using a straightforward depth-first algorithm we then calculate the minimum number of steps (via transition states) for every minimum to the minima in the fastest paths, with separate lists for the number of steps to the path endpoints, and to the full path. To study the convergence of the FPT as more minima are retained, states can be systematically added for an increasing number of steps (see the ESI,† for figures illustrating convergence).
Keeping minima on the fastest paths helps to preserve shorter time peaks in the FPT distribution, but retaining only these minima is insufficient. Retaining minima surrounding the fastest paths helps to protect them from the effects of GT and includes more routes for the flow of probability. Removal of a node via GT increases the waiting time for all directly connected nodes. If adjacent minima to the fastest paths are not retained then, as more minima are removed, the time taken to traverse the fastest path will increase.
To demonstrate the power of pGT, we revisit the nine community network presented in ref. 30, for which the disconnectivity graph is shown in Fig. 6. Instead of looking at transitions between metastable communities, we compute the FPT distribution between a high energy minimum and one of minima at the bottom of a basin (Fig. 7). When only the minima at the bottom of the nine trapping basins, plus the source minimum are retained, only the long time peaks in the FPT distribution are preserved. To maintain the full FPT distribution under pGT, we compute the fastest path between the source and the sink, which are labelled 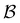 and
and  in Fig. 6, respectively. We then additionally retain the fastest path and its first and second neighbouring minima, to produce a reduced network of 84 states, which is shown in blue in Fig. 6. The FPT distributions computed from the full 994 state network and the pGT reduced 84 state network match, which shows that we can reduce the size of a network by an order of magnitude, and still preserve the full FPT distribution. As for the previous model landscape, we work in reduced units. All these calculations correspond to T = 1, where eigendecomposition is tractable on the full 994 state network.
in Fig. 6, respectively. We then additionally retain the fastest path and its first and second neighbouring minima, to produce a reduced network of 84 states, which is shown in blue in Fig. 6. The FPT distributions computed from the full 994 state network and the pGT reduced 84 state network match, which shows that we can reduce the size of a network by an order of magnitude, and still preserve the full FPT distribution. As for the previous model landscape, we work in reduced units. All these calculations correspond to T = 1, where eigendecomposition is tractable on the full 994 state network.
 | ||
Fig. 6 Disconnectivity graphs36,37 for a model energy landscape consisting of nine traps.30 The scale bar corresponds to five energy units and the source and sink states  and and  are marked. (a) Graph for the full system. The states that are on the fastest path between are marked. (a) Graph for the full system. The states that are on the fastest path between  and and 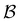 and first and second neighbouring minima surrounding the fastest path, are marked in blue. (b) Graph for the pGT reduced system, computed using the method described in Section IV. We retain the global minimum of each trap, and all the states marked in blue in (a). and first and second neighbouring minima surrounding the fastest path, are marked in blue. (b) Graph for the pGT reduced system, computed using the method described in Section IV. We retain the global minimum of each trap, and all the states marked in blue in (a). | ||
 | ||
Fig. 7 First passage time distributions for relaxation from  to to  (left) and (left) and  to to  (right), of the nine community network at T = 1.0, as shown in Fig. 6. The distributions are computed using eigendecomposition for the full network with 994 minima (thick grey line), and two different partial GT reduced networks consisting of, 10 states including the nine trap global minima and state (right), of the nine community network at T = 1.0, as shown in Fig. 6. The distributions are computed using eigendecomposition for the full network with 994 minima (thick grey line), and two different partial GT reduced networks consisting of, 10 states including the nine trap global minima and state  (thin light blue line), and a network of 84 states that additionally contains the states on the fastest path between (thin light blue line), and a network of 84 states that additionally contains the states on the fastest path between  and and 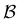 and the first and second neighbouring minima surrounding the fastest path (dashed blue line). Only the minima at the bottom of the traps are required to retain long time behaviour, whilst minima on and around the fastest path help pick out the short time peaks. and the first and second neighbouring minima surrounding the fastest path (dashed blue line). Only the minima at the bottom of the traps are required to retain long time behaviour, whilst minima on and around the fastest path help pick out the short time peaks. | ||
As well as reducing the network size, partial graph transformation can decrease the number of eigenmodes that contribute significantly to the first passage time distribution. The five eigenvalues smallest in magnitude agree to three significant figures for the full and reduced networks in Fig. 6. The slowest peak can be approximated by the eigenmode with the smallest magnitude eigenvalue, and the slowest two peaks can be reproduced from the modes corresponding to the five smallest magnitude eigenvalues. To reproduce the full distribution, the summation over eigenmodes in eqn (4) must include the 40 eigenmodes with the largest |A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) | values for the full network, compared to just 28 modes for the pGT reduced network. Alternatively, if we sum over the modes in order of decreasing magnitude for λ
| values for the full network, compared to just 28 modes for the pGT reduced network. Alternatively, if we sum over the modes in order of decreasing magnitude for λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , 234 terms are required to reproduce the distribution for the full network, and only 39 modes for the pGT reduced system. (see ESI,† for more information).
, 234 terms are required to reproduce the distribution for the full network, and only 39 modes for the pGT reduced system. (see ESI,† for more information).
B. Results for an atomic cluster: LJ38
Our third example is the atomic cluster of 38 atoms bound by the Lennard-Jones potential (LJ38),66 which has become a standard benchmark for enhanced sampling methods.40,67–81 This system exhibits a double-funnel energy landscape37,40,41,72,82 caused by competition between the global potential energy minimum, a truncated octahedron (Oh symmetry), and an incomplete Mackay icosahedron (C5v symmetry), which is the second lowest minimum. The barrier between these structures is large at the temperature where they are in equilibrium, leading to broken ergodicity and a low temperature heat capacity feature. These thermodynamic signatures have been investigated extensively in previous work. Analysis of the kinetics provides a complementary viewpoint, where the double-funnel landscape is associated with multiple relaxation time scales.72Here we considered a database with 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 minima in the connected component of interest, and 123
887 minima in the connected component of interest, and 123![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 transition states, which is available for download from the Cambridge Landscape Database.83 As in previous work, five low energy minima from the Oh funnel and 395 minima from the C5v funnel are chosen for the
561 transition states, which is available for download from the Cambridge Landscape Database.83 As in previous work, five low energy minima from the Oh funnel and 395 minima from the C5v funnel are chosen for the 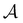 and
and 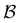 states. Results corresponding to these sets are colour-coded red
states. Results corresponding to these sets are colour-coded red 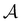 and blue
and blue  , respectively, in the figures.
, respectively, in the figures.
Our objective was to reduce the number of minima in the database using graph transformation as far as possible, while preserving the full first passage time distribution to a good approximation. We chose to run this part of the analysis at 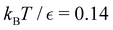 , which is somewhat higher than the equilibrium temperature for the Oh and C5v sets, but still low enough for broken ergodicity effects and separate relaxation time scales to be clearly manifested. At this temperature it is feasible to calculate converged first passage time distributions using a leapfrog kinetic Monte Carlo scheme6 and 200
, which is somewhat higher than the equilibrium temperature for the Oh and C5v sets, but still low enough for broken ergodicity effects and separate relaxation time scales to be clearly manifested. At this temperature it is feasible to calculate converged first passage time distributions using a leapfrog kinetic Monte Carlo scheme6 and 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories. We additionally ran 400
000 trajectories. We additionally ran 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories for the first passage time to
000 trajectories for the first passage time to 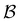 , and found that the distribution did not change. Standard kinetic Monte Carlo runs are feasible for the reduced network described below, and give very similar results for the first passage time distributions in each case, providing a further consistency check.
, and found that the distribution did not change. Standard kinetic Monte Carlo runs are feasible for the reduced network described below, and give very similar results for the first passage time distributions in each case, providing a further consistency check.
We investigate the FPT for relaxation from a high energy minimum to both the  and
and 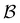 sets. We compute the shortest (fastest) path, as defined in Section IVA, between all pairs of the lowest minima in
sets. We compute the shortest (fastest) path, as defined in Section IVA, between all pairs of the lowest minima in 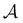 and
and 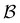 and the starting minimum at
and the starting minimum at 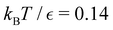 , producing a set of pathway minima,
, producing a set of pathway minima,  . We then find the distance in terms of the shortest discrete path from every other minimum to
. We then find the distance in terms of the shortest discrete path from every other minimum to  and separately, the distance to the combined set of the lowest minima in
and separately, the distance to the combined set of the lowest minima in  ,
,  and the starting minimum. We retain the 2500 states with the highest equilibrium occupation probabilities from the combined first- and second-neighbour set, from the latter definition, as well as every minimum in
and the starting minimum. We retain the 2500 states with the highest equilibrium occupation probabilities from the combined first- and second-neighbour set, from the latter definition, as well as every minimum in 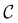 itself. The branching probabilities employed in the fastest path calculation are temperature dependent, and we analysed the effect of changing the temperature from
itself. The branching probabilities employed in the fastest path calculation are temperature dependent, and we analysed the effect of changing the temperature from 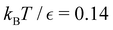 . The retained states do not change very much over a wide range of T, and the effect on the calculated FPT is negligible (see ESI†). The results for this database of 2506 states are shown in Fig. 8, with the corresponding free energy disconnectivity graph in Fig. 9. The FPT results for the renormalised database can be converged even closer to the KMC results shown in Fig. 8 if more states are retained in the renormalised database (ESI†). Using the properties of the left and right eigenvectors of the transition matrix
. The retained states do not change very much over a wide range of T, and the effect on the calculated FPT is negligible (see ESI†). The results for this database of 2506 states are shown in Fig. 8, with the corresponding free energy disconnectivity graph in Fig. 9. The FPT results for the renormalised database can be converged even closer to the KMC results shown in Fig. 8 if more states are retained in the renormalised database (ESI†). Using the properties of the left and right eigenvectors of the transition matrix 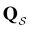 , as described in the previous section, we can now assign the peaks in this first passage time distribution and understand their heights.
, as described in the previous section, we can now assign the peaks in this first passage time distribution and understand their heights.
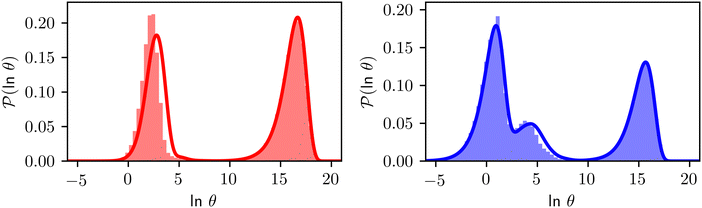 | ||
Fig. 8 First passage time distributions for relaxation to the  and and  (right) states of the LJ38 cluster at (right) states of the LJ38 cluster at 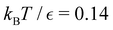 where ε is the pair well depth. The initial probability distribution corresponds to a single higher energy minimum, selected to highlight the separation of relaxation time scales. The histogram corresponds to 200 where ε is the pair well depth. The initial probability distribution corresponds to a single higher energy minimum, selected to highlight the separation of relaxation time scales. The histogram corresponds to 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kinetic Monte Carlo trajectories run for the full database with 71 000 kinetic Monte Carlo trajectories run for the full database with 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 connected minima using the leapfrog algorithm.6 The solid curves were calculated using the eigendecomposition formulation in eqn (4) for a database of 2506 minima resulting from partial graph transformation, as described in the text. 887 connected minima using the leapfrog algorithm.6 The solid curves were calculated using the eigendecomposition formulation in eqn (4) for a database of 2506 minima resulting from partial graph transformation, as described in the text. | ||
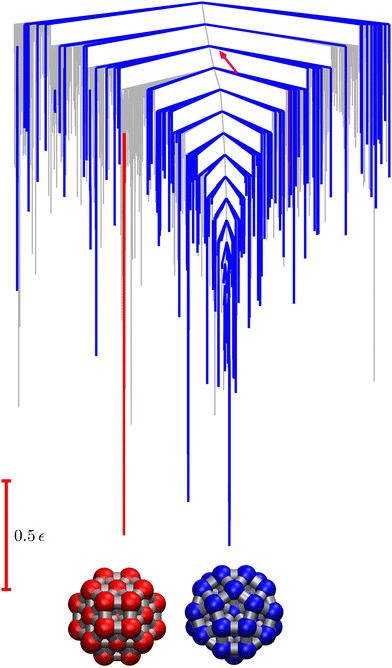 | ||
Fig. 9 Disconnectivity graph36,37 for the LJ38 database renormalised down to 2506 states, which produces the 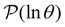 distributions in Fig. 8. The free energies of the minima and transition states are defined to reproduce the equilibrium occupation probabilities and rates for the network that results after partial graph transformation at distributions in Fig. 8. The free energies of the minima and transition states are defined to reproduce the equilibrium occupation probabilities and rates for the network that results after partial graph transformation at 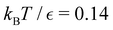 , defined in eqn (15). Branches corresponding to minima in the original , defined in eqn (15). Branches corresponding to minima in the original 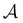 and and 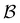 sets are coloured red and blue, respectively. The source state for the FPT calculations is a higher energy minimum; its position in the graph is marked with a magenta arrow. sets are coloured red and blue, respectively. The source state for the FPT calculations is a higher energy minimum; its position in the graph is marked with a magenta arrow. | ||
Analysis of wR![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) provides further insight into the first passage time distribution and global dynamics of the LJ38 cluster. In this case, we find that the peaks in Fig. 8 corresponding to the slow relaxation time scale can be assigned to a single eigenvalue of the transition matrix
provides further insight into the first passage time distribution and global dynamics of the LJ38 cluster. In this case, we find that the peaks in Fig. 8 corresponding to the slow relaxation time scale can be assigned to a single eigenvalue of the transition matrix 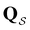 , and the components of the corresponding eigenvector are strongly localised on low-lying minima at the bottom of the competing funnel that acts as a kinetic trap. In fact, there are eigenvalues corresponding to slower relaxation times that do not produce features in
, and the components of the corresponding eigenvector are strongly localised on low-lying minima at the bottom of the competing funnel that acts as a kinetic trap. In fact, there are eigenvalues corresponding to slower relaxation times that do not produce features in 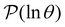 , as we noted before.42 These eigenvalues correspond to minima that are almost disconnected from the rest of the network because they are separated by very high barriers. For most initial probability distributions
, as we noted before.42 These eigenvalues correspond to minima that are almost disconnected from the rest of the network because they are separated by very high barriers. For most initial probability distributions 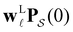 is too small to produce a significant feature in
is too small to produce a significant feature in 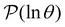 for these modes. The right eigenvector is localised on the corresponding dead-end minimum (or minima), providing a straightforward interpretation.
for these modes. The right eigenvector is localised on the corresponding dead-end minimum (or minima), providing a straightforward interpretation.
In contrast to the simple model landscape shown in Fig. 1, the 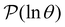 peaks corresponding to the faster relaxation time scales in Fig. 8 do not correspond to a single eigenvalue of
peaks corresponding to the faster relaxation time scales in Fig. 8 do not correspond to a single eigenvalue of 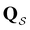 . For relaxation to the fcc structure
. For relaxation to the fcc structure  the fast peak at around ln
the fast peak at around ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 3 is a result of contributions from 13 eigenmodes with |A
θ = 3 is a result of contributions from 13 eigenmodes with |A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /e| > 0.01. For relaxation to the
/e| > 0.01. For relaxation to the  states the largest peak around ln
states the largest peak around ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0.6 results from two eigenvalues with A
θ = 0.6 results from two eigenvalues with A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /e values of 0.243 and − 0.154. The shoulder peak around ln
/e values of 0.243 and − 0.154. The shoulder peak around ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 4 results from 45 modes with |A
θ = 4 results from 45 modes with |A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /e| > 0.01, again including positive and negative contributions. The decomposition of the faster relaxation peak as a superposition results from the denser spectrum of eigenvalues for the transition matrix compared to the slow relaxation. We expect to see a similar effect in molecular and condensed matter systems if a slow relaxation time scale is associated with a well-defined rate-determining step, while faster relaxation can occur via a number of alternative pathways.
/e| > 0.01, again including positive and negative contributions. The decomposition of the faster relaxation peak as a superposition results from the denser spectrum of eigenvalues for the transition matrix compared to the slow relaxation. We expect to see a similar effect in molecular and condensed matter systems if a slow relaxation time scale is associated with a well-defined rate-determining step, while faster relaxation can occur via a number of alternative pathways.
As we have found before, whilst full eigendecomposition of the transition matrix provides over 2000 eigenvalues, only a small number of them contribute significantly to the first passage time distribution. The distribution for relaxation to  can be reproduced from eqn (4) by summing over only the 200 eigenvalues with the largest |A
can be reproduced from eqn (4) by summing over only the 200 eigenvalues with the largest |A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) | values. In contrast, if we sum over the modes in order of decreasing magnitude for λ
| values. In contrast, if we sum over the modes in order of decreasing magnitude for λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , we require 1934 terms to reproduce the FPT distribution (see ESI†).
, we require 1934 terms to reproduce the FPT distribution (see ESI†).
This scan over sources following state reduction with partial GT provides an automated analysis of the dependence on initial conditions, which can then be used for further analysis and to suggest experiments that will highlight multiple relaxation time scales.
Some examples are shown for the LJ38 cluster in Fig. 10. 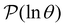 is illustrated for four sources that produce multiple peaks, including the source that was used for the analysis in Section IVB. Identifying initial conditions that produce the most interesting structure in the first passage time distribution, coupled with assignments based on the right eigenvector, has enabled us to analyse kinetic transition networks for a wide variety of systems. Some further examples are presented below. New studies, ranging from proteins and nucleic acids the photosystem II light-harvesting supercomplex, will be presented elsewhere.
is illustrated for four sources that produce multiple peaks, including the source that was used for the analysis in Section IVB. Identifying initial conditions that produce the most interesting structure in the first passage time distribution, coupled with assignments based on the right eigenvector, has enabled us to analyse kinetic transition networks for a wide variety of systems. Some further examples are presented below. New studies, ranging from proteins and nucleic acids the photosystem II light-harvesting supercomplex, will be presented elsewhere.
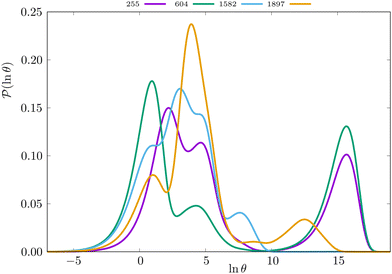 | ||
Fig. 10 First passage time distributions for relaxation to the  state of the LJ38 cluster at state of the LJ38 cluster at 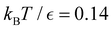 for initial probability distributions localised in four different minima, as labelled in the legend. The selected minima were chosen to highlight structure in the for initial probability distributions localised in four different minima, as labelled in the legend. The selected minima were chosen to highlight structure in the  distribution. Starting minimum 604 corresponds to the results in Fig. 8. distribution. Starting minimum 604 corresponds to the results in Fig. 8. | ||
V. Accessing longer time scales I: peak fitting
Reducing the network using partial graph transformation enables us to use a full eigendecomposition approach for the FPT distribution. However, at sufficiently low temperature this approach inevitably fails because the problem becomes increasingly ill-conditioned.24 The formulation of in eqn (4) suggests that we might be able to predict the distribution at lower temperature by fitting the λ
in eqn (4) suggests that we might be able to predict the distribution at lower temperature by fitting the λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and A
and A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as a function of temperature for the regime where eigendecomposition is tractable.
as a function of temperature for the regime where eigendecomposition is tractable.
For the model landscape in Fig. 1 accurate fits can be obtained with an Arrhenius form for λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and a simple polynomial for A
and a simple polynomial for A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (see ESI†). However, for the more realistic case of the LJ38 cluster fitting to the individual eigenmodes is problematic, because the spectrum of λ
(see ESI†). However, for the more realistic case of the LJ38 cluster fitting to the individual eigenmodes is problematic, because the spectrum of λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is far more dense, especially for the faster relaxations. However, we have found an alternative approach that works well. For a temperature range where the number of peaks in the FPT distribution is constant, we treat each peak position and height as if they were the result of a single eigenmode α with effective values of −ln
is far more dense, especially for the faster relaxations. However, we have found an alternative approach that works well. For a temperature range where the number of peaks in the FPT distribution is constant, we treat each peak position and height as if they were the result of a single eigenmode α with effective values of −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λα and Aα/e. These effective amplitudes and eigenvalues provide good approximations to the true peaks, particularly when the range of eigenvalues contributing to a given peak is small. To test the procedure we compare the reference FPT distribution with the full fit using all temperatures, and for fits where the data is divided into two parts to produce high and low temperature fits. The performance of the high temperature fit at low temperature is the main point of interest, and some example results are shown for LJ38 in Fig. 11. Eigendecomposition was performed at regular temperature increments of 0.001 in reduced units, in the range from 0.1 to 0.15. The fitted distributions are shown for four temperatures, and indicate that the true distributions can be reproduced with useful accuracy.
λα and Aα/e. These effective amplitudes and eigenvalues provide good approximations to the true peaks, particularly when the range of eigenvalues contributing to a given peak is small. To test the procedure we compare the reference FPT distribution with the full fit using all temperatures, and for fits where the data is divided into two parts to produce high and low temperature fits. The performance of the high temperature fit at low temperature is the main point of interest, and some example results are shown for LJ38 in Fig. 11. Eigendecomposition was performed at regular temperature increments of 0.001 in reduced units, in the range from 0.1 to 0.15. The fitted distributions are shown for four temperatures, and indicate that the true distributions can be reproduced with useful accuracy.
 | ||
Fig. 11 First passage time distributions for the LJ38 database for relaxation to the 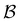 state renormalised down to 2506 states at state renormalised down to 2506 states at 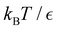 values of (a) 0.10, (b) 0.12, (c) 0.13, and (d) 0.14. The starting state is the same as for Fig. 8. There are four plots in each panel, showing the full eigendecomposition results (full black), fits to the full temperature range (long orange dashed), fits to the high temperature range (green dashed) and fits to the low temperature range (blue dashed), as described in the text. values of (a) 0.10, (b) 0.12, (c) 0.13, and (d) 0.14. The starting state is the same as for Fig. 8. There are four plots in each panel, showing the full eigendecomposition results (full black), fits to the full temperature range (long orange dashed), fits to the high temperature range (green dashed) and fits to the low temperature range (blue dashed), as described in the text. | ||
VI. Accessing longer time scales II: a hybrid scheme
As in previous work, we compared the performance of eigendecomposition using LAPACK routines84 DSYEVR and DGEEV for symmetrised and unsymmetrical matrix formulations, along with the Implicitly Restarted Lanczos Method implementation in ARPACK.85 The symmetrised rate matrix is obtained by a standard similarity transformation, which is applicable under the detailed balance conditions that apply in all our formulations. The symmetrised formulation did not prove to be significantly more stable. For example, the lowest temperatures at which eigendecomposition for the model landscape shown in Fig. 1, produces first passage times that agree with the MFPT generated from GT are: T = 0.93 for DGEEV, T = 0.89 for DSYEVR, T = 0.92 for ARPACK using mode 1 of DSAUPD and T = 0.87 for ARPACK using mode 3 of DSAUPD and with DGETRF for LU decomposition and DGETRI for inverse computation. After pGT, FPTs can be computed at slightly lower temperatures, and DGEEV works down to T = 0.80. Here we define the FPT to agree with GT if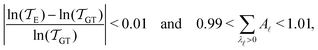 | (16) |
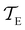 and
and 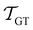 are the MFPTs computed using eigenvalue methods and GT, respectively. We were able to reach lower temperatures using ARPACK routines, but the eigenvalues corresponding to the slowest relaxations also became unreliable as the temperature decreased. In contrast, the eigenvalues and eigenvectors associated with the faster relaxations remained accurate, particularly for LAPACK, even at relatively low temperatures. We can therefore combine the eigendecomposition results for the faster relaxations with the accurate mean first passage time from graph transformation to produce a hybrid scheme.
are the MFPTs computed using eigenvalue methods and GT, respectively. We were able to reach lower temperatures using ARPACK routines, but the eigenvalues corresponding to the slowest relaxations also became unreliable as the temperature decreased. In contrast, the eigenvalues and eigenvectors associated with the faster relaxations remained accurate, particularly for LAPACK, even at relatively low temperatures. We can therefore combine the eigendecomposition results for the faster relaxations with the accurate mean first passage time from graph transformation to produce a hybrid scheme.
The different eigendecomposition routines performed similary for the LJ38 network, and, with the exception of mode 3 DSAUPD, produced accurate FPT distributions down to around T = 0.07. Mode 3 does not reproduce the short time peaks properly unless T > 0.1, and the computation for the slowest mode fails at a similar temperature to the other routines. The lowest temperatures we could reach with the other routines for LJ38 were:
We are grateful to a referee for suggesting alternative eigendecomposition approaches based on Krylov subspace iteration, which might be combined with hybrid schemes in future work. A related hybrid method, employing Krylov projection for the slowest relaxation time and some faster relaxation modes, has recently been used to analyse vacancy kinetics in aluminum.86 The numerical stability was sufficient to access the largest (numerically smallest) eigenvalue for relevant temperatures in that work, potentially providing another way to reach longer time scales for our applications. The assignments and dependence of first passage time peaks on initial conditions might also be connected with the Krylov projection, and we will explore these possibilities in the future.
If the eigenvalues and eigenvectors are trustworthy up to mode α, in order of increasing time scale, then the remaining amplitude in the first passage time distribution is 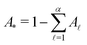 . Assuming that the distribution has one missing peak at long time, we can calculate an effective value for a missing eigenvalue, λ*, that gives a mean first passage time in agreement with the graph transformation result,
. Assuming that the distribution has one missing peak at long time, we can calculate an effective value for a missing eigenvalue, λ*, that gives a mean first passage time in agreement with the graph transformation result, 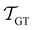 :
:
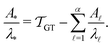 | (17) |
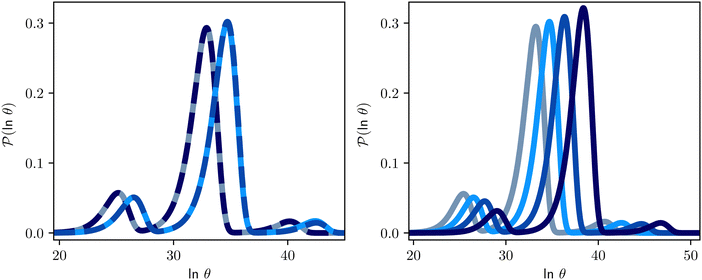 | ||
| Fig. 12 First passage time distributions for the model landscape shown in Fig. 1. At the lower temperatures considered here, standard eigendecomposition for the full network breaks down. The amplitude of the first peak in Fig. 2 becomes very small, and we focus on the three peaks corresponding to the slower relaxation modes. Left: Comparison of standard eigendecomposition for the pGT reduced network with the hybrid method applied to the full network. The plots are for the hybrid method at T = 0.85 (solid grey) and T = 0.80 (solid light blue), and eigendecomposition T = 0.85 (dashed dark blue) and T = 0.80 (dashed blue). Right: The distributions change smoothly with temperature: T = 0.84 (grey) T = 0.80 (light blue), T = 0.76 (blue) and T = 0.72 (dark blue). | ||
For LJ38 we compare the hybrid scheme with the peak fitting approach of Section V. The results in Fig. 13 are for 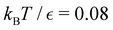 , and illustrate the good agreement between the two methods in terms of both peak positions and heights. Here, the peak fitting employed temperatures from
, and illustrate the good agreement between the two methods in terms of both peak positions and heights. Here, the peak fitting employed temperatures from 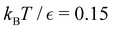 to 0.1 at intervals of 0.001. This shows that incorrect computation of eigenmodes with the smallest magnitude eigenvalues, does not mean that all eigenmodes are incorrect. We also verified that the hybrid scheme produced consistent results for cutoffs in λα ranging over several orders of magnitude, so long as the cutoff is not too small.
to 0.1 at intervals of 0.001. This shows that incorrect computation of eigenmodes with the smallest magnitude eigenvalues, does not mean that all eigenmodes are incorrect. We also verified that the hybrid scheme produced consistent results for cutoffs in λα ranging over several orders of magnitude, so long as the cutoff is not too small.
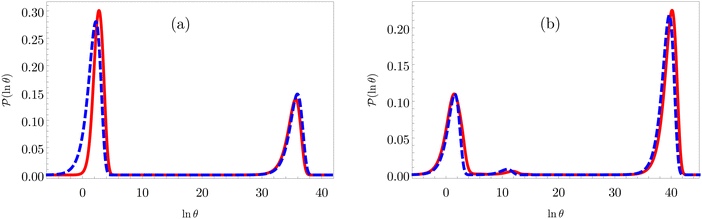 | ||
Fig. 13 First passage time distributions for the LJ38 database renormalised down to 2506 states comparing the hybrid scheme (Section VI solid red curves) with fits to higher temperature results (Section V dashed blue curves). (a) and (b) Are for relaxation to the  and and  states; the starting state is the same as for Fig. 8. For these examples states; the starting state is the same as for Fig. 8. For these examples 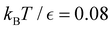 , in the regime where eigendecomposition begins to produce positive eigenvalues for the modes that don't significantly contribute to the FPT, and below the temperature where the truncated octahedral ( , in the regime where eigendecomposition begins to produce positive eigenvalues for the modes that don't significantly contribute to the FPT, and below the temperature where the truncated octahedral ( ) and incomplete icosahedral ( ) and incomplete icosahedral (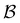 ) morphologies are in equilibrium, which is around ) morphologies are in equilibrium, which is around 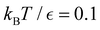 . . | ||
Fig. 14 shows results for LJ38 with the hybrid scheme for 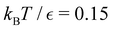 to 0.06 at intervals of 0.01. The systematic variation in the FPT is consistent for a wide range of eigenvalue cutoff thresholds. These results cover time scales for the slow relaxation that vary by over 20 orders of magnitude. Plotting the slow peak position or −ln
to 0.06 at intervals of 0.01. The systematic variation in the FPT is consistent for a wide range of eigenvalue cutoff thresholds. These results cover time scales for the slow relaxation that vary by over 20 orders of magnitude. Plotting the slow peak position or −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ*versus 1/T produces straight line plots for relaxation to both
λ*versus 1/T produces straight line plots for relaxation to both 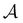 and
and 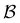 (see ESI†), which shows how these kinetics manifest an apparently simple Arrhenius temperature dependence. The peak position corresponding to the faster relaxation is much less sensitive to temperature, because it corresponds to a lower effective energy barrier. In fact, this peak results from a superposition of contributions from a number of different eigenmodes, and we would not necessarily expect the temperature dependence to be Arrhenius.
(see ESI†), which shows how these kinetics manifest an apparently simple Arrhenius temperature dependence. The peak position corresponding to the faster relaxation is much less sensitive to temperature, because it corresponds to a lower effective energy barrier. In fact, this peak results from a superposition of contributions from a number of different eigenmodes, and we would not necessarily expect the temperature dependence to be Arrhenius.
 | ||
Fig. 14 First passage time distributions for the LJ38 database renormalised down to 2506 states calculated with the hybrid scheme described in Section VI. (a) and (b) are for relaxation to the  and and  states; the starting state is the same as for Fig. 8. In each case the states; the starting state is the same as for Fig. 8. In each case the 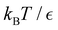 values range from 0.15 to 0.04 in steps of 0.01, and the peak corresponding to the slow relaxation (trapping) steadily shifts to larger values of ln values range from 0.15 to 0.04 in steps of 0.01, and the peak corresponding to the slow relaxation (trapping) steadily shifts to larger values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ. | ||
Approximating the missing amplitude by a single effective mode should produce an accurate representation of the FPT if the long time kinetics is dominated by one slow process. Otherwise we will have a single long time peak that simply reproduces the MFPT by construction. We can check whether a large spectral gap opens up between the two slowest relaxations as the temperature decreases in the range where full eigendecomposition is possible. The systematic variation of the slow peak position in Fig. 14 provides a direct visual report on this spectral gap condition.
Some networks support modes that do not produce detectable peaks in the FPT (Section IIIA); the corresponding amplitudes are negligible for initial conditions of interest. Hence the relevant spectral gap may correspond to the slowest two modes that result in resolvable peaks. We note that it may still be possible to define a quasi-stationary distribution87,88 (QSD) if this gap is large enough, and the projection of the initial condition onto slower modes is sufficiently small. The QSD is defined as the occupation probability distribution in the long time limit conditional on not being adsorbed in the product states.87,88 Usually, this distribution is proportional to wR1. However, for some sources and sinks, the MFPT is significantly smaller than the mixing time for the full network, if we define this quantity as 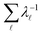 (the Kemeny constant89–91). If there are slow modes with negligible projection onto the initial conditions then a QSD may still exist on practical experimental time scales, but proportional to the right eigenvector for the slowest visible relaxation mode. This effective QSD will then correspond to the slowest resolvable peak in the FPT distribution.
(the Kemeny constant89–91). If there are slow modes with negligible projection onto the initial conditions then a QSD may still exist on practical experimental time scales, but proportional to the right eigenvector for the slowest visible relaxation mode. This effective QSD will then correspond to the slowest resolvable peak in the FPT distribution.
The hybrid approach seems particularly attractive, since it does not involve fitting, and it should work for distributions that feature a well separated slow relaxation time scale, where choosing a suitable cutoff for the eigenvalues is straightforward. Such distributions are likely to be typical for systems featuring rare event dynamics and competing structures, with a wide variety of potential applications in biophysics and materials science.86
VII. CD4 receptor peptide
To test the hybrid scheme for a challenging example corresponding to an important biomolecule we consider the disordered CD4 peptide, PDB code 2KLU,93 which has a multifunnel landscape.92 This peptide corresponds to residues 402–419 in the membrane-proximal region of the cytoplasmic tail of human cluster of differentiation 4 (CD4), and is implicated in HIV-1 infection.94–97 Circular dichroism and NMR experiments suggested α-helical structure,98 which is consistent with binding of HIV-1 viral proteins Nef (negative factor) and Vpu (viral protein U).96,99–102 Previous simulations indicated a relatively flat free energy landscape.103For the FPT analysis we used an existing kinetic transition network created using discrete path sampling;19,20 for full details of this database we refer readers to the original report.92 The potential employed for this particular database was the properly symmetrised104 AMBER ff99SB-ILDN force field,105 with implicit solvent GB-Neck2,106 which produced the best agreement with experiment.92 Similar multifunnel landscapes, featuring a variety of low energy structures with variable α-helix content, were obtained with alternative potentials.92
We surveyed the FPT distributions for different choices of target product state and source state. The distributions can exhibit multiple relaxation times, with peaks at ln(θ/s) values ranging between around −27 to 12. Fig. 16 shows one specific example corresponding to the source and target states highlighted in the landscapes illustrated in Fig. 15. Here we constructed the list of retained minima by calculating the Dijkstra fastest path between source and sink, again using edge weights that depend on branching probabilities, as described in Section IVA. We found that the two main peaks appeared converged when minima on this path and up to two steps away (in terms of connections via transition states) were included. The smaller peak at longer time appeared when one more minimum was added, corresponding to a possible trap connected to the same funnel as the source, giving a renormalised database of 234 states.
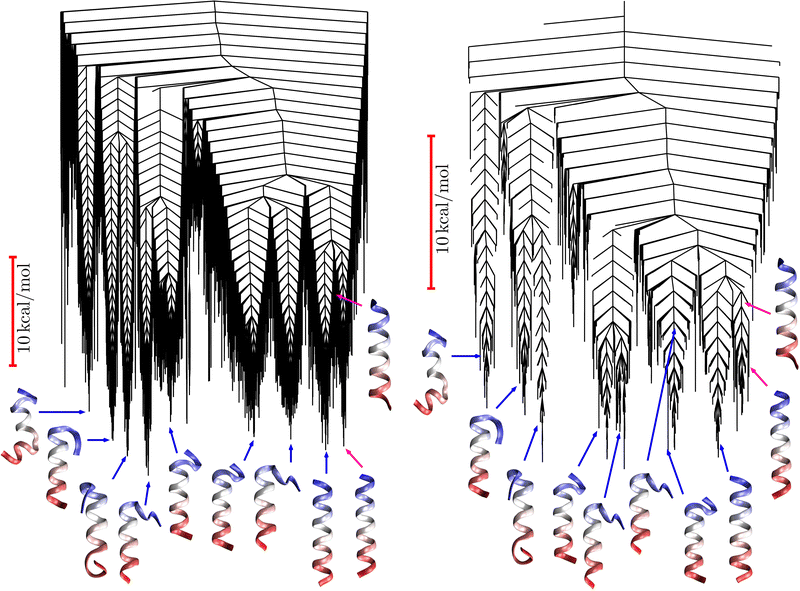 | ||
| Fig. 15 Disconnectivity graphs for the CD4 receptor peptide. Left: Original potential energy graph92 with the secondary structure of selected low energy minima illustrated. Right: the free energy graph for a renormalised landscape at 302 K containing 3580 selected minima. The FPT calculations considered relaxation to a low-lying helical minimum indicated in the graphs with a magenta arrow. The source state above it is highlighted with an arrow of the same color. | ||
To assess the convergence of the FPT we compared with systematically larger sets of retained minima obtained from the fastest paths between the nine potential energy funnel bottoms in Fig. 15. Here we used the minima on the fastest paths, then added minima one step away, two steps away, etc. The FPT was identical to the result obtained for the smaller set for 3500 minima and above, at which point all members of the smaller set were included.
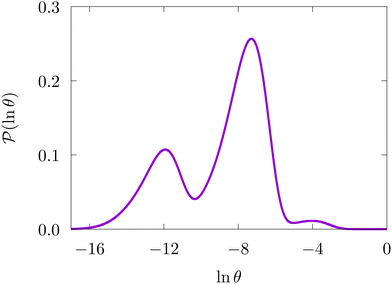 | ||
| Fig. 16 First passage time distribution at 302 K for the CD4 database renormalised down to 234 states calculated with the hybrid scheme described in Section VI. These results correspond to the free energy disconnectivity graph in Fig. 15. θ is the first passage time in seconds. | ||
For this relatively complex multifunnel landscape we find that the FPT distribution depends strongly on the choice of initial and final states. Hence it would be essential to know what these end points are for a given experiment in order to make a proper comparison. If the experiment can probe alternative end points then it would be possible to build up a picture of the global landscape in a systematic fashion. For CD4 we have found combinations that produce up to three well-defined peaks in the FPT distribution. Although the spectrum of relaxation times defined by the eigenvalues λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is not affected by the source state, the amplitudes in the FPT depend on the corresponding component of the left eigenvector. Only a few of these amplitudes are likely to be resolvable for a particular source, but in principle it is possible to probe the whole spectrum if the initial state can be controlled. Theory could play an important role in designing and interpreting such experiments in the future. For example, understanding the subtle differences between alternative low-lying minima, and how these structures interconvert, could be helpful in drug design efforts that mimic the interaction of the cytoplasmic tail of CD4 with HIV-1 accessory proteins.107,108
is not affected by the source state, the amplitudes in the FPT depend on the corresponding component of the left eigenvector. Only a few of these amplitudes are likely to be resolvable for a particular source, but in principle it is possible to probe the whole spectrum if the initial state can be controlled. Theory could play an important role in designing and interpreting such experiments in the future. For example, understanding the subtle differences between alternative low-lying minima, and how these structures interconvert, could be helpful in drug design efforts that mimic the interaction of the cytoplasmic tail of CD4 with HIV-1 accessory proteins.107,108
VIII. Conclusions
Our key objective in this work is to calculate and understand first passage time distributions for energy landscapes that support multiple relaxation time scales. In the present contribution we first considered partial graph transformation30 for reducing the dimension of a kinetic transition network while preserving the full first passage time distribution, p(θ), as far as possible. The renormalised network can be visualised using free energy disconnectivity graphs, which reproduce the stationary distribution and rates. Eigendecomposition can be applied to solve the master equation for the kinetics and calculate the full first passage time distribution. The peaks in this distribution, expressed as a function of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, can be investigated in terms of right eigenvectors of the rate matrix,
θ, can be investigated in terms of right eigenvectors of the rate matrix, 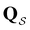 , and assigned to distinct features of the energy landscape in favourable cases. The number of peaks in
, and assigned to distinct features of the energy landscape in favourable cases. The number of peaks in 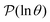 can be scanned systematically for all the possible source states in the network using the left eigenvectors of
can be scanned systematically for all the possible source states in the network using the left eigenvectors of 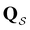 , which highlights starting conditions that are predicted to reveal the competing relaxation time scales.
, which highlights starting conditions that are predicted to reveal the competing relaxation time scales.
Landscapes featuring rare events and multiple time scales are particularly interesting, partly because of potential applications, such as molecular switches and multifunctional materials. However, the eigendecomposition approach suffers from numerical problems for such systems, preventing access to the longest relaxation time, which may be the most important property. We have presented two approaches to tackle this problem. The first uses a fit to the peaks of 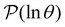 calculated in the tractable temperature range. The second approach is a hybrid scheme, which combines eigendecomposition for faster relaxations with graph transformation for the mean first passage time. The two methods give consistent results for time scales that are beyond the reach of eigendecomposition. The hybrid scheme is particularly attractive, requiring only a choice for a time scale that lies between the slowest relaxation mode and the faster modes. This approach is now being applied to existing kinetic transition networks to extract new insight into the competing pathways. The kinetic information associated with alternative paths is averaged out when a single rate is associated with the mean first passage time. However, we now have a powerful tool to investigate competing pathways, which may be useful in future projects to understand and design new molecules and materials with target properties that depend upon their dynamical response.
calculated in the tractable temperature range. The second approach is a hybrid scheme, which combines eigendecomposition for faster relaxations with graph transformation for the mean first passage time. The two methods give consistent results for time scales that are beyond the reach of eigendecomposition. The hybrid scheme is particularly attractive, requiring only a choice for a time scale that lies between the slowest relaxation mode and the faster modes. This approach is now being applied to existing kinetic transition networks to extract new insight into the competing pathways. The kinetic information associated with alternative paths is averaged out when a single rate is associated with the mean first passage time. However, we now have a powerful tool to investigate competing pathways, which may be useful in future projects to understand and design new molecules and materials with target properties that depend upon their dynamical response.
Multifunnel landscapes may also exhibit thermodynamic signatures of broken ergodicity, especially low temperature peaks in the heat capacity.40,67,71,73–78,80,81 These features can be associated with specific sets of local minima,109 where transitions occur between alternative structures. Analysing the FPT provides a complementary approach to probe the structure of the landscape based on kinetics. Combining these thermodynamic and kinetic perspectives will enable us to understand and predict molecular properties at a fundamental level, resolved in terms of the locally stable structures and the pathways that connect them.
Software and data availability
All the calculations were performed with the open source program PATHSAMPLE, available for download from https://www-wales.ch.cam.ac.uk.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We are very grateful to Prof. Jerelle Joseph for her assistance with the CD4 database. As mentioned in the text, we are very grateful to the referees for their suggestions, especially the potential for exploiting Krylov approaches in future work. EJW gratefully acknowledges support from the Engineering and Physical Sciences Research Council [grant numbers EP/R513180/1, EP/N509620/1]. DJW gratefully acknowledges financial support from the Engineering and Physical Sciences Research Council [grant number EP/N035003/1].References
- X. Li and A. B. Kolomeisky, J. Chem. Phys., 2013, 139, 144106 CrossRef PubMed.
- A. L. Thorneywork, J. Gladrow, Y. Qing, M. Rico-Pasto, F. Ritort, H. Bayley, A. B. Kolomeisky and U. F. Keyser, Sci. Adv., 2020, 6, eaaz4642 CrossRef CAS PubMed.
- M. Athènes and V. V. Bulatov, Phys. Rev. Lett., 2014, 113, 230601 CrossRef PubMed.
- R. Elber, A. Fathizadeh, P. Ma and H. Wang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1512 CAS.
- R. Wang, H. Wang, W. Liu and R. Elber, Approximating First Hitting Point Distribution in Milestoning for Rare Event Kinetics, 2023 Search PubMed.
- D. J. Wales, J. Phys. Chem. Lett., 2022, 13, 6349–6358 CrossRef CAS PubMed.
- Y. Chebaro, A. J. Ballard, D. Chakraborty and D. J. Wales, Sci. Rep., 2015, 5, 10386 CrossRef PubMed.
- J. A. Joseph, K. Roder, D. Chakraborty, R. G. Mantell and D. J. Wales, Chem. Commun., 2017, 53, 6974–6988 RSC.
- K. Roder, J. A. Joseph, B. E. Husic and D. J. Wales, Adv. Theory Simul., 2019, 2, 1800175 CrossRef.
- C. Schütte, A. Fischer, W. Huisinga and P. Deuflhard, J. Comput. Phys., 1999, 151, 146–168 CrossRef.
- M. Shirts and V. S. Pande, Science, 2000, 290, 1903–1904 CrossRef CAS PubMed.
- N. Singhal, C. D. Snow and V. S. Pande, J. Chem. Phys., 2004, 121, 415–425 CrossRef CAS PubMed.
- W. C. Swope, J. W. Pitera and F. Suits, J. Phys. Chem. B, 2004, 108, 6571–6581 CrossRef CAS.
- J. D. Chodera, K. A. Dill, N. Singhal, V. S. Pande, W. C. Swope and J. W. Pitera, J. Chem. Phys., 2007, 126, 155101 CrossRef PubMed.
- V. S. Pande, K. Beauchamp and G. R. Bowman, Methods, 2010, 52, 99–105 CrossRef CAS PubMed.
- J. H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schütte and F. Noé, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- B. E. Husic and V. S. Pande, J. Am. Chem. Soc., 2018, 140, 2386–2396 CrossRef CAS PubMed.
- T. D. Swinburne and D. Perez, Phys. Rev. Mater., 2018, 2, 053802 CrossRef CAS.
- D. J. Wales, Mol. Phys., 2002, 100, 3285–3306 CrossRef CAS.
- D. J. Wales, Mol. Phys., 2004, 102, 891–908 CrossRef CAS.
- N. G. van Kampen, Stochastic processes in physics and chemistry, North-Holland, Amsterdam, 1981 Search PubMed.
- S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2006, 124, 234110 CrossRef PubMed.
- D. J. Wales, J. Chem. Phys., 2009, 130, 204111 CrossRef PubMed.
- J. D. Stevenson and D. J. Wales, J. Chem. Phys., 2014, 141, 041104 CrossRef PubMed.
- R. S. MacKay and J. D. Robinson, Philos. Trans. R. Soc., A, 2018, 376, 20170232 CrossRef PubMed.
- T. D. Swinburne and D. J. Wales, J. Chem. Theory Comput., 2020, 16, 2661–2679 CrossRef CAS PubMed.
- A. B. Bortz, M. H. Kalos and J. L. Lebowitz, J. Comput. Phys., 1975, 17, 10–18 CrossRef.
- A. F. Voter, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 6819–6829 CrossRef CAS PubMed.
- K. A. Fichthorn and W. H. Weinberg, J. Chem. Phys., 1991, 95, 1090–1096 CrossRef CAS.
- E. J. Woods, D. Kannan, D. J. Sharpe, T. D. Swinburne and D. J. Wales, Philos. Trans. R. Soc., A, 2023, 381, 20220245 CrossRef PubMed.
- D. J. Sharpe and D. J. Wales, J. Chem. Phys., 2020, 153, 024121 CrossRef CAS PubMed.
- M. Athènes, S. Kaur, G. Adjanor, T. Vanacker and T. Jourdan, Phys. Rev. Mater., 2019, 3, 103802 CrossRef.
- G. Hummer and A. Szabo, J. Phys. Chem. B, 2015, 119, 9029–9037 CrossRef CAS PubMed.
- A. Kells, Z. E. Mihalka, A. Annibale and E. Rosta, J. Chem. Phys., 2019, 150, 134107 CrossRef PubMed.
- D. Kannan, D. J. Sharpe, T. D. Swinburne and D. J. Wales, J. Chem. Phys., 2020, 153, 244108 CrossRef CAS PubMed.
- O. M. Becker and M. Karplus, J. Chem. Phys., 1997, 106, 1495–1517 CrossRef CAS.
- D. J. Wales, M. A. Miller and T. R. Walsh, Nature, 1998, 394, 758–760 CrossRef CAS.
- S. V. Krivov and M. Karplus, J. Chem. Phys., 2002, 117, 10894–10903 CrossRef CAS.
- D. A. Evans and D. J. Wales, J. Chem. Phys., 2003, 118, 3891–3897 CrossRef CAS.
- J. P. K. Doye, M. A. Miller and D. J. Wales, J. Chem. Phys., 1999, 110, 6896–6906 CrossRef CAS.
- D. J. Wales and T. V. Bogdan, J. Phys. Chem. B, 2006, 110, 20765–20776 CrossRef CAS PubMed.
- T. D. Swinburne, D. Kannan, D. J. Sharpe and D. J. Wales, J. Chem. Phys., 2020, 153, 134115 CrossRef CAS PubMed.
- F. Noé and S. Fischer, Curr. Opin. Struct. Biol., 2008, 18, 154–162 CrossRef PubMed.
- D. Prada-Gracia, J. Gomez-Gardenes, P. Echenique and F. Falo, PLoS Comput. Biol., 2009, 5, e1000415 CrossRef PubMed.
- D. J. Wales, Curr. Opin. Struct. Biol., 2010, 20, 3–10 CrossRef CAS PubMed.
- R. E. Kunz, Dynamics of First-Order Phase Transitions, Deutsch, Thun, 1995 Search PubMed.
- V. Lecomte, C. Appert-Rolland and F. van Wijland, J. Stat. Phys., 2007, 127, 51–106 CrossRef.
- L. B. Newcomb, M. Alaghemandi and J. R. Green, J. Chem. Phys., 2017, 147, 034108 CrossRef PubMed.
- J. H. Prinz, B. Keller and F. Noé, Phys. Chem. Chem. Phys., 2011, 13, 16912–16927 RSC.
- B. G. Keller, J. H. Prinz and F. Noé, J. Chem. Phys., 2012, 396, 92–107 CAS.
- Y. Nagahata, S. Maeda, H. Teramoto, T. Horiyama, T. Taketsugu and T. Komatsuzaki, J. Phys. Chem. B, 2016, 120, 1961–1971 CrossRef CAS PubMed.
- T. J. Frankcombe and S. C. Smith, Theor. Chem. Acc., 2009, 124, 303–317 Search PubMed.
- B. Philippe, Y. Saad and W. J. Stewart, Oper. Res., 1992, 40, 1156–1179 Search PubMed.
- C. D. Meyer Jr., SIAM J. Matrix Anal. Appl., 1994, 15, 715–728 CrossRef.
- C. D. Meyer Jr., SIAM Rev., 1989, 31, 240–272 CrossRef.
- S. A. Trygubenko and D. J. Wales, Mol. Phys., 2006, 104, 1497–1507 CrossRef CAS.
- R. S. MacKay and J. D. Robinson, Philos. Trans. Roy. Soc., A, 2018, 376, 20170232 CrossRef PubMed.
- M. A. Novotny and S. M. Wheeler, Computer Simulations of Surfaces and Interfaces, Springer, Netherlands, 2003, pp. 225–235 Search PubMed.
- M. A. Novotny, Phys. Rev. Lett., 1995, 74, 1–5 CrossRef CAS PubMed.
- D. J. Sharpe and D. J. Wales, J. Chem. Phys., 2020, 153, 024121 CrossRef CAS PubMed.
- M. C. Anderson, E. J. Woods, T. P. Fay, D. J. Wales and D. T. Limmer, J. Phys. Chem. Lett., 2023, 14, 6888–6894 CrossRef CAS PubMed.
- E. W. Dijkstra, Numerische Math., 1959, 1, 269–271 CrossRef.
- J. M. Carr, S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2005, 122, 234903 CrossRef PubMed.
- J. M. Carr and D. J. Wales, Latest Advances in Atomic Cluster Collisions: Structure and Dynamics from the Nuclear to the Biological Scale, London, 2008, pp. 321–330 Search PubMed.
- M. Bastian, S. Heymann and M. Jacomy, International AAAI Conference on Weblogs and Social Media, 2009.
- J. E. Jones and A. E. Ingham, Proc. R. Soc. A, 1925, 107, 636–653 CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372 CrossRef CAS PubMed.
- M. T. Oakley, R. L. Johnston and D. J. Wales, Phys. Chem. Chem. Phys., 2013, 15, 3965–3976 RSC.
- M. Dittner and B. Hartke, Comput. Theor. Chem., 2017, 1107, 7–13 CrossRef CAS.
- J. P. K. Doye, D. J. Wales and M. A. Miller, J. Chem. Phys., 1998, 109, 8143–8153 CrossRef CAS.
- M. A. Miller, J. P. K. Doye and D. J. Wales, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 3701–3718 CrossRef CAS PubMed.
- F. Calvo, J. P. Neirotti, D. L. Freeman and J. D. Doll, J. Chem. Phys., 2000, 112, 10350–10357 CrossRef CAS.
- J. P. Neirotti, F. Calvo, D. L. Freeman and J. D. Doll, J. Chem. Phys., 2000, 112, 10340–10349 CrossRef CAS.
- D. J. Wales, Energy Landscapes, Cambridge University Press, Cambridge, 2003 Search PubMed.
- P. A. Frantsuzov and V. A. Mandelshtam, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 037102 CrossRef PubMed.
- C. Predescu, P. A. Frantsuzov and V. A. Mandelshtam, J. Chem. Phys., 2005, 122, 154305 CrossRef PubMed.
- H. B. Liu and K. D. Jordan, J. Phys. Chem. B, 2005, 109, 5203–5207 CrossRef CAS PubMed.
- G. Adjanor, M. Athênes and F. Calvo, Eur. Phys. J. B, 2006, 53, 47–60 CrossRef CAS.
- V. A. Sharapov and V. A. Mandelshtam, J. Phys. Chem. A, 2007, 111, 10284–10291 CrossRef CAS PubMed.
- V. A. Sharapov, D. Meluzzi and V. A. Mandelshtam, Phys. Rev. Lett., 2007, 98, 105701 CrossRef PubMed.
- M. A. Miller, J. P. K. Doye and D. J. Wales, J. Chem. Phys., 1999, 110, 328–334 CrossRef CAS.
- D. J. Wales, The Cambridge Landscapes Database, URL https://www-wales.ch.cam.ac.uk/CCD.html.
- E. Anderson, Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney and D. Sorensen, LAPACK Users’ Guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, 3rd edn, 1999 Search PubMed.
- R. Lehoucq, K. Maschhoff, D. Sorensen and C. Yang, ARPACK, a collection of Fortran77 subroutines designed to solve large scale eigenvalue problems, https://www.caam.rice.edu/software/ARPACK/.
- S. Kaur, M. Athènes and J. Creuze, J. Comput. Phys., 2022, 454, 110987 CrossRef CAS.
- J. N. Darroch and E. Seneta, J. App. Prob., 1967, 4, 192–196 CrossRef.
- C. Le Bris, T. Lelievre, M. Luskin and D. Perez, Monte Carlo Methods and Applications, 2012, 18, 119–146 Search PubMed.
- J. G. Kemeny and J. L. Snell, Finite Markov Chains, Van Nostrand, New Jersey, USA, 1960 Search PubMed.
- J. G. Kemeny, Linear Algebra Appl., 1981, 38, 193–206 CrossRef.
- A. Kells, V. Koskin, E. Rosta and A. Annibale, J. Chem. Phys., 2020, 152, 104108 CrossRef CAS PubMed.
- J. A. Joseph and D. J. Wales, J. Phys. Chem. B, 2018, 122, 11906–11921 CrossRef CAS PubMed.
- M. Wittlich, P. Thiagarajan, B. W. Koenig, R. Hartmann and D. Willbold, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 122–127 CrossRef CAS PubMed.
- M. Y. Chen, F. Maldarelli, M. K. Karczewski, R. L. Willey and K. Strebel, J. Virol., 1993, 67, 3877–3884 CrossRef CAS PubMed.
- M. J. Vincent, N. U. Raja and M. A. Jabbar, J. Virol., 1993, 67, 5538–5549 CrossRef CAS PubMed.
- C. Aiken, J. Konner, N. R. Landau, M. E. Lenburg and D. Trono, Cell, 1994, 76, 853–864 CrossRef CAS PubMed.
- S. J. Anderson, M. Lenburg, N. R. Landau and J. V. Garcia, J. Virol., 1994, 68, 3092–3101 CrossRef CAS PubMed.
- D. Willbold and P. Rosch, J. Biomed. Sci., 1996, 3, 435–441 CAS.
- X.-J. Yao, J. Friborg, F. Checroune, S. Gratton, F. Boisvert, R. P. Sekaly and E. A. Cohen, Virology, 1995, 209, 615–623 CrossRef CAS PubMed.
- E. Tiganos, X.-J. Yao, J. Friborg, N. Daniel and E. A. Cohen, J. Virol., 1997, 71, 4452–4460 CrossRef CAS PubMed.
- A. Preusser, L. Briese and D. Willbold, Biochem. Biophys. Res. Commun., 2002, 292, 734–740 CrossRef CAS PubMed.
- S. K. Singh, L. Mockel, P. Thiagarajan-Rosenkranz, M. Wittlich, D. Willbold and B. W. Koenig, FEBS J., 2012, 279, 3705–3714 CrossRef CAS PubMed.
- N. Ahalawat, S. Arora and R. K. Murarka, J. Phys. Chem. B, 2015, 119, 11229–11242 CrossRef CAS PubMed.
- E. Małolepsza, B. Strodel, M. Khalili, S. Trygubenko, S. N. Fejer and D. J. Wales, J. Comput. Chem., 2010, 31, 1402–1409 CrossRef PubMed.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror, D. E. Shaw, K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958 CrossRef CAS PubMed.
- H. Nguyen, D. R. Roe and C. Simmerling, J. Chem. Theory Comput., 2013, 9, 2020–2034 CrossRef CAS PubMed.
- F. Curreli, Y. Do Kwon, H. Zhang, Y. Yang, D. Scacalossi, P. D. Kwong and A. K. Debnath, Antimicrob. Agents Chemother., 2014, 58, 5478–5491 CrossRef PubMed.
- J. Richard, M. Veillette, N. Brassard, S. S. Iyer, M. Roger, L. Martin, M. Pazgier, A. Schon, E. Freire and J.-P. Routy, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E2687–E2694 CAS.
- D. J. Wales, Phys. Rev. E, 2017, 95, 030105(R) CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04199a |
| This journal is © the Owner Societies 2024 |