Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum chemistry and kinetics of hydrogen sulphide oxidation†
M.
Monge-Palacios‡
 *a,
Q.
Wang‡
*a,
Q.
Wang‡
 *a,
A.
Alshaarawi
b,
A. C. Cavazos
Sepulveda
b and
S. M.
Sarathy
*a,
A.
Alshaarawi
b,
A. C. Cavazos
Sepulveda
b and
S. M.
Sarathy
 a
a
aKing Abdullah University of Science and Technology, Thuwal (Makkah) 23955, Saudi Arabia. E-mail: manuel.mongepalacios@kaust.edu.sa; qi.wang@kaust.edu.sa
bExploration and Petroleum Engineering Center-Advanced Research Center (EXPEC ARC), Saudi Aramco, Dhahran 34465, Saudi Arabia
First published on 28th December 2023
Abstract
A fundamental understanding of the acid gas (H2S and CO2) chemistry is key to efficiently implement the desulphurisation process and even the production of clean fuels such as hydrogen or syngas. In this work, we developed a new kinetic model for the pyrolysis and oxidation of hydrogen sulphide by merging two previously reported models with the goal of covering a wider range of conditions and including the effect of carbon dioxide. The resulting model, which consists of 75 species and 514 reactions, was used to conduct rate of production and sensitivity analysis in plug flow reactor simulations, and the results were used to determine the most prominent reactions in which hydrogen sulphide, molecular hydrogen, and sulphur monoxide are involved. The resulting list of important reactions was screened and the kinetics of three of them, i.e., SO2 + S2 → S2O + SO, S2O + S2 → S3 + SO, and SO + SH → S2 + OH, was found to warrant further investigation. With the goal of improving the accurancy of our new kinetic model, we carried out a robust quantum chemistry and Rice–Ramsperger–Kassel–Marcus master equation study to obtain, for the first time, the forward and reverse rate constants for those three reactions at temperatures and pressures of interest for combustion and atmospheric chemistry. This work is the first step of a kinetic study that is aimed at improving the understanding of the chemistry of the pyrolysis and oxidation of H2S, highlighting the importance of sulphur–sulphur interactions and providing a fundamental basis for future kinetic models of H2S not only in the field of combustion, but also in atmospheric chemistry.
Introduction
Raw natural gas (NG) contains levels of hydrogen sulphide (H2S) ranging from a few ppm up to 5%.1 Due to the high toxicity of H2S,2 worldwide health and safety agencies demand the concentration of H2S not to exceed 5 ppm in NG before end use.3 In addition, corrosive H2S and other acid gases must be removed from natural gas before pipeline transportation. For the H2S removal process, a well-known industrial treatment is the Claus process,4 in which H2S is fully oxidized and converted into solid sulphur and water. Although the main purpose of H2S removal is to sweeten NG, H2S can also be used to produce clean fuels. For example, partial oxidation of H2S may yield hydrogen (H2), similarly to methane (CH4) combustion under rich conditions.5 Another feasible treatment is the thermal decomposition of acid gas, i.e., H2S and carbon dioxide (CO2), which yields syngas (H2 and carbon monoxide, CO)6 that can be used either directly as a fuel7 or in fuel syntheses (e.g., methanol or Fischer–Tropsch fuels).8,9 This partial removal of CO2 in NG is also beneficial since the CO2 level needs to be below 2% in pipeline-grade methane1 due to the lack of heating value of CO2.The above-described methods to convert the highly toxic species H2S into valuable products can be only optimized and made more efficient by achieving a deep fundamental understanding of the kinetics of the oxidation of acid gas. Therefore, developing an accurate combustion mechanism of H2S in the presence of CO2 is of pivotal importance and is the key to optimize and evaluate the performance of desulphurisation processes and the revalorization of H2S, i.e., its conversion into sulphur or the fuels syngas or H2.
Nevertheless, both experimental and theoretical works on H2S combustion are scarce due to, respectively, the safety issues with H2S experimentation and the complexity of the interactions between sulphur species. Binoist et al.10 investigated the pyrolysis of H2S in a continuous perfectly mixed quartz tube reactor in the temperature range of 800–1000 °C and proposed a kinetic mechanism with 22 elementary reactions. Zhou et al.11 studied the oxidation of H2S in an atmospheric pressure flow reactor from 950 to 1150 K under fuel-lean conditions and developed a kinetic mechanism with 41 species and 277 reactions. The effect of CO2 on the partial oxidation of H2S was investigated by Li et al.12via tube furnace experiments, who developed a kinetic mechanism with 90 species and 596 reactions. More recently, Stagni et al.13 studied the pyrolysis and oxidation of H2S under fuel-lean conditions with jet stirred reactor and flow reactor experiments across a wider range of operating conditions and proposed a kinetic model with 30 species and 156 reactions.
Despite those efforts, discrepancies between experiments and current model predictions remain significant. For example, the discrepancies in the onset of the SO2 mole fraction profiles, as well as in the peak of the H2 mole fraction profiles, observed by Stagni et al.13 indicate that reactions in their recent H2S combustion mechanism need to be examined further.
At a fundamental level, the interactions between sulphur species under combustion conditions have been rarely studied. Unlike elementary reactions directly related to H2S (e.g., hydrogen abstraction from H2S by various species), which have been studied by experiments and ab initio calculations,13 reaction pathways and kinetic parameters of most bimolecular reactions involving sulphur-species such as S2, SO2, S2O and SO in kinetic models have been crudely estimated.11 As an example, the rate constants of 142 out of the 277 reactions in Zhou's model11 were estimated, and most of these estimated reactions are sulphur–sulphur interactions involving the species S2, SO2, S2O and/or SO. Despite those estimations, this model has been often used as a reference or base model for H2S oxidation in later kinetic models, and the same estimations were inherited to even the most up-to-date ones.12,13 These sulphur species (e.g., SO and S2O) represent important intermediates in H2S combustion, which are hard to characterize by experiments due to their detection limit. Ab initio and kinetic calculations are also complicated due to features such as the multi-reference character, formation of numerous intermediates and saddle points, and pressure effects.
As Raj et al.14 pointed out in a review article, those sulphur–sulphur interactions are extremely important in H2S oxidation even under fuel-lean conditions. Therefore, studying the most important reactions of that kind would help to not only improve the performance of current kinetic mechanisms, but also assess the accuracy of the estimations currently being used in these mechanisms.
Under such considerations, this work aims to shed light into the chemistry of H2S combustion by first establishing a kinetic model applicable across a wider range of conditions and then by performing quantum chemistry and Rice-Ramsperger-Kassel–Markus master equation (RRKM–ME) calculations15–17 on some of the most important reactions in the developed model. Therefore, this work highlights the importance of sulphur–sulphur interactions and provides a fundamental basis for future kinetic models of H2S oxidation in combustion applications.
Moreover, the chemistry of sulphur species in the atmosphere of the Earth and other planets is limited and thus not very well understood. Given the low temperature and pressure regimes achieved in our computational kinetic study, the reported rate constants may be also of interest for the development of atmospheric chemistry models that target polluted environments by sulphur emissions18 or the chemistry of sulphur-containing species in the atmosphere of other planets.
Computational details and methodology
Kinetic modelling
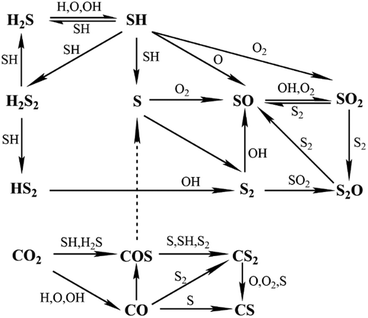
Our kinetic model aims to cover a wider range of conditions than former ones and also at including the effect of CO2 in H2S (acid gas) oxidation. Therefore, we merged Li's model for fuel-rich conditions in which the effect of CO2 was considered12 and Stagni's model for fuel-lean conditions.13 Since the latter was developed more recently and included updated rate constants from new ab initio calculations and literature, it was used as the base model. When the same reaction was included in both models the corresponding rate constants from Stagni's model were used.The sub-mechanism for the C/H/O system from Li's model was taken from GRI-3.0,19 which contains nitrogen chemistry. Since nitrogen chemistry was not anticipated to be relevant in the current H2S combustion mechanism, related reactions were removed from the merged model, reducing it by 17 species and 106 reactions. The new H2S mechanism contains a total of 75 species and 514 reactions. Fig. 1 shows the corresponding simplified H2S reaction path diagram, where it can be seen that in addition to the direct pyrolysis and oxidation products disulphur (S2) and sulphur dioxide (SO2), intermediates such as sulphur monoxide (SO) and disulphur monoxide (S2O) are also important in H2S oxidation. Moreover, the reaction path diagram indicates that carbonyl sulphide (COS) is crucial for understanding the effect of CO2 on H2S combustion.
Plug flow reactor (PFR) simulations with CHEMKIN-PRO software20 using our new model were conducted to get insights into the oxidation of H2S. The PFR configuration is the same as Li's experiment setup,12 namely, with an inner diameter of 16 mm, a length of 800 mm, and an inlet flow rate of 20 cm3 s−1. The simulated conditions are selected as to study the partial oxidation of H2S under fuel-rich conditions, in which H2 and numerous other intermediate species are likely to be formed,14i.e., temperatures between 1300 K and 1900 K, fuel composition H2S/CO2/H2O ranging from 18%/81%/1% to 97%/2%/1%, oxidizer composition from air to pure oxygen, and equivalence ratio between 2.0 and 3.0.
Rate of production (ROP) and sensitivity analysis (SA) were performed for the species of interest, namely H2S, H2, and SO, to identify the most important reactions. H2S is the fuel component, thus the ROP and SA were evaluated when its consumption rate is maximized. H2 is one of the desired products, i.e., a clean fuel, and thus it was analysed when its production rate is maximized. However, since SO is an important partial oxidation intermediate, the corresponding analysis was carried out when its concentration is maximized. The most important reactions were identified and listed at different temperatures, fuel/oxidizer compositions, and equivalence ratios.
It should be noted that the merged kinetic mechanism obtained in this work is being currently validated by means of kinetic modelling and experiments, and it was exclusively used in the current study for the identification of important reactions in the oxidation of H2S whose kinetics need to be revisited.
Quantum chemistry calculations: characterization of the potential energy surfaces
The potential energy surfaces (PESs) of the selected reactions were characterized with the W3X//CCSD/aug-cc-pVDZ, W3X//CCSD/6-311++G(d,p), and W3X//CCSD/jun-cc-pVTZ single point levels of theory, considering their electronic ground-states. Geometries and vibrational frequencies were obtained with the CCSD method21 and the jun-cc-pVTZ,22 aug-cc-pVDZ,22 and 6-311++G(d,p)23 basis sets depending on the size of the chemical system, and the energy was refined with the composite W3X method.24 The W3X method incorporates post-CCSD(T) wave function components and complete basis set (CBS) extrapolation schemes in order to estimate highly accurate CCSDT(Q)/CBS energies. Furthermore, thanks to the implementation of the quasi-perturbative quadruple excitations (Q) in the wave function, this method represents a good approach to handle chemical systems with marked multi-reference character or static correlation,25,26 such as some of those investigated in our work. The optimization and characterization of the stationary points were conducted with the Gaussian16 software27 and the energy calculations with the W3X method were carried out with the Molpro28,29 and MRCC software.30,31The minimum energy paths (MEPs) of the investigated reactions were calculated with the Gaussrate17 software32 by using the Page-McIver method33 with a mass scaling factor and a stepsize of, respectively, 1.0 amu and 0.02 Å, over the reaction coordinate range −2.0 to +2.0 Å and evaluating the Hessian matrix every other point. Those MEPs were obtained at the CCSD/jun-cc-pVTZ, CCSD/may-cc-pVTZ or CCSD/6-311++G(d,p) levels of theory depending on the chemical system, and were scaled to reproduce the corresponding W3X single point energy barrier heights for the kinetic calculations. The calculated MEPs were used to confirm the connectivity of the optimized saddle points, reaction intermediates, reactants and products of a given reaction since they were calculated by following the eigenvector of the imaginary frequency and the maximum gradient down from the saddle point. This information is necessary for the RRKM–ME kinetic study, as will be explained in the next Section.
Rate constant calculations
Using the information of the PES obtained in the previous step for the investigated reactions, we conducted a RRKM–ME kinetic study to calculate the microcanonical flux coefficients and rate constants. The software used for the RRKM–ME calculations was the version 3.1 of TUMME,34 in which a non-conservative ME with bimolecular pairs was set up and solved to obtain the rate constants of the investigated reactions. The main feature of TUMME is its ability to calculate those microcanonical flux coefficients with the inclusion of torsional and multi-structural anharmonicity, variational, and curvature tunnelling corrections, resulting in accurate rate constants.First, the high pressure limit rate constants for each of the multiple steps of the selected reactions that have a saddle point were calculated with the Polyrate 2016-2A software35 using the canonical variational transition state theory (CVT)36,37 with small curvature tunneling corrections (SCT) and the harmonic oscillator approach (HO),38 which is defined as
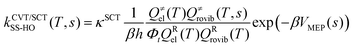 | (1) |
| Qe = 2 + 2·exp(−ε/kBT) | (2) |
Second, the density of states of the reaction intermediates and saddle points of those reactions, including torsional anharmonicity, was calculated with the MSTor 2017 software.40 As for the MSTor calculations, it should be noted that none of those intermediates and saddle points has multiple conformers, and thus multi-structural anharmonicity effects were not implemented in the MSTor calculations.
Finally, the calculated high pressure limit CVT rate constants, together with the corresponding SCT coefficients (CVT/SCT), transition states, and density of states, were provided to TUMME for the RRKM–ME calculations at 0.1, 1.0, 10.0 and 100.0 atm using octuplet precision in the temperature range of 200 K to 3000 K. The bath gas considered for our pressure dependent rate constant calculations was N2, and the corresponding Lennard-Jones (LJ) and energy-transfer-down parameters were provided as ε = 56.993 cm−1, σ = 3.740 Å, and ΔEd = 200(T/300)0.85 cm−1.41 Given the limited existing works for sulfur-containing species, ΔEd was selected based on former works for different hydrocarbon and oxygenated reacting species in which N2 was also used as bath gas.42–45 For the intermediate species of reactions R1, R2, and R3, which will be defined in the next Section, we used σ = 4.175 Å, σ = 4.189 Å, and σ = 3.000 Å, respectively, and ε = 187.980 cm−1; the value of ε for those intermediates, which is not available in the literature, was derived from the Berthelot combination rule46 by considering the ε values of the SO2 and SO3 species, i.e., 335.4 K47 and 218.1 K,48 respectively.
The rate constants of the barrierless steps of reactions R2 and R3 (see Fig. 4 of the next section) were calculated by providing as input to the master equation the corresponding microcanonical flux coefficients. Those microcanonical flux coefficients were obtained by inverse Laplace transform of the canonical hard-sphere collision flux coefficient, which is calculated as follows for the case of formation of an intermediate INT from a pair of reactants R
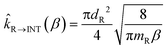 | (3) |
Results and discussion
Rate of production and sensitivity analysis
Rate of production and sensitivity analysis were performed for H2S, H2, and SO for 81 different combinations of reactor temperatures and inlet compositions to identify the most important reactions. It was observed that the top few reactions for each species are the same when changing the inlet compositions (fuel/oxidation compositions and equivalence ratios), and that their prominence depends mainly on the reactor temperature. For the sake of clarity, only a few representative cases are shown in the discussion below for the following initial conditions: 1600 K, fuel composition H2S/CO2/H2O = 58%/41%/1%, oxidizer as pure oxygen, and equivalence ratios of 2.0, 2.5, and 3.0.When the H2S consumption rate is maximized, the most important reactions are those of H2S reacting with OH, H, O, S, and S2. All these reactions have been studied either experimentally or computationally and thus the rate constants are considered as adequate for the new mechanism.2,13,51,52
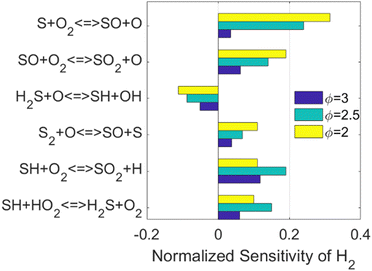
The important reactions directly responsible for H2 production and consumption are well-studied in the literature as well. Therefore, the sensitivity analysis was conducted to investigate how the H2 production is affected by other reactions and species, as shown in Fig. 2.
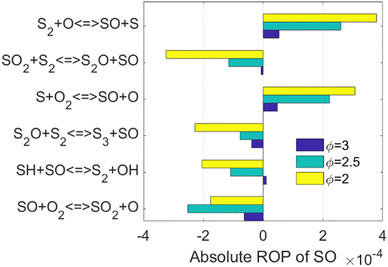
The kinetics of the reactions listed in Fig. 2 have been addressed either experimentally or computationally.13,52–55 However, it is worth noticing that three out of the top six reactions are related to the species SO. As concluded when the simplified reaction path diagram (Fig. 1) was discussed, SO related reactions play an important role in H2 production and consumption since SO is a key intermediate in H2S partial oxidation under fuel-rich conditions. Therefore, we looked into the ROP results for SO, and the top six reactions when the SO concentration is maximized are shown in Fig. 3.
The kinetics of three of the six reactions highlighted in Fig. 3, i.e., the reactions of SO with S,56 O,53 and O2,54 has already been investigated. However, for the SO2 + S2, S2O + S2, and SH + SO cases, not only their rate constants were estimated in former models, but also their products, i.e., S2O + SO, S3 + SO, and S2 + OH, respectively, were assumed.11 To the best of our knowledge, the kinetics and energetics of the different reaction pathways that those three reactions can go through have not been investigated. Therefore, the reactions SO2 + S2 → S2O + SO, S2O + S2 → S3 + SO, and SO + SH → S2 + OH, hereafter reactions R1, R2, and R3, respectively, were selected as the target of the current computational kinetic study, which is described in the next Sections.
The rate constants calculated in this work for the selected reactions R1, R2, and R3 will be used to update the newly developed kinetic mechanism.
Topology of the potential energy surfaces of the target reactions
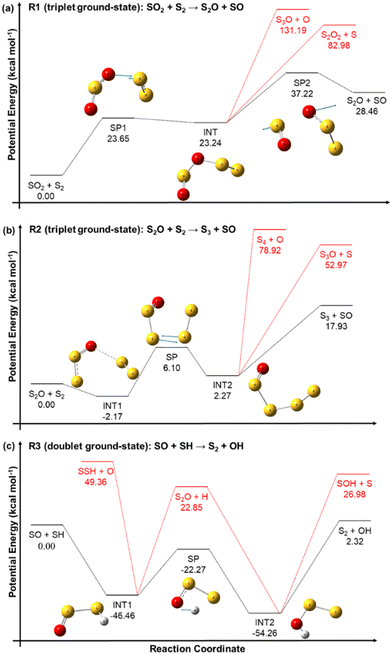
The reactant pairs SO2 + S2 and S2O + S2 can react on the triplet ground-state and singlet excited-state electronic PESs, yielding ground-state triplet and excited singlet SO, respectively. Similarly, the reactants SO + SH can react either on a doublet ground-state or on a quartet excited state PES, yielding triplet ground-state or singlet excited state S2, respectively. Our computational chemistry study focuses on the more kinetically important electronic ground-states, and the corresponding potential energy profiles of reactions R1, R2 and R3, indicating the connectivity between the different stationary points confirmed by the calculated MEPs, are shown in the panels (a), (b), and (c), respectively, of Fig. 4. Different dissociation channels for the reaction intermediates are displayed by the black and red lines, being those highlighted in red not energetically favoured and thus not kinetically competitive. Therefore, in our RRKM–ME kinetic study, only the pathways represented by black lines were implemented.The PESs of the three reactions confirm that they take place through a step-wise mechanism with one or more reaction intermediates and saddle points, and thus their rate constants are expected to be not only temperature dependent, but also pressure dependent. With the exception of INT1 of reaction R2, which is an intermediate complex that is probably formed by a dipole-induced dipole weak intermolecular interaction, all the intermediates are covalently bonded species.
The reaction intermediate INT of reaction R1 is more likely to dissociate via the S–O bond scission that yields the SO rather than by the S–O bond scission that yields S3O + O or the S–S one. Similarly, the reaction intermediate INT2 of reaction R2 is also more prone to dissociate via the S–S bond breaking that yields SO. These observations seem to support the importance of the SO species, as discussed before.
The inclusion of the zero point energy corrections in the reaction energies of reactions R1 and R3 to derive the corresponding heat of reactions at 0 K can help with the evaluation of our energy values by comparing them to those derived from the enthalpies of formation tabulated in the Active Thermochemical Tables (ATcT).57 The heat of reactions ΔHR(0 K) predicted by our calculations for reactions R1 and R3 are, respectively, 28.00 kcal mol−1 and 3.2 kcal mol−1, which are in good agreement with the values of 29.23 kcal mol−1 and 3.8 kcal mol−1 obtained from the ATcT.
Rate constants
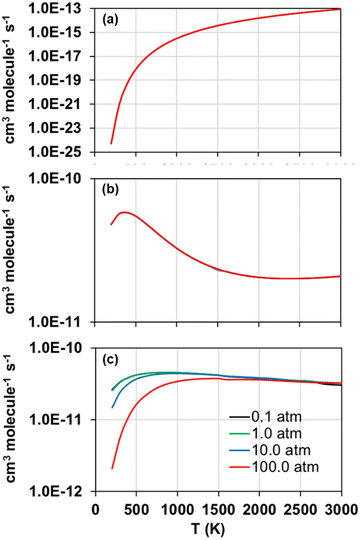
The forward and reverse rate constants of the step-wise reactions R1, R2, and R3 were calculated with the TUMME software as explained previously in the Rate constant calculations Section. The strongly coupled scheme implemented in MSTor was used for the treatment of torsional anharmonicity of the reaction intermediates and saddle points with more than one torsion, except for the saddle point of reaction R2, in which both torsional motions were considered as nearly separable.The calculated forward rate constants of reactions R1, R2, and R3 are represented as a function of temperature in Fig. 5(a), 5(b), and 5(c), respectively, at 0.1, 1.0, 10.0 and 100.0 atm, and the corresponding reverse rate constants are plotted in Fig. 6(a), 6(b), and 6(c). The forward rate constants that Li et al.12 estimated and implemented in their model, which were considered pressure independent, are also plotted for comparison purposes in Fig. 5(a)–(c).
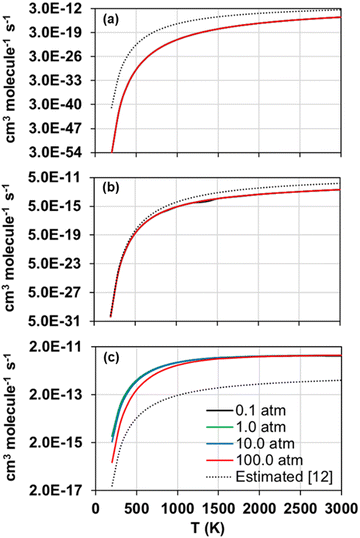 | ||
| Fig. 5 Calculated (solid lines) forward rate constants of reactions R1 (a), R2 (b), and R3 (c) as a function of temperature at pressures 0.1, 1.0, 10.0 and 100.0 atm. The rate constants estimated by Li et al. in their model12 are also plotted (dotted lines). | ||
 | ||
| Fig. 6 Calculated reverse rate constants of reactions R1 (a), R2 (b), and R3 (c) as a function of temperature at pressures 0.1, 1.0, 10.0 and 100.0 atm. | ||
Reaction R3 shows the largest forward rate constants due to its significantly lower endothermicity and barrier height as well as to the significantly larger stability of its reaction intermediates, which make it energetically and kinetically more favoured. On the contrary, reaction R1, with the largest endothermicity and barrier heights as well as less stabilized reaction intermediates, is the slowest one. Therefore, in the updated model, reaction R2 should control the yield of SO to a larger extent than R1, especially at lower temperatures when the differences between their rate constants are more pronounced.
The comparison between our calculated forward rate constants and those estimated by Li et al.12 pertain to two aspects. First, the bimolecular products assumed by those authors, which seem to be the correct ones as they are the bimolecular pairs that are most energetically favoured and were confirmed with our MEP calculations as per the connectivity between the different stationary points of the PESs. And second, the value of the rate constants for each reaction, which shows large deviations with respect to our calculations in the case of reactions R1 and R3, with differences of several orders of magnitude and a severe underestimation in the case of reaction R3; on the contrary, the rate constants estimated and calculated for reaction R2 are in much closer agreement, with the largest differences at high temperatures below one order of magnitude. This comparison highlights the need of accurate ab initio and kinetic calculations, including pressure dependency, for these and other important reactions whose rate constants were estimated in former kinetic models in order to improve the accuracy of the future kinetic models addressing the combustion and atmospheric chemistry of H2S.
As for the reverse rate constants, their temperature dependence shows different trends in the three considered reactions, with an Arrhenius behaviour in the case of reaction R1 but a non-Arrhenius behaviour in the case of reactions R2 and R3; the reverse reaction R1 is the only one with a positive barrier associated to the saddle point SP2, while the other two reverse reactions have submerged barriers that are responsible for the observed non-Arrhenius behaviour, which is usually explained by a change in the sign of the activation energy at a given temperature.58,59
Regarding the observed pressure effects in both, forward and reverse reactions, only the rate constants of reaction R3 turned out pressure dependent, showing the typical trend of a chemical activation mechanism involving association intermediates that can be stabilized at high pressures and low temperatures.60 Li et al.12 and Zhou et al.11 did not estimate pressure effects not only for any of the three considered reactions in this work, but also for many others whose rate constants were also estimated in their model, suggesting that the kinetics of other reactions may also need to be revisited.
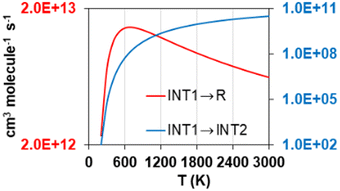
Another distinctive feature of the reverse rate constants of reaction R2 is their positive temperature dependence observed below 400 K, which results in a maximum rate constant value of 4.78·10−11 cm3 molecule−1 s−1 at that temperature. This is attributed to the fate of the intermediate INT1, which is ruled by its decomposition into the reactants S2O + S2, whose rate constants are significantly larger than those of its transformation into INT2. The former, i.e., the step INT1 → S2O + S2, shows rate constants with a similar trend to those of the reverse reaction R2, as shown in Fig. 7, where it can be seen that at 700 K they drop to much lower values as temperature decreases. We attribute this change in the rate constants trend of the step INT1 → S2O + S2, and thus that in the rate constants of the reverse reaction R2 (Fig. 6(b)), to the fact that the other competing consumption channel of INT1, i.e., INT1 → INT2, becomes prominent enough at 700 K to also rule the fate of INT1 together with the INT1 → S2O + S2 channel. In other words, the consumption of INT1 through the INT1 → INT2 channel, which is not kinetically favoured compared to the alternative consumption channel INT1 → S2O + S2, hinders the latter channel by lowering its reaction flux only when a high enough temperature is achieved to surmount the barrier associated to the saddle point SP that connects INT1 and INT2.
The values of the different sets of rate constants plotted in Fig. 5 and 6 within the temperature range 200–3000 K are tabulated in Tables 1 and 2, respectively, and they were fitted to the following extended Arrhenius equations (A in cm3 mol−1 s−1, n unitless, and Ea in kcal mol−1) where f and r refer to forward and reverse rate constants, respectively
| kR1,f = 7.94 × 108·T1.074·e(−39000/RT) | (4) |
| kR2,f = 1.00 × 1013·T0.029·e(−17956/RT) | (5) |
| k0.1atmR3,f = 2.51 × 1015·T−0.687·e(−4105/RT) | (6) |
| k1atmR3,f = 1.58 × 1015·T−0.624·e(−4064/RT) | (7) |
| k10atmR3,f = 3.16 × 1015·T−0.704·e(−4386/RT) | (8) |
| k100atmR3,f = 7.94 × 1015·T−0.797·e(−5414/RT) | (9) |
| kR1,r = 3831·T2.250·e(−9598/RT) | (10) |
| kR2,r = 6.31 × 1015·T−0.796·e(−420.3/RT) | (11) |
| k0.1atmR2,r = 1.26 × 1015·T−0.504·e(−723.0/RT) | (12) |
| k1atmR3,r = 1.26 × 1015·T−0.502·e(−742.1/RT) | (13) |
| k10atmR3,r = 1.58 × 1015·T−0.523·e(−980.6/RT) | (14) |
| k100atmR3,r = 2.00 × 1015·T−0.531·e(−1864/RT) | (15) |
| T (k) | k R1,f | k R2,f | k 0.1atm R3,f | k 1atm R3,f | k 10atm R3,f | k 100atm R3,f |
|---|---|---|---|---|---|---|
| 200 | 1.19 × 10−54 | 2.09 × 10−30 | 3.84 × 10−15 | 3.74 × 10−15 | 2.16 × 10−15 | 3.07 × 10−16 |
| 298 | 2.53 × 10−41 | 5.33 × 10−24 | 7.20 × 10−14 | 7.10 × 10−14 | 5.19 × 10−14 | 1.23 × 10−14 |
| 400 | 3.05 × 10−34 | 1.10 × 10−20 | 3.33 × 10−13 | 3.31 × 10−13 | 2.74 × 10−13 | 9.48 × 10−14 |
| 500 | 4.97 × 10−30 | 8.95 × 10−19 | 8.23 × 10−13 | 8.19 × 10−13 | 7.24 × 10−13 | 3.25 × 10−13 |
| 600 | 3.55 × 10−27 | 1.59 × 10−17 | 1.48 × 10−12 | 1.48 × 10−12 | 1.35 × 10−12 | 7.23 × 10−13 |
| 700 | 4.18 × 10−25 | 1.20 × 10−16 | 2.25 × 10−12 | 2.24 × 10−12 | 2.11 × 10−12 | 1.29 × 10−12 |
| 800 | 1.58 × 10−23 | 5.33 × 10−16 | 3.04 × 10−12 | 3.04 × 10−12 | 2.91 × 10−12 | 1.98 × 10−12 |
| 900 | 2.76 × 10−22 | 1.67 × 10−15 | 3.83 × 10−12 | 3.82 × 10−12 | 3.70 × 10−12 | 2.72 × 10−12 |
| 1000 | 2.82 × 10−21 | 4.09 × 10−15 | 4.55 × 10−12 | 4.55 × 10−12 | 4.44 × 10−12 | 3.46 × 10−12 |
| 1100 | 1.94 × 10−20 | 8.48 × 10−15 | 5.22 × 10−12 | 5.22 × 10−12 | 5.12 × 10−12 | 4.18 × 10−12 |
| 1200 | 9.84 × 10−20 | 1.55 × 10−14 | 5.81 × 10−12 | 5.81 × 10−12 | 5.73 × 10−12 | 4.84 × 10−12 |
| 1300 | 3.96 × 10−19 | 2.58 × 10−14 | 6.33 × 10−12 | 6.33 × 10−12 | 6.26 × 10−12 | 5.45 × 10−12 |
| 1400 | 1.33 × 10−18 | 3.99 × 10−14 | 6.77 × 10−12 | 6.77 × 10−12 | 6.71 × 10−12 | 5.98 × 10−12 |
| 1500 | 3.84 × 10−18 | 5.84 × 10−14 | 7.15 × 10−12 | 7.15 × 10−12 | 7.10 × 10−12 | 6.44 × 10−12 |
| 1600 | 9.81 × 10−18 | 8.16 × 10−14 | 7.20 × 10−12 | 7.33 × 10−12 | 7.31 × 10−12 | 6.70 × 10−12 |
| 1800 | 4.81 × 10−17 | 1.44 × 10−13 | 7.67 × 10−12 | 7.84 × 10−12 | 7.85 × 10−12 | 7.36 × 10−12 |
| 2000 | 1.76 × 10−16 | 2.29 × 10−13 | 8.00 × 10−12 | 8.23 × 10−12 | 8.24 × 10−12 | 7.94 × 10−12 |
| 2200 | 5.21 × 10−16 | 3.38 × 10−13 | 8.23 × 10−12 | 8.51 × 10−12 | 8.52 × 10−12 | 8.26 × 10−12 |
| 2400 | 1.31 × 10−15 | 4.74 × 10−13 | 8.39 × 10−12 | 8.70 × 10−12 | 8.69 × 10−12 | 8.48 × 10−12 |
| 2600 | 2.89 × 10−15 | 6.36 × 10−13 | 8.48 × 10−12 | 8.85 × 10−12 | 8.69 × 10−12 | 8.64 × 10−12 |
| 2800 | 5.78 × 10−15 | 8.23 × 10−13 | 8.38 × 10−12 | 8.78 × 10−12 | 8.89 × 10−12 | 8.89 × 10−12 |
| 3000 | 1.06 × 10−14 | 1.04 × 10−12 | 8.38 × 10−12 | 8.94 × 10−12 | 8.94 × 10−12 | 8.94 × 10−12 |
| T (K) | k R1,r | k R2,r | k 0.1atm R3,r | k 1atm R3,r | k 10atm R3,r | k 100atm R3,r |
|---|---|---|---|---|---|---|
| 200 | 4.97 × 10−25 | 4.78 × 10−11 | 2.63 × 10−11 | 2.56 × 10−11 | 1.48 × 10−11 | 2.11 × 10−12 |
| 298 | 8.71 × 10−22 | 5.67 × 10−11 | 3.38 × 10−11 | 3.34 × 10−11 | 2.44 × 10−11 | 5.76 × 10−12 |
| 400 | 5.82 × 10−20 | 5.78 × 10−11 | 3.90 × 10−11 | 3.87 × 10−11 | 3.20 × 10−11 | 1.11 × 10−11 |
| 500 | 7.98 × 10−19 | 5.47 × 10−11 | 4.25 × 10−11 | 4.23 × 10−11 | 3.74 × 10−11 | 1.68 × 10−11 |
| 600 | 5.05 × 10−18 | 4.97 × 10−11 | 4.43 × 10−11 | 4.41 × 10−11 | 4.05 × 10−11 | 2.16 × 10−11 |
| 700 | 2.02 × 10−17 | 4.46 × 10−11 | 4.54 × 10−11 | 4.53 × 10−11 | 4.26 × 10−11 | 2.62 × 10−11 |
| 800 | 6.03 × 10−17 | 3.99 × 10−11 | 4.59 × 10−11 | 4.58 × 10−11 | 4.38 × 10−11 | 2.98 × 10−11 |
| 900 | 1.47 × 10−16 | 3.60 × 10−11 | 4.59 × 10−11 | 4.59 × 10−11 | 4.44 × 10−11 | 3.26 × 10−11 |
| 1000 | 3.08 × 10−16 | 3.26 × 10−11 | 4.56 × 10−11 | 4.56 × 10−11 | 4.45 × 10−11 | 3.46 × 10−11 |
| 1100 | 5.80 × 10−16 | 2.99 × 10−11 | 4.51 × 10−11 | 4.51 × 10−11 | 4.43 × 10−11 | 3.61 × 10−11 |
| 1200 | 1.00 × 10−15 | 2.77 × 10−11 | 4.45 × 10−11 | 4.45 × 10−11 | 4.38 × 10−11 | 3.71 × 10−11 |
| 1300 | 1.62 × 10−15 | 2.60 × 10−11 | 4.38 × 10−11 | 4.38 × 10−11 | 4.33 × 10−11 | 3.77 × 10−11 |
| 1400 | 2.48 × 10−15 | 2.45 × 10−11 | 4.29 × 10−11 | 4.29 × 10−11 | 4.25 × 10−11 | 3.79 × 10−11 |
| 1500 | 3.63 × 10−15 | 2.34 × 10−11 | 4.21 × 10−11 | 4.21 × 10−11 | 4.18 × 10−11 | 3.80 × 10−11 |
| 1600 | 5.12 × 10−15 | 2.25 × 10−11 | 4.04 × 10−11 | 4.07 × 10−11 | 4.08 × 10−11 | 3.66 × 10−11 |
| 1800 | 9.33 × 10−15 | 2.12 × 10−11 | 3.90 × 10−11 | 3.94 × 10−11 | 3.97 × 10−11 | 3.67 × 10−11 |
| 2000 | 1.55 × 10−14 | 2.05 × 10−11 | 3.77 × 10−11 | 3.82 × 10−11 | 3.86 × 10−11 | 3.64 × 10−11 |
| 2200 | 2.39 × 10−14 | 2.01 × 10−11 | 3.66 × 10−11 | 3.70 × 10−11 | 3.76 × 10−11 | 3.55 × 10−11 |
| 2400 | 3.50 × 10−14 | 2.00 × 10−11 | 3.55 × 10−11 | 3.54 × 10−11 | 3.54 × 10−11 | 3.45 × 10−11 |
| 2600 | 4.88 × 10−14 | 2.01 × 10−11 | 3.45 × 10−11 | 3.49 × 10−11 | 3.38 × 10−11 | 3.36 × 10−11 |
| 2800 | 6.60 × 10−14 | 2.04 × 10−11 | 3.14 × 10−11 | 3.29 × 10−11 | 3.34 × 10−11 | 3.29 × 10−11 |
| 3000 | 8.64 × 10−14 | 2.08 × 10−11 | 3.04 × 10−11 | 3.25 × 10−11 | 3.25 × 10−11 | 3.28 × 10−11 |
Conclusions
A new chemical kinetic model for the oxidation and pyrolysis of H2S has been developed by merging the previously developed kinetic models by Li et al.12 for fuel-rich conditions, which includes the chemistry of CO2, and that by Stagni et al.13 for fuel-lean conditions. The new model is expected to cover a wider range of conditions than former ones, and was used to carry out plug flow reactor simulations under conditions in which H2, which is targeted as a clean fuel, is more likely to be yielded. From the simplified reaction path diagram of the new model we concluded that the species SO, SO2 and S2O play a pivotal role in the oxidation of H2S. Moreover, the sensitivity analysis for H2 revealed that its production is largely affected by reactions involving SO, and thus a rate of production analysis was conducted for SO when its concentration was maximized. From that rate of production analysis, we concluded that the kinetics of three of the six more important reactions, i.e., SO2 + S2 → S2O + SO, S2O + S2 → S3 + SO, and SO + SH → S2 + OH, has been just estimated in previous kinetic models due to the lack of kinetic data for sulphur-related reactions.Therefore, a robust quantum chemistry and Rice-Ramsperger-Kassel–Markus master equation kinetic study have been also conducted in this work for those three reactions, which turned out to proceed through a complex potential energy surface with several intermediates and saddle points. The resulting forward and reverse rate constants, obtained within the wide temperature and pressure ranges of 200–3000 K and 0.1–100 atm, respectively, revealed important pressure effects in the reaction SO + SH → S2 + OH, whereas the kinetics of the reactions SO2 + S2 → S2O + SO and S2O + S2 → S3 + SO is not pressure sensitive. Furthermore, our rate constants calculations also point out large discrepancies with those estimations implemented in former models.
The calculated forward and reverse rate constants for the three selected reactions have been implemented in our new kinetic model with the goal of improving its general performance in the description of the hydrogen sulphide oxidation process, but more specifically, its description of the yield of H2 under different conditions as a clean fuel that can be produced from the H2S carrier.
Moreover, given the low temperatures and pressures considered in our computational kinetic study, we expect our calculated rate constants to also contribute to unravel the chemistry that takes place in polluted environments by sulphur emissions or in the atmosphere of planets that are known to contain sulphur species.
Author contributions
M. Monge-Palacios and Q. Wang conceptualized the idea of this work, conducted the formal analysis and data curation, and wrote the original draft. M. Monge-Palacios carried out the quantum chemistry and kinetic calculations, and Q. Wang built the updated model and performed the numerical simulations. A. Shaarawi and A. C. Cavazos Sepulveda reviewed the kinetic model, and S. M. Sarathy was responsible for funding acquisition, project administration and supervision, and also reviewed the original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research reported in this publication was supported by the Supercomputer Laboratory at King Abdullah University of Science and Technology (KAUST). We would also like to acknowledge the developers of the TUMME software for providing us with the version 3.1 of the software that was used for the kinetics calculations of this work, and specially Dr Rui Ming Zhang for his advice during the setup of the calculations.References
- L. Wang and R. T. Yang, Front. Chem. Sci. Eng., 2014, 8, 8–19 CrossRef CAS.
- T. L. Guidotti, Int. J. Toxicol., 2010, 29, 551–637 CrossRef PubMed.
- M. Rezakazemi, I. Heydari and Z. Zhang, J. CO2 Util., 2017, 18, 362–369 CrossRef CAS.
- J. S. Eow, Environ. Prog., 2002, 21, 143–162 CrossRef CAS.
- Y. Wang, Y. Li, Z. Wang and X. He, Int. J. Hydrogen Energy, 2017, 42, 14301–14311 CrossRef CAS.
- A. M. El-Melih, S. Ibrahim, A. K. Gupta and A. Al Shoaibi, Appl. Energy, 2016, 164, 64–68 CrossRef CAS.
- C. Ghenai, Adv. Mech. Eng., 2010, 2, 342357 CrossRef.
- X. Cui and S. K. Kær, Chem. Eng. J., 2020, 393, 124632 CrossRef CAS.
- D. Selvatico, A. Lanzini and M. Santarelli, Fuel, 2016, 186, 544–560 CrossRef CAS.
- M. Binoist, B. Labégorre, F. Monnet, P. D. Clark, N. I. Dowling, M. Huang, D. Archambault, E. Plasari and P.-M. Marquaire, Ind. Eng. Chem. Res., 2003, 42, 3943–3951 CrossRef CAS.
- C. Zhou, K. Sendt and B. S. Haynes, Proc. Combust. Inst., 2013, 34, 625–632 CrossRef CAS.
- Y. Li, X. Yu, H. Li, Q. Guo, Z. Dai, G. Yu and F. Wang, Appl. Energy, 2017, 190, 824–834 CrossRef CAS.
- A. Stagni, S. Arunthanayothin, L. Pratali Maffei, O. Herbinet, F. Battin-Leclerc and T. Faravelli, Chem. Eng. J., 2022, 446, 136723 CrossRef.
- A. Raj, S. Ibrahim and A. Jagannath, Prog. Energy Combust. Sci., 2020, 80, 100848 CrossRef.
- R. A. Marcus, J. Chem. Phys., 2004, 20, 359–364 CrossRef.
- H. M. Rosenstock, M. B. Wallenstein, A. L. Wahrhaftig and H. Eyring, Proc. Natl. Acad. Sci. U. S. A., 1952, 38, 667–678 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 2004, 45, 2630–2638 CrossRef.
- C. N. Hewitt, Atmos. Environ., 2001, 35, 1155–1170 CrossRef CAS.
- D. M. G. G. P. Smith, M. Frenklach, N. W. Moriarty, B. Eiteneer, M. Goldenberg, C. T. Bowma, R. K. Hnason, S. Song, W. C. Gardiner Jr., V. V. Lissianski and Z. Qin, https://combustion.berkeley.edu/gri-mech/.
- CHEMKIN-PRO, Reaction Design, 2019.
- R. J. Bartlett, J. Phys. Chem., 1989, 93, 1697–1708 CrossRef CAS.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- K. B. Wiberg, J. Comput. Chem., 1986, 7, 379 CrossRef.
- B. Chan and L. Radom, J. Chem. Theory Comput., 2013, 9, 4769–4778 CrossRef CAS PubMed.
- M. Monge-Palacios and S. M. Sarathy, Phys. Chem. Chem. Phys., 2018, 20, 4478–4489 RSC.
- J. E. Chavarrio Cañas, M. Monge-Palacios, X. Zhang and S. M. Sarathy, Combust. Flame, 2022, 235, 111708 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 software, 2016.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Biosci., 2012, 2, 242–253 CrossRef CAS.
- H.-J. Werner, et al., MOLPRO, version 2012, a package of ab initio programs, 2012.
- M. Kállay, et al., MRCC, a quantum chemical program suite.
- M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz, J. Chem. Phys., 2020, 152, 074107 CrossRef PubMed.
- J. Zheng, et al., Gaussrate 17, University of Minnesota, Minneapolis, MN, 2017.
- M. Page and J. W. McIver, Jr., J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS.
- R. M. Zhang, X. Xu and D. G. Truhlar, Comput. Phys. Commun., 2022, 270, 108140 CrossRef CAS.
- J. B. J. Zheng, R. Meana-Paneda, S. Zhang, B. Lynch, J. C. Corchado, Y. Chuang, P. Fast, W. Hu, Y. Liuet al., Polyrate 2016-2A software, Minneapolis University of Minnesota, 2016.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 2008, 70, 1593–1598 CrossRef.
- B. Garrett and D. Truhlar, J. Phys. Chem., 1983, 87, 4553 Search PubMed.
- R. T. Skodje, D. G. Truhlar and B. C. Garrett, J. Chem. Phys., 1982, 77, 5955–5976 CrossRef CAS.
- M. W. Chase, Jr., J. L. Curnutt, J. R. Downey, Jr., R. A. McDonald, A. N. Syverud and E. A. Valenzuela, J. Phys. Chem. Ref. Data, 1982, 11, 695–940 CrossRef.
- J. Zheng, S. L. Mielke, K. L. Clarkson and D. G. Truhlar, Comput. Phys. Commun., 2012, 183, 1803–1812 CrossRef CAS.
- B. E. Poling, J. M. Prausnitz and J. P. O’Connell, Properties of Gases and Liquids, McGraw-Hill Education, New York, 5th edn, 2001 Search PubMed.
- J. P. Senosiain, S. J. Klippenstein and J. A. Miller, J. Phys. Chem. A, 2006, 110, 6960–6970 CrossRef CAS PubMed.
- M. Akbar Ali, V. T. Dillstrom, J. Y. W. Lai and A. Violi, J. Phys. Chem. A, 2014, 118, 1067–1076 CrossRef CAS PubMed.
- M. Akbar Ali and A. Violi, J. Org. Chem., 2013, 78, 5898–5908 CrossRef CAS PubMed.
- R. M. Zhang, W. Chen, D. G. Truhlar and X. Xu, Faraday Discuss., 2022, 238, 431–460 RSC.
- J. Wisniak, Educ. Quim., 2010, 21, 155–162 CAS.
- J. R. Elliott, V. Diky, T. A. I. V. Knotts and W. V. Wilding, Properties of Gases and Liquids, McGraw-Hill Education, New York, 6th edn, 2023 Search PubMed.
- X. Tang, P. H. Koenig and R. G. Larson, J. Phys. Chem. B, 2014, 118, 3864–3880 CrossRef CAS PubMed.
- Y. Georgievskii and S. J. Klippenstein, J. Chem. Phys., 2003, 118, 5442–5455 CrossRef CAS.
- Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 9776–9781 CrossRef CAS.
- K. Sendt, M. Jazbec and B. S. Haynes, Proc. Combust. Inst., 2002, 29, 2439–2446 CrossRef CAS.
- C. Wang, G. Zhang, Z. Wang, Q. S. Li and Y. Zhang, J. Mol. Struct.: THEOCHEM, 2005, 731, 187–192 CrossRef CAS.
- C.-W. Lu, Y.-J. Wu, Y.-P. Lee, R. S. Zhu and M. C. Lin, J. Phys. Chem. A, 2003, 107, 11020–11029 CrossRef CAS.
- N. L. Garland, Chem. Phys. Lett., 1998, 290, 385–390 CrossRef CAS.
- C. Zhou, K. Sendt and B. S. Haynes, J. Phys. Chem. A, 2009, 113, 2975–2981 CrossRef CAS PubMed.
- C. Zhou, Kinetic study of the oxidation of hydrogen sulfide, PhD thesis, The University of Sydney, 2009.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- S. Y. Mohamed, M. Monge-Palacios, B. R. Giri, F. Khaled, D. Liu, A. Farooq and S. M. Sarathy, Phys. Chem. Chem. Phys., 2022, 24, 12601–12620 RSC.
- M. Monge-Palacios, C. Rangel, J. C. Corchado and J. Espinosa-GarcÍA, Int. J. Quantum Chem., 2012, 112, 1887–1903 CrossRef CAS.
- E. Grajales-González, M. Monge-Palacios and S. M. Sarathy, Combust. Flame, 2021, 225, 485–498 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04535h |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2024 |