Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy landscape of perylenediimide chromophoric aggregates†
Pallavi
Panthakkal Das‡
 ,
Aniruddha
Mazumder‡
,
Aniruddha
Mazumder‡
 ,
Megha
Rajeevan
,
Megha
Rajeevan
 ,
Rotti Srinivasamurthy
Swathi
,
Rotti Srinivasamurthy
Swathi
 * and
Mahesh
Hariharan
* and
Mahesh
Hariharan
 *
*
School of Chemistry, Indian Institute of Science Education and Research Thiruvananthapuram, Maruthamala P.O., Vithura, Thiruvananthapuram, Kerala 695551, India. E-mail: swathi@iisertvm.ac.in; mahesh@iisertvm.ac.in
First published on 4th December 2023
Abstract
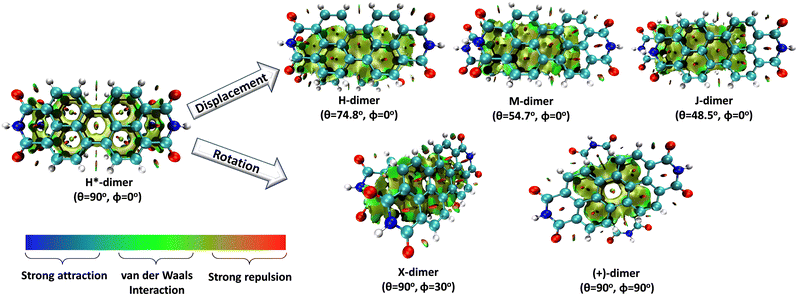
Understanding the self-assembly of conjugated organic materials at the molecular level is crucial in their potential applications as active components in electronic and optoelectronic devices. The type of aggregation significantly influences the intriguing electronic and optical characteristics differing from their constituent molecules. Perylenediimides (PDIs), electron-deficient molecules exhibiting remarkable n-type semiconducting properties, are among the most explored organic fluorescent materials due to their high fluorescence efficiency, photostability, and optoelectronic properties. PDI derivatives are reported to form well-tailored supramolecular architectures: cofacial with minor slip (H-aggregates), staggered with major slip (J-aggregates), magic angle stacking (M-aggregates), rotated (X-aggregates), rotated orthogonal ((+)-aggregates), etc. H*-aggregates are defined here as an ideal case of H-aggregate with an eclipsed configuration. Although numerous reports regarding the formation and optical properties of various PDI aggregates are known, the key driving force within the PDI units guiding the self-assembly to form distinct aggregate systems remains elusive. To unravel the molecular-level mechanisms behind the self-assembly of PDI units by probing the intermolecular interactions, symmetry-adapted perturbation theory-based energy decomposition, potential energy surface scans, and non-covalent interaction index analyses were employed on PDI dimer models. Quantum theory of atoms in molecules and frontier molecular orbital analyses were implemented on the dimer models to comprehend the effect of heteroatoms and orbital interactions in stabilising the X-aggregates over the other PDI aggregate systems. Competition between the attractive and repulsive non-covalent interactions dictates a stability order of X > H > J > M > (+) > H* for the PDI aggregate system, while in the parent perylene system, the stability order was found to be X > (+) > H > M > J > H*.
Introduction
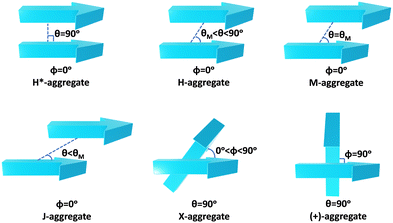
Molecular aggregates are an important class of materials exhibiting optical properties generally different from their constituent molecules.1,2 Molecular coalition of π-conjugated organic materials into three-dimensional supramolecular assemblies has been utilised efficiently in photonic and optoelectronic devices.3 The relative spatial orientation,4 interplanar distance, and the non-covalent interactions5 between the chromophores dictate the electronic communication, thereby governing the photophysical properties of the aggregate systems.6 The self-assembly process hinges on non-covalent interactions, which essentially decide the packing and relative orientation of the chromophores, thereby determining the nature and strength of the electronic interactions. Understanding the strength of non-covalent interactions is quintessential in realising the structure–property relationships in aggregates.7,8 Based on the relative orientation of transition dipole moments corresponding to S0 → S1 transition in two monomer units, quantified by the slip angle (θ), molecular exciton theory9,10 categorises aggregates into different classes (Fig. 1). In H-aggregates, transition dipoles are arranged head-to-head (θM < θ < 90°), while J-aggregates have a slip-stacked head-to-tail arrangement (θ < θM), where θM = 54.7° is called the magic angle.1,11–13 H- and J-aggregates exhibit positive and negative Coulombic coupling, respectively.12 Another interesting class of aggregates is the M-aggregates14 or magic angle stacking possessing θ = 54.7°, an orientation at which Coulombic coupling is predicted to vanish.12 X-aggregates exhibit cross-dipole stacking with a rotation offset (ϕ) in between 0° and 90°.15 (+)-aggregates (Greek cross-aggregates) are found to have an orthogonal arrangement of the transition dipoles and exhibit monomer-like optical properties owing to the null exciton coupling between the monomers.15–17 H*-aggregates (ideal H-aggregates) have the monomers oriented in an eclipsed configuration (without any rotation or displacement offsets). Hunter and Sanders proposed that the structure of π-aggregates is determined by electrostatic interactions. When there is a rotation or displacement offset between the monomers, repulsive π–π interaction is outweighed by the π–σ attractions between the positive σ framework and the negative π electron density.16 However, the symmetry-adapted perturbation theory (SAPT) contradicted the model by showing electrostatic energy contribution as negative (attractive) for such structures due to the charge-penetration effect.18–21SAPT22 has emerged as a powerful tool for probing non-covalent interaction energies between molecules using intermolecular perturbation theory to compute the strength and assess the nature of the intermolecular interactions. The density-fitting density functional theory symmetry-adapted perturbation theory (DF-DFT-SAPT) method performed on π-stacked dimers suggests that the dispersion and other contributions are maximised at the parallel displaced conformation than at the sandwiched (eclipsed) conformation. A qualitative stack bond order (SBO) description of the orbital interactions supplemented the understanding of the underlying non-covalent interactions.23 A molecular orbital-based model for rationalising the exchange-repulsion contribution to the total interaction energy in aggregates over electrostatic models was proposed using SAPT by Fink and co-workers.24 SAPT-based approach was employed in pentacene and N-heteropentacenes to assess the impact of heteroatom substitution on the strength of the various non-covalent intermolecular interactions and intermolecular electronic couplings.25
Perylenediimides (PDIs) are a class of electron-deficient molecules exhibiting remarkable n-type semiconducting properties and excellent photostability. PDI derivatives are reported to form well-defined supramolecular assemblies.26 Long-standing efforts to understand the mechanism of self-assembly in PDI chromophores have been stimulating. Kaupp, Fink, Engels and co-workers have employed extensive theoretical methods to explain the crystal structures and visible light absorption properties in a PDI dimer model system.27 By exploring the non-covalent interactions to understand self-assembly, a parallel step-wise H-type aggregation pattern was observed in the oligomers of perylene, PDI, and thionated PDI.28 Despite PDI forming different aggregate systems depending on substituents at the imide and bay positions, twisted core, H-bonding, etc.,26 the driving force within the PDI structure for self-assembly into H-, J-, X-, M-, and (+)-aggregates remains elusive.
In this work, SAPT based energy decomposition analysis along with potential energy surface (PES) scan and non-covalent interaction (NCI) index analyses were implemented to evaluate the nature and strength of the interactions between the monomers. Five classes of PDI aggregate systems: H (cofacial with minor slip), J (staggered with major slip), M (magic angle stacking), X (rotated) and (+) (rotated orthogonal) were studied with a dimer model29 for understanding their formation favourability over H*-aggregate (eclipsed) with maximum dispersion force to bind the monomers. The terminology used for the dimer systems pertains to Kasha's exciton model for molecular aggregates. However, herein, the non-covalent interactions between the monomers are explored to apprehend the ground state stabilities of different supramolecular motifs. Previous studies have provided evidence supporting the use of dimer-based models to accurately represent the properties exhibited by the larger aggregate systems.27,29–31 Topological analysis based on Bader's quantum theory of atoms in molecules (QTAIM) was employed to probe the non-covalent interactions between the heteroatom functionalities and HOMO isosurfaces traced the orbital interactions between the two monomers in the dimers. The obtained interaction energies for the PDI dimers were compared to the analogous perylene dimers, to delineate the exclusive influence of the aromatic π-core in stabilising the aggregate systems.
Computational methods
The PDI monomer geometry was obtained from the previously reported crystal structure of PDI and was used for the analysis without optimisation.32 For the parent perylene molecule, an optimised monomer geometry was used as the initial geometry. Geometry optimisation of perylene monomer and selected PDI dimers, frequency calculations on the selected PDI dimers, potential energy surface scans and single point energy calculations were performed employing Gaussian 1633 using the ωB97XD functional and 6-311+G(d,p) basis set at the density functional theory (DFT) level of theory in vacuum. ωB97XD was shown to predict the energetics of polyaromatic hydrocarbon aggregates accurately.34 HOMO orbital isosurfaces were generated after performing single point energy calculations at dimer geometries.Fig. 2 depicts the axes labels used for the computational analyses. The origin of the coordinate system is established at the centroid of one of the monomers (reference monomer), X and Y are the long and short axes respectively, and Z is the interplanar axis. The interplanar distance between the monomers is fixed at 3.4 Å based on the reported crystal structures of PDI and perylene derivatives (Fig. S1 and Table S1, ESI†).1,14,15,27,32,35–37 Starting from the eclipsed configuration (H*-dimer), one of the monomer units was systematically rotated along the interplanar axis Z by an angle ϕ (0° ≤ ϕ ≤ 90°) with a step size of 2° to generate dimer geometries of X-aggregates and the (+)-aggregate. Displacing the monomer along the long axis X (0 Å ≤ X ≤ 13.4 Å) and short axis Y (0 Å ≤ Y ≤ 3.2 Å) by a step size of 0.2 Å generated H- and J-dimer geometries for SAPT scans. As the transition dipole moment of PDI lies along the long axis (Fig. S2a, ESI†), the slip angle θ is defined as the angle between the line joining the centroids of two monomers and the long axis of the reference monomer.12 As it was computationally challenging to perform two-dimensional SAPT scan, as a large number of input geometries had to be generated, we resorted to a two-dimensional rigid PES scan using the DFT method. We then investigated the non-covalent interactions in each of the stationary points obtained from the PES scan using the SAPT method.
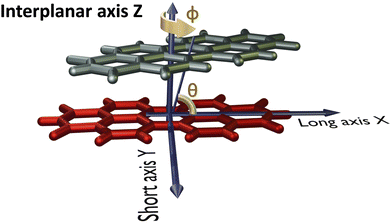 | ||
| Fig. 2 Dimer model of the perylenediimide chromophore showing axes labels, rotation angle (ϕ) and slip angle (θ). | ||
Symmetry-adapted perturbation theory (SAPT)22,38,39
SAPT analysis was carried out using AUG-cc-pVDZ basis set employing the Psi4 code.40 One-dimensional SAPT scans were employed to investigate the changes in the intermolecular non-covalent interactions corresponding to the displacement of one monomer along long or short axes or rotation about the interplanar axis from the eclipsed configuration. SAPT computes the interaction energy between two molecules and decomposes the interaction energy into physically meaningful components: i.e., electrostatic, exchange, induction, and dispersion. SAPT(0) is the simplest truncation of SAPT. The SAPT(0) analysis results comprise a second-order perturbation expansion constituting first-order electrostatic and exchange energy parts and second-order dispersion, induction, and their exchange counterparts as the perturbation terms.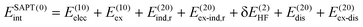 | (1) |
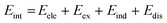 | (2) |
Potential energy surface (PES) analysis
Two-dimensional rigid PES scan was performed at the ωB97XD/6-311+G(d,p) level of theory using Gaussian 16 to comprehend the trends in interaction energies starting from the eclipsed configuration, by displacing one monomer along both long and short axes simultaneously. Counterpoise correction41 was employed to compensate for the overestimation of the interaction energies in the dimer due to the basis set superposition error.42 Keeping the reference monomer fixed, the other monomer was displaced along both long and short axes without any rotation offset (ϕ = 0°) with a step size of 0.1 Å to obtain dimer energy (Edimer) at each point. The total interaction energy between the monomers was calculated using the equation:43| Eint = Edimer – 2Emonomer | (3) |
Monomer energy (Emonomer) was calculated by performing a single point energy calculation at the monomer geometry.
Non-covalent interactions (NCI) index analysis44,45
NCI analysis, also called reduced gradient density method employs an index based on electron density and its derivatives to identify non-covalent interactions. Reduced density gradient is given by: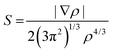 | (4) |
Quantum theory of atoms in molecules (QTAIM)48
QTAIM analysis assists in describing the interatomic interactions in terms of electron density (ρ(r)) and its Laplacian (▽2ρ(r)) in dimers as well as higher-order aggregate structures. The critical points (CPs) appear when the first derivative of the electron density approaches a near-zero value, and the sign of the second derivative of electron density determines the shape in real space. In Bader's AIM theory, the appearance of a (3, −1) CP called bond critical point (BCP) usually implies a local aggregation of electron density, commonly appearing on a bond path or between atoms having attractive interactions. The (3, +1) CP implies local electron density depletion and indicates a steric effect. The value of real space functions at BCP have great significance; for example, the value of ρ and the sign of ∇2ρ at BCP are closely related to bond strength and bond type, respectively, for analogous bonds. van der Waals interaction regions always have very small ρ.Results and discussion
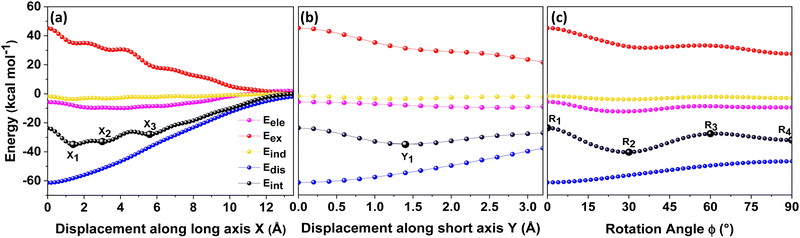
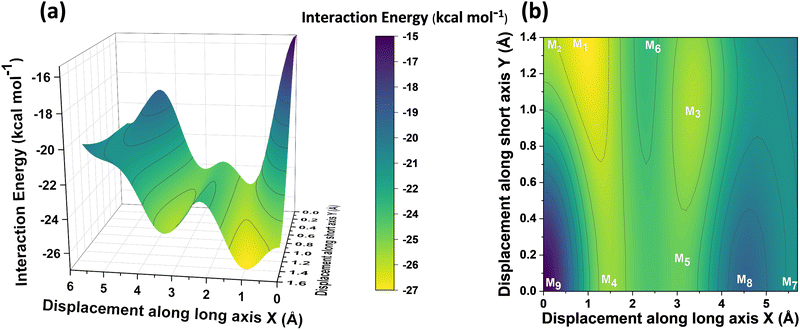
Different non-covalent interactions stabilising the dimer systems were examined using SAPT analysis. Fig. 3 shows the variation of different non-covalent interactions and total interaction energy (Eint) as a function of displacement along long axis X, short axis Y, and rotation about the interplanar axis Z. The effect of interplanar distance on interaction energy is shown in Fig. S3a (ESI†). The competition between attractive dispersion interaction binding the monomer units and repulsive exchange interaction plays a pivotal role in dictating stability of aggregates. The H*-dimer exhibits the least stability due to the high exchange interaction i.e., Pauli repulsion between equivalent orbitals, which is inadequately compensated by the other three stabilising interactions (electrostatics, induction and dispersion). Fig. 3a and b show the effect of displacing one of the monomers in one dimension (1D) along the long and short axes, respectively on the interactions within the dimers, and the degree to which the displacement influences the interactions. The obtained minima (X1 = 1.4 Å; X2 = 3.0 Å; X3 = 5.6 Å; and Y1 = 1.4 Å) are a manifestation of relatively lower contribution from the exchange interactions. As the displacement increases, the dispersion interaction becomes less negative. Fig. 3c shows the effect of rotation on the stability of the dimers. At the minimum R2 (ϕ = 30°), the exchange interaction appears relatively weak and strong stabilisation due to the electrostatic interactions is observed. Conversely, a maximum is observed at R3 (ϕ = 60°) due to decreased attractive electrostatic and dispersion interactions along with increased exchange interactions. Though the dispersion is least in R4 (ϕ = 90°), (+)-dimer forms a minimum due to low exchange and moderately high electrostatic interactions. Therefore, X-dimer close to a rotation angle of 30° is energetically more favoured than the (+)-dimer with a rotation angle of 90°. The R2 configuration is consistent with the global minimum previously reported using DFT.27 The H*-dimer, R1 (ϕ = 0°) is energetically less favoured and rarely observed.49R1 (X = 0 Å, Y = 0 Å, θ = 90°, ϕ = 0°), R2 (X = 0 Å, Y = 0 Å, θ = 90°, ϕ = 30°) and R4 (X = 0 Å, Y = 0 Å, θ = 90°, ϕ = 90°) are considered as the representatives of H*-, X- and (+)-dimer respectively. Frontier molecular orbital (FMO) analysis through HOMO isosurfaces of the stationary geometries obtained from the 1D SAPT scan in Fig. S4 (ESI†) portray a qualitative picture of the orbital interactions between the monomers. The dimer devoid of rotation and displacement offsets (R1) exhibits strong destructive overlaps between the orbitals, as evinced by the orbital lobes of different phases interacting in an antibonding fashion. With displacing one of the monomers, a reduction in repulsive exchange interactions and an increase in the constructive π–π interactions occurs (Fig. S4a, ESI†). The R2 and R4 geometries show prominent orbital overlaps between the lobes of same phases, whereas R3 geometry displays destructive overlap between the orbital lobes of the monomers (Fig. S4b, ESI†). FMO analysis provides key physical insights into the orbital contribution towards the manifestation of the minima and maxima in the 1D SAPT scans of PDI dimers.In order to understand the interaction energy profiles in H- and J-dimers of PDI, a two-dimensional rigid PES scan was performed as shown in Fig. 4a. Two-dimensional map of interaction energy showing stationary points (M1 to M9) is depicted in Fig. 4b and the corresponding interaction energies are tabulated in Table S2 (ESI†). Minima obtained from PES correlates well with the minima obtained from corresponding 1D SAPT scans. Fig. S5 (ESI†) shows geometries of dimers at stationary points and Table S3 (ESI†) provides information on the SAPT analysis conducted on these stationary points. Among the stationary points, M1 (X = 1.0 Å, Y = 1.4 Å, θ = 74.8°, ϕ = 0°) exhibits the highest interaction energy and represents an H-dimer. M5 (X = 3.0 Å, Y = 0.2 Å, θ = 48.5°, ϕ = 0°) possesses the highest interaction energy among the J-dimers. For further analyses, M1 and M5 are considered as representatives of the H- and J-dimer systems, respectively. The rigid PES scan computed as a function of rotation of one monomer about the interplanar axis Z for the PDI dimers shows similar interaction energy trends in comparison to the obtained SAPT(0) energies (Fig. S6, ESI†). Further geometry optimisations were performed on H-, J-, M-, X- and (+)-dimer structures and no imaginary frequencies were observed (Table S4, ESI†).
Table 1 provides a summary of the total interaction energy calculated through SAPT for the different PDI dimer systems (Fig. 5). The rotated or the X-dimer, characterised by the highest electrostatic and induction interactions, moderately low exchange interaction, and high dispersion interaction, exhibits the maximum intermolecular interaction strength (Eint = −40.49 kcal mol−1). Following in stability is the H-dimer or the cofacially stacked dimer with minor slip (Eint = −36.93 kcal mol−1), possessing low exchange interaction and high stabilising interactions. The J- (staggered with major slip), M- (magic angle stacking), and (+)- (rotated orthogonal) dimers display similar interaction energy values of −33.32 kcal mol−1, −32.71 kcal mol−1 and −32.06 kcal mol−1 respectively, and exhibit higher electrostatic interaction compared to the H-dimer. On the other hand, the H*-dimer (eclipsed) demonstrates the highest repulsive exchange interaction and the lowest electrostatic and induction interactions, making it the least stable configuration with a low interaction energy of −23.82 kcal mol−1. The DFT (ωB97XD/6-311+G(d,p)) predicted interaction energies of these dimer systems are tabulated in Table S5 (ESI†). The DFT interaction energy trend is in line with the computed SAPT(0) interaction energies, where X-dimer exhibits the highest interaction energy strength and the H*-dimer (eclipsed dimer) shows the lowest intermolecular interaction energy strength.
| Dimer system | Coordinate (Å) | Rotation angle, ϕ (°) | Slip angle, θ (°) | E ele | E ex | E ind | E dis | E int |
|---|---|---|---|---|---|---|---|---|
| X-dimer | (0,0,3.4) | 30 | 90 | −12.33 | 32.32 | −4.06 | −56.43 | −40.49 |
| H-dimer | (1.0,1.4,3.4) | 0 | 74.8 | −8.93 | 29.71 | −3.78 | −53.93 | −36.93 |
| J-dimer | (3,0.2,3.4) | 0 | 48.5 | −9.96 | 31.96 | −3.30 | −52.02 | −33.32 |
| M-dimer | (2.5,0.9,3.4) | 0 | 54.7 | −9.77 | 34.35 | −2.87 | −54.42 | −32.71 |
| (+)-dimer | (0,0,3.4) | 90 | 90 | −9.67 | 27.72 | −3.17 | −46.94 | −32.06 |
| H*-dimer | (0,0,3.4) | 0 | 90 | −5.82 | 45.25 | −1.81 | −61.44 | −23.82 |
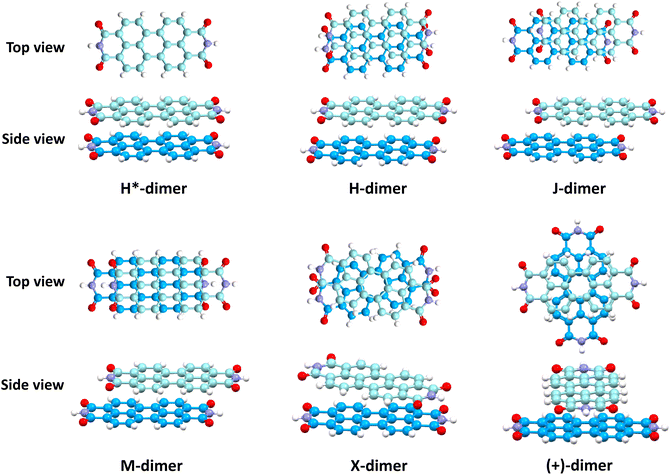
Fig. 6 shows NCI isosurfaces in different PDI dimer systems. In the H*-dimer, the ring centres align, leading to multiple voids within the green isosurface, indicating the presence of weak intermolecular π–π interactions arising from strong repulsive forces between the molecules. In addition to van der Waals interactions, X-dimer showcases a strong electrostatic attractive interaction between the partially positive imide nitrogen and partially negative carbonyl oxygen located in close proximity within the opposite imide rings. The interaction mentioned above is absent in (+)-dimer, and the interacting surface is mainly on four core rings. The NCI isosurface is enhanced with displacement, indicating the increment in stabilising interactions compared to the H*-dimer. Notably, the enhancement in NCI isosurface is more pronounced in the H-dimer than in J- and M-dimers. NCI analysis qualitatively elucidated the increase in non-covalent interactions with displacement and rotation from the eclipsed configuration. NCI isosurfaces of all stationary points computed through 1D SAPT scan for rotation along interplanar axis and PES scan are provided in Fig. S7 in ESI.† Geometries forming minima in 1D-rotational SAPT scans and PES (R2, R4, M1 to M5 and M7) have continuous NCI isosurfaces without any voids. However, the NCI isosurfaces of maxima geometries (R1, R3, M6, M8, and M9) are intermittent, with multiple voids indicating weak intermolecular interactions.
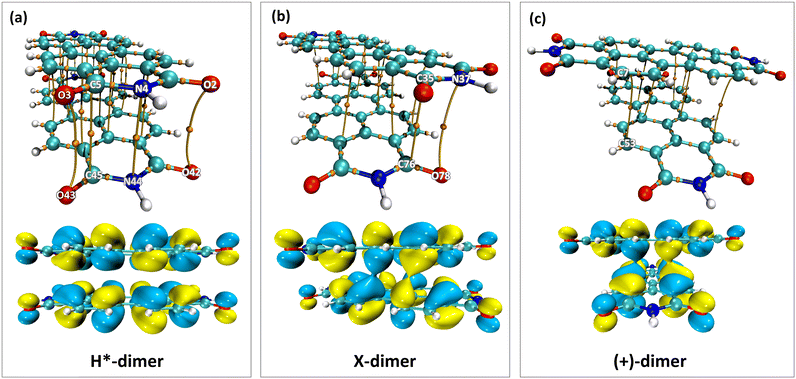
The impact of heteroatoms on enhancing the stability of X-aggregates in PDI was evaluated using QTAIM analysis.50 The H*-dimer exhibited C⋯C, N⋯N and O⋯O interactions (Fig. 7a-top). While rotating one monomer from the H*-dimer configuration, a bond critical point (BCP-109) with (3, −1) nature was observed between the imide nitrogen and carbonyl oxygen (N37⋯O78) (Fig. 7b-top). The obtained BCP strongly confirms the presence of a non-covalent interaction between the different functional groups of the two monomers in the X-dimer. Fig. 7c-top shows the C⋯C interactions in the (+)-dimer and heteroatom interactions were not realised due to the large distance between the functional groups in the (+)-dimer. The observed BCP-109 in the X-dimer corresponding to the heteroatom interaction was not observed in any of the dimer systems obtained through displacement offsets from the eclipsed configuration (Fig. S8, ESI†). Selected BCPs and the associated ρ(r) and ∇2ρ(r) values have been summarised in Table S6 (ESI†) for all the dimer systems studied. FMO analysis was utilised to describe the orbital interactions leading to the stability of different PDI dimers. In the X-dimer, the interactions between HOMO orbitals demonstrate a favorable interaction, as the orbital lobes of the two monomers with same phase overlap, indicating strong π orbital interactions (Fig. 7b-bottom). Conversely, in the H*-dimer, a pronounced repulsive interaction between the orbitals of the monomers exhibiting destructive overlap is present (Fig. 7a-bottom). It is intriguing that at least a slight deviation such as displacement or rotation away from the eclipsed configuration is quintessential for the monomer orbitals to interact constructively (Fig. 7c-bottom and Fig. S8, ESI†).
To discern the contribution of aromatic core interactions to the total interaction energies in PDI aggregates, 1D SAPT scans and PES analyses were performed on comparable perylene dimer geometries (Fig. S9, ESI†). The coordinate system used for the perylene dimer is similar to that of the PDI dimer, with long axis X, short axis Y, and interplanar axis Z. The transition dipole moment vector for the perylene monomer is along the long axis (Fig. S2b, ESI†). 1D SAPT scan along the interplanar axis Z, displayed similar interaction energy trends for perylene as well as PDI dimers (Fig. S3b, ESI†). Displacement along the long and short axes revealed energy minima at X1′ = 1.4 Å and Y1′ = 1.4 Å (Fig. S10, ESI†). Rotational SAPT analysis showed minima at 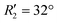 and
and 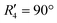 , although the stabilisation effect was less pronounced than in analogous PDI dimers. The energy difference between the two minima in PDI (R2 and R4) was 8.40 kcal mol−1 and it is merely 1.11 kcal mol−1 in perylene dimer (
, although the stabilisation effect was less pronounced than in analogous PDI dimers. The energy difference between the two minima in PDI (R2 and R4) was 8.40 kcal mol−1 and it is merely 1.11 kcal mol−1 in perylene dimer (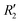 and
and 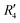 ). Fig. S11 (ESI†) depicts the PES of the perylene dimer, while Tables S7 and S8 (ESI†) list the stationary points and their interaction energies computed by PES and SAPT, respectively. Previous studies on coplanar perylene dimers based on long-range corrected functionals exhibit similar binding energy trends and stabilities, which are in line with the SAPT(0) interaction energy trends observed in our study for the parent perylene dimers.51 SAPT analysis was carried out on
). Fig. S11 (ESI†) depicts the PES of the perylene dimer, while Tables S7 and S8 (ESI†) list the stationary points and their interaction energies computed by PES and SAPT, respectively. Previous studies on coplanar perylene dimers based on long-range corrected functionals exhibit similar binding energy trends and stabilities, which are in line with the SAPT(0) interaction energy trends observed in our study for the parent perylene dimers.51 SAPT analysis was carried out on 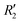 (X-dimer),
(X-dimer), 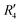 ((+)-dimer),
((+)-dimer),  (H-dimer),
(H-dimer),  (J-dimer),
(J-dimer),  (H*-dimer), and M-dimer geometries (Table S9, ESI†) to compare the stability order of different perylene and PDI aggregate systems. Unlike in PDI, (+)-aggregate was energetically more favourable in perylene next to H-aggregates. M- and J-aggregates have comparable stability in terms of their total intermolecular interaction strengths. Therefore, a stability order of X > H > J > M > (+) > H* was observed for PDI aggregates (Fig. 8a), whereas the parent perylene aggregates displayed a stability order of X > (+) > H > M > J > H* with respect to the interaction energies (Fig. 8b). In general, the interaction strengths are lower in perylene aggregates than in corresponding PDI aggregates due to the low magnitudes of stabilising interactions.
(H*-dimer), and M-dimer geometries (Table S9, ESI†) to compare the stability order of different perylene and PDI aggregate systems. Unlike in PDI, (+)-aggregate was energetically more favourable in perylene next to H-aggregates. M- and J-aggregates have comparable stability in terms of their total intermolecular interaction strengths. Therefore, a stability order of X > H > J > M > (+) > H* was observed for PDI aggregates (Fig. 8a), whereas the parent perylene aggregates displayed a stability order of X > (+) > H > M > J > H* with respect to the interaction energies (Fig. 8b). In general, the interaction strengths are lower in perylene aggregates than in corresponding PDI aggregates due to the low magnitudes of stabilising interactions.
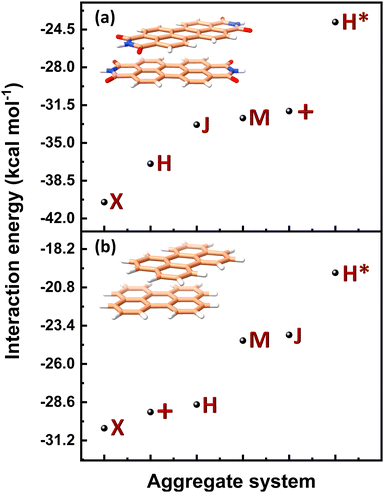 | ||
| Fig. 8 Interaction energy profiles of different dimer systems of (a) PDI and (b) perylene aggregate systems computed through SAPT. | ||
Conclusions
In summary, we have investigated the ground state stability order and formation favourability of perylenediimide aggregates by performing quantum chemical calculations on various dimer models. Critical insights into the nature and strength of the non-covalent interactions predominant in PDI dimer systems were obtained using SAPT, PES and NCI analyses. Generally, PDIs prefer to form X-(rotated) or H-(cofacially stacked with minor slip) aggregates due to favourable π–π interactions.1 X-dimer or the rotated dimer with additional stabilising electrostatic interactions constitutes the global minimum and is the most favoured configuration among the dimer systems studied. J-(staggered with major slip), M-(magic angle stacking) and (+)-(rotated orthogonal) dimers have relatively similar interaction energies and fine-tuning of the PDI monomer through substitution is necessary for directing the self-assembly to J-, M- and (+)-type aggregation. Though with a maximum dispersion interaction, the H*-dimer (eclipsed dimer) is the most unstable dimer due to the strong repulsive exchange interactions between monomers. NCI analysis on PDI dimers portrayed a qualitative picture of the enhancement of non-covalent interactions, with displacement and rotation from the eclipsed H*-dimer configuration. QTAIM topological analysis unveiled the imide-N⋯O-carbonyl interaction in X-dimer, which is absent in other PDI dimer systems. HOMO isosurfaces ascertained the enhancement in the constructive orbital overlap between the two monomers, when rotation or displacement offset is present from the eclipsed configuration. SAPT analysis on analogous perylene dimers showed lower interaction strengths than in corresponding PDI dimers. The above result verifies the role of functional groups in gaining additional stabilisation favouring the formation of X-aggregate systems in PDI.Our findings shed light on the key interactions within the PDI units, favouring the self-assembly process into distinct supramolecular arrangements. These computational efforts can be extended to other chromophoric systems to predict the structure–property relationships and the concomitant photophysics.
Author contributions
P. P. D., A. M., and M. H. conceived the project. P. P. D., A. M. and M. R. carried out the calculations. P. P. D., A. M. and M. R. analysed the results. P. P. D., A. M., M. R., R. S. S. and M. H. wrote the manuscript. M. H. supervised the research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. H. and R. S. S. thank the Nanomission project (DST/NM/TUE/EE01/2019) of the Department of Science and Technology (DST), Government of India, for financial support. We greatly acknowledge the support for high-performance computing time at the Padmanabha cluster, IISER Thiruvananthapuram, India. A. M. and M. R. thank IISER TVM for the financial assistance.References
- M. Hecht and F. Würthner, Acc. Chem. Res., 2021, 54, 642–653 CrossRef CAS PubMed.
- S. Ma, S. Du, G. Pan, S. Dai, B. Xu and W. Tian, Aggregate, 2021, 2, 1–15 CrossRef.
- S. K. Park, J. H. Kim and S. Y. Park, Adv. Mater., 2018, 30, 1–26 Search PubMed.
- H. Zhang, Z. Zhang, K. Ye, J. Zhang and Y. Wang, Adv. Mater., 2006, 18, 2369–2372 CrossRef CAS.
- S. Sanyal, A. Painelli, S. K. Pati, F. Terenziani and C. Sissa, Phys. Chem. Chem. Phys., 2016, 18, 28198–28208 RSC.
- S. J. Yoon, J. W. Chung, J. Gierschner, K. S. Kim, M. G. Choi, D. Kim and S. Y. Park, J. Am. Chem. Soc., 2010, 132, 13675–13683 CrossRef CAS PubMed.
- Y. Dai, M. Zubiria-Ulacia, D. Casanova and F. Negri, Computation, 2022, 10, 18 CrossRef.
- M. Zubiria-Ulacia, J. M. Matxain and D. Casanova, Phys. Chem. Chem. Phys., 2020, 22, 15908–15918 RSC.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- A. S. Davydov, Uspekhi Fiz. Nauk, 1964, 82, 393–448 CrossRef CAS.
- E. E. Jelley, Nature, 1936, 138(3502), 1009–1010 CrossRef CAS.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- G. Scheibe, Angew. Chem., 1937, 50, 212–219 CrossRef CAS.
- J. Zhou, W. Zhang, X. F. Jiang, C. Wang, X. Zhou, B. Xu, L. Liu, Z. Xie and Y. Ma, J. Phys. Chem. Lett., 2018, 9, 596–600 CrossRef CAS PubMed.
- E. Sebastian, A. M. Philip, A. Benny and M. Hariharan, Angew. Chem., Int. Ed., 2018, 57, 15696–15701 CrossRef CAS PubMed.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- M. P. Lijina, A. Benny, E. Sebastian and M. Hariharan, Chem. Soc. Rev., 2023, 52, 6664–6679 RSC.
- C. D. Sherrill, Acc. Chem. Res., 2013, 46, 1020–1028 CrossRef CAS PubMed.
- J. M. Herbert, J. Phys. Chem. A, 2021, 125, 7125–7137 CrossRef CAS PubMed.
- K. Carter-Fenk and J. M. Herbert, Chem. Sci., 2020, 11, 6758–6765 RSC.
- E. G. Hohenstein, J. Duan and C. D. Sherrill, J. Am. Chem. Soc., 2011, 133, 13244–13247 CrossRef CAS PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- P. B. Lutz and C. A. Bayse, Phys. Chem. Chem. Phys., 2013, 15, 9397–9406 RSC.
- J. Henrichsmeyer, M. Thelen, M. Bröckel, M. Fadel, S. Behnle, M. Sekkal-Rahal and R. F. Fink, Chem. Phys. Chem., 2023, 24, e202300097 CrossRef CAS PubMed.
- C. Sutton, C. Risko and J. L. Brédas, Chem. Mater., 2016, 28, 3–16 CrossRef CAS.
- F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Chem. Rev., 2016, 116, 962–1052 CrossRef PubMed.
- H. M. Zhao, J. Pfister, V. Settels, M. Renz, M. Kaupp, V. C. Dehm, F. Würthner, R. F. Fink and B. Engels, J. Am. Chem. Soc., 2009, 131, 15660–15668 CrossRef CAS PubMed.
- S. Parida, S. K. Patra and S. Mishra, Chem. Phys. Chem., 2022, 23, e202200361 CrossRef CAS PubMed.
- B. Engels and V. Engel, Phys. Chem. Chem. Phys., 2017, 19, 12604–12619 RSC.
- C. Walter, V. Krämer and B. Engels, Int. J. Quantum Chem., 2017, 117, 1–14 CrossRef.
- G. Wu, F. Li, B. Tang and X. Zhang, J. Am. Chem. Soc., 2022, 144, 14962–14975 CrossRef CAS PubMed.
- K. Tojo and J. Mizuguchi, Z. Krist.- New Cryst. St, 2002, 217, 45–46 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. James and R. S. Swathi, J. Phys. Chem. A, 2022, 126, 3472–3485 CrossRef CAS PubMed.
- E. Hädicke and F. Graser, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 195–198 CrossRef.
- E. Hädicke and F. Graser, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 189–195 CrossRef.
- G. Klebe, F. Graser, E. Hädicke and J. Berndt, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 69–77 CrossRef.
- G. Jansen, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2014, 4, 127–144 CrossRef CAS.
- K. Szalewicz, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 254–272 CrossRef CAS.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031 CrossRef CAS.
- M. Oltean, G. Mile, M. Vidrighin, N. Leopold and V. Chiş, Phys. Chem. Chem. Phys., 2013, 15, 13978–13990 RSC.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- G. W. Coates, A. R. Dunn, L. M. Henling, D. A. Dougherty and R. H. Grubbs, Angew. Chem., Int. Ed. Engl., 1997, 36, 248–251 CrossRef CAS.
- P. S. V. Kumar, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527–1536 CrossRef CAS.
- D. Casanova, Int. J. Quantum Chem., 2015, 115, 442–452 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04609e |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2024 |