Open Access Article
Open Access ArticleMechanistic insights into the co-recovery of nickel and iron via integrated carbon mineralization of serpentinized peridotite by harnessing organic ligands†
Shreya
Katre
 ab,
Prince
Ochonma
ab,
Prince
Ochonma
 c,
Hassnain
Asgar
c,
Hassnain
Asgar
 a,
Archana M
Nair
a,
Archana M
Nair
 b,
Ravi
K
b,
Ravi
K
 b and
Greeshma
Gadikota
b and
Greeshma
Gadikota
 *ac
*ac
aSchool of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
bDepartment of Civil Engineering, Indian Institute of Technology Guwahati, Assam 781039, India
cSmith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA. E-mail: gg464@cornell.edu; Tel: +1 607-255-4796
First published on 19th February 2024
Abstract
The rising need to produce a decarbonized supply chain of energy critical metals with inherent carbon mineralization motivates advances in accelerating novel chemical pathways in a mechanistically-informed manner. In this study, the mechanisms underlying co-recovery of energy critical metals and carbon mineralization by harnessing organic ligands are uncovered by investigating the influence of chemical and mineral heterogeneity, along with the morphological transformations of minerals during carbon mineralization. Serpentinized peridotite is selected as the feedstock, and disodium EDTA dihydrate (Na2H2EDTA·2H2O) is used as the organic ligand for metal recovery. Nickel extraction efficiency of ∼80% and carbon mineralization efficiency of ∼73% is achieved at a partial pressure of CO2 of 50 bars, reaction temperature of 185 °C, and 10 hours of reaction time in 2 M NaHCO3 and 0.1 M Na2H2EDTA·2H2O. Extensive magnesite formation is evidence of the carbon mineralization of serpentine and olivine. An in-depth investigation of the chemo-morphological evolution of the CO2–fluid–mineral system during carbon mineralization reveals several critical stages. These stages encompass the initial incongruent dissolution of serpentine resulting in a Si-rich amorphous layer acting as a diffusion barrier for Mg2+ ions, subsequent exfoliation of the silica layer to expose unreacted olivine, and the concurrent formation of magnesite. Organic ligands such as Na2H2EDTA·2H2O aid the dissolution and formation of magnesite crystals. The organic ligand exhibits higher stability for Ni-complex ions than the corresponding divalent metal carbonate. The buffered environment also facilitates concurrent mineral dissolution and carbonate formation. These two factors contribute to the efficient co-recovery of nickel with inherent carbon mineralization to produce magnesium carbonate. These studies provide fundamental insights into the mechanisms underlying the co-recovery of energy critical metals with inherent carbon mineralization which unlocks the value of earth abundant silicate resources for the sustainable recovery of energy critical metals and carbon management.
1 Introduction
The rising need to create a decarbonized supply chain of energy critical metals motivates scientific advances in material-efficient pathways to harness earth abundant silicate resources.1–4 The opportunity to fix anthropogenic CO2 emissions via thermodynamically downhill carbon mineralization routes while co-recovering energy critical metals such as nickel and iron motivates scientific advances in accelerating these pathways.1–3,5,6 Prior advances in this field were exclusively focused on carbon mineralization with limited attention being given to the co-recovery of energy critical metals that are present in earth abundant silicate resources such as serpentine (Mg3Si2O5(OH)4) and olivine ((Mg,Fe)2SiO4).1–4,7 However, recent advances have shown that organic ligands such as ethylenediaminetetraacetic acid (EDTA) are effective in facilitating the co-recovery of energy critical metals such as nickel, while enabling accelerated carbon mineralization. However, scalable realization of these pathways remains limited by the lack of mechanistic insights into the complex chemo-morphological interactions underlying the co-recovery of energy critical metals with inherent carbon mineralization. Prior studies unlocked the role of siliceous materials and carbon mineralization in enabling enhanced H2 generation,8–10 creating carbonate-bearing construction materials,11 hydroxide/silica production,12,13 and low carbon and clean manufacturing.10,14–16 However, the co-recovery of energy critical metals with inherent carbon mineralization remains underexplored despite its transformative potential.Carbon mineralization of siliceous materials generally involves three primary reactions, as illustrated in Fig. 1. In the first step, gaseous CO2 undergoes hydration on contact with the aqueous phase resulting in the formation of carbonic acid, which dissociates to generate bicarbonate ions, carbonate ions, and protons, based on the pH of the system.17 CO2 hydration precedes mineral dissolution, a process facilitated by acidic pH conditions. The incorporation of buffering agents like sodium bicarbonate modulates mineral dissolution and carbonate precipitation reactions.18–21 Reactions between bicarbonate ions and divalent metals originating from olivine play a crucial role in the overall carbon mineralization process.2,22,23 The third step involves carbonate formation, wherein the dissolved species interact and precipitate as carbonate minerals.24,25Fig. 1 illustrates the sequence of these reactions in the carbon mineralization of Mg-rich olivine and serpentine minerals. It has been reported that CO2 hydration, mineral dissolution and carbonate precipitation may be the rate-limiting processes during carbon mineralization.22,23,26–30 Several approaches have been proposed to accelerate the overall rate of carbon mineralization including mineral pre-treatment,31,32 use of chemical additives,8,22,28 and tuning of experimental conditions such as temperature, pH, and CO2 partial pressure.6,20,27,33 While the chemical reactions underlying CO2–water–rock interactions have been studied in the context of carbon mineralization reactions, the morphological evolution of the underlying silicates and this impact on the kinetics of mineralization and metal release have not yet been systematically elucidated. Furthermore, the influence of organic ligands on the coupled interactions involving CO2 hydration, mineral dissolution and carbonate precipitation remain unresolved.
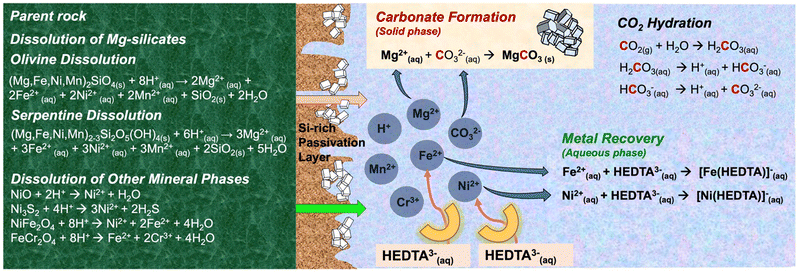 | ||
| Fig. 1 Schematic representation of the reaction pathways for direct carbon mineralization with concurrent metal recovery. | ||
Magnesium-rich ultramafic rocks are favored feedstocks for carbon mineralization, given their substantial abundance as Mg-bearing silicate minerals such as olivine ((Mg,Fe)2SiO4) and serpentine (Mg3Si2O5(OH)4).33–35 Hydration of olivine from peridotite results in partially serpentinized peridotite.36 Notably, ultramafic rocks also contain significant quantities of iron (Fe) and a high concentration of energy critical metals such as nickel (Ni), cobalt (Co), chromium (Cr), and manganese (Mn). These elements are commonly present within the crystalline matrices of minerals such as magnesium silicates, magnesium hydroxides, sulfides, oxides, as well as alloy minerals including chromite, heazlewoodite, trevorite, spinel, awaruite, wairauite, among others.37–39 These metals mobilize or disperse throughout the sample during the mineral dissolution step of the carbon mineralization process.5,40–43 These metals are often co-present with the Mg carbonate matrix after carbon mineralization.42 Efforts have been made to enhance the mobilization and recovery of these metals into the aqueous phase.1,5,44–47 For example, CO2 mineralization can be harnessed as a pre-treatment step to enhance the efficiency of nickel extraction by 25–35%.5 Notably, a comparative analysis demonstrated a substantial enhancement in the leaching efficiency of nickel in fully carbonated olivine compared to fresh olivine, particularly when leached with HCl or HNO3 acid. This work also reports increased dispersion of nickel throughout the sample after complete carbon mineralization, a precursor for enhanced extraction efficiency.
Thus far, the majority of the work on aqueous phase metal recovery from various sources, such as ultramafic mine tailings, alkaline red mud, and laterite ore, primarily has relied on a multi-step approach which commonly use sulfuric, nitric, and hydrochloric acids for the initial extraction of metals followed by carbonate precipitation.7,44,45 In a recent study, Sim et al.46 investigated a novel approach for CO2 fixation and rare earth element (REE) recovery by employing NaOH and oxalic acid-assisted pH swing carbon mineralization of blast furnace slag. Similarly, Gao et al.47 investigated waste iron(II) sulfate as a reagent to extract Mg and Ni from laterite ore for simultaneous Ni recovery and carbon mineralization, achieving optimal extraction efficiencies of 94% for Mg and 87% for Ni with subsequent addition of Na2SO4, followed by mineralization using (NH4)2CO3. Despite the potential benefits of these processes, the extensive use of acids and slow reaction kinetics raise uncertainties in the development of ex situ indirect carbon mineralization methodology.
To overcome these challenges associated with indirect carbon mineralization, direct aqueous carbon mineralization has been proposed. Direct aqueous carbon mineralization is a single step process wherein three key reactions during the carbon mineralization process operate concurrently within a single reactor.31,33 For example, Wang et al.48 leveraged the contrasting solubilities of Mg and Ni carbonates compared to sulfides to facilitate nickel sulfide (NiS) and magnesium carbonate (MgCO3) production from olivine containing Ni. The dissolution of olivine in 1.5 M sodium bicarbonate (NaHCO3) resulted in a carbon mineralization efficiency exceeding 80% at temperatures ranging from 115 °C to 150 °C, and a Ni to NiS conversion efficiency of 32%. However, the use of hazardous gases such as H2S, low NiS selectivity due to the co-precipitation of by-products such as iron sulfide, and competition between carbonate versus sulfide precipitation pose a significant concern to the environmental and economic viability of this approach. More recently, the use of organic ligands such as EDTA have been investigated for integrated carbon mineralization and selective metal recovery from olivine, as shown in Fig. 1.1 The process has been reported to be a highly selective single-step process reaching Ni and Co extraction efficiencies above 90%, and simultaneous carbon mineralization efficiencies of 90%.1 Interestingly, the addition of EDTA in the aqueous phase during CO2 mineralization resulted in both improved critical metal recovery efficiencies and accelerated carbon mineralization by transitioning from a diffusion-controlled to surface-reaction-controlled mechanism. It was reported that the formation of a patchy porous carbonate layer on unreacted olivine enables EDTA to extract metals from the shrinking core.1,7 Similar advantages have been observed with other organic ligands such as oxalate which leads to enhanced mineral dissolution. However, in the case of oxalate, the formation of a secondary solid phase known as glushinskite (magnesium oxalate) is noted, which limits further extraction.49 Further, EDTA can be easily regenerated when utilized at temperatures below 175 °C and has been used extensively in mineral processing practices.7
While enhanced carbon mineralization and metal recovery efficiencies have been extensively reported during direct carbon mineralization, the impact of chemical and mineralogical heterogeneity on this integrated process remains poorly understood. Metal recovery during the carbon mineralization relies on the mobilization of various metals from their respective mineral structures.5,41 Consequently, scalable advances require a comprehensive understanding of the influence of chemical additives or physical processes that may govern the migration of metals during carbon mineralization. Another crucial but understudied aspect of simultaneous carbon mineralization and metal recovery pertains to changes in the structural and morphological characteristics of minerals, including pore volume, surface area, and particle size, which may significantly influence metal leaching. Moreover, the effect of chemical additives, such as organic ligands or acids, on the morphology of the unreacted and carbonate-bearing products has not been thoroughly investigated. This work advances the knowledge on ex situ direct aqueous carbon mineralization of serpentinized peridotite and concurrent recovery of energy critical metals using Na2H2EDTA·2H2O as the organic ligand. In this regard, the specific research questions that are addressed in this current study are: (1) What are the chemo-morphological mechanisms underlying carbon mineralization and the recovery of nickel and iron from serpentinized peridotite? (2) What is the role of organic ligands, such as Na2H2EDTA·2H2O, on the efficiency of carbon mineralization and metal recovery? (3) How can the physico-chemical parameters be tuned to achieve >70% conversion of CO2 to magnesium carbonate and nickel recovery?
2 Experimental methods
2.1 Characterization of materials
A sample of ultramafic igneous rock is obtained by grab sampling from the Mayodia-Hunli region of Dibang valley ophiolitic sequence located in Arunachal Pradesh, India. To establish a representative chemical composition of the rock sample, the entire specimen is finely ground and thoroughly mixed using a lab-scale bench-top mixer mill (8000 M Mixer/Mill® by SPEX® Sample Prep), with a small subsample selected for further analysis. The particle size of the powdered samples is determined using a Laser Diffraction Particle Size Analyzer (Anton Paar). X-ray fluorescence (XRF) spectroscopy (Thermo ARL Perform’X) is used to analyze the elemental composition of the crushed rock. Information about the structural arrangement and chemical phases present in the crushed mineral and carbonate-bearing products is obtained using an X-ray diffractometer (XRD) (Bruker D8 Advance ECO Powder Diffractometer), which uses Cu Kα radiation, and is operated with an acceleration voltage of 40 kV, and current of 25 mA. The XRD patterns are obtained in the range of 2θ = 20°–80°. The specific surface area and pore volume of the powdered sample are determined using the Brunauer–Emmett–Teller technique (BET, Quantachrome Autosorb iQ Analyzer, Boynton Beach, FL) by obtaining N2 adsorption–desorption isotherms at 77 K. Prior to conducting the adsorption–desorption isotherms, the samples are outgassed at 120 °C for 24 hours. Thermogravimetric analysis (TGA) is carried out in the temperature range of 30–1000 °C to determine any pre-existing phases, which are sensitive to thermal perturbations. The measurements are performed using a Thermogravimetric Analyzer (TA Instruments, SDT650, New Castle, DE) at a ramp rate of 10 °C min−1 with N2 purged at 50 mL min−1.2.2 Carbon mineralization of serpentinized peridotite
The direct aqueous carbon mineralization experiments are carried out using a 50 mL stainless steel batch reactor (Micro Bench Top Reactor, Parr Instrument Company) under high pressure and temperature conditions. A schematic representation of the reactor is shown in Fig. 2.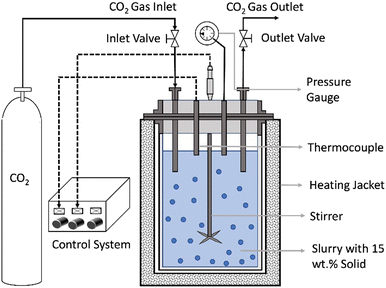 | ||
| Fig. 2 Schematic of the experimental setup for direct carbon mineralization with co-recovery of energy critical metals. | ||
In important studies that informed our reagent selection, Wang and Dreisinger,1 Wang et al.,8 Gadikota et al.,28 and Gadikota et al.30 extensively investigated olivine carbon mineralization in CO2-saturated aqueous solutions under varying temperature and CO2 partial pressure conditions, incorporating sodium bicarbonate. These studies revealed a significant enhancement in carbon mineralization efficiency with the increasing concentration of NaHCO3. Specifically, the carbon mineralization efficiency increased from 15% to a peak of 76% as the NaHCO3 addition escalated from 0 to 2 M. Sodium bicarbonate played a pivotal role in facilitating the transfer of CO2 from the gas phase to aqueous phase, accelerating the diffusion of aqueous silica for carbon mineralization, and establishing a buffered system with carbonic acid to regulate pH during mineral carbonate precipitation. The only distinction between direct aqueous carbon mineralization and simultaneous enhanced metal recovery lies in the addition of the metal-complexing ligand. Wang and Dreisinger1 demonstrated the efficiency of 0.1 M Na2EDTA in recovering nearly 90% of nickel and cobalt from olivine. Hence, in our study, we maintained an optimal 0.1 M Na2H2EDTA·2H2O and 2 M NaHCO3 dosage across all experimental conditions.
In each run, a slurry of 20 mL consisting of 15 wt% ground minerals is suspended in a reaction fluid composed of deionized water, 2 M sodium bicarbonate (NaHCO3), and 0.1 M Na2H2EDTA·2H2O. The reactor, containing the slurry, is sealed tightly, and a constant stirring rate of 500 rpm is maintained throughout the experiment. After approximately 40 minutes, when the reactor reached the specified temperature, the pressure inside is increased to the desired level of CO2 partial pressure (PCO2), marking the beginning of the experiment. The experiments are conducted under a range of reaction conditions, including CO2 partial pressures of 35 and 50 bars, reaction temperatures of 155 and 185 °C, and varying reaction times from 1 hour to 18 hours. The specific combinations of these reaction parameters are listed in Table S1 (ESI†). To replicate the conditions of purified and pressurized CO2 streams obtained after CO2 capture, ultra-high-purity grade CO2 (99.99%) is used in these experiments.
Upon completion of the designated reaction time, the temperature of the reactor is gradually decreased to a level below 60 °C over a duration of approximately 50 minutes. Subsequently, the reactor is depressurized and all the solid and liquid samples are collected. The interior of the reactor is thoroughly rinsed with water, and the resulting aqueous solution is carefully filtered to capture any solid residues that may have adhered to or formed on the reactor walls. Following this, the resultant solution is centrifuged for 15 minutes at the rate of 4000 rpm for effective separation of solid–liquid phases. The solid fraction is subjected to multiple rinses with deionized water until a colorless liquid is obtained during the separation process, with each resulting liquid being collected. Subsequently, the solid component is dried for 24 hours at a temperature of 70 °C in an oven. The liquid fraction, after being filtered through a 0.45 μm filter paper, undergoes further analysis.
2.3 Characterization of the reaction products
 | (1) |
 | (2) |
TCA, in conjunction with the TGA technique, is employed to evaluate the extents of carbon mineralization. It is important to highlight that the solid product obtained after the carbon mineralization process is washed rigorously, involving four to five cycles of rinsing with deionized water. This approach dissolves any potential NaHCO3 and Na2H2EDTA·2H2O molecules that may have been adsorbed on the surface of the sample. The presence of these molecules has the potential to interfere with the precise determination of the total carbon content, which, in the context of this study, is not relevant as it does not contribute to the formation of carbonates. The quantification of total carbon in the carbonate-bearing samples is performed at the Cornell Soil Health Laboratory, utilizing a dry combustion furnace with controlled temperature. Sets of crucibles, which are dried in an oven and contained around 0.3 g of soil each, are prepared and processed by the autosampler for subsequent analysis. The determination of total carbon in a given sample involved the complete oxidation of sample carbon into CO2 through high-temperature combustion at 1100 °C. To estimate the degree of carbon mineralization using TCA, the equation proposed by Gadikota et al.28 as shown in eqn (3) is used:
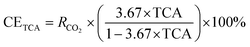 | (3) |
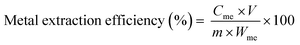 | (4) |
3 Results
3.1 Characterization of serpentinized peridotite
The ultramafic rock sample in this study contains a significantly higher amount of magnesium as determined using XRF spectroscopy (Table 1).| Major oxides | wt% | Trace elements | ppm |
|---|---|---|---|
| SiO2 | 41.65 | Ni | 2547 |
| Al2O3 | 1.58 | Cr | 3154 |
| Fe2O3 | 7.83 | V | 37 |
| MgO | 42.84 | Sc | 10 |
| CaO | 0.58 | Cu | 18 |
| Loss On Ignition (LOI) (%) | 4.43 | Sr | 1 |
| Y | 3 | ||
| Zr | 6.2 | ||
| Ce | 8 | ||
| Nd | 2 |
Briefly, the sample comprises 42.84% MgO, followed by SiO2 (41.65%), Fe2O3 (7.83%), Al2O3 (1.58%) and CaO (0.58%). Notably, significant amounts of Ni and Cr metals are present in the sample, measuring 2547 ppm and 3154 ppm, respectively. Based on the X-ray diffraction analyses (discussed in more detail in Section 3.3), the antigorite polymorph of the serpentine mineral group (Mg3Si2O5(OH)4) and forsterite (Mg2SiO4) are the prominent mineral phases in the unreacted sample. The powdered sample has an average particle size of 9.24 μm, with over 90% of the material consisting of particles smaller than 22.24 μm. The specific surface area, pore volume, and pore diameter of the sample are 7.67 m2 g−1, 0.021 cc g−1, and 2.12 nm, respectively.
The weight loss (%) vs. temperature (°C) plot of unreacted sample, obtained from TGA, shows a weight loss of 3.79%, at temperatures between 600 to 800 °C, which corresponds to the dehydroxylation process of antigorite, as indicated in Section 3.2. The observed temperature range at which the major decomposition of antigorite into forsterite and silica takes place aligns well with existing literature50,51 as shown in reaction (R1):
 | (R1) |
3.2 Carbon mineralization and metal recovery efficiencies
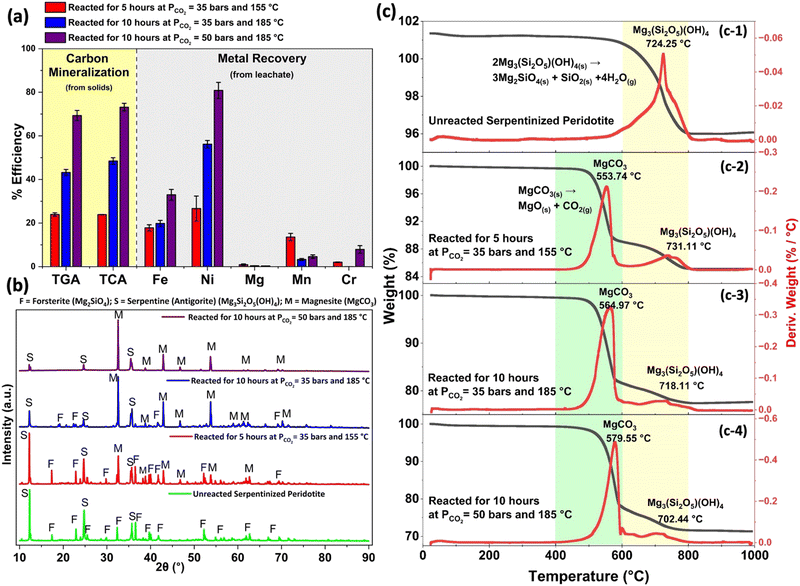
This study investigates the combined effects of CO2 partial pressure, temperature, and reaction time on the kinetics of carbon mineralization of serpentinized peridotite. Additionally, the study seeks to examine the extent to which energy critical metals can be extracted from the mineral matrix and recovered in an aqueous solution using organic ligands. Through the examination of these factors, a more profound insight into the chemical and morphological dynamics of this multiphase reaction environment during the processes of carbon mineralization and concurrent metal recovery is achieved. The primary aim is to uncover mechanistic insights into the phenomena underlying the use of organic ligands for concurrent recovery of energy critical metals and carbon mineralization. To this end, Table 2 and Fig. 3(a) present the metal extraction efficiencies and extents of carbon mineralization for serpentinized peridotite under various reaction conditions.| P CO2 (bar) | T (°C) | Reaction time (h) | Chemical additives | Mean particle size (μm) | pH of the post-reaction liquid | Carbon mineralization efficiency (%) | Metal recovery (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TGA | TCA | Fe | Ni | Mn | Cr | Mg | ||||||
| 35 | 155 | 5 | 2 M NaHCO3; 0.1 M Na2H2EDTA·2H2O | 17.85 | 10.38 | 23.95 ± 0.78 | 23.89 ± 0.09 | 17.79 ± 1.43 | 26.68 ± 5.73 | 13.58 ± 1.69 | 2.02 ± 0.14 | 0.91 ± 0.37 |
| 35 | 185 | 10 | 19.17 | 9.21 | 43.26 ± 1.35 | 48.49 ± 1.49 | 19.81 ± 1.42 | 56.19 ± 1.72 | 3.3 ± 0.47 | 0 | 0.39 ± 0.03 | |
| 35 | 185 | 18 | 9.94 | 8.69 | 66.05 ± 3.98 | 76.36 ± 4.25 | 16.41 ± 1.39 | 78.59 ± 2.15 | 3.16 ± 0.25 | 2.09 ± 0.11 | 0.07 ± 0.02 | |
| 50 | 185 | 1 | 15.28 | 9.35 | 42.52 ± 0.86 | 44.37 ± 0.37 | 17.67 ± 1.40 | 38.82 ± 1.06 | 3.11 ± 0.42 | 3.17 ± 0.25 | 0.28 ± 0.02 | |
| 50 | 185 | 3 | 16.69 | 8.86 | 59.64 ± 1.91 | 63.26 ± 1.45 | 19.69 ± 1.88 | 41.12 ± 2.50 | 6.24 ± 1.35 | 3.22 ± 0.21 | 1.26 ± 0.51 | |
| 50 | 185 | 6 | 16.96 | 9.23 | 66.68 ± 2.00 | 70.01 ± 1.62 | 21.23 ± 2.81 | 60.94 ± 3.34 | 2.13 ± 0.62 | 1.81 ± 0.33 | 0.43 ± 0.16 | |
| 50 | 185 | 10 | 25.38 | 9.04 | 69.35 ± 2.33 | 73.19 ± 1.74 | 32.96 ± 2.46 | 80.87 ± 3.69 | 4.6 ± 0.81 | 7.92 ± 1.73 | 0.32 ± 0.01 | |
| 35 | 185 | 10 | 2 M NaHCO3 | 9.54 | 9.1 | 37.38 ± 2.11 | 38.65 ± 2.34 | 0.1 | 0.183 | 0 | 0.042 | 0.03 |
| 50 | 185 | 10 | 2 M NaHCO3 | 10.73 | 8.89 | 64.81 ± 5.54 | 69.55 ± 6.86 | 0.107 | 0.365 | 0 | 0.063 | 0.029 |
The reacted mineral samples are analyzed by TGA and TCA to determine the extents of carbon mineralization. It is worth noting that the extents of carbon mineralization derived from both the TGA and TCA methods are generally in agreement, except for instances with notably high carbon mineralization efficiencies achieved during longer reaction time of 10 and 18 hours. To maintain uniformity in our observations, the carbon mineralization efficiency values discussed in the subsequent sections are exclusively based on the TCA method.
The initial set of experiments is guided by the optimized conditions for integrated carbon mineralization and concurrent metal recovery proposed by Wang and Dreisinger.1 The carbon mineralization reaction is started at 155 °C, with a PCO2 of 35 bars, and involves the addition of 2 M NaHCO3 and 0.1 M Na2H2EDTA·2H2O. The reaction proceeds for 5 hours, with a solid concentration of 15 wt% and a stirring rate of 500 rpm. Under these conditions, the carbon mineralization efficiency is found to be 24%, which is determined based on the formation of magnesium carbonate. Further details on post-reaction carbonate phases are discussed later in this section. The aqueous phase recovery efficiencies for Fe, Ni, Mn, Cr, and Mg are ∼18%, 27%, 14%, 2%, and 1%, respectively, based on the compositions of the post-reaction liquid sample. Higher carbon mineralization efficiencies of 49% and 76% are observed at extended reaction times of 10 and 18 hours respectively at 185 °C, under similar conditions of CO2 partial pressure and solvent concentration. Similarly, an increase in the Ni extraction efficiencies from 56% to 79% is observed when the reaction time is increased from 10 hours to 18 hours at 185 °C. However, the increased reaction temperature and extended reaction time does not significantly affect the extraction efficiencies of other metals, as shown in Table 2.
A second set of experiments is performed to probe the effect of increased partial pressure of CO2 on the extent of carbon mineralization and metal recovery efficiencies. Under similar solvent concentration of 2 M NaHCO3 and 0.1 M Na2H2EDTA·2H2O in 20 ml slurry consisting of 15 wt% solids and stirring rate of 500 rpm, reactions are carried out at 185 °C with PCO2 of 50 bars for 1, 3, 6 and 10 hours. Extents of carbon mineralization of 44%, 63%, 70%, and 73% are observed for reaction times of 1, 3, 6, and 10 hours, respectively. Similarly, Ni extraction efficiency increases from approximately 39% to 81% between 1–10 hours of reaction as shown in Table 2. By increasing PCO2 from 35 bars to 50 bars, a significant increase in Fe extraction efficiencies from ∼20% to 33% and Ni extraction efficiencies from ∼56% to 81% is also observed for reaction time of 10 hours at 185 °C. These findings suggest the potential for effective metal recovery during carbon mineralization using olivine and serpentine minerals under appropriate reaction conditions.
To gain important insights into the underlying mechanisms that govern the simultaneous carbon mineralization and metal recovery process, and the resulting chemical and morphological changes under different reaction conditions, three case scenarios from prior experimental results were selected for further analysis as discussed below.
Case I: reaction conducted for a duration of 5 hours at a temperature of 155 °C and PCO2 of 35 bars with CETCA ≈ 25% and metal extraction efficiency for Ni ≈ 27% and for Fe ≈ 18%.
Case II: reaction conducted for a duration of 10 hours at a temperature of 185 °C and PCO2 of 35 bars with CETCA ≈ 49% and metal extraction efficiency for Ni ≈ 56% and for Fe ≈ 20%.
Case III: reaction conducted for a duration of 10 hours at a temperature of 185 °C and a PCO2 of 50 bars with CETCA ≈ 73% and metal extraction efficiency for Ni ≈ 81% and for Fe ≈ 33%.
For all three cases, the experiments were conducted with 15 wt% solid in an aqueous environment comprising, 2 M sodium bicarbonate and 0.1 M Na2H2EDTA·2H2O, and a stirring rate of 500 rpm. Detailed mechanistic insights into the reactivity of these multiphase reaction systems are obtained through a systematic investigation of the effects of the partial pressure of CO2 (or PCO2), reaction temperature, reaction time, and fluid composition.
3.3 Chemical and crystallographic phase changes during carbon mineralization
The emergence of carbonate phases after reaction is validated using X-ray diffraction (Fig. 3(b)). The unreacted sample primarily consists of the antigorite polymorph of the serpentine mineral group (Mg3Si2O5(OH)4) and forsterite (Mg2SiO4) as the prominent mineral phases.52 The morphology of the resulting post-reaction products may be impacted by the presence of various carbonate mineral phases. Prior investigations have highlighted the significance of reaction temperature in regulating the precipitation of various carbonate minerals. Magnesite forms preferentially rather than hydrated magnesium carbonate minerals at higher temperatures.24,28 In this study, XRD patterns of reacted products indicated the prevalence of magnesite (MgCO3) as the dominant carbonate phase present in all three cases. Moreover, the significant reduction in the relative peak intensities of serpentine in Case II and III, compared to Case I, implies either the complete dissolution of serpentine into the aqueous phase or its conversion into forsterite (Mg2SiO4) or (MgCO3). The increasing trend in the magnesite peaks for Cases II and III, in contrast to Case I, aligns with the diminishing peaks of serpentine and forsterite. The quantitative XRD data aligns with the observed trends, indicating an increased intensity of magnesite and concurrent reduction in the intensities of olivine and serpentine phases (Table S2, ESI†). These findings collectively suggest the transformation of serpentine and forsterite into magnesite during the carbon mineralization process.Further evidence of the presence of antigorite and subsequent magnesite formation during CO2 mineralization is observed using TGA (see Fig. 3(c)). While TGA can be used to identify different phases, such as hydroxides and carbonates, based on their respective decomposition temperatures, the presence of overlapping weight drop curves poses a challenge in accurately determining phase proportions, particularly for samples where minerals such as serpentine and carbonates coexist. The thermal decomposition of serpentine, magnesite, and calcite occurs within a temperature range of 400 °C to 800 °C, resulting in overlapping peaks. Consequently, it is challenging to distinctly quantify the weight loss solely associated with carbonates. In this study, the weight loss occurring within the temperature range of 400 °C to 600 °C is assigned to the thermal decomposition of magnesite,53 while the weight loss within the range of 600 °C to 800 °C is attributed to the thermal breakdown of serpentine.50,51 Since the phase identification analysis conducted using XRD does not detect the presence of any crystalline calcium carbonate phase such as calcite, the calculation of carbon mineralization efficiency is restricted to the formation of magnesite alone. Consequently, the carbon mineralization efficiency is calculated based on the weight loss between 400 °C to 600 °C. In the unreacted sample, weight loss of 3.79% is observed in the temperature range of 600 °C to 800 °C corresponding to the dehydroxylation of antigorite (Fig. 3(c-1)), as discussed in Section 3.1. The observed temperatures at which the major decomposition of antigorite into forsterite and silica occurs align well with existing literature.50,51 Weight loss in the temperature range of 400 °C to 600 °C in all products corresponds to the decomposition of MgCO3 to produce MgO and CO2. The associated weight losses for Cases I, II, and III are 10.92 ± 0.8%, 16.01 ± 1.4%, and 21.45 ± 2.3%, respectively (Fig. 3(c-2)–(c-4)). These weight losses are used to estimate the carbon mineralization efficiency. Notably, the percentage weight loss between 600 °C to 800 °C increases in Cases II and III compared to the unreacted sample. This observation can be attributed to the leaching of metals and other phases into the aqueous solution, resulting in serpentine becoming a more prominent phase in relation to the total weight of the sample. Also, XRD analysis shows reduced intensity or nearly complete disappearance of forsterite, resulting in serpentine as the predominant remaining mineral from the original sample.
X-ray photoelectron spectroscopy (XPS) survey scans were employed to examine the chemical states and surface compositions of unreacted serpentinized peridotite and the three carbon mineralization cases. XPS survey scans reveal that the relative intensities of Si exhibited slight variations, although they display qualitative similarities (Fig. 4). Notably, a significant disparity is observed in the Mg peak intensities between all three cases and the unreacted sample. Further analysis of the survey scans showed a decline in the Mg/Si atomic concentration ratio, with values of 1.56 for the unreacted sample, 0.84, 0.45, and 0.23 for Cases I, II, and III, respectively (Fig. 4). This observation suggests an enrichment of silica on the surface, which can be attributed to the initial incongruent dissolution of serpentine. This process involves the rapid exchange of Mg2+ and H+ ions from the octahedral brucite-type layer, leaving behind a silica-rich layer.54,55 Moreover, the re-precipitation of silica from the solution is expected to have contributed to the progressive thickening of the Si-rich layer on the unreacted particle surface. Previous studies have noted that elevated pH (>6) and temperature conditions (60–75 °C) can re-precipitate extracted silica from the solution during thermally activated serpentine dissolution.56–58 In our study, the pH of the solution after completion of the reaction was reported as 10.4, 9.2, and 9.04 for Cases I, II, and III, respectively (Table 2). It has also been observed that amorphous silica, a relatively soluble form of Si, tends to precipitate at lower temperatures (T < 90 °C), while the less soluble and thermodynamically stable quartz phase is favored at higher temperatures (T ≥ 90 °C).57,59 This re-precipitated silica layer covering the unreacted particles subsequently hinders the rate of magnesium extraction as the reaction progresses.56,57,59 Interestingly, the XRD analysis does not reveal the presence of any crystalline phase rich in silica, indicating the potential existence of a glassy SiO2 or Si-rich amorphous coating that may be increasingly prevalent from Case I to Case III. Additionally, in the unreacted sample, Mg is dispersed throughout the sample in the form of olivine and serpentine. However, as carbon mineralization progresses, Mg content preferentially precipitates as MgCO3 and concentrates as a singular mineral form as noted from the high-resolution scans of Mg 1s shown in Fig. 5(a-3)–(d-3). Further, the enrichment of the surface with silica is corroborated by the O/Si percentage atomic concentration ratio, which has a value of 3.84 for the unreacted sample, and subsequently decreases to 2.3 for Case III. This finding is further supported by SEM EDS analysis, as indicated in Fig. S1 (ESI†). The intermediate carbon mineralization reaction cases exhibit a gradual decrease in both the Mg/Si and O/Si ratios, in alignment with the evolving surface composition during the carbon mineralization process, as reported in Table S3 (ESI†).
Additional insights into the chemical evolution during carbon mineralization are obtained from high-resolution XPS elemental scans of individual elements such as silicon (Si), oxygen (O), carbon (C), and magnesium (Mg) (Fig. 5). The binding energies determined using XPS for high-resolution scans are listed in Table S3 (ESI†). Broad peaks in the spectra of all these elements indicate the coexistence of diverse chemical structures across all four samples. All the spectra are calibrated based on the adventitious carbon C–C (284.8 eV) peak.60,61 Additional carbon peaks ranging from 286.4 eV to 287 eV are identified as C–O–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds.61 Peaks observed between 289.5 eV and 289.7 eV are attributed to carbonate (CO32−) species.60–62 The CasaXPS curve resolution platform is used to analyze the peaks of interest using a combination of 30/70% Lorentzian/Gaussian functions, along with a Shirley background. The relative ratios of % atomic concentrations are determined using empirical sensitivity factors derived specifically for the XPS operating conditions employed in this study. The C 1s peak values at 289.6 eV, 289.9 eV, and 289.7 eV for Cases I, II and III, respectively, are indicative of the presence of MgCO3 in the carbonate-bearing samples.60,63 Notably, the intensity of the peak associated with carbonate exhibits a notable increase from Case I to III (Fig. 5(a-4)–(d-4)), signifying a higher concentration of MgCO3 in the samples as carbon mineralization progresses.
O bonds.61 Peaks observed between 289.5 eV and 289.7 eV are attributed to carbonate (CO32−) species.60–62 The CasaXPS curve resolution platform is used to analyze the peaks of interest using a combination of 30/70% Lorentzian/Gaussian functions, along with a Shirley background. The relative ratios of % atomic concentrations are determined using empirical sensitivity factors derived specifically for the XPS operating conditions employed in this study. The C 1s peak values at 289.6 eV, 289.9 eV, and 289.7 eV for Cases I, II and III, respectively, are indicative of the presence of MgCO3 in the carbonate-bearing samples.60,63 Notably, the intensity of the peak associated with carbonate exhibits a notable increase from Case I to III (Fig. 5(a-4)–(d-4)), signifying a higher concentration of MgCO3 in the samples as carbon mineralization progresses.
Deconvolution of the Si 2p core region results in a broad peak at the binding energy of 102.7 eV for unreacted serpentinized peridotite, as shown in Fig. 5(a-1). The Si 2p spectra of all cases are subjected to deconvolution, separating them into Si 2p3/2 and Si 2p1/2 peaks. The spin–orbit splitting parameters for Si 2p are assigned with atomic values, resulting in a separation of 0.617 eV between the two peaks, while the intensity of Si 2p1/2 is fixed at 50% of Si 2p3/2. Additionally, all peaks and their corresponding components are constrained to have identical fullwidth-at-half-maximum (fwhm) values. For the unreacted sample, the binding energies of the observed peaks for Si 2p1/2 and Si 2p3/2 are 102.1 eV and 102.9 eV, respectively which indicate the presence of serpentine in the form of Si–O–Mg–OH and olivine in the presence of silicate tetrahedra SiO4, respectively.55,60–66 As a result of carbon mineralization, a shift in the peak affiliated with Si 2p3/2 to a higher binding energy of approximately 103.2 eV is observed in Cases II and III, indicating a Si-rich surface layer of a SiO2 type silica. In addition, higher binding energies of 103.8, 103.9 and 104 eV for the Si 2p1/2 peaks in Cases I to III are also observed (Fig. 5(a-1)–(d-1)), which indicates the presence of a complex amorphous silica phase containing siloxane Si–O–Si and silanol Si–OH bonds.61
Evidence of multiple oxygen atom chemistries is also observed by deconvoluting the O 1s spectra shown in Fig. 5(a-2)–(d2). A weaker intensity O 1s peak at 530.57 eV is identified as the non-bridging OH–Mg–O–Si serpentine bond,55 while the O 1s binding energy around 531.4 eV is attributed to tetrahedral silicates in the forsterite surface group.55,60,61,63,65–67 In Cases I, II, and III, the respective O 1s binding energy peaks at 532.8, 532.61, and 532.65 eV are observed, which are higher than that of standard olivine (531.2 eV).64,67 This increase in binding energy suggests the presence of electronegative elements in close proximity to oxygen atoms, possibly indicating the existence of a silicon-rich amorphous phase comprising siloxane and silanol components. These findings align with the observations made with the Si 2p spectra. The carbonate-bearing products exhibit even higher binding energies for O 1s, measuring 533.26 eV, 533.74 eV, and 533.5 eV for Cases I–III, respectively, indicating the presence of Mg carbonates.68
In the Mg 1s core region (Fig. 5(a-3)–(d-3)), two peaks at 1303.8 eV and 1304.28 eV are noted for the unreacted sample. These peaks correspond to Mg species found in the serpentine and forsterite mineral phases of the raw sample.64,67 The trends noted for Mg 1s align well with those observed for Si 2p and O 1s, showing similar binding energy value ranges (1303.8–1304.28 eV and 1304.8–1305.6 eV) for unreacted and carbonate-bearing products. In the case of the carbonate-bearing samples (Cases I–III), the higher binding energies for Mg 1s indicate a slight oxidation of magnesium, suggesting the presence of carbonate species in the reacted sample.61,62
The Fe 2p region in both unreacted and carbonate-bearing samples exhibit an asymmetric shape with a significant split of approximately 13.1 eV between the spin orbit components Fe 2p1/2 and Fe 2p3/2 (Fig. S2, ESI†). The Fe 2p3/2 binding energy at approximately 710.4 eV aligns well with Mg-dominated olivine.67 The obtained Fe 2p spectra for the carbonate-bearing products show a slight shift of the Fe 2p3/2 peak towards higher energies, located at around 712.6, 712.4, and 711.49 for Cases I, II, and III, respectively. This shift implies a higher degree of iron oxidation at the surface of the carbonate-bearing samples, aligning with the formation of Fe2O3.62,67
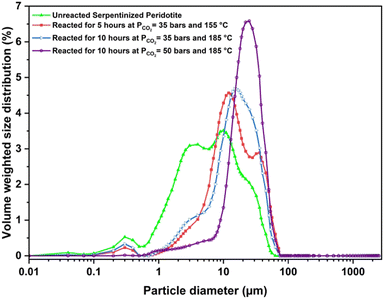
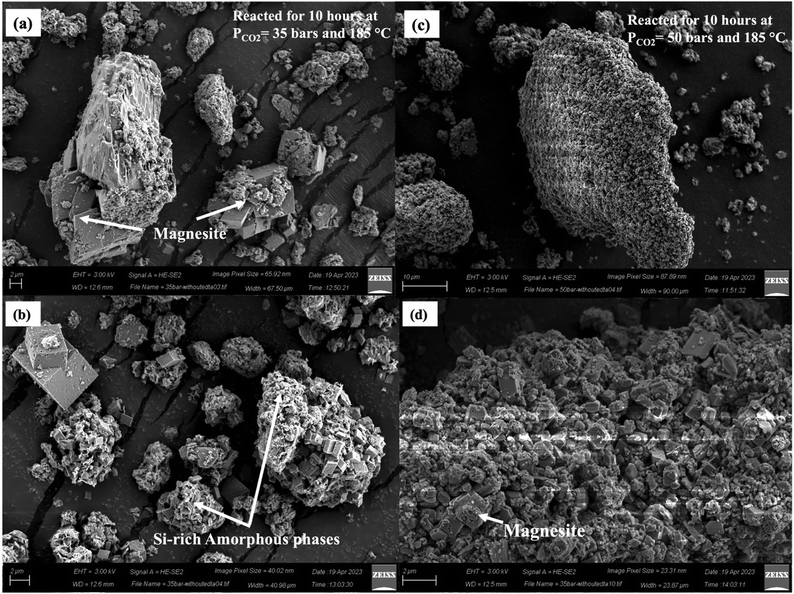
To delineate the morphological changes during the carbon mineralization reaction and the effect on mineral dissolution chemistries, the changes in the morphology of serpentinized peridotite on carbon mineralization, specifically focusing on surface area, particle size, and pore volume distributions are determined. Through a comparison of particle size distributions pre- and post-reaction in Case I, it is observed that fine particles with sizes smaller than 10 μm exhibit a higher dissolution rate in comparison to coarser grains. As a consequence, the particle size distribution becomes narrower, while the overall particle size increases (Fig. 6). Mean particle size of 17.85 μm is observed for Case I, which is considerably larger than the mean particle size of the unreacted sample (9.24 μm). Furthermore, the particle size distribution curve obtained in Case I exhibits a bimodal feature, indicating the presence of two prominent peaks (Fig. 6). This represents a shift from the multimodal curve observed in the particle size distribution of the unreacted sample, where different particle size populations co-existed. In Case II, where the reaction temperature is increased to 185 °C, a narrower range of grain size variability is observed compared to Case I. However, a simultaneous increase in the number of fines (particle size < 10 μm) is also observed in Case II relative to Case I. We hypothesize that this can be attributed to smaller silica particles that are detached from the surfaces of incongruently dissolved serpentine and olivine, or small newly nucleated magnesite crystals, as revealed by the SEM images (Fig. 7(c)). This trend aligns with the findings of Gadikota et al.28 for carbon mineralization of olivine at a reaction temperature of 90 °C. In Case III, which shows an extent of carbon mineralization of 73%, the size distribution is narrower and well defined with a mean particle size of 25.38 μm. An increase in the carbon mineralization efficiency achieved at higher pressure and temperature in Case III corresponds to a significant growth of magnesite crystals, leading to the formation of larger crystals. The morphological evolution of the CO2–water–rock system, as shown in Fig. 8, with increasing carbon mineralization efficiency and under variable reaction conditions, has a significant impact on the morphology, size, and shape of the magnesite crystals (Fig. 8 and 9). This aspect is further discussed in detail in Sections 4.2 and 4.3.
 | ||
| Fig. 8 Schematic representation of the reaction mechanism and morphological evolution of serpentinized peridotite during carbon mineralization with concurrent metal recovery. | ||
The effect of carbon mineralization and metal recovery on the pore volume and surface area of serpentinized peridotite is also investigated using the Brunauer–Emmett–Teller (BET) method with N2 adsorption at 77 K. The average pore size, surface area, and pore diameter of the unreacted and carbonate-bearing samples are summarized in Table 3. In Case I, the surface area and pore volume decrease from the initial values of 7.67 m2 g−1 and 0.021 cc g−1 to 5.53 m2 g−1 and 0.014 cc g−1, respectively. This reduction suggests the rapid dissolution of fine particles with high surface-to-volume ratios and the growth of carbonate precipitates. This finding aligns well with the earlier work on the direct carbon mineralization of olivine, where magnesium carbonate is produced.28,30
| Surface area (m2 g−1) | Pore volume (cc g−1) | Pore diameter (nm) | |
|---|---|---|---|
| Unreacted sample | 7.67 ± 1.08 | 0.021 ± 0.001 | 2.12 ± 0.001 |
| Case I | 5.53 ± 2.49 | 0.014 ± 0.006 | 2.85 ± 0.774 |
| Case II | 27.57 ± 0.86 | 0.093 ± 0.002 | 3.94 ± 0.001 |
| Case III | 4.71 ± 0.88 | 0.019 ± 0.003 | 2.97 ± 0.690 |
However, Case II exhibits a slightly different trend, where a significant increase in surface area and pore volume is noted compared to the unreacted sample (Table 3). This can be attributed to the presence of large intergrown clusters of magnesite and a Si-rich amorphous layer, a trend also observed in the SEM image of the carbonate-bearing sample for Case II (Fig. 7(c)). The higher temperature and the presence of the organic ligand Na2H2EDTA·2H2O promote enhanced growth and size modulation of magnesite crystals, resulting in larger particle size, and rapid formation of the Si-rich amorphous phase, leading to a higher surface area. This hypothesis is also supported with the experiments conducted in the absence of Na2H2EDTA·2H2O. The magnesite crystal size reduces significantly in the absence of Na2H2EDTA·2H2O, as shown in Fig. 10 (additional details are provided in Section 4.4).
Similar increases in surface area and pore volume have been observed in the carbon mineralization of fly ash and waste ash in the presence of monoethanolamine and sodium glycinate.69 Furthermore, as discussed earlier, the particle size distribution for Case II shows a higher number of fine particles compared to Case I, which contributes to the higher surface area observed in Case II. A similar observation should be expected for Case III. However, a decrease in the surface area to 4.71 m2 g−1 and pore volume to 0.019 cc g−1 is observed. SEM images of Case III reveal weathered and broken crystals of magnesite (Fig. 7(d) and Fig. S3, ESI†). The intergrown clusters of magnesite crystals and Si-rich amorphous phase are disrupted due to fluid saturation, resulting in reduced surface area and pore volume. Remarkably, Case III exhibited the highest carbon mineralization efficiency of 74%, along with notable metal recovery rates for Ni (81%) and Fe (33%). The elevated level of nickel recovery indicates enhanced dissolution of the native minerals present in the sample, which may have leached into the pore spaces of the Si-rich amorphous phase, potentially influencing the surface area and pore volume.
4 Discussion
4.1 Effect of chemical additives and mineral chemistry on integrated carbon mineralization and metal recovery
The influence of chemical additives, including bicarbonate compounds like NaHCO3, and organic ligands such as Na2H2EDTA·2H2O, have been investigated for their individual effects on carbon mineralization efficiency in direct carbon mineralization studies.2,8,22,28,30,31,48,70–74 It has been reported that the addition of 2 M NaHCO3 significantly enhances the carbon mineralization efficiency by approximately 50–60%.8,28 Upon dissolution in the aqueous phase, NaHCO3 dissociates to produce bicarbonate ions (R2). The dissociation and transformation of NaHCO3 to carbonate ion results in generation of local protons (see R2–R4). Further, the high pH of this system also promotes the reaction of hydroxide ion with CO2, leading to formation of bicarbonate ions while promoting CO2 hydration (R3). Thus, NaHCO3 facilitates CO2 hydration and olivine dissolution during the carbon mineralization process.8| NaHCO3 → HCO3− + Na+ | (R2) |
| OH− + CO2 → HCO3− | (R3) |
| HCO3− → CO32− + H+ | (R4) |
In addition to aiding dissolution and carbonate formation, NaHCO3 enhances the diffusion of aqueous silica and prevents iron oxide precipitation on the reactive mineral surface to accelerate carbon mineralization.28,30,71 The introduction of Na2H2EDTA·2H2O into the system facilitate the presence of HEDTA3− ions, which have been reported to be the dominant EDTA species at pH 7–10 and the pH range at which the carbon mineralization process is occurring (R6).8,73–76 The formation of HEDTA3− ions facilitates a catalytic effect on carbon mineralization due to their chelation effect (R7).73,74 Thus, NaHCO3 and Na2H2EDTA·2H2O creates a buffered system, contributing to the regulation of pH for mineral dissolution, metal chelation, and magnesium carbonate precipitation as shown in reactions, R5–R8 below.
| NaHCO3− + OH− + CO2 → 2CO32− + 2H+ + Na+ | (R5) |
| Na2H2EDTA·2H2O → HEDTA3− + H+ + 2Na+ + 2H2O | (R6) |
| (Mg,Fe)SiO4(s) + 4Haq+ + HEDTA3− → Mgaq2+ + [Fe(HEDTA)](aq)− + SiO2(aq) + 2H2O | (R7) |
| Mgaq2+ + CO32− → MgCO3 | (R8) |
Also, Na2H2EDTA·2H2O, containing a diamine group, possesses a strong affinity towards CO2, thereby facilitating CO2 hydration.77,78 Primary diamines, like ethylenediamine, exhibit high CO2 adsorption capacity compared to other amines and CO2 can be bound as bicarbonate, carbonate, carbamate or dicarbamate during chemical adsorption of CO2 in aqueous diamine systems.79 In this study, an optimum Na2H2EDTA·2H2O dosage of Na2H2EDTA·2H2O/TNi = 2 and 2 M NaHCO3 were maintained throughout all experimental conditions.1,8 The addition of Na2H2EDTA·2H2O increased carbon mineralization efficiencies from 39% and 69% to 48% and 73% for Case II and Case III, respectively. Thus, the combination of NaHCO3 and Na2H2EDTA·2H2O can create a buffered system and foster a catalytic effect for enhancing carbon mineralization while facilitating metal recovery.1
In contrast to previous studies that employed EDTA for enhanced mineral dissolution,49,54,73 our research focused on the metal extraction from minerals with the controlled Na2H2EDTA·2H2O dosage. The findings, as discussed in Section 3.2 and presented in Fig. 3(a), reveal that the extraction efficiency of Ni with 0.1 M Na2H2EDTA·2H2O is significantly higher compared to the extraction of other metals. This discrepancy can be attributed to the higher stability constant of Ni–EDTA relative to that of Mg–EDTA, and Ca–EDTA, leading to the preferential formation of Ni–EDTA complexes (Table S4, ESI†). In contrast, the Mg2+ ions originating from dissolved serpentine and olivine tend to precipitate as stable mineral carbonates when exposed to limited amounts of Na2H2EDTA·2H2O in the solution owing to their least stable complex with Na2H2EDTA·2H2O compared to other common multivalent cations (Table S4, ESI†).
Despite chromium (Cr3+) having a stability constant of 23.4 (Table S4, ESI†), which surpasses that of Ni–EDTA, we observe a very low concentration of Cr3+ in the post-carbon mineralization liquid samples even though the raw sample has more chromium content (3154 ppm) than nickel (2547 ppm). Numerous previous studies, such as those conducted by Terzano et al.,80 Jean-Soro et al.,81 and Jean et al.,82 have reported similar trends in the leaching efficiencies of Ni and Cr by EDTA, supporting the notion that Ni is more effectively leached by EDTA compared to Cr. Therefore, the effectiveness of EDTA in leaching Cr is not directly influenced by the thermodynamics of complexation. Rather, it can be attributed to Cr phases within different mineralogical structure of the host rock. Cr primarily resides in highly refractory chromite or chrome spinel minerals in the ultramafic rocks of ophiolitic settings, while Ni is predominantly present in serpentine, trevorite, or Ni-spinel type minerals.39,83,84 The studied sample, belonging to the Mayodia ophiolitic sequence, exhibits economically valuable chrome spinel minerals (Mg,Fe)2+(Cr,Al,Fe)23+O4.84–86 It comprises Cr-rich chlorite inclusions embedded within a matrix consisting of Cr-rich serpentine. Additionally, the sample displays notable compositional enrichment in Cr and Fe species in the form of ferrous chromite.84,86 Furthermore, as discussed in Section 3.3, XPS spectra of the Fe 2p region for the unreacted sample show the presence of the Fe2+ state, while the carbonate-bearing samples of all cases exhibit a shift in the binding energy towards higher values, indicating a higher degree of iron oxidation at the surface of the carbonate-bearing samples, consistent with the formation of Fe2O3. The low Ksp values reported for Fe3+ ions hinder their dissolution, possibly explaining the slow leaching of Fe from the carbonate-bearing samples.87 Consequently, the slow leaching of Cr and Fe corresponds to the slow dissolution of the mineral matrix, most likely involving chrome spinel and iron oxide dissolution. As indicated in Table S5 (ESI†), minerals such as bunsenite, heazlewoodite, trevorite, and Ni-spinel with lower formation constants and less negative Gibbs free energy values exhibit a higher propensity for dissolution compared to chromite, which possesses higher formation constants. The potential influence of higher Na2H2EDTA·2H2O dosages on the leaching of iron or chromium into the solution remains an intriguing aspect for future investigation. Increasing the dosage of Na2H2EDTA·2H2O could potentially enhance the dissolution of Fe or Cr-containing minerals, leading to a greater release of these metals into the solution.
4.2 Morphological evolution during direct carbon mineralization with concurrent metal recovery
A qualitative morphological analysis of surfaces of unreacted and carbonate-bearing samples using SEM provide detailed insights into the morphological transformations during carbon mineralization and metal recovery. Prior to the reaction, the surface of the forsterite powder appears featureless or displays the typical texture resulting from the conchoidal fracturing of ground olivine88 (Fig. 7(a)). However, after the reaction (Case I), distinct features emerged on the surfaces of the olivine particles. These features include elevated regions (referred to as mammillary structures),89,90 tooth-like edges (known as denticular margins),90 and small cavities (etch pits)89,91 (Fig. 7(b)). These structures have been previously observed in experiments studying natural olivine dissolution92 and in naturally weathered samples.89,91 The formation of such structures is attributed to the anisotropic nature of olivine dissolution, wherein certain surfaces are preferentially dissolved. However, the exact mechanism governing the rate-determining step based on crystallographic orientation is still not fully understood.90,93 The morphological examination of the carbonate-bearing sample in Case II revealed that the formation of elevated regions (humps) during the experiments exhibited a dependence on crystallographic orientation, as they are observed only on specific surfaces of individual grains. Fig. 7(b) illustrates mammillary structures pointing in one direction on a particular surface of the reacted particles, coinciding with the nucleation of magnesite crystals.X-ray diffraction analyses reveal the presence of forsterite, serpentine, and magnesite crystallographic phases in carbonate-bearing samples. However, field-emission scanning electron microscopy (FESEM) of the carbon mineralization products unveils two distinct particle morphologies: well-ordered structures and irregular-shaped particles, as shown in Fig. 7(c) and (d). These ordered and irregular-shaped particles are often observed individually but are also found intergrown in the clusters. Energy-dispersive X-ray spectroscopy (EDS) (Fig. S1(a)–(d) ESI†) confirms that the irregular particles exhibit strong signals for Si and O, consistent with silica, while the polyhedral crystals display strong signals for Mg and O, indicative of magnesite. The EDS analysis of the amorphous material indicates the presence of a significant silicon peak, suggesting that this phase is enriched in silica.94 However, there are still detectable but reduced amounts of Mg and Fe, indicating the presence of the original olivine within this amorphous phase. The presence of silica in the amorphous layer is also supported by the XPS analysis of individual spectra of the Si 2p and O 1s peaks revealing the presence of a complex matrix containing Si–O–Si and Si–OH (Fig. 5(a-1)–(d-1) and (a-2)–(d-2)). The formation of this Si-rich amorphous layer can be associated with the initial rapid incongruent dissolution of serpentine or Si re-precipitation from the solution phase post-dissolution of serpentine or olivine.28,54–56,75 Serpentine is a mineral composed of sheet-like structures, characterized by a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 arrangement resulting from the alternating layers of SiO4 tetrahedra and Mg octahedral brucite-type layers. These layers are interconnected through –Si–O–Si– bonds. Notably, the brucite-like layer exhibits higher reactivity and dissolves at a faster rate compared to the adjacent Si-rich tetrahedral layer.40,54,95 Therefore, the dissolution of serpentine is hypothesized to occur through the rapid breakdown of Mg-octahedral brucite-like layers (Fig. 8(a)). Subsequently, the dissolution of the highly polymerized silica sheets takes place at a slower rate, acting as the controlling factor in the process. This observation agrees with the previous observations of the concentrations of dissolved Mg2+ ions, which are approximately twice as high as those of Si in serpentine dissolution experiments conducted with a reaction time of 6–10 hours in the presence of 0.5 M Na3Citrate at 120 °C under 20 bars of PCO2.96 Previous studies90,97,98 have postulated the existence of a Mg-depleted gel-like glassy SiO2 layer, commonly known as a silica-rich passivating layer, that remains on the mineral surface during the process of mineral dissolution. It has been observed that the thickness of this layer increases as the re-precipitation of Si from the solution phase and serpentine dissolution continues over time (Fig. 8(b)). Furthermore, EDS analyses in Fig. S1 (ESI†) indicate the absence of a pure amorphous silica phase devoid of Mg. Two possible explanations can be proposed to elucidate the consistent occurrence of Mg in the amorphous phase, as suggested by Schulze et al.55 First, the reaction does not reach complete conversion, resulting in the formation of a mixed Mg–Si oxide as a by-product. Second, as previously discussed, the initial stage of the reaction involves the disintegration of the serpentine crystal structure, starting from the brucite-like layer leaving behind a Si-rich amorphous layer. As the reaction proceeds, magnesite grows from this amorphous product, with the diffusion of Mg2+ ions out of the amorphous phase, which could potentially serve as the rate-limiting step (Fig. 8(b)).
1 arrangement resulting from the alternating layers of SiO4 tetrahedra and Mg octahedral brucite-type layers. These layers are interconnected through –Si–O–Si– bonds. Notably, the brucite-like layer exhibits higher reactivity and dissolves at a faster rate compared to the adjacent Si-rich tetrahedral layer.40,54,95 Therefore, the dissolution of serpentine is hypothesized to occur through the rapid breakdown of Mg-octahedral brucite-like layers (Fig. 8(a)). Subsequently, the dissolution of the highly polymerized silica sheets takes place at a slower rate, acting as the controlling factor in the process. This observation agrees with the previous observations of the concentrations of dissolved Mg2+ ions, which are approximately twice as high as those of Si in serpentine dissolution experiments conducted with a reaction time of 6–10 hours in the presence of 0.5 M Na3Citrate at 120 °C under 20 bars of PCO2.96 Previous studies90,97,98 have postulated the existence of a Mg-depleted gel-like glassy SiO2 layer, commonly known as a silica-rich passivating layer, that remains on the mineral surface during the process of mineral dissolution. It has been observed that the thickness of this layer increases as the re-precipitation of Si from the solution phase and serpentine dissolution continues over time (Fig. 8(b)). Furthermore, EDS analyses in Fig. S1 (ESI†) indicate the absence of a pure amorphous silica phase devoid of Mg. Two possible explanations can be proposed to elucidate the consistent occurrence of Mg in the amorphous phase, as suggested by Schulze et al.55 First, the reaction does not reach complete conversion, resulting in the formation of a mixed Mg–Si oxide as a by-product. Second, as previously discussed, the initial stage of the reaction involves the disintegration of the serpentine crystal structure, starting from the brucite-like layer leaving behind a Si-rich amorphous layer. As the reaction proceeds, magnesite grows from this amorphous product, with the diffusion of Mg2+ ions out of the amorphous phase, which could potentially serve as the rate-limiting step (Fig. 8(b)).
The progressive increase in the thickness of the Si-rich amorphous layer serves as an impediment, restraining the subsequent mechanism by hindering the diffusion and exchange of reactive species such as Mg2+ and H+.55,90,97 This observation substantiates the presence of Mg within the Si-rich amorphous phase, thereby limiting the formation of pure SiO2. Additionally, it accounts for the common occurrence of isolated magnesite crystals exhibiting a minimal encircling amorphous phase.55 Specifically, Mg diffuses out of the amorphous phase, resulting in the formation of magnesite at the periphery, rather than the expulsion of SiO2 from the growing magnesite, as observed in Fig. 7(c) and (d). The diffusion of Mg from this intricate Si–O–Si–OH amorphous phase is considered to be the rate-limiting step in the carbon mineralization reaction of natural samples comprising serpentine as a primary mineral alongside olivine. It is noteworthy that not only Mg, but also trace metals like Fe or Cr, can become entrapped within this amorphous phase. The SEM-EDS analysis (Fig. S1, ESI†) shows the presence of Cr and Fe within the amorphous silica phase. Furthermore, the continuous reaction leads to the exfoliation of the Si-rich amorphous layer (Fig. 8(c)) from the surface of the olivine due to volumetric differences and resulting stresses between the olivine crystal and the layer depleted of Mg and O.70,98,99 The exfoliation rate depends on the thickness of the passivation layer. The hydrothermal deposition of silica is known to contribute to the irregular surface morphology of the amorphous layer, leading to the formation of brittle silica.97 Hence, the combination of brittle silica and interfacial stresses renders silica-rich passivating layers highly prone to fracture and exfoliation. This cyclic process continues until the amorphous layer reaches a critical threshold, inducing stresses that lead to the detachment of the silica layer. The exfoliation of the silica layer creates pathways for the exchange of Mg2+, H+, CO32− species, and HEDTA3−, enabling the extraction of trace metals from the dissolved minerals (Fig. 8(c)).
To validate the proposed step-by-step mechanism, we conducted experiments under the best-case scenario (Case III) with varying reaction times of 1 hour, 3 hours, and 6 hours and observed the morphological changes, as shown in Fig. 9 and Fig. S4 (ESI†). During the initial hour of the reaction, complete coverage of the particles with an amorphous layer is observed, indicating the rapid dissolution of serpentine at the onset of the reaction (Fig. 9(a) and (b)). The presence of some magnesite crystals on the surface can be attributed to the incongruent dissolution process, where specific constituents migrate rapidly. In this case, Mg diffuses quickly into the aqueous phase, leaving behind a silicon-enriched layer and forming few magnesite crystals. Following this initial stage of incongruent dissolution, the subsequent dissolution is anticipated to proceed uniformly and congruently. As the reaction time is increased from 1 hour to 3 hours, the carbon mineralization efficiency increases from 44% to 63%, indicating an enhanced diffusion of Mg over time from the silica-rich amorphous phase. This observation supports the hypothesis that the exfoliation of the amorphous layer allows for the re-exposure of unreacted olivine, facilitating the carbon mineralization process. However, the extraction efficiencies of Ni and Fe did not show significant improvement, remaining at 39% and 18%, respectively, for the 1 hour reaction duration, and increasing only slightly to 41% and 20% for the 3 hours reaction duration. Thus, in the short-duration experiments, carbon mineralization is the preferred reaction over metal recovery. After reaction for 6 hours, a gradual increase in the thickness of the Si-rich passivating layer and the number of magnesite crystals is observed, as shown in Fig. 9(e), resulting in a carbon mineralization efficiency of 70%. However, no significant improvement in carbon mineralization efficiency is observed beyond 6 hours of reaction time with a carbon mineralization efficiency of 73% being observed after 10 hours. This indicates that almost all of the serpentines have dissociated, and the mass transfer limitation becomes more prominent due to slower exfoliation of the Si-rich amorphous layer and a low concentration of free magnesium ions.100 It is important to note that in contrast to slower carbon mineralization efficiencies after longer reaction times, the Ni recovery efficiency continues to increase rapidly, reaching 61% and 81% for 6 hours and 10 hours, respectively. Similarly, the Fe recovery efficiency increased to 22% and 33% for the corresponding reaction times. Hence, it can be concluded that, given sufficient time, carbon mineralization and metal recovery processes are equally facilitated through chemical and morphological evolution of the Mg-silicate mineral substrates.
4.3 Effect of reaction kinetics on the morphology of the magnesite crystals
Magnesium carbonate is consistently formed in all experiments. Case II exhibits well-defined, sharp-faced euhedral rhombohedral magnesite crystals (Fig. 7(c)), while Case III shows weathered corners and surfaces of the magnesite crystals (Fig. 7(d)). The morphology of the large Mg carbonate crystals is found to be dependent on the saturation level of the CO2–fluid–mineral system. Increasing the CO2 partial pressure from 35 bars (Case II) to 50 bars (Case III) results in a significant alteration in the crystal morphology, transitioning from well-defined edges and smooth faces to fractured and worn-out corners. Prior studies attribute such weathered surfaces to high stirring speeds and particle–particle/particle–wall collisions during the reaction process.94,97 However, in our experiments, both Cases II and III are conducted at identical stirring speeds of 500 rpm. Thus, this weathering phenomenon is not attributed to stirring speed but to other factors.To probe this phenomenon further, we conducted additional experiments under conditions similar to Case II with a constant CO2 partial pressure of 35 bars and stirring speed of 500 rpm, while extending the reaction time to 18 hours. The carbon mineralization efficiency increases to 82.36% and significant changes in crystal morphology (Fig. S5, ESI†) are observed compared to Case II with a carbon mineralization efficiency of approximately 49%. This suggests that the degradation of magnesite particles is influenced by CO2 hydration, which increases with longer reaction times. Interestingly, the morphology of magnesite crystals obtained at CO2 partial pressure of 50 bars and reaction durations of 1 hour (CETCA = 44%) and 3 hours (CETCA = 63%) (Fig. 9(a)–(d)) closely resemble the morphology observed in reactions conducted at a CO2 partial pressure of 35 bars and a reaction duration of 10 hours (Fig. 7(c)) (Case II) (CETCA = 49%). This observation highlights a strong correlation between the magnesite crystal morphology and carbon mineralization efficiency. In summary, our findings demonstrate that the morphology of Mg carbonate crystals is influenced by the saturation level of the CO2–fluid–mineral system, which is facilitated under high CO2 partial pressure conditions and longer reaction times with all other conditions remaining unchanged. This observation can be expressed from another perspective of aging. The aging process of carbonate crystals exhibits a direct correlation with the increasing efficiency of carbon mineralization. The observed changes in crystal morphology emphasize the need for tuning the carbon mineralization process to achieve the desired crystal structures and maximize the efficiency of carbon mineralization.
4.4 Effect of Na2H2EDTA·2H2O on the morphology of the magnesite crystals
The introduction of Na2H2EDTA·2H2O has a notable positive effect on both the carbon mineralization efficiency and the size and morphology of magnesite crystals. In the absence of Na2H2EDTA·2H2O, the carbon mineralization efficiencies for Case II and Case III decreased to 39% and 69% from their respective values of 48% and 73%. Fig. 10 and Fig. S6 (ESI†) show the SEM and EDS analyses, respectively, of the carbonate-bearing product for Case II and Case III without Na2H2EDTA·2H2O. Particularly for Case III, where the partial pressure of CO2 is maintained at 50 bars and the temperature at 185 °C, the magnesite crystals are observed to have a size smaller than 2 μm in the absence of Na2H2EDTA·2H2O (Fig. 10(c) and (d)). However, in Case III with Na2H2EDTA·2H2O, larger magnesite crystals with dimensions on the order of 10 μm are observed (Fig. 7(d)). This observation is further supported by the particle size distribution analysis for Case II and Case III in the absence of Na2H2EDTA·2H2O (Fig. S6, ESI†). The mean particle size decreases to 9.54 μm and 10.73 μm from the values of 19.17 μm and 25.38 μm for Case II and Case III, respectively, in the absence of Na2H2EDTA·2H2O. Also, we observe a well-distributed and well-sorted particle size distribution of carbonate-bearing mineral when Na2H2EDTA·2H2O is present in the CO2–fluid–mineral system (Fig. 6). However, in the absence of Na2H2EDTA·2H2O, the grain size distribution of carbonate-bearing particles was bimodal and poorly sorted, as shown in Fig. S6 (ESI†). As discussed in Section 4.1, Na2H2EDTA·2H2O, containing a diamine group, possesses a strong affinity towards CO2, thereby facilitating CO2 hydration and promoting enhanced growth and size modulation of magnesite crystals. It has been shown that EDTA and its disodium salts exhibit stability to heat, even up to 190–200 °C.101 Beyond 200 °C, decomposition occurs in the presence of metal ions, leading to the formation of iminodiacetate and other degradation products.102 The decomposition of Na2H2EDTA·2H2O can also be influenced by factors such as acidity and the reaction medium. In instances of a strong acidic environment, such as hydrochloric acid in the presence of 1,2-phenylenediamine, the decomposition of EDTA may occur at a moderately lower temperature of 110 °C.101 Consequently, Na2H2EDTA·2H2O is a viable option for use in carbon mineralization studies, and it can be recycled as long as temperatures below 190 °C are employed. The presence of Na2H2EDTA·2H2O likely facilitates the formation of more favorable reaction environments, fostering the efficiency of carbon mineralization and growth of larger magnesite crystals.5 Conclusions
This study presents a comprehensive investigation into concurrent recovery of energy critical metals and carbon mineralization of serpentinized peridotite using organic ligands such as Na2H2EDTA·2H2O through a direct carbon mineralization process. Calibrated tuning of the physico-chemical parameters such as CO2 partial pressure, reaction temperature, and reaction time unlocked fundamental insights into the chemo-morphological transformations associated with observed carbon mineralization and metal recovery efficiencies.The best-case scenario for achieving maximum carbon mineralization efficiency was observed at 185 °C, CO2 partial pressure of 50 bars, a reaction time of 10 hours in an aqueous fluid with 2 M NaHCO3 plus 0.1 M Na2H2EDTA·2H2O at a stirring rate of 500 rpm and slurry composition of 15 wt%. At these conditions, a carbon mineralization efficiency of 73% and nickel and iron extraction efficiencies of 81% and 33%, respectively, were achieved for serpentinized peridotite. Additionally, significant morphological changes were observed in the reacted rocks, with a shift in particle size distribution towards larger sizes and faster dissolution of particles smaller than 10 μm. The mean particle size was found to be directly proportional to the carbon mineralization efficiency. Weathering of the magnesite crystals was also observed with increasing carbon mineralization efficiency, indicating a direct relationship between efficiency and the aging of the magnesite crystals.
A thorough investigation into the reaction mechanisms and morphological evolution during the metal recovery and carbon mineralization process of serpentinized peridotite revealed that these multiphase chemical reactions proceed via the following major steps:
(1) Initial incongruent dissolution of serpentine, with rapid exchange of Mg2+ and H+ cations, results in a silica-rich gel-like layer forming on the surface of the unreacted sample.
(2) Diffusion of Mg2+ ions and other critical metals out of the complex amorphous silica layer, accompanied by the exchange of H+ and CO32− ions, which becomes the rate-limiting step.
(3) Exfoliation of the amorphous silica layer due to stresses between the reaction layer and olivine, leading to the re-exposure of unreacted olivine and an increase in carbon mineralization efficiency in longer duration experiments.
(4) Saturation of the CO2–fluid–mineral system, resulting in the erosion of corner edges and defects on the surface of magnesite crystals at higher carbon mineralization efficiencies.
Organic ligands such as Na2H2EDTA·2H2O facilitated solvation of nickel and iron in serpentinized peridotite while enabling carbon mineralization to produce magnesite. Conditions that favor high carbon mineralization extents also enable high recovery efficiencies of nickel and iron. HEDTA3− forms more stable complexes with nickel and iron compared to magnesium ions, which facilitates the partitioning of nickel and iron into the solution phase, while precipitating magnesite. Furthermore, the presence of Na2H2EDTA·2H2O improved the morphology and crystal size of the formed magnesium carbonates. These results unlock the feasibility of using suitable ligands for the co-recovery of energy critical metals from complex mineral substrates while enabling carbon mineralization.
Author contributions
Shreya Katre: writing – original draft, concept, data curation, formal analysis, investigation, methodology, validation; Prince Ochonma: writing – review & editing, formal analysis, investigation, methodology, validation; Hassnain Asgar: writing – review & editing, formal analysis; Archana M Nair: writing – review & editing, supervision, conceptualization, formal analysis; Ravi K: writing – review & editing, supervision, conceptualization; Greeshma Gadikota: writing – concept, review & editing, supervision, conceptualization, resources, formal analysis.Conflicts of interest
G. G. is the co-founder of Carbon To Stone, a company focused on commercializing technologies for industrial decarbonization.Acknowledgements
This research was supported by the Fulbright-Kalam climate Fellowship to S. K. (Award No. 2737/FKDR/2022-2023) funded by the United States-India Educational Foundation (USIEF) and the Institute of International Education (IIE). All the analytical lab work has been performed at the School of Civil and Environmental Engineering, Cornell University. The authors acknowledge the use of facilities and instrumentation supported by NSF through the Cornell University Materials Research Science and Engineering Center DMR-1719875. Authors are thankful to Cornell Soil Health Laboratory for ICP-AES and TCA analysis, and to Hamilton Analytical Laboratory for XRF analysis. Besides, the authors gratefully acknowledge Adnan Ahmed (Guwahati) and Dr Biraj Borgohain (Mumbai) for providing the sample used in the study. S. K. would also like to thank the Indian Institute of Technology, Guwahati for providing the necessary research facilities. P. O.’s efforts are supported by the Link Energy Fellowship. G. G. acknowledges the support of a DOE CAREER Award from the Office of Basic Energy Sciences (Award #: DE-SC0020263), Cornell SPROUT Award awarded in Spring 2023, and ARPA-E MINER Program (Award #: DE-AR0001721) for enabling this effort.References
- F. Wang and D. Dreisinger, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2203937119 CrossRef CAS PubMed
.
- F. Wang, D. Dreisinger and Y. Xiao, J. Cleaner Prod., 2023, 393, 136345 CrossRef CAS
.
- F. Wang and D. Dreisinger, Sep. Purif. Technol., 2023, 321, 124268 CrossRef CAS
.
- R. Castro-Amoedo, J. Granacher, M. Abou Daher and F. Maréchal, Energy Environ. Sci., 2023, 16, 4356–4372 RSC
.
- R. M. Santos, A. Van Audenaerde, Y. W. Chiang, R. I. Iacobescu, P. Knops and T. Van Gerven, Metals, 2015, 5, 1620–1644 CrossRef
.
- A. Sanna, M. Uibu, G. Caramanna, R. Kuusik and M. Maroto-Valer, Chem. Soc. Rev., 2014, 43, 8049–8080 RSC
.
- S. Wilson and J. L. Hamilton, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2212424119 CrossRef CAS PubMed
.
- F. Wang, D. Dreisinger, M. Jarvis and T. Hitchins, Miner. Eng., 2019, 131, 185–197 CrossRef CAS
.
- P. Ochonma, C. Blaudeau, R. Krasnoff and G. Gadikota, Front. Energy Res., 2021, 9, 742323 CrossRef
.
- P. Ochonma, C. Noe, S. Mohammed, A. Mamidala and G. Gadikota, React. Chem. Eng., 2023, 8, 1943–1959 RSC
.
- S. Zhang, Z. Ghouleh, A. Mucci, O. Bahn, R. Provençal and Y. Shao, J. Cleaner Prod., 2022, 342, 130948 CrossRef CAS
.
- S. Stopic, C. Dertmann, I. Koiwa, D. Kremer, H. Wotruba, S. Etzold, R. Telle, P. Knops and B. Friedrich, Metals, 2019, 9, 708 CrossRef CAS
.
- P. Ochonma, X. Gao and G. Gadikota, Acc. Chem. Res., 2024, 57, 267–274 CrossRef CAS PubMed
.
- R. Zhang, A. Arrigoni and D. K. Panesar, Cem. Concr. Compos., 2021, 124, 104263 CrossRef CAS
.
- H. Ostovari, L. Muller, J. Skocek and A. Bardow, Environ. Sci. Technol., 2021, 55, 5212–5223 CrossRef CAS PubMed
.
- J. Skocek, M. Zajac and M. Ben Haha, Sci. Rep., 2020, 10, 5614 CrossRef CAS PubMed
.
- X. Wang, W. Conway, R. Burns, N. McCann and M. Maeder, J. Phys. Chem. A, 2010, 114, 1734–1740 CrossRef CAS PubMed
.
- A. Awad, A. K. Van Groos and S. Guggenheim, Geochim. Cosmochim. Acta, 2000, 64, 1765–1772 CrossRef CAS
.
- E. H. Oelkers, Chem. Geol., 2001, 175, 485–494 CrossRef CAS
.
- D. E. Giammar, R. G. Bruant Jr and C. A. Peters, Chem. Geol., 2005, 217, 257–276 CrossRef CAS
.
- M. Hänchen, V. Prigiobbe, G. Storti, T. M. Seward and M. Mazzotti, Geochim. Cosmochim. Acta, 2006, 70, 4403–4416 CrossRef
.
-
G. Gadikota and A.-H. A. Park, Carbon Dioxide Utilisation, Elsevier, 2015, pp. 115–137 Search PubMed
.
- E. C. La Plante, I. Mehdipour, I. Shortt, K. Yang, D. Simonetti, M. Bauchy and G. N. Sant, ACS Sustainable Chem. Eng., 2021, 9, 10727–10739 CrossRef CAS
.
- M. Hänchen, V. Prigiobbe, R. Baciocchi and M. Mazzotti, Chem. Eng. Sci., 2008, 63, 1012–1028 CrossRef
.
- G. D. Saldi, J. Schott, O. S. Pokrovsky, Q. Gautier and E. H. Oelkers, Geochim. Cosmochim. Acta, 2012, 83, 93–109 CrossRef CAS
.
- S. R. Gislason, D. Wolff-Boenisch, A. Stefansson, E. H. Oelkers, E. Gunnlaugsson, H. Sigurdardottir, B. Sigfusson, W. S. Broecker, J. M. Matter and M. Stute,
et al.
, Int. J. Greenhouse Gas Control, 2010, 4, 537–545 CrossRef CAS
.
- I. M. Power, A. L. Harrison, G. M. Dipple, S. Wilson, P. B. Kelemen, M. Hitch and G. Southam, Rev. Mineral. Geochem., 2013, 77, 305–360 CrossRef CAS
.
- G. Gadikota, J. Matter, P. Kelemen and A.-H. A. Park, Phys. Chem. Chem. Phys., 2014, 16, 4679–4693 RSC
.
-
G. Gadikota, K. Fricker, S.-H. Jang and A.-H. A. Park, in Advances in CO2 Capture, Sequestration, and Conversion, ACS Publications, 2015, pp. 295–322 Search PubMed
.
- G. Gadikota, J. Matter, P. Kelemen, P. V. Brady and A.-H. A. Park, Fuel, 2020, 277, 117900 CrossRef CAS
.
- J. Li, M. Hitch, I. M. Power and Y. Pan, Minerals, 2018, 8, 147 CrossRef
.
- S. J. Gerdemann, W. K. O’Connor, D. C. Dahlin, L. R. Penner and H. Rush, Environ. Sci. Technol., 2007, 41, 2587–2593 CrossRef CAS PubMed
.
- A. A. Olajire, J. Pet. Sci. Eng., 2013, 109, 364–392 CrossRef CAS
.
- P. B. Kelemen and J. Matter, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17295–17300 CrossRef CAS
.
- P. B. Kelemen, J. Matter, E. E. Streit, J. F. Rudge, W. B. Curry and J. Blusztajn, Annu. Rev. Earth Planet. Sci., 2011, 39, 545–576 CrossRef CAS
.
- S. R. Scott, K. W. Sims, B. R. Frost, P. B. Kelemen, K. A. Evans and S. M. Swapp, Geochim. Cosmochim. Acta, 2017, 215, 105–121 CrossRef CAS
.
- J. Olsson, S. Stipp and S. Gislason, Mineral. Mag., 2014, 78, 1479–1490 CrossRef
.
- J. M. Morrison, M. B. Goldhaber, C. T. Mills, G. N. Breit, R. L. Hooper, J. M. Holloway, S. F. Diehl and J. F. Ranville, Appl. Geochem., 2015, 61, 72–86 CrossRef CAS
.
- A. Dey, M. F. Hussain and M. N. Barman, Geosci. Front., 2018, 9, 517–529 CrossRef CAS
.
- F. Zaccarini, A. K. Singh and G. Garuti, Can. Mineral., 2016, 54, 409–427 CrossRef CAS
.
- J. L. Hamilton, S. Wilson, B. Morgan, C. C. Turvey, D. J. Paterson, S. M. Jowitt, J. McCutcheon and G. Southam, Int. J. Greenhouse Gas Control, 2018, 71, 155–167 CrossRef CAS
.
- J. L. Hamilton, S. A. Wilson, B. Morgan, A. L. Harrison, C. C. Turvey, D. J. Paterson, G. M. Dipple and G. Southam, Econ. Geol., 2020, 115, 303–323 CrossRef
.
- J. L. Hamilton, S. Wilson, B. Morgan, C. C. Turvey, D. J. Paterson, C. MacRae, J. McCutcheon and G. Southam, Int. J. Greenhouse Gas Control, 2016, 55, 73–81 CrossRef CAS
.
- P. B. Kelemen, N. McQueen, J. Wilcox, P. Renforth, G. Dipple and A. P. Vankeuren, Chem. Geol., 2020, 550, 119628 CrossRef CAS
.
- K. Kashefi, A. Pardakhti, M. Shafiepour and A. Hemmati, J. Environ. Chem. Eng., 2020, 8, 103638 CrossRef CAS
.
- G. Sim, S. Hong, S. Moon, S. Noh, J. Cho, P. T. Triwigati, A.-H. A. Park and Y. Park, J. Environ. Chem. Eng., 2022, 10, 107327 CrossRef CAS
.
- Y. Gao, X. Jin, L. Teng, S. Rohani, M. He, J. Li, S. Ren, Q. Liu, J. Huang and H. Duan,
et al.
, Fuel, 2023, 331, 125750 CrossRef CAS
.
- F. Wang, D. Dreisinger, M. Jarvis, T. Hitchins and L. Trytten, Chem. Eng. J., 2021, 406, 126761 CrossRef CAS
.
- B. Bonfils, C. Julcour-Lebigue, F. Guyot, F. Bodénan, P. Chiquet and F. Bourgeois, Int. J. Greenhouse Gas Control, 2012, 9, 334–346 CrossRef CAS
.
- S. Zahid, H. C. Oskierski, I. Oluwoye, H. E. Brand, F. Xia, G. Senanayake, M. Altarawneh and B. Z. Dlugogorski, Miner. Eng., 2022, 184, 107630 CrossRef CAS
.
- B. Z. Dlugogorski and R. D. Balucan, Renewable Sustainable Energy Rev., 2014, 31, 353–367 CrossRef CAS
.
- C. E. Abi, S. Gürel, D. Kılınç and Ö. Emrullahoglu, Adv. Powder Technol., 2015, 26, 947–953 CrossRef
.
- S. J. Kemp, A. L. Lewis and J. C. Rushton, Appl. Geochem., 2022, 146, 105465 CrossRef CAS
.
- A.-H. A. Park and L.-S. Fan, Chem. Eng. Sci., 2004, 59, 5241–5247 CrossRef CAS
.
- R. K. Schulze, M. A. Hill, R. D. Field, P. A. Papin, R. J. Hanrahan and D. D. Byler, Energy Convers. Manage., 2004, 45, 3169–3179 CrossRef CAS
.
- F. Farhang, T. Oliver, M. Rayson, G. Brent, T. Molloy, M. Stockenhuber and E. Kennedy, J. CO2 Util., 2019, 30, 123–129 CrossRef CAS
.
- M. Werner, S. Hariharan and M. Mazzotti, Phys. Chem. Chem. Phys., 2014, 16, 24978–24993 RSC
.
- S. Hong, S. Moon, G. Sim and Y. Park, J. CO2 Util., 2023, 69, 102418 CrossRef CAS
.
- G. Rim, N. Roy, D. Zhao, S. Kawashima, P. Stallworth, S. G. Greenbaum and A.-H. A. Park, Faraday Discuss., 2021, 230, 187–212 RSC
.
- F. Larachi, I. Daldoul and G. Beaudoin, Geochim. Cosmochim. Acta, 2010, 74, 3051–3075 CrossRef CAS
.
- K.-H. Tan, A. Iqbal, F. Adam, N. A. Bakar, M. Ahmad, R. M. Yusop and H. Pauzi, RSC Adv., 2019, 9, 38760–38771 RSC
.
- A. Dufourny, C. Julcour, J. Esvan, L. Cassayre, P. Laniesse and F. Bourgeois, Front. Climate, 2022, 4, 946735 CrossRef
.
- J. H. Kwak, J. Z. Hu, R. V. Turcu, K. M. Rosso, E. S. Ilton, C. Wang, J. A. Sears, M. H. Engelhard, A. R. Felmy and D. W. Hoyt, Int. J. Greenhouse Gas Control, 2011, 5, 1081–1092 CrossRef CAS
.
- C. Davoisne, H. Leroux, M. Frère, J. Gimblot, L. Gengembre, Z. Djouadi, V. Ferreiro, L. d’Hendecourt and A. Jones, Astron. Astrophys., 2008, 482, 541–548 CrossRef CAS
.
- J. Esvan, G. Berger, S. Fabre, E. Bêche, Y. Thébault, A. Pages and C. Charvillat, Geochim. Cosmochim. Acta, 2022, 335, 124–136 CrossRef CAS
.
- J. S. Loring, J. Chen, P. Benezeth, O. Qafoku, E. S. Ilton, N. M. Washton, C. J. Thompson, P. F. Martin, B. P. McGrail and K. M. Rosso,
et al.
, Langmuir, 2015, 31, 7533–7543 CrossRef CAS PubMed
.
- H. Seyama and M. Soma, J. Chem. Soc., Faraday Trans. 1, 1985, 81, 485–495 RSC
.
- V. Rheinheimer, C. Unluer, J. Liu, S. Ruan, J. Pan and P. J. Monteiro, Materials, 2017, 10, 75 CrossRef PubMed
.
- T. Yin, S. Yin, A. Srivastava and G. Gadikota, Resour., Conserv. Recycl., 2022, 180, 106209 CrossRef CAS
.
- A. V. Chizmeshya, M. J. McKelvy, K. Squires, R. W. Carpenter and H. Béarat, A novel approach to mineral carbonation: Enhancing carbonation while avoiding mineral pretreatment process cost, Arizona State University, Tempe, AZ (United States), technical report, 2007 Search PubMed.
- J. Wang, K. Nakamura, N. Watanabe, A. Okamoto and T. Komai, IOP Conf. Ser.: Earth Environ. Sci., 2019, 257, 012017 CrossRef
.
- F. Wang, D. Dreisinger, M. Jarvis, T. Hitchins and D. Dyson, Chem. Eng. J., 2019, 360, 452–463 CrossRef CAS
.
- S. Yang, L. Mo and M. Deng, Cem. Concr. Compos., 2021, 118, 103948 CrossRef CAS
.
- T. Chen, Y. Xue, X. Zhao and J. Liu, J. Mater. Cycles Waste Manage., 2023, 25, 1498–1508 CrossRef CAS
.
- A.-H. A. Park, R. Jadhav and L.-S. Fan, Can. J. Chem. Eng., 2003, 81, 885–890 CrossRef CAS
.
-
G. D. Christian, P. K. Dasgupta and K. A. Schug, Analytical chemistry, John Wiley & Sons, 2013 Search PubMed
.
- T. Zelenka, K. Simanova, R. Saini, G. Zelenkova, S. P. Nehra, A. Sharma and M. Almasi, Sci. Rep., 2022, 12, 17366 CrossRef CAS PubMed
.
- J. G. Vitillo, M. Savonnet, G. Ricchiardi and S. Bordiga, ChemSusChem, 2011, 4, 1281–1290 CrossRef CAS PubMed
.
- A. F. Ciftja, A. Hartono and H. F. Svendsen, Energy Proc., 2013, 37, 1605–1612 CrossRef CAS
.
- R. Terzano, M. Spagnuolo, B. Vekemans, W. De Nolf, K. Janssens, G. Falkenberg, S. Fiore and P. Ruggiero, Environ. Sci. Technol., 2007, 41, 6762–6769 CrossRef CAS PubMed
.
- L. Jean-Soro, F. Bordas and J.-C. Bollinger, Environ. Pollut., 2012, 164, 175–181 CrossRef CAS PubMed
.
- L. Jean, F. Bordas and J.-C. Bollinger, Environ. Pollut., 2007, 147, 729–736 CrossRef CAS PubMed
.
- S. Sengupta, S. Acharyya, H. Van Den Hul and B. Chattopadhyay, J. Geol. Soc., 1989, 146, 491–498 CrossRef CAS
.
- S. Roy, D. Bandyopadhyay, T. Morishita, A. Dhar, M. Koley, S. Chattopadhaya, A. Karmakar and B. Ghosh, Lithos, 2022, 420, 106719 CrossRef
.
-
N. C. Ghose, N. Chatterjee and A. Fareeduddin, A petrographic atlas of ophiolite: an example from the Eastern India-Asia collision zone, Springer, 2014 Search PubMed
.
- B. Ghosh, J. Mahoney and J. Ray, J. Geol. Soc. India, 2007, 70, 595 CAS
.
- U. Schwertmann, Plant Soil, 1991, 130, 1–25 CrossRef CAS
.
- J. Olsson, N. Bovet, E. Makovicky, K. Bechgaard, Z. Balogh and S. Stipp, Geochim. Cosmochim. Acta, 2012, 77, 86–97 CrossRef CAS
.
- M. Velbel and J. Ranck, Mineral. Mag., 2008, 72, 145–148 CrossRef CAS
.
- H. E. King, O. Plümper and A. Putnis, Environ. Sci. Technol., 2010, 44, 6503–6509 CrossRef CAS PubMed
.
- M. A. Velbel, Am. Mineral., 2014, 99, 2227–2233 CrossRef
.
- D. Grandstaff, Geochim. Cosmochim. Acta, 1978, 42, 1899–1901 CrossRef CAS
.
- Y. Liu, A. A. Olsen and J. D. Rimstidt, Am. Mineral., 2006, 91, 455–458 CrossRef CAS
.
-
M. J. McKelvy, A. Chizmeshya, J. Diefenbacher, H. Béarat, R. Carpenter, G. Wolf and D. Gormley, EPD Congress, 2005, pp. 1133–1147 Search PubMed
.
- C. J. Thompson, J. S. Loring, K. M. Rosso and Z. Wang, Int. J. Greenhouse Gas Control, 2013, 18, 246–255 CrossRef CAS
.
- S. C. Krevor and K. S. Lackner, Int. J. Greenhouse Gas Control, 2011, 5, 1073–1080 CrossRef CAS
.
- H. Béarat, M. J. McKelvy, A. V. Chizmeshya, D. Gormley, R. Nunez, R. Carpenter, K. Squires and G. H. Wolf, Environ. Sci. Technol., 2006, 40, 4802–4808 CrossRef PubMed
.
- K. Jarvis, R. Carpenter, T. Windman, Y. Kim, R. Nunez and F. Alawneh, Environ. Sci. Technol., 2009, 43, 6314–6319 CrossRef CAS PubMed
.
- Y. Kim, R. Nunez, R. Carpenter, A. V. Chizmeshya and M. J. McKelvy, Microsc. Microanal., 2005, 11, 1530–1531 Search PubMed
.
- S. T. Mergelsberg, B. P. Rajan, B. A. Legg, L. Kovarik, S. D. Burton, G. M. Bowers, M. E. Bowden, O. Qafoku, C. J. Thompson and S. N. Kerisit,
et al.
, Environ. Sci. Technol. Lett., 2023, 10, 98–104 CrossRef CAS
.
- J. Chen, J. Gao and X. Wang, J. Braz. Chem. Soc., 2006, 17, 880–885 CrossRef CAS
.
- D. L. Venezky and W. E. Rudzinski, Anal. Chem., 1984, 56, 315–317 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04996e |
| This journal is © the Owner Societies 2024 |