Metallicity and chemical bonding in anti-anatase Mo₂N

Abstract

Here we present a detailed analysis of the structure, bonding character, and electronic structure of anti-anatase β-Mo₂N using density functional theory calculations. We analyze the crystal orbital Hamilton populations, phonon band structure, and electronic structure calculations to explain its low energy transport behavior. We further examine the electronic structures of (anti-)rutile and (anti-)anatase M_3−nX_n (X = N,O; n = 1,2) M = Ti and Mo nitrides and oxides to show that the atomic structure of anti-anatase leads to metallic behavior independent of the metal and ligand chemistry. Finally, we assess whether these anti-anatase compounds are viable electrides using electron density maps and electron localization functions. Our work shows anti-structures of known binary compounds can expand the phase space of available metallic ceramics beyond layered, hexagonal carbides and nitrides, e.g., M_n+1A_n (MAX) where n = 1–4.

---

1 Introduction

Crystal structure discovery is fundamental in order to increase the available materials options for future applications, particularly in understudied fields such as advanced, metallic ceramics.^1–4 Advanced metallic ceramics can be used as catalysts, diffusion resistant thin-films, and thermal barriers. Traditionally, semiconductivitity or metallicity in oxide ceramics is realized through introducing partially filled conduction bands (nominal metal), extended d-orbitals and hybridization, and highly overlapped metal–metal bonds. However, there are few metallic ceramics, primarily because of oxygen's high electronegativity and coulombic potential⁵ that localize electron bonding orbitals. Important counterexamples include alkali metal oxides and correlated metals, such as VO₂,⁶ ReO₃, RuO₂, SrFeO₃, (Pd,Pt)Co₂, which are of particular importance for electronics applications.

Recent research has shown promising structural and property differences for the less electronegative nitrides, carbides, and chalcogenides when compared to oxides, such as for MAX phases and electrides, necessitating further exploration. Carbides provide increased electrical conductivity when compared to oxides and nitrides due to their delocalized electronic structure. Transition metal monocarbides like TiC⁷ and its derivatives are well-known metallic ceramics. Nitrides generally have good mechanical properties and are most likely to exhibit cation charge disorder due to the nominal oxidation state of nitrogen, yielding interesting electronic properties.^3,4,8 However, nitrides are challenging to synthesize owing to their lower energetic stability.⁴ Heteroanionic materials, which contain two or more anions, have also captured attention due to increased local interactions and symmetry breaking, providing more variables for tuning to create emerging functionality.^2,3

Binary anti-structures, such as anti-anatase, accessible through anion and cation chemical substitution, advanced synthesis techniques, and computational probing, present viable opportunities to manifest functional properties. We can realize a wider range of properties, including negative thermal expansion and superconductivity, through the consideration of anti-structures, such as those found upon switching between perovskite and anti-perovskite.⁹ Anti-structures are more accessible through the application of non-oxygen anions, which modifies the nominal electron count and fosters different bonding environments. This is apparent when we consider that both Ti₂N anti-rutile and anti-anatase are reported anti-structures of their well-known rutile and anatase TiO₂ polymorphs (Fig. 1).

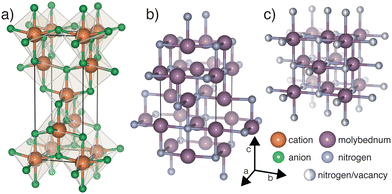Fig. 1 Structures displaying (a) generic anatase (b) anti-anatase β-Mo₂N and (c) γ-Mo₂N, where the anion site is statistically filled at 50%.

Anatase, whose generic structure is shown in Fig. 1a, most often refers to a metastable TiO₂ phase.¹⁰ Anatase titanium dioxide does not contain 1D cation chains like the brookite and rutile phases, yielding a larger electronic band gap.^11,12 The octahedra, which zig-zag along [001], are half edge-sharing and half vertex-sharing, and exhibit large distortions.¹³ Anatase and its anti-structure, anti-anatase (Fig. 1b), are less dense than many other ordered AB₂ phases, leading to decreased mechanical properties and increased compressibility. The anti-anatase structure was first reported as the δ′-Ti₂N phase,^14,15 and was described as a tetragonal NaCl-defect structure with locally ordered vacancies (Fig. 1b). The switch to anti-anatase creates a single cation Wyckoff position which is surrounded by anions connected in (100) or (010) at 90°, yielding a T-shaped, 3 anion coordinated cation. The 1D cation chains, bridged by obtuse cation–anion–cation bond(s), create shorter distances for electron hopping between cation sites and support potential metal bonding through extended d orbitals.

Metallic molybdenum nitrides are generally known to have excellent mechanical properties e.g. extreme hardness, high melting points, deformation resistance, and superconductivity.^16,17 Therefore, molybdenum nitrides find use in fast digital circuits, anodes of pseudocapacitors,¹⁸ coatings,^16,19 and in catalysis due to their high specific surface area.²⁰ Its members include δ-MoN, and the lesser reported γ-Mo₂N and β-Mo₂N.^16,21 The recorded thermodynamic ground state structure of Mo₂N is an anti-anatase compound exhibiting I4₁/amd symmetry, shown in Fig. 1b. Few publications report on its electronic structure and its other physical properties. Moreover, the high temperature γ phase (Fig. 1c) undergoes a phase transition as its defect structure disorders and adopts a statistical occupation.

Here, we examine role of structure on metallicity in the anti-anatase phase with first principles DFT calculations on the experimentally reported β-Mo₂N compound. To provide intuition on anti-anatase's properties, we construct a MX₂ model that compares the electronic behavior for different atomic substitutions and (anti-)structures. We also explore whether Mo₂N is a potential electride, analyze its band structure, and explain increases in stability gained in the β →γ transition. We argue that chemical substitution and leveraging unconventional structures, like anti-structures, are imperative to realizing the potential of the advanced ceramics field.

2 Computational methods

2.1 Electronic structure calculations

Density functional theory calculations were performed using the Vienna Ab initio Simulation Package (VASP)^22–25 utilizing the GGA functional Perdew–Burke–Ernzerhof revised for solids (PBEsol).^26–29 Structures were optimized and converged electronically to 10⁻⁷ eV and to 10⁻⁵ eV Å⁻¹ for forces. For general calculations, the plane wave cutoff was set to 600 eV. Gamma centered k-point meshes were used with at least 4000 k-points per reciprocal atom (KPPRA). The International Crystal Structures Database³⁰ was used to find structures from experimental databases. Anatase MoO₂ was initialized in the ferromagnetic spin configuration. We note the self-interaction error correction +U was not included within our framework, as the Mo-d states are itinerant. A benchmark analysis demonstrates that only small changes to the Mo₂N and MoO₂ electronic density of states occurs with and without the ad hoc +U as shown in Fig. S21 (ESI†).

To calculate the electronic density of states, a self-consistent calculation with the tetrahedron method with Blöchl corrections was performed. Electronic band structures were calculated from a non-self consistent calculation with Gaussian smearing. Ground state phonon calculations were performed based on the quasi-harmonic approximation³¹ with Phonopy³² at 0 K with a 2 × 2 × 2 supercell constructed from the primitive cell. 0 K and finite temperature phonon calculations were performed on a 4 × 4 × 4 supercell with the temperature-dependent effective potential (TDEP) method utilizing ab initio molecular dynamics.^33–35 All band structure calculations utilized the K-path in reciprocal space for the primitive cell recommended by SeeK-path: the k-path finder and visualizer.^36,37

Topological behavior was probed with the VASP2Trace program and the Bilbao Crystallographic Server's Check Topological Material feature.³⁸ The BoltzTraP2 program was used to calculate transport properties.³⁹ Crystal orbital Hamilton populations (COHP) were found with VASP and the LOBSTER package to create atom projected density of states for Mo₂N.^40–45 The electron localization function (ELF) was calculated with the approach developed by A.D. Becke et al., implemented within VASP.⁴⁶

3 Results

In the following sections, we detail a structural and electronic description of anti-anatase, an electronic behavior model for titanium and molybdenum oxide and nitride (anti-)structures, β-Mo₂N bonding character and low energy electronic behavior, and methods to probe the potential electride character of anti-anatase. In all cases, we use DFT structurally optimized atomic structures. We find the lattice parameters a = 4.22 Å and c = 7.96 Å for tetragonal β-Mo₂N. Bond-length and bond-angle distortions are present in anti-anatase to accommodate cation/anion size mismatch, including a shorter z direction Mo–N bond length and angular distortion of the N–Mo–N angle away from the 90° ideal. In comparison to Ti₂N anti-anatase, the angular distortion is more pronounced.The full crystal structure information for all computed compounds is available in Tables S1–S3 (ESI†).

3.1 Anti-anatase electronic model

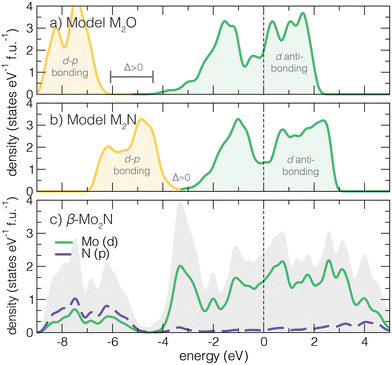
Structurally, the anti-anatase phase can promote high electronic transport through its conductive 1D cation chains. None of these mechanisms are available to the parent anatase. Moreover, the high cation:anion ratio should yield a higher filling of d orbitals and ill-defined cation oxidation state, thus preventing explicit insulating behavior from band theory and simple 2-electron bond arguments. With this understanding, we next sketch the expected electronic density of states (DOS) for an anti-rutile oxide (Fig. 2a) and an anti-anatase nitride (Fig. 2b). Based on electron filling, 6 electrons that form a closed shell anion configuration will first fill the valence band, composed of primarily p–d anion–cation states located well below the Fermi level. Then, at an energy gap of Δ above the valence band top, d states form a wide conduction band. The anti-anatase DOS generally present as small-gap semi-metals where E_f sits somewhere in the middle of the conduction band.

Fig. 2 (a) and (b) Schematic electronic DOS for anti-rutile and anti-anatase. Oxides generally a wider gap Δ (E_g between d–p bonding metal–metal bonding overlap in the conduction band). E_f is higher in the conduction band due to electronegativity and electron filling differences. (c) DFT calculated DOS for β-Mo₂N. Disperse d orbitals dominate the wide conduction band.

The position of the Fermi level, relative to the hybridized dp band, in the mainly d derived states is determined by how many remaining electrons are contributed by the cation. For a transition metal (TM) oxide in the anti-anatase structure the d derived band is partially filled when dⁿ, n ≥ 2 (Fig. 2a). TM nitrides (Fig. 2b) complete the valence band and start to fill the conduction band at d electrons. Most TM cations will easily fill d–p bands and partially fill the d dominated conduction bands. We find this behavior in anti-anatase β-Mo₂N (Fig. 2c), where p–d valence bonding states range from −9.5 to −5 eV (E_f = 0 eV). The d orbital dominated conduction band spreads between −5–6 eV. From here, we find that: (i) the change in the principal quantum number from 3d to 4d/5d increases the conduction bandwidth due to larger orbital size; (ii) increases in the oxidation state of the anion shifts E_f towards higher energy into the conduction band; and (iii) switching from anatase to anti-anatase reduces the chemical dependence on metallicity. To support this description, we next examine changes in the electronic structure for other (anti-)structure MX₂ compositions.

3.2 Substituted (anti-)MX₂ comparisons

Switching from structure to anti-structure modifies the cation/anion coordination number, increases the cation:anion ratio, and alters the bonding strengths due to shifts in orbital energies. We examine M_{3 −a}X_a (M = Ti, Mo; X = N,O; a = 1,2) compositions in (anti-)rutile and (anti-)anatase structures. Both rutile and anatase are well known titanium dioxide structures, and the nitrides of titanium in both anti-phases are reported. The crystallographic information for the DFT relaxed structures is reported in Table S2 (ESI†).

We first investigate how the effect of 3d versus 4d with atomic structure affects the d-orbital dominated electronic states about the Fermi level. Fig. 3 summarizes the compositions and phases varied, and their electronic behavior as described by the calculated conduction band energy ranges, normalized to the Ti core state of the rutile structure given by the σ bonding maximum near −20 eV (see ESI†). All DOS show insulating or semi-metallic character, where E_f is located in the middle of the nominal conduction band (except for anatase Ti₂X, where E_f is located in the nominal valence band). For nitrides, we observe the predicted shift down in E_f within the conduction band due to the decreased anion electronegativity and the additional cation-donated electron in the p–d valence band. Furthermore, Mo (4d) substitution for Ti (3d) yields larger bonding energy ranges due to the increase in principal quantum number and number of valence electrons. The 6 electron valence band is filled in all anti-structure cases, requiring that E_f is located within the middle of the conduction band. This should provide for robust metallic behavior for the anti-structures. For anti-anatase, we highlight that the conduction bandwidth increases with the substitution of Mo for Ti (≈ 1–2 eV change). Upon inspection of the β-Mo₂N orbital projected density of states, we find the d-orbitals are almost completely degenerate and delocalized (Fig. S4, ESI†).

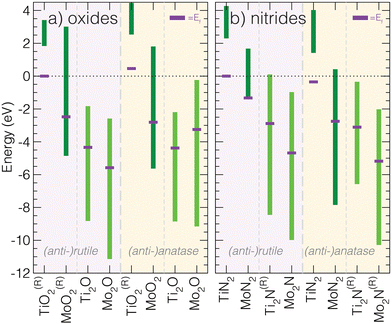Fig. 3 Calculated conduction band energy ranges of the 16 M_3−aX_a (X = N,O; a = 1,2) (anti-)rutile and (anti-)anatase phases. All materials are either calculated to be insulators or occur as semimetals, where E_f is located in the middle of the conduction band. Compared to other structures types, anti-anatase appears metallic independent of the composition (similar to anti-rutile). The superscript (R) indicates the phase is reported experimentally: rutile and anatase TiO₂,^47,48 rutile MoO₂,⁴⁹ anti-rutile and anti-anatase Ti₂N,^14,15,50,51 anti-anatase Mo₂N.⁵²

We also examined key characteristics of the valence band and and total density of states characters, visualized for all 16 phases in the ESI† (Fig. S4–S7). Upon inspection of the total DOS, it is apparent the valence band localizes upon the switch to an anti-structure, but is generally insensitive to the principal quantum number of the transition metal and electrons it contributes. Upon going from 3d to 4d and increasing the number of valence electrons, e.g., comparing isostructural TiO₂ (d⁰) and MoO₂ (d²), we find the conduction band shifts to lower energy and touches the valence band such that Δ = 0 and E_f is located in the conduction band. Additionally, the substitution of oxides for nitrides produces a larger Δ. Structurally, moving from anatase to anti-anatase, i.e., anatase MoO₂ to anti-anatase Mo₂O, introduces more states around E_f. Interestingly, we observe a lower valence band maximum for anti-anatase structures, indicating strong anion–cation bonding. We point out that additional electrons due to chemical substitution will lead to filling of the conduction band and a shift of E_f farther into the conduction band.

To summarize this analysis, we find that anti-anatase induces robust metallic character. This behavior is likely chemically invariant, owing to the small valence d–p band and a disperse conduction band dominated by low energy d orbital hybridization, and is distinct when compared to other A_x+1B_2−x (x = 0,1) compounds.

3.3 Bonding character of Mo₂N

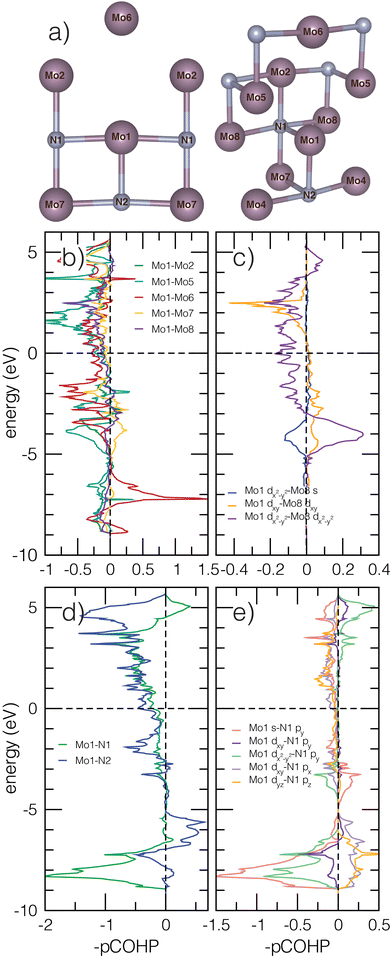
We next evaluate the projected crystal orbital Hamilton populations (pCOHP) of β-Mo₂N to better understand how the Mo–N bonding, facilitated by the atomic structure, affects stability, structural distortions, and electronic behavior in anti-anatase. Pair bonding interactions are indicated by positive −pCOHP magnitudes, while anti-bonding interactions are identified by negative −pCOHP values. All Mo cations are coordinated to three nearest neighbor nitrogen atoms and 13 nearest neighbor Mo atoms within a 4 Å cutoff. By symmetry, there are are six inequivalent Mo–Mo pairs and two inequivalent nearest neighbor Mo–N bonds with significant overlap. Fig. 4a depicts multiple views of the atomic structure to fully visualize the bonds. All Mo–N bonds in the N centered octahedra are equivalent except those in the (001) plane. The N-p_z orbitals are higher in energy and contribute to a shorter Mo–N bond. The N-p_x and N-p_y orbitals are degenerate and the greater bonding overlap can be seen in the orbital projected DOS (Fig. S1, ESI†). It is important to note that COHP calculations are defined only for cohesive energy contributions and are thus limited in their description of ionic bonding. Utilizing analyses by P.C. Müller et al.,⁵³ we find the Mo–N bonds contain roughly 0.18 ionicity (a value of 1 would indicate fully ionic bonding), indicating covalent contributions are significant.

Fig. 4 The projected crystal orbital Hamilton population (COHP) of select molybdenum and nitrogen bonding pairs throughout the β-Mo₂N structure, shown in (a). (b) and (c) Mo–Mo pairs exhibit strong bonding character (positive −pCOHP) around −10 eV below the Fermi level. (d) and (e) Mo1–N bonding in the (100) and (001) planes is shown. Significant anti-bonding character (negative −pCOHP) around −9 to −7 eV from the Mo1–N1 interaction is noted, and attributed to Mo1 s-N1 p_y (or p_x, Mo site dependent) and Mo1 d-N1 p_y overlap.

Fig. 4b and c shows the Mo–Mo −pCOHP. N is nominally 3–, meaning there are 9 electrons per Mo₂ unit available for metallic bonding. The pairs considered are Mo1–Mo2 (2.89 Å), Mo1–Mo5 (2.78 Å), Mo1–Mo6 (3.80 Å), Mo1–Mo7 (3.01 Å), and Mo1–Mo8 (2.98 Å). Mo1–Mo4 is not shown due to nearly identical overlap with Mo1–Mo2. In Fig. 4b, filled Mo–Mo interactions within 10 eV below E_f are dominated by prominent anti-bonding character. Despite these relatively long Mo–Mo bonds lengths, due to high Mo electron count, the lack of full bridging anions for most Mo–Mo bonds allows for Mo₂N to sit in an intermediate region where conventional orbital ordering is balanced by through-bond M–X–M interactions.⁵⁴ The unbridged Mo1–Mo2 and Mo1–Mo5 retain significant out-of-phase orbital overlap around −5 to −3 eV. The greatest bonding behavior occurs around −7 eV and −3 eV for Mo1–Mo6 interactions parallel to the c-axis (propagated almost exclusively by d_z² overlap). Nearly all unfilled states are strongly anti-bonding. In Fig. 4c, some 1D cation chains with a single N bridge in the (110) plane, associated with Mo1–Mo8 pairs, exhibit bonding contributions through d orbital interactions at about −4 eV, but show destructive interference closer to E_f and for d_xy–d_x²–y² and d_z²–d_x²–y² orbital overlap. We note that significant filled anti-bonding states are found in the elemental bcc molybdenum COHP as well (Fig. S3, ESI†). Based on the elemental COHP and previous literature, we connect anti-anatase to covalent anti-bonding interactions through metal–metal bonding and strong hybridization of Mo 4d orbitals.⁵⁴

Anti-bonding behavior is also present for filled Mo–N bonds near and below E_f (Fig. 4d and e). The negative Mo1–N1 interactions in the (100) −pCOHP values are attributed to p_y orbitals. Mo1–N2 interactions parallel to the c axis feature some small positive −pCOHP contributions. The filled anti-bonding Mod–Np states indicate some structure instability in the Mo₂N and stronger ionic interactions. We explain the high anti-bonding contribution to Mod–Np bonding at the Brillion zone boundary through the anti-symmetric nature of Np orbitals, which are restricted by k-space and cannot constructively overlap. On the other hand, the unrestricted (001) direction allows for significant bonding overlap. Finally, we note the longer Mo–N bond in the xy plane will shift the energy of the anti-bonding states down, leading to increased likelihood they will be filled.⁵⁵ We underscore that the filled anti-bonding orbitals will decrease the stability of anti-anatase and Mo₂N. Additionally, increased cation electron count (dⁿ, n > 2) accommodated through anti-bond conduction band filling should increase structural distortion and likely leads to a soft limit in electron count, which can be tuned by cation substitution. Presumably, because fewer electrons will fill the anti-bonding conduction band for M₂N than for M₂O, nitrides are more amenable to anti-anatase structures.

Finally, we note β-Mo₂N will spontaneously form point defects leading to the β → γ transformation. We hypothesize a driving force for this order–disorder transition in anti-anatase structures is the reduction of anti-bonding states at the Fermi level and the creation of variable oxidation states.⁵⁶ In Fig. S8 (ESI†), we show that γ- and β-Mo₂N with and without nitrogen vacancy defects exhibit decreased electronic states and anti-bonding character near E_f when nitrogen vacancies are disordered, supporting γ-Mo₂N stability and anion-vacancy disorder as a common defect in other anti-anatase phases.

3.4 Low energy and transport behavior

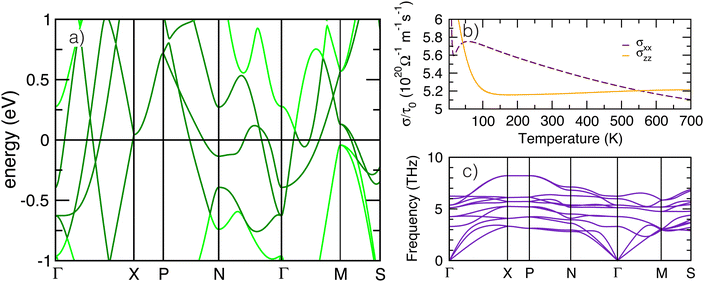
To better understand the low energy electronic behavior of anti-anatase, shown to be composed of anti-bonding d states, we calculated the unfolded electronic band structure for β-Mo₂N (Fig. 5a). Parabolic trajectories from crossings near E_f throughout the Brillion zone, originating from three Mo-d bands, signify metallic behavior. These bands are weakly dispersing, ranging only from about −1 eV below to 1.5 eV. Hybridized metal–metal bonding is indicated by overlapping d bands from near N (q = 0, 0.5, 0) to to Γ (q = 0, 0, 0). The sharp peaks from high velocity electrons reflect low effective mass throughout the Brillion zone, and indicate the conductivity is largely isotropic. We note that β-Mo₂N is an enforced semi-metal with a Fermi-degeneracy when including SOC. The electronic band structure exhibits weak dependence on spin–orbit coupling, especially near Γ and X (see Fig. S15, ESI†). Topologically relevant points close to the Fermi level include electron and hole pockets near E_f around the Γ high symmetry point, shown here in the paths Γ → X and Γ → M. Moreover, the electron pocket near Γ forms a three dimensional cone with high velocity and nearly linear dispersion similar to semi-metals.⁵⁷

Fig. 5 (a) The unfolded electronic band structure of β-Mo₂N from −1 eV < E_f < 1 eV. (b) Simulated electrical conductivity from 0–700 K at μ = ε_f. (c) Phonon band calculations at 300 K. In the total band structure, significant parabolic band crossings indicate metallic behavior. Darker green bands indicate those that cross E_f. Conductivity calculations demonstrate significant anisotropic behavior between about 50–550 K. At around T = 550 K the anisotropy reverses and σ_zz > σ_xx, where σ_zz roughly looses its temperature dependence after 100 K. The phonon band structure demonstrates dynamic stability at room temperature, with flat degenerate transverse acoustic modes near X and P.

We next calculate the transport behavior of anti-anatase Mo₂N focusing on the electronic conductivities σ_xx and σ_zz (Fig. 5b), presented from approximately 0 K to 700 K. Between about 50 K and 550 K σ_xx > σ_zz, whereas at room temperature and just below, conductivity through the anti-bonding Mo–Mo chains is most substantial.⁵⁸ However, at low and high temperatures, σ_zz is greater than σ_xx. σ_zz is largely temperature invariant after 100 K, but σ_xx decreases nearly linearly after 50 K. The multiple equivalence points (σ_xx = σ_zz) demonstrate that anti-anatase should exhibit temperature and chemistry tunable conductivity, where we expect filling of the anti-bonding dominated conduction band to dictate the extent of electrical transport anisotropy at the operating temperatures. Finally, we calculated the room temperature (300 K) phonon dispersions of the primitive cell utilizing a 4 × 4 × 4 supercell (Fig. 5c). Acoustic bands reach up to nearly 4 THz and are nearly flat throughout most of the Brillion zone, overlapping with an optical band between X and P (q = 0.25, 0.25, 0.25) and later with three bands on Γ → M → S. The set of lower frequency optical bands, ranging from about 3 to 8 THz, are also generally flat implying low phonon group velocities. The dispersion over an extended path at 0 K, 50 K, and 300 K appears in Fig. S16–S18 (ESI†). The 0 K phonon band structure indicates small instabilities at a number of points, including Γ, N, and P (method dependent, See ESI†). Modulation of the negative Γ mode yields a lower energy, ground state Imma structure (see ESI†). We note that due to N lone pairs, structural distortions in the anti-anatase bonding, and vacancies in the structure,⁵⁹ Mo₂N phonons were found to be anharmonic and tools that rely on the quasi-harmonic approximation³¹ produced slightly different phonon band structures. Anharmonic phonon behavior, which can be important for electrides and non-oxide advanced ceramics, was calculated with TDEP.^33–35,59 Experimentally, the anharmonic phonon spectra are measured with inelastic neutron scattering and inelastic X-ray scattering through the whole Brillion zone, and probed near the zone center using visible light and infrared absorption spectroscopies.⁵⁹

3.5 Probing potential ambient and high-pressure electride character

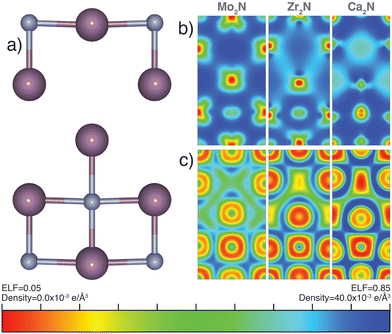
There has been significant research effort dedicated to the discovery of electrides since the synthesis and characterization of the first room temperature stable electride [Ca₂₄Al₂₈O₆₄]⁴(4e⁻).^60,61 An electride is a compound with an electron acting as an anion. Quantum trapping of electrons in F-centers have been found in 0D, 1D, 2D, or even 3D. Design principles based on experimental characterization and high-throughput computation, using charge density and localization function mapping,^62–64 loosely define native electride design rules as (i) possessing a well defined vacant (multi-dimensional) cavity for electron confinement, (ii) a cavity size which can effectively support and protect a stable anionic electron at room temperature, (iii) excess electrons to act as anions, and (iv) a strong cation to offset the concentrated negative charge of the confined electron.^63–68 Most experimentally verified and computationally predicted electrides contain closed shell cations, however partially filled d-shell transition metal electrides have been reported.⁶⁹ Mo₂N and the general anti-anatase structure can fit these minimum design requirements; we therefore explore its potential electride character.

Our electron localization function (ELF) analysis reveals highly ionic Mo–N bonds (Fig. 6b), indicated by the large ELF contours between the two ions. There is also considerable metallic bonding between Mo sites. The partial electron charge density mapping of Mo₂N (Fig. 6c) depicts the distribution of electrons in the range of −1.0 eV ≤ E_f ≤ 0.5 eV. The density supports d orbital extension throughout and conduction channels between some neighboring cations. There is little electron density near the vacancy, which would be expected for an electride. Although it follows the aforementioned design rules, we conclude that Mo₂N is not a native electride. We note that Mo₂N shows no electron vacancy confinement under applied hydrostatic pressures up to 500 GPa based on ELF and partial charge density mapping verifying β-Mo₂N is not a high pressure electride.

Fig. 6 Visualized bonding character of anti-anatase, where (a) is the structure in the (100) plane. The structural slice shows an ordered vacancy, surrounding by Mo atoms, in addition to a the highly coordinated anion site. (b) Electron localization function (ELF) and (c) electron density map from −1.0 eV < E_f − E < 0.5 eV. The ELF demonstrates metal–metal bonding of the molybdenum atoms. Additionally, the low ELF values directly between N and Mo supports highly ionic bonding. The electron charge density shows some Mo–Mo bonding and conduction channels through slightly increased electron density between Mo atoms. No charge is found in the vacancy site near the Fermi level, indicating β-Mo is not an electride. The maximum charge density is 40 × 10⁻³e Å⁻³ except for Mo₂N, where the maximum charge density is 75 × 10⁻³e Å⁻³.

We were prompted to explore the electride behavior in cation-substituted anti-anatase compounds. We investigated the isoelectric, anti-anatase 3d Zr₂N, whose charge density map and ELF do not support electride behavior (Fig. 6b and c). Next we attempted substitution of closed shell calcium, which should nominally donate 1e⁻ in anti-anatase Ca₂N, and has already been synthesized as a 2D electride in the anti-CdCl₂ structure.⁶⁵ Based on the charge density mapping and ELF, we observe electronically confined channels, demonstrating potential electride like behavior. We conclude that while Mo₂N is not an electride, the anti-anatase structure may support electride character. Furthermore, additional design rules are necessary to explain the formation of electrides. In particular, exclusionary rules and an increase in vacancy structures considered such as M₂X anti-structures of typical oxides, will aide in future electride prediction.

4 Conclusions

We investigated the structure, bonding, and electronic behavior of anti-anatase, primarily through first principles DOS, COHP, and band structure calculations of β-Mo₂N and complementary compounds. We predict that anti-anatase (i) is robustly metallic with a partially filled and broad conduction band for most chemistries, (ii) contains significant metal–metal bonding and symmetry supported anti-bonding, and (iii) exhibits interesting electronic behavior, including multiple conductivity equivalence points (σ_xx = σ_zz) and chemistry dependent electride behavior. The significant metal–metal bonding is tied to hybridized Mo-d orbitals in 1D cation chains and strong orbital overlap across the periodic anion vacancy, both of which make anti-anatase a robust electrical conductor.

We also described an electron filling model, wherein cations contributing 2 or more d electrons to an anti-anatase nitride phase will have additional electrons fill an anti-bonding, d state dominated conduction band that should remain robustly metallic. By exploring titanium and molybdenum (anti-)rutile and (anti-)anatase structures, we found both anti-structures contain highly metallic, disperse conduction bands regardless of chemistry. COHP calculations confirmed that the conduction band is primarily anti-bonding, implying that late transition metals with more d electrons are less likely to adopt the anti-anatase structure owing to occupation of these destabilizing states. We further emphasize that because most transition metal cation choices should locate E_f within a d-orbital dominated conduction band, other properties, such as mechanical properties or surface energy, can be tuned without sacrificing metallicity.

The under-studied anti-anatase crystal structure promises a unique template for designing interesting properties. Anti-anatase accommodates significant anti-bonding between cations, as indicated by a COHP analysis of β-Mo₂N. Filled anti-bonding states prompt intrinsic instability and potential for interesting property design through distortion and subsequent symmetry breaking. Structural anisotropy also presents an interesting design component. The predicted temperature dependent, anisotropic electronic conductivity for β-Mo₂N revealed in our study is expected to persist for others in the anti-anatase family, pointing to hypothetical chemically tunable transport behavior. Moreover, we explored whether anti-anatase, due to its periodic vacancies, may enable electride character in β-Mo₂N and other A₂N nitrides through chemical substitution. We found that anti-anatase Ca₂N is indeed predicted to have trapped anionic electrons. Future exploration into s-block metal carbides or nitrides within the cation-rich anti-anatase may lead to new electride prediction.

Throughout this study we highlight the importance of future investigations of anti-anatase as well as explore possible mechanisms to increase the conductivity (anion substitution and unfamiliar anti-structure exploration) of other advanced ceramics candidates. Coupling of relevant chemistries with structures that support industrial applications, e.g., in the form of electrical interconnects for microelectronics, is essential for rational materials design and should be leveraged. We assert that the wider composition-structure space comprising carbides, nitrides, chalcogenides, heteroanionic materials, etc., should be investigated. Given the advent of high-throughput computational prediction of synthesizability and properties, and significant advances in synthesis science, we believe this area of research is overdue for discovery of novel functional materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

L.N.W. was supported by the National Science Foundations (NSF) MRSEC program (DMR-1720139) at the Materials Research Center of Northwestern University. J.M.R. was was supported in part by SUPREME, one of seven centers in JUMP 2.0, a Semiconductor Research Corporation (SRC) program sponsored by DARPA. Calculations were performed using the QUEST HPC Facility at Northwestern University and at the Extreme Science and Engineering Discovery Environment (NSF, ACI-1548562). L.N.W. thanks Dr A.B. Georgescu and K.D. Miller for comments on earlier versions of this manuscript.

References

1. M. Srinivasan and W. Rafaniello, Carbide, Nitride and Boride Materials Synthesis and Processing, Springer, Netherlands, 1997, pp. 3–42.
2. S. T. Hartman, First-principles Studies of Anion Engineering in Functional Ceramics, 2020, https://openscholarship.wustl.edu/eng_etds/544.
3. J. K. Harada, N. Charles, K. R. Poeppelmeier and J. M. Rondinelli, Adv. Mater., 2019, 31, 1805295.
4. W. Sun, C. J. Bartel, E. Arca, S. R. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. M. Holder and G. Ceder, Nat. Mater., 2019, 18, 732–739.
5. N. Haddad, E. Garcia-Caurel, L. Hultman, M. W. Barsoum and G. Hug, J. Appl. Phys., 2008, 104, 023531.
6. D. Lee, B. Chung, Y. Shi, G.-Y. Kim, N. Campbell, F. Xue, K. Song, S.-Y. Choi, J. P. Podkaminer, T. H. Kim, P. J. Ryan, J.-W. Kim, T. R. Paudel, J.-H. Kang, J. W. Spinuzzi, D. A. Tenne, E. Y. Tsymbal, M. S. Rzchowski, L. Q. Chen, J. Lee and C. B. Eom, Science, 2018, 362, 1037–1040.
7. A. M. Shul’pekov and G. V. Lyamina, Inorg. Mater., 2011, 47, 722–727.
8. W. Lengauer, J. Alloys Compd., 1992, 186, 293–307.
9. Y. Wang, H. Zhang, J. Zhu, X. Lü, S. Li, R. Zou and Y. Zhao, Adv. Mater., 2020, 32, 1905007.
10. R. Asahi, Y. Taga, W. Mannstadt and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7459–7465.
11. J. Pascual, J. Camassel and H. Mathieu, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 5606–5614.
12. H. Tang, F. Lévy, H. Berger and P. E. Schmid, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 7771–7774.
13. A. Stepanov, X. Xiao and F. Ren, Implantation of titanium dioxide with transition metalions, Nova Science Publishers, Inc., 2013, pp. 59–83.
14. A. N. Christensen, A. Alamo and J. P. Landesman, Acta Cryst. C, 1985, 41, 1009–1011.
15. P. Ehrlich, Z. Anorg. Chem., 1949, 259, 1–41.
16. I. Jauberteau, A. Bessaudou, R. Mayet, J. Cornette, J. Jauberteau, P. Carles and T. Merle-Méjean, Coatings, 2015, 5, 656–687.
17. S. Wang, D. Antonio, X. Yu, J. Zhang, A. L. Cornelius, D. He and Y. Zhao, Sci. Rep., 2015, 5.
18. D. P. Dubal, S. Abdel-Azeim, N. R. Chodankar and Y.-K. Han, iScience, 2019, 16, 50–62.
19. K. Khojier, M. R. K. Mehr and H. Savaloni, J. Nanostruct. Chem., 2013, 3, 5.
20. V. Tagliazucca, M. Leoni and C. Weidenthaler, Phys. Chem. Chem. Phys., 2014, 16, 6182–6188.
21. K. Inumaru, K. Baba and S. Yamanaka, Chem. Mater., 2005, 17, 5935–5940.
22. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
23. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
24. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
25. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
26. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
27. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
28. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
29. G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. T. Philipsen, S. Lebégue, J. Paier, O. A. Vydrov and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155107.
30. A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Cryst. B, 2002, 58, 364–369.
31. B. Fultz, Prog. Mater. Sci., 2010, 55, 247.
32. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
33. O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 180301.
34. O. Hellman and I. A. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 144301.
35. O. Hellman, P. Steneteg, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104111.
36. Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comp. Mat. Sci., 2017, 128, 140–184.
37. A. Togo and I. Tanaka, Spglib: a software library for crystal symmetry search, 2018.
38. M. G. Vergniory, L. Elcoro, C. Felser, N. Regnault, B. A. Bernevig and Z. Wang, Nature, 2019, 566, 480–485.
39. G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145.
40. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
41. V. L. Deringer, A. L. Tchougreéff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
42. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
43. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
44. S. Maintz, M. Esser and R. Dronskowski, Acta Phys. Pol., B, 2016, 47, 1165.
45. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
46. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
47. Y. Liu and A. R. West, J. Am. Ceram. Soc., 2013, 96, 218–222.
48. H. G. Yang, C. H. Sun, S. Z. Qiao, J. Zou, G. Liu, S. C. Smith, H. M. Cheng and G. Q. Lu, Nature, 2008, 453, 638–641.
49. G. A. Seisenbaeva, M. Sundberg, M. Nygren, L. Dubrovinsky and V. G. Kessler, Mater. Chem. Phys., 2004, 87, 142–148.
50. M. Dalal, A Textbook of Inorganic Chemistry, Dalal Institute, Rohtak, Haryana, India, 2017.
51. B. Holmberg, M. Yhland, R. Dahlbom, J. Sjövall, O. Theander and H. Flood, Acta Chem. Scand., 1962, 16, 1255–1261.
52. P. Ettmayer, Monatsh. Chem., 1970, 101, 127–140.
53. P. C. Müller, C. Ertural, J. Hempelmann and R. Dronskowski, J. Phys. Chem. C, 2021, 125(14), 7959–7970.
54. T. Hughbanks and R. Hoffmann, J. Am. Chem. Soc., 1983, 105, 3528–3537.
55. X.-S. Zhao, Y.-R. Ge, X. Zhao and H. Zhao, Physical Mechanism of Superconductivity, arXiv, 2010, arXiv.1012.0879 DOI:10.48550/arXiv.1012.0879.
56. M. Pouchard and A. Villesuzanne, Condens. Matter, 2020, 5, 67.
57. T. Wehling, A. Black-Schaffer and A. Balatsky, Adv. Phys., 2014, 63, 1–76.
58. L. Xi, Y. B. Zhang, X. Y. Shi, J. Yang, X. Shi, L. D. Chen, W. Zhang, J. Yang and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155201.
59. B. Wei, Q. Sun, C. Li and J. Hong, Sci. China: Phys., Mech. Astron., 2021, 64.
60. K. Hayashi, S. Matsuishi, T. Kamiya, M. Hirano and H. Hosono, Nature, 2002, 419, 462–465.
61. S. Matsuishi, Science, 2003, 301, 626–629.
62. S. G. Dale and E. R. Johnson, J. Phys. Chem. A, 2018, 122, 9371–9391.
63. L. A. Burton, F. Ricci, W. Chen, G.-M. Rignanese and G. Hautier, Chem. Mater., 2018, 30, 7521–7526.
64. Y. Zhang, H. Wang, Y. Wang, L. Zhang and Y. Ma, Phys. Rev. X, 2017, 7, 011017.
65. K. Lee, S. W. Kim, Y. Toda, S. Matsuishi and H. Hosono, Nature, 2013, 494, 336–340.
66. S. W. Kim, T. Shimoyama and H. Hosono, Science, 2011, 333, 71–74.
67. S. G. Dale, A. O. De-la Roza and E. R. Johnson, Phys. Chem. Chem. Phys., 2014, 16, 14584–14593.
68. S. G. Dale and E. R. Johnson, Phys. Chem. Chem. Phys., 2017, 19, 27343–27352.
69. P. Chanhom, K. E. Fritz, L. A. Burton, J. Kloppenburg, Y. Filinchuk, A. Senyshyn, M. Wang, Z. Feng, N. Insin, J. Suntivich and G. Hautier, J. Am. Chem. Soc., 2019, 141, 10595–10598.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05054h

---