Theoretical trends in the dynamics simulations of molecular machines across multiple scales

Abstract

Over the past few decades, molecular machines have been extensively studied, since they are composed of single molecules for functional materials capable of responding to external stimuli, enabling motion at scales ranging from the microscopic to the macroscopic level within molecular aggregates. This advancement holds the potential to efficiently transform external resources into mechanical movement, achieved through precise control of conformational changes in stimuli-responsive materials. However, the underlying mechanism that links microscopic and macroscopic motions remains unclear, demanding computational development associated with simulating the construction of molecular machines from single molecules. This bottleneck has impeded the design of more efficient functional materials. Advancements in theoretical simulations have successfully been developed in various computational models to unveil the operational mechanisms of stimulus-responsive molecular machines, which could help us reduce the costs in experimental trial-and-error procedures. It opens doors to the computer-aided design of innovative functional materials. In this perspective, we have reviewed theoretical approaches employed in simulating dynamic processes involving conformational changes in molecular machines, spanning different scales and environmental conditions. In addition, we have highlighted current challenges and anticipated future trends in the collective control of aggregates within molecular machines. Our goal is to provide a comprehensive overview of recent theoretical advancements in the field of molecular machines, offering valuable insights for the design of novel smart materials.

---

From left to right: Haoyang Xu, Jin Wen, Weijia Xu and Yuanda Tao

Weijia Xu and Yuanda Tao are currently pursuing their master's degrees in Professor Wen's research group at Donghua University. Haoyang Xu obtained his master's degree in Materials Science and Engineering from Donghua University in 2021 and is currently working towards his doctoral degree within Professor Wen's research team. Professor Jin Wen completed her PhD in Chemistry at Nanjing University under the supervision of Prof. Jing Ma in 2012. Subsequently, she held positions as an associate scientist at the Academy of Sciences of the Czech Republic and as a project leader at the University of Vienna before joining Donghua University in 2020. Her research is primarily focused on method development for theoretical simulations in ultrafast processes of photochemistry and photophysics, with specific interests in singlet fission and molecular machines.

1 Introduction

Over the preceding four decades, chemists have ingeniously conceived a wide array of molecular machines, which convert chemical, electrical, and photonic stimuli into intricate mechanical responses. Since the prestigious Nobel Prize was bestowed upon Jean-Pierre Sauvage, Sir J. Fraser Stoddart, and Bernard L. Feringa in 2016, the realm of molecular machines has undergone swift advancement.¹ Progressing through the range from individual molecules to the domain of complex systems, molecular machines have shown immense potential in energy conversion, mechanical devices, artificial muscles, drug delivery, and sensing and detection.^2,3

The coupling between molecular machines and external stimuli, such as light,⁴ pH,⁵ or electrical stimulation,⁶ plays a crucial role in determining the amplitude and speed of molecular motions. Therefore, optimizing parameters for these stimuli is essential for efficiently regulating motion in molecular machines. While it is possible to regulate the motion of single molecules, especially in solutions, their collective motion becomes random when they aggregate.⁷ To address this issue, directional motion can be achieved by attaching molecular machines to solid surfaces, thereby confining their spatial movement. This approach not only improves surface properties but also amplifies microscopic motion, resulting in greater mechanical work production.^7,8 Surface-mounted molecular machines hold significant promise for functional materials. Additionally, self-assembled molecular machines can respond reversibly to external stimuli, functioning as molecular switches.⁷

Understanding the driving forces behind the response of molecular machines to external stimuli is essential for improving and designing new molecular machines. For instance, in solution, properties of the solvent, such as polarity and viscosity, and charge distribution on the molecular machine, impact the rotational movement of molecular machines.⁹ Controlling the surface diffusion or motion of molecules on solid surfaces and their specific moving direction is challenging.² Theoretical modeling offers valuable insights by simulating the interactions between molecular machines and their environments along reaction coordinates.^10,11 Computational simulations help determine the reaction pathways. Activation barriers along the potential energy surface reflect the likelihood and speed of motion in molecular machines. Therefore, adjusting the profile of the potential energy surface can accelerate reactions by reducing these activation barriers, resulting in a more efficient process. Increasing the reaction temperature is another option, but it requires more resources and may not be optimal. Therefore, a practical strategy for improving the functions of molecular machines involves revealing and reshaping the potential energy surfaces through the design of novel chemical structures.

Extensive reviews have comprehensively explored research related to molecular machines,^3,7,12 but our focus is squarely on highlighting the recent advancements that have emerged in the past few years. With the advancement of computational chemistry techniques and the continuous improvement in computer performance, we are now capable of investigating reaction mechanisms within large-scale molecular machines. This encompasses predicting molecular properties, determining structures, assessing performance, and aiding in the discovery and design of new materials. In this perspective, we aim to provide a concise overview of the current state of research and the challenges encountered in both computational and experimental settings for molecular machines. Our discussion is structured into three main sections: beginning with the study of individual molecules, progressing to surface-mounted and self-assembled supramolecules, and concluding with the exploration of the domain of polymers. Accordingly, we will introduce various computational methods tailored to different scales of molecular systems to offer a comprehensive theoretical and simulation framework. This will empower researchers to effectively and precisely select suitable computational protocols for various scales of molecular machines.

2 Recent progress in molecular machines and their applications

2.1 Molecular machine functioning as a solitary molecule

Molecular machines exhibit diverse classifications grounded in their functional components and mechanical behaviors. In contrast to molecular shuttles, in which back-and-forth translation is utilized by reversible binding sites under chemical and photochemical stimuli (Fig. 1a),¹³ a molecular motor manifests the unique capacity to convert external energy into a continuous circular rotation.¹⁴ Pioneered by harnessing the photoisomerization of a C=C double bond in a chiral overcrowded alkene, light-driven molecular motors were facilitated by alternate light and heat sources to achieve their unidirectional motion. While three generations of motors have undergone advancements in rotational efficiency, the practical application of molecular motors remains hindered by the rate-determining step of thermal helix inversion, governed by ambient temperature. The thermal reaction is significantly behind the photoisomerization step by orders of magnitude.¹⁵ An all-photochemical motor exhibits potential advantages over the prior generation, due to its temperature independence. A breakthrough emerged in hemithioindigo- and alkene-based motors for all-light-driven rotation, which improved the efficiency of photon conversion.^16,17 Illustrated in Fig. 1b, irradiation on the stable configurations of this novel alkene-based motor at −50 °C gives rise to the appearance of four isomers within the photostationary state.¹⁷

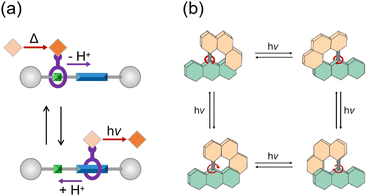Fig. 1 (a) A “molecular transporter” based on a controllable molecular shuttle and operated by two independent external stimuli (base/acid and dark/light).¹³ (b) All-light-driven rotational cycle of the novel alkene-based molecular motor.¹⁷

2.2 Molecular machine operating as a collective of molecules

Beyond the single molecules, characterized by stochastic molecular collisions and vibrations, the collective motion of molecular machines faces challenges imposed by unpredictable dynamics in molecular assembly owing to Brownian motion. Therefore, the development of functional molecular machines with controllable motion becomes imperative for molecular aggregates.

Surface-mounted molecular machines have emerged as a viable solution to diminish the impact of random motion through chemical or physical adsorption onto solid surfaces. This approach serves a dual purpose. Firstly, it enables the controlled motion of molecular machines, facilitating the manipulation of surface properties. Secondly, this strategy provides the potential to capture and amplify nanoscale energy, thereby generating substantial mechanical work. An innovative approach presented by Magnussen et al. involved designing an azobenzene-based photo-reactive switch with its axis aligned parallel to the metal surface, enabling horizontal rotation (Fig. 2a).¹⁸ In addition to surface-mounted molecular machines, advanced designs have also explored surface inclusion. For instance, a unidirectionally rotating molecular motor has been embedded into nanocrystals, forming two-dimensional ordered arrays with photo-responsive capabilities on the surface (Fig. 2b).¹⁹ This approach offers a promising strategy for achieving organized arrays and synchronized rotation of molecular motors on two-dimensional surfaces.

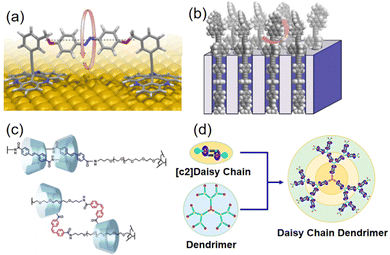Fig. 2 (a) Molecular machine parallel to the molecular surface. Adapted with permission from ref. 18. Copyright 2019 American Chemical Society. (b) Surface inclusion molecular motor. Adapted with permission from ref. 19. Copyright 2017 American Chemical Society. (c) Photoisomerization of azobenzene causes shrinking [c2]daisy chains. Adapted with permission from ref. 20. Copyright 2018 American Chemical Society. (d) Dendritic cyclophane polymers. Adapted with permission from ref. 21. Copyright 2020 American Chemical Society.

Beyond the surface-mounted molecular machines, the manipulation of reversible non-covalent interactions has proven instrumental in crafting multifunctional materials, which are composed of macrocyclic hosts and compatible guests. These materials exhibit mechanical motion enabled by configurational changes in guest molecules in response to external stimuli, altering their positioning relative to the host. The development of such supramolecular systems with precisely controllable motion opens new avenues for enhancing the operational efficiency of molecular machines. For instance, azobenzene-based polymer chains induce the shrinking of [c2]daisy chains within cyclodextrin-based hydrogels through photoisomerization. This leads to subsequent volume reduction and macroscopic bending deformation (Fig. 2c).²⁰ Furthermore, to achieve more extensive movement, Yang et al. have synthesized dendritic polymers resembling daisy chains. In these structures, external stimuli trigger collective motion by amplifying the movements of individual cyclophanes along the dendritic polymer chains (Fig. 2d).²¹ This approach offers a reversible and controllable means of modifying thin film deformations.

2.3 Molecular machine operating as a component within complex systems

Beyond self-assembly, molecular machines exhibit the ability to construct complex systems, in which mechanical movement responds functionally to stimuli. These complex systems can be classified based on the sequence of responsive reactions they utilize. Some systems achieve their functions within the domain of their stimulus-responsive unit, while others induce motion by modifying their structural components through responsive units, particularly evident in host–guest systems.

For instance, a rotaxane-based metal–organic framework (MOF) is depicted in Fig. 3a. Here, the capture and release of guest molecules occur via alternating hydrogen bonding, enabled by the photoisomerization of guests.²² Another noteworthy example involves microgels, which are composed of cyclodextrin aggregates within cross-linked networks. These microgels exhibit the ability to adjust their swelling capacity, responding sensitively to variations in pH and thermal conditions.²⁵ This attribute suggests their potential utility in drug release applications. In the case of pseudorotaxane-based MOFs, the photochemical reactions of guest molecules occur within the host structure, resulting in a reduction of the host's diameter.²³ Of particular interest is the captivating phenomenon of macroscopic deformation that accumulates along a crystal direction (Fig. 3b). Likewise, molecular-machine-based liquid crystal polymers (LCPs) exhibit fascinating behavior.^24,26–28 The photo-responsive groups within these LCPs induce different shapes of mesogenic units, which subsequently trigger macroscopic deformation (Fig. 3c). In addition, when the molecular motor is incorporated as cross-linker units within a polyurethane network, it results in the amplification of macroscopic movement in light-activated materials, endowing them with shape-memory functionality.²⁹ These responsive molecular machines have shown significant potential for advanced applications in areas such as actuators, artificial muscles, and drug delivery systems.

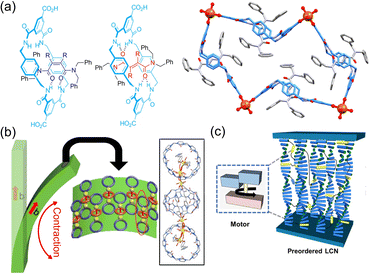Fig. 3 (a) In a MOF composed of rotane and copper ions photoisomerization controls the entry and exit of cargo. Adapted with permission from ref. 22. Copyright 2020 American Chemical Society. (b) The polymerization reaction of the object leads to the contraction of the subject, ultimately leading to deformation. Adapted with permission from ref. 23. Copyright 2022 Springer Nature. (c) The rotation of the motors as a cross-linkers leads to the formation of crystals. Adapted with permission from ref. 24. Copyright 2022 American Chemical Society​.

3 Multiscale modeling in molecular machines

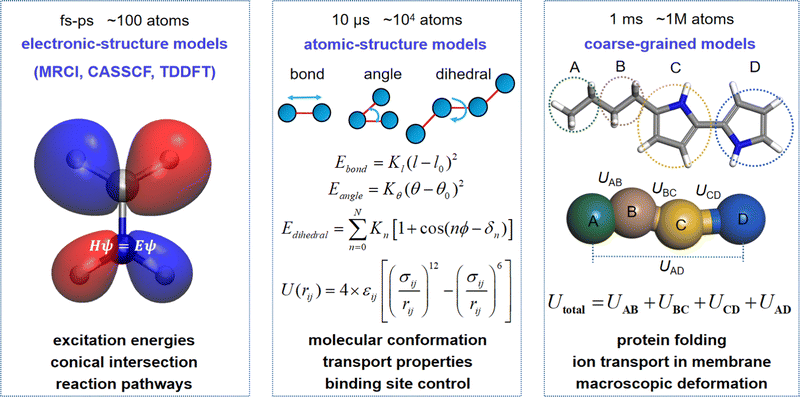
The dynamics and mechanisms that underlie the intricate movement of molecular machines remain puzzling, even with the development of advanced techniques aimed at unveiling their intermediate configuration. These include achieving precise control over single molecules and self-assembled complexes, hampered by low energy conversion efficiency, and understanding the mechanisms governing responsive behavior to external stimuli. However, a new avenue emerges through computational simulations, allowing for the exploration of molecular machine dynamics from single molecular to aggregate and self-assembly at the mesoscale scale. Theoretical chemists are actively pursuing innovative methodologies for conducting long-term simulations in the motion of molecular machines in a cost-effective manner.³⁰ This pursuit extends to both quantum mechanics (QM) and molecular mechanics (MM) levels, benefiting from the facilitation provided by machine learning models. Therefore, theoretical research plays a crucial role in providing insights into the rational design and precise control of molecular machines.

3.1 Electronic-structure calculations

3.1.1 Electronic configurations in excited states. It is crucial to choose an appropriate method in electronic-structure calculations (Fig. 4a), as the accuracy of these calculations affects the topology of the potential energy surfaces (PESs), particularly in the excited state. Moreover, the rotational speed within molecular machines is determined by the PESs in both ground and excited states under the influence of light irradiation. Notably, the conical intersection (CI) plays an important role in a variety of molecular motors and switches during the photoisomerization processes,^31–34 which determines the product and the quantum yield of the photo reactions. To obtain an accurate topology of the energy profile and electronic configuration around CI, multiconfigurational methods, such as complete active space self-consistent field (CASSCF) and multireference configuration interaction (MRCI) methods are required.^35,36 However, the computational demands associated with CASSCF and MRCI methods render their application to larger systems impractical due to the computational cost. The single- and multi-reference approaches were compared to investigate molecular switches and motors in our recent studies,^37–39 revealing that the single-reference method could replicate the experimental absorption spectrum,⁴⁰ however, it failed to obtain CI where the nonadiabatic coupling is too large. A spin–flip time-dependent density functional theory (SF-TDDFT) provides an efficient and promising solution, by including a higher spin configuration as a ref. 41, thus it offers a reasonable description of the crossing region between the electronic states in molecular machines.^31,42

Fig. 4 Theoretical calculation methods based on different time scales.

3.1.2 Non-adiabatic molecular dynamics simulations. The direction of motion within molecular machines can be finely adjusted through the influence of external fields, such as optical, electric, and magnetic fields. This manipulation could improve the overall energy conversion efficiency.^43–45 To unveil the photochemical processes within molecular machines, it is essential to consider the energy profiles along the reaction pathways in both ground and excited states. This can be accomplished through non-adiabatic molecular dynamics (NAMD) simulations. Additionally, the control of vibrational excitations can be achieved using infrared pulses, which could be described by the quantum dynamics (QD) approach. Remarkably, this approach has demonstrated that laser pulses with far-infrared frequencies can induce directional rotation in molecular motors.^43,46 This is exemplified in Fig. 5b, where the phase in the superposition of rotational states can be precisely adjusted by introducing laser fields.

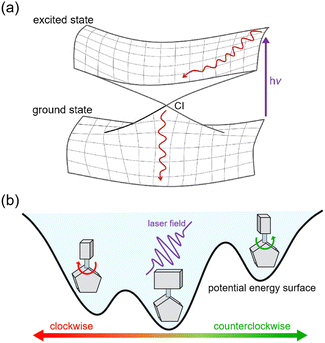Fig. 5 (a) The nonadiabatic dynamics process from excited state to ground state via CI. (b) The directional rotation controlled by laser field in a chiral molecular motors.

In addition, laser fields offer an exciting avenue for tuning electronic excitations in molecular motors, with potential applications in rationally designing the evolution of chemical reactions within these machines. By precisely adjusting the delay time of a laser pulse to resonate with a specific excited state, it becomes possible to control and direct chemical reactions in molecular machines.^47,48 The fewest-switches surface hopping (FSSH) method is a practical approach for handling large systems that involve laser-induced excitation.^49,50 However, performing FSSH simulations, especially with a high number of trajectories, can be computationally intensive, which limits their utility in photochemical studies. Previous simulations relying on electronic structure calculations were carried out in a short timescale, typically within a few picoseconds.^51–53 However, recent advancements in machine learning (ML) have revolutionized NAMD simulations.^54,55 ML enables the analytical construction of PESs with electronic structure-level accuracy, extending NAMD simulations to encompass large-scale photochemical reactions at a low computational cost.^56–59 We have recently developed a machine learning model combined with force fields, specifically designed to construct PESs for a large system in photodynamics simulations.³⁹ Notably, our results align with experimental observations, presenting the potential for broader applications in this field.

ML-based NAMD simulations have significant success in accelerating excited-state dynamics simulations. Despite this progress, several challenges still remain. One of the main obstacles is the need for extensive computational resources and precise electronic structure methods to acquire abundant high-quality training data for constructing high-dimensional PESs. Additionally, choosing the appropriate ML algorithm and input features is crucial, as it directly affects the accuracy and efficiency of the PES. Active learning offers a promising solution by identifying the most informative data points for labeling.^60,61 This approach not only reduces computational demands but also enhances the efficiency of the ML algorithm in simulating photodynamics for molecular machines.

3.2 Molecular-structure calculations

3.2.1 MM and QM/MM simulatioms. In contrast to photodynamics simulations conducted using QM methods on single molecules, studying configurational transitions in complex environments for large systems presents a formidable challenge. This challenge stems from the significant number of degrees of freedom involved in the reactions, the extensive computational resources required, and the extended timescales necessary for simulations. Consequently, the development of multi-scale simulation methods for complex systems becomes imperative.

For large systems, classical dynamics simulations based on molecular mechanics offer a cost-effective and computationally efficient approach to studying molecular motion. Molecular mechanics simplifies the representation of molecular structures by employing a force field at the atomic level (Fig. 4b). This force field describes intermolecular interactions using a potential energy function derived from either experimental data or high-level QM calculations. More than ten force fields have been developed to suit a wide array of molecular systems at present. Bao et al., for example, conducted all-atom molecular dynamics simulations to elucidate that light-driven molecular motors can achieve K⁺ transportation within a lipid bilayer (Fig. 6a).⁶² However, it's important to note that while molecular mechanics provides a computationally efficient approach, it may lack precision in describing certain intermolecular interactions due to limitations in experimental data used for force field parameterization.

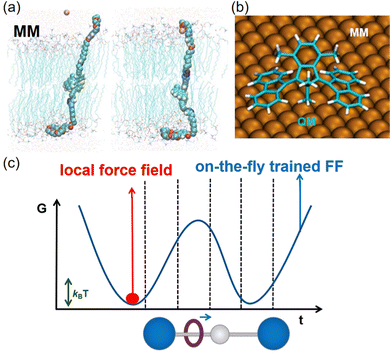Fig. 6 (a) Light-driven molecular motors capture potassium ions. Adapted with permission from ref. 62. Copyright 2022 WILEY-VCHGmbH. (b) QM/MM in a surface-mounted molecular machine. Adapted with permission from ref. 63. Copyright 2023 American Chemical Society. (c) Schematic diagram of on-the-fly trained force field.⁶⁴

The quantum mechanics/molecular mechanics (QM/MM) method integrates the advantages of both the precision of quantum chemistry and the efficiency of molecular mechanics, making it a rapidly evolving approach.⁶⁵ This method is crucial for applying quantum mechanics to address the reactive regions of complex systems, which are of primary interest. Simultaneously, a simplified molecular mechanics model can be employed to account for the surrounding environment. When theoretical simulations involve the study of dynamics in molecular machines in solution, the polarity and viscosity of the solvents play a significant role in influencing the motions of molecular machines. Therefore, it is crucial to consider the interactions between solvents and molecular machines in a cluster model that explicitly includes the first solvation shell. If the cluster model proves to be computationally expensive for quantum mechanics (QM) calculations, a multiscale approach combining quantum mechanics and molecular mechanics (QM/MM) can be utilized. This QM/MM model has proven instrumental in investigating the impact of solvents on the thermal inversion of molecular motors.⁶⁶ This research revealed that solvents can influence the rotation of molecular motors, particularly those with large dipole moments. Additionally, Srivastava et al. utilized an MM model to characterize the metal surface, shedding light on the mechanism governing the forward motion of molecular motors on metal surfaces (Fig. 6b).⁶³

The challenge of accuracy and universal applicability still persists, even with the powerful QM/MM and MM methods for simulating molecular machine motions. The manual parameterization of force fields often requires prior knowledge and can be nontrivial and relatively cumbersome. Novel methods for optimizing force field parameters are needed to accelerate dynamics simulations. An on-the-fly training algorithm has been introduced to simplify parameter optimization automatically. This approach aims to address inaccuracies in force fields resulting from inadequate phase space sampling (Fig. 6c) by the development of machine learning models, which offers an efficient means to enhance force field accuracy.^64,67 This methodology involves generating initial trajectories using low-level methods and then employing machine learning to reduce the discrepancies between low-level and high-level calculations of energies and gradients. Molecular machines’ conformations can vary based on the environment, causing charge redistribution due to environmental polarization effects. Updating charges, especially in the presence of strong interactions, considering intermolecular interactions can be exceptionally time-consuming. Developing a real-time charge updating protocol is imperative for handling molecular machines in diverse environments.

3.2.2 Enhanced sampling. Capturing the configuration adaptation in response to external stimuli through molecular dynamics (MD) simulations within millisecond timescales can be challenging due to the vast number of configurations and the length of simulations involved. Particularly in such complex systems for molecular machines, utilization of enhanced sampling methods becomes imperative to achieve comprehensive simulation results within a finite timeframe.

There are two categories of enhanced sampling techniques, depending on how collective variables (CVs) are defined. In the first category, CVs are predefined as reaction coordinates, and an external biasing force is introduced to accelerate the simulation efficiency. This category includes approaches like metadynamics, umbrella sampling, and ABF adaptive biasing force techniques (ABF), which require prior knowledge of reaction pathways. In the ABF method, four CVs were introduced to elucidate the shuffling process of rotaxane motion by obtaining its free energy landscape across two transition states (Fig. 7a).⁶⁸ Additionally, Parrinello and colleagues employed the Gaussian mixture-based enhanced sampling (GAMBES) method to explore how solvent impacts the binding affinity of host–guest complexes, significantly expediting the determination of guest molecule residence times.⁶⁸ Several metadynamics techniques, including well-tempered metadynamics (WT-MetaD), were employed to achieve extensive sampling of metastable states during the rotational motion of four macrocycles. This enabled the reconstruction of the potential energy surface and provided insights into the shuttle mechanism (Fig. 7b).⁶⁹ This research presents a promising and potentially universal approach for studying the key factors influencing the dynamics of various host–guest supramolecules.

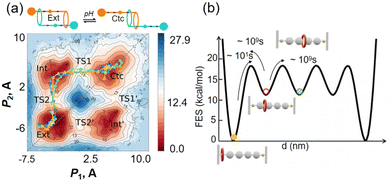Fig. 7 (a) Free-energy landscape of contraction/extension of the [c2]daisy chain computed by adaptive biasing force techniques calculations. Adapted with permission from ref. 68. Copyright 2021 American Chemical Society. (b) Free energy and barriers of each state. Adapted with permission from ref. 69. Copyright 2023 Royal Society of Chemistry.

When dealing with multidimensional motions in molecular machines that can’t be deduced intuitively, another approach is needed where CVs are unknown beforehand.³⁰ The replica exchange molecular dynamics (REMD) method is particularly suitable for simulating the relative motion within molecular machines in multidimensional space. In summary, enhanced sampling methods have been widely applied in the study of molecular machines to reduce the computational cost for MD simulations in molecular motions. Especially in simulating rare events, enhanced sampling not only aids in reconstructing more accurate PESs in the investigation of thermodynamics and kinetics of molecular reactions, but also allows for exploration of the influence of the surrounding environment on molecular machine motions. This provides valuable insights for the improved design and control of molecular machines.

3.3 Coarse-grained simulations

All-atom molecular dynamics (AAMD) simulations offer a detailed description of molecular and material evolution at the atomic level, however, when dealing with complex systems beyond the microscopic scale during reactions that span nanoseconds, AAMD simulations become computationally expensive. In such cases, coarse-grained molecular dynamics (CGMD) and dissipative particle dynamics (DPD) simulations present viable alternatives for investigating phase transitions, as well as chemical and physical properties. Employing multi-scale simulations of molecular machines, ranging from microscale to mesoscale, and even macroscale, provides comprehensive tools for illustrating the assembly's evolution and its response to external fields.

To accurately capture the atomic-level deformation of polymers induced by photo-responsive units, a reactive rotational potential is applied, transitioning from AAMD to CGMD. This transition enables the simulation of disordered morphologies in photo-mechanical response liquid crystal polymers when azobenzene sub-units respond to thermal or photo conditions.^70,72 As depicted in Fig. 8a, this model can predict mechanical properties and macroscopic transitions resulting from photoresponsive structures. Beyond AAMD, CGMD could be employed to investigate the self-assembly process in polymers, where the atomic configuration is not critical in determining the morphology. For instance, macroscopic stress within polymer backbones arises from the reorientation of azobenzene molecules in the case of photo-induced stress polymers. Dynamical properties as simulated by CGMD, have effectively illustrated the relationship between polymer orientation and light intensity and density.⁷³ Furthermore, CGMD simulations have shed light on how the morphology of self-assembled structures can be tuned. For example, in peptide-based hydrogels, CGMD investigations have revealed that the stacking of azobenzene molecules and the arrangement of peptide units play a crucial role in determining the self-assembly's morphology.⁷⁴ Therefore, CGMD has proven its capability in simulating phase transitions and dynamical properties within self-assembled complex systems.

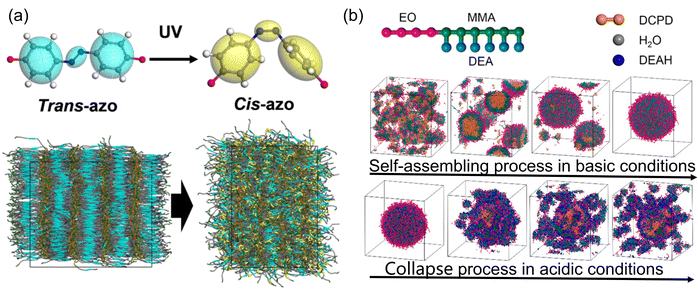Fig. 8 (a) Combined coarse-grained molecular dynamics and finite-element study of light-activated deformation of liquid crystal polymer. Adapted with permission from ref. 70. Copyright 2021 American Physical Society. (b) Dissipative particle dynamics simulations on a pH-responsive drug delivery diblock copolymer hydrogels. Adapted with permission from ref. 71. Copyright 2017 American Chemical Society.

While atomic simulations are indispensable for providing static information and translation rates within hierarchical multifunctional systems at the equilibrium stage,⁷⁵ they may fall short when addressing phase transitions in self-assembly that extend beyond equilibrium. In such cases, DPD simulations come to the fore. Consider the example of drug release, achieved by shifting the chemical environment from neutral to acidic conditions. This transition has been effectively demonstrated through DPD simulations in pH-responsive hydrogels,^71,76 as illustrated in Fig. 8b. DPD simulations have unveiled that drug release occurs due to the repulsive forces between protonated molecular chains. Moreover, DPD simulations have illuminated how interactions between drugs and solvents can impact the amount of released drugs in self-assembled amphiphilic block copolymers and nanoparticles, providing valuable insights into the kinetics of drug release.⁷⁷

While simulating macroscopic motions in molecular machine-integrated complex systems remains a challenge, machine learning models offer a potent means to bridge the gap between microscopic and macroscopic movements. These ML models have accelerated the prediction of hydrogel properties, based on the relationships between chemical structure and properties.⁷⁸ Moreover, by effectively identifying key parameters in the driving forces behind macroscopic transformations, ML models have demonstrated their ability to accurately predict properties that respond to external stimuli within these materials.^79,80

The relationship between microscopic responses to stimuli and macroscopic movements has been investigated through both computational simulations and experimental measurements. However, designing a practical strategy to precisely tune the macroscopic movement and responsive behavior of functional groups remains a challenge. Integrating atomic-level simulations with coarse-grained molecular dynamics shows promise in revealing the intricate connections between microscopic composition, structure, morphology, and macroscopic movement. This approach has the potential to significantly enhance our understanding of complexity and expedite the development of innovative responsive materials.

3.4 Challenges in collective motion of molecular assemblies

At scales beyond the molecular level, precise control over collective motion within molecular aggregates is crucial for optimizing the functionality of molecular machines. Recent studies have focused on utilizing the driving forces efficiently at larger length scales to induce macroscopic movements.^3,81,82 Investigations have revealed that the dynamic nature of molecular interactions, particularly fluctuations within parts of molecular aggregates, can impact neighboring components, potentially disrupting assembled behavior. This poses a significant challenge when integrating molecular machines into nano-materials. The main challenges and obstacles are outlined as follows. Firstly, achieving synchronized movement among molecular aggregates is crucial but challenging. The movement of one molecule can disturb the equilibrium state of surrounding molecules, creating difficulties. Solutions inspired by nature, such as enzymes capable of triggering coordinated or cooperative actions, provide insights into overcoming this challenge. Another difficulty arises from the uncontrollable motion in collective assembly due to intermolecular interactions in multiple dimensions. While dynamic bonds offer controllable deformation in supramolecules, tuning parameters in the external field is nontrivial. Therefore, optimal parameters can be obtained through computational simulations when the external field is included in non-equilibrium dynamics simulations.⁸³

As discussed above, theoretical simulations provide valuable insights into the formation of dynamic structures and their interactions with the environment, serving as a solid foundation for the design of innovative molecular machines. Exploring the multi-body interactions inherent in molecular machines, Kapral utilized a coarse-grained model to delineate the chemical interactions between fluid flow and molecular machines. This approach acts as a driving force in the formation of clusters, as demonstrated in his work.⁸⁴ Several strategies have been employed to effectively control the transition from the motion of individual molecules to the movement of the entire assembly.

Firstly, supramolecular arrangements have been successfully reported to amplify motions resulting from π–π, hydrogen bonding, and hydrophobic interactions.^81,82 Upon exposure to external stimuli, supramolecular structures undergo reversible changes by disrupting their dynamic chemical bonds.⁸⁴ It's noteworthy that the collective motions of supramolecular aggregates can be influenced by chemical gradients generated by the surrounding medium. From a microscopic perspective, the individual motion of a single molecular machine could be amplified into collective motions, when the interaction between the molecules and the chemical gradients are manipulated properly.

Secondly, surface-mounted molecular assemblies offer an effective approach to drive molecular rotation or translation, resulting in spatially directed collective motion. Physical parameters such as conductivity, wettability, and coverage can be precisely tuned to organize molecules into ordered arrays, thereby enhancing their collective motion.^3,81,82 Following irradiation or other stimuli, densely packed arrays can undergo switching due to fluctuations in neighboring molecules. Even though conformational changes may lead to unstable isomers, rapid growth of newly ordered structural domains could be obtained when spatial adjustments among neighboring molecules decrease.

The introduction of external fields with tunable characteristics, such as electric fields and polarized light, could effectively regulate the configurational changes of molecular machines.^84,85 Achieving directional motions of molecular aggregates on the surface could be accomplished by aligning the external field with the dipole moments of molecular machines, thereby reducing their rotational energy barriers. Recently, it has been reported that molecular switches have been fabricated on surfaces using tip-enhanced Raman spectroscopy,⁸⁶ achieving fast configuration transformation. Computational models could be employed in external field manipulation, exploring potential energy surfaces along with the projection of the dipole moment of the rotator of molecular machines, as shown in our previous work.⁸³ The computational results provided insight into the direction of the electric field along the transition, where the dipole moments change significantly.

While various theoretical approaches have been proposed to study molecular machines across different scales, research on the cooperative dynamics of molecular machines at large-length scales remains limited.⁸⁴ In complex systems, computational modeling has primarily focused on the rotational moieties within molecular machines, using accurate methods. However, accurately describing the propagation of motion at the same level, as illustrated in Fig. 9, has proven challenging. The dynamic disorder in self-assembled systems arises from non-equilibrium transitions, making it computationally demanding to capture collective motions. The directional motion of molecular machines could be finely tuned by investigating the potential energy surface and projection of dipole moments of molecular assembly. The orientation of the electric field could be manipulated to align with the changes of dipole moments along the potential energy surface, as shown in Fig. 9(b). Future advancements in computational methods could enable the modeling of non-equilibrium processes, especially in the presence of controllable external fields, to facilitate simulations of long-time-scale dynamics.

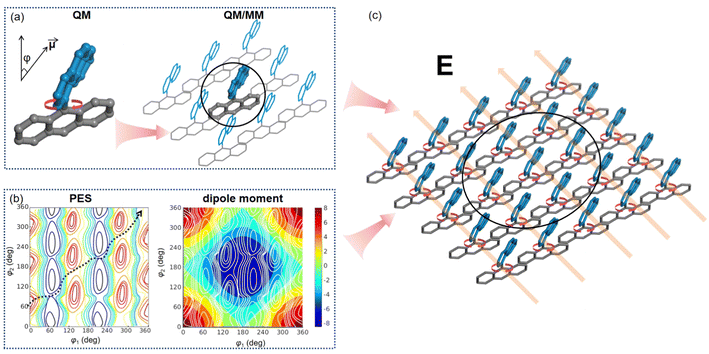Fig. 9 Computational simulations, employing multiscale models (a), are utilized to regulate the collective motion of an array of molecular rotors through external fields. (b) Illustration of the potential energy surfaces (left) and projection of dipole moments (right) of molecular rotors. The rotational direction (dashed line) is manipulated by regulating the electric field (c). Adapted with permission from ref. 83. Copyright 2019 American Chemical Society.

4 Conclusions and outlook

Molecular machines have been under development for decades, however, their potential applications remain constrained to specific operating conditions. Realizing the full potential of molecular machines demands a delicate balance between intricate organic synthesis and precise device manipulation. While experimental advancements have been substantial, theoretical progress can play a pivotal role in guiding experimental synthesis and modifications. Progress has been achieved in three aspects of theoretical simulations. Firstly, electronic structure calculations in the ground state have successfully extended to large systems. However, studying the potential energy surfaces in excited states remains a challenge for light-driven molecular machines. The complexity arises due to the large number of degrees of freedom in these systems, resulting in high-dimensional PESs that demand substantial computational resources for an accurate description of electronic structures in excited states. Future efforts could focus on developing cost-effective methods, possibly utilizing machine learning tools, to obtain precise PESs. This advancement could significantly accelerate photodynamics simulations for light-driven molecular machines.

Secondly, simulating the transitions between different equilibrium states poses challenges not only in terms of time but also due to the lack of efficient theoretical approaches. In real systems, non-equilibrium reaction processes occur relatively slowly, often at the nanosecond level. While coarse-grained models can effectively capture these non-equilibrium processes in molecular machines, they often miss out on molecular-level motions, leading to inaccuracies in describing configurational changes. Finding the right balance between computational demand and accuracy is crucial. Hence, there is a need for a hybrid model that incorporates atomic-level information about molecular configurations alongside coarse-grained approaches. This hybrid approach is essential to quantitatively characterize transitions from equilibrium to non-equilibrium processes induced by external stimuli.

Thirdly, the selection of collective variables (CVs) for sampling is a critical step, as these variables need to distinguish not only between the initial and final states but also guide the reaction path along the lowest free energy profile. Introducing bias ensures a reasonable transition rather than navigating through high free energy pathways, leading to faster convergence and a more accurate representation of the free energy landscape. However, identifying suitable CVs can be challenging and requires prior knowledge. In complex systems, multiple CVs are often employed to assess the system's reaction process. Biases can also be introduced to the potential energy surface in enhanced sampling methods, especially when dealing with rare events, as obtaining accurate rate constants is nearly impossible due to statistical uncertainties. Recent approaches have utilized neural networks (NNs) to enhance the construction of free energy profiles by selecting effective CVs. Training data points are sampled from trajectories in molecular dynamics simulations. While the training set may not cover the entire configuration space, an iterative active learning approach can be employed to explore new configurational spaces and improve the potential energy surface automatically. However, this protocol is still limited to small systems due to the computational resources required to construct accurate potential energy surfaces from multiple trajectories. Consequently, exploring complex molecules remains challenging, along with the need to improve the transferability of machine learning models.

In summary, improving the accuracy of electronic structure calculations for describing excited states and enhancing sampling approaches are crucial steps in simulating the stimuli-responsive behavior of molecular machines. This progress can be further supported by the development of accurate molecular machine models. Furthermore, integrating atomic-level molecular simulations with coarse-grained methods enables simulations on a larger scale, aiding in predicting molecular-level configurational deformations. This, in turn, facilitates the rational design of smart materials, ensuring efficient macroscopic mechanical movements.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. W. thanks the financial support by the Fundamental Research Funds for the Central Universities (2232023A-02), Shanghai Municipal Science and Technology Commission (22511103900), and National Natural Science Foundation of China (22173017).

Notes and references

1. V. Richards, Nat. Chem., 2016, 8, 1755–4349.
2. V. Balzani, A. Credi, F. M. Raymo and J. F. Stoddart, Angew. Chem., Int. Ed., 2000, 39, 3348–3391.
3. D. Dattler, G. Fuks, J. Heiser, E. Moulin, A. Perrot, X. Yao and N. Giuseppone, Chem. Rev., 2020, 120, 310–433.
4. D. R. Pooler, A. S. Lubbe, S. Crespi and B. L. Feringa, Chem. Sci., 2021, 12, 14964–14986.
5. J. Beswick, V. Blanco, G. De Bo, D. A. Leigh, U. Lewandowska, B. Lewandowski and K. Mishiro, Chem. Sci., 2015, 6, 140–143.
6. Y. Liu, A. H. Flood, P. A. Bonvallet, S. A. Vignon, B. H. Northrop, H.-R. Tseng, J. O. Jeppesen, T. J. Huang, B. Brough, M. Baller, S. Magonov, S. D. Solares, W. A. Goddard, C.-M. Ho and J. F. Stoddart, J. Am. Chem. Soc., 2005, 127, 9745–9759.
7. V. García-López, D. Liu and J. M. Tour, Chem. Rev., 2020, 120, 79–124.
8. N. Katsonis, M. Lubomska, M. M. Pollard, B. L. Feringa and P. Rudolf, Prog. Surf. Sci., 2007, 82, 407–434.
9. M. R. Panman, B. H. Bakker, D. Den Uyl, E. R. Kay, D. A. Leigh, W. J. Buma, A. M. Brouwer, J. A. Geenevasen and S. Woutersen, Nat. Chem., 2013, 5, 929–934.
10. L. Andreoni, M. Baroncini, J. Groppi, S. Silvi, C. Taticchi and A. Credi, Energy Fuels, 2021, 35, 18900–18914.
11. E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2007, 46, 72–191.
12. F. Lancia, A. Ryabchun and N. Katsonis, Nat. Rev. Chem., 2019, 3, 536–551.
13. C. Schäfer, G. Ragazzon, B. Colasson, M. La Rosa, S. Silvi and A. Credi, ChemistryOpen, 2016, 5, 120–124.
14. I. N. Unksov, C. S. Korosec, P. Surendiran, D. Verardo, R. Lyttleton, N. R. Forde and H. Linke, ACS Nanosci. Au, 2022, 2, 140–159.
15. D. R. Pooler, A. S. Lubbe, S. Crespi and B. L. Feringa, Chem. Sci., 2021, 12, 14964–14986.
16. A. Gerwien, P. Mayer and H. Dube, J. Am. Chem. Soc., 2018, 140, 16442–16445.
17. G. B. Boursalian, E. R. Nijboer, R. Dorel, L. Pfeifer, O. Markovitch, A. Blokhuis and B. L. Feringa, J. Am. Chem. Soc., 2020, 142, 16868–16876.
18. T. R. Rusch, A. Schlimm, N. R. Krekiehn, B. M. Flöser, F. Röhricht, M. Hammerich, I. Lautenschläger, T. Strunskus, R. Herges, F. Tuczek and O. M. Magnussen, J. Phys. Chem. C, 2019, 123, 13720–13730.
19. J. Kaleta, J. Chen, G. Bastien, M. Dracínský, M. Mašát, C. T. Rogers, B. L. Feringa and J. Michl, J. Am. Chem. Soc., 2017, 139, 10486–10498.
20. S. Ikejiri, Y. Takashima, M. Osaki, H. Yamaguchi and A. Harada, J. Am. Chem. Soc., 2018, 140, 17308–17315.
21. W.-J. Li, W. Wang, X.-Q. Wang, M. Li, Y. Ke, R. Yao, J. Wen, G.-Q. Yin, B. Jiang, X. Li, P. Yin and H.-B. Yang, J. Am. Chem. Soc., 2020, 142, 8473–8482.
22. A. Saura-Sanmartin, A. Martinez-Cuezva, D. Bautista, M. R. Marzari, M. A. Martins, M. Alajarin and J. Berna, J. Am. Chem. Soc., 2020, 142, 13442–13449.
23. J.-s Geng, L. Mei, Y.-y Liang, L.-y Yuan, J.-p Yu, K.-q Hu, L.-h Yuan, W. Feng, Z.-f Chai and W.-q Shi, Nat. Commun., 2022, 13, 2030.
24. J. Hou, G. Long, W. Zhao, G. Zhou, D. Liu, D. J. Broer, B. L. Feringa and J. Chen, J. Am. Chem. Soc., 2022, 144, 6851–6860.
25. T. Kureha, D. Aoki, S. Hiroshige, K. Iijima, D. Aoki, T. Takata and D. Suzuki, Angew. Chem. Int. Ed., 2017, 56, 15393–15396.
26. M. P. Da Cunha, E. A. van Thoor, M. G. Debije, D. J. Broer and A. P. Schenning, J. Mater. Chem. C, 2019, 7, 13502–13509.
27. S. Iamsaard, E. Anger, S. J. Aßhoff, A. Depauw, S. P. Fletcher and N. Katsonis, Angew. Chem., 2016, 128, 10062–10066.
28. W.-J. Li, W. Wang, X.-Q. Wang, M. Li, Y. Ke, R. Yao, J. Wen, G.-Q. Yin, B. Jiang and X. Li, et al. , J. Am. Chem. Soc., 2020, 142, 8473–8482.
29. J. Bao, Z. Wang, C. Song, Y. Zhang, Z. Li, L. Zhang, R. Lan and H. Yang, Adv. Mater., 2023, 2302168.
30. H. Fu, X. Shao and W. Cai, Phys. Chem. Chem. Phys., 2022, 24, 1286–1299.
31. Y. Li, F. Liu, B. Wang, Q. Su, W. Wang and K. Morokuma, J. Chem. Phys., 2016, 145, 244311.
32. X. Pang, X. Cui, D. Hu, C. Jiang, D. Zhao, Z. Lan and F. Li, J. Phys. Chem. A, 2017, 121, 1240–1249.
33. M. J. Bearpark, F. Bernardi, S. Clifford, M. Olivucci, M. A. Robb and T. Vreven, J. Phys. Chem. A, 1997, 101, 3841–3847.
34. T. Ishikawa, T. Noro and T. Shoda, J. Chem. Phys., 2001, 115, 7503–7512.
35. B. O. Roos, Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2, 1987, vol. 69, pp. 399–445.
36. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814.
37. J. Wen, Z. Tian and J. Ma, J. Phys. Chem. C, 2013, 117, 19934–19944.
38. Z. Tian, J. Wen and J. Ma, J. Chem. Phys., 2013, 139, 014706.
39. H. Xu, B. Zhang, Y. Tao, W. Xu, B. Hu, F. Yan and J. Wen, J. Phys. Chem. A, 2023, 127, 7682–7693.
40. J. Wen, S. Mai and L. Gonzalez, J. Phys. Chem. A, 2023, 127, 9520–9529.
41. A. I. Krylov and C. D. Sherrill, J. Chem. Phys., 2002, 116, 3194–3203.
42. F. Romeo-Gella, I. Corral and S. Faraji, J. Chem. Phys., 2021, 154, 064111.
43. L. Pfeifer, N. V. Hoang, M. Scherübl, M. S. Pshenichnikov and B. L. Feringa, Sci. Adv., 2020, 6, eabb6165.
44. J. S. Seldenthuis, F. Prins, J. M. Thijssen and H. S. van der Zant, ACS Nano, 2010, 4, 6681–6686.
45. S. Stolz, O. Gröning, J. Prinz, H. Brune and R. Widmer, Proc. Natl. Acad. Sci. U.S. A., 2020, 117, 14838–14842.
46. M. Yamaki, K. Hoki, Y. Ohtsuki, H. Kono and Y. Fujimura, J. Am. Chem. Soc., 2005, 127, 7300–7301.
47. K. Hoki, M. Sato, M. Yamaki, R. Sahnoun, L. González, S. Koseki and Y. Fujimura, J. Phys. Chem. B, 2004, 108, 4916–4921.
48. M. Yamaki, K. Hoki, H. Kono and Y. Fujimura, Chem. Phys., 2008, 347, 272–278.
49. P. Marquetand, M. Richter, J. González-Vázquez, I. Sola and L. González, Faraday Discuss., 2011, 153, 261–273.
50. M. Heindl and L. González, J. Chem. Phys., 2021, 154, 144102.
51. M. Filatov, M. Paolino, S. K. Min and K. S. Kim, J. Phys. Chem. Lett., 2018, 9, 4995–5001.
52. M. Filatov, M. Paolino, R. Pierron, A. Cappelli, G. Giorgi, J. Léonard, M. Huix-Rotllant, N. Ferré, X. Yang and D. Kaliakin, et al. , Nat. Commun., 2022, 13, 6433.
53. A. Nikiforov, J. A. Gamez, W. Thiel and M. Filatov, J. Phys. Chem. Lett., 2016, 7, 105–110.
54. D. Hu, Y. Xie, X. Li, L. Li and Z. Lan, J. Phys. Chem. Lett., 2018, 9, 2725–2732.
55. W.-K. Chen, X.-Y. Liu, W.-H. Fang, P. O. Dral and G. Cui, J. Phys. Chem. Lett., 2018, 9, 6702–6708.
56. J. Westermayr, M. Gastegger and P. Marquetand, J. Phys. Chem. Lett., 2020, 11, 3828–3834.
57. J. Li, P. Reiser, B. R. Boswell, A. Eberhard, N. Z. Burns, P. Friederich and S. A. Lopez, Chem. Sci., 2021, 12, 5302–5314.
58. S. Axelrod, E. Shakhnovich and R. Gómez-Bombarelli, Nat. Commun., 2022, 13, 3440.
59. J. Behler, Chem. Rev., 2021, 121, 10037–10072.
60. J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903.
61. J. Westermayr, M. Gastegger, M. F. Menger, S. Mai, L. González and P. Marquetand, Chem. Sci., 2019, 10, 8100–8107.
62. H. Yang, J. Yi, S. Pang, K. Ye, Z. Ye, Q. Duan, Z. Yan, C. Lian, Y. Yang and L. Zhu, et al. , Angew. Chem., 2022, 134, e202204605.
63. G. Srivastava, P. SÌŒtacko, J. I. Mendieta-Moreno, S. Edalatmanesh, J. C. Kistemaker, G. H. Heideman, L. Zoppi, M. Parschau, B. L. Feringa and K.-H. Ernst, ACS Nano, 2023, 17, 3931–3938.
64. E. Kolodzeiski and S. Amirjalayer, J. Chem. Theory Comput., 2021, 17, 7010–7020.
65. G. Monard and K. M. Merz, Acc. Chem. Res., 1999, 32, 904–911.
66. J. Wen, M. Zhu and L. González, Chemistry, 2022, 4, 185–195.
67. O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schuitt, A. Tkatchenko and K.-R. Muiller, Chem. Rev., 2021, 121, 10142–10186.
68. F. E. Blanc and M. Cecchini, J. Phys. Chem. Lett., 2021, 12, 3260–3265.
69. L. Leanza, C. Perego, L. Pesce, M. Salvalaglio, M. von Delius and G. M. Pavan, Chem. Sci., 2023, 14, 6716–6729.
70. J. Moon, H. Chung and M. Cho, Phys. Rev. E, 2021, 103, 012703.
71. Z. Wang, J. Gao, V. Ustach, C. Li, S. Sun, S. Hu and R. Faller, Langmuir, 2017, 33, 7288–7297.
72. J. Moon, B. Kim, J. Choi and M. Cho, Macromolecules, 2019, 52, 2033–2049.
73. J. M. Ilnytskyi, V. Toshchevikov and M. Saphiannikova, Soft Matter, 2019, 15, 9894–9908.
74. X. Wang, Y. Wang, J. Wang, Z. Li, J. Zhang and J. Li, Colloids Surf. A Physicochem. Eng. Asp., 2023, 663, 131020.
75. E. Kolodzeiski and S. Amirjalayer, Sci. Adv., 2022, 8, eabn4426.
76. S. Zeng, X. Quan, H. Zhu, D. Sun, Z. Miao, L. Zhang and J. Zhou, Langmuir, 2021, 37, 1225–1234.
77. L. Jia, R. Wang and Y. Fan, Soft Matter, 2020, 16, 3088–3095.
78. F. Li, J. Han, T. Cao, W. Lam, B. Fan, W. Tang, S. Chen, K. L. Fok and L. Li, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11259–11264.
79. C. Boztepe, A. Künkül and M. Yüceer, J. Drug Delivery Sci. Technol., 2020, 57, 101603.
80. K. Ishizaki, R. Sugimoto, Y. Hagiwara, H. Koshima, T. Taniguchi and T. Asahi, CrystEngComm, 2021, 23, 5839–5847.
81. E. Moulin, L. Faour, C. C. Carmona-Vargas and N. Giuseppone, Adv. Mater., 2020, 32, 1906036.
82. J. M. Abendroth, O. S. Bushuyev, P. S. Weiss and C. J. Barrett, ACS Nano, 2015, 9, 7746–7768.
83. J. Kaleta, G. Bastien, J. Wen, M. Dracínský, E. Tortorici, I. Císarová, P. D. Beale, C. T. Rogers and J. Michl, J. Org. Chem., 2019, 84, 8449–8467.
84. B. Robertson, M.-J. Huang, J.-X. Chen and R. Kapral, Acc. Chem. Res., 2018, 51, 2355–2364.
85. Y. Yuan, G. N. Abuhaimed, Q. Liu and I. I. Smalyukh, Nat. Commun., 2018, 9, 5040.
86. L.-Q. Zheng, S. Yang, J. Lan, L. Gyr, G. Goubert, H. Qian, I. Aprahamian and R. Zenobi, J. Am. Chem. Soc., 2019, 141, 17637–17645.

---