Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of urea in formation of the sodium acetate trihydrate (SAT)–urea eutectic liquid: a neutron diffraction and isotopic substitution study†
Emily L.
Byrne
 a,
Sanskrita
Madhukailya
a,
Sanskrita
Madhukailya
 a,
Oliver L. G.
Alderman
b,
Marijana
Blesic
a,
Oliver L. G.
Alderman
b,
Marijana
Blesic
 a and
John D.
Holbrey
a and
John D.
Holbrey
 *a
*a
aThe QUILL Research Centre, School of Chemistry and Chemical Engineering, Queen's University Belfast, David Keir Building, Stranmillis Road, Belfast BT9 5AG, UK. E-mail: j.holbrey@qub.ac.uk
bISIS, Rutherford Appleton Laboratory, Harwell Science & Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
First published on 22nd December 2023
Abstract
Neutron diffraction with isotopic substitution has been used to investigate the structure of the liquid sodium acetate trihydrate–urea eutectic (mole fraction (χurea) of 0.60) at 50 °C. Urea competes with acetate anions and water molecules in the solvation of sodium ions, displacing water and, simultaneously, stabilising the liberated ‘excess’ water through hydrogen bonding between water and urea molecules in the eutectic liquid. This provides a direct insight into the role of urea as both denaturant and hydrogen-bond network former in generating eutectic liquids.
Introduction
Phase change materials (PCMs) are of interest for latent heat thermal energy storage devices across a range of temperature scales to capture and release heat energy at defined temperatures through melting/freezing phase transitions. As thermal energy storage media, PCMs have uses in solar energy storage, heat management in buildings, industrial exhaust heat recovery, and thermal management systems.1 A wide range of materials have been explored for applications as PCMs including molecular organics (paraffins, polyols, fatty acids etc.), organic2 and inorganic3 salts.Inorganic salt hydrates,4 that combine large heat capacities with high energy density and low cost, are desirable materials. However, instability through loss of water can lead to phase segregation and extensive supercooling that inhibits crystallisation can both be significant challenges to their practical application. Sodium acetate trihydrate (SAT) is one example of a salt hydrate that has been widely studied as a PCM for potential thermal management and storage applications.5,6 The low melting point (58–58.4 °C) and large enthalpy of fusion (ΔHfus 264.0 kJ kg−1) are highly desirable characteristics, however incongruent melting forming liquid sodium acetate n-hydrate and solid anhydrous sodium acetate causes problematic phase segregation.7 The addition of urea to SAT leads to melting point depression and the formation of a pseudo-ternary SAT–urea eutectic at 40 wt% urea (mole fraction, χurea of 0.60, see Fig. 1).8 This eutectic composition melts congruently at 31.4 °C while retaining a large latent heat of fusion (ΔHfus 205.3 kJ kg−1). As well as interest as a potential PCM, the SAT–urea eutectic liquid has also been explored as a non-toxic solvent for use in chemical synthesis,9 solubilisation and extraction of oligosaccharides, antioxidants and proteins from waste biomass,10 and for preparation of gelatin films.11
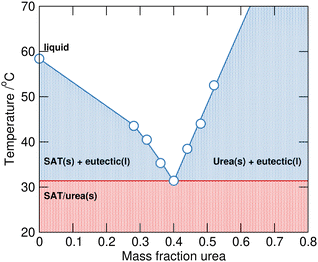 | ||
| Fig. 1 The SAT–urea solid–liquid equilibrium phase diagram plotted with data taken from Li et al.6 | ||
The SAT–urea liquid offers opportunities to study the potential competitive and/or collaborative interactions between urea and water in concentrated ionic liquids bridging between molten salt hydrates12 and inorganic salt–urea eutectic liquids.13 Moreover, the interactions between urea and water in organic deep eutectic liquids such as choline chloride–urea14 and choline acetate–urea15 are of interest, with the former reported to retain a remarkable degree of ionic liquid structural integrity even after addition of large mole fractions of water16 whereas choline acetate–urea exhibits loss of ionic structure on addition of water.17
Here we describe the liquid structure of liquid SAT–urea studied at the eutectic composition, comparing the competing interactions between the different components present in the melt (sodium and acetate ions, water and urea), using neutron diffraction on the SANDALS diffractometer at the ISIS pulsed neutron source in order to investigate the role of urea as a eutectic former.
Experimental
Materials
All chemicals (anhydrous sodium acetate, sodium acetate-d3, urea, urea-d4, and D2O with purities >99% except urea-d4 which was 98 atom%) were purchased from Merck (Sigma-Aldrich). Seven isotopomeric SAT–urea samples were prepared with the H/D-distributions between acetate, water, and urea shown in Table 1 at the eutectic composition of the fully protiated system (0.40 mole fraction sodium acetate trihydrate and 0.60 mole fraction urea). SAT–urea samples were prepared by mixing appropriate quantities of the corresponding protic or deuterated anhydrous sodium acetate, water and urea in sealed glass vials and then heating at 50 °C until homogeneous liquids were obtained.Neutron scattering experiments
Total neutron scattering data were collected from the seven SAT–urea samples shown in Table 1 using the SANDALS diffractometer at the ISIS pulsed neutron source. Samples were loaded into ‘null scattering’ Ti0.68Zr0.32 flat plate cells with internal geometries of 1 × 35 × 35 mm with a wall thickness of 1 mm. SANDALS has a wavelength range of 0.05–4.95 Å, and data were collected above the melting points for all the H/D-isotopomeric compositions (as shown from the measurements in Fig. 2) at 50 °C over a Q range from 0.1–50 Å−1 (with Q = 2π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ, where 2θ = scattering angle and λ = wavelength). During measurements, the cell was maintained at a temperature of 50 °C using a recirculating heater (Julabo FP50).
θ/λ, where 2θ = scattering angle and λ = wavelength). During measurements, the cell was maintained at a temperature of 50 °C using a recirculating heater (Julabo FP50).
Experimental sample densities (Table 1) and scattering levels obtained were consistent with the isotopic compositions of the samples. Absolute values of the differential cross sections were obtained from the raw scattering data by normalising against a 3.1 mm thick null-scattering vanadium–niobium alloy (0.9485![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0515) standard and correcting for background and multiple scattering, container scattering and self-attenuation, using GUDRUN.18 The neutron structure factors obtained from GUDRUN were further analysed by fitting to atomistic models using Empirical Potential Structure Refinement (EPSR).19 Details of the GUDRUN and EPSR input files are included in ESI.†
0.0515) standard and correcting for background and multiple scattering, container scattering and self-attenuation, using GUDRUN.18 The neutron structure factors obtained from GUDRUN were further analysed by fitting to atomistic models using Empirical Potential Structure Refinement (EPSR).19 Details of the GUDRUN and EPSR input files are included in ESI.†
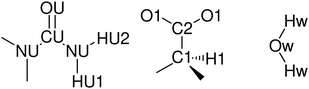
The EPSR approach consists of a Monte Carlo simulation, using Lennard-Jones potentials with atom-centred point charges that are combined with basic information about the structure of the atoms or molecules present in the system and total atomic densities of the system to constrain the model in a chemically and physically reasonable manner. By comparing the differences between calculated and experimental structure factors in Q-space for each data set, an empirical perturbation potential is determined. This is combined with the reference potential and used as the new potential for simulations, iteratively driving the model towards agreement with experimental data. EPSR of the liquid was performed against the experimental data for all seven isotopologues simultaneously over the range (Q = 0.1–30 Å−1). Initial interatomic distance constraints used to define the basic molecular geometries were obtained from MOPAC with the AM1 model, and Lennard-Jones reference potentials for each atom type were taken from OPLS-AA20 and, for water, SPC21 non-bonded parameters. Atom types are defined based on unique positions in the molecular skeletons (Fig. 3). Full parameters of the reference potential and interatomic distance and angular constraints used to define the basic molecular geometries are given in Table 2 and 3.
| Atom label | ε/kJ mol−1 | σ/Å | q/e |
|---|---|---|---|
| Sodium | |||
| Na | 0.0117 | 3.33 | 0.8000 |
| Acetate | |||
| C1 | 0.2761 | 3.50 | −0.2240 |
| C2 | 0.4393 | 3.75 | 0.5600 |
| O1 | 0.6500 | 2.96 | −0.6400 |
| H1 | 0.1255 | 0.25 | 0.0480 |
| Water | |||
| Ow | 0.6364 | 3.15 | −0.6672 |
| Hw | 0.0000 | 0.00 | 0.3336 |
| Urea | |||
| CU | 0.4393 | 3.75 | 0.5455 |
| OU | 0.8786 | 2.96 | −0.4378 |
| NU | 0.7113 | 3.25 | −0.4826 |
| HU1 | 0.0000 | 0.00 | 0.2145 |
| HU2 | 0.0000 | 0.00 | 0.2145 |
| Bond distance/Å | Bond angle/Å | ||
|---|---|---|---|
| Acetate | |||
| C1–C2 | 1.52 | C2–C1–H1 | 109.96 |
| C1–H1 | 1.09 | H1–C1–H1 | 109.09 |
| C2–O1 | 1.25 | C1–C2–O1 | 117.30 |
| O1–C2–O1 | 126.00 | ||
| Water | |||
| Ow–Hw | 0.96 | Hw–Ow–Hw | 103.51 |
| Urea | |||
| OU–CU | 1.22 | OU–CU–NU | 119.91 |
| CU–NU | 1.34 | NU–CU–NU | 120.18 |
| NU–HU1 | 1.01 | CU–NU–HU1 | 120.13 |
| NU–HU2 | 1.01 | CU–NU–HU2 | 120.14 |
| HU1–NU–HU2 | 119.74 | ||
EPSR models were equilibrated for over ca. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles before accumulating and averaging structural data. The EPSR refinement was initialised using an equilibrated Monte Carlo simulation containing 2600 discrete species (400 Na+, 400 [OAc]−, 1200 waters and 600 ureas) in a cubic box of size 48.85 Å. The atom density of the simulation box used (0.0992 atoms Å−3) was the experimental density, averaged across all seven isotopomeric SAT–urea eutectic liquids at 50 °C (Table 1) which varied between 1.285–1.369 g cm2 (0.09896–0.09944 atoms Å−3) depending on the extent of deuteriation.
000 cycles before accumulating and averaging structural data. The EPSR refinement was initialised using an equilibrated Monte Carlo simulation containing 2600 discrete species (400 Na+, 400 [OAc]−, 1200 waters and 600 ureas) in a cubic box of size 48.85 Å. The atom density of the simulation box used (0.0992 atoms Å−3) was the experimental density, averaged across all seven isotopomeric SAT–urea eutectic liquids at 50 °C (Table 1) which varied between 1.285–1.369 g cm2 (0.09896–0.09944 atoms Å−3) depending on the extent of deuteriation.
Results and discussion
SAT–urea samples 1–7 were prepared at χurea = 0.60, e.g. 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 sodium acetate trihydrate
3 sodium acetate trihydrate![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
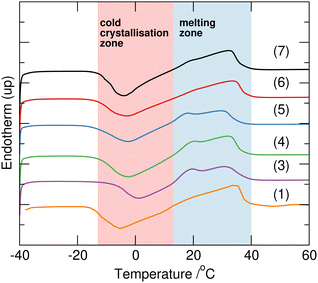
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) urea, using combinations of protiated and deuteriated sodium acetate, water and urea as shown in Table 1. This composition is that representing the eutectic reported for the fully hydrogenous system. All samples 1–7 melted upon heating to 40 °C forming clear homogeneous liquids. Interestingly, after subsequent cooling to 5 °C, 4, 5 and 6 completely solidified, whereas 2 remained a liquid, and 1, 3 and 7 produced crystals within a bulk liquid phase, and remained in these forms for over three months under ambient conditions. There was no clear correlation of this behaviour with the H/D-composition which could be attributed to differences in eutectic behaviour as a function of H/D-substitution, as seen, for example in mixtures of H/D-water/tetrahydrofuran.22 Using differential scanning calorimetry (TA Instruments Q2000 DSC), with a repeat cycle of three cooling and heating steps at 2 °C min−1 between −90 and 70 °C in sealed Tzero aluminium pans, all the samples displayed extensive supercooling to below −40 °C. On heating, cold crystallisation as a broad exotherm between −5 and 15 °C was followed by melting between 15 and 35 °C (Fig. 2). The exception to this behaviour was 2 which did not show any phase transitions in the DSC, but did slowly solidify after storing at −15 °C suggesting that crystallisation is kinetically slow for this composition (sodium acetate-d3 with mixed H/D-urea and water).
urea, using combinations of protiated and deuteriated sodium acetate, water and urea as shown in Table 1. This composition is that representing the eutectic reported for the fully hydrogenous system. All samples 1–7 melted upon heating to 40 °C forming clear homogeneous liquids. Interestingly, after subsequent cooling to 5 °C, 4, 5 and 6 completely solidified, whereas 2 remained a liquid, and 1, 3 and 7 produced crystals within a bulk liquid phase, and remained in these forms for over three months under ambient conditions. There was no clear correlation of this behaviour with the H/D-composition which could be attributed to differences in eutectic behaviour as a function of H/D-substitution, as seen, for example in mixtures of H/D-water/tetrahydrofuran.22 Using differential scanning calorimetry (TA Instruments Q2000 DSC), with a repeat cycle of three cooling and heating steps at 2 °C min−1 between −90 and 70 °C in sealed Tzero aluminium pans, all the samples displayed extensive supercooling to below −40 °C. On heating, cold crystallisation as a broad exotherm between −5 and 15 °C was followed by melting between 15 and 35 °C (Fig. 2). The exception to this behaviour was 2 which did not show any phase transitions in the DSC, but did slowly solidify after storing at −15 °C suggesting that crystallisation is kinetically slow for this composition (sodium acetate-d3 with mixed H/D-urea and water).
Neutron diffraction data
Data were collected from the seven H/D-substituted SAT–urea samples shown in Table 1 and after reduction and normalisation, were analysed using EPSR.19Good fits were obtained between the experimental and simulated data in F(Q) and real space g(r) (Fig. 4). Small discrepancies are evident in the low Q region of 3 and 7 which have the largest isotopic contrast between the acetate and water/urea components. This is commonly ascribed to limitations in correcting for inelastic scattering in the experimental structure factors.23 Centre of mass radial distribution functions (COM RDFs) from the EPSR model (Fig. S1, ESI†) reveal acetate, water, and urea within the sodium first coordination shell, with the sodium–acetate correlation most predominant. However, COM RDFs give a distorted view of coordination environments and interactions due to discrepancies in the positions of maxima that reflect the differences in distance of COM from the points of association, especially between components of dissimilar sizes or where the interaction sites are significantly offset from the centre of mass.
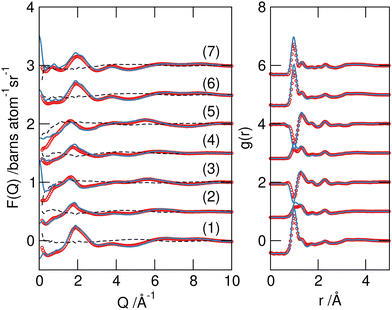 | ||
| Fig. 4 Experimental F(Q) data (red symbols), EPSR models for the data (blue lines) and residual differences between simulated and experimental data (dashed lines) (left), and the Fourier transform to real space g(r) (right) for the seven isotopomeric SAT/urea samples from Table 1. The curves are offset for clarity. | ||
A more detailed investigation of the nature of these associations can be made by examination of site–site partial RDFs. Selected pRDFs for principle interactions in the SAT–urea liquid are plotted in Fig. 5, with the positions of the first maxima (rmax) in the correlations and coordination number (Ncoord) calculated to the minimum after this peak (rmin) listed in Table 4.
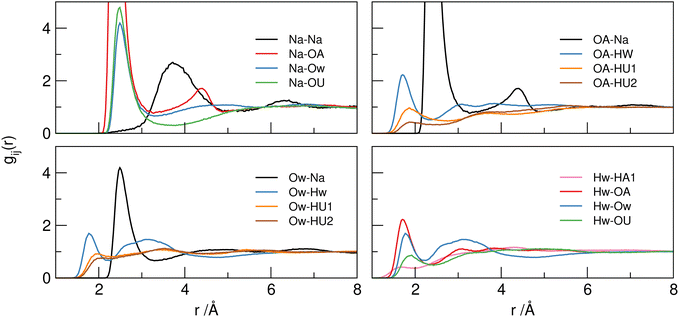 | ||
| Fig. 5 Selected principle site–site pRDFs showing around sodium ions (top left), acetate OA (top right), water Hw (bottom left) and water Ow (bottom right) sites. | ||
| Atomic pairs | r max/Å | r min/Å | N coord | Atomic pairs | r max/Å | r min/Å | N coord |
|---|---|---|---|---|---|---|---|
| Na–Na | 3.72 | 5.00 | 2.27 ± 1.43 | ||||
| Na–OA | 2.35 | 3.33 | 2.96 ± 1.43 | OA–Na | 2.35 | 3.33 | 1.47 ± 0.90 |
| Na–Ow | 2.47 | 3.30 | 1.81 ± 1.09 | Ow–Na | 2.47 | 3.30 | 0.64 ± 0.67 |
| Na–OU | 2.46 | 3.40 | 0.95 ± 0.93 | OU–Na | 2.46 | 3.40 | 0.70 ± 0.62 |
| OA–OA | 3.38 | 4.00 | 2.33 ± 1.32 | ||||
| OA–Hw | 1.70 | 2.32 | 0.89 ± 0.90 | Hw–OA | 1.70 | 2.32 | 0.31 ± 0.48 |
| OA–HU1 | 1.84 | 2.50 | 0.32 ± 0.69 | HU1–OA | 1.84 | 2.77 | 0.24 ± 0.44 |
| OA–HU2 | 1.85 | 2.50 | 0.19 ± 0.43 | HU2–OA | 1.86 | 2.50 | 0.14 ± 0.36 |
| Ow–Ow | 2.72 | 4.20 | 3.57 ± 1.56 | ||||
| Ow–Hw | 1.76 | 2.20 | 1.24 ± 0.93 | Hw–Ow | 1.76 | 2.20 | 0.62 ± 0.70 |
| Ow–HU1 | 1.95 | 2.50 | 0.33 ± 0.63 | HU1–Ow | 1.95 | 2.30 | 0.35 ± 0.51 |
| Ow–HU2 | 1.98 | 2.50 | 0.32 ± 0.53 | HU2–Ow | 1.98 | 2.30 | 0.32 ± 0.51 |
| OU–Hw | 1.90 | 2.50 | 0.58 ± 0.70 | Hw–OU | 1.90 | 2.50 | 0.14 ± 0.36 |
| OU–HU1 | 2.00 | 2.50 | 0.20 ± 0.48 | HU1–OU | 2.00 | 2.50 | 0.12 ± 0.33 |
| OU–HU2 | 2.00 | 2.50 | 1.40 ± 0.78 | HU2–OU | 2.00 | 2.50 | 0.71 ± 0.58 |
The pRDFs show that the first shell coordination environment around sodium cations contains oxygen atoms arising from acetate (OA), water (Ow), and urea (OU). In each case the first peak in each pRDF has a maximum between 2.4–2.5 Å showing similar strength of association in each case with coordination numbers (determined to the minimum around 3.3 Å) of 2.96 ± 1.43 for Na–OA, 1.81 ± 1.09 for Na–Ow, and 0.95 ± 0.93 for Na–OU. Hence, the sodium cations have an average coordination environment containing six oxygen atoms at 2.4–2.5 Å. A representative snapshot of the coordination environment around sodium ions is shown in Fig. 6 illustrating a typical coordination to six oxygens from three acetates, two waters, and one urea. However the degree of order within the liquid is small as evident from the large standard deviations in Ncoord values indicating that the sodium ion experiences a dynamic environment in terms of the specific oxygen-donating species present.
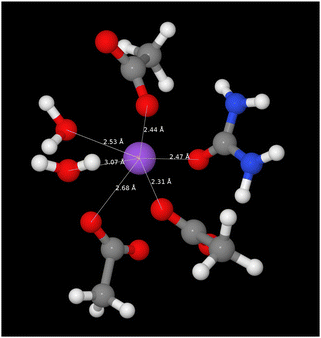 | ||
| Fig. 6 A snapshot from EPSR model of the SAT–urea eutectic showing the first correlation shell environment about a single representative sodium site with coordination to three acetate OA (2.31, 2.44, 2.68 Å), two water Ow (2.53, 3.07 Å) and one urea OU (2.47 Å). The full distribution in the numbers of acetate, water, and urea molecules within the first correlation shell are shown in Fig. 7. | ||
The variation in the coordination environment of sodium ions in SAT–urea is illustrated in Fig. 7 where the coordination number probabilities for OA, OU and Ow oxygens within the sodium first shell are plotted showing approximately equal probabilities (35% and 45% for either one urea or no ureas present coordinating to sodium. Similarly, a broad distribution of waters within the first shell is evident with the highest probability (40%) for one water followed by a progressive decrease in the likelihood of two (28%) or three (17%) waters present. The sodium–acetate coordination number has a Gaussian distribution with the maximum probability (32%) at three OA sites consistent with the summed coordination numbers.
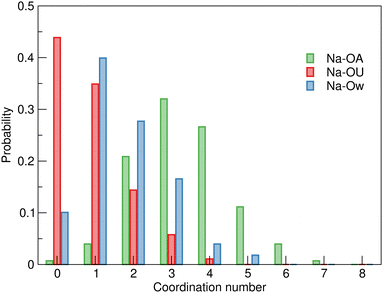 | ||
| Fig. 7 Distribution of Ow, OA, and OU coordination numbers around sodium ions in the EPSR model of SAT–urea eutectic showing variability in the presence of urea within the sodium first shell coordination environment with similar probabilities for either zero or one urea OU oxygens to be present. Numerical data is available in Table S1, ESI.† | ||
The first sodium–water (Na–Ow) correlation in the pRDF at 2.47 Å, and much broader second maxima at ca. 4.4 Å, are similar to the correlation distances reported in aqueous 3 molar NaCl solution (2.38 Å) where approximately six-fold coordination which preserved even up to gigapascal compression.24 Similarly, in crystalline SAT25 sodium ions are coordinated to six water and acetate oxygens atoms in a distorted octahedral environment with Na–O distances between 2.35–2.56 Å. The retention of six-fold coordination of sodium ions is conserved in the SAT–urea melt, even with a range of competing oxygen-donors (water, acetate, and urea) contributing to the coordination environment.
The Na–OA (acetate) pRDF has a first peak with an average Ncoord of 2.96 ± 1.43 acetate oxygens per sodium and 1.47 ± 0.90 sodium per oxygen site at a distance of 2.4 Å suggesting that acetate could coordinate to sodium through both bidentate and bridging modes. The locations of Na–OA associations in the spatial distributions around acetate and the presence of the second peak in the Na–OA RDF at 4.3 Å are both evidence for the acetate bridging between neighbouring sodium ions. This is consistent with aqueous sodium acetate where contact ion pairs with Na–OA separation of 2.30 Å have been reported.26 Acetate oxygens (OA) also interact strongly with both water (Hw) and urea (HU1/2) hydrogen-bond donor sites with rmax at 1.70 Å (Hw), 1.84 Å (HU1), and 1.85 Å (HU2) respectively. Correlations with HU1 and particularly with HU2 have lower intensities than to Hw, with Ncoord values of 0.89 ± 0.90, 0.32 ± 0.69 and 0.19 ± 0.43, respectively. In contrast to the strong correlations evident to the carboxylate-OA sites, only weak correlations of the acetate –CH3 group to other –CH3 hydrogens, water (HW) and urea (HU1/2) are evident as dispersive contacts at the VDW separation distance. These do not contribute to structure-forming interactions.
Comparing the water–water correlations, Hw–Hw, Hw–Ow and Ow–Ow RDFs, to bulk water it is clear there are significant differences. Maxima in the pRDFS for Ow–Hw (1.76 Å) and Ow–Ow (2.72 Å) in Fig. 5 show the presence of association, however the Ow–Ow maxima is slightly compressed compared to bulk water (2.86–2.90 Å),23 and the absence of a higher order peak at 4.5 Å is indicative that the characteristic tetrahedral ordering is absent (more clearly shown in Fig. S2, ESI†) suggesting that water–water correlations occur as a consequence of association with other components in the mixture, for example due to vicinal solvation of sodium cations.
Urea can function as both a hydrogen-bond donor (from HU1/HU2 sites) and Lewis base/hydrogen-bond acceptor (at the carbonyl OU site). The most dominant correlation evident from the pRDFs is that from OU to sodium, as previously mentioned in the context of the sodium environment. The large maximum in the Na–OU pRDF at 2.48 Å is evidence of the importance of this Lewis acid function to insert urea into the sodium coordination shell, although the large standard deviations in Ncoord for Na–OU of 0.95 ± 0.93 and OU–Na of 0.70 ± 0.62 indicate that this dynamic and fluxional with sodium ions associated with one or more urea OU centres 66% of the time (Fig. 7).
In addition to association with Na+ as a Lewis base, the urea carbonyl OU site acts as a hydrogen-bond acceptor site through a range of weaker interactions with water Hw, showing a small first peak in the OU–Hw pRDF at 1.90 Å (with an average 0.58 Hw coordinating to OU). This contact is ca. 0.2 Å longer than that between Hw and acetate oxygens, but is 0.10 Å shorter than for the corresponding urea–urea cluster hydrogen-bonding interactions through HUn–OU associations (rmax = 2.00 Å). This urea-urea self-association is most clearly seen from correlations between HU2 and OU in Table 4 where Ncoord is between six to seven times greater than from HU1 (1.40 vs. 0.20 for OU→HUn and 0.71 vs. 0.12 for HUn → OU). The coordination of the urea OU site comprises, on average, 0.58 water Hw, 0.20 HU1 and 1.40 HU2 urea hydrogens, and 0.70 sodium ions.
In addition to urea–urea hydrogen-bonding which is most dominant from HU2, suggesting propagation of double two-center hydrogen bonds as identified in the majority of crystals containing urea–urea hydrogen bonding.,27 water–urea mixing is evident with hydrogen-bonding equally from HU1/2 to Ow and from Hw to OU acting as a Lewis basic hydrogen-bond acceptor. Both HU1 and HU2 show equal degrees of hydrogen-bonding with water (rmax = 1.95–1.98, Ncoord = 0.32–0.35), whereas Ncoord to acetate OA from HU1 is approximately 30% greater than that from HU2, again reflecting the propensity for urea to form chelated complexes with ditopic hydrogen bond acceptors such as carboxylates28 and allowing differentiation between urea–acetate correlations at HU1 and urea–urea correlations through HU2. These distinctions are evident in the spatial distribution functions plotted in Fig. 8 for the first shell correlations around ureas in SAT–urea.
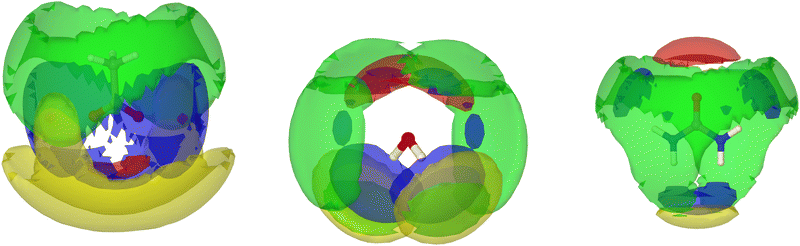 | ||
| Fig. 8 Centre of mass spatial distribution function plots showing the distribution of water (blue), urea (green), acetate (yellow) and sodium ions (red) around central acetate (left), water (centre) and urea (right) in the first shell of the SAT–urea eutectic liquid. SDFs plotted encompass the top 15% acetate/water), 10% (urea) and 25% (sodium) probability within the first correlation shell determined from the COM RDFs in Fig. S1, ESI.† | ||
Spatial distributions
Spatial distribution functions (SDFs) in Fig. 8 show the regions of highest probability for association between the different species present (sodium, urea, acetate, and water) around each molecular component in the SAT–urea liquid. SDFs are plotted to identify the regions with the top 15% probability for correlations to take place for acetate and water, top 10% for urea (the diffusivity of urea COM distributions as a consequence of the relatively large size of urea and that the principle interaction sites, HU1, HU2, and OU, are all offset from the COM by approximately 2.0 Å) and top 25% for sodium.Strong coordination of sodium by the three oxygens of acetate, urea, and water is clearly identifiable with single nodes in the spatial distribution between sodium and water and urea associated with the Ow and OU sites, and a pair of nodes in the sodium–acetate SDF associated with monodentate and bi-dentate coordination to the carboxylate OA atoms. Water molecules are similarly distributed around acetate in the same regions as sodium cations. The acetate–acetate correlation, which has a carboxylate–carboxylate rmax of ca. 5 Å suggests bridging though coordinated sodium ions.
The spatial correlation between urea and acetate –CH3 groups is broad and unstructured, consistent with non-directional contacts at van der Waals separation distances. One origin of this correlation can be seen from the close proximities of urea-NH2 and acetate-CH3 groups coordinated to sodium in Fig. 6 whereas the strongest correlation of acetate around urea is through hydrogen-bond donation from both urea HU1 sites to OA.
The directionality of hydrogen-bonding from water Hw to oxygens of water (Ow), acetate (OA) and to urea (OU) as seen in the pRDFs (Fig. 5) is confirmed through the presence of correlation nodes in the SDFs directed along the Ow–Hw bond. It is notably, that with the congruent positions of these three distributions, there is competition for between water–acetate, water–water, and water–urea association. Additional water–urea spatial correlations are evident in the broad, diffuse distributions of urea molecules over each face of water molecules. This correlation is associated with interaction of urea HU1/2 sites with water as can be from the four sites of association of water molecules with urea along the directions of N–HU1 and N–HU2 bonds.
Water–water correlations are restricted because water molecules are either strongly bound to Na, or are associated with urea. Urea–urea correlations present a broad diffusive band in the urea-centred SDF that links each NH site (HU1/HU2) through HU1/2→OU association, which leads to the absence of water–water correlation nodes associated with Ow hydrogen bond acceptor positions. Previous experimental and MD studies on urea/water mixtures has identified clustering and urea–urea self-aggregation29 at high urea content and accommodation of urea into the water network without significant perturbation through formation of hydrogen bonded chains or clusters with stacked ‘head to tale’ urea molecules.30 This gives rise to ‘in-plane’ and ‘edge-to-face’ correlations from HU2→OU and a more suppressed HU1–OU edge-face association. The same pattern of urea–urea spatial correlation is observable in the SAT–urea liquid and, combined with the urea–water correlations to both HU1 and HU2 in the SDF illustrate the capacity for the excess water molecules, liberated by competitive coordination of urea OU oxygens to sodium, to then become associated with urea through hydrogen bonding to HU1 and HU2.
Role of urea as both Lewis basic ligand, hydrogen-bond acceptor and hydrogen-bond donor
The contribution of urea as an oxo-ligand to the coordination of sodium leads to stabilisation of fully solvated, but only partially hydrated sodium ions in the SAT–urea melt enabling formation of the eutectic liquid. Urea–acetate interactions enable insertion of urea into the sodium solvation shell where the urea can compete with, and displace, water. At the same time, urea–water hydrogen-bonding (from both HU1/2–Ow and Hw–OU) reduce the availability of water molecules to hydrate sodium. Thus the association between sodium, acetate, and water, and urea are sensitive to the presence of each other, with overall reduction in sodium–acetate and sodium–water correlations compared to those reported for neat and hydrated SAT. This may mimic the effects of urea in protein denaturisation31,32 where urea molecules displace water from a proteins first solvation shell by forming strong hydrogen bonds to functional groups such as carboxylates in Asp/Glu residues and simultaneously associate with the displaced water molecules.33Hence the role of urea as a base, coordinating to Na+ and to water and other urea Hw/HU1/HU2 hydrogen-bond donor sites is clearly important as well as the more usual, and dominant focus in the literature, on the role of hydrogen-bond donation in the function of urea across a range of applications from anion recognition to formation of deep eutectic solvents.13,34,35 Hydrogen-bonding through the HU1/HU2 sites of urea appears to play a disruptive role in the liquid, generating a number of short but low intensity associations with acetate methyl (HA1), water–Ow, and self-association with OU. Most of these first correlations in the respective pRDFs show only low probabilities, often less than unity, and correspondingly low coordination numbers.
Mixtures of SAT with a series of substituted ureas; 1,3-dimethylurea (mp 104 °C), 1,1-dimethylurea (mp 178–183 °C) and 1,1,3,3-tetramethylurea (mp −1.2 °C), were examined using temperature-controlled polarising optical microscopy (Olympus BX50 with Linkam TP92 stage) to screen for eutectic formation36 in order to explore whether any insights could be gained from simple structure–property relationships. Unfortunately, and to our disappointment, no evidence for the generation of eutectics was observed with any of the alkylated ureas. With 1,1-dimethylurea, the two solids remained immiscible up to the (partial) melting of SAT at 59 °C. In contrast, with 1,3-dimethylurea, around 55–60 °C, the powdered dimethylurea appears to undergo a change in morphology although no liquid phase was formed. One possible explanation is that a 1,3-dimethylurea hydrate is generated by abstraction of water from SAT around its melting point as the peritectic transformation point of SAT to sodium acetate is reached.8N-Alkylsubstitution increases the denaturing strength of ureas,37 which would be consistent with an enhanced affinity for water, however in the absence of liquid phase relevant to the application of eutectic liquids as solvents or PCMs this was not investigated further. With the liquid tetramethylurea, SAT crystals remained immiscible and suspended in the fluid until they melted around 58–60 °C.
Conclusions
Experimental neutron scattering data has been collected for a range of H/D isotopically substituted sodium acetate trihydrate–urea samples (χurea = 0.60) at 50 °C and the liquid structure was examined using EPSR.The liquid structure contains predominantly six coordinate sodium ions associated with, on average, two water molecules, one urea and three acetate oxygens through both bidentate and bridging modes, with the acetate anions coordinated to water molecules through the carboxylate group. Approximately two-thirds of the water molecules present are associated with sodium ions. The ‘excess’ water is inhibited from hydrating sodium ions through competition in the sodium coordination shell by urea acting as an oxygen donor via OU, and is stabilised through a network of urea–water HU→Ow and Hw→OU hydrogen bonds with urea acting as a denaturing hydrogen bond donor/acceptor. These dual roles of urea, competing with acetate and water molecules in the coordination shell of sodium ions and through water–urea association, appears to enable the low melting point and congruent melting of the SAT–urea eutectic composition. This mimics the well known, but molecularly poorly understood, denaturing effects of urea through both displacement of water from the acetate solvation shell and simultaneously increasing the degree of urea-acetate interactions.
These observations support the importance of the extensive, and directional hydrogen-bond donation available in urea providing interactions with water that disrupt association and generate the eutectic composition. However, it is important to note that urea is not unique in combining these characteristics. For example, glycerol, which forms eutectic liquids with choline chloride,14 has been reported to inhibit crystallisation of SAT38 and SAT–glycerol mixtures have been described as deep eutectic solvents, although with no evidence for formation of a eutectic.39
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Queen's University Belfast and Tezpur University Collaborative Research Degree Programme for support to SM. Beam time for the experiments carried out on the SANDALS instrument at the ISIS Pulsed Neutron and Muon Source, STFC Rutherford Appleton Laboratory, UK, was awarded by ISIS through allocation RB2000229. Experimental data is available at https://doi.org/10.5286/ISIS.E.RB2000229.References
- (a) K. Pielichowska and K. Pielichowski, Prog. Mater. Sci., 2014, 65, 67–123 CrossRef CAS; (b) L. F. Cabeza, A. Castell, C. Barreneche, A. de Gracia and A. I. Fernandez, Renewable Sustainable Energy Rev., 2011, 15, 1675–1695 CrossRef CAS; (c) F. Agyenim, N. Hewitt, P. Eames and M. Smyth, Renewable Sustainable Energy Rev., 2010, 14, 615–628 CrossRef CAS; (d) A. Sharma, V. V. Tyagi, C. R. Chen and D. Buddhi, Renewable Sustainable Energy Rev., 2009, 13, 318–345 CrossRef CAS; (e) M. Farid, A. Khudhair, S. Razack and S. Al-Hallaj, Energy Convers. Manage., 2004, 45, 1597–1615 CrossRef CAS; (f) B. Zalba, J. M. Marín, L. F. Cabeza and H. Mehling, Appl. Therm. Eng., 2003, 23, 251–283 CrossRef CAS.
- (a) K. Matuszek, R. Vijayaraghavan, M. Kar, S. Mahadevan and D. R. MacFarlane, ChemSusChem, 2021, 14, 2757–2762 CrossRef CAS PubMed; (b) K. Matuszek, R. Vijayaraghavan, M. Kar and D. R. MacFarlane, Cryst. Growth Des., 2019, 20, 1285–1291 CrossRef.
- Q. Li, C. Li, Z. Du, F. Jiang and Y. Ding, Appl. Energy, 2019, 255, 113806 CrossRef.
- P. Dixit, V. J. Reddy, S. Parvate, A. Balwani, J. Singh, T. K. Maiti, A. Dasari and S. Chattopadhyay, J. Energy Storage, 2022, 51, 104360 CrossRef.
- (a) J.-H. Li, G. en Zhang and J.-Y. Wang, Sol. Energy, 1991, 47, 443–445 CrossRef CAS; (b) W. Cui, Y. Yuan, L. Sun, X. Cao and X. Yang, Renewable Energy, 2016, 99, 1029–1037 CrossRef CAS; (c) W. Fu, T. Zou, X. Liang, S. Wang, X. Gao, Z. Zhang and Y. Fang, Appl. Therm. Eng., 2018, 138, 618–626 CrossRef CAS; (d) W. Fu, T. Zou, X. Liang, S. Wang, X. Gao, Z. Zhang and Y. Fang, Appl. Therm. Eng., 2019, 162, 114253 CrossRef CAS; (e) X. Li, Z. Fu, Y. Qiao, Z. Zhang, Y. Zhou, C. Hai, Y. Shen, Y. Sun, J. Zeng and X. Ren, Energy Fuels, 2020, 34, 6439–6447 CrossRef CAS; (f) Z. Ling, S. Li, C. Cai, S. Lin, X. Fang and Z. Zhang, Appl. Therm. Eng., 2021, 193, 117002 CrossRef CAS.
- M. Li, Z. Lin, Y. Sun, F. Wu, T. Xu, H. Wu, X. Zhou, D. Wang and Y. Liu, Renewable Energy, 2020, 157, 670–677 CrossRef CAS.
- (a) K. K. Meisingset and F. Grønvold, J. Chem. Thermodyn., 1984, 16, 523–536 CrossRef CAS; (b) D. E. Oliver, A. J. Bissell, X. Liu, C. C. Tang and C. R. Pulham, CrystEngComm, 2021, 23, 700–706 RSC.
- T. Wada, F. Kimura and R. Yamamoto, Bull. Chem. Soc. Jpn., 1983, 56, 1223–1226 CrossRef CAS.
- C. A. Navarro, C. A. Sierra and C. Ochoa-Puentes, RSC Adv., 2016, 6, 65355–65365 RSC.
- (a) X. Rico, E.-M. Nuutinen, B. Gullón, V. Pihlajaniemi and R. Yáñez, Food Bioprod. Process., 2021, 130, 216–228 CrossRef CAS; (b) C. Gallego, H. Rodriguez and A. Soto, Int. J. Mol. Sci., 2023, 24, 1550 CrossRef CAS PubMed.
- (a) Y. Cui, Y. Zhu, R. Dai, Z. Shan, J. Yi and H. Chen, Colloids Surf., A, 2021, 625, 126916 CrossRef CAS; (b) T. Wu, R. Dai, Z. Shan, H. Chen, M. W. Woo and J. Yi, Process Biochem., 2022, 118, 32–40 CrossRef CAS; (c) Y. Cui, M. He, R. Dai, H. Chen and Y. Wang, J. Am. Leather Chem. Assoc., 2023, 118, 95–101 CrossRef CAS.
- S. Lenton, N. H. Rhys, J. J. Towey, A. K. Soper and L. Dougan, Nat. Commun., 2017, 8, 919 CrossRef PubMed.
- A. P. Abbott, J. C. Barron, K. S. Ryder and D. Wilson, Chem. – Eur. J., 2007, 13, 6495–6501 CrossRef CAS PubMed.
- (a) E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082 CrossRef CAS PubMed; (b) O. S. Hammond, D. T. Bowron and K. J. Edler, Green Chem., 2016, 18, 2736–2744 RSC; (c) A. H. Turner and J. D. Holbrey, Phys. Chem. Chem. Phys., 2019, 21, 21782–21789 RSC.
- A. Triolo, M. E. D. Pietro, A. Mele, F. L. Celso, M. Brehm, V. D. Lisio, A. Martinelli, P. Chater and O. Russina, J. Chem. Phys., 2021, 154, 244501 CrossRef CAS PubMed.
- (a) O. S. Hammond, D. T. Bowron and K. J. Edler, Angew. Chem., Int. Ed., 2017, 56, 9782–9785 CrossRef CAS PubMed; (b) M. M. Nolasco, S. N. Pedro, C. Vilela, P. D. Vaz, P. Ribeiro-Claro, S. Rudić, S. F. Parker, C. S. Freire, M. G. Freire and A. J. D. Silvestre, Front. Phys., 2022, 10, 834571 CrossRef.
- M. E. Di Pietro, M. Tortora, C. Bottari, G. Colombo Dugoni, R. V. Pivato, B. Rossi, M. Paolantoni and A. Mele, ACS Sustainable Chem. Eng., 2021, 9, 12262–12273 CrossRef CAS.
- A. K. Soper, GudrunN and GudrunX: Programs for correcting raw neutron and X-ray diffraction data to differential scattering cross section, RAL-TR-2011-013, Rutherford Appleton Laboratory Technical Report, 2011 Search PubMed.
- (a) A. K. Soper, Chem. Phys., 1996, 202, 295–306 CrossRef CAS; (b) A. K. Soper, Mol. Phys., 2001, 99, 1503–1516 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- C. Y. Jones, J. S. Zhang and J. W. Lee, J. Thermodyn., 2010, 2010, 1–6 CrossRef.
- A. K. Soper, ISRN Phys. Chem., 2013, 2013, 1–67 CrossRef.
- T. Yamaguchi, N. Fukuyama, K. Yoshida and Y. Katayama, J. Phys. Chem. Lett., 2020, 12, 250–256 CrossRef PubMed.
- (a) T. S. Cameron, K. M. Mannan and M. O. Rahman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 87–90 CrossRef; (b) V. A. Efremov, N. O. Endeladze, V. M. Agre and V. K. Trunov, J. Struct. Chem., 1986, 27, 498–501 CrossRef; (c) K.-T. Wei and D. L. Ward, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 522–526 CrossRef.
- (a) E. F. Aziz, N. Ottosson, S. Eisebitt, W. Eberhardt, B. Jagoda-Cwiklik, R. Vácha, P. Jungwirth and B. Winter, J. Phys. Chem. B, 2008, 112, 12567–12570 CrossRef CAS PubMed; (b) H. V. R. Annapureddy and L. X. Dang, J. Phys. Chem. B, 2012, 116, 7492–7498 CrossRef CAS PubMed.
- A. Olejniczak, K. Ostrowska and A. Katrusiak, J. Phys. Chem. C, 2009, 113, 15761–15767 CrossRef CAS.
- M. P. Hughes and B. D. Smith, J. Org. Chem., 1997, 62, 4492–4499 CrossRef CAS PubMed.
- (a) P.-O. Åstrand, A. Wallqvist and G. Karlstroem, J. Phys. Chem., 1994, 98, 8224–8233 CrossRef; (b) A. Idrissi, F. Sokolic and A. Perera, J. Chem. Phys., 2000, 112, 9479–9488 CrossRef CAS; (c) F. Sokolic, A. Idrissi and A. Perera, J. Mol. Liq., 2002, 101, 81–87 CrossRef CAS; (d) F. Sokolic, A. Idrissi and A. Perera, J. Chem. Phys., 2002, 116, 1636–1646 CrossRef CAS; (e) A. Soper, E. Castner and A. Luzar, Biophys. Chem., 2003, 105, 649–666 CrossRef CAS PubMed; (f) M. C. Stumpe and H. Grubmüller, J. Phys. Chem. B, 2007, 111, 6220–6228 CrossRef CAS PubMed.
- R. C. Burton, E. S. Ferrari, R. J. Davey, J. Hopwood, M. J. Quayle, J. L. Finney and D. T. Bowron, Cryst. Growth Des., 2008, 8, 1559–1565 CrossRef CAS.
- (a) C. Tanford, Protein Denaturation, Elsevier, 1970, pp. 1–95 Search PubMed; (b) G. I. Makhatadze, J. Phys. Chem. B, 1999, 103, 4781–4785 CrossRef CAS.
- C. Pace, Enzyme Structure Part L, Academic Press, 1986, vol. 131, pp. 266–280 Search PubMed.
- (a) A. Das and C. Mukhopadhyay, J. Phys. Chem. B, 2008, 112, 7903–7908 CrossRef CAS PubMed; (b) A. Das and C. Mukhopadhyay, J. Phys. Chem. B, 2009, 113, 12816–12824 CrossRef CAS PubMed; (c) I. P. de Oliveira and L. Martínez, Phys. Chem. Chem. Phys., 2020, 22, 354–367 RSC.
- (a) A. P. Abbott, G. Capper, D. L. Davies, K. J. McKenzie and S. U. Obi, J. Chem. Eng. Data, 2006, 51, 1280–1282 CrossRef CAS; (b) V. Amendola, D. Esteban-Gómez, L. Fabbrizzi and M. Licchelli, Acc. Chem. Res., 2006, 39, 343–353 CrossRef CAS PubMed; (c) K. Choi and A. D. Hamilton, Coord. Chem. Rev., 2003, 240, 101–110 CrossRef CAS; (d) M. G. Chudzinski, C. A. McClary and M. S. Taylor, J. Am. Chem. Soc., 2011, 133, 10559–10567 CrossRef CAS PubMed; (e) B. P. Hay, T. K. Firman and B. A. Moyer, J. Am. Chem. Soc., 2005, 127, 1810–1819 CrossRef CAS PubMed; (f) Y. Takemoto, Org. Biomol. Chem., 2005, 3, 4299 RSC; (g) D. V. Wagle, H. Zhao and G. A. Baker, Acc. Chem. Res., 2014, 47, 2299–2308 CrossRef CAS PubMed.
- B. B. Hansen, S. Spittle, B. Chen, D. Poe, Y. Zhang, J. M. Klein, A. Horton, L. Adhikari, T. Zelovich, B. W. Doherty, B. Gurkan, E. J. Maginn, A. Ragauskas, M. Dadmun, T. A. Zawodzinski, G. A. Baker, M. E. Tuckerman, R. F. Savinell and J. R. Sangoro, Chem. Rev., 2021, 121, 1232–1285 CrossRef CAS PubMed.
- G. Diarce, L. Quant, A. Campos-Celador, J. Sala and A. García-Romero, Sol. Energy Mater. Sol. Cells, 2016, 157, 894–906 CrossRef CAS.
- U. Kaatze, J. Chem. Phys., 2018, 148, 014504 CrossRef PubMed.
- L. Yuan, Q. Ge, H. Fu, G. Jiang, Z. Yu, Q. Zheng, Y. Lv, J. Zhao and J. Yu, J. Energy Eng., 2018, 144, 04018022 CrossRef.
- W. Sun, Q. Liu, J. Zhao, H. M. Ali, Z. Said and C. Liu, J. Mol. Liq., 2023, 372, 121164 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Centre of mass radial distribution functions between sodium, acetate, urea and water, and water (Ow/Hw) partial radial distribution functions, scripts for treatment of experimental data from SANDALS with GUDRUN and EPSR. See DOI: https://doi.org/10.1039/d3cp05516g |
| This journal is © the Owner Societies 2024 |