Quantum chemical modeling of hydrogen binding in metal–organic frameworks: validation, insight, predictions and challenges†
Romit
Chakraborty
 *ab,
Justin J.
Talbot
*ab,
Justin J.
Talbot
 b,
Hengyuan
Shen
b,
Yuto
Yabuuchi
b,
Hengyuan
Shen
b,
Yuto
Yabuuchi
 ab,
Kurtis M.
Carsch
b,
Henry Z. H.
Jiang
b,
Hiroyasu
Furukawa
ab,
Kurtis M.
Carsch
b,
Henry Z. H.
Jiang
b,
Hiroyasu
Furukawa
 ab,
Jeffrey R.
Long
ab,
Jeffrey R.
Long
 abc and
Martin
Head-Gordon
abc and
Martin
Head-Gordon
 *bd
*bd
aMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
bDepartment of Chemistry, University of California, Berkeley, CA 94720, USA. E-mail: m_headgordon@berkeley.edu
cDepartment of Chemical and Biomedical Engineering, University of California, Berkeley, CA 94720, USA
dChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 31st January 2024
Abstract
A detailed chemical understanding of H2 interactions with binding sites in the nanoporous crystalline structure of metal–organic frameworks (MOFs) can lay a sound basis for the design of new sorbent materials. Computational quantum chemical calculations can aid in this quest. To set the stage, we review general thermodynamic considerations that control the usable storage capacity of a sorbent. We then discuss cluster modeling of H2 ligation at MOF binding sites using state-of-the-art density functional theory (DFT) calculations, and how the binding can be understood using energy decomposition analysis (EDA). Employing these tools, we illustrate the connections between the character of the MOF binding site and the associated adsorption thermodynamics using four experimentally characterized MOFs, highlighting the role of open metal sites (OMSs) in accessing binding strengths relevant to room temperature storage. The sorbents are MOF-5, with no open metal sites, Ni2(m-dobdc), containing Lewis acidic Ni(II) sites, Cu(I)-MFU-4l, containing π basic Cu(I) sites and V2Cl2.8(btdd), also containing π-basic V(II) sites. We next explore the potential for binding multiple H2 molecules at a single metal site, with thermodynamics useful for storage at ambient temperature; a materials design goal which has not yet been experimentally demonstrated. Computations on Ca2+ or Mg2+ bound to catecholate or Ca2+ bound to porphyrin show the potential for binding up to 4 H2; there is precedent for the inclusion of both catecholate and porphyrin motifs in MOFs. Turning to transition metals, we discuss the prediction that two H2 molecules can bind at V(II)-MFU-4l, a material that has been synthesized with solvent coordinated to the V(II) site. Additional calculations demonstrate binding three equivalents of hydrogen per OMS in Sc(I) or Ti(I)-exchanged MFU-4l. Overall, the results suggest promising prospects for experimentally realizing higher capacity hydrogen storage MOFs, if nontrivial synthetic and desolvation challenges can be overcome. Coupled with the unbounded chemical diversity of MOFs, there is ample scope for additional exploration and discovery.
1 Introduction
Touted as the Swiss Army Knife for decarbonization, hydrogen provides a versatile alternative to fossil fuels applicable across multiple economic sectors, including transportation, power generation, chemical production (e.g. hydrocarbons, ammonia), and industrial manufacturing (e.g. steel).1,2 The future hydrogen economy3–5 will be driven by clean hydrogen, using the reactive H–H chemical bond as the medium for energy storage. Fuel cell-based energy release from H2 consumption yields only water, which can, in turn, be regenerated into H2via the reverse processes of water oxidation and proton reduction, resulting in minimal CO2 generation if green electricity is used. Four serious barriers stand in the way of this vision: (i) obtaining H2 from green sources at a viable cost, (ii) the storage challenge (which is the motivating issue for this work), (iii) efficient and economical fuel cells, and (iv) implementation of large-scale infrastructure.The H2 storage challenge is well-recognized6–17 with potential solutions ranging from storage at cryogenic temperatures, or under high pressures,18,19 or in materials like metal hydrides20,21 and nanoporous frameworks.22–27 The low volumetric energy density of hydrogen when compared to gasoline22 leads to storage at pressures above 350 bar or at liquid hydrogen temperatures, each with very significant handling costs.28,29 Metal–organic frameworks (MOFs) potentially solve this problem since they densify hydrogen in the solid state, allowing its storage and release at more modest pressures.22,23
The original goal of hydrogen storage research was to address light vehicle needs. In pursuit of H2 powered vehicles, the U.S. Department of Energy (DOE) has set a volumetric capacity target of 40 g L−1 for the year 2025 at temperatures in the range of −40 to 60 °C (233 K to 333 K), and a delivery pressure in the range of 5 to 12 bar.15,30 To meet the system level targets, the storage capacity of material-based solutions likely needs to match the density of liquid H2 (71 g L−1) due to the limited tank space in light-duty vehicles. Consequently, the US DOE has been exploring the potential use of H2 for heavy-duty applications (e.g., trucks, rail, maritime) as well as power sector applications (e.g., backup and stationary power).31 Indeed, recent techno-economic analysis suggests that the cost of hydrogen storage in MOFs for backup power could be lower than the cost of a liquid hydrogen storage system and comparable to the cost of compressed H2 at 350 bar,29 although significant improvements in materials design and manufacturing are necessary for the practical realization of a MOF-based technology. Use of MOFs for H2 storage stands in the context of the explosion of exciting MOF-based science32,33 that makes this area an active frontier of chemistry and materials science,34 across areas ranging from gas separation35 to water purification36 to catalysis.37,38
Towards the goal of rational materials design for H2 storage in MOFs, it is essential to understand the interactions between hydrogen and MOFs at a fundamental level. As we shall see, it is particularly interesting to explore the interactions between hydrogen and open metal sites in MOFs. In a general sense, these interactions originate from the normal driving forces of host–guest binding: permanent and induced electrostatics, dispersion, charge-transfer, and Pauli repulsions.39–41 However, the details of site-specific binding can be quite complex and multi-faceted, encompassing a range of weak dispersion interactions as well as stronger associations with local charges or an accessible metal site. MOFs, with their high surface-to-volume ratio, are ideally suited for van der Waals interactions with H2,42,43 but these weak interactions alone do not suffice for storage under ambient or near-ambient conditions (down to −50 °C).22,23 Put simply, molecular H2 is relatively inert in its interactions with the stable organic linkers.
Fortunately, the modular nature of MOFs allows for the incorporation of more diverse binding motifs, either at open (coordinately unsaturated) metal sites (OMSs)44,45 or on linkers46 which may themselves be metal-decorated.47 While outside our present scope, other porous materials can also support OMSs, such as zeolites where cation exchange reactions can replace protons with metal ions, such as alkalis, alkaline earths or transition metals.48 The flexibility of MOFs makes them unique in this arena and enables tuning of hydrogen interactions with the MOF surface through judicious chemical modifications, albeit subject to the constraints of synthetic feasibility and suitable mechanical stability of the resulting MOF. A great amount of experimental effort over the past two decades has resulted in considerable progress toward this objective.22,23,44–46 Our purpose here is not to review that ground-breaking work, but rather to present computational explorations that illustrate some key aspects of the prospects for going further, particularly with regard to potential binding site design paradigms. The first main topic is discussing optimal binding site characteristics based on thermodynamic considerations that maximize the usable storage capacity of H2 in MOFs at ambient to near-ambient temperatures under the constraints of a fixed pressure swing between loading and unloading conditions.49–51 This analysis leads to an optimal value of the binding free energy for chosen working conditions. In turn, this determines a set of optimal enthalpy–entropy tradeoffs that are coupled to optimizing the density of accessible sites.
The exploration of hydrogen-binding interactions in MOFs that have been prepared or are possible candidates for preparation is possible with accurate modern density functional theory (DFT).52,53 As we discuss in the second section, such calculations yield good numerical predictions on the one hand, and, on the other hand, insights into the origin of binding strength via the tools of energy decomposition analysis (EDA).54,55 The fidelity of the calculations depends upon the model of the MOF: we use cluster calculations that aim to capture all relevant structural and electronic features close to a hydrogen binding site; cluster modeling is also reviewed.
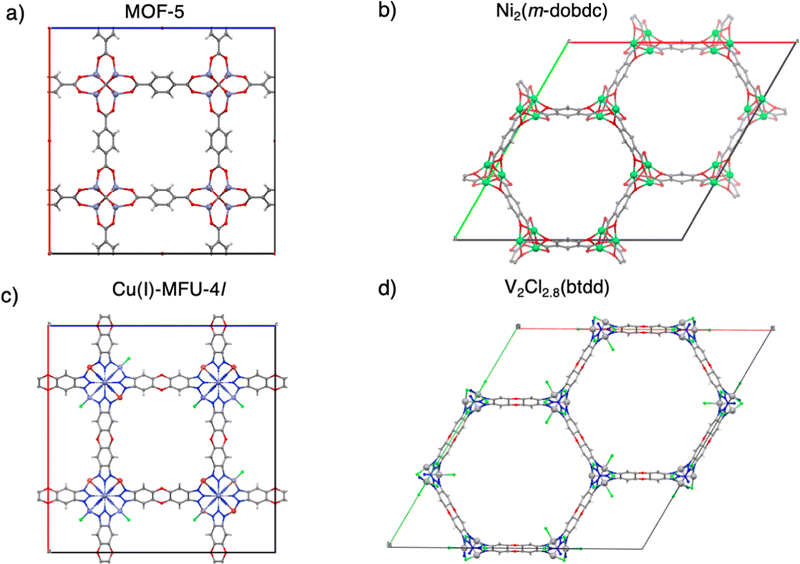
The third section summarizes DFT calculations on H2 binding in four separate MOFs, each of which has already been experimentally characterized. These examples span a range of H2 binding energies spanning the physisorption regime through to relatively strong chemisorption. From weakest binding to strongest binding, we begin with MOF-5 (Zn4O(bdc)3, bdc2− = 1,4-benzenedicarboxylate),56 which lacks open metal sites, followed by Ni2(m-dobdc) (m-dobdc4− = 4,6-dioxido-1,3-benzenedicarboxylate) which has Ni(II) sites,25,57 and then the exceptionally strong H2 binding in Cu(I)-MFU-4l.58,59 The role of open transition metal sites in MOFs is one pathway to go beyond physisorption binding strengths,44 and even in the case of Cu(I)-MFU-4l, to a binding that is stronger than optimal. The final example of this section is the near-optimal binding in V2Cl2.8(btdd) (H2btdd = bis(1H-1,2,3-triazolo[4,5-b],[4′,5′-i])dibenzo[1,4]dioxin).27 These MOFs are each illustrated in Fig. 1.
The final topic we address is the question of binding multiple H2 molecules to a single site with appropriate binding energy. Whilst well-recognized as a goal that could be a critical multiplier to the site density in terms of usable storage capacity, it has not yet been realized experimentally, notwithstanding exciting progress60 and a range of predictions.61–70 In the fourth section, we review two promising existing suggestions, and also present some new computational results. We first consider the use of main group ions, Ca2+ and Mg2+, binding to catecholate functional groups,68 which are derivatives of MOF linkers, and therefore represent a pathway to post-synthetic modification of MOFs. Additionally, we present new calculations on calcium porphyrin. We then turn to explore other open transition metal sites, beginning with our previous DFT calculations that demonstrated the feasibility of two hydrogen molecules coordinating at each V(II) site of V(II) exchanged MFU-4l.70 Exploring the rare +1 oxidation state, we predict the coordination of three hydrogen molecules is possible at each Sc(I) or Ti(I) metal site in metal exchanged MFU-4l. We conclude with some discussion on the prospects for future advances in MOF-based storage materials, as well as identifying areas where progress in computational modeling would be desirable.
2 Optimal binding for hydrogen storage
Bhatia and Myers pioneered the understanding of optimal hydrogen storage conditions in porous adsorbents.49 They proposed an optimal enthalpy change (ΔH) of −15.1 kJ mol−1 for hydrogen storage at 298 K and a pressure swing of 1.5–30 bar, presuming a standard entropy change ΔS° ≈ −8R. Their standard entropy change is derived from a Langmuirian analysis of H2 adsorption in cylindrical pores of silica and slit pores of carbon. However, Bae and Snurr have shown that Bhatia and Myers' entropy change assumption might not hold for materials with strong H2 binding sites. By utilizing Grand Canonical Monte Carlo (GCMC) simulations, Bae and Snurr deduced an optimal isosteric heat −Qst = ΔHads for H2 binding at around −20 kJ mol−1 under a slightly different pressure swing of 1.5–120 bar at 298 K.71 Experimental studies on zeolites have estimated the optimal enthalpy to be in the range of −22 to −25 kJ mol−1 for 1.5–30 bar pressure swing at 298 K.72Despite its limitations, the Langmuir model still offers valuable insights into the thermodynamics of H2 adsorption at specific binding sites within a MOF. This model, rooted in the balance between the energy lowering upon H2 binding and its entropic drive to gain translational freedom, suggests that the surface coverage (θ) at thermal equilibrium can be defined as 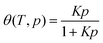 . Here, p is the relative pressure to a reference pressure P0 of 1 bar. The binding constant K(T), which reflects the ratio of adsorbed vs free adsorbate molecules, can be determined by the standard free energy change ΔG°(T) = −RT
. Here, p is the relative pressure to a reference pressure P0 of 1 bar. The binding constant K(T), which reflects the ratio of adsorbed vs free adsorbate molecules, can be determined by the standard free energy change ΔG°(T) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K on binding at the reference pressure.
K on binding at the reference pressure.
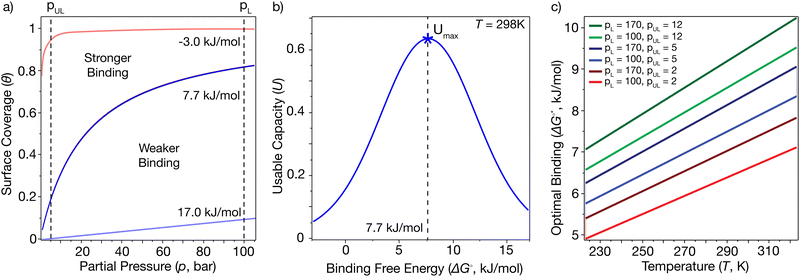
Examples of hypothetical binding isotherms are shown in Fig. 2(a). The usable coverage, represented by U, is calculated as the difference in site coverage between loading and unloading pressures (pL and pUL) expressed as U(T,pL,pUL) = θ(T,pL) − θ(T,pUL). This dimensionless usable coverage is multiplied by the density of binding sites in the material to obtain the volumetric capacity, which is commonly expressed in g L−1. The usable coverage describes the amount of hydrogen desorbed at pUL after being loaded at pL, for a specific temperature. Our problem is to maximize usable capacity by tailoring the material properties of the MOF. The amount of gas released is greater when the pressure swing (from pL to pUL) has surface coverage approaching the saturation limit at pL and as close to zero as possible at pUL. Given that pL, pUL and T should be viewed as specified device parameters, the development of an optimal MOF, therefore, amounts to optimizing the binding constant K(T) to maximize usable coverage for those constraints. Separately, the site density should also be optimized to maximize usable capacity. As illustrated in Fig. 2(a), it is important to avoid steep uptake at very low pressures (i.e. at pUL), which occurs with strong binding, as well as small uptake at low to moderate pressures (i.e. at pL), which occurs with weak physisorption. The optimal standard binding free energies, ΔG°*(T), which maximize usable capacity, can be found by variation.49
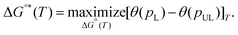 | (1) |
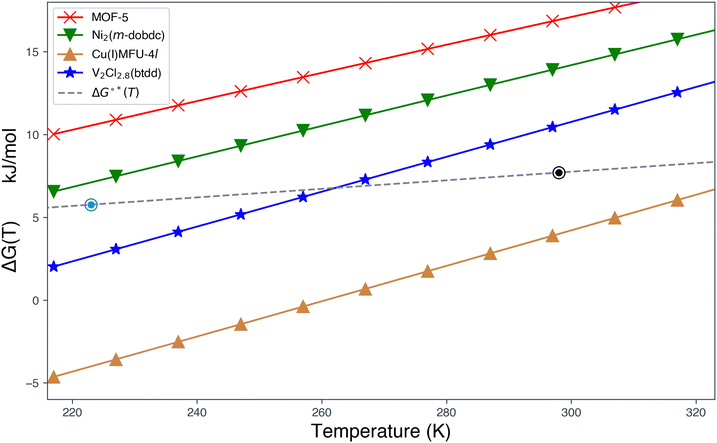
Fig. 2(b) shows that U(T) is maximal for a binding free energy change of +7.7 kJ mol−1 at 298 K for a pressure swing of 5–100 bar. This optimal binding isotherm for single-site Langmuir adsorption corresponds to the blue curve at the centre of Fig. 2(a), and can utilize 63% of the available binding sites to release hydrogen from the material.
ΔG°* depends on both temperature and the chosen pressure swing. Fig. 2(c) charts ΔG°* from 223 to 323 K (−50 to 50 °C) for loading pressures pL = 100 and 170 bar and unloading pressures pUL = 2, 5 and 12 bar. This data shows that the optimal standard free energy change ΔG°*(T) that enables maximal recovery of hydrogen from the sorbent lies in the range of 5–10 kJ mol−1 under ambient to moderately cooled conditions and these chosen pressure swings.
While we quantify optimality conditions in terms of the standard free energy change on H2 binding based on the Langmuir model, this is admittedly an approximation, and there may be coupling between binding sites if they are close. While simplified enthalpy–entropy correlation functions for H2 binding in nanoporous frameworks exist,73 they are not readily generalizable across different framework topologies and binding sites, particularly when the binding arises from the synergy between the molecular orbitals of the adsorbate and the host. Therefore, optimal binding interactions are best described in terms of the binding free energy without loss of generality. Clearly, a range of different enthalpy–entropy tradeoffs can achieve a particular target free energy of binding. All else being equal, the most desirable tradeoff, from a heat management perspective in H2 storage, is the least loss of entropy and least gain in enthalpy upon binding.
3 Models
With some idea of the target binding free energy and binding enthalpy in mind from the previous section, we consider how to computationally predict and understand the H2 binding energy (Fig. 3). As illustrated in Fig. 1, H2 binding sites in MOFs exist inside a periodic three-dimensional material, and upon the approach of a guest molecule to a metal site, there may be strong binding contributions reflecting local chemical interactions at the site, supplemented by weaker long-range dispersion interactions. Three approximations are needed to (approximately) predict binding energies. First, the binding site is modelled, either using a periodic boundary condition (PBC) approximation that neglects disorder or a cluster model that neglects long-range interactions. Second, the exact equations of quantum mechanics are replaced by a density functional theory (DFT) model, which reduces the formal exponential complexity to polynomial (roughly cubic scaling in the number of atoms). Third, the DFT equations are solved using a finite basis set to make the prefactor of polynomial scaling manageable. We shall elaborate briefly on all three of these aspects in the remainder of this section, as well as discuss a fourth issue, which is how to obtain some physical insight from the calculations beyond predicted observables.The choice between a PBC model and a cluster model is made for MOF binding site modeling based on two considerations. First is physical appropriateness. The PBC approach is most appropriate when long-range interactions are important. However, using the most accurate density functionals such as ωB97M-V is not presently computationally tractable with PBC approaches. Hence, the cluster approach is often favoured when an accurate description of local binding is of primary importance. PBC models are advantageous for examining multiple site adsorption, including adsorption on linkers and interactions over larger scales of the framework, which complements the localized interaction studies provided by cluster models presented here.
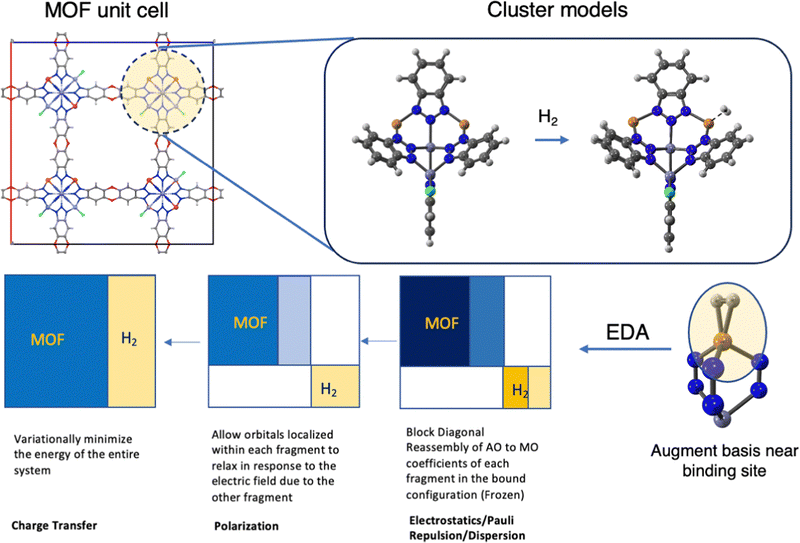 | ||
| Fig. 3 Workflow for DFT cluster calculations of H2 binding in MOFs. The top panel illustrates the selection of an appropriate cluster model from crystallographic data. The cluster should be centered on the binding site, with all chemically important functional groups around that site included, followed by addition of suitable passivating groups to terminate all dangling bonds at the cluster periphery. The cluster is then DFT-optimized to obtain equilibrium geometries with and without H2 ligation. The lower panel (going right to left) is a schematic illustration of the energy decomposition analysis (EDA) used to understand the main physical contributions to binding, ΔEads, typically using a larger basis set that is augmented on atoms near the binding site. The boxes schematically illustrate EDA constraints that isolate those physical contributions by controlling the atomic orbital to molecular orbital transformations on each fragment (MOF and H2) at each stage of the EDA sequence.55 | ||
All subsequent figures illustrating MOF modeling show the cluster chosen to replace the extended framework. Computational tractability versus physical reality likewise governs the choice of the cluster because a factor of two increase in the number of atoms leads to almost an order of magnitude increase in compute costs. On the other hand, the ideal cluster model should accurately capture metal–ligand interactions at short distances while adequately accounting for the dominant dispersion forces at comparatively longer ranges that govern binding in MOF pores. As an example of the considerations involved, we can examine the binding of H2 at the Cu(I) site in MFU-4l. This scenario can be depicted through a cluster model of the node truncated at its benzotriazolate extremities such that the arene is capped with hydrogen atoms (Fig. 3). These models allow us to validate binding energies and geometries against experimental crystal structure data and measured isosteric heats.58,59 These validations, in turn, enable the application of a smaller cluster model for computations of higher computational demand, such as frequency calculations. Complete ab initio relaxation of the cluster was performed in response to H2 loading for MOF topologies that can represent the nodal unit as a closed geometric shape, like in MOFs with a cubic crystalline structure such as MOF-5 and MFU-4l. The MOF V2Cl2.8(btdd), which features 1D dimensional chains truncated to the two nearest neighbours, was also subjected to a full cluster relaxation based on its extensive experimental validation.27 On the other hand, Ni2(m-dobdc), a MOF exhibiting similar 1D chains, the optimization of the cluster was achieved by fixing the bare node's coordinates using values from neutron diffraction data, an approach that has been previously demonstrated to be effective.57 A comprehensive understanding of the cluster models utilized in this work can be found in the original literature.27,57,59,70,74
4 Methods
Turning to density functional theory, modern DFT is based on an in-principle exact mapping of the 3n-dimensional many electron integro-differential Schrödinger equation onto a set of n coupled 3-dimensional equations, the Kohn–Sham equations.75 However, the KS equations depend on an unknown universal functional that describes exchange and correlation (XC), which in practice is modelled. The resulting approximate functionals are commonly grouped onto five rungs of a metaphorical Jacob's ladder that ascends from the primordial ooze of the Hartree world, where electron correlation is not described at all, to the heaven of chemical accuracy.76 In practice, functionals on rungs 1–3 (the local spin density approximation (LSDA), generalized gradient approximations (GGAs) and meta-GGAs) can be tractably evaluated with PBC models. Hybrid density functionals on rung 4, which include a portion of exact exchange,77 are computationally more demanding than local or semi-local functionals. This can make calculations with PBC models using hybrid functionals particularly resource-intensive, especially for large systems. However, the accuracy achievable at the 4th rung is known to be substantially higher across a range of chemical energy differences76,78 that include the noncovalent interactions critical to H2 binding. The comparative performance is illustrated for 275 H2 binding energies52 (ranging from very weak to very strong) in Fig. 4. It is to gain the benefit of this higher accuracy that we employ cluster modeling in this work.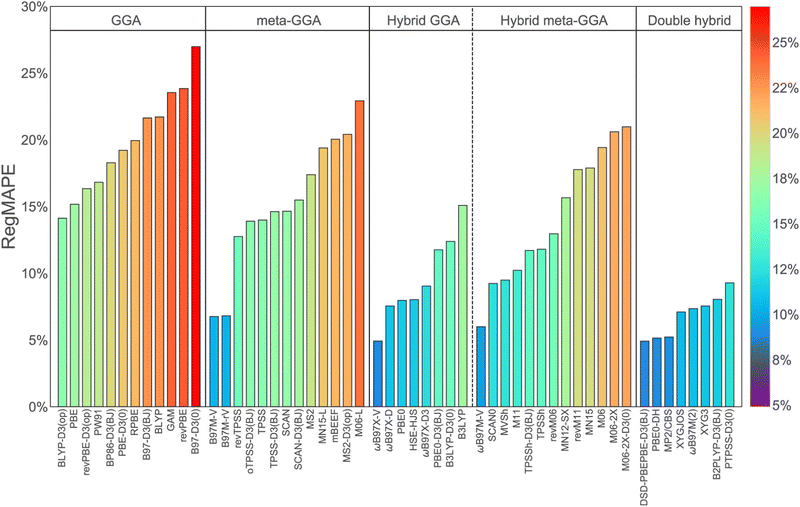 | ||
| Fig. 4 Regularized mean absolute percent errors (RegMAPE) (in percent) for a wide range of density functionals assessed against high accuracy benchmarks for 275 H2 binding energies (defining the H2bind275 dataset). The results are arranged according to the rungs of Jacobs ladder. The error metric, RegMAPE, is constructed to give most weight to binding energies in the key interaction range of 15–25 kJ mol−1 (see ref. 52 for definition). Reproduced from Veccham et al., J. Chem. Theory Comput., 2020, 16(8), 4963–4982; Copyright 2020 American Chemical Society. | ||
Specifically, we employ the ωB97M-V functional,79 which is an accurate range-separated hybrid meta-GGA that includes non-local VV10 dispersion,80 designed by the combinatorial “survival of the most transferable” protocol.76 The VV10 non-local correlation functional provides a proper description of long-range electron correlation responsible for non-covalent interactions.80 Metal–ligand interactions due to charge-induced dipoles and orbital overlap entail accurate prediction of main group-transition metal chemistry. ωB97M-V is the top-performing hybrid density functional in several large assessments, including the MGC84 database,76 the large and diverse GMTKN55 benchmark dataset,78,81,82 and the TMC151 transition metal database.83 These findings are buttressed by an extensive benchmark52,53 of density functionals for hydrogen storage.
Once a density functional is selected, the next step in cluster modeling is to choose an appropriate atomic orbital (AO) basis set, which is used to represent the unknowns, the KS molecular orbitals (MOs). The compute cost of rung 4 DFT calculations rises as the 4th power of the number of AOs per atom,84 so again, there is a steep computational penalty to using very large basis sets. At the same time, not every property is equally sensitive to the quality (i.e. size) of the AO basis. In particular, optimized geometries offer the possibility of cancelling the basis set incompleteness error from one set of coordinates to another nearby set of coordinates with virtually identical chemistry and bonding. Therefore geometries are far less basis set sensitive (and are also less functional sensitive) than absolute binding energies since the latter is the difference between two very different configurations.
With these considerations in mind, geometries were optimized in this work using the relatively small def2-SVP basis,85 which contains f-polarization at the transition metal site, and p-polarization on H to account for polarization adequately. The ωB97M-V functional was used (with a few exceptions discussed where relevant when B3LYP-D2 was used). Geometries were converged to 3 × 10−4 kJ mol−1 in energy, and 3 × 10−5 a.u. in the maximum gradient component. Single point calculations for electronic binding energy, ΔEads, utilized ωB97M-V with the augmented def2-TZVPPD basis85 at the metal site and dihydrogen, which includes 2f and 1g polarization functions at the metal site and 3p and 1d polarization functions for hydrogen. All single point energy calculations were counterpoise corrected for basis set superposition error, following best practices with basis sets of this size.76
Thermochemistry was determined using the B3LYP functional with Grimme's empirical dispersion corrections86 in the def2-SVP basis with the same convergence criteria mentioned above, followed by Hessian evaluations at the minimum energy configuration. The total enthalpy change (ΔH(T)) was calculated as ΔH(T) = ΔEads + ΔZPVE + ΔHvib(T) + ΔnRT, with the free energy of binding estimated as ΔH(T) − TΔS(T), with ΔS(T) and ΔH(T) computed using the rigid–rotor–harmonic oscillator (RRHO) approximation. Low-frequency normal modes (≤100 cm−1) were set to 100 cm−1 to account for soft vibrations.87 All computations were conducted using QChem 5.3 software88 and a development version of Q-Chem 6.1.
If the approximations described above were well chosen, the resulting DFT calculations should be a reliable numerical experiment that yields the thermodynamic and structural information needed to characterize H2 binding in MOFs. To provide additional insight into why those properties take the values they do, we employ the absolutely localized molecular orbital (ALMO)-EDA to reveal the interaction energy as being due to distinct physically interpretable components,54,55,89–91 relative to the noninteracting MOF and H2. The electronic component of the adsorption enthalpy is expressed as:
| ΔEads = ΔPrep + ΔFrzDF + ΔDisp + ΔPol + ΔCT | (2) |
5 Characterizing open metal sites for H2 storage
MOF-5
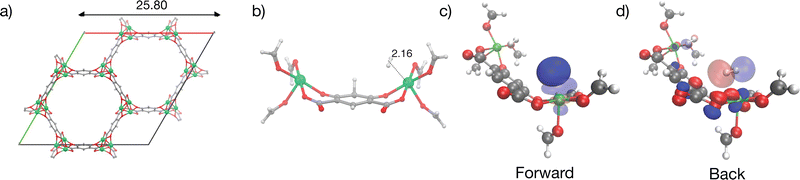
MOF-5 has been extensively studied due to its potential for hydrogen storage and is an archetypal metal–organic framework with broad implications for gas storage and separation applications.32,34,56,94–97 A MOF with no open metal sites, MOF-5 is composed of Zn4O(bdc)3 (bdc2− = 1,4-benzenedicarboxylate) units forming a cubic three-dimensional extended porous structure with the unit cell pictured in Fig. 5a. H2 binds to MOF-5 in an array of binding sites classified as α, β, γ and L depending on its relative positioning with respect to the interstitial oxide at the centre of the Zn4O tetrahedra, and the linker.98,99 The strongest binding α site in MOF-5 depicted with a cluster model in Fig. 5b binds H2 with an experimentally measured enthalpy of −7 kJ mol−1 between 60 to 70 K100 (lower values of ∼3.5 kJ mol−1 have also been reported101). Our calculations suggest that hydrogen binds at the cup site α in MOF-5 at a distance of 3.43 Å from the interstitial oxide at the centre of the node with ΔE = −8.6 kJ mol−1, which is in qualitative agreement (slightly stronger) than the experiment, and previous computations of H2 binding in the material at the MP2 level of theory.99 This binding is driven primarily by dispersion, as seen by the large ΔDisp of −16.3 kJ mol−1 and weak ΔPol and ΔCT terms (see Fig. 9). A secondary charge transfer energy lowering of −3.4 kJ mol−1 dominated by back-donation from lone pairs on polarized oxygens of the bdc2− linkers to the hydrogen σ* is visualized in Fig. 5c.We must also consider the intricacies of zero-point vibrational energy change in our computational models of MOF-5. Earlier simulations by Sillar, Hoffman, and Sauer have demonstrated that hydrogen molecules exhibit free rotational movement when bound to MOF-5's cup sites.99 Using MP2 simulations in conjunction with the multi-site Langmuir model, they were able to replicate experimental binding curves, assuming H2 retains its rotational freedom in the adsorbed state. In alignment with this, our calculations employ a simplified formate model for the cup site described in previous work74,99 for thermochemistry calculations and assume unhindered rotation of H2 in its bound state. This methodological choice leads to predicted binding enthalpies of −10.0 kJ mol−1 at 77 K, which, although stronger than the experimentally observed −7.7 kJ mol−1, serves to illuminate future avenues for refining vibrational ground state predictions. The limitations of the RRHO approximation become particularly pronounced for light elements like hydrogen, especially when interacting anharmonically with MOF-5's delocalized soft modes. A comprehensive solution would necessitate computations of the vibrational ground state allowing full nodal relaxation in response to H2 uptake and anharmonic coupling between delocalized modes of the framework, posing a formidable computational challenge and presents an avenue for future methodological development.
Contributors to binding due to frozen (which includes the effect of electrostatic or Coulomb interactions and Pauli repulsion), dispersion, polarization, and charge transfer are summarized in Fig. 9.
Ni2(m-dobdc)
A MOF with Ni(II) sites, Ni2(m-dobdc) has surpassed the volumetric usable capacity of MOF-5 under ambient conditions.25 As the leading MOF for ambient temperature hydrogen storage, Ni2(m-dobdc)'s volumetric usable capacity has been measured at 11.0 g L−1 at 298 K at a pressure swing of 5–100 bar (and 23.0 g L−1 with a temperature swing between 198 K and 298 K). This MOF is characterized by the m-dobdc linker, and derives from MOF-74 family of metal–organic frameworks25,57,102–109 which feature hexagonally packed cylindrical channels with cross-sections that are lined with Ni(II) sites at a high volumetric density (see Fig. 6a).Given its significance for storage and sequestration applications, MOF-74 and its derivatives have been simulated extensively with electronic structure methods,57,108,110 and with force fields.111,112Fig. 6b shows the DFT optimized geometry for a two-site model of the Ni2(m-dobdc) node where H2 binds at the distorted octahedral Ni(II) sites (shown in green) at centre of mass (COM) distances of 2.16 Å away from the Ni(II) site (powder neutron diffraction indicates a COM distance of 2.18 Å).57Fig. 9, Column II shows binding energy estimates for H2 binding to the open metal site. The net electronic energy lowering in Ni2(m-dobdc) (ΔE = −14.5 kJ mol−1) is stronger than MOF-5 and driven by a predilection for polarization (ΔPol = −15.9 kJ mol−1) and charge transfer (ΔCT = −23.8 kJ mol−1). Charge-flow is dominated by the forward donation from H2 σ to the metal d manifold visualized in Fig. 6(c). Our ΔH(T) of −14.3 kJ mol−1 under ambient conditions aligns well with the experimentally measured value of 13.7 kJ mol−1.25 Though the polarization of H2 by the local charge at the Ni(II) centres makes H2 binding enthalpy in this framework stronger than MOF-5, it still falls short of the optimal range sought for attaining maximum usable coverage in sorbent materials.
Simulations of the 2-site cluster model of the node were performed with MOF coordinates fixed, a constraint encapsulated in ΔPrep, the energy required to achieve the bound configurations for both the node and H2. Geometry optimizations with the MOF cluster fixed led to SCF convergence problems with our preferred functional, ωB97M-V, which we circumvented by employing B3LYP-D2 for geometry optimizations and frequency analysis. Single-point vertical EDA computations were conducted using ωB97M-V. Thermochemical calculations accounted for partial Hessian evaluations of the bound H2 using the RRHO approximation. It's worth noting that, akin to the case of MOF-5, we assumed free rotation of H2 in its bound state. This assumption is in line with prior literature and serves as a simplification that achieves better agreement with experimental observables. However, it should be acknowledged that this approximation reflects limitations in vibrational modeling, and future methodological improvements would be desirable.
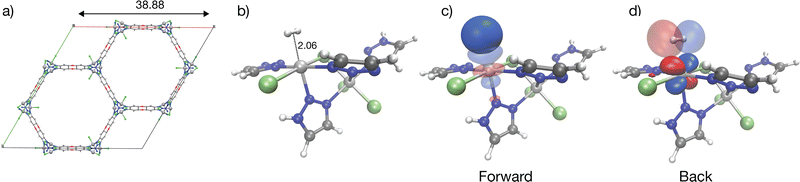
Cu(I)-MFU-4l
With an isosteric heat of −32 kJ mol−1, one of the strongest for H2 binding in MOFs, Cu(I)-MFU-4l has been of interest with regard to H2 binding.58,59,113,114 This material comprises cubic unit cells (Fig. 7a) with Kuratowski Secondary Binding Units (SBUs)115 (Fig. 7b), which feature coordinatively unsaturated and initially trigonal pyramidal Cu(I) sites which become pseudo-tetrahedral upon H2 coordination. The binding enthalpy of H2 to the Cu(I) site is driven by charge transfer to and from the metal site (see Column III in Fig. 9). H2 approach to the binding site results in a pyramidalization at the binding Cu(I) site reflected by a large ΔPrep or geometric distortion term, resulting in a destabilization of the dxz, dyz orbitals that can back-donate effectively to the hydrogen σ*.59 However, the binding in Cu(I)-MFU-4l is excessively strong, with the standard change in binding free energy predicted to be 2.39 kJ mol−1 at a temperature of 298 K, which falls outside the desirable range of between 5–10 kJ mol−1. Additionally, the density of open metal sites within MFU-4l is relatively low, necessitating refinement of both the local composition at the binding site and the global framework topology to establish this material as a viable option for high-capacity hydrogen storage. Within the context of strong Cu(I)-H2 interactions in a metal–organic framework, there is a recent report that 1% of Cu sites in NU-2100 exhibited high isosteric heat of adsorption (32 kJ mol−1).116 However, computations of the material with periodic DFT at the PBE-D3BJ level of theory predict weaker binding with adsorption energies between −9 to −11 kJ mol−1.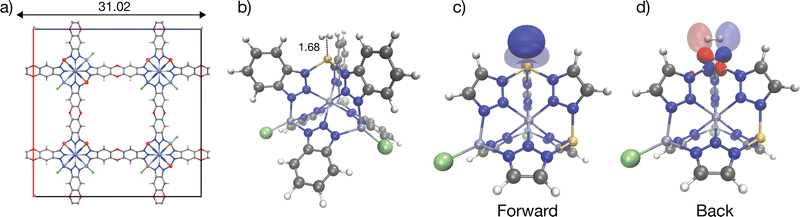 | ||
| Fig. 7 Illustration of strong H2 binding at the Cu(I) site in Cu(I)-MFU-4l. Panel (a) shows the cubic unit cell of the material, and (b) shows the cluster model representation H2 binding in Cu(I)-MFU-4l; note the short 1.7 Å Cu–H2 distance. Tetrahedral Cu(I) binding site with significant charge transfer orbitals for forward- and back-donation are shown in (c) and (d). Cu(I)-H2 back-bonding interactions are strong at this binding site (see also Fig. 9). Distances are labelled in Å with Zn(II) rendered in blue-grey, Cu(I) in bronze, N in blue, H in light grey, C in dark grey, and Cl in light-green. The orbitals were plotted with an isosurface of ±0.07 Å. A smaller cluster model truncated at triazolate extremities was used for the visualization of charge transfer orbitals. | ||
V2Cl2.8(btdd)
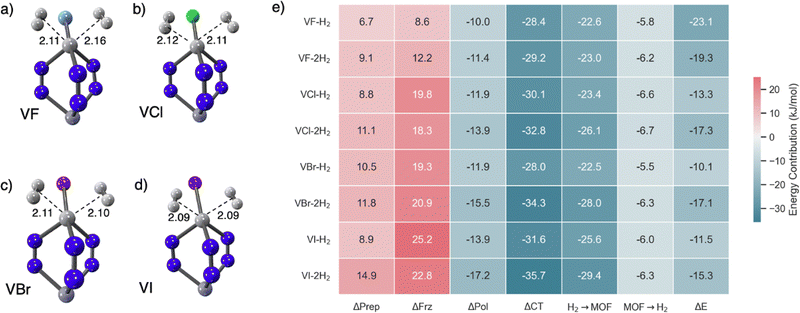
Gagliardi et al. initially put forth V(II)-MOF-74 as a candidate for the separation of N2 and CH4.108 Subsequently, Jaramillo et al. synthesized coordinatively unsaturated dicationic V(II) substitution in V2Cl2.8(btdd) (depicted in Fig. 8),117 thereby demonstrating the viability of this material for chemical handle-based separation through the preferential activation of π* orbitals in guest molecules. Further research has revealed the material's efficacy for H2 storage under ambient conditions.27 This MOF has a mixture of V(II) and V(III) sites that are formed by oxidation of V(II) during synthesis and, therefore, can be effectively modeled as a two-site cluster with a halide capping the V(III) site adjacent to the V(II) OMS where H2 can coordinate (see Fig. 8(b)). A mechanism similar to that in Ni2(m-dobdc) prevails here where ΔPol = −6.1 kJ mol−1 polarizes the H2 in preparation for charge transfer. ΔCT, however is much stronger than Ni2(m-dobdc) for H2 binding to the π-basic V(II) site (see column IV of Fig. 9) with back-bonding attenuated when compared to Cu(I) in MFU-4l. The acceptor orbital for forward donation from H2 has dz2 character on V. Back donation occurs from the dπ orbital to the H2 σ* orbital.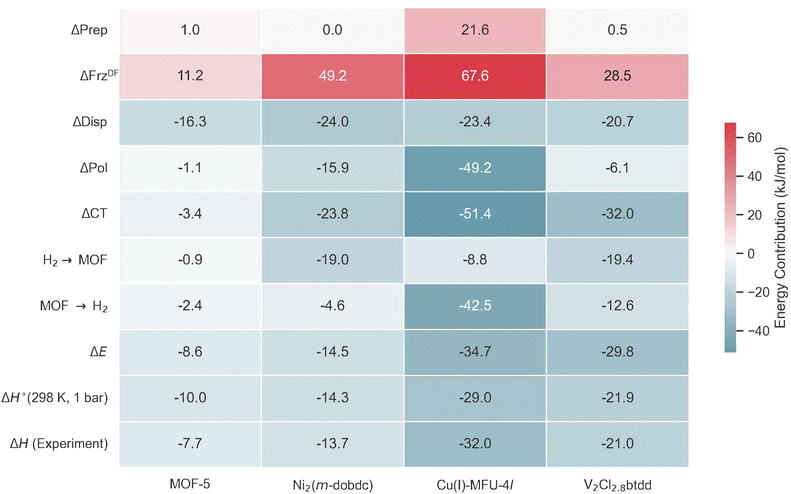 | ||
| Fig. 9 A comparative summary of energy decomposition analysis (EDA) (see eqn (2) for definition of terms) of H2 binding to four MOFs. ΔCT contains forward (H2 → MOF) and back-donation (MOF → H2) contributions. The MOFs are MOF-5, a material with no open metal sites (see Fig. 5), the Lewis acidic Ni(II) site in Ni2(m-dobdc) (see Fig. 6), and π-basic Cu(I) and V(II) sites in Cu(I)-MFU-4l (see Fig. 7) and V2Cl2.8(btdd) (see Fig. 8) respectively. ΔH°(T) values are reported at 298 K and 1 bar, and compared to experimental values. | ||
Comparative analysis
This EDA provides insight into the chemical factors governing optimal interactions for high-capacity hydrogen storage, underscoring the significance of precise modulation of open metal site interactions as a primary design principle. Despite considering 4 quite distinct binding sites, the range of dispersion stabilization for H2 binding spans a fairly compact range from −16.0 to −24.0 kJ mol−1. Unique characteristics of the open metal sites in each framework lead to divergent adsorption behaviour. In MOF-5, dispersion dominates binding at the cup site, while the polarization of H2 by unscreened charges at open metal sites facilitates stronger binding in Ni2(m-dobdc). The Lewis acidic Ni(II) in Ni2(m-dobdc) exhibits forward-dominant charge transfer, whereas Cu(I) in MFU-4l and V(II) in V2Cl2.8(btdd) act as π bases. Excessive charge transfer at the π-basic Cu(I) site in MFU-4l leads to chemisorption and a strongly repulsive ΔFrz arising from increased occupation pressure. In contrast, attenuated back-bonding at the more diffuse and electropositive V(II) site results in near-optimal binding enthalpy for H2 storage under ambient conditions.Fig. 10 delineates the predicted ΔG°(T) values for H2 binding across the four investigated MOFs, spanning temperatures from 223 K (−50 °C) to 323 K (50 °C) under the RRHO approximation. MOF-5, devoid of open metal sites, exhibits binding enthalpies that are insufficient for maximizing room-temperature capacities. In contrast, Ni2(m-dobdc) offers stronger binding but still fails to meet the requisite threshold for ambient storage. Intriguingly, Cu(I)-MFU-4l, characterized by its strongly π-basic sites, binds H2 too strongly for practical ambient storage. Among the candidates, V2Cl2.8(btdd) stands out for its near-optimal enthalpy–entropy trade-off, boasting an H2 binding enthalpy of ΔH(298 K, 1 bar) = −21.9kJ mol−1. This enthalpy, in conjunction with a predicted binding free energy change of 10.0 kJ mol−1 at 298 K and 1 bar, places it within the optimal range for maximizing deliverable H2 capacity under ambient conditions as evidenced by its proximity to the dashed grey curve for optimal free energy of binding ΔG°*(T) under a pressure swing of 5–100 bar. The optimal binding free energy change of 7.7 kJ mol−1 at 298 K (25 °C), and 5.8 kJ mol−1 at 223 K (−50 °C) with this pressure swing are shown by black and blue encircled points. Ni2(m-dobdc) is closer to optimality conditions for hydrogen storage under moderately chilled conditions. Finally, it is worth recalling that the density of strong binding sites is critical to usable storage capacity. In fact, V2Cl2.8(btdd) does not have a high enough site density to compete with the usable capacity of Ni2(m-dobdc) at ambient temperature despite its superior binding characteristics.
6 Prospects for multi-H2 coordination at open metal sites
The case studies in the previous section illustrated several main points. Perhaps the most important point, now generally accepted, is that the chemical diversity of MOFs permits the realization of binding sites that can closely approach the ideal hydrogen binding free energy. This maximizes the usable capacity for room-temperature H2 storage given a specific site density. A second important point is that quantum chemical cluster calculations using high-quality density functionals can accurately evaluate the binding energy, as evidenced by good agreement with binding enthalpies. Contributions associated with vibrational motion, such as the binding entropy and the ZPE contribution to binding, are the most challenging, and there is room for further methodology improvements.Relative to the binding of a single H2 per site, the volumetric and gravimetric storage capacity of a MOF-based material could be greatly enhanced if a given open metal site could bind multiple hydrogen molecules. While fully exposed metal ions can bind many H2 molecules, the challenge for a viable material is having partially exposed metal sites that are still stable. Indeed, many calculations on specific material designs allude to this possibility.61–68,70 There is a reported instance of multiple H2 molecules ligating at Mn in MOF, albeit with a weak interaction with the second H2 interactions.60 Nonetheless, the experimental demonstration of reversible binding of multiple hydrogens in the first coordination sphere of an open metal site with standard binding enthalpies of −20 kJ mol−1 or higher at room temperature remains elusive. There are substantial experimental hurdles to achieving this goal, including appropriate materials design, successful synthesis, and full desolvation of the resulting open metal sites. Exploratory quantum chemical calculations can provide insight into binding sites capable of accommodating multiple H2 molecules in the desired range, and the purpose of this section is to review and extend some existing work towards this goal.
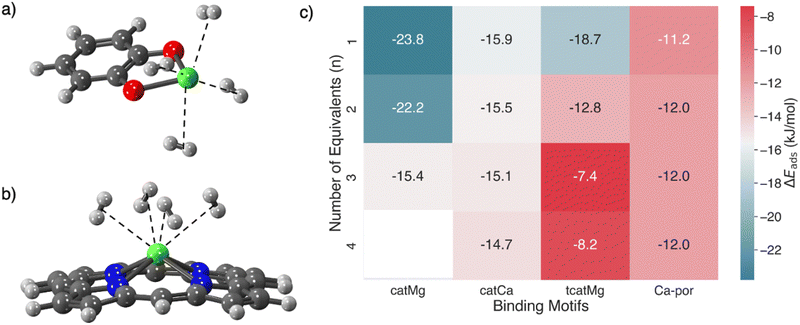
Catecholates are the doubly deprotonated forms of catechols (for which the parent compound is 1,2-benzenediol, or 2-hydoxyphenol). The resulting dianion can form strong chelating bonds with divalent metal ions of appropriate size,118 where the doubly coordinated metal is significantly exposed. In the context of hydrogen storage, the idea of a quite open metal site on a catecholate, with only 2-fold coordination, is potentially exciting because of the prospect that strong yet reversible binding of more than one H2 could be achieved, thereby allowing for higher-density storage. Furthermore, incorporating the catechol functionality on a MOF linker119 potentially opens the door for post-synthetic modifications to incorporate the open metal sites. Indeed, there are successful synthetic precedents for incorporating catechol-based linkers into MOFs,120,121 and demonstrating postsynthetic metalation.119 That progress has synergized with and inspired a range of computational studies of metal-catecholates,122–124 including for storage of multiple hydrogens at a single site.66,68
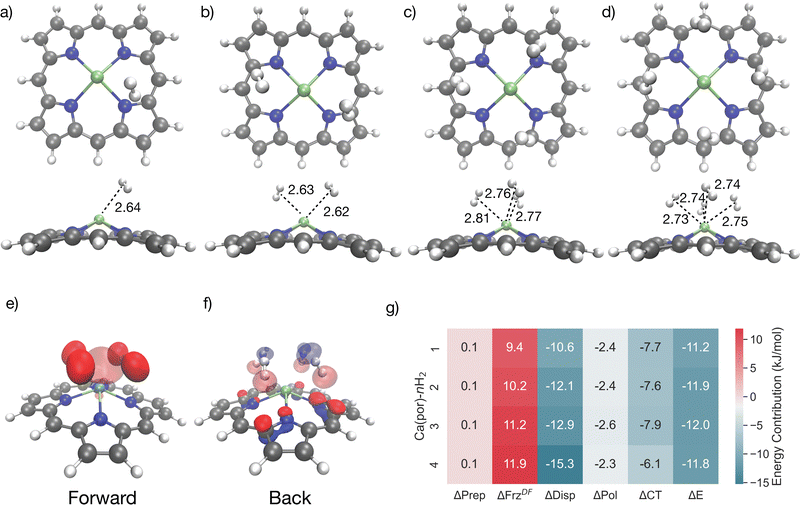
In particular, magnesium and calcium catechols have demonstrated the capability of binding multiple equivalents of H2, where the electronic binding energy ΔEads of each hydrogen may exceed −20 kJ mol−1.68Fig. 11 shows the binding of four equivalents of H2 in calcium catecholate and a summary of the binding energies of multiple H2 equivalents in catecholate-decorated MOFs. It is promising that the binding energies of more than one H2 at a single Mg and Ca catecholate site are in the ideal range for usable capacity with a 5–100 bar pressure swing. However, the highly exposed alkaline earth metal binding site will strongly coordinate with the solvent as well, and therefore, part of the synthetic challenge will be the problem of desolvation. If even partial desolvation is possible, then there may still be potential for a usable material because computations have demonstrated that Ca-catecholate can bind two hydrogen equivalents in the ideal range even when there is a residual solvent molecule (acetonitrile) still coordinated at the binding site.68 On the other hand, in the corresponding catMg material, the H2 binding energies were significantly reduced by the presence of a coordinating CH3CN molecule.
Multiple hydrogen ligation at an open metal site can also be realized through metal porphyrins, which can be incorporated as linkers in porous materials.125–130 PCN-224131 and PCN-221132 are examples of MOFs incorporating metallated porphyrins. The study of dihydrogen adduct formation in calcium-containing porphyrin systems is significant due to calcium's abundance and the capacity of Ca-porphyrin to support up to four dihydrogen adducts.133 Past endeavours at quantifying the binding of these H2 adducts in Ca-porphyrin have used the local density approximation (LDA), and the generalized gradient approximation (GGA) with periodic DFT, giving binding estimates of −24.1 kJ mol−1, and −9.6 kJ mol−1 per hydrogen respectively. In light of the significant difference in predicted binding energies between the LDA and GGA approximations, their limited treatment of dispersion effects, and the improvements that are possible with high-level functionals,52,53 we employ one such functional here. This ωB97M-V functional79 employs the non-local and highly effective VV10 form80 for capturing dispersion interactions and is well-suited for quantifying binding at these sites.52,53Fig. 11 compares differential binding energies for the sequential ligation of multiple equivalents of H2 in Ca-porphyrin and compares them with calcium and magnesium catecholate functionalized materials that have been investigated earlier.68 It is evident that the Ca-porphyrin binding energies are only a little weaker than ideal (∼−12 kJ mol−1) and, furthermore, are remarkably invariant through the binding of 4 H2 molecules.
Fig. 12 shows Ca-porphyrin binding one, two, three, and four H2 molecules. The Ca2+ ion (shown in green in Fig. 12) in Ca-porphyrin is raised from the plane of the porphyrin ring, and this pyramidalization is supported by experimental evidence on the crystallized Ca-porphyrin.129 The hydrogen molecules are bound close to the Ca2+ ion, assuming positions within the six-membered pockets that interlace the modified pyrrole subunits at distances ranging from 2.64 Å to 2.75 Å for the sequential ligation of four equivalents. The bound H2 molecules are little perturbed from the gas phase, as ascertained by a 0.76 Å H–H distance (compared to 0.74 Å in the gas phase) that remains consistent across the board.134
 | ||
| Fig. 12 Front-on and sideways perspectives for 4 H2 molecules binding to Ca-porphyrin with distances from H2 centre of mass to Ca site (green) labelled in Å (a)–(d), showing a striking invariance to the number of coordinated H2 molecules. Charge transfer orbitals engaged in forward- and back-donation to and from the metal site for the case of 4 coordinated H2 (e) and (f). EDA (see eqn (2) for definitions) of the differential ΔEads for the ligation of 4 H2 molecules in Ca-porphyrin (g), showing a key role for dispersion (ΔDisp) and a secondary role for charge transfer (ΔCT). The orbitals were plotted with an isosurface of ±0.07 Å. | ||
Fig. 12g presents the electronic interaction energy ΔE and energy decomposition analysis for the sequential binding of four H2 molecules near Ca-porphyrin. The binding strength for each hydrogen is stronger than −10 kJ mol−1, with dispersion forces contributing significantly to the overall binding, providing >10 kJ mol−1 of stabilization in each instance. Short-range interactions such as polarization and charge transfer also contribute to the binding, with charge transfer playing a role in the net binding energy albeit to a lesser extent when compared to the binding of H2 to Ni(II), Cu(I), and V(II) OMS in MOFs studied earlier. Fig. 12e and f shows charge transfer orbitals for forward and back-donation. While the Ca2+ ion does accept charge from the ligating hydrogens (Fig. 12e), back-donation occurs primarily from the nitrogen atoms on the porphyrin ring (Fig. 12f), which indicates that the ring itself an active participant in the binding. In summary, our findings corroborate that the binding mechanism of H2 to Ca-porphyrin is slightly stronger than −10 kJ mol−1 and is largely controlled by dispersion effects augmented by charge transfer. This is in contrast to binding in metallated porphyrins containing transition metals like Ti, where the Kubas interaction plays a significant role in dihydrogen binding.133
Therefore, a broader potential for multiple H2 coordination lies within the open transition metal sites of MOFs (or, possibly, decoration of linkers with transition metals, although that can also readily lead to overly strong binding135). Owing to their unique electronic configurations, some open transition metal sites offer the potential for binding multiple hydrogen molecules, thereby setting the stage for improved usable hydrogen storage capacities. Our recent investigation70 focused on the open metal site of V(II)-exchanged MFU-4l, where the parent scaffold supports tetrahedral V(II) sites.136 Utilizing state-of-the-art density functional theory calculations, we predicted the binding of two hydrogen molecules at V(II), where the V(II) site starts off with four-coordinate pseudo-tetrahedral coordination.70 This binding site also exhibited the potential for tuning the H2 binding strength by varying the adjacent first coordination sphere halide counterion. Fig. 13(a)–(d) shows V(II) sites in MFU-4l binding 2 H2 molecules and summarizes the quite wide range of associated adsorption energies with EDA components for each (Fig. 13(e)). While the strongest binding was predicted for F− substituted nodes, the heavier halides exhibited stronger ΔEads for binding the second equivalent of H2 in V(II)-MFU-4l when compared to the first. The orbital synergy between the ligating H2 molecules and V(II) underpinned the binding, characterized by robust forward donation and uniformly weaker back-bonding stabilization. In particular, the binding strengths for each hydrogen for fluoride substituted nodes in V(II)-MFU-4l were predicted to be around −20 kJ mol−1, which makes it a viable candidate for H2 storage under ambient or moderately chilled conditions.
Intrigued by the prospect that a monovalent metal without the halide at the peripheral site of the MFU-4l node could accommodate three equivalents of H2 on the completion of its octahedral sphere, we performed a computational search of metal-substituted nodes with monovalent first-row transition metals in their high-spin configuration. In pursuit of identifying monovalent first-row transition metals capable of accommodating three H2 molecules within the MFU-4l node, we employed a hierarchical computational strategy. Initial screening relied on a truncated small cluster model, focusing on the triazolate-terminated node. This exploratory phase singled out Sc(I) and Ti(I) within the MFU-4l framework as the most promising candidates for binding 3 H2 molecules at a single site, presumably enabled by the relatively large size of these ions relative to later members of the first transition series. Despite the formidable challenge of synthesizing these unusual metal substitutions in MFU-4l, there are synthetic precedents for these metals in their +1 oxidation states in the literature.138,139
For more accurate modeling, we then switched to larger benzotriazolate-terminated nodes near the binding sites to refine the Sc(I) and Ti(I) results. The OMSs for Sc(I) and Ti(I) were modelled in their high-spin ground states with S = 1, and 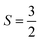 respectively.
respectively.
The results reported were based on geometry optimizations and thermochemistry calculations (vibrational corrections) at the B3LYP-D2 level of theory, while the electronic energies and the associated EDA analysis were evaluated with the ωB97M-V functional. The more computationally expensive frequency calculations for these systems were performed with the model of the node truncated at triazolate extremities.
Fig. 14 illustrates the coordination of 1, 2 and then 3-H2 molecules to the Sc(I)-MFU-4l site. All three coordination numbers show similar centre of mass distances to the OMS (Fig. 14). Distances to the closest contact at the node for the step-wise attachment of three hydrogens is shown in purple. It is particularly striking that many of these contact distances (each to another hydrogen) are inside the sum of van der Waals radii of two hydrogens (∼2.4 Å). Sc(I) exhibits a ΔEads range of −30 to −35 kJ mol−1, slightly weaker than Ti(I), while its ΔH(T) at standard temperature and pressure ranges between −24.7 and −26.9 kJ mol−1 (see Table S2, ESI†), also attenuated compared to Ti(I)-substituted MFU-4l. To further characterize these results, we will discuss EDA, thermochemistry, and binding curves to predict the usable capacities of transmetalated MFU-4l and MFU-4 that has these sites embedded within the material.
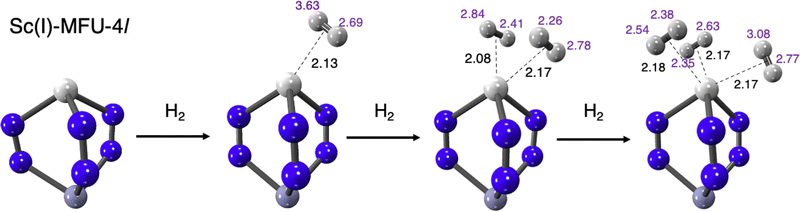 | ||
| Fig. 14 Summary of computational predictions of the ligation of three equivalents of H2 at the Sc(I) core in Sc(I)-MFU-4l. Distances to the H2 centre of mass are labeled in black. The quite striking invariance of this distance to the number of ligated H2 corresponds to very similar binding energies (see Fig. 15 for details), and is a very desirable feature of this binding site. Distances to the closest contact at the node for the bound hydrogens are shown in purple. All distances are in Å. | ||
Fig. 15 reports EDA for binding each of the 3 hydrogens at Sc(I) and Ti(I) sites, respectively. As is the case with our analysis of the four extensively characterized MOFs discussed in the previous section, the dispersion stabilization contributions to the binding energy stay consistent across the board.
 | ||
| Fig. 15 Binding energies and their EDA (see eqn (2)) for the binding of three equivalents of H2 at Sc(I) and Ti(I) sites in MFU-4l. The Sc(I) sites demonstrate a weak dependence of binding on the number of bound H2, which is desirable for H2 storage purposes. By contrast, the Ti(I) sites show fall-off in binding with number of bound H2. See text and Fig. 16 for the origin of the remarkable change in the ΔFrzDF and ΔPol EDA components for the Sc(I) site with 2 bound H2. | ||
The electronic binding energy, ΔEads, is comparable for all three hydrogens. However, the EDA results indicate that when the second hydrogen binds to Sc(I), the Pauli repulsion component in ΔFrz is remarkably large in magnitude. Moreover, its ΔPol counterpart is also remarkably large and attractive compared to the first and third hydrogens. We turned to the recently developed polarization analysis137 to seek an explanation, resulting in the POL COVPs shown in Fig. 16. Fig. 16(b) reveals that Sc d-orbital occupation changes to relieve Pauli repulsions (i.e. nearly an entire electron promoted from occupied to virtual) for the binding of the second H2.
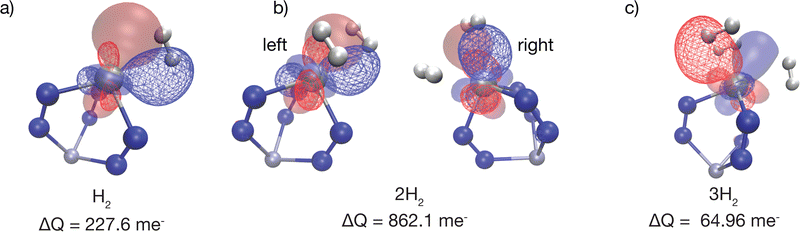 | ||
| Fig. 16 The polarization COVPs (see ref. 137 for theory) associated with relaxing the Sc(I) site upon (a) binding the first H2, (b) binding the second H2, and (c) binding the third H2. Each COVP consists of a donor orbital shown as a solid surface and an acceptor orbital shown as a triangulated surface. The number of electrons rearranged is shown in millielectrons, and it is evident that nearly an entire Sc d electron is rearranged upon the binding of the 2nd H2; this is the origin of the remarkable EDA results shown in Fig. 15. The orbitals were plotted with an isosurface of ±0.07 Å. | ||
The fact that the largest value of ΔPol appears to reflect relief of Pauli repulsion rather than conventional electrostatic polarization is not unprecedented: we also recently observed this in computations of the binding of water to Cu(I)-MFU-4l.140 Both the structural factors discussed above and the EDA results indicate how effectively the Sc(I) site serves to pack together the 3 H2 molecules that it binds.
This sequential binding of three H2 molecules at a single binding site can be described by the reactions 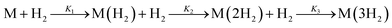 . This process can be represented by the binding polynomial, Q(p)
. This process can be represented by the binding polynomial, Q(p)
| Q = 1 + K1p + K1K2p2 + K1K2K3p3, | (3) |
The average ligand occupancy v(p,T) at a given temperature and pressure is determined by 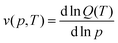 , enabling the derivation of the binding isotherm, which in turn predicts the material's usable capacity. Distinct from a conventional multi-site Langmuir model, which assumes site independence, the stoichiometric sequential multi-site model incorporates higher-order polynomial terms to account for cooperative ligand binding effects.99,141 This leads to a sigmoidal binding isotherm in some cases (e.g., Sc(I) in Fig. 17a).
, enabling the derivation of the binding isotherm, which in turn predicts the material's usable capacity. Distinct from a conventional multi-site Langmuir model, which assumes site independence, the stoichiometric sequential multi-site model incorporates higher-order polynomial terms to account for cooperative ligand binding effects.99,141 This leads to a sigmoidal binding isotherm in some cases (e.g., Sc(I) in Fig. 17a).
The binding of three hydrogen molecules at the Sc(I) site in MFU-4l results in a binding isotherm that affords steep uptake at room temperature and at a pressure swing between 5–100 bar. Since the binding in Ti(I) in MFU-4l is considerably stronger, the corresponding binding curve shows strong uptake at pressures below 5 bar. These binding curves are compared with that of single H2 binding in Cu(I)-MFU-4l to provide perspective on the enhancement of site coverage facilitated by multiple H2 binding at a single open metal site.
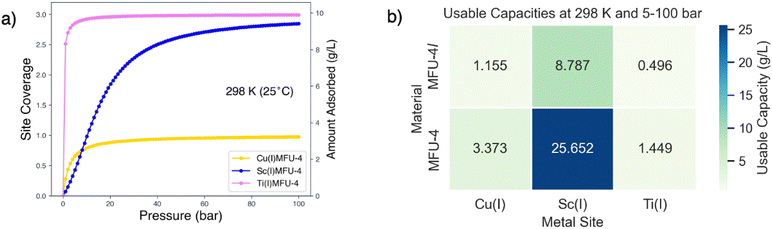
The surface coverage can be translated to capacity given the density of open metal sites, for instance, from crystallographic data. Considering the relatively low density of open metal sites in the MFU-4l, we anticipate that the adsorption capacity in g L−1 will be higher for MFU-4, a material with a similar topology but a higher density of binding sites. The MFU-4l unit cell, cubic with an edge of 30.91 Å, comprises eight nodes, each with four tetrahedral sites. The hydrogen adsorption amount is 3.63 g L−1, if we assume that each site is binding a single hydrogen molecule. The smaller unit cell in MFU-4, 21.63 Å, leads to denser metal site packing and a maximum uptake of 10.59 g L−1 if each site can bind only a single molecule, and presuming consistent unit cell dimensions after metal exchange. These estimates focus on hydrogen binding at the OMS, excluding additional adsorption within pores. For comprehensive uptake predictions, Grand Canonical Monte Carlo (GCMC) models, which factor in MOF surface area and free volume, can be utilized.71,142
Room temperature binding curves parameterized from the free energies of binding are shown in Fig. 17a along with estimates of usable capacity for the MFU-4 and MFU-4l families of materials (see Fig. 17b) for a pressure swing of 5–100 bar. Our results indicate that the multi-ligation of H2 in Sc(I)-MFU-4 yields impressive usable capacities of 25.65 g L−1 under these conditions, which results from the synergy between multiple H2 binding, and the nearly 3-fold increase in OMS density from using MFU-4 rather than MFU-4l. These estimates for usable capacities are conservative lower bounds since they do not account for dispersion stabilized H2 within the MOF pores.
7 Conclusions and outlook
Decarbonization of the world economy is an urgent challenge to address the increasingly alarming rate of climate change arising from greenhouse gas emission from legacy hydrocarbon-based transportation, heating and electricity generation applications. Hydrogen has tremendous promise as a clean fuel, but this promise is inhibited by the challenge of economically transporting it from the point of generation to the point of application, dispensing it, and even storing it from time of generation to time of consumption: this is the hydrogen storage problem. One approach to the as-yet not practically solved H2 storage problem is the use of sorbents, such as MOFs.In this perspective article, we have discussed computational quantum chemistry modeling of H2 binding in MOFs, across topics ranging from thermodynamic generalities to specific strengths and weaknesses of our chosen simulation methods to a range of comparisons between theory and experiment and a range of predictions. To summarize the generalities first, MOF materials design focuses on achieving maximal density of H2 binding sites that individually possess near-optimal thermodynamic characteristics for ambient temperature storage. Of course that is subject to suitable materials robustness, cost constraints, and synthetic realizability, which are topics we do not dwell upon in this computational perspective. In principle, optimal binding at 300 K should correspond to ΔG ∼ +8 kJ mol−1 to optimize usable capacity for a 5–100 bar pressure swing, or ΔG ∼ +9 kJ mol−1 to optimize usable capacity for a 5–170 bar swing. Given at least partial enthalpy–entropy compensation, an optimal range for binding enthalpies emerges that is between roughly −15 and −25 kJ mol−1.
Computational quantum chemistry permits, in principle, near-exact solution of the potential energy surface based on well-defined approximations to quantum mechanics. In practice, of course, there are a range of tradeoffs between the accuracy of results and the feasibility of calculations for a given system size. We have summarized key advances in the accuracy associated with DFT calculations on cluster models of H2 binding sites of MOFs. From the perspective of H2 binding, the best modern density functionals on rungs 3 (meta-GGAs) and 4 (hybrids) of the Jacob's ladder classification are capable of results that are typically within a few kJ mol−1 of the true result for the electronic binding energy. It is worth remembering that the worst are much poorer! We also reviewed and employed the latest EDA to unravel the main driving forces behind H2 binding. EDA permits the separation of the electronic binding energy into a frozen contribution containing Pauli repulsions and permanent electrostatics, a dispersion contribution, polarization (induced electrostatics/relief of Pauli repulsions), and charge-transfer (donor–acceptor) contributions. The latter three contributions are purely attractive.
About simulation accuracy, the situation is considerably less satisfactory for the corrections due to the vibrational motion that is necessary to obtain thermodynamic functions such as the enthalpy, entropy and free energy changes associated with binding. The standard rigid–rotor harmonic oscillator (RRHO) approach can be ineffective, and it is necessary to carefully consider that bound H2 retains motional freedom beyond that captured in the RRHO. For instance, in line with earlier work by Sauer and colleagues,99 we assumed free rotational movement of H2 when bound to the cup site in MOF-5, and to Ni(II) in Ni2(m-dobdc). The RRHO model also has known limitations when dealing with delocalized soft modes within the framework. These complexities remind us that each framework possesses unique vibrational characteristics that require customized computational approaches. They also point to a compelling avenue for future methodological refinements.
Improved computational predictions of free energies of hydrogen binding in metal–organic frameworks are challenging due to the anharmonic vibrations and coupling between multiple vibrational modes of the material; they are known to play a role in MOFs.143,144 An in-principle exact approach comes from the path integral formulation of quantum mechanics,145 which leads to well-developed path-integral methods146 that require either molecular dynamics or Monte Carlo sampling. While path integrals are the right ultimate goal, their expense is prohibitive, and more approximate methods are necessary, until automatic development of cheap force fields that accurately approximate our expensive quantum mechanical calculations becomes possible, or computing power advances a few more orders of magnitude. Beyond the RRHO model, and the simple corrections we have employed are a range of approaches that should offer higher accuracy than RRHO with cost still far less than path integrals.147 More work in this area would be beneficial to enable routine treatment of the beyond-harmonic quantum aspects of nuclear motion such as anharmonic couplings between MOF phonons and bound H2 modes, which is crucial for precise predictions of free energies of hydrogen binding.
As validation examples, as well as specific cases of H2 binding in MOFs to be analyzed and understood, we report calculations examining MOF-5, Ni2(m-dobdc), Cu(I)-MFU-4l, and V2Cl2.8(btdd). MOF-5 represents the extreme of overly weak binding, as it displays exceptional hydrogen storage capabilities only at low temperatures because H2 molecules are attracted to the framework via van der Waals forces. The other examples involve open metal sites, demonstrating the importance of orbital synergy in H2 binding within these frameworks. Specifically, V2Cl2.8(btdd) exhibits slightly stronger charge transfer interactions than Ni2(m-dobdc), and slightly attenuated back-bonding compared to Cu(I)-MFU-4l, resulting in near-optimal binding for storage at ambient conditions. V2Cl2.8(btdd) is, however, less promising for deployment than Ni2(m-dobdc) because of lower usable capacity due to its lower site density in addition to air sensitivity.
Densification of H2 with MOFs could be greatly enhanced by the binding of more than one H2 at a specific open metal site. We have reviewed and extended existing calculations that probe the candidate sites for binding multiple H2 molecules, starting with metal catecholates, which present very exposed metal sites which are capable of binding either 2 (Mg-catecholate) or 4 (Ca-catecholate) H2 with binding affinities that are stronger than physisorption though likely weaker than optimal. Turning to metals, the MFU-4l and MFU-4 family of materials offer a unique tetrahedral coordination scaffold stabilising transition metal sites. If a suitable metal ion replaces Zn, our calculations show that this allows for the binding of two equivalents of H2 in the case of divalent V(II) and three equivalents in monovalent Sc(I) or Ti(I).
As already discussed, the Sc(I) and Ti(I) oxidation states are exotic, and it may therefore not be possible to achieve post-synthetic modification of the MFU-4l and MFU-4 frameworks to create these novel low-valent sites. We do note that MFU-4l is known to support Ti(IV) and Ti(III),148 which can serve as a high-valent starting point for attempting chemical reduction for instance using sodium naphthalene. Regardless, the binding of three H2 at, e.g. Sc(I)-MFU-4l (or MFU-4) is striking for the density with which the H2 molecules pack with near-optimal binding enthalpies. Our optimized structures reveal many contacts inside the nominal van der Waals contact distance in the ligated structures, as well as an estimate of usable capacity of ∼25 g L−1 at ambient conditions. Both these aspects point to exciting potential for future discoveries which yield similar binding features and packing densities in synthetically realizable MOFs.
Author contributions
RC and MHG conceptualized the manuscript and formulated the methodology for this work. RC curated the data and wrote the original draft. RC, JT, HS and KMC visualized the data. HS implemented and provided some of the software code for the simulations. HZHJ provided insight into optimal binding conditions for hydrogen storage. MHG substantially edited the initial drafts to create the article that was then reviewed by JT, HS, YY, KMC, HF, and JRL.Conflicts of interest
MHG is a part-owner of Q-Chem Inc., whose software was used for the calculations reported here.Acknowledgements
The authors gratefully acknowledge research support from the Hydrogen Materials Advanced Research Consortium (HyMARC), established as part of the Energy Materials Network under the U.S. DOE, Office of Energy Efficiency and Renewable Energy, under Contract No. DE-AC02-05CH11231. Work on energy decomposition analysis was supported by the U.S. National Science Foundation through Grants No. CHE-1955643 and CHE-2313791. Work on vibrational contributions to thermodynamic functions was supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. DOE under contract no. DE-AC02-05CH11231, through the Gas Phase Chemical Physics Program. KMC acknowledges the Arnold O. Beckman Foundation for financial support.Notes and references
- E. L. Miller, S. T. Thompson, K. Randolph, Z. Hulvey, N. Rustagi and S. Satyapal, MRS Bull., 2020, 45, 57–64 CrossRef.
- A. M. Oliveira, R. R. Beswick and Y. Yan, Curr. Opin. Chem. Eng., 2021, 33, 100701 CrossRef.
- G. W. Crabtree, M. S. Dresselhaus and M. V. Buchanan, Phys. Today, 2004, 57, 39–44 CrossRef CAS.
- B. C. Tashie-Lewis and S. G. Nnabuife, Chem. Eng. J. Adv., 2021, 8, 100172 CrossRef CAS.
- S. K. Kar, S. Harichandan and B. Roy, Int. J. Hydrogen Energy, 2022, 47, 10803–10824 CrossRef CAS.
- H.-M. Cheng, Q.-H. Yang and C. Liu, Carbon, 2001, 39, 1447–1454 CrossRef CAS.
- I. Jain, C. Lal and A. Jain, Int. J. Hydrogen Energy, 2010, 35, 5133–5144 CrossRef CAS.
- D. P. Broom, Hydrogen storage materials: the characterisation of their storage properties, Springer, 2011, vol. 1 Search PubMed.
- Y.-h Zhang, Z.-c Jia, Z.-m Yuan, T. Yang, Y. Qi and D.-l Zhao, J. Iron Steel Res. Int., 2015, 22, 757–770 CrossRef.
- Q. Lai, M. Paskevicius, D. A. Sheppard, C. E. Buckley, A. W. Thornton, M. R. Hill, Q. Gu, J. Mao, Z. Huang, H. K. Liu, Z. Guo, A. Banerjee, S. Chakraborty, R. Ahuja and K. F. Aguey-Zinsou, ChemSusChem, 2015, 8, 2789–2825 CrossRef CAS PubMed.
- E. Rivard, M. Trudeau and K. Zaghib, Materials, 2019, 12, 1973 CrossRef CAS.
- J. O. Abe, A. Popoola, E. Ajenifuja and O. M. Popoola, Int. J. Hydrogen Energy, 2019, 44, 15072–15086 CrossRef CAS.
- M. R. Usman, Renewable Sustainable Energy Rev., 2022, 167, 112743 CrossRef CAS.
- D. Wei, X. Shi, R. Qu, K. Junge, H. Junge and M. Beller, ACS Energy Lett., 2022, 7, 3734–3752 CrossRef CAS.
- M. D. Allendorf, Z. Hulvey, T. Gennett, A. Ahmed, T. Autrey, J. Camp, E. S. Cho, H. Furukawa, M. Haranczyk and M. Head-Gordon, et al. , Energy Environ. Sci., 2018, 11, 2784–2812 RSC.
- M. D. Allendorf, V. Stavila, J. L. Snider, M. Witman, M. E. Bowden, K. Brooks, B. L. Tran and T. Autrey, Nat. Chem., 2022, 14, 1214–1223 CrossRef CAS PubMed.
- M. Wieliczko and N. Stetson, MRS Energy Sustainability, 2020, 7, E41 CrossRef.
- H. Barthélémy, Int. J. Hydrogen Energy, 2012, 37, 17364–17372 CrossRef.
- C. Chilev and F. D. Lamari, Int. J. Hydrogen Energy, 2016, 41, 1744–1758 CrossRef CAS.
- A. Schneemann, J. L. White, S. Kang, S. Jeong, L. F. Wan, E. S. Cho, T. W. Heo, D. Prendergast, J. J. Urban, B. C. Wood, M. D. Allendorf and V. Stavila, Chem. Rev., 2018, 118, 10775–10839 CrossRef CAS.
- A. Schneemann, L. F. Wan, A. S. Lipton, Y. S. Liu, J. L. Snider, A. A. Baker, J. D. Sugar, C. D. Spataru, J. Guo, T. S. Autrey, M. Jørgensen, T. R. Jensen, B. C. Wood, M. D. Allendorf and V. Stavila, ACS Nano, 2020, 14, 10294–10304 CrossRef CAS.
- M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782–835 CrossRef CAS.
- L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314 RSC.
- A. G. Wong-Foy, A. J. Matzger and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 3494–3495 CrossRef CAS.
- M. T. Kapelewski, T. Runčevski, J. D. Tarver, H. Z. Jiang, K. E. Hurst, P. A. Parilla, A. Ayala, T. Gennett, S. A. Fitzgerald, C. M. Brown and J. R. Long, Chem. Mater., 2018, 30, 8179–8189 CrossRef CAS.
- J. Purewal, M. Veenstra, D. Tamburello, A. Ahmed, A. J. Matzger, A. G. Wong-Foy, S. Seth, Y. Liu and D. J. Siegel, Int. J. Hydrogen Energy, 2019, 44, 15135–15145 CrossRef CAS.
- D. E. Jaramillo, H. Z. Jiang, H. A. Evans, R. Chakraborty, H. Furukawa, C. M. Brown, M. Head-Gordon and J. R. Long, J. Am. Chem. Soc., 2021, 143, 6248–6256 CrossRef CAS PubMed.
- H. Nazir, N. Muthuswamy, C. Louis, S. Jose, J. Prakash, M. E. Buan, C. Flox, S. Chavan, X. Shi and P. Kauranen, et al. , Int. J. Hydrogen Energy, 2020, 45, 20693–20708 CrossRef CAS.
- P. Peng, A. Anastasopoulou, K. Brooks, H. Furukawa, M. E. Bowden, J. R. Long, T. Autrey and H. Breunig, Nat. Energy, 2022, 7, 448–458 CrossRef.
- U. D. of Energy, DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles, https://www.energy.gov/eere/fuelcells/doe-technica-targets-onboard-hydrogen-storage-light-duty-vehicles, 2017, Accessed on: October 2023.
- U.S. Department of Energy under the Biden-Harris Administration, US releases National Clean Hydrogen Strategy and Roadmap, MRS Bull., 2023, 48, 707–708 DOI:10.1557/s43577-023-00574-9.
- H. Furukawa, K. E. Cordova, M. OKeeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- H. B. Wu and X. W. Lou, Sci. Adv., 2017, 3, eaap9252 CrossRef PubMed.
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS.
- R.-B. Lin, S. Xiang, H. Xing, W. Zhou and B. Chen, Coord. Chem. Rev., 2019, 378, 87–103 CrossRef CAS.
- S. Rojas and P. Horcajada, Chem. Rev., 2020, 120, 8378–8415 CrossRef CAS PubMed.
- Q. Wang and D. Astruc, Chem. Rev., 2020, 120, 1438–1511 CrossRef CAS PubMed.
- A. Bavykina, N. Kolobov, I. S. Khan, J. A. Bau, A. Ramirez and J. Gascon, Chem. Rev., 2020, 120, 8468–8535 CrossRef CAS PubMed.
- J. Y. Saillard and R. Hoffmann, J. Am. Chem. Soc., 1984, 106, 2006–2026 CrossRef CAS.
- R. C. Lochan and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 1357–1370 RSC.
- P. R. Kemper, P. Weis, M. T. Bowers and P. Matre, J. Am. Chem. Soc., 1998, 120, 13494–13502 CrossRef CAS.
- E. Tsivion, J. R. Long and M. Head-Gordon, J. Am. Chem. Soc., 2014, 136, 17827–17835 CrossRef CAS PubMed.
- D. Zhao, X. Wang, L. Yue, Y. He and B. Chen, Chem. Commun., 2022, 58, 11059–11078 RSC.
- M. Dincă and J. R. Long, Angew. Chem., Int. Ed., 2008, 47, 6766–6779 CrossRef.
- Ü. Kökçam-Demir, A. Goldman, L. Esrafili, M. Gharib, A. Morsali, O. Weingart and C. Janiak, Chem. Soc. Rev., 2020, 49, 2751–2798 RSC.
- S. A. A. Razavi and A. Morsali, Coord. Chem. Rev., 2019, 399, 213023 CrossRef.
- X. Zou, M.-H. Cha, S. Kim, M. C. Nguyen, G. Zhou, W. Duan and J. Ihm, Int. J. Hydrogen Energy, 2010, 35, 198–203 CrossRef CAS.
- M. Babucci, A. Guntida and B. C. Gates, Chem. Rev., 2020, 120, 11956–11985 CrossRef CAS.
- S. K. Bhatia and A. L. Myers, Langmuir, 2006, 22, 1688–1700 CrossRef CAS PubMed.
- Y.-S. Bae and R. Q. Snurr, Microporous Mesoporous Mater., 2010, 132, 300–303 CrossRef CAS.
- C. M. Simon, J. Kim, L.-C. Lin, R. L. Martin, M. Haranczyk and B. Smit, Phys. Chem. Chem. Phys., 2014, 16, 5499–5513 RSC.
- S. P. Veccham and M. Head-Gordon, J. Chem. Theory Comput., 2020, 16, 4963–4982 CrossRef CAS PubMed.
- S. P. Veccham and M. Head-Gordon, J. Phys. Chem. A, 2021, 125, 4245–4257 CrossRef CAS PubMed.
- P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079 RSC.
- Y. Mao, M. Loipersberger, P. R. Horn, A. Das, O. Demerdash, D. S. Levine, S. Prasad Veccham, T. Head-Gordon and M. Head-Gordon, Ann. Rev. Phys. Chem., 2021, 72, 641–666 CrossRef CAS PubMed.
- N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keeffe and O. M. Yaghi, Science, 2003, 300, 1127–1129 CrossRef CAS PubMed.
- M. T. Kapelewski, S. J. Geier, M. R. Hudson, D. Stück, J. A. Mason, J. N. Nelson, D. J. Xiao, Z. Hulvey, E. Gilmour, S. A. Fitzgerald, M. Head-Gordon, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 12119–12129 CrossRef CAS PubMed.
- D. Denysenko, M. Grzywa, J. Jelic, K. Reuter and D. Volkmer, Angew. Chem., Int. Ed., 2014, 53, 5832–5836 CrossRef CAS PubMed.
- B. R. Barnett, H. A. Evans, G. M. Su, H. Z. H. Jiang, R. Chakraborty, D. Banyeretse, T. J. Hartman, M. B. Martinez, B. A. Trump, J. D. Tarver, M. N. Dods, L. M. Funke, J. Börgel, J. A. Reimer, W. S. Drisdell, K. E. Hurst, T. Gennett, S. A. FitzGerald, C. M. Brown, M. Head-Gordon and J. R. Long, J. Am. Chem. Soc., 2021, 143, 14884–14894 CrossRef CAS PubMed.
- T. Runčevski, M. T. Kapelewski, R. M. Torres-Gavosto, J. D. Tarver, C. M. Brown and J. R. Long, ChemComm, 2016, 52, 8251–8254 RSC.
- T. Sagara, J. Klassen, J. Ortony and E. Ganz, J. Chem. Phys., 2005, 123, 014701 CrossRef PubMed.
- E. Klontzas, A. Mavrandonakis, E. Tylianakis and G. E. Froudakis, Nano Lett., 2008, 8, 1572–1576 CrossRef PubMed.
- A. Mavrandonakis, E. Klontzas, E. Tylianakis and G. E. Froudakis, J. Am. Chem. Soc., 2009, 131, 13410–13414 CrossRef CAS PubMed.
- E. Klontzas, E. Tylianakis and G. E. Froudakis, J. Phys. Chem. C, 2009, 113, 21253–21257 CrossRef CAS.
- T. Stergiannakos, E. Tylianakis, E. Klontzas and G. E. Froudakis, J. Phys. Chem. C, 2010, 114, 16855–16858 CrossRef CAS.
- R. B. Getman, J. H. Miller, K. Wang and R. Q. Snurr, J. Phys. Chem. C, 2011, 115, 2066–2075 CrossRef CAS.
- E. Klontzas, E. Tylianakis and G. E. Froudakis, J. Phys. Chem. Lett., 2011, 2, 1824–1830 CrossRef CAS.
- E. Tsivion, S. P. Veccham and M. Head-Gordon, ChemPhysChem, 2017, 18, 184–188 CrossRef CAS PubMed.
- H. Tachikawa and T. Iyama, J. Phys. Chem. C, 2019, 123, 8709–8716 CrossRef CAS.
- R. Chakraborty, K. M. Carsch, D. E. Jaramillo, Y. Yabuuchi, H. Furukawa, J. R. Long and M. Head-Gordon, J. Phys. Chem. Lett., 2022, 13, 10471–10478 CrossRef CAS PubMed.
- Y. S. Bae and R. Q. Snurr, Microporous Mesoporous Mater., 2010, 132, 300–303 CrossRef CAS.
- E. Garrone, B. Bonelli and C. Otero Areán, Chem. Phys. Lett., 2008, 456, 68–70 CrossRef CAS.
- S. M. Chavan, O. Zavorotynska, C. Lamberti and S. Bordiga, Dalton Trans., 2013, 42, 12586–12595 RSC.
- E. Tsivion and M. Head-Gordon, J. Phys. Chem. C, 2017, 121, 12091–12100 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- J. Lee, A. Rettig, X. Feng, E. Epifanovsky and M. Head-Gordon, J. Chem. Theory Comput., 2022, 18, 7336–7349 CrossRef CAS PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- A. Najibi and L. Goerigk, J. Chem. Theory Comput., 2018, 14, 5725–5738 CrossRef CAS PubMed.
- G. Santra and J. M. Martin, Some observations on the performance of the most recent exchange-correlation functionals for the large and chemically diverse GMTKN55 benchmark, AIP Conf Proc., 2019, 2186, 030004 CrossRef CAS.
- B. Chan, P. M. W. Gill and M. Kimura, J. Chem. Theory Comput., 2019, 15, 3610–3622 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al. , J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765 CrossRef CAS PubMed.
- D. S. Levine, P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 4812–4820 CrossRef CAS PubMed.
- D. S. Levine and M. Head-Gordon, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12649–12656 CrossRef CAS PubMed.
- P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2016, 144, 114107 CrossRef PubMed.
- P. R. Horn and M. Head-Gordon, J. Chem. Phys., 2015, 143, 114111 CrossRef PubMed.
- N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keeffe and O. M. Yaghi, Science, 2003, 300, 1127–1129 CrossRef CAS PubMed.
- J. L. Rowsell and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 1304–1315 CrossRef CAS PubMed.
- D. Dubbeldam, K. S. Walton, D. E. Ellis and R. Q. Snurr, Angew. Chem., Int. Ed., 2007, 46, 4496–4499 CrossRef CAS PubMed.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781 CrossRef CAS PubMed.
- J. L. Rowsell, E. C. Spencer, J. Eckert, J. A. Howard and O. M. Yaghi, Science, 2005, 309, 1350–1354 CrossRef CAS PubMed.
- K. Sillar, A. Hofmann and J. Sauer, J. Am. Chem. Soc., 2009, 131, 4143–4150 CrossRef CAS PubMed.
- F. M. Mulder, T. J. Dingemans, H. G. Schimmel, A. J. Ramirez-Cuesta and G. J. Kearley, Chem. Phys., 2008, 351, 72–76 CrossRef CAS.
- S. Bordiga, J. G. Vitillo, G. Ricchiardi, L. Regli, D. Cocina, A. Zecchina, B. Arstad, M. Bjørgen, J. Hafizovic and K. P. Lillerud, J. Phys. Chem. B, 2005, 109, 18237–18242 CrossRef CAS PubMed.
- H. Deng, S. Grunder, K. E. Cordova, C. Valente, H. Furukawa, M. Hmadeh, F. Gándara, A. C. Whalley, Z. Liu and S. Asahina, et al. , Science, 2012, 336, 1018–1023 CrossRef CAS PubMed.
- N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504–1518 CrossRef CAS PubMed.
- P. D. Dietzel, Y. Morita, R. Blom and H. Fjellvåg, Angew. Chem., 2005, 117, 6512–6516 CrossRef.
- T. Xiao and D. Liu, Microporous Mesoporous Mater., 2019, 283, 88–103 CrossRef CAS.
- S. R. Caskey, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2008, 130, 10870–10871 CrossRef CAS PubMed.
- A. F. Cozzolino, C. K. Brozek, R. D. Palmer, J. Yano, M. Li and M. DincaÌ, J. Am. Chem. Soc., 2014, 136, 3334–3337 CrossRef CAS PubMed.
- K. Lee, W. C. Isley, A. L. Dzubak, P. Verma, S. J. Stoneburner, L. C. Lin, J. D. Howe, E. D. Bloch, D. A. Reed, M. R. Hudson, C. M. Brown, J. R. Long, J. B. Neaton, B. Smit, C. J. Cramer, D. G. Truhlar and L. Gagliardi, J. Am. Chem. Soc., 2014, 136, 698–704 CrossRef CAS PubMed.
- E. Haldoupis, J. Borycz, H. Shi, K. D. Vogiatzis, P. Bai, W. L. Queen, L. Gagliardi and J. I. Siepmann, J. Phys. Chem. C, 2015, 119, 16058–16071 CrossRef CAS.
- K. Lee, J. D. Howe, L. C. Lin, B. Smit and J. B. Neaton, Chem. Mater., 2015, 27, 668–678 CrossRef CAS.
- A. L. Dzubak, L.-C. Lin, J. Kim, J. A. Swisher, R. Poloni, S. N. Maximoff, B. Smit and L. Gagliardi, Nat. Chem., 2012, 4, 810–816 CrossRef CAS PubMed.
- A. Kundu, K. Sillar and J. Sauer, Chem. Sci., 2020, 11, 643–655 RSC.
- S. A. FitzGerald, D. Mukasa, K. H. Rigdon, N. Zhang and B. R. Barnett, J. Phys. Chem. C, 2019, 123, 30427–30433 CrossRef CAS.
- G. M. Su, H. Wang, B. R. Barnett, J. R. Long, D. Prendergast and W. S. Drisdell, Chem. Sci., 2021, 12, 2156–2164 RSC.
- S. Biswas, M. Tonigold, M. Speldrich, P. Kögerler, M. Weil and D. Volkmer, Inorg. Chem., 2010, 49, 7424–7434 CrossRef CAS PubMed.
- D. Sengupta, P. Melix, S. Bose, J. Duncan, X. Wang, M. R. Mian, K. O. Kirlikovali, F. Joodaki, T. Islamoglu and T. Yildirim, et al. , J. Am. Chem. Soc., 2023, 145, 20492–20502 CrossRef CAS PubMed.
- D. E. Jaramillo, D. A. Reed, H. Z. Jiang, J. Oktawiec, M. W. Mara, A. C. Forse, D. J. Lussier, R. A. Murphy, M. Cunningham, V. Colombo, D. K. Shuh, J. A. Reimer and J. R. Long, Nat. Mater., 2020, 19, 517–521 CrossRef CAS PubMed.
- M. J. Sever and J. J. Wilker, Dalton Trans., 2004, 1061–1072 RSC.
- H. Fei, J. Shin, Y. S. Meng, M. Adelhardt, J. Sutter, K. Meyer and S. M. Cohen, J. Am. Chem. Soc., 2014, 136, 4965–4973 CrossRef CAS PubMed.
- M. Hmadeh, Z. Lu, Z. Liu, F. Gándara, H. Furukawa, S. Wan, V. Augustyn, R. Chang, L. Liao and F. Zhou, et al. , Chem. Mater., 2012, 24, 3511–3513 CrossRef CAS.
- D. Rankine, T. D. Keene, C. J. Doonan and C. J. Sumby, Cryst. Growth Des., 2014, 14, 5710–5718 CrossRef CAS.
- S. J. Stoneburner, V. Livermore, M. E. McGreal, D. Yu, K. D. Vogiatzis, R. Q. Snurr and L. Gagliardi, J. Phys. Chem. C, 2017, 121, 10463–10469 CrossRef CAS.
- H. Chen and R. Q. Snurr, J. Phys. Chem. C, 2021, 125, 21701–21708 CrossRef CAS.
- S. J. Stoneburner and L. Gagliardi, J. Phys. Chem. C, 2018, 122, 22345–22351 CrossRef CAS.
- S. De, T. Devic and A. Fateeva, Dalton Trans., 2021, 50, 1166–1188 RSC.
- D. W. Smithenry, S. R. Wilson and K. S. Suslick, Inorg. Chem., 2003, 42, 7719–7721 CrossRef CAS PubMed.
- K. S. Suslick, P. Bhyrappa, J.-H. Chou, M. E. Kosal, S. Nakagaki, D. W. Smithenry and S. R. Wilson, Acc. Chem. Res., 2005, 38, 283–291 CrossRef CAS PubMed.
- E.-Y. Choi, P. M. Barron, R. W. Novotney, C. Hu, Y.-U. Kwon and W. Choe, CrystEngComm, 2008, 10, 824–826 RSC.
- L. Bonomo, M.-L. Lehaire, E. Solari, R. Scopelliti and C. Floriani, Angew. Chem., Int. Ed., 2001, 40, 771–774 CrossRef CAS PubMed.
- S. Muniappan, S. Lipstman, S. George and I. Goldberg, Inorg. Chem., 2007, 46, 5544–5554 CrossRef CAS PubMed.
- J. Wang, Y. Fan, Y. Tan, X. Zhao, Y. Zhang, C. Cheng and M. Yang, ACS Appl. Mater. Interfaces, 2018, 10, 36615–36621 CrossRef CAS PubMed.
- D. Feng, H.-L. Jiang, Y.-P. Chen, Z.-Y. Gu, Z. Wei and H.-C. Zhou, Inorg. Chem., 2013, 52, 12661–12667 CrossRef CAS PubMed.
- J. Ryou, G. Kim and S. Hong, J. Chem. Phys., 2011, 134, 234701 CrossRef PubMed.
- G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205 CrossRef CAS PubMed.
- R. C. Lochan, R. Z. Khaliullin and M. Head-Gordon, Inorg. Chem., 2008, 47, 4032–4044 CrossRef CAS PubMed.
- R. J. Comito, Z. Wu, G. Zhang, J. A. Lawrence, M. D. Korzyński, J. A. Kehl, J. T. Miller and M. Dincă, Angew. Chem., Int. Ed., 2018, 57, 8135–8139 CrossRef CAS PubMed.
- H. Shen, S. P. Veccham and M. Head-Gordon, J. Chem. Theory Comput., 2023, 19, 8624–8638 CrossRef CAS PubMed.
- P. L. Arnold, F. G. N. Cloke, P. B. Hitchcock and J. F. Nixon, J. Am. Chem. Soc., 1996, 118, 7630–7631 CrossRef CAS.
- F. Calderazzo, I. Ferri, G. Pampaloni, U. Englert and M. L. Green, Organometallics, 1997, 16, 3100–3101 CrossRef CAS.
- J. J. Talbot, R. Chakraborty, H. Shen and M. Head-Gordon, J. Phys. Chem. Lett., 2023, 14, 5432–5440 CrossRef CAS PubMed.
- K. A. Dill, S. Bromberg and D. Stigter, Molecular driving forces: statistical thermodynamics in biology, chemistry, physics, and nanoscience, Garland Science, 2010, p. 563 Search PubMed.
- H. Frost and R. Q. Snurr, J. Phys. Chem. C, 2007, 111, 18794–18803 CrossRef CAS.
- A. Lamaire, J. Wieme, S. M. Rogge, M. Waroquier and V. Van Speybroeck, J. Chem. Phys., 2019, 150, 094503 CrossRef PubMed.
- V. Kapil, J. Wieme, S. Vandenbrande, A. Lamaire, V. Van Speybroeck and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 3237–3249 CrossRef CAS PubMed.
- D. Chandler and P. G. Wolynes, J. Chem. Phys., 1981, 74, 4078–4095 CrossRef CAS.
- C. P. Herrero and R. Ramirez, J. Phys.: Condens. Matter, 2014, 26, 233201 CrossRef CAS PubMed.
- V. Kapil, E. Engel, M. Rossi and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 5845–5857 CrossRef CAS PubMed.
- R. J. Comito, K. J. Fritzsching, B. J. Sundell, K. Schmidt-Rohr and M. Dincă, J. Am. Chem. Soc., 2016, 138, 10232–10237 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Coordinates for all converged geometries. See DOI: https://doi.org/10.1039/d3cp05540j |
| This journal is © the Owner Societies 2024 |