Open Access Article
Open Access ArticleVibrational and electronic spectra of protonated vanillin: exploring protonation sites and isomerisation†
Alejandro
Gutiérrez-Quintanilla
ab,
Baptiste
Moge
c,
Isabelle
Compagnon
 c and
Jennifer A.
Noble
c and
Jennifer A.
Noble
 *a
*a
aCNRS, Aix Marseille Univ., PIIM, Physique des Interactions Ioniques et Moléculaires, UMR 7345, 13397 Marseille, France. E-mail: jennifer.noble@univ-amu.fr
bUniversité de Pau et des Pays de l’Adour, E2S UPPA, CNRS, IPREM, Pau, France
cUniv. Lyon, Université Claude Bernard Lyon 1, CNRS, Institut Lumière Matière, F-69622 Villeurbanne, France
First published on 13th May 2024
Abstract
Photofragmentation spectra of protonated vanillin produced under electrospray ionisation (ESI) conditions have been recorded in the 3000–3700 cm−1 (vibrational) and 225–460 nm (electronic) ranges, using room temperature IRMPD (infrared multiphoton dissociation) and cryogenic UVPD (ultraviolet photodissociation) spectroscopies, respectively. The cold (∼50 K) electronic UVPD spectrum exhibits very well resolved vibrational structure for the S1 ← S0 and S3 ← S0 transitions, suggesting long excited state dynamics, similar to its simplest analogue, protonated benzaldehyde. The experimental data were combined with theoretical calculations to determine the protonation site and configurational isomer observed in the experiments.
1 Introduction
Aromatic derivatives are a diverse family of compounds having a long list of possible substituents, including, among others, amino (–NH2), carboxyl (–COOH), hydroxyl (–OH), methoxy (–OCH3), and formyl (–CHO). Depending on the nature of each group and their relative positions in the aromatic ring (or rings), several (one- or multiple-) competing protonation sites can be observed.1–4 The photophysics of different possible protonated isomers (protomers) in aromatic derivatives and similar compounds may exhibit substantial differences.5–10 In such a case, the reactivity of a protonated molecule in this family of compounds or its photodegradation mechanisms may depend on the favoured protomer.11Protonated aromatic species play a crucial role in various processes and environments, existing as transient short- and long-lived intermediates and in some cases as stable entities. Examples of these processes are chemical reactions,12 hydrocarbon plasmas13 and jet engine exhaust.14 From a more fundamental point of view, there is also a particular interest in these derivatives and their photophysics and dynamics in the gas phase.2,15–19
Aromatic aldehydes are a particular subfamily having a formyl group as substituent. With the exception of studies performed on benzaldehyde and hydroxybenzaldehydes isomers, the systematic study of the protonation and the photophysics on more complex aromatic aldehydes in the gas phase has not been extensively addressed. The formyl group present in aldehydes has a high proton affinity, usually leading to a preferential protonation on the corresponding oxygen, as observed for benzaldehyde and hydroxybenzaldehydes isomers in the gas phase.20,21 Some research performed in the liquid phase also supports this conclusion.22 Understanding how protonation evolves in this compound family under the influence of more complex substitution patterns is the next step. This examination sets the stage for a thorough understanding of the molecular dynamics at play.
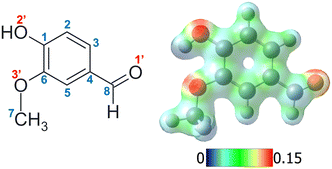
In addition, protonation of the formyl oxygen can introduce more complex isomeric patterns. Two possible isomers (cis/trans) with low relative energy difference can be formed, depending on the relative position of the hydroxyl hydrogen (O2′–H, see Fig. 1 for numbering) with respect to the phenyl ring. We need to add to this scenario that, when a second (or more) non-symmetric substituent is present in the aldehyde aromatic compound, like in hydroxybenzaldehydes, different isomers can be produced in the protonated species, differing in the relative position of the C8–OH with respect to the other substituents in the aromatic ring (noted as syn/anti to differentiate it from the previous cis/trans classification, as used in Chiavarino et al.21). This implies that a complex configurational space, with isomers obtained by the different possible cis/trans–syn/anti combinations, needs to be added to the diverse number of possible protomers.23 Achieving the exact determination of the formed protomer along with its precise configurational or conformational isomer in room temperature gas-phase experiments is not always an easy task.
Previous studies using laser action spectroscopy, such as infrared multiphoton dissociation (IRMPD) and cold ion trap ultraviolet photodissociation (UVPD), have reported the observation of only one of the possible isomers in the case of benzaldehyde and ortho- and para-hydroxybenzaldehyde, and two isomeric forms of meta-hydroxybenzaldehyde.21,24 The individual use of these techniques have been shown to be very suitable for the study of protonated species, especially when the ions are prepared at cryogenic temperatures.25–28 However, the combined utilisation of IRMPD and UVPD is less commonly found in the literature, although very interesting works have been published.11,29–31 To the best of our knowledge, none of these works take advantage of the use of cryogenic temperatures.25
Vanillin (3-methoxy-4-hydroxybenzaldehyde, Fig. 1) is a suitable candidate to begin evaluating how more complex substitution patterns affect protonation, isomerism, and dynamics in protonated aromatic aldehydes. The introduction of a methoxy group, compared to hydroxybenzaldehyde, allows the inclusion of a new intramolecular hydrogen bond interaction. Vanillin is a volatile organic compound (VOC) most commonly associated with its role in the complex mixture of compounds related to vanilla's natural odour. This aromatic derivative has been widely studied due to its antioxidant properties, its UV protective properties in plants, and its role as a possible base unit for renewable polymers, amongst others.32,33 Along with other aromatic molecules, vanillin is also commonly produced in biomass burning emissions, specifically as a by-product of lignin, and consequently can participate as a precursor in the formation of secondary organic aerosols (SOA). The unique and highly acidic conditions often found in these aerosols could promote the formation of protonated species, thus altering the reactivity, as well as its spectroscopic and physicochemical properties.34 In fact, previous studies have demonstrated how the optical properties (absorption and fluorescence) of aqueous solutions of vanillin depend on pH.22 However, protonated vanillin has thus far received limited attention, in contrast to its neutral molecular counterparts. This aspect has also motivated our interest in choosing vanillin as a first model system.
Hereafter, we present a combined experimental and theoretical study on the protonation sites of vanillin under electrospray ionisation (ESI) conditions, as well as the structures of the resulting observed gas phase isomers and their electronic excitation energies. We provide a detailed study of the vibrational ground-state spectrum (IRMPD) and the vibrationally resolved electronic spectrum (UVPD) of protonated vanillin in the gas phase by means of photofragmentation spectroscopy. Geometry optimisations, frequency calculations, and determination of vertical excitations were performed at the DFT (TD-DFT) and CC2 levels of theory in the ground and excited states. Comparison with hydroxybenzaldehyde and especially benzaldehyde, a simple analogue, with respect to the protonation site, stable isomeric structures, and dynamics is also included in the Discussion section.
2 Methods
2.1 Chemicals and sample preparation
Vanillin (C8H8O3, M = 152.15 g mol−1, 99% purity) was purchased from Sigma-Aldrich. Solutions were prepared according to standard conditions used to obtain protonated species in the ESI sources. The solution was prepared at 10−5 M for UVPD and 6.10−5 M for IRMPD, using a water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol mixture at 50
methanol mixture at 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio as solvent and adding acetic acid (∼0.1%) to promote protonation of the solute.
50 ratio as solvent and adding acetic acid (∼0.1%) to promote protonation of the solute.
2.2 Room temperature IRMPD spectroscopy (RT-IRMPD)
IRMPD studies were carried out at the ILM Institute in Lyon. The IRMPD apparatus consists of a commercial mass spectrometer equipped with an electrospray ion source and a linear ion trap (Thermo Scientific LTQ-XL) at room temperature modified to allow irradiation of the trapped ions by a tunable IR OPO laser system (M Squared Firefly) operating at 150 kHz. The pulse duration is shorter than 10 ns and the pulse energy is 1 μJ throughout the spectral range. A continuous CO2 laser simultaneously irradiates the ion cloud. This irradiation increases the internal energy of the ions, facilitating their photodissociation by subsequent absorption of the photons produced by the OPO laser. CO2 laser output power can be manually selected, and has been shown to enhance the IRMPD yields obtained.35,36 Mass-selected ions (here m/z = 153 amu) are isolated for 720 ms and then irradiated for 700 ms. The resulting photofragmentation mass spectrum is averaged three times. The photofragmentation yield is calculated using the following variation of the Beer–Lambert formula: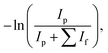 | (1) |
2.3 Cryogenic ion-trap UVPD spectroscopy
UVPD studies were carried out in the PIIM laboratory in Marseille. The photofragmentation spectrum of protonated vanillin was obtained in a cryogenically cooled Paul trap. The set-up has been extensively described elsewhere15 and is similar to those developed in various research groups based on the original concept of Wang and Wang.37,38 Protonated ions are produced in an electrospray source39 and, once extracted from an initial octopole trap, are guided towards the Paul trap with electrostatic lenses and deviation plates and decelerated to a few electron-Volts (∼5 eV) before entering the trap. The ions are trapped for several tens of ms. During this time, they are thermalised to a temperature of around 50 K by collisions with cold helium buffer gas,40 which is constantly removed by pumping.In this experimental setup, photodissociation of the trapped ions is accomplished with a tuneable UV-Vis OPO laser (EKSPLA), which has a 10 Hz repetition rate, 10 ns pulse width, a spectral resolution of ∼10 cm−1 and a minimum scanning step of 0.02 nm in the range 225–700 nm. The laser is shaped to a 1 mm2 spot to fit the entrance hole of the trap, and the laser power is around 2 mJ per pulse in the UV spectral region. The precursor and photofragment product ions are extracted from the trap after each laser shot and separated in a 1.2 m long time-of-flight (TOF) tube before being detected using a microchannel plate (MCP) detector. The UV-Vis photofragmentation spectra were recorded by simultaneously detecting the selected ion signals as a function of the excitation energy.
The laser interacts only once with the ion cloud. The signal is typically averaged over eight shots at each wavelength, and the spectra are recorded up to ten times and then averaged. No smoothing procedure was used, and noise is due either to statistical uncertainty, instability of the ESI source, or minor fluctuations in the laser power (which were not corrected for). We note that we are working in the one-photon absorption regime in these experimental conditions (see ESI in ref. 17).
2.4 Quantum chemistry calculations
Ab initio calculations were performed with the Gaussian1641 program and TURBOMOLE (V6.6) package,42 making use, for the latter, of the resolution-of-the-identity (RI) approximation for the evaluation of the electron-repulsion integrals.43–45 The optimised equilibrium geometries of ground state (S0) species were first determined at DFT level using the B3LYP functional and the cc-pVDZ basis set.46 The CAM-B3LYP functional47 (including Grimme's D3 dispersion correction48) and second-order Møller–Plesset (MP2) method were employed in a second step with the aug-cc-pVDZ basis set.46 Frequency calculations were performed in each case to confirm the presence of a minimum energy geometry, to include zero-point energy (ZPE) corrections to electronic energies, and to obtain the vibrational spectrum of each isomer. Since very similar results were obtained in all three cases, only CAM-B3LYP computed spectra are discussed hereafter. An empirical scaling factor of 0.942 was used for comparison with the experimental IRMPD spectra. The scaling factor was chosen to globally fit the theoretical νOH high-frequency mode to the corresponding high-frequency experimental band, considering the whole set of theoretical isomers (see Fig. S4 and S5, ESI†). In this way, we focus on the relative position between both O–H bands and not on their actual excitation energy. Anharmonic frequency calculations were also performed on the lowest energy isomers. Theoretical infrared intensities are represented in the spectra by the convolution of the transition line with a Gaussian function of FWHM = 10 cm−1. Ground-state structures were also optimised at the CAM-B3LYP/aug-cc-pVDZ level in water and methanol considering the default implicit solvation model (SCRF: self-consistent reaction field) implemented in Gaussian16.49Vertical excitation energies and ZPE corrected adiabatic excitation energies of the lowest excited singlet states were determined at two different levels of theory: CC2/cc-pVDZ (second-order approximate coupled-cluster) and TD-DFT CAM-B3LYP/aug-cc-pVDZ (time-dependent density functional theory) levels. Ground and excited state structures and vibrations were calculated with both CC2/cc-pVDZ and CAM-B3LYP/aug-cc-pVDZ, and the vibronic spectrum was simulated at the former level using PGOPHER software for Franck–Condon analysis.50 One limit to the choice of this simulation method is that Hertzberg–Teller coupling can not be applied in PGopher. Excitations to triplet states are not included in the discussion because they exhibit almost zero oscillator-strength for the protonated species at the level of theory we use. The mapped electrostatic potential (MEP) was visualised with the Chemcraft v1.8 software, by using the output file from geometry optimisation at the CAM-B3LYP/aug-cc-pVDZ level.51
3 Results and discussion
In order to determine the structure of the possible isomers of protonated vanillin (protonation site and configuration), we followed a methodology in which the number of possible candidates is progressively reduced by using information from (i) theoretical DFT energy calculations, (ii) room temperature IRMPD experiments, and (iii) cryogenic UVPD experiments. The results are thus presented following the same order, while the underlying photophysics is discussed at the end.3.1 Calculations: relative energy analysis
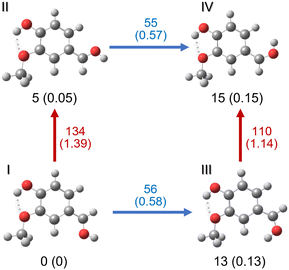
Different protonation sites could be present in vanillin, although chemical intuition readily suggests that the carbonylic oxygen has the greatest proton affinity. Indeed, an analysis of the individual electronic effects of each substituent indicates that the two other oxygens are likely to delocalise their lone pairs into the aromatic ring. This results in a notable reduction in their proton affinity, in contrast to the behaviour exhibited by the carbonyl oxygen. On the other hand, the carbon atoms of the aromatic ring are quite unlikely to be protonated in this molecule, as can be observed from the mapped electrostatic potential (MEP) of the molecule (see Fig. 1). The MEP indicates that oxygen atoms, and particularly carbonyl oxygen, are more prone to protonation than carbon atoms. Similar results have been reported in other simple protonated aromatic analogues presenting a carbonyl group.2,24 However, while chemical intuition would suggest that protonation “should” occur on the carbonyl oxygen, this molecule includes three different functional groups which can modify the electron density distribution, and there are multiple examples in the literature of “unexpected” protonation on e.g. carbon atoms in the aromatic cycle due to mesomeric effects.15,52 In order to perform a rigorous study, we do not totally exclude these chemically less probable protomers from our analysis until we have compared our calculations to our experimental data.A first, rough exploration of the configuration space was performed by computing and comparing the zero-point corrected energies at the CAM-B3LYP-D3/aug-cc-pVDZ level on the optimised structures of the different species protonated on carbons or oxygens without a specific conformational search. Then, considering that (i) isomers protonated on carbonyl oxygen should be more stable, (ii) in these particular isomers the three functional groups maintain a planar symmetry, and (iii) only two conformations per group are usually stable (similar to cis/trans), we performed geometry optimisations on the different combinations to achieve a more refined search for the lowest energy isomers. As expected, the results confirm that the lowest energy isomers correspond to structures protonated on the oxygen atom of the carbonyl functional group (Fig. S1, ESI†), leading to the formation of oxonium ions. These species are at least 50 kJ mol−1 (∼0.52 eV) more stable than any other structure (see Fig. S1 and S2, ESI†). Furthermore, structures presenting the “closed” intramolecular hydrogen bond interaction between hydroxilic hydrogen and methoxy oxygen (Fig. S1 and S2, ESI†) are stabilised by about 20 kJ mol−1 (∼0.2 eV) compared to their “open” analogues. This value can also be taken as an approximate rough measure of the strength of such an interaction, which is, in fact, very similar to that obtained in the case of neutral vanillin.53 The four most stable isomers are depicted in Fig. 2.
The relative energy order of these four isomers is not modified in the solvated medium. Calculations performed in water and methanol using SCRF implicit solvation model (CAM-B3LYP-D3/aug-cc-pVDZ) show a relative energy lowering of 1 kJ mol−1 for isomers II (4 kJ mol−1) and IV (11 kJ mol−1), and 3 kJ mol−1 lowering for isomer III (9 kJ mol−1) compared to the gas phase. We highlight that the energy difference between the two lowest isomers, I and II in the gas phase and in solution, is almost within the error limit of the method (∼4 kJ mol−1), indicating that they could be very close in energy. The same energy difference was also obtained in the vacuum with the B3LYP/cc-pVDZ method.
A very similar result is obtained at the MP2/aug-cc-pVDZ level of theory for the set of eight lowest energy isomers in the gas phase. Considering this and the fact that the isomers in Fig. 2 are well separated (in energy) from the other candidates, it is very tempting to completely reduce the search space to these four isomers. However, it is known that the gas phase protonated isomers produced by the ESI technique can sometimes differ not only from the expected lowest energy structures obtained by theoretical calculations (vacuum and solvent included), but also from the experimental structures observed in solution.15,54–56 Thus, we retained the whole set to compare their vibrational spectra in the next step, bearing in mind that the most probable candidates should be among the four lowest in energy.
We note that, although the relative energy difference between the four main isomers is small, the relaxed rotational barriers between the isomers are higher than 50 kJ mol−1. This means that once the protonated species is formed in the gas phase, it will be kinetically trapped (low collision regime, far from thermodynamic equilibrium), and no conversion should occur between isomers. It should be noted that the optimised structures for the lowest-energy isomers (protonated on O1′) have a Cs symmetry. This implies that one of the hydrogen atoms on the methyl group is in the plane of the molecule. Indeed, the most stable minimum for the methyl group position corresponds to that shown for the four isomers represented in Fig. 2, where the hydrogen atom in the plane of the molecule is in the “anti” position with respect to the aromatic ring. The “eclipsed” position is higher in energy (∼10 kJ mol−1).
Finally, a comparison with the theoretical lowest energy isomers of other carbonyl- or hydroxyl-substituted aromatic compounds (e.g. benzaldehyde, phenol, hydroxybenzaldehyde, anisol and guaiacol) can provide a more complete picture of the role of these groups as possible proton acceptors in vanillin. Previous theoretical and experimental works on protonated benzaldehyde (Ph-CHO, where Ph stands for phenyl), the simplest carbonyl-containing aromatic compound, have reported that the most stable isomer corresponds to the protonation site on the oxygen atom of the carbonyl group.20,23,24,57 The same conclusion was reached for ortho, meta and para hydroxybenzaldehyde (HO-Ph-CHO) isomers,21 where hydroxyl and carbonyl groups are present. On the contrary, according to DFT and MP2 calculations, protonation in phenol (Ph-OH) is predicted to be more stable on carbon atoms in the para position.58–60 Experiments in the acidic aqueous phase support these results for phenol, and also for anisol (Ph-OCH3).61 In the case of protonated guaiacol (ortho HO-Ph-OCH3), Gondarry and Mayer62 found by theoretical calculations that the most probable protonation site, by more than 25 kJ mol−1 (0.26 eV), is the aromatic carbon in the para position with respect to the hydroxyl group, as in phenol. These experimental results and the theoretical results on vanillin align well with chemical intuition, predicting that species formed by protonation at the formyl group are highly favoured due to a higher proton affinity of this group. Furthermore, carbon aromatic sites are only protonated when the electron-donating substituents OH and OCH3 are the only ones present in the molecule.
After this first energy exploration of the possible protonation sites, more refined data about the structure and the vibrational and electronic spectra were obtained from experimental laser action spectroscopies.
3.2 Room temperature IRMPD spectroscopy
The IRMPD fragmentation pattern at different irradiation wavelengths exhibits 28 amu (carbon monoxide, CO) loss as the main fragmentation channel (see Fig. S3, ESI†). The IRMPD spectrum of protonated vanillin recorded by following this mass fragment in our experimental conditions is presented in Fig. 3. The spectrum clearly shows the presence of at least two distinct types of O–H vibrations. According to their frequencies, one must correspond to a free O–H oscillator (3576 cm−1) while the second, redshifted, belongs to an associated O–H (3470 cm−1). A closer look at the experimental data shows that what could have been attributed to a second component of the signal associated with the higher frequency O–H band is just an artefact. Thus, only one component is present in this band. Finally, no clear signals are observed in the C–H stretching mode region (∼3060 cm−1) under our experimental conditions.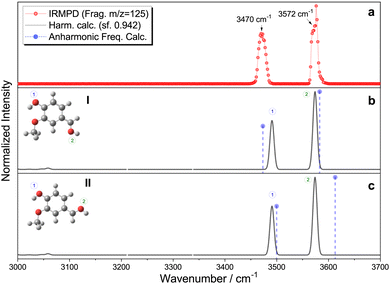 | ||
| Fig. 3 (a) Experimental IRMPD spectrum of protonated vanillin, (b) and (c) theoretical harmonic infrared spectra for carbonyl protonated isomers I and II, respectively (black line), and the corresponding anharmonic frequencies (violet circle/dash-line). Theoretical calculations at the CAM-B3LYP-D3/aug-cc-pVDZ level of theory, with harmonic frequencies corrected by a 0.942 scaling factor, chosen to globally fit the theoretical νOH high-frequency mode to the corresponding high-frequency experimental band, considering the whole set of theoretical isomers (see Fig. S4 and S5, ESI†). | ||
Comparison with the IRMPD spectra of protonated benzaldehyde20 and two of the three isomers of hydroxybenzaldehyde (meta and para)21 indicates that the high frequency mode can effectively correspond to an OH obtained by protonation of the oxygen atom in the formyl group. The frequency of this particular mode in the aforementioned protonated molecules covers a range spanning 25 cm−1 (3551–3576 cm−1). The observed value in vanillin is almost identical to that obtained in para-hydroxybenzaldehyde, which is the closest structural analogue to vanillin in this series of isomers.
The most important result from the comparison between experimental RT-IRMPD and infrared theoretical calculations within the harmonic approximation is that the two lowest-energy isomers, named I and II, of vanillin protonated on the carbonyl group match the experimental spectrum quite well (Fig. 3). When considering relative frequencies, these two conformers share an almost identical theoretical frequency spectrum in the O–H region. The comparison of the relative frequencies (wavenumbers) in the experiment and the simulation of these two bands for all the other possible isomers formed by protonation on the carbonyl oxygen atom reveals a poor correspondence (Fig. S4, ESI†). The simulated vibrational spectra of isomers obtained by protonation on the benzene ring do not show two bands because they only have one O–H vibration (Fig. S5, ESI†). The relative intensities are not included in the comparison because calculated IR intensities can greatly differ from experimental IRMPD ones, mainly due to the different physical origin of the vibrational signal in each case (linear absorption versus multiphotonic/action spectroscopy). Local anharmonic frequency calculations, performed on the two lowest isomers (I and II), also show a very good match with the IRMPD spectrum (Fig. 3). Theoretical infrared spectra indicate that, in principle, other isomers could also contribute to the high frequency band (see Fig. S4 and S5, ESI†). However, these isomers are either very high in energy compared to I and II (∼90 kJ mol−1) because of protonation on the aromatic ring, or because of the absence of the intramolecular hydrogen bond leading also to higher relative energies (∼20–35 kJ mol−1). In fact, previous IRMPD studies show that isomers of more than 10 kJ mol−1 of relative energy with respect to the lowest energy one are usually not observed when using this technique with an ESI source.63 This supports the exclusion of isomers other than the four lowest in energy (i.e. I, II, III and IV) from any subsequent analysis. Thus, combining theoretical and IRMPD results allows us to conclude that isomers I and II (or one of them) are mainly present in the gas phase under the employed experimental conditions.
Finally, the IRMPD spectra of protonated vanillin can offer information about the intramolecular hydrogen bond. A comparison of the infrared spectrum of neutral vanillin and neutral guaiacol with respect to the intramolecular O–H mode is established primarily for this purpose. The IR–UV double resonance experiments in cold supersonic jets of Longarte et al.64 on guaiacol indicates that this mode appears at 3599 cm−1. There are no vibrational data on neutral vanillin under the same conditions, but if we use as a reference the room temperature gas phase infrared spectrum given on the Spectrabase website,65 we clearly observe a band centred at 3575 cm−1. In both cases, the O–H mode appears at higher wavenumber compared to protonated vanillin. It is clear that the addition of the carbonyl group to the aromatic ring (neutral vanillin) and its subsequent protonation, both have a direct impact on the strength of the O–H⋯O intramolecular hydrogen bond (Fig. 2), which contrasts with the approximate energetic analysis mentioned in the previous section.
3.3 Cryogenic UVPD
At this point, theoretical energy calculations and RT-IRMPD allow a reduction of the set of possible candidates observed under ESI conditions. Additional and complementary information about the protonated isomers formed, i.e. their structure and excited state dynamics, is also obtained by means of the UVPD technique in the cryogenic ion trap. This technique is sensitive to isomerism, especially when a clear vibronic structure is observed.66 However, we must consider that the different excitation process and the differences in temperatures used in RT-IRMPD (room temperature) and cryogenic UVPD (∼50 K), as well as subtle differences in ESI ionisation conditions in the two experimental setups can sometimes lead to different observed isomers, even within the same technique.54–56 Note the use of the word “observed” instead of “produced” or “present” to highlight, or avoid confusion about, the information provided by these techniques.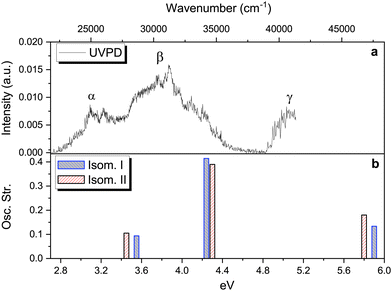 | ||
| Fig. 4 Upper panel: Photofragmentation action spectrum of protonated vanillin obtained through the UVPD technique (see text and Fig. S7 (ESI†) for more details). Lower panel: The three lowest singlet–singlet vertical electronic excitation energies for the two lowest energy isomers obtained through TD-DFT calculations at the CAM-B3LYP/aug-cc-pVDZ level of theory. | ||
At least three main bands can be distinguished in the experimental spectrum, labelled α, β and γ. Comparison with the theoretical TD-DFT spectrum (Fig. 4, panel b) suggests that these bands correspond to the first three singlet–singlet electronic transitions of isomers protonated on carbonyl oxygen (O1′). All three excitations involve π → π* orbital transitions (see Fig. S8, ESI†). Fig. 4 (panel b) shows the TD-DFT singlet–singlet vertical excitations of the two lowest energy isomers. The values of excitation energy and oscillator strength for each isomer are included in Table S1 (ESI†). Three electronic transitions are also observed for isomers III and IV, with the highest energy excitation well separated from the two others. This set of isomers (I–IV) all reproduce the trend observed on the experimental spectrum. However, the average shift in energy (∼0.7 eV) is, at least for S1 ← S0 and S2 ← S0 transitions, around 0.2 eV higher than the typical range of 0.5 eV observed in other protonated molecules (for the S1 ← S0 transition) using TD-DFT calculations methods, but still within the maximum deviation range (∼0.8 eV).69
Despite the fact that the theoretical UV absorption spectra (vertical excitation) of O1′(I–IV) protonated isomers (lowest in energy) reproduce the experimental trend well, there is still the question of whether or not there are contributions coming from other isomers, not observed in the IRMPD experiment. A detailed comparison of the theoretical vertical excitations (see Table S1, ESI†) with the UVPD experimental spectrum shows that some of the isomers protonated on the benzene ring, i.e. C1, C4 and C6, exhibit numerous transitions within the energy range which are not actually observed, especially in the 4.3–4.8 eV range. This is also the case for the S2 ← S0 transition of C3. Combining this information with that obtained from IRMPD and theoretical energy calculations, we confirm that the O1′(I) and O1′(II) isomers are the most probable candidates to reproduce the observed UVPD spectrum.
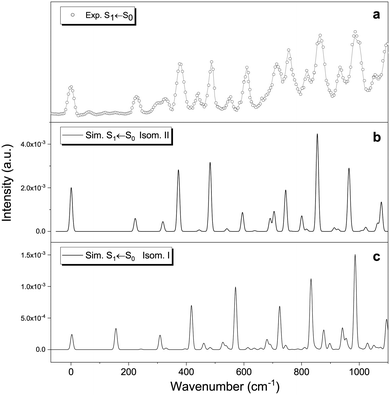
Fig. 5 shows the theoretical Frank–Condon factors obtained with PGopher for isomers I and II compared to the origin of the experimental S1 ← S0 transition. The agreement with the experimental spectrum is much better for isomer II than for isomer I. The good match suggests that the most important features of the spectrum are, overall, well reproduced by including four active modes of isomer II: ν35 (222 cm−1), ν34 (318 cm−1), ν33 (373 cm−1) and ν32 (483 cm−1), including overtones and combination bands. These four modes correspond to ring breathing and in-plane bending of the three functional groups (Table 1), indicating that the molecule keeps the planar structure in the S1 excited state. Similar to protonated benzaldehyde, theoretical calculations predict rather small geometry differences between the ground and first singlet states (see xyz file in Tables S2 and S3, ESI†). The predicted structural change mainly concerns an overall lengthening of the C–C bonds in the aromatic ring (∼0.04 Å), the decrease of the C2C1C6, C5C6O3′ and C4C8O1′ angles (∼−4°), and the increase of the C6O3′C7 angle (∼4°). In addition, the increase of the O1′⋯O3′ distance, coupled with the slight decrease of the O2′–H bond and the O2′⋯H–O3′ angle point to a decrease in the strength of the intramolecular hydrogen bond (Fig. 2) in the S1 (ππ*) excited state.
| Exp. | Calc. | Mode | Description |
|---|---|---|---|
| Δ: ring-breathing, δ: in-plane bending. | |||
| 0 | 0–0 | ||
| 226 | 222 | ν 35 | δ O3′C6C1 |
| 326 | 318 | ν 34 | Δ |
| 379 | 373 | ν 33 | Δ |
| 440 | 443 | 2ν35 | |
| 488 | 483 | ν 32 | δ C7O3′C6 |
| 549 | 540 | ν 35 + ν34 | |
| 610 | 595 | ν 35 + ν33 | |
| ν 30 | Δ/δC4C8O1′ | ||
| 690 | ν 34 + ν33 | ||
| 714 | 705 | ν 35 + ν32 | |
| 721 | ν 29 | Δ | |
| 756 | 745 | 2ν33 | |
| 819 | 800 | ν 34 + ν32 | |
| 861 | 855 | ν 33 + ν32 | |
| 931 | 913 | ν 35 + ν34 + ν33 | |
| 990 | 964 | 2ν32, ν35 + 2ν33, ν33 + 2ν30 | |
| 1051 | 1022 | ν 35 + ν34 + ν32 | |
| 1096 | 1077 | ν 35 + ν33 + ν32, ν32 + ν30 | |
The FC result allows us to conclude that isomer II is the one mainly observed with the UVPD technique. However, this only implies that this particular isomer is formed under our experimental conditions, but not necessarily as a major species. In fact, if we assume that the sample entering the ion trap is only composed of isomers I and II and consider that the protonation process leads to a thermodynamic equilibrium in the gas phase, we should have around 12% of isomer II at 298 K, and less than 5 × 10−3% at 50 K (using the CAM-B3LYP-D3 energy difference). These ratios are only slightly modified if we use energies from the implicit solvation model, i.e. considering that protonation and equilibration occur in the liquid phase rather than once the ions are in the gas phase. Moreover, even if we consider that the protonation process is not thermodynamically controlled and that there is a slightly higher percentage of isomer II in the ion trap, there are other parameters to consider (e.g. possible differences in fragmentation yields). More importantly, transition intensity is determined by the multiplication of oscillator strength and the Franck–Condon factor. The oscillator strengths (from the vertical transitions) are very close in both cases (0.094 for I and 0.105 for II, see Table S1, ESI†), but the FC factors are between 3 to 10 times higher in II compared to I (see ordinate axis in Fig. 5, and Fig. S9 for a better comparison, ESI†). Thus, no definitive conclusion can be easily drawn from the experimental UVPD spectrum. In any case, it is also important to highlight that the result is coherent with the information provided by RT-IRMPD spectroscopy, and by theoretical calculations, showing that isomer II is very low in energy. This is not evident, especially if we consider that, in some systems, different isomer populations can be obtained by slight changes in ESI ionisation conditions.15,56 We recall here that isomers I and II are almost isoenergetic within the uncertainty of the level of theory used.
The question remains as to whether or not isomer I is observed in the UVPD spectrum. Most of the experimental bands are well reproduced by isomer II. However, vertical excitation energies indicate that isomer I absorbs at higher energies (+552 cm−1 shift), which implies that some of the bands could come from this particular isomer (Fig. S10, ESI†). Again, no definitive conclusion can be drawn in this regard within the experimental framework employed in this work. Other approaches should be considered to resolve this question, for instance, double resonance experiments and ion mobility spectroscopy (IMS) are especially suited for this purpose.
We were not able to obtain an optimised Cs structure in the S3 state for the O1′(II) isomer with CAM-B3LYP/aug-cc-pVDZ. The structure converges to a clear non-planar geometry, mainly caused by deformation of the aromatic ring. However, the difference between vertical and adiabatic transition energies is about 0.5 eV (vertical: 5.80 eV, adiabatic: 5.34 eV, Table 2) which is usually associated to a small geometry change.66 Optimisation with CC2/cc-pVDZ did not converge for this excited state. Despite this, the experimental spectrum shows some similarities with the S1 ← S0 transition with respect to vibrational structure and narrow bandwidth. As in the S1 ← S0 transition, a mode around 400 cm−1 is clearly active during the transition (Fig. S11, ESI†). Despite these slight complications with the calculations at high energy, this does not change our main conclusion that the molecule protonates on O1′. The “puckering” of the molecule in the S3 state hints at some excited state mechanisms such as crossing between states or the presence of a conical intersection,17,70 and as such we propose that protonated vanillin represents a good candidate for study at higher levels of theory (e.g. CASPT2) in its excited states.
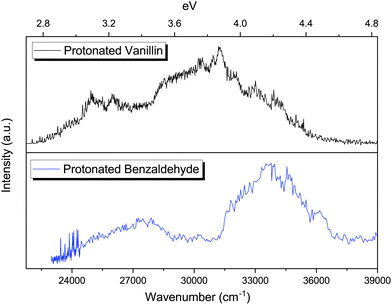
The photofragmentation spectra of protonated benzaldehyde and protonated vanillin share the presence of two clear absorption bands in the 2.7–4.6 eV region (Fig. 6). As in the case of protonated vanillin, these two transitions in benzaldehyde are related to π → π* orbital transitions. There is a clear blueshift for benzaldehyde bands compare to vanillin (0.18 eV for S1 ← S0 and ∼0.28 eV for S2 ← S0). This can be explained by the presence of a destabilising electron-withdrawing inductive effect (–I) on vanillin due to the –OH and –OCH3 groups, which is greater for the HOMO orbital (Δ = 1.38 eV) than for the LUMO (Δ = 0.68 eV).72
4 Conclusions
We have presented here a combined experimental and theoretical study of the vibrational and electronic spectroscopy of protonated vanillin. Theoretical energy calculations predict that, as expected, protonation is more likely to occur on the oxygen of the carbonyl group (O1′) in vanillin, and not on the aromatic ring or other oxygens, which is in line with chemical intuition and what is thus observed in similar systems.21 We have found that the second-lowest energy calculated isomer, O1′(II), is able to reproduce both RT-IRMPD and UVPD spectra. However, the energy difference between the two lowest-energy isomers in the vacuum is close to the error range of the theoretical methods used to compute this magnitude. Thus, they could be closer in energy than predicted, or even the energy order may be inverted. In any case, the result indicates that production of this particular isomer is favoured under the ESI ionisation conditions of the setups used in both spectroscopic techniques. However, we highlight that no quantitative conclusion can be actually drawn from the observed spectra, and that other isomers, e.g. O1′(I), may also be formed, but that we are not able to observe them, or discriminate them from the signal of isomer II.The present research reveals a situation where the analysis of experimental data may not exclusively rely on the lowest calculated energy isomer, especially for low energetic differences. Similar conclusions have been previously obtained by other research groups on different systems,6,9,66 although, to our knowledge, this is the first work focused on aromatic aldehydes. In addition, this work adds to the growing list of examples showing the power of combining IRMPD and UVPD spectroscopies to determine the molecular structure and/or isomerism (e.g. protonation site, configurational isomers, tautomers, etc.), although the use of the cryogenic conditions (implemented in this work for UVPD) is not yet widely extended.29–31,75 We highlight that these techniques would ideally be combined in the form of IR/UV double resonance experiments to obtain more precise information. For a more in-depth analysis of the conformer ratios generated in the sources and the parameters influencing this ratio, the coupling of action spectroscopies with other techniques sensitive and selective to conformation, such as ion mobility spectroscopy, can also be envisaged.
Author contributions
AGQ: investigation, visualization, writing – original draft, BM and IC: investigation, writing – review & editing, JAN: conceptualization, investigation, funding acquisition, project administration, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the computing center MésoLUM managed by ISMO (UMR8214) and LPGP (UMR8578), University Paris-Saclay (France). JAN acknowledges funding from the Agence Nationale de la Recherche (ANR, HYDRAE project ANR-21-CE30-0004-01). The authors thank Christophe Jouvet and Karinne Miqueu for helpful discussions.Notes and references
- S. Warnke, J. Seo, J. Boschmans, F. Sobott, J. H. Scrivens, C. Bleiholder, M. T. Bowers, S. Gewinner, W. Schöllkopf, K. Pagel and G. von Helden, J. Am. Chem. Soc., 2015, 137, 4236–4242 CrossRef CAS PubMed.
- K. Hirata, F. Haddad, O. Dopfer, S.-I. Ishiuchi and M. Fujii, Phys. Chem. Chem. Phys., 2022, 24, 5774–5779 RSC.
- O. J. Shiels, S. J. P. Marlton and A. J. Trevitt, J. Am. Chem. Soc., 2023, 145, 15024–15029 CrossRef CAS PubMed.
- B. Ucur, O. J. Shiels, S. J. Blanksby and A. J. Trevitt, J. Am. Soc. Mass Spectrom., 2023, 34, 1428–1435 CrossRef CAS PubMed.
- M. Broquier, S. Soorkia, G. Pino, C. Dedonder-Lardeux, C. Jouvet and G. Grégoire, J. Phys. Chem. A, 2017, 121, 6429–6439 CrossRef CAS PubMed.
- S. J. P. Marlton, B. I. McKinnon, B. Ucur, A. T. Maccarone, W. A. Donald, S. J. Blanksby and A. J. Trevitt, Faraday Discuss., 2019, 217, 453–475 RSC.
- S. J. P. Marlton, B. I. McKinnon, B. Ucur, J. P. Bezzina, S. J. Blanksby and A. J. Trevitt, J. Phys. Chem. Lett., 2020, 11, 4226–4231 CrossRef CAS PubMed.
- N. J. A. Coughlan, P. J. J. Carr, S. C. Walker, C. Zhou, M. Guna, J. L. Campbell and W. S. Hopkins, J. Am. Soc. Mass Spectrom., 2020, 31, 405–410 CrossRef CAS PubMed.
- N. Mashmoushi, D. R. Juhász, N. J. A. Coughlan, B. B. Schneider, J. C. Y. Le Blanc, M. Guna, B. E. Ziegler, J. L. Campbell and W. S. Hopkins, J. Phys. Chem. A, 2021, 125, 8187–8195 CrossRef CAS PubMed.
- F. V. Heldmaier, N. J. A. Coughlan, A. Haack, R. Huard, M. Guna, B. B. Schneider, J. C. Y. Le Blanc, J. L. Campbell, M. Nooijen and W. S. Hopkins, Phys. Chem. Chem. Phys., 2021, 23, 19892–19900 RSC.
- J. A. Berenbeim, N. G. K. Wong, M. C. R. Cockett, G. Berden, J. Oomens, A. M. Rijs and C. E. H. Dessent, J. Phys. Chem. A, 2020, 124, 2919–2930 CrossRef CAS PubMed.
- G. A. Olah, Acc. Chem. Res., 1971, 4, 240–248 CrossRef CAS.
- S. Pasquiers, Eur. Phys. J.: Appl. Phys., 2004, 28, 319–324 CrossRef CAS.
- A. Kiendler and F. Arnold, Atmos. Environ., 2002, 36, 2979–2984 CrossRef CAS.
- J. A. Noble, M. Broquier, G. Grégoire, S. Soorkia, G. Pino, E. Marceca, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2018, 20, 6134–6145 RSC.
- J. N. Bull, E. Carrascosa, N. Mallo, M. S. Scholz, G. da Silva, J. E. Beves and E. J. Bieske, J. Phys. Chem. Lett., 2018, 9, 665–671 CrossRef CAS PubMed.
- J. A. Noble, E. Marceca, C. Dedonder, W. Phasayavan, G. Féraud, B. Inceesungvorn and C. Jouvet, Phys. Chem. Chem. Phys., 2020, 22, 27280–27289 RSC.
- J. T. Buntine, E. Carrascosa, J. N. Bull, U. Jacovella, M. I. Cotter, P. Watkins, C. Liu, M. S. Scholz, B. D. Adamson, S. J. P. Marlton and E. J. Bieske, Rev. Sci. Instrum., 2022, 93, 043201 CrossRef CAS PubMed.
- N. G. K. Wong, C. D. Rankine, C. S. Anstöter and C. E. H. Dessent, Phys. Chem. Chem. Phys., 2022, 24, 17068–17076 RSC.
- S. Chakraborty, A. Patzer and O. Dopfer, J. Chem. Phys., 2010, 133, 044307 CrossRef PubMed.
- B. Chiavarino, O. Dopfer, M. E. Crestoni, D. Corinti, P. Maître and S. Fornarini, ChemPhysChem, 2020, 21, 749–761 CrossRef CAS PubMed.
- O. K. Bazyl, V. Y. Artyukhov, G. V. Mayer, P. P. Pershukevich, M. V. Belkov, O. I. Shadyro and S. N. Samovich, Opt. Spectrosc., 2020, 128, 473–480 CrossRef CAS.
- B. Chiavarino, M. E. Crestoni, S. Fornarini, O. Dopfer, J. Lemaire and P. Maître, J. Phys. Chem. A, 2006, 110, 9352–9360 CrossRef CAS PubMed.
- I. Alata, R. Omidyan, C. Dedonder-Lardeux, M. Broquier and C. Jouvet, Phys. Chem. Chem. Phys., 2009, 11, 11479 RSC.
- O. V. Boyarkin, Int. Rev. Phys. Chem., 2018, 37, 559–606 Search PubMed.
- S. J. P. Marlton and A. J. Trevitt, Chem. Commun., 2022, 58, 9451–9467 RSC.
- T. Khuu, T. Schleif, A. Mohamed, S. Mitra, M. A. Johnson, J. Valdiviezo, J. P. Heindel and T. Head-Gordon, J. Phys. Chem. A, 2023, 127, 7501–7509 CrossRef CAS PubMed.
- S. J. Stropoli, K. Greis, T. Schleif and M. A. Johnson, J. Phys. Chem. A, 2023, 127, 4269–4276 CrossRef CAS PubMed.
- M. A. Halim, M. Girod, L. MacAleese, J. Lemoine, R. Antoine and P. Dugourd, J. Am. Soc. Mass Spectrom., 2016, 27, 1435–1442 CrossRef CAS PubMed.
- M. Lesslie, J. T. Lawler, A. Dang, J. A. Korn, D. Bím, V. Steinmetz, P. Maître, F. Tureček and V. Ryzhov, ChemPhysChem, 2017, 18, 1293–1301 CrossRef CAS PubMed.
- J. Paris, A. Theisen, B. P. Marzullo, A. Haris, T. E. Morgan, M. P. Barrow, J. O’Hara and P. B. O’Connor, J. Am. Soc. Mass Spectrom., 2022, 33, 1126–1133 CrossRef CAS PubMed.
- M. Fache, B. Boutevin and S. Caillol, Eur. Polym. J., 2015, 68, 488–502 CrossRef CAS.
- S. S. Kumar, K. I. Priyadarsini and K. B. Sainis, Redox Rep., 2002, 7, 35–40 CrossRef CAS PubMed.
- M. A. Freedman, E.-J. E. Ott and K. E. Marak, J. Phys. Chem. A, 2019, 123, 1275–1284 CrossRef CAS PubMed.
- O. Yeni, B. Schindler, B. Moge and I. Compagnon, Analyst, 2022, 147, 312–317 RSC.
- B. Moge, O. Yeni, A. Infantino and I. Compagnon, Int. J. Mass Spectrom., 2023, 490, 117071 CrossRef CAS.
- X.-B. Wang and L.-S. Wang, Rev. Sci. Instrum., 2008, 79, 073108 CrossRef PubMed.
- L.-S. Wang, J. Chem. Phys., 2015, 143, 040901 CrossRef PubMed.
- J. U. Andersen, H. Cederquist, J. S. Forster, B. A. Huber, P. Hvelplund, J. Jensen, B. Liu, B. Manil, L. Maunoury, S. Brøndsted Nielsen, U. V. Pedersen, J. Rangama, H. T. Schmidt, S. Tomita and H. Zettergren, Phys. Chem. Chem. Phys., 2004, 6, 2676–2681 RSC.
- N. Esteves-López, C. Dedonder-Lardeux and C. Jouvet, J. Chem. Phys., 2015, 143, 074303 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- TURBOMOLE V6.6 2011, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available fromhttps://www.turbomole.com.
- C. Hättig, J. Chem. Phys., 2003, 118, 7751–7761 CrossRef.
- C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- D. E. Woon, J. Dunning and H. Thom, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242 CrossRef CAS.
- Chemcraft - graphical software for visualization of quantum chemistry computations, https://www.chemcraftprog.com, Version 1.8, build 654.
- J. A. Noble, C. Dedonder-Lardeux, J. Mascetti and C. Jouvet, Chem. – Asian J., 2017, 12, 1523–1531 CrossRef CAS PubMed.
- X. Wu, X. Zhou, S. Bjelić, P. Hemberger and A. Bodi, J. Phys. Chem. A, 2021, 125, 3327–3340 CrossRef CAS PubMed.
- J. R. Joyce and D. S. Richards, J. Am. Soc. Mass Spectrom., 2011, 22, 360–368 CrossRef CAS PubMed.
- D. Schröder, M. Buděšínský and J. Roithová, J. Am. Chem. Soc., 2012, 134, 15897–15905 CrossRef PubMed.
- H. Xia and A. B. Attygalle, Anal. Chem., 2016, 88, 6035–6043 CrossRef CAS PubMed.
- I. Antol, M. Eckert-Maksić and M. Klessinger, THEOCHEM, 2003, 664–665, 309–317 CrossRef CAS.
- N. Solcà and O. Dopfer, Chem. Phys. Lett., 2001, 342, 191–199 CrossRef.
- G. Bouchoux, D. Defaye, T. McMahon, A. Likholyot, O. Mó and M. Yáñez, Chem. – Eur. J., 2002, 8, 2900 CrossRef CAS PubMed.
- M. Katada and A. Fujii, J. Phys. Chem. A, 2018, 122, 5822–5831 CrossRef CAS PubMed.
- R. F. Childs and B. Parrington, Can. J. Chem., 1974, 52, 3303–3312 CrossRef CAS.
- S. Gondarry and P. M. Mayer, J. Phys. Chem. A, 2022, 126, 9051–9058 CrossRef CAS PubMed.
- L. Barnes, A.-R. Allouche, S. Chambert, B. Schindler and I. Compagnon, Int. J. Mass Spectrom., 2020, 447, 116235 CrossRef.
- A. Longarte, C. Redondo, J. A. Fernández and F. Castaño, J. Chem. Phys., 2005, 122, 164304 CrossRef PubMed.
- J. Wiley and S. Inc., SpectraBase: Vanillin, https://spectrabase.com/spectrum/4sk2VtOvBc5, 2023.
- G. Féraud, N. Esteves-López, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2015, 17, 25755–25760 RSC.
- P. Neta, Y. Simón-Manso, Y. Liang and S. E. Stein, Rapid Commun. Mass Spectrom., 2014, 28, 1871–1882 CrossRef CAS PubMed.
- N. G. K. Wong, C. D. Rankine and C. E. H. Dessent, J. Phys. Chem. Lett., 2021, 12, 2831–2836 CrossRef CAS PubMed.
- M. Berdakin, G. Féraud, C. Dedonder-Lardeux, C. Jouvet and G. A. Pino, Phys. Chem. Chem. Phys., 2014, 16, 10643–10650 RSC.
- R. Mansour, S. Mukherjee, M. Pinheiro, J. A. Noble, C. Jouvet and M. Barbatti, Phys. Chem. Chem. Phys., 2022, 24, 12346–12353 RSC.
- B. S. Freiser and J. L. Beauchamp, J. Am. Chem. Soc., 1977, 99, 3214–3225 CrossRef CAS.
- L. Klasinc, B. Kovac and H. Gusten, Pure Appl. Chem., 1983, 55, 289–298 CrossRef CAS.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- H. Kang, C. Jouvet, C. Dedonder-Lardeux, S. Martrenchard, G. Grégoire, C. Desfrançois, J.-P. Schermann, M. Barat and J. A. Fayeton, Phys. Chem. Chem. Phys., 2005, 7, 394–398 RSC.
- M. A. Halim, L. MacAleese, J. Lemoine, R. Antoine, P. Dugourd and M. Girod, J. Am. Soc. Mass Spectrom., 2018, 29, 270–283 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05573f |
| This journal is © the Owner Societies 2024 |