Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploration of biochemical reactivity with a QM/MM growing string method†
Neil R.
McFarlane
 and
Jeremy N.
Harvey
and
Jeremy N.
Harvey
 *
*
Department of Chemistry, KU Leuven, B-3001 Leuven, Celestijnenlaan 200f, 2404, Belgium. E-mail: jeremy.harvey@kuleuven.be
First published on 26th January 2024
Abstract
In this work, we have implemented the single-ended growing string method using a hybrid internal/Cartesian coordinate scheme within our in-house QM/MM package, QoMMMa, representing the first implementation of the growing string method in the QM/MM framework. The goal of the implementation was to facilitate generation of QM/MM reaction pathways with minimal user input, and also to improve the quality of the pathways generated as compared to the widely used adiabatic mapping approach. We have validated the algorithm against a reaction which has been studied extensively in previous computational investigations – the Claisen rearrangement catalysed by chorismate mutase. The nature of the transition state and the height of the barrier was predicted well using our algorithm, where more than 88% of the pathways generated were deemed to be of production quality. Directly compared to using adiabatic mapping, we found that while our QM/MM single-ended growing string method is slightly less efficient, it readily produces reaction pathways with fewer discontinuites and thus minimises the need for involved remapping of unsatisfactory energy profiles.
Introduction
Successfully describing biochemical reaction pathways and, crucially, how enzymes accelerate the rate of these reactions is central both from a fundamental point-of-view,1,2 and for applications ranging from drug development3,4 to industrial biocatalysis.5,6 However, due to the short-lived nature of a transition state (TS), these pathways can be challenging to characterise experimentally. Allowing the modelling of reaction pathways and TSs, computational methodology is an attractive alternative which is widely used.7–9In studying these reaction pathways, it is often desirable to include in the model not only the substrates and the catalytic site amino acid residues, but also the wider protein and solvent environment. Hybrid quantum mechanics/molecular mechanics (QM/MM) is one of the commonly used methods that can satisfy this.10–14 However, by its very nature, a hybrid QM/MM model invokes a significant number of degrees of freedom, and thus finding the minimum energy pathway (MEP) between reactant and product is seldom straightforward.
In the QM/MM formalism, one may obtain the MEP as either a free energy surface by using dynamic techniques, or as a potential energy surface through the use of static techniques.15 While dynamic techniques such as umbrella sampling,16–18 free energy perturbation methods,19–22 and thermodynamic integration23–27 provide an attractively systematic approach to describing reactivity, they are also quite demanding in a QM/MM context, since they require sampling of the potential energy surface at the QM/MM level. Doing so adequately in the context of QM/MM simulations may become computationally unfeasible when using more accurate QM methods.23 While various techniques exist to minimise this computational expense, static techniques are attractive in that they do not require simulation at the QM/MM level of theory. Instead, starting from one or more initial structures, a MEP of discrete structures leading from reactants to products is obtained, and the potential energy barrier along this path is used to estimate the activation free energy for the reaction.28 This estimate of the free energy barrier is not exact, and, as will be discussed below, meaningful estimation of the barrier often requires obtaining multiple MEPs, somewhat restricting the relative computational efficiency compared to dynamic approaches. Nevertheless, these static approaches are valuable, and improved algorithms for identifying MEPs are hence desirable.
Broadly, two classes of static technique to find a MEP exist: double- and single-ended methodologies. Double-ended methodologies start from a pair of structures, often corresponding typically to reactant and product minima, and then iteratively connect them via a MEP.29 Single-ended methods only require a single starting structure, typically a reactant or product minimum. One also needs to provide some definition of the desired reaction coordinate.7,29
With a double-ended methodology, the reactant and product structures need to be configurationally coupled, i.e. the two input structures need to be as geometrically similar as possible given the required changes in chemical bonding occurring during the reaction. This can be viewed as an application of the principle of least motion.30 Rather problematically, due to the very large number of degrees of freedom, independently-generated reactant and product structures are very likely to differ in many ‘spectator’ degrees of freedom.31
On the other hand, careful application of single-ended methodologies has the advantage that the obtained MEP is more likely to connect two structures that are configurationally coupled in the sense discussed above. However, the large number of degrees of freedom to be optimised means that during optimisation of the MEP with single-ended methods, structural changes in ‘spectator’ degrees of freedom are frequently observed, leading to MEPs that include one or several discontinuities in the energy profile.7 One contributing factor to this behaviour is the definition of a reaction coordinate once and only once at the start of the pathway optimisation. In cases with conformationally flexible groups or solvent molecules near the reacting site, many degrees of freedom can couple strongly to the bonding change and accurately defining the reaction coordinate can be challenging, and less accurate reaction pathways may be obtained.7 Hence, there is scope for a single-ended QM/MM technique which improves upon the method for construction of a reaction coordinate, and this would be expected to improve MEP quality.
The growing string method (GSM) was first proposed in 2004 by Peters et al.32 as an improvement upon other double-ended techniques such as the nudged elastic band (NEB)33,34 and other string methods.35,36 This double-ended variant of GSM (DE-GSM) was developed further, and used in a number of computational investigations.37–40 However, the need for configurationally coupled reactant and product structures means that double-ended reaction pathway optimisation techniques are not always readily applicable to large systems. In 2015, Zimmerman developed a single-ended variant of GSM (SE-GSM).41 It is broadly similar to the DE-GSM approach, with both algorithms having a two-stage methodology in which the pathway is first ‘grown’ by adding discrete structures along the pathway, and then optimised with an additional reparameterization step between optimisation cycles.39,41 The method uses a delocalised internal coordinate (DLC) scheme, which allows for the reaction coordinate constraints to be expressed in a flexible way as a combination of all relevant internal coordinates.42–44
In this work, we describe what is, to the best of our knowledge, the first implementation of SE-GSM within the QM/MM framework. We use a hybrid coordinate system, where the QM region is described by DLCs, and the MM region by Cartesian coordinates.45 As mentioned above, the SE-GSM algorithm has two stages, where the initial reaction coordinate used during the growth phase is user-defined (this phase is in many ways similar to the adiabatic mapping method14), and the reaction coordinates used in the subsequent optimisation phase are allowed to vary along the pathway. This variable reaction coordinate should, in principle, have an improved propensity to obtain continuous MEPs.
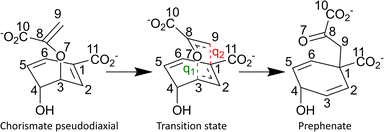
As an initial test and validate of our implementation, we have selected a well-understood biomolecular reaction, the Claisen rearrangement catalysed by chorismate mutase (CM), where the substrate chorismate is converted to prephenate in a single step.46–49 The choice was based upon a number of factors, including ease of system preparation, wealth of computational investigations already performed, and system size. The mechanism of catalysis by CM does not involve any covalent bond formation between the substrate and the enzyme, as the enzyme is a member of the rare class of pericyclic catalysing enzymes.50,51 In bacterial systems, CM plays a part in the shikimate metabolic pathway, ultimately leading to the production of aromatic amino acids phenylalanine and tyrosine.52,53 The reaction mechanism is illustrated in Fig. 1.
Perhaps the most computationally investigated form of chorismate mutase is that from Bacillus subtilis (BsCM),54 presumably due to availability of high-resolution crystal structures containing transition state analogues (TSA). Consequently, BsCM was the enzyme used in this work. Extensive QM/MM studies have been carried out on this reaction using BsCM as the starting structure, so the TS relative energy and structure are well known,55–66 hence providing an excellent benchmark for our study.
In this paper, we describe a new implementation of the SE-GSM methodology within the QM/MM framework (in our in-house QM/MM code QoMMMa).67 We find that the dynamic definition of the reaction coordinate during pathway optimisation improves reaction pathway smoothness, at least for the case of BsCM. We also find that the SE-GSM approach provides an easier and more robust single-ended method for evaluating reaction pathways compared to the adiabatic mapping approach. We describe below the algorithmic details of this implementation, including the coordinate system used and the SE-GSM methodology, as well as the details of the computations on the BsCM test case, and evaluate the quality of the reaction pathways obtained in that case.
Algorithm details
Hybrid delocalised internal coordinates
Our optimisation uses hybrid DLCs as these yield faster optimisation than Cartesian coordinates, fewer degrees of freedom,68,69 and they also facilitate the implementation of multi-component constraints.42–44 In addition, DLCs can be generated completely automatically from a set of Cartesian coordinates. These advantages outweigh the computational expense required to generate them for large systems, and the need for an iterative back-transformation procedure between optimisation cycles to Cartesian coordinates that does not always converge.42–44 By using a hybrid DLC scheme where DLCs are used for the QM region, and Cartesian coordinates for the MM region,45 the expense is in any case negligible, while convergence of the back-transformation can be ensured by taking relatively small geometry update steps with a robust algorithm.The process of generating and constraining a set of DLCs has been described previously,42–45 here only a brief outline is given. To generate a set of DLCs, primitive internal coordinates are first generated completely automatically. This set of nq primitive internal coordinates, q, fully describe the internal degrees of freedom of a system of n atoms and nx = 3n Cartesian coordinates. Our implementation allows for q either a complete set of interatomic distances (a ‘total connectivity’ scheme) or a covalently defined set of bonds, angles, and dihedral torsions. To describe the system accurately, nq must be at least equal to nx − 6, or nx − 5 for linear molecules. It may, however, be greater, and the precise choice made is not critical for the optimisation algorithm.42
In our implementation, q and the subsequently formed DLCs are only generated for the QM region – a previously validated partitioning scheme for QM/MM calculations.45 In an additive scheme, the QM and MM regions are independently optimised, but are polarised by one another via point charges. This independent optimisation means that treating the two regions with different coordinate types is straightforward. Any link atoms introduced by scission of a covalent bond across the QM-MM boundary can be seamlessly included in the generation of q and hence DLCs. Moreover, the microiterative scheme as implemented in QoMMMa where the entire MM region is optimised at each macrocyle67 is preserved whilst still optimising the QM region with DLCs, thereby improving performance at low computational expense.70,71 Optimisation steps involve updating initially the DLCs, which can be seamlessly converted to a step in q space. The resulting updated structures then need to be converted back to Cartesian coordinates, as will be discussed below. Coordinate interconversion steps make use of the Wilson B matrix (see eqn (1)), whose elements are structure-dependent.72
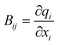 | (1) |
Forming the DLCs uses the symmetric matrix, G, the product of B with its transpose (see eqn (2)).72 Diagonalisation of G (eqn (3)) yields nx − 6 non-zero eigenvalues, and corresponding eigenvectors, which form a sub-matrix U of P, and describe the non-redundant combinations of q. The remaining eigenvectors spanning the redundant space are discarded.
| G = BBT | (2) |
| G = P−1ΛP | (3) |
The DLCs, s, of which there are nx − 6, are formed by linear combinations of q as described by U as shown in eqn (4).
| s = UTq | (4) |
This coordinate set, s, can be taken as the working set for any optimisation procedure. The gradient and (optionally) Hessian that are needed for optimisation in DLC coordinates are obtained as previously described.42 In our implementation, optimisation of the QM region can be carried out using either first-derivative based steepest descent (SD), or the second-derivative based Broyden–Fletcher–Goldfarb–Shanno (BFGS) scheme.73,74 A combination of a few steps of SD then switching to BFGS is currently found to work well, though implementation of other often more efficient algorithms74–77 is also possible. After each structure update for the QM region, the DLCs must be back-transformed to Cartesian coordinates, and problems in this step are avoided by limiting the magnitude of optimisation steps, in a manner that has been previously recommended and applied successfully.78
For reaction pathway optimisation, constraints are needed, and their introduction in a DLC-based algorithm is relatively straightforward. The constraint imposed can, in principle, be applied to any linear combination of several primitive internal coordinates,42,43 and can be imposed exactly. The constraint is expressed initially as a linear combination of primitive internal coordinates in terms of the unit length vector C, which is then is projected onto DLC subspace as shown in eqn (5).
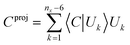 | (5) |
The orthogonal complement of the (nx − 6) vectors of the DLC transformation set, U, with respect to the normalised Cproj then form an nx − 7 space in which to perform optimisation. This exact projection approach is typically more accurate than alternative approaches based on applying geometrical restraints in terms of Cartesian coordinates.79
Single-ended growing string method
As noted in the introduction, all single-ended methodologies begin with just one structure, and incrementally adjust the structure subject to some reaction coordinate.29 However, a poorly-defined reaction coordinate can result in a discontinuous reaction pathway. The SE-GSM partly mitigates this problem due to its two-stage nature, whereby the user-defined reaction coordinate is only used initially in the growth phase, while a structure-dependent reaction coordinate is used during the optimisation phase. Furthermore, during each cycle of the optimisation phase, a reparameterization step is carried out, where the set of discrete structures (or so-called nodes) are equally distributed along the reaction path – thus ensuring even spacing of nodes.41In the growth phase, the user defines an initial, guess reaction coordinate known as the primitive driving coordinate, qinit. qinit may be a combination of any number of primitive internal coordinates, and it does not need to describe the reaction perfectly. It should, however, capture the anticipated changes in chemical bonds, angles, and dihedral torsions. Unlike in usual single-ended methodologies, the range over which the reaction coordinate should be incremented is not required as input but handled internally. In order to generate a new node (i.e., to ‘grow’ the string), for each element of qinit, linear steps of 0.1 Å and 5° are taken for bonds and valence and/or dihedral angles, respectively. These steps may be either in the positive or negative direction depending on the exact definition of qinit. While the size of these steps is the default, we note that for cases where qinit contains many components, it may be desirable to reduce the magnitude of the overall step taken so that the structure of the newly generated node is not severely different from that of the previous one. For the system studied here, we have verified the magnitude of these steps by performing five pathway optimisations using half the step-size. We found that, in this particular case, the five pathways obtained were similar in shape and showed the same barrier height – see Fig. S7 (ESI†). However, we note that for cases where the TS is structurally very similar to either reactant or product, it may be preferable to take smaller steps.
In detail, the growth phase operates as follows: starting with primitive internal coordinate structure qi, structure qi+1 is formed by taking a linear displacement along qinit. Subsequently, qi+1 is converted to DLCs (forming si+1), constrained using eqn (5) (where, C = qinit), and QM/MM optimisation cycles are performed, where the convergence criteria used here are relatively ‘loose’ (see the ESI† for these criteria), and a maximum of 5 optimisation steps per node is taken. This cycle is repeated until the QM/MM energy of structure qi+1 is lower than the QM/MM energy of structure qi – hence a barrier has been surmounted. In this way, it is worth mentioning that this algorithm is limited to reactions with a measurable potential energy barrier. The growth phase is completed by first adding an equal number of nodes on the other side of the barrier and performing a constrained optimisation on each of these nodes, also following qinit. However, as postulated by Hammond,80 other than for thermoneutral reactions, barriers are not symmetric. Therefore, to ensure that the product has been reached, an unconstrained optimisation is performed on the final node in the string. In the following optimisation phase, this final node is fixed, meaning that the node density along the string may change in the following stages of the algorithm. In the description thus far, SE-GSM bears resemblance to adiabatic mapping, but the pathway obtained at this stage is much more approximate than with adiabatic mapping,14 and the pathway will subsequently be refined in the optimisation phase.
In the optimisation phase, qinit is discarded and, instead, the change in q for each pair of neighbouring nodes qi and qi+1 is taken and used to define the reaction coordinate, henceforth τi,i+1, as shown in eqn (6).
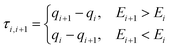 | (6) |
Not every single element of q will be included in τi,i+1, but only those which exceed an internally-defined cut-off threshold going from structure qi to qi+1. By default, these cut-offs are defined as 0.05 Å and 2.5° for bonds and valence and/or dihedral angles, respectively. To minimise any possibility of kinks in the string, Henkelman's upwinding principle is obeyed, wherebyτi,i+1 is defined to point in the direction of increasing energy,81 as indicated in eqn (6). This definition of the reaction coordinate is dynamic, and captures aspects of the reaction coordinate which were not predicted initially in qinit. In this phase, no new nodes are added, but each node is constrained using eqn (5) (where now, C = τi,i+1), and optimised this time with usual convergence criteria (see the ESI† for these criteria) and now a maximum of 25 optimisation steps. Since the reaction coordinate is no longer equivalent at each node, the spacing of nodes will not be even, so a reparameterization step is taken. During this step, the overall difference in q between the reactant and (now fixed) product node is calculated, and each node is linearly spaced along this tangent. The cycle of optimisation phase and reparameterization step is repeated until the constrained QM/MM optimisation of every node on the string is converged, and SE-GSM algorithm is complete.
With the algorithm complete and a MEP obtained, the activation energy can be easily approximated. It is worth noting that, in its current implementation, the activation energy and hence the TS geometry are strictly-speaking an approximation as an eigenvector following TS search algorithm has not yet been implemented.40,45,82 This is something we bear in mind for future development, but the primary goal of this work was to improve the quality of reaction pathways generated.
Given the algorithmic similarity,32,39,40 we have also implemented DE-GSM into QoMMMa. However, due to the aforementioned reasons, it is not necessarily useful for biomolecular QM/MM reaction pathway calculations. It may, however, be useful in other QM/MM reaction pathway applications. QoMMMa has been made publicly available on GitHub with all that has been described in this work.‡
Computational details
For modelling the Claisen rearrangement in BsCM,54 the starting point was a crystal structure containing a transition state analogue (TSA) was used (pdb: 2CHT),83 where Bartlett's inhibitor is used as the TSA.842CHT is a homotrimer with three active sites each situated between two of the monomers, and the site at interface between chains A and B was modelled here. Missing residues at both the C- and N-terminus of chains A and B were ignored due to their distance from the active site. As in previous work,60 a gas-phase optimised (B3LYP/6-311G85–89 with Grimme's D3 dispersion correction and the BJ damping function90,91) structure of chorismate was placed in the active site after aligning it to the TSA. The DFT calculations were performed using Gaussian 16.92 Forcefield parameters for the chorismate co-factor were generated using CGenFF93 with the geometry obtained from the gas-phase optimisations of chorismate; the initially suggested parameters were used without additional validation (see ESI† for parameters). Protonation states of all titratable amino acid side-chains were predicted using PropKa.94 The system (protein and chorismate) was solvated using the TIP3P model95 and placed in a rhombic dodecahedron with the protein at least 10 Å from the box edge. The total charge of the system was neutralised with Na+ and Cl− ions, and set to a physiological concentration of NaCl (0.15 M).96 To remove any initial bad contacts, an energy minimisation procedure was performed. Following this, NVT and NPT simulations were performed for 100 ps each, using Berendsen thermostats and pressure couplings with positional restraints on all heavy atoms, thus equilibrating the system at 300 K and 1 bar. Lastly, positional restraints were relaxed, and a 200 ns simulation was performed in the NPT ensemble with Parrinello–Rahman pressure coupling. All molecular dynamics (MD) simulations were performed within GROMACS97,98 and used the CHARMM36/CGenFF forcefield.93,99 Along the course of the simulation, the root-mean-square deviation (RMSD) of the polypeptide α-carbons was monitored (see Fig. S1, ESI†), and stabilised after approximately 65 ns at 0.098 nm. Starting from 68 ns, 132 snapshots were selected after each ns of simulation and, without any further pre-screening, used as starting points for QM/MM calculations.In preparation for the QM/MM calculations, water molecules further than 15 Å from the centre-of-mass of the chorismate co-factor were deleted giving a total of 6010 atoms. An energy minimisation (with an RMS gradient criterion of 0.001 kcal mol−1 Å−1) was performed on the resulting large cluster model using the same CHARMM36/CGenFF93,99 forcefield in the Tinker program package,100 with atoms > 10 Å from the centre-of-mass of the chorismate frozen. For all QM/MM calculations, the calculations for QM and MM regions of the system were performed with two different packages – Gaussian 09101 and Tinker,100 respectively. The QM and MM parts of the system are combined as a QM/MM calculation using our in-house package QoMMMa.67 The chorismate co-factor was chosen as the QM region, and the remaining protein and solvent was the MM region – resulting in no link atoms between the QM and MM regions, and a QM region size of 24 atoms. For the QM region, all calculations used B3LYP/6-31G(d)85–89 and Grimme's D3 dispersion correction with the BJ damping function.90,91 The MM region was described using the CHARMM36 forcefield.99 For each snapshot, an unconstrained optimisation using DLC for the QM region with usual convergence criteria was performed (see the ESI† for these criteria) was performed to ensure a meaningful starting structure for the pathway evaluations. The primitive driving coordinate, qinit selected was the difference between the forming bond and the breaking bond, i.e. qinit = d(C3–O7) − d(C1–C9) (illustrated in Fig. 1). To minimise any structural changes in distant MM atoms, and ultimately improve reaction pathway continuity, any atoms which were > 10 Å from the centre-of-mass of chorismate were frozen.7
Results and discussion
Pathway quality with QM/MM SE-GSM
Of the 132 pathways obtained, a number were found to be discontinuous based on an analysis of the QM, MM and QM/MM energies for neighbouring nodes along the MEP. If the QM, MM, or QM/MM energy difference to one side of a given node differed too strongly from that on the other side (i.e., if Ek−1 − Ek differed by more than 6 kcal mol−1 from Ek − Ek+1), this was considered to possibly be a discontinuous path to be verified by visual inspection. The threshold of 6 kcal mol−1 was based on inspection of the visibly discontinuous paths in their QM/MM energy profiles, and a sensitivity analysis of this threshold where it was changed by ±1 kcal mol−1 did not cause any variation in the number of discarded pathways. For examples of reaction pathways with discontinuous QM/MM energy profiles, see Fig. S9 (ESI†). Ultimately, 15 of the pathways were discarded using this analysis. The remaining 117 pathways were considered to be sufficiently smooth, although we note that minor discontinuities may still be present. While the reaction catalysed by CM is known to be a favourable case for optimisation of continuous or near-continuous reaction paths, which have been obtained in many studies using adiabatic mapping,55–66 the fact that starting from 132 randomly-selected initial structures and using an automated protocol, we have obtained over 88% success in generating near-continuous pathways is encouraging in terms of the applicability of the SE-GSM. Performance for other types of reaction will need to be tested in future work.To understand the accuracy and efficiency of the QM/MM SE-GSM versus adiabatic mapping, we have calculated five reaction pathways using adiabatic mapping and compared the number of gradient evaluations to SE-GSM reaction pathways which used the same starting geometry. Looking at the barrier heights, both techniques predict approximately the same barrier height, with average difference in barrier heights across the five pathways being 0.6 kcal mol−1. Turning to the question of efficiency, the average number of gradient calls required to reach a smooth pathway were 745 and 627 for SE-GSM and adiabatic mapping, respectively, so that the latter is slightly more efficient. However, SE-GSM is a more streamlined procedure as one does not need to manually define a reaction coordinate with appropriate range, but instead one provides a guess of the reaction coordinate components. Also, the five pathways generated from SE-GSM were already smooth and therefore meaningful, whereas two of the pathways generated using adiabatic mapping were initially not continuous and required refining. This is a common experience with adiabatic mapping studies of reaction pathways and may be due to the fact that the constraint is applied along the same pre-assumed reaction coordinate along the whole reaction pathway. In any case, discontinuities in QM/MM energy profiles are quite common when using adiabatic mapping, so that to achieve a smooth profile, one needs to perform quite tedious reverse mapping.7 Hence, even though the total number of gradient calls required to generate smooth pathways was slightly lower with adiabatic mapping, the ease of generating smooth pathways with SE-GSM is a considerable benefit. In general, we attribute the quality of pathways generated by SE-GSM to the relatively ‘loose’ convergence criteria in the growth phase (see the ESI† for these criteria). This means that discontinuities in the QM energy profile are less likely to occur as compared to adiabatic mapping. Moreover, we expect that any discontinuities in the QM energy profile which emerge following the growth phase should be smoothed-out by the flexibility of the optimisation phase reaction coordinate. The primary limitation in generating quality pathways lies in the choice of qinit, as it must represent the main changes in chemical bonding for the reaction under study – something which is not always trivial to understand. However, the selection of an appropriate qinit can in principle be done automatically.102–104
Prediction of the TS in BsCM
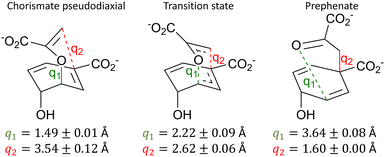
As the potential energy surface in BsCM was sampled extensively using the MD snapshot methodology, there is a degree of variation in predicted barrier heights from different starting snapshots (see Fig. S8 for a histogram of all barrier heights, ESI†). Of the 117 reaction pathways, the standard deviation of the barrier height was ±2.8 kcal mol−1 and the maximum and minimum barrier heights were 9.3 kcal mol−1 and 24.2 kcal mol−1, respectively. This discrepancy in barrier heights is not unusual for static QM/MM reaction pathway calculations and highlights the importance of appropriate sampling.7 In the case herein, given the relatively modest standard deviation, we are satisfied with the extent of sampling.We have used two commonly used methods to evaluate the average barrier height across all 117 snapshots: the arithmetic average of all barrier heights 16.8 kcal mol−1, while exponential averaging yields a value of 12.0 kcal mol−1. The exponential averaging technique has been shown to be preferable for approximating the free energy of the barrier, as lower energy barriers contribute more to the average barrier height,28 hence our discussion below will focus on exponential averaging (even though this does not yield a rigorous estimate of the activation free energy). The calculated barrier height of 12.0 kcal mol−1 calculated herein agrees well with both the average of previous DFT-based computational investigations of 12.7 kcal mol−1, and with the experimental barrier of 12.7 kcal mol−1 – as summarised in Table S1 (ESI†) and the accompanying text. The key bond lengths (including their standard deviations) for the reactant, TS, and product are summarised in Fig. 2.
The predicted TS structures are rather similar to those reported previously, e.g. q1 = 2.14 ± 0.05 Å and q2 = 2.64 ± 0.05 Å from ref. 64 or q1 = 2.28 Å and q2 = 2.58 Å from ref. 61. Given this favourable agreement, and the rather low standard deviations of the key bond lengths around the TS, we have some confidence that the QM/MM SE-GSM with hybrid DLCs approximates the TS well for this reaction. With reference to Fig. 2, one may note that the standard deviation of q2 for the reactant structures is larger than that of any other primitive internal coordinate, indicating that some reactant structures are considerably ‘closer’ to the TS than others, reflecting also the unbiased nature of the sampling of reactant structure from the MD trajectory. Indeed, the variance of the obtained barrier heights and reactant structures is greater than in previous investigations of this system, which typically involved some degree of manual selection of initial structures.
For all pathways, we have also calculated the so-called near-attack conformation (‘NAC’) angle105 for the reactant geometry and plotted this against the barrier height – see Fig. S2 (ESI†). The activation energy has been suggested to be directly dependent on this ‘NAC’ angle, where a lower ‘NAC’ angle suggests that the reactant geometry is predisposed to form the TS, thus lowering the barrier height. In this work, we note some (albeit quite small) correlation between the ’NAC’ angle and the barrier height, where a lower angle gives a lower barrier height. Since all the reactant conformations used in this work were in the pseudodiaxial form of chorismate, and therefore all more-or-less a ’NAC’, seeing only a minor correlation is not unexpected. An alternative theory argues that the primary effect in lowering the barrier height is TS stabilisation by the enzyme environment via electrostatic preorganisation.60–62,106 For the present purposes, whether the ‘NAC’ or electrostatic preorganisation theory is the main barrier lowering effect is perhaps less important given that the structural features leading to TS stabilisation are also expected to stabilise ‘NAC's and hence lead to their observation.
Hybrid DLCs and dynamic reaction coordinate
The hybrid DLC scheme as applied to additive QM/MM calculations is not new,45 but specifically in the case of GSM where the reaction coordinate does not change linearly, it was not clear whether this scheme could be seamlessly implemented. In the current implementation, the QM region is the DLC region by default. However, in principle, the choice of DLC region in a hybrid DLC scheme need not be limited to simply the QM region, but could also include particularly important MM atoms, or indeed a smaller subset of the QM region atoms. Including MM region atoms requires modification of the Hessian matrices used for optimisation,45 and it is not clear to us if there is a significant benefit to using a scheme such as this given that the most significant structural changes typically occur in the QM region. Moreover, selection of important MM atoms requires more user intervention – something which we aimed to minimise in the QM/MM SE-GSM methodology. We do, however, note that in cases where it is desirable to use a particularly large QM region,107 but only one part of it undergoes any significant structural changes, it could be useful to use DLC for only this part. Therefore, the repeated diagonalisation procedure required to generate the DLC could be made faster.When compared to adiabatic mapping, our implementation of SE-GSM offers a dynamic definition of reaction coordinate during the optimisation phase, and the improvement over adiabatic mapping can largely be ascribed to this. This benefit is less important in a simple case study as described herein, but for calculations on more complex biochemical systems, this may be critical to achieve a smooth MEP. The effect of the dynamic reaction coordinate can be clearly seen in the components of the reaction coordinate as the optimisation phase proceeded, where a number of additional interatomic distances emerged as important. These are summarised alongside the original primitive internal coordinates within qinit in Table 1.
| Internal coordinate | Definition | Distance (Å) | ||
|---|---|---|---|---|
| Reactant | TS | Product | ||
| q 1 | d(C3–O7) | 1.49 ± 0.01 | 2.22 ± 0.09 | 3.63 ± 0.08 |
| q 2 | d(C1–C9) | 3.54 ± 0.12 | 2.62 ± 0.06 | 1.60 ± 0.00 |
| q 3 | d(C1–C11) | 1.35 ± 0.00 | 1.40 ± 0.01 | 1.51 ± 0.00 |
| q 4 | d(C2–C3) | 1.50 ± 0.01 | 1.38 ± 0.01 | 1.34 ± 0.00 |
| q 5 | d(O7–C8) | 1.39 ± 0.01 | 1.28 ± 0.01 | 1.22 ± 0.00 |
| q 6 | d(C8–C9) | 1.34 ± 0.00 | 1.39 ± 0.01 | 1.53 ± 0.01 |
From Table 1 it can be seen that not only do the components of the initial driving coordinate play a part in the reaction, but so do some other relevant distances, albeit to a lesser extent. In this way, we have included other reaction coordinate components entirely automatically. The components of the initial primitive driving coordinate (q1 and q2) continue to have the largest weight in the reaction coordinate, but this is to be expected given the relatively simple nature of this reaction. However, for more complex biochemical reactions in which one is unsure of which internal coordinates aid in reaction catalysis, their contribution could be captured during pathway optimisation. There are no discontinuities in q1 and q2, and the same is true for all other interatomic distances shown in Table 1 (see Fig. S3 and S5, ESI†). We have also plotted the variation of q1 and q2 for four sample pathways, highlighting the smoothness of the reaction coordinate for individual pathways – see Fig. S4 (ESI†). Given that this was generated only from an initial guess of the driving coordinate, not a specific constrained range nor any biased selection of MD snapshots, the result is quite pleasing. Besides these distances, a large number or valence and dihedral angles also played a part in the reaction coordinate. Regardless of the reaction, this will, always happen as there are many valence and dihedral angles dependent on the position of a given atom. Due to their large number, we do not report all of them here, but we have plotted the two known important dihedral angles found in this reaction (see Fig. S6, ESI†), aligning well with previous investigations.64
Conclusions
In this article, we have described the single-ended growing string method as implemented in our code QoMMMa. The implementation of this method in a QM/MM framework is, to the best of our knowledge, novel. As a validation case study, we have successfully applied our algorithm to a well-known biochemical system – the Claisen rearrangement of chorismate to prephenate catalysed by chorismate mutase. We find that the algorithm generates useful pathways for the reaction and aligns well with previous computational investigations. Moreover, the algorithm appears to more reliably generate continuous pathways than the usually employed single-ended methods. We attribute this improvement to the fact that constraints applied to the discrete structures along the reaction coordinate are better able to adapt to the local nature of chemical changes taking place. In the algorithm validation process, we generated many continuous reaction pathways, possibly the most that have been generated for this system in a given study.Author contributions
Neil R. McFarlane: conceptualisation, data curation, formal analysis, software, visualisation, writing – original draft, writing – review & editing; Jeremy N. Harvey: conceptualisation, software, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding through KULeuven grants CELSA/19/017 and C14/22/087.Notes and references
- G. G. Hammes, S. J. Benkovic and S. Hammes-Schiffer, Biochemistry, 2011, 50, 10422–10430 CrossRef CAS PubMed
.
- P. K. Agarwal, Biochemistry, 2019, 58, 438–449 CrossRef CAS PubMed
.
- G. A. Holdgate, T. D. Meek and R. L. Grimley, Nat. Rev. Drug Discovery, 2018, 17, 115–132 CrossRef CAS PubMed
.
- A. C. Rufer, Drug Discovery Today, 2021, 26, 875–886 CrossRef CAS PubMed
.
- E. M. M. Abdelraheem, H. Busch, U. Hanefeld and F. Tonin, React. Chem. Eng., 2019, 4, 1878–1894 RSC
.
- A. Guarneri, W. J. van Berkel and C. E. Paul, Curr. Opin. Biotechnol, 2019, 60, 63–71 CrossRef CAS PubMed
.
- R. Lonsdale, J. N. Harvey and A. J. Mulholland, Chem. Soc. Rev., 2012, 41, 3025 RSC
.
- S. Ahmadi, L. Barrios Herrera, M. Chehelamirani, J. Hostaš, S. Jalife and D. R. Salahub, Int. J. Quantum Chem., 2018, 118, e25558 CrossRef
.
- A. J. Mulholland, Drug Discovery Today, 2005, 10, 1393–1402 CrossRef CAS PubMed
.
- R. P. Magalhães, H. S. Fernandes and S. F. Sousa, Isr. J. Chem., 2020, 60, 655–666 CrossRef
.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed
.
- C. E. Tzeliou, M. A. Mermigki and D. Tzeli, Molecules, 2022, 27, 2660 CrossRef CAS PubMed
.
- M. G. Quesne, T. Borowski and S. P. de Visser, Chem. - Eur. J., 2016, 22, 2562–2581 CrossRef CAS PubMed
.
- K. E. Ranaghan and A. J. Mulholland, Int. Rev. Phys. Chem., 2010, 29, 65–133 Search PubMed
.
-
G. Groenhof, in Biomolecular Simulations, ed. L. Monticelli and E. Salonen, Humana Press, Totowa, NJ, 2013, vol. 924, pp. 43–66 Search PubMed
.
- J. Kästner, WIREs Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed
.
- W. You, Z. Tang and C. A. Chang, J. Chem. Theory Comput., 2019, 15, 2433–2443 CrossRef CAS PubMed
.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS
.
- H. Hu and W. Yang, Annu. Rev. Phys. Chem., 2008, 59, 573–601 CrossRef CAS PubMed
.
- H. Hu, Z. Lu, J. M. Parks, S. K. Burger and W. Yang, J. Chem. Phys., 2008, 128, 034105 CrossRef PubMed
.
- H. Hu, Z. Lu and W. Yang, J. Chem. Theory Comput., 2007, 3, 390–406 CrossRef CAS PubMed
.
- Y. Zhang, H. Liu and W. Yang, J. Chem. Phys., 2000, 112, 3483–3492 CrossRef CAS
.
- J. Kästner, H. M. Senn, S. Thiel, N. Otte and W. Thiel, J. Chem. Theory Comput., 2006, 2, 452–461 CrossRef PubMed
.
- J. G. Kirkwood, J. Chem. Phys., 2004, 3, 300–313 CrossRef
.
- M. Sprik and G. Ciccotti, J. Chem. Phys., 1998, 109, 7737–7744 CrossRef CAS
.
- J. Schlitter and M. Klähn, J. Chem. Phys., 2003, 118, 2057–2060 CrossRef CAS
.
- W. K. den Otter and W. J. Briels, J. Chem. Phys., 1998, 109, 4139–4146 CrossRef CAS
.
- A. M. Cooper and J. Kästner, ChemPhysChem, 2014, 15, 3264–3269 CrossRef CAS PubMed
.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, WIREs Comput. Mol. Sci., 2018, 8, 1–20 Search PubMed
.
-
M. L. Sinnott, in Advances in Physical Organic Chemistry, ed. D. Bethell, Academic Press, 1988, vol. 24, pp. 113–204 Search PubMed
.
- P. E. M. Siegbahn and T. Borowski, Faraday Discuss., 2010, 148, 109–117 RSC
.
- B. Peters, A. Heyden, A. T. Bell and A. Chakraborty, J. Chem. Phys., 2004, 120, 7877–7886 CrossRef CAS PubMed
.
-
H. Jónsson, G. Mills and K. W. Jacobsen, Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, LERICI, Villa Marigola, 1998, pp. 385–404 Search PubMed
.
- S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2004, 120, 2082–2094 CrossRef CAS PubMed
.
- W. E. W. Ren and E. Vanden-Eijnden, J. Phys. Chem. B, 2005, 109, 6688–6693 CrossRef PubMed
.
- W. E. W. Ren and E. Vanden-Eijnden, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 052301 CrossRef
.
- A. Behn, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2011, 7, 4019–4025 CrossRef CAS PubMed
.
- M. Jafari and P. M. Zimmerman, J. Comput. Chem., 2017, 38, 645–658 CrossRef CAS PubMed
.
- P. M. Zimmerman, J. Chem. Phys., 2013, 138, 184102 CrossRef PubMed
.
- P. Zimmerman, J. Chem. Theory Comput., 2013, 9, 3043–3050 CrossRef CAS PubMed
.
- P. M. Zimmerman, J. Comput. Chem., 2015, 36, 601–611 CrossRef CAS PubMed
.
- J. Baker, A. Kessi and B. Delley, J. Chem. Phys., 1996, 105, 192–212 CrossRef CAS
.
- J. Baker, J. Comput. Chem., 1997, 18, 1079–1095 CrossRef CAS
.
- J. Baker, D. Kinghorn and P. Pulay, J. Chem. Phys., 1999, 110, 4986–4991 CrossRef CAS
.
- S. R. Billeter, A. J. Turner and W. Thiel, Phys. Chem. Chem. Phys., 2000, 2, 2177–2186 RSC
.
- X. Zhang, X. Zhang and T. C. Bruice, Biochemistry, 2005, 44, 10443–10448 CrossRef CAS PubMed
.
- C. C. Galopin, Tetrahedron Lett., 1996, 37, 8675–8678 CrossRef CAS
.
- A. L. Lamb, Biochemistry, 2011, 50, 7476–7483 CrossRef CAS PubMed
.
- N. A. Khanjin, J. P. Snyder and F. M. Menger, J. Am. Chem. Soc., 1999, 121, 11831–11846 CrossRef CAS
.
- P. R. Andrews, G. D. Smith and I. G. Young, Biochemistry, 1973, 12, 3492–3498 CrossRef CAS PubMed
.
- S. D. Copley and J. R. Knowles, J. Am. Chem. Soc., 1987, 109, 5008–5013 CrossRef CAS
.
- E. Pérez, M. B. Rubio, R. E. Cardoza, S. Gutiérrez, W. Bettiol, E. Monte and R. Hermosa, Front. Microbiol., 2015, 6, 1181 Search PubMed
.
- V. Tzin and G. Galili, Arab. Book Am. Soc. Plant Biol., 2010, 8, e0132 Search PubMed
.
- Y. M. Chook, H. Ke and W. N. Lipscomb, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 8600–8603 CrossRef CAS PubMed
.
- P. D. Lyne, A. J. Mulholland and W. G. Richards, J. Am. Chem. Soc., 1995, 117, 11345–11350 CrossRef CAS
.
- M. M. Davidson, I. R. Gould and I. H. Hillier, J. Chem. Soc., Perkin Trans. 2, 1996, 525–532 RSC
.
- R. J. Hall, S. A. Hindle, N. A. Burton and I. H. Hillier, J. Comput. Chem., 2000, 21, 1433–1441 CrossRef CAS
.
- S. Martí, J. Andrés, V. Moliner, E. Silla, I. Tuñón, J. Bertrán and M. J. Field, J. Am. Chem. Soc., 2001, 123, 1709–1712 CrossRef PubMed
.
- Y. S. Lee, S. E. Worthington, M. Krauss and B. R. Brooks, J. Phys. Chem. B, 2002, 106, 12059–12065 CrossRef CAS
.
- K. E. Ranaghan, L. Ridder, B. Szefczyk, W. A. Sokalski, J. C. Hermann and A. J. Mulholland, Mol. Phys., 2003, 101, 2695–2714 CrossRef CAS
.
- K. E. Ranaghan, L. Ridder, B. Szefczyk, W. A. Sokalski, J. C. Hermann and A. J. Mulholland, Org. Biomol. Chem., 2004, 2, 968 RSC
.
- F. Claeyssens, K. E. Ranaghan, F. R. Manby, J. N. Harvey and A. J. Mulholland, Chem. Commun., 2005, 5068 RSC
.
- F. Claeyssens, J. N. Harvey, F. R. Manby, R. A. Mata, A. J. Mulholland, K. E. Ranaghan, M. Schütz, S. Thiel, W. Thiel and H.-J. Werner, Angew. Chem., Int. Ed., 2006, 45, 6856–6859 CrossRef CAS PubMed
.
- F. Claeyssens, K. E. Ranaghan, N. Lawan, S. J. Macrae, F. R. Manby, J. N. Harvey and A. J. Mulholland, Org. Biomol. Chem., 2011, 9, 1578 RSC
.
- X. Pan, R. Van, E. Epifanovsky, J. Liu, J. Pu, K. Nam and Y. Shao, J. Phys. Chem. B, 2022, 126, 4226–4235 CrossRef CAS PubMed
.
- S. A. Siddiqui and K. D. Dubey, Phys. Chem. Chem. Phys., 2022, 24, 1974–1981 RSC
.
- J. N. Harvey, Faraday Discuss., 2004, 127, 165 RSC
.
- H. B. Schlegel, Int. J. Quantum Chem., 1992, 44, 243–252 CrossRef
.
- E. F. Koslover and D. J. Wales, J. Chem. Phys., 2007, 127, 234105 CrossRef PubMed
.
- R. B. Murphy, D. M. Philipp and R. A. Friesner, J. Comput. Chem., 2000, 21, 1442–1457 CrossRef CAS
.
- T. Vreven, K. Morokuma, Ö. Farkas, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 2003, 24, 760–769 CrossRef CAS PubMed
.
- E. B. Wilson, J. C. Decius, P. C. Cross and B. R. Sundheim, J. Electrochem. Soc., 1955, 102, 235 CrossRef
.
- P. Debye, Math. Ann., 1909, 67, 535–558 CrossRef
.
-
R. Fletcher, Practical Methods of Optimization, Wiley, 1987 Search PubMed
.
- L. De Vico, M. Olivucci and R. Lindh, J. Chem. Theory Comput., 2005, 1, 1029–1037 CrossRef CAS PubMed
.
- H. B. Schlegel, WIREs Comput. Mol. Sci., 2011, 1, 790–809 CrossRef CAS
.
- I. F. Galván, G. Raggi and R. Lindh, J. Chem. Theory Comput., 2021, 17, 571–582 CrossRef PubMed
.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed
.
- J. Baker and D. Bergeron, J. Comput. Chem., 1993, 14, 1339–1346 CrossRef CAS
.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- Y. M. Chook, J. V. Gray, H. Ke and W. N. Lipscomb, J. Mol. Biol., 1994, 240, 476–500 CrossRef CAS PubMed
.
- P. A. Bartlett and C. R. Johnson, J. Am. Chem. Soc., 1985, 107, 7792–7793 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, 2016 Search PubMed
.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. MacKerell, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS PubMed
.
- M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed
.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS
.
- G. A. Ross, A. S. Rustenburg, P. B. Grinaway, J. Fass and J. D. Chodera, J. Phys. Chem. B, 2018, 122, 5466–5486 CrossRef CAS PubMed
.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- J. Huang and A. D. MacKerell, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed
.
- J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schnieders, J.-P. Piquemal, P. Ren and J. W. Ponder, J. Chem. Theory Comput., 2018, 14, 5273–5289 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09, 2009 Search PubMed
.
- E. Martínez-Núñez, G. L. Barnes, D. R. Glowacki, S. Kopec, D. Peláez, A. Rodríguez, R. Rodríguez-Fernández, R. J. Shannon, J. J. P. Stewart, P. G. Tahoces and S. A. Vazquez, J. Comput. Chem., 2021, 42, 2036–2048 CrossRef PubMed
.
- P. M. Zimmerman, J. Comput. Chem., 2013, 34, 1385–1392 CrossRef CAS PubMed
.
- A. Nakao, Y. Harabuchi, S. Maeda and K. Tsuda, Phys. Chem. Chem. Phys., 2022, 24, 10305–10310 RSC
.
- S. Hur and T. C. Bruice, J. Am. Chem. Soc., 2003, 125, 10540–10542 CrossRef CAS PubMed
.
- M. Štrajbl, A. Shurki, M. Kato and A. Warshel, J. Am. Chem. Soc., 2003, 125, 10228–10237 CrossRef PubMed
.
- H. Kang and M. Zheng, Comput. Theor. Chem., 2021, 1204, 113399 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05772k |
| ‡ The QM/MM program described herein, QoMMMa, has been made publicly available on GitHub: https://github.com/NeilMcFarlane-gh/QoMMMa. |
| This journal is © the Owner Societies 2024 |