Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Activation of H2 using ansa-aminoboranes: solvent effects, dynamics, and spin hyperpolarization†
Karolina
Konsewicz‡
a,
Gergely
Laczkó‡
bc,
Imre
Pápai
 b and
Vladimir V.
Zhivonitko
b and
Vladimir V.
Zhivonitko
 *a
*a
aNMR Research Unit, Faculty of Science, University of Oulu, P.O. Box 3000, Oulu, 90014, Finland. E-mail: vladimir.zhivonitko@oulu.fi
bInstitute of Organic Chemistry, Research Centre for Natural Sciences, Magyar Tudósok Körútja 2, H-1117 Budapest, Hungary
cHevesy György PhD School of Chemistry, Eötvös Loránd University, P.O. Box 32, H-1518 Budapest, Hungary
First published on 22nd December 2023
Abstract
Spin hyperpolarization generated upon activation of parahydrogen, the spin-0 isomer of H2, by ansa-aminoboranes (AABs) constitutes a rare but interesting example of applied metal-free catalysis in parahydrogen-induced polarization (PHIP). AAB molecular moieties made of light elements would be useful in important areas of NMR, such as chemosensing and the production of hyperpolarized substances, or generally in NMR sensitivity enhancement. At the same time, little is known about the detailed mechanistic aspects of underlying chemical processes. Herein, we present a joint experimental-computational study of the kinetic and thermodynamic aspects of H2 activation by AABs, for the first time providing molecular-level details and results of PHIP experiments with AABs in various solvents. Specifically, a large number of kinetic and thermodynamic parameters are measured experimentally for H2 activation by 2-aminophenylboranes of variable steric bulkiness of the boryl site. A clear correlation between the experimental and DFT-predicted thermochemical parameters is observed. PHIP effects in toluene, dichloromethane, and acetonitrile are characterized and rationalized based on the use of the kinetic and nuclear spin relaxation parameters. Altogether, the obtained results provide valuable information for the further rational design of efficient AAB catalysts for metal-free PHIP based on frustrated Lewis pair (FLP) chemistry.
1. Introduction
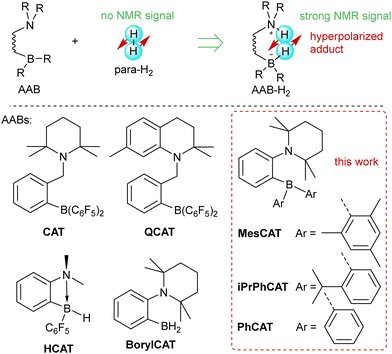
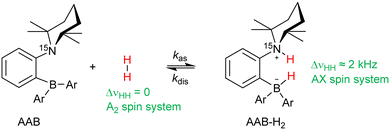
The metal-free activation of small molecules has garnered considerable attention due to its potential for the development of new catalysts based on abundant main group elements.1,2 In addition, it can likely be utilized in the design of chemosensors that are sensitive to small molecules. For instance, metal-free ansa-aminoboranes that can activate molecular hydrogen were shown to activate parahydrogen, the spin-0 isomer of H2, which leads to strongly enhanced signals in 1H NMR spectra (Scheme 1).3,4 With ortho-phenylene-based ansa-aminoboranes, spontaneous 15N and 11B hyperpolarization using parahydrogen was also demonstrated,5 potentially opening the possibility of background-free NMR chemosensing of parahydrogen utilizing these species. Moreover, ansa-aminoboranes CAT, QCAT and HCAT (Scheme 1) were shown to act as efficient catalysts in the hydrogenation of alkynes and imines leading to hyperpolarized alkenes and amines, respectively.6,7 To a certain extent, this class of catalytic materials can be considered as a more sustainable and environmentally friendly alternative to transition metal catalysts usually employed in parahydrogen-based spin hyperpolarization techniques.8Understanding the mechanism of H2 activation by ansa-aminoboranes on both macroscopic and microscopic levels can provide detailed insights into the molecular features facilitating the activation process. This can be used in the design of new ansa-aminoboranes with desired kinetic and thermodynamic properties, dramatically increasing the nuclear spin hyperpolarization efficiency. It is worth noting that other metal-free compounds such as triphosphabenzene9 and pnictogen biradicals10,11 and tetraradicals12 have also been documented to exhibit hyperpolarization effects with parahydrogen. However, we believe that ansa-aminoboranes provide the most versatile metal-free scaffold for parahydrogen activation. It is worth noting that the intramolecular nature of ansa-aminoboranes is crucial for the observation of parahydrogen-induced polarization (PHIP), since attempts to use intermolecular FLPs did not reveal any hyperpolarization effects.7 However, the solvent effects on H2 activation using these interesting compounds in conjunction with PHIP have never been studied.
In the realm of catalytic research, PHIP is a particularly valuable nuclear spin hyperpolarization technique due to the fact that hyperpolarization transpires organically when H2 molecules enriched in the para nuclear spin isomer are chemically activated.13,14 Mechanistic insights can be obtained by observing the significantly amplified NMR signals of the reaction intermediates or final products when a catalyst is used to activate parahydrogen. To see the hyperpolarization, it is necessary for H2 activation to be pairwise, implying that the H atom pair must not be completely separated, at least during the initial parahydrogen activation phase.8 In particular, the ability of PHIP to identify dihydride intermediates has been illustrated through its application in elucidating the hydrogenation mechanisms of numerous metal complex catalysts.8,15 As intriguing examples, the kinetics of the formation of [IrCO(H)2I(PPh3)2] subsequent to the reductive elimination of hydrogen induced by light was investigated using parahydrogen,16 cationic RhI intermediates with coordinated arene rings were detected;17 the pathways of H2 exchange in (μ-H)2Os3(CO)10 clusters were determined;18 ligand exchange in [IrCO(H)2Cl(PPh3)2] and [IrH2Cl(PPh3)3] was understood;19 and many other important mechanistic studies8,15,20 were done, including also those of heterogeneous catalytic systems.21,22
In this paper, we discuss for the first time the key factors influencing the activation of molecular hydrogen by a selection of PHIP-relevant ortho-phenylene ansa-aminoboranes in various solvents. These factors are crucial for the observation of PHIP in general. We report a significant amount of experimentally measured kinetic and thermodynamic data for MesCAT, iPrPhCAT, and PhCATansa-aminoboranes (Scheme 1), model species with variable steric bulkiness at the boron center. We describe the observed parameters based on DFT calculations, showing that the applied computational approach can be used to predict these parameters with good accuracy. Both experiments and computations show a stabilization effect of the ansa-aminoborane-H2 adduct in polar solvents. Altogether, kinetic, thermodynamic, relaxation, and computational data are used to rationalize the observed nuclear spin hyperpolarization effects observed in activation parahydrogen using the studied ansa-aminoboranes in toluene, dichloromethane, and acetonitrile as representative solvents of variable polarity that do not interact with the FLP centers.
2. Methods
2.1 Chemicals and materials
Ansa-Aminoborane compounds were synthesized according to the previously described methods.4,5 All the required chemicals were purchased from commercial sources. Deuterated solvents were dried under molecular sieves (3 Å). Parahydrogen-enriched H2 gas (92%), referred to simply as “parahydrogen” in the following discussion, was produced using a Bruker parahydrogen generator.2.2 Parahydrogen experiments
PHIP NMR experiments were performed on a Bruker AV 400 NMR spectrometer operating at 400 MHz 1H resonance frequency and equipped with a broad-band 5 mm RF probe. A standard temperature control unit of the instrument was used to maintain the desired sample temperature.In a typical experiment, a 5 mm sample tube (Wilmad) containing a ca. 0.05 M solution of 15N-labeled ansa-aminoboranes MesCAT, iPrPhCAT, or PhCAT in degassed dry toluene-d6 or acetonitrile-d3 was placed inside the NMR magnet, and parahydrogen was bubbled through the solution for 10 s. Then the parahydrogen flow was abruptly switched off, and an 1H NMR experiment using π/4-pulse was started. 11B decoupling (WALTZ16) was used for the acquisitions. Parahydrogen was supplied to the bottom of the sample tube through 1/32′′ PTFE tubing under a pressure of 5 bar. The enhancement factors were determined by comparing the integral amplitudes of individual components of the enhanced 1H NMR antiphase doublets to those in the thermal spectrum.
2.3 Kinetic and thermodynamic measurements
Measurements of kinetic rate constants were performed using the spin saturation transfer method23–25 on a Bruker Avance III 600 MHz spectrometer, similarly to those described in ref. 4. A valved 5 mm NMR tube from Wilmad was used in the experiments. The samples were prepared by charging the tube with AAB solutions (∼0.05 M) and 5 bars of normal (thermal) H2. 15N decoupling (WALTZ16) was used for all acquisitions. The thermally polarized NH group proton signals were used to determine the rate constants for the dissociation of AAB-H2 adducts into AAB and H2 (kdis, see eqn (1) in Section 3.1). The constants were calculated from the ratios of the signals in the normal spectra and in the spectra acquired with presaturation of the ortho-H2 resonance at ca. 4.6 ppm. To determine kdis, the following expression was used: kdis = (Sn/Ss − 1)/TNH1, in which Sn is the signal intensity in the normal spectrum, Ss is the signal intensity in the spectrum with saturation, and TNH1 is the relaxation time of the proton in the NH group. The saturation-recovery protocol with irradiation of H2 resonance during the recovery delays was used to determine TNH1 as described in ref. 4.Equilibrium constants Kc (see eqn (2)) were determined using signal ratios of AAB, AAB-H2, and H2 in the thermal 1H NMR spectra of the samples. Concentration scaling was required for the conversion from signal amplitude units to concentrations, which was done using the signal integrals and the known initial concentration of AABs. The association rate constant is derived as kas = Kckdis. The standard enthalpies and entropies of the reaction were determined from Kc values at different temperatures using the equation of chemical reaction isotherm.
The enthalpy and entropy activation parameters for the AAB-H2 dissociation were determined by the linear regression procedure of Eyring26 plots. The corresponding data are shown in ESI† (Fig. S1–S6).
2.4 Computational methods
Density functional theory (DFT) was applied to identify the most stable forms of H2 adducts of ansa-aminoboranes, the transition states of the H2 activation process, and also to characterize the conformational changes. The ωB97X-D functional was chosen for DFT calculations, which is a dispersion-corrected, range-separated hybrid exchange–correlation functional developed by Chai and Head-Gordon.27–29 The geometries were optimized at the ωB97X-D/6-311G** level of theory, and the thermal and entropic corrections were also estimated at this level. Single point solvation Gibbs free energies were calculated with the SMD model30 using the gas phase structures for all relevant solvents. Electronic energies were recalculated at the more accurate ωB97X-D/6-311++G(3df,3pd) level. All calculations were carried out with the Gaussian 16 package.313. Results and discussion
In the following sections, we present and discuss the activation of H2 by ansa-aminoboranes from the perspectives of chemical kinetics (Section 3.1), microscopic dynamics (Section 3.2), and spin hyperpolarization (Section 3.3) to build a reasonably full picture describing observations in parahydrogen experiments.3.1 Kinetics and thermodynamics of H2 activation
Formally, H2 activation by ansa-aminoboranes is a second order kinetic process in the forward (association) direction and a first order process in the reverse (dissociation) direction with rate constants kas and kdis, respectively,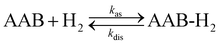 | (1) |
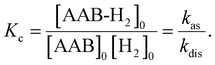 | (2) |
| AAB | Solvent | T (K) | k dis (s−1) | k as (M−1 s−1) | K c (M−1) | [AAB-H2]0/[AAB]0 | [AAB-H2]0/[H2]0 | T NH1 (s) |
|---|---|---|---|---|---|---|---|---|
| a This work. b Taken from ref. 4. | ||||||||
| MesCAT | tola | 293 | 1.5 ± 0.1 | 0.30 ± 0.04 | 0.20 ± 0.05 | 2.8 × 10−3 | 6.9 × 10−3 | 0.29 ± 0.03 |
| 299 | 3.2 ± 0.4 | 0.53 ± 0.06 | 0.16 ± 0.03 | 2.3 × 10−3 | 5.4 × 10−3 | 0.32 ± 0.02 | ||
| 304 | 5.3 ± 0.5 | 0.71 ± 0.07 | 0.13 ± 0.03 | 1.9 × 10−3 | 4.1 × 10−3 | 0.32 ± 0.02 | ||
| dcmb | 283 | 0.02 ± 0.01 | 0.10 ± 0.01 | 5.2 ± 1.1 | 0.11 | 0.22 | 0.38 ± 0.04 | |
| 293 | 0.10 ± 0.02 | 0.20 ± 0.02 | 2.3 ± 0.4 | 0.05 | 0.10 | 0.42 ± 0.04 | ||
| 303 | 0.32 ± 0.03 | 0.32 ± 0.04 | 1.0 ± 0.2 | 0.03 | 0.05 | 0.49 ± 0.06 | ||
| acna | 298 | 0.040 ± 0.003 | 0.52 ± 0.06 | 13.0 ± 2.2 | 0.22 | 0.05 | 0.55 ± 0.05 | |
| 304 | 0.07 ± 0.01 | 0.59 ± 0.05 | 8.6 ± 1.4 | 0.15 | 0.07 | 0.57 ± 0.04 | ||
| 310 | 0.15 ± 0.01 | 1.0 ± 0.1 | 6.7 ± 1.4 | 0.11 | 0.11 | 0.64 ± 0.06 | ||
| iPrPhCAT | tola | 293 | 0.25 ± 0.02 | 8.6 ± 0.9 | 34 ± 8 | 0.48 | 0.99 | 0.30 ± 0.03 |
| 299 | 0.78 ± 0.09 | 21 ± 2 | 27 ± 6 | 0.37 | 0.74 | 0.32 ± 0.04 | ||
| 304 | 1.58 ± 0.15 | 34 ± 3 | 22 ± 3 | 0.31 | 0.58 | 0.33 ± 0.04 | ||
| dcmb | 283 | 0.010 ± 0.005 | 12 ± 1 | 1200 ± 270 | 20 | 1.20 | 0.30 ± 0.04 | |
| 293 | 0.040 ± 0.006 | 20 ± 2 | 462 ± 90 | 8 | 0.99 | 0.35 ± 0.04 | ||
| 303 | 0.18 ± 0.02 | 36 ± 4 | 192 ± 50 | 4 | 0.80 | 0.42 ± 0.05 | ||
| acna | 319 | 0.17 ± 0.02 | 109 ± 13 | 643 ± 100 | 12 | 0.84 | 0.63 ± 0.05 | |
| 322 | 0.23 ± 0.02 | 115 ± 11 | 502 ± 90 | 10 | 0.75 | 0.64 ± 0.07 | ||
| 327 | 0.39 ± 0.05 | 144 ± 12 | 369 ± 90 | 7 | 0.67 | 0.70 ± 0.05 | ||
| PhCAT | tola | 287 | 17 ± 2 | 509 ± 50 | 29.6 ± 5.4 | 0.41 | 1.10 | 0.22 ± 0.02 |
| 293 | 30 ± 3 | 703 ± 70 | 23.4 ± 5.7 | 0.33 | 0.77 | 0.24 ± 0.02 | ||
| 299 | 59 ± 4 | 1093 ± 90 | 18.6 ± 4.5 | 0.26 | 0.58 | 0.24 ± 0.03 | ||
| dcmb | 283 | 0.40 ± 0.04 | 840 ± 70 | 2110 ± 300 | 26 | 2.56 | 0.28 ± 0.03 | |
| 293 | 1.6 ± 0.1 | 1440 ± 170 | 800 ± 180 | 10 | 2.15 | 0.32 ± 0.03 | ||
| 303 | 5.4 ± 0.6 | 1620 ± 160 | 320 ± 80 | 5 | 1.76 | 0.38 ± 0.03 | ||
| acna | 298 | 0.7 ± 0.1 | 600 ± 50 | 858 ± 170 | 15 | 1.44 | 0.46 ± 0.04 | |
| 310 | 2.2 ± 0.2 | 915 ± 80 | 415 ± 70 | 8 | 1.34 | 0.52 ± 0.05 | ||
| 316 | 3.9 ± 0.4 | 1102 ± 80 | 282 ± 70 | 5 | 1.30 | 0.54 ± 0.06 | ||
The experimental data reveal a strong dependence of the kinetic parameters, kdis and kas, as well as the equilibrium constant, Kc, on the solvent used. Specifically, the adduct dissociation constant, kdis, revealed a significant dependence on the solvent polarity. For all studied ansa-aminoboranes, this parameter has the highest value in toluene (non-polar solvent) and the lowest value in acetonitrile (polar solvent) under otherwise similar conditions and reaction temperatures. Dichloromethane experiments provided some intermediate values, correlating with its polarity. In contrast, the association constant, kas, showed much weaker solvent dependence. Together, the solvent effects stemming from the kinetics of the reversible H2 activation affected the equilibrium constant Kc = kas/kdis, making it also solvent dependent.
The overall trend is that the higher polarity of the solvent shifts the equilibrium towards the formation of AAB-H2 adducts. Kc values in toluene are approximately two orders of magnitude smaller than in acetonitrile, which dramatically changes the [AAB-H2]0/[AAB]0 equilibrium ratio, implying that the concentration of the AAB-H2 adduct is significantly smaller in non-polar toluene than in polar acetonitrile for a given initial concentration of ansa-aminoborane (see Table 1 for data).
The strong dependence of the AAB-H2 dissociation step on the solvent is clearly visible in the analysis of standard activation Gibbs free energies ΔG#dis (298 K) derived from the experimentally measured kinetic data by using Eyring plot analysis (see Section 2.3), Table 2. The free energies of dissociation are lower by approximately 2 kcal mol−1 in toluene as compared to acetonitrile for all studied ansa-aminoboranes, implying that the energetic barrier for elimination of H2 is significantly smaller in the non-polar solvent. The reasons for such an effect can be attributed to the stabilization/destabilization influence of solvation on either the AAB-H2 adduct molecule or on the corresponding transition state. These details are discussed below based on the microscopic picture provided by DFT calculations. However, looking at the standard enthalpies of the overall reaction, ΔHr, we can deduce that polar solvents lead to the clear thermal stabilization of AAB-H2 adducts, as the use of acetonitrile leads to an enthalpic drop of at least 6 kcal mol−1 as compared to the toluene data. This seems to be well justified, as the adduct has a zwitterionic structure that must be stabilized by the solvation effects in polar solvents.
| AAB | Solvent | ΔG#dis (298 K) kcal mol−1 | ΔH#dis kcal mol−1 | ΔS#dis cal mol−1 K−1 | ΔHr kcal mol−1 | ΔSr cal mol−1 K−1 |
|---|---|---|---|---|---|---|
| a This work. b Taken from ref. 4. ΔG#dis is given for 298 K. | ||||||
| MesCAT | tola | 16.8 | 19 ± 2 | 6 ± 6 | −7 ± 1 | −28 ± 7 |
| dcmb | 18.4 | 23 ± 8 | 16 ± 25 | −14 ± 4 | −48 ± 27 | |
| acna | 19.4 | 22 ± 2 | 7 ± 8 | −13 ± 2 | −40 ± 15 | |
| iPrPhCAT | tola | 17.6 | 20 ± 1 | 8 ± 4 | −10 ± 1 | −27 ± 10 |
| dcmb | 18.9 | 23 ± 1 | 13 ± 3 | −15 ± 2 | −39 ± 14 | |
| acna | 19.8 | 19 ± 3 | −2 ± 8 | −16 ± 2 | −38 ± 15 | |
| PhCAT | tola | 15.1 | 16 ± 1 | 2 ± 5 | −8 ± 1 | −21 ± 13 |
| dcmb | 16.8 | 21 ± 1 | 15 ± 2 | −17 ± 3 | −44 ± 10 | |
| acna | 17.7 | 18 ± 1 | 0 ± 1 | −13 ± 1 | −32 ± 7 | |
3.2 Microscopic picture of H2 activation
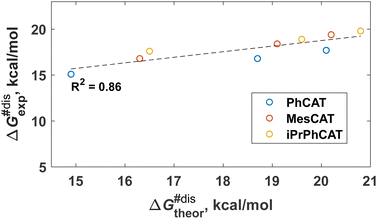
The formal kinetic and thermodynamic considerations described above give an overall picture of H2 activation without specific mechanistic details. Microscopically, however, the activation of H2 by ansa-aminoboranes has features that are useful to bear in mind for the parahydrogen experiments and are important for understanding the reaction mechanism in general. Our DFT calculations indicate that the H2 activation occurs via the concerted action of Lewis acidic and basic sites of the ansa-aminoborane. The identified transition states reflect the general characteristics of FLP-assisted heterolytic H2 splitting, namely the end-on N⋯H2 and side-on H2⋯B interactions, which is consistent with the electron transfer (ET) reactivity model.32 The corresponding reaction pathways for the studied ansa-aminoboranes are illustrated in the supporting animation (see ESI†). All the H2 activation transition states have an early nature in that their structures resemble closely to those of the corresponding AAB + H2 states. In terms of the AAB-H2 → AAB + H2 dissociation processes, these transition states have a late nature, so one expects notable entropic contributions to the free energy barriers of H2 elimination reactions. Interestingly, the measured entropic contributions reported in Table 2 are not so significant (3–5 kcal mol−1).It is noticeable that the DFT analysis revealed a clear correlation between the computed activation free energies and the experimentally observed ones presented in Table 2. Specifically, Fig. 1 shows the computed vs. experimental ΔG#dis (298 K) data plot for the dissociation step. The correlation is quite encouraging considering that both experimental and computational data have their intrinsic uncertainties. The uncertainty of the measurements typically ranges from 1 to 3 kcal mol−1, depending on the case, and one expects similar uncertainties for the DFT predictions as well. The reasonable agreement between theory and experiment implies that the presented computational approach could be used for the estimation of the thermochemical parameters for additional structures of ansa-aminoboranes in future studies. Another important outcome of this comparison is that it provides support for the reaction mechanism established from computational studies, enriching the information content with fine details inaccessible by the formal kinetic approach.
The computed thermodynamic stabilities of AAB-H2 adducts in the form for the Gibbs free energies of reaction (eqn (1)) are compiled in Table 3. The data indicate that the introduction of electron donating alkyl groups (Me or iPr) on the borane phenyl substituents reduces the thermodynamic feasibility of H2 activation. This is likely due to electronic effects (the borane unit becomes less acidic), but steric effects may also influence the thermodynamics. The substituent effect is particularly notable for MesCAT. It is also apparent that the relative stability of the adduct states is fairly sensitive to the polarity of the solvent since the zwitterionic AAB-H2 products are stabilized by more polar solvents. We note that the barrier of H2 splitting is much less influenced by the polarity of the solvent, which can be associated with the early nature of the transition states.
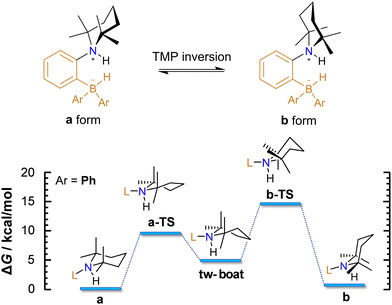
At the microscopic level, the H2 activation process is accompanied by molecular rearrangements, which will be discussed herein. Concerning the AAB-H2 adducts of the studied ansa-aminoboranes, two internal structural rearrangements are important: (1) inversion of the 2,2,6,6-tetramethylpiperidine (TMP) ring (Fig. 2) and (2) rotation of the –BHAr2 unit of the adduct (Fig. 3).
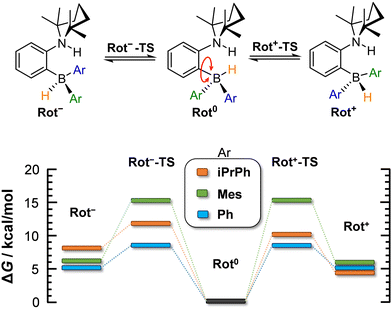 | ||
| Fig. 3 Computed energetics corresponding to borohydride site rotation in AAB-H2 adducts (in DCM). ΔG is given for 298 K. | ||
According to DFT calculations, TMP inversion that interconnects the a and b forms of AAB-H2 adducts proceeds in two steps, as exemplified in the reaction with PhCAT (Fig. 2). Herein, the chair structure of form a first transforms into a twisted boat conformer (viaa-TS), which is then converted to form b (viab-TS). The second transition state is predicted to be higher in free energy, but the overall barrier of TMP inversion (14.0 kcal mol−1) is lower than that of H2 elimination (18.7 kcal mol−1). Calculations predict the a and b forms to have similar stabilities; they differ only by 0.4 kcal mol−1. These results suggest fast dynamic exchange between these two forms of AAB-H2 adducts, so it is impossible to distinguish between them in 1H NMR spectra under ambient conditions.
In contrast, the rotation of –BHAr2 groups can lead to rotamers (rotated forms) that are significantly different in free energy. The rotation of the borohydride unit was investigated with all the three AABs, but only in their a forms. The barriers of the rotation and the stabilities of the rotamers are summarized in Fig. 3. In the most stable forms of AAB-H2, the H atoms originating from H2 atoms are close to each other, which is due to the stabilization effect of dihydrogen bonding in the AAB-H2 adducts.4 The rotamers in which the borohydride groups are rotated by 120° (Rot− and Rot+ forms) are predicted to be 5–6 kcal mol−1 higher for PhCAT-H2 and MesCAT-H2. In the Rot− form of iPrPhCAT-H2, the steric hindrance is enhanced, resulting in a less favoured structure lying at 8 kcal mol−1 in free energy (see ESI,† for structures). Nevertheless, the rotation is actually feasible in all AAB-H2 adducts, as the free energy barriers of rotations are notably lower than those of the corresponding adduct dissociation processes, and therefore they allow for fast intramolecular structural rearrangements on the time scale of dissociation.
The barrier of the rotation is predicted to be lowest for PhCAT-H2 (8.7 kcal mol−1), but it becomes significantly higher with MesCAT-H2 (15.1 kcal mol−1). The destabilization of the related transition states Rot−-TS and Rot+-TS is evidenced by the distorted mesityl units of these structures (see ESI†). Although BHAr2 rotation appears to be feasible kinetically, the relative stabilities computed for the rotated structures of AAB-H2 (5–8 kcal mol−1) suggest a very low population of these states (<1% at room temperature).
3.3 Parahydrogen experiments
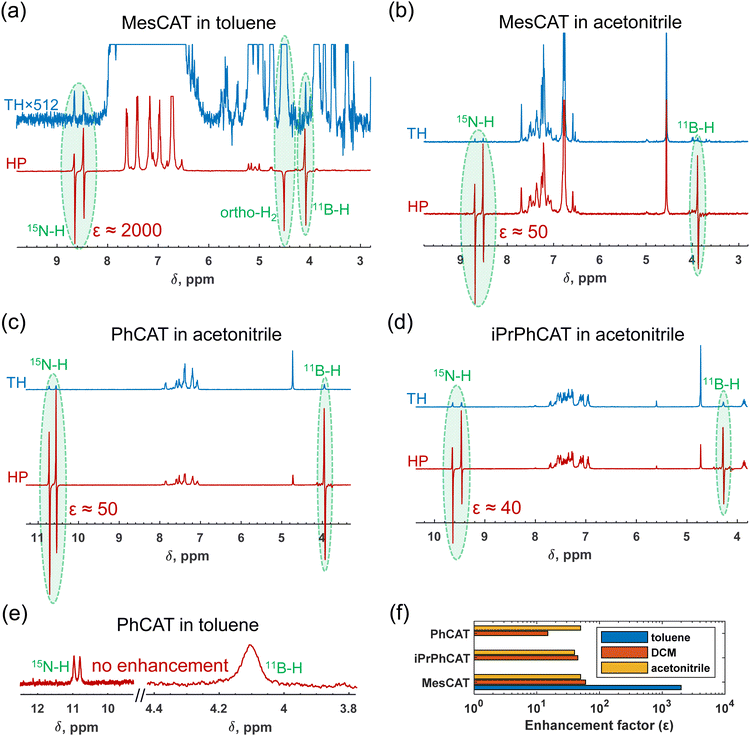
Based on observations, the use of parahydrogen as H2 feedstock in the activation process with ansa-aminoboranes leads to nuclear spin hyperpolarization of AAB-H2 species due to the dynamic chemical equilibrium characterized above. To demonstrate this effect in different solvents, we performed reference experiments by bubbling parahydrogen (92%, 5 bar) through 0.05 M solutions of ansa-aminoboranes (MesCAT, iPrPhCAT, PhCAT) in toluene-d8 and acetonitrile-d3 at room temperature, which culminated in the consequent acquisition of 1H NMR spectra. π/4-pulses were used for the radio-frequency (RF) excitation to maximize signal amplitudes according to the PASADENA protocol for weakly coupled correlated spins.33 Similar experiments utilizing dichloromethane as a solvent have been reported previously.4Fig. 4 provides an overview of how the hyperpolarization exhibits a strong dependence on the solvent used and the AAB structure.Specifically, MesCAT showed antiphase doublets, indicating the formation of the hyperpolarized MesCAT-H2 adduct in both toluene and acetonitrile solvents (Fig. 1a and b). In contrast, iPrPhCAT and PhCAT demonstrated the formation of corresponding hyperpolarized adducts with parahydrogen only in acetonitrile (Fig. 1c and d). Signals of only thermally polarized species were observed in toluene for these ansa-aminoboranes. Interestingly, all AABs showed some degree of hyperpolarization in dichloromethane-d2, as was reported previously in ref. 4.
Measured signal enhancements reveal an ambiguous trend with respect to the solvent and ansa-aminoborane used. For instance, the summarizing histogram in Fig. 1f shows that as high as 2000-fold signal enhancement was observed in toluene in the case of MesCAT, whereas it was 50-fold in the case of acetonitrile. In contrast, the reaction with PhCAT in toluene resulted in the absence of signal enhancement (no hyperpolarization), whereas in acetonitrile, AAB-H2 signals were again enhanced by a factor of 50.
As presented in Section 3.1, the kinetic and thermodynamic parameters of H2 activation (kas, kdis, Kc) also reveal significant differences between the solvents (Table 1). It is obvious that the observed hyperpolarization effects are dependent on those parameters, and this is the origin of the solvent dependence of the hyperpolarization. To elaborate on this implication in more detail, the processes leading to hyperpolarization can be understood as follows: during parahydrogen bubbling through the solutions of ansa-aminoboranes, the reversible chemical activation of H2 leads to the accumulation of a non-equilibrium nuclear spin order in the corresponding hydrogen adduct molecules (Scheme 2). To understand the general features of the resulting hyperpolarization, as a first approximation, it is sufficient to consider only a pair of parahydrogen originating hydrogen nuclei in the adduct molecules, neglecting long-range spin–spin couplings to any other protons as they are small.
Parahydrogen is a source of singlet nuclear spin order:13
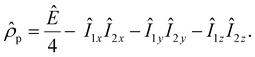 | (1) |
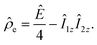 | (2) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e in the H2 and AAB-H2 pools during parahydrogen bubbling. Assuming the thermodynamic chemical equilibrium in Scheme 1, the formal kinetic equations describing this process can be read as
e in the H2 and AAB-H2 pools during parahydrogen bubbling. Assuming the thermodynamic chemical equilibrium in Scheme 1, the formal kinetic equations describing this process can be read as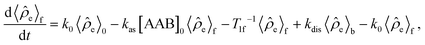 | (3) |
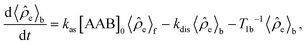 | (4) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e〉0 is the rate of
e〉0 is the rate of ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e supply induced by parahydrogen bubbling through AAB solutions, whereas T1f and T1b are the relaxation times of this spin order in the forms of free H2 and bound H2 in AAB-H2, respectively. To a good approximation, the relaxation in the free form can be neglected since it is much slower as compared to that in the bound form. If the lifetime of AAB-H2 species is comparable with T1b, the relaxation will significantly decrease 〈
e supply induced by parahydrogen bubbling through AAB solutions, whereas T1f and T1b are the relaxation times of this spin order in the forms of free H2 and bound H2 in AAB-H2, respectively. To a good approximation, the relaxation in the free form can be neglected since it is much slower as compared to that in the bound form. If the lifetime of AAB-H2 species is comparable with T1b, the relaxation will significantly decrease 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e〉b. At the same time, if the association of AAB and parahydrogen defined by kas[AAB]0 is fast, then the fast relaxation in the bound form will also noticeably destroy 〈
e〉b. At the same time, if the association of AAB and parahydrogen defined by kas[AAB]0 is fast, then the fast relaxation in the bound form will also noticeably destroy 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e〉f – the non-equilibrium spin order in the free species. Generally, kinetics and relaxation have a complex influence on the amplitude of generated 〈
e〉f – the non-equilibrium spin order in the free species. Generally, kinetics and relaxation have a complex influence on the amplitude of generated 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e〉b and 〈
e〉b and 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e〉f. For instance, after a long enough time of parahydrogen bubbling through AAB solutions, a stationary state will be reached in which, according to eqn (3) and (4), theoretically achieved fractions of
e〉f. For instance, after a long enough time of parahydrogen bubbling through AAB solutions, a stationary state will be reached in which, according to eqn (3) and (4), theoretically achieved fractions of ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e in H2 (εf) and AAB-H2 (εb) pools have the following functional dependencies, respectively,
e in H2 (εf) and AAB-H2 (εb) pools have the following functional dependencies, respectively,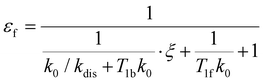 | (5) |
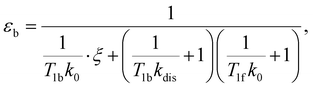 | (6) |
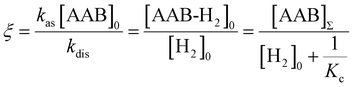 | (7) |
The time evolution before reaching the stationary state and after interruption of parahydrogen bubbling is a complex process reflecting the interplay between mass transport of parahydrogen, the kinetics and thermodynamics of H2 activation, and the relaxation processes leading to the decay of the non-equilibrium nuclear spin order. It is difficult to find simple analytical expressions describing these transient processes. The numerical solutions presented in Fig. 5 illustrate the basic features of accumulation and decay of the longitudinal two spin order (![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e, eqn (2)) for PhCAT and MesCAT in toluene based on the corresponding experimental kinetic and thermodynamic parameters from Table 1. The stationary state for
e, eqn (2)) for PhCAT and MesCAT in toluene based on the corresponding experimental kinetic and thermodynamic parameters from Table 1. The stationary state for ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e is reached after ca. 2 and 10 s for PhCAT (Fig. 5a) and MesCAT (Fig. 5b), respectively. The concentration normalized amplitudes (
e is reached after ca. 2 and 10 s for PhCAT (Fig. 5a) and MesCAT (Fig. 5b), respectively. The concentration normalized amplitudes (![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e/[C]), however, differ by an order of magnitude, indicating much weaker stationary hyperpolarization in the case of PhCAT. This state is preserved for both H2 and AAB-H2 pools until the moment when the parahydrogen supply is stopped at t = 25 s. After this point, the accumulated non-equilibrium order starts to decay to zero, thus it is important to apply the read π/4-pulse and detect the signal as soon as possible after parahydrogen supply (e.g., bubbling) is stopped. Importantly, in the case of PhCAT, this decay is very fast, leading to 95% of the spin order drop after 1 s (Fig. 5a). Both the low stationary level and fast decay of the spin order result in the absence of hyperpolarization effects for PhCAT in toluene (Fig. 4e). In contrast, the situation is significantly more favorable in the case of MesCAT (Fig. 5b), since both the higher stationary spin order amplitude and the relatively slow decay should result in strong hyperpolarization effects observed experimentally (Fig. 4a).
e/[C]), however, differ by an order of magnitude, indicating much weaker stationary hyperpolarization in the case of PhCAT. This state is preserved for both H2 and AAB-H2 pools until the moment when the parahydrogen supply is stopped at t = 25 s. After this point, the accumulated non-equilibrium order starts to decay to zero, thus it is important to apply the read π/4-pulse and detect the signal as soon as possible after parahydrogen supply (e.g., bubbling) is stopped. Importantly, in the case of PhCAT, this decay is very fast, leading to 95% of the spin order drop after 1 s (Fig. 5a). Both the low stationary level and fast decay of the spin order result in the absence of hyperpolarization effects for PhCAT in toluene (Fig. 4e). In contrast, the situation is significantly more favorable in the case of MesCAT (Fig. 5b), since both the higher stationary spin order amplitude and the relatively slow decay should result in strong hyperpolarization effects observed experimentally (Fig. 4a).
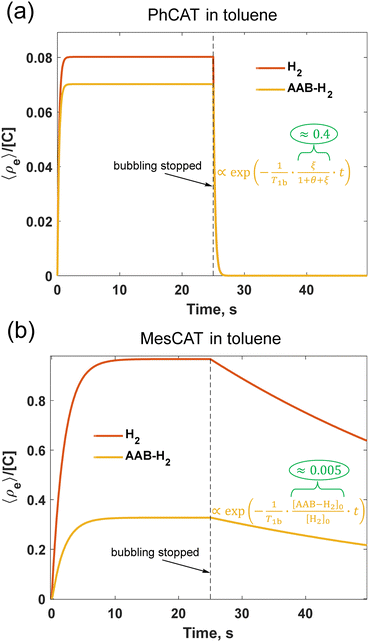 | ||
| Fig. 5 Dynamics of the longitudinal nuclear spin order in 0.05 M solutions of PhCAT (a) and MesCAT (b) at 298 K in toluene-d8 according to the kinetic model described by eqn (3) and (4) with experimentally measured reaction rate parameters of Table 1. The first half of the graphs illustrates accumulation (“pumping”) of the spin order during the parahydrogen bubbling, and the second half correspond to the decay of the order after the parahydrogen supply was stopped (see ESI,† for details of the modelling; θ = 1/kdisT1b). | ||
It is worth noting that this discussion primarily concerns the AAB-H2 pool since the hyperpolarization is revealed when the parahydrogen-originating protons are inequivalent (AX spin system). Indeed, the accumulated longitudinal two-spin order in the free H2 hydrogen pool, 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e〉f, to a first approximation, is not observable by π/4-pulse pulse method in the same way as for AAB-H2, since the antiphase transverse magnetization does not evolve into its observable in-phase counterpart due to the equality of the observed Larmor frequencies of nuclei, i.e., strong coupling. If the frequencies are equal, the density operator derived from Î1xÎ2z + Î1zÎ2x always commutes with the scalar term in the spin Hamiltonian during the time evolution. However, some subtle effects, such as the partially negative line (PNL) effect for orthohydrogen, can reveal specific manifestations of the generated non-equilibrium order.4,35 Effectively, this happens due to the fact that chemical exchange can slightly alter the observed resonance frequencies, breaking the symmetry of the isotropic spin Hamiltonian. In addition, cross-correlated relaxation can transform the longitudinal two-spin order of
e〉f, to a first approximation, is not observable by π/4-pulse pulse method in the same way as for AAB-H2, since the antiphase transverse magnetization does not evolve into its observable in-phase counterpart due to the equality of the observed Larmor frequencies of nuclei, i.e., strong coupling. If the frequencies are equal, the density operator derived from Î1xÎ2z + Î1zÎ2x always commutes with the scalar term in the spin Hamiltonian during the time evolution. However, some subtle effects, such as the partially negative line (PNL) effect for orthohydrogen, can reveal specific manifestations of the generated non-equilibrium order.4,35 Effectively, this happens due to the fact that chemical exchange can slightly alter the observed resonance frequencies, breaking the symmetry of the isotropic spin Hamiltonian. In addition, cross-correlated relaxation can transform the longitudinal two-spin order of ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) e into single spin longitudinal magnetization in some cases, which leads to the enhanced in-phase negative magnetization of orthohydrogen (see, for instance, Fig. 1a).4–7 Both of these effects are observable in experiments with ansa-aminoboranes, but they are typically minor, and their description is much more complicated to analyze precisely. Therefore, we focus on the antiphase magnetization in AAB-H2, the major hyperpolarization effect, to characterize different ansa-aminoboranes in different solvents.
e into single spin longitudinal magnetization in some cases, which leads to the enhanced in-phase negative magnetization of orthohydrogen (see, for instance, Fig. 1a).4–7 Both of these effects are observable in experiments with ansa-aminoboranes, but they are typically minor, and their description is much more complicated to analyze precisely. Therefore, we focus on the antiphase magnetization in AAB-H2, the major hyperpolarization effect, to characterize different ansa-aminoboranes in different solvents.
Based on the known experimental kinetic and relaxation parameters (Table 1), we can model the response of the nuclear spin order buildup on an alternation of experimental conditions to optimize the observed hyperpolarization signals. For instance, the absence of hyperpolarization in the case of the 0.05 M solution of PhCAT in toluene is probably the clearest example of suboptimal conditions for the hyperpolarization. In spite of the fact that the kinetics of the reaction is fast in both directions, the enhanced signals were not observed since the nuclear spin relaxation effectively destroys the hyperpolarization due to the rapid formation of a large rapidly relaxing PhCAT-H2 pool. This makes a clear difference with MesCAT, for which the MesCAT-H2 pool is two orders of magnitude smaller than the slowly relaxing H2 pool (see [AAB-H2]0/[H2]0 ratios in Table 1). This implies that the size variation of these pools can influence the observed polarization level. Note that eqn (6) explicitly includes concentration factor (eqn (7)) dependence, which we can vary in experiments.
Indeed, when we used a diluted sample with a decreased concentration of PhCAT by 50 times in toluene while keeping the other parameters and the parahydrogen pressure at the same level, strong hyperpolarization was detected (Fig. 6). From the no enhancement, the dilution led to a 100-fold amplification of the parahydrogen-originating protons in PhCAT-H2 (see antiphase NH and BH signals). Of course, one needs to keep in mind that this was done at the price of decreased amplitudes of the thermal signals, but this can be beneficial in certain situations, for instance, when it is not preferable to use concentrated samples. Overall, this experiment demonstrated that knowledge of the reaction kinetics and mechanism can provide freedom in selecting one or another ansa-aminoborane for PHIP experiments.
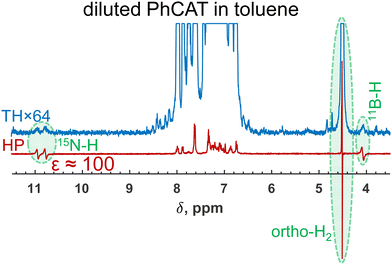 | ||
| Fig. 6 1H NMR spectra measured after parahydrogen bubbling through a 0.001 M solution of PhCAT that demonstrate the observation of strongly enhanced antiphase doublets of the parahydrogen-originating protons of PhCAT-H2. Note that the 50 times more concentrated solution did not result in any hyperpolarization effects (see Fig. 2e), clearly illustrating the influence of the concentration factor. Additionally, a partially negative line effect is observed for the orthohydrogen resonance. | ||
4. Conclusions
Ansa-aminoboranes can provide interesting capabilities for the activation of molecular hydrogen and, generally, for hydrogenation catalysis without metals. Characterization of the mechanistic details of the activation can be very helpful in designing highly efficient metal-free catalysts. In this study, we consider this process on both macroscopic and microscopic levels. Utilizing these data, we rationalize experimental observations of nuclear spin hyperpolarization effects in different solvents when parahydrogen was used as H2 feedstock. We show that the presented vast amount of experimentally measured kinetic and thermodynamic parameters for MesCAT, iPrPhCAT, and PhCATansa-aminoboranes can be employed to find optimal conditions for the observation of strong spin hyperpolarization. The discussed microscopic picture of the activation process shows the active dynamics around the FLP centers, such as inversion of the TMP ring and rotation of the boryl site. Nevertheless, our DFT calculations reveal that the most stable forms of H2 adducts are those where the two hydrogen atoms are in close proximity to each other, which is attributed to the stabilization effect of dihydrogen bonding. Moreover, it is shown experimentally and computationally that the polarity of the solvent is an important factor that shifts the chemical equilibrium towards the formation of H2 adducts and decreases the adduct dissociation rate. It is demonstrated that the computed thermochemical parameters match the experimentally measured ones to a good accuracy level, opening an avenue for extensive modelling of molecular metal-free catalysts for parahydrogen-induced polarization studies. Altogether, this gives a solid foundation for further rational design of efficient metal-free catalytic systems for NMR sensitivity enhancement and NMR sensing applications based on ansa-aminoboranes.Author contributions
K. K.: investigation, validation, writing – review and editing; G. L.: investigation, validation, visualization, writing – review and editing; I. P.: conceptualization, funding acquisition, resources, supervision, validation, writing – review and editing; V. V. Z.: conceptualization, funding acquisition, resources, supervision, validation, visualization, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for the support of this work by the Academy of Finland (grant no. 323480) and the University of Oulu (Kvantum Institute). Financial support from the National Research, Development, and Innovation Office (NKFIH) is gratefully acknowledged (grant K-142486). We thank Dr Konstantin Chernichenko, Dr Kristina Sorochkina and Prof. Timo Repo from the University of Helsinki for their assistance with the synthesis of ansa-aminoborane samples for the experiments. V. V. Z. wishes to acknowledge CSC – IT Center for Science, Finland, for computational resources (CSC project 2004016).Notes and references
- J. Lam, K. M. Szkop, E. Mosaferi and D. W. Stephan, Chem. Soc. Rev., 2019, 48, 3592–3612 RSC.
- A. R. Jupp and D. W. Stephan, Trends Chem., 2019, 1, 35–48 CrossRef CAS.
- V. V. Zhivonitko, V.-V. Telkki, K. Chernichenko, T. Repo, M. Leskelä, V. Sumerin and I. V. Koptyug, J. Am. Chem. Soc., 2014, 136, 598–601 CrossRef CAS PubMed.
- V. V. Zhivonitko, K. Sorochkina, K. Chernichenko, B. Kotai, T. Földes, I. Pápai, V.-V. Telkki, T. Repo and I. Koptyug, Phys. Chem. Chem. Phys., 2016, 18, 27784–27795 RSC.
- K. Sorochkina, V. V. Zhivonitko, K. Chernichenko, V. V. Telkki, T. Repo and I. V. Koptyug, J. Phys. Chem. Lett., 2018, 9, 903–907 CrossRef CAS PubMed.
- D. O. Zakharov, K. Chernichenko, K. Sorochkina, S. Yang, V. V. Telkki, T. Repo and V. V. Zhivonitko, Chem. – Eur. J., 2022, 28, e202103501 CrossRef CAS PubMed.
- D. O. Zakharov, K. Chernichenko, K. Sorochkina, T. Repo and V. V. Zhivonitko, Dalton Trans., 2022, 51, 13606–13611 RSC.
- B. J. Tickner and V. V. Zhivonitko, Chem. Sci., 2022, 13, 4670–4696 RSC.
- L. E. Longobardi, C. A. Russell, M. Green, N. S. Townsend, K. Wang, A. J. Holmes, S. B. Duckett, J. E. McGrady and D. W. Stephan, J. Am. Chem. Soc., 2014, 136, 13453–13457 CrossRef CAS PubMed.
- V. V. Zhivonitko, J. Bresien, A. Schulz and I. V. Koptyug, Phys. Chem. Chem. Phys., 2019, 21, 5890–5893 RSC.
- V. V. Zhivonitko, H. Beer, D. O. Zakharov, J. Bresien and A. Schulz, ChemPhysChem, 2021, 22, 813–817 CrossRef CAS PubMed.
- E. Zander, J. Bresien, V. V. Zhivonitko, J. Fessler, A. Villinger, D. Michalik and A. Schulz, J. Am. Chem. Soc., 2023, 145, 14484–14497 CrossRef CAS PubMed.
- C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645–2648 CrossRef CAS PubMed.
- C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542 CrossRef CAS.
- S. B. Duckett and N. J. Wood, Coord. Chem. Rev., 2008, 252, 2278–2291 CrossRef CAS.
- B. Procacci, P. M. Aguiar, M. E. Halse, R. N. Perutz and S. B. Duckett, Chem. Sci., 2016, 7, 7087–7093 RSC.
- R. Giernoth, P. Huebler and J. Bargon, Angew. Chem., Int. Ed., 1998, 37, 2473–2475 CrossRef CAS PubMed.
- S. Aime, W. Dastru, R. Gobetto, F. Reineri, A. Russo and A. Viale, Organometallics, 2001, 20, 2924–2927 CrossRef CAS.
- C. J. Sleigh, S. B. Duckett and B. A. Messerle, Chem. Commun., 1996, 2395–2396 RSC.
- S. B. Duckett, in Encyclopedia of Spectroscopy and Spectrometry, ed. J. C. Lindon, G. E. Tranter and D. W. Koppenaal, Elsevier, 3rd edn, 2016, pp. 527–534 DOI:10.1016/B978-0-12-409547-2.12126-2.
- K. V. Kovtunov, O. G. Salnikov, V. V. Zhivonitko, I. V. Skovpin, V. I. Bukhtiyarov and I. V. Koptyug, Top. Catal., 2016, 59, 1686–1699 CrossRef CAS.
- K. V. Kovtunov, V. V. Zhivonitko, I. V. Skovpin, D. A. Barskiy and I. V. Koptyug, Top. Curr. Chem., 2013, 338, 123–180, DOI:10.1007/128_2012_371.
- R. L. Jarek, R. J. Flesher and S. K. Shin, J. Chem. Educ., 1997, 74, 978 CrossRef CAS.
- M. Montag, J. Zhang and D. Milstein, J. Am. Chem. Soc., 2012, 134, 10325–10328 CrossRef CAS PubMed.
- W. G. Wang, T. B. Rauchfuss, L. Y. Zhu and G. Zampella, J. Am. Chem. Soc., 2014, 136, 5773–5782 CrossRef CAS PubMed.
- P. W. Atkins and J. De Paula, in Physical chemistry, W. H. Freeman, Oxford University Press, Peter Atkins, Julio de Paula, New York, Oxford, 9th edn, 2010 Search PubMed.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. E.01, Wallingford CT, 2016 Search PubMed.
- T. A. Rokob, I. Bako, A. Stirling, A. Hamza and I. Pápai, J. Am. Chem. Soc., 2013, 135, 4425–4437 CrossRef CAS PubMed.
- C. R. Bowers, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, Wiley, Chichester, 2002, vol. 9, pp. 750–769 Search PubMed.
- J. Natterer and J. Bargon, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 293–315 CrossRef.
- A. S. Kiryutin, G. Sauer, A. V. Yurkovskaya, H. H. Limbach, K. L. Ivanov and G. Buntkowsky, J. Phys. Chem. C, 2017, 121, 9879–9888 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Description of experiments; theory and computations; animation of H2 activation. See DOI: https://doi.org/10.1039/d3cp05816f |
| ‡ Both authors contributed equally to this manuscript. |
| This journal is © the Owner Societies 2024 |