Wolfium bonds in homodimers of MX₄Y (M = Mo, W; X = F, Cl, Br; Y = O, S, Se)

Abstract

The term “wolfium bond” has been recently introduced to describe the noncovalent attraction between an atom of group 6 and a nucleophile via a σ-hole binding site. Crystal structures commonly contain a motif wherein two MX₄Y units are arranged in close proximity, where M represents either Mo or W, and X and Y refer to halogen and chalcogen atoms respectively. DFT calculations were thus applied to a wide range of homodimers of these molecules so as to assess their preferred arrangements, and to characterize the types of bonding that are present in each in a systematic manner. The most stable Dual-X configuration is symmetric and contains a pair of equivalent M⋯X bonds. The interaction energies range from −8 to −29 kcal mol⁻¹, and are largest for X = F, Y = O, and M = W. The X electron donor is replaced by Y, and the two wolfium bonds are reduced to one, in the less stable Mono-Y structure, with interaction energies between −2 and −10 kcal mol⁻¹. There is some question as to whether the weaker bonds of this type constitute true wolfium bonds.

---

Introduction

Our understanding of noncovalent interactions is in a state of continual renewal, fostered by studies over the last few years. Some examples of interactions that have received renewed attention of late are halogen and chalcogen bonds, both of which have been the beneficiaries of official IUPAC recognition and definition^1,2 Politzer and coworkers began a systematic understanding of these and related bonds^3–8via the σ-hole concept. Within the context of the halogen bond, a σ-hole represents a small region of charge depletion and positive electrostatic potential located along the extension of the RX (X = halogen) covalent bond.^9–11 Despite the overall negative charge on X, this polar hole can interact with a nucleophile in much the same way as the overall positive charge on the H atom within an H-bond. This same idea has been extended to a wide range of closely related atoms: chalcogens,¹² pnicogens,¹³ tetrels,¹⁴ triels^15,16 and so forth. And each ensuing bond is categorized under the rubric of the family of the bridging atom.

Continuing research has demonstrated a number of principles guiding the strengths of this set of bonds. For example, the obvious electrostatic or Coulombic attraction involving the σ-hole is supplemented by charge transfer, polarization, and dispersion.^17–22 A major addition arises from the charge that is transferred from the nucleophile to the antibonding σ*(RX) orbital of the Lewis acid. It is not always possible to treat the σ-hole as connected to a single atom, but may be due to the distribution of the electron density throughout the entire molecule.²³ For example, a number of molecules contain a so-called π-hole where the positive region lies usually above the molecular plane. As an intriguing side-issue, the potential of the σ-hole does not have to be positive per se, so long as it is less negative than its surroundings.²⁴

Ongoing research has led to further extension of these ideas to bridging atoms that are not main-group elements. A diverse group of the transition metals can play a very similar role. Such bonding interactions have acquired tentative names such as regium (group 11),^25–29 spodium (group 12),^30–34 matere (group 7)^35–37 and osme (group 8)^38–40 bonds. As an example, the regium bond has been documented in the metal–DNA complexes, involving Cu(II), Ag(I), Au(I) and Au(III).²⁹ Among the spodium bonds, both H-bonds and π-stacking interactions were observed as supplements in the solid state structure of Zn(II) with tetradentate secondary diamine ligands.⁴¹ The properties of interactions in this co-crystal were evaluated by X-ray diffraction analysis and DFT calculations. The matere bond has been described within the framework of crystallographic and theoretical evidence. Combined CSD (Cambridge Structure Database) and DFT work noted that Tc⋯nucleophile contacts are present in a variety of configurations as di-matere bonds, Lewis acid–Lewis base complexes (Tc⋯S, Tc⋯O, Tc⋯Cl interactions), anion–Lewis base (Tc⋯N) systems, anion–cation (Tc⋯S) or even anion–anion interactions (Tc⋯N).³⁵ The influence of the latter was confirmed in other work where self-assembling architectures based on matere bonds were examined.³⁶

To add to this growing array of transition metal bridging atoms, the newly christened wolfium bond⁴² was originally grounded in protein–ligand complexes with Mo or W atoms wherein molecular electrostatic potential (MEP) analysis confirmed a σ-hole on the metal atoms. In order to augment their observations within protein systems, the authors carried out calculations on a series of dimers pairing MF₂O and MF₄O (M = Mo, W) with electron rich species CO, NCH, OCN⁻ and SCN⁻. However, to this point the study of the wolfium bond remains rather sparse in comparison with the variety of other noncovalent bonds.

Our Cambridge Structural Database (CSD) survey identified five structures^43–46 that pointed toward the possible presence of a wolfium bond between neutral molecules, in addition to a more numerous sample involving the Mo(V) oxidation state within the context of (MoCl₄L)⁻ where L = O, S, Se (see below for more details). Given the tendency in the literature for molecules of this type to aggregate with one another within a crystal environment, and the presence of both electrophilic and nucleophilic sites, it was thought important to examine the mode and strength of interaction between them. For this purpose, a set of MX₄Y molecules was constructed which covers a wide range of metal and substituents, with Mo and W both being considered for the central metal atom M, X halogens include F, Cl, and Br, and the chalcogen atoms Y cover O, S, and Se, for a total of 18 different molecules. For each pair of molecules placed together in a homodimer, the potential energy surface was extensively searched for all minima via DFT calculations. The bonding present within each complex was dissected through a combination of various means of quantum chemical analysis, so as to better understand the nature of this newly uncovered form of noncovalent bond.

Computational details

Quantum chemical calculations were carried out using the Gaussian 16 (revision C.01)⁴⁷ set of codes. The M06-2X functional⁴⁸ was applied along with the def2-TZVPP^49,50 basis set. It has been repeatedly shown that this functional is among the most accurate for interactions like those of interest here.^51–58 Optimized geometries were verified as true minima by the absence of any imaginary vibrational frequencies. The energy of interaction E_int is defined in eqn (1) as the difference between the total energy of the two subunits in the geometry that they adopt within the AB complex and the energy of the full complex. Binding energies E_b were computed in a similar way in eqn (2) but refer to the fully optimized monomers. E_int and E_b were corrected for basis set superposition error (BSSE) by the counterpoise procedure.⁵⁹

E_int = E(AB) − {E(A_comp) + E(B_comp)} (1)

E_b = E(AB) − {E(A_mon) + E(B_mon)} (2)

The Multiwfn program⁶⁰ was used to establish the position and magnitude of the extrema of the molecular electrostatic potential (MEP) on the ρ = 0.001 a.u. isosurface of electron density⁶¹ and for reduced density gradient (RDG) analysis⁶² as well as to perform NCI (non-covalent index) analysis. The electron density topology, including bond paths and associated bond critical points (BCPs) was evaluated by the Quantum Theory of Atoms in Molecules (QTAIM) protocol⁶³ using the AIMAll program.⁶⁴ Interorbital charge transfer was assessed by the natural bond orbital (NBO) procedure^65,66 using NBO 7 software.⁶⁷ Symmetry adapted perturbation theory (SAPT0)⁶⁸ was performed at the MP2/6-31G*⁶⁹ level of theory, applying the ASVP basis set⁷⁰ for the Mo and W atoms, to decompose the total interaction energies via the Molpro 2022.2.3^71–73 program. The Cambridge Structural Database (CSD) survey^74–76 was performed using the ConQuest suite of programs.⁷⁶ Structures were visualized via the VMD and Chemcraft programs.^77,78

Results

Monomers

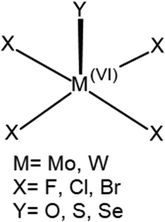
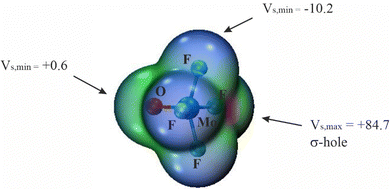
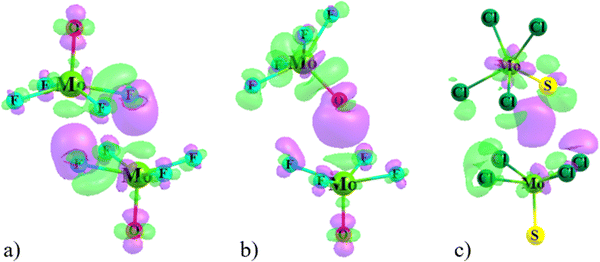
The overall geometry of each of the MX₄Y monomers (M = Mo, W; X = F, Cl, Br; Y = O, S, Se) with C_4v symmetry is indicated in Scheme 1. The square pyramidal shape places a chalcogen Y atom at the apex, and a halogen X atom at each of the four leg positions. Elucidation of the three-dimensional molecular electrostatic potential (MEP) surrounding this molecule provide clues as to the preferred orientations of the two units with respect to one another. As visualized in Fig. 1, there is a single, narrow positive σ-hole lying directly along the extension of the MY (C₄ axis) axis and four equivalent local minima situated near each of the X atoms; some of the monomers contain additional minima near the Y atom.

Scheme 1 Schematic representation of studied monomers with C_4v symmetry.

Fig. 1 MEPs of MoF₄O monomer on an 0.001 a.u. of electron density. The σ-hole maximum and negative extrema positions are indicated by arrows. In the case of minima, only one out of the four equivalent minima at F atoms are indicated. Numbers in kcal mol⁻¹. MEP coloring: from blue (negative) to red (positive).

The values of the MEP extrema on a 0.001 a.u. isodensity surface are gathered in Table 1 as V_s,max and V_s,min. The V_s,max quantities that characterize the σ-hole on M diminish along with a lowering electronegativity of X = F > Cl > Br, and the same is true for the opposite Y atom σ-hole O > S > Se. The transition from Mo to W also yields a modest 5–8 kcal mol⁻¹ enlargement of V_s,max. Of the molecules considered here it is WF₄O that contains the deepest σ-hole with V_s,max equal to 89 kcal mol⁻¹, and the shallowest at 23 kcal mol⁻¹ is that of MoBr₄Se. The minima of the MEP on the X atoms are of considerably smaller magnitude, in the range between −2 and −15 kcal mol⁻¹. The minima on F are the most negative, and this quantity enlarges (absolute value) as Y is made less electronegative. Only 6 of the 18 monomers contain a secondary minimum, and these are only on the O atoms. Earlier calculations by Bauzá and Frontera⁴² found similar MEP extrema for MoF₄O and WF₄O molecules.

Table 1 Maxima and minima on 0.001 a.u. isodensV_s,max and V_s,min values for optimized MX₄Y on 0.001 a.u. isodensity surface. Data in kcal mol⁻¹

Monomer	V s,max	V s,min	V s,min on Y atom
MoF4O	84.7	−10.2	0.6
MoCl4O	45.5	−2.2	−0.7
MoBr4O	37.6	−2.1	−2.0
MoF4S	62.6	−14.6	—
MoCl4S	32.0	−7.5	—
MoBr4S	25.9	−6.7	—
MoF4Se	58.1	−15.2	—
MoCl4Se	28.9	−8.4	—
MoBr4Se	23.1	−7.6	—
WF4O	89.3	−8.8	−6.9
WCl4O	54.3	−6.8	−6.8
WBr4O	45.2	−7.5	−7.5
WF4S	68.7	−12.0	—
WCl4S	39.8	−5.6	—
WBr4S	32.6	−5.4	—
WF4Se	64.0	−12.3	—
WCl4Se	36.4	−6.3	—
WBr4Se	29.6	−6.0	—

---

Dimers

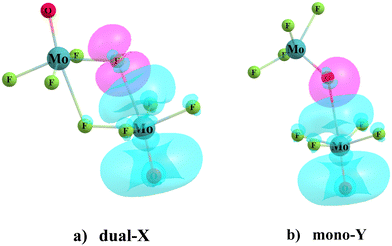
Geometry optimizations of the homodimers from a variety of different starting points yielded as many as four different minima on the potential energy surface. The two configurations that were identified for all dimers, and were the most stable, are displayed in Fig. 2 for the MoF₄O dimer, along with a definition of the geometrical parameters of interest. The Dual-X shape in Fig. 2(a) contains a pair of equivalent O–Mo⋯F wolfium bonds with the two equivalent M⋯X distances defined as R. This sort of arrangement is sometimes referred to in the literature as “square” although its true shape more closely resembles a parallelogram. The F atom lies close to the O–Mo bond extension as indicated by F–Mo–O angle θ_a. The other angle θ_b(MoF⋯Mo) refers to the relative orientation around the F. The mono-Y configuration arises when the electron donor atom is switched from F to O, as illustrated in Fig. 2(b), and contains a single wolfium bond.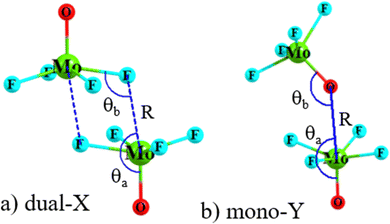

Fig. 2 Geometry of (a) dual-X and (b) mono-Y conformers of MoF₄O homodimers, with definitions of selected geometrical parameters (numeric values of the geometrical parameters are defined in Table 2).

The intermolecular geometries for these two configurations are summarized in Table 2 for all of the homodimers. Considering first the M⋯X distances in the first two columns, these values of course rise as the X atom enlarges from F to Cl to Br. For any given X atom, there is a progressive lengthening of distance as the Y atom becomes less electronegative in the O < S < Se order. This pattern is sensible in the reduced depth of the σ-hole on the M with which the X is interacting. The change from Mo to W has only a small and erratic effect on this distance R. The R(M⋯Y) distances in the mono-Y structures of course elongate as the Y atom grows larger. It is shortest for X = F, consistent again with deeper σ-holes for these monomers.

Table 2 Selected geometrical parameters of homodimers defined in Fig. 2. Distances in Å, angles in degs

	R		R N		θ a		θ b
	Dual-X	Mono-Y	Dual-X	Mono-Y	Dual-X	Mono-Y	Dual-X	Mono-Y
a R divided by sum of atomic van der Waals (vdW) radii of respective atoms.
(MoF4O)2	2.365	2.645	0.605	0.670	170.6	177.0	110.5	137.2
(MoCl4O)2	3.144	2.812	0.736	0.712	177.6	179.2	103.6	148.6
(MoBr4O)2	3.405	2.767	0.790	0.701	178.5	179.5	102.6	155.8
(MoF4S)2	2.445	3.405	0.625	0.785	171.1	177.5	110.8	104.0
(MoCl4S)2	3.318	3.817	0.777	0.879	178.8	166.6	103.9	107.0
(MoBr4S)2	3.590	3.823	0.833	0.881	179.8	167.8	102.9	113.9
(MoF4Se)2	2.477	3.522	0.633	0.825	171.3	176.3	110.9	100.0
(MoCl4Se)2	3.359	3.888	0.787	0.911	179.1	166.0	103.8	103.8
(MoBr4Se)2	3.629	3.788	0.842	0.887	179.9	174.3	103.0	113.4
(WF4O)2	2.359	2.535	0.585	0.623	170.0	177.3	111.1	139.4
(WCl4O)2	3.118	2.661	0.710	0.654	177.3	179.1	103.5	151.9
(WBr4O)2	3.375	2.569	0.762	0.631	178.3	179.6	102.4	162.5
(WF4S)2	2.450	3.375	0.608	0.757	171.0	178.5	111.6	103.9
(WCl4S)2	3.342	3.694	0.761	0.828	178.7	175.1	104.3	116.7
(WBr4S)2	3.603	3.711	0.813	0.832	179.7	175.6	103.1	122.4
(WF4Se)2	2.487	3.506	0.617	0.799	171.3	178.0	111.7	99.3
(WCl4Se)2	3.389	3.806	0.772	0.867	179.0	175.0	104.2	112.6
(WBr4Se)2	3.643	3.830	0.822	0.872	180.0	175.3	103.1	117.9

---

The next two columns report the normalized intermolecular distance R_N whereby each R is divided by the sum of the van der Waals radii of the two atoms involved.⁷⁹ It is first apparent that these normalized contact distances are all substantially less than unity, signifying a real noncovalent attractive force, i.e. a wolfium bond. Like their non-normalized correlates, R_N rises for the Dual-X dimers as the X atoms grows larger, reinforcing the idea of a weakened interaction. This same lengthening of intermolecular distance occurs for the Mono-Y structures as X grows larger, albeit to a lesser degree. The enlargement of the Y atom has a pronounced lengthening effect on R_N for the Mono-Y structures, clear evidence of a weakening wolfium bond. The normalized distances are shorter for W as compared to Mo, an indirect sign of a stronger bond.

The θ_a angles of the Dual-X configurations are all within 10° of 180°, particularly so for X = Cl and Br. Although also nearly linear, these same angles are a bit more erratic for the Mono-Y structures, with some values less than 170°. The θ_b angles which describe the orientation around the X atom in the Dual-X geometries tend toward 111° for X = F and are somewhat smaller, around 103° for the two larger X atoms. These same θ_a angles describe the M–Y⋯M orientation for Mono-Y. There is a significant variation depending upon the X atoms, rising as X enlarges from F to Cl to Br. This angle is most sensitive to the nature of the Y atom, diminishing substantially as the O atom is enlarged to S and Se.

Energetics

The energies of these dimers are reported in Table 3 where the interaction energy refers to the geometries of the monomers within the dimer, whereas the binding energy relates to the fully optimized monomer geometries. These quantities cover a wide range, with E_int varying between −2 and −29 kcal mol⁻¹. These dimer energies exhibit several interesting patterns. In the first place the Dual-X complexes are bound considerably more strongly than are the corresponding Mono-Y configurations. Part of this larger binding energy rests on the presence of two wolfium bonds in Dual-X, which reinforce one another in a cooperative fashion as each monomer acts simultaneously as electron donor and acceptor. The high electron accepting ability of F is apparent in the much larger interaction energies of the Dual-X geometries with X = F, twice as large as for Cl or Br. This stronger interaction is also controlled by the deeper M σ-holes of the monomers containing F (see Table 1). The bonding is also weakened as the Y atom is enlarged from O to S to Se, again consonant with the trends in V_s,max. Also mirroring the σ-hole depths, the interaction energies are slightly larger for W than for Mo.

Table 3 BSSE-corrected interaction E_int and binding E_b energies of homodimers, in kcal mol⁻¹

Homodimer	−Eint		−Eb
	Dual-X	Mono-Y	Dual-X	Mono-Y
(MoF4O)2	26.96	5.65	16.41	4.89
(MoCl4O)2	13.23	5.61	9.68	5.11
(MoBr4O)2	12.31	6.47	9.78	5.76
(MoF4S)2	19.42	2.23	13.01	2.08
(MoCl4S)2	9.15	4.68	7.98	4.40
(MoBr4S)2	9.16	5.80	8.47	5.42
(MoF4Se)2	17.57	2.59	11.99	2.41
(MoCl4Se)2	8.47	5.12	7.57	4.75
(MoBr4Se)2	8.60	5.93	8.08	5.73
(WF4O)2	28.91	9.70	17.72	8.23
(WCl4O)2	14.43	8.25	10.33	7.07
(WBr4O)2	13.32	9.22	10.35	7.58
(WF4S)2	20.16	3.06	13.52	2.85
(WCl4S)2	9.48	4.22	8.25	4.15
(WBr4S)2	9.51	5.03	8.74	4.95
(WF4Se)2	17.95	3.32	12.31	3.08
(WCl4Se)2	8.76	4.57	7.82	4.48
(WBr4Se)2	8.94	5.44	8.35	5.32

---

The energies of the Mono-Y configurations are quite different in a number of respects. These bonds are much weaker, all less than −10 kcal mol⁻¹. There is little sensitivity to the nature of the particular atoms. Enlarging Y, and therefore reducing its electron-accepting capability, appears to reduce the interaction energy, but only slightly. There is a tendency for the interaction energies to rise slightly as X is enlarged, contrary to the pattern observed in Dual-X or in the M σ-holes.

E _b differs from E_int only in the reference of monomer geometries that is used, so their difference is equal to the deformation energy E_def required to distort the optimized monomers into the geometry they adopt within the complex. This quantity is rather small for the Mono-Y configurations but is quite sizable in several Dual-X geometries. Taking the (MoF₄O)₂ dimer as an example, E_def is equal to 10.5 kcal mol⁻¹ for Dual-X but only 0.8 kcal mol⁻¹ for Mono-Y. One can trace this large deformation in the former to two primary factors. First, the Mo–F bond length stretches from 1.830 Å within the optimized monomer to 1.937 Å within the Dual-X homodimer. Secondly, this elongation is coupled with a 4.5° reduction in the internal O–Mo–F angle as the MoF₄O fragment flattens out to a certain extent. The internal distortions within the Mono-Y structure are more modest, the largest of which is a 0.013 Å stretch of the Mo=O bond within the electron acceptor unit.

Analysis of electronic structures

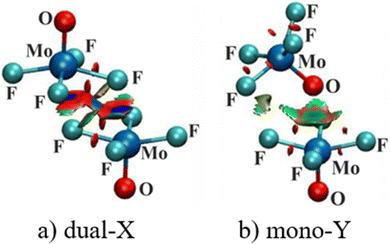
Atoms in molecules (AIM) analysis provides a measure of bond strength derived from the topology of the electron density. The AIM diagrams of the two configurations of (MoF₄O)₂ are displayed in Fig. 3 wherein broken lines indicate bond paths, for which the density at the bond critical point (BCP) is shown explicitly. BCP are such points that are stationary points of the electron density function for which the number of non-zero eigenvalues of the hessian is 3 while the value of the sum of their signs is −1. The primary bond paths concern the two M⋯X bonds for Dual-X and the Mono-Y contain the expected M⋯Y path. Corresponding AIM diagrams of all of the homodimers are contained in Fig. S1 (ESI†), where it may be noted that some of these structures are characterized by supplementary bond paths, although their associated BCP densities are rather small. For example, several of the dimers hint at possible weak X⋯X interactions, but with densities much less than 0.010 a.u. of electron density.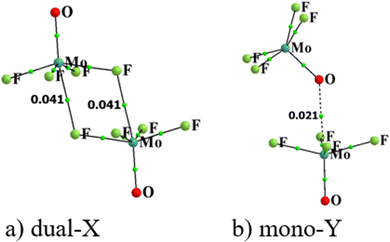

Fig. 3 QTAIM molecular diagrams for (a) dual-X and (b) mono-Y conformers of MoF₄O homodimer. Small green dots represent bond critical points, with their density displayed in a.u.

Various quantities concerning the critical point lying along the principal M⋯X or M⋯O bond paths are listed in Table 4, including its density and the density Laplacian. The ratio between the kinetic (G) and potential (V) energy densities G/V represents another assessment of the character of each bond,⁸⁰ as does the total energy density H. The interdependencies between these parameters have been discussed in a general sense elsewhere.^81–89 As there are two equivalent M⋯X wolfium bonds in the Dual-X geometries, values of electron density (ρ) at the BCP of these two bonds have been summed in the first column so as to provide a more accurate assessment of the interaction energy. Like the σ-hole depths and interaction energies of Dual-X, both ρ and ∇²ρ are largest for the F substituents, and drop down as the Y atom grows from O to S to Se. The densities also mirror the trend of higher values for W than for Mo. Positive density Laplacians are indicative of closed–shell interactions. The G/V ratios hover around unity or slightly higher. The near-zero values of H are indicative of little covalent character in these wolfium bonds. Like the energies, ρ is considerably smaller for the Mono-Y configurations. Indeed not all of the Mono-Y dimers contain a bond path between M and Y. This point is addressed further. As a point of comparison, it might be noted that Bauzá and Frontera⁴² calculated a set of critical point densities in the same range level as observed here for their set of Mo and W σ-hole donors with other bases, such as CO, NCH, OCN, and SCN.

Table 4 QTAIM-derived electron density (ρ), Laplacian of electron density, −G/V ratio and total energy density H measured at BCPs of Mo/W⋯X or M⋯Y bond paths in homodimers. Data in a.u. of electron density

Homodimer	ρ	∇^2ρ	−G/V ratio	H
a Sum of the values of electron density (ρ) at BCP of two M⋯X bonds for Mono-X.
Dual-X
(MoF4O)2	0.082	0.197	0.99	0.000
(MoCl4O)2	0.030	0.049	1.10	0.001
(MoBr4O)2	0.024	0.033	1.05	0.000
(MoF4S)2	0.068	0.161	1.03	0.001
(MoCl4S)2	0.022	0.033	1.10	0.001
(MoBr4S)2	0.018	0.023	1.06	0.000
(MoF4Se)2	0.064	0.150	1.04	0.001
(MoCl4Se)2	0.020	0.031	1.17	0.001
(MoBr4Se)2	0.016	0.021	1.06	0.000
(WF4O)2	0.088	0.194	0.94	−0.003
(WCl4O)2	0.034	0.049	1.00	0.000
(WBr4O)2	0.026	0.034	1.01	0.000
(WF4S)2	0.071	0.156	0.98	−0.001
(WCl4S)2	0.022	0.033	1.11	0.001
(WBr4S)2	0.018	0.023	1.09	0.000
(WF4Se)2	0.066	0.142	1.00	0.000
(WCl4Se)2	0.020	0.030	1.12	0.001
(WBr4Se)2	0.018	0.021	1.09	0.000
Mono-Y
(MoF4O)2	0.021	0.097	1.10	0.002
(MoCl4O)2	0.014	0.067	1.17	0.002
(MoBr4O)2	0.016	0.075	1.19	0.002
(MoF4S)2	0.010	0.026	1.09	0.000
(MoCl4S)2	—	—	—	—
(MoBr4S)2	—	—	—	—
(MoF4Se)2	0.010	0.022	1.04	0.000
(MoCl4Se)2	—	—	—	—
(MoBr4Se)2	—	—	—	—
(WF4O)2	0.030	0.122	0.98	−0.001
(WCl4O)2	0.022	0.094	1.04	0.001
(WBr4O)2	0.028	0.118	1.00	0.000
(WF4S)2	0.011	0.028	1.08	0.000
(WCl4S)2	—	—	—	—
(WBr4S)2	—	—	—	—
(WF4Se)2	0.011	0.024	1.03	0.000
(WCl4Se)2	0.007	0.015	1.13	0.000
(WBr4Se)2	—	—	—	—

---

While AIM analysis provides clues as to which atoms interact with one another, NBO analysis delves into the particular orbitals of the two subunits. The left section of Table 5 lists the donor and acceptor orbitals for the Dual-X configurations. Taking the (MoF₄O)₂ dimer in the first row as an example, the bulk of the transfer extracts density from the lone pairs of the F atom involved in the Mo⋯F bond, with some going into a σ*(Mo–O) antibonding orbital. Another portion of charge is transferred into what NBO designates as an empty orbital with the general shape of a Mo lone pair. The overlap between these two MOs is clear from Fig. 4(a). (In some of the other Dual-X structures, the M antibonding lone pair LP* orbital designation is switched by NBO to a Rydberg orbital.)

Table 5 NBO E⁽²⁾ energies (E⁽²⁾, in kcal mol⁻¹) and overall charge transfer (CT, in me) for homodimers from upper to lower subunit (see Fig. 4)

	Dual-X				Mono-Y
Homodimer	Donor	Acceptor	E ^(2)	CT	Donor	Acceptor	E ^(2)	CT
(MoF4O)2	LP F	LP* Mo	18.94	0.01	LP O	LP* Mo	75.96	51.2
	LP F	BD* Mo–O	16.37		LP O	BD* Mo–O	2.18
(MoCl4O)2	LP Cl	RY* Mo	16.48	0.16	LP O	LP* Mo	11.62	43.2
	LP Cl	BD* Mo–O	12.20		LP O	BD* Mo–O	10.70
(MoBr4O)2	LP Br	RY* Mo	12.99	0.39	LP O	RY* Mo	14.44	46.5
	LP Br	BD* Mo–O	8.14		LP O	BD* Mo–O	14.64
(MoF4S)2	LP F	LP* Mo	27.83	0.02	LP S	LP* Mo	3.17	38.9
	LP F	BD* Mo–S	8.77		LP S	BD* Mo–S	0.15
(MoCl4S)2	LP Cl	RY* Mo	14.90	0.12	LP S	LP* Mo	0.95	4.5
	LP Cl	BD* Mo–S	3.38		LP S	BD* Mo–S	0.12
(MoBr4S)2	LP Br	RY* Mo	7.53	0.16	LP S	LP* Mo	1.46	1.7
	LP Br	BD* Mo–S	2.27		LP S	BD* Mo–S	0.05
(MoF4Se)2	LP F	BD* Mo–F	14.92	0.45	LP Se	LP* Mo	3.19	46.2
	LP F	BD* Mo–Se	4.87		LP Se	BD* Mo–Se	0.20
(MoCl4Se)2	LP Cl	RY* Mo	11.80	0.17	LP Se	LP* Mo	1.17	7.2
	LP Cl	BD* Mo–S	2.23		LP Se	BD* Mo–Se	0.12
(MoBr4Se)2	LP Br	RY* Mo	5.41	0.03	LP Se	RY* Mo	1.14	17.4
	LP Br	BD* Mo–Se	1.40		LP Se	BD* Mo–Se	0.41
(WF4O)2	LP F	LP* W	21.75	0.08	LP O	LP* W	6.17	47.6
	LP F	BD* W–O	9.55		LP O	BD* W–O	9.64
(WCl4O)2	LP Cl	LP* W	17.41	0.03	LP O	LP* W	15.26	58.3
	LP Cl	BD* W–O	16.92		LP O	BD* W–O	15.15
(WBr4O)2	LP Br	RY* W	14.16	0.00	LP O	RY* W	20.70	68.0
	LP Br	BD* W–O	0.14		LP O	BD* W–O	25.68
(WF4S)2	LP F	LP* W	18.69	0.11	LP S	LP* W	8.86	47.5
	LP F	BD* W–S	6.29		LP S	BD* W–S	0.08
(WCl4S)2	LP Cl	RY* W	14.47	0.33	LP S	LP* W	6.38	28.4
	LP Cl	BD* W–S	3.78		LP S	BD* W–S	0.18
(WBr4S)2	LP Br	RY* W	10.59	0.02	LP S	LP* W	7.14	27.0
	LP Br	BD* W–S	3.57		LP S	BD* W–S	0.48
(WF4Se)2	LP F	LP* W	18.35	0.27	LP Se	LP* W	9.11	56.3
	LP F	BD* W–Se	4.69		LP Se	BD* W–Se	0.11
(WCl4Se)2	LP Cl	RY* W	11.70	0.23	LP Se	LP* W	6.76	34.6
	LP Cl	BD* W–Se	2.69		LP Se	BD* W–Se	0.09
(WBr4Se)2	LP Br	RY* W	6.69	0.06	LP Se	LP* W	7.16	32.1
	LP Br	BD* W–Se	2.52		LP Se	BD* W–Se	0.06

---

Fig. 4 Overlaps between orbitals of two interacting subunits in (a) dual-X and (b) mono-Y configurations of MoF₄O homodimer. Red color designates the occupied F or O lone pair (LP) orbital, and the corresponding empty LP*(Mo) orbital of the partner subunit is shown in blue. Isosurfaces refer to ρ = 0.055 a.u. of electron density.

It should be recalled that these two aforementioned transfers in this particular Mo⋯F bond are mirrored by nearly identical charge transfers in the opposite direction pertaining to the second Mo⋯F bond. Consequently, the overall intermolecular charge transfer CT in the final column is vanishingly small. Overall, the patterns of E⁽²⁾ in Table 5 are generally consistent with the binding energetics in Table 3. That is, E⁽²⁾ drops as the X or Y atom grows larger, but rises when Mo is replaced by W.

Turning next to the Mono-Y configurations in the right half of Table 5, the CT originates in both Y atom lone pairs. The overlapping orbitals within this configuration are illustrated in Fig. 4(b). Most of these quantities are substantially smaller than in the Dual-X cases with some interesting exceptions. For instance, there is a particularly large E⁽²⁾ for the (MoF₄O)₂ dimer. Indeed, these quantities tend toward large magnitude for the other MX₄O dimers as well, albeit not quite as large. It is notable that even in those cases where AIM analysis did not indicate a M⋯Y bond path in some of these dimers, the NBO treatment provided evidence of such a wolfium bond. The large sizes of some of these E⁽²⁾ energies are mirrored in the total amount of charge transferred from the upper unit to the lower (as in Fig. 4), as indicated by the CT quantities in Table 5.

The AIM view of the electron density topology can be supplemented by an NCI three-dimensional view of the reduced density gradient. Fig. 5 presents such a plot for the sample (MoF₄O)₂ dimer where blue regions represent strong noncovalent bonding, red indicates repulsion, with green an intermediate weak attraction. The strong Mo⋯F wolfium bonds in Fig. 5(a) are clearly confirmed by the blue regions lying between these two atoms corresponding to the attractive interaction zone. The Mo⋯O bond in the mono-Y structure in Fig. 5(b) is weaker, as evidenced by its green color. The NCI diagrams for all of these homodimers in Fig. S2 (ESI†) confirm the presence of wolfium bonds, even in those cases where there is no AIM bond path.

Fig. 5 NCI molecular diagrams of (a) dual-X and (b) mono-Y configurations of MoF₄O. Blue isosurfaces represent areas of strong noncovalent contacts, while green and red correspond to weaker contacts and repulsions, respectively. RDG isosurface shown is 0.05 a.u. of electron density and blue and red colors refer specifically to −0.03 and +0.03 a.u. of electron density for ρ·sign(λ₂).

Rather than considering charge transfers between individual orbitals, the displacements of electron density caused by the complexation can be viewed in a more global sense. Fig. 6 illustrates this motion by way of the difference in density over all space between the full complex and the sum of the densities of the individual subunits, namely electron density shift produced by the Chemcraft software. The system chosen for illustration is again the (MoF₄O)₂ dimer in a and b where purple regions designate density gain, and loss is indicated in green. Because the shifts are larger in magnitude in the dual-X configuration, the density difference contour applied in Fig. 6(a) is ±0.003 a.u. and that in Fig. 6(b) is ±0.001 a.u. More to the point, the two diagrams present similar shift patterns. In either case, there is a purple region of gain on the F or O atom that serves as electron donor in the wolfium bond, which is enabled by the internal polarizations consisting of green depletions in other segments of the molecule. One may also observe a green density loss directly above the Mo atom along the Mo⋯F/O axis. All of these features are characteristic of the entire family of noncovalent bonds, including H-bonds, halogen bonds and so on.

Fig. 6 Electron density difference maps of (a) dual-X and (b) mono-Y configurations of MoF₄O dimer, and (c) mono-Y of MoCl₄S dimer. Purple and green areas indicate respectively gain or loss of density upon complexation. Contours shown are ±0.003 a.u. of electron density in frame (a), ±0.001 a.u. in (b), and ±0.0004 a.u. in (c).

Fig. 6(c) presents the density shift diagram of the Mono-Y configuration of (MoCl₄S)₂ as an example of a case for which AIM and NBO disagree as to the presence of a Mo⋯S wolfium bond. The magnitudes of the density shifts here are rather small, so the contours shown are ±0.0004 a.u. The pattern is fairly similar to that in Fig. 6(b), in that there is the purple region of density accretion below the S atom of the upper unit (refer to the Fig. 6). On the other hand, there is no green density loss above the lower Mo atom. The polarization patterns in the other segments of the two subunits are generally similar. On balance, then, one might take the similarities between Fig. 6(b) and (c) as confirmation of a wolfium bond in both.

An alternative sort of insight into the nature of the bonding can be gleaned by a partitioning of the total interaction energy into several physically meaningful components. The results of such a SAPT0 energy partitioning are presented in Table 6. The electrostatic component makes up some 40–57% of the total of three attractive elements in the Dual-X dimers. This contribution is largest for the subunits containing F. The electrostatic fraction is lower for Mono-Y, in some cases quite a bit smaller. The fractional dispersion contribution is quite variable, and tends toward higher amounts for the larger X atoms. Induction energy is also rather variable, generally following an opposite trend of diminishing for heavier X. Overall, there is a heavier dispersion contribution for the Mono-Y in comparison to Dual-X. This percentage hovers around 60% for some of the Mono-Y configurations.

Table 6 SAPT0 decomposition of interaction energies and percentage contribution of all attractive terms at the 6-31G*/ASVP level of theory. Labelling of terms: E_ele – electrostatic energy, E_exch – exchange (repulsion), E_ind – induction, E_disp – dispersion, E_tot – total SAPT0 interaction energy. All in kcal mol⁻¹

Dual-X
Dimer	E ele	%	E exch	E ind	%	E disp	%	E tot
(MoF4O)2	−47.31	56	52.92	−25.79	31	−10.93	13	−31.12
(MoCl4O)2	−22.00	48	38.75	−11.67	26	−11.81	26	−6.72
(MoBr4O)2	−20.28	44	37.35	−9.35	20	−16.87	36	−9.15
(MoF4S)2	−37.74	57	43.44	−17.40	27	−10.22	16	−21.91
(MoCl4S)2	−14.48	48	27.36	−5.70	19	−10.09	33	−2.91
(MoBr4S)2	−13.68	41	27.04	−4.55	14	−14.84	45	−6.03
(MoF4Se)2	−34.47	57	40.14	−15.50	26	−10.12	17	−19.95
(MoCl4Se)2	−13.15	47	25.41	−4.84	17	−10.13	36	−2.71
(MoBr4Se)2	−12.58	40	25.40	−3.90	13	−14.60	47	−5.68
(WF4O)2	−51.98	55	56.37	−30.73	33	−11.18	12	−37.51
(WCl4O)2	−23.67	46	41.40	−15.06	29	−12.83	25	−10.16
(WBr4O)2	−21.86	42	39.64	−12.32	24	−17.47	34	−12.01
(WF4S)2	−39.87	57	45.52	−20.00	28	−10.39	15	−24.74
(WCl4S)2	−14.05	45	26.54	−6.52	21	−10.49	34	−4.52
(WBr4S)2	−13.68	40	26.73	−5.32	16	−14.86	44	−7.13
(WF4Se)2	−35.90	57	41.54	−17.35	27	−10.20	16	−21.91
(WCl4Se)2	−12.54	44	24.21	−5.42	19	−10.29	35	−4.03
(WBr4Se)2	−12.64	40	25.17	−4.55	14	−14.62	46	−6.64

---

Mono-Y
Dimer	E ele	%	E exch	E ind	%	E disp	%	E tot
(MoF4O)2	−7.06	38	13.65	−6.08	33	−5.22	28	−4.73
(MoCl4O)2	−7.60	40	16.83	−3.55	19	−7.66	41	−1.98
(MoBr4O)2	−10.04	39	21.74	−4.06	16	−11.72	45	−4.07
(MoF4S)2	−0.36	5	7.74	−2.66	37	−4.22	58	0.50
(MoCl4S)2	−3.49	32	11.91	−0.99	9	−6.48	59	0.95
(MoBr4S)2	−4.85	29	14.46	−1.17	7	−10.43	64	−2.00
(MoF4Se)2	−0.96	11	8.17	−3.00	34	−4.77	55	−0.55
(MoCl4Se)2	−4.46	33	13.38	−1.33	10	−7.68	57	−0.10
(MoBr4Se)2	−4.97	28	14.91	−1.81	12	−11.03	60	−2.91
(WF4O)2	−14.68	46	20.41	−11.06	35	−6.25	20	−11.58
(WCl4O)2	−13.31	45	23.51	−7.37	25	−9.22	31	−6.40
(WBr4O)2	−17.59	43	31.82	−9.56	23	−13.54	34	−8.87
(WF4S)2	−1.99	19	9.45	−3.85	36	−4.73	45	−1.12
(WCl4S)2	−2.44	24	10.15	−1.46	14	−6.27	62	−0.02
(WBr4S)2	−4.02	26	13.22	−1.45	10	−9.79	64	−2.05
(WF4Se)2	−2.54	21	9.90	−4.13	35	−5.20	44	−1.98
(WCl4Se)2	−2.44	24	10.15	−1.46	14	−6.27	62	−0.08
(WBr4Se)2	−4.54	27	13.84	−1.67	10	−10.62	63	−3.01

---

Additional structures

In several cases, the Dual-X and Mono-Y structures are not the only minima present on the potential energy surface of a particular dimer. In some cases, the upper unit in the Mono-Y geometry (see Fig. 2) can bend around so that the MY⋯M arrangement becomes almost linear, which is designated as Lin-Y. A second alternative to the Dual-X changes the mutual orientation so that there is but a single M⋯X bond, termed a Mono-X structure. Both of these possibilities are illustrated in Fig. S3 (ESI†) for the MoF₄O dimer, and the intermolecular distances and interaction energies contained in Table S1 (ESI†).

The Dual-X configuration is universally the most stable for all dimers. Table S2 (ESI†) relates the relative energies of all other possible geometries. In many cases Lin-Y does not represent a true minimum, and converged to the Mono-Y geometry, as indicated in Table S2 (ESI†). In those cases where such a minimum is present, it is slightly higher in energy than Mono-Y. The loss of one of the two M⋯X wolfium bonds destabilizes each dimer by a varying amount, ranging from less than −1 kcal mol⁻¹ to as much as −9 kcal mol⁻¹. As one might expect, the destabilization is roughly proportional to the interaction energy, largest for X = F, Y = O, and M = Mo. The greater strength of the M⋯X versus M⋯Y can be seen in that, in many cases, even the single former bond in the Mono-X is lower in energy than it is in Mono-Y.

Correlations between properties

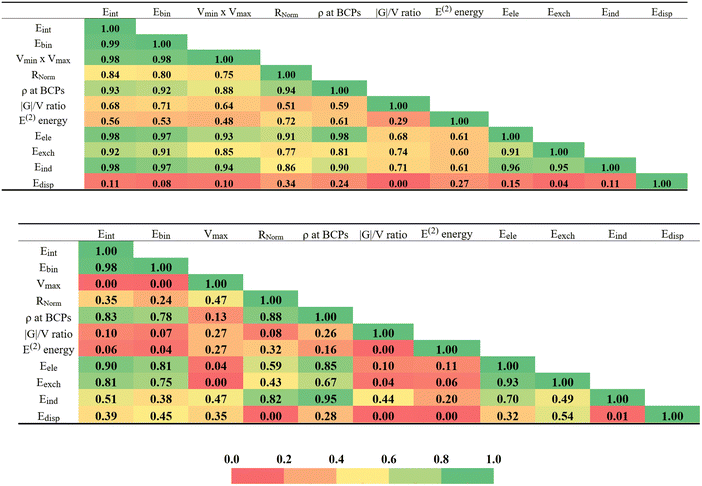
There are a number of different parameters that have been described above. All of them have some relationship with the strength of the interaction within each homodimer. The measure by which they are all correlated with one another is viewed as a color-coded matrix in Fig. 7. The green colors indicate strong correlations, change color to yellow and then to red as the correlation deteriorates, with R² fading from 1.0 to 0.0. The upper diagram refers to the Dual-X configurations where the interaction energy is most closely mirrored by the product of V_max × V_min and the sum of the two bond critical point densities, with respective correlation coefficients of 0.98 and 0.93. Within the context of decomposition components, these are the electrostatic and induction energies that most closely reproduce E_int, both with R² = 0.98. As evidenced by the reddish hue of the lowermost row of Fig. 7, dispersion is a particularly poor indicator of bond strength. It is perhaps surprising that E⁽²⁾ and E_ind, which are both related in some way to charge transfer, correlate with one another only modestly, with R² = 0.61.

Fig. 7 Correlation matrices with correlation coefficients (R²) of selected features obtained for investigated Dual-X (top matrix) and Mono-Y (bottom matrix) homodimers. The strongest NBO E⁽²⁾ energies were taken for this analysis. The E_ele, E_exch, E_ind and E_disp abbreviations represent the electrostatic, exchange, induction and dispersion terms, respectively, derived from the SAPT0 decomposition of the interaction energies.

The lower half of Fig. 7 is concerned with the Mono-Y configurations. In the absence of a V_min on most of the pertinent Y atoms, the V_max × V_min product is replaced with just V_max which correlates much more poorly than does the product for the Dual-X structures. Note however, that the interaction energy does correlate reasonably well with the full E_ele. Although not quite as good as in the Dual-X, the interaction energy of the Mono-Y geometries still correlates fairly well with the AIM BCP density. Overall, the more red hues of the Mono-Y matrix indicate a generally set of poorer correlations for these more weakly held complexes.

Discussion

Some of the findings in this work are consistent with prior results, both computational and experimental. The earlier calculations of Bauzá and Frontera⁴² paired the same Lewis acids (MoF₄O and WF₄O) with a variety of bases and computed interaction energies within an −8 to −46 kcal mol⁻¹ range. These authors also found somewhat stronger binding by W as compared to Mo by some 1 to 5 kcal mol⁻¹. There are no other works in the literature that explicitly treat wolfium bonding interactions.

Regarding elements in adjacent group 7 in the periodic table, neutral matere bonded complexes preferred a bridge configuration similar to Dual-X, with a total interaction energy derived from two Tc⋯Cl contacts of −11.0 kcal mol⁻¹.³⁵ Moving over another group, osme bonds comprising Os⋯Cl interactions lay in the range between −3.3 and −13.8 kcal mol⁻¹.³⁸ Mono Os⋯N/O contacts were observed in OsO₄ adducts with 4,4′-bipyridine and [4,4′-bipyridine]1,1′-dioxide in a recent work by Pizzi et al.³⁹ The complexes stabilized by Os⋯O osme bonds mimic the Mono-Y homodimers presented here. The authors of mentioned work found evidence that these osme interactions contain all the features typical of a σ-hole interaction, including a positive σ-hole at the metal atom.

Regarding the structures of the complexes considered here, there is ample precedent in the crystal literature for these geometries. Fig. S4 (ESI†) illustrates a number of examples drawn from the CSD database.^90–93 The MATCOD geometry places a Se atom along the Se–W axis of a WCl₄Se molecule in a structure similar to the Lin-Y geometries, that were found here to be so similar in energy to Mono-Y. This type of structure occurs also when WCl₄S is paired with an eight-membered S ring in JITRUZ or with a thioether in KUDFOH and KUDGEY. Not only chalcogen bases prefer this sort of structure, but nitrogen as well as in PHASOM, where N lies along the O–Mo axis of MoCl₄O. The anionic forms of these units naturally fall into bridged pairings with one another, highly reminiscent of Dual-X. Fig. S5 (ESI†)^94–96 illustrates the manner in which POSWIF adopts this structure precisely between a pair of MoCl₄O units where the Mo⋯Cl distances are 2.96 Å, slightly shorter than our computed distance of 3.14 Å. IHODAM alters the geometry to Mono-X; in fact, this intermolecular geometry serves as a template for the formation of an infinite chain of MoCl₄O units, all bound together by such Mono-X type bonds. NABQIQ falls into the alternative Lin-Y category. Crystal intermolecular distances tend to be slightly shorter than the computed values, due to crystal packing forces.

Conclusions

MX₄Y homodimers prefer to arrange themselves in two primary ways. The more strongly bound Dual-X complexes are symmetric in the sense that they contain a pair of equivalent M⋯X noncovalent bonds. Their interaction energies span a range between −8 and −29 kcal mol⁻¹. An alternate Mono-Y structure replaces the two M⋯X bonds with a single and weaker M⋯Y bond; the interaction energies here are in the −2 to −10 kcal mol⁻¹ range. The replacement of F by Cl or Br weakens the Dual-X bonds while strengthening Mono-Y. Enlarging the Y atom from O to S or Se reduces the bonding strength of both sorts of dimers. The Mono-Y dimers are bound weakly enough that there is some question as to whether they constitute true bonds, as AIM does not indicate an M⋯Y bond path for all such dimers, although NBO, RDG, and density difference maps do suggest such a bond. In contrast to Dual-X where electrostatics tends to be the primary attractive component, this role is largely usurped by dispersion forces for Mono-Y.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge Polish high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) for providing computer facilities and support within computational grant no. PLG/2023/016853, Wrocław Center for Networking and Supercomputing (WCSS). This material is also based upon work supported by the U.S. National Science Foundation under grant no. 1954310 to SS. This research was funded by the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology under grant no. 8211104160/K14W03D10 and by the US National Science Foundation under grant no. 1954310.

References

1. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
2. C. B. Aakeroy, D. L. Bryce, G. Desiraju, A. Frontera, A. C. Legon, F. Nicotra, K. Rissanen, S. Scheiner, G. Terraneo, P. Metrangolo and G. Resnati, Pure Appl. Chem., 2019, 91, 1889–1892.
3. P. Politzer, J. S. Murray and P. Lane, Int. J. Quantum Chem., 2007, 107, 3046–3052.
4. P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2007, 13, 643–650.
5. P. Politzer, P. Lane, M. C. Concha, Y. G. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311.
6. J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2007, 107, 2286–2292.
7. J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
8. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
9. P. Politzer, J. S. Murray, T. Clark and G. Resnati, Phys. Chem. Chem. Phys., 2017, 19, 32166–32178.
10. P. Politzer and J. S. Murray, Crystals, 2017, 7, 212.
11. C. B. Aakeroy, S. Alavi, L. Brammer, D. L. Bryce, T. Clark, J. E. Del Bene, A. J. Edwards, C. Esterhuysen, T. N. G. Row, P. Kennepohl, A. C. Legon, G. O. Lloyd, J. S. Murray, W. T. Pennington, P. Politzer, K. E. Riley, S. V. Rosokha, S. Scheiner, S. Tsuzuki and I. Vargas-Baca, Faraday Discuss., 2017, 203, 131–163.
12. W. Wang, B. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132–8135.
13. S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288.
14. A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Rec., 2016, 16, 473–487.
15. S. J. Grabowski, Struct. Chem., 2017, 28, 1163–1171.
16. S. J. Grabowski, ChemPhysChem, 2014, 15, 2985–2993.
17. P. Politzer and J. S. Murray, ChemPhysChem, 2020, 21, 579–588.
18. T. Clark, J. S. Murray and P. Politzer, Aust. J. Chem., 2014, 67, 451–456.
19. S. J. Ang, A. M. Mak and M. W. Wong, Phys. Chem. Chem. Phys., 2018, 20, 26463–26478.
20. T. Clark, J. S. Murray and P. Politzer, Phys. Chem. Chem. Phys., 2018, 20, 30076–30082.
21. K. E. Riley, J. S. Murray, J. Fanfrlik, J. Rezac, R. J. Sola, M. C. Concha, F. M. Ramos and P. Politzer, J. Mol. Model., 2013, 19, 4651–4659.
22. K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2013, 15, 17742–17751.
23. P. Politzer and J. S. Murray, Theor. Chem. Acc., 2021, 140, 7.
24. J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e13260.
25. M. D. Pina, A. Frontera and A. Bauzá, J. Phys. Chem. Lett., 2020, 11, 8259–8263.
26. G. Sanchez-Sanz, C. Trujillo, I. Alkorta and J. Elguero, ChemPhysChem, 2019, 20, 1572–1580.
27. A. Bauza and A. Frontera, Inorganics, 2018, 6, 64.
28. M. Khera, Anchal and N. Goel, J. Phys. Chem. A, 2023, 127, 6953–6961.
29. S. Burguera, A. Frontera and A. Bauza, Inorg. Chem., 2023, 62, 6740–6750.
30. H. S. Biswal, A. Kumar Sahu, A. Frontera and A. Bauzá, J. Chem. Inf. Model., 2021, 61, 3945–3954.
31. T. Xia, D. Li and L. J. Cheng, Chem. Phys., 2020, 539, 110978.
32. G. Mahmoudi, S. E. Lawrence, J. Cisterna, A. Cardenas, I. Brito, A. Frontera and D. A. Safin, New J. Chem., 2020, 44, 21100–21107.
33. M. Karmakar, A. Frontera, S. Chattopadhyay, T. J. Mooibroek and A. Bauza, Int. J. Mol. Sci., 2020, 21, 7091.
34. A. Bauzá, I. Alkorta, J. Elguero, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2020, 59, 17482–17487.
35. S. Burguera, R. M. Gomila, A. Bauza and A. Frontera, Crystals, 2023, 13, 187.
36. G. Resnati, A. Pizzi and M. Calabrese, Acta Crystallogr., Sect. A: Found. Adv., 2022, 78, E200–E200.
37. R. M. Gomila and A. Frontera, Molecules, 2022, 27, 6597.
38. R. M. Gomila and A. Frontera, Inorganics, 2022, 10, 133.
39. A. Pizzi, A. Daolio, M. Calabrese, G. Terraneo, A. Frontera and G. Resnati, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C800–C800.
40. A. Daolio, A. Pizzi, M. Calabrese, G. Terraneo, S. Bordignon, A. Frontera and G. Resnati, Angew. Chem., Int. Ed., 2021, 60, 20723–20727.
41. P. Middya, M. Karmakar, R. M. Gomila, M. G. B. Drew, A. Frontera and S. Chattopadhyay, New J. Chem., 2023, 47, 9346–9363.
42. A. Bauzá and A. Frontera, Chem. – Eur. J., 2022, 28, e202201660.
43. V. K. Greenacre, A. L. Hector, R. Huang, W. Levason, V. Sethi and G. Reid, Dalton Trans., 2022, 51, 2400–2412.
44. D. L. Hughes, J. D. Lane and R. L. Richards, J. Chem. Soc., Dalton Trans., 1991, 1627–1629,  10.1039/DT9910001627.
45. D. E. Smith, V. K. Greenacre, A. L. Hector, R. Huang, W. Levason, G. Reid, F. Robinson and S. Thomas, Dalton Trans., 2020, 49, 2496–2504.
46. F. Weller, U. Müller, U. Weiher and K. Dehnicke, Z. Anorg. Allg. Chem., 1980, 460, 191–199.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford, CT, USA, 2016.
48. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
49. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
50. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
51. B. S. D. R. Vamhindi and A. Karton, Chem. Phys., 2017, 493, 12–19.
52. R. Podeszwa and K. Szalewicz, J. Chem. Phys., 2012, 136, 161102.
53. S. Karthikeyan, V. Ramanathan and B. K. Mishra, J. Phys. Chem. A, 2013, 117, 6687–6694.
54. M. Majumder, B. K. Mishra and N. Sathyamurthy, Chem. Phys., 2013, 557, 59–65.
55. M. A. Vincent and I. H. Hillier, Phys. Chem. Chem. Phys., 2011, 13, 4388–4392.
56. A. D. Boese, ChemPhysChem, 2015, 16, 978–985.
57. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600.
58. L. F. Molnar, X. He, B. Wang and K. M. Merz, J. Chem. Phys., 2009, 131, 065102.
59. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
60. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
61. P. V. Bijina and C. H. Suresh, J. Chem. Sci., 2016, 128, 1677–1686.
62. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
63. R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Clarendon Press, Oxford, 1990.
64. A. T. Keith, AIMAll (Version 14.11.23), TK Gristmill Software, Overland Park, KS, USA, 2014.
65. A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073.
66. A. E. Reed, F. Weinhold, L. A. Curtiss and D. J. Pochatko, J. Chem. Phys., 1986, 84, 5687–5705.
67. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0 software, 2018.
68. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
69. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
70. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
71. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
72. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, III, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
73. H.-J. Werner, P. J. Knowles and others, MOLPRO, version, a package of ab initio programs, see https://www.molpro.net.
74. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
75. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470.
76. I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2002, 58, 389–397.
77. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
78. Chemcraft – graphical software for visualization of quantum chemistry computations. Version 1.8, build 682. https://www.chemcraftprog.com.
79. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
80. M. Ziolkowski, S. J. Grabowski and J. Leszczynski, J. Phys. Chem. A, 2006, 110, 6514–6521.
81. R. F. W. Bader and H. Essen, J. Chem. Phys., 1984, 80, 1943–1960.
82. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
83. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
84. S. J. Grabowski, Chem. Rev., 2011, 111, 2597–2625.
85. G. V. Baryshnikov, B. F. Minaev, V. A. Minaeva, A. T. Podgornaya and H. Ågren, Russ. J. Gen. Chem., 2012, 82, 1254–1262.
86. S. J. Grabowski, J. Phys. Chem. A, 2012, 116, 1838–1845.
87. N. N. Karaush, G. V. Baryshnikov and B. F. Minaev, RSC Adv., 2015, 5, 24299–24305.
88. P. S. V. Kumar, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527–1536.
89. A. S. Novikov, Inorg. Chim. Acta, 2018, 471, 126–129.
90. F. Weller, U. Muller, U. Weiher and K. Dehnicke, Z. Anorg. Allg. Chem., 1980, 460, 191–199.
91. D. E. Smith, V. K. Greenacre, A. L. Hector, R. M. Huang, W. Levason, G. Reid, F. Robinson and S. Thomas, Dalton Trans., 2020, 49, 2496–2504.
92. D. L. Hughes, J. D. Lane and R. L. Richards, J. Chem. Soc., Dalton Trans., 1991, 1627–1629,  10.1039/dt9910001627.
93. V. K. Greenacre, A. L. Hector, R. M. Huang, W. Levason, V. Sethi and G. Reid, Dalton Trans., 2022, 51, 2400–2412.
94. M. Bortoluzzi, G. Bresciani, F. Marchetti, G. Pampaloni and S. Zacchini, Dalton Trans., 2015, 44, 10030–10037.
95. C. Limberg, R. Boese and B. Schiemenz, J. Chem. Soc., Dalton Trans., 1997, 1633–1637,  10.1039/a700083i.
96. F. Marchetti, G. Pampaloni and S. Zacchini, Polyhedron, 2015, 85, 369–375.

---

Footnote

† Electronic supplementary information (ESI) available: The characteristics of monomers, and the additional QTAIM and NCI data. Also included are the Cartesian coordinates of all relevant monomers and dimers along with the specifics of the CSD survey (DOC). See DOI: https://doi.org/10.1039/d3cp05867k

---