Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Martinoid: the peptoid martini force field†
Hamish W. A.
Swanson
 ,
Alexander
van Teijlingen
,
Alexander
van Teijlingen
 ,
King Hang Aaron
Lau
,
King Hang Aaron
Lau
 * and
Tell
Tuttle
* and
Tell
Tuttle
 *
*
Department of Pure and Applied Chemistry, University of Strathclyde, 295 Cathedral Street, Glasgow G1 1XL, UK. E-mail: aaron.lau@strath.ac.uk; tell.tuttle@strath.ac.uk
First published on 22nd January 2024
Abstract
Many exciting innovations have been made in the development of assembling peptoid materials. Typically, these have utilised large oligomeric sequences, though elsewhere the study of peptide self-assembly has yielded numerous examples of assemblers below 6–8 residues in length, evidencing that minimal peptoid assemblers are not only feasible but expected. A productive means of discovering such materials is through the application of in silico screening methods, which often benefit from the use of coarse-grained molecular dynamics (CG-MD) simulations. At the current level of development, CG models for peptoids are insufficient and we have been motivated to develop a Martini forcefield compatible peptoid model. A dual bottom-up and top-down parameterisation approach has been adopted, in keeping with the Martini parameterisation methodology, targeting the reproduction of atomistic MD dynamics and trends in experimentally obtained log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 partition coefficients, respectively. This work has yielded valuable insights into the practicalities of parameterising peptoid monomers. Additionally, we demonstrate that our model can reproduce the experimental observations of two very different peptoid assembly systems, namely peptoid nanosheets and minimal tripeptoid assembly. Further we can simulate the peptoid helix secondary structure relevant for antimicrobial sequences. To be of maximum usefulness to the peptoid research community, we have developed freely available code to generate all requisite simulation files for the application of this model with Gromacs MD software.
D7.4 partition coefficients, respectively. This work has yielded valuable insights into the practicalities of parameterising peptoid monomers. Additionally, we demonstrate that our model can reproduce the experimental observations of two very different peptoid assembly systems, namely peptoid nanosheets and minimal tripeptoid assembly. Further we can simulate the peptoid helix secondary structure relevant for antimicrobial sequences. To be of maximum usefulness to the peptoid research community, we have developed freely available code to generate all requisite simulation files for the application of this model with Gromacs MD software.
Introduction
Peptoids are synthetic structural isomers of peptides in which sidechains are attached through the amide nitrogen centre, as opposed to the backbone alpha-carbon. Consequently, the rigidity of the amide linker is lessened, and the backbone may occupy both cis and trans ω torsions.1,2 Interest in peptoids has been steadily growing since the introduction of a facile submonomer solid phase synthesis method for generating sequence-specific peptoids in the 1990s.3 Since this time, there has been an expanding library of amines from which to select sidechains,4,5 and emerging green synthesis methods.6 Peptoids have also been utilised in biomedical sciences,7,8 among which protein recognition and antimicrobial/antifungal activity are two prominent examples.9,10 Recently Sharol et al. generated a small library of organogelators with which the antibiotic metronidazole could be encapsulated and released with significant activity against E. coli,11 further demonstrating the potential of this research area. Peptoid materials research has yielded a diversity of function, ranging from novel anti-freeze materials12 to anti-fouling coatings.13,14The study of self-assembling peptoids has been an area of particular interest15,16 and a varied range of assembly morphologies have been reported to date including nanosheets,17 nanotubes,18 superhelices,19 micelles and polymersomes.20 Many of these are generated using relatively long amphiphilic sequences, and rationally designed block copolymers are common.21 Overall, diverse properties and chemical functionality can be achieved in the design of peptoids. This positions them as a molecular platform for solving a range of challenges, from tackling anti-microbial resistance to developing sustainable materials.
There is comparatively little exploration of the assembly of short peptoids, or ‘minimal’ sequences, i.e., below 6–8 units in length. This is surprising given the extensive field of interesting assemblies reported for short peptides to date.22–24 Some initial work had shown that oligopeptoid assembly required hybridization with peptides25 or organic solvent mixtures.26 However, recently Lau et al. demonstrated that the dipeptoid Ac–Nf–Nf may assemble into amorphous nanosheets or macroscopic crystalline needles depending on the solvent environment.27 It was shown that tripeptoids inspired by the tripeptide assemblers, FKF28,29 and KFF,30 assemble into water soluble nanofibers, or globular vesicle structures, depending on the sequence and sidechain length of a cationic lysine mimic.31 This demonstrated that peptoids generate morphologies distinct from analogous peptide sequences,32,33 evidencing that peptoid assemblies are possible in aqueous environments, despite the expanded ϕ/ψ/ω space34 and the removal of hydrogen bond donors along the backbone.
The discovery of peptoid materials is currently by trial-and-error and can be readily accelerated using in silico approaches. A strong need to develop a flexible and transferable coarse-grained (CG) peptoid force field for peptoid assembly exists. CG molecular dynamics (CG-MD) has previously been used through unbiased screening approaches to yield reliable data on peptide assembly which follows experimental trends35,36 and more recently an active learning machine algorithm approach was able to identify the top assembling sequences from these initial efforts using a fraction of the number of necessary simulations,37 making the screening of sequences up to hexapeptides feasible. Considering these developments and the powerful opportunities presented by combining computational and experimental design endeavours, a CG force field for peptoids would be beneficial.24
Herein, we report our contribution to this effort built within the popular and transferable Martini forcefield framework, ubiquitous in the simulation of biomolecular systems due to its ability to access the necessary system sizes and spatiotemporal requirements. Indeed, it has been in use for twenty years and it is now in its 3rd iteration of development.38,39 Our work has been stimulated by previous CG-MD peptoid forcefield developments. Haxton et al. had first developed the MFCGTOID model in 2015,40,41 which was a bespoke implicit solvent model for simulation of nanosheet-forming, long, diblock sequences in which monomers were minimally represented with single backbone and sidechain units. To compensate for the loss of dynamic detail anisotropic interaction sites were used, with an independently fluctuating symmetry axis. A total of 115 parameters were fit using combined simulation and experimental data from an all-atom (AA) MFTOID model42 and nanosheet structural measurements obtained by X-ray scattering. The model successfully reproduced experimentally observed properties indicative of metastable and assembled states observed during nanosheet formation. Subsequently, this model was applied to understanding the role of charged sidechain arrangements in monolayer to bilayer buckling which occurs in nanosheet formation.41 However, this model is not compatible with other CG forcefields and application to other systems would require complete re-parameterization of the relevant parameters.
Zhao et al. developed a Martini-based model with a pseudo united-atom (UA) character43 that targeted simulation of a series of halophenyl amphiphilic peptoids that assemble into nanosheets and nanotubes.18,44 The mapping strategy follows that of Gao and Tartakovsky,45 which places the backbone bead in the geometric centre of the C–N amide bond of each monomer such that a given bead ‘straddles’ the previous and proceeding residues. A new ‘PA’ backbone bead type was parametrised, and the key bromine within the bromobenzene sidechain was modelled using an existing bead on the basis that this same type is used in the Martini model for chlorobenzene.46 As a result mass conservation was not achieved, as a 45 amu bead was used to represent an 80 amu atom. Moreover, to reproduce the dihedral rotations between the peptoid backbone and the sidechain benzene along an ethyl linkage (Ntoid–Cα–Cβ–Cγ) a non-standard 14 amu bead, coined a ‘CC’ bead, was developed giving this model a UA component and limiting the use of large timesteps. For the UA beads CHARMM forcefield interaction parameters for CH2 groups were used.47 While an iterative Boltzmann inversion (IBI) procedure gave generally good convergence onto PBMetaD AA MFTOID simulations that obtained adequate sampling of peptoid backbone cis/trans dynamics, and the model was able to reproduce experimental findings, the introduction of a UA component minimises the potential benefits that can be derived from coarse-graining.
Most recently Banerjee et al. parameterised a CG forcefield for simulation of peptoid helices48 that assemble into microspheres.49,50 A rigorous parameterisation based on AA MFTOID simulations, IBI procedures and force matching (FM) gave good agreements between CG and atomistic potentials. However, 1-3-5 backbone potentials were required to remediate differences between atomistic and accurate CG helical secondary structure. The resulting model was able to simulate (hemi)spherical assembly and showed this was driven by aromatic sidechain interactions and aromatic stacking between peptoids. The mapping scheme used ranges from 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 heavy atoms per bead, thus a short timestep of 2 fs was again required for this system, which precluded the simulation of large numbers of molecules.
1 heavy atoms per bead, thus a short timestep of 2 fs was again required for this system, which precluded the simulation of large numbers of molecules.
Herein, we present a transferable Martini based peptoid CG forcefield, called ‘Martinoid’. This is parameterised using a dual bottom-up and top-down approach, targeting the reproduction of dynamics derived from AA-MD simulations obtained using a CHARMM General Force Field (CGenFF) developed for peptoids.51 The top-down parameterisation focuses on reproducing trends in experimentally obtained log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 data. In this effort we hope to contribute a generalizable tool to the wider community and accelerate the discovery of novel peptoid materials.
D7.4 data. In this effort we hope to contribute a generalizable tool to the wider community and accelerate the discovery of novel peptoid materials.
Model development
Nomenclature in this work is in accordance with the ‘Glasgow Convention’ for peptoid naming. Briefly, for a given residue, the characteristic peptoid ‘N’ is retained for familiarity, followed by the lower-case letter corresponding to the most closely related amino acid single letter code. While new letters can be assigned for novel residues with no structural similarity to amino acids, the third and fourth letters are intended to encode sidechain modifications or atom substitutions, and the degree of deviation from an amino acid analogue can be discerned by the number of letters used in the name. An in-depth overview can be found at the following ref. 52.Bonded interactions within the Martinoid model use the same potentials as employed in the Martini 2.1 model for proteins based on earlier versions (eqn (1)–(4)).53,54 Acting between bonded sites i, j, k and l with equilibrium distance db, angle ϕa and dihedral angles φd and φid:
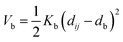 | (1) |
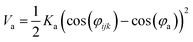 | (2) |
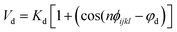 | (3) |
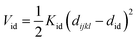 | (4) |
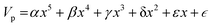 | (5) |
Non-bonded interactions are dealt with in the same way as in the standard Martini forcefield, specifically with all particle pairs i and j at distance rij interacting via a Lennard-Jones (LJ) potential:
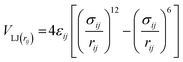 | (6) |
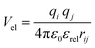 | (7) |
In the Martinoid model we use the same relative dielectric constant, εrel = 15, as in previous non-polarized Martini models, while no testing of the model was done with polarizable water, we anticipate that the model would be compatible with a polarizable water model,56 using a relative dielectric constant εrel = 2.5. Throughout this work we used the Martini 2.1 models for water, antifreeze water and ions directly without modification.
In the calculation of nonbonded interactions the Martini straight potential energy scheme is followed. In this approach Lennard Jones (LJ) potential and electrostatic terms are both shifted to a cutoff at 1.1 nm. For the coulombic terms a reaction-field treatment of electrostatics is used due to its improved performance efficiency.57
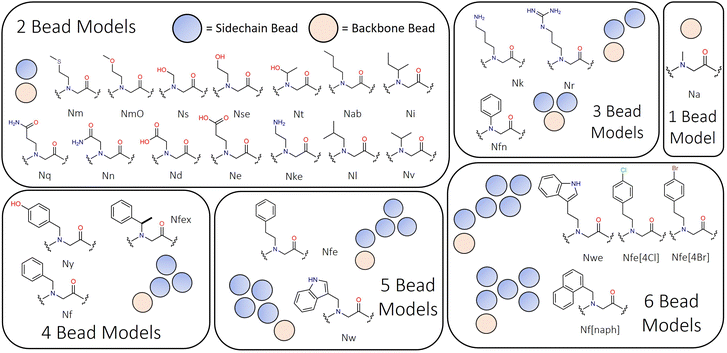
Mapping of peptoid monomers follows directly the classical Martini convention with 4–5 heavy atoms being described by beads with 72 amu mass, and 2–3 heavy atoms being combined into smaller 45 amu beads for the preservation of ring planarity or where sidechains were small, such as Ns, Nt and Nv (i.e., analogues of serine, S, threonine, T, and valine, V). Our approach is sensitive to the ‘bond length effect’ described by Alessandri et al., in which it is observed that shorter bond lengths tend to produce more hydrophobic behaviour through increased solvent–solute interactions.58 This is found to be most significant at and below the 0.2 nm bond scale and thus we sought to avoid such dimensionality where possible. In the Martini peptoid model formulated by Zhao et al., bond lengths on the order of 0.16–0.2 nm are used throughout.43 The structural characteristics of the monomers present within this model range in size from single beads (e.g., Na, the alanine analogue, a.k.a. sarcosine) to six beads (e.g., Nf[naph]; see Fig. 1). In peptoid sequence design, the use of chiral branched sequences (e.g., Nfes or Nfer) are commonplace to enforce specific amide conformations; while it is not possible to have specific chirality at this level of molecular resolution, we introduce a residue Nfex which represents both chirality's as a single residue.
In the Martini 2.1. forcefield there are a total of 18 bead types, capturing four main types of interaction sites: polar (P), nonpolar (N), apolar (C) and charged (Q). These are then subdivided into categories, either by a letter describing their hydrogen-bonding character (d = donor, a = acceptor, da = both and 0 = none) or by a number representing their degree of polarity (from 1 = low polarity to 5 = high polarity). The interactions between the different bead types (e.g., ranging from uber attractive to super repulsive) defined in the Martini 2.1 interaction matrix are used directly within Martinoid without modification.
Given the close chemical relationship between peptoids and peptides we decided to adopt generally the same bead typing approach as in the Martini 2.1 protein forcefield for analogous residues. Aliphatic type species (Nab, Nl, Ni, Nv, and Nm) are represented with C-type beads. Aromatic type ring systems (e.g., Nf, Nfe, Nfex, Nw, Nwe, and Nf[naph]) are similarly represented using the ‘small’ C-type beads. Polar uncharged residues (e.g., Ns, Nse, Nt, Nq, NmO and Nn) are represented using P-type beads of regular and small sizes where appropriate. Unlike the Martini peptide models, [2,2.2,3] bead typing for specific secondary structures is not currently applied. However, this as an area for future development.
The appropriateness of bead type selection was assessed by comparing simulation Aggregation Propensity (AP), which in an assembly simulation refers to the ratio of Solvent Accessible Surface Area (SASA) at the beginning of the simulation in the non-aggregated state (SASAinitial) verses this same property in the final frame of the simulation (SASAfinal) (eqn (8)). When simulating in an aqueous solvent, one would expect an apolar species to have an AP score >1.0, while charged or polar character would have an AP score of ∼1.0. This metric is well established in rationalising CG assembly.35–37,59 We also compare experimental and computationally evaluated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg measurements obtained for a series of peptoid monomers to select the most applicable bead types (eqn (9)).
Dcg measurements obtained for a series of peptoid monomers to select the most applicable bead types (eqn (9)).
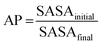 | (8) |
ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(P) ln(P) | (9) |
Bonded terms fitting was done against AA MD dynamics target data to conform with the bottom-up component of the Martini parameterisation scheme. This was generated using a recently re-parameterised CGenFF peptoid forcefield developed in our lab.51 An acetyl-capped peptoid dimer of each monomer of interest was solvated in TIP3P water and neutralised with counter ions where required. This system was then simulated at 298.15 K and 1 atmospheric pressure for 10 ns with the dimer in both the cis and trans conformation (therefore 20 ns total run time for each dimer) in the NPT ensemble, thus yielding two atomistic trajectories (see ESI,† Section 5 for additional details). In all cases the starting structure for the simulation was the lowest energy conformer in the gas phase which was obtained using the GFN-FF based metadynamics conformer/rotameter ensemble sampling tool (CREST).60 Initial CG parameters were then obtained for each dimer in both conformations using SWARM-CG with standard optimisation settings and a centre of mass (COM) mapping scheme (scg_optimise). The optimised parameters obtained from the conformers were then superimposed (averaged).
We assessed the validity of the above methodology by comparing aggregation propensity (AP) scores for the same molecule using the different parameters. In doing so it was possible to assess the impact on a property relevant to self-assembly screening, a key parameterisation goal of this work. Importantly, the SWARM-CG parameters were treated as a starting point and subsequent tuning and parameter selection was then performed manually using the model evaluation tool (scg_evaluate). For bonded term evaluation, complementary CG simulations of the prospective model were performed for 25 ns solvated in Martini water with ions as required. CG simulation details can be found in ESI,† Section 5.
Once sidechain and backbone parameters had been obtained at the peptoid dimer level, we performed simulations 100 ns simulations of single peptoids trimer sequences in TIP3P water with ions, in all amide sequence states (i.e., cis–cis, cis–trans, trans–cis and trans–trans). The backbone angle distributions were then compared to a CG representation of the same molecule in Martini water, and the force constant/equilibrium angle which gave the best agreement with the distribution obtained from the population was selected. This comparison was also done against a population of 25 molecules which were simulated for 50 ns, similar results were obtained for the selected parameters (ESI,† Section 5.3). For specific secondary structures, such as the peptoid helix, we performed mapping to obtain appropriate angle and dihedral terms to enforce this arrangement.
The selection and optimisation of backbone dihedral angle parameters has been a focus of previous CG peptoid forcefield optimisation.40,43,48 While the parameterisation discussed here is targeted at short peptoid sequences, we include a dihedral parameter from the Martini protein forcefield with an equilibrium angle of 180° and a loose force constant of 10 kJ mol−1. To validate this choice, we performed simulations of peptoid nanosheet forming polymers which gave agreement with experimental observations.61 We thus have confidence that this is a reasonable initial choice.
Nonbonded parameterisation employed umbrella sampling was used to evaluate the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg values via the generation of an unbiased potential of mean force (PMF) which was derived from these simulations using weighted analysis histogram method (WHAM). These estimations were performed in triplicate for each monomer (Tables S48–S57, ESI†) and we validated the method against known amino acid log
Dcg values via the generation of an unbiased potential of mean force (PMF) which was derived from these simulations using weighted analysis histogram method (WHAM). These estimations were performed in triplicate for each monomer (Tables S48–S57, ESI†) and we validated the method against known amino acid log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values (ESI,† Section 7 and Tables S27–S47). In our parameterisation we sought to reproduce trends experimentally determined trends in log
P values (ESI,† Section 7 and Tables S27–S47). In our parameterisation we sought to reproduce trends experimentally determined trends in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D data between residues of interest. Additional information on the procedure can be found in the Experimental section. Furthermore, we performed free assembly simulations of peptoid monomers to assess whether these choices were reasonable against chemical expectations.
D data between residues of interest. Additional information on the procedure can be found in the Experimental section. Furthermore, we performed free assembly simulations of peptoid monomers to assess whether these choices were reasonable against chemical expectations.
Results and development
Bonded term parameterisation
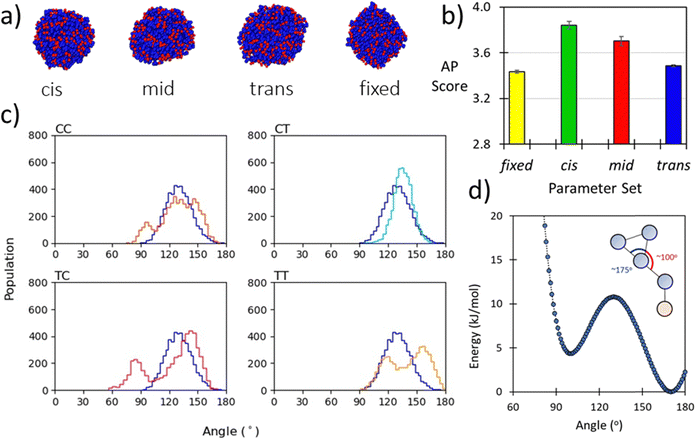
The backbone to sidechain bond (BB–SC) for a given residue are obtained by taking the average of parameters (e.g., mid) obtained for dimers in the cis and trans backbone state. Previously we have shown that backbone state and sidechain dynamics are coupled in a manner which effects molecular self-assembly propensity;51 however, at the CG level of theory, where this resolution is lacking, similar assembly morphologies are obtained irrespective of the use of cis, trans, or mid parameters (Fig. 2a). Comparison of AP scores indicates a compromise (Fig. 2b). Using the SWARM-CG optimised parameters the sidechain–sidechain (SC–SC) ring constraint was ∼0.23 nm, however in the Martini 2 model rings have a 0.27 nm bond length. With this consideration we introduced a fixed parameter set which was composed of the mid parameter and with this lengthened SC–SC contact. The impact of this on the resultant AP score is non-trivial and so for forcefield compatibility we use this contact length for all aromatic ring systems. For all parameter sets the AP score is high, e.g., ≥3.4., which agrees with experiment, where it was found that Ac–(Nf)2 is insoluble in water and assembles upon aqueous dilution of an acetonitrile stock solution.27 In a screening protocol, this would be sufficient to flag a given sequence as an assembler which is a goal of our model. Lastly, the globular assembilies formed, are distinct from the kinds of structures obtained from FF.35 Providing confirmation that Martinoid is not a peptide forcefield of a different name.Experimental data, such as NMR correlation, can be used to infer the relative population of peptoid backbone conformations and inform parameter development. This is particularly successful when enhanced sampling molecular dynamics or Bayesian inference methods such as BICePs62 as developed by Voelz et al. are used.63 However, obtaining the experimental data is non-trivial. Sampling all possible conformational states with higher accuracy simulations is also intractable beyond short sequences, as the number of cis/trans states scales as 4n−1.64 While our model may lose specific detail through parameter superimposition, the use of CG MD accelerates the testing of sequences. Higher accuracy studies may then be performed to refine understanding of screening hits. To gauge how well superimposed parameters agree with their cis and trans atomistic distributions we present the CG bonded term distributions and both atomistic distributions. Generally, we found good compromises for all residues (ESI,† Section 6, Fig. S44–S92).
The backbone-to-backbone bond (BB–BB) is set to a fixed length for simplicity as it was found that differences between the cis and trans states were generally on the sub-nanometre scale, with a maximum deviation in the SWARM-CG fitting of 0.7 Å. During the fitting process an average value of 0.34 nm and a force constant of 8515 kJ nm−2 mol−1 was found to give good agreement for most dimers. We regard this as a reasonable choice for several reasons. Firstly, previous atomistic simulations of peptoid nanosheet, arguably the most well characterised assembled peptoid structure, found sequences in both all-cis and all-trans conformations with mean lengths per residue of 0.305 nm in the former and 0.384 nm in the latter.61 The median therefore being ∼0.34 nm. A similar bond length was used by Zhao et al. in their CG model for the peptoid BB–BB bond distance.43 Secondly, in the Martini Protein forcefield this contact is set at 0.35 nm giving a similar equilibrium distance, notably in this model a considerably smaller force constant was used 1250 kJ nm−2 mol−1 for an extended protein secondary structure, though our selection agrees with atomistic mapping showing the force constant is sensible.
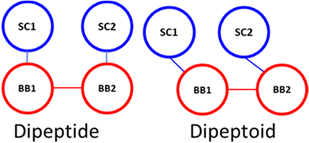
The sidechain to backbone angle (SC–BB–BB) which is used to constrain the sidechain position with respect to the backbone, and to adapt the Martini bead approach to accommodate the sidechain attachment on the backbone N-atom. In our dimer simulations we assumed this would have the same equilibrium angle whether defined for the N-terminal or C-terminal sidechain. However, a bimodal distribution resulted with a sharp population around ∼60° and broader distribution ∼120°. Initially we interpreted this as being due to their being two ‘dynamic states’ of a given peptoid sidechain. Closer inspection of atomistic trajectories revealed that this was not the case.
Instead, this is a consequence of the fact that the COM of the sidechain (SC) is ‘to the left’ of the backbone bead (BB) COM, e.g., approximately in line with the Cα. Therefore, the angle defined as SC1–BB1–BB2 (at the N-termini) is inequivalent to SC2–BB2–BB1 (at the C-termini), the former being obtuse and the latter acute (this is illustrated in Scheme 1). This situation describes peptides well and the sidechain adopts a more symmetric position, approximately in the plane of the backbone COM. Accordingly, this angle is generalised and non-directional in the Martini model for proteins such that an angle of 100° is obtained with a force constant of 25 kJ mol−1.
To describe peptoid sequences, defining an angle from the N-terminus sidechain bead to the following backbone beads, as SC1–BB1–BB2, an obtuse angle is obtained, ∼110°. However, starting at the C-terminus and then defining an angle in the same manner, as SC2–BB2–BB1, an acute angle is obtained, ∼70°. Therefore, we define these two angles separately at the termini of peptoids—an equilibrium angle of 65° and 80 kJ mol−1 is defined at the C-terminus and all other positions are described with an equilibrium angle of 110° and a force constant of 20 kJ mol−1. By separating these terms, we were able to better reproduce the angle distributions within the dimer simulations (ESI,† Section 6).
The backbone to backbone angle (BB–BB–BB) was fit by comparing atomistic sampling distributions of this angle for the known self-assembling peptoid trimers31 and other short trimeric peptoid motifs. It was found that generally an equilibrium angle of ∼100–150° was obtained for both single molecules and across a population of 25 molecules (Section 5.3, ESI†). To achieve this distribution in our model, it was necessary to set the equilibrium angle at 138° with a force constant of 50 kJ mol−1 (example for Nk–Nf–Nf, Fig. 2c). This a slightly larger angle than that obtained by Zhao et al. where an equilibrium angle of ∼125–130° was obtained from all-atom simulations.
Lastly, we found it necessary to include some specific sidechain–sidechain angles for aromatic sidechains with extended unbranched linkers (e.g., Nfe and its derivatives; see Fig. 1). The angle linker bead (SC1) and those in the benzene ring (SC2–SC3) and (SC2–SC4) was found to oscillate between ∼100° and ∼170°. To reproduce this dynamic behaviour in our model, we used an asymmetric double well-potential with minima at these equilibrium positions using a tabulated bonded potential within Gromacs. Recently Sami et al. used this same tabulated potential based approach in a reactive Martini context.65 The ∼100° well was set to be 4.35 kJ mol−1 higher than the 170° well which we set to 0.0 kJ mol−1, with a barrier of 10.8 kJ mol−1 between the wells (Fig. 2d). Then both angles SC1–SC2–SC3 and SC1–SC2–SC4 are defined using the same potential form. The consequence of this is that when angle i is in the global minima then by definition angle j is in a local minimum. This means that the two angles are in perpetual competition for the same objective, i.e., occupancy of the global minima, and as this cannot be achieved for both angles simultaneously a regular oscillating motion is obtained. A requisite of this approach is the use of a 1–3 exclusion between SC1–SC3 and SC1–SC4. While this term is only applicable to a small number of residues, it is important in distinguishing the dynamic behaviour of these residues from other aromatic sidechains within the model. This has no discernible impact on simulation performance.
The peptoid helix secondary structure is a notable target for parameterisation, peptoid 1–3 helices arising from sequences of amphiphilic trimer repeating motifs. This structure brought early attention to peptoid research66,67 and found particular application as a template for mimicking facial amphiphilic antimicrobial peptides.68–70 To obtain atomistic MD data for such sequences, we built a (Nk–Nfes–Nfes)2 structure using a peptide polyproline type I (PPI) helix as the backbone with ω ≈ 0°, ϕ ≈ −70° and ψ ≈ 180°, which is consistent with an Nfes derived right-handed helix.64,71 This was then simulated in TIP3P water with counter ions for 100 ns (ESI,† Section 5.4) and CG parameters were tuned to reproduce backbone angle and dihedral distributions obtained from the atomistic trajectory (Fig. 3a and c). Atomistic Ramachandran plots can be seen in Fig. S42 (ESI†).
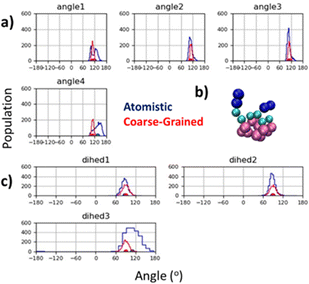 | ||
| Fig. 3 (a) Agreement between atomistic and CG backbone angle distributions for peptoid helix structure; (b) screenshot of CG model for (Nk–Nfex–Nfex)2 showing facial amphiphilicity, a key feature of this sequence design and central to its mimicry of the antimicrobial peptide Magainin;72 and (c) agreement between equilibrium dihedral angles for atomistic and CG model. Duplicate mapping data can be found in ESI,† Fig. S43. | ||
Good agreement between angle and dihedral distributions are obtained for most of the inter-relations measured (Fig. 3a and c). This was obtained using an equilibrium backbone angle (BB–BB–BB) of 110° and a force constant of 300 kJ mol−1, combined with an equilibrium backbone dihedral angle (BB–BB–BB–BB) of 90° and a force constant of 100 kJ mol−1. These optimized parameters can be applied to a given backbone sequence with the Martinoid structure building script, using the keyword ‘helical’ in the structure generating command line execution of: “python-m Martinoid-helical”. Some deviation occurs at the N- and C-termini which is also found in the atomistic simulations and is likely due to increase degrees of freedom at these locations. Notwithstanding, facial amphiphilicity of the helix sequence is captured, which agrees with previous structural data obtained for the helical secondary structure (Fig. 3b).67,72,73
Non-bonded term parameterisation
In the original screening study for di- and tripeptide assemblers performed by Fredrix et al. the extended secondary structure (E) was used, in which the backbone bead is represented by an Nda bead-type. This bead type has a semi-attractive LJ interaction with water (P4 bead type) while other Martini 2 secondary structures such as coil, free and bend have a P5 backbone bead with an attractive LJ interaction with water. Given that peptoids have less hydrogen bonding potential along the backbone than peptides,7 we would expect this to be manifest in a reduced backbone hydrophilicity. For these reasons we chose to represent the peptoid backbone and the elementary sarcosine unit with an Na bead, which due to substitution of hydrogens with the peptoid sidechain precludes ‘d’ donor type hydrogen bonding intermolecular interactions. Thus, we draw a distinction between minimal peptoid and peptide sequences.Amidation of the peptoid C-terminus is widespread in peptoid chemistry, arising from the convenience of chemically synthesizing peptoids from rink amide solid resin supports.3 For this reason, we propose that an Nda bead is the most appropriate choice for the peptoid C-terminus, capturing its propensity for hydrogen bonding74 and reflecting its reduced polarity and non-polar character with respect to an amino acid backbone. Emerging peptoid chemistries can also yield carboxylate peptoid C-termini6,75 and we include the possibility of placing a Qa (charged)/P3 (uncharged) bead at this position in our model.
The peptoid N-terminus, when charged, is represent with a Qd bead and, when uncharged, an Nda bead for acceptor type interactions via the carbonyl group. Using a Qda bead has limited impact on the assembly of representative sequence Nf–Nke–Nf (vide infra, ESI,† Section 8, Fig. S93) and in using this bead choice we follow the precedent of the Martini 2.1. protein forcefield, in which the same selection is made for the N-terminus. Lastly, an Na bead is also used if the N-terminus is acylated.
In the Martini parameterisation methodology, bead types are chosen to reproduce experimental partition free energies between polar and apolar phases.53 To remain consistent with this methodology we sought to assign peptoid bead types to reproduce trends in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 partition coefficients (between n-octanol/PBS7.4) for various peptoid monomers. Acetamide monomer versions of key residues were synthesised using either solid-phase or solution phase methods to suit synthetic and purification convenience (see ESI,† Sections 1 and 3 for details), and log
D7.4 partition coefficients (between n-octanol/PBS7.4) for various peptoid monomers. Acetamide monomer versions of key residues were synthesised using either solid-phase or solution phase methods to suit synthetic and purification convenience (see ESI,† Sections 1 and 3 for details), and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 measurements were compared with model values estimated according to the method of Bolt et al.76
D7.4 measurements were compared with model values estimated according to the method of Bolt et al.76
To assess the validity of this approach, we firstly compared the partition coefficients of amidated L-phenylalanine (H-Phe-NH2) and the peptoid analogue (H-Nf-NH2). Additionally, we estimated the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 of L-phenylalanine to compare with reported literature values (Table 1). Log
D7.4 of L-phenylalanine to compare with reported literature values (Table 1). Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 of −1.45 ± 0.04 was obtained for L-phenylalanine, which agrees with literature values ranging from −1.35 to −1.52 obtained using similar conditions,77–79 and little difference was found between Nf-NH2 and Phe-NH2 (Table 1; difference ∼0.05
D7.4 of −1.45 ± 0.04 was obtained for L-phenylalanine, which agrees with literature values ranging from −1.35 to −1.52 obtained using similar conditions,77–79 and little difference was found between Nf-NH2 and Phe-NH2 (Table 1; difference ∼0.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D units). These measurements indicate that the substitution of a peptoid nitrogen is less impactful on overall monomer hydrophobicity than may have been previously thought. Based on this closeness in partitioning behaviour, we concluded that importing Martini bead types for direct amino acid analogues in the Martinoid model would be reasonable, and additional log
D units). These measurements indicate that the substitution of a peptoid nitrogen is less impactful on overall monomer hydrophobicity than may have been previously thought. Based on this closeness in partitioning behaviour, we concluded that importing Martini bead types for direct amino acid analogues in the Martinoid model would be reasonable, and additional log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 comparison further validated this approach (Table 3).
D7.4 comparison further validated this approach (Table 3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 values for phenylalanine and its derivatives as determined in this work
D7.4 values for phenylalanine and its derivatives as determined in this work
| Species | Grand average |
|---|---|
| H-Phe-OH | −1.45 ± 0.04 |
| H-Nf-NH2 | 0.01 ± 0.02 |
| H-Phe-NH2 | −0.04 ± 0.03 |
In the analysis of Nf and Phe above, the rings in both are composed of three SC4 beads (i.e., SC4–SC4–SC4). This might seem at odds with the subsequent development of protein model version 2.2, in which phenylalanine was re-parameterised to be represented by three SC5 beads instead (i.e., SC5–SC5–SC5), to improve reproduction of several properties, including partitioning across a lipid bilayer, Wimley-White peptide membrane binding, and dimerization free energy in water.80 However it has been shown that this modification also prevents Martini models 2.2 onwards to reproduce self-assemblies formed with phenylalanine containing peptides,59 most critically the widely recognized FF motif, the assembly of which is reproduced well by Martini 2.1.35,81 With this in mind and the goal of developing Martinoid as a forcefield for discovering new self-assembling materials, we decided to continue with the ‘overly’ hydrophobic but useful SC4 representation of benzene rings.
Peptoid aromatic sidechains
For additional analogues of Nf with no natural counterpart in the Martini protein model, e.g., Nfe, Nfex, Nfe[4Cl], Nfe[4Br], Nfn and Nf[naph], we fit bead-types to obtain increases relative to Nf and performed additional parameterisations. This approach is in the spirit of the Hansch hydrophobicity constant, denoted π, which relates to the difference in the partition coefficient of a parent compound and its substituted derivatives.82 Fauchere and Pilska applied this approach to determine hydrophobicity parameters of the amino acid sidechains by comparing the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values obtained for a given acetyl amino acid amide and that of glycine.82 The N/C-termini were capped to enable isolation of distribution behaviour due to the sidechain as opposed to relative ionised/unionized populations within the aqueous phase.
D values obtained for a given acetyl amino acid amide and that of glycine.82 The N/C-termini were capped to enable isolation of distribution behaviour due to the sidechain as opposed to relative ionised/unionized populations within the aqueous phase.
Our approach assumes that the pKa of the peptoid N-terminus is similar across the monomers studied, so that the relative populations of material in the n-octanol and water are only dependant on the sidechain chemistry of a given group. Nonetheless, we note that the relative increase in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 between Nf and Nfe of 0.12 through chain extension (e.g., methyl to ethyl linkage) is challenging to reproduce (Table 2). Firstly, our representation of Nfe is a four-bead model following the precedent of Zhao et al.43 meaning that the number of interaction sites in Nfe is greater than Nf. Secondly the granularity of apolar bead types from which to select is small (i.e., SC1–SC5). The closeness of log
D7.4 between Nf and Nfe of 0.12 through chain extension (e.g., methyl to ethyl linkage) is challenging to reproduce (Table 2). Firstly, our representation of Nfe is a four-bead model following the precedent of Zhao et al.43 meaning that the number of interaction sites in Nfe is greater than Nf. Secondly the granularity of apolar bead types from which to select is small (i.e., SC1–SC5). The closeness of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg values for these species reflects a leveraging of these two constraints. However, they are still distinct in terms of physical construction, which will serve to mitigate this to an extent. We found more favourable agreement comparing Nf and Nfex, with a relative increase in computed log
Dcg values for these species reflects a leveraging of these two constraints. However, they are still distinct in terms of physical construction, which will serve to mitigate this to an extent. We found more favourable agreement comparing Nf and Nfex, with a relative increase in computed log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg of 0.45 units which complements an experimental difference of 0.40 (Table 2). In this case, a three-bead model is used in which the sidechain linker is a C3 (72 amu) bead, as opposed to a small bead. While this is a slight over mapping, the effect on log
Dcg of 0.45 units which complements an experimental difference of 0.40 (Table 2). In this case, a three-bead model is used in which the sidechain linker is a C3 (72 amu) bead, as opposed to a small bead. While this is a slight over mapping, the effect on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg makes it a worthwhile compromise.
Dcg makes it a worthwhile compromise.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for aromatic peptoid monomers
D values for aromatic peptoid monomers
| Species | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 D7.4 |
Relative log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 D7.4 |
Calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg Dcg |
CG Relative log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg Dcg |
|---|---|---|---|---|
a This log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D value is estimated based on other experimentally obtained log D value is estimated based on other experimentally obtained log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for benzene and bromobenzene. D values for benzene and bromobenzene.
|
||||
| H-Nf-NH2 | 0.01 ± 0.02 | — | 4.74 ± 0.09 | — |
| H-Nfe-NH2 | 0.13 ± 0.02 | 0.12 | 4.93 ± 0.20 | 0.19 |
| H-Nfes-NH2 | 0.41 ± 0.02 | 0.40 | 5.19 ± 0.10 | 0.45 |
| H-Nfe[4Cl]-NH2 | 0.90 ± 0.04 | 0.89 | 5.53 ± 0.10 | 0.79 |
| H-Nfe[4Br]-NH2 | — | — | 5.67 ± 0.04a | 0.93a |
Halogenation has been utilized in peptoid research to promote self-assembly as well as in attempts to attenuate properties of antimicrobial peptoid sequences.83,84 The halogenation series benzene (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = 2.13) > 1-chlorobenzene (log
D = 2.13) > 1-chlorobenzene (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = 2.84) > 1-bromobenzene (log
D = 2.84) > 1-bromobenzene (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = 2.99) as evaluated by Hansch79 would crudely imply a Δlog
D = 2.99) as evaluated by Hansch79 would crudely imply a Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D of 0.71 through chlorination and 0.86 through bromination. Experimentally, we observe a substantial increase in log
D of 0.71 through chlorination and 0.86 through bromination. Experimentally, we observe a substantial increase in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 towards lower partitioning in water between Nf and Nfe[4Cl]. For both Nfe[4Cl] and Nfe[4Br] we use a five-bead model which share the same bead-typing as Nfe except at the ‘para’ position which represents the halogen unit. In the chlorinated monomer we use a SC5 bead, which is consistent with the Martini model for chlorobenzene46 and obtain a relative increase in log
D7.4 towards lower partitioning in water between Nf and Nfe[4Cl]. For both Nfe[4Cl] and Nfe[4Br] we use a five-bead model which share the same bead-typing as Nfe except at the ‘para’ position which represents the halogen unit. In the chlorinated monomer we use a SC5 bead, which is consistent with the Martini model for chlorobenzene46 and obtain a relative increase in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg of 0.79 units, which agrees with the experimental difference of 0.89 units with Nf. For Nfe[4Br] we use a C5 bead to ensure a reasonable conservation of mass between the all-atom and CG representations (Table 3). In this instance, we obtain a Δlog
Dcg of 0.79 units, which agrees with the experimental difference of 0.89 units with Nf. For Nfe[4Br] we use a C5 bead to ensure a reasonable conservation of mass between the all-atom and CG representations (Table 3). In this instance, we obtain a Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg of 0.93 which is consistent with the Δlog
Dcg of 0.93 which is consistent with the Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dexp from benzene to 1-bromobenzene, and similarly a 0.13 unit increase in Δlog
Dexp from benzene to 1-bromobenzene, and similarly a 0.13 unit increase in Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg relative to Nfe[4Cl] which also agrees with the difference between free benzene derivatives (Δlog
Dcg relative to Nfe[4Cl] which also agrees with the difference between free benzene derivatives (Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dexp = 0.15).
Dexp = 0.15).
| Sidechain | Sidechain bead type | Sidechain | Sidechain bead type |
|---|---|---|---|
| Na | Backbone only (Na) | Nke | Qd/P1 (uncharged) |
| Nab | C1 | Nl | C1 |
| Nd | Qa/P3 (uncharged) | Nm | C5 |
| Ne | Qa/P1 (uncharged) | NmO | N0 |
| Nfn | SC4–SC4 | Nn | P5 |
| Nf | SC4–SC4–SC4 | Nq | P4 |
| Nfe | SC1–SC5–SC5–SC5 | Nr | N0–Qd/N0–P4 (uncharged) |
| Nfex | C3–SC4–SC4 | Ns | SP1 |
| Nfe[4Br] | SC3–SC4–SC5–SC5–C5 | Nse | P2 |
| Nfe[4Cl] | SC2–SC5–SC5–SC5–SC5 | Nt | SP1 |
| Nf[naph] | SC4–SC4–SC4–SC4–SC4 | Nv | SC2 |
| Nk | C5–Qd/C5–P1 (uncharged) | Nw | SP1–SC4–SC4–SC4 |
| Ny | SC4–SC4–SP1 | Nwe | SC5–SP1–SC4–SC4–SC4 |
| Ni | C1 |
Additional aromatic peptoid analogues of tryptophan like, e.g., Nw and Nwe, have been parameterised for the Martinoid model owing to their use in antimicrobial peptoids development.85 Bead type selection for Nw follows that of the Martini 2.1 on the principle previously established (calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg = 4.17 ± 0.07). However, bead type selection for Nwe is still required. A five-bead model was used, in which an SC5 bead represents the ethyl linker (log
Dcg = 4.17 ± 0.07). However, bead type selection for Nwe is still required. A five-bead model was used, in which an SC5 bead represents the ethyl linker (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg = 4.68 ± 0.24). The Δlog
Dcg = 4.68 ± 0.24). The Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg between these Trp analogues was 0.51 units. This is larger than anticipated compared to the increase from Nf to Nfe, though use of a less hydrophobic linker bead is not possible, and we accept this as a potential overestimate in log
Dcg between these Trp analogues was 0.51 units. This is larger than anticipated compared to the increase from Nf to Nfe, though use of a less hydrophobic linker bead is not possible, and we accept this as a potential overestimate in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg.
Dcg.
Naphthalene containing sidechains are also relevant to peptoid secondary structure formation86 and antimicrobial peptoids.69,87,88 Furthermore, they are likely to be relevant for self-assembling peptoid design given the proclivity of application of N-terminal naphthal in short peptide assembling material design.22 The structure of this residue is a five-membered ring resembling a St Andrew's cross (Fig. 1). To fit the hydrophobicity of this group we compared the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values for benzene and naphthalene, noting that the former is 2.13 compared to 3.3 units,89 giving a Δ
P values for benzene and naphthalene, noting that the former is 2.13 compared to 3.3 units,89 giving a Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of 1.17 units. When a ring of SC4 beads is used to represent the group, a much more hydrophobic value than Nf is obtained (7.00 ± 0.39; Δ
P of 1.17 units. When a ring of SC4 beads is used to represent the group, a much more hydrophobic value than Nf is obtained (7.00 ± 0.39; Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg = 2.27). However, using a ring of SC5 beads yielded log
Dcg = 2.27). However, using a ring of SC5 beads yielded log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg values like Nf which is not chemically accurate and thus the overestimation is the better choice.
Dcg values like Nf which is not chemically accurate and thus the overestimation is the better choice.
Lastly, we felt it would be an interesting to include in the Martinoid model Nfn, the peptoid analouge of phenylglycine, which has been reported to enforce trans amide conformations within peptoid backbones90 and for which a peptide analogue Phg–Phg was shown to form closed-cage nanostructures.91 Nfn is represented by a triangular structure in which the backbone bead is connected to two SC4 beads (Fig. 1). Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 data is not available for this species, though we find that its log
D7.4 data is not available for this species, though we find that its log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg value (3.69 ± 0.11) is less than that of Nf which we might expect and on a first approximation we anticipate the selection of bead types is appropriate.
Dcg value (3.69 ± 0.11) is less than that of Nf which we might expect and on a first approximation we anticipate the selection of bead types is appropriate.
Aliphatic and polar sidechains
Bead type fitting for the peptoid analogues of lysine, Nk and Nke, was performed through the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 comparison for tert-butyloxycarbonyl (boc) protected monomers of these species. This was necessary as purified forms of the unprotected monomers could not be obtained. The species were found to decompose during an acidic deprotection step involved in the synthesis (e.g., using TFA resin cleavage or aqueous HCl: acetone solvent conditions) via what was suspected to be an oxopiperazine formation reaction as previously described by Seo et al.92 In the Martini protein model, lysine is represented by two sidechain beads C3–Qd (C3–P1, uncharged), with the C3 bead capturing the hydrophobicity of the butyl-CH2-linker. This structuring is retained Martinoid. We tuned the linker ‘C’ type bead to balance the hydrophobicity of Nk against the Nke residue which is a two-bead model (e.g., Nke indicates it is the ethyl linker only). In this comparison, the backbone was an Nda bead in both cases and a P1 bead was used as the amine sidechain was boc-protected and thus uncharged. It was found that a C5 bead gave the best possible agreement between experimental relative hydrophobicity of −0.73 units and the CG difference of −1.08
D7.4 comparison for tert-butyloxycarbonyl (boc) protected monomers of these species. This was necessary as purified forms of the unprotected monomers could not be obtained. The species were found to decompose during an acidic deprotection step involved in the synthesis (e.g., using TFA resin cleavage or aqueous HCl: acetone solvent conditions) via what was suspected to be an oxopiperazine formation reaction as previously described by Seo et al.92 In the Martini protein model, lysine is represented by two sidechain beads C3–Qd (C3–P1, uncharged), with the C3 bead capturing the hydrophobicity of the butyl-CH2-linker. This structuring is retained Martinoid. We tuned the linker ‘C’ type bead to balance the hydrophobicity of Nk against the Nke residue which is a two-bead model (e.g., Nke indicates it is the ethyl linker only). In this comparison, the backbone was an Nda bead in both cases and a P1 bead was used as the amine sidechain was boc-protected and thus uncharged. It was found that a C5 bead gave the best possible agreement between experimental relative hydrophobicity of −0.73 units and the CG difference of −1.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg units (Table 4).
Dcg units (Table 4).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for polar and aliphatic peptoid monomers
D values for polar and aliphatic peptoid monomers
| Species | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 D7.4 |
Relative log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 D7.4 |
Calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg Dcg |
CG Relative log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg Dcg |
|---|---|---|---|---|
| a Denotes that H-Nkeboc-NH2 is relative to H-Nkboc-NH2. b Indicates that H-Nab-NH2 is relative to Nf-NH2. | ||||
| H-Nkboc-NH2 | 0.00 ± 0.03 | — | 1.14 ± 0.07 | — |
| H-Nkeboc-NH2 | −0.73 ± 0.01 | −0.73a | 0.06 ± 0.06 | −1.08 |
| H-Nab-NH2 | −1.23 ± 0.03 | −1.24b | 3.45 ± 0.16 | −1.29 |
For the butyl sidechain containing residue, Nab, monomer we opted to try a C1 bead, noting that this same bead is used in the Martini model for aliphatic moieties leucine and isoleucine. We compare the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 for this Nk species with the aliphatic sidechain to Nf, which represents aromatic hydrophobicity. Experimentally, Δ
D7.4 for this Nk species with the aliphatic sidechain to Nf, which represents aromatic hydrophobicity. Experimentally, Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 was found to be −1.23, and we obtain a Δ
D7.4 was found to be −1.23, and we obtain a Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg = −1.29 for the C1 bead, in good agreement. Therefore, we proceed with the use of a C1 bead for Nab, Nl and Ni within the Martinoid model.
Dcg = −1.29 for the C1 bead, in good agreement. Therefore, we proceed with the use of a C1 bead for Nab, Nl and Ni within the Martinoid model.
Additional choices
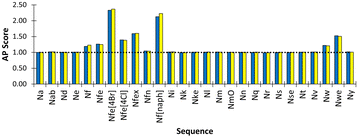
The ether sidechain peptoid, NmO is defined as a N0 bead, as the methoxyethane building block was also represented with this bead type in the Martini model.53 Note we make use of small beads for Ns, Nt and Nv owing to the criticism of Martini 2.1, in which it is recognised that over-massing beads is problematic for solvation and entropy within the Martini model.58Aggregation propensity (AP) score evaluation was then used to further validate our selection of bead types and demonstrate consistency with chemical expectations, we performed aggregation/self-assembly screening for all peptoid monomers we have now developed in this first report of the Martinoid model. For each monomer, 600 molecules with charged N-termini (termini Qd, acidic to neutral conditions) were placed in a water box of dimensions 12.5 × 12.5 × 12.5 nm and simulated for 200 ns. AP scores >1.0 are considered indicative of aggregation.
We found that Nfe[4Br] had the highest AP score of 2.72 (Fig. 4) and formed sheets with a defined hydrophobic core, which is consistent with the use of this monomer in oligomers which are very effective in forming well defined nanosheets and nanotubes.18,44 Nf[naph] with naphthalene sidechains and an AP score of 2.33 formed a fibrous mesh in which the polar backbone beads face into the surrounding solvent and ions. Importantly, it was found that other aromatic derivatives Nf, Nfe, Nfex and Nfe[4Cl] only clustered but were not observed to assemble into extended structures. This is consistent with our observations in the laboratory, where it is found that all these monomers readily dissolved in D2O and PBS solutions, indicating a phenylene sidechain on its own is not hydrophobic enough to cause aggregation when considered together with the polar termini of the peptoid backbone. The Martinoid bead choices are therefore reasonable and reproduce the chemical characteristics of peptoid monomers. The assembly potential of Nfe[4Br] and Nf[naph] is of interest and will be the focus of future work.
Application to peptoid assembly systems
To further assess the applicability of the Martinoid model, we applied it to two systems encompassing well characterized and distinct assembly behaviour: peptoid trimer assembly and peptoid nanosheets.Assembly of tripeptoid Nf–Nke–Nf
The tripeptoid Nf–Nke–Nf forms well defined bundles of nanofibrillar assemblies indicated by fine striations of uniform widths of ∼6 nm, as observed by Cyro-EM (Fig. 5a). Previously, using various computational approaches, we attributed this extended molecular organisation to complementary intramolecular edge-to-face and face-to-face organisation of aromatic groups which flank the central charged Nke unit.51 However a conceptual barrier to further exploration of this system at atomistic resolution was the ambiguity of relative populations of amide sequence states, alongside the inherent computational limitations on system size and simulation duration implicit with this level of theory.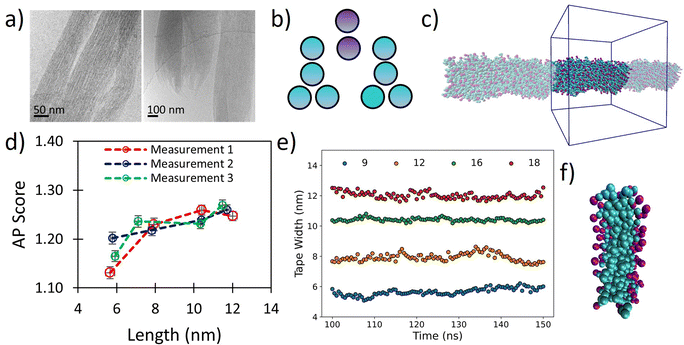 | ||
| Fig. 5 (a) Cryo-TEM images of tripeptoid Nf–Nke–Nf assembled into nanofibrous bundles reproduced with permission from ref. 31. Copyright RSC 2020, (b) CG structure of Nf–Nke–Nf tripeptoid, (c) screenshots of resultant tape after 150 ns, showing highly organised aromatic region which agrees with a benzyl fluorescence shift observed experimentally for this sequence, (d) AP score verses average fibre length for various starting widths of Nf–Nke–Nf showing that growth occurs between 6–8 nm after which further AP increases are less substantial indicating that growth dimensions are emergent, (e) average tape width verses time for different numbers of starting molecules, (f) a close up image of tape cross section showing a well-defined hydrophobic domain defined by benzene side chains. | ||
We hypothesized that the observed individual fibre widths represent some equilibrium local limitation balancing intermolecular interactions and sequence arrangement. Although cryo-EM was not able to resolve the cross-sectional shape of the nanofibrils, we posit that at small length scales around this size any distinction between tapes and fibrils would be relatively small. To probe whether the width of the individual fibrils may indeed represent an equilibrium structure, we therefore used our Martinoid model to build nano-tapes of a range of starting molecular widths to investigate whether the Nf–Nke–Nf assembly would approach an apparent limit in width analogous to the observed equilibrium fibre dimension.
Tapes of ‘infinite’ length, continuous in the z-dimension, composed of 9, 12, 16 and 18 molecular layers stacked along the short axis were made (Fig. 5b and c) and these were simulated for 150 ns. The tapes initially disassembled in a process driven by electrostatic repulsion of charged termini/sidechains. Overtime, however, the tapes reformed with relatively homogenous widths (Fig. 5e) and the peptoids were found to organise with charged residues presented towards the surrounding water (Fig. 5f). Notably, we observed ‘freezing’ of the Martini water which is indicative of the emergence of repeating ordered structures within the system,53 and so it was necessary to include 10% antifreeze water beads.
Visually, the aromatic groups also appear to be optimally orientated (Fig. 5f), which agrees with the benzyl fluorescence shift consistent with sidechain π–π stacking found experimentally for this sequence.31 Furthermore, the present Martinoid CG-MD can reproduce a tape thickness of ∼6 nm starting with assemblies composed of 9 and 12 molecules. The Nf–Nke–Nf peptoid is an amphiphilic sequence and the experimentally observed width of the self-assembly is expected to have emerged from a balance of electrostatic repulsion versus favourable hydrophobic residue burial, constrained by solvation of polar residues and conformational energetics. To assess whether this width is indeed an emergent property of the system, we measured the AP score reached at the end of the simulations. It was revealed that there was a significant increase in the AP score between an initial width of 9 molecules in the cross-section to 12 molecules, and then the AP score plateaued for larger widths (Fig. 5d). The initial gain in the AP score moving from a small (9) to intermediate number of molecules (12) in the cross section could be indicative of an increased ability of the system to bury the hydrophobic sidechains. The limit in the AP score at increasing molecular width could then indicate a different thermodynamic control. Furthermore, free assembly simulations of Nf–Nke–Nf also yielded flat and tapelike extended structures with similar dimensions to those obtained for the periodically fixed assemblies (Fig. S94, ESI†).
Peptoid monolayer structuring
We also validated the Martinoid model by studying the self-organisation of long 28-mer (Nke–Nfe)7–(Ne–Nfe)7 amphiphilic sequences at an oil–water interface, which has been shown to be a critical first step in the assembly of a class of bilayered peptoid nanosheets.93 This nanostructure is considered a major development because it demonstrated the ability of achiral peptoid chains to access a novel “Σ-strand” secondary structure not available to natural peptides.61 While the initial experimental report of nanosheet assembly was performed at an air–water interface, simulation of interactions at such an interface is inherently challenging in molecular dynamics and in the peptoid domain this required bespoke simulation system design.41 Later work by Robertson et al. showed with an oil–water interface that the selection of the non-aqueous, oleophilic phase is critical to the formation of nanosheets.93 Therefore, we simulated peptoid monolayers at the oil–water interface using two organic solvents, chloroform and hexadecane, that have been shown to accommodate suitable interactions for nanosheet assembly. According to experimental observations, the peptoid chains were arranged with antiparallel packing, aromatic sidechains from Nfe residues facing the oil-phase, and oppositely charged residues from adjacent chains paired with one another (Fig. S95, ESI†). The assemblies consisted of 14 extended oligomers and were simulated to 250 ns, with a 10 fs timestep.Over the simulation, we observe that a well-defined sheet structure was retained, and 20% anti-freeze water was required due to prevent the emergence of crystallinity between Martini water molecules, which is expected from seeding by the well-packed sequences and the relatively small system size. Analysis of our peptoid monolayer returned an end-to-end length of ∼76–77 Å for individual sequences (Fig. S95, ESI†). Elsewhere Hudson et al. estimated the width of the peptoid 28mer in a cis Σ-strand configuration as being 79.8 Å by all atom MD simulations of peptoid nanosheets.61 Thus, although the parameterisation of Martinoid is focused on short sequences, it can reproduce behaviour of polymer like chains with reasonable accuracy.
Experimental
Materials and methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50/v, Fluorochem, Glossop, UK) for 40 minutes with shaking. The resin was subsequently filtered and washed four times with DMF and two times with NMP. The resin was then treated with the amine required for each type of sidechain (Table S1, ESI†) dissolved in NMP (8.8 mL, 1.5 M) with shaking for 40 minutes. The resin was then alternately washed with methanol and DCM three times and dried. The resin was twice treated with cleavage solution (95% TFA: 2.5% H2O: 2.5% TIPS) with shaking for 20 minutes each time. The two batches of TFA with the cleaved peptoid was separately collected, and the TFA was removed by rotary evaporation leaving a yellow oil, this was solubilised in a mixture of H2O and acetonitrile, transferred to a pre-weighed vial and freeze-dried.
50/v, Fluorochem, Glossop, UK) for 40 minutes with shaking. The resin was subsequently filtered and washed four times with DMF and two times with NMP. The resin was then treated with the amine required for each type of sidechain (Table S1, ESI†) dissolved in NMP (8.8 mL, 1.5 M) with shaking for 40 minutes. The resin was then alternately washed with methanol and DCM three times and dried. The resin was twice treated with cleavage solution (95% TFA: 2.5% H2O: 2.5% TIPS) with shaking for 20 minutes each time. The two batches of TFA with the cleaved peptoid was separately collected, and the TFA was removed by rotary evaporation leaving a yellow oil, this was solubilised in a mixture of H2O and acetonitrile, transferred to a pre-weighed vial and freeze-dried.
Preparative reverse phase HPLC (RP-HPLC) was used to purify the peptoids. Stock solutions of the crude material were prepared in mixtures of H2O (Fischer Scientific, HPLC Gradient Grade) and acetonitrile (Fischer Scientific, HPLC Gradient Grade) which were filtered through 0.2-micron syringe filters to remove any solids. Preparative RP-HPLC was performed on a Jupiter C18 column (Phenomenex, 90 Å, 250 × 10.0 mm) to purify the material using an isocratic eluent mixture of 2% acetonitrile: 98% H2O with 0.1% TFA. Higher acetonitrile percentages were found to preclude material partitioning onto the solid phase, with the material eluting as the injection peak. 1 mL of crude stock at concentrations from 2–25 mg mL−1 were injected across different preparative runs and fractions were collected every 30 or 60 seconds. The HPLC fractions with matching UV absorbance peak features (data at 220 nm and 254 nm) were combined, and solvent was removed successively by a centrifugal evaporation (heating at 30 °C; to reduce volume to a few millilitres) and by freeze-drying. A fluffy white crystalline solid was obtained for Nfe and Nfes, while for the product for Nfe was more granular in nature. The identity and final purity of the product was characterized by NMR (see ESI,† Section 2).
Acetonitrile was selected as the preferred polar aprotic solvent as several of the monomer products precipitated in this solvent which was convenient for work-up. In initial synthesis batches, 1 equivalent of diisopropylethylamine (DIPEA, Alfa Aesar) was used as a complementary base to neutralise the equivalent of hydrogen bromide formed by the reaction. Through X-ray crystallography characterization, it was confirmed that the final product was a bromide salt (results not shown). It was found in subsequent batches that similar yields could be obtained with the omission of DIPEA, as well as resulting in faster precipitate formation and reduced adhesion to glassware. For all batches, after 12–24 h the precipitate was recrystallised in hot acetonitrile: methanol (approximately 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/v). For Nke it was necessary to use acetone as the recrystallisation solvent. Although this monomer is unstable in acetone over extended periods (suspected imine formation), it is found to be sufficiently stable for our protocol with a short recrystallisation step (e.g., rapid transfer of hot liquor into ice-bath). All solids were filtered and washed with the relevant recrystallization solution. The identity and final purity of the product was characterized by NMR (see ESI,† Section 2).
1/v). For Nke it was necessary to use acetone as the recrystallisation solvent. Although this monomer is unstable in acetone over extended periods (suspected imine formation), it is found to be sufficiently stable for our protocol with a short recrystallisation step (e.g., rapid transfer of hot liquor into ice-bath). All solids were filtered and washed with the relevant recrystallization solution. The identity and final purity of the product was characterized by NMR (see ESI,† Section 2).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) D measurement method.
The method described by Cobb et al.76 was broadly followed in this work: 500 μL of octanol (Sigma Aldrich) measured by weight was placed in an HPLC vial and 500 μL of PBS solution was added (Gibco 10× diluted as required), into which peptoid material was diluted to the concentration range 0.3–5 mg mL−1 as required for a given species. More material was required for aliphatic monomers (e.g., Nle, Nab or boc-Nk) as opposed to their aromatic counterparts (e.g., Nf, Nfe, Nfes or Nfe[4Cl]). This vial was then sealed and agitated at 150 rpm for ∼24 h in an incubator to maintain a constant temperature of 25 °C. Then a portion of both phases (∼100 μL) was analysed using reversed-phase high performance liquid chromatography (HPLC) using a Luna 5 μm C18 column (Phenomenex, 100 Å, 100 × 4.6 mm) with a gradient of 2 to 45% acetonitrile water over either 15 or 30 minutes with 0.1% trifluoroacetic acid as an additive. The resultant peak areas were integrated (peak area per minute) and compared between the two phases.
D measurement method.
The method described by Cobb et al.76 was broadly followed in this work: 500 μL of octanol (Sigma Aldrich) measured by weight was placed in an HPLC vial and 500 μL of PBS solution was added (Gibco 10× diluted as required), into which peptoid material was diluted to the concentration range 0.3–5 mg mL−1 as required for a given species. More material was required for aliphatic monomers (e.g., Nle, Nab or boc-Nk) as opposed to their aromatic counterparts (e.g., Nf, Nfe, Nfes or Nfe[4Cl]). This vial was then sealed and agitated at 150 rpm for ∼24 h in an incubator to maintain a constant temperature of 25 °C. Then a portion of both phases (∼100 μL) was analysed using reversed-phase high performance liquid chromatography (HPLC) using a Luna 5 μm C18 column (Phenomenex, 100 Å, 100 × 4.6 mm) with a gradient of 2 to 45% acetonitrile water over either 15 or 30 minutes with 0.1% trifluoroacetic acid as an additive. The resultant peak areas were integrated (peak area per minute) and compared between the two phases.
Starting structures for atomistic mapping simulations were obtained using the Conformer/Rotameter Ensemble Sampling Tool (CREST).60 These were solvated in 3.8 × 3.8 × 3.8 nm boxes with TIP3P water using either Gromacs ver. 2020.3 or 2020.7, which were also used for subsequent simulations.98 The TopoTools99 plugin in VMD95 plugin was used to convert these to Gromacs compatible parameters.
Treatment of non-bonded parameters within the atomistic simulations was as follows: a Verlet cutoff scheme was used, LJ interactions were calculated below a cutoff of 1.2 nm, with a force-switch modifier being used after 1.0 nm. Local electrostatic interactions were calculated below the 1.2 nm cutoff, beyond which particle–mesh Ewald (PME) summation was used to calculate long-range interactions, with a grid spacing of 0.12 nm.
Starting velocities were generated to a Maxwell distribution at 298.15 K, both the velocity rescaling and Nosé–Hoover thermostats were used within the equilibration and production procedure. The Parrinello–Rahman barostat was used to maintain a pressure of 1.0325 bar with a compressibility of 4.5 × 10−5 bar−1. Throughout these simulations hydrogen bonds were constrained using the LINCS algorithm.100 Specific details of simulations can be found in ESI,† Section 5.
The general simulation procedure was that of a minimisation, followed by a short equilibration using the Berendsen barostat, followed by a production simulation using the Parrinello–Rahman barostat to maintain either isotropic or semiisotropic pressure control, with a reference pressure of 1.01325 bar and compressibility of 3 × 10−4 bar−1 being used throughout. The velocity rescaling algorithm was used to maintain a temperature of 298.15 K and starting velocities were generated to a Maxwell distribution. For specific simulation details see ESI,† Section 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) D estimation.
Umbrella sampling was used to evaluate the partition free energies of the peptoid monomers, we used an umbrella sampling method in which we sampled positions from 0.0–4.0 nm across a water–octanol interface using a spacing of 0.1 nm. To retain the monomer at the position of interest a harmonic potential, of force constant 1100 kJ mol−1 nm−2 was used and each window was simulated for 5 ns. The weighted analysis histogram method (WHAM) implemented using Gromacs (gmx wham) was then used to extract an unbiased PMF.101 The highest energies obtained within pure water (0–0.5 nm) and in octanol (3.5–4.0 nm) were compared to obtain ΔG and hence compute the log
D estimation.
Umbrella sampling was used to evaluate the partition free energies of the peptoid monomers, we used an umbrella sampling method in which we sampled positions from 0.0–4.0 nm across a water–octanol interface using a spacing of 0.1 nm. To retain the monomer at the position of interest a harmonic potential, of force constant 1100 kJ mol−1 nm−2 was used and each window was simulated for 5 ns. The weighted analysis histogram method (WHAM) implemented using Gromacs (gmx wham) was then used to extract an unbiased PMF.101 The highest energies obtained within pure water (0–0.5 nm) and in octanol (3.5–4.0 nm) were compared to obtain ΔG and hence compute the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dcg (performed in triplicate for each monomer of interest, Tables S48–S57, ESI†). Additionally, we validated this method against known amino acid log
Dcg (performed in triplicate for each monomer of interest, Tables S48–S57, ESI†). Additionally, we validated this method against known amino acid log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values (ESI,† Section 7, Tables S27–S47). More information on this method can be found at ref. 102.
P values (ESI,† Section 7, Tables S27–S47). More information on this method can be found at ref. 102.
Conclusions
We present Martinoid, a Martini-compatible peptoid forcefield built for the simulation of a wide range of peptoid chemistries and applications. In this work we have performed parameterisation in a dual bottom-up and top-down approach targeting atomistic molecular dynamics simulations and the reproduction of trends in experimentally obtained log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D measurements, respectively. It has been shown to be applicable to several peptoid assembly systems of various sizes, including monomers, trimers, and 28-mer sequences.
D measurements, respectively. It has been shown to be applicable to several peptoid assembly systems of various sizes, including monomers, trimers, and 28-mer sequences.
Simplicity and transferability of parameters has been a central concern of our development approach. This follows the spirit of the Martini forcefield. We hope that the community may find the model widely applicable and provide an edge to peptoid materials development through computational sequence discovery, which we feel has been lacking to date. All parameters reported in this work and the Martinoid script for structure generation can be obtained at our GitHub repository. (https://github.com/Tuttlelab/MartinoidPeptoidCG).
Author contributions
HWAS designed the forcefield, performed all parameterisation, small molecule synthesis, experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D7.4 characterisation and drafted the manuscript. AVT and HWAS jointly developed the Martinoid code and AVT set-up the GitHub. KHAL and TT supervised the project and edited the manuscript.
D7.4 characterisation and drafted the manuscript. AVT and HWAS jointly developed the Martinoid code and AVT set-up the GitHub. KHAL and TT supervised the project and edited the manuscript.
Data availability
All computational data described in this publication are openly available from the University of Strathclyde KnowledgeBase at https://doi.org/10.15129/e51b58cd-110a-4eee-83f7-c84383ed3519.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
HWAS thanks the Carnegie Trust for funding. Computational results were obtained using the EPSRC funded ARCHIE WeSt High – Performance Computer (www.archie-west.ac.uk; EPSRC grant no. EP/K000586/1).References
- Q. Sui, D. Borchardt and D. L. Rabenstein, J. Am. Chem. Soc., 2007, 129, 12042–12048 CrossRef CAS PubMed.
- J. R. B. Eastwood, E. I. Weisberg, D. Katz, R. N. Zuckermann and K. Kirshenbaum, Pept. Sci., 2023, 115, e24307 CrossRef CAS.
- R. N. Zuckermann, J. M. Kerr, S. B. H. Kent and W. H. Moos, J. Am. Chem. Soc., 1992, 114, 10646–10647 CrossRef CAS.
- A. S. Culf and R. J. Ouellette, Molecules, 2010, 15, 5282–5335 CrossRef CAS PubMed.
- C. M. Davern, B. D. Lowe, A. Rosfi, E. A. Ison and C. Proulx, Chem. Sci., 2021, 12, 8401–8410 RSC.
- N. Soumanou, D. Lybye, T. Hjelmgaard and S. Faure, Green Chem., 2023, 25, 3615–3623 RSC.
- Y. U. Kwon and T. Kodadek, J. Am. Chem. Soc., 2007, 129, 1508–1509 CrossRef CAS PubMed.
- J. M. Astle, D. G. Udugamasooriya, J. E. Smallshaw and T. Kodadek, Int. J. Pept. Res. Ther., 2008, 14, 223–227 CrossRef CAS.
- S. M. Miller, R. J. Simon, S. Ng, R. N. Zuckermann, J. M. Kerr and W. H. Moos, Drug Dev. Res., 1995, 35, 20–32 CrossRef CAS.
- K. L. Bicker and S. L. Cobb, Chem. Commun., 2020, 56, 11158–11168 RSC.
- E. Y. S. Sebastian, P. Bhardwaj, M. Maruthi, D. Kumar and M. K. Gupta, J. Mater. Chem. B, 2023, 9975–9986 RSC.
- M. L. Huang, D. Ehre, Q. Jiang, C. H. Hu, K. Kirshenbaum and M. D. Ward, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19922–19927 CrossRef CAS PubMed.
- K. H. A. Lau, T. S. Sileika, S. H. Park, A. M. L. Sousa, P. Burch, I. Szleifer and P. B. Messersmith, Adv. Mater. Interfaces, 2015, 2, 1400225 CrossRef PubMed.
- A. Hasan, K. Lee, K. Tewari, L. M. Pandey, P. B. Messersmith, K. Faulds, M. Maclean and K. H. A. Lau, Chem. – Eur. J., 2020, 26, 5789–5793 CrossRef CAS PubMed.
- A. Battigelli, Biopolymers, 2019, 110, e23265 CrossRef PubMed.
- M. F. Zhao, Biopolymers, 2021, 112, e23469 CrossRef CAS PubMed.
- K. T. Nam, S. A. Shelby, P. H. Choi, A. B. Marciel, R. Chen, L. Tan, T. K. Chu, R. A. Mesch, B. C. Lee, M. D. Connolly, C. Kisielowski and R. N. Zuckermann, Nat. Mater., 2010, 9, 454–460 CrossRef CAS PubMed.
- H. B. Jin, Y. H. Ding, M. M. Wang, Y. Song, Z. H. Liao, C. J. Newcomb, X. P. Wu, X. Q. Tang, Z. Li, Y. H. Lin, F. Yan, T. Y. Jian, P. Mu and C. L. Chen, Nat. Commun., 2018, 9, 270 CrossRef PubMed.
- H. K. Murnen, A. M. Rosales, J. N. Jaworsk, R. A. Segalman and R. N. Zuckermann, J. Am. Chem. Soc., 2010, 132, 16112–16119 CrossRef CAS PubMed.
- C. Fetsch, J. Gaitzsch, L. Messager, G. Battaglia and R. Luxenhofer, Sci. Rep., 2016, 6, 33491 CrossRef PubMed.
- M. E. Y. Hamish, W. A. Swanson, A. Jawed, V. Saxena, M. G. L. Merrilees, T. Tuttle, L. M. Pandey, I. W. Hamley and K. Hang Aaron Lau, in Supramolecular Nanotechnology: Advanced Design of Self-Assembled Functional Materials, ed. M. C.-S. Omar Azzaroni, Wiley-VCH GmbH, 2023, vol. 3, ch. 36, pp. 969–999 Search PubMed.
- S. Fleming and R. V. Ulijn, Chem. Soc. Rev., 2014, 43, 8150–8177 RSC.
- A. Lampel, R. V. Ulijn and T. Tuttle, Chem. Soc. Rev., 2018, 47, 3737–3758 RSC.
- M. Ramakrishnan, A. van Teijlingen, T. Tuttle and R. V. Ulijn, Angew. Chem., Int. Ed., 2023, e20221806 Search PubMed.
- Z. D. Wu, M. Tan, X. M. Chen, Z. M. Yang and L. Wang, Nanoscale, 2012, 4, 3644–3646 RSC.
- H. P. R. Mangunuru, H. Yang and G. J. Wang, Chem. Commun., 2013, 49, 4489–4491 RSC.
- V. Castelletto, A. M. Chippindale, I. W. Hamley, S. Barnett, A. Hasan and K. H. A. Lau, Chem. Commun., 2019, 55, 5867–5869 RSC.
- Z. Shlomo, T. P. Vinod, R. Jelinek and H. Rapaport, Chem. Commun., 2015, 51, 3154–3157 RSC.
- Z. Azoulay, P. Aibinder, A. Gancz, J. Moran-Gilad, S. Navon-Venezia and H. Rapaport, Acta Biomater., 2021, 125, 231–241 CrossRef CAS PubMed.
- G. G. Scott, P. J. McKnight, T. Tuttle and R. V. Ulijn, Adv. Mater., 2016, 28, 1381–1386 CrossRef CAS PubMed.
- V. Castelletto, J. Seitsonen, K. M. Tewari, A. Hasan, R. M. Edkins, J. Ruokolainen, L. M. Pandey, I. W. Hamley and K. H. A. Lau, ACS Macro Lett., 2020, 9, 1415–1416 CrossRef CAS PubMed.
- M. Reches and E. Gazit, Science, 2003, 300, 625–627 CrossRef CAS PubMed.
- M. Reches and E. Gazit, Isr. J. Chem., 2005, 45, 363–371 CrossRef CAS.
- S. Alamdari and J. Pfaendtner, J. Phys. Chem. B, 2023, 127, 6163–6170 CrossRef CAS PubMed.
- P. W. J. M. Frederix, R. V. Ulijn, N. T. Hunt and T. Tuttle, J. Phys. Chem. Lett., 2011, 2, 2380–2384 CrossRef CAS PubMed.
- P. W. J. M. Frederix, G. G. Scott, Y. M. Abul-Haija, D. Kalafatovic, C. G. Pappas, N. Javid, N. T. Hunt, R. V. Ulijn and T. Tuttle, Nat. Chem., 2015, 7, 30–37 CrossRef CAS PubMed.
- A. van Teijlingen and T. Tuttle, J. Chem. Theory Comput., 2021, 17, 3221–3232 CrossRef CAS PubMed.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grunewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domanski, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed.
- S. J. Marrink, L. Monticelli, M. N. Melo, R. Alessandri, D. P. Tieleman and P. C. T. Souza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1620 Search PubMed.
- T. K. Haxton, R. V. Mannige, R. N. Zuckermann and S. Whitelam, J. Chem. Theory Comput., 2015, 11, 303–315 CrossRef CAS PubMed.
- T. K. Haxton, R. N. Zuckermann and S. Whitelam, J. Chem. Theory Comput., 2016, 12, 345–352 CrossRef CAS PubMed.
- D. T. Mirijanian, R. V. Mannige, R. N. Zuckermann and S. Whitelam, J. Comput. Chem., 2014, 35, 360–370 CrossRef CAS PubMed.
- M. F. Zhao, J. Sampath, S. Alamdari, G. Shen, C. L. Chen, C. J. Mundy, J. Pfaendtner and A. L. Ferguson, J. Phys. Chem. B, 2020, 124, 7745–7764 CrossRef CAS PubMed.
- H. B. Jin, F. Jiao, M. D. Daily, Y. L. Chen, F. Yan, Y. H. Ding, X. Zhang, E. J. Robertson, M. D. Baer and C. L. Chen, Nat. Commun., 2016, 7, 12252 CrossRef CAS PubMed.
- P. Gao and A. Tartakovsky, arXiv, 2019, preprint, arXiv:1903.01975 DOI:10.48550/arXiv.1903.01975.
- R. Alessandri, J. J. Uusitalo, A. H. de Vries, R. W. A. Havenith and S. J. Marrink, J. Am. Chem. Soc., 2017, 139, 3697–3705 CrossRef CAS PubMed.
- P. Bjelkmar, P. Larsson, M. A. Cuendet, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2010, 6, 459–466 CrossRef CAS PubMed.
- A. Banerjee and M. Dutt, J. Chem. Phys., 2023, 158, 114105 CrossRef CAS PubMed.
- M. L. Hebert, D. S. Shah, P. Blake and S. L. Servoss, Coatings, 2013, 3, 98–107 CrossRef CAS.
- M. L. Hebert, D. S. Shah, P. Blake, J. P. Turner and S. L. Servoss, Org. Biomol. Chem., 2013, 11, 4459–4464 RSC.
- K. H. A. L. Hamish, W. A. Swanson and T. Tuttle, J. Phys. Chem. B, 2023, 10601–10614 Search PubMed.
- K. H. A. L. Hamish, W. A. Swanson and T. Tuttle, A Convention for Peptoid Monomer Naming, The University of Strathclyde, 2023 Search PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2008, 4, 819–834 CrossRef CAS PubMed.
- C. Empereur-Mot, L. Pesce, G. Doni, D. Bochicchio, R. Capelli, C. Perego and G. M. Pavan, ACS Omega, 2020, 5, 32823–32843 CrossRef CAS PubMed.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810 CrossRef PubMed.
- D. H. de Jong, S. Baoukina, H. I. Ingolfsson and S. J. Marrink, Comput. Phys. Commun., 2016, 199, 1–7 CrossRef CAS.
- R. Alessandri, P. C. T. Souza, S. Thallmair, M. N. Melo, A. H. de Vries and S. J. Marrink, J. Chem. Theory Comput., 2019, 15, 5448–5460 CrossRef CAS PubMed.
- A. van Teijlingen, M. C. Smith and T. Tuttle, Acc. Chem. Res., 2023, 56, 644–654 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- B. C. Hudson, A. Battigelli, M. D. Connolly, J. Edison, R. K. Spencer, S. Whitelam, R. N. Zuckermann and A. K. Paravastu, J. Phys. Chem. Lett., 2018, 9, 2574–2578 CrossRef CAS PubMed.
- Y. H. Ge and V. A. Voelz, J. Phys. Chem. B, 2018, 122, 5610–5622 CrossRef CAS PubMed.
- M. F. D. Hurley, J. D. Northrup, Y. H. Ge, C. E. Schafineister and V. A. Voelz, J. Chem. Inf. Model., 2021, 61, 2818–2828 CrossRef CAS PubMed.
- R. K. Spencer, G. L. Butterfoss, J. R. Edison, J. R. Eastwood, S. Whitelam, K. Kirshenbaum and R. N. Zuckermann, Biopolymers, 2019, 110, e2326 CrossRef PubMed.
- S. Sami and S. J. Marrink, J. Chem. Theory Comput., 2023, 4040–4046 CrossRef CAS PubMed.
- K. Kirshenbaum, A. E. Barron, R. A. Goldsmith, P. Armand, E. K. Bradley, K. T. V. Truong, K. A. Dill, F. E. Cohen and R. N. Zuckermann, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 4303–4308 CrossRef CAS PubMed.
- T. J. Sanborn, C. W. Wu, R. N. Zuckerman and A. E. Barron, Biopolymers, 2002, 63, 12–20 CrossRef CAS PubMed.
- J. A. Patch and A. E. Barron, J. Am. Chem. Soc., 2003, 125, 12092–12093 CrossRef CAS PubMed.
- A. Hasan, V. Saxena, V. Castelletto, G. Zimbitas, J. Seitsonen, J. Ruokolainen, L. M. Pandey, J. Sefcik, I. W. Hamley and K. H. A. Lau, Front. Chem., 2020, 8, 416 CrossRef CAS PubMed.
- J. E. Nielsen, M. A. Alford, D. B. Y. Yung, N. Molchanova, J. A. Fortkort, J. S. Lin, G. Diamond, R. E. W. Hancock, H. Jenssen, D. Pletzer, R. Lund and A. E. Barron, ACS Infect. Dis., 2022, 8, 533–545 CrossRef CAS PubMed.
- P. Armand, K. Kirshenbaum, A. Falicov, R. L. Dunbrack, K. A. Dill, R. N. Zuckermann and F. E. Cohen, Folding Design, 1997, 2, 369–375 CrossRef CAS PubMed.
- N. P. Chongsiriwatana, J. A. Patch, A. M. Czyzewski, M. T. Dohm, A. Ivankin, D. Gidalevitz, R. N. Zuckermann and A. E. Barron, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2794–2799 CrossRef CAS PubMed.
- C. W. Wu, T. J. Sanborn, K. Huang, R. N. Zuckermann and A. E. Barron, J. Am. Chem. Soc., 2001, 123, 6778–6784 CrossRef CAS PubMed.
- K. Huang, C. W. Wu, T. J. Sanborn, J. A. Patch, K. Kirshenbaum, R. N. Zuckermann, A. E. Barron and I. Radhakrishnan, J. Am. Chem. Soc., 2006, 128, 1733–1738 CrossRef CAS PubMed.
- P. Ghosh, G. L. Ruan, N. Fridman and G. Maayan, Chem. Commun., 2022, 58, 9922–9925 RSC.
- H. L. Bolt, C. E. J. Williams, R. V. Brooks, R. N. Zuckermann, S. L. Cobb and E. H. C. Bromley, Biopolymers, 2017, 108, e23014 CrossRef PubMed.
- R. A. Klein, M. J. Moore and M. W. Smith, Biochim. Biophys. Acta, 1971, 233, 420–433 CrossRef CAS PubMed.
- L. M. Yunger and R. D. Cramer, Mol. Pharmacol., 1981, 20, 602–608 CAS.
- A. Leo, C. Hansch and D. Elkins, Chem. Rev., 1971, 71, 525–616 CrossRef CAS.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schafer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697 CrossRef CAS PubMed.
- C. Guo, Y. Luo, R. H. Zhou and G. H. Wei, ACS Nano, 2012, 6, 3907–3918 CrossRef CAS PubMed.
- J. L. Fauchere and V. Pliska, Eur. J. Med. Chem., 1983, 18, 369–375 CAS.
- H. L. Bolt, G. A. Eggimann, C. A. B. Jahoda, R. N. Zuckermann, G. J. Sharples and S. L. Cobb, MedChemComm, 2017, 8, 886–896 RSC.
- N. Molchanova, J. E. Nielsen, K. B. Sorensen, B. K. Prabhala, P. R. Hansen, R. Lund, A. E. Barron and H. Jenssen, Sci. Rep., 2020, 10, 14805 CrossRef CAS PubMed.
- B. Mojsoska, G. Carretero, S. Larsen, R. V. Mateiu and H. Jenssen, Sci. Rep., 2017, 7, 42332 CrossRef CAS PubMed.
- J. R. Stringer, J. A. Crapster, I. A. Guzei and H. E. Blackwell, J. Am. Chem. Soc., 2011, 133, 15559–15567 CrossRef CAS PubMed.
- T. S. Ryge and P. R. Hansen, J. Pept. Sci., 2005, 11, 727–734 CrossRef CAS PubMed.
- M. L. Huang, S. B. Y. Shin, M. A. Benson, V. J. Torres and K. Kirshenbaum, ChemMedChem, 2012, 7, 114–122 CrossRef CAS PubMed.
- C. Hansch, A. Leo and D. Hoekman, Exploring QSAR - Hydrophobic, Electronic, and Steric Constants, American Chemical Society, Washington, DC, 1995 Search PubMed.
- D. Kalita, B. Sahariah, S. P. Mookerjee and B. K. Sarma, Chem. – Asian J., 2022, 17, e202200 CrossRef PubMed.
- M. Reches and E. Gazit, Nano Lett., 2004, 4, 581–585 CrossRef CAS.
- Y. Lee and J. Seo, Tetrahedron Lett., 2018, 59, 3946–3949 CrossRef CAS.
- E. J. Robertson, G. K. Oliver, M. Qian, C. Proulx, R. N. Zuckermann and G. L. Richmond, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13284–13289 CrossRef CAS PubMed.
- A. Salaün, A. Favre, B. Le Grel, M. Potel and P. Le Grel, J. Org. Chem., 2006, 71, 150–158 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14.1, 33–38 CrossRef PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernandez, C. R. Schwantes, L. P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- T. M. M. J. Abraham, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- J. V. Vermaas, D. J. Hardy, J. E. Stone, E. Tajkhorshid and A. Kohlmeyer, J. Chem. Inf. Model., 2016, 56, 1112–1116 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- Martini tutorials: Free energy techniques https://cgmartini.nl/index.php/tutorials-general-introduction-gmx5/partitioning-techniques, Accessed 2023.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05907c |
| This journal is © the Owner Societies 2024 |