Improving the estimation accuracy of confined vapor–liquid equilibria by fine-tuning the pure component parameter in the PC-SAFT equation of state
Received
8th December 2023
, Accepted 3rd April 2024
First published on 8th April 2024
Abstract
We propose a thermodynamic model that combines the Young–Laplace equation and perturbed chain-statistical associating fluid theory (PC-SAFT) equation of state to estimate capillary condensation pressure in microporous and mesoporous sorbents. We adjust the PC-SAFT dispersion-energy parameter when the pore size becomes comparable to the molecular dimension. This modelling framework is applied to diverse systems containing associating and non-associating gases, various sorbents, and a wide range of temperatures. Our simulation results show that under extreme confinement, a higher value of the dispersion-energy parameter (ε) is required. Furthermore, using the experimental saturation pressure data for 18 different associating and non-associating confined fluids, we find that the shift in the PC-SAFT dispersion energy correlates with the ratio of the sorbent mean pore size to the PC-SAFT segment size (rp/σ). By fitting to the capillary condensation data, the relative deviation between the confined and bulk PC-SAFT dispersion energy parameter is only 0.1% at rp/σ = 15; however, this deviation starts to increase exponentially as rp/σ decreases. For a sorbent with large pores, when rp/σ > 15, the capillary condensation pressure results from our model are similar to the predictions from the Kelvin equation. Using a dataset containing 235 saturation pressure data points composed of 18 pure gases and 4 binary mixtures, the overall AARD% from our model is 12.26%, which verifies the good accuracy of our model. Because the mean sorbent pore radius (rp), the PC-SAFT energy parameter (ε), and segment size (σ) are known a priori, our model estimates the corrected energy parameter for small pores and, thus, extends its applicability.
1 Introduction
Mesoporous and microporous adsorbents have extensive applications, including CO2 capture,1–3 drug delivery,4,5 industrial wastewater treatment,6–8 hydrogen production,9,10 gas dehumidification,11,12 energy storage,13 reactions,14 and catalysts.15,16 Over the past two decades, considerable advancement has been made in understanding adsorption phenomena and the behavior of confined fluids in porous materials.17 The adsorption process becomes complicated in microporous materials because of deviation in phase equilibria, including capillary condensation, upon extreme confinement (for pore radii of at least 0.5 nm). The Kelvin equation describes the curvature-dependency of vapor pressure for the nanoconfined fluids;18 it predicts that the vapor pressure of a confined wetting fluid becomes smaller than that of the bulk phase,19 allowing capillary condensation in small pores. The Kelvin effect was directly measured for the first time by Fisher and Israelachvili.20
Despite the success of the Kelvin equation in estimating the vapor pressure of confined fluids, there is a debate on its validity for small pores with meniscus radii ranging 1–100 nm;20 however, it has been experimentally verified that in principle, the thermodynamic basis for the Kelvin equation holds for the radii of curvature down to 4 nm.21 The Kelvin equation is observed to overestimate capillary condensation pressure in microporous adsorbents; therefore, its thermodynamic framework must be modified under an extreme confinement (radii of curvature < 4 nm).22 In recent years, various methodologies have emerged to improve the thermodynamic modeling performance for confined phase equilibria, including capillary condensation. In addition to including the capillary pressure effect in the phase equilibria framework, researchers have suggested several other modifications that consider, for example, the curvature-dependency of surface tension using the Tolman parameter,23 heterogeneous density distribution due to solid–liquid interactions near the pore walls,24 correction to the curvature value due to the adsorbed layer,25 adjustments to the critical properties of the confined fluid,26 and solid–confined liquid interaction energy.27,28
Most of the studies on confined phase equilibria are limited to the phase behavior application for reservoir fluids confined in tight shale formations.29 In general, the confined phase equilibria are studied using thermodynamic frameworks such as density functional theory;30–33 molecular dynamics simulation;34,35 lattice Boltzmann method,36 and equation of state (EoS) approach combined with Young–Laplace equation,27,37,38 or modified Young–Laplace equation where the effect of the adsorbed layer is considered.33,39 In this study, we use the EoS approach to model the capillary condensation pressure. In the literature, the Peng–Robinson equation of state (PR-EoS) is commonly used with the Young–Laplace equation, and the critical properties are adjusted under confinement.40,41 Moreover, in some studies, the solid–liquid interaction energy is included in the van der Waals EoS thermodynamic modeling framework.28,42 In general, the cubic EoSs are less accurate for modeling the behavior of associating fluids.43 Also, they need critical properties as the input parameters; thus, the cubic EoS application can become challenging for the fluids for which the critical properties cannot be measured. For example, many ionic liquids start to decompose when the temperature approaches the normal boiling point.44 To correct the cubic EoS models under extreme confinement, researchers often use the ratio of the Lennard-Jones size parameter to the pore radius (σLJ/rp) to estimate the shift in the critical properties. Nonetheless, the Lennard-Jones potential is better suited for describing small nonpolar molecules.45
There are only a few studies in the literature on confined phase equilibria using thermodynamic EoS models that consider association. Xiong et al.27 used cubic-plus association equation of state (CPA-EoS) to estimate confined phase equilibria for 10 non-associating fluids and two associating fluids (water and ethanol) in SBA-15, MCM-41, and Vycor® glass. They modified the energy parameter a in the CPA-EoS model by shifting the critical temperature and pressure upon confinement.27 In another study, Tan and Piri39 used perturbed chain statistical association fluid theory (PC-SAFT) EoS to model the phase behavior of different gases in SBA-15 and MCM-41. They also used a modified Young–Laplace equation by subtracting the thickness of the adsorbed layer prior to condensation from the pore radius value. Later, they used the PC-SAFT EoS to model the capillary condensation, including the retrograde condensation for reservoir fluids at the reservoir operating conditions.46
Unlike other EoS models, the PC-SAFT model does not rely on the critical properties and is suitable for both associating and non-associating molecules of varying sizes.47,48 Therefore, we use the PC-SAFT model integrated with the Young–Laplace equation to calculate the capillary condensation pressure under confinement from dew point pressure calculations.49 We test the thermodynamic model for various systems using associating and non-associating fluids at different temperature and composition levels. The pure and binary fluid mixtures that are studied are confined in micro- and mesoporous materials such as SBA-15, MCM-41, and Vycor® glass with a known pore size distribution, assuming a zero contact angle (complete wetting condition). For smaller pores, we adjust the PC-SAFT dispersion energy parameter (ε) to obtain more accurate capillary condensation pressure estimates from the model. Finally, we propose a general correlation for the adjustment factor (Δε) with the ratio of the average pore radius to the PC-SAFT segment diameter (rp/σ), which holds for all components tested. Because Δε can be obtained a priori, our predictive model can estimate the capillary condensation pressure for associating and non-associating fluids even when the pore size becomes comparable to the molecular size. The structure of our paper is as follows: after the introduction, Section 2 discusses the thermodynamic framework of the PC-SAFT model and capillary effects in the phase equilibria calculations; Section 3 presents the results for pure component and binary gas systems; finally, the conclusion remarks are given in Section 4.
2 Thermodynamic frameworks
2.1 Confined phase equilibria for multicomponent systems
The equality of fugacity for each mixture component in the available phases dictates the thermodynamics of phase equilibria. The equilibrium condition for the vapor–liquid equilibria (VLE) is given by eqn (1):45| | 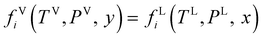 | (1) |
where fi is the fugacity of component i; T and P are the temperature and pressure, respectively; x and y represent the mole fractions in the liquid and vapor phases, respectively; and the superscripts V and L indicate the vapor and liquid phases, respectively. The fugacity of each component in the liquid and vapor phases can be written in terms of their fugacity coefficients using eqn (2):45| | 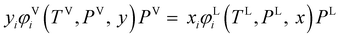 | (2) |
where φi is the fugacity coefficient of component i, that is computed using the PC-SAFT model.
The equilibrium conditions given by eqn (1) and (2) are valid for both the bulk and confined phase equilibria. In most applications, the thermal equilibrium condition predicts similar temperature values for the vapor and liquid phases (TV = TL), in both the bulk and confined systems. However, contrary to the bulk phase equilibria, the mechanical equilibrium condition in the confined fluids predicts different pressures for the vapor and liquid phases across a curved interface. The difference in the phase pressures is dictated by capillary pressure, which according to the Laplace equation, is related to the interfacial tension (γ) and the radius of curvature (r).25 For a gas–liquid system confined in a cylindrical capillary tube and under equilibrium, the capillary pressure simplifies to the Young–Laplace equation, as presented in eqn (3):50
| | 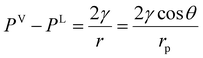 | (3) |
γ is the interfacial tension;
rp is the capillary tube pore radius; and
θ is the contact angle. Often, the calculations are simplified by assuming complete wetting in pores, which is quantified by zero contact angle.
27,39,51 We also make a similar assumption because the contact angle values are not available in the capillary condensation experiments conducted in nanocapillaries. Interfacial tension is an important parameter that affects the capillary pressure. In multicomponent systems, the solubility of a gas in the confined liquid changes the interfacial tension, and consequently, capillary pressure.
52 For a multicomponent system, the interfacial tension can be estimated using a so-called parachor method that is shown in
eqn (4):
52| | 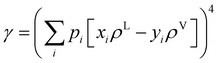 | (4) |
where
pi represents the parachor of component
i and
ρ is the fluid density, which is estimated from the PC-SAFT model in this study.
The Kelvin equation is fundamental in interfacial thermodynamics, relating the saturation pressure of the confined and bulk fluids to curvature, as expressed in eqn (5):50
| | 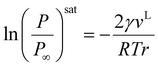 | (5) |
where
γ represents the interfacial tension;
vL is the molar volume of the liquid phase;
r is the mean radius of curvature for the condensed liquid;
Psat and
Psat∞ are the vapor pressure of confined and bulk phases, respectively;
T represents the temperature; and
R is the universal gas constant.
2.2 PC-SAFT model
We use PC-SAFT EoS to calculate the fugacity coefficient and density of confined fluids. The PC-SAFT model was proposed by Gross and Sadowski47,48 in the context of molecular thermodynamics and statistical mechanics. It considers molecules as chains with a different number of segments and sizes interacting with each other. Because PC-SAFT considers the molecular interactions, it is especially suitable for calculating phase equilibria and physical properties of systems that involve associating fluids, polymers, and colloids.47
The PC-SAFT model is formulated using dimensionless residual Helmholtz energy contributions from hard-chain, dispersion, and association as illustrated in eqn (6):47,48,53–55
| | 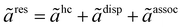 | (6) |
The dimensionless dispersion contribution term for the residual Helmholtz energy is given by
eqn (7):
47| | 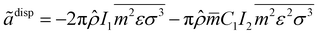 | (7) |
where
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif)
is the total number density of the molecules and is related to density and Avogadro's number (
NA) using
eqn (8):
| | 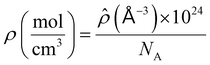 | (8) |
The intermediate variables in eqn (7) are defined by eqn (9)–(17):47
| | 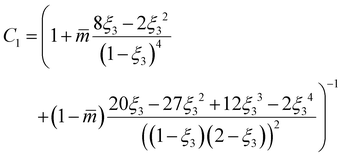 | (9) |
| | 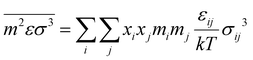 | (10) |
| | 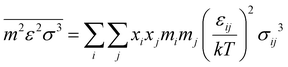 | (11) |
| | 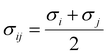 | (12) |
| | 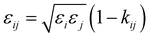 | (13) |
| | 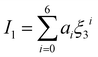 | (14) |
| | 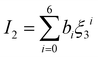 | (15) |
| | 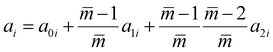 | (16) |
| | 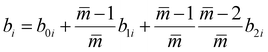 | (17) |
where
mi,
σi and
εi are the segment number per chain, segment diameter, and the dispersion-energy parameter for component
i, respectively, and are among the PC-SAFT pure component parameters; and
k is the Boltzmann constant. In addition,
kij is the binary interaction parameter in the PC-SAFT model. The values of the model universal constants
a0i,
a1i,
a2i,
b0i,
b1i, and
b2i are available in the literature.
47
Furthermore, ξn (n = 0, 1, 2, 3) and di are defined by eqn (18) and (19), respectively.
| | 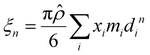 | (18) |
| | 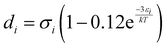 | (19) |
The dimensionless hard-chain and association contribution terms to the residual Helmholtz energy (
ãhc and
ãassoc) are given in Appendix A.
To obtain the fugacity coefficient of a pure component or that of a component in the mixture, the following equations are employed:47
| | 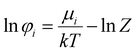 | (20) |
| | 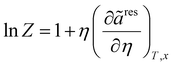 | (21) |
| | 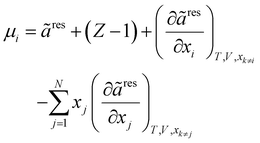 | (22) |
In
eqn (20),
Z and
μ represent the compressibility factor and chemical potential, respectively. In addition,
η is the packing fraction and is equal to
ξ3 (see
eqn (18)). Details on the partial derivative terms in
eqn (21) and (22) can be found in the literature.
47
2.3 Dispersion-energy parameter of the PC-SAFT model for confined fluids
It is noted in the literature that including the capillary pressure in the framework of flash calculation alone does not always provide an accurate estimation of the confined vapor–liquid equilibria (VLE).52 For pores of nm size, further adjustments to the confined VLE calculations using EoS models are required.27,52 Yang et al.52 used PR-EoS for confined phase equilibria and found it essential to adjust the critical pressure and critical temperature parameters, particularly when the ratio of pore radius to the Lennard-Jones diameter (rp/σLJ) is less than 20. Furthermore, Xiong et al.27 employed CPA-EoS for confined phase equilibria and concluded that for rp/σLJ < 10, it becomes important to adjust the CPA energy parameter.
The molecular interactions between a confined fluid and the pore wall surface intensify the van der Waals forces of the fluid.56,57 In a nanoconfined fluid, the effect of solid pore boundary is more pronounced, and the molecules experience attractive forces not only with each other but also with the molecules at the confining surfaces.56,57 This allows molecules to come into a closer contact, enhancing the van der Waals interactions. The stronger van der Waals forces perturb the phase equilibrium by affecting the fugacity coefficient of the confined phase in eqn (2). In the PC-SAFT model, the van der Waals forces are incorporated in the dispersion energy term (eqn (7)). Hence, we adjust the dispersion energy parameter of the PC-SAFT model (ε) to obtain a better estimation of capillary condensation pressure in nanopores.
To model the system under extreme confinement, we use PC-SAFT confined dispersion energy parameter (εc) that is correlated to the conventional PC-SAFT dispersion-energy parameter (ε) through a so-called dimensionless adjustment factor (Δε) as shown in eqn (23):
The subscript c represents the confinement condition. Using experimental data of capillary condensation, we will later correlate the dimensionless adjustment factor (Δ
ε) to the ratio of pore radius to the PC-SAFT segment size (
rp/
σ). To obtain the correction term, Δ
ε for pure components under confinement conditions, experimental capillary condensation pressures are collected from literature for associating and non-associating pure and binary systems as detailed in
Table 1. Then, the saturation pressure for the pure components is calculated from
eqn (2) and (3) using the PC-SAFT EoS.
Table 1 List of experimental adsorption isotherms from which the capillary condensation data are derived
| Adsorbate |
Porous medium |
Temperature (K) |
Mean pore radius (nm) |
Ref. |
| Name |
Formula |
| Nitrogen |
N2 |
MCM-48 |
55–115 |
1.9 |
58
|
| Nitrogen |
N2 |
MCM-41 |
65–115 |
1.2–2.2 |
59 and 60
|
| Nitrogen |
N2 |
SBA-15 |
68–120 |
3.0–3.9 |
59
|
| Argon |
Ar |
MCM-41 |
57–135 |
1.2–2.2 |
41, 60 and 61
|
| Argon |
Ar |
MCM-48 |
87 |
1.1–1.5 |
62
|
| Oxygen |
O2 |
MCM-41 |
70–140 |
1.8, 2.2 |
60 and 61
|
| Carbon dioxide |
CO2 |
MCM-41 |
200–260 |
1.8, 2.2 |
61 and 63
|
| Carbon dioxide |
CO2 |
SBA-15 |
245–295 |
2.45, 3.3 |
64
|
| Ethane |
C2H6 |
SBA-15 |
263–300 |
3.04, 4.07 |
64
|
| Ethylene |
C2H4 |
MCM-41 |
144–148 |
1.8 |
60
|
| Propane |
C3H8 |
MCM-41 |
278.5–322.5 |
1.3–3.0 |
65
|
|
n-Butane |
n-C4H10 |
MCM-41 |
281.8–301.4 |
1.3–3.0 |
65
|
|
n-Pentane |
n-C5H12 |
MCM-41 |
258–298 |
1.4–3.2 |
63
|
|
n-Hexane |
n-C6H14 |
MCM-41 |
298–323 |
1.2–2.2 |
66 and 67
|
|
n-Hexane |
n-C6H14 |
SBA-15 |
293.2 |
3.4 |
68
|
|
c-Hexane |
c-C6H12 |
SBA-15 |
293.2 |
3.4 |
68
|
| 3-Methyl pentane |
C6H14 |
SBA-15 |
293.2 |
3.4 |
68
|
|
n-Heptane |
n-C7H16 |
SBA-15 |
298.15–308.15 |
2.3–3.9 |
68 and 69
|
| Benzene |
C6H6 |
MCM-41 |
273.15–303.15 |
1.3–2.2 |
70 and 71
|
| Toluene |
C7H8 |
SBA-15 |
293.2 |
3.4 |
68
|
| Methanol |
CH3OH |
MCM-41 |
298 |
1.2–2.2 |
71
|
| Ethanol |
C2H5OH |
MCM-41 |
273.15–303.15 |
1.3–2.1 |
70
|
| Water |
H2O |
MCM-41 |
298.2 |
1–2.1 |
72
|
| Water |
H2O |
SBA-15 |
293.2–298.2 |
2.5–3.3 |
72 and 73
|
| Water |
H2O |
OMC |
294.5 |
3.1–4.6 |
74
|
| Water |
H2O |
MCM-48 |
293.15 |
1.4 |
73
|
| Methane + Ethane |
CH4 + C2H6 |
SBA-15 |
236–277 |
3.28 |
75
|
| Methane + Ethane |
CH4 + C2H6 |
MCM-41 |
264.75 |
1.95 |
76
|
| Methane + Carbon dioxide |
CH4 + CO2 |
SBA-15 |
240–280 |
3.28 |
75
|
| Ethane + Carbon dioxide |
C2H6 + CO2 |
MCM-41 |
264.6 |
1.35 |
77
|
| Nitrogen + Water |
N2 + H2O |
Mica |
294 |
0.5–3.0 |
78
|
To find the adjustment factor (Δε) for each component, genetic algorithm optimization method is used. We minimize the average absolute relative deviation (AARD) between the experimental and computed capillary condensation pressure data as the objective function, as shown in eqn (24).
| | 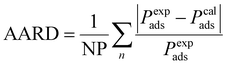 | (24) |
NP is the number of datapoints, and
Pads is the capillary condensation pressure. The superscripts exp and cal indicate experimental and calculated (from the model), respectively. To use the PC-SAFT EoS, the model parameters for all components are required, which are obtained from literature and summarized in
Table 2.
Table 2 PC-SAFT pure component parameters and parachor
| Component |
PC-SAFT pure parameters |
Ref. |
Parachor |
Ref. |
|
m
|
σ
|
ε/k (K) |
k
AB
|
ε
AB/k (K) |
| The parachor (p) for methanol, ethanol, and water are obtained from the literature and are correlated with temperature (T in K): * p = 82.07 + 0.0212T, ** p = 113.6 + 0.0602T − 5.013 × 10−5T2, and *** p = 91.7714 − 0.3517T + 1.176 × 10−3T2 − 1.7636 × 10−6T3 + 1.0023 × 10−9T4. |
| Non-associating fluids |
| N2 |
1.2053 |
3.3130 |
90.96 |
— |
— |
47
|
60.5 |
27
|
| Ar |
0.9285 |
3.4784 |
122.23 |
— |
— |
47
|
54.0 |
27
|
| O2 |
1.1335 |
3.1947 |
114.43 |
— |
— |
79
|
53.6 |
27
|
| CO2 |
2.0729 |
2.7852 |
169.21 |
— |
— |
47
|
77.5 |
80
|
| CH4 |
1.0000 |
3.7039 |
150.03 |
— |
— |
47
|
72.6 |
80
|
| C2H6 |
1.6069 |
3.5206 |
191.42 |
— |
— |
47
|
110.5 |
80
|
| C2H4 |
1.5930 |
3.4450 |
176.47 |
— |
— |
47
|
99.5 |
80
|
| C3H8 |
2.0020 |
3.6184 |
208.11 |
— |
— |
47
|
150.8 |
80
|
|
n-C4H10 |
2.3316 |
3.7086 |
222.88 |
— |
— |
47
|
190.3 |
80
|
|
n-C5H12 |
2.6896 |
3.7729 |
231.20 |
— |
— |
47
|
231.0 |
80
|
|
n-C6H14 |
3.0576 |
3.7983 |
236.77 |
— |
— |
47
|
270.8 |
80
|
|
c-C6H12 |
2.5303 |
3.8499 |
278.11 |
— |
— |
47
|
241.7 |
80
|
| C6H14 |
2.8852 |
3.8605 |
240.48 |
— |
— |
47
|
267.9 |
80
|
|
n-C7H16 |
3.4831 |
3.8049 |
238.40 |
— |
— |
47
|
311.3 |
80
|
| C6H6 |
2.4653 |
3.6478 |
287.35 |
— |
— |
47
|
205.7 |
80
|
| C7H8 |
2.8149 |
3.7169 |
285.69 |
— |
— |
47
|
245.7 |
80
|
|
|
| Associating fluids (2B scheme) |
| CH3OH |
1.5255 |
3.2300 |
188.90 |
0.035176 |
2899.5 |
48
|
* |
80
|
| C2H5OH |
2.3827 |
3.1771 |
198.24 |
0.032384 |
2653.4 |
48
|
** |
80
|
| H2O |
1.0656 |
3.0007 |
366.51 |
0.034868 |
2500.7 |
48
|
*** |
27
|
To create a generalized correlation for Δε, we relate the dimensionless adjustment factor to the ratio of rp/σ; rp represents the mean pore radius; and σ is the segment diameter in the PC-SAFT EoS. Therefore, for the situations when the pore radius becomes comparable to the molecular diameter, the inclusion of capillary pressure in the VLE calculations alone is not sufficient to predict the confined phase behavior. In such cases, we modify ε to improve the accuracy of the confined VLE calculation for the extremely small pores.
3 Results and discussion
3.1 Capillary condensation pressure for pure gases
The dimensionless energy adjustment factor (Δε) is determined using a dataset comprising 78 data points, which include 18 different components such as permanent and noble gases, various hydrocarbons, alcohols, and water. This adjustment factor is calculated individually for all components to predict the capillary condensation pressure experiments at given pore sizes. We find Δε to be independent of temperature. The resulting adjustment factor (Δε) is shown in Fig. 1 as a function of the dimensionless parameter rp/σ. Fig. 1 shows positive values for the adjustment factor, indicating that the dispersion-energy parameter for the confined fluids is greater than that of the bulk fluids (εc > ε). In addition, Fig. 1 demonstrates that the adjustment factor increases exponentially as the rp/σ ratio decreases. Conversely, the adjustment factor approaches zero with the increase in the rp/σ ratio. It signifies that the PC-SAFT dispersion-energy parameter for the confined fluids approaches that of the bulk fluids when pores become large compared to the molecular dimension (rp/σ > 15).
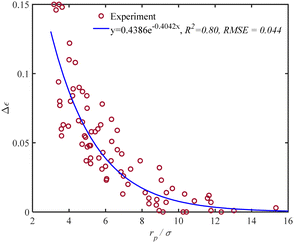 |
| | Fig. 1 Adjustment factor Δε of PC-SAFT for confined fluids vs. rp/σ, a comparison between data and proposed correlation using 18 different adsorbate species, six different adsorbents, and at different ranges of temperature and pore size, as listed in Table 1. | |
This adjustment factor, as shown in Fig. 1, fits well to (rp/σ), which considers the ratio of characteristic sizes of porous media (rp: pore radius) and the confined fluid molecular size (σ: the PC-SAFT segment diameter). Both rp and σ are known a priori for most fluids, and the correlation in eqn (25) provides a general modification, which is valid for the wide ranges of temperature, pressure, and components used, as summarized in Table 1.
In addition, to provide a generalized representation of the adjustment factor, a correlation is introduced to link the (rp/σ) ratio to the adjustment factor, as given by eqn (25).
| | 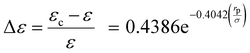 | (25) |
The t-test analysis on the regression parameters shows that the coefficient and exponent parameters are statistically significant at a 95% confidence level. According to the correlation, when the ratio (rp/σ) = 15, the adjustment factor (Δε) is only 0.001. This implies that the PC-SAFT dispersion-energy parameter for the confined fluids is 99.9% of that for the bulk fluid (εc = 0.999ε). Therefore, for (rp/σ) > 15, there is no need for adjusting the PC-SAFT dispersion energy parameter to estimate the capillary condensation pressure. Note that for the range of pore radius corresponding to 15 < (rp/σ) < 100, capillary pressure should still be integrated with the PC-SAFT model to accurately estimate the capillary condensation pressure; however, using the PC-SAFT dispersion energy parameter from bulk (ε) is satisfactory. For (rp/σ) < 15, confined VLE phase equilibria predictions using the PC-SAFT model deviate from experimental data; we find that by using the confined dispersion energy parameter (εc) instead of the conventional dispersion energy parameter (ε) in the PC-SAFT model, the VLE prediction error reduces significantly.
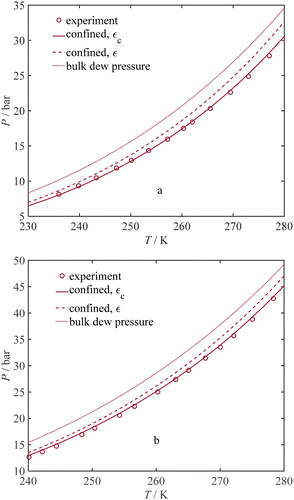
In the following, we compare the experimental adsorption saturation pressure data for pure fluids with the proposed model. We use the PC-SAFT model with the Young–Laplace equation and assume complete wetting conditions. The proposed correlation shown in eqn (25) is used to modify the PC-SAFT EoS dispersion energy parameter when the pore size becomes comparable to the molecular dimension. Using the thermodynamic framework discussed and performing dew point calculations, we estimate the mean pressure at which capillary condensation occurs in different mesoporous silica and at different temperature levels.
Using the entire dataset listed in Table 1, the estimated capillary condensation pressure values from our thermodynamic model are compared with the experimental data for 18 different pure gases at various temperatures and sorbent pore sizes, as illustrated in Fig. 2a. Using 235 data points gathered in our dataset from the literature, the AARD% value of 12.26% is achieved. The maximum relative deviation is observed in the case of benzene (C6H6) in MCM-41 with a pore radius of 1.3 nm and at a temperature of 273.15 K. Although the AARD% value for the maximum deviation is relatively large, the absolute error value is low; in this system, the experimental capillary condensation pressure is only 0.47 kPa, while the model estimation is 0.21 kPa, resulting in the maximum RD% of 57%. To show the importance of using the adjustment factor, we compare the experimental adsorption saturation pressure data for pure fluids with the model by employing the conventional dispersion energy parameter (ε), as shown in Fig. 2b. Consequently, an AARD% value of 40.28% is attained. A comparison of the AARDs reveals a notable enhancement in the adsorption saturation pressure predictions for pure fluids with the current model. Another observation arising from the comparison between Fig. 2a and b is that using the conventional dispersion energy parameter (ε) results in an overestimation of the adsorption saturation pressure. This overestimation is evident in Fig. 2b, where most data points lie above the y = x line.
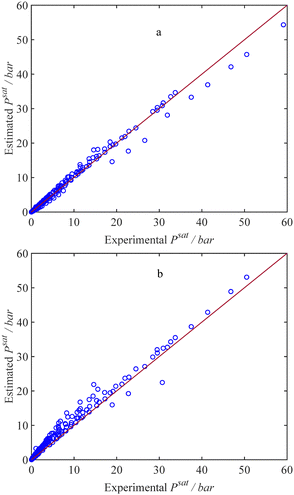 |
| | Fig. 2 Estimated and experimental confined saturation pressure for 235 datapoints that include 18 different pure gas components at various temperatures and porous materials, as listed in Table 1. Markers: datapoints, solid line: y = x, (a) with εc, (b) with ε. | |
To show the trends in capillary condensation pressure with temperature for different gases and for porous media with different average pore sizes, the model results are compared to the experimental data in Fig. 3. The solid lines show the saturation pressure of confined fluids from the model; the dashed lines represent the saturation pressure for the bulk condition; and the symbols denote the experimental data for capillary condensation pressure. Fig. 3 covers the adsorbate-adsorbent literature data for 13 different pure gas components, including associating fluids (such as water and alcohols) and non-associating fluids (such as the atmospheric gases and hydrocarbons). The capillary condensation pressure data from the literature are related to different porous materials such as MCM-41, MCM-48, OMC, Mica, and SBA-15 with different pore sizes. Fig. 3 explores the influence of temperature and pore radius size on the capillary condensation pressure for various gas components, showing an excellent fit to the experimental data for all components tested. As expected, with an increase in temperature, the condensation pressure increases for a given pore size. Also, from Fig. 3, it follows that the rate of change (increase) in condensation pressure increases with temperature; at a given temperature, the rate of change in saturation pressure with temperature decreases under confinement such that as the pore size decreases, the rate of change in the capillary condensation pressure with temperature decreases. Also, in agreement with the Kelvin equation, at a given temperature, the saturation pressure is less for smaller pores. Alternatively, to achieve the same saturation pressure, a higher temperature is required when pores become smaller.
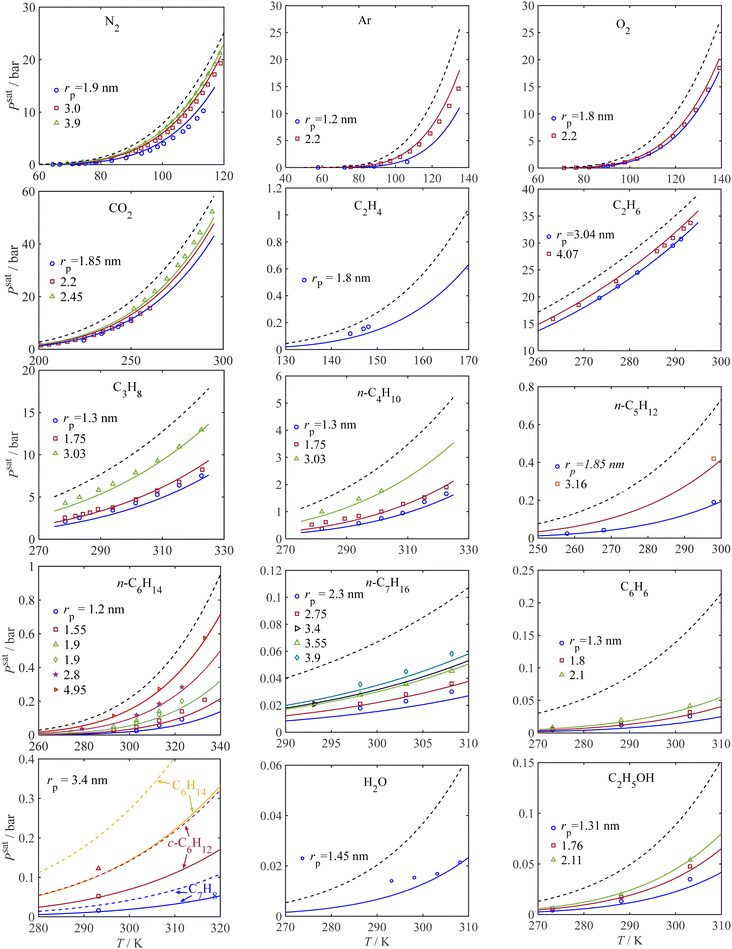 |
| | Fig. 3 Pure component condensation pressure for bulk and confined fluids from the current model and experimental data. Symbols: experiment, solid lines: model for confined fluid, and dashed line: bulk. Data sources: (N2) ○,58 □, Δ;59 (Ar) ○,60 □;61 (O2) ○,60 □;61 (CO2) ○,63 □,61 Δ,64 (C2H6),64 (C3H8),65 (n-C4H10),65 (n-C5H12),63 (n-C6H14) □ and ▷,66 others,67 (n-C7H16) ▷68 others,69 (C2H5OH),70 (C6H6),70 (H2O),73 (c-C6H12),68 (C6H8),68 (C6H14).68 | |
Furthermore, to assess the significance of our fine-tuned model, we compare capillary condensation pressure from the Kelvin equation (eqn (5)) and experiments with our model with and without adjustments to the dispersion energy parameter in Fig. 4 (by employing εc and ε, respectively). According to Fig. 4, the ratio of the confined saturation pressure to the bulk saturation pressure is plotted against the pore radius. The comparison is made for C6H6 and CH3OH at 298 K,71 and H2O at 294.5 K.74Fig. 4 shows that the Kelvin equation and the current model without adjusting the dispersion energy parameter, both start to overestimate the saturation pressure when pores become small while our model (using εc) consistently provides a significantly better agreement with the experimental data even for smaller pore sizes. An analysis of the results in Fig. 4 shows that for C6H6, our model gives an AARD of 14.71%, while the Kelvin equation results in a notably higher AARD of 124.03%. In the case of CH3OH, our model yields an AARD of 13.34%, whereas the Kelvin equation leads to a comparatively higher AARD of 48.20%. For H2O, our model shows an exceptionally low AARD of 0.75%, while the Kelvin equation results in an AARD of 1.96%. In Fig. 4, we also show the location of (rp/σ) = 15, at which the dispersion-energy parameter for the confined fluid is nearly identical to that of the bulk fluid (εc = 0.999ε). As observed in Fig. 4, for larger pores where (rp/σ) > 15, the results from the Kelvin equation and our model are similar.
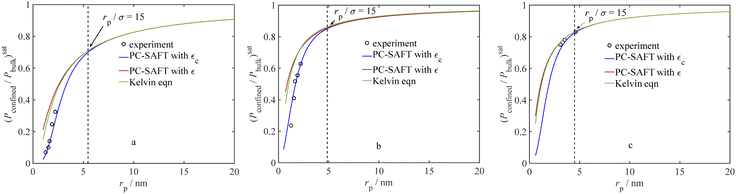 |
| | Fig. 4 Ratio of confined saturation pressure to bulk saturation pressure vs. pore radius; a comparison between the current model (with and without ε adjustment) and experiments: (a) C6H6 at 298 K,71 (b) CH3OH at 298 K,71 (c) H2O at 294.5 K.74 | |
As discussed in Section 2.3, we adjust the dispersion energy parameter (ε) in the PC-SAFT model to address the increased van der Waals interactions upon fluid confinement. Fig. 5 represents the impact of adjusting the dispersion energy parameter on the van der Waals interactions for confined fluids. In this figure, we plot the ratio of the dispersion contribution to the Helmholtz energy for confined water to that of bulk fluid against the dimensionless variable (rp/σ) with and without the correction for the dispersion energy parameter. The adjusted dispersion energy parameter is shown with εc in which the subscript c highlights correction for confinement condition, and the conventional dispersion energy parameter is shown with ε, which represents its value for the bulk phase.
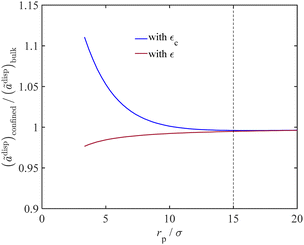 |
| | Fig. 5 The ratio of the dispersion energy of confined water to that of bulk water vs. the dimensionless variable rp/σ, with and without ε adjustment. | |
When correcting for the confinement effects by using εc instead of ε, the model predicts an interplay between two conflicting factors that together affect ãdisp with varying the pore size. When decreasing the pore radius of a nanoconfined fluid, the adjusted PC-SAFT model uses a larger value for the dispersion energy parameter (εc), as proposed in Fig. 1, which increases ãdisp as it is expected from eqn (7). On the contrary, when decreasing the pore radius, the Young–Laplace equation predicts a lower pressure for the wetting liquid at a fixed gas pressure. At a lower liquid pressure, the number density decreases (in eqn (8), also reducing the intermediate terms I1, I2, and ξn in eqn (14) and (18), respectively), which reduces ãdisp accordingly. The overall observation is an increase in the dispersion contribution to the Helmholtz energy of the confined fluid, which is in agreement with the literature.56,57 In the conventional modelling approach using ε (knowing that ε < εc), the PC-SAFT model overlooks the van der Waals interactions for the liquid molecules and pore surface that is expected for confined fluids. Thus, as can seen in Fig. 5, when using the conventional energy parameter ε in the PC-SAFT model, the ãdisp term for the nanoconfined fluid can become less than that of the bulk phase. The reason is that, in this case, the effect of confinement is only implemented through reduced liquid pressure (that eventually approaches a negative value) from the Young–Laplace equation, which consequently reduces ãdisp.
3.2 Capillary condensation pressure for binary gas mixtures
As previously explained, the capillary condensation pressure of mixtures under confinement conditions can be determined by performing dew point calculations using an EoS in conjunction with the Young–Laplace equation. To assess the model's predictive capabilities in estimating the capillary condensation pressure in binary mixtures, we compare experimental capillary condensation pressure data with those from our model. However, compared to pure gases, the experimental data on capillary condensation pressure of binary mixtures in porous materials are rather limited.
The binary interaction parameter of the PC-SAFT model (kij) for the confined fluid is adopted from those related to the bulk condition, as listed in Table 3. For mixtures of C2H6 + CO2 and N2 + H2O, the binary interaction parameters are estimated due to the lack of available data in the literature. The comparisons between the current model results and experimental data are visualized in Fig. 6–9 for four different binary systems. Overall, excellent model predictions are observed when compared to the experimental data of the binary mixtures.
Table 3 Binary interaction parameters of PC-SAFT at the bulk condition
| Mixtures |
k
ij
|
Ref. |
| CH4 + C2H6 |
0 |
81
|
| CH4 + CO2 |
0.065 |
47
|
| C2H6 + CO2 |
0.085 |
This work |
| N2 + H2O (2B scheme) |
−0.055 |
This work |
 |
| | Fig. 6 Saturation pressure of isochoric binary gas mixtures versus temperature in bulk and in SBA-15: (a) CH4 + C2H6 with xCH4 = 0.15 and rp = 3.28 nm, (b) CH4 + CO2 with xCH4 = 0.12 and rp = 3.28 nm; symbols: experimental data under confinement condition from ref. 75. | |
 |
| | Fig. 7
P-xy diagram for C2H6 + CO2 mixture at 264.6 K and rp = 1.35 nm, under bulk and confined (with and without ε adjustment) conditions in MCM-41; symbols: experimental data under confinement condition from ref. 77. | |
 |
| | Fig. 8
P-xy diagram for the CH4 + C2H6 mixture at 264.75 K and rp = 1.95 nm under bulk and confined (with and without ε adjustment) conditions in MCM-41; symbols: experimental data under confinement condition from ref. 76. | |
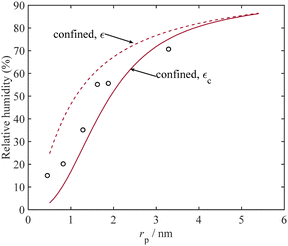 |
| | Fig. 9 Relative humidity required for H2O condensation in a binary mixture of H2O + N2 in mica with different pore sizes at 294 K and the atmospheric pressure from model and experimental data.78 | |
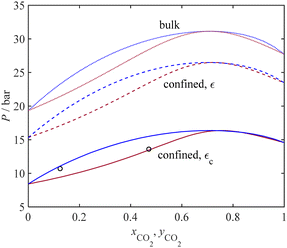
Fig. 6 shows a P–T diagram of capillary condensation pressure for binary gas mixtures at different temperatures; the corresponding dew pressure curves for these mixtures in the bulk phase (using PC-SAFT model) are also shown for comparison. The sorbent used in Fig. 6 is SBA-15 with an average pore radius of 3.28 nm, and the binary mixtures are CH4 + C2H6 (15% CH4) and CH4 + CO2 (12% CH4). The binary interaction parameter is set to zero, which is consistent with the literature reports.
Fig. 6 reveals a remarkable agreement between the results obtained from our model and the experimental data. The results show that under confined conditions in SBA-15, the capillary pressure values for these binary mixtures are consistently lower by approximately 2.0 to 4.4 bar compared to bulk conditions at all temperature levels studied in this work. This agreement highlights the model's ability to predict the capillary condensation pressure in these mixtures effectively.
Fig. 7 presents a P-xy diagram for the C2H6 + CO2 binary system at 264.6 K under bulk conditions (dashed lines) and under confinement conditions (solid lines). The sorbent is MCM-41, with an average pore radius of 1.35 nm. Fig. 7 displays a comparison between our model results obtained and the limited experimental data for adsorption capillary pressure. Despite the relatively narrow two-phase region band in Fig. 7, our results show a good agreement between the dew curve obtained by the model under confinement conditions (represented by the dark red solid line) and those limited experimental data. Furthermore, a comparison between the confinement and bulk conditions highlights that the dew pressure under confinement is consistently lower by about 10 and 14 bar, respectively. This significant reduction in the dew pressures for the confined compared to the bulk phases is attributed to the small pore size (1.35 nm) of the MCM-41 adsorbent used.
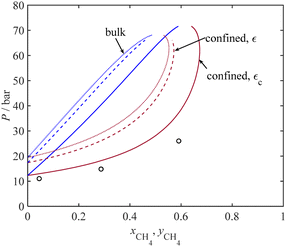
Fig. 8 presents a comparison between the P-xy diagram for the bulk (dashed lines) and confined (solid lines) mixtures of CH4 + C2H6 at 264.75 K and experimental adsorption capillary pressure data using MCM-41 with an average pore radius of 1.95 nm. According to Fig. 8, a good agreement is observed between the experimental results and the predicted dew data under confinement conditions, represented by the dark red solid line.
Furthermore, a comparison between the two-phase region under confinement conditions and bulk conditions reveals a notable shift of the P-xy diagram to higher temperature values. As it can be seen in Fig. 8, for mixtures with xCH4 > 0.55, condensation does not occur at the bulk condition. However, for the confined mixtures with a CH4 mole fraction of up to 0.67, condensation can still occur. For instance, at a temperature of 264.75 K, a mixture with a CH4 mole fraction of 0.6 does not condense under the bulk conditions. However, the experiments show that it can be condensed at 26 bar; our model estimates the condensation pressure to be 37 bar in MCM-41 with an average pore size of 1.95 nm. This observation underscores the significant impact of confinement on the phase behavior of these mixtures.
Capillary condensation has applications in dehumidification and atmospheric water harvesting.82Fig. 9 illustrates the relative humidity level that is required for water condensation from a binary mixture of H2O + N2 at 294 K using mica as the adsorbent. As depicted in Fig. 9, the experimental data closely matches the results obtained from our thermodynamic model. These findings, as evident in Fig. 9, suggest that the wet nitrogen gas mixture can undergo dehumidification under ambient conditions in mica, even when the relative humidity percent for nitrogen is as low as 10%, which exists in arid climate conditions.
4 Conclusions
The importance of capillary condensation in micro- and mesoporous sorbents has motivated us to build a reliable model that can predict the capillary condensation pressure of associating and non-associating fluids. Our thermodynamic model uses PC-SAFT EoS and includes the effect of capillary pressure on dew point pressure by including the Young–Laplace equation for fluids confined in different sorbents such as MCM-41, MCM-48, SBA-15, mica, and Vycor® glass, and at different temperature values. A dataset of 235 capillary condensation data is collected for 18 pure gases (including permanent gases, hydrocarbons, alcohols, and water) and four binary gas mixtures (CH4/C2H6, CH4/CO2, C2H6/CO2, and N2/H2O), in sorbents with various mean pore sizes in the range 1 nm to 5 nm, under different temperature conditions.
To enhance the model accuracy, we adjust the PC-SAFT dispersion-energy parameter (ε) for confined fluids when the pore size becomes comparable to the adsorbate molecular size. By fitting the experimental data of capillary condensation pressure, our model results demonstrate that for the confined fluids, a higher PC-SAFT energy parameter should be used. Also, we find that the energy parameter increases as the sorbent pores become smaller. To extend the predictability of our model under extreme confinement, we develop a correlation that estimates the adjusted PC-SAFT energy parameter from a priori model and sorbent data. Using 78 experimental data for the 18 pure fluids, the adjustment factor (ε) of the PC-SAFT dispersion-energy parameter is found to correlate with the ratio of the sorbent mean pore radius to the PC-SAFT segment diameter (rp/σ). This modification to the PC-SAFT energy parameter significantly improves the accuracy of calculations, especially for sorbents that feature small pores such that (rp/σ) < 15. The modification is however not required for larger pores. We conclude that for (rp/σ) ≥ 15, the capillary condensation pressure behavior from our model behaves similar to the Kelvin equation.
To assess the reliability of our model, we predict the dew point conditions for the bulk and confined fluids and compare them to the experimental data. The results show that the overall AARD% is 12.3% for a total of 235 data points, revealing an acceptable accuracy. We also compare our model results with those from the Kelvin equation. The values of AARD% in the ratio of confined-to-bulk saturation pressure for pure C6H6, CH3OH, and H2O are 14.71%, 13.34%, and 0.75%, respectively, using our model, and 124.03%, 48.2%, and 1.96%, respectively, using the Kelvin equation. Moreover, we employ our model to estimate the saturation pressure for four binary gas mixtures for which the PC-SAFT binary interaction parameters are taken from bulk conditions. The model results show that after correcting the PC-SAFT binary interaction parameter, the capillary condensation pressures obtained from the fine-tuned model match exceptionally well with the experimental data.
Author contributions
Aliakbr Roosta: conceptualization, data collection, programming, analysis, writing – review and editing. Sohrab Zendehboudi: analysis, writing – review and editing. Nima Rezaei: conceptualization, supervision, writing – review and editing.
Conflicts of interest
There are no conflicts to declare.
Appendices
Appendix A
The hard-chain contribution to the Helmholtz energy is described by eqn (A1):47| | 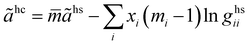 | (A1) |
ãhs is the dimensionless residual Helmholtz energy of the hard-sphere obtained for each segment from eqn (A2); and ghsii is the radial distribution function of the hard-sphere fluid defined by eqn (A3).| | 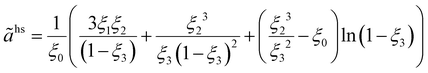 | (A2) |
| | 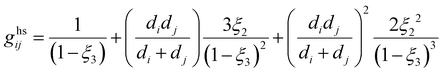 | (A3) |
The association contribution to the dimensionless residual Helmholtz energy is described by eqn (A4)–(A8):48,54| | 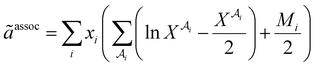 | (A4) |
| | 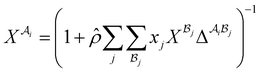 | (A5) |
| | 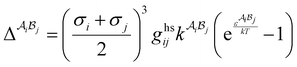 | (A6) |
| | 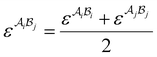 | (A7) |
| | 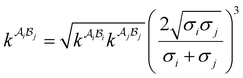 | (A8) |
where 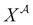 is the mole fraction of molecules that are not bonded at site
is the mole fraction of molecules that are not bonded at site 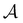 and Mi is the number of association sites on each molecule. In this study, we consider Mi = 2 for all associating molecules because of using the 2B association scheme. Furthermore,
and Mi is the number of association sites on each molecule. In this study, we consider Mi = 2 for all associating molecules because of using the 2B association scheme. Furthermore, 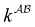 and
and 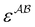 are the associating component parameters of the PC-SAFT EoS related to the effective association volume and the association energy, respectively. For non-associating molecules, these parameters are set to zero.
are the associating component parameters of the PC-SAFT EoS related to the effective association volume and the association energy, respectively. For non-associating molecules, these parameters are set to zero.
Acknowledgements
The authors wish to acknowledge Jane and Aatos Erkko Foundation (JAES) in Finland for providing research funding for our project (210053) that enabled this research.
References
- A. A. Azmi and M. A. A. Aziz, Mesoporous adsorbent for CO2 capture application under mild condition: a review, J. Environ. Chem. Eng., 2019, 7, 103022 CrossRef CAS
 .
.
- J. Jiao, J. Cao, Y. Xia and L. Zhao, Improvement of adsorbent materials for CO2 capture by amine functionalized mesoporous silica with worm-hole framework structure, Chem. Eng. J., 2016, 306, 9–16 CrossRef CAS
 .
.
- H. F. Hasan, F. T. Al-Sudani, T. M. Albayati, I. K. Salih, H. N. Harharah, H. S. Majdi, N. M. C. Saady, S. Zendehboudi and A. Amari, Synthesizing and Characterizing a Mesoporous Silica Adsorbent for Post-Combustion CO2 Capture in a Fixed-Bed System, Catalysts, 2023, 13, 1267 CrossRef CAS
 .
.
- F. Farjadian, A. Roointan, S. Mohammadi-Samani and M. Hosseini, Mesoporous silica nanoparticles: Synthesis, pharmaceutical applications, biodistribution, and biosafety assessment, Chem. Eng. J., 2019, 359, 684–705 CrossRef CAS
 .
.
- D. Bhatane, S. R. Pamshong, S. Sarnaik and P. A. Amit Alexander, Potential applications of mesoporous silica nanoparticles for the treatment of neurological disorders, J. Drug Delivery Sci. Technol., 2023, 104970 CrossRef CAS
 .
.
- N. Kumar, A. Pandey, Rosy and Y. C. Sharma, A review on sustainable mesoporous activated carbon as adsorbent for efficient removal of hazardous dyes from industrial wastewater, J. Water Process Eng., 2023, 54, 104054 CrossRef
 .
.
- H. Zhang, Y. Zhang, Y. Pan, F. Wang, Y. Sun, S. Wang, Z. Wang, A. Wu and Y. Zhang, Efficient removal of heavy metal ions from wastewater and fixation of heavy metals in soil by manganese dioxide nanosorbents with tailored hollow mesoporous structure, Chem. Eng. J., 2023, 459, 141583 CrossRef CAS
 .
.
- D. Gang, Z. Uddin Ahmad, Q. Lian, L. Yao and M. E. Zappi, A review of adsorptive remediation of environmental pollutants from aqueous phase by ordered mesoporous carbon, Chem. Eng. J., 2021, 403, 126286 CrossRef CAS
 .
.
- Z. Taherian, A. Khataee, N. Han and Y. Orooji, Hydrogen production through methane reforming processes using promoted-Ni/mesoporous silica: a review, J. Ind. Eng. Chem., 2022, 107, 20–30 CrossRef CAS
 .
.
- P. García-Muñoz, N. P. Zussblatt, B. F. Chmelka, V. A. de la Peña O’Shea and F. Fresno, Production of hydrogen from gas-phase ethanol dehydrogenation over iron-grafted mesoporous Pt/TiO2 photocatalysts, Chem. Eng. J., 2022, 450, 138450 CrossRef
 .
.
- L. Ge, Y. Feng, Y. Dai, R. Wang and T. Ge, Imidazolium-based ionic liquid confined into ordered mesoporous MCM-41 for efficient dehumidification, Chem. Eng. J., 2023, 452, 139116 CrossRef CAS
 .
.
- M. Zhang, B. Sun, K. Wei Shah and X. Zhang, Molecular dynamics study on electric field-facilitated separation of H2O/O2 through nanoporous graphene oxide membrane, J. Mol. Liq., 2022, 351, 118634 CrossRef CAS
 .
.
- G. D. Park, J. Lee, Y. Piao and Y. C. Kang, Mesoporous graphitic carbon-TiO2 composite microspheres produced by a pilot-scale spray-drying process as an efficient sulfur host material for Li–S batteries, Chem. Eng. J., 2018, 335, 600–611 CrossRef CAS
 .
.
- K. K. Gill, R. Gibson, K. H. C. Yiu, P. Hester and N. M. Reis, Microcapillary film reactor outperforms single-bore mesocapillary reactors in continuous flow chemical reactions, Chem. Eng. J., 2021, 408, 127860 CrossRef CAS
 .
.
- M. N. Gebresillase, D. Ho Hong, J.-H. Lee, E.-B. Cho and J. Gil Seo, Direct solvent-free selective hydrogenation of levulinic acid to valeric acid over multi-metal [NixCoyMnzAlw]-doped mesoporous silica catalysts, Chem. Eng. J., 2023, 472, 144591 CrossRef CAS
 .
.
- G. Luo, Z. Li, Q. Liu, S. Guo, X. Pei, J. Lv, S. Huang, Y. Wang and X. Ma, Enhanced synthesis of C2+ alcohols from syngas over a Co–CO2C catalyst supported on mesoporous carbon–silica composites, Chem. Eng. J., 2023, 475, 146206 CrossRef CAS
 .
.
- K. Cychosz Struckhoff, M. Thommes and L. Sarkisov, On the Universality of Capillary Condensation and Adsorption Hysteresis Phenomena in Ordered and Crystalline Mesoporous Materials, Adv. Mater. Interfaces, 2020, 7 DOI:10.1002/admi.202000184
 .
.
- L. R. Fisher, R. A. Gamble and J. Middlehurst, The Kelvin equation and the capillary condensation of water, Nature, 1981, 290, 575–576 CrossRef CAS
 .
.
- J. Huang, X. Yin, M. Barrufet and J. Killough, Lattice Boltzmann simulation of phase equilibrium of methane in nanopores under effects of adsorption, Chem. Eng. J., 2021, 419, 129625 CrossRef CAS
 .
.
- L. R. Fisher and J. N. Israelachvili, Direct experimental verification of the Kelvin equation for capillary condensation, Nature, 1979, 277, 548–549 CrossRef CAS
 .
.
- L. R. Fisher and J. N. Israelachvili, Experimental studies on the applicability of the Kelvin equation to highly curved concave menisci, J. Colloid Interface Sci., 1981, 80, 528–541 CrossRef CAS
 .
.
- I. Al-Kindi and T. Babadagli, Revisiting Kelvin equation and Peng–Robinson equation of state for accurate modeling of hydrocarbon phase behavior in nano capillaries, Sci. Rep., 2021, 11, 6573 CrossRef CAS PubMed
 .
.
- R. C. Tolman, The Effect of Droplet Size on Surface Tension, J. Chem. Phys., 1949, 17, 333–337 CrossRef CAS
 .
.
- Z. Li, Z. Jin and A. Firoozabadi, Phase Behavior and Adsorption of Pure Substances and Mixtures and Characterization in Nanopore Structures by Density Functional Theory, SPE J., 2014, 19, 1096–1109 CrossRef
 .
.
- D. R. Sandoval, W. Yan, M. L. Michelsen and E. H. Stenby, Influence of Adsorption and Capillary Pressure on Phase Equilibria inside Shale Reservoirs, Energy Fuels, 2018, 32, 2819–2833 CrossRef CAS
 .
.
- G. J. Zarragoicoechea and V. A. Kuz, van der Waals equation of state for a fluid in a nanopore, Phys. Rev. E, 2002, 65, 021110 CrossRef PubMed
 .
.
- W. Xiong, Y.-L. Zhao, J.-H. Qin, S.-L. Huang and L.-H. Zhang, Phase equilibrium modeling for confined fluids in nanopores using an association equation of state, J. Supercrit. Fluids, 2021, 169, 105118 CrossRef CAS
 .
.
- L. Travalloni, M. Castier, F. W. Tavares and S. I. Sandler, Thermodynamic modeling of confined fluids using an extension of the generalized van der Waals theory, Chem. Eng. Sci., 2010, 65, 3088–3099 CrossRef CAS
 .
.
- S. Salahshoor, M. Fahes and C. Teodoriu, A review on the effect of confinement on phase behavior in tight formations, J. Nat. Gas Sci. Eng., 2018, 51, 89–103 CrossRef
 .
.
- J. Wu, Density functional theory for chemical engineering: From capillarity to soft materials, AIChE J., 2006, 52, 1169–1193 CrossRef CAS
 .
.
- E. A. Ustinov and D. D. Do, Modeling of Adsorption in Finite Cylindrical Pores by Means of Density Functional Theory, Adsorption, 2005, 11, 455–477 CrossRef CAS
 .
.
- T. Ren, C.-Y. Wang, R. Huang, C. Deng, Y. Xu, A. Majumder, J. Ra, K. Shen, J. M. Vohs, J. J. de Pablo, R. J. Gorte and D. Lee, Understanding polymer-porous solid interactions based on small gas molecule adsorption behavior, Chem. Eng. J., 2023, 473, 145220 CrossRef CAS
 .
.
- Y. Liu, Z. Jin and H. A. Li, Comparison of Peng–Robinson Equation of State With Capillary Pressure Model With Engineering Density-Functional Theory in Describing the Phase Behavior of Confined Hydrocarbons, SPE J., 2018, 23, 1784–1797 CrossRef CAS
 .
.
- M. Sedghi and M. Piri, Capillary condensation and capillary pressure of methane in carbon nanopores: Molecular Dynamics simulations of nanoconfinement effects, Fluid Phase Equilib., 2018, 459, 196–207 CrossRef CAS
 .
.
- H. Hu, Q. Li, S. Liu and T. Fang, Molecular dynamics study on water vapor condensation and infiltration characteristics in nanopores with tunable wettability, Appl. Surf. Sci., 2019, 494, 249–258 CrossRef CAS
 .
.
- M. B. Asadi, A. De Rosis and S. Zendehboudi, Central-Moments-Based Lattice Boltzmann for Associating Fluids: A New Integrated Approach, J. Phys. Chem. B, 2020, 124, 2900–2913 CrossRef CAS PubMed
 .
.
- Y. Wang and S. A. Aryana, Coupled confined phase behavior and transport of methane in slit nanopores, Chem. Eng. J., 2021, 404, 126502 CrossRef CAS
 .
.
- G. J. Zarragoicoechea and V. A. Kuz, Critical shift of a confined fluid in a nanopore, Fluid Phase Equilib., 2004, 220, 7–9 CrossRef CAS
 .
.
- S. P. Tan and M. Piri, Equation-of-state modeling of confined-fluid phase equilibria in nanopores, Fluid Phase Equilib., 2015, 393, 48–63 CrossRef CAS
 .
.
- M. Thommes and G. H. Findenegg, Pore Condensation and Critical-Point Shift of a Fluid in Controlled-Pore Glass, Langmuir, 1994, 10, 4270–4277 CrossRef CAS
 .
.
- K. Morishige and M. Shikimi, Adsorption hysteresis and pore critical temperature in a single cylindrical pore, J. Chem. Phys., 1998, 108, 7821–7824 CrossRef CAS
 .
.
- L. Travalloni, M. Castier, F. W. Tavares and S. I. Sandler, Critical behavior of pure confined fluids from an extension of the van der Waals equation of state, J. Supercrit. Fluids, 2010, 55, 455–461 CrossRef CAS
 .
.
- M. B. Asadi and S. Zendehboudi, Hybridized method of pseudopotential lattice Boltzmann and cubic-plus-association equation of state assesses thermodynamic characteristics of associating fluids, Phys. Rev. E, 2019, 100, 043302 CrossRef CAS PubMed
 .
.
- J. O. Valderrama and P. A. Robles, Critical Properties, Normal Boiling Temperatures, and Acentric Factors of Fifty Ionic Liquids, Ind. Eng. Chem. Res., 2007, 46, 1338–1344 CrossRef CAS
 .
.
-
J. Prausnitz, R. Lichtenthaler and E. G. de Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice Hall PTR, New Jersey, 3ed edn, 1999 Search PubMed
 .
.
- S. P. Tan and M. Piri, Retrograde behavior revisited: implications for confined fluid phase equilibria in nanopores, Phys. Chem. Chem. Phys., 2017, 19, 18890–18901 RSC
 .
.
- J. Gross and G. Sadowski, Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules, Ind. Eng. Chem. Res., 2001, 40, 1244–1260 CrossRef CAS
 .
.
- J. Gross and G. Sadowski, Application of the Perturbed-Chain SAFT Equation of State to Associating Systems, Ind. Eng. Chem. Res., 2002, 41, 5510–5515 CrossRef CAS
 .
.
- A. A. Shapiro and E. H. Stenby, Kelvin equation for a non-ideal multicomponent mixture, Fluid Phase Equilib., 1997, 134, 87–101 CrossRef CAS
 .
.
-
R. J. Stokes and D. F. Evans, Fundamentals of Interfacial Engineering, Wiley, Germany, 1997 Search PubMed
 .
.
- G. Yang, Z. Fan and X. Li, Determination of confined fluid phase behavior using extended Peng–Robinson equation of state, Chem. Eng. J., 2019, 378, 122032 CrossRef CAS
 .
.
- G. Yang, Z. Fan and X. Li, Determination of confined fluid phase behavior using extended Peng–Robinson equation of state, Chem. Eng. J., 2019, 378, 122032 CrossRef CAS
 .
.
- J. Gross and G. Sadowski, Reply to Comment on “Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules”, Ind. Eng. Chem. Res., 2019, 58, 5744–5745 CrossRef CAS
 .
.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, New reference equation of state for associating liquids, Ind. Eng. Chem. Res., 1990, 29, 1709–1721 CrossRef CAS
 .
.
- W. A. Cañas-Marín, D. L. González and B. A. Hoyos, Comment on “Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules”, Ind. Eng. Chem. Res., 2019, 58, 5743 CrossRef
 .
.
- L. Kong and H. Adidharma, Adsorption of simple square-well fluids in slit nanopores: Modeling based on Generalized van der Waals partition function and Monte Carlo simulation, Chem. Eng. Sci., 2018, 177, 323–332 CrossRef CAS
 .
.
- L. Travalloni, M. Castier, F. W. Tavares and S. I. Sandler, Thermodynamic modeling of confined fluids using an extension of the generalized van der Waals theory, Chem. Eng. Sci., 2010, 65, 3088–3099 CrossRef CAS
 .
.
- K. Morishige, N. Tateishi and S. Fukuma, Capillary Condensation of Nitrogen in MCM-48 and SBA-16, J. Phys. Chem. B, 2003, 107, 5177–5181 CrossRef CAS
 .
.
- K. Morishige and M. Ito, Capillary condensation of nitrogen in MCM-41
and SBA-15, J. Chem. Phys., 2002, 117, 8036–8041 CrossRef CAS
 .
.
- K. Morishige, H. Fujii, M. Uga and D. Kinukawa, Capillary Critical Point of Argon, Nitrogen, Oxygen, Ethylene, and Carbon Dioxide in MCM-41, Langmuir, 1997, 13, 3494–3498 CrossRef CAS
 .
.
- K. Morishige and Y. Nakamura, Nature of Adsorption and Desorption Branches in Cylindrical Pores, Langmuir, 2004, 20, 4503–4506 CrossRef CAS PubMed
 .
.
- M. Thommes, R. Köhn and M. Fröba, Sorption and Pore Condensation Behavior of Nitrogen, Argon, and Krypton in Mesoporous MCM-48 Silica Materials, J. Phys. Chem. B, 2000, 104, 7932–7943 CrossRef CAS
 .
.
- E. Barsotti, S. Saraji, S. P. Tan and M. Piri, Capillary Condensation of Binary and Ternary Mixtures of n-Pentane–Isopentane–CO2 in Nanopores: An Experimental Study on the Effects of Composition and Equilibrium, Langmuir, 2018, 34, 1967–1980 CrossRef CAS PubMed
 .
.
- X. Qiu, S. P. Tan, M. Dejam and H. Adidharma, Isochoric measurement of the evaporation point of pure fluids in bulk and nanoporous media using differential scanning calorimetry, Phys. Chem. Chem. Phys., 2020, 22, 7048–7057 RSC
 .
.
- E. Barsotti, S. P. Tan, M. Piri and J.-H. Chen, Phenomenological Study of Confined Criticality: Insights from the Capillary Condensation of Propane, n-Butane, and n-Pentane in Nanopores, Langmuir, 2018, 34, 4473–4483 CrossRef CAS PubMed
 .
.
- S. Z. Qiao, S. K. Bhatia and D. Nicholson, Study of Hexane Adsorption in Nanoporous MCM-41 Silica, Langmuir, 2004, 20, 389–395 CrossRef CAS PubMed
 .
.
- N. Tanchoux, P. Trens, D. Maldonado, F. Di Renzo and F. Fajula, The adsorption of hexane over MCM-41 type materials, Colloids Surf., A, 2004, 246, 1–8 CrossRef CAS
 .
.
- E. Van Bavel, V. Meynen, P. Cool, K. Lebeau and E. F. Vansant, Adsorption of Hydrocarbons on Mesoporous SBA-15 and PHTS Materials, Langmuir, 2005, 21, 2447–2453 CrossRef CAS PubMed
 .
.
- H. Vinh-Thang, Q. Huang, M. Eić, D. Trong-On and S. Kaliaguine, Adsorption of C7 Hydrocarbons on Biporous SBA-15 Mesoporous Silica, Langmuir, 2005, 21, 5094–5101 CrossRef PubMed
 .
.
- C. Nguyen, C. G. Sonwane, S. K. Bhatia and D. D. Do, Adsorption of Benzene and Ethanol on MCM-41 Material, Langmuir, 1998, 14, 4950–4952 CrossRef CAS
 .
.
- M. M. L. Ribeiro Carrott, A. J. E. Candeias, P. J. M. Carrott, P. I. Ravikovitch, A. V. Neimark and A. D. Sequeira, Adsorption of nitrogen, neopentane, n-hexane, benzene and methanol for the evaluation of pore sizes in silica grades of MCM-41, Microporous Mesoporous Mater., 2001, 47, 323–337 CrossRef CAS
 .
.
- S. Kittaka, S. Ishimaru, M. Kuranishi, T. Matsuda and T. Yamaguchi, Enthalpy and interfacial free energy changes of water capillary condensed in mesoporous silica, MCM-41 and SBA-15, Phys. Chem. Chem. Phys., 2006, 8, 3223 RSC
 .
.
- J. S. Oh, W. G. Shim, J. W. Lee, J. H. Kim, H. Moon and G. Seo, Adsorption Equilibrium of Water Vapor on Mesoporous Materials, J. Chem. Eng. Data, 2003, 48, 1458–1462 CrossRef CAS
 .
.
- K. Morishige, T. Kawai and S. Kittaka, Capillary Condensation of Water in Mesoporous Carbon, J. Phys. Chem. C, 2014, 118, 4664–4669 CrossRef CAS
 .
.
- X. Qiu, H. Yang, M. Dejam, S. P. Tan and H. Adidharma, Experiments on the Capillary Condensation/Evaporation Hysteresis of Pure Fluids and Binary Mixtures in Cylindrical Nanopores, J. Phys. Chem. C, 2021, 125, 5802–5815 CrossRef CAS
 .
.
- J.-H. Yun, T. Düren, F. J. Keil and N. A. Seaton, Adsorption of Methane, Ethane, and Their Binary Mixtures on MCM-41: Experimental Evaluation of Methods for the Prediction of Adsorption Equilibrium, Langmuir, 2002, 18, 2693–2701 CrossRef CAS
 .
.
- Y. He and N. A. Seaton, Experimental and Computer Simulation Studies of the Adsorption of Ethane, Carbon Dioxide, and Their Binary Mixtures
in MCM-41, Langmuir, 2003, 19, 10132–10138 CrossRef CAS
 .
.
- Q. Yang, P. Z. Sun, L. Fumagalli, Y. V. Stebunov, S. J. Haigh, Z. W. Zhou, I. V. Grigorieva, F. C. Wang and A. K. Geim, Capillary condensation under atomic-scale confinement, Nature, 2020, 588, 250–253 CrossRef CAS PubMed
 .
.
- S. Gast, J. H. Matthies, U. S. Tuttlies and U. Nieken, A Novel Experimental Setup for Kinetic Studies of Toluene Oxidation in the Homogeneous Liquid Phase, Chem. Eng. Technol., 2017, 40, 1445–1452 CrossRef CAS
 .
.
- O. R. Quayle, The Parachors of Organic Compounds. An Interpretation and Catalogue, Chem. Rev., 1953, 53, 439–589 CrossRef CAS
 .
.
- M. Ma, S. Chen and J. Abedi, Binary interaction coefficients of asymmetric CH4, C2H6, and CO2 with high n-alkanes for the simplified PC-SAFT correlation and prediction, Fluid Phase Equilib., 2015, 405, 114–123 CrossRef CAS
 .
.
- J. Wu, H. Zhou, H. Wang, H. Shao, G. Yan and T. Lin, Novel Water Harvesting Fibrous Membranes with Directional Water Transport Capability, Adv. Mater. Interfaces, 2019, 6 DOI:10.1002/admi.201801529
 .
.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
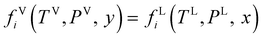
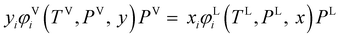
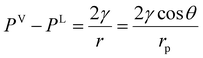
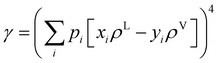

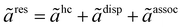
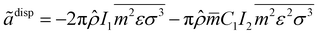
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) is the total number density of the molecules and is related to density and Avogadro's number (NA) using eqn (8):
is the total number density of the molecules and is related to density and Avogadro's number (NA) using eqn (8):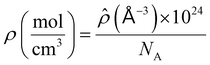
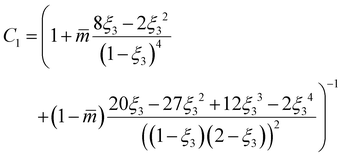
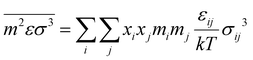
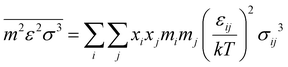
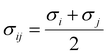
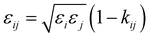
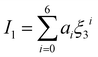
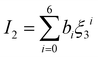
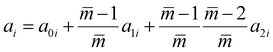
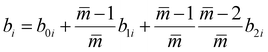
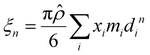
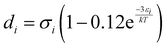
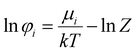
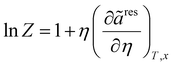
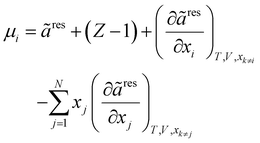
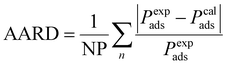

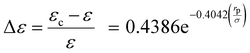








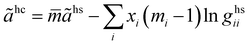
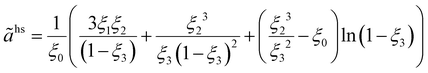
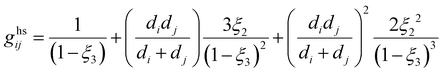
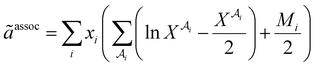
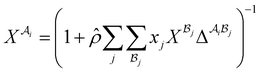
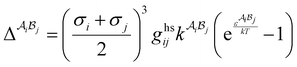
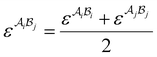
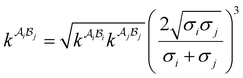
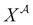 is the mole fraction of molecules that are not bonded at site
is the mole fraction of molecules that are not bonded at site 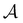 and Mi is the number of association sites on each molecule. In this study, we consider Mi = 2 for all associating molecules because of using the 2B association scheme. Furthermore,
and Mi is the number of association sites on each molecule. In this study, we consider Mi = 2 for all associating molecules because of using the 2B association scheme. Furthermore, 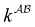 and
and 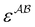 are the associating component parameters of the PC-SAFT EoS related to the effective association volume and the association energy, respectively. For non-associating molecules, these parameters are set to zero.
are the associating component parameters of the PC-SAFT EoS related to the effective association volume and the association energy, respectively. For non-associating molecules, these parameters are set to zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
