Microhydration of small protonated polyaromatic hydrocarbons: a first principles study

Abstract

Using first principles methodology, we investigate the microsolvation of protonated benzene (BzH⁺), protonated coronene (CorH⁺) and protonated dodecabenzocoronene (DbcH⁺). Gas phase complexes of these small protonated polyaromatic hydrocarbons (H⁺PAHs) with mono-, di-, and tri-hydrated water molecules are considered. Their most stable forms are presented, where we discuss their structural, energetic aromaticity and IR and UV spectral features. In particular, we focus on the analysis of the bonding and various non-bonded interactions between these protonated aromatics and water clusters. The strength of non-bonded interactions is quantified and correlated with their electron density profiles. Furthermore, insights into the interfacial interactions and stability of these complexes were obtained through non-covalent index and symmetry-adapted perturbation theory (SAPT0) analyses. We also discuss the effects of the extension of the π aromatic cloud on the water solvation of these protonated aromatics. In particular, we extended our predictions for the S₀ → S₁ and S₀ → T₁ wavelength transitions of micro hydrated H⁺PAHs to deduce those of these species solvated in aqueous solution. The present findings should be useful for understanding, at the microscopic level, the effects of water interacting with H⁺PAHs, which are relevant for organic chemistry, astrochemistry, atmospheric chemistry, combustion and materials science.

---

I. Introduction

Polyaromatic hydrocarbons (PAHs) are aromatic organic compounds of great importance in atmospheric chemistry,^1,2 materials science^3,4 and combustion.^5–9 For instance, they can be formed during the incomplete combustion of organic compounds and be found in various environmental and atmospheric media such in air, food, soil and water with serious drawbacks for the health of humans, animals and plants because of their wide structural distribution and potential toxicity.^10–12 Besides, PAHs are very important in astrochemistry.^13–15 Indeed, they are highly suspected to be present in interstellar media (ISM) and on the origin of the unidentified infrared emission bands (UIR). Although the characteristics of some of the vibrations of PAHs are closely similar to those recorded in surveys, several features remain unassigned. In this context, several PAH (ionized or nitrogen or silicon containing) derivatives and clusters were proposed instead. Indeed, the recent detections of small aromatics (e.g., benzonitrile,¹⁶ 1-cyanonaphthalene and 2-cyanonaphthalene,¹⁷ 1-cyano-cyclopentadiene,¹⁸ cyclopentadiene and indene¹⁹) and of the commonly admitted chemical intermediates for their formation in the ISM (e.g., 1-ethynyl-cyclopentadiene and 2-ethynyl-cyclopentadiene²⁰ and fulvenallene²¹) are very encouraging towards their definitive identification and for the understanding of their physical chemistry there. In particular, protonated PAHs (H⁺PAHs) were proposed as important intermediates in the chemical models leading to PAHs, since some protonated compounds were also detected in the ISM.²² Therefore, these results motivated extensive spectroscopic laboratory investigations of protonated aromatics targeting their detection in astrophysical media.^23–31

PAHs are formed by fused aromatic rings with wide π-electron delocalization. A priori, several protonation sites of these aromatics are possible resulting in: (i) a σ complex where the proton is attached to an external carbon of the aromatic compound (i.e., aliphatic sp³ C–H⁺); (ii) a π complex where the proton interacts with the π orbital of these aromatics; and (iii) a σ complex where the proton is attached to an internal carbon of PAHs possessing more than one aromatic ring. The identification of the protonation site, the relative stability of the corresponding protonated aromatic compound and the nature of their mutual interactions motivated intensive theoretical and experimental investigations during the two last decades.

Back to 2001, the computational study of Frash et al.³² showed that the proton attaches preferentially to one carbon atom (either external or internal) of corannulene, forming a σ-complex. Then, Solcà and Dopfer²⁹ and Jones et al.³³ showed that a σ-complex (case (i)) is obtained upon attaching a proton to benzene forming a benzenium ion through the analysis of the corresponding IR spectrum. For the benzenium ion, Duncan and co-workers^34–36 confirmed these findings using infrared and photodissociation spectroscopy (IRPD) combined with ab initio and DFT computations. Later on, Knorke et al.²⁸ and Lorenz et al.³⁷ extended such investigations to gas phase protonated naphthalene, anthracene, tetracene, pentacene, and coronene. Indeed, these authors produced various protonated forms of such polyaromatic ring compounds. They characterized them by IR multiple-photon dissociation (IRMPD) spectroscopy. Through comparison to their computed DFT IR spectra, these authors confirmed the formation of case (i) ions. For protonated naphthalene and protonated coronene, Bahou et al.^30,38 recorded highly resolved IR spectra of these molecular cations trapped in cold solid para-hydrogen matrices. Through the analysis of these spectra, these authors came to the conclusion that H⁺PAHs might be among the carriers of UIR bands in the ISM.

Besides, UV-vis absorption and fluorescence spectroscopies were used to give insights into the pattern of the electronic excited states of H⁺PAHs and on their photophysics. Experimentally, vibrationally resolved electronic spectra of protonated species of benzene, toluene, naphthalene, anthracene, and tetracene were recorded.^39–44 Maier and co-workers^45–49 extended these studies to larger H⁺PAHs, such as protonated pyrene and protonated coronene in addition to protonated naphthalene. These cations were trapped in cold solid neon matrices or in ion traps combined with collisional cooling. Such experimentally very cold media (T ∼ 15 K) mimic the ISM temperature allowing stating, nevertheless, that these cations are not possible carriers of any known diffuse interstellar band. Moreover, these works showed that protonation strongly affects the electronic structure of the respective PAHs resulting in an unusually large red shift with respect to the corresponding neutral bands. The theoretical investigations^50–56 of the S₀ → S₁ transition of such protonated PAHs showed that this transition exhibits a charge transfer character as observed experimentally. Complex dynamics on the electronic states of H⁺PAHs was noticed, such as reversible photoisomerization of protonated naphthalenes. Very recently, Laws et al.⁵⁷ recorded highly resolved excitation spectra of very cold protonated anthracene cations obtained by triple-resonance dissociation spectroscopy. These spectra present the rich structure signature of a symmetry-breaking intramolecular charge-transfer process through active Herzberg–Teller progressions. In fact, these authors revealed that the electronic structure and photophysics of H⁺PAHs, either isolated or interacting with inert ligands, are still challenging and worth investigating in-depth.

Although H⁺PAHs were extensively studied, this is not the case, however, of their complexes with ligands such as water or rare gases. Back to 2003, Solcà and Dopfer⁵⁸ detected protonated benzene – complexed with various inert ligands, including water (W). They identified the protonated benzene–water dimer (BzH⁺–W) by IRPD spectroscopy complemented by MP2/6-311G(2df,2pd) computations for assignment. In 2012, the structures, bonding, and IR spectra of protonated benzene (BzH⁺)_n–W_m (with n and/or m up to 3) clusters were studied by Duncan and co-workers^59,60 using IRPD spectroscopy and quantum chemical approaches. They found that specific induced shifts on IR bands compared to bare protonated benzene allow identification of the corresponding cluster. Also, Jouvet and co-workers^61,62 treated experimentally the effects on the electronic spectra of protonated naphthalene caused by microhydration or its clustering with Ar. Complex vibrationally resolved photodissociation spectral features were recorded, for which assignments were achieved using quantum chemical calculations and Franck–Condon simulations of the vibrational bands. More recently, Chatterjee and Dopfer⁶³ used IRPD and B3LYP-D3/aug-cc-pVTZ computations, in the C–H and O–H stretch spectral range (2750–3800 cm⁻¹), to probe clustering induced shifts on bare and Ar-tagged protonated naphthalene–W_n complexes (n ≤ 3). Interestingly, they found a solvation-dependent intracluster proton transfer where a proton is attached to naphthalene for n = 1, whereas the proton binds preferentially to water clusters for n ≥ 2.

Previous theoretical and experimental studies proved that the most stable protonated aromatic species correspond to case (i) cations. They showed also that IR and UV-vis spectroscopies combined with first principles computations represent powerful tools and a critical probe of the structure, the bonding and the electronic, vibrational and rotational spectra of organic/aromatic–W_n complexes. The present study uses such first principles methodologies to investigate the structural stability, IR and UV-vis spectra and energetics of water cluster networks (W_n, where n = 1 to 3) interacting with three different protonated aromatic carbon compounds of increasing size (i.e. benzene (BzH⁺), coronene (CorH⁺) and dodecabenzocoronene (DbcH⁺). We thus aim at understanding the effect of the aromatic π-extension from benzene to coronene to dodecabenzocoronene. These extended models are considered to mimic the effect of large, protonated PAH–water cluster interactions. Although computations and experiments on the latter are challenging, recent investigations showed, indeed, that studying the series of small PAHs with increasing size gives several insights on the larger ones.^64–66 Besides, we target shedding light on the microsolvation induced effect of these H⁺PAHs targeting their physical chemical properties in aqueous solutions.

II. Computational methods

We focus on the structures, stabilities, energetics, electron density profiles, and nature of the interfacial interactions within BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters, and on their clustering induced IR and UV-vis spectral features. For these clusters, we thus perform geometry optimizations, frequency calculations, bonding and intermonomer analyses, binding energy calculations and IR and UV spectra determinations. For electronic structure calculations and spectroscopic investigations, we use the Gaussian 16⁶⁷ suite of programs. For all species, we carry out computations at the PBE0/6-311++G** and PBE0-D3/6-311++G** levels, where D3 corresponds to the Grimme's dispersion correction to account for dispersion.⁶⁸ As established in the literature,^66,69 the PBE0-D3/6-311++G** level of theory is accurate enough to describe such protonated aromatic–water clusters since benchmarks revealed that PBE0-D3/6-311++G** competes with MP2/CBS and CCSD(T)/CBS, whereas a strong reduction in computational costs is noticed. In particular, we carried out additional MP2/6-311++G** calculations for BzH⁺–W_n (n = 1–3) clusters. These results are provided in Fig. S1 and Table S1 of the ESI.† These MP2 computations show that the O–H⁺⋯π mode of interaction is more favorable than the C–H⁺⋯O interaction. Indeed, all PBE0-D3 optimized CH⁺⋯O isomers convert into O–H⁺⋯π isomers. This is due to the strong inductive effect that stabilizes the Cation⁺⋯π complex (see ref. 83 for more details). Nevertheless, PBE0-D3 describes well σ C–H⁺⋯O interaction with reduced computational cost. Since this is the focus of the present work, we will adopt PBE0-D3 for all electronic computations of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) complexes.

For visualization, we use Gauss View 6.0 with Chemcraft software.^70,71 We also do an energy decomposition analysis (EDA) at the SAPT0/aug-cc-pVDZ level. For these symmetry-adapted perturbation theory (SAPT) computations, we use PSI-4 software.^72,73

For cluster optimizations, several initial configurations are considered. Using the Conformer–Rotamer ensemble sampling tool (CREST) technique, which is based on the semiempirical tight-binding quantum chemistry methods (GFN1-xTB and GFN2-xTB), the conformational space for clusters is sampled.^74–76 Within the framework of meta-dynamics (MTD), the semiempirical tight-binding based quantum chemistry approach GFN-xTB is utilized to explore the different chemical compounds, conformers, and reaction space. First, geometries are pre-optimized with the semi-empirical tight-binding XTB2 method.⁷⁷ The corresponding results are listed in Table S2 of the ESI.†

We set very low convergence criteria since the intermonomer interactions are weak and these clusters are floppy resulting in flat potentials close to equilibria. We check on the minimal nature of the optimized stationary points by having all positive vibrational frequencies. Afterwards, only the most stable minimum structures of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3)-type clusters are retained for further treatment. Thus, we deduce their anharmonic frequencies by scaling the harmonic ones by a factor of 0.9593⁷⁸ and compute their IR spectra and their UV-vis absorption spectra. In addition, we perform full anharmonic frequency calculations for BzH⁺–W_n (n = 1–3) and CorH⁺–W_n (n = 0–2) species using perturbation theory as implemented in Gaussian 16. For electronic excited states and UV-vis spectra calculations, we use the time-dependent density functional theory (TD-DFT) technique as implemented in Gaussian 16. All TD-DFT calculations are carried out on the PBE0/6-311++G** optimized geometries of the clusters, where the TD = (Nstates = 30, 50–50) keywords for the singlet and triplet excited states are used. Furthermore, to study the aromatic character of the protonated species after incorporation of water molecules, nucleus independent chemical shift (NICS) values are computed at the center of the ring (NICS (0 Å)_zz) and at 1 Å above (NICS (1 Å)_zz) for all the clusters.

To characterize the bonding and the intermonomer interactions within these complexes, we carry out atoms-in-molecules (AIM) electron density and non-covalent interaction (NCI) index analyses using AIM 2000⁷⁹ and Multiwfn⁸⁰ software, respectively. We also compute their binding energies (BE_(AB)) at the PBE0(-D3)/6-311++G** level. For BzH⁺-containing clusters, we derive also their BEs using MP2/6-311++G**. BE_(AB) is calculated within the supramolecular approach and corrected for basis set superposition error using the counterpoise method:⁸¹

BE_(AB) = [E_(AB) − (E_(A) + E_(B))] (1)

where E_(AB) is the total energy of BzH⁺–W_n or CorH⁺–W_n or DbcH⁺–W_n, where n = 1–3; E_(A) is the total energy of BzH⁺ or CorH⁺ or DbcH⁺. E_(B) is the total energy of W_n (n = 1–3), respectively. The total energies of the (A) and (B) monomers are evaluated in the basis set of the respective (AB) cluster.

III. Results

1. Most stable forms of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (where n = 1–3) clusters

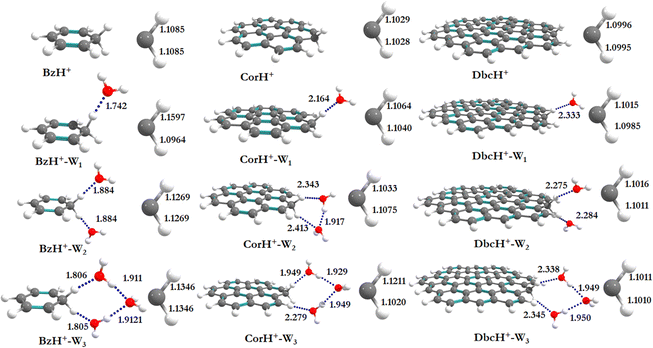
Fig. 1 shows the PBE0-D3/6-311++G** optimized geometries of BzH⁺, CorH⁺, DbcH⁺ and of their clusters with water (i.e., BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3). The coordinates obtained from the PBE0-D3/6-311++G** method are provided in Table S3 of the ESI,† where we also list those obtained without D3 correction (Table S4, ESI†) and the MP2/6-311++G** (Table S5, ESI†) methods. Only in case (i), protonated aromatics are considered as interacting with water molecules since their monohydrates are the most stable ones. Indeed, this was already confirmed for BzH⁺ hydrates and we show in Tables S4 and S5 (ESI†) that this is also the case for CorH⁺ and for CorH⁺–W₁. Strictly speaking, upon protonation, BzH⁺ species are no more aromatic; however, those containing CorH⁺ and DbcH⁺ are still aromatic.

Fig. 1 PBE0-D3/6-311++G** optimized equilibrium structures of BzH⁺, CorH⁺ and DbcH⁺ and of the most stable forms of the BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) complexes. Close views of the sp³ C–H bond distances (before and after hydration) and the intermonomer distances (in Å) are given.

Fig. 1 reveals that, after optimization, the proton remains attached to the aromatic, where the water molecules form an H-bonded network in its vicinity. For instance, we have an H-bond between the excess proton (i.e., sp³ C–H⁺ site) and the oxygen of a water molecule for the BzH⁺–W₁, CorH⁺–W₁ and DbcH⁺–W₁ complexes. We have also the establishment of H-bonds between the hydrogens attached to the sp³ carbon of BzH⁺, CorH⁺ and DbcH⁺ and an oxygen of the water molecule for BzH⁺–W₂, CorH⁺–W₂ and DbcH⁺–W₂, without interaction between the two water molecules. Nevertheless, a H₂O–H₂O–H₂O network is formed while attaching three water molecules to BzH⁺, CorH⁺ and DbcH⁺ to form BzH⁺–W₃, CorH⁺–W₃ and DbcH⁺–W₃, where an H-bond network involving the hydrogens of the sp³ carbon of BzH⁺, CorH⁺ and DbcH⁺ and H/O of the water molecules is observed.

Specifically, the optimized geometries of BzH⁺–W_n (n = 1–3) clusters (Fig. 1) reveal that the excess proton is always localized/attached to Bz establishing H-bond interactions with the neighbouring water molecules. The corresponding H-bond distances vary from 1.742 (1.776) Å, to 1.884 (1.905) Å, to 1.805 (1.825) Å for BzH⁺–W₁, BzH⁺–W₂, and BzH⁺–W₃, respectively, where parenthesised values are obtained without D3 correction. The corresponding distances calculated using the MP2/6-311++G** method are 1.674 Å, 1.941 Å, and 1.849 Å (Fig. S1, ESI†). The comparison of these distances reveals that the incorporation of D3 correction significantly strengthens the H-bonds. The MP2 distances exhibit a similar trend upon attaching water molecules and remain close to those deduced using PBE0-D3/6-311++G**.

For BzH⁺–W_n (n = 1–3), the calculated sp³ C–H bond distances of bare BzH⁺ are ∼1.11 Å, whereas hydrated BzH⁺ C–H bond distances vary from 1.096 to 1.160 Å. This is due to the formation of a H-bonded network with water clusters. The mono-hydrated protonated Bz has the shortest distance with water when compared to di-hydrated (i.e., bifurcated) ones. When n = 3, water molecules form a cyclic H-bonded network, which has a close resemblance with the tetrameric form of such water clusters with different charged species.^82,83 While considering CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters, we have similar findings. Indeed, monohydrated CorH⁺ and DbcH⁺ are stabilised by an intermonomer H-bond. Di-hydrated CorH⁺ and DbcH⁺ consist of two water molecules establishing H-bonds, each with an aliphatic C–H of CorH⁺ or DbcH⁺. For CorH⁺–W₃ and DbcH⁺–W₃, we have a network of three water molecules bonded by four H-bonds. In addition, Fig. 1 shows that extending the aromatic π-clouds affects the H-bond distances and geometrical parameters. For example, the primary shell H-bond distance in BzH⁺–W₁ is ∼1.742 Å, which is lengthened, due to the H-bond strength weakening, to 2.164 Å and 2.333 Å in CorH⁺–W and in DbcH⁺–W, respectively. A similar trend is observed for CorH⁺–W₂, CorH⁺–W₃, DbcH⁺–W₂ and DbcH⁺–W₃ clusters. In sum, the extension of the π-aromatic cloud significantly influences the strength of C–H⁺⋯O and O–H⋯O interactions, i.e. it reduces the strength of the hydration/solvation structure. In contrast, the proton transfer process enhances the H-bonding strength as well as shortens the water–water interactions in protonated water PAH clusters.⁶⁶

2. Binding energies of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (where n = 1–3) complexes

Table 1 lists the BEs of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) complexes as computed at the PBE0/6-311++G** and PBE0-D3/6-311++G** levels i.e., without and with considering the D3 dispersion correction. This table shows that dispersion correction leads to 5–10% larger BEs (in absolute values). This is due to the better consideration of the long-range interactions within the complexes. This table shows that MP2 leads to less deep potential wells compared to PBE0-D3, whereas the differences remain small. Hereafter, we will refer to the PBE0-D3/6-311++G** data.

Table 1 PBE0/6-311++G** (first entry), PBE0-D3/6-311++G** (second entry) and MP2/6-311++G** (third entry) binding energies (BEs, in kcal mol⁻¹) of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) complexes

N	BzH^+–Wn	CorH^+–Wn	DbcH^+–Wn
a Taken from ref. 66 and 69. b Using the aug-cc-pVTZ basis set. Taken from ref. 69. c This geometry is from this work for the cyclic H-bonded water cluster model.
1	−12.76^a (−11.92)^b	−7.09	−5.40
	−13.97	−8.17	−6.55
	−13.15^b	—	—
2	−21.49^a (−19.84)^b	−13.40	−9.92
	−24.10	−13.46	−13.03
	−19.44 (−20.07)^b	—	—
3	−36.40^a (−34.17)^b	−25.24	−20.91
	−32.69	−21.2	−17.1
	−28.16^c	—	—

---

For BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters, Table 1 shows that, for a given number of water molecules, the C–H⁺⋯O H-bond interaction energies decrease, in absolute values, while increasing the size of the aromatic compound. For instance, we compute BEs of −13.97, −8.17, and −6.55 in kcal mol⁻¹ for BzH⁺–W₁, CorH⁺–W₁ and DbcH⁺–W₁, respectively. Thus, the reduction in the strength reaches up to 40 to 50% upon extending the π-cloud. In fact, the extension of the aromatic surface leads to a decrease of the interaction strength irrespective of the nature of the water clusters signature of the decrease of the hydration energy of the proton when the excess proton is attached to such an organic surface model.

In contrast, the |BEs| increase while increasing the number of water molecules surrounding protonated BzH⁺, CorH⁺ or DbcH⁺, where we observe an increase of 3–4 times when going from the mono- to di- to tri-hydrated respective clusters. Interestingly, our work shows that we can modulate, via the extension of the size of the aromatic, the interaction, at the microscopic level, between the protonated sp³ carbon of the aromatic compounds, and the neighboring network of water molecules participating in the solvation of these species. This may result in the activation of the solvated compound as we noticed for CO₂ interacting, via σ H-bond or π stacking interactions, with organic molecules, metal surfaces or ionic liquids.^84–86 We expect applications of these findings at least in organic chemistry where protonated aromatics are important intermediates, for instance, in electrophilic substitutions.

3. Analyses of non-covalent interactions.
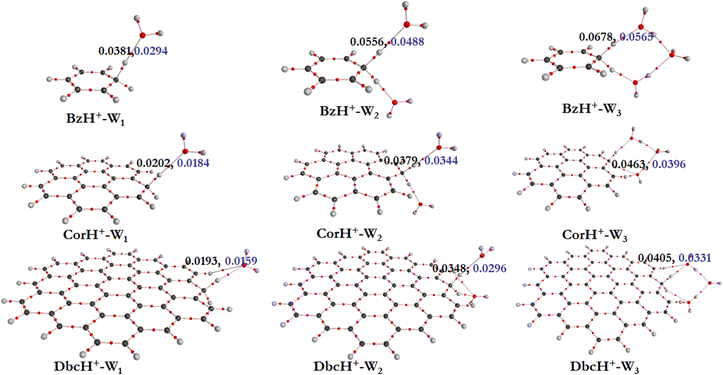
a. AIM electron density topography. To get some insights into the interfacial interactions, the AIM approach is used. This allows description of the non-covalent interactions between BzH⁺, CorH⁺ and DbcH⁺ and water clusters, where topological parameters at bond critical points (BCPs) are determined. Indeed, the strength and the nature of non-covalent interactions are connected to the electron density (ρ(r_c)) and its Laplacian (∇²ρ(r_c)) values at BCPs. Fig. 2 shows the electron density analysis at H-bonded critical points (HBCPs) and non-bonded critical points (NBCPs) for BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3). This figure reveals that there are several kinds of non-covalent interactions stabilizing these complexes, where various bond paths are formed between protonated aromatic compounds and water clusters.

Fig. 2 PBE0/6-311++G** molecular topography analyses of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters as determined from the corresponding total electron densities. Red dots correspond to bond critical points (BCPs). We give also their total electron density ρ(r_c) (in black color) and ∇²ρ(r_c) (in blue color). These values are shown in a.u.

For BzH⁺–W₁, the calculated ρ(r_c) and ∇²ρ(r_c) values at the HBCP of C–H⁺⋯O interaction are 0.0381 and 0.0294 a.u., respectively. In the case of BzH⁺–W₂ and BzH⁺–W₃ clusters, the ρ(r_c) (∇²ρ(r_c)) values at the HBCP are 0.0556 (0.0488) and 0.0678 (0.0565) a.u. It is worth noticing that the electron density increases while increasing the hydration number. This reveals that there is no proton migration to water clusters i.e., the excess proton remains localized at the aromatic organic side as discussed above. Also, it is interesting to note that when the hydration number increases from 1 to 3, the H-bond strength gradually decreases. This is due to the charge distribution over the whole cluster. This is in line with the lengthening of the H-bond(s) between BzH⁺ upon increasing the number of water molecules attached to BzH⁺. Similar effects are found for the protonated CorH⁺/DbcH⁺ hydrates.

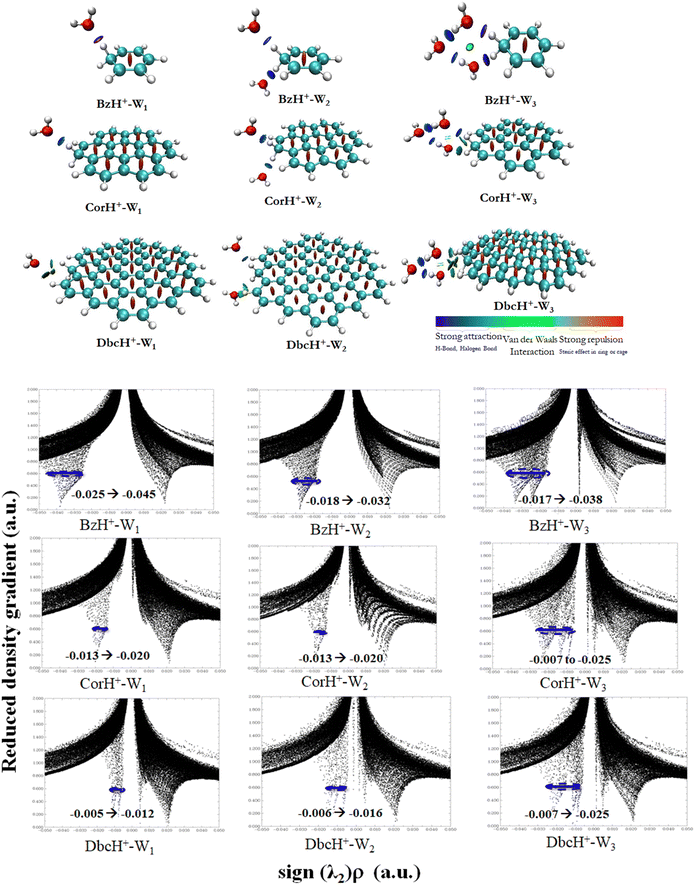
b. Non-covalent interaction indexes. Non-covalent interaction indexes allow the quantitative assessment of the non-covalent interactions established between water clusters and protonated aromatics. Fig. 3 shows the NCI plots of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters. We observe the existence of strong interaction regions (in blue) between water clusters and these aromatics. In addition, we notice the further stabilization of some water clusters via weak van der Waals interactions (in green). The relative contribution of both kinds of interactions depends on the cluster type.

Fig. 3 Top: NCI indexes of the BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters with an isosurface of 0.59 a.u. We show the strong and weak interaction regions in blue and green, respectively. Bottom: Bi-dimensional plots of reduced density gradient RDG versus sign (λ₂)*ρ of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters.

Mainly, strong interactions dominate within BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) clusters. Therefore, similar covalent and non-covalent interactions, with various strengths, are in action for the stabilization of these clusters whatever the extension of the π-aromatic cloud. The bi-dimensional plots of reduced density gradient RDG versus sign (λ₂)*ρ (Fig. 3) allow the assessment of quantitative information about the strength of H-bonded interaction within these various clusters. The strong repulsion and attraction in van der Waals interactions are represented in red and green areas, respectively; meanwhile, the H-bonds are represented by blue area.

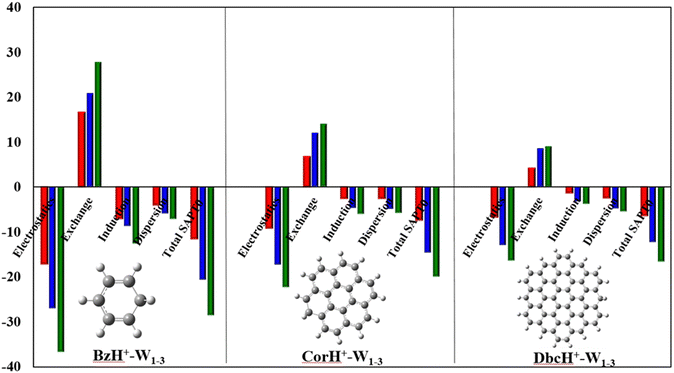
c. Energy decomposition analysis (EDA). As revealed by the NCI analyses, various terms contribute to the intermonomer interactions within BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3). Such effects can be quantified via energy decomposition analyses, which allow an understanding of the different energy contributions. At present, these are done at the SAPT0/aug-cc-pVDZ level as implemented in PSI-4. Within this approach, the total interaction energy (IE_total) contains the following contributions: electrostatic (E_{(electrostatic)}), exchange-repulsion (E_{(exchange-repulsion)}), induction (E_(induction)), and dispersion (E_(dispersion)) energies:

IE_total = E_{(electrostatic)} + E_{(exchange-repulsion)} + E_(induction) + E_(dispersion) (2)

Fig. 4 plots the individual contributions for BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) complexes. This figure shows that the E_{(electrostatic)}, E_(induction) and E_(dispersion) energies are negative, favouring thus the stability of these weakly bound complexes. The dominant stabilising contributions are of electrostatic nature since |E_{(electrostatic)}| is the largest. E_{(exchange-repulsion)} energies are, however, positive and thus contribute to the non-stability of these molecular species. Nevertheless, the sum of E_{(electrostatic)}, E_(induction) and E_(dispersion) is larger, in absolute value, than E_{(exchange-repulsion)} leading to negative IE_total energies, which are in line with the stable character of the clusters under study as certified by their negative BEs and AIM analyses. Moreover, Fig. 4 reveals that the IE_total energies and their various terms increase, in absolute value, upon increasing the number of water molecules because of the establishment of additional σ-type H-bonded interactions within such species. In contrast, the opposite trend is observed when the π-cloud is extended from Bz to Cor to Dbc.

Fig. 4 SAPT0/aug-cc-pVDZ energy decomposition analyses of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) complexes. The mono-, di- and tri-hydrated values are given in red, blue and green, respectively. All values are in kcal mol⁻¹.

d. Vibrational analyses and IR spectra. Previous works showed that IR spectroscopy is useful to characterize protonated aromatic compounds in the gas phase and to probe the interfacial interactions between organic compounds and water molecules. We thus computed, at the PBE0(-D3)/6-311++G** level, the vibrational harmonic frequencies of bare BzH⁺, CorH⁺ and DbcH⁺ and those of their complexes with one, two and three water molecules. Afterwards we deduced the corresponding anharmonic frequencies by scaling the harmonic ones. They are listed as ν_s in Tables 2 and 3. For BzH⁺–W_n (n = 0–3) and CorH⁺–W_n (n = 0–1), we have also computed their anharmonic frequencies at the PBE0 + D3/6-311++G** level and using perturbation theory (PT2) as implemented in Gaussian 16. The latter are denoted as ν_p in Tables 2 and 3. In the following, we will concentrate on the anharmonic frequencies > 2500 cm⁻¹. Mainly, they correspond to the C–H⁺ (sp³) and the C–H (sp²) stretchings and those arising from the complexation with water molecules. The latter are classified as A_water, AA_water and AD_water for single acceptor, double acceptor and single acceptor-single donor H-bonded stretching in water molecules, respectively. We give also the respective complexation induced shifts. The shifted frequencies were evaluated as the differences between the frequencies of the bare protonated aromatic and water molecule and those of this compound complexed with water clusters. For an isolated water molecule, the experimental and calculated stretching frequencies are 3757 cm^−1 87 and 3824 cm⁻¹, respectively. Note that free sp³ C–H stretchings have low IR intensities and they will not be discussed further.

Table 2 Main anharmonic vibrational frequencies (in cm⁻¹) of BzH⁺–W_n (n = 0–3) as computed using the PBE0/6-311++G** and PBE0+D3/6-311++G** methods. ν_s and ν_p correspond to scaled harmonic frequencies and to perturbatively determined anharmonic frequencies. The complexation induced shifts (in cm⁻¹) are given between parentheses. A_water, AA_water and AD_water denote the single acceptor, double acceptor and single acceptor single donor H-bonded stretching in water molecules, respectively

n	Assignment	PBE0	PBE0-D3
		ν s	ν s	ν p
a Experimental IR spectroscopy in the gas phase. Ref. 29. b Experimental IR spectroscopy in the gas phase. Ref. 36. c Experimental IR spectroscopy in the gas phase. Ref. 33. d Experimental IR spectroscopy in the gas phase. Ref. 36.
0	Aliphatic sp^3 C–H^+ stretching	2856	2858	2977
		2810^a
		2820^b
		2700–3200^c
		2891^d
	Aromatic sp^2 C–H stretching	3080	3079	3210
		3110^a
		3006^b
1	Free sp^3 C–H^+ stretching mode	2952 (−96)	2964 (−106)	3089 (−112)
	Free sp^2 C–H stretching	3082 (−2)	3081 (−2)	3211 (−1)
	H-bonded C–H^+ stretching to Awater (νss)	2323 (533)	2269 (589)	2365 (612)
	Free O–H stretching in Awater (νas)	3793 (31)	3794 (31)	3955 (35)
2	Free sp^3 C–H^+ stretching	Absence of sp^3 C–H^+ stretching
	Free sp^2 C–H stretching	3080 (0)	3079 (0)	3209 (1)
	H-bonded C–H^+ stretching to Awater (νas)	2637 (219)	2581 (277)	2690 (287)
	Free O–H stretching in Awater (νas)	3800 (24)	3801 (26)	3938 (52)
3	Free sp^2 C–H stretching	3070 (10)	3080 (−1)	3210 (0)
	H-bonded C–H^+ stretching to ADwater	2577 (279)	2447 (411)	2679 (298)
	H-bonded O–H stretching in ADwater (νas)	3780 (48)	3780 (47)	3943 (47)
	Free O–H stretching in AAwater (νas)	3776 (52)	3778 (49)	3938 (52)

---

Table 3 Main anharmonic (ν_s and ν_p in cm⁻¹) vibrational frequencies of CorH⁺–W_n and DbcH⁺–W_n (n = 0–3) as computed at the PBE0/6-311++G** and PBE0+D3/6-311++G** levels. ν_s (ν_p) correspond to scaled harmonic (perturbatively determined) ones (cf. text). The complexation induced shifts (in cm⁻¹) are given between parentheses. A_water, AA_water and AD_water denote the single acceptor, double acceptor and single acceptor single donor H-bonded stretching in water molecules, respectively

n	Assignment	CorH^+–Wn			DbcH^+–Wn
		PBE0	PBE0-D3		PBE0	PBE0-D3
		ν s	ν s	ν p	ν s	ν s
a Experimental IR spectroscopy in the gas phase. Ref. 38.
0	Aliphatic sp^3 C–H^+ stretching	2898	2899	3022	2926	2926
		2813^a
	Aromatic sp^2 C–H stretching	3085	2954	3215	3082	3081
1	Free sp^3 C–H^+ stretching mode	2900 (−2)	2843 (56)	3003 (19)	2887 (39)	2890 (30)
	Free sp^2 C–H stretching	3084 (1)	2956 (−2)	3197 (18)	3064 (18)	3080 (−1)
	H-bonded C–H^+ stretching to Awater (νss)	2771 (127)	2841 (58)	2961 (61)	2926 (0)	2928 (−2)
	Free O–H stretching in Awater (νas)	3807 (20)	3802 (25)	3963 (27)	3805 (19)	3805 (22)
2	Free sp^3 C–H^+ stretching	Absence of sp^3 C–H^+ stretching
	Free sp^2 C–H stretching	3083 (2)	3071 (−117)	3190 (25)	3081 (1)	3080 (−154)
	H-bonded C–H^+ stretching to Awater (νss)	2791 (107)	2840 (100)	2962 (60)	2846 (80)	2883 (43)
	Free O–H stretching in Awater (νas)	3807 (20)	3786 (41)	3946 (44)	3807 (20)	3807 (20)
3	Free sp^2 C–H stretching	3068 (17)	3071 (−117)	—	3064 (18)	3081 (0)
	H-bonded C–H^+ stretching to ADwater	2693 (205)	2668 (72)	—	2891 (35)	2905 (21)
	H-bonded O–H stretching in ADwater (νas)	3780 (47)	3781 (46)	—	3782 (45)	3782 (45)
	Free O–H stretching in AAwater (νas)	3785 (42)	3786 (41)	—	3790 (37)	3791 (36)

---

Tables 2 and 3 show that the PBE0 and PBE0-D3 ν_s values are very close, whereas the corresponding data are quite different from the respective ν_p, questioning thus the validity of the scaling factor used and of the applicability of perturbation theory to deduce such a quantity. Indeed, the scaling factor was derived ∼20 years ago and it should be updated. Besides, perturbation theory may not be well suited for such weakly bound complexes, which exhibit low frequency modes, possibly inducing some divergences upon determination of the derivatives needed for anharmonicity effect evaluations, even for modes > 2500 cm⁻¹. One needs highly resolved IR spectra for validation. Interestingly, the complexation induced shifts are not affected, where we have similar shifts either including D3 or not and either scaled or PT2 anharmonic frequencies.

For the benzenium cation, the PBE0 and PBE0-D3 C–H⁺ (sp³) and the C–H (sp²) stretching ν_s are computed as ∼2856 and ∼3080 cm⁻¹, respectively. These values are close to the experimental ones. For instance, the C–H⁺ (sp³) stretching was measured as 2810, 2820, 2700–3200, and 2891 cm^{−1 29,33,36} and the C–H (sp²) stretching was determined as 3110 and 3006 cm⁻¹.^29,36 Our computed values are also close to those determined using the B3LYP/6-311+G(d,p) method (i.e. the C–H⁺ (sp³) stretching = 2887 cm⁻¹ and the C–H (sp²) stretching = 3114 cm⁻¹).³⁶ In contrast, the corresponding ν_p values are relatively high (= 2977 and 3210 cm⁻¹, respectively). A priori, this validates the use of the scaling factor and not of PT2 for BzH⁺.

Table 3 gives the ν_s values of CorH⁺–W_n and DbcH⁺–W_n clusters. In the following we will quote those computed at the PBE0-D3/6-311++G** level. For CorH⁺, we calculate 2899 cm⁻¹ and 2954 cm⁻¹ for the C–H⁺ (sp³) and C–H (sp²) stretchings, which compare favorably with the experimental value of aliphatic sp³ C–H⁺ stretching (2813 cm⁻¹).³⁸ For bare DbcH⁺, our predictions for these modes are 2926 cm⁻¹ and 3081 cm⁻¹, respectively. The existence of H-bonded interactions between aliphatic C–H⁺ and water molecule(s) may influence the C–H stretching modes. The conventional H-bonded interactions induce a shift in frequency. For monohydrates of BzH⁺, CorH⁺ and DbcH⁺, the H-bonded aliphatic C–H⁺ stretchings are reduced upon increasing the aromatic π-clouds. Indeed, we compute a redshift of 589 cm⁻¹ for BzH⁺–W₁ that drops to 58 cm⁻¹ for CorH⁺–W₁ and vanishes for DbcH⁺–W₁. Besides, there is a blue shift in free aliphatic C–H stretching in BzH⁺–W₁. This stretching mode in the extended π-cloud in CorH⁺–W₁ and DbcH⁺–W₁ is predicted to be 2843 and 2890 cm⁻¹. Interestingly, the free aliphatic sp³ C–H⁺ stretching mode in BzH⁺ is blue shifted, whereas in DbcH⁺ it is redshifted (by ∼30 cm⁻¹). This important finding shows how the extension of the π-cloud influences the non-H-bonded C–H stretching modes via the perturbation of the electronic structure of the aromatic rings.

For dihydrates of BzH⁺, CorH⁺ and DbcH⁺, both aliphatic sp³ C–H⁺ modes are directly involved in the H-bonded stretching to water molecules. For these clusters, Tables 2 and 3 show that the water stretching redshift values are decreasing, while increasing the aromatic π-cloud. Indeed, the corresponding redshift values are 277 cm⁻¹, 100 cm⁻¹ and 43 cm⁻¹ for BzH⁺–W₂, CorH⁺–W₂ and DbcH⁺–W₂, respectively. In trihydrated clusters of BzH⁺, CorH⁺ and DbcH⁺, the H-bond to water is observed in both the hydrogens present in sp³ carbon and stretching redshift values are affected due to the third AA (double acceptor)-water present in between them, where the water molecules form a cyclic structure with the hydrogen atom. The redshifts for BzH⁺–W₃, CorH⁺–W₃ and DbcH⁺–W₃ are 411 cm⁻¹, 72 cm⁻¹ and 21 cm⁻¹, respectively. As expected, the free sp² C–H stretchings are slightly affected by microhydration of BzH⁺, CorH⁺ and DbcH⁺.

Fig. 5 displays the IR spectra of bare BzH⁺, CorH⁺ and DbcH⁺, and of their mono-, di and trihydrates as computed using the PBE0-D3/6-311++G** method. For the clusters not probed yet by IR, these spectra may be used for the assignment of the corresponding spectra whenever measured. In particular, they can help to disentangle the IR spectra of protonated aromatics interacting with water clusters and those of aromatics interacting with protonated water clusters in a mixture using the presently computed IR spectra and those of Bz–H⁺W_n, Cor–H⁺W_n and Dbc–H⁺W_n (n = 1–3) as given in ref. 66. Indeed, different spectral shapes are computed for each set of complexes.

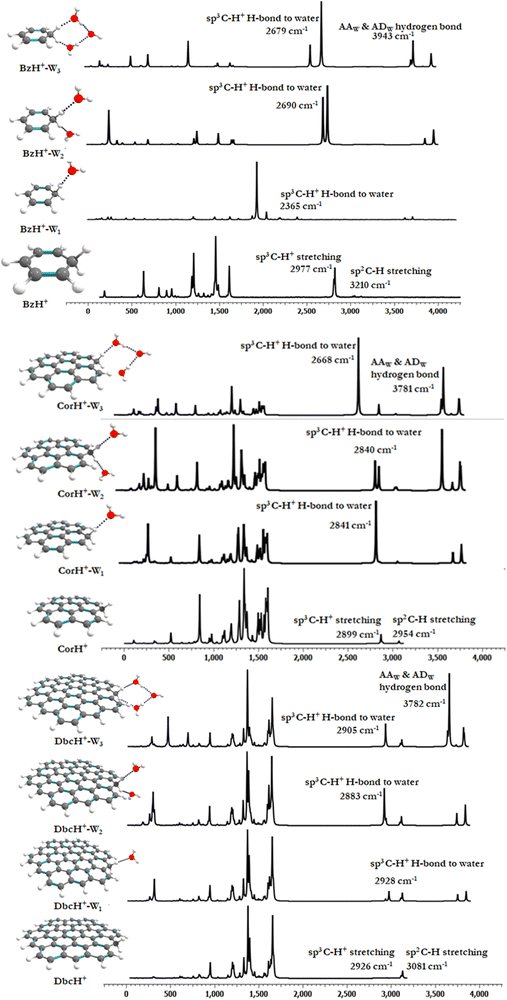Fig. 5 IR spectra of bare BzH⁺, CorH⁺ and DbcH⁺ and of their clusters with water as computed at the PBE0-D3/6-311++G** level.

e. UV-vis spectra. The full set of singlet and triplet electronic states of BzH⁺, CorH⁺ and DbcH⁺, and of their clusters with water (i.e., BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3)) is listed in Tables S6 and S7 (ESI†) for transitions with λ > 200 nm. These data are obtained at the TD-DFT PBE0/6-311++G** level. We give also their tentative assignments. Mostly, they correspond to the promotion of one electron from the occupied highest molecular orbital (MO) to the lowest unoccupied MO. These MOs are depicted in Fig. S2–S4 (ESI†), which show that they are mainly located on the organic part with some contributions on the water clusters. Although, the lowest singlets of BzH⁺ and of CorH⁺ were studied both theoretically and experimentally (Table 4),^{39–41,44,46} the singlet states of DbcH⁺ and those of their mono-, di- and trihydrates are treated here for the first time. Also, the results on the triplets represent predictions.

Table 4 Lowest S₀ → S₁ and S₀ → T₁ vertical transitions energies (E, in eV) of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 0–3) species. We give also the corresponding transition wavelength (λ, in nm) and oscillator strength (f). The experimental values are given between parentheses. The full set of singlet and triplet electronic states, electron transitions and oscillator strengths are listed in Tables S6 and S7 (ESI). We give also the λ extrapolated values (i.e., λ_+∞) for n → + ∞. See text for more details

n	Transition	E	λ	f
a Adiabatic electronic excitation transition.
BzH^+
0	S0 → T1	2.21	560
	S0 → S1	4.24	292	0.12
			(330)^40,41
			(325)^39
			(325)^44	(0.14)^44
1	S0 → T1	2.51	493
	S0 → S1	4.40	281	0.11
2	S0 → T1	2.52	492
	S0 → S1	4.38	282	0.11
3	S0 → T1	2.65	467
	S0 → S1	4.45	278	0.10
+∞	S0 → T1		464 ± 50
			413^89
	S0 → S1		277 ± 15
			284^88
CorH^+
0	S0 → T1	1.20	1031
	S0 → S1	2.08	595	0.08
		(1.78)^46^a	(695.6)^46^a
1	S0 → T1	1.28	961
	S0 → S1	2.16	573	0.08
2	S0 → T1	1.36	905
	S0 → S1	2.23	555	0.08
3	S0 → T1	1.39	889
	S0 → S1	2.25	549	0.08
+∞	S0 → T1		849 ± 50
	S0 → S1		534 ± 15
DbcH^+
0	S0 → T1	0.87	1411
	S0 → S1	1.48	836	0.14
1	S0 → T1	0.91	1356
	S0 → S1	1.51	816	0.14
2	S0 → T1	0.96	1287
	S0 → S1	1.56	791	0.15
3	S0 → T1	0.97	1273
	S0 → S1	1.57	785	0.15
+∞	S0 → T1		1196 ± 50
	S0 → S1		754 ± 15

---

The UV-vis absorption spectra of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) are shown in Fig. 6. This figure reveals that different UV-vis spectra are computed for each molecular species, depending on the extension of the aromatic compound and on the number of water molecules clustered with them. For instance, Fig. 6 shows that the characteristic peaks of BzH⁺–W₁, CorH⁺–W₁ and DbcH⁺–W₁ clusters have different energy positions from those of BzH⁺, of CorH⁺, and of DbcH⁺, where shorter wavelengths are computed upon attaching water molecules to these H⁺PAHs. This trend is found for BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n clusters upon increasing n. This is further confirmed by the computed vertical transition energies/wavelengths given in Table 4. Indeed, we compute S₀ → S₁ transitions at 292, 281, 282 and 278, in nm, for BzH⁺, BzH⁺–W₁, BzH⁺–W₂ and BzH⁺–W₃, respectively. For CorH⁺–W_n clusters, we also have such a decrease of wavelengths upon increasing the number of water molecules interacting with Cor⁺, where we compute S₀ → S₁ transitions at 595, 573, 555 and 549 nm for n = 0, 1, 2 and 3, respectively. The S₀ → S₁ transitions for DbcH⁺–W_n (n = 0, 1, 2 and 3) are predicted at 836, 816, 791 and 785 nm.

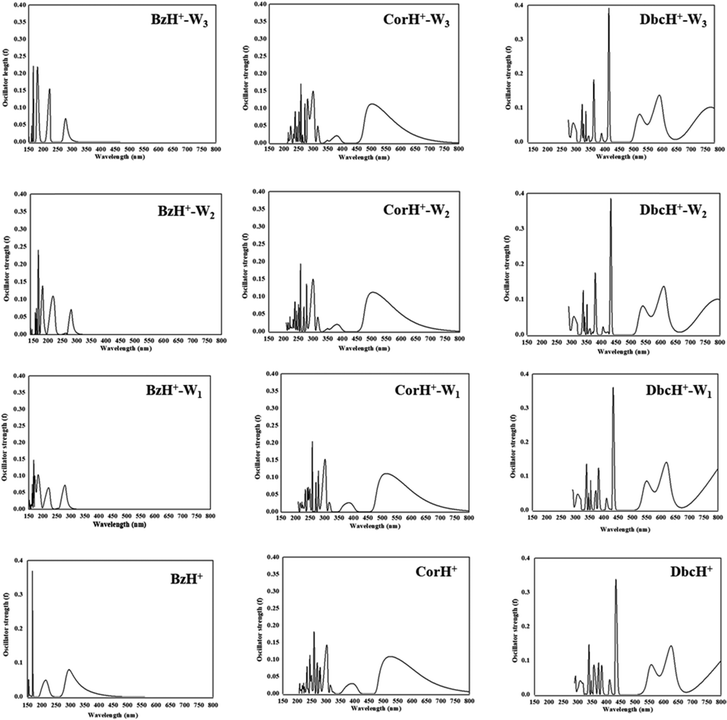Fig. 6 UV-vis spectra of bare BzH⁺, CorH⁺ and DbcH⁺, and of their clusters with water BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (where n = 1–3) as computed at the TD-DFT PBE0/6-311++G** level.

Fig. 6 shows that bands appear in the visible domain upon extending the π-aromatic cloud from BzH⁺ to CorH⁺ to DbcH⁺ as already noticed experimentally for the extension from BzH⁺ to CorH^+ 44,46 and for other isolated H⁺PAHs such as protonated naphthalene, protonated anthracene, protonated tetracene, and protonated pyrene.^42,43,46 We have a similar trend for these protonated species complexed with water molecules. For illustration, Table 4 shows that the S₀ → T₁ and S₀ → S₁ transition wavelengths increase upon extending the π-aromatic cloud for these bare H⁺PAHs. For the S₀ → S₁ transitions, they are predicted at 292 nm, 595 nm and 836 nm for BzH⁺, CorH⁺ and DbcH⁺, respectively. Also, Table 4 shows that this trend is observed for the S₀ → T₁ transitions of all species and for the S₀ → S₁ transitions of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3). For instance, the computed λ values are 493 nm, 961 nm and 1356 nm for the S₀ → T₁ BzH⁺–W₁, CorH⁺–W₁ and DbcH⁺–W₁ transitions, respectively. Note that our calculated S₀ → S₁ wavelengths for BzH⁺ and CorH⁺ are slightly lower than the measured ones. The differences may come from perturbations of the singlets states by vibronic or Herzberg–Teller couplings as pointed out in ref. 39–41, 44 and 46 not accounted for in the present computations.

The trends upon the extension of the π-aromatic cloud or upon adding water molecules can be explained by examining the frontier MOs given in Fig. S2–S4 (ESI†). Indeed, the S₀ → T₁ and S₀ → S₁ transitions are associated with the promotion of an electron from the HOMO to the LUMO (Tables S6 and S7, ESI†). Fig. S2–S4 (ESI†) show that the HOMOs of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) species are destabilized by the anti-bounding nature of the interaction between the organic and the water molecules’ MOs. This results in the increase of the energies of these HOMOs, whereas we observe a favorable bonding between both entities in the LUMOs. In total, we have reduction of their HOMO–LUMO gaps and the increase of the corresponding wavelength transitions.

Besides, the S₀ → T₁ and S₀ → S₁ transition wavelengths decrease by increasing the number of water molecules attached to the protonated aromatics. For instance, the S₀ → S₁ transition wavelengths change from 292 nm to 278 nm for BzH⁺–W_n (n = 0–3), from 595 nm to 549 nm for CorH⁺–W_n (n = 0–3) and from 836 nm to 785 nm for DbcH⁺–W_n (n = 0–3). For the S₀ → T₁ transitions, these values change from 560 nm to 467 nm, from 1031 nm to 889 nm and from 1411 nm to 1273 nm in the same order. These evolutions are non-monotonic and they can be fitted by A + B × exp(−C × n), where n is the number of water molecules attached to these protonated aromatics. In this formula, the A parameter corresponds to the λ_+∞ wavelength transition for n → +∞ and thus could be assumed to be the value of the wavelength transition for these H⁺PAHs in aqueous media. Table 4 gives the values of λ_+∞ for the S₀ → S₁ and S₀ → T₁ transitions. We show also the λ values of BzH⁺ dissolved in liquid hydrogen fluoride containing boron trifluoride and of BzH⁺MX₄⁻ (MX₄⁻ = BF₄⁻, AlCl₄⁻, AlBr₄⁻, GaCl₄⁻, GaBr₄⁻) ion pair in an organic solvent solution as measured by Reid⁸⁸ and by Perkampus and Baumgarten,⁸⁹ respectively. Although relatively old, these data correspond to the unique data available for BzH⁺ in the condensed phase to compare with.

For BzH⁺, the extrapolated S₀ → S₁ wavelength transition is λ_+∞ = 277 ± 15 nm, which agrees quite well with the 284 nm wavelength measured for BzH⁺ ions dissolved in liquid hydrogen fluoride containing boron trifluoride.⁸⁸ However, the 413 nm value measured for the BzH⁺MX₄⁻ (MX₄⁻ = BF₄⁻, AlCl₄⁻, AlBr₄⁻, GaCl₄⁻, GaBr₄⁻) ion pair in organic solvents⁸⁹ is obviously far from the present λ_+∞ and that of ref. 88. Thus, it cannot be assigned to the S₀ → S₁ transition. Instead, our extrapolated value for the S₀ → T₁ transition (λ_+∞ = 464 ± 50 nm) is closer and falls within both experimental and theoretical error bars. Accordingly, we suggest to reassign this band to the BzH⁺ S₀ → T₁ transition, although it is spin-forbidden. Anyway, such transitions become slightly allowed in emission and responsible for the phosphorescence spectra of molecules. Back to the 1940's, Lewis and Kasha^90,91 proved that such S–T absorption transitions can be viewed as a reverse process of phosphorescence and become slightly allowed under spin–orbital perturbations, for instance, by surrounding compounds⁹² such as solvents or the MX₄⁻ anion within the BzH⁺MX₄⁻ ion pair. Since then, such S–T transitions were detected for several compounds⁹³ and even for some neutral PAHs such as anthracene and its derivatives.⁹³ For CorH⁺ in aqueous solution, we predict S₀ → T₁ and S₀ → S₁λ_+∞'s at 849 ± 50 nm and 534 ± 15 nm, respectively. These values decrease to λ_+∞ = 1196 ± 50 and λ_+∞ = 754 ± 15 nm for DbcH⁺ in a water solvent. Generally, the wavelength transitions in the condensed phase are quite different from those of gas phase species, which illustrates the drastic impact of the surroundings on these H⁺PAH optical properties. These predictions are worth investigating experimentally. Such experiments are challenging since the extinction coefficients for the singlet–triplet transitions are several orders of magnitude smaller than the values for the singlet–singlet transitions.⁹³

f. Nucleus-independent chemical shift (NICS) analysis. In ref. 94–96 a methodology was proposed to quantify the nature of aromaticity for any molecular system using nucleus independent chemical shifts (NICS) as the negative of the absolute magnetic shielding. The latter is here calculated at the center of the ring (0 Å) and 1 Å above resulting in NICS (0 Å)_zz and NICS (1 Å)_zz, respectively. The calculated NICS isotropic terms are shown in Table 5. Calculations suggest that the protonation of the PAH significantly reduces the aromatic character at both 0 and 1 Å. In contrast, incorporation of water molecules to the protonated PAH moiety leads to an enhancement of the NICS values (more negative terms mean more aromatic character). Overall, the aromatic character at 1 Å is always higher than at the center of the ring irrespective of the nature of the considered H⁺PAH and size of the water cluster. In particular, the binding of excess protons on the Bz ring affects NICS (0 Å)_zz, whereas the NICS (1 Å)_zz terms are slightly affected. At the same time, the extension of the PAH with H-bonded water clusters enhances the aromaticity, and this will help in the stability of the molecular clusters. It is interesting to note that the NICS (0 Å)_zz and NICS (1 Å)_zz values of bare Cor are significantly lower, in absolute value, at the center of the ring than in the outer ring, where we compute values of −9.6 ppm and −11.3 ppm, respectively. In fact, Cor systems are slightly more aromatic than Bz systems and less aromatic than Dbc ones. This effect is due to the dual aromaticity that exists in the Cor surface. It is also the case in the presence of proton and water clusters attached at the Cor surface.

Table 5 PBE0/6-311++G** calculated NICS isotropic values (in ppm) at the center of the PAH rings and respective protonated counterparts with and without water (W_n; where n = 1–3) clusters. NICS (0 Å)_zz and NICS (1 Å)_zz represent the values computed at the center of the ring and above the plane of the aromatic ring (i.e., 1 Å), respectively

PAH	Bz		Cor^a		Dbc
	NICS (0 Å)zz	NICS(1 Å)zz	NICS (0 Å)zz	NICS (1 Å)zz	NICS (0 Å)zz	NICS (1 Å)zz
a For Cor, two types of aromaticity exist in the inner and outer rings. The calculated NICS (0 Å)zz and NICS (1 Å)zz for the outer ring of COR are provided in parenthesis.
Bare PAH	−8.2	−10.4	−0.1 (−9.6)	−4.6 (−11.3)	−12.9	−15.6
H^+PAH	−0.5	−5.9	−1.6 (−8.4)	−5.7 (−10.9)	−2.9	−6.9
H^+PAH-W1	−2.0	−6.9	−1.5 (−8.7)	−5.9 (−12.0)	−3.8	−7.7
H^+PAH-W2	−1.9	−6.9	−1.4 (−8.9)	−5.6 (−11.5)	−4.6	−8.3
H^+PAH-W3	−2.5	−7.2	−1.3 (−7.3)	−5.7 (−10.5)	−4.6	−8.4

---

IV. Conclusions

The structure, energetic stability, aromaticity, IR and UV-vis features of various H⁺PAHs with W_n clusters (where n = 1–3) have been computed. It is interesting to note that the extension of the π-cloud directly influences the structure, energetic stability and spectral features of hydrated H⁺PAH cations. Also, we show that there is a substantial amount of reduction in the energetics, which does not disturb the hydration pattern irrespective of the size of the H⁺PAH cations. For explanation, we found that this is due to noncovalent interactions that are dominating the microsolvation of H⁺PAH cations. Furthermore, NICS(0 Å)_zz and NICS(1 Å)_zz calculations confirm the aromatic character of the Cor and Dbc bearing clusters.

The present work shows that the mode of interaction plays a vital role in understanding the strength and stability of the proton at the interface and different vibrational shifts were computed for the complexes under study. The calculated induced complexation shifts are large enough to be probed by IR. Also, computations reveal that the UV-vis spectral fingerprints are specific for each compound. Indeed, different UV-vis spectra are computed depending on the extended aromatic compound and on the number of water molecules interacting with these protonated aromatics. In particular, we show that UV-vis spectroscopy can be used to probe complexation induced effects of H⁺PAHs upon microhydration. Besides, this spectroscopy can be used to identify the excess proton localized in either the carbon surface or water clusters after comparison of the present spectra to those predicted recently for Bz–H⁺W_n, Cor–H⁺W_n and Dbc–H⁺W_n (n = 1–3) clusters.⁶⁶ Indeed, the presently computed UV-vis band wavelengths are significantly lower than those when the excess proton is localized at the water clusters.

Finally, our work allows filling the gap between the gas phase H⁺PAH properties and those of these species in aqueous solution. In particular, we characterized the S₀–S₁ and S₀–T₁ transitions of BzH⁺–W_n, CorH⁺–W_n and DbcH⁺–W_n (n = 1–3) in both gas and condensed phases. Although the intensities of the latter are expected to be weak, the direct population of triplet states is important for applications such as designing materials targeting visible-light excitable organic afterglow and for the development of triplet-state involved organic optoelectronic technologies.⁹⁷

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. R. M., N. G. L., and C. G. acknowledge the SRM Institute of Science and Technology (SRM-IST) Research Fellowship for their research work. M. P. thanks the Department of Science and Technology, Science and Engineering Research Board (DST-SERB) of India for financial support from the CRG scheme. The authors also thank SRM Supercomputer Centre (HPCC), SRM Institute of Science and Technology for providing the computational facility and financial support.

References

1. K.-H. Kim, S. A. Jahan, E. Kabir and R. J. Brown, Environ. Int., 2013, 60, 71–80.
2. I. J. Keyte, R. M. Harrison and G. Lammel, Chem. Soc. Rev., 2013, 42, 9333–9391.
3. J. E. Anthony, Angew. Chem., Int. Ed., 2008, 47, 452–483.
4. J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048.
5. M. Frenklach, Phys. Chem. Chem. Phys., 2002, 4, 2028–2037.
6. K.-H. Homann, Angew. Chem., Int. Ed., 1998, 37, 2434–2451.
7. H. Wang, Proc. Combust. Inst., 2011, 33, 41–67.
8. H. Richter and J. B. Howard, Prog. Energy Combust. Sci., 2000, 26, 565–608.
9. K. O. Johansson, M. P. Head-Gordon, P. E. Schrader, K. R. Wilson and H. A. Michelsen, Science, 2018, 361, 997–1000.
10. G. R. Sampaio, G. M. Guizellini, S. A. da Silva, A. P. de Almeida, A. C. C. Pinaffi-Langley, M. M. Rogero, A. C. de Camargo and E. A. F. S. Torres, Int. J. Mol. Sci., 2021, 22, 6010.
11. O. Idowu, K. T. Semple, K. Ramadass, W. O’Connor, P. Hansbro and P. Thavamani, Environ. Int., 2019, 123, 543–557.
12. N. Premnath, K. Mohanrasu, R. Guru Raj Rao, G. H. Dinesh, G. S. Prakash, V. Ananthi, K. Ponnuchamy, G. Muthusamy and A. A. Arun, Chemosphere, 2021, 280, 130608.
13. C. Joblin and A. G. G. M. Tielens, PAHs and the Universe, EDP Sciences, 2021, ISBN: 978-2-7598-0624-9.
14. D. S. N. Parker and R. I. Kaiser, Chem. Soc. Rev., 2017, 46, 452–463.
15. R. I. Kaiser, D. S. Parker and A. M. Mebel, Annu. Rev. Phys. Chem., 2015, 66, 43–67.
16. B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205.
17. B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii, M. A. Siebert, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Science, 2021, 371, 1265–1269.
18. M. C. McCarthy, K. L. K. Lee, R. A. Loomis, A. M. Burkhardt, C. N. Shingledecker, S. B. Charnley, M. A. Cordiner, E. Herbst, S. Kalenskii, E. R. Willis, C. Xue, A. J. Remijan and B. A. McGuire, Nat. Astron., 2021, 5, 176–180.
19. J. Cernicharo, M. Agúndez, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2021, 649, L12.
20. J. Cernicharo, M. Agúndez, R. I. Kaiser, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2021, 655, L1.
21. J. Cernicharo, R. Fuentetaja, M. Agúndez, R. I. Kaiser, C. Cabezas, N. Marcelino, B. Tercero, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2022, 663, L9.
22. https://www.astrochymist.org/astrochymist_ism.html .
23. A. G. G. M. Tielens, Annu. Rev. Astron., 2008, 46, 337.
24. D. M. Hudgins, C. W. Bauschlicher and L. J. Allamandola, Spectrochim. Acta, Part A, 2001, 57, 907.
25. O. Dopfer, Laboratory Spectroscopy of Protonated PAH Molecules Relevant For Interstellar Chemistry in PAHs and the Universe, ed C. Joblin and A. G. G. M. Tielens, EAS Publications Series, 2011, vol. 46, pp. 103–108.
26. M. Hammonds, A. Pathak, A. Candian and P. J. Sarre, Spectroscopy of Protonated and Deprotonated PAHs in PAHs and the Universe, ed C. Joblin and A. G. G. M. Tielens, EAS Publications Series, 2011, vol. 46, pp. 373–379.
27. A. L. F. de Barros, A. L. Mattioda, A. Ricca, G. A. Cruz-Diaz and L. J. Allamandola, Astrophys. J., 2017, 848, 112.
28. H. Knorke, J. Langer, J. Oomens and O. Dopfer, Astrophys. J., 2009, 706, L66–L70.
29. N. Solcà and O. Dopfer, Angew. Chem., Int. Ed., 2002, 41, 3628–3631.
30. M. Bahou, Y. J. Wu and Y. P. Lee, Angew. Chem., Int. Ed., 2014, 53, 1021–1024.
31. V. A. Kapinus, Photophysical Properties of Protonated Aromatic Hydrocarbons, PhD, California Institute of Technology Pasadena, California, 2005 (Defended December 14, 2004).
32. M. V. Frash, A. C. Hopkinson and D. K. Bohme, J. Am. Chem. Soc., 2001, 123(27), 6687–6695.
33. W. Jones, P. Boissel, B. Chiavarino, M. E. Crestoni, S. Fornarini, J. Lemaire and P. Maitre, Angew. Chem., Int. Ed., 2003, 42, 2057–2059.
34. Michael A. Duncan, J. Phys. Chem. A, 2012, 116, 11477–11491.
35. T. C. Cheng, B. Bandyopadhyay, J. D. Mosley and M. A. Duncan, J. Am. Chem. Soc., 2012, 134, 13046–13055.
36. G. E. Douberly, A. M. Ricks, P. V. R. Schleyer and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 4869–4874.
37. U. J. Lorenz, N. Solcà, J. Lemaire, P. Maître and O. Dopfer, Angew. Chem., Int. Ed., 2007, 46, 6714–6716.
38. M. Bahou, Y. J. Wu and Y. P. Lee, Phys. Chem. Chem. Phys., 2013, 15, 1907–1917.
39. I. Garkusha, J. Fulara, A. Nagy and J. P. Maier, J. Am. Chem. Soc., 2010, 132, 14979.
40. B. S. Freiser and J. L. Beauchamp, J. Am. Chem. Soc., 1976, 98, 3136.
41. B. S. Freiser and J. L. Beauchamp, J. Am. Chem. Soc., 1977, 99, 3214.
42. I. Alata, C. Dedonder, M. Broquier, E. Marceca and C. Jouvet, J. Am. Chem. Soc., 2010, 132, 17483–17489.
43. I. Alata, R. Omidyan, M. Broquier, C. Dedonder, O. Dopfer and C. Jouvet, Phys. Chem. Chem. Phys., 2010, 12, 14456–14458.
44. N. E.-López, C. D.-Lardeux and C. Jouvet, J. Chem. Phys., 2015, 143, 074303.
45. F.-X. Hardy, O. Gause, C. A. Rice and J. P. Maier, Astrophys. J., Lett., 2013, 778, L30.
46. I. Garkusha, J. Fulara, P. J. Sarre and J. P. Maier, J. Phys. Chem. A, 2011, 115, 10972–10978.
47. I. Garkusha, A. Nagy, J. Fulara, M. F. Rode, A. L. Sobolewski and J. P. Maier, J. Phys. Chem. A, 2013, 117, 351–360.
48. I. Garkusha, J. Fulara and J. P. Maier, J. Mol. Struc., 2012, 1025, 147–150.
49. C. A. Rice, F. X. Hardy, O. Gause and J. P. Maier, J. Phys. Chem. Lett., 2014, 5, 942–945.
50. B. Saed and R. Omidyan, J. Phys. Chem. A, 2013, 117, 2499–2507.
51. R. Omidyan, Chem. Phys. Lett., 2011, 518, 15–20.
52. J. F. Li, G. Tian, Y. Luo and Z. Cao, Chem. Phys. Lett., 2015, 641, 57–61.
53. J. Li, Y. Luo and J. Zhang, Spectrochim. Acta, Part A, 2018, 205, 520–527.
54. J. Li and Y. Luo, Spectrochim. Acta, Part A, 2021, 244, 118832.
55. J. Li and N. Li, Comput. Theor. Chem., 2023, 1221, 114028.
56. C. H. Chin and S. H. Lin, Phys. Chem. Chem. Phys., 2016, 18, 14569–14579.
57. B. A. Laws, O. Krechkivska, K. Nauta, S. H. Kable and T. W. Schmidt, Phys. Chem. Chem. Phys., 2023, 25, 19524–19531.
58. N. Solcà and O. Dopfer, Chem. – Eur. J., 2003, 9, 3154–3163.
59. M. A. Duncan, J. Phys. Chem. A, 2012, 116, 11477–11491.
60. T. C. Cheng, B. Bandyopadhyay, J. D. Mosley and M. A. Duncan, J. Am. Chem. Soc., 2012, 134, 13046–13055.
61. I. Alata, M. Broquier, C. Dedonder-Lardeux, C. Jouvet, M. Kim, W. Y. Sohn, S. Kim, H. Kang, M. Schütz, A. Patzer and O. Dopfer, J. Chem. Phys., 2011, 134, 074307.
62. A. Patzer, M. Schütz, C. Jouvet and O. Dopfer, J. Phys. Chem. A, 2013, 117, 9785–9793.
63. K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2020, 124, 1134–1151.
64. A. M. Santa Daría, L. González-Sánchez and S. Gómez, Phys. Chem. Chem. Phys., 2024, 26, 174–184.
65. J. Bourgalais, X. Mercier, M. Mogren Al-Mogren and M. Hochlaf, J. Phys. Chem. A, 2023, 127, 8447–8458.
66. M. Prakash, K. R. Maiyelvaganan, N. G. Lakshman, M. Mogren Al-Mogren and M. Hochlaf, ChemPhysChem, 2023, 24, e202300267.
67. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, N. R. J. Gao, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Wallingford CT, 2016.
68. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
69. K. R. Maiyelvaganan, M. K. Ravva, M. Prakash and V. Subramanian, Theor. Chem. Acc., 2020, 139, 1–14.
70. R. Dennington, T. A. Keith and J. M. Millam, GaussView 6.0.16, Shawnee Mission, Semichem Inc, 2016.
71. G. A. Zhurko and D. A. Zhurko, Chemcraft Program, academic version 1.8, 2015.
72. B. P. Pritchard, A. Kumar, A. C. Simmonett, F. A. Evangelista, K. Patkowski, A. E. DePrince, J. M. Turney, M. Saitow, R. A. King, R. Di Remigio, D. G. A. Smith, U. Bozkaya, P. Verma, A. Y. Sokolov, E. F. Valeev, E. G. Hohenstein, C. D. Sherrill, R. M. Richard, A. M. James, T. D. Crawford, R. M. Parrish, H. F. Schaefer, L. A. Burns, H. R. McAlexander, X. Wang and J. F. Gonthier, J. Chem. Theory Comput., 2017, 13, 3185–3197.
73. K. Morokuma, J. Chem. Phys., 1971, 55, 1236.
74. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
75. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
76. S. Grimme, C. Bannwarth, S. Dohm, A. Hansen, J. Pisarek, P. Pracht, J. Seibert and F. Neese, Angew. Chem., Int. Ed., 2017, 56, 14763–14769.
77. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
78. Y. Tantirungrotechai, K. Phanasanta, S. Roddecha, P. Surawatanawonga, V. Sutthikhum and J. Limtrakul, THEOCHEM, 2006, 760, 189–192.
79. F. Biegler-Konig, J. Schonbohm, R. Derdau, D. Bayles and R. F. W. Bader, AIM 2000, Bielefeld, Germany, 2000.
80. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
81. F. Bernardi and S. F. Boys, Mol. Phys., 1970, 19, 553–566.
82. M. Prakash, K. Gopalsamy and V. Subramanian, J. Chem. Phys., 2011, 135, 214308.
83. K. R. Maiyelvaganan, M. K. Ravva and M. Prakash, J. Phys. Chem. A, 2020, 124, 3364–3373.
84. M. Prakash, K. Mathivon, D. M. Benoit, G. Chambaud and M. Hochlaf, Phys. Chem. Chem. Phys., 2014, 16, 12503–12509.
85. S. Kamalakannan, K. R. Maiyelvaganan, K. Palanisamy, A. Thomas, R. B. Said, M. Prakash and M. Hochlaf, Chemosphere, 2022, 286, 131612.
86. S. Kamalakannan, K. Palanisamy, M. Prakash and M. Hochlaf, Photocatalysis for Environmental Remediation and Energy Production, ed. S. Garg and A. Chandra, Green Chemistry and Sustainable Technology, 2023, p. 329.
87. https://webbook.nist.gov/ .
88. C. Reid, J. Am. Chem. Soc., 1954, 76, 3264–3268.
89. H. H. Perkampus and E. Baumgarten, Angew. Chem., Int. Ed. Engl., 1964, 3, 776.
90. G. N. Lewis and M. Kasha, J. Am. Chem. Soc., 1945, 67, 994.
91. G. N. Lewis and M. Kasha, J. Am. Chem. Soc., 1944, 66, 2100.
92. S. K. Lower and M. A. El-Sayed, Chem. Rev., 1966, 66, 199.
93. M. A. Omary and H. H. Patterson, Organic Luminophores in Encyclopedia of Spectroscopy and Spectrometry, ed J. C. Lindon, G. E. Tranter and D. W. Koppenaal, 3rd edn, 2017, ISBN: 978-0-12-803224-4.
94. C. Corminboeuf, T. Heine, G. Seifert, P. Von Ragué Schleyer and J. Weber, Phys. Chem. Chem. Phys., 2004, 6, 273–276.
95. H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Org. Lett., 2006, 8, 863–866.
96. R. Báez-Grez, L. Ruiz, R. Pino-Rios and W. Tiznado, RSC Adv., 2018, 8, 13446–13453.
97. J. Yuan, R. Chen, X. Tang, Y. Tao, S. Xu, L. Jin, C. Chen, X. Zhou, C. Zheng and W. Huang, Chem. Sci., 2019, 10, 5031.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06000d

‡ These authors contributed equally to this work.

---