Correction: Extracting accurate information from triplet–triplet annihilation upconversion data with a mass-conserving kinetic model

Abstract

Correction for ‘Extracting accurate information from triplet–triplet annihilation upconversion data with a mass-conserving kinetic model’ by Abhishek Kalpattu et al., Phys. Chem. Chem. Phys., 2022, 24, 28174–28190, https://doi.org/10.1039/D2CP03986A.

---

The authors would like to make the changes described below to their published article. The corrected supplementary information is provided in the modified Supplementary Information published alongside the original published article.

In the published article, the upconversion quantum yield, Φ_UC, was calculated using the quadratic model, and the steady-state rate of excitation in the system was approximated as k_exI[S]₀. However, saturation occurs at high irradiance, and so the steady-state rate of excitation should instead have been given by k_exI[S]_SS. In other words, the quartic model should be used in the high irradiance limit, because in the saturation regime the concentration of ground-state sensitizers available to absorb light is considerably smaller than the initial concentration of sensitizers. The major conclusions of the published paper remain unchanged, but here we correct some details regarding the behavior of Φ_UC at high irradiance.

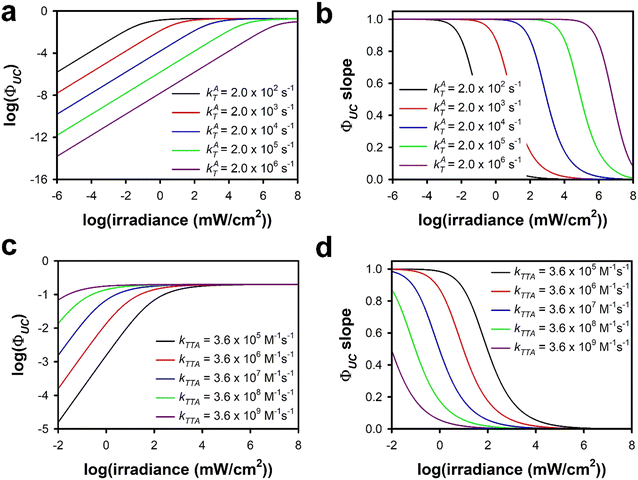
As shown in the new Fig. 6, when the quartic model is used, Φ_UC does not decrease upon the onset of saturation; rather the rate of increase in Φ_UC with respect to irradiance decreases until the maximum value for Φ_UC is reached as I → ∞. This behaviour arises at high irradiance because the rate of excitation and F_SS both saturate. As a result, Φ_UC continues to approach an asymptote with increasing irradiance even after the onset of saturation. The conclusions regarding Φ_UC should be modified as follows:

Fig. 6 The dependence of the upconversion quantum yield and its slope on irradiance for (a) and (b), respectively, different values of k^A_T, and (c) and (d), respectively, different values of k_TTA. See Table S1 for the values of the other parameters.

1. On page 28182, “Because F_SS is proportional to I^n(I), we can conclude that Φ_UC must be proportional to I^n(I)−1.” should be replaced with “Because F_SS is proportional to I^n(I), we can conclude that Φ_UC must be proportional to I^n(I)−q(I), where 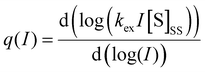is the local slope of a log–log plot of the sensitizer excitation rate as a function of irradiance. Far below the saturation regime, q(I) has a value of unity.”

2. On page 28182, “When n(I) is unity, Φ_UC ∝ I⁰. The TTA-UC quantum yield reaches its maximum value at this irradiance, and decreases at higher irradiances.” should be replaced with “Φ_UC grows slowly with I as both n(I) and q(I) fall below unity, and Φ_UC becomes independent of I as n(I) approaches 0.”

3. On page 28182, “Thus, for any TTA-UC system, peak performance is achieved when the relationship between F_SS and I becomes strictly linear. As n(I) approaches 0, Φ_UC becomes inversely proportional to I. As a result, Φ_UC decreases at irradiances high enough to saturate the intensity of upconverted fluorescence.” should be removed, although this statement holds true in the context of the external quantum yield (vide infra).

4. On page 28183, “As shown in Fig. 6b and d, the slope for the quantum yield of the data in Fig. 6a and c undergoes a smooth transition from a value of 1 at low irradiance, to a value of 0 when n(I) is 1, and then finally to a value of −1 at high irradiances.” should be replaced with “As shown in Fig. 6b and d, the slope for the quantum yield of the data in Fig. 6a and c undergoes a smooth transition from a value of 1 at low irradiance to a value of 0 as n(I) approaches 0.”

5. On page 28184, the value of Φ_UC,max in the discussion for the system with a k^A_T = 2 × 10² s⁻¹ should be changed from 99.5% to 99.7%. The value for Φ_UC,max for the system with k^A_T = 2 × 10⁴ s⁻¹ should be changed from 99.6% to 99.5%. The value for Φ_UC,max for the system with k^A_T = 2 × 10⁶ s⁻¹ should be changed from 51% to 81.7%.

Φ _UC values in Fig. S8, S9, S11 and S12 were also corrected. The discussion in the main text regarding Fig. S8 and S9 is correct, because the trend in Φ_UC and [capital Phi, Greek, macron]_UC as n(I) decreases from a value of 2 to a value of 1 is unchanged. Similarly, the main trends in Fig. S11 and S12 remain the same.

To provide further insight into the behaviour of Φ_UC upon the onset of saturation, in Fig. S22 we show the trends in n(I) and q(I) when k^A_T = 2 × 10² s⁻¹ and when k^A_T = 2 × 10⁵ s⁻¹. Φ_UC attains its maximum value when n(I) = q(I). When k^A_T = 2 × 10² s⁻¹, the n(I) curves overlap completely once n(I) is unity (the irradiance at which n(I) = 1 is indicated by the vertical dotted line). However, when k^A_T = 2 × 10⁵ s⁻¹, n(I) > q(I) when n(I) = 1, and the q(I) and n(I) curves only converge as n(I) approaches 0. The precise point at which Φ_UC becomes independent of I, and hence is maximized, is when n(I) = 0. However, for ideal TTA-UC systems, Φ_UC is close to Φ_UC,max at the irradiance for which n(I) = 1.

From a practical perspective, the external quantum efficiency Φ_UC,ext (the ratio of the steady-state rate of fluorescence emission, F_SS, to the rate of exposure to photons) is more important than the internal quantum efficiency that we treated in this article. Φ_UC,ext necessarily decreases in the saturation regime, as there are fewer ground-state sensitizers available to absorb photons. In the original article we expressed Φ_UC as F_SS/k_exI[S]₀. Multiplying this quantity by hω_exk_ex[S]₀/A, where A is the area of the excitation beam and ω_ex is the frequency of the excitation light, gives Φ_UC,ext. Thus, with this factor, the Φ_UC values in the original Fig. 6a, c and Fig. S8, S9, S11 and S12 can be converted to the correct corresponding Φ_UC,ext values. Fig. 6b and d in the original paper are correct if Φ_UC is replaced with Φ_UC,ext in the title of the y-axis. Please refer to revised version of the ESI (https://doi.org/10.1039/D2CP03986A) for the corrected S8, S9, S11 and S12 figures.

Acknowledgements

This work was supported by the National Science Foundation, grant CHE-1800491 (J. T. F. and A. K.) and DMR-1752782 (K. H. and T. D.). A. K. would also like to thank the University of Maryland’s Graduate School and the Department of Materials Science and Engineering for supporting this research through a Summer Graduate Research Fellowship. We are grateful to the reviewer for bringing the point regarding Φ_UC,ext to our attention.

The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.

---