Similarity scores of vibrational spectra reveal the atomistic structure of pentapeptides in multiple basins†
Hiroki
Otaki
 a,
Shun-ichi
Ishiuchi
a,
Shun-ichi
Ishiuchi
 b,
Masaaki
Fujii
b,
Masaaki
Fujii
 c,
Yuji
Sugita
c,
Yuji
Sugita
 def and
Kiyoshi
Yagi
def and
Kiyoshi
Yagi
 *d
*d
aCenter for Bioinformatics and Molecular Medicine, Graduate School of Biomedical Sciences, Nagasaki University, 1-14 Bunkyo, Nagasaki, Nagasaki 852-8521, Japan
bDepartment of Chemistry, School of Science, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo, 152-8550, Japan
cSchool of Life Science and Technology, Tokyo Institute of Technology, 4259 Nagatsuta-cho, Midori-ku, Yokohama, Kanagawa 226-8503, Japan
dTheoretical Molecular Science Laboratory, RIKEN Cluster for Pioneering Research, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan. E-mail: kiyoshi.yagi@riken.jp
eComputational Biophysics Research Team, RIKEN Center for Computational Science, 7-1-26 Minatojima-Minamimachi, Chuo-ku, Kobe, Hyogo 650-0047, Japan
fLaboratory for Biomolecular Function Simulation, RIKEN Center for Biosystems Dynamics Research, 1-6-5 Minatojima-Minamimachi, Chuo-ku, Kobe, Hyogo 650-0047, Japan
First published on 7th March 2024
Abstract
Vibrational spectroscopy combined with theoretical calculations is a powerful tool for analyzing the interaction and conformation of peptides at the atomistic level. Nonetheless, identifying the structure becomes increasingly difficult as the peptide size grows large. One example is acetyl-SIVSF-N-methylamide, a capped pentapeptide, whose atomistic structure has remained unknown since its first observation [T. Sekiguchi, M. Tamura, H. Oba, P. Çarçarbal, R. R. Lozada-Garcia, A. Zehnacker-Rentien, G. Grégoire, S. Ishiuchi and M. Fujii, Angew. Chem., Int. Ed., 2018, 57, 5626–5629]. Here, we propose a novel conformational search method, which exploits the structure-spectrum correlation using a similarity score that measures the agreement of theoretical and experimental spectra. Surprisingly, the two conformers have distinctly different energy and geometry. The second conformer is 25 kJ mol−1 higher in energy than the other, lowest-energy conformer. The result implies that there are multiple pathways in the early stage of the folding process: one to the global minimum and the other to a different basin. Once such a structure is established, the second conformer is unlikely to overcome the barrier to produce the most stable structure due to a vastly different hydrogen bond network of the backbone. Our proposed method can characterize the lowest-energy conformer and kinetically trapped, high-energy conformers of complex biomolecules.
Introduction
Advanced technologies in gas-phase vibrational spectroscopy have made it feasible to elucidate the structure and interaction of complex molecules and clusters. Various systems have been studied to date; for example, ionic liquid,1–4 protonated water clusters,5–10 metal oxide clusters,11–15 and so on. Conformer-selective vibrational spectra of polypeptides16–26 have been measured with the usage of infrared (IR) and ultraviolet (UV) double resonance spectroscopy and supersonic jet expansions. We have developed cryogenic ion traps27 combined with an electrospray ion source,28,29 which efficiently produce peptides and peptide–ligand complexes in the gas phase. The method has been applied to building blocks of the receptor domain of ion channels,30–32 β2-adrenoceptors,33,34 and kinase35 to elucidate the mechanism for molecular recognition.As the molecule grows complex, theoretical analysis plays a crucial role in assigning spectral peaks and molecular structures.36 One of the common approaches is to optimize the geometry of candidate structures and calculate their harmonic vibrational spectra using electronic structure calculations. However, the agreement between harmonic spectra and the experiment is insufficient due to the lack of anharmonicity. Notably, NH/OH groups, which form hydrogen bond (HB) networks, induce strong anharmonic couplings. Furthermore, polypeptides have many possible conformers due to their flexibility. In the previous work, we proposed a method that combines conformational sampling, clustering analysis, geometry optimization, and anharmonic vibrational analysis (Fig. 1a).37 We used the replica-exchange molecular dynamics (REMD) method38–41 and the second-order vibrational quasi-degenerate perturbation theory (VQDPT2),42,43 for sampling and vibrational calculations, respectively. The method has been applied to a pentapeptide, Ser-Ile-Val-Ser-Phe (SIVSF-NH2) (Fig. 2a), which is a partial sequence of the binding site of the β2-adrenoceptor.26 Our method reproduced the experimental IR spectrum in a range of 3100–3700 cm−1 with a mean absolute deviation (MAD) of 11.2 cm−1, and determined the peptide structure.
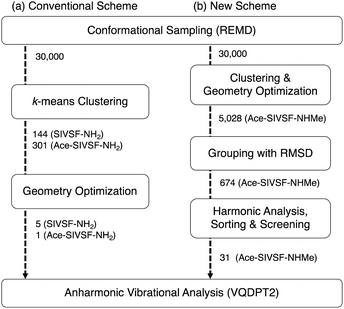 | ||
| Fig. 1 Schematic illustration of (a) the conventional conformational search scheme used in the previous work (ref. 37) and (b) that of the present work. The numbers indicate the number of candidate structures in each process. | ||
Nevertheless, the method faces a challenge when multiple conformers are observed in the experiment. In Fig. 1a, the clustering and the geometry optimization aim to find energetically stable structures. However, the observed conformers may not appear in the energetic order. For example, Gloaguen et al. studied a model dipeptide, N-acetyl-(Ala)2-O-benzyl, and observed IR spectra of two conformers.25 With the aid of theoretical calculations, the two conformers have been assigned to the most stable folded structure and a fully extended backbone structure. Notably, the extended structure is higher in energy than the folded structure by ca. 16 kJ mol−1.
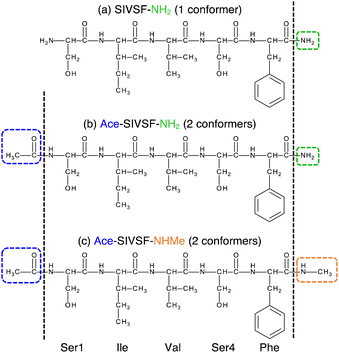
In this study, we investigate the structure of Ace-SIVSF-NH2 and Ace-SIVSF-NHMe (Fig. 2b and c, respectively). Previously, we found two conformers of Ace-SIVSF-NHMe by the IR/UV double resonance spectroscopy.34 However, the conformer structures have remained tentative. In addition, we carried out a similar measurement for Ace-SIVSF-NH2 and found two conformers (Section S2, ESI†). Revealing the structures of these conformers poses a challenge.
Here, we develop a new conformational search method that exploits the correlation between structure and spectrum as a guiding principle (Fig. 1b). In this new method, candidate structures are categorized based on their structural differences, and the conformer is determined by comparing the theoretical and experimental spectrum. For this purpose, we have incorporated similarity scores (see Methods), which objectively measure the agreement between two spectra. These scores prove to be useful tools in selecting the calculated spectrum that most accurately matches with the experimental one, without any subjective bias. The structural search reveals that the two conformers of Ace-SIVSF-NH2 come from the same basin, whereas those of Ace-SIVSF-NHMe have distinctly different geometry (Table 1).
| Peptide | Conformer name | ID |
|---|---|---|
| Ace-SIVSF-NH2 | P | A′ |
| Q | f28623 | |
| Ace-SIVSF-NHMe | X | f19375 |
| Y | f389 |
Results
Conformational search of Ace-SIVSF-NH2
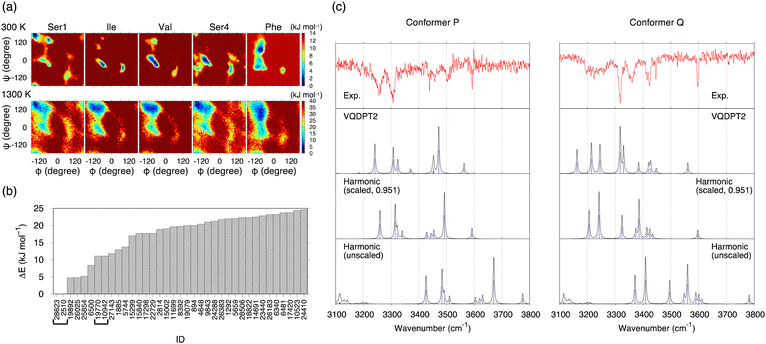
The potential of mean forces (PMFs) obtained by REMD simulations are shown in Fig. 3a. The PMF is plotted as a function of backbone dihedral angles ϕ and ψ for each residue. Notably, the PMF of all residues resembles each other at 1300 K, indicating that the simulation samples a sufficiently wide conformational space. A random walk is achieved in replica, temperature, and potential energy space (Fig. S9, ESI†). 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 snapshot structures obtained from the REMD trajectory at 300 K are referred to by an ID number from 1 to 30
000 snapshot structures obtained from the REMD trajectory at 300 K are referred to by an ID number from 1 to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 with the prefix “f”.
000 with the prefix “f”.
The conformational search was carried out in the conventional scheme. First, k-means clustering analysis was used to find representative structures from the trajectory. The clustering analysis yielded 301 structures by setting the clustering radius to 1.6 Å. Then, these structures were geometry optimized by the density functional theory (DFT) at the level of B3LYP/6-31(++)G**. [This level was used to be consistent with the previous work on SIVSF-NH2.37 The quality of this calculation is assessed in the Discussion section.] Fig. 3b shows the relative energies of the optimized structures. The most stable structure, f28623, is a strong candidate for the experimentally observed conformer.
One of the two spectra of Ace-SIVSF-NH2, conformer P, is very similar to that of SIVSF-NH2 (Fig. S7, ESI†). Therefore, we have manually constructed a conformer of Ace-SIVSF-NH2 by modifying conformer A of SIVSF-NH2 found in the previous study.37 The N-terminal of SIVSF-NH2 is replaced with an acetyl group, and the geometry is optimized at the B3LYP/6-31(++)G** level. We call this structure conformer A′. conformer A′ is 4.72 kJ mol−1 higher in energy than f28623. The molecular structures of conformer A′ and f28623 are compared in Fig. S11 (ESI†).
Fig. 3c shows the IR spectra of conformer A′ and f28623 calculated by the harmonic approximation and the VQDPT2 method together with the experimental spectra. The peak positions obtained from the harmonic approximation deviate from the experimental ones by more than 100 cm−1, suggesting strong anharmonic effects on the N–H and O–H stretching vibration. Scaled harmonic spectra, in which the frequencies are scaled so that the highest frequency peak matches the experiment, show a substantial improvement. However, the agreement with the experiment is insufficient, especially for conformer Q. In contrast, VQDPT2 not only corrects the position to the right place but also yields overtones and combination bands due to Fermi resonance. Consequently, VQDPT2 spectra agree quantitatively with the experimental spectra. The MAD of the peak position between conformer P and conformer A′, and conformer Q and f28623 are obtained as 14.9 and 13.5 cm−1, respectively. The accuracy is comparable to the previous work on SIVSF-NH2 (MAD = 11.2 cm−1), in which the calculation was done in the same procedure.37 We therefore conclude that the experimentally observed conformer P and conformer Q are assigned to conformer A′ and f28623, respectively.
The details on the peak assignment and the Fermi resonance are provided in ESI† (Section S3.3).
Conformational search of Ace-SIVSF-NHMe
REMD simulations were carried out for Ace-SIVSF-NHMe in the same way. Again, a random walk is achieved in replica, temperature, and potential energy space (Fig. S12, ESI†). 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 snapshot structures were obtained from trajectories at 300 K and used for the conformational search.
000 snapshot structures were obtained from trajectories at 300 K and used for the conformational search.
The conventional scheme was first employed to find the two conformers observed in the experiment (conformer X and conformer Y). Consequently, conformer X was assigned to the energetically most stable conformer, f19375, but conformer Y was not found among the five lowest energy structures (Section S4.2, ESI†). We then improved the search algorithm by incorporating hierarchical clustering analyses based on the principal component analysis (PCA) and Ward's method (Section S4.3, ESI†). Despite all these efforts, the structure of conformer Y remained unknown (Section S4.4, ESI†).
The failure of the conventional method and its variant has prompted us to develop a conceptually different approach, i.e., a method that does not rely on the energetics but extensively exploits the structure-spectrum correlation. The new method outlined in Fig. 1b was carried out in the following steps: (1) the energetics (i.e., the geometry optimization) were used for pre-screening, leaving more than 5000 candidate structures. (2) Similar structures were classified into 674 groups based on an RMSD of backbone and important sidechain atoms. (3) The representative structure of each group was used for the harmonic vibrational analysis. Then, 56 low-energy structures were selected, and 25 structures were ruled out because the harmonic spectrum was qualitatively wrong. (4) VQDPT2 calculations were carried out for the remaining 31 structures. Finally, the conformers were assigned based on a similarity score, which measures the difference between the experimental and VQDPT2 spectra. Further details on calculation protocols, used programs, and computational costs are given in Section S1 (ESI†).
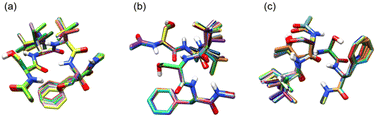
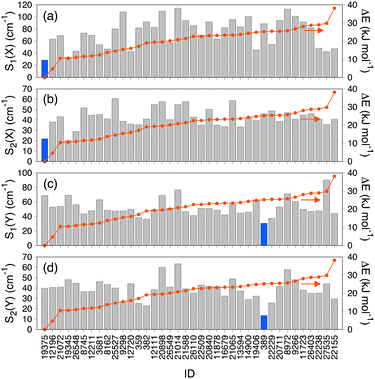
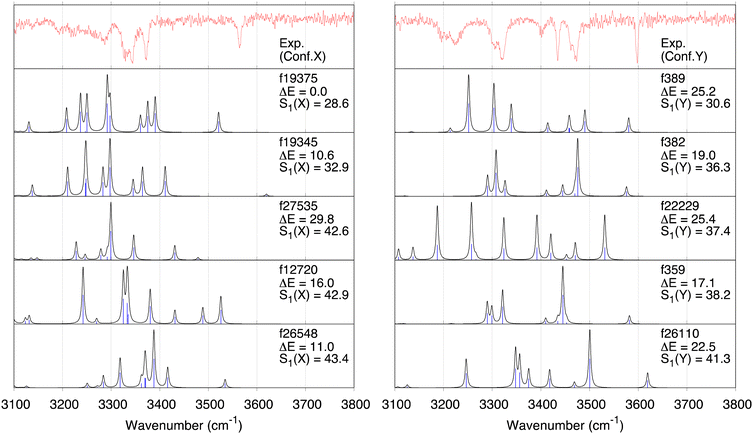
Fig. 4 shows superpositions of conformers of the three most populated groups obtained in step (2). The conformers are found to be well overlapped, demonstrating the usefulness of the proposed grouping procedure. Fig. 5 compares similarity scores, S1 and S2, of the computed conformers. (The spectra are shown in Fig. S19, ESI.†) In Fig. 5a and b, f19375 gives the smallest S1(X) and the second smallest S2(X) among the calculated conformers, reinforcing the assignment of conformer X to f19375. In Fig. 5c and d, one of the conformers, f389, gives a distinctly small value of S1(Y) = 30.6 cm−1. It is notable that f389 is less stable than f19375 by 25.2 kJ mol−1. Fig. 6 compares the experimental spectrum with the theoretical spectra of five conformers in increasing order of S1. The IR spectrum of conformer X and conformer Y agrees best with that of f19375 and f389, respectively, as indicated by the value of S1. We therefore conclude that conformer X and conformer Y are assigned to f19375 and f389, respectively. The details on the peak assignment are provided in Section S4.6 (ESI†).
Discussion
We have carried out REMD simulations, conformational searches, and VQDPT2 calculations to determine the atomistic structure of two conformers of capped SIVSF peptides, Ace-SIVSF-NH2 and Ace-SIVSF-NHMe, observed in the gas-phase IR spectroscopy. Although the conventional scheme found one of the conformers (the lowest-energy structure), it failed to reveal the second conformer. Here, we have developed a new scheme that exploits the structure-spectrum correlation: (1) the candidate conformers are grouped based on structural features, and (2) the conformer is assigned utilizing similarity scores of the calculated VQDPT2 spectrum compared to the experimental one. Using the proposed approach, we have determined the structure of all conformers of capped SIVSF peptides observed in the experiment.Fig. 7 shows the structure of SIVSF revealed in the present and previous works, together with a diagram of HB networks. Hereafter, we denote the OH, NH, and CO groups of residue R as OHR, NHR, and COR, respectively. Two conformers of Ace-SIVSF-NH2 are different only in the HB of OHSer1. OHSer1 is hydrogen bonded to COVal in conformer A′, whereas it is bonded to COAce in f28623. Other HBs are common: NHCter–COSer4 (γ-turn), NHPhe–COIle (β-turn), NHVal–COSer1 (γ-turn), NHIle–COPhe, and NHCter–OHSer1. In addition, the OH–π interaction between OHSer4 and the phenyl ring of Phe (OHSer4–PhPhe) is also found in both conformers. Conformer A′ is 4.72 kJ mol−1 less stable in energy than f28623 and is found to be the second lowest energy conformer among all the calculated ones. The structural similarity and the slight energy difference indicate that these conformers belong to the same basin. The result is in line with the previous report by Chin et al.,44–47 where three conformers of Ace-Phe-NH2 and two conformers of Ace-Phe-Val-NH2 observed simultaneously have been found from the same basin of the conformational landscape within ca. 4 kJ mol−1 of the relative energy.
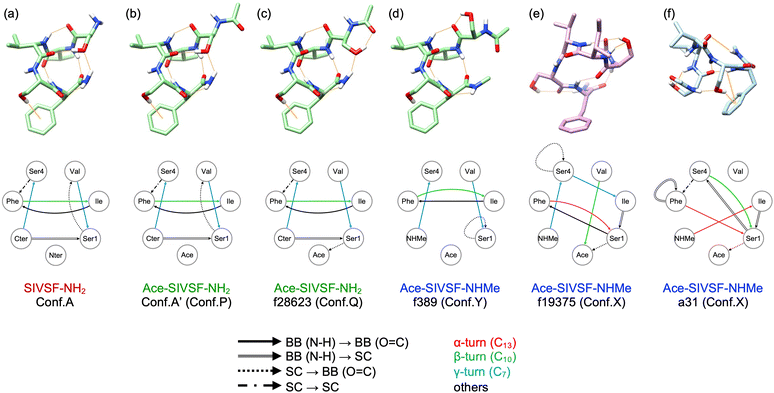 | ||
| Fig. 7 Molecular structures and diagrams of HB networks of SIVSF. (a) Conformer A of SIVSF-NH2. (b) and (c) conformer A′ and f28623 of Ace-SIVSF-NH2. (d) and (e) f389 and f19375 of Ace-SIVSF-NHMe. (f) a31 of Ace-SIVSF-NHMe obtained in ref. 34. Hydrogen atoms except for OH and NH are omitted for clarity. Hydrogen bonds are shown in orange lines. | ||
On the other hand, the second conformer of Ace-SIVSF-NHMe (f389) is 25.2 kJ mol−1 higher in energy than the most stable one (f19375). Notably, the energy difference is significantly larger than that of Ace-SIVSF-NH2. The diagram of HB networks in Fig. 7 demonstrates that f19375 and f389 are quite different in geometry. f19375 has eight HBs in total, whereas f389 has only five. The larger number of HBs stabilizes the structure of f19375. The difference in structure and energy suggests that f19375 belongs to a different basin from f389.
Interestingly, f389 has a similar HB network to conformers of Ace-SIVSF-NH2, which forms HBs between NHNHMe–COSer4 (γ-turn), NHPhe–COIle (β-turn), NHVal–COSer1 (γ-turn), NHIle–COPhe, and OHSer4–PhPhe. Note that OHSer4–PhPhe is absent in f389 because one geometrical parameter is slightly out of the range of Malone's criteria for D–H⋯π interactions (Fig. S21, ESI†).48 Thus, the three conformers, f28623, conformer A′, and f389, are different only in the orientation of OHSer1. The structures of these conformers are overlapped in Fig. S22 (ESI†). This is because OHSer1 avoids the steric hindrance with the methyl group of the C-terminal cap. Consequently, f389 lacks in the HB between NHNHMe–OHSer1.
The distinct geometry between f19375 and f389 is fascinating, suggesting multiple pathways in the early stage of the folding process. One is a pathway to the global minimum, but the other path leads to a different basin. From the observation that f389 has a similar structure to SIVSF-NH2 and Ace-SIVSF-NH2, we speculate that the sequence, SIVSF, has an intrinsic folding propensity of the backbone, i.e., NHCter–COSer4 (γ-turn), NHPhe–COIle (β-turn), NHVal–COSer1 (γ-turn), and NHIle–COPhe. The pathway leads to forming the most stable conformer in SIVSF-NH2 and Ace-SIVSF-NH2 but not in Ace-SIVSF-NHMe due to an instability caused by the N-methyl cap. Nonetheless, once such a structure is formed, it is difficult to overcome the barrier to produce the most stable structure, i.e., f19375, because the HB network of the backbone is vastly different. Consequently, two conformers are produced in Ace-SIVSF-NHMe.
One of the characteristic structures of f19375 is the α-turn, which has been rarely reported in spectroscopic studies of neutral peptides.25 Abo-Riziq et al.17 reported that the α-turn is formed in a pentapeptide FDASV, although the conformer is not the most stable one. They assigned the band at 3322 cm−1 to ν(NH) of the α-turn. As for charged peptides, Stearns et al.29 reported that alanine-rich polypeptide Ace-Phe-(Ala)10-Lys-H+ has α-helical structures and that the frequency of ν(NH) in α-helix is in a range of 3320–3350 cm−1. In the present study, ν(NHPhe) is assigned to a band observed at 3371.7 cm−1 (Fig. S20 and Table S5, ESI†), consistent with the reported value.
Another interesting HB is OHSer1–COAce, found in f19375 of Ace-SIVSF-NHMe and f28623 of Ace-SIVSF-NH2. ν(OHSer1) is assigned to a weak band at 3223.7 cm−1 in conformer X and to a sharp band at 3317.8 cm−1 in conformer Q. The result suggests that these HBs are extremely strong, yielding a large red-shift relative to ν(OH) of the free OH group (∼3600 cm−1). Note that OHSer1–COAce forms a seven-membered ring analogous to the γ-turn. The γ-turn is well known to be a strong HB exhibiting a significant red shift of the amide A band, i.e., ν(NH).44 On the other hand, the HB of the OH group and the backbone CO group is scarcely documented.25 Abo-Riziq et al.17 reported that the HB of serine OHi and COi−1 (i is the residue number) exhibited a red-shift of 210 cm−1 in FDASV. The OH group of the C-terminal COOH should be able to form a seven-membered-ring HB with the backbone CO.25 However, to our knowledge, the peak of such ν(OH) has never been characterized. In Gly-Trp-COOH, the COOH group was suggested to be hydrogen bonded with the backbone CO, but the peak of ν(OH) was not detected in the IR spectrum. The authors concluded that the peak was hidden in a broad band due to a strong HB.49 The present study provides a clear-cut assignment of the OH stretching frequency of the OH group involved in seven-membered-ring HBs.
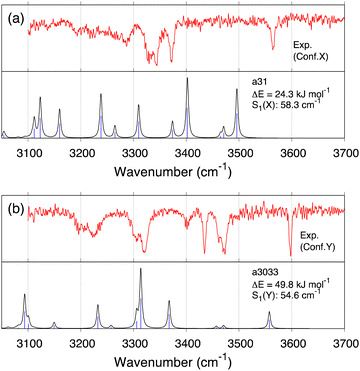
In the previous work,34 conformer X and conformer Y were tentatively assigned to a31 and a3033 (we refer to the conformer ID in ref. 34 with prefix “a”) obtained by the geometry optimization and the harmonic vibrational calculation at the level of RI-B97-D3/TZVPP.50–54 To compare with the present result, we re-optimized the geometry and computed the VQDPT2 spectrum of a31 and a3033 at the B3LYP/6-31(++)G** level.
Fig. 8 shows the calculated IR spectra, similarity scores, and the relative energy of a31 and a3033. (The peak assignment is given in Fig. S23 and Tables S7, S8, ESI.†) The calculated spectra agree poorly with the experimental ones, yielding S1(X) = 58.3 and S1(Y) = 54.6 cm−1. Furthermore, these conformers are unfavorable in terms of the energy as well. Therefore, the present calculation does not support the assignment of the previous work. We emphasize that the scaled harmonic spectra of a31 obtained by the RI-B97-D3/TZVPP method showed reasonable agreement with the experiment (see the ESI† of ref. 34), which was misleading. Nevertheless, both f19375 and a31 have α-turn between NHPhe–COSer1 (Fig. 7), which was the main finding about the atomistic structure of conformer X in the previous study.34
We now assess the quality of the DFT calculation used in this work, i.e., B3LYP/6-31(++)G**. The relative energies of the conformers of Ace-SIVSF-NHMe calculated at the B3LYP-D3/6-311(++)G(3df,3pd) level are compared with those obtained by various levels of electronic structure theory (Fig. S24, ESI†). Notably, f19375 is the most stable conformer, irrespective of the level of electronic structure calculations. However, the B3LYP/6-31(++)G** level gives the lowest correlation coefficient of 0.75. Incorporating the dispersion correction53 (B3LYP-D3/6-31(++)G**) dramatically improves the coefficient to 0.99. The relative energy of low-energy conformers obtained by B3LYP and B3LYP-D3, shown in Fig. S25 (ESI†), suggests that some conformers agree well within 5 kJ mol−1, while others deviate by more than 20 kJ mol−1. The structures of f19375, f389, and f21065 optimized by B3LYP and B3LYP-D3 are superimposed in Fig. S26 (ESI†). In f21065, B3LYP-D3 changes the orientation of the C-terminus and forms new HBs, thereby stabilizing the energy by more than 20 kJ mol−1. Therefore, incorporating the dispersion correction is generally crucial. Nevertheless, the structural change is little in the case of f19375 and f389 (RMSD = 0.30 and 0.45 Å, respectively). Since the effect of dispersion on the vibrational frequency is known to be minor,55,56 the conformer assignment is valid with the use of B3LYP/6-31(++)G** in this study.
Considering the large computational cost of anharmonic calculations, it is interesting to check the performance of similarity scores obtained from scaled harmonic frequencies and intensities, which are shown in Fig. S27 (ESI†). The minimum values of S1 are given by conformers f26549 (S1(X) = 24.4 cm−1) and f359 (S1(Y) = 34.6 cm−1). The values of S1 for f19375 and f389 (the assigned conformers) are found to be larger than these values: S1(X) = 42.3 cm−1 and S1(Y) = 34.8 cm−1, respectively. Therefore, anharmonic calculations are required for a correct assignment of the conformers. Nevertheless, the similarity score obtained from the harmonic spectrum predicts the trend and thus can be used for selecting the candidate conformers for anharmonic calculations. For example, we checked the peak position of ν(OHSer) by eye and rejected the conformers when they appeared in the wrong region. This step may be automated using the similarity score based on the harmonic results.
The present study demonstrates that the conventional conformational search of polypeptides based on the energetics may be imperfect, particularly, when multiple conformers are observed, because not only the most stable conformer(s) but also conformers that belong to a high energy basin can be produced in the experiment. The proposed scheme remedies the drawback by exploiting the structure-spectrum correlation. The grouping based on RMSD classifies the structural features, and the similarity score quantifies the agreement of theoretical and experimental spectra without a subjective point of view. Combined with enhanced sampling simulations (REMD) and anharmonic vibrational calculations (VQDPT2), these methods provide a general workflow to analyze the IR spectrum of large, complex systems, e.g., longer polypeptides and molecular complexes.
Methods
Similarity score
The comparison of experimental and theoretical spectra is crucial in spectroscopic studies to verify the validity of theory and interpret experiments. However, the comparison becomes difficult as the spectrum grows complex. To resolve this issue, Pendry57 has proposed a factor that quantifies the agreement of two spectra. Pendry's reliability factor is widely used in low-energy electron diffraction (LEED). The factor has also been used to analyze the vibrational spectra of polypeptides.58,59Following these works, we propose a score to evaluate the similarity of the two spectra. The score is obtained as follows.
(1) Obtain a set of frequency and intensity for each peak of the spectrum. We assume that the two spectra to be compared, spectrum-1 and spectrum-2, have N1 and N2 peaks, respectively. We can set N1 ≤ N2 without loss of generality. The intensities are normalized so that the maximum value in each spectrum is equal to one.
(2) Select N1 peaks from spectrum-2, which are compared with the N1 peaks of spectrum-1. The frequencies and intensities of spectrum-1 and 2 can be written as,
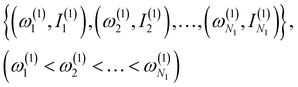 | (1) |
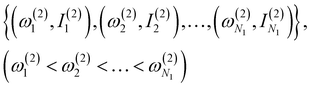 | (2) |
(3) Calculate a score S1 defined as,
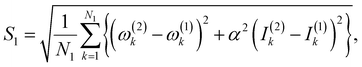 | (3) |
(4) Steps 2 and 3 are iterated over all the combinations to choose N1 peaks out of N2 peaks. The number of combinations is equal to 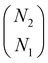 . The combination with the lowest S1 is taken as the final value of S1.
. The combination with the lowest S1 is taken as the final value of S1.
(5) Using the N1 peaks of spectrum-2 selected in step 4, we calculate another score S2 defined as,
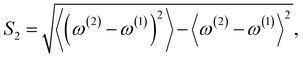 | (4) |
Note that the final assignment should be determined not only from the values of the scores S1 and S2, but also with a visual inspection of the spectra. Because S1 and S2 are evaluated from a subset of the peaks of spectrum-2, it is important to check how the overall shape look alike.
In this study, we used the peak with the frequency higher than 3100 cm−1 and intensity larger than 10.0 km mol−1 to construct the set of peaks for VQDPT2 spectra. Note that VQDPT2 distributes the intensity of fundamental modes to many states that are dark in the harmonic approximation and thus produces many peaks. As for the experimental spectrum, the frequencies and intensities are obtained by fitting the spectrum to Lorentz functions. Since the scores depend on the quality of the fitting of the experimental spectrum, small and broad bands need to be fitted carefully (Section S2, ESI†).
Computational programs
The MD and REMD simulations were carried out using the NAMD software (version 2.9).62 The geometry optimization and the harmonic vibrational analysis at the DFT level were carried out using Gaussian09.63 The single point energy at the RI-MP2/def2-TZVP(-df) level was calculated using ORCA program package (version 3.0.3).64 VQDPT2 calculation was carried out with SINDO program.65 UCSF Chimera (version 1.12)66 was used for molecular drawing. HB diagrams were drawn using Cytoscape (version 3.8.0).67Data availability
The data that support the findings of this study are openly available in the ESI† and Zenodo at https://www.doi.org/10.5281/zenodo.7580818. The script for evaluating the similarity scores can be found at https://github.com/hotaki/similarity-score.Author contributions
H. O.: data curation, formal analysis, funding acquisition, investigation, methodology, software, visualization, writing – original draft. S. I.: data curation, formal analysis, funding acquisition, investigation, visualization, writing – original draft. M. F.: conceptualization, funding acquisition, resources, supervision, writing – review & editing. Y. S.: conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing. K. Y.: funding acquisition, project administration, software, visualization, writing – original draft, review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Hiroya Asami (Gakushuin Univ.) for helpful comments on the manuscript. This research was partially supported by RIKEN Pioneering Research Projects (Biology of Intracellular Environments/Glycolipidologue Initiative) (to YS), Program for Promoting Research on the Supercomputer Fugaku (Biomolecular dynamics in a living cell (JPMXP 1020200101)/MD-driven Precision Medicine (JPMXP 1020200201)), MEXT/KAKENHI Grants No. JP19K16058 (to HO), JP20K20446, JP20H00372 (to MF and SI), JP19H05645, JP21H05249 (to YS) and JP20H02701, JP22H04761 (to KY). We used the computer system HOKUSAI provided by the RIKEN Information System Division.References
- T. Niemann, A. Strate, R. Ludwig, H. J. Zeng, F. S. Menges and M. A. Johnson, Angew. Chem., Int. Ed., 2018, 57, 15364–15368 CrossRef CAS PubMed.
- D. A. Thomas, M. Marianski, E. Mucha, G. Meijer, M. A. Johnson and G. von Helden, Angew. Chem., Int. Ed., 2018, 57, 10615–10619 CrossRef CAS PubMed.
- H. J. Zeng, T. Khuu, S. D. Chambreau, J. A. Boatz, G. L. Vaghjiani and M. A. Johnson, J. Phys. Chem. A, 2020, 124, 10507–10516 CrossRef CAS PubMed.
- H. J. Zeng, F. S. Menges, T. Niemann, A. Strate, R. Ludwig and M. A. Johnson, J. Phys. Chem. Lett., 2020, 11, 683–688 CrossRef CAS PubMed.
- J. A. Fournier, C. J. Johnson, C. T. Wolke, G. H. Weddle, A. B. Wolk and M. A. Johnson, Science, 2014, 344, 1009–1012 CrossRef CAS PubMed.
- C. T. Wolke, J. A. Fournier, L. C. Dzugan, M. R. Fagiani, T. T. Odbadrakh, H. Knorke, K. D. Jordan, A. B. McCoy, K. R. Asmis and M. A. Johnson, Science, 2016, 354, 1131–1135 CrossRef CAS PubMed.
- N. Yang, C. H. Duong, P. J. Kelleher, A. B. McCoy and M. A. Johnson, Science, 2019, 364, 275–278 CrossRef CAS PubMed.
- N. Yang, S. C. Edington, T. H. Choi, E. V. Henderson, J. P. Heindel, S. S. Xantheas, K. D. Jordan and M. A. Johnson, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 26047–26052 CrossRef CAS PubMed.
- J. Liu, J. Yang, X. C. Zeng, S. S. Xantheas, K. Yagi and X. He, Nat. Commun., 2021, 12, 6141 CrossRef CAS PubMed.
- M. R. Fagiani, H. Knorke, T. K. Esser, N. Heine, C. T. Wolke, S. Gewinner, W. Schöllkopf, M.-P. Gaigeot, R. Spezia, M. A. Johnson and K. R. Asmis, Phys. Chem. Chem. Phys., 2016, 18, 26743–26754 RSC.
- J. Sauer and H.-J. Freund, Catal. Lett., 2015, 145, 109–125 CrossRef CAS.
- M. L. Weichman, S. Debnath, J. T. Kelly, S. Gewinner, W. Schöllkopf, D. M. Neumark and K. R. Asmis, Top. Catal., 2018, 61, 92–105 CrossRef CAS.
- S. Debnath, H. Knorke, W. Schöllkopf, S. Zhou, K. R. Asmis and H. Schwarz, Angew. Chem., Int. Ed., 2018, 57, 7448–7452 CrossRef CAS PubMed.
- Y.-K. Li, S. Debnath, M. Schlangen, W. Schöllkopf, K. R. Asmis and H. Schwarz, Angew. Chem., Int. Ed., 2019, 58, 18868–18872 CrossRef CAS PubMed.
- F. Müller, J. B. Stückrath, F. A. Bischoff, L. Gagliardi, J. Sauer, S. Debnath, M. Jorewitz and K. R. Asmis, J. Am. Chem. Soc., 2020, 142, 18050–18059 CrossRef PubMed.
- J. M. Bakker, C. Plützer, I. Hünig, T. Häber, I. Compagnon, G. von Helden, G. Meijer and K. Kleinermanns, ChemPhysChem, 2005, 6, 120–128 CrossRef CAS PubMed.
- A. Abo-Riziq, J. E. Bushnell, B. Crews, M. Callahan, L. Grace and M. S. de Vries, Chem. Phys. Lett., 2006, 431, 227–230 CrossRef CAS.
- A. Abo-Riziq, B. O. Crews, M. P. Callahan, L. Grace and M. S. de Vries, Angew. Chem., Int. Ed., 2006, 45, 5166–5169 CrossRef CAS PubMed.
- T. D. Vaden, S. A. N. Gowers, T. S. J. A. de Boer, J. D. Steill, J. Oomens and L. C. Snoek, J. Am. Chem. Soc., 2008, 130, 14640–14650 CrossRef CAS PubMed.
- T. D. Vaden, S. A. N. Gowers and L. C. Snoek, Phys. Chem. Chem. Phys., 2009, 11, 5843–5850 RSC.
- T. D. Vaden, S. A. N. Gowers and L. C. Snoek, J. Am. Chem. Soc., 2009, 131, 2472–2474 CrossRef CAS PubMed.
- A. M. Rijs, M. Kabeláč, A. Abo-Riziq, P. Hobza and M. S. de Vries, ChemPhysChem, 2011, 12, 1816–1821 CrossRef CAS PubMed.
- G. D. Santis, N. Takeda, K. Hirata, K. Tsuruta, S. Ishiuchi, S. S. Xantheas and M. Fujii, J. Am. Chem. Soc., 2022, 144, 16698–16702 CrossRef CAS PubMed.
- A. M. Rijs and J. Oomens, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, Springer International Publishing, Cham, 2015, pp. 1–42 Search PubMed.
- E. Gloaguen, M. Mons, K. Schwing and M. Gerhards, Chem. Rev., 2020, 120, 12490–12562 CrossRef CAS PubMed.
- S. Ishiuchi, K. Yamada, H. Oba, H. Wako and M. Fujii, Phys. Chem. Chem. Phys., 2016, 18, 23277–23284 RSC.
- S. Ishiuchi, H. Wako, D. Kato and M. Fujii, J. Mol. Spectrosc., 2017, 332, 45–51 CrossRef CAS.
- O. V. Boyarkin, S. R. Mercier, A. Kamariotis and T. R. Rizzo, J. Am. Chem. Soc., 2006, 128, 2816–2817 CrossRef CAS PubMed.
- J. A. Stearns, O. V. Boyarkin and T. R. Rizzo, J. Am. Chem. Soc., 2007, 129, 13820–13821 CrossRef CAS PubMed.
- S. Ishiuchi, Y. Sasaki, J. M. Lisy and M. Fujii, Phys. Chem. Chem. Phys., 2019, 21, 561–571 RSC.
- T. Negoro, K. Hirata, J. M. Lisy, S. Ishiuchi and M. Fujii, Phys. Chem. Chem. Phys., 2021, 23, 12045–12050 RSC.
- R. Otsuka, K. Hirata, Y. Sasaki, J. M. Lisy, S. Ishiuchi and M. Fujii, ChemPhysChem, 2020, 21, 712–724 CrossRef CAS PubMed.
- M. Tamura, T. Sekiguchi, S. Ishiuchi, A. Zehnacker-Rentien and M. Fujii, J. Phys. Chem. Lett., 2019, 10, 2470–2474 CrossRef CAS PubMed.
- T. Sekiguchi, M. Tamura, H. Oba, P. Çarçarbal, R. R. Lozada-Garcia, A. Zehnacker-Rentien, G. Grégoire, S. Ishiuchi and M. Fujii, Angew. Chem., Int. Ed., 2018, 57, 5626–5629 CrossRef CAS PubMed.
- J. H. Kwon, M. J. Lee, G. Song, K. Tsuruta, S. Ishiuchi, M. Fujii and H. Kang, J. Phys. Chem. Lett., 2020, 11, 7103–7108 CrossRef CAS PubMed.
- K. A. Tanemura, S. Das and K. M. Merz, Jr., J. Chem. Inf. Model., 2021, 61, 1647–1656 CrossRef CAS PubMed.
- H. Otaki, K. Yagi, S. Ishiuchi, M. Fujii and Y. Sugita, J. Phys. Chem. B, 2016, 120, 10199–10213 CrossRef CAS PubMed.
- Y. Sugita and Y. Okamoto, in Computational Methods for Macromolecules: Challenges and Applications, ed. T. Schlick and H. H. Gan, Springer Berlin Heidelberg, Berlin, Heidelberg, 2002, pp. 304–332 Search PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 2000, 329, 261–270 CrossRef CAS.
- Y. Sugita, M. Kamiya, H. Oshima and S. Re, in Biomolecular Simulations: Methods and Protocols, ed. M. Bonomi and C. Camilloni, Springer New York, New York, NY, 2019, pp. 155–177 Search PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- K. Yagi and H. Otaki, J. Chem. Phys., 2014, 140, 084113 CrossRef PubMed.
- K. Yagi, S. Hirata and K. Hirao, Phys. Chem. Chem. Phys., 2008, 10, 1781–1788 RSC.
- W. Chin, F. Piuzzi, I. Dimicoli and M. Mons, Phys. Chem. Chem. Phys., 2006, 8, 1033–1048 RSC.
- W. Chin, M. Mons, J.-P. Dognon, F. Piuzzi, B. Tardivel and I. Dimicoli, Phys. Chem. Chem. Phys., 2004, 6, 2700–2709 RSC.
- W. Chin, M. Mons, J.-P. Dognon, R. Mirasol, G. Chass, I. Dimicoli, F. Piuzzi, P. Butz, B. Tardivel, I. Compagnon, G. von Helden and G. Meijer, J. Phys. Chem. A, 2005, 109, 5281–5288 CrossRef CAS PubMed.
- W. Chin, F. Piuzzi, J.-P. Dognon, I. Dimicoli and M. Mons, J. Chem. Phys., 2005, 123, 084301 CrossRef PubMed.
- J. F. Malone, C. M. Murray, M. H. Charlton, R. Docherty and A. J. Lavery, J. Chem. Soc., Faraday Trans., 1997, 93, 3429–3436 RSC.
- I. Hunig and K. Kleinermanns, Phys. Chem. Chem. Phys., 2004, 6, 2650–2658 RSC.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759–1787 RSC.
- C. Puzzarini, J. Bloino, N. Tasinato and V. Barone, Chem. Rev., 2019, 119, 8131–8191 CrossRef CAS PubMed.
- J. B. Pendry, J. Phys. C: Solid State Phys., 1980, 13, 937–944 CrossRef CAS.
- M. Rossi, V. Blum, P. Kupser, G. von Helden, F. Bierau, K. Pagel, G. Meijer and M. Scheffler, J. Phys. Chem. Lett., 2010, 1, 3465–3470 CrossRef CAS.
- F. Schubert, M. Rossi, C. Baldauf, K. Pagel, S. Warnke, G. von Helden, F. Filsinger, P. Kupser, G. Meijer, M. Salwiczek, B. Koksch, M. Scheffler and V. Blum, Phys. Chem. Chem. Phys., 2015, 17, 7373–7385 RSC.
- B. Galabov, Y. Yamaguchi, R. B. Remington and H. F. Schaefer, J. Phys. Chem. A, 2002, 106, 819–832 CrossRef CAS.
- P. Seidler, J. Kongsted and O. Christiansen, J. Phys. Chem. A, 2007, 111, 11205–11213 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- K. Yagi, SINDO 4.0, 2019, https://tms.riken.jp/en/research/software/sindo/.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- P. Shannon, A. Markiel, O. Ozier, N. S. Baliga, J. T. Wang, D. Ramage, N. Amin, B. Schwikowski and T. Ideker, Genome Res., 2003, 13, 2498–2504 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details and supporting results. See DOI: https://doi.org/10.1039/d4cp00064a |
| This journal is © the Owner Societies 2024 |