Predicting two-dimensional semiconductors using conductivity effective mass

Abstract

In this paper we investigate the relationship between the conductivity effective mass and exfoliation energy of materials to assess whether automatic sampling of the electron band structure can predict the presence of and ease of separating chemically bonded layers. We assess 22 976 materials from the Materials Project database, screen for only those that are thermodynamically stable and identify the 1000 materials with the highest standard deviation for p-type and the 1000 materials with the highest standard deviation for n-type internal conductivity effective mass tensors. We calculate the exfoliation energy of these 2000 materials and report on the correlation between effective mass and exfoliation energy. A relationship is found which is used to identify a previously unconsidered two-dimensional material and could streamline the modelling of other two-dimensional materials in the future.

---

Introduction

For decades it was thought that two-dimensional crystals were not possible,^1,2 until the successful preparation of monolayer graphene with mechanical exfoliation³ proved that two-dimensional planar crystal structures could be isolated.^4–6 These layers are not only stable but also exhibit remarkable physical and chemical properties not found in their parent materials.^7,8 For example, the thermal conductivity of suspended monolayer graphene is as high as 5000 W m⁻¹ K⁻¹ as measured by Raman spectroscopy, a value much higher than that of bulk diamond or graphite.⁹ Similarly, at room temperature, the carrier mobility in graphene can also reach much higher values of up to 15 000 cm² V⁻¹ s⁻¹ and is less dependent on temperature than in its bulk counterpart.¹⁰ Because of these outstanding properties, graphene can be used in high-speed electronics,¹¹ optical devices,¹² chemical sensors,^10,13 energy production and storage,^12,14,15 and DNA sequencing^16,17 among many other fields.

The successful preparation of graphene led to a growing number of other two-dimensional materials being reported.¹⁸ Similar to graphene, transition metal dichalcogenides (TMDs) have been studied for some time, with the structure of TMDs first reported by Linus and colleagues as early as 1923.¹⁹ By the 1960s, about 60 TMDs materials had been reported, of which at least 40 exhibit layered structures,²⁰ for example MoS₂, MoSe₂, WS₂ and WSe₂, among others. These layered crystals not only have a thickness comparable to that of graphene, but additionally have an intrinsic band gap, which gives them the potential to be used in a new generation of small, low energy-consuming transistor materials. The semiconductor industry is driven by the continued reduction in transistor size, with Moore's law stating that the number of transistors that can fit on an integrated circuit doubles approximately every eighteen months.²¹ These days, the state-of-the-art silicon-based transistor has all but reached its fundamental limit and, to further break through the gate length of silicon-based field-effect transistors,²² materials that can achieve smaller sizes than silicon are sought. Two-dimensional (2D) materials have an inherent advantage for transistor applications because they are intrinsically stable at atomic thicknesses and still have robust and well-characterized electrostatic properties.²³ In a study by Xie et al. it was noted that in field effect transistors prepared from MoS₂, channel lengths of down to 4 nm could be reliably achieved;²⁴ owing to the planar confinement of the 2D material effectively suppressing short channel effects. By comparison, the minimum channel length that can be achieved in state-of-the-art silicon-based transistors is around 5 nm, which is difficult to reduce further without the device failing.¹⁸ Thus, it is expected that TMDs will be able to enable further reduction in transistor size beyond the intrinsic limit of silicon.²⁵

There are also other 2D materials that have been successfully exfoliated from their parent materials apart from TMDs, such as phosphole, arsenene, hexagonal boron nitride and C₃N₄, which have crystal structures similar to that of graphene.^26–29 In general, these 2D materials have great potential for applications in sensors, batteries, transistors and many other fields, as shown in the Fig. 1. Therefore, there is strong motivation to explore new two-dimensional materials and as such, an expansion of the tools used by researchers to identify and understand 2D materials is desirable for the research community.

Fig. 1 Overview of the multiple possible applications of two-dimensional materials in several fields.¹⁴

The varied nature of 2D materials has defied facile classification thus far owing to the numerous atomic structures and the myriad arrangements with which bonded layers may nestle together. However, the poor bonding in the interlayer direction should always be observable in the electronic band structure of the material; see for example the band structures of the archetypal 2D materials WSe₂, MoS₂, WS₂ and MoSe₂ in Fig. 2.³⁰ The curvature of the bands is known to correlate with degree of bonding and each of these materials has a noticeable contraction to flat bands in the specific path of the Brillouin zone that corresponds to the interlayer crystallographic direction. This band curvature is often quantified or expressed as conductivity effective mass; with positive (p-type) charge effective mass arising from the curvature in the occupied valence bands and negative (n-type) charge effective mass arising from the curvature of the unoccupied conduction bands. These days, publicly available codes and open-source software exist that can calculate the conductivity effective mass automatically and indeed have already been deployed on repositories of many thousands of materials.³¹ In this paper we assess whether such automated analysis can recover the likelihood of 2D nature of a material based on the conductivity effective masses arising from the band structure by calculating the exfoliation energy of the two thousand stable materials reported to have the most anisotropic conductivity effective mass tensors.

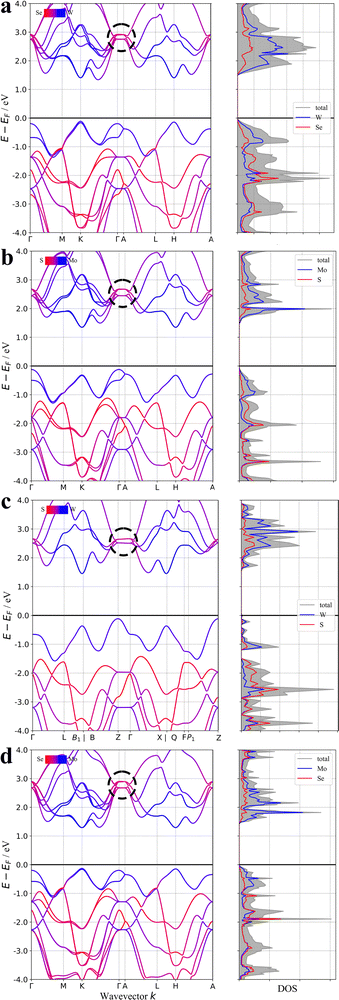Fig. 2 The band structures of (a) WSe₂ (b) MoS₂ (c) WS₂ and (d) MoSe₂. The flat bands that correspond to the weak inter-layer bonding are circled in each case.

Methods

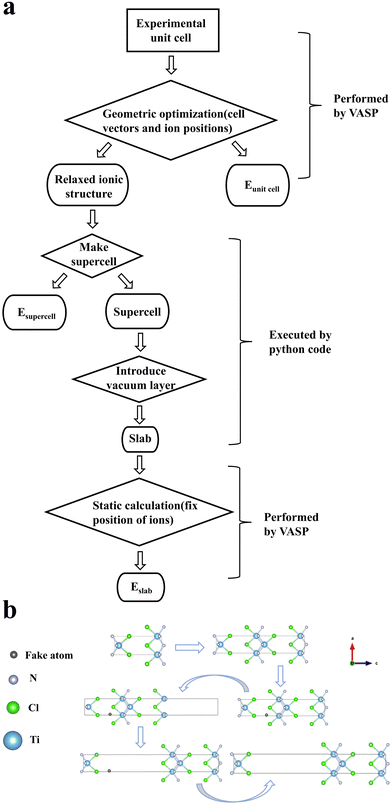
There are two publicly available repositories that form the basis of this work. First is the database of information on conductivity effective mass for 22 976 materials published by Ricci et al.³¹ The second is the structures and values of energy above convex hull from the Materials Project database.³² We use the energy above convex hull as a metric of thermodynamic stability for the first screening criterion. Then, we cross-reference the remaining stable materials with their corresponding values of conductivity effective masses of carriers in three crystallographic directions from the repository of Ricci et al. Next, we eliminate any materials containing F-block elements due to their scarcity. Finally, we select the one thousand materials each of p-type and n-type that have the largest standard deviation of effective mass. For these materials, we automatically construct slabs and calculate their exfoliation energy with density functional theory (DFT). Ultimately, we explore the relationship between exfoliation energy and standard deviation of the effective mass. A schematic of the screening workflow of this paper is shown in Fig. 3.

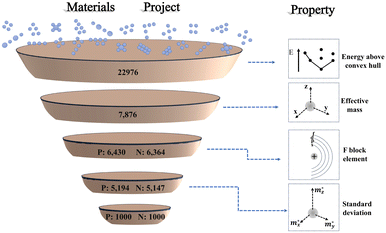Fig. 3 Material screening workflow diagram, showing the process of the screening procedure used in this work. On the right is the representation of property screened at each stage.³⁴ P and N refer to doping type and the number corresponds to the number of candidates remaining.

The DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP) version 5.4.4,^33,34 which uses the projector augmented wave (PAW) method for modelling core and valence electrons.^35,36 The Perdew–Burke–Enzerhof (PBE) exchange correlational functional of the generalized gradient approximation (GGA) was chosen.^37,38 For the long-range, non-local interactions that give rise to the van der Waals force, the D-3 method correction proposed by Grimme was used to describe the van der Waals interaction where indicated in this work.^39,40

All of the VASP input files were automatically generated using pymatgen “io.vasp.sets” module,⁴¹ however the magnetic moment of atoms and the spin polarization effect were not considered to allow for convergence of structural relaxation of slab calculations containing surface terminations.

The data of the conductivity effective masses was obtained from the work of Ricci et al.,³¹ which is based on the Boltzmann transport theory. The BoltzTraP software was used to calculate the conductivity, Seebeck coefficient, effective masses and other transport properties of the materials. BoltzTrap uses the relaxation time approximation and the k-point interpolation method based on a Fourier expansion to calculate conductivity effective mass, which is dependent on temperature T and doping level.³¹ In this work, the data we used were found at a temperature of 300 K and a doping concentration of 10¹⁸ cm⁻³.

To create the slab structures for high-throughput ab initio calculations, we developed a python code with the help of the pymatgen toolkit to expand the relaxed crystal cell along the axis in which the effective mass has its largest value,⁴¹ so that the unit cell length is not less than 15 Å. Then, the code adds a fake atom incrementally throughout the lattice space and collects the distance from that atom to its closest other atom (i.e. the nearest neighbour distance). After doing this 1600 times across the unit cell, the code reports back the position of the fake atom that gives the maximum nearest neighbour distance. Once the coordinates of fake atom have been determined, the code will pull the crystallographic supercell apart by 10 Å (to ensure that the periodic boundaries don’t allow the surfaces to interact with themselves) along the high-effective mass axis, creating a so-called slab. A summary of this process and example slab construct can be seen in Fig. 4(b).

Fig. 4 (a) Representation of the calculation flow chart used to obtain exfoliation energy. E_slab and E_supercell are the total energies from the corresponding calculations used to calculate exfoliation energy. (b) An example corresponding slab structure construction process for TiNCl (mp-27850).

All of these slabs were subject to static calculations to obtain internal energy without ionic relaxation at the PBE or PBE + vdW level of theory. The exfoliation energy could then be obtained by the formula:

E_f = (E_slab − E_supercell)/A (1)

On the left side of the equation E_f is the exfoliation energy, E_slab on the right is the total energy from the slab structure and E_supercell is the total energy from the supercell structure. The distinction between slab and supercell models is that the slab contains the supercell and the empty vacuum layer, implicitly creating a surface that allows for the simulation of the exfoliation process. A is the surface area of structure after relaxation. Practically the exfoliation energy reflects the relative ease of separating atomic layers of a material.

Results and discussion

Since, the inverse of the effective mass is the second-order partial derivative of the energy on the k-point in the energy band diagram dividing the square of the Planck constant; the effective mass reflects the degree of dispersity or bending of the electronic energy band. When the value of the effective mass is very large, it indicates that the band is flat and barely diverges at that point in the Brillouin zone, akin to the features of the band structures shown in Fig. 2. Conversely, if the effective mass value is low, there should be high dispersion of the bands in that region of the Brillouin zone. We posit therefor that a 2-dimensional material should exhibit a relatively high conductivity effective mass in the inter-layer direction of a 2D crystal and a relatively low effective mass in the two bonded crystallographic directions. Overall, this behaviour should be possible to capture and quantify in the single value of standard deviation for the conductivity effective mass tensor.

Firstly, we identify the materials from the Materials Project that present with an energy above convex hull of 0 eV.³² These materials IDs are then cross-referenced with the publicly available database of calculated conductivity effective mass values of Ricci et al.³¹ While the known examples of 2D materials have band contraction in the conduction band (see Fig. 2), it may not necessarily be the case for all 2D materials. As a result, we consider datasets for both p- and n-type effective mass in parallel.

Among the screening candidates identified to be on the convex hull, 3938 n-type materials show their standard deviation of effective mass less than one, which indicates that most stable materials are electronically isotropic, as is perhaps to be expected. By comparison however, the maximum standard deviation of effective mass for n-type materials reaches an outlandish 1 910 154. Such a huge standard deviation as this is meaningless and arises as an artefact from the effective mass. Because the derivative of a perfectly flat band is infinite, there is no upper limit to the value that can be presented by the standard deviation. What exactly is a high enough effective mass for the band to be considered flat is entirely arbitrary and so a heuristic approach is still needed. As examples for comparison, we include experimentally reported values of effective mass in Table 1.^42,43 We include more details on the effective mass at a, b and c crystallographic directions for the selected 1000 p-type and 1000 n-type materials in the ESI† (see Fig. S1 and S2).

Table 1 Values of effective mass determined by a least-squares fit along the ΓX[100], ΓL[111] and ΓK[110] directions. The experimental data is from Vurgaftman et al. and the theoretical data is from Kim et al.^42,43 PBE, MBJLDA and HSE are increasingly expensive levels of density functional theory

Material	Method	γ 1	γ 2	γ 3
InP	PBE	8.01	2.91	3.49
	MBJLDA	4.53	1.28	1.80
	HSE	5.27	1.63	2.14
	Expt.	5.08	1.60	2.10
InAs	MBJLDA	12.53	5.10	5.73
	HSE	16.50	6.77	7.64
	Expt.	20.00	8.50	9.20
InSb	MBJLDA	22.26	9.47	10.31
	MBJLDA	36.13	16.49	17.27
	HSE	29.44	12.79	13.85
	Expt.	34.80	15.50	16.50
GaAs	PBE	15.29	6.16	6.96
	MBJLDA	5.79	1.60	2.32
	MBJLDA	7.45	2.37	3.12
	HSE	7.51	2.22	3.07
	Expt.	6.98	2.06	2.93
GaSb	MBJLDA	10.13	3.27	4.26
	HSE	12.69	4.31	5.43
	Expt.	13.40	4.70	6.00

---

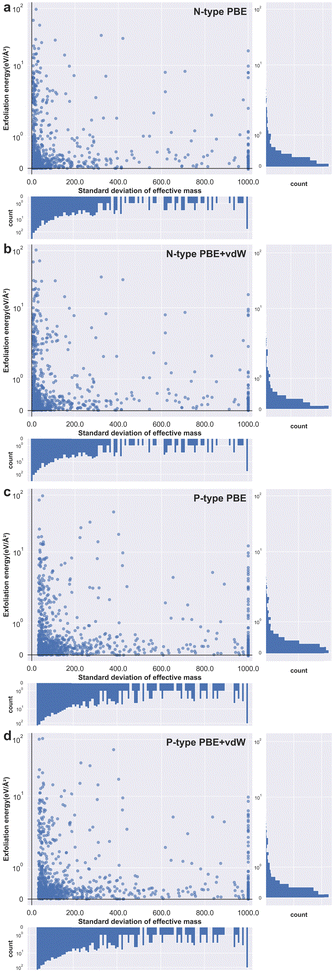
Next, we identify both the 1000 materials with the highest effective mass standard deviation for n-type doping and 1000 of the highest for p-type doping. For these 2000 materials we automatically create slab simulations and calculate exfoliation energies for each. We do this for two levels of DFT: PBE and PBE with van der Waals corrections (PBE + vdW); meaning a total of four thousand data points. These are plotted as four separate panels in Fig. 5 by taking the logarithm of the exfoliation energy against a truncated standard deviation of conductivity effective mass. Fig. 5a and b show the results obtained for n-type materials at the PBE and PBE + vdW functional levels, respectively. And Fig. 5c and d are the results obtained for p-type materials at the PBE and PBE + vdW functional levels, respectively. Detailed information on the structure of these materials and related information, as well as the structures that did not converge during the calculations, can be found in the ESI† (see Fig. S3–S6).

Fig. 5 Exfoliation energy versus standard deviation of effective mass. The exfoliation energies were calculated with PBE or PBE + vdW, (a) and (c) show n- and p-type materials with PBE and (b) and (d) show n- and p-type materials at PBE + vdW. The subplots show the count for the data on the relevant axis.

From Fig. 5, we can see that the distribution characteristics of the p-type and the n-type material scatters are very similar, the data points are mainly concentrated in the lower left corner and a few isolated points are distributed up the middle area of the graphs. This relationship shows the expected behaviour posited at the start of this paper – that as the standard deviation of conductivity effective mass approaches zero the exfoliation energy rises rapidly- indeed the exfoliation energy appears to increase exponentially. The subplot on the right indicates that most materials have a small exfoliation energy, even though we selected those with the highest standard of effective mass from all stable compounds. This observation is to be expected given that of the many thousands of known materials, only a few dozen two-dimensional materials have been successfully prepared experimentally.⁴⁴ The subplot underneath each panel shows similarly that most materials have a relatively low standard deviation of effective mass. From this we can infer that a material with a standard deviation of effective mass of more than 100, for example, is already exceptional relative to almost all known cases (see Fig. S7 for the interval distribution of the conductivity effective mass for each of the 1000 materials datasets, ESI†).

We also confirm this behaviour with the effect of van der Waals interaction included for the exfoliation energy calculations for both n-type and p-type materials (images b and d in Fig. 5). The effect of the vdW corrections serves to raise the exfoliation energy values higher than those obtained using the PBE functional, which is to be expected given that the instantaneous dipoles create forces of attraction and therefore make materials harder to pull apart. The nature of the relationship between exfoliation energy and effective mass standard deviation remains unchanged at this higher level of theory. This is a fortuitous result as it benefits the community to be able to screen for 2D materials at as rapid a level of theory as possible. However, we note that when the van der Waals interaction is not considered, there are several materials that show negative values for the exfoliation energy (see Fig. S8 in the ESI† for the specific cases). This should not be possible, as negative exfoliation energies imply that the structure of the material is unstable prior to layer separation, even though we screened for only thermodynamically stable materials. The expected positive exfoliation energies are obtained when the total energy of the structure is calculated considering van der Waals interactions, however. As such, we encourage other researchers to include van der Waals corrections in any future studies involving the calculation of exfoliation energies.

We note that there is a discrepancy between the values of standard deviation of charge effective mass for the p- and n-type datasets, observable in Fig. 5. Whereas the smallest standard deviation for the n-type results is 5.14, the smallest value for the p-type results is 31.1. This indicates that sampling the conduction band can give a broader range of values across the same set of materials than does the valence band and is perhaps therefore a more suitable resource for use in future screening. Once again, this observation is somewhat intuitive and relatable to fundamental materials physics in that higher energy bands in general are less likely to be strongly bonding when compared to lower energy bands due to the shielding effects of the deeper core states of the material. With less strong bonding, the bands are likely to be relatively flatter and hence give rise to a greater standard deviation for the charge effective mass tensor.

As a whole, we believe there is a clear relationship between the two properties considered in this work. However, there are multiple outliers in the data which we investigate further. From the datasets represented in Fig. 5, we take three p-type and three n-type materials from the upper left, lower left and lower right parts of the scatter plot as examples for further scrutiny. The atomic structures for the n-type materials selected from the top left, bottom left and bottom right of Fig. 5b are shown in Fig. 6a, b and c respectively. The atomic structures for the p-type materials selected from the top left, bottom left and bottom right of Fig. 5d are shown in Fig. 6d, e and f, respectively.

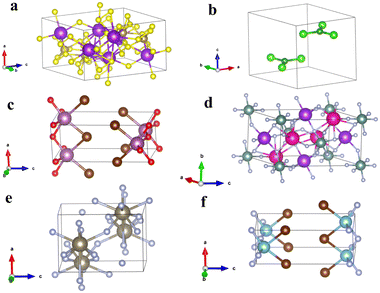Fig. 6 (a)–(c) Are the unit cells of three n-type materials from the upper left, lower left and lower right zones of Fig. 5b respectively. (d)–(f) Are the unit cells of three p-type materials from the upper left, lower left and lower right zones of Fig. 5d respectively. Information about all these materials can be found in Table 2.

For the n-type materials, Fig. 6a (from the top left section of Fig. 5b) is K₄Ta₂S₁₁ which presents an atomic structure that immediately appears not amenable to exfoliation. The anions and cations are reasonably interspersed throughout the structure and there is a high density of bonds present. This is to be expected given the compound's position high on the graph, as pulling apart oppositely charged ions and breaking bonds is certain to lead to a high exfoliation energy. It is also in line with the premise of the paper; since the material is to the left of the graph it has a relatively isotropic charge effective mass tensor yielding one of the lowest standard deviations of effective mass. Fig. 6b shows the material BCl₃ that immediately seems quite amenable to exfoliation and unsurprisingly presents in the lower quadrant of the graph for exfoliation energy. Interestingly this material was extracted as being relatively isotropic in effective mass tensor. We believe that perhaps this can be explained by an interaction between cations and anions in the interlayer direction. It can be seen that the oppositely charged ions almost eclipse one another when viewed along the c axis, and so are likely to have electrostatic interactions that can give rise to some degree of dispersion of the electronic bands. Finally, Fig. 6c shows ScBrO a material that has both a low exfoliation energy and high standard deviation of effective mass. When contrasted with BCl₃, it can be seen that this material does not have potential anion–cation interactions between the layers, instead the structure is composed of anion terminated bonded layers, similar to MoS₂, MoSe₂, WS₂ and WSe₂ and we predict to be ScBrO to be an unequivocal two-dimensional material. To the knowledge of the authors, this is the first time this compound has been highlighted as a two-dimensional material.

Fig. 6d–f are p-type materials selected from the top left, bottom left and bottom right of Fig. 5d, respectively. Fig. 6d shows the compound KRb₂YF₆, which, like K₄Ta₂S₁₁ has a high density of bonds and interspersed oppositely charged anions that explain the high exfoliation energy. Fig. 6e shows the compound TlF₃, which does appear to be possible to separate into constituent layers. Like BCl₃, TlF₃ has potential interactions between the cations and anions, visible as long bonds in the centre of the unit cell in this case. We believe this explains how the material (like BCl₃) exhibits both a relatively isotropic effective mass tensor and a relatively low exfoliation energy. Finally, we again end with a material that has both a high standard deviation of effective mass and a low exfoliation energy in TiBrN. Again, like ScBrO, we believe this material is highly likely to be an inherent 2D material as it has a bonded layer structure, and these bonded layers are terminated in anions as in the case of the archetypal 2D materials.

These two sets of sample materials, whose information is summarized in Table 2, lends confidence to our initial premise, that the conductivity effective mass tensor can provide a summary of chemical structure and the likeliness of manifesting a layered nature. Based on our results it seems that n-type and p-type conductivity effective mass sampling perform equally well in estimating 2D nature. Furthermore, we remind the reader that our slabs were constructed without human intervention. We believe these results also corroborate our simplistic automated exfoliation approach.

Table 2 Properties of the layered materials shown in Fig. 6 and Fig. 2

Materials Project ID	Formula	Space group	Standard deviation of effective mass	E f (eV Å^−2)	Doping-type
mp-18664^45	K4Ta2S11	P1̄	7.005	20.739	n-type
mp-23184^46,47	BCl3	P63/m	5.267	0.009	n-type
mp-546279^48	ScBrO	Pmmn	1000.000	0.015	n-type
mp-7012^49	KRb2YF6	P21/c	31.408	21.638	p-type
mp-2632^50,51	TlF3	Pnma	32.158	0.045	p-type
mp-27849^52,53	TiBrN	Pmmn	1000.000	0.016	p-type
mp-2815^54,55	MoS2	P63/mmc	2.510	0.029	n-type
mp-9813^56,57	WS2	R3m	0.320	0.037	n-type
mp-1634^54,58	MoSe2	P63/mmc	5.869	0.028	p-type
mp-1821^59	WSe2	P63/mmc	3.305	0.030	p-type

---

Returning to the material TlF₃ (Fig. 6e), its ease of exfoliation is perhaps surprising as at first glance there is no obvious layered sub-structure (only upon closer inspection are the elongated bonds noticeable: 2.42 vs. 2.15 angstroms). This observation suggests that significant lattice gaps in the atomic structure are not necessary for a material to have a small exfoliation energy. Even if a bulk material does not exhibit layered structure, it may have the potential to be stripped down into a two-dimensional layer. In fact, non-van der Waals layered materials have been successfully exfoliated recently in experiment. Ilmenene, for example, has been exfoliated from the naturally occurring titanite ore ilmenite (FeTiO₃) by employing liquid phase exfoliation in a dimethylformamide solvent by ultrasonic bath sonication.⁶⁰ Similarly, a new two-dimensional material ‘hematene’ has been successfully obtained from the natural iron ore hematite (α-Fe₂O₃), by means of liquid exfoliation.⁶¹ Finally, In the work of Ma et al.⁶² they report successful exfoliate of stable monolayer wurtzite semi-conductors from bulk materials that are non-vdW material and show isotropic in three crystallographic directions. This is a fascinating and surprising new avenue of research in the field of 2D materials, and it is hoped that the tools and data presented in this work can be brought to bear in understanding this new phenomenon in future work.

It should also be noted that theoretical tools for the calculation of charge mobilities are continuously improving in both accuracy and efficiency. Density functional perturbation theory combined with Wannier interpolation can yield highly accurate predictions of electron mobility and conductivity in semiconductors and does not rely on the constant relaxation time approximation for example, unlike the BoltzTrap method.^63–66 New open-source tools have also been released recently lending such advanced techniques to high-throughput screening, which could provide an even better basis for large-scale analysis projects such as this in the future.^67,68

Finally, we highlight that according to our data WS₂ – one of the archetypal 2-dimensional materials – has very small standard deviation of conductivity effective mass for both p-type and n-type sampling and has a small exfoliation energy (see Table 2) and does have anion terminated bonded layers in its crystal structure. The atomic structures of the four archetypal 2D materials are shown in Fig. S9 (ESI†). This places one of the most important 2D materials outside of the premise of our paper. Together with the several outliers that can be seen in Fig. 5, we conclude that while the conductivity effective mass tensor can be instructive in the field, the relationship between it and exfoliation energy is not absolute in applicability. On the other hand, we do find that the conductivity effective mass tensor is very useful in predicting the crystallographic direction along which a material can be exfoliated. The code used in this work was designed according to this principle.

Conclusions

In summary, we have investigated whether the conductivity effective mass can be used to evaluate the likely ease of exfoliation for a given material using high-throughput calculation and find several results of note.

We found that the conductivity effective mass tensor was able to reliably provide the crystallographic direction along which a material could be exfoliated in conjunction with an automated script, an example of which we release with this article for free use (both online and in the ESI†).‡ Such a simplistic approach, which requires no human intervention, can significantly facilitate materials screening for technologically relevant applications with machine learning or high-throughput methods for example.

Subsequently, we calculated the exfoliation energy of one thousand p-type materials and one thousand n-type materials that have highest standard deviation of effective mass and compared them at the PBE and PBE + vdW level. We find that the use of a vdW correction is highly recommended for any calculation of accurate exfoliation energy, successfully erasing aberrant results that arose at the PBE level. By knowing the exfoliation energy and conductivity effective mass we were able to predict physiological and structural features of a range of materials. Not least among which, we were able to identify at least one material that to our knowledge has not been considered as a two-dimensional material previously but that exhibits the physical hallmarks of such compounds. We provide the full dataset of our results in the ESI† (Tables S1 and S2) and encourage the reader to explore further, bearing in mind that there are known exceptions to the proposed relationship (specifically WS₂ in this case).

Finally, we suggest future work in the area could consider the newly reported cases of stable layers from materials that are not considered intrinsically two-dimensional such as hematene from hematite among others. This recent development will undoubtedly expand the area of 2D materials significantly.

Overall, we find that conductivity of effective mass can be a useful tool for quickly accessing information pertaining to the electronic structure of materials without requiring full band structures or high levels of theory.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support of the Shanghai Municipal Science and Technology Commission Program, number 19010500500, and the Natural National Science Foundation of China (NSFC) number 51950410585. L. A. B. also acknowledges the support of the Ilby and Aladar Fleischman Faculty of Engineering, Tel Aviv University.

References

1. R. Peierls, Quelques Propriétés Typiques Des Corps Solides, Ann. Inst. Henri Poincare, 1935, 5(3), 177–222.
2. A. Münster, Zur Theorie Der Umwandlungen II. Ordnung, Z. Für Phys. Chem., 1954, 1, 259–274,  DOI:10.1524/zpch.1954.1.5_6.259.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306(5696), 666–669,  DOI:10.1126/science.1102896.
4. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Two-Dimensional Gas of Massless Dirac Fermions in Graphene, Nature, 2005, 438(7065), 197–200,  DOI:10.1038/nature04233.
5. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Two-Dimensional Atomic Crystals, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(30), 10451–10453,  DOI:10.1073/pnas.0502848102.
6. Y. B. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Experimental Observation of the Quantum Hall Effect and Berry's Phase in Graphene, Nature, 2005, 438(7065), 201–204,  DOI:10.1038/nature04235.
7. S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Graphene-Based Composite Materials, Nature, 2006, 442(7100), 282–286,  DOI:10.1038/nature04969.
8. J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, The Structure of Suspended Graphene Sheets, Nature, 2007, 446(7131), 60–63,  DOI:10.1038/nature05545.
9. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Superior Thermal Conductivity of Single-Layer Graphene, Nano Lett., 2008, 8(3), 902–907,  DOI:10.1021/nl0731872.
10. A. K. Geim and K. S. Novoselov, The Rise of Graphene, Nat. Mater., 2007, 6(3), 183–191,  DOI:10.1038/nmat1849.
11. Y.-M. Lin, C. Dimitrakopoulos, K. A. Jenkins, D. B. Farmer, H.-Y. Chiu and A. Grill, Avouris, Ph. 100-GHz Transistors from Wafer-Scale Epitaxial Graphene, Science, 2010, 327(5966), 662,  DOI:10.1126/science.1184289.
12. M. Liu, X. Yin, E. Ulin-Avila, B. Geng, T. Zentgraf, L. Ju, F. Wang and X. Zhang, A Graphene-Based Broadband Optical Modulator, Nature, 2011, 474(7349), 64–67,  DOI:10.1038/nature10067.
13. M. Deng, X. Yang, M. Silke, W. Qiu, M. Xu, G. Borghs and H. Chen, Electrochemical Deposition of Polypyrrole/Graphene Oxide Composite on Microelectrodes towards Tuning the Electrochemical Properties of Neural Probes, Sens. Actuators, B, 2011, 158(1), 176–184,  DOI:10.1016/j.snb.2011.05.062.
14. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Large-Scale Pattern Growth of Graphene Films for Stretchable Transparent Electrodes, Nature, 2009, 457(7230), 706–710,  DOI:10.1038/nature07719.
15. Y. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Carbon-Based Supercapacitors Produced by Activation of Graphene, Science, 2011, 332(6037), 1537–1541,  DOI:10.1126/science.1200770.
16. S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Graphene as a Subnanometre Trans-Electrode Membrane, Nature, 2010, 467(7312), 190–193,  DOI:10.1038/nature09379.
17. M. Xu, Y. Gao, X. Yang and H. Chen, Unique Synthesis of Graphene-Based Materials for Clean Energy and Biological Sensing Applications, Chin. Sci. Bull., 2012, 57(23), 3000–3009,  DOI:10.1007/s11434-012-5128-9.
18. Y. Wang, L. Wang, X. Zhang, X. Liang, Y. Feng and W. Feng, Two-Dimensional Nanomaterials with Engineered Bandgap: Synthesis, Properties, Applications, Nano Today, 2021, 37, 101059,  DOI:10.1016/j.nantod.2020.101059.
19. R. G. Dickinson and L. Pauling, THE CRYSTAL STRUCTURE OF MOLYBDENITE, J. Am. Chem. Soc., 1923, 45(6), 1466–1471,  DOI:10.1021/ja01659a020.
20. J. A. Wilson and A. D. Yoffe, The Transition Metal Dichalcogenides Discussion and Interpretation of the Observed Optical, Electrical and Structural Properties, Adv. Phys., 1969, 18(73), 193–335,  DOI:10.1080/00018736900101307.
21. G. E. Moore, Cramming More Components onto Integrated Circuits, Proc. IEEE, 1998, 86(1), 4.
22. D. Akinwande, C. Huyghebaert, C.-H. Wang, M. I. Serna, S. Goossens, L.-J. Li, H.-S. P. Wong and F. H. L. Koppens, Graphene and Two-Dimensional Materials for Silicon Technology, Nature, 2019, 573(7775), 507–518,  DOI:10.1038/s41586-019-1573-9.
23. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutierrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Terrones, W. Windl and J. E. Goldberger, Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene, ACS Nano, 2013, 7(4), 2898–2926,  DOI:10.1021/nn400280c.
24. L. Xie, M. Liao, S. Wang, H. Yu, L. Du, J. Tang, J. Zhao, J. Zhang, P. Chen, X. Lu, G. Wang, G. Xie, R. Yang, D. Shi and G. Zhang, Graphene-Contacted Ultrashort Channel Monolayer MoS2 Transistors, Adv. Mater., 2017, 29(37), 1702522,  DOI:10.1002/adma.201702522.
25. F. Schwierz, J. Pezoldt and R. Granzner, Two-Dimensional Materials and Their Prospects in Transistor Electronics, Nanoscale, 2015, 7(18), 8261–8283,  10.1039/c5nr01052g.
26. P. Miro, M. Audiffred and T. Heine, An Atlas of Two-Dimensional Materials, Chem. Soc. Rev., 2014, 43(18), 6537–6554,  10.1039/c4cs00102h.
27. G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, Recent Advances in Two-Dimensional Materials beyond Graphene, ACS Nano, 2015, 9(12), 11509–11539,  DOI:10.1021/acsnano.5b05556.
28. A. Gupta, T. Sakthivel and S. Seal, Recent Development in 2D Materials beyond Graphene, Prog. Mater. Sci., 2015, 73, 44–126,  DOI:10.1016/j.pmatsci.2015.02.002.
29. M. Xu, T. Liang, M. Shi and H. Chen, Graphene-Like Two-Dimensional Materials, Chem. Rev., 2013, 113(5), 3766–3798,  DOI:10.1021/cr300263a.
30. J. A. Champion, Some Properties of (Mo, W) (Se, Te)2, Br. J. Appl. Phys., 1965, 16(7), 1035,  DOI:10.1088/0508-3443/16/7/418.
31. F. Ricci, W. Chen, U. Aydemir, G. J. Snyder, G.-M. Rignanese, A. Jain and G. Hautier, An Ab Initio Electronic Transport Database for Inorganic Materials, Sci. Data, 2017, 4(1), 170085,  DOI:10.1038/sdata.2017.85.
32. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1(1), 011002,  DOI:10.1063/1.4812323.
33. G. Kresse and J. Furthmuller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
34. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561,  DOI:10.1103/PhysRevB.47.558.
35. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
36. P. E. Blochl, C. J. Forst and J. Schimpl, Projector Augmented Wave Method: Ab Initio Molecular Dynamics with Full Wave Functions, Bull. Mater. Sci., 2003, 26(1), 33–41,  DOI:10.1007/BF02712785.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78(7), 1396,  DOI:10.1103/PhysRevLett.78.1396.
38. M. Xu, C. Wang, B. J. Morgan and L. A. Burton, Hydride Ion Intercalation and Conduction in the Electride Sr₃CrN₃, J. Mater. Chem. C, 2022, 10(17), 6628–6633,  10.1039/D1TC05850A.
39. K. Berland, V. R. Cooper, K. Lee, E. Schroeder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, van der Waals Forces in Density Functional Theory: A Review of the vdW-DF Method, Rep. Prog. Phys., 2015, 78(6), 066501,  DOI:10.1088/0034-4885/78/6/066501.
40. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
41. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319,  DOI:10.1016/j.commatsci.2012.10.028.
42. Y.-S. Kim, M. Marsman, G. Kresse, F. Tran and P. Blaha, Towards Efficient Band Structure and Effective Mass Calculations for III-V Direct Band-Gap Semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(20), 205212,  DOI:10.1103/PhysRevB.82.205212.
43. I. Vurgaftman, J. R. Meyer and L. R. Ram-Mohan, Band Parameters for III–V Compound Semiconductors and Their Alloys, J. Appl. Phys., 2001, 89(11), 5815–5875.
44. N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Two-Dimensional Materials from High-Throughput Computational Exfoliation of Experimentally Known Compounds, Nat. Nanotechnol., 2018, 13(3), 246.
45. S. Herzog, C. Naether and W. Bensch, Dimorphism of K4Ta2S11: Syntheses, Crystal Structures and Properties of Two Alkali Metal Tantalum Sulfides, Z. Fuer Anorg. Allg. Chem., 1999, 625, 969–974.
46. M. Atoji and W. N. Lipscomb, B-Cl Distance in Boron Trichloride, J. Chem. Phys., 1957, 27, 195.
47. M. A. Rollier and A. Riva, Determinazione Roentgenografica Della Struttura Cristallina Del Cloruro e Del Bromuro Di Boro Allo Stato Solido, Gazzetta Chim. Ital., 1947, 77, 361–366.
48. L. Jongen and G. Meyer, Scandium(III) Oxide Bromide, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, i153–i154.
49. H. Guengard, J. Grannec and P. Gravereau, Structure Cristalline de Rb2 K Y F6 a Temperature Ambiante, C. R. Seances Acad. Sci., Ser. 2, 1993, 317, 37–42.
50. C. Hebecker, Die Kristallstruktur von Thalliumtrifluorid, Z. Anorg. Allg. Chem., 1972, 393, 223–229.
51. C. Hebecker, Zur Kristallstruktur von Indium- Und Thalliumtrifluorid, Naturwissenschaften, 1966, 53, 104.
52. B. Altintas, Structural and Electronic Properties of Alpha-Ti N X (X: F, Cl, Br, I). An Ab Initio Study, J. Theor. Comput. Chem., 2011, 10, 65–74.
53. R. Juza and J. Ueber Nitridhalogenide Des Titans Und Zirkons Heners, Z. Anorg. Allg. Chem., 1964, 332, 159–172.
54. C. Lee, J. Hong, W. R. Lee, D. Y. Kim and J. H. Shim, Density Functional Theory Investigation of the Electronic Structure and Thermoelectric Properties of Layered Mo S2, Mo Se2 and Their Mixed-Layer Compound, J. Solid State Chem., 2014, 211, 113–119.
55. M. A. Py and R. R. Haering, Structural Destabilization Induced by Lithium Intercalation in Mo S2 and Related Compounds, Can. J. Phys., 1983, 61, 76–84.
56. W. J. Schutte, J. L. de Boer and F. Jellinek, Crystal Structures of Tungsten Disulfide and Diselenide, J. Solid State Chem., 1987, 70, 207–209.
57. J. C. Wildervanck and F. Jellinek, Preparation and Crystallinity of Molybdenum and Tungsten Sulfides, Z. Anorg. Allg. Chem., 1964, 328, 309–318.
58. B. L. Evans and R. A. Hazelwood, Optical and Structural Properties of Mo Se2, Phys. Status Solidi A, 1971, 4, 181–192.
59. V. L. Kalikhman, E. P. Gladchenko and L. L. Pravoverova, Crystal Structure of Quasibinary Alloys of the System W Se2 - Nb Se2, Inorg. Mater., 1972, 8, 1020–1022.
60. A. Puthirath Balan, S. Radhakrishnan, R. Kumar, R. Neupane, S. K. Sinha, L. Deng, C. A. de los Reyes, A. Apte, B. M. Rao, M. Paulose, R. Vajtai, C. W. Chu, G. Costin, A. A. Martí, O. K. Varghese, A. K. Singh, C. S. Tiwary, M. R. Anantharaman and P. M. Ajayan, A Non-van der Waals Two-Dimensional Material from Natural Titanium Mineral Ore Ilmenite, Chem. Mater., 2018, 30(17), 5923–5931,  DOI:10.1021/acs.chemmater.8b01935.
61. A. Puthirath Balan, S. Radhakrishnan, C. F. Woellner, S. K. Sinha, L. Deng, C. Reyes, B. M. Rao, M. Paulose, R. Neupane, A. Apte, V. Kochat, R. Vajtai, A. R. Harutyunyan, C.-W. Chu, G. Costin, D. S. Galvao, A. A. Martí, P. A. van Aken, O. K. Varghese, C. S. Tiwary, A. Malie Madom Ramaswamy Iyer and P. M. Ajayan, Exfoliation of a Non-van der Waals Material from Iron Ore Hematite, Nat. Nanotechnol., 2018, 13(7), 602–609,  DOI:10.1038/s41565-018-0134-y.
62. Z. Ma, P. Huang, J. Li, P. Zhang, J. Zheng, W. Xiong, F. Wang and X. Zhang, Multiferroicity and Giant In-Plane Negative Poisson's Ratio in Wurtzite Monolayers, Npj Comput. Mater., 2022, 8(1), 1–11.
63. S. Poncé, E. R. Margine, C. Verdi and F. Giustino, EPW: Electron–Phonon Coupling, Transport and Superconducting Properties Using Maximally Localized Wannier Functions, Comput. Phys. Commun., 2016, 209, 116–133.
64. L. A. Agapito and M. Bernardi, Ab Initio Electron-Phonon Interactions Using Atomic Orbital Wave Functions, Phys. Rev. B, 2018, 97(23), 235146.
65. G. Brunin, H. P. C. Miranda, M. Giantomassi, M. Royo, M. Stengel, M. J. Verstraete, X. Gonze, G.-M. Rignanese and G. Hautier, Phonon-Limited Electron Mobility in Si, GaAs, and GaP with Exact Treatment of Dynamical Quadrupoles, Phys. Rev. B, 2020, 102(9), 094308.
66. X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J.-M. Beuken, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, N. Brouwer, F. Bruneval, G. Brunin, T. Cavignac, J.-B. Charraud, W. Chen, M. Côté, S. Cottenier, J. Denier, G. Geneste, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, X. He, N. Helbig, N. Holzwarth, Y. Jia, F. Jollet, W. Lafargue-Dit-Hauret, K. Lejaeghere, M. A. L. Marques, A. Martin, C. Martins, H. P. C. Miranda, F. Naccarato, K. Persson, G. Petretto, V. Planes, Y. Pouillon, S. Prokhorenko, F. Ricci, G.-M. Rignanese, A. H. Romero, M. M. Schmitt, M. Torrent, M. J. van Setten, B. Van Troeye, M. J. Verstraete, G. Zérah and J. W. Zwanziger, The Abinitproject: Impact, Environment and Recent Developments, Comput. Phys. Commun., 2020, 248, 107042.
67. J.-J. Zhou, J. Park, I.-T. Lu, I. Maliyov, X. Tong and M. Bernardi, Perturbo: A Software Package for Ab Initio Electron–Phonon Interactions, Charge Transport and Ultrafast Dynamics, Comput. Phys. Commun., 2021, 264, 107970.
68. A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Efficient Calculation of Carrier Scattering Rates from First Principles, Nat. Commun., 2021, 12(1), 2222.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00277f

‡ https://github.com/bmd-lab/mss_auto

---