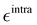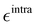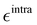Dynamic effects on the nonlinear optical properties of donor acceptor stenhouse adducts: insights from combined MD + QM simulations†
Received
23rd January 2024
, Accepted 5th March 2024
First published on 12th March 2024
Abstract
The second-order nonlinear optical (NLO) responses of a donor–acceptor stenhouse adduct (DASA) are investigated by using a computational approach combining molecular dynamics simulations and density functional theory (DFT) calculations. Specific force fields for the open and closed photoswitching forms are first parameterized and validated according to the Joyce protocol, in order to finely reproduce the geometrical features and potential energy surfaces of both isomers in chloroform solution. Then, DFT calculations are performed on structural snapshots extracted at regular time steps of the MD trajectories to address the influence of the thermalized conformational dynamics on the NLO responses related to hyper-Rayleigh scattering (HRS) experiments. We show that accounting for the structural dynamics largely enhances the HRS hyperpolarizability (βHRS) compared to DFT calculations considering solely equilibrium geometries, and greatly improves the agreement with experimental measurements. Furthermore, we show that the NLO responses of the NLO-active open form are correlated with the bond order alternation along the triene bridge connecting the donor and acceptor moieties, which is rationalized using simple essential state models.
1 Introduction
Stenhouse donor–acceptor adducts (DASAs) are a class of organic molecules first synthesized by Read De Alanis and colleagues in 2014,1,2 that have attracted much interest over the past decade due to unique reverse photochromic properties. The structure of these systems comprises an amine donor and a dicarboxylate acceptor from either Meldrums or barbituric acids at the terminal positions of a π-conjugated triene bridge. When exposed to visible light, DASAs photoisomerize from the thermodynamically stable conjugated (open) form to a non-conjugated cyclic (closed) form, undergoing a loss of color that reversibly recovers in the dark. The design of successive generations of DASAs upon variation of the substitution pattern, rationalized by quantum chemistry calculations, further demonstrated high tunability in their photoswitching behavior and excellent fatigue resistance.3–16 In addition, the significant change in (photo)physical and chemical properties upon photoisomerization makes DASAs very useful for many applications, ranging from colorimetric sensing to photo-induced drug-delivery systems.17,18 Recently, the potential of DASAs for exploitation within light-responsive nonlinear optical (NLO) materials and devices has also been demonstrated. Quantum-chemical calculations performed on a large number of DASA derivatives predicted that the alteration of the π-electron conjugation along the photocommutation should induce a significant contrast in the first hyperpolarizability (β),19,20 which was subsequently proved experimentally by means of hyper-Rayleigh scattering (HRS) measurements.21 These extensive experimental and theoretical investigations allowed to identify the BA4 derivative (Fig. 1), incorporating a barbituric acid (BA) acceptor moiety and a tertiary amine donor, as a highly effective NLO switch due to its fast and efficient photoconversion, intermediate time constant for the back reaction, and high contrast in the second-harmonic (SH) intensity.
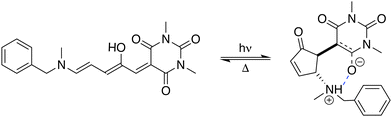 |
| | Fig. 1 Photocommutation between the open and zwitterionic closed forms of BA4. | |
In this theoretical contribution, we investigate further the second-order NLO responses of BA4 in both its closed and open forms, by taking into account the effects of thermally-induced fluctuations in the geometry of the chromophore. Indeed, molecular hyperpolarizabilities are highly sensitive to geometrical distortions, and structural dynamic effects have been shown to play a leading role in the NLO properties of organic dyes.22 The computational approach involves classical molecular dynamics (MD) simulations and subsequent quantum chemistry (QM) calculations performed at the density functional theory (DFT) level on statistical samplings of uncorrelated molecular snapshots extracted from the MD trajectories. This sequential MD + QM (or MD + DFT) scheme23–26 has been previously employed to characterize the SH responses of various organic species in solution, including photochromic compounds.27–35 For example, it was shown to drastically improve the description of the first hyperpolarizability contrast between the open and closed forms of switchable indolino-oxazolidine derivatives.28
However, this computational strategy requires the development of highly accurate and system-specific force fields (FFs), as the NLO properties targeted by DFT calculations have high sensitivity to geometrical changes. Therefore, the first part of this work was dedicated to the derivation of force-fields able to precisely reproduce the structural features of BA4 in both its open and closed forms. Concretely, two quantum mechanically derived force-fields (QMD-FFs36–38) were specifically tailored for either the open or closed BA4 forms, based on QM descriptors purposely computed at the DFT level. In the second part, the second-order NLO responses of BA4 and their variation upon switching were computed at the DFT level along the MD trajectories obtained with the QMD-FFs and validated against previously reported experimental data.21 The influence of dynamic geometrical distortions was then analyzed in detail and rationalized in the light of simple essential state models.
2 Theory and methods
2.1 Training molecular descriptors
To build the training database required by the QMD-FF parameterization, selected molecular descriptors were computed at QM (DFT) level for both the open and closed form of BA4. In fact, as previously reported,21,39 DASA derivatives incorporating non-symmetric amines can adopt two different conformations in their open form (Fig. 2), the first one with the smaller substituent in the upper position being slightly more stable (with a Gibbs free energy difference of 0.45 kcal mol−1 at 298 K). Moreover, the most stable closed form of BA4 in chloroform adopts a zwitterionic structure, as illustrated in Fig. 2. Following the standard Joyce procedure,36,37 the QM training data set for each form is composed by the optimized geometry, its Hessian matrix and relaxed torsional energy scans along the most flexible coordinates. To this end, reference geometries for both forms of BA4 were obtained by optimizing all coordinates using DFT, and the Hessian matrices were computed at these conformations. In addition, the relaxed energy profiles were obtained by minimizing all internal coordinates but the scanned dihedral. All DFT calculations were performed using the Gaussian16 package,40 employing the M06-2X41 exchange–correlation functional (XCF) with the aug-cc-pVDZ basis set, accounting for dispersion effects by means of the Grimme's D3 correction42 and for solvent effects (here chloroform) by using the solvation model based on density (SMD),43 which was shown to reproduce the relative thermal stability of open and closed DASA isomers more accurately than other polarizable continuum models.21 At this level of approximation, selected according to benchmark calculations reported in ref. 21, the open-to-closed Gibbs isomerization energy is equal to 6.73 kcal mol−1.
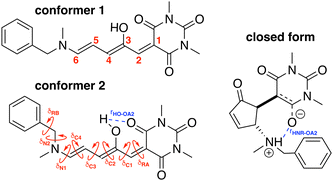 |
| | Fig. 2 Possible open conformers (left) and zwitterionic closed form (right) of BA4. Torsional angles and intramolecular non-bonded interactions discussed in the text are also displayed. | |
2.2 QMD-FF parameterization
Based on the aforementioned QM training molecular descriptors, two separate QMD-FFs, for either BA4 open and closed forms, were parameterized exploiting the standard partition38,44–46 of the total QMD-FF energy, EtotalQMD-FF, in an intramolecular contribution, ruling the molecular flexibility and an intermolecular term, which describes the interaction with the solvent:| | | EtotalQMD-FF = EintraQMD-FF + EinterQMD-FF | (1) |
The interactions between the BA4 solute and the surrounding chloroform molecules, is hence accounted as:| | 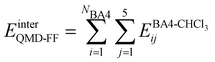 | (2) |
where i and j run on the atoms of the NBA4 solute and CHCl3 solvent, respectively, whereas 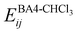 takes the standard expression:
takes the standard expression:| | 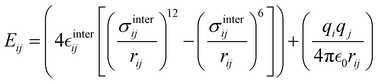 | (3) |
The first term in square brackets on the right side of eqn (3) is the standard 12–6 Lennard-Jones (LJ) potential, while the second term accounts for the Coulomb charge–charge interactions. In the present work, only the latter term was derived from QM data, whereas the LJ intermolecular parameters, consistently with the description chosen for the CHCl3 solvent, were transferred from the OPLS database.47,48 Conversely, the point charges were specifically derived through the RESP method from the DFT electronic density of either the open or closed isomers, exploiting their optimized geometries computed for the Joyce parameterization. A full list of the intermolecular parameters for both forms is reported in the ESI† (Tables S1 and S7).
The QMD-FF parameterization of the intramolecular term in eqn (1) was carried out according to the Joyce protocol,36,37 thus computing EintraQMD-FF as:
| | 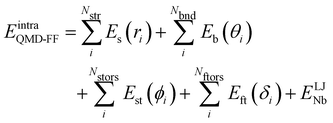 | (4) |
where the first two terms describe stretching and bending contributions, respectively:
| | 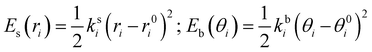 | (5) |
being
ks(
kb) and
r0(
θ0) the harmonic force constants and equilibrium values. According to the standard Joyce procedure,
26,36,46,49 the same harmonic expression is employed to describe dihedrals,
ϕ, which are expected to be subjected to small oscillations around their equilibrium position, as those ruling the planarity of stiff aromatic rings or double bonds,
i.e.:
| | 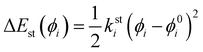 | (6) |
where
ksti and
ϕ0i are the force constant and equilibrium angle for the stiff torsion
i. Conversely, the more flexible dihedrals
δ are described through sums of Fourier-like terms:
| | 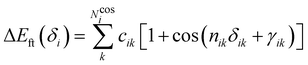 | (7) |
Finally, as the MD runs are expected to explore a large portion of the potential energy surface (PES) of the target molecule, in which the open form might be found in varied conformations, intramolecular non-bonded interactions were introduced between selected atom pairs, to account for both the steric repulsion between close atoms and the possible intramolecular hydrogen bonds (HBs). Following the Joyce protocol, such interactions can be introduced through specific LJ intramolecular model functions as:
| | 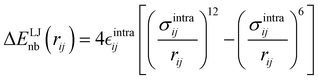 | (8) |
It is worth noticing that
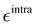
and
σintra, the intramolecular LJ parameters entering in the above equation and describing the interaction between selected atom pairs belonging to the same molecule (BA4), differ from
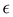
and
σ reported in
(3), which were instead designed to mimic the interaction among atoms pertaining to two different molecules (here BA4 and chlorofrom).
Once all potential terms have been assigned to each coordinate, the QMD-FF parameters (i.e. all equilibrium coordinates and force constants) were simultaneously determined from the stored QM molecular descriptors with the Joyce software,50 by minimizing the standard36,37 objective function:
| | 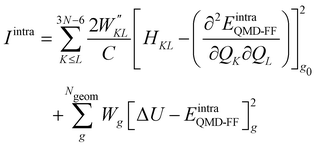 | (9) |
where the sum in the first term runs over the 3
N − 6 dye's normal modes (
Q),
C is a normalization factor, and
HKL an element of the QM Hessian matrix, evaluated in the minimum energy geometry (
g0). In the second term, Δ
Ug is the QM computed energy difference between the
g and
g0 geometries, while
Ngeom is the number of different geometrical arrangements sampled along the QM relaxed energy scans. The weights
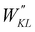
and
Wg were set, as in most recent applications,
37,38,46,49,51,52 to 2500 (for
K ≠
L), 5000 (for the diagonal elements) and 1.0 for all
g geometries.
2.3 Molecular dynamics
MD simulations were carried out with the Gromacs code53 employing the parameterized QMD-FFs, either on each isolated (gas phase) DASA isomer or on a system consisting of one open or closed isomer and ∼1000 explicit chloroform molecules. Simulations were performed in the NVT ensemble at 298 K for the isolated molecule in the gas phase and at constant pressure and temperature (NPT, 1 atm and 298 K) in solution. For the isolated molecule, a 5 ns trajectory at 298 K was produced, storing DASA's conformations every 100 ps. Conversely, the solvated system was equilibrated in the NPT ensemble for 5 ns, keeping temperature (298 K) and pressure (1 atm) constant in the NPT ensemble through the Berendsen algorithm.54 Thereafter, a 10 ns production run was carried out, keeping the same temperature and pressure constant through the Bussi–Parrinello55 and Parrinello–Rahman56 schemes, which are capable to preserve the correct statistics in the NPT ensemble. In all runs, unless otherwise stated, no bond length was constrained and the time step was set to 0.25 fs. A cut-off distance of 12 Å was employed for short-range interactions, and the standard correction for energy and virial applied to LJ potentials. Long range electrostatic was accounted for by the particle mesh Ewald scheme (PME). Temperature and pressure coupling constants τT and τP were set to 0.1 ps and 5 ps, respectively.
2.4 Reference molecular properties
The parameterized QMD-FFs were validated by comparing geometrical, electronic and optical properties calculated using MD geometries with those obtained from reference DFT calculations. Concerning the structural descriptors, particular attention was paid to the torsional degrees of freedom defined by the dihedral angles (δ) shown in Fig. 2 (see Fig. 3 and 4 for 3D representations), and to the length of intramolecular HBs (rHO–OA2 and rHNR–OA2).
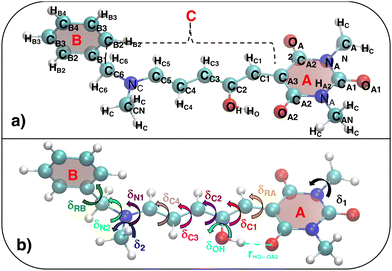 |
| | Fig. 3 (a) Specific atom labeling adopted during the Joyce parameterization for the open DASA isomer. Only symmetry- or chemically equivalent atoms share the same label. All label suffixes refer to the fragmentation scheme evidenced with the red letters: A (ring A), B (ring B) and C (Chain). (b) Definition and labeling of the most flexible dihedrals of the open DASA isomer, all handled by the QMD-FF through eqn (7), unless otherwise stated. The internal non-bonded coordinate rHO⋯OA2 (see eqn (8)) is also evidenced with a dashed cyan line. | |
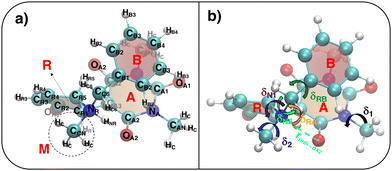 |
| | Fig. 4 (a) Specific atom labeling adopted during the Joyce parameterization for the closed DASA isomer. Only symmetry- or chemically equivalent atoms share the same label. All label suffixes refer to the fragmentation scheme evidenced with the red letters: A (ring A), B (ring B) and R (ring C) and M (methyl). (b) Definition and labeling of the most flexible dihedrals of the closed DASA isomer, all handled by the QMD-FF through eqn (7). The internal non-bonded coordinate rHNR⋯OA2 (eqn (8)), is also evidenced with a dashed cyan line. | |
For the conjugated open form, the planarity of the central part is measured through the dihedral angle ξ = 1-2-5-6 (see Fig. 2 for atom labels), while the overall molecular length is estimated through the OA1–NC distance (see Fig. 3). Additionally, bond length alternation (BLA) and bond order alternation (BOA) along the triene bridge are defined as:
| | 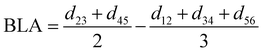 | (10) |
| | 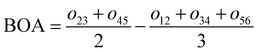 | (11) |
where
dij and
oij are bond distances and bond orders between atoms
i and
j, respectively. The bond order
oij estimates the number of electrons fluctuating concurrently between atoms
i and
j. The different atoms are defined according to the quantum theory of atoms in molecules (QTAIM)
57 and their corresponding overlap integrals were obtained from the AIMAll software.
58 Finally, the bond orders were calculated using the ESI-3D code
59–61 using the following expression:
62,63| | 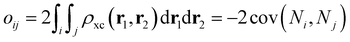 | (12) |
where
Ni and
Nj are the atomic populations and
ρxc(
r1,
r2) is the exchange–correlation density. Note that, while π-conjugation metrics like BLA and BOA are known to be highly sensitive to the choice of XCF,
64–66 the M06-2X XCF was shown to reliably describe these indicators for extended π-conjugated systems.
67,68
Turning to the optical properties, the Franck–Condon vertical absorption energies between the ground and first excited states, as well as the second-order NLO responses, were calculated using time-dependent (TD) DFT at the SMD:M06-2X/6-311+G(d) level. More specifically, the investigated NLO responses are related to hyper-Rayleigh scattering (HRS) experiments, in which the intensity of the light at the second harmonic frequency, collected perpendicularly to the incident laser beam, is proportional to the square of the first hyperpolarizability of the molecular scatterers. Assuming a vertical polarization of the scattered light (parallel to the Z axis of the laboratory frame) and a non-polarized incident light (i.e. including both vertical and horizontal components along Z and X, respectively), the HRS hyperpolarizability reads:
| | 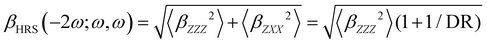 | (13) |
where the 〈
βZZZ2〉 and 〈
βZXX2〉 rotational averages can be written in terms of molecular
β tensor components as follows:
| |  | (14) |
| | 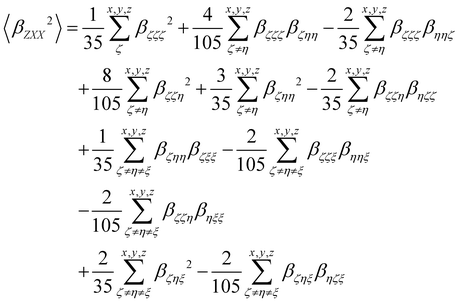 | (15) |
The depolarization ratio (DR in
eqn (13)) is defined as the ratio between these two components and provides information on the symmetry of the second harmonic scatterer. It ranges from 3/2 for pure octupolar compounds to 9 for pure dipolar ones. For strong push–pull π-conjugated molecules, the hyperpolarizability tensor is largely dominated by the diagonal component of the
β tensor oriented along the charge transfer axis (
βzzz); in this case, the NLO scatterers are said “one-dimensional” (1D) and the DR value is equal to 5.
βHRS and DR values were computed in the static limit (
ω → 0 in
eqn (13)), as well as in the dynamic regime using an incident wavelength of 1300 nm as used in the experiments.
21 All
β values reported hereafter are given in atomic units (1 a.u. of
β = 3.6310
−42 m
4 V
−1 = 3.2063 × 10
−53 C
3 m
3 J
−2 = 8.641 × 10
−33 esu) and assume a Taylor series expansion of the molecular induced dipoles with respect to the external electric fields, according to the T convention.
69
All the computed geometrical and optical reference molecular descriptors, obtained on the considered QM optimized conformers, are collected in Table 1.
Table 1 Reference geometrical and optical descriptors for open and closed forms of BA4 used for QMD-FF validation (torsional angles δ and ξ (degrees) and distances rHO–OA2, rHNR–OA2 and rOA1–NC (Å), see Fig. 2 for definitions), bond length alternation (BLA, Å) and bond order alternation (BOA) along the triene bridge, calculated at the SMD:M06-2X-D3/aug-cc-pVDZ level; vertical S0 → S1 absorption energy (ΔE01, eV), first hyperpolarizability (βHRS, a.u.) and depolarization ratio (DR) computed for an incident wavelength of 1300 nm and in the static limit at the SMD:M06-2X/6-311+G(d) level. For the open form, Boltzmann-averaged values calculated according the relative populations of the two conformers at room temperature are also reported
|
|
Open |
Closed |
| Conformer 1 |
Conformer 2 |
Averaged |
|
δ
RA
|
0 |
0 |
0 |
47 |
|
δ
RB
|
37 |
46 |
40 |
108 |
|
δ
C1
|
180 |
180 |
180 |
— |
|
δ
C2
|
180 |
180 |
180 |
— |
|
δ
C3
|
180 |
180 |
180 |
— |
|
δ
C4
|
179 |
179 |
179 |
— |
|
δ
N1
|
176 |
1 |
— |
142 |
|
δ
N2
|
70 |
80 |
73 |
170 |
|
ξ
|
180 |
180 |
180 |
— |
|
r
HO–OA2
|
1.575 |
1.575 |
1.575 |
— |
|
r
HNR–OA2
|
— |
— |
— |
1.832 |
|
r
OA1–NC
|
11.44 |
11.46 |
11.45 |
4.51 |
|
|
| BLA |
−0.001 |
−0.006 |
−0.003 |
— |
| BOA |
−0.017 |
−0.038 |
−0.024 |
— |
|
|
| ΔE01 |
2.53 |
2.54 |
2.53 |
3.63 |
|
β
HRS (1300 nm) |
4860 |
6133 |
5267 |
292 |
| DR (1300 nm) |
2.69 |
3.16 |
2.84 |
2.38 |
|
β
HRS (static) |
3669 |
4381 |
3897 |
344 |
| DR (static) |
2.52 |
2.81 |
2.61 |
2.29 |
3 Results
3.1 QMD-FF parameterization
3.1.1 Open form.
As detailed in Fig. 3a, the first step for the QMD-FF parameterization of the open form consisted in assigning specific atom types, taking into account the different (internal) chemical background experienced by each atom. Next, by looking at its chemical structure, it can be hypothesized that the open BA4 isomer is characterized by a certain degree of flexibility. Beside the trivial rotation of the methyl groups (δ1 and δ2) and the one around the C–OH bond (δOH, influenced by the intramolecular HB), possible dihedral distortions can also take place along the conjugated chain, i.e. δRA, δC1–δC4, δN1, and most likely, δRB and δN2. A summary of all possible flexible dihedrals is sketched in Fig. 3b.
The Joyce parameterization was initially carried out with varied choices concerning the flexible dihedrals and the model potential energy function (8) to the internal rHO⋯OA2 distance, which led to the refinement of three different sets of QMD-FF parameters, hereafter labeled as FF1, FF2, and FF3. Concretely, for all FFs, the stretching, bending and stiff dihedrals coordinates were described through the harmonic terms (5) and (6), whereas the flexible dihedrals δ2, δRA, δRB, δC2, δC3, δOH, δN1 and δN2 were instead modeled with the Fourier-like term (7). Note that in consideration of the high barriers and the rather unfavourable local minima found in QM scans required by the training data base, dihedrals δC1 and δC4 were treated as flexible torsions only in the first two QMD-FFs, while in FF3 they were considered as stiff torsions, and hence approximated through harmonic terms (see also Table 2).
Table 2 Summary of the different parameterization settings for the QMD-FFs of the DASA open form. All 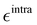 and σintra parameters are reported in kJ mol−1 and Å, respectively. Atom labeling refers to Fig. 3
and σintra parameters are reported in kJ mol−1 and Å, respectively. Atom labeling refers to Fig. 3
| QMD-FF |
E
tors(δC1) |
E
tors(δC4) |
LJ HO⋯OA2 |
LJ HC⋯HB |
LJ HCk⋯HBk |
|
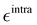
|
σ
intra
|
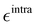
|
σ
intra
|
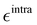
|
σ
intra
|
|
FF1
|
Cos |
Cos |
0.33209 |
1.750 |
0.125 |
2.46 |
— |
— |
|
FF2
|
Cos |
Cos |
15.000 |
1.410 |
0.125 |
2.46 |
0.125 |
2.46 |
|
FF3
|
Harm |
Harm |
15.000 |
1.410 |
0.125 |
2.46 |
0.125 |
2.46 |
Additionally, it is worth stressing that the rHO⋯OA2 distance between the hydroxyl proton HO and either one of the carboxyl oxygen atoms OA2 is involved in two different mechanisms, and hence pivotal to determine the BA4 open form conformations: (i) the internal HO⋯OA2 hydrogen bond, and (ii) the co-planarity of the C and A fragments, which in turn affects the delocalization of the electron cloud from the ring to the chain. For this reason, particular attention was paid to the LJ parameters entering eqn (8) for the HO/OA2 pair, and different sets of σintra and 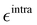 parameters were evaluated for each considered FF, as summarized in Table 2.
parameters were evaluated for each considered FF, as summarized in Table 2.
Once the LJ intramolecular parameters have been assigned, all the remaining QMD-FF parameters were determined with the Joyce code, by minimizing the standard objective function (9). All parameters are reported in Tables S2–S6 (ESI†).
3.1.2 Closed form.
A specific QMD-FF was also parameterized for the closed conformer, applying the Joyce protocol, but, as discussed in the following, with slight different settings with respect to the open form, due to the very different shape and flexibility exhibited by the two isomers.
In fact, as evident in Fig. 4, the formation of the five-membered ring (R) from the conjugated chain (C, in open DASA, see Fig. 3) implies a chemical change in the involved atoms, which leads to different atom types and to a significant reduction of the flexible dihedrals since, apart for δ1 and δ2, the only allowed internal rotations are those around the σ bonds connecting the four A, C, R and M fragments, as evidenced in Fig. 4b. Yet, despite the reduced number of torsional degrees of freedom, the QM relaxed torsional scans required to build the Joyce training data set revealed a significant complexity of the conformational space accessible to the DASA closed form. Such features are mainly caused by both the steric hindrance of the rotable groups (that may “hit” onto each other upon rotation) and by the delicate interplay settled among different kind of “through space” intramolecular interactions, as the π-stacking between the A and B rings, or the internal HB between HNR and OA2 atoms, in turn affected by possible rotations. To account for these features, the sole use of bonded valence term is clearly not sufficient, and the sum in the intramolecular non bonded energy term in eqn (8) has to be extended to a larger number of interacting pairs. Such procedure has been here performed specifically for the target molecule, manually selecting the most plausible interacting pairs, defining them through 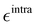 and σintra sets tuned to reproduce a particular interaction, e.g. OPLS47,48 parameters between heavy atoms of ring B and ring A for mimicking π–π stacking, or scaled parameters to simply account for steric repulsion. Such set of intramolecular LJ parameters, reported in detail in Tables S12 and S13 (ESI†), was fixed at the beginning of the Joyce parameterization, which was carried out on all the remaining harmonic and cosine force constants, according, as for the open form, to eqn (5)–(9). All parameters obtained for the closed form are reported in Tables S8–S13 (ESI†).
and σintra sets tuned to reproduce a particular interaction, e.g. OPLS47,48 parameters between heavy atoms of ring B and ring A for mimicking π–π stacking, or scaled parameters to simply account for steric repulsion. Such set of intramolecular LJ parameters, reported in detail in Tables S12 and S13 (ESI†), was fixed at the beginning of the Joyce parameterization, which was carried out on all the remaining harmonic and cosine force constants, according, as for the open form, to eqn (5)–(9). All parameters obtained for the closed form are reported in Tables S8–S13 (ESI†).
3.2 QMD-FF validation along the QM PES
To judge the performance of the different FFs, we have monitored some of the specific geometrical descriptors discussed in the previous sections. Firstly, FF1 presented an issue in preserving the intramolecular hydrogen bond during the conformational dynamics occuring in MD simulations. In fact, as appears by looking at Fig. S1 (ESI†), the average rHO–OA2 distance (>2 Å), registered in the MD runs carried out on the isolated molecules, deviates significantly from the QM reference values (1.575 Å, see also Table 1), hence suggesting that the intramolecular HB is not adequately described. To overcome this lack, the FF2 force field was designed by refining the intramolecular LJ parameters as summarized in Table 2. The resulting change in the distribution of rHO–OA2 from FF1 to FF2 can be monitored in Fig. S1 (ESI†). Notwithstanding the correct treatment of the intramolecular hydrogen bond obtained through the LJ refinement, some additional issues were found on the structures produced with FF2, revealed by both a structural analysis and preliminary calculations of the β responses. In fact, few snapshots revealed an anomalous twist of the backbone (see Fig. S3, ESI†), implying a distortion of the ξ dihedral, which in turn leads to a decrease of the molecular length (rOA1–NC, see Table 1) and eventually to critical overestimation of the computed first hyperpolarizability. To avoid such inconvenience, as previously mentioned, a third QMD-FF (FF3) was prepared, where δC1 and δC4 are considered as stiff torsions and hence described with harmonic potentials (see Table 2). As a consequence, a slight reduction in the standard deviation of both ξ and the molecular elongation has been observed and illustrated in Fig. S1 and S2 (ESI†). A final validation on the intramolecular terms of FF3 was carried out by computing selected linear and nonlinear optical properties along the trajectory in solution for the open form (Table S14, ESI†). The addition of the planarity constrains contributes to slightly reduce the standard deviation of the corresponding NLO response. The aforementioned observations have led us to the choice of FF3 as the best fit among the built FFs for the case of open DASA. In the following, we will therefore refer to FF3 for the discussion on the results obtained for the open form.
The parameterization of the FFs yielded standard deviations of the objective function (9) respectively of 0.8 and 1.9 kJ mol−1 for the open and closed isomers, and, as shown in Fig. 5, a good general agreement between the QM and QMD-FF optimized structures and vibrational modes. A more quantitative evaluation of the accuracy of the QMD-FF in reproducing the target QM data in a local harmonic approximation is given in Table 3, where the deviation between the two structures is reported in terms of internal coordinates. Excellent agreement is obtained for all coordinates in both cases, with the exception of the deviation found in the dihedrals (>10°) for the open form, which lies essentially in a misalignment of a CH3 rotation, hence negligible to our scopes.
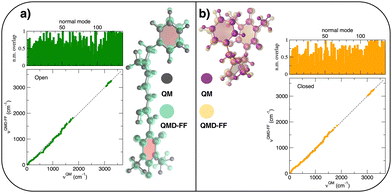 |
| | Fig. 5 (a) Open conformer: overlap between QM (gray solid spheres) and QMD-FF (transparent green spheres) optimized geometries (right) and comparison of QM and QMD-FF frequencies and normal mode overlap (left). (b) Closed conformer: overlap between QM (purple solid spheres) and QMD-FF (transparent orange spheres) optimized geometries (left) and comparison of QM and QMD-FF frequencies and normal mode overlap (right). | |
Table 3 RMSD between QM and QMD-FF optimized geometries in terms of bond lengths, bending angles, dihedrals and molecular normal modes (total) for the open and closed DASA isomers
| Conformer |
Bond lengths (Å) |
Bending angles (degr) |
Dihedrals (degr) |
Total (Å) |
| Open |
0.000 |
0.096 |
14.00 |
0.31 |
| Closed |
0.001 |
0.305 |
3.43 |
0.22 |
Besides well reproducing the optimized conformers and their oscillations around the respective equilibrium structures, to reliably sample the conformational space explored by MD, it is pivotal to accurately account for the flexibility of the target molecules. For these reason all the relaxed torsional scans were recomputed at QMD-FF level, and compared to the corresponding QM profiles in Fig. 6 and 7. All the QM torsional scans computed for the open isomer appear to be well reproduced by the FF3, with high accuracy obtained for both the most flat profiles (δ2, δRB and δN2) and the ones presenting higher barriers, as δRA, δC2, δC3 and δN1. Furthermore, the choice of representing δC1 and δC4 with harmonic potentials does not seem to introduce significant errors: the steepness of the repulsive branches around the minimum (180°) is in nice agreement with the one found at the QM level, whereas the QM barrier that should be crossed to populate the (high energy) local minima at 0° are located at energies well above 10kBT, excluding such possibility.
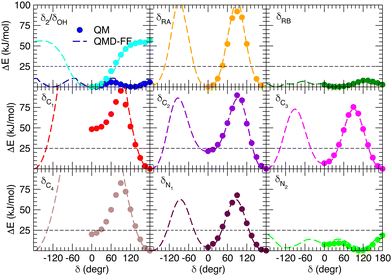 |
| | Fig. 6 Comparison of QM (full circles) and QMD-FF (FF3, dashed lines) relaxed torsional energy profiles for all the scanned dihedrals of the open isomer. In all panels, a dashed line is drawn to show 10kBT (25 kJ mol−1). | |
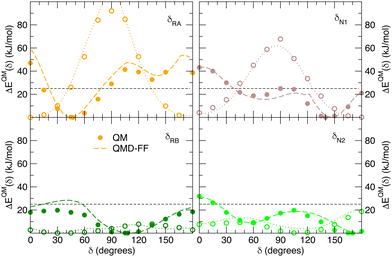 |
| | Fig. 7 Comparison of QM (full circles) and QMD-FF (dashed lines) relaxed torsional energy profiles for all the scanned dihedrals of the closed isomer. The results obtained for the same dihedrals in the open form is also drawn with empty circles (QM) and dotted lines (QMD-FF, FF3). In all panels, a dashed line is drawn to show 10kBT (25 kJ mol−1). | |
Fig. 7 displays the QMD-FF torsional profiles for the closed form, focusing on the four most important dihedrals by comparing them with both their QM counterparts and with the open form profiles of the same dihedrals. Notwithstanding a slightly worse agreement, due to the aforementioned complexity of the closed isomer PES, the QMD-FF appears to be capable to catch all minima and barriers of the reference QM data, and, most importantly, the completely different profiles resulting after the open-to-closed interconversion.
3.3 QMD-FF validation on geometrical properties
Choosing FF3 as the best option among the constructed FFs, we considered 1000 structural snapshots from MD trajectories carried out in chloroform solution, and investigated first the evolution of the geometrical and electronic parameters of both the open and closed forms of BA4. Considering the open isomer, preliminary MD runs were carried out to investigate the equilbrium between the two conformers shown in Fig. 2. To this end we chose to extend the simulation time to 50 ns, yet constraining all bonds through the LINCS algorithm70 and using an increased time step of 1 fs. Fig. 8 shows the time evolution of the δN1 dihedral along such MD runs, starting either from conformer 1 or 2, as well as the relative populations of the two conformers. At room temperature, this time range is not sufficient to observe interconversion between the two conformers. However, if the temperature is raised to 500 K, conformer 2 does indeed convert to conformer 1, which is slightly favored. This result demonstrates that FF3 is suitable for studying the conformational equilibrium in the open form of BA4, and that the interconversion barrier could be crossed with longer observation times. However, since conformer 2 is not populated along the 50 s MD run performed at room temperature, the geometrical and optical properties obtained using the MD + DFT approach are compared hereafter to DFT results calculated for conformer 1.
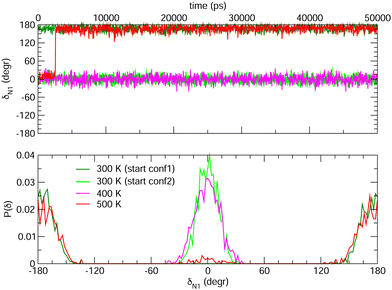 |
| | Fig. 8 Time evolution of the δN1 dihedral in the open form (top) and relative populations of conformers 1 and 2 (bottom) along MD trajectories of 50 ns at various temperatures. | |
As shown in Table 4, average values of geometrical parameters computed using the MD + DFT scheme are consistent with DFT calculations on the equilibrium geometry. However, large standard deviations are observed for dihedral angles, reflecting the high structural flexibility of the chromophore. In the open form, very broad statistical distributions are found for the δRB and δN2 torsional angles (Fig. S4, ESI†), as expected from the low rotational barriers shown Fig. 6. Similarly, BLA and BOA values computed using the DFT-optimized geometry (referred to as “rigid” calculations hereafter) are very close to average values issued from the sequential MD + QM approach, while structural fluctuations induce broad distributions in the values of these two parameters, which are expected to have significant impact on the NLO responses (see Fig. 9). We should also keep in mind that our classical MD sampling leads, for high frequency motions as those behind the fluctuations of the BLA, to narrower conformational distributions as compared to a fully quantum treatment.71 Therefore, we can expect such fluctuations to be even larger. This outcome could be achieved through methods that ensure a QM sampling, such as Path-Integral MD,72 or by adopting hybrid quantum-classical schemes,49 which allow treating the high frequency motions at QM level, while retaining the classical description for low frequency ones. For the purposes of the present investigation, though, the adopted fully classical sampling completely fulfills our needs in an efficient way.
Table 4 Geometric and electronic parameters computed at the SMD:M06-2X-D3/aug-cc-pVDZ level for the open and closed form, using their equilibrium geometry (conformer 1 for the open form), and using the MD + DFT scheme. All angles are in degrees, all distances in Å
|
|
Open |
Closed |
| DFT |
MD + DFT |
DFT |
MD + DFT |
|
δ
RA
|
0 |
1 ± 10 |
47 |
40 ± 6 |
|
δ
RB
|
37 |
80 ± 54 |
108 |
116 ± 13 |
|
δ
C1
|
180 |
180 ± 9 |
— |
— |
|
δ
C2
|
180 |
180 ± 11 |
— |
— |
|
δ
C3
|
180 |
180 ± 10 |
— |
— |
|
δ
C4
|
179 |
180 ± 9 |
— |
— |
|
δ
N1
|
176 |
179 ± 14 |
142 |
133 ± 62 |
|
δ
N2
|
70 |
82 ± 24 |
170 |
55 ± 65 |
|
ξ
|
180 |
180 ± 19 |
— |
— |
|
r
HO–OA2
|
1.575 |
1.675 ± 0.168 |
— |
— |
|
r
HNR–OA2
|
— |
— |
1.832 |
1.933 ± 0.389 |
| BLA |
−0.001 |
−0.001 ± 0.025 |
— |
— |
| BOA |
−0.017 |
−0.005 ± 0.066 |
— |
— |
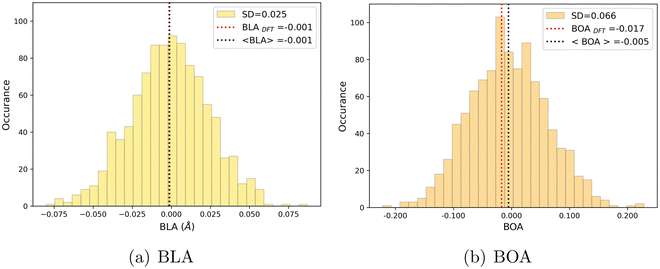 |
| | Fig. 9 Statistical distribution of BLA (a) and BOA (b) values, calculated using the MD + DFT scheme at the SMD:M06-2X-D3/aug-cc-pVDZ level. Vertical dotted lines show the average value, and the value computed at the DFT level using the equilibrium geometry (conformer 1) of the chromophore. | |
We can also note that BLA and BOA, which both measure the extent of the π-conjugation in the open form, show an expected inverse correlation, as illustrated in Fig. S5 (ESI†). In our simulations, we did not find any direct correlation between the bond length/order alternation and any of the torsional parameters if taken individually (see Fig. S6, ESI†). The fact that BOA is directly correlated to BLA but not to the dihedrals may be attributed to the complete lack of conjugation effects in our FF. Such effects could be incorporated through explicit coupling terms,37 also implemented in Joyce, but at the price of a much more complex parameterization procedure.
As found for the open form, the rotational motions associated with the terminal phenyl ring in the closed form have also low energy constraints (see Fig. 7), leading to broad distributions of the δRB and δN2 angles. Compared to the open isomer, the distribution of δRB is less spread, due to the proximity of the rings RA and RB, which develop larger non-covalent van der Waals interactions that reduce the rotational flexibility of the RB fragment. Reversely, the δN2 distribution is more spread in the closed form than in the open form, which comes from the greater ease of rotation around a sp3-hybridized nitrogen compared to a sp2-hybridized one, for which the rotation breaks the π-conjugation. We also note the larger average length of the hydrogen bond (compare rHO–OA2 to rHNR–OA2 in Table 4), consistently associated with a larger standard deviation.
4 Discussion
4.1 Dynamic behavior and nonlinear optical properties
We monitor in this section the fluctuations of the optical properties of the open and closed forms along the MD runs, focusing on transition energies from the ground to the lowest-energy bright excited states as well as on HRS responses at 1300 nm. The data computed at the DFT and MD + DFT levels are collected in Table 5. Note that for the open form, three structural snapshots were considered as outliers and excluded from the statistics, as they provide very low ΔE01 values (<2.0 eV) and massive NLO signal (>105 a.u.) due to frequency dispersion effects. For consistency, these outliers were removed from all statistics on the open form.
Table 5 Linear and nonlinear optical properties computed at the SMD:M06-2X/6-311+G(d) level for the open and closed forms, using their equilibrium geometry (conformer 1 for the open form), and using the MD + DFT scheme. Transition energy (ΔE01) and hyperpolarizability (β) values are in eV and a.u., respectively
|
|
Open |
Closed |
| DFT |
MD + DFT |
DFT |
MD + DFT |
| ΔE01 |
2.53 |
2.46 ± 0.10 |
3.63 |
3.62 ± 0.14 |
| ΔE02 |
— |
— |
4.17 |
4.07 ± 0.16 |
|
β
HRS (1300 nm) |
4860 |
10969 ± 5999 |
292 |
343 ± 41 |
| DR (1300 nm) |
2.69 |
3.69 ± 0.77 |
2.38 |
2.21 ± 0.26 |
|
β
HRS (static) |
3669 |
5525 ± 2169 |
335 |
369 ± 36 |
| DR (static) |
2.52 |
3.35 ± 0.74 |
2.03 |
2.15 ± 0.22 |
The MD + DFT probability distributions of vertical transition energies (related to the S0 → S1 transition for the open form and to the S0 → S1 and S0 → S2 transitions for the closed form) are plotted in Fig. 10 against the absorption spectra simulated at the DFT level and the experimental spectrum for the open conformer. For the closed form, the average ΔE01 value calculated with the MD + DFT approach coincides with the maximal absorption energy calculated using DFT, while geometrical fluctuations induce a redshift of 0.1 eV of the S0 → S2 transition. Similarly, the S0 → S1 transition energy calculated for the open form using MD + DFT is 0.07 eV lower than that predicted using the S0 equilibrium geometry of the chromophore. However, it is still significantly overestimated compared to experiments (2.46 eV vs. 2.18 eV as reported in ref. 21). This discrepancy can be mainly attributed to the inherent limitations of the DFT approximation, but also, to a lesser extent originates from the fact that vertical transitions provided by TD-DFT calculations are not strictly comparable to experimental maximal absorption energies. In addition, although the MD configurations sample (albeit classically) the different vibrational degrees of freedom, the MD + DFT approach fails in reproducing the band shape asymmetry observed experimentally, which broadens in the high-energy region (Fig. S7, ESI†). Similar discrepancy of the sequential MD + DFT approach was previously reported for another DASA derivative,73 suggesting that this failure is intrinsic to the computational approach irrespective of the force field used in the MD simulations, and that more robust comparisons with experiments require the calculation of vibrationally resolved spectra using full QM approaches, as reported in ref. 74.
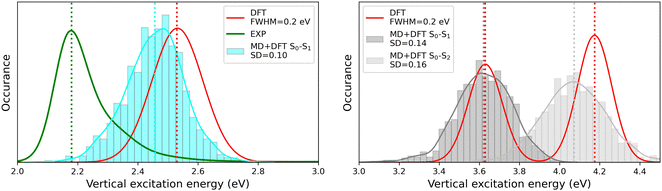 |
| | Fig. 10 Statistical distribution of the vertical S0 → S1 transition energies of the open (left) and closed (right) forms, calculated using the MD + DFT scheme at the SMD:M06-2X/6-311+G(d) level. Vertical dotted lines indicate either average values, values computed at the DFT level using the equilibrium geometry of the chromophore (conformer 1 in the case of the open form), or experimental absorption maxima.21 SD = standard deviation. | |
As illustrated in Fig. 11, geometrical fluctuations also largely affect the NLO properties, giving rise to broad distributions of βHRS and DR values. The βHRS distribution of the more flexible open form is much broader than that of the closed form as reflected in their standard deviation, which represents about 12% of the average value for the closed form and reaches 55% for the open form. Taking dynamic fluctuations into account for the open form also induces a dramatic increase (+125%) in βHRS compared to rigid DFT calculations, whereas a much smaller increase of 17% is observed for the closed form. Accordingly, the NLO contrast upon photo-isomerization, defined as η = βopenHRS/βclosedHRS, also increases when accounting for structural dynamics: η = 32 from the MD + DFT approach versus η = 17 from rigid DFT calculations. It is also important to note that the βHRS value calculated using MD + DFT is in better agreement with experimental measurements (βHRS = 8600 ± 390 a.u.). However, it is 27% overestimated, which may be attributed to an overly simple treatment of solvent effects, as interactions between the chromophore and chloroform molecules are not explicitly taken into account by the continuum solvation model.
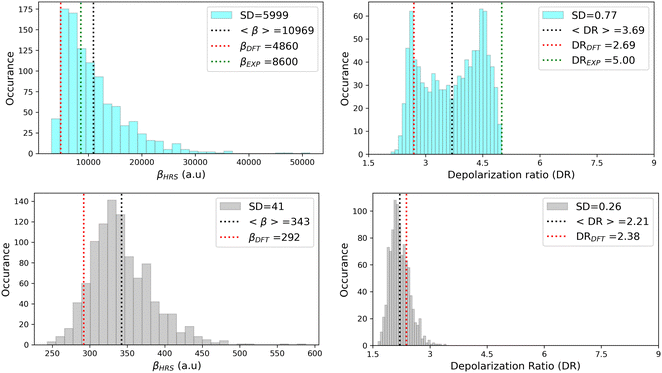 |
| | Fig. 11 Statistical distribution of the dynamic (1300 nm) HRS first hyperpolarizability and depolarization ratio of the open (top) and closed (bottom) forms, calculated using the MD + DFT scheme at the SMD:M06-2X/6-311+G(d) level. Vertical dotted lines indicate either average values, values computed at the DFT level using the equilibrium geometry of the chromophore (conformer 1 in the case of the open form), or experimental values.21 SD = standard deviation. | |
The depolarization ratios of both DASA isomers are also spread over a broad range of values, again with a larger standard deviation in the case of the more flexible open form. The MD + DFT scheme provides a DR value larger than that issued from rigid DFT calculations and in closer agreement with experiments (DR = 5.00 ± 0.3), despite it remains significantly underestimated.
Finally, additional MD simulations were performed for the open form starting from conformer 2. The resulting distributions of the NLO responses have the same profiles as obtained from the MD sampling starting from conformer 1, leading to very similar average βHRS and DR values (Fig. S8 and Table S15, ESI†). Moreover, estimating the NLO response using rigid DFT calculations by weighting the responses of conformers 1 and 2 by their relative Maxwell–Boltzmann populations (Table S15, ESI†) still provides largely underestimated βHRS values compared to experiments, showing that dynamic effects must be taken into account to obtain reliable estimates of the NLO responses in these systems.
4.2 Structure/NLO properties relationships in the open form
Although NLO responses of the open form are highly sensitive to geometrical fluctuations, βHRS values do not show direct correlation with any of the individual torsional parameters (Fig. S9, ESI†). However, as illustrated in Fig. 12, βHRS and DR values display a clear dependence on BOA and both present a minimum for BOA = 0, corresponding to the so-called cyanine limit for which the π-electron conjugation between the donor and acceptor parts is maximal. Note that, although BOA and BLA are inversely correlated (Fig. S5, ESI†), the correlation between the NLO responses and BLA is much less clear (Fig. S10, ESI†), indicating that the fluctuations of βHRS and DR are better described using an electronic metric rather a structural metric of the π-conjugation.
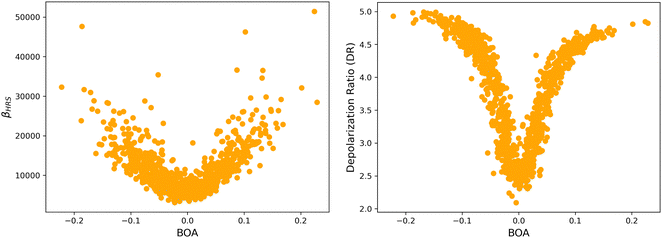 |
| | Fig. 12 Distribution of βHRS (left) and DR (right) values as a function of the bond order alternation (BOA) for the open form. | |
The changes in the magnitude of the HRS hyperpolarizability with respect to the BOA fluctuations can be further rationalized using the two-state approximation (TSA).75 This approximation is based on the perturbative sum-over-state expansion of the second-order NLO response and assumes that the only non-negligible contribution arises from the first dipole-allowed electronic excited state (S1), leading to a very simple expression of the dynamic HRS hyperpolarizability in terms of spectroscopic quantities. Limiting the β tensor to its single diagonal βzzz component, with z the charge-transfer axis of the molecule, it yields:
| | 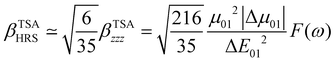 | (16) |
where Δ
E01 is the S
0 → S
1 excitation energy,
μ01 is the associated
z-component of the transition dipole, and
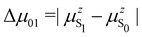
is the change in the permanent dipole moment between the two electronic states.
F(
ω) is a factor accounting for frequency dispersion, which depends on the energy of the incident photons (
ħω = 0.95 eV for a 1300 nm wavelength):
| | 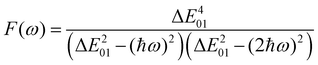 | (17) |
The suitability of the TSA for describing the effect of structural fluctuations on the molecular first hyperpolarizability is demonstrated in Fig. S11 (ESI†), which shows a good linear correlation between the βHRS values calculated at the TDDFT level and those estimated using eqn 16 in both the static and the dynamic regimes. Moreover, the frequency dispersion factor estimated using eqn 17 provides a good estimate of the resonance effects in the range of ΔE01 values spanned by the dynamics (Fig. S11, ESI†). Although neither ΔE01 nor μ01 correlate with BOA (Fig. S12, ESI†), Fig. 13a clearly shows that Δμ01 linearly decreases with BOA, and is equal to zero when BOA = 0. We can therefore conclude that the variations of βHRS shown in Fig. 12 are mainly driven by the variations of Δμ01, as further illustrated in Fig. 13b.
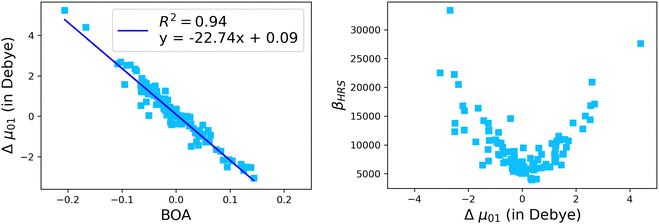 |
| | Fig. 13 Evolution of Δμ01 of the open form as a function of the BOA (left), and evolution of βHRS of the open form as a function of Δμ01. The calculations have been performed for 100 structural snapshots taken every 10 picoseconds of the MD trajectory. | |
In turn, the variation of Δμ01 with respect to BOA can be rationalized by means of the valence bond-charge transfer (VB-CT) model,76–79 which assumes that the (orthogonal) wavefunctions of the electronic ground and excited states, |ψS0〉 and |ψS1〉, can be expressed as linear combinations of two VB resonance structures, namely a weakly polar |DA〉 form and a highly polar zwitterionic form |D+A−〉 corresponding to the transfer of one electron from the amine donor (D) to the barbituric acceptor (A):
| | 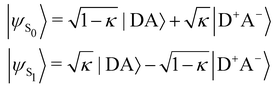 | (18) |
where
κ ranges between 0 and 1 and measures the π-electron charge transfer between the D and A units in the ground state. By definition, the cyanine limit (BOA = 0) is associated to a value of
κ equal to 1/2, which corresponds to equal weights for the |DA〉 and |D
+A
−〉 forms in both electronic states. According to the VB-CT model and assuming no dipolar coupling between the |DA〉 and |D
+A
−〉 forms (〈DA|
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif)
|D
+A
−〉 = 0), the dipole moment variation upon the S
0 → S
1 transition can be written as:
| | | Δμ01 = (2κ − 1)μDA + (1 − 2κ)μD+A− | (19) |
where
μDA and
μD+A− are the dipole moments of the |DA〉 and |D
+A
−〉 forms, respectively. Therefore, Δ
μ01 = 0 if
κ = 1/2,
i.e. if BOA = 0, as it is observed in
Fig. 13a. The contribution of the excited state participating the most to the NLO response is thus cancelled out in the cyanine limit, which explains the minimum reached by the
βHRS values in
Fig. 12a, and the reason why taking geometric fluctuations into account increases the magnitude of the second-order NLO response compared with rigid DFT calculations, which only consider a single cyanine-type conformer.
The evolution of the depolarization ratio DR with respect to the BOA shown in Fig. 12b can also be simply rationalized, considering a few simplifications. First, let's assume that, in addition to SHG (degenerated sum-frequency generation), Kleinman's permutation rules apply, so that βijk = βikj = βjik = βjki = βkij = βkji for any component of the molecular β tensor. Note that Kleinman's conditions require to be far from any resonance between the absorption bands of the chromophore and the second harmonic light at 650 nm (∼1.9 eV), which is a reasonable approximation according to the absorption spectrum shown in Fig. 10a. Second, let's assume that the chromophore possesses a pseudo-planar C2v symmetry, as it was considered in number of previous studies for push–pull systems.80–83 With z the axis parallel to the C2 (charge transfer) axis and x the transverse direction within the molecular plane, one has: (βxxx = βxyy = βxzz = βxyz = βyxx = βyyy = βyzz = 0, βzzz ≠ 0, and βzxx ≠ 0). Furthermore, we assume that βzyy = 0, as this tensor component is expected to be small with respect to βzzz and βzxx. In that case, the depolarization ratio can be simply expressed as a function of the ratio R = βzxx/βzzz between the only two non-zero β components:
| | 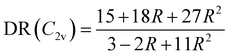 | (20) |
According to
eqn (20), DR converges towards the value of 27/11 ≃ 2.45 when
R → ∞,
i.e. when
βzzz (and thus
βHRS) tends to zero. This value of ≃2.45 corresponds to the minimum reached by the DR values when BOA = 0 in
Fig. 12, and is close to the DR value of 2.69 calculated for the equilibrium geometry of the chromophore (
Table 5). Reversely,
R = 0 corresponds to DR = 5, which is typical of “1D” push–pull chromophores in which the
βzzz component dominates the
β tensor. One can see in
Fig. 12b that this situation corresponds to the largest absolute values of BOA, and therefore that dynamic fluctuations enhance the 1D NLO character of the chromophore.
The validity of the above considerations for the open form of BA4 is demonstrated in Fig. 14a, which illustrates the evolution with BOA of absolute R values calculated without assuming Kleinman or full C2v symmetry (see ESI,† for details on the calculation of R). One can indeed observe that |R| diverges when BOA equals 0, whereas it vanishes for large absolute BOA values. Fig. 14b further shows that the evolution of DR with respect to R qualitatively follows the ideal Kleinman-C2v behavior, although computed DR values are limited in the 2.1–5.0 range, whereas they show a greater amplitude (from 1.5 to 6.75) for pure C2v systems.
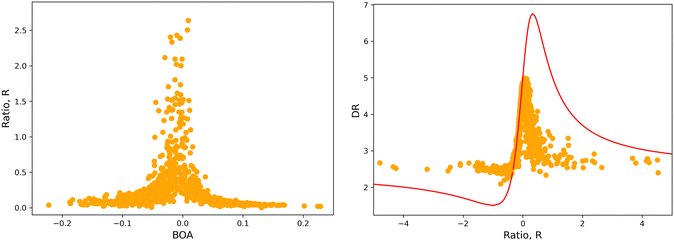 |
| | Fig. 14 (left) Evolution of |R| as a function of BOA (truncated to |R| < 3); (right) evolution of DR with respect to R in the case of an ideal Kleinman C2v symmetry (eqn (20), red line) and using computed values (orange dots). | |
5 Conclusion
In this work, we carried out classical MD simulations on both the open and closed isomers of a DASA derivative in chloroform solution, by using specific force fields derived by means of the Joyce protocol. Subsequent DFT calculations performed on structural snapshots extracted from the MD trajectories enabled us to demonstrate the significant impact of geometric fluctuations on the second-order NLO responses associated with hyper-Rayleigh scattering experiments. In particular, taking structural dynamics into account considerably increases the first hyperpolarizability of the NLO-active open form compared with DFT calculations performed on Maxwell–Boltzmann-weighted sets of conformers, and provides an average βHRS value in better agreement with experimental data. However, the depolarization ratio predicted by the MD + DFT scheme remains significantly underestimated with respect to experiments, a discrepancy that may be attributed to the use of a continuum solvation model to describe solute–solvent interactions. Further work implying calculations of the NLO properties of the DASA chromophore surrounded by explicit chloroform molecules is in progress.
MD + DFT calculations also revealed that the large enhancement of βHRS induced by the dynamic fluctuations in the open isomer are correlated with the changes in the bond order alternation along the π-conjugated bridge linking the amine donor and the barbituric acid acceptor. Structural distortions take the molecule out of its cyanine-type equilibrium geometry, moving the bond order alternation away from its zero value and increasing the second-order NLO response. An interesting correlation was also found between the bond order alternation and the depolarization ratio, which could be qualitatively rationalized by using simple symmetry assumptions.
At last, this work demonstrates the reliability of the sequential application of classical MD and DFT calculations for the accurate prediction of the NLO responses of conjugated organic molecular systems in dilute solution. In addition, this computational strategy enables us to better understand the important role of dynamic fluctuations and the interaction between electron conjugation within the molecule and its NLO properties.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank Dr Eduard Matito for kindly providing us the ESI-3D code for computing the bond orders. A. D. and F. C. thank Prof. Benoît Champagne for helpful discussions. C. N. acknowledges the DIPC for his postdoctoral PhD grant. This work was supported by the French National Research Agency (grant number ANR-20-CE29-0009-01) and by the Transnational Common Laboratory QuantumChemPhys (Theoretical Chemistry and Physics at the Quantum Scale, grant number ANR-10-IDEX-03-02) established between the Université de Bordeaux (UB), Euskal Herriko Unibertsitatea (UPV/EHU) and the Donostia International Physics Center (DIPC). Calculations were performed using the computing facilities provided by the Mésocentre de Calcul Intensif Aquitain (MCIA) of UB and of the Université de Pau et des Pays de lAdour. J. C. thanks the Ministerio de Universidades, Plan de Recuperación, Transformación y Resiliencia and UAM for funding the research stay in Pisa with a requalification program (CA2/RSUE/2021-00890). G. P. thanks the financial support from ICSC – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU – PNRR, Missione 4 Componente 2 Investimento 1.4.
References
- S. Helmy, F. A. Leibfarth, S. Oh, J. E. Poelma, C. J. Hawker and J. R. De Alaniz, Photoswitching using visible light: a new class of organic photochromic molecules, J. Am. Chem. Soc., 2014, 136, 8169–8172 Search PubMed.
- S. Helmy, S. Oh, F. A. Leibfarth, C. J. Hawker and J. Read de Alaniz, Design and Synthesis of Donor–Acceptor Stenhouse Adducts: A Visible Light Photoswitch Derived from Furfural, J. Org. Chem., 2014, 79, 11316–11329 Search PubMed.
- J. R. Hemmer, S. O. Poelma, N. Treat, Z. A. Page, N. D. Dolinski, Y. J. Diaz, W. Tomlinson, K. D. Clark, J. P. Hooper, C. Hawker and J. Read De Alaniz, Tunable Visible and Near Infrared Photoswitches, J. Am. Chem. Soc., 2016, 138, 13960–13966 Search PubMed.
- M. M. Lerch, S. J. Wezenberg, W. Szymanski and B. L. Feringa, Unraveling the Photoswitching Mechanism in Donor-Acceptor Stenhouse Adducts, J. Am. Chem. Soc., 2016, 138, 6344–6347 Search PubMed.
- N. Mallo, P. T. Brown, H. Iranmanesh, T. S. C. MacDonald, M. J. Teusner, J. B. Harper, G. E. Ball and J. E. Beves, Photochromic switching behaviour of donoracceptor Stenhouse adducts in organic solvents, Chem. Commun., 2016, 52, 13576–13579 Search PubMed.
- M. D. Donato, M. M. Lerch, A. Lapini, A. D. Laurent, A. Iagatti, L. Bussotti, S. P. Ihrig, M. Medved, D. Jacquemin, W. Szymański, W. J. Buma, P. Foggi and B. L. Feringa, Shedding Light on the Photoisomerization Pathway of Donor–Acceptor Stenhouse Adducts, J. Am. Chem. Soc., 2017, 139, 15596–15599 Search PubMed.
- M. M. Lerch, W. Szymański and B. L. Feringa, The (photo)chemistry of Stenhouse photoswitches: guiding principles and system design, Chem. Soc. Rev., 2018, 47, 1910–1937 Search PubMed.
- M. M. Lerch, M. Di Donato, A. D. Laurent, M. Medved’, A. Iagatti, L. Bussotti, A. Lapini, W. J. Buma, P. Foggi, W. Szymański and B. L. Feringa, Solvent Effects on the Actinic Step of Donor–Acceptor Stenhouse Adduct Photoswitching, Angew. Chem., Int. Ed., 2018, 57, 8063–8068 Search PubMed.
- R. F. A. Gomes, J. A. S. Coelho and C. A. M. Afonso, Synthesis and Applications of Stenhouse Salts and Derivatives, Chem. – Eur. J., 2018, 24, 9170–9186 Search PubMed.
- J. R. Hemmer, Z. A. Page, K. D. Clark, F. Stricker, N. D. Dolinski, C. J. Hawker and J. Read De Alaniz, Controlling Dark Equilibria and Enhancing Donor-Acceptor Stenhouse Adduct Photoswitching Properties through Carbon Acid Design, J. Am. Chem. Soc., 2018, 140, 10425–10429 Search PubMed.
- C. García-Iriepa, M. Marazzi and D. Sampedro, From Light Absorption to Cyclization: Structure and Solvent Effects in Donor-Acceptor Stenhouse Adducts, ChemPhotoChem, 2019, 3, 866–873 Search PubMed.
- H. Zulfikri, M. A. J. Koenis, M. M. Lerch, M. D. Donato, W. Szymański, C. Filippi, B. L. Feringa and W. J. Buma, Taming the complexity of donor-acceptor stenhouse adducts: Infrared motion pictures of the complete switching pathway, J. Am. Chem. Soc., 2019, 141, 7376–7384 Search PubMed.
- M. Ugandi and M. Roemelt, An Ab Initio Computational Study of Electronic and Structural Factors in the Isomerization of Donor-Acceptor Stenhouse Adducts, J. Phys. Chem. A, 2020, 124, 7756–7767 Search PubMed.
- D. M. Sanchez, U. Raucci, K. N. Ferreras and T. J. Martínez, Putting Photomechanical Switches to Work: An Ab Initio Multiple Spawning Study of Donor-Acceptor Stenhouse Adducts, J. Phys. Chem. Lett., 2020, 11, 7901–7907 Search PubMed.
- C. Xiong, G. Xue, L. Mao, L. Gu, C. He, Y. Zheng and D. Wang, Carbon Spacer Strategy: Control the Photoswitching Behavior of Donor-Acceptor Stenhouse Adducts, Langmuir, 2021, 37, 802–809 Search PubMed.
- S. W. Connolly, R. Tiwari, S. J. Holder and H. J. Shepherd, A simple strategy to overcome concentration dependence of photoswitching properties in donor-acceptor Stenhouse adducts, Phys. Chem. Chem. Phys., 2021, 23, 2775–2779 Search PubMed.
- S. O. Poelma, S. S. Oh, S. Helmy, A. S. Knight, G. L. Burnett, H. T. Soh, C. J. Hawker and J. Read de Alaniz, Controlled drug release to cancer cells from modular one-photon visible light-responsive micellar system, Chem. Commun., 2016, 52, 10525–10528 Search PubMed.
- M. Clerc, S. Sandlass, O. Rifaie-Graham, J. A. Peterson, N. Bruns, J. Read de Alaniz and L. F. Boesel, Visible light-responsive materials: the (photo)chemistry and applications of donor–acceptor Stenhouse adducts in polymer science, Chem. Soc. Rev., 2023, 52, 8245–8294 Search PubMed.
- C. Tonnelé, B. Champagne, L. Muccioli and F. Castet, Second-order nonlinear optical properties of Stenhouse photoswitches: insights from density functional theory, Phys. Chem. Chem. Phys., 2018, 20, 27658–27667 Search PubMed.
- Y. Yao, H.-L. Xu and Z.-M. Su, Switching of second-order nonlinear response effected by different acceptors: The impacts of environment and frequency dispersion, Dyes Pigm., 2021, 193,
109502 Search PubMed.
- S. Dubuis, A. Dellai, C. Courdurié, J. Owona, A. Kalafatis, L. Vellutini, E. Genin, V. Rodriguez and F. Castet, Nonlinear Optical Responses of Photoswitchable Donor–Acceptor Stenhouse Adducts, J. Am. Chem. Soc., 2023, 145, 10861–10871 Search PubMed.
- F. Castet, C. Tonnelé, L. Muccioli and B. Champagne, Predicting the Second-Order Nonlinear Optical Responses of Organic Materials: the Role of Dynamics, Acc. Chem. Res., 2022, 55, 3716–3726 Search PubMed.
-
K. Coutinho and S. Canuto, Solvent Effects from a Sequential Monte Carlo – Quantum Mechanical Approach, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, J. R. Sabin, M. C. Zerner, J. Karwowski and M. Karelson, Academic Press, 1997, vol. 28, pp. 89–105 Search PubMed.
- R. C. Barreto, K. Coutinho, H. C. Georg and S. Canuto, Combined Monte Carlo and quantum mechanics study of the solvatochromism of phenol in water. The origin of the blue shift of the lowest π–π* transition, Phys. Chem. Chem. Phys., 2009, 11, 1388–1396 Search PubMed.
- N. De Mitri, S. Monti, G. Prampolini and V. Barone, Absorption and Emission Spectra of a Flexible Dye in Solution: A Computational Time-Dependent Approach, J. Chem. Theory Comput., 2013, 9, 4507–4516 Search PubMed.
- I. Cacelli, A. Ferretti and G. Prampolini, Perturbative multireference configuration interaction (CI-MRPT2) calculations in a focused dynamical approach: A computational study of solvatochromism in pyrimidine, J. Phys. Chem. A, 2015, 119, 5250–5259 Search PubMed.
- J. Quertinmont, B. Champagne, F. Castet and M. Hidalgo Cardenuto, Explicit versus Implicit Solvation Effects on the First Hyperpolarizability of an Organic Biphotochrome, J. Phys. Chem. A, 2015, 119, 5496–5503 Search PubMed.
- K. Pielak, C. Tonnelé, L. Sanguinet, E. Cariati, S. Righetto, L. Muccioli, F. Castet and B. Champagne, Dynamical Behavior and Second Harmonic Generation Responses in Acido-Triggered Molecular Switches, J. Phys. Chem. C, 2018, 122, 26160–26168 Search PubMed.
- T. Giovannini, M. Ambrosetti and C. Cappelli, A polarizable embedding approach to second harmonic generation (SHG) of molecular systems in aqueous solutions, Theor. Chem. Acc., 2018, 137, 74 Search PubMed.
- T. N. Ramos, S. Canuto and B. Champagne, Unraveling the Electric Field-Induced Second Harmonic Generation Responses of Stilbazolium Ion Pairs Complexes in Solution Using a Multiscale Simulation Method, J. Chem. Inf. Model., 2020, 60, 4817–4826 Search PubMed.
- J. Seibert, B. Champagne, S. Grimme and M. de Wergifosse, Dynamic Structural Effects on the Second-Harmonic Generation of Tryptophane-Rich Peptides and Gramicidin A, J. Phys. Chem. B, 2020, 124, 2568–2578 Search PubMed.
- T. Hrivnák, H. Reis, P. Neogrády, R. Zaleśny and M. Medved’, Accurate Nonlinear Optical Properties of Solvated para-Nitroaniline Predicted by an Electrostatic Discrete Local Field Approach, J. Phys. Chem. B, 2020, 124, 10195–10209 Search PubMed.
- T. N. Ramos, F. Castet and B. Champagne, Second Harmonic Generation Responses of Ion Pairs Forming Dimeric Aggregates, J. Phys. Chem. B, 2021, 125, 3386–3397 Search PubMed.
- C. Naim, R. Vangheluwe, I. Ledoux-Rak, B. Champagne, C. Tonnelé, M. BlanchardDesce, E. Matito and F. Castet, Electric-field induced second harmonic generation responses of push–pull polyenic dyes: experimental and theoretical characterizations, Phys. Chem. Chem. Phys., 2023, 25, 13978–13988 Search PubMed.
- C. Bouquiaux, P. Beaujean, T. N. Ramos, F. Castet, V. Rodriguez and B. Champagne, First hyperpolarizability of the di-8-ANEPPS and DR1 nonlinear optical chromophores in solution. An experimental and multi-scale theoretical chemistry study, J. Chem. Phys., 2023, 159,
174307 Search PubMed.
- I. Cacelli and G. Prampolini, Parametrization and Validation of Intramolecular Force Fields Derived from DFT Calculations, J. Chem. Theory Comput., 2007, 3, 1803–1817 Search PubMed.
- J. Cerezo, G. Prampolini and I. Cacelli, Developing accurate intramolecular force fields for conjugated systems through explicit coupling terms, Theor. Chem. Acc., 2018, 137, 80 Search PubMed.
- G. Prampolini, L. G. D. Silveira, J. G. Vilhena and P. R. Livotto, Predicting Spontaneous Orientational Self-Assembly: In Silico Design of Materials with Quantum Mechanically Derived Force Fields, J. Phys. Chem. Lett., 2022, 13, 243–250 Search PubMed.
- N. Mallo, E. D. Foley, H. Iranmanesh, A. D. Kennedy, E. T. Luis, J. Ho, J. B. Harper and J. E. Beves, Structure-function relationships of donor-acceptor Stenhouse adduct photochromic switches, Chem. Sci., 2018, 9, 8242–8252 Search PubMed.
-
M. J. Frisch, et al., Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132,
154104 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 Search PubMed.
- I. Cacelli, A. Cimoli, P. R. Livotto and G. Prampolini, An Automated Approach for the Parameterization of Accurate Intermolecular Force-Fields: Pyridine as a Case Study, J. Chem. Theory Comput., 2012, 33, 1055 Search PubMed.
- G. Prampolini, P. R. Livotto and I. Cacelli, Accuracy of Quantum Mechanically Derived Force-Fields Parameterized from Dispersion-Corrected DFT Data: The Benzene Dimer as a Prototype for Aromatic Interactions, J. Chem. Theory Comput., 2015, 11, 5182–5196 Search PubMed.
- G. Prampolini, F. Ingrosso, J. Cerezo, A. Iagatti, P. Foggi and M. Pastore, Shortand Long-Range Solvation Effects on the Transient UV–Vis Absorption Spectra of a Ru(II)–Polypyridine Complex Disentangled by Nonequilibrium Molecular Dynamics, J. Phys. Chem. Lett., 2019, 10, 2885–2891 Search PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 Search PubMed.
- W. L. Jorgensen and J. Tirado-Rives, Potential Energy Functions for Atomic-Level Simulations of Water and Organic and Biomolecular Systems, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 Search PubMed.
- J. Cerezo, D. Aranda, F. J. Avila Ferrer, G. Prampolini and F. Santoro, AdiabaticMolecular Dynamics Generalized Vertical Hessian Approach: A Mixed Quantum Classical Method to Compute Electronic Spectra of Flexible Molecules in the Condensed Phase, J. Chem. Theory Comput., 2020, 16, 1215–1231 Search PubMed.
-
I. Cacelli, J. Cerezo, N. De Mitri and G. Prampolini, Joyce2.10, a Fortran 77 code for intra-molecular force field parameterization, available free of charge at https://www.iccom.cnr.it/en/joyce-2/, last consulted May 2022. 2019.
- R. Pawlak, J. G. Vilhena, P. D’Astolfo, X. Liu, G. Prampolini, T. Meier, T. Glatzel, J. A. Lemkul, R. Häner, S. Decurtins, A. Baratoff, R. Pérez, S.-X. Liu and E. Meyer, Sequential Bending and Twisting around C–C Single Bonds by Mechanical Lifting of a Pre-Adsorbed Polymer, Nano Lett., 2020, 20, 652–657 Search PubMed.
- A. Segalina, J. Cerezo, G. Prampolini, F. Santoro and M. Pastore, Accounting for Vibronic Features through a Mixed Quantum-Classical Scheme: Structure, Dynamics, and Absorption Spectra of a Perylene Diimide Dye in Solution, J. Chem. Theory Comput., 2020, 16, 7061–7077 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 Search PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126,
014101 Search PubMed.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 Search PubMed.
-
R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
-
T. A. Keith, AIMAll (Version 14.11.23), TK Gristmill Software, Overland Park KS, USA, 2014.(aim.tkgristmill.com) Search PubMed.
-
E. Matito, ESI-3D: Electron Sharing Indices Program for Molecular Space Partitioning. 2023; nstitute of Computational chemistry and Catalysis (IQCC), University of Girona, Catalonia, Spain (2006–2015) and Donostia International Physics Center (DIPC), Euskadi, Spain (2015-2023).
- E. Matito, M. Solà, P. Salvador and M. Duran, Electron sharing indexes at the correlated level. Application to aromaticity calculations, Faraday Discuss., 2007, 135, 325–345 Search PubMed.
- E. Matito, M. Duran and M. Solà, The aromatic fluctuation index (FLU): a new aromaticity index based on electron delocalization, J. Chem. Phys., 2005, 122,
014109 Search PubMed.
- R. F. W. Bader and M. E. Stephens, Spatial localization of the electronic pair and number distributions in molecules, J. Am. Chem. Soc., 1975, 97, 7391–7399 Search PubMed.
- X. Fradera, M. A. Austen and R. F. W. Bader, The Lewis Model and Beyond, J. Phys. Chem. A, 1999, 103, 304–314 Search PubMed.
- D. Jacquemin, E. A. Perpète, I. Ciofini and C. Adamo, Assessment of recently developed density functional approaches for the evaluation of the bond length alternation in polyacetylene, Chem. Phys. Lett., 2005, 405, 376–381 Search PubMed.
- D. Jacquemin, A. Femenias, H. Chermette, I. Ciofini, C. Adamo, J.-M. André and E. A. Perpète, Assessment of Several Hybrid DFT Functionals for the Evaluation of Bond Length Alternation of Increasingly Long Oligomers, J. Phys. Chem. A, 2006, 110, 5952–5959 Search PubMed.
- D. Jacquemin, E. A. Perpète, H. Chermette, I. Ciofini and C. Adamo, Comparison of theoretical approaches for computing the bond length alternation of polymethineimine, Chem. Phys., 2007, 332, 79–85 Search PubMed.
- M. Torrent-Sucarrat, S. Navarro, F. P. Cossío, J. M. Anglada and J. M. Luis, Relevance of the DFT method to study expanded porphyrins with different topologies, J. Comput. Chem., 2017, 38, 2819–2828 Search PubMed.
- I. Casademont-Reig, T. Wöller, J. Contreras-García, M. Alonso, M. TorrentSucarrat and E. Matito, New electron delocalization tools to describe the aromaticity in porphyrinoids, Phys. Chem. Chem. Phys., 2018, 20, 2787–2796 Search PubMed.
- H. Reis, Problems in the comparison of theoretical and experimental hyperpolarizabilities revisited, J. Chem. Phys., 2006, 125,
014506 Search PubMed.
- B. Hess, B. Bekker, H. Berendsen and J. G. E. M. Fraaije, LINCS: a linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 Search PubMed.
- J. Cerezo, F. Santoro and G. Prampolini, Comparing classical approaches with empirical or quantum-mechanically derived force fields for the simulation electronic lineshapes: application to coumarin dyes, Theor. Chem. Acc., 2016, 135, 143 Search PubMed (1–21).
- T. E. Markland and M. Ceriotti, Nuclear quantum effects enter the mainstream, Nat. Rev. Chem., 2018, 2, 0109 Search PubMed.
- C. García-Iriepa and M. Marazzi, Level of theory and solvent effects on DASA absorption properties prediction: Comparing TD-DFT, CASPT2 and NEVPT2, Materials, 2017, 10, 1025 Search PubMed.
- A. D. Laurent, M. Medved and D. Jacquemin, Using Time-Dependent Density Functional Theory to Probe the Nature of Donor–Acceptor Stenhouse Adduct Photochromes, ChemPhysChem, 2016, 1846–1851 Search PubMed.
- J. L. Oudar and D. S. Chemla, Hyperpolarizabilities of the nitroanilines and their relations to the excited state dipole moment, J. Chem. Phys., 1976, 66, 2664–2668 Search PubMed.
- D. Lu, G. Chen, J. W. Perry and W. A. I. Goddard, Valence-Bond Charge-Transfer Model for Nonlinear Optical Properties of Charge-Transfer Organic Molecules, J. Am. Chem. Soc., 1994, 116, 10679–10685 Search PubMed.
- F. Meyers, S. R. Marder, B. M. Pierce and J. L. Bredas, Electric Field Modulated Nonlinear Optical Properties of Donor-Acceptor Polyenes: Sum-Over-States Investigation of the Relationship between Molecular Polarizabilities (.alpha.,.beta., and.gamma.) and Bond Length Alternation, J. Am. Chem. Soc., 1994, 116, 10703–10714 Search PubMed.
- M. Barzoukas, C. Runser, A. Fort and M. Blanchard-Desce, A two-state description of (hyper) polarizabilities of push-pull molecules based on a two-form model, Chem. Phys. Lett., 1996, 257, 531–537 Search PubMed.
- P. Beaujean and B. Champagne, Unraveling the Symmetry Effects on the Second-Order Nonlinear Optical Responses of Molecular Switches: The Case of Ruthenium Complexes, Inorg. Chem., 2022, 61, 1928–1940 Search PubMed.
- L. Sanguinet, J. L. Pozzo, V. Rodriguez, F. Adamietz, F. Castet, L. Ducasse and B. Champagne, Acido- and Photo-triggered NLO Properties Enhancement, J. Phys. Chem. B, 2005, 109, 11139–11150 Search PubMed.
- A. Plaquet, M. Guillaume, B. Champagne, L. Rougier, F. Mancois, V. Rodriguez, J.-L. Pozzo, L. Ducasse and F. Castet, Investigation on the Second-Order Nonlinear Optical Responses in the Keto-Enol Equilibrium of Anil Derivatives, J. Phys. Chem. C, 2008, 112, 5638–5645 Search PubMed.
- F. Mancois, J.-L. Pozzo, J. Pan, F. Adamietz, V. Rodriguez, L. Ducasse, F. Castet, A. Plaquet and B. Champagne, Two-Way Molecular Switches with Large Nonlinear Optical Contrast, Chem. – Eur. J., 2009, 15, 2560–2571 Search PubMed.
- A. Plaquet, B. Champagne, J. Kulhánek, F. Bure
![[s with combining breve]](https://www.rsc.org/images/entities/char_0073_0306.gif) , E. Bogdan, F. Castet, L. Ducasse and V. Rodriguez, Effects of the Nature and Length of the π-Conjugated Bridge on the Second-Order Nonlinear Optical Responses of Push–Pull Molecules Including 4,5-Dicyanoimidazole and Their Protonated Forms, ChemPhysChem, 2011, 12, 3245–3252 Search PubMed.
, E. Bogdan, F. Castet, L. Ducasse and V. Rodriguez, Effects of the Nature and Length of the π-Conjugated Bridge on the Second-Order Nonlinear Optical Responses of Push–Pull Molecules Including 4,5-Dicyanoimidazole and Their Protonated Forms, ChemPhysChem, 2011, 12, 3245–3252 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: QMD-FF parameters; Complementary data on geometrical and electronic parameters and on optical properties; details on the calculation of the βzxx/βzzz ratio. See DOI: https://doi.org/10.1039/d4cp00310a |
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Carmelo
Naim
*a,
Carmelo
Naim
 ab,
Javier
Cerezo
ab,
Javier
Cerezo
 c,
Giacomo
Prampolini
c,
Giacomo
Prampolini
 *d and
Frédéric
Castet
*d and
Frédéric
Castet
 *a
*a

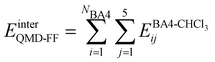
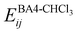 takes the standard expression:
takes the standard expression: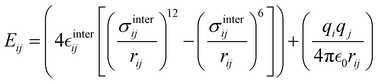
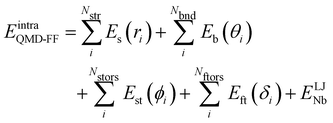
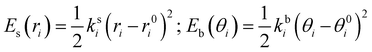
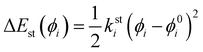
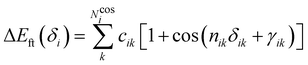

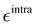 and σintra, the intramolecular LJ parameters entering in the above equation and describing the interaction between selected atom pairs belonging to the same molecule (BA4), differ from
and σintra, the intramolecular LJ parameters entering in the above equation and describing the interaction between selected atom pairs belonging to the same molecule (BA4), differ from  and σ reported in (3), which were instead designed to mimic the interaction among atoms pertaining to two different molecules (here BA4 and chlorofrom).
and σ reported in (3), which were instead designed to mimic the interaction among atoms pertaining to two different molecules (here BA4 and chlorofrom).
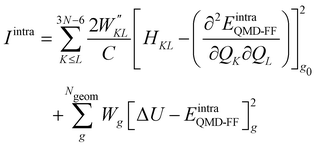
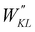 and Wg were set, as in most recent applications,37,38,46,49,51,52 to 2500 (for K ≠ L), 5000 (for the diagonal elements) and 1.0 for all g geometries.
and Wg were set, as in most recent applications,37,38,46,49,51,52 to 2500 (for K ≠ L), 5000 (for the diagonal elements) and 1.0 for all g geometries.


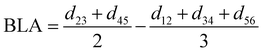
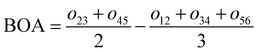
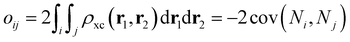
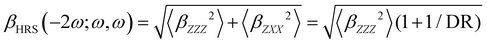

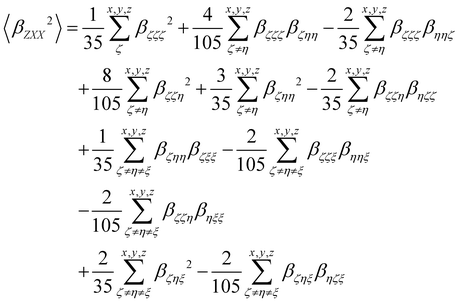
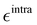 and σintra parameters are reported in kJ mol−1 and Å, respectively. Atom labeling refers to Fig. 3
and σintra parameters are reported in kJ mol−1 and Å, respectively. Atom labeling refers to Fig. 3
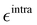 parameters were evaluated for each considered FF, as summarized in Table 2.
parameters were evaluated for each considered FF, as summarized in Table 2.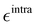 and σintra sets tuned to reproduce a particular interaction, e.g. OPLS47,48 parameters between heavy atoms of ring B and ring A for mimicking π–π stacking, or scaled parameters to simply account for steric repulsion. Such set of intramolecular LJ parameters, reported in detail in Tables S12 and S13 (ESI†), was fixed at the beginning of the Joyce parameterization, which was carried out on all the remaining harmonic and cosine force constants, according, as for the open form, to eqn (5)–(9). All parameters obtained for the closed form are reported in Tables S8–S13 (ESI†).
and σintra sets tuned to reproduce a particular interaction, e.g. OPLS47,48 parameters between heavy atoms of ring B and ring A for mimicking π–π stacking, or scaled parameters to simply account for steric repulsion. Such set of intramolecular LJ parameters, reported in detail in Tables S12 and S13 (ESI†), was fixed at the beginning of the Joyce parameterization, which was carried out on all the remaining harmonic and cosine force constants, according, as for the open form, to eqn (5)–(9). All parameters obtained for the closed form are reported in Tables S8–S13 (ESI†).



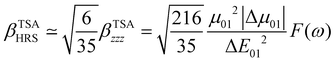
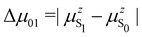 is the change in the permanent dipole moment between the two electronic states. F(ω) is a factor accounting for frequency dispersion, which depends on the energy of the incident photons (ħω = 0.95 eV for a 1300 nm wavelength):
is the change in the permanent dipole moment between the two electronic states. F(ω) is a factor accounting for frequency dispersion, which depends on the energy of the incident photons (ħω = 0.95 eV for a 1300 nm wavelength):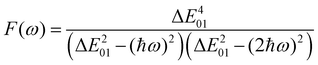
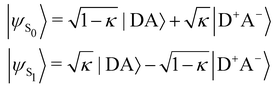
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |D+A−〉 = 0), the dipole moment variation upon the S0 → S1 transition can be written as:
|D+A−〉 = 0), the dipole moment variation upon the S0 → S1 transition can be written as: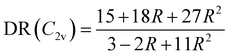

![[s with combining breve]](https://www.rsc.org/images/entities/char_0073_0306.gif) , E. Bogdan, F. Castet, L. Ducasse and V. Rodriguez, Effects of the Nature and Length of the π-Conjugated Bridge on the Second-Order Nonlinear Optical Responses of Push–Pull Molecules Including 4,5-Dicyanoimidazole and Their Protonated Forms, ChemPhysChem, 2011, 12, 3245–3252 Search PubMed.
, E. Bogdan, F. Castet, L. Ducasse and V. Rodriguez, Effects of the Nature and Length of the π-Conjugated Bridge on the Second-Order Nonlinear Optical Responses of Push–Pull Molecules Including 4,5-Dicyanoimidazole and Their Protonated Forms, ChemPhysChem, 2011, 12, 3245–3252 Search PubMed.