A density functional theory study on interactions in water-bridged dimeric complexes of lignin†
Jurgen Lange
Bregado
 *a,
Argimiro R.
Secchi
*a,
Argimiro R.
Secchi
 ab and
Frederico W.
Tavares
ab and
Frederico W.
Tavares
 ab
ab
aChemical Engineering Program, COPPE, Universidade Federal do Rio de Janeiro, Cidade Universitária, Rio de Janeiro, CP: 21941-914, Brazil. E-mail: jurgenlange1967@gmail.com
bChemical and Biochemical Process Engineering Program, Escola de Química, Universidade Federal do Rio de Janeiro, Cidade Universitária, Rio de Janeiro, CP: 21941-909, Brazil
First published on 22nd February 2024
Abstract
Lignin is the main plant cell wall component responsible for recalcitrance in the process of lignocellulosic biomass conversion into biofuels. The recalcitrance and insolubility of lignin in different reaction media are due in part to the hydrogen bonds and π interactions that hold syringyl (S) and guaiacyl (G) units together and promote the formation of stable water-bridged dimeric complexes (WBDCs): S⋯G and S⋯S, in native lignin. The current understanding of how each type of interaction influences the stability of these complexes within lignin native cell walls is still limited. Here, we found by DFT calculations that hydrogen bonding is more dominant than π-stacking interaction between aromatic rings of WBDCs. Although there is a stronger interaction of hydrogen bonds between subunits and water and higher π-stacking interaction in the S⋯S complex compared to the S⋯G complex, the former complex is less thermodynamically stable than the latter due to the entropic contribution coming from the methoxy substituents in the S-unit. Our results demonstrate that the methoxylation degree of lignin units does not significantly influence the structural geometries of WBDCs; if anything, an enhanced dispersion interaction between ring aromatics results in quasi-sandwich geometries as found in “coiled” lignin structures in the xylem tissue of wood. In the same way as that with ionic liquids, polar solvents can dissolve S-lignin by favorable interactions with the aliphatic hydroxyl group in the α-position as the key site or the aromatic hydroxyl group as the secondary site.
1. Introduction
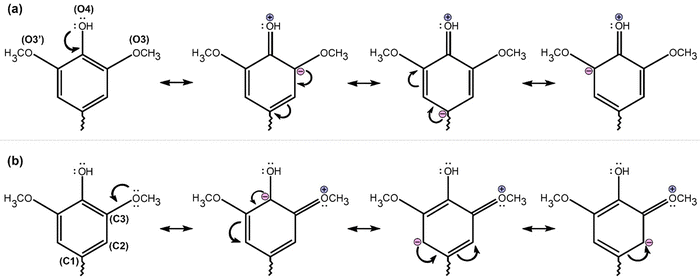
Lignin, one of the main components of lignocellulosic biomass, is a crucial structural component preserving the integrity of the plant cell wall, imparting stiffness and strength of vascular plants, enabling the transport of water and solutes through the tracheary elements in the vasculature system, and affording physical barriers against invasions of phytopathogens, and other environmental stresses.1–3 In nature, this component is primarily produced by enzymatic dehydrogenation and oxidative coupling of three hydroxycinnamyl alcohols or monolignols, namely, p-coumaryl alcohol, coniferyl alcohol, and sinapyl alcohol (Fig. 1), which are the origin of the p-hydroxyphenyl (H), guaiacyl (G), and syringyl (S) units following incorporation into the lignin polymer chains.4–8 Thus, lignin is a plant-originated polymer with a three-dimensional supramolecular structure of dimethoxylated (S), monomethoxylated (G), and non-methoxylated (H) phenylpropanoid and acetylated units linked by various types of C–O and C–C bonds, including α-O-4, β-O-4, β-5, 5-5, 4-O-5, β-1 and β-β linkages.9 Lignins generally have β-O-4 (alkyl aryl ether) as the majority bond, accounting for 45–60% of monomer connectivity.1,10,11 Based on its polyphenolic structure, lignin is a large-scale renewable feedstock composed of aromatics from biomass and can be used as a potential source of phenolic compounds to substitute for petroleum-derived chemicals.12–15The formulation of lignin and the ratio of the three units change with the type of cell and type of plant. For example, grasses are built up from H, G, and S units; softwood lignin (SL) or G-lignin essentially consists of G units; hardwood lignin (HL) of G and S units.16–18 G units constitute approximately 90% of SL from the gymnosperm plant, while roughly equal proportions of G units and S units appear in HL from the angiosperm plant.18–20 However, out of this classification, some species diverging from angiosperm plants can synthesize S-lignin having a high content of syringyl units.21 The hydrogen bonds (H-bonds) between neighboring hydroxyl groups and ether groups, as well as π–π interactions between aromatic groups, are responsible for the associated and complicated structures of lignin.22 These interactions hold lignin units together23,24 and promote the formation of stable water-bridged dimeric complexes (WBDCs), as shown in Fig. 2.25–27 In fact, the existence of WBDCs: G⋯S and S⋯S in native lignin is a consequence of the association of monolignols and its radicals in aqueous solution during their (bio)polymerization2,28–31 rendering lignols in folded and extended-chain structures mediated by hydrogen bonding interactions between close HO4–O4 and HO7–O7 hydroxyl groups (Fig. 2a),8 which participate in “coiled” structures found in the xylem tissue of tracheary elements of wood.32,33
 | ||
| Fig. 2 Molecular model of water-bridged dimeric complexes (WBDCs). (a)A crumpled globule structure of softwood lignin under normal conditions obtained via molecular dynamics simulation (left panel)26 and a coiled chain extracted from this structure (right panel). (b) Illustration of two S units (S⋯S) in the “coiled” chain (a) interacting with a hydration layer of three water molecules. Atom notations are specified as in the CHARMM topology file and other studies.34,35 Methyl groups (dotted circle) are inserted at the O8 position to represent etherification by β-O-4 linkages. (c) Depicts each fragment or lignin substructure (unit) and water molecules within WBDCs in different colors. By convenience in the text, we denote the water molecules: water 1, water 2, and water 3 as W1, W2, and W3 fragments, respectively. | ||
A fundamental understanding of how non-covalent interactions influence lignin stability at the microstructural level (e.g., in WBDCs) is key in the search for robust solvents to deconstruct lignocellulosic biomass or to prepare biopolymers by lignin aggregation in nanoparticles/colloids for environmentally friendly various applications.9,36–44 Like solubilization and aggregation phenomena, the structural stability of lignin is connected to the strength of H-bonds and π–π interactions, which in turn is linked to the number of methoxy groups (–OCH3) in their units.25,38,45 From a π interaction perspective, lignins rich in G units (less methoxylated) could be better π-stacked than those rich in S units (more methoxylated), thus allowing better self-aggregation with poorer solubility.38 In contrast, some studies45,46 showed that lignins rich in S units collapse better due to the hydrophobic effect, so they would have less solubility than lignins rich in G units. Apart from the hydrophobic effect and π interactions, hydrogen bonding is another type of interaction considered in the structural stability and solubility of lignin. Kubo et al.,25 using simple model compounds of lignins with S units in aqueous media, revealed “strong” H-bonds between aromatic groups, which could be a factor hindering solubility and favoring self-aggregation of lignins rich in S units compared to those rich in G units. The above is an example, based only on physical interactions, that the degree of lignin aggregation and its stability in a solvation media depends on the competition between the repulsion force, intermolecular hydrogen bonding as well as hydrophobic interactions (π–π interactions) between lignin's subunits.38
The current understanding of how each type of these interactions impacts the stability of complexes within lignin native cell walls is still limited. To our knowledge, few studies have considered the interaction between lignin units in aqueous media. Earlier studies investigated the association between monolignol radicals and monomers to reveal the lignin biosynthesis mechanism rather than the interaction between phenolic substructures constituting the natural lignin polymer. Li and Eriksson28 performed molecular dynamics (MD) simulations to examine the association of some monolignol dimers – coumaryl and coniferyl alcohols – in water. However, the study of such interactions between coniferyl and sinapyl alcohols (Fig. 1), which constitute primary alcohols in HL subunits, was not addressed. Chen and Sarkanen47 analyzed interactions between aromatic moieties in lignin chains, but some complexes involving lignin residues alone were probed. In a recent study,26 we determined by molecular dynamics the most stable conformation of the hydrated G⋯G complex into crumpled globules of softwood lignin. However, a quantitative understanding of non-covalent interaction strength governing its structural stability was not provided. Such an understanding could be obtained more efficiently by electronic structure calculations due to the complex nature of non-covalent interactions involving different types of energetic contributions such as electrostatics, charge transfer, orbital repulsion, electron dispersion, and so on.48–50
Electronic structure calculations using density functional theory (DFT) have been used to understand the solubility of different lignin types in organic solvents and green reaction media,9,42,51–54 as well as the inter/intramolecular interactions between components of the lignocellulosic biomass.28,55,56 Nevertheless, lignin is a complex aromatic biopolymer and a rather expensive one using which quantum mechanical DFT calculations are performed. From a total of approximately 200 density functionals used in DFT,57 three types of hybrid functionals are most commonly used in lignin or monolignols: B3LYP,9,22,28,55,56,58–63 Minnesota's suite (e.g. M05-2X, M06-2X)52,56,64–66 and B97-family (e.g. B97-D, ωB97M-V, ωB97D-2).22,51,54,67,68 The M05-2X and M06-2X hybrid meta-density functional series have broader accuracy than previous popular functionals (e.g. B3LYP) and provide an adequate representation of nonbonded interactions such as hydrogen bonding and dispersion forces,69–71 which are important in molecular systems containing phenolic moieties as lignin. These functionals account for “medium-range” electron correlation, sufficient to describe the dispersion interactions within many complexes.72 DFT calculations at the M05-2X/6-31+G(d,p) level of theory were performed to estimate interaction energies between lignol radicals and aromatic substructures in lignin and thus demonstrate that a template polymerization process is reasonable during lignin biosynthesis.47 Hohenstein et al.73 demonstrated that the M06-2X functional is better than the M05-2X functional at capturing “medium-range” (<= 5 Å) electron correlation, allowing accurate description of the stacking interactions when the electron clouds of each monomer for stacked base pairs are in relative proximity to one another. The M06-2X/6-31+G(d) level of theory was able to reproduce stacking interaction energies in benzene sandwich dimers substituted with the –OCH3 group comparable to CCSD(T)/aug-cc-pVTZ, but at a drastically reduced computational cost.74,75
Some analysis using DFT calculations can be performed to obtain more information about the nature of non-covalent interactions, such as natural bond orbital (NBO) analysis,76,77 atoms in molecules (AIM) theory,77–81 the reduced density gradient (RDG) method,82,83 and the Shubin Liu's energy decomposition scheme (EDA-SBL).25,84–86 These analyzes can be performed together with DFT calculations because the key quantity estimated is the quantum-mechanical electron density (ρ), from which all chemical properties can, in principle, be obtained.87 Some of these analyses have recently been performed to understand the key interactions between a variety of solvents with lignocellulose biomass components;9,42,54 however they have not been used to investigate interactions between lignin units in cell walls so far.
The primary goal of this work is to corroborate, from a quantum mechanical modeling point of view, the formation of stable WBDCs: S⋯G and S⋯S in native lignin, which influences conformation, stability and dissolution of lignin. Another purpose is to examine all energetic components engaged with non-covalent interactions affecting the structural stability of these complexes; for hydrogen bonds: electrostatic and charge-transfer, and for π–π interaction: electrostatic, London dispersion and repulsion, which are much difficult to study by MD simulations. Our interest is unraveling how the strength of these interactions depends on the methoxylation degree of lignin and which of them governs the WBDC interaction networks. Here, we address the study of complexes with S units because of the importance of the syringyl constituent in facilitating overall lignin degradation for more efficient materials and energy production from angiosperm than from gymnosperm wood.88–90 Beyond intermolecular interactions, this study finds the relationship between these interactions and thermodynamic parameters (enthalpy and entropy) of stability in WBDCs, which are important in the rational design of new solvents for the dissolution of lignin rich in S-units. Herein, if some assumption is made about the solvent design based on DFT calculations, it applies more to the depolymerization of lignin that has many S-units (hardwood or syringil lignins) in its composition and not to softwood lignin, which has almost no S-units and it is more branched.
2. Computational methodology
2.1. Optimization of geometries
All calculations were performed using Gaussian 09 (revision D.01) package91 with the M06-2X functional and 6-31++g(d,p) basis set at a temperature of 298 K and pressure of 1 atm. Although a medium-size basis set, this basis set shows a good estimation of interaction energy for π–π stacked complexes. For example, DFT calculations at the M05-2X/6-31++g(d,p) level of theory yielded a mean unsigned error of just 1.2 kcal mol−1 relative to the best estimates for nucleobase π–π stacking energies.47,92 The nature of π-stacking interactions in various models of DNA base pairs,93,94 structure and energies of dilignols,60 hydrogen bonding network in woody biomass55 and the mechanism of lignin solubilization in ionic liquids (ILs)9,53 were also satisfactorily described using this basis set. Using 6-31G enables an excellent compromise between the computational cost and the accuracy of the computational results.9 In principle, + and ++ diffuse functions might be indistinctly used in the basis sets for modeling lignocellulose materials since they do not significantly affect the calculation of interaction energy, H-bonding, and O–H stretching frequencies.54,95 However, diffuse polarization functions on the second-row elements (d,p) must always be used in the basis set to successfully describe the interactions of components in woody biomass.55Before optimization, the WBDC geometries, S⋯G and S⋯S, were created starting from π–π stacked conformation for G⋯G dimers found via MD simulation (structure in Fig. 2 by removing –OCH3 groups).26 Thus, to obtain the methoxylated complexes S⋯G and S⋯S, one and two –OCH3 groups were introduced into G units, respectively. This study was performed for simple lignin complexes having a high content of –OCH3 in their units because the S-unit shows less crosslinking in the native lignin's network.90 For comparison, we leave the same number of water molecules in all WBC geometries.
The electronic energy minimization of these complexes was carried out in the gas phase employing a tight self-consistent field convergence criterion and ultrafine integration grid. This grid, having 99 radial shells and 590 angular points per shell, is recommended for optimizations of molecules with many soft modes, such as methyl rotations, making such optimizations more reliable.96 The stability of the optimized WBDCs was certified by harmonic vibrational frequency analyses. Harmonic vibrational frequencies were computed for all WBDC optimized structures in order to characterize the stationary points. No imaginary frequencies were obtained, confirming that each geometry has a minimum on the potential energy surface.
It is important to stress that the aim of this work is not to derive new structures for WBDCs starting from randomly different configurations but rather to corroborate that there may be structures whose geometries are like those estimated with MD simulations26 trapped in a nearby local minimum of energy landscapes estimated with DFT calculations.
2.2. Calculation of thermodynamic properties
The interaction energy (ΔE, eqn (1) and (2)) of the different configurations has been expressed as the electronic energy difference of WBDCs: ES⋯G and ES⋯S (Fig. 2a) and the corresponding optimized isolated geometries (EG, ES and Ewater).97 Zero-point energy corrections and basis superposition set error (BSSE) were included in the ΔE calculation. The BSSE-correction scheme was based on the counterpoise (CP) method developed by Boys and Bernardi98 to account for basis set superposition errors resulting from using finite basis sets.| ΔES⋯G = 627.591 [ES⋯G − (EG + ES + 3Ewater)] in kcal mol−1 | (1) |
| ΔES⋯S = 627.591 [ES⋯S − (2ES + 3Ewater)] in kcal mol−1 | (2) |
The interaction enthalpy (ΔH), entropy (ΔS) and Gibbs energy (ΔG) of the formation of these complexes were calculated employing the same formulation used to estimate the interaction energy (eqn (1) and (2)). The Gibbs energy (G) and enthalpy (H) for all optimized configurations were obtained by adding the thermal corrections to the electronic energy calculated at the theory level. The volume variation (ΔV) during the formation of the complex was determined using the relationship (ΔH − ΔE)/P, where P (= 1 atm) is the pressure. A more negative ΔG correspond to a higher thermodynamic stability of the formed complex.
2.3. Topological analysis of bonding interactions
 ,81,101 where G(r) is the electronic kinetic energy density, which is always positive, and V(r) is the electronic potential energy density that must be negative.102 A negative ∇2ρ shows the excess potential energy at the BCP, which indicates that electronic charges are concentrated in the inter-nuclear region, and, therefore, shared by two nuclei by covalent bonding.103 On the other hand, a positive ∇2ρ shows the excess kinetic energy at the BCP, which reveals that electronic charges are depleted between nuclei as in conventional hydrogen bonding and ionic bonds.9,80 However, the extremely strong H-bonds can also have negative Laplacian values. For conventional H-bonds in neutral molecules (closed-shell molecules), the electron density and Laplacian value should be positive within the ranges of 0.002–0.035 a.u. and 0.024–0.139 a.u., respectively.80 The Multiwfn software104 was employed to determine all BCPs in the hydrogen bonding network of each WBDCs studied. A Python script was used to extract all BCPs that fulfil the requirements for conventional H-bonds.
,81,101 where G(r) is the electronic kinetic energy density, which is always positive, and V(r) is the electronic potential energy density that must be negative.102 A negative ∇2ρ shows the excess potential energy at the BCP, which indicates that electronic charges are concentrated in the inter-nuclear region, and, therefore, shared by two nuclei by covalent bonding.103 On the other hand, a positive ∇2ρ shows the excess kinetic energy at the BCP, which reveals that electronic charges are depleted between nuclei as in conventional hydrogen bonding and ionic bonds.9,80 However, the extremely strong H-bonds can also have negative Laplacian values. For conventional H-bonds in neutral molecules (closed-shell molecules), the electron density and Laplacian value should be positive within the ranges of 0.002–0.035 a.u. and 0.024–0.139 a.u., respectively.80 The Multiwfn software104 was employed to determine all BCPs in the hydrogen bonding network of each WBDCs studied. A Python script was used to extract all BCPs that fulfil the requirements for conventional H-bonds.
 | (3) |
2.4. Energetics of bonding interactions
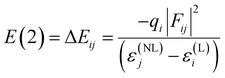 | (4) |
 | ||
| Fig. 3 2e-stabilizing interaction between a filled donor orbital ε(L)i and vacant acceptor orbital ε(NL)j, leading to energy lowering ΔEij.107 Here, L and NL stand for Lewis-type and non-Lewis type natural bonding orbitals (NBOs), respectively. The σ, π donor orbitals and lone electron pairs (Lp) of an atom in one molecule can overlap with the vacant σ* or π* acceptor orbital of another molecule. The figure illustrates the interaction (n → π*) between the lone electron pair (n) as the donor orbital and π* as the vacant acceptor orbital leading to mixing (delocalization) by connecting the NL type NBOs with L NBOs. | ||
In the NBO analysis, E(2) is used to describe the intensity of orbital interaction between electron donors and electron acceptors. The higher the value of E(2), the more the electrons transfer from the donor, increasing the bond strength.9 The Gaussian 09 package was used to make such an analysis employing pop = nbo and nboread keywords. The visualization of NBO was carried out with the Multiwfn software.
| E[ρ] = Es[ρ] + Ee[ρ] + Eq[ρ] | (5) |
 | (6) |
 | (7) |
The quantum term (Eq[ρ] = EXC[ρ] + EPauli[ρ]) is the energy purely caused by the quantum effect, which can be broken down into exchange–correlation energy (EXC[ρ]) and Pauli energy (EPauli[ρ]). According to the Kohn and Sham (KS) formalism, EXC[ρ] can be calculated as follows:54
 | (8) |
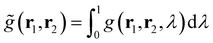 and g(r1, r2, λ) stand for the electron pair correlation function in a range of interaction strengths (λ). The shape of the
and g(r1, r2, λ) stand for the electron pair correlation function in a range of interaction strengths (λ). The shape of the ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) (r1, r2) function is precisely determined using the DFT functional used in calculations. For hybrid meta-density functionals such as M06-2X used in this work,
(r1, r2) function is precisely determined using the DFT functional used in calculations. For hybrid meta-density functionals such as M06-2X used in this work, ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) (r1, r2) depends on ρ, ∇ρ, and ∇2ρ (included in the kinetic energy density). EXC[ρ] describes the long-range attractive dispersion energetic component (e.g., London-dispersion forces) acting between aromatic rings, which is negative. This dispersion energy depends on explicit electron–electron correlations,108 which are associated with overlapping of π–π and π–σ orbitals.109EPauli[ρ] is also known as exchange repulsion and it is determined by subtracting the Weizsäcker kinetic energy (eqn (6)) from the exact kinetic energy of the non-interacting electron system defined using KS-DFT theory.105 From a physical point of view, it represents a short-range repulsion effect between electrons in occupied orbitals, which is always positive.
(r1, r2) depends on ρ, ∇ρ, and ∇2ρ (included in the kinetic energy density). EXC[ρ] describes the long-range attractive dispersion energetic component (e.g., London-dispersion forces) acting between aromatic rings, which is negative. This dispersion energy depends on explicit electron–electron correlations,108 which are associated with overlapping of π–π and π–σ orbitals.109EPauli[ρ] is also known as exchange repulsion and it is determined by subtracting the Weizsäcker kinetic energy (eqn (6)) from the exact kinetic energy of the non-interacting electron system defined using KS-DFT theory.105 From a physical point of view, it represents a short-range repulsion effect between electrons in occupied orbitals, which is always positive.
The contribution of each type of energy to the overall interaction energy was calculated from 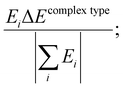 where i represents the energy type: steric, electrostatic, exchange–correlation, and Pauli repulsion, and the complex type is S⋯G or S⋯S. Here
where i represents the energy type: steric, electrostatic, exchange–correlation, and Pauli repulsion, and the complex type is S⋯G or S⋯S. Here  .
.
3. Results and discussion
3.1. Geometric characteristics and interaction energy of the complexes
The optimized structures of WBDCs (Fig. 4) by DFT were like the starting structures guessed by molecular dynamics calculations26 in terms of dimer ring orientation (Fig. S1, ESI†). This indicates that new parameterizations of the CHARMM force field for lignin34 adequately reproduce structural features of lignin dimers with hydrogen bonding. DFT dimerization energy landscapes of studied complexes may be well captured by the CHARMM force field, as observed for pairs of ring-containing amino acids in proteins when comparing CHARMM27 or OPLS-AA force fields with the MP2 method.108 If there is any structural discrepancy between the DFT and MD results, it is attributed to the inability of force fields based on fixed partial charges centered on the atoms to reproduce the effects related to the partially covalent character of hydrogen bonding, such as higher-order multipoles and electronic polarization. On the other hand, it is also noteworthy that the initial structures used in the optimization by DFT were derived from MD simulations using radial distribution functions, which provide average distances between water molecules and hydroxyl groups so that the positions of the H-bonds can be somewhat different between DFT and MD (Fig. S1, ESI†). | ||
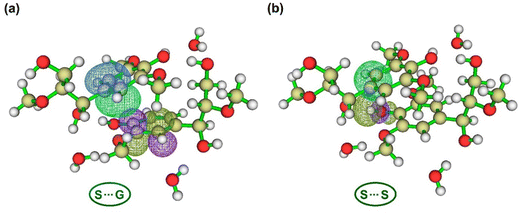
| Fig. 4 Optimized water-bridged dimeric complex (WBDC) structures: S⋯G and S⋯S using DFT at the M06-2X/6-31++g(d,p) theory level. Carbon, oxygen, and hydrogen atoms are represented by gray, red, and white balls, respectively. In these WBDCs, the bonding critical points (BCPs) of hydrogen bonds (H-bonds) are illustrated by blue balls connecting with dashed green lines between oxygen and hydrogen atoms. In dashed black lines, the distance (d) from centroids and interplanar angle (θ)108 between aromatic rings. The BCPs with circled number 1 are H-bonds formed between HO7 of fragment 1 and oxygen of water 1 ([1] O7H⋯O [W1]), while the BCPs with circled number 2 are H-bonds formed between O7 of fragment 1 and HO4 of fragment 2 ([1] O7⋯HO4 [2]). Fig. 2 illustrates the nomenclature of atoms in each fragment and the numbering of water molecules in these WBDCs. | ||
A glance at Fig. 4 reveals that the methoxylation degree of subunits in WBDCs does not significantly influence their molecular geometries. For example, the estimated distance of the center of mass (d) and interplanar angle (θ) between aromatic rings slightly decreases with the increasing number of –OCH3 groups in WBDCs (Table 1). For the studied WBDCs, the d values agree with those found for benzene sandwich dimers (∼3.8 Å, Fig. 5a)109 and double veratrylglycerol-β-guaiacyl ether dimers (3.643 Å).43 The value of d is somewhat higher for the S⋯G complex than for the S⋯S complex, which indicates a more favorable interaction in the latter complex, as shown by interaction energy (ΔE) values in Table 1. The above agrees with theoretical results, wherein it was demonstrated that –OCH3 substituents in lignin led to the strengthening of lignin/lignin effective interactions in aqueous media.45 Also, the ΔE results obtained by DFT in this study are in line with those estimated by MD for lignin constituents in water,28 in which the estimated potential energy of interactions between coumaryl (H) dimers was lower (−41.4 kcal mol−1) than that between coniferyl (G) dimers (−80.8 kcal mol−1). On the other hand, the hydration favors interunit interactions in these complexes since the values of ΔE calculated for these complexes without water were lower (e.g., ΔE = −17.34 kcal mol−1 for S⋯G) compared to those reported here (Table 1). However, even without water molecules, these complexes can be stabilized by intermolecular hydrogen bonding as O7⋯HO4 and O4⋯HO9 (Fig. S2 in the ESI†).
| WBDCs | Number of methoxy groups | d [Å] | θ [°] | ΔEb [kcal mol−1] | ΔHb [kcal mol−1] | ΔV × 10−4 [cm−3] | TΔSc [kcal mol−1] | ΔGb [kcal mol−1] |
|---|---|---|---|---|---|---|---|---|
| a d and θ mean the distance and interplanar angle between aromatic rings (Fig. 4a). b The values of E, H, S and G for each optimized configuration involved in the formation of WBDCs are assembled in Table S5 (ESI). c T means the temperature and is equal to 298 K. | ||||||||
| S⋯G | 3 | 3.60 | 23.74 | −40.33 | −49.29 | −2.17 | −43.66 | −5.63 |
| S⋯S | 4 | 3.52 | 23.11 | −40.63 | −50.53 | −2.39 | −45.70 | −4.83 |
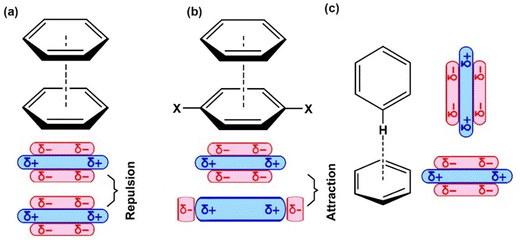 | ||
| Fig. 5 (a) and (b) Cofacial “sandwich” π-stacked configurations, (c) edge-to-face T-shaped geometry.114,117 The delocalized π electrons impart a quadrupole moment with partial negative charge (δ−) above both aromatic faces and a partial positive charge (δ+) on hydrogen atoms around the periphery.49,118 (b) A favored cofacial “sandwich” π-stacked configuration between electron-rich and electron-deficient aromatic rings, which is accompanied by close contact between π orbitals of adjacent molecules.118 X symbolizes electron-withdrawing substituting groups. | ||
The values of θ around 23–29° (Table 1) suggest the existence of parallel-displaced geometry in the π-stacking,110,111 showing a quasi-sandwich (Fig. 5) character. This geometry justifies transition structures acting in the growing mechanism of dilignols to oligolignols in the plant cell.8 It has been suggested that the coniferyl alcohol radical may be oriented in the transition state during cross-coupling so that its aromatic ring is parallel to the guaiacyl ring at the growing end by the formation of a π-complex like a “sandwich transition state”.112
3.2. Calculation of thermodynamic properties in the complex formation
Although the interaction energy (ΔE) appears to be a dominant force in the stabilization of the complexes through the highly exothermic enthalpic component (ΔH) (Table 1), calculations of Gibbs energy (ΔG) of the formation of these complexes must be performed to harshly judge their stability. The calculated ΔG values are collected in Table 1, where it can be seen that ΔG for the S⋯G complex is slightly more negative (−5.63 kcal mol−1) than for the S⋯S complex (−4.83 kcal mol−1), revealing a superior thermodynamic stability for the S⋯G complex. The above can be rationalized on the basis of entropic contributions coming from the methoxy group to the Gibbs energy (ΔG = ΔH − TΔS) of complex formation. Despite more favorable interactions (with more negative ΔH) during the formation of the S⋯S complex, it shows a more negative ΔS (Table 1) during its formation, which causes a less negative ΔG for the S⋯S complex compared to the S⋯G complex. That is, the increase of S-unit entropy (Table S5, ESI†) coming from the methoxy substituent provokes a more accentuated decrease in ΔS in the formation of the S⋯S complex. Such a diminution of ΔS is in turn accompanied by favored interactions between the S⋯S complex's units, leading to a slightly larger decrease in ΔV (or contraction) for the S⋯S complex, as shown in Table 1. This outcome is in consonance with the lower value of distance (d) between aromatic rings for the S⋯S complex (3.52 Å) compared to the S⋯G (3.60 Å) complex. The higher thermodynamic stability of S⋯G in relation to S⋯S justifies the greater recalcitrance in biomass dissolution found for lignins containing higher contents of guaiacil (G) units.88 On the other hand, taking into account the thermodynamic stability of these complexes, it can be inferred that solvents with some polarity (between ethanol and DMSO)35 can favor the dissolution of lignin rich in S units, as found for hardwood lignin.42 Possibly, it is due to the interaction of hydrogen bonding between lignin units with the solvent, which decreases the entropy (SS⋯S) and increases the enthalpy (HS⋯S) of S-units into complexes compared to the dissociated state (e.g., SS), thus disfavoring complexation (or increase in ΔG) with improved lignin solvation.Despite the fact that the entropic component drives the stability of WBDCs under ambient conditions, the interaction energy is an opposite force and not much less important than the entropy, which is worth investigating. In fact, as beforementioned, the interaction energy influences the geometry and stability of these complexes. An explanation of the interaction forces driving the formation of parallel-displaced or sandwich geometries in π-stacking is still unclear, and various models have been proposed for specific systems. According to the “π/polar or electrostatic model” developed by Hunter and Sanders,113 sandwich geometries might be stabilized by decreasing quadrupolar electrostatic interactions between aromatic rings competing with London dispersion that favor cofacial π-stacking.49,113 However, this intuitive electrostatic model has been criticized for considering only the electrostatic forces as dominant and not considering other phenomena, such as charge penetration, to explain parallel-displaced structures in π-stacking.114 Also, the quadrupolar repulsion cannot account for the structures adopted by larger polycyclic aromatics and geometries of larger graphene analogues, which may be better understood via Pauli repulsion models whose origin is quantum. Another proposed model, the “direct-interaction model”,74,75,115,116 which conflicts with the electrostatic model, states that substituent effects in the benzene sandwich dimer are relatively unimportant in the π-system of the substituted benzene and rather dominate the electron-withdrawing character of the substituent in the σ-bonds.
Since the overall nature of substituent effects on π stacking involves the interplay of several competing factors, including electrostatics, dispersion, and direct substituent-ring interactions, a careful investigation should be performed to unravel which of them is predominant in WBDC interaction networks. However, the picture of the interaction in WBDCs goes beyond such interactions that only participate in π-stacking. The WBDC geometries (Fig. 4) may result from intermolecular H-bonding interactions between the water molecules and the units, as well as between the units themselves, overcoming repulsive interactions (e.g., Pauli repulsion) between aromatic rings. Just considering that π–π interaction energies for the benzene dimer in stable geometries (parallel displacement or T-shape) have a contribution of around 2.7 kcal mol−1,74,119,120 and that the calculated overall interaction energy is approximately 40 kcal mol−1 (Table 1), other energetic contributions are expected to predominate in the association of units in WBDCs. In the next sections, we examined each type of these interactions engaged in the stability of WBDCs.
3.3. Topological analysis of hydrogen bonding interactions
The AIM theory was used to analyze hydrogen bonding characteristics to obtain information about the interactions in these studied complexes. Using this theory, different bond critical points (BCPs) were found for all studied WBDCs (Fig. S3, ESI†). From these BCPs, those related to conventional H-bond type (3, −1) could be obtained, as shown in Fig. 4. The values of electron density (ρBCP), its Laplacian (∇2ρBCP), and energy density (HBCP) for these H-bonds are listed in Table 2. We can observe that the values of ρBCP and ∇2ρBCP lie in the relative proposed ranges for conventional H-bonds, and strongest H-bonds like O7H⋯O and O7⋯HO4 have the highest values for S⋯G and S⋯S complexes. From a geometric point of view, these H-bonds show shorter bond lengths and angles close to 180° (Table 2), which favor strong hydrogen donor–acceptor interactions.9,121,122 These H-bonds show negative values of HBCP, which reveals electronic shared interactions or covalent within the WBDCs.102 They have partially covalent and partially electrostatic properties and can be classified as strong H-bonds.123 The strongest H-bonds at O7 and HO4 interactions in these complexes are consistent with theoretical findings reported for lignin dissolution with ILs.9 Zhang et al., using the guaiacyl glycerol-β-guaiacyl ether (GG) model with imidazolium-based ionic liquids, found that the α-OH group (in our case O7–HO7 in WBDCs) is the key site when ion pairs interact with GG, while the p-OH (O4–HO4 in WBDCs) is the secondary site favorable for H-bonds.| WBDCs | H-Bondsa | Length [Å] | Angle [°] | ρ BCP | ∇2ρBCP | H BCP × 10−3 [a.u.] |
|---|---|---|---|---|---|---|
| a The numbers 1 and 2 in brackets represent the fragments 1 and 2 from which the oxygen or hydrogen atoms in the H-bonds come from. Here the notations [W1], [W2], and [W3] also indicate fragments, but they are referred to as water molecules: water 1, water 2, and water 3, respectively (Fig. 2). | ||||||
| S⋯G | [1] O7H⋯O [W1] | 1.859 | 148.94 | 0.0302 | 0.0995 | −0.0160 |
| [1] O7⋯HO4 [2] | 1.838 | 171.14 | 0.0318 | 0.0978 | −0.0230 | |
| [1] O4H⋯O [W2] | 2.072 | 119.38 | 0.0201 | 0.0729 | −0.2050 | |
| [1] O4⋯HO9 [2] | 2.012 | 131.83 | 0.0227 | 0.0784 | −0.2080 | |
| [1] O3⋯HO9 [2] | 2.398 | 146.13 | 0.0093 | 0.0357 | 0.7580 | |
| [1] O4⋯H9 [2] | 2.559 | 110.15 | 0.0102 | 0.0388 | 1.0950 | |
| [1] O3⋯H8 [2] | 2.596 | 141.11 | 0.0084 | 0.0276 | 0.6118 | |
| [2] O3⋯H [W1] | 1.924 | 141.28 | 0.0258 | 0.0868 | −0.2591 | |
| [2] O9⋯H [W2] | 1.962 | 150.23 | 0.0251 | 0.0755 | −0.8722 | |
| [2] O7H⋯O8 [2] | 1.997 | 117.29 | 0.0256 | 0.0986 | 0.2999 | |
| [2] O7⋯H [W3] | 1.897 | 166.27 | 0.0261 | 0.0866 | −0.3020 | |
| [2] H103⋯O [W3] | 2.349 | 154.76 | 0.0122 | 0.0394 | 0.3487 | |
| [2] H2⋯O [W3] | 2.453 | 123.88 | 0.0096 | 0.0410 | 1.6779 | |
| S⋯S | [1] O7H⋯O [W1] | 1.852 | 150.78 | 0.0308 | 0.1006 | −0.03094 |
| [1] O7⋯HO4 [2] | 1.866 | 171.29 | 0.0299 | 0.0908 | −0.19783 | |
| [1] O4H⋯O [W2] | 1.966 | 131.89 | 0.0243 | 0.0816 | −0.28417 | |
| [1] O4⋯HO9 [2] | 1.941 | 137.45 | 0.0252 | 0.0878 | −0.02348 | |
| [1] H103′⋯O3′ [2] | 2.452 | 120.01 | 0.0112 | 0.0389 | 0.79105 | |
| [1] O3⋯H8 [2] | 2.369 | 96.74 | 0.0125 | 0.0378 | 0.09377 | |
| [2] O3⋯H [W1] | 1.907 | 129.72 | 0.0266 | 0.0903 | −0.1382 | |
| [2] O9⋯H [W2] | 1.971 | 145.84 | 0.0250 | 0.0754 | −0.9600 | |
| [2] O7H⋯O8 [W2] | 1.952 | 118.74 | 0.0277 | 0.1058 | 0.1942 | |
| [2] O7⋯H [W3] | 1.900 | 164.16 | 0.0256 | 0.0861 | −0.3397 | |
| [2] H103⋯O [W3] | 2.382 | 151.28 | 0.0156 | 0.0376 | 0.4226 | |
| [2] H2⋯O [W3] | 2.411 | 132.25 | 0.0102 | 0.0433 | 0.0016 | |
On the other hand, the weakest H-bond interactions correspond to those formed between hydrogen atoms attached to carbon atoms in a unit and some type of oxygen from water (e.g., W3) or neighbor unit: O3⋯H8, O4⋯H9, H103′⋯O3′, H103⋯O, and H2⋯O. These H-bonds have positive values of HBCP, which discloses the electrostatic nature of them. This is a consequence of low partial positive charges, ranging from 0.101 to 0.405 (Table S2, ESI†) of aliphatic hydrogen bond donors: H8, H9, H103, and H103′, by successive Sigma bond polarizations on carbon skeleton. This polarization is mediated by the inductive (−I) effect of electron-withdrawing oxygen atoms (O3, O3′, O8, and O9) attached to carbon atoms adjacent (C10, C10′, C8, and C9) to these hydrogen atoms.
For the case of H2 atoms, belonging to the aromatic ring and involved in H2⋯O hydrogen bonds, its low partial positive charge is caused by the positive mesomeric effect (+M) (Scheme 1). The –OCH3 substituent added at the C3 position of the aromatic ring increases the negative charge on the C2 carbon (from −0.373 in S⋯G to −0.436 in S⋯S), decreasing the partial positive charge on the H2 atom (from 0.109 in S⋯G to 0.103 in S⋯S, Table S2, ESI†). Actually, H2⋯O is the weakest bond of all H-bonds having an electrostatic attraction force (Table S2, ESI†) of −318 and 330 pN for S⋯G and S⋯S, respectively, which is in the range of −75.8 to −521 pN found for a diversity of planar complexes with H-bonds dominated by electrostatic interactions.124 The geometry of this H-bond is similar to that found between the anions of ILs and GG, wherein there is an anchoring of the anion (in our case water) between the –OCH3 group and the α-OH position of GG.9 Curiously, the O3⋯HO9 hydrogen bond, which should be of moderate strength in the S⋯G complex, it is a weak H-bond considering low ρBCP (Table 2) and electrostatic force values (Table S2, ESI†). The weakness of this H-bond can be explained in light of that lone electron pairs of O3 atoms are delocalized by the +M effect (Scheme 1),125 resulting in low partial negative charges (−0.264, Table S2, ESI†) on the O3 atom.
In general, intermolecular H-bonds (e.g., H103⋯O[W3], O7⋯H[W3], O4H⋯O[W2], H2⋯O[W3]) related to hydration of units are stronger in the S⋯S complex than in the S⋯G complex, due to the +M effect of extra –OCH3 group in the aromatic ring (Scheme 1). This effect augments the partial positive charges on O4H and H103 and decreases that on H2, whereas the partial negative charge increases on the O7 atom. The oxygen atoms (O[W2] and O[W3]) of water molecules involved in these H-bonds appear to increase the negative charge due to the polarization effect by surrounding units, leading to a net augmentation of the attractive electrostatic forces and diminution of distance for these H-bonds (Table S2, ESI†). The better hydration observed in the S⋯S complex caused by H-bond interactions is in line with theoretical evidence about S-units that shows higher interactions of hydrogen bonding in water than in G-units.35 However, on analyzing the values of ρBCP (Table 2) corresponding to H-bonds involved with interunit interactions (O7⋯HO4, O4⋯HO9, O3⋯HO9, O4⋯H9, O3⋯H8, and H103′⋯O3′), there is no clear trend to claim that the S⋯S complex has stronger interaction than the S⋯G complex (Table 1). That is, when the values of ρBCP for each of these interactions are compared individually, sometimes they appear to be higher for S⋯S and other times for S⋯G as shown in Table 2. In this case, it is necessary to apply another auxiliary method, as will be seen in the next sections, to obtain detailed information about the energy values of each hydrogen bonding. Then, the sum of these energy values encompassing H-bonds related to an interaction type (e.g., interunit or hydration) can inform their contribution to the interaction overall energy.
3.4. NBO analysis
| WBDCs | H-Bonda | Donor (i) | Acceptor (j) | E(2) [kcal mol−1] |
|---|---|---|---|---|
| a The numbers 1 and 2 in brackets, respectively, represent the fragments 1 and 2 from which the oxygen or hydrogen atoms in the H-bonds come from. Here the notations [W1], [W2], and [W3] also indicate fragments, but they are referred to as water molecules: water 1, water 2, and water 3, respectively (Fig. 2). | ||||
| S⋯G | [1] O7H⋯O [W1] | Lp O | σ* O7–H | 15.74 |
| [1] O7⋯HO4 [2] | Lp O7 | σ* O4–H | 17.47 | |
| [1] O4H⋯O [W2] | Lp O | σ* O4–H | 6.17 | |
| [1] O4⋯HO9 [2] | Lp O4 | σ* O9–H | 7.56 | |
| [1] O3⋯HO9 [2] | Lp O3 | σ* O9–H | 1.72 | |
| [1] O4⋯H9 [2] | Lp O4 | σ* C9–H9 | 0.51 | |
| [1] O3⋯H8 [2] | Lp O3 | σ* C8–H8 | 0.60 | |
| [2] O3⋯H [W1] | Lp O3 | σ* O–H | 1.66 | |
| [2] O9⋯H [W2] | Lp O9 | σ* O–H | 2.39 | |
| [2] O7H⋯O8 [2] | Lp O8 | σ* O7–H | 3.28 | |
| [2] O7⋯H [W3] | Lp O7 | σ* O–H | 6.38 | |
| [2] H103⋯O [W3] | Lp O | σ* C10–H103 | 6.49 | |
| [2] H2⋯O [W3] | Lp O | σ* C2–H2 | 0.36 | |
| S⋯S | [1] O7H⋯O [W1] | Lp O | σ* O7–H | 19.65 |
| [1] O7⋯HO4 [2] | Lp O7 | σ* O4–H | 15.20 | |
| [1] O4H⋯O [W2] | Lp O | σ* O4–H | 7.63 | |
| [1] O4⋯HO9 [2] | Lp O4 | σ* O9–H | 8.43 | |
| [1] H103′⋯O3′ [2] | Lp O3′ | σ* C10′–H103′ | 0.98 | |
| [1] O3⋯H8 [2] | Lp O3 | σ* C8–H8 | 2.48 | |
| [2] O3⋯H [W1] | Lp O3 | σ* O–H | 3.13 | |
| [2] O9⋯H [W2] | Lp O9 | σ* O–H | 2.48 | |
| [2] O7H⋯O8 [2] | Lp O8 | σ* O7–H | 3.85 | |
| [2] O7⋯H [W3] | Lp O7 | σ* O–H | 6.78 | |
| [2] H103⋯O [W3] | Lp O | σ* C10–H103 | 2.94 | |
| [2] H2⋯O [W3] | Lp O | σ* C2–H2 | 0.68 | |
Summing up all E(2) values of H-bonds between water molecules and units in the WBDCs (e.g., for S⋯G: O7H⋯O, O4H⋯O, O3⋯H, O9⋯H, O7⋯H, H103⋯O, and H2⋯O), we have, respectively, 39.19 and 43.29 kcal mol−1 for S⋯G and S⋯S complexes, which indicates a better interaction of water molecules with the S⋯S complex. Thus, a greater number of S-units would allow a more effective degree of hydration in lignin complexes, which is in consonance with a higher bound water/free water ratio found in HL (more methoxylated lignin) than in SL127 and lower absolute aqueous solvation free energy for S-lignin.35,45 Thus, the increase of the S-unit content in lignin would impede polymer extension and solvation (dissolution) with solvents, due possibly to strong interactions between units and water making lignin structures more compact.35 On the other hand, by summing up all E(2) values for H-bonds related to interactions between units (e.g., O7⋯HO4, O4⋯HO9, O3⋯HO9, O4⋯H9, O3⋯H8, and H103′⋯O3′), we have 27.86 and 27.09 kcal mol−1 for S⋯G and S⋯S, respectively. This suggests that interunit interactions in the S⋯G complex are slightly stronger than in the S⋯S complex, which shows that hydration is one of the phenomena contributing to favor interactions in WBDCs of lignin. However, another type of interaction, such as π interaction between aromatic rings, might also contribute to the overall interaction energy of WBDCs, which should be analyzed in detail.
The shorter distance (d) and lower interplanar angle (θ) between centroids in the S⋯S complex, with a more parallel (stacked) geometry, enables a better overlap by the contribution of dispersion forces.128 Because of the higher polarizability of electrons in the S⋯S complex (348.4 a.u.) than in the S⋯G complex (332.2 a.u.), the dispersion forces are stronger129 in the first complex. As is well known, higher polarizability enables electrons to more easily redistribute and allows the formation of stronger poles, which creates a higher attractive London dispersion energy (eqn (9)).130
 | (9) |
As found in organometallic complexes,130 the attractive London dispersion forces might benefit electron transfer from a Lewis base (e.g., π donor orbitals) to a σ* antibonding orbital in the S⋯S complex, in which there is a contribution of 1 kcal mol−1 promoted solely by the interaction between π C1–C6 [1] and σ* O4–HO4 [2] (Fig. 7b). Here, instead of an appropriate π stacking interaction, a local direct interaction is observed between a substituent (e.g., hydroxyl group) of one aromatic ring and the nearby vertex of the other ring115 (e.g., C1–C6) by π–σ* orbital interaction. Possibly this local interaction is predominant in the S⋯S complex because –OCH3 is an electron-withdrawing group, which manifests on the σ-bonding of the aromatic ring, thereby the σ-withdrawing character dominates the effects of substituents in WBDCs.74,75 In addition to this effect, the electrostatic attraction in H-bonds holding the rings closer in the S⋯S complex would allow stronger local direct interactions between substituents of a ring and the nearby vertex of the other ring,33,129 as discussed above. There may be certain cooperativity of hydrogen bonding and π-stacking in WBDCs. Unlike the S⋯S complex, π–σ* interactions are not abundant in the S⋯G complex (Fig. S4, ESI†), but rather predominate π–π* interactions. The most predominant interaction in the S⋯G complex was π C1–C2 [1] and π* C2–C3 [2] (Fig. 7a) with the value of E(2) of 0.55 kcal mol−1.
All results show that π interactions are relatively much weaker than H-bonds, but they contribute positively to the hydration of units, thus favoring interactions between units in WBDCs. At a supramolecular level, the combined interaction of hydrogen bonding and π-stacking stabilize lignin xylem tissue of tracheary elements of wood whose main function is water conduction.32,33 Based on the similar structures found in the complexes forming quasi-sandwich geometries between the centroids of the aromatic ring, it is quite likely that S–G lignins and S-lignins have similar “coiled” structures in the xylem tissue of wood. However, S-lignins are expected to show more coiled spiral conformation than S–G lignins, which have a higher content of β–β and β-5 bonds.131
3.5. Energy decomposition by the EDA-SBL scheme
Up to now, we have only considered attractive forces (H-bonds and London dispersion) in the interaction networks of WBDCs, but there are others forces involved in them, such as steric and Pauli repulsion corresponding to the electronic interaction between orbitals. Such repulsive effects of these forces can be measured by decomposing the total interaction energy into different types of energy using an energy partition scheme, such as EDA-SBL. Fig. 8 shows the breakdown of the molecular total energy of S⋯G and S⋯S complexes into steric, electrostatic, exchange–correlation, and Pauli dispersion energetic components using the EDA-SBL scheme. Calculating the energy difference of each contribution in Fig. 8, we found that the addition of one –OCH3 group to the S⋯G complex to produce the S⋯S complex provides an increase in steric and Pauli repulsion in 0.22 and 0.08 kcal mol−1, while there is also an increase in attractive electrostatic and dispersion forces in 0.58 and 0.03 kcal mol−1, respectively. On the one hand, the results show that the electrostatic term is dominant and controls the geometric preference of WBDCs in a quasi-sandwich conformation instead of other interactions coming from dispersion and repulsion due to electronic delocalization of the aromatic rings.49 The net contribution of the stacking interactions to the overall interaction energy is surprisingly small in these complexes, as observed in H-bonded “zipper” complexes.132On the other hand, the better electrostatic stabilization of the S⋯S complex relative to the S⋯G complex comes precisely from the additional –OCH3 substituent group, which explains the higher interaction energy for S⋯S than for S⋯G (Table 1). In fact, by summing the found differences values by the EDA-SBL scheme, an energy difference between S⋯G and S⋯S equal to −0.31 kcal mol−1 is obtained, which corresponds to the difference calculated between interaction energies (−0.3 kcal mol−1, Table 1) of these complexes. Assuming that there exists substituents additivity on interaction energy of WBDCs, as found in benzene dimers,75 one can validate this energy difference between WBDCs. By ab initio calculations, the interaction energy of benzene sandwich dimers when substituted with a –OCH3 group relative to the unsubstituted benzene dimer was in the range of −0.3 to −0.6 kcal mol−1,74 while the computed difference (−0.31 kcal mol−1) in our work falls in this range.
All the above results indicate that attractive electrostatic forces and London dispersion forces are positive contributors, while steric and Pauli repulsion forces are negative contributors in the interaction networks of WBDCs. The attractive electrostatic forces (Table S2, ESI†) are the major source of interactions in these dimers by H-bonds, overcoming the steric and Pauli repulsion effects (Fig. 8). The greater number of –OCH3 substituents in the S⋯S complex enhances the London dispersion energy133 due to the increase in polarizability of the aromatic ring (eqn (9)), but also there is an increase in the Pauli repulsion energy because –OCH3 is a π donor group. In other words, the additional –OCH3 substituent in the S⋯S complex relative to the S⋯G complex provides a slight increase of electron density in the internuclear region of aromatic rings (Fig. 9), hindering the stacking interaction as has been evidenced in the π/polar or electrostatic model.49,74 Herein, although the role of dispersion interactions is overweighted by performing the calculations in the gas phase,129 such interactions show to be even smaller than Pauli repulsion, which indicates that quantum effects contribute to the destabilization in WBDCs.
 | ||
| Fig. 9 Molecular electrostatic potential map for guaiacyl (G) and syringyl (S) units in the gaseous phase calculated at the M06-2X/6-31++g(d,p) theory level. The S unit has a richer π electron cloud than the G unit in the center of the substituted rings because –OCH3 is a π donor group,125 which increases the π-electron density by conjugating the lone electron pair of oxygen with the π-cloud of the aromatic ring by resonance effects (the resonance parameter for –OCH3 is −0.56).74 | ||
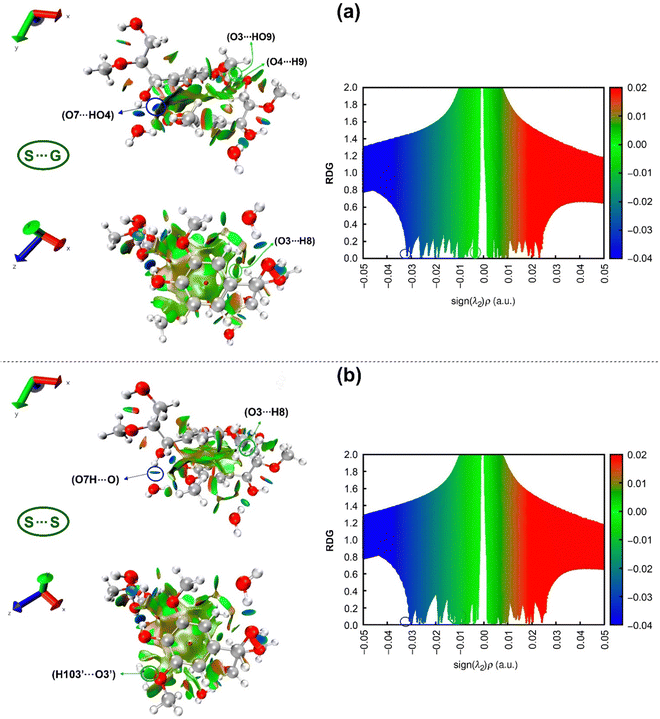
3.6. RDG analysis of the complexes
The reduced density gradient (RDG) analysis is employed as another useful method to further study non-covalent interactions, which can supply more reliable data compared to the AIM method and visualize them. The studied non-covalent interactions are revealed with RDG vs. the sign of the second Hessian eigenvalue (sing(λ2)ρ),82 as shown in Fig. 10.RDG scatter points in Fig. 10 indicate H-bonding attractive interactions at a negative scale (blue color) less than −0.01, van der Waals interactions (green color) at a scale from −0.01 to 0.01,134 and steric repulsions at the positive scale of sign(λ2)ρ greater than 0.01 “red color”. Although the difference between these two RDG scatters appears to be subtle, some differentiating details between S⋯G and S⋯S complexes can be drawn from them. The hydrogen bond AIM analysis states that the strongest intermolecular H-bond for the S⋯G complex is O7⋯HO4, while for the S⋯S complex, it is O7H⋯O, which are visualized with spikes at values of sign(λ2)ρ, respectively of −0.0318 and −0.0308 a.u. These spikes are marked by blue circles on the right-hand side of Fig. 10, corresponding to blue circled disk-shaped blocks in the structures on the left-hand side of this figure. The more negative values of sign(λ2)ρ for O7H⋯O, O4H⋯O, O3⋯H, H103⋯O and H2⋯O define a higher spike density zone in the RDG plot for the S⋯S complex, which is an indication of its higher hydration capacity than the S⋯G complex, in consonance with NBO analysis. Around −0.01 a.u., it is possible to observe a higher spike density for the S⋯S complex than for the S⋯G complex due to the attractive stronger O3⋯H8 interunit interaction located at −0.0125 a.u. and the appearance of a new interaction (H103′⋯O3′) at −0.0112 a.u. binding two S units in the S⋯S complex.
Interestingly, introducing a –OCH3 group in the S⋯G complex turns off the weak O3⋯HO9 and O4⋯H9 interactions at −0.0093 and −0.0102 a.u., respectively (Table 2). This is caused by the +M effect of the –OCH3 group, which depletes the negative charge on O3 and O4 atoms and decreases the attractive electrostatic forces in such interactions (Table S2, ESI†). It is important to highlight that although O3⋯H8, H103′⋯O3′, O3⋯HO9 and O4⋯H9 interactions are classified as van der Waals interactions according to the value of sign(λ2)ρ (around −0.01), they are likely “Keesom”135 interactions given by dipole/dipole forces governed by electrostatic effects. Finally, analyzing the steric repulsion at values of sign(λ2) ρ > 0.01 in RDG scatter points (the red region in Fig. 10), it can be noted that in the S⋯S complex, there is a slightly higher density of spikes than in the S⋯G complex. The above reveals that the additional –OCH3 group in the S⋯S complex induces steric repulsions between carbon (e.g., C10) of this group and carbons belonging to the aromatic ring (e.g., C2) (Fig. 2), besides the intrinsic electronic repulsion between centers of the aromatic rings (Pauli repulsion), as indicated by the red ellipsoid in the structures of the left panel in Fig. 10.
4. Conclusions
We have carried out DFT calculations at a reliable theory level (M06-2X/6-31+G(d,p)) on S⋯G and S⋯S complexes forming “coiled” structures into globular conformations of lignin. Regarding dimer ring orientation, the optimized structures of WBDCs by DFT were like the starting structures achieved by molecular dynamics studies. This indicates that new parameterizations of the CHARMM force field for lignin adequately reproduce structural features of lignin dimers with hydrogen bonding. The analysis methods (AIM, NBO, EDA-SBL, and RDG) suggest that in the S⋯S complex there is a stronger intermolecular interaction than in the S⋯G complex due to the interaction of the H-bonds with the water molecules acting as the glue between the units and π–σ* local direct-interaction between the substituent of one aromatic ring and the nearby vertex of the other ring. The hydrogen bonding interactions are predominant relative to π-stacking interactions, which include London dispersion and Pauli repulsion. Electrostatic interactions control the quasi-sandwich geometries between centroids of aromatic rings in these complexes and not by π–π interactions, in consonance with other studies of aromatic systems in the literature. However, despite the more favorable interactions in the S⋯S complex, it shows a less thermodynamic stability than the S⋯G complex due to the entropic contributions coming from the presence of the methoxy group in the S-unit. From a physical interaction point of view, our computational results suggest that S–G lignins are more stable or recalcitrant than S-lignins in biomass dissolution, even when branched interunit bonds (e.g., β–β and β-5) were not considered in our simple models. The similarity of WBDC structures indicates that S–G lignins and S-lignins are likely to have similar coiled structures in the xylem tissue of wood, but the stronger intermolecular interaction between S units mediated by H-bonds in S-lignins leads to somewhat more coiled and compact structures. Thus, as a biorefinery strategy to fraction lignin rich in S units might be used in polar solvents to replace intermolecular hydrogen bonds between S units and water molecules due to the increased hydration capacity of the S⋯S complex compared to the S⋯G complex. In the same way that with ionic liquids, polar solvents can dissolve S-lignin through favorable interactions with the aliphatic hydroxyl group in the α-position as the key site or the aromatic hydroxyl group as the secondary site. Future DFT calculations should be performed with these complexes using solvents different from water to evaluate which solvent system is better for dissolving them.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the COPPETEC foundation and partially by Programa de Recursos Humanos (PRH) da Agência Nacional do Petróleo (ANP), Gás Natural e Biocombustíveis with funds from the investment of oil companies qualified in the R&DI Clause of ANP Resolution 50/2015 (Grant No. 041319) and. The authors thank the Centro Nacional de Processamento de Alto Desempenho em São Paulo (CENAPAD-SP). We also wish to express our gratitude to the reviewers for the rigorous peer-review of this manuscript and constructive suggestions.References
- W. Boerjan, J. Ralph and M. Baucher, Lignin biosynthesis, Annu. Rev. Plant Biol., 2003, 54, 519, DOI:10.1146/annurev.arplant.54.031902.134938.
- J. Ralph, K. Lundquist, G. Brunow, F. Lu, H. Kim, P. F. Schatz, J. M. Marita, R. D. Hatfield, S. A. Ralph, J. H. Christensen and W. Boerjan, Lignins: natural polymers from oxidative coupling of 4-hydroxyphenylpropanoids, Phytochem. Rev., 2004, 3, 29, DOI:10.1023/B:PHYT.0000047809.65444.a4.
- Q. Liu, L. Luo and L. Zheng, Lignins: Biosynthesis and Biological Functions in Plants, Int. J. Mol. Sci., 2018, 19, 335, DOI:10.3390/ijms19020335.
- J. C. Río, J. Rencoret, A. Gutiérrez, T. Elder, H. Kim and J. Ralph, Lignin Monomers from beyond the Canonical Monolignol Biosynthetic Pathway: Another Brick in the Wall, ACS Sustainable Chem. Eng., 2020, 8, 4997, DOI:10.1021/acssuschemeng.0c01109.
- X. Li, J.-K. Weng and C. Chapple, Improvement of Biomass Through Lignin Modification, Plant J., 2008, 54, 569, DOI:10.1111/j.1365-313X.2008.03457.x.
- R. Vanholme, B. Demedts, K. Morreel, J. Ralph and W. Boerjan, Plant Physiol., 2010, 153, 895, DOI:10.1104/pp.110.155119.
- C.-J. Liu, Deciphering the Enigma of Lignification: Precursor Transport, Oxidation, and the Topochemistry of Lignin Assembly, Mol. Plant, 2012, 5, 304, DOI:10.1093/mp/ssr121.
- N. Terashima, M. Yoshida, J. Hafrén, K. Fukushima and U. Westermark, Proposed supramolecular structure of lignin in softwood tracheid compound middle lamella regions, Holzforschung, 2012, 66, 907, DOI:10.1021/acsapm.9b01007.
- Y. Zhang, H. He, K. Dong, M. Fan and S. Zhang, A DFT study on lignin dissolution in imidazolium-based ionic liquids, RSC Adv., 2017, 7, 12670, 10.1039/C6RA27059J.
- H. Luo and M. M. Abu-Omar, Encyclopedia of Sustainable Technologies, 2017, vol. 3, p. 573 DOI:10.1016/B978-0-12-409548-9.10235-0.
- Y. Pu, F. Hu, F. Huang, B. H. Davison and A. J. Ragauskas, Assessing the Molecular Structure Basis for Biomass Recalcitrance During Dilute Acid and Hydrothermal Pretreatments, Biotechnol. Biofuels, 2013, 6, 15, DOI:10.1186/1754-6834-6-15.
- R. Paliwal, K. Giri and J. Rai, in Handbook of Research on Uncovering New Methods for Ecosystem Management through Bioremediation. Chapter: Microbial Ligninolysis: Avenue for Natural Ecosystem Management, ed. P. A. Hershey, S. O. Singh and K. Shriwastav, IGI Global, USA, 2015 DOI:10.4018/978-1-4666-8682-3.ch006.
- A. J. Ragauskas, G. T. Beckham, M. J. Biddy, R. Chandra, F. Chen, M. F. Davis, B. H. Davison, R. A. Dixon, P. Gilna, M. Keller, P. Langan, A. K. Naskar, J. N. Saddler, T. J. Tschaplinski, G. A. Tuskan and C. E. Wyman, Lignin Valorization: Improving Lignin Processing in the Biorefinery, Science, 2014, 344, 1246843, DOI:10.1126/science.1246843.
- C. O. Tuck, E. Pérez, I. T. Horváth, R. A. Sheldon and M. Poliakoff, Valorization of Biomass: Deriving More Value from Waste, Science, 2012, 337, 695, DOI:10.1126/science.1218930.
- Q. Meng, J. Yan, R. Wu, H. Liu, Y. Sun, N. Wu, J. Xiang, L. Zheng, J. Zhang and B. Han, Sustainable production of benzene from lignin, Nat. Commun., 2021, 12, 4534, DOI:10.1038/s41467-021-24780-8.
- F. Huang, in Materials for Biofuels, ed. A. J. Ragauskas, World Scientific Publishing Co., 2013, pp. 1–26 Search PubMed.
- E. Dorrestijn, L. J. J. Laarhoven, I. W. C. E. Arends and P. Mulder, The Occurrence and Reactivity of Phenoxyl Linkages in Lignin and Low Rank Coal, J. Anal. Appl. Pyrolysis, 2000, 54, 153, DOI:10.1016/S0165-2370(99)00082-0.
- B. Kamm, P. R. Gruber and M. Kamm, Biorefineries – Industrial Processes and Products, Wiley Online Library, 2007 Search PubMed.
- M. Poletto, Lignin – Trends and Applications, 2018 DOI:10.5772/intechopen.68464.
- K. Osakabe, C. C. Tsao, L. Li, J. L. Popko, T. Umezawa, D. T. Carraway, D. T. Smeltzer, C. P. Joshi and V. L. Chiang, Coniferyl aldehyde 5-hydroxylation and methylation direct syringyl lignin biosynthesis in angiosperms, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 8955, DOI:10.1073/pnas.96.16.895.
- J.-K. Weng, X. Li, J. Stout and C. Chapple, Independent origins of syringyl lignin in vascular plants, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 7887, DOI:10.1073/pnas.0801696105.
- B. J. Janesko, Modeling interactions between lignocellulose and ionic liquids using DFT-D, Phys. Chem. Chem. Phys., 2011, 13, 11393, 10.1039/C1CP20072K.
- M. Yang, W. Zhao, S. Singh, B. Simmons and G. Cheng, On the solution structure of kraft lignin in ethylene glycol and its implication for nanoparticle preparation, Nanoscale Adv., 2019, 1, 299, 10.1039/c8na00042e.
- S. Bylin, T. Wells, Q. Sun, A. Ragauskas and H. Theliander, Lignin structure and aggregation behavior in a two-component ionic liquid solvent system, BioResources, 2014, 9, 6002 CrossRef.
- S. Kubo and J. Kadla, Hydrogen Bonding in Lignin: A Fourier Transform Infrared Model Compound Study, Biomacromolecules, 2005, 6, 2815, DOI:10.1021/bm050288q.
- J. L. Bregado, F. Souto, A. R. Secchi, F. W. Tavares and V. Calado, Molecular Dynamics Study of Thermophysical and Mechanical Properties in Hydrated Lignin with Compositions Close to Softwood, ACS Sustainable Chem. Eng., 2023, 11, 238, DOI:10.1021/acssuschemeng.2c05264.
- T. Vu, A. Chaffee and I. Yarovsky, Investigation of Lignin-water Interactions by Molecular Simulation, Mol. Simul., 2002, 28, 981, DOI:10.1080/089270204000002610.
- X. Y. Li and L. A. Eriksson, Molecular dynamics study of lignin constituents in water, Holzforschung, 2005, 59, 253, DOI:10.1515/HF.2005.042.
- K. Freudenberg and A. C. Neish, Constitution and Biosynthesis of Lignin, Springer-Verlag, Berlin, Germany, 1968, p. 132, ISBN 978-3-540-04274-7 Search PubMed.
- in Lignins, occurrence, formation, structure and reactions, ed. K. V. Sarkanen and C. H. Ludwig, Wiley-Interscience, California, 1971, p. 916, ISBN 0471754226 Search PubMed.
- G. Brunow, K. Lundquist and G. Gellerstedt, Lignin, in Analytical Methods in Wood Chemistry, Pulping and Papermaking, ed. E. Sjöström and R. Alén, Springer-Verlag, Berlin, Germany, 1999, pp. 77–124 Search PubMed.
- A. Emonet and A. Hay, Development and diversity of lignin patterns, Plant Physiol., 2022, 190, 31, DOI:10.1093/plphys/kiac261.
- H. S. Abreu, J. V. F. Latorraca, R. P. W. Pereira, M. B. O. Monteiro, F. A. Abreu and K. F. Amparado, A supramolecular proposal of lignin structure and its relation with the wood properties, An. Acad. Bras. Cienc., 2009, 81, 137 CrossRef CAS PubMed.
- J. V. Vermaas, L. Petridis, J. Ralph, M. F. Crowley and G. T. Beckham, Systematic Parameterization of Lignin for the CHARMM Force Field, Green Chem., 2019, 21, 109, 10.1039/C8GC03209B.
- J. V. Vermaas, M. F. Crowley and G. T. Beckham, Molecular Lignin Solubility and Structure in Organic Solvents, ACS Sustainable Chem. Eng., 2020, 8, 17839, DOI:10.1021/acssuschemeng.0c07156.
- M. Takada, R. P. Chandra and J. N. Saddler, The influence of lignin migration and relocation during steam pretreatment on the enzymatic hydrolysis of softwood and corn stover biomass substrates, Biotechnol. Bioeng., 2019, 116, 2864, DOI:10.1002/bit.27137.
- L. Petridis and J. C. Smith, Molecular-level driving forces in lignocellulosic biomass deconstruction for bioenergy, Nat. Rev. Chem., 2018, 2, 382, DOI:10.1038/s41570-018-0050-6.
- W. Zhao, L.-P. Xiao, G. Song, R.-C. Sun, L. He, S. Singh, B. A. Simmons and G. Cheng, From lignin subunits to aggregates: insights into lignin solubilization, Green Chem., 2017, 19, 3272, 10.1039/C7GC00944E.
- A. Guerra, A. R. Gaspar, S. Contreras, L. A. Lucia, C. Crestini and D. S. Argyropoulos, Phytochemistry, 2007, 68, 2570–2583, DOI:10.1016/j.phytochem.2007.05.026.
- Y. Qian, Y. Deng, X. Qiu, H. Li and D. Yang, Formation of uniform colloidal spheres from lignin, a renewable resource recovered from pulping spent liquor, Green Chem., 2014, 16, 2156, 10.1039/c3gc42131g.
- A. A. Myint, H. W. Lee, B. Seo, W.-S. Son, J. Yoon, T. J. Yoon, H. J. Park, J. Yu, J. Yoon and Y.-W. Lee, One pot synthesis of environmentally friendly lignin nanoparticles with compressed liquid carbon dioxide as an antisolvent, Green Chem., 2016, 18, 2129, 10.1039/c5gc02398j.
- V. Ponnuchamy, O. Gordobil, R. H. Diaz, A. Sandak and J. Sandak, Fractionation of lignin using organic solvents: a combined experimental and theoretical study, Int. J. Biol. Macromol., 2021, 168, 792, DOI:10.1016/j.ijbiomac.2020.11.139.
- H. Ji and P. Lv, Mechanistic insights into the lignin dissolution behaviors of a recyclable acid hydrotrope, deep eutectic solvent (DES), and ionic liquid (IL), Green Chem., 2020, 22, 1378, 10.1039/C9GC02760B.
- Q. Xia, Y. Liu, J. Meng, W. Cheng, W. Chen, S. Liu, Y. Liu, J. Li and H. Yu, Multiple hydrogen bond coordination in three-constituent deep eutectic solvents enhances lignin fractionation from biomass, Green Chem., 2018, 20, 2711, 10.1039/C8GC00900G.
- R. L. Silveira, S. R. Stoyanov, S. Gusarov, M. S. Skaf and A. Kovalenko, Supramolecular Interactions in Secondary Plant Cell Walls: Effect of Lignin Chemical Composition Revealed with the Molecular Theory of Solvation, J. Phys. Chem. Lett., 2015, 6, 206, DOI:10.1021/jz502298q.
- L. Petridis, R. Schulz and J. C. Smith, Simulation Analysis of the Temperature Dependence of Lignin Structure and Dynamics, J. Am. Chem. Soc., 2011, 133, 20277, DOI:10.1021/ja206839u.
- Y.-R. Chen and S. Sarkanen, Macromolecular replication during lignin biosynthesis, Phytochemistry, 2010, 71, 453, DOI:10.1016/j.phytochem.2009.11.012.
- P. Hobza and J. Šponer, Toward True DNA Base-Stacking Energies: MP2, CCSD(T), and Complete Basis Set Calculations, J. Am. Chem. Soc., 2002, 124, 11802, DOI:10.1021/ja026759n.
- C. A. Hunter and J. K. M. Sanders, The nature of. π–π interactions, J. Am. Chem. Soc., 1990, 112, 5525, DOI:10.1021/ja00170a016.
- S. C. C. van der Lubbe and C. F. Guerra, The Nature of Hydrogen Bonds: A Delineation of the Role of Different Energy Components on Hydrogen Bond Strengths and Lengths, Chem. – Asian J., 2019, 14, 2759, DOI:10.1002/asia.201900717.
- J. Wang, X. Shi, X. Du and W. Cao, A DFT investigation on interactions between lignin and ionic liquids, Russ. J. Phys. Chem., 2017, 91, 1468, DOI:10.1134/S0036024417080155.
- X. Mu, Z. Han, C. Liu and D. Zhang, Mechanistic Insights into Formaldehyde-Blocked Lignin Condensation: A DFT Study, J. Phys. Chem. C, 2019, 123(14), 8640, DOI:10.1021/acs.jpcc.9b00247.
- Z. Ju, W. Xiao, X. Yao, X. Tan, B. A. Simmons, K. L. Sale and N. Sun, Theoretical study on the microscopic mechanism of lignin solubilization in Keggin-type polyoxometalate ionic liquids, Phys. Chem. Chem. Phys., 2020, 22, 2878, 10.1039/C9CP05339E.
- V. Ponnuchamy, A. Sandak and J. Sandak, Multiscale modelling investigation of wood modification with acetic anhydride, Phys. Chem. Chem. Phys., 2020, 22, 28448, 10.1039/D0CP05165A.
- X. Zhang, W. Yang and W. Blasiak, Modeling Study of Woody Biomass: Interactions of Cellulose, Hemicellulose, and Lignin, Energy Fuels, 2011, 25, 4786, DOI:10.1021/ef201097d.
- H. Yang, H. D. Watts, V. Gibilterra, T. B. Weiss, L. Petridis, D. J. Cosgrove and J. D. Kubicki, Quantum Calculations on Plant Cell Wall Component Interactions, Interdiscip Sci., 2019, 11, 485, DOI:10.1007/s12539-018-0293-4.
- N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115, 2315, DOI:10.1080/00268976.2017.1333644.
- Y. Elrhayam and A. Elharfi, 3D-QSAR studies of the chemical modification of hydroxyl groups of biomass (cellulose, hemicelluloses and lignin) using quantum chemical descriptors, Heliyon, 2019, 5, e02173, DOI:10.1016/j.heliyon.2019.e02173.
- T. Zhang, Y. Zhang, Y. Wang, F. Huo, Z. Li, Q. Zeng, H. He and X. Li, Theoretical Insights into the Depolymerization Mechanism of Lignin to Methyl p-hydroxycinnamate by [Bmim][FeCl4] Ionic Liquid, Front. Chem., 2019, 7, 446, DOI:10.3389/fchem.2019.00446.
- B. Durbeej and L. A. Eriksson, A Density Functional Theory Study of Coniferyl Alcohol Intermonomeric Cross Linkages in Lignin – Three-Dimensional Structures, Stabilities and the Thermodynamic Control Hypothesis, Holzforschung, 2003, 57, 150, DOI:10.1515/HF.2003.024.
- H. D. Watts, M. N. A. Mohamed and J. D. Kubicki, Comparison of Multistandard and TMS-Standard Calculated NMR Shifts for Coniferyl Alcohol and Application of the Multistandard Method to Lignin Dimers, J. Phys. Chem. B, 2011, 115, 1958, DOI:10.1021/jp110330q.
- P. Bock, P. Nousiainen, T. Elder, M. Blaukopf, H. Amer, R. Zirbs, A. Potthast and N. Gierlinger, Infrared and Raman spectra of lignin substructures: dibenzodioxocin, J. Raman Spectrosc., 2020, 51, 422, DOI:10.1002/jrs.5808.
- C. A. C. Kramer, A. R. L. Silva and L. S. Carvalho, Influence of phenylpropanoid units of lignin and its oxidized derivatives on the stability and βO4 binding properties: DFT and QTAIM approach, Org. Biomol. Chem., 2020, 18, 5897, 10.1039/D0OB01171A.
- Y. Zhu, J. Yan, C. Liu and D. Zhang, Modeling interactions between a β-O-4 type lignin model compound and 1-allyl-3-methylimidazolium chloride ionic liquid, Biopolymers, 2017, 107, e23022, DOI:10.1002/bip.23022.
- T. Elder, Bond Dissociation Enthalpies of a Pinoresinol Lignin Model Compound, Energy Fuels, 2014, 28, 1175, DOI:10.1021/ef402310h.
- R. Parthasarathi, R. A. Romero, A. Redondo and S. Gnanakaran, Theoretical study of the remarkably diverse linkages in lignin, J. Phys. Chem. Lett., 2011, 2, 2660, DOI:10.1021/jz201201q.
- N. Mardirossian and M. Head-Gordon, ωB97M-V: a combinatorially optimized, range-separated hybrid, meta-GGA density functional with VV10 nonlocal correlation, J. Chem. Phys., 2016, 144, 214110, DOI:10.1063/1.4952647.
- V. Ponnuchamy and E. S. Esakkimuthu, Density functional theory study of lignin, carboxymethylcellulose and unsustainable binders with graphene for electrodes in lithium-ion batteries, Appl. Surf. Sci., 2022, 573, 151461, DOI:10.1016/j.apsusc.2021.151461.
- Y. Zhao and D. G. Truhlar, Density functionals with broad applicability in chemistry, Acc. Chem. Res., 2008, 41, 157, DOI:10.1021/ar700111a.
- Y. Zhao and D. G. Truhlar, Applications and validations of the Minnesota density functionals, Chem. Phys. Lett., 2011, 502, 1, DOI:10.1016/j.cplett.2010.11.060.
- M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions, J. Phys. Chem. A, 2013, 117(47), 12590, DOI:10.1021/jp408166m.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215, DOI:10.1007/s00214-007-0310-x.
- E. G. Hohenstein, S. T. Chill and C. D. Sherrill, Assessment of the Performance of the M05-2X and M06-2X Exchange-Correlation Functionals for Noncovalent Interactions in Biomolecules, J. Chem. Theory Comput., 2008, 4, 1996, DOI:10.1021/ct800308k.
- S. E. Wheeler, A. J. McNeil, P. Muller, T. M. Swager and K. N. Houk, Probing Substituent Effects in Aryl-Aryl Interactions Using Stereoselective Diels-Alder Cycloadditions, J. Am. Chem. Soc., 2010, 132, 3304, DOI:10.1021/ja903653j.
- S. E. Wheeler and K. N. Houk, Substituent Effects in the Benzene Dimer are Due to Direct Interactions of the Substituents with the Unsubstituted Benzene, J. Am. Chem. Soc., 2008, 130, 10854, DOI:10.1021/ja802849j.
- E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1, DOI:10.1002/wcms.51.
- S. J. Grabowski, Non-covalent interactions – QTAIM and NBO analysis, J. Mol. Model., 2013, 19, 4713, DOI:10.1007/s00894-012-1463-7.
- R. F. W. Bader, Encyclopedia of Computational Chemistry, John Wiley & Sons, Ltd, 2002 Search PubMed.
- J. Cioslowski, Atoms in molecules: a quantum theory, Science, 1991, 252, 1566, DOI:10.1126/science.252.5012.1566-a.
- R. G. Parr, Horizons of Quantum Chemistry, Springer, 1980, pp. 5–15 Search PubMed.
- R. F. W. Bader, Atoms in molecules, Acc. Chem. Res., 1985, 18, 9, DOI:10.1021/ar00109a003.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498, DOI:10.1021/ja100936w.
- R. A. Boto, J.-P. Piquemal and J. Contreras-García, Revealing strong interactions with the reduced density gradient: a benchmark for covalent, ionic and charge-shift bonds, Theor. Chem. Acc., 2017, 136, 138, DOI:10.1007/s00214-017-2169-9.
- S. Liu, Steric effect: a quantitative description from density functional theory, J. Chem. Phys., 2007, 126, 244103-1, DOI:10.1063/1.2747247.
- S. Liu, Origin and Nature of Bond Rotation Barriers: A Unified View, J. Phys. Chem. A, 2013, 117, 962, DOI:10.1021/jp312521z.
- V. G. Tsirelson, A. I. Stash and S. Liu, Quantifying steric effect with experimental electron density, J. Chem. Phys., 2010, 133, 114110, DOI:10.1063/1.3492377.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864, DOI:10.1103/PhysRev.136.B864.
- V. L. Chiang and M. Funaoka, The Difference between Guaiacyl and Guaiacyl-Syringyl Lignins in their Responses to Kraft Delignification, Holzforschung, 1990, 44, 309, DOI:10.1515/hfsg.1990.44.4.309.
- J. J. Stewart, T. Akiyama, C. Chapple, J. Ralph and S. D. Mansfield, The Effects on Lignin Structure of Overexpression of Ferulate 5-Hydroxylase in Hybrid Poplar, Plant Physiol., 2009, 150, 621, DOI:10.1104/pp.109.137059.
- C. Buhl, R. Meilan and R. L. Lindroth, Genetic Modification of Lignin in Hybrid Poplar (Populus alba
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
× ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Populus tremula) Does Not Substantially Alter Plant Defense or Arthropod Communities, J. Insect. Sci., 2017, 17, 76, DOI:10.1093/jisesa/iex052.
Populus tremula) Does Not Substantially Alter Plant Defense or Arthropod Communities, J. Insect. Sci., 2017, 17, 76, DOI:10.1093/jisesa/iex052. - M. J. Frisch, G. W. Trucks and H. B. Schlegelet al.Gaussian 09, Revision D. 01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions, J. Chem. Theory Comput., 2006, 2, 364, DOI:10.1021/ct0502763.
- J. Šponer, J. Leszczyski and P. Hobza, Nature of Nucleic Acid-Base Stacking: Nonempirical ab Initio and Empirical Potential Characterization of 10 Stacked Base Dimers. Comparison of Stacked and H-Bonded Base Pairs, J. Phys. Chem., 1996, 100, 5590, DOI:10.1021/jp953306e.
- J. Šponer, J. Leszczynski and P. Hobza, Hydrogen Bonding and Stacking of DNA Bases: A Review of Quantum-chemical ab initio Studies, J. Biomol. Struct. Dyn., 1996, 14, 117, DOI:10.1080/07391102.1996.10508935.
- J. D. Kubicki, M. N. A. Mohamed and H. D. Watts, Quantum mechanical modeling of the structures, energetics and spectral properties of Iα and Iβ cellulose, Cellulose, 2013, 20, 9, DOI:10.1007/s10570-012-9838-6.
- Expanding the limits of computational chemistry, https://gaussian.com/integral/. Accessed 04/2023.
- J. Šponer, P. Hobza and J. Leszczynski, Chapter 3 – Computational Approaches to the Studies of the Interactions of Nucleic Acid Bases, Theor. Comput. Chem., 1999, 8, 85, DOI:10.1016/S1380-7323(99)80078-8.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553, DOI:10.1080/00268977000101561.
- R. Lü, J. Lin and Z. Qu, Theoretical study on interactions between ionic liquids and organosulfur compounds, Comput. Theor. Chem., 2012, 1002, 49, DOI:10.1016/j.comptc.2012.10.002.
- M. Moosavi, N. Banazadeh and M. Torkzadeh, Structure and Dynamics in Amino Acid Choline-Based Ionic Liquids: A Combined QTAIM, NCI, DFT, and Molecular Dynamics Study, J. Phys. Chem. B, 2019, 123, 4070, DOI:10.1021/acs.jpcb.9b01799.
- R. F. W. Bader, Atoms in molecules: a quantum theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- R. F. W. Bader, A Bond Path:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Universal Indicator of Bonded Interactions, J. Phys. Chem. A, 1998, 102, 7314, DOI:10.1021/jp981794v.
A Universal Indicator of Bonded Interactions, J. Phys. Chem. A, 1998, 102, 7314, DOI:10.1021/jp981794v. - R. F. W. Bader and H. Essén, The characterization of atomic interactions, J. Chem. Phys., 1984, 80, 194, DOI:10.1063/1.446956.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580, DOI:10.1002/jcc.22885.
- Multiwfn software manual (version 3.8), https://sobereva.com/multiwfn, Accessed 14/3/2023.
- A. E. Reed, F. Weinhold, L. A. Curtiss and D. J. Pochatko, Natural bond orbital analysis of molecular interactions: theoretical studies of binary complexes of HF, H2O, NH3, N2, O2, F2, CO, and CO2 with HF, H2O, and NH3, J. Chem. Phys., 1986, 84, 5687, DOI:10.1063/1.449928.
- F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, John Wiley & Sons, New Jersey, 2012 Search PubMed.
- A. V. Morozov, K. M. S. Misura, K. Tsemekhman and D. Baker, Comparison of Quantum Mechanics and Molecular Mechanics Dimerization Energy Landscapes for Pairs of Ring-Containing Amino Acids in Proteins, J. Phys. Chem. B, 2004, 108, 8489, DOI:10.1021/jp037711e.
- X.-X. Fu, J.-F. Li and R.-Q. Zhang, Strong Orbital Interaction in pi–pi Stacking System, arXiv, 2016, preprint, arXiv.1601.01150 DOI:10.48550/arXiv.1601.01150.
- L.-J. Riwar, N. Trapp and B. Kuhn, F. Diederich. Substituent Effects in Parallel-Displaced π–π Stacking Interactions: Distance Matters, Angew. Chem., 2017, 56, 11252, DOI:10.1002/anie.201703744.
- M. O. Sinnokrot, E. F. Valeev and C. D. Sherrill, Estimates of the Ab Initio Limit for π−π Interactions:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) The Benzene Dimer, J. Am. Chem. Soc., 2002, 124, 10887, DOI:10.1021/ja025896h.
The Benzene Dimer, J. Am. Chem. Soc., 2002, 124, 10887, DOI:10.1021/ja025896h. - G. Brunow, I. Kilpiläinen, J. Sipilä, K. Syrjänen, P. Karuhnen, H. Setälä and P. Rummako, Oxidative coupling of phenols and the biosynthesis of lignin, in Lignin and Lignans, ed. N. G. Lewis and S. Sarkanen, ACS Symposium Series 697, American Chemical Society, Washington DC, USA, 1996, pp. 131–147 Search PubMed.
- C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, Aromatic interactions, J. Chem. Soc., Perkin Trans. 2, 2001, 651, 10.1039/b008495f.
- K. Carter-Fenk and J. M. Herbert, Electrostatics does not dictate the slip-stacked arrangement of aromatic π–π interactions, Chem. Sci., 2020, 11, 6758, 10.1039/D0SC02667K.
- S. E. Wheeler, Local Nature of Substituent Effects in Stacking Interactions, J. Am. Chem. Soc., 2011, 133, 10262, DOI:10.1021/ja202932e.
- S. E. Wheeler and K. N. Houk, Substituent Effects in the Benzene Dimer are Due to Direct Interactions of the Substituents with the Unsubstituted Benzene, J. Am. Chem. Soc., 2008, 130, 10854, DOI:10.1021/ja802849j.
- R. Thakuria, N. K. Nath and B. K. Saha, The Nature and Applications of π–π Interactions: A Perspective, Cryst. Growth Des., 2019, 19, 523, DOI:10.1021/acs.cgd.8b01630.
- C. R. Martinez and B. L. Iverson, Rethinking the term “pi-stacking”, Chem. Sci., 2012, 3, 2191, 10.1039/c2sc20045g.
- T. Janowski and P. Pulay, High accuracy benchmark calculations on the benzene dimer potential energy surface, Chem. Phys. Lett., 2007, 447, 27, DOI:10.1016/j.cplett.2007.09.003.
- J. R. Grover, E. A. Walters and E. T. Hui, Dissociation energies of the benzene dimer and dimer cation, J. Phys. Chem., 1987, 91, 3233, DOI:10.1021/j100296a026.
- G. R. Desiraju, A Bond by Any Other Name, Angew. Chem., Int. Ed., 2011, 50, 52, DOI:10.1002/anie.201002960.
- A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441, DOI:10.1021/j100785a001.
- A. H. Pakiari and K. Eskandari, The chemical nature of very strong hydrogen bonds in some categories of compounds, THEOCHEM, 2006, 759, 51, DOI:10.1016/j.theochem.2005.10.040.
- M. K. Tiwari and K. Vanka, Exploiting directional long range secondary forces for regulating electrostatics-dominated noncovalent interactions, Chem. Sci., 2017, 8, 1378, 10.1039/C6SC03642B.
- L. A. Wiles, The methoxyl group, Chem. Rev., 1956, 56, 329, DOI:10.1021/cr50008a005.
- S. J. Grabowski, Theoretical studies of strong hydrogen bonds, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 131, 10.1039/B417200K.
- F. Longuetaud, F. Mothe, M. Fournier, J. Dlouha, P. Santenoise and C. Deleuze, Within-stem maps of wood density and water content for characterization of species: a case study on three hardwood and two softwood species, Ann. Forest Sci., 2016, 73, 601, DOI:10.1007/s13595-016-0555-4.
- J. R. T. Arendorf, A study of some non-covalent functional group pi interactions, PhD thesis, University CollegeLondon, 2011, https://discovery.ucl.ac.uk/id/eprint/1334083/1/1334083.pdf Search PubMed.
- J. Hwang, B. E. Dial, P. Li, M. E. Kozik, M. D. Smith and K. D. Shimizu, How important are dispersion interactions to the strength of aromatic stacking interactions in solution?, Chem. Sci., 2015, 6, 4358, 10.1039/C5SC01370D.
- D. J. Liptrot and P. P. Power, London dispersion forces in sterically crowded inorganic and organometallic molecules, Nat. Rev. Chem., 2017, 1, 0004, DOI:10.1038/s41570-016-0004.
- K. E. Achyuthan, A. M. Achyuthan, P. D. Adams, S. M. Dirk, J. C. Harper, B. A. Simmons and A. K. Singh, Supramolecular Self-Assembled Chaos: Polyphenolic Lignin's Barrier to Cost-Effective Lignocellulosic Biofuels, Molecules, 2010, 15, 8641, DOI:10.3390/molecules15118641.
- S. L. Cockroft, C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, Electrostatic Control of Aromatic Stacking Interactions, J. Am. Chem. Soc., 2005, 127, 8594, DOI:10.1021/ja050880n.
- M. O. Sinnokrot and C. D. Sherrill, Unexpected Substituent Effects in Face-to-Face π-Stacking Interactions, J. Phys. Chem., 2003, 107, 8378, DOI:10.1021/jp030880e.
- S. Ullah, H. Sadia, F. Ullah and T. Jadoon, Inclusive DFT insight into sensing mechanism of cyclotetrapyrole towards lung irritants, J. Mol. Model., 2022, 28, 110, DOI:10.1007/s00894-022-05100-3.
- W. H. Keesom, The second viral coefficient for rigid spherical molecules, whose mutual attraction is equivalent to that of a quadruplet placed at their centre, in KNAW, Proceedings, 18 I, 1915, Amsterdam, 1915, pp. 636–646.
Footnote |
| † Electronic supplementary information (ESI) available: Comparison of WBDCs inferred by radial distribution functions from MD simulations and DFT calculations. Optimized structures of S⋯G without water using DFT calculations. Structures of WBDCs: S⋯G and S⋯S showing all bonding critical points estimated using AIM's theory. Comparison of the geometric characteristics of WBDCs using DFT calculations and MD simulations. Electrostatic properties of hydrogen bonds in WBDCs. The main electron donor–acceptor interactions in π-stacking for WBDCs and their second-order perturbation stabilization energies at the M06-2X/6-31++g(d,p) level. Energetic contribution of π–π* and π-σ* interactions in WBDCs. Values of thermodynamic properties of units (S, G, and water) and WBDCs (S⋯S and S⋯G) calculated at the M06-2X/6-31++g(d,p) level. See DOI: https://doi.org/10.1039/d4cp00312h |
| This journal is © the Owner Societies 2024 |