Open Access Article
Open Access ArticleUltrafast control of the LnF+/LnO+ ratio from Ln(hfac)3
Jiangchao
Chen
,
Xi
Xing
,
Roberto
Rey-de-Castro
and
Herschel
Rabitz
 *
*
Department of Chemistry, Princeton University, Princeton, New Jersey 08544, USA. E-mail: hrabitz@princeton.edu
First published on 19th April 2024
Abstract
The photo-induced dissociative ionization of lanthanide complexes Ln(hfac)3 (Ln = Pr, Er, Yb) is studied using ultrafast shaped laser pulses in a time-of-flight (TOF) mass spectrometry setup. Various fluorine and Ln-containing mass fragments were observed, which can be interpreted by the photo-fragmentation mechanistic pathway involving C–C bond rotation processes proposed previously. A set of experiments used pulse shaping guided by closed-loop feedback control to identify pulses that optimize the ratio of LnF+/LnO+. In agreement with previous studies in which very little LnO+ was observed, broad pulses were found to maximize the LnF+/LnO+ ratio, which involves metal–ligand bond-breaking followed by bond rotation and bond rearrangement. In contrast, a transform limited (TL) pulse favored the formation of LnO+. Finally, the recently developed experimental control pulse slicing (CPS) technique was applied to elucidate the dynamics induced by fields that either maximize or minimize the LnF+/LnO+ ratio, which also indicates that longer laser pulses facilitate LnF+ formation during the C–C bond rotation dissociative-ionization process.
I. Introduction
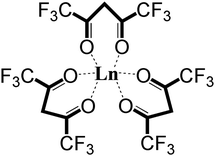
There are potentially wide applications of lanthanide oxides and fluorides in the field of materials science. For example, thin film lanthanide oxides are good candidates as gate materials in metal-oxide semiconductor field effect transistors (MOSFETs)1 due to their high electric permittivity and the potential of reducing the film thickness. Lanthanide fluorides constitute a common inorganic matrix for phosphors due to their low degree of phonon energy coupling.2 Additionally, an efficient energy transfer from Yb to Er has been obtained in a NaYF4 matrix to form highly luminescent NIR-to-visible up-conversion nanocrystals, β-NaYF4:Er,Yb.3 The β-diketonate complexes, such as Ln(thd)3 (thd- = 2,2,6,6-tetramethyl-3,5-heptanedionate), are traditional precursors for thin films of lanthanide materials during metal–organic chemical vapor deposition (MOCVD).4 Fluorinated lanthanide complexes, Ln(hfac)3 (hfac = hexafluoroacetylacetonate) (shown in Fig. 1) and Ln(fod)3 (fod = 1,1,1,2,2,3,3-heptafluoro-7,7-dimethyl-4,6-octanedionate), are also commonly used as precursors in MOCVD, because of their high thermal stability, volatility,5,6 and superior mass transport properties.7,8 Even though Ln(hfac)3 and Ln(fod)3 are both oxygen-coordinated complexes, they are still excellent candidates for deposition of lanthanide fluorides.8,9 Additionally, it is currently difficult to form lanthanide oxides from Ln(hfac)3 or Ln(fod)3 alone. In order to generate lanthanide oxides, a common strategy is to apply a co-precursor and post-deposition treatment.10Previous studies have considered the photofragmentation mechanisms of Ln(hfac)3 and Ln(fod)3, as well as the propensity for gas-phase formation of lanthanide fluorides.7,11–13 Gas-phase metal fluoride formation is consistent with earlier results by Zink et al.12 who observed the spectroscopic signature of CrF following Cr(hfac)3 photolysis with a ns laser at ∼400 nm. As shown in Fig. 2, they proposed a unimolecular reaction that was initiated by a metal-oxide bond elongation under laser field excitation, followed by Cα–C(O) bond rotation bringing the CF3 group into proximity to the metal.12 A similar rotation-based mechanism was proposed by Condorelli et al. as a reasonable means for explaining the production of SrF2 from the MOCVD of Sr(hfac)2tetraglyme.13 Pollard et al. further observed that the metal fluoride formation would be accompanied by the elimination of CO.7
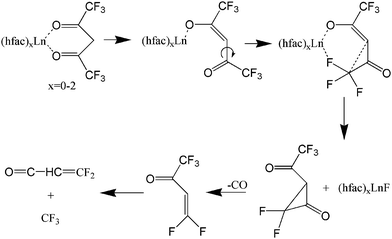 | ||
| Fig. 2 Lanthanide fluoride compounds resulting from C–C bond rotation according to ref. 7 and 11–13 The focus is in a single ligand with other possibly present as well. | ||
Furthermore, the metal oxides have been rarely observed using Ln(hfac)3 or Ln(fod)3 as precursors in previous laser dissociation-ionization experiments. Small amounts of oxide fragments from Pr(hfac)3 and Pr(fod)3 were reported, but no oxides were observed for the europium, terbium, or gadolinium analogues with CW and ns lasers.11
Intense, ultrashort laser pulses are capable of strongly interacting with matter resulting in phenomena such as above threshold ionization,14,15 high harmonic generation,16–18 Coulomb explosion,19 nonadiabatic excitation of polyatomic molecules,20,21 and even neutron emission.22,23 Nakashima, et al. found that strong molecular fragmentation often occurs when the excitation wavelength is resonant with cation electronic levels.24 For excitation at non-resonant wavelengths, a sufficiently intense short pulse is often necessary to achieve significant parent molecular ionization, while suppressing further molecular fragmentation.24
In our previous study of Ln(hfac)3,25 we showed that intense femtosecond laser pulses can generate a variety of high mass fluorine-containing metal fragments, indicating that two of the three ligands are involved in metal fluorination. In this paper, in contrast with previous other studies,11 we observed large LnO+ peaks with the precursors Pr(hfac)3, Er(hfac)3, and Yb(hfac)3. According to the fluoride formation mechanism proposed by Zink et al.,12 the Cα–C(O) bond rotation brings the CF3 group into proximity to the metal. The bond rotation is thought to take hundreds of picoseconds, and in the previous experiments with CW or ns lasers the rotation should be finished long before the laser interaction is over. In the experiments reported in this paper, sub-picosecond appropriately tailored laser pulses are found to greatly enhance LnO+ generation and restrict bond rotation. Our findings are also supported by the results of time-resolved measurements taken under the control pulse slicing (CPS) mechanism analysis protocol.26 CPS is a versatile technique that allows for extracting time-resolved information from laser-control experiments, including those involving an optimally determined laser field, E(t). The CPS data is attained through a series of experiments in which a pulse's time profile E(t) is “sliced-off” after a time t = τ (i.e., E(t) is smoothly made equal to 0 for t > τ). The physical system's response to the sliced field gives information about processes that are triggered or frustrated by the removed part of the field after t = τ. The evolution of signals (in this case the intensity of the various fragments) corresponding to slicing the field at various times t = τ can then aid in piecing together what parts of E(t) are relevant to the underlying physical processes. As discussed below, the CPS results indicate that a short pulse favors oxide formation because the Cα–C(O) bond does not have enough time to rotate. And, as the pulse is stretched, the formation of PrF+ is more favorable.
The paper is organized as follows: Section II describes the experimental setup including the laser system, the means for sample delivery, and the vacuum system. Section III presents the results and a discussion focused on the following two aspects: (1) controlling the fragmentation ratio of LnO+ and LnF+ using shaped fs laser pulses, and (2) understanding the mechanism for controlling the fragment ratio of PrF+/PrO+ with shaped pulses. Section IV provides a conclusion for the mechanistic understanding of the dissociative ionization studies of the PrF+/PrO+ ratio with shaped fs laser pulses.
II. Experimental setup
As described in more detail previously27 a linear time-of-flight mass spectrometer (Jordan TOF) was used to detect laser induced positively charged fragments. The laser employed in the experiments is a fs Ti:Sapphire laser system consisting of an oscillator and a multi-pass amplifier (KMlab, Dragon) operating at a repetition rate of 3 kHz with pulses of ∼35 fs width at ∼785 nm. A pulse shaper with a dual-mask liquid crystal SLM containing 640 pixels (CRI, SLM-640), was used to generate linearly chirped pulses as well as arbitrarily shaped laser pulses. Each TL pulse with ∼200 μJ energy, was then focused with a fused silica lens of f = 20 cm into an optically-accessible vacuum chamber (part of the mass spectrometer), to a spot size of ∼50 μm diameter; each pulse is estimated to have a maximum peak intensity of ∼3 × 1014 W cm−2 focused in between the repeller plate (3 kV) and extraction grid (2 kV) of the mass spectrometer.The precursor molecules as solids, Pr(hfac)3, Er(hfac)3, and Yb(hfac)3, were purchased from Sterm Chemicals, Inc. and used without further treatment. Each solid sample (i.e., handled separately) was slowly heated inside the vacuum chamber stepwise up to approximately 120–140 °C, slightly above the sublimation temperature, while pyrolysis was minimized, which normally occurs at much higher temperature above 200 °C. We assume that, only the precursor molecules (i.e., Ln(hfac)3) can enter the gas phase for further laser ionization and fragmentation, while any metal-containing pyrolysis products, if they arise, would stay in the solid phase because of their much higher sublimation temperature due to increased polarity upon the loss of ligands. The sample holder was home-made, consisting of a metal reservoir, which was wrapped with heating tape and attached to a thermocouple, allowing for both heating in vacuum and monitoring the temperature. The sample holder had a small opening (∼0.5 mm) into a 0.5 mm diameter tube of 2 cm length pointing towards the focus of the laser lens. As the solid sample was transformed into the gas phase by heating, it effusively leaked through the tube and reached the laser focus for dissociative ionization and subsequent mass spectral (MS) detection. The distance between the tip of the tube and the laser focus could be adjusted for optimal gas density. The pressure of the vacuum chamber was between 1 × 10−6 torr and 5 × 10−6 torr under effusive entry of the heated sample. Ion signals were collected and amplified with a 40 mm diameter microchannel plate, which was coupled to a digital oscilloscope (Lecroy 104MXi) for signal averaging and processing.
III. Results and discussion
This section presents our experimental results and discusses the following two aspects of laser-driven dissociative-ionization: (1) control of the fragmentation ratio LnF+/LnO+ using shaped fs laser pulses, and (2) presentation of a mechanistic analysis, aided by CPS, for controlling the ratio of PrF+/PrO+ with shaped pulses.III.1. Controlling the fragmentation ratio of LnO+ and LnF+ using shaped fs laser pulses
The MS observations presented in our previous study,25 corresponding to a transform limited (TL) pulse, suggest that C–C bond rotation plays an important role in the formation of fluorinated metal compounds. Furthermore, the overall mechanism in that paper is argued to be strongly influenced by laser peak intensity. However, further subtle mechanistic processes may be altered by changing features in the control pulse shape, which were not explored in that work. In particular, as mentioned above, the C–C bond rotation process involves the breaking of the Ln–O metal ligand bond and the formation of new Ln–F bonds by substitution. In order to explore the extent to which this process can be laser pulse shape controlled and to gain an understanding of the associated mechanisms, we applied adaptive feedback control to manipulate the fragmentation ratio of PrF+/PrO+. The optimizations, carried out using a genetic algorithm (GA) utilizing phase-only control variables with 80 pixel bundles (i.e., 8 neighboring pixels formed a bundle), showed that the PrF+/PrO+ ratio can be modified by nearly a factor of 3 by phase shaping (i.e., the pulse energy was fixed) under our experimental conditions. With the TL pulse, the PrO+ signal can be twice as large as that for PrF+, which is shown is Fig. 3.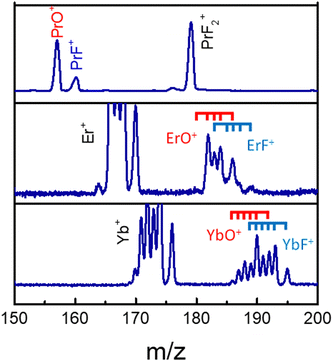 | ||
| Fig. 3 The LnO+ and LnF+ arising from Pr(hfac)3 (top), Er(hfac)3 (middle), and Yb(hfac)3 (bottom) with a TL pulse. The blue and red ticks indicate isotope variants of Ln. | ||
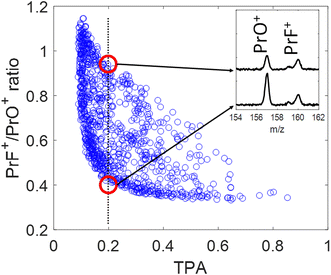
We further explore the behavior of the PrF+/PrO+ ratio by comparing it to the two-photon-absorption (TPA) signals (i.e., a measure of the pulse intensity) corresponding to a large number of uniquely-shaped pulses. A polynomial spectral phase function Φ (i.e., Φ(Ω) = AΩ2+ BΩ3+ CΩ4, where Ω is spectral frequency) with three parameters (A, B, C) were used here to generate ∼1000 different pulse shapes by randomly sampling the parameters. We recorded the mass spectra and TPA signal for each pulse.
The blue circles in Fig. 4 show the correlation between the PrF+/PrO+ ratio and the measured TPA signal for each shaped pulse using the polynomial phase sampling scheme explained above. The TPA signal was normalized so that TPA = 1 corresponds to the TL pulse. The pulse gets more stretched at lower TPA signals, where the ratio also generally increases, favoring the formation of PrF+ at the expense of PrO+. At high TPA signals (>0.6) the PrF+/PrO+ ratio stays within a narrow range around the relatively low value of ∼0.35. On the other hand, when the TPA signal is low (<0.4) the PrF+/PrO+ ratio spreads over a large dynamic range approximately from 0.4 to 1.1. The maximum and minimum attainable ratios are close to the ones obtained during the GA optimization shown in Fig. 5(a) and (c). The two red circles in Fig. 4 correspond to two pulses with almost identical TPA signals but with very distinct PrF+/PrO+ ratios (their associated mass spectra are shown in the inset of Fig. 4). Inspection of Fig. 4 shows that, even for pulses with comparable peak intensity, the formation of PrF+ and PrO+ could be controlled over a large dynamic range. Insights into the control mechanism behind this phenomenon can be extracted using the control pulse slicing (CPS) technique, described in the following section.
III.2. Understanding the mechanism for controlling the fragment ratio of PrF+/PrO+ with shaped pulses
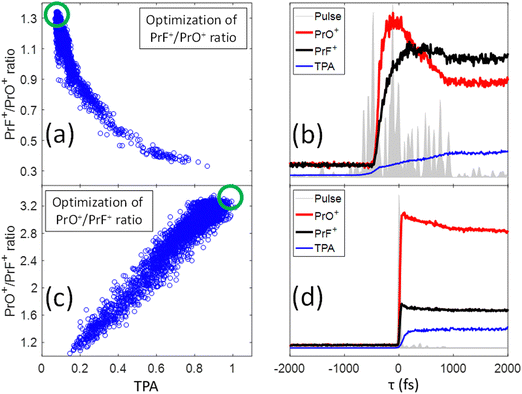
In our previous study,25 we presented evidence suggesting that the formation of PrF+ could be understood in terms of the pathway involving C–C bond-rotation.25 We also saw that the yield of PrF+ relative to PrO+ could be controlled to some degree by simply chirping fs laser pulses (i.e., stretching the laser pulses tends to increase the PrF+/PrO+ ratio). In this section, we apply control pulse slicing (CPS)26 to provide insights into the control mechanism for this phenomenon. Two pulses (obtained through a GA optimization with a pixel basis as controls) that either maximize or minimize the PrF+/PrO+ ratio were selected for CPS analysis. The goal here is to better understand the relationship between pulse shape and control outcome. The blue circles in Fig. 5(a) and (c) depict the two different target ratios as a function of TPA signal for each pulse during the optimization. The green circles define the regions of the optimal pulses for maximizing and minimizing the labelled ratio, respectively. The temporal amplitudes for the two optimal pulse fields in Fig. 5(a) and (c) were calculated from their frequency dependent spectral phase and amplitude and plotted as the grey areas in Fig. 5(b) and (d), respectively. While the optimal pulse that maximizes the PrF+/PrO+ spans over 2 ps with a complex structure, the pulse that minimizes the ratio is short and nearly transform limited (TL). The red and black curves in Fig. 5(b) and (d) show the dynamical evolution of the fragment yields for PrO+ and PrF+ extracted by the CPS scan (see Section I for a brief description of the CPS technique26). The CPS scans were achieved by continuously varying the slicing time τ experimentally to generate a series of shaped pulses corresponding to the rear portion (i.e., t > τ) of the original control pulse being sliced off.The CPS results for the optimal PrF+/PrO+ pulse in Fig. 5(b) show that the early portion of the pulse starting around −500 fs gives rise to both PrO+ and PrF+, but with PrO+ initially being the dominant signal up to ∼350 fs. As the pulse evolves beyond ∼350 fs, the signal for PrF+ dominants while the signal for PrO+ significantly decreases. The anti-correlation of the yields between PrF+ and PrO+ during this time window (i.e., 1000 fs > τ ≥ 350 fs) may suggest that the metal–ligand and Pr–O bond breaking is in competition with Pr–F bond formation. The latter agrees well with the C–C bond rotation pathway described in our previous study.25 The final fragment yields after the completion of the entire optimal pulse shape gives rise to an enhanced PrF+/PrO+ ratio, which was not observed for the compressed TL pulse in Fig. 4 that instead minimizes the same ratio. The CPS plot for the TL pulse (i.e., being optimal for the ratio PrO+/PrF+) in Fig. 5(d) shows much higher yields for PrO+ than PrF+ throughout the scan for τ ≥ 0, indicative of a reduced influence from C–C rotation. The C–C rotation is a slow process that usually takes much longer than 1 ps consistent with the latter behavior in Fig. 5(b). The closed-loop optimization and CPS analysis of the optimal pulses suggest that longer pulse durations are advantageous to this process when PrF+ is the goal. In order to confirm this observation we performed a chirp scan. During the scan, a 2nd order chirp phase term AΩ2 was added to the TL laser pulse, and A was progressively increased from −40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fs2 to +40
000 fs2 to +40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fs2.
000 fs2.
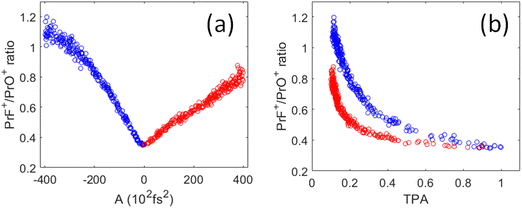
As shown in Fig. 6(a), the PrF+/PrO+ ratio is at minimum when A = 0 (i.e., corresponding to the TL pulse), which then maximally favors the oxidation product. The ratio becomes larger as the pulses are stretched. Interestingly, the change of the ratio versus the chirp parameter is asymmetric for positive and negative chirp. As a result, the ratio versus TPA plot shown in Fig. 6(b) consists of two trajectories corresponding to negative and positive chirp. We may understand the asymmetric nature of the chirped plots in Fig. 6 by the following assessment. First, for a negatively chirped pulse, the blue portion of the light comes first followed by red. For ionization induced by a multiphoton process, a fs pulse needs to overcome a minimum peak intensity threshold in order to initiate ionization. Since the blue photon has a higher energy than the red photon. Thus, fewer blue photons are needed to go above the ionization threshold, and that effectively lowers the peak intensity threshold when the blue photon comes first. So, the pulse effectively appears to be “shorter”.26 This explains why the negatively chirped pulse is more effective for increasing the PrF+/PrO+ ratio.
Naturally, elucidating mechanism information from computational studies would be valuable. In the present case of Ln(hfac)3, such computations would involve electronic excitation, bond breaking, bond formation and ionization. The simulation would need to be done in the strong field regime where multi-photon processes are present, and the overall physics will surely be complex. While such a simulation would be desirable, it is beyond the scope of the present paper. Rather, we took an alternative experimental approach in the section to gain insight into the control mechanism by the CPS analysis and the explanation is in good agreement with the observation from Chirp scans, along with the prior literature on the role of bond rotation in laser-driven dynamics of Ln(hfac)3. The achieved overall experimental view of the mechanism leaves an important goal for future numerical simulations to fill in additional details.
IV. Conclusion
This paper presents the results of a series of experiments for the dissociative-ionization of Ln(hfac)3 driven by both TL and shaped ultrafast fs laser pulses. Various fluorine and Ln containing mass fragments were observed (only PrO+ and PrF+ are reported in this work), which can be explained by C–C bond rotation processes. A discussion of the full mass fragmentation pattern can be found in ref. 25. The relative photofragment yields of PrO+ and PrF+ were optimized with shaped fs laser pulses during adaptive feedback control experiments. The laser pulse duration at fixed pulse energy was shown to readily affect the relative yields between the fluoride and oxide products. While the oxide formation favors shorter pulse duration, fluoride formation corresponds to longer pulse duration. This behavior is evident in the results of CPS scans, chirp scans, and in the pulse shapes obtained by GA optimizations. The CPS technique was applied to further probe the mechanism behind the optimized fields. The results of the latter experiments confirmed the importance of C–C rotation pathway during the formation of PrF+ at large time scales.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Department of Energy (DE-FG02-02ER15344).References
- M. Houssa, High-K gate dielectrics, Institute of Physics, 2004 Search PubMed.
- S. Wilhelm, T. Hirsch, W. M. Patterson, E. Scheucher, T. Mayr and O. S. Wolfbeis, Theranostics, 2013, 3, 239 CrossRef CAS PubMed.
- C. Lin, M. T. Berry, R. Anderson, S. Smith and P. S. May, Chem. Mater., 2009, 21, 3406 CrossRef CAS.
- K. J. Eisentraut and R. E. Sievers, J. Am. Chem. Soc., 1965, 87, 5254 CrossRef CAS.
- M. F. Richardson, W. F. Wagner and D. E. Sands, J. Inorg. Nucl. Chem., 1968, 30, 1275 CrossRef CAS.
- C. S. Springer, D. W. Meek and R. E. Sievers, Inorg. Chem., 1967, 6, 1105 CrossRef CAS.
- K. D. Pollard, H. A. Jenkins and R. J. Puddephatt, Chem. Mater., 2000, 12, 701 CrossRef CAS.
- G. Malandrino, O. Incontro, F. Castelli, I. L. Fragalà and C. Benelli, Chem. Mater., 1996, 8, 1292 CrossRef CAS.
- G. Malandrino and I. L. Fragalà, Coord. Chem. Rev., 2006, 250, 1605 CrossRef CAS.
- R. Lo Nigro, R. Toro, G. Malandrino and I. L. Fragalà, Chem. Mater., 2003, 15, 1434 CrossRef CAS.
- Q. Meng, R. J. Witte, P. S. May and M. T. Berry, Chem. Mater., 2009, 21, 5801 CrossRef CAS.
- D. S. Talaga, S. D. Hanna and J. I. Zink, Inorg. Chem., 1998, 37, 2880 CrossRef CAS.
- G. G. Condorelli, A. Baeri and I. L. Fragala, Chem. Mater., 2002, 14, 4307 CrossRef CAS.
- U. Mohideen, M. H. Sher, H. W. K. Tom, G. D. Aumiller, O. R. Wood, R. R. Freeman, J. Boker and P. H. Bucksbaum, Phys. Rev. Lett., 1993, 71, 509 CrossRef CAS PubMed.
- R. R. Freeman, P. H. Bucksbaum, H. Milchberg, S. Darack, D. Schumacher and M. E. Geusic, Phys. Rev. Lett., 1987, 59, 1092 CrossRef CAS PubMed.
- T. Brabec and F. Krausz, Rev. Mod. Phys., 2000, 72, 545 CrossRef CAS.
- T. Popmintchev, M.-C. Chen, A. Bahabad, M. Gerrity, P. Sidorenko, O. Cohen, I. P. Christov, M. M. Murnane and H. C. Kapteyn, Proc. Natl. Acad. Sci., 2009, 106, 10516 CrossRef CAS PubMed.
- J. Mauritsson, P. Johnsson, E. Gustafsson, A. L’Huillier, K. J. Schafer and M. B. Gaarde, Phys. Rev. Lett., 2006, 97, 013001 CrossRef CAS PubMed.
- K. Codling and L. J. Frasinski, J. Phys. B: At., Mol. Opt. Phys., 1993, 26, 783 CrossRef CAS.
- M. Lezius, V. Blanchet, D. M. Rayner, D. M. Villeneuve, A. Stolow and M. Y. Ivanov, Phys. Rev. Lett., 2001, 86, 51 CrossRef CAS PubMed.
- A. N. Markevitch, S. M. Smith, D. A. Romanov, H. Bernhard Schlegel, M. Y. Ivanov and R. J. Levis, Phys. Rev. A, 2003, 68, 011402 CrossRef.
- K. W. D. Ledingham, P. McKenna and R. P. Singhal, Science, 2003, 300, 1107 CrossRef CAS PubMed.
- T. Ditmire, J. Zweiback, V. P. Yanovsky, T. E. Cowan, G. Hays and K. B. Wharton, Nature, 1999, 398, 489 CrossRef CAS.
- N. Nakashima and T. Yatsuhashi, In Progress in Ultrafast Intense Laser Science II, Springer Berlin, Heidelberg, Berlin, Heidelberg, 2007, pp. 25 Search PubMed.
- J. Chen, X. Xing, R. Rey-de-Castro and H. Rabitz, Sci. Rep., 2020, 10, 7066 CrossRef CAS PubMed.
- X. Xing, R. Rey-de-Castro and H. Rabitz, J. Phys. Chem. A, 2017, 121, 8632 CrossRef CAS PubMed.
- K. M. Tibbetts, X. Xing and H. Rabitz, J. Chem. Phys., 2013, 139(14), 144201 CrossRef PubMed.
| This journal is © the Owner Societies 2024 |