Unrivaled accuracy in measuring rotational transitions of greenhouse gases: THz CRDS of CF4†
Fabien
Simon
 a,
Arnaud
Cuisset
a,
Arnaud
Cuisset
 *a,
Coralie
Elmaleh
*a,
Coralie
Elmaleh
 a,
Francis
Hindle
a,
Francis
Hindle
 a,
Gaël
Mouret
a,
Gaël
Mouret
 a,
Michaël
Rey
a,
Michaël
Rey
 b,
Cyril
Richard
b,
Cyril
Richard
 c and
Vincent
Boudon
c and
Vincent
Boudon
 c
c
aLaboratoire de Physico-Chimie de l’Atmosphère, UR 4493, LPCA, Université du Littoral Côte d’Opale, F-59140 Dunkerque, France. E-mail: arnaud.cuisset@univ-littoral.fr
bGroupe de Spectrométrie Moléculaire et Atmosphérique, UMR CNRS 7331, BP 1039, F-51687, Reims Cedex 2, France
cLaboratoire Interdisciplinaire Carnot de Bourgogne, UMR 6303 CNRS - Université de Bourgogne, 9 Av. A. Savary, BP 47870, F-21078 Dijon Cedex, France
First published on 15th March 2024
Abstract
Tetrafluoromethane CF4 is the most abundant perfluorocarbon in the atmosphere, where it is designated as PFC-14. This greenhouse gas is very stable, has an atmospheric lifetime of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years, and a high greenhouse warming potential 6500 times that of CO2. Over the last 15 years, its atmospheric concentration has increased at a rate of 0.8 ppt per year. The accurate quantification of CF4 is key to understanding the contribution of its emissions to the radiative forcing budget, and the most precise spectroscopic parameters possible are hence required. In this study, a novel high finesse THz cavity, providing an interaction length in excess of 1 km, has enabled highly resolved spectra, and quantification of the weak transitions of CF4 by cavity ring-down spectroscopy (CRDS). More than 50 pure rotational P6 − P6
000 years, and a high greenhouse warming potential 6500 times that of CO2. Over the last 15 years, its atmospheric concentration has increased at a rate of 0.8 ppt per year. The accurate quantification of CF4 is key to understanding the contribution of its emissions to the radiative forcing budget, and the most precise spectroscopic parameters possible are hence required. In this study, a novel high finesse THz cavity, providing an interaction length in excess of 1 km, has enabled highly resolved spectra, and quantification of the weak transitions of CF4 by cavity ring-down spectroscopy (CRDS). More than 50 pure rotational P6 − P6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν3 − ν3 lines of CF4 have been measured, yielding both position and intensity with unequalled precision. Several tetrahedral splittings are fully resolved and measured with sub-MHz accuracy. Moreover, CRDS-THz allows determining absolute intensities and, using a global fit of the ν2 polyad series, a CF4 dipole parameter, namely
ν3 − ν3 lines of CF4 have been measured, yielding both position and intensity with unequalled precision. Several tetrahedral splittings are fully resolved and measured with sub-MHz accuracy. Moreover, CRDS-THz allows determining absolute intensities and, using a global fit of the ν2 polyad series, a CF4 dipole parameter, namely ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3,3, has been fitted to 106.38(53) mD. This value is in very good agreement with that of the ab initio-based parameter deduced from a dipole moment surface. For the first time, a set of ab initio effective dipole moment parameters is derived for the computation of the transitions of the type Pn − Pn (n = 0,…, 8) and the resulting line list composed of 25
3,3, has been fitted to 106.38(53) mD. This value is in very good agreement with that of the ab initio-based parameter deduced from a dipole moment surface. For the first time, a set of ab initio effective dipole moment parameters is derived for the computation of the transitions of the type Pn − Pn (n = 0,…, 8) and the resulting line list composed of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863 transitions can be used to model the whole CF4 rotational spectrum. Finally, the TFMeCaSDa database is updated and is available for future spectroscopic and monitoring activities.
863 transitions can be used to model the whole CF4 rotational spectrum. Finally, the TFMeCaSDa database is updated and is available for future spectroscopic and monitoring activities.
1 Introduction
It is generally accepted in the public consciousness that greenhouse gases are synonymous with carbon dioxide CO2. The media warn of the need to reduce CO2 emissions. All over the world, carbon capture use and storage (CCUS) technologies are being developed to achieve zero-carbon emissions, CO2 being the principal target. However, the contribution of other greenhouse gases to global warming, which may be less abundant than CO2, is far from negligible. This is typically the case for tetrafluoromethane CF4: with an atmospheric concentration almost five million times weaker than that of CO2, this molecule has a warming power 6500 times greater and a lifetime 200 times longer (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years) in the atmosphere.1 Although less abundant, CF4's residual radiative forcing is much greater, and our atmosphere takes much longer to get rid of it. As a result, we can expect CF4's contribution to global warming from greenhouse gases to increase over the next few years. A study published in 2016 warned of a slowdown in the decline in perfluorocarbon (PFC) emissions and urged PFC generating industries especially aluminium and semiconductor manufacturing industries to continue to reduce the emissions of these potent greenhouse gases, which, once emitted, will stay in the atmosphere essentially permanently (on human timescales) and contribute to radiative forcing.2 More recently, long-lived atmospheric greenhouse gases have been compared using IASI/Metop and ACE-FTS satellite and AGAGE ground-based measurements over the last 15 years.3 These three instruments were found to demonstrate a remarkable degree of agreement in monitoring the atmospheric CF4, and the concentration has been increasing linearly at a rate of 0.8 ppt per year (≃1% of the average atmospheric concentration) since 2008. These analyses were based on the inversion of the absorption spectrum of the strong ν3 stretching fundamental band of CF4 observed in the 1283 cm−1 region.1
000 years) in the atmosphere.1 Although less abundant, CF4's residual radiative forcing is much greater, and our atmosphere takes much longer to get rid of it. As a result, we can expect CF4's contribution to global warming from greenhouse gases to increase over the next few years. A study published in 2016 warned of a slowdown in the decline in perfluorocarbon (PFC) emissions and urged PFC generating industries especially aluminium and semiconductor manufacturing industries to continue to reduce the emissions of these potent greenhouse gases, which, once emitted, will stay in the atmosphere essentially permanently (on human timescales) and contribute to radiative forcing.2 More recently, long-lived atmospheric greenhouse gases have been compared using IASI/Metop and ACE-FTS satellite and AGAGE ground-based measurements over the last 15 years.3 These three instruments were found to demonstrate a remarkable degree of agreement in monitoring the atmospheric CF4, and the concentration has been increasing linearly at a rate of 0.8 ppt per year (≃1% of the average atmospheric concentration) since 2008. These analyses were based on the inversion of the absorption spectrum of the strong ν3 stretching fundamental band of CF4 observed in the 1283 cm−1 region.1
Therefore, the accuracy of CF4 monitoring depends on the accuracy of modelling of the ν3 rovibrational band including line frequencies, intensities, air-broadening coefficients and profiles up to high J levels. In addition to the fundamental band, the main hot bands involving the lower rovibrational levels such as ν3 + νi − νi with i = 1, 2 and 4 must be included since they contribute 92% of the total absorption at room temperature. This was the objective of a study in which a global analysis of 17 rovibrational bands of CF4 was undertaken.4 The first Terahertz (THz) measurements of the very weak rotational transitions of CF4 in the ν3 = 1 state (ν3 − ν3 hot band) were included. Synchrotron-based Fourier transform spectroscopy was used with an optical path of 150 m with a white-type multipass cell, allowing recording of R(20) to R(37) line clusters in the 20–37 cm−1 (600–921 GHz) region at a resolution of 0.1 cm−1. Due to a lack of sensitivity and resolution, the recorded THz lines were pressure-broadened (P ≃100 mbar) and largely averaged (5000 co-additions).5 As a result, these measurements are characterised by high levels of uncertainty both in frequency and in intensity. Moreover, the tetrahedral splitting of CF4 rotational lines was only very partially resolved. More recently, it has been demonstrated6 that THz Fabry–Perot absorption spectroscopy with a km effective path length allowed detection of CF4 THz lines with intensities lower than 1 × 10−27 cm−1 / (molecule cm−2) and full resolution of the tetrahedral splitting. In this study, only the R(20) cluster was measured with the unique consideration of line frequencies.
Here, a similar experimental setup described previously7 is used, a cavity ring-down spectroscopy (CRDS) configuration has enabled the direct measurement of the absorption coefficient.8R(19) to R(30) and Q(32) to Q(34) line clusters are measured both in frequency and intensity with unequalled precision. CRDS THz line frequencies and intensities are included in a global fit of the ν2 polyad (see Section 5.1) allowing an improvement of the RMS deviation and an accurate determination of the μ3,3 dipole moment parameter specific to the ν3 − ν3 CF4 transitions. Fluoride-containing molecules are heavy species with highly congested spectra composed of many hot bands, even at room temperature. Recently, the complete elucidation of the dense and complex band structure in the rotationally resolved spectra of the greenhouse CF4 and SF6 molecules was made possible using accurate ab initio and variational calculations.9,10 In this work, a non-empirical, ab initio-based effective model has been derived for the first time for the modelling of the whole CF4 rotational spectrum. The quality of the resulting calculated line list has been validated by a direct comparison with experiment. Finally, this work has enabled an updated line list of CF4 to be tabulated in the TFMeCaSDa database while the ab initio predictions pave the way for future experimental studies and line-by-line analyses.
2 THz cavity ring-down spectrometer
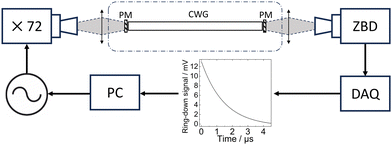
Observation of the weak CF4 transitions around 20 cm−1 is beyond the sensitivity limits of a standard spectrometer with a single path absorption cell.11 To perform high-resolution measurements of weakly absorbing species in this region, we have developed a cavity assisted THz spectrometer.7,8 The excellent resolution is provided by an electronic source, which is an amplified multiplier chain (AMC). A standard microwave synthesizer is used to feed the AMC with 0 dBm in the range from 7.92 to 8.75 GHz. Once the frequency of the synthesizer has been multiplied by the AMC (×72) it directly addresses the range from 570 to 630 GHz, or 19 to 21 cm−1. Typical power levels in the rectangular waveguide at the AMC output are −2 dBm. The excellent resolution that can be achieved by such sources is possible due to their spectral purity, the emission linewidth is estimated to be around 1 kHz. Up-converting a microwave synthesizer provides two useful advantages. First, it allows the source to be readily modulated in both frequency and amplitude, and second, a traceable reference frequency can be easily introduced, in our case, a timing signal generated by a GPS receiver (Spectracom EC20S) was employed.In order to increase the available sensitivity and consequently the accuracy of line measurements, a high finesse cavity was used to extend the interaction length between the sample gas and the THz radiation. The cavity is composed of two photonic mirrors and a corrugated waveguide, both designed for operation around 20 cm−1. The radiation from the AMC source is launched into free space with a horn antenna before being coupled to the cavity using a TPX lens, see Fig. 1. The output of the cavity is refocused using a second TPX lens onto a zero biased detector (ZBD). The cavity has a free spectral range of 310 MHz, and finesse values of 4000 are routinely obtained, providing an interaction length of 1.2 km for a measurement cell that has a physical length of around 50 cm. To measure the narrow molecular transitions, both the AMC frequency and cavity mode must be simultaneously scanned over the zone of interest. This is achieved by finely adjusting the cavity length by means of two piezoelectric actuators; further details can be found elsewhere.7 This instrument can be used to make not only cavity enhanced absorption spectroscopy (CEAS) measurements but also CRDS, the latter is of particular interest and has been used for this study as it directly gives a quantitative value of the absorption coefficient.8
The principle of CRDS is to measure the residency time τ of the photons in the cavity. The presence of an absorbing gas in the cavity will lead to a decrease in τ compared to the initial value under vacuum conditions. To measure the cavity ring-down time τ the AMC must be coupled to the cavity to allow the intracavity power to build up. Once a stable power level is obtained the source must be rapidly removed, achieved using pulse modulation, and the acquisition process is triggered. The light exiting the cavity is measured as a function of time and averaged for a large number of ring-down events, in our case 5 × 104 events per second. The signal from the detector is amplified and then measured using a dedicated data acquisition card (Spectrum Instruments) that samples at 1.25 GS s−1 and calculates the average waveform in real time. Each average waveform is fitted by an exponential function to give the value of τ.
3 Experimental results
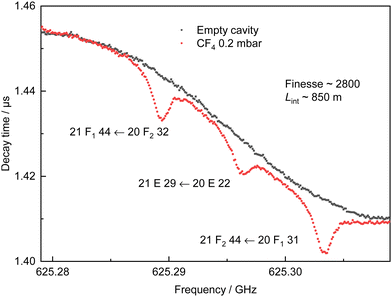
Pure CF4 (>99.997%) purchased from Messer was introduced into the empty measurement chamber. A pressure of 0.2 mbar was selected to maximise the molecular signal while maintaining narrow linewidths, optimising the available molecular signal to noise ratio (SNR). The cavity is sensitive to temperature which results in slow changes to the baseline. A second spectrum is recorded, with an empty chamber, immediately after the acquisition of the molecular spectrum. The total duration is a compromise between the degree of data accumulation that is employed and the minimisation of the variation of the baseline. The measurement of a single line with its baseline is typically completed within 10 minutes. If no baseline spectrum is available a synthetic baseline can be produced using a suitable low order polynomial function. All CRDS spectra have been obtained at room temperature (294.0(15) K), with a frequency step size of 100 kHz. This step size was selected to match the mode width of the cavity, which provides around 20 measurement points within the FWHM of the lines. A typical example spectrum with its baseline is shown in Fig. 2. The difference in the cavity ring-down time with and without gas is clearly distinguished for three molecular lines of CF4 separated by about 7 MHz (0.0002 cm−1). The equivalent interaction length here is calculated to be 850 m with a cavity finesse of 2800. A total of 54 transitions, from 577.405 GHz to 629.164 GHz (19.26 cm−1 to 20.99 cm−1), have been probed in this study. Nineteen of them are isolated so they have been individually resolved, while the remaining 35 could not be individually isolated due to the Doppler broadening at room temperature (≃0.8 MHz (FWHM)). In this case, the measured absorption results from two or three overlapping molecular transitions. The use of CRDS has enabled the quantification of 28 (single or multiplet) line intensities.The cavity ring-down time with and without gas, τ(ν) and τ0(ν), respectively, are directly related to the molecular absorption coefficient α(ν) (cm−1):12
 | (1) |
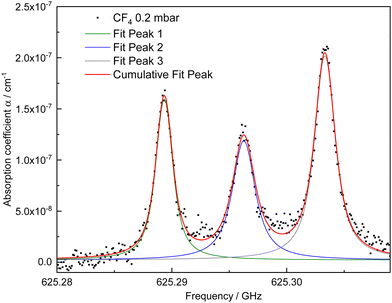 | ||
| Fig. 3 The absorption coefficient spectrum determined from the CRDS spectrum in Fig. 2. Three Voigt functions sharing the same Gaussian line broadening contribution are used to obtain the cumulative fit of these transitions with overlapping tails (21 F1 44 ← 20 F2 32), (21 E 29 ← 20 E 22), and (21 F2 44 ← 20 F1 31). | ||
The spectra measured in this way are fitted with a Voigt profile, whose parameters are all free other than Doppler broadening which is fixed to its calculated value. No Voigt profile variations may be observed due to the limited SNR of the weak intensities of the CF4 rotational transitions. The integrated absorption coefficient  in cm−2, line centre frequency νexp and linewidth in cm−1 are extracted from the fitting procedure. The transition line intensity Iexp is determined by dividing A by the molecular density n in molecule cm−3 determined by the gas equation
in cm−2, line centre frequency νexp and linewidth in cm−1 are extracted from the fitting procedure. The transition line intensity Iexp is determined by dividing A by the molecular density n in molecule cm−3 determined by the gas equation  , while νexp is compared with the calculated value νcalc, as presented in Table 1. The precision of νexp is estimated using the measured linewidth and SNR, as explained in the following section. For multiplet lines, we indicate in Table 1 the different assignments and calculated frequencies; we detail this case in Section 5.2. For example, in Fig. 4, the three transitions are fitted using a single Voigt function of fixed Gaussian contribution.
, while νexp is compared with the calculated value νcalc, as presented in Table 1. The precision of νexp is estimated using the measured linewidth and SNR, as explained in the following section. For multiplet lines, we indicate in Table 1 the different assignments and calculated frequencies; we detail this case in Section 5.2. For example, in Fig. 4, the three transitions are fitted using a single Voigt function of fixed Gaussian contribution.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio are the intensities obtained from the ab initio effective model (see Section 5.3). For unresolved line clusters, the experimental intensity Iexp is that of the cluster as a whole and the intensity of each component can be obtained through eqn (7). Line frequencies are given in GHz. Line intensities in units of cm−1 / (molecule cm−2) which have been multiplied by 1 × 1027. The experimental uncertainties are given in parentheses
initio are the intensities obtained from the ab initio effective model (see Section 5.3). For unresolved line clusters, the experimental intensity Iexp is that of the cluster as a whole and the intensity of each component can be obtained through eqn (7). Line frequencies are given in GHz. Line intensities in units of cm−1 / (molecule cm−2) which have been multiplied by 1 × 1027. The experimental uncertainties are given in parentheses
| Transition | ν exp / GHz | ν calc / GHz | I exp × 1027 | I calc × 1027 |
I
ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio
× 1027 initio
× 1027 |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| J′′ | C′′ | α′ | J′ | C′ | α′ | cm−1 / (molecule cm−2) | ||||
| 19 | A 2 | 11 | 20 | A 1 | 15 | 595.825800(106) | 595.825626 | 4.57(54) | 3.75 | 4.22 |
| 19 | A 2 | 12 | 20 | A 1 | 16 | 596.518640(272) | 596.518587 | 3.00(54) | 2.71 | 3.05 |
| 19 | A 1 | 10 | 20 | A 2 | 14 | 595.848490(110) | 595.848163 | 2.77(56) | 3.69 | 4.14 |
| 19 | F 2 | 30 | 20 | F 1 | 41 | 595.832630(175) | 595.832384 | 2.77(55) | 2.24 | 2.51 |
| 19 | F 2 | 31 | 20 | F 1 | 42 | 596.205100(285) | 596.205017 | 1.32(30) | 1.91 | 2.15 |
| 19 | F 1 | 31 | 20 | F 2 | 42 | 595.840010(179) | 595.839828 | 2.85(48) | 2.23 | 2.50 |
| 19 | F 1 | 32 | 20 | F 2 | 43 | 596.114480(329) | 596.114288 | — | — | — |
| 19 | F 1 | 33 | 20 | F 2 | 44 | 596.311630(380) | 596.311646 | — | — | — |
| 20 | A 2 | 11 | 21 | A 1 | 14 | 625.730970(39) | 625.731006 | 4.62(25) | 3.50 | 3.93 |
| 20 | A 1 | 12 | 21 | A 2 | 16 | 625.584540(48) | 625.584555 | 4.96(36) | 3.77 | 4.29 |
| 20 | A 1 | 13 | 21 | A 2 | 17 | 626.471100(47) | 626.471092 | 2.04(21) | 2.21 | 2.49 |
| 20 | E | 22 | 21 | E | 29 | 625.296260(75) | 625.296234 | 1.74(23) | 1.65 | 1.86 |
| 20 | E | 24 | 21 | E | 31 | 626.464170(165) | 626.464052 | — | — | — |
| 20 | F 2 | 32 | 21 | F 1 | 44 | 625.289340(57) | 625.289361 | 2.54(25) | 2.48 | 2.80 |
| 20 | F 2 | 33 | 21 | F 1 | 45 | 625.656590(91) | 625.656716 | 2.01(22) | 2.09 | 2.45 |
| 20 | F 2 | 34 | 21 | F 1 | 46 | 625.839690(78) | 625.839690 | 2.10(28) | 1.97 | 2.29 |
| 20 | F 1 | 31 | 21 | F 2 | 44 | 625.303320(50) | 625.303327 | 3.38(23) | 2.47 | 2.77 |
| 20 | F 1 | 32 | 21 | F 2 | 45 | 625.617060(80) | 625.617183 | 1.93(19) | 2.20 | 2.50 |
| 20 | F 1 | 34 | 21 | F 2 | 47 | 626.466270(116) | 626.466375 | — | — | — |
| 27 | A 1 | 16 | 28 | A 2 | 21 | 587.307807 | 1.94 | 2.23 | ||
| 27 | E | 33 | 28 | E | 43 | 587.307750(110) | 587.307609 | 4.21(43) | 0.77 | 0.89 |
| 27 | F 1 | 51 | 28 | F 2 | 64 | 587.307807 | 1.16 | 1.32 | ||
| 27 | F 2 | 48 | 28 | F 1 | 63 | 589.437590(73) | 589.437532 | 4.19(27) | 1.58 | 1.82 |
| 27 | F 1 | 50 | 28 | F 2 | 65 | 589.437528 | 1.58 | 1.83 | ||
| 28 | A 2 | 17 | 29 | A 1 | 21 | 610.106098 | 2.77 | 3.20 | ||
| 28 | E | 34 | 29 | E | 44 | 610.106060(38) | 610.106093 | 5.64(26) | 1.11 | 1.27 |
| 28 | F 2 | 51 | 29 | F 1 | 67 | 610.106095 | 1.66 | 1.91 | ||
| 28 | A 1 | 16 | 29 | A 2 | 19 | 586.724152 | 1.64 | 1.77 | ||
| 28 | E | 30 | 29 | E | 35 | 586.724190(71) | 586.724132 | 3.21(28) | 0.66 | 0.70 |
| 28 | F 1 | 44 | 29 | F 2 | 53 | 586.724139 | 0.99 | 1.05 | ||
| 29 | A 2 | 16 | 30 | A 1 | 19 | 606.278291 | 2.35 | 2.53 | ||
| 29 | E | 30 | 30 | E | 37 | 606.278270(41) | 606.278287 | 4.27(20) | 0.94 | 1.00 |
| 29 | F 2 | 45 | 30 | F 1 | 53 | 606.278288 | 1.41 | 1.51 | ||
| 29 | A 2 | 19 | 30 | A 1 | 24 | 628.490594 | 2.18 | 2.52 | ||
| 29 | E | 35 | 30 | E | 46 | 628.490650(36) | 628.490688 | 4.72(29) | 0.87 | 1.00 |
| 29 | F 2 | 53 | 30 | F 1 | 67 | 628.490657 | 1.31 | 1.50 | ||
| 30 | A 2 | 16 | 31 | A 1 | 19 | 626.603820 | 1.84 | 1.98 | ||
| 30 | E | 32 | 31 | E | 37 | 626.603890(49) | 626.603964 | 3.52(22) | 0.74 | 0.79 |
| 30 | F 2 | 48 | 31 | F 1 | 58 | 626.603916 | 1.11 | 1.19 | ||
| 30 | F 2 | 47 | 31 | F 1 | 57 | 626.381980(35) | 626.381977 | 3.63(24) | 1.48 | 1.58 |
| 30 | F 1 | 46 | 31 | F 2 | 55 | 626.381973 | 1.48 | 1.58 | ||
| 31 | A 1 | 16 | 31 | A 2 | 24 | 577.405098 | 2.21 | 2.46 | ||
| 31 | E | 32 | 31 | E | 47 | 577.405100(148) | 577.405104 | 3.74(54) | 0.88 | 0.99 |
| 31 | F 1 | 49 | 31 | F 2 | 70 | 577.405102 | 1.33 | 1.48 | ||
| 32 | A 1 | 18 | 32 | A 2 | 24 | 592.046796 | 1.70 | 1.90 | ||
| 32 | E | 34 | 32 | E | 49 | 592.046540(64) | 592.046330 | 3.11(20) | 0.68 | 0.76 |
| 32 | F 1 | 50 | 32 | F 2 | 73 | 592.046486 | 1.02 | 1.14 | ||
| 32 | F 2 | 50 | 32 | F 1 | 72 | 594.991100(118) | 594.991007 | 3.73(52) | 1.36 | 1.52 |
| 32 | F 1 | 49 | 32 | F 2 | 74 | 594.991008 | 1.36 | 1.52 | ||
| 33 | A 2 | 18 | 33 | A 1 | 24 | 612.305429 | 2.31 | 2.55 | ||
| 33 | E | 34 | 33 | E | 50 | 612.305440(49) | 612.305457 | 4.69(22) | 0.93 | 1.03 |
| 33 | F 2 | 51 | 33 | F 1 | 76 | 612.305448 | 1.39 | 1.54 | ||
| 34 | F 2 | 53 | 34 | F 1 | 77 | 629.163980(66) | 629.163941 | 2.76(20) | 1.39 | 1.55 |
| 34 | F 1 | 52 | 34 | F 2 | 78 | 629.164005 | 1.39 | 1.55 | ||
4 Uncertainties
The experimental uncertainty of νexp is evaluated by eqn (2) where FWHM is the linewidth and δν is the frequency step size.13 | (2) |
The FWHM is obtained from the Voigt fitting procedure, and in our case δν was held constant at 100 kHz. As regards the evaluation of the SNR, a prudent estimation was adopted. The signal amplitude was simply the maximum value of the absorption coefficient. The noise amplitude was determined from the maximum peak-to-peak value present in the first and last 5 percent of the spectrum.
The line intensity uncertainty ΔIexp was calculated by taking into account the precision of the pressure gauge, knowledge of the measurement cell temperature and the quality of the fitted absorption profile. The pressure gauge error is smaller than 0.001 mbar, and the temperature was controlled at 294.0(15) K. The quality of the fit is limited by the stability of the baseline which is not always perfectly removed, as can be observed in Fig. 4. The Voigt profile was minimised using OriginLab® software which provides a confidence interval ΔA equal to the estimated standard deviation of A. The different contributions were combined by eqn (3) and are included in Table 1.
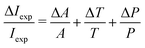 | (3) |
The average relative uncertainties of the CRDS measurements are ≃10−5% for the frequencies and ≃10% for the intensities. Compared to the synchrotron FT-IR measurements,14 the frequency and intensity uncertainties are improved by factors 200 and 2, respectively. In a weighted global fit including IR data, such an accuracy improvement yields a significant influence of the THz rotational lines even with a modest number of lines. This was demonstrated for the THz measurements of the CH4 centrifugal distortion induced rotational transitions,15 in the case of CF4 it will be verified in Section 5.1.
5 Analysis and discussion
The idea of introducing effective Hamiltonians![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) for the modelling of absorption spectra of molecules whose energy levels are organized as small groups of nearly degenerate vibrational states, called polyads, has been well established for decades.16,17 Currently, there exists two different ways for constructing effective Hamiltonians:
) for the modelling of absorption spectra of molecules whose energy levels are organized as small groups of nearly degenerate vibrational states, called polyads, has been well established for decades.16,17 Currently, there exists two different ways for constructing effective Hamiltonians:
Case 1: effective parameters of a phenomenological model are obtained by a direct fit to experiment using a least-squares method (see Section 5.1). The same holds for the construction of an effective dipole moment operator (see Section 5.2). In this context, the approach proposed in ref. 18 is relevant for spherical top molecules.
Case 2: a non-empirical effective model is derived by applying a series of unitary transformations to the nuclear-motion Hamiltonian, composed of a kinetic energy operator and an ab initio potential energy surface (PES). Here, the numerical method proposed in ref. 19 is preferred to the commonly used Van Vleck transformations because the dipole moment parameters can be obtained from a dipole moment surface (DMS) without performing tedious algebraic calculations (see Section 5.3).
For both cases, each polyad is characterized by a polyad number
P = c1ν1 + c2ν2 +⋯ + cNmνNm(ci ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) >0), >0), | (4) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) }P is obtained either by direct fitting to experimental data (Case 1) or from ab initio PESs (Case 2). In eqn (4), νi is the vibrational quantum numbers and Nm is the number of vibrational modes. By definition, the first polyad is P = 0, or simply denoted as P0. Although the second polyad does not necessarily equal P = 1, it is denoted as P1, and so on. Success in the line-by-line analysis of high-resolution spectra thus lies in a convenient choice of the polyad vector c = (c1, c2,⋯, cNm)t in order to include the most relevant resonance coupling terms. In the case of quite isolated polyads with few vibrational bands, the approach proposed in (case 1) allows obtaining very accurate results using few parameters. Conversely, for more complex polyads containing many vibrational bands, a proper characterization of all the resonance couplings becomes a challenging task. In this case, missing information on the so-called “dark” states may lead to a poor determination of some resonance coupling parameters, making the approach defined in (case 2) more relevant.
}P is obtained either by direct fitting to experimental data (Case 1) or from ab initio PESs (Case 2). In eqn (4), νi is the vibrational quantum numbers and Nm is the number of vibrational modes. By definition, the first polyad is P = 0, or simply denoted as P0. Although the second polyad does not necessarily equal P = 1, it is denoted as P1, and so on. Success in the line-by-line analysis of high-resolution spectra thus lies in a convenient choice of the polyad vector c = (c1, c2,⋯, cNm)t in order to include the most relevant resonance coupling terms. In the case of quite isolated polyads with few vibrational bands, the approach proposed in (case 1) allows obtaining very accurate results using few parameters. Conversely, for more complex polyads containing many vibrational bands, a proper characterization of all the resonance couplings becomes a challenging task. In this case, missing information on the so-called “dark” states may lead to a poor determination of some resonance coupling parameters, making the approach defined in (case 2) more relevant.
Note that the accuracy of the ab initio effective parameters {![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) }Pab
}Pab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio derived in (case 2) is typically that of the PES. These parameters can be thus further optimized by fine tuning to experimental data as in (case 1). We can also mention that for heavy molecules like CF4 the density of lines dramatically increases because of the tremendous number of hot bands, resulting in strongly congested spectra, even at room temperature.
initio derived in (case 2) is typically that of the PES. These parameters can be thus further optimized by fine tuning to experimental data as in (case 1). We can also mention that for heavy molecules like CF4 the density of lines dramatically increases because of the tremendous number of hot bands, resulting in strongly congested spectra, even at room temperature.
5.1 Inclusion in the global fit of line positions
Here, we used the present high-precision line positions to include them in the so-called “ν2” polyad scheme already used in ref. 4. This scheme corresponds to a polyad vector c = (0, 2, 6, 3)t in which the v3 = 1 level falls into the P6 polyad (along with v4 = 2). We can note that in this scheme, the ν1 mode is ignored and there is no P1 polyad (see the discussion in Section 5.4).The general theory of the tensorial effective Hamiltonian can be found in many papers. The reader can for instance refer to ref. 18 and references therein. Let us just recall that for each polyad Pk, the effective Hamiltonian can be written in the form
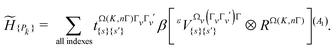 | (5) |
In this equation,  are parameters to be determined, while
are parameters to be determined, while  and RΩ(K,nΓ) are vibrational and rotational operators, respectively. For each term, Ωv and Ω represent the degree in elementary vibrational operators (creation a+ and annihilation a operators), and rotational operators (components Jx, Jy and Jz of the angular momentum), respectively. β is a factor that allows the scalar terms (terms with Γ = A1, the totally symmetric irreducible representation of Td) to match the “usual'” contributions like B0J2, etc. The order of each individual term is defined as Ω + Ωv−2.
and RΩ(K,nΓ) are vibrational and rotational operators, respectively. For each term, Ωv and Ω represent the degree in elementary vibrational operators (creation a+ and annihilation a operators), and rotational operators (components Jx, Jy and Jz of the angular momentum), respectively. β is a factor that allows the scalar terms (terms with Γ = A1, the totally symmetric irreducible representation of Td) to match the “usual'” contributions like B0J2, etc. The order of each individual term is defined as Ω + Ωv−2.
Using this theory, we simply added the 54 ν3 − ν3 (as part of P6 − P6 transitions) line positions of Table 1 in the same “ν2” global fit as in ref. 4 (see, in particular, Table 5 of this reference), using the XTDS20 software package. We also took this opportunity to “clean” the fit by removing many duplicate assignments. A few ν3 − ν3 line positions that were already present in the fit were replaced with values from the present work. Thus, the P6 − P6 assignments has raised from 268 to 316. In Table 2, we compare the new fit statistics with those of ref. 4Fig. 5 displays the fit residuals for line positions for the different transitions included in this global fit. Fig. 6 details the ν3 − ν3 (P6 − P6) part.
| Transitions | Ref. 4 | This work | ||||||
|---|---|---|---|---|---|---|---|---|
| Nb. data | J max | σ | d RMS/1 × 10−3 cm | Nb. data | J max | σ | d RMS/1 × 10−3 cm−1 | |
| P 2 − P0:ν2 | 4686 | 82 | 0.9984 | 1.027 | 3744 | 82 | 1.009 | 1.043 |
| P 3 − P0:ν4 | 2254 | 72 | 1.276 | 1.276 | 2198 | 72 | 1.115 | 1.115 |
| P 4 − P0:2ν2 | 823 | 42 | 0.7757 | 0.7757 | 602 | 42 | 0.989 | 0.989 |
| P 5 − P0:ν2 + ν4 | 877 | 39 | 1.188 | 1.188 | 862 | 39 | 1.188 | 1.188 |
| P 6 − P0:ν3/2ν4 | 2930 | 53 | 0.9847 | 1.161 | 2686 | 53 | 1.153 | 1.332 |
| P 8 − P0:ν2 + (ν3/2ν4) | 4763 | 49 | 1.167 | 1.167 | 3554 | 49 | 1.176 | 1.177 |
| P 4 − P2:2ν2 − ν2 | 803 | 68 | 0.7758 | 0.7758 | 803 | 68 | 0.7588 | 0.7588 |
| P 6 − P4:ν3 − 2ν2 | 222 | 37 | 1.189 | 1.189 | 222 | 37 | 1.063 | 1.063 |
| P 6 − P6:ν3 − ν3 | 268 | 37 | 0.9173 | 33.64 MHz | 316 | 37 | 2.858 | 31.43 MHz |
| Total | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 626 |
82 | 1.076 | 1.116 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 987 |
82 | 1.159 | 1.126 |
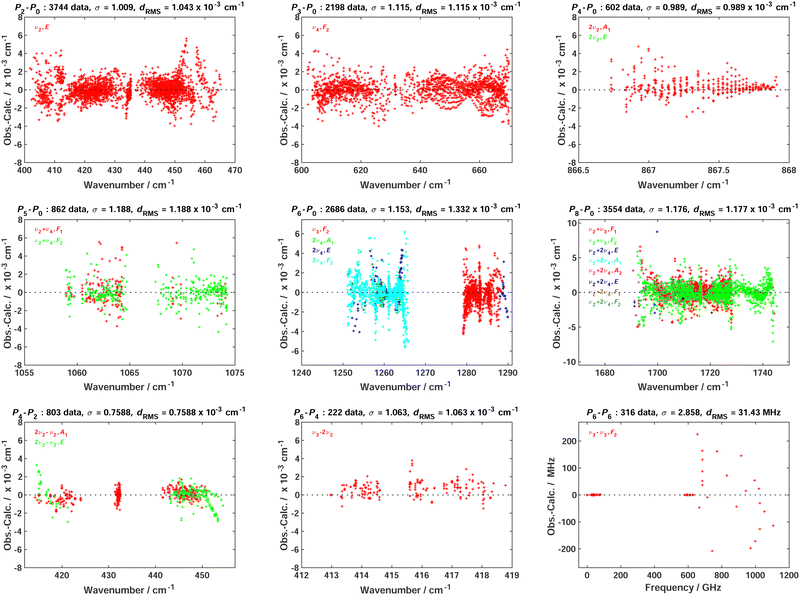 | ||
| Fig. 5 Fit residuals for line positions in the global fit; each panel corresponds to a set of transitions between two polyads (see the text for polyad definition); σ is the dimensionless standard deviation and dRMS is the root mean square deviation. This is to be compared with the equivalent Fig. 3 in ref. 4 | ||
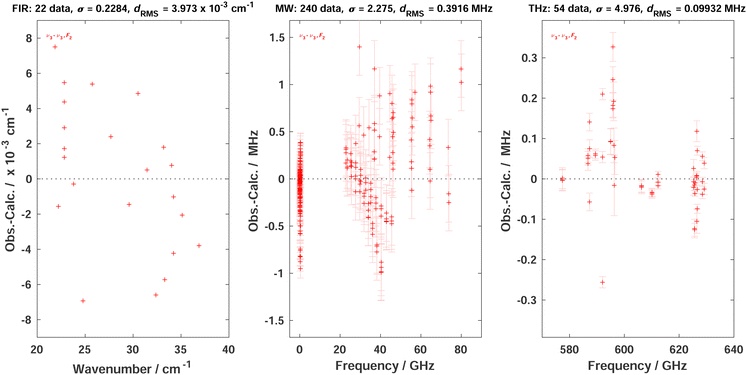 | ||
| Fig. 6 Fit residuals for line positions in the global fit in the case of P6 − P6; σ is the dimensionless standard deviation and dRMS is the root mean square deviation. The three panels detail these residuals for far-infrared (FIR) lines from ref. 5 infrared-microwave/radiofrequency (MW) lines from ref. 21, 22 and THz line from the present work. The last two panels also display experimental line position error bars. It should be noted that ref. 4 did not mention the MW lines from Takami et al. but those were already included in the global fit of this paper. | ||
Although the combination of the elimination of duplicate lines and the introduction of the present new high-precision THz lines renders the comparison with the previous work somewhat tricky, we can tell that (i) we start from a more reliable line assignment list and (ii) the ν3 − ν3 region fit is influenced by the new lines. The overall root mean squares (RMS) deviation in the THz region has slightly decreased from 33.64 to 31.43 MHz. The 4.976 weighted standard deviation for the new THz lines may seem high, but this is due to strong constraints between data with very diverse experimental precisions in this fit; anyway, their RMS deviation of ca. 99 kHz is satisfactory. Some RMS deviations for other transitions have slightly increased compared to ref. 4 but, again, this is due to the “cleaning” of the global fit that has changed the weight of many lines with the removal of duplicates. In any case, it was mandatory to re-do the global fit of line positions in order to obtain consistent eigenvectors for the line intensity analysis. We give the full list of effective Hamiltonian parameters resulting from the present fit as ESI.†
5.2 Fit of effective dipole moment parameter
As a spherical top, CF4 has no permanent dipole moment. But, following the same theory as the one explained in ref. 5, we consider here the effective dipole moment operator for ν3 − ν3 transitions in the form | (6) |
This contains two terms in the right member. The first one, μ{GS–GS}〈μ3–μ3〉 corresponds to a centrifugal distortion-induced dipole moment in the ground state (GS) and should be very small. The second term is the dipole moment derivative that is specific to ν3 − ν3 transitions. The corresponding parameter μ3,3 can be fitted using the present intensity data.
The main problem when fitting effective dipole moment parameters using experimental data is that one needs to find and assign isolated lines in order to determine intensities of single transitions. However, as previously mentioned, for quite heavy molecules, there are generally line clusters consisting of superimposed transitions that cannot be resolved experimentally. This is the case for CF4. Let us take an example from Table 1, the line at 587.307750 cm−1 is a triplet consisting of an A1 → A2, an E → E and an F1 → F2 transition. But the measured intensity, 4.21 × 1027 cm−1 / (molecule cm−2), is the sum for these three transitions. Among the 30 measured intensities, 13 are such multiplets: 4 doublets and 9 triplets, the remaining 17 measurements corresponding to singlets. We have thus a potential of 52 transitions (which is much better than just using the 17 isolated lines), if we can extract individual line intensities for the multiplets. This is possible, since we know their assignments, that is the transitions that compose them. The idea is to split experimental intensities between the multiplet components using the following procedure.
Due to the 1/2 spin of the F ligands, CF4 have spin statistical weights wi for each Td symmetry species A1, A2, E, F1 or F2. It is easy to show23 that these weights are 3, 3, 2, 5 and 5, respectively. Thus, for a cluster of n = 2 or 3 lines with experimental total intensity Iexp, the intensity of the “subline” i can be extracted as follows:
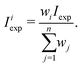 | (7) |
We thus obtained 52 individual line intensities that we introduced in a fit, again using XTDS.20 The 2 transitions 20 F2 43 ← 19 F1 32 (the line is too distorted to be fitted) and 20 F2 44 ← 19 F1 33 (Iexp = 1.15 × 10−27 cm−1 / (molecule cm−2), uncertainty 34%) shown in Table 1 have not been taken in consideration for the line strength global fit, for experimental reasons (very low finesse attributed to a misalignment of the mirrors; one mirror may have hit against the waveguide during the experiment). It also appeared that two line intensities were outliers that were removed from that fit. These 2 transitions, 21 E 31 ← 20 E 24 and 21 F2 47 ← 20 F1 34, separated by only 2.1 MHz, they are too close from each other to be reliably fitted for quantification.‡ These four transitions have been included in the global fit of line positions but, consequently, we finally end up with a fit of 50 experimental intensities. The resulting relative RMS deviation is 16.6% and the standard deviation is 1.706. We obtain the following parameters:
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3,3 = 106.38(53) mD 3,3 = 106.38(53) mD | (8) |
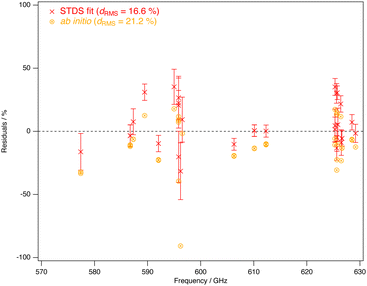 | ||
| Fig. 7 Relative fit residuals for fitted and ab initio line intensities for the presently measured ν3 − ν3 THz lines, as a function of the frequency. | ||
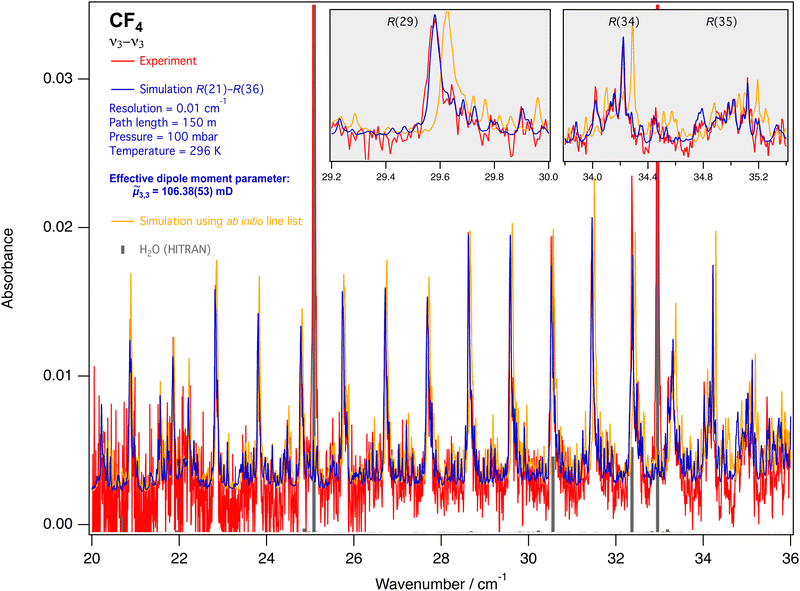 | ||
| Fig. 9 FTIR spectrum of ν3 − ν3 lines in the R branch (from ref. 5), compared to the simulation. Grey ticks show water lines taken from the HITRAN database.25 The insets detail three line clusters. The ab initio line list – with errors on the line positions estimated between 0.01 and 0.05 cm−1 – can be found in the ESI.† | ||
5.3 Derivation of ab initio effective dipole moment parameters
In ref. 9, more than 700 vibrational bands and subbands were predicted for CF4 to construct a variationally computed line list up 4000 cm−1, composed of 2 billion rovibrational transitions at 296 K. Such a density of lines is obtained in methane spectra at 1000 K.26 This list is freely available on the TheoReTS27 webpages https://theorets.univ-reims.fr, https://theorets.tsu.ru. The accuracy of our ab initio line intensities was recently validated in different spectral ranges by a direct comparison with experiment.28 Due to its relatively low-lying vibrational modes compared to other spherical top molecules like methane, the CF4 rotational spectrum is composed of successive hot band transitions of the type Pn − Pn (n = 1, 2,…). We have fitted the parameter μ33(8) of P6 − P6 using the “ν2” polyad scheme.For the modelling of the very crowded CF4 spectra, we can consider an approach which is complementary to the one presented in Sections 5.1 and 5.2 and that combines both the small dimensionality of the spectroscopic models and the completeness of the variational calculation. Within that context, a novel methodology has been recently proposed in ref. 19 to construct an ab initio effective rotation–vibration spectroscopic model directly from a PES and a DMS. Very briefly, let H(J,C) be the matrix representation of the complete nuclear-motion Hamiltonian for a given symmetry block (J,C), computed in a basis set {|γ; J,C〉} where γ denotes all other symmetry labels and quantum numbers (vi, etc.). For the CF4 molecule, the ab initio PES and DMS of ref. 9 were employed and the Eckart–Watson Hamiltonian29 was used to build H(J,C) using harmonic oscillator basis functions. Then, we search for a unitary transformation 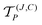 that brings H(J,C) into block diagonal form up to a maximum polyad PNP
that brings H(J,C) into block diagonal form up to a maximum polyad PNP
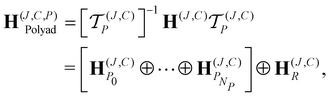 | (9) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (J,C)P. The choice of this polyad scheme compared to the one proposed in Section 5.1 will be discussed in Section 5.4.
(J,C)P. The choice of this polyad scheme compared to the one proposed in Section 5.1 will be discussed in Section 5.4.
At this stage, it is worth mentioning that H(J,C,P)Polyad in eqn (9) is nothing but a matrix representation of an effective Hamiltonian in a basis {|γ;J,C,P〉}, with a set of parameters {![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) }ab
}ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initioP to be determined. The strategy thus consists in considering an effective Hamiltonian
initioP to be determined. The strategy thus consists in considering an effective Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) of the type (5) whose effective parameters are determined for each polyad P such that the matrix elements of
) of the type (5) whose effective parameters are determined for each polyad P such that the matrix elements of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) match the elements of H(J,C,P)Polyad. To this end, we follow the iterative procedure (19) of ref. 19. For line intensity calculation, we can define the transformed matrix
) match the elements of H(J,C,P)Polyad. To this end, we follow the iterative procedure (19) of ref. 19. For line intensity calculation, we can define the transformed matrix
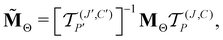 | (10) |
 computed in the same primitive basis as the Hamiltonian. Here, M(Γ)α ≡ M(Γ)α(μ) (α = x, y, z) are the molecular-fixed frame dipole moment components and the μ's are the ab initio DMS parameters of ref. 9.
computed in the same primitive basis as the Hamiltonian. Here, M(Γ)α ≡ M(Γ)α(μ) (α = x, y, z) are the molecular-fixed frame dipole moment components and the μ's are the ab initio DMS parameters of ref. 9.  is the tensor counterpart32 of the direction cosines λΘα. Similarly, we determine the parameters
is the tensor counterpart32 of the direction cosines λΘα. Similarly, we determine the parameters ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) of an effective normal-mode dipole moment operator
of an effective normal-mode dipole moment operator ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) (Γ)α(
(Γ)α(![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) ) (see eqn (6)) such that the matrix elements of
) (see eqn (6)) such that the matrix elements of  match
match ![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) Θ. Only transitions with J ≤ 2 are required to determine the effective dipole moment parameters.
Θ. Only transitions with J ≤ 2 are required to determine the effective dipole moment parameters.
In this work, we have developed the effective Hamiltonian (5) at order 8 up to the eighth polyad, except that the resulting 964 parameters have been determined directly from the PES, without any fit to experimental data. The effective dipole moment of the type (6) has been expended at order 6 and 723 vibrational parameters were simultaneously determined from the DMS for all the transitions Pn − Pn, n = 0,…, 8. We have shown in this work that the contribution of the rovibrational terms to the line intensities of Pn − Pn was negligible, by at least 4 orders of magnitude. Only one rotational parameter was included in the model for computing the P0 − P0 transitions and one rovibrational parameter was determined for ν2 − ν2, for which purely vibrational terms are not allowed by symmetry. Some terms of the tensor dipole moment are given below, with parameters in units of 10−4 Debye:
 | (11) |
Note that the definition of the irreducible tensor vibrational operators33 used in eqn (11) differs from those in eqn (6) whereas the rotational part in the effective Hamiltonian and dipole moment operator is unchanged. We can show that these two sets of vibrational operators can be related by following Appendix of ref. 19. We have plotted in Fig. 10 (upper panel) the strongest line intensities between 5 and 80 cm−1 using the ab initio dipole moment parameters. The line positions were computed from the pure ab initio effective Hamiltonian parameters at an accuracy estimated between 0.01 and 0.05 cm−1. The line list is provided in the ESI.† Finally, in the experimental spectral range considered in this work, only ν3 − ν3 transitions have been observed (see Fig. 10, bottom panel). The corresponding ab initio effective parameter can be easily converted to the STDS formalism as
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) ab ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio3,3 = 117.8 mD. initio3,3 = 117.8 mD. | (12) |
Line intensities of ν3 − ν3 in the observed spectral range and computed from the parameter ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) ab
ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio3,3 are given in the last column of Table 1. We can also compute the experimental and calculated (fit and ab initio) sum of intensities S (×1026) in this range. We obtain Sexp = 9.36, Sfit = 8.87 and Sab
initio3,3 are given in the last column of Table 1. We can also compute the experimental and calculated (fit and ab initio) sum of intensities S (×1026) in this range. We obtain Sexp = 9.36, Sfit = 8.87 and Sab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio = 9.91 cm−1 / (molecule cm−2) and we can see that Sexp is between the two calculated values. Note that the two calculated sums differ by 10.5%, while a comparison between the fitted parameter
initio = 9.91 cm−1 / (molecule cm−2) and we can see that Sexp is between the two calculated values. Note that the two calculated sums differ by 10.5%, while a comparison between the fitted parameter ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3,3(8) and the ab initio parameter
3,3(8) and the ab initio parameter ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) ab
ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio3,3 (12) would suggest a difference of 21%. A brief inspection of the eigenvector decomposition showed that the treatment of the resonance coupling for the dyad system ν3/2ν4 slightly differs between the fitted and ab initio effective models. This thus explains why the difference between Sab
initio3,3 (12) would suggest a difference of 21%. A brief inspection of the eigenvector decomposition showed that the treatment of the resonance coupling for the dyad system ν3/2ν4 slightly differs between the fitted and ab initio effective models. This thus explains why the difference between Sab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio is not that expected.
initio is not that expected.
5.4 Effective versus “ab initio” polyad scheme: discussion
The choice of a relevant polyad scheme 4 is partly conditioned by the available observed data. In ref. 4 and in this work, the so-called “ν2” polyad scheme was employed to build the empirically fitted effective Hamiltonian and dipole moment because of the lack of data for ν1. The same holds for the bands ν1 + ν2 and 3ν2 which were omitted in the polyad called P5. For the construction of the ab initio model presented in Section 5.3, only PES and DMS are required. Most of the resonance couplings are taken into account in the ab initio model, even those associated with “dark” states that are not directly observable. Thus, the choice (4) based on some “resonance” conditions between the vibrational modes does not depend on available experimental data.The “ab initio” polyad vector (0.8, 0.4, 1.2, 0.6)t, also equals to (4, 2, 6, 3)t, should allow inclusion of all possible resonance coupling terms inside a given polyad. In order to see the impact of removing ν1 and its overtones, as in Section 5.1, an ab initio model was built using the scheme (0,2,6,3)t and the results have been compared to the “full” model. For a proper comparison, ν1 + ν2 and 3ν2 were also removed from the model. Not surprisingly, many line positions of the “light” model were slightly shifted for the Pn–Pm (n ≠ m) transitions with respect to the “full” model while both the line positions and line intensities of Pn − Pn were similar in the range considered in this work. This can be explained by quite weak resonance couplings between ν1 + ν2/3ν2 and ν3/2ν4, making the “ν2” polyad scheme relevant for the present study. For example, in the “full” model the rovibrational state  involved in the first transition in Table 1 decomposes as ∼91.5% of |ν3〉, ∼8.5% of |2ν4〉 and less than 0.01% of |ν1 + ν2〉 and |3ν2〉.
involved in the first transition in Table 1 decomposes as ∼91.5% of |ν3〉, ∼8.5% of |2ν4〉 and less than 0.01% of |ν1 + ν2〉 and |3ν2〉.
6 CF4 database update
The Dijon CF4 database, also called TFMeCaSDa for tetrafluoromethane calculated spectroscopy database, and previously built using three different polyad schemes,36 has been reviewed and updated. The third scheme, initially used to describe these pure rotational lines of ν3 = 1, and based on earlier work by Boudon et al.14 has been removed. Instead, we have defined P6 − P6 in scheme 1, adding 284![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 new transitions in the 1 to 114 cm−1 range. This update is already available at https://vamdc.icb.cnrs.fr/PHP/CF4.php and will be the subject of a forthcoming publication detailing the latest major update to the Dijon CaSDa24 databases. Table 3 summarizes the changes in the database using this global approach. The total number of calculated lines has increased slightly, but their accuracy is better, as explained in Section 5.
350 new transitions in the 1 to 114 cm−1 range. This update is already available at https://vamdc.icb.cnrs.fr/PHP/CF4.php and will be the subject of a forthcoming publication detailing the latest major update to the Dijon CaSDa24 databases. Table 3 summarizes the changes in the database using this global approach. The total number of calculated lines has increased slightly, but their accuracy is better, as explained in Section 5.
| Transitions | Nb. dipolar | Dipolar wavenumber / cm−1 | Dipolar intensity / (cm−1 / (molecule cm−2)) |
|---|---|---|---|
| Scheme 1 (0, 2, 6, 3)t | |||
| P 6 − P0 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086 086 |
1230–1305 | 8 × 10−25–8 × 10−22 |
| P 3 − P0 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149 149 |
583–682 | 8 × 10−27–8 × 10−24 |
| P 8 − P2 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430 430 |
1231–1330 | 8 × 10−25–1 × 10−20 |
| P 6 − P6 | 284![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 350 |
1–114 | 1 × 10−30–8 × 10−27 |
| Scheme 2 (3, 0, 4, 2)t | |||
| P 6 − P0 | 3408 | 1270–1283 | 8 × 10−25–1 × 10−21 |
| Total | 375![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423 423 |
||
7 Conclusions
Using THz CRDS, more than 50 pure rotational transitions P6 − P6:ν3 − ν3 of CF4 have been measured both in frequency and intensity with unequalled precision. The experimental data have been included in a global fit of the ν2 polyad series allowing “cleaning” of the previous line list and slight improvement of the overall RMS in the THz region. Moreover, it was possible for the first time to fit a CF4 dipole moment parameter using absolute absorption coefficient measurements of individual tetrahedral splitting components, namely the![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3,3 parameter fitted to 106.38(53) mD. For the modelling of the whole rotational spectrum, a set of ab initio effective dipole moment parameters was also derived for the first time. The value of the ab initio effective parameter
3,3 parameter fitted to 106.38(53) mD. For the modelling of the whole rotational spectrum, a set of ab initio effective dipole moment parameters was also derived for the first time. The value of the ab initio effective parameter ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) ab
ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) initio3,3 of 117.8 mD is in good agreement with the fitted value. The ab initio line list shows that CF4 rotational transitions belonging to other vibrational states will be accessible in other spectral ranges with the actual degree of sensitivity of the CRDS-THz setup. For example, the ν3–2ν4 vibrational state transitions will be accessible at THz frequencies using an AMC covering higher frequencies with a pair of photonic mirrors of suitable dimensions. Nevertheless, the transitions belonging to other fundamental states such as GS–GS or ν4 − ν4 are too weak to be measured with this setup, and a sensitivity improvement of several orders is required for their observation. The improvement of cavity stability by its thermal management will allow a higher degree of accumulation to be undertaken.
initio3,3 of 117.8 mD is in good agreement with the fitted value. The ab initio line list shows that CF4 rotational transitions belonging to other vibrational states will be accessible in other spectral ranges with the actual degree of sensitivity of the CRDS-THz setup. For example, the ν3–2ν4 vibrational state transitions will be accessible at THz frequencies using an AMC covering higher frequencies with a pair of photonic mirrors of suitable dimensions. Nevertheless, the transitions belonging to other fundamental states such as GS–GS or ν4 − ν4 are too weak to be measured with this setup, and a sensitivity improvement of several orders is required for their observation. The improvement of cavity stability by its thermal management will allow a higher degree of accumulation to be undertaken.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Marc Fourmentin (LPCA) for writing the procedure to automatically extract the cavity ring down time from the averaged time domain data of each frequency point. The authors would like to acknowledge the financial support from the French Agence Nationale de la Recherche via the projects ANR TIGER (ANR-21-CE30-0048), and ANR METIS (ANR-20-ASTR-0016), the Région Hauts-de-France, the Ministère de l'Enseignement Supérieur et de la Recherche and the European Fund for Regional Economic Development for via the CPER ECRIN program, the Région Hauts-de-France via the STIMULE project Deus Marooner. AC is part of the ATMOS project no872081 funded by the H2020-MSCA-RISE-2019 program.Notes and references
- V. Boudon, J.-P. Champion, T. Gabard, G. Pierre, M. Loëte and C. Wenger, Environ. Chem. Lett., 2003, 1, 86–91 CrossRef CAS.
- C. M. Trudinger, P. J. Fraser, D. M. Etheridge, W. T. Sturges, M. K. Vollmer, M. Rigby, P. Martinerie, J. Mühle, D. R. Worton, P. B. Krummel, L. Paul Steele, B. R. Miller, J. Laube, F. S. Mani, P. J. Rayner, C. M. Harth, E. Witrant, T. Blunier, J. Schwander, S. O'Doherty and M. Battle, Atmos. Chem. Phys., 2016, 16, 11733–11754 CrossRef CAS.
- H. De Longueville, L. Clarisse, S. Whitburn, C. Clerbaux, G. Lecomte and P. Coheur, J. Quant. Spectrosc. Radiat. Transfer, 2023, 311, 108755 CrossRef CAS.
- M. Carlos, O. Gruson, C. Richard, V. Boudon, M. Rotger, X. Thomas, C. Maul, C. Sydow, A. Domanskaya, R. Georges, P. Soulard, O. Pirali, M. Goubet, P. Asselin and T. Huet, J. Quant. Spectrosc. Radiat. Transfer, 2017, 201, 75–93 CrossRef CAS.
- V. Boudon, M. Carlos, C. Richard and O. Pirali, J. Mol. Spectrosc., 2018, 348, 43–46 CrossRef CAS.
- A. Cuisset, F. Hindle, G. Mouret, R. Bocquet, J. Bruckhuisen, J. Decker, A. Pienkina, C. Bray, E. Fertein and V. Boudon, Appl. Sci., 2021, 11, 1229 CrossRef CAS.
- F. Hindle, R. Bocquet, A. Pienkina, A. Cuisset and G. Mouret, Optica, 2019, 6, 1449 CrossRef CAS.
- C. Elmaleh, F. Simon, J. Decker, J. Dumont, F. Cazier, M. Fourmentin, R. Bocquet, A. Cuisset, G. Mouret and F. Hindle, Talanta, 2023, 253, 124097 CrossRef CAS.
- M. Rey, I. S. Chizhmakova, A. V. Nikitin and V. G. Tyuterev, Phys. Chem. Chem. Phys., 2018, 20, 21008–21033 RSC.
- M. Rey, I. S. Chizhmakova, A. V. Nikitin and V. G. Tyuterev, Phys. Chem. Chem. Phys., 2021, 23, 12115–12126 RSC.
- G. Mouret, M. Guinet, A. Cuisset, L. Croize, S. Eliet, R. Bocquet and F. Hindle, IEEE Sens. J., 2013, 13, 133–138 CAS.
- J. van Helden, R. Peverall and G. Ritchie, Cavity Ring-Down Spectroscopy: Techniques and Applications, Wiley, 2010, pp. 27–56 Search PubMed.
- D. A. Landman, R. Roussel-Dupre and G. Tanigawa, Astrophys. J., 1982, 261, 732 CrossRef.
- V. Boudon, M. Carlos, C. Richard and O. Pirali, J. Mol. Spectrosc., 2018, 348, 43–46 CrossRef CAS.
- C. Bray, A. Cuisset, F. Hindle, G. Mouret, R. Bocquet and V. Boudon, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 349–354 CrossRef CAS.
- M. R. Aliev and J. K. G. Watson, Higher-order effects in the vibration-rotation spectra of semirigid molecules, Academic Press, London, 1985 Search PubMed.
- D. Papousek and M. R. Aliev, Molecular vibrational-rotational spectra, Elsevier Scientific Publishing Company, Amsterdam-Oxford-New York, 1982 Search PubMed.
- V. Boudon, J.-P. Champion, T. Gabard, M. Loëte, M. Rotger and C. Wenger, Handbook of High-Resolution Spectroscopy, Wiley, Chichester, West Sussex, United Kingdom, 2011, vol. 3, pp. 1437–1460 Search PubMed.
- M. Rey, J. Chem. Phys., 2022, 156, 224103 CrossRef CAS.
- C. Wenger, V. Boudon, M. Rotger, J. P. Sanzharov and J. P. Champion, J. Mol. Spectrosc., 2008, 251, 102–113 CrossRef CAS.
- M. Takami, J. Chem. Phys., 1980, 73, 2665–2672 CrossRef CAS.
- M. Takami, J. Chem. Phys., 1981, 74, 4276–4285 CrossRef CAS.
- H. Berger, J. Phys., 1977, 38, 1371–1375 CrossRef CAS.
- J. V. Auwera, 2023, Private Communication.
- I. E. Gordon, L. S. Rothman, R. V. C. Hill, Y. Tan, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, B. J. Drouin, J.-M. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, V. I. Perevalov, A. Perrin, K. P. Shine, M.-A. H. Smith, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, A. Barbe, A. Csaszar, M. V. Devi, T. Furtenbacher, J. J. Harrison, A. Jolly, T. Johnson, T. Karman, I. Kleiner, A. A. Kyuberis, J. Loos, O. M. Lyulin, S. T. Massie, S. N. Mikhailenko, N. Moazzen-Ahmadi, H. S. P. Müller, O. V. Naumenko, A. V. Nikitin, O. L. Polyansky, M. Rey, M. Rotger, S. Sharpe, K. Sung, E. Starikova, S. A. Tashkun, J. V. Auwera, G. Wagner, J. Wilzewski, P. Wcislo, S. Yu and E. J. Zak, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 3–69 CrossRef CAS.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, Adtrophys. J., 2017, 847, 1 CrossRef.
- M. Rey, A. V. Nikitin, Y. L. Babikov and V. G. Tyuterev, J. Mol. Spectrosc., 2016, 327, 138–158 CrossRef CAS.
- A. Domanskaya, K. Berezkin, G. Li, H. Bohlius, M. Kim, J. Harrison and V. Ebert, J. Quant. Spectrosc. Radiat. Transf., 2023, 311, 108790 CrossRef CAS.
- J. K. G. Watson, Mol. Phys., 1968, 15, 479–490 CrossRef CAS.
- V. Tyuterev, S. Tashkun, M. Rey and A. Nikitin, Mol. Phys., 2022, 120, e2096140 CrossRef.
- J. Van Vleck, Phys. Rev., 1929, 33, 467 CrossRef.
- J. P. Champion, M. Loëte and G. Pierre, in Spherical Top Spectra, eds K. N. Rao, A. Weber, Academic Press, San Diago, 1992 Search PubMed.
- A. V. Nikitin, J. P. Champion and V. G. Tyuterev, J. Mol. Spectrosc., 1997, 182, 72–84 CrossRef CAS.
- V. Boudon, O. Pirali, P. Roy, J.-B. Brubach, L. Manceron and J. Vander Auwera, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 1117–1129 CrossRef CAS.
- M. Rey, A. V. Nikitin and V. G. Tyuterev, Phys. Chem. Chem. Phys., 2013, 15, 10049–10061 RSC.
- C. Richard, V. Boudon and M. Rotger, J. Quant. Spectrosc. Radiat. Transfer, 2020, 251, 107096 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: (1) Full list of fitted effective Hamiltonian parameters. (2) Room-temperature CF4 line list in the range of 4–82 cm−1 calculated from an ab initio effective model. See DOI: https://doi.org/10.1039/d4cp00653d |
‡ NB: A multi Voigt fit with fixed frequency centers gives respectively  = 8.71 × 10−28 cm−1 / (molecule cm−2) uncertainty 17% and = 8.71 × 10−28 cm−1 / (molecule cm−2) uncertainty 17% and  = 1.11 × 10−27 cm−1 / (molecule cm−2) uncertainty 15%. If the frequency centers are let free, the fit diverges. = 1.11 × 10−27 cm−1 / (molecule cm−2) uncertainty 15%. If the frequency centers are let free, the fit diverges. |
| This journal is © the Owner Societies 2024 |