Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Smallest unit of maximal entropy as novel experimental criterion for parametric characterization of middle- and high-entropy materials
Alexander
Khort
 *a,
Alexander
Dahlström
a,
Sergey
Roslyakov
b and
Inger
Odnevall
*a,
Alexander
Dahlström
a,
Sergey
Roslyakov
b and
Inger
Odnevall
 acd
acd
aKTH Royal Institute of Technology, Stockholm, 10044, Sweden. E-mail: khort@kth.se
bUniversity of Science and Technology ‘‘MISIS’’, Moscow, 119049, Russia
cAIMES – Center for the Advancement of Integrated Medical and Engineering Sciences at Karolinska Institutet and KTH Royal Institute of Technology, Stockholm, Sweden
dKarolinska Institutet, Department of Neuroscience, Stockholm SE-171 77, Sweden
First published on 26th March 2024
Abstract
Materials with multiple principal elements (middle- and high-entropy materials), are used in emerging applications in various fields due to their unique properties, driven by configuration entropy. Improved understanding and experimental investigations of the impact of the entropy of mixing on the properties of these materials are of large practical interest. Here we show a simplified limited area calculation approach for assessing the entropy of mixing using a CoCuFeNi model nanoalloy. Based on our calculations we propose a new parametric entropy-based criterion, which defines critical scale parameter transition from the maximal entropy state to the entropy-depleted state of the system. The criterion could be used for generalized mechanistic assessment of the effect of the entropy of mixing on the characteristics of the materials with multiple principal elements and for the development and characterization of existing and new middle- and high-entropy materials with both simple single-, and more complex, multiple-sublattice structures.
1. Introduction
Middle- and high-entropy materials (ME and HE, respectively) are a class of materials, composed of multiple (4 for ME and ≥5 for HE) principal elements in proportions varying from 5 to 35 at%, which form a single crystal phase driven by the configuration entropy.1–3 Such a combination of elements of different types in a wide range of concentrations in the same crystal lattice could lead to the emergence of entropy-related configuration effects, including lattice distortion, high-entropy effect, and cocktail effect, to name a few. These effects are often accompanied by the appearance of unpredictable and unique properties in the materials that surpass those of their single-element counterparts.2–4 For instance, HE materials show superb catalytic activity5–8 and thermoelectric properties,9,10 while HE ceramics exhibit excellent oxidation resistance and mechanical characteristics.11–14 HE oxides are used as advanced materials for energy storage and conversion.15–18 However, the degree of manifestation of the entropy effects is related to the configurational entropy of the structure. Its highest state is achieved only in a random mixed system and can be expressed through the entropy of mixing (Smix), described by Boltzmann's equation (eqn (1)):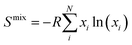 | (1) |
Here we described a simple experimental approach for the assessment of the Smix and propose a new entropy-based parametric criterion that can be potentially used for the prediction of the impact of the Smix on the properties of ME and HE materials. The experimental approach and criterion calculation allow consideration of the real distribution of the atoms of different types in the crystal structure and to define critical scale parameters transition from the maximal entropy state to the entropy-depleted state of the system.
2. Experimental
2.1. Chemicals and synthesis
MEA NPs of CoCuFeNi were prepared via the sol–gel (auto)combustion synthesis (SGCS) using a mixture of copper nitrate trihydrate (Cu(NO3)2·3H2O, 99.99%; Sigma-Aldrich, USA), cobalt nitrate hexahydrate (Co(NO3)2·6H2O), iron nitrate nonahydrate (Fe(NO3)3·9H2O), and nickel nitrate hexahydrate (Ni(NO3)2·6H2O) as a corresponding metal atoms sources and oxidizers, as well as hexamethylenetetramine (C6H12N4, HTM) (all 98% purity, Chimmed, Russia) as an organic fuel/reducer. All chemicals were used without any additional purification. For the synthesis, the required amount of metal nitrates with a nominal equiatomic molar concentration of metal atoms was first dissolved in a minimal volume of hot distilled water. The HTM fuel was then gradually added to the solution of nitrates upon continuously stirring. The reducer-to-oxidized molar ratio (φ) was kept at 3 to create a reducing atmosphere during the synthesis.24,25 The obtained solution was dried in a ceramic beaker for the next 24 h at 80 °C until all unbound water was completely evaporated and a gel-like precursor formed. The auto-combustion reaction in the precursor was initiated in a constant pressure lab reactor by means of a resistively heated wire at an inert ambient Ar atmosphere. A homogeneous powder of the ME alloy (MEA) NPs was formed as a result of a rapid self-sustained high-temperature combustion wave propagating through the gel.2.2. Characterization
3. Results
The CoCuFeNi NPs obtained by the SGCS approach have a microstructure, typical for the materials synthesized by the combustion type method.29,30 The SEM images of the NPs (Fig. 1a and b) show the NPs to be agglomerated into rough, both large- (up to tens of μm) and small-sized (tens of nm) dendritic structures. The NPs are stacked upon the surface of each other, forming separate layers of flat structures as a direct consequence of the combustion wave propagation during the synthesis.The detailed investigation of the NPs by means of TEM showed that the separate layers, forming during intensive tip sonication, consist of aggregated NPs (sized ∼5–10 nm) covered with a thin carbon (graphene) layer. Such types of structures, as well as mechanisms of graphene formation in (metal nitrate)–(organic fuel) systems during self-combustion type synthesis, are described elsewhere.31,32
The XRD profile of the synthesized CoCuFeNi NPs revealed (Fig. 2a and Table 1) a homogeneous polymetallic phase composition with a face-centered cubic (fcc) polymorph (Fm3m space group) with the main XRD peaks observed at 43.757° (111), 50.964° (200), and 74.929° (220). No other crystalline phases were observed. According to the results of the Rietveld refinement, the cell parameter a value was 3.5834 Å, which is close to the previously reported Co0.25Cu0.25Fe0.25Ni0.25 crystal phase.33 The calculated size of the crystallites of the material was 23.8 nm.
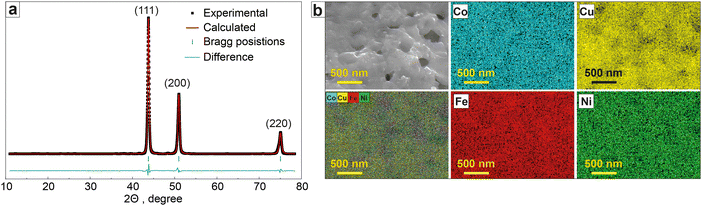 | ||
| Fig. 2 Phase and chemical composition of the CoCuFeNi NPs. (a) Rietveld refined the XRD profile and (b) EDX elemental mapping (Co, Cu, Fe, Ni). | ||
| Material | Crystal structure | a, Å | V, Å3 | d, nm | Goodness of fit |
|---|---|---|---|---|---|
| CoCuFeNi | Cubic Fm3m | 3.5834 | 46.0136 | 23.8 | 0.55 |
The elemental mapping results (Fig. 2b) show a close to homogeneous distribution of the metal atoms in the material structure. The metal content of the CoCuFeNi NPs was shown to be close to equal for all 4 metals in the NPs; 26.6 at% Co, 24.8 at% Fe, 24.5 at% Ni, and 24.1 at% Cu. The content of carbon and oxygen was excluded as adhesive tape was used for the sample preparation, containing both elements.
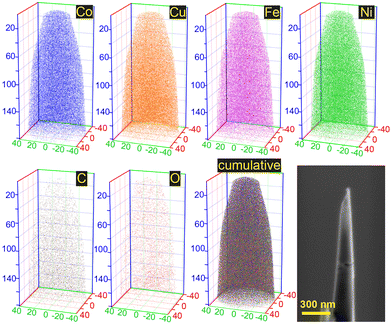
Based on the analysis of the data provided by XRD and EDX, it was concluded that the CoCuFeNi NPs had a sufficient homogeneity of structure and randomness of elements distribution to be classified as middle-entropy alloy according to the commonly accepted practice, i.e. ideal mixing assumption (IMA).34,35 APT investigations were conducted to gain a more detailed understanding of the features of the CoCuFeNi structure and composition. A visual representation of the measured atom distribution density is presented in Fig. 3.
From the analysis of the distribution of the nearest neighbours in the APT spectra of the CoCuFeNi sample, we can conclude a good homogeneous distribution of the metal atoms across the whole structure of the sample. However, the calculation of the metal composition revealed a slightly higher bulk concentration of Ni (30.6 at%) compared to the concentration of the other metal atoms (26.7 at% Cu, 21.9 at% Co and 20.8 at% Fe) in the investigated area.
The presence of the carbon and oxygen atoms could be explained by the presence of the graphene (Fig. 1c) and other forms of carbon with adsorbed oxygen-containing groups, residual from fuel decomposition. Furthermore, oxygen could indicate the presence of metal oxides, which were formed in the intermediate stages of the synthesis and not fully reduced.25,36
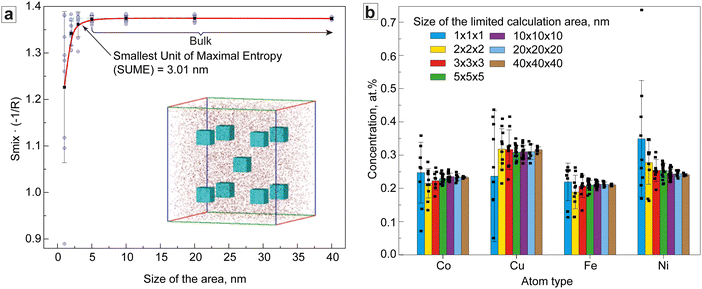
A more detailed investigation of the structural characteristics and Smix of the CoCuFeNi composite required a detailed analysis of the APT data on the distribution of the atoms in the NP structure. For this purpose, a limited area calculation (LAC) approach to the element distribution and Smix concentration was developed and employed. At first, a cubic area sized 40 × 40 × 40 nm inside the sample, reasonably far from the sample's edges, was selected. This area was in turn divided into smaller cubes (20 × 20 × 20 nm), which were also divided. This was repeated until a cube size of 1 × 1 × 1 nm was obtained, see Fig. 4a (insert). 5 (for 40 × 40 × 40 nm) and 9 (all other sizes) cubes were chosen for further calculation of the concentration of atoms and subsequent calculation of the average Smix for every area size (Smix/area) by using eqn (1). The results of the calculation of the Smix/area are presented in Fig. 4a.
The results of Fig. 4a show that the Smix/area for the areas sized > 5 × 5 × 5 nm inclusive was equal to the bulk Smix/APT (−1.373R) and decreased with decreased area size to a level of −1.226R ± 0.16 for the 1 × 1 × 1 nm area. The intersection tangent to the linear sections of the ‘bulk’ and ‘descending’ branches of the curve was 3.01 × 3.01 × 3.01 nm. The reduction of Smix/area is mainly associated with the clustering of the Ni and Cu atoms, noticeably manifested below the scale of 3 × 3 × 3 nm and seen from the increasing standard deviation of the concentration of the different metals (Fig. 4b). This is a common phenomenon and has been reported earlier.37 The results further show that the concentration of the atoms above the 3 × 3 × 3 nm scale shows a low variability with increasing calculation area size.
4. Discussion
The Smix of the 4-component ideal equimolar randomly mixed system calculated by eqn (1) is −1.386R, representing the highest possible entropy of the system. The EDX-calculated composition of the metals of the CoCuFeNi NPs is very close to an equimolar mixture of the components. The EDX-calculated value of entropy of mixing Smix/EDX using the IMA approach equals −1.385R. In comparison, the APT-calculated entropy of mixing Smix/APT value as the bulk concentration of the metallic atoms of all types in the system equals −1.373R. In both cases, the calculated Smix/EDX and Smix/APT values are less than 1R% smaller than Smix values calculated for the ideal equimolar randomly mixed system. However, it should be noted, that any bulk-based assessment of the phase composition and elemental distribution cannot provide sufficient information regarding the degrees of local randomness of distribution of the atoms and SRO in the system. Thus, any calculation of the Smix based on this assessment of the bulk concentrations, using IMA where the ideal case would be an equal probability of occupation of the equivalent position in the crystal structure by the 4 metal atoms, cannot automatically be considered equivalent to the real Smix/real. In the latter case, the complexity of mixing of atoms of different types, the tendency of formation of the clusters of the atoms of the same type during the NPs crystallite formation, and the SRO effect could reduce the values of the entropy of the mixing in the local area Smix/loc in separate areas of the NPs. From this follows that the Smix/real should be represented as the sum of the Smix/loc of areas m considering the concentrations of the specific atoms xi in the area j, and the fractions of all atoms η present in the specific area j, as described by eqn (2).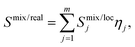 | (2) |
From this follows a modified eqn (1) as described in eqn (3):
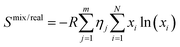 | (3) |
The number of the local areas depends on the size of the NPs, i.e. the number of atoms in the crystal structure which are the individual area centres. The size of these local areas is defined by the choice of the order of the closest neighbours included. Thus, the smallest area includes only the central atom and the first-order neighbours (only the central atom will not form any crystal structure and cannot be considered), and the largest area includes the entire NP. It should be noted that there is a minimal size transition area where Smix/loc becomes ≈Smix/real, which can be considered as the smallest unit of maximal entropy (SUME). In the case of ideal random mixing of atoms of different types, the SUME has the size of one or several crystal cells, where there are enough atoms for the formation of a structure with a random distribution of atoms with concentrations of elements equal to the bulk concentration. However, despite that the APT measurements were able to provide the necessary data for the calculation of the Smix/loc, the calculation of the Smix/real for any large enough sample with millions of atoms by eqn (3) would require a significant amount of computation time to complete the computational calculations. The simplified approach, as described above, was therefore applied.
Analysis of Fig. 4a shows, that in the case of the CoCuFeNi sample, the SUME was ∼(3.01)3 nm. Considering the XRD-calculated fcc crystal cell parameter of 3.5834 Å, the SUME hence consists of ∼594 cells and exceeds angstrom-level SRO. Below that number of cells, the deviation in composition of the separate areas became high enough to affect the general entropy of mixing of the area, i.e. separate clusters of metals of one of several types can be detected on this scale. This may already be considered as phase separation and could thus require the use of sublattice (SL) or many phase models for calculating Smix for all phases separately instead of Boltzmann's equation.37 In any case, the Smix/area of the chosen area will be smaller compared with the Smix of the SUME. Thus, the SUME value can potentially be used as a characteristic scale parameter for the assessment of the effect of the Smix on the properties of the ME and HE materials. For instance, we can speculate, that the materials with SUME values comparable to SRO distance should show enhanced mechanical properties, defined by the SRO effect.20,23 If the SUME value exceeds SRO distance, the effect of SRO on the properties should decrease while influence of Smix-related effects increases. In this case, it should be expected that for the materials with the same nominal composition, one with a smaller SUME value should show a more pronounced SRO or cocktail effect, whereas the effect will be negligible for large SUMEs. Furthermore, the SUME could be an important criterion for the characterization of extremely small MEA and HEA NPs. In this case, SUME is a significant part of the NPs volume of the size A, thus the effect of Smix will only be well pronounced for NPs with large A/SUME ratios. Overall, the difference in the SUME may be one of the explanations for the difference in the properties of the nominally similar ME and HE materials.
We believe that the same LAC approach for the assessment of the SUME can also be used for ME and HE materials with more complex structures containing two or more sublattices, like AB alloys, carbides, oxides, etc. In these cases, the calculation of Smix/area requires consideration of the concentration of all elements in all sublattices and can be assessed using SL or entropy metric38 approaches.
5. Conclusions
In summary, the current study addresses the fundamental need for the development of an experimental approach to calculate the Smix of ME and HE materials. Our limited area calculation approach has enabled the development of a new fundamental entropy-based parametric criterion representing the smallest unit of maximal entropy. The criterion defines the critical scale parameters of transition from the maximal entropy state to the entropy-depleted state of the system. The criterion holds the potential for mechanistically predicting the degree to which entropy-related effects influence the properties of both ME and HE materials.Author contributions
A. K.: conceptualization; methodology; investigation; formal analysis; visualization; data curation writing – original draft. A. D.: investigation; formal analysis; visualization; data curation; writing – review & editing. S. R.: investigation; resources; writing – review & editing. I.O.: conceptualization; writing – review & editing; supervision; funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work forms part of the Mistra Environmental Nanosafety program, Sweden. Financial support from Mistra, the Swedish Foundation for Strategic Environmental Research, is highly acknowledged. Part of this work was conducted with financial support from the Russian Science Foundation (Grant no. 20-79-10257).References
- J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS.
- C. Oses, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2020, 5, 295–309 CrossRef CAS.
- D. B. Miracle and O. N. Senkov, Acta Mater., 2017, 122, 448–511 CrossRef CAS.
- M. Li, C. Huang, H. Yang, Y. Wang, X. Song, T. Cheng, J. Jiang, Y. Lu, M. Liu, Q. Yuan, Z. Ye, Z. Hu and H. Huang, ACS Nano, 2023, 17, 13659–13671 CrossRef CAS PubMed.
- Y. Yao, Z. Huang, P. Xie, S. D. Lacey, R. J. Jacob, H. Xie, F. Chen, A. Nie, T. Pu, M. Rehwoldt, D. Yu, M. R. Zachariah, C. Wang, R. Shahbazian-Yassar, J. Li and L. Hu, Science, 2018, 359, 1489–1494 CrossRef CAS PubMed.
- H. Wu, Q. Lu, Y. Li, M. Zhao, J. Wang, Y. Li, J. Zhang, X. Zheng, X. Han, N. Zhao, J. Li, Y. Liu, Y. Deng and W. Hu, J. Am. Chem. Soc., 2023, 145, 1924–1935 CrossRef CAS PubMed.
- C. Riley, A. De La Riva, J. E. Park, S. J. Percival, A. Benavidez, E. N. Coker, R. E. Aidun, E. A. Paisley, A. Datye and S. S. Chou, ACS Appl. Mater. Interfaces, 2021, 13, 8120–8128 CrossRef CAS PubMed.
- X. Wang, H. Yao, Z. Zhang, X. Li, C. Chen, L. Yin, K. Hu, Y. Yan, Z. Li, B. Yu, F. Cao, X. Liu, X. Lin and Q. Zhang, ACS Appl. Mater. Interfaces, 2021, 13, 18638–18647 CrossRef CAS PubMed.
- B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, Science, 2021, 371, 830–834 CrossRef CAS PubMed.
- D. Moskovskikh, S. Vorotilo, V. Buinevich, A. Sedegov, K. Kuskov, A. Khort, C. Shuck, M. Zhukovskyi and A. Mukasyan, Sci. Rep., 2020, 10, 19874 CrossRef CAS PubMed.
- S. Yudin, A. Sedegov, D. Moskovskikh, S. Volodko, K. Kuskov, V. Suvorova, S. Danilova-Tretiak, S. Vorotilo, A. Nepapushev and A. Khort, Mater. Des., 2023, 231, 112048 CrossRef CAS.
- G. Wang, J. Xu, S. Peng, Z.-H. Xie and P. Munroe, Vacuum, 2023, 211, 111974 CrossRef CAS.
- Z. Wen, Z. Tang, Y. Liu, L. Zhuang, H. Yu and Y. Chu, Adv. Mater., 2024, e2311870, DOI:10.1002/adma.202311870.
- Z. Lun, B. Ouyang, D. H. Kwon, Y. Ha, E. E. Foley, T. Y. Huang, Z. Cai, H. Kim, M. Balasubramanian, Y. Sun, J. Huang, Y. Tian, H. Kim, B. D. McCloskey, W. Yang, R. J. Clement, H. Ji and G. Ceder, Nat. Mater., 2021, 20, 214–221 CrossRef CAS PubMed.
- T. X. Nguyen, Y. C. Liao, C. C. Lin, Y. H. Su and J. M. Ting, Adv. Funct. Mater., 2021, 2101632, DOI:10.1002/adfm.202101632 ARTN .
- B. Xiao, G. Wu, T. Wang, Z. Wei, Y. Sui, B. Shen, J. Qi, F. Wei and J. Zheng, Nano Energy, 2022, 95, 106962 CrossRef CAS.
- Q. Zheng, Z. Ren, Y. Zhang, T. Qin, J. Qi, H. Jia, L. Jiang, L. Li, X. Liu and L. Chen, ACS Appl. Mater. Interfaces, 2023, 15, 4643–4651 CrossRef CAS PubMed.
- H. Gao, N. Guo, Y. Gong, L. Bai, D. Wang and Q. Zheng, Nanoscale, 2023, 15, 19469–19474 RSC.
- J. B. Seol, W. S. Ko, S. S. Sohn, M. Y. Na, H. J. Chang, Y. U. Heo, J. G. Kim, H. Sung, Z. Li, E. Pereloma and H. S. Kim, Nat. Commun., 2022, 13, 6766 CrossRef CAS PubMed.
- Q. Ding, Y. Zhang, X. Chen, X. Fu, D. Chen, S. Chen, L. Gu, F. Wei, H. Bei, Y. Gao, M. Wen, J. Li, Z. Zhang, T. Zhu, R. O. Ritchie and Q. Yu, Nature, 2019, 574, 223–227 CrossRef CAS PubMed.
- Z. Lei, X. Liu, Y. Wu, H. Wang, S. Jiang, S. Wang, X. Hui, Y. Wu, B. Gault, P. Kontis, D. Raabe, L. Gu, Q. Zhang, H. Chen, H. Wang, J. Liu, K. An, Q. Zeng, T. G. Nieh and Z. Lu, Nature, 2018, 563, 546–550 CrossRef CAS PubMed.
- R. Zhang, S. Zhao, J. Ding, Y. Chong, T. Jia, C. Ophus, M. Asta, R. O. Ritchie and A. M. Minor, Nature, 2020, 581, 283–287 CrossRef CAS PubMed.
- A. Khort, S. Roslyakov and P. Loginov, Nano-Struct. Nano-Objects, 2021, 26, 100727 CrossRef CAS.
- A. Khort, K. Podbolotov, R. Serrano-Garcia and Y. Gun'ko, Inorg. Chem., 2018, 57, 1464–1473 CrossRef CAS PubMed.
- D. J. Larson, R. M. Ulfig, D. R. Lenz, J. H. Bunton, J. D. Shepard, T. R. Payne, K. P. Rice, Y. Chen, T. J. Prosa, D. J. Rauls, T. F. Kelly, N. Sridharan and S. Babu, JOM, 2018, 70, 1776–1784 CrossRef CAS.
- F. De Geuser and B. Gault, Acta Mater., 2020, 188, 406–415 CrossRef CAS.
- K. Thompson, D. Lawrence, D. J. Larson, J. D. Olson, T. F. Kelly and B. Gorman, Ultramicroscopy, 2007, 107, 131–139 CrossRef CAS PubMed.
- A. Khort, K. Podbolotov, R. Serrano-García and Y. K. Gun’ko, J. Solid State Chem., 2017, 253, 270–276 CrossRef CAS.
- A. Varma, A. S. Mukasyan, A. S. Rogachev and K. V. Manukyan, Chem. Rev., 2016, 116, 14493–14586 CrossRef CAS PubMed.
- A. Khort, V. Romanovski, D. Leybo and D. Moskovskikh, Sci. Rep., 2020, 10, 16104 CrossRef CAS PubMed.
- A. Khort, V. Romanovski, V. Lapitskaya, T. Kuznetsova, K. Yusupov, D. Moskovskikh, Y. Haiduk and K. Podbolotov, Inorg. Chem., 2020, 59, 6550–6565 CrossRef CAS PubMed.
- Journal.
- K. Guruvidyathri, M. Vaidya and B. S. Murty, Scr. Mater., 2020, 188, 37–43 CrossRef CAS.
- X. Yang and Y. Zhang, Mater. Chem. Phys., 2012, 132, 233–238 CrossRef CAS.
- S. Roslyakov, Z. Yermekova, G. Trusov, A. Khort, N. Evdokimenko, D. Bindiug, D. Karpenkov, M. Zhukovskyi, A. Degtyarenko and A. Mukasyan, Nano-Struct. Nano-Objects, 2021, 28, 100796 CrossRef CAS.
- L. J. Santodonato, Y. Zhang, M. Feygenson, C. M. Parish, M. C. Gao, R. J. Weber, J. C. Neuefeind, Z. Tang and P. K. Liaw, Nat. Commun., 2015, 6, 5964 CrossRef PubMed.
- O. F. Dippo and K. S. Vecchio, Scr. Mater., 2021, 201, 113974 CrossRef CAS.
| This journal is © the Owner Societies 2024 |