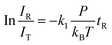Size-dependent reactivity of VnO+ (n = 1–9) clusters with ethane†
Hang
Zhou
a,
Man
Ruan
b,
Qing-Yu
Liu
bc,
Yan-Xia
Zhao
bc,
Rui-Yong
Wang
 a,
Yuan
Yang
*a and
Sheng-Gui
He
a,
Yuan
Yang
*a and
Sheng-Gui
He
 *bcd
*bcd
aHenan Key Laboratory of Crystalline Molecular Functional Materials, College of Chemistry, Zhengzhou University, Zhengzhou 450001, P. R. China. E-mail: yangy@zzu.edu.cn
bState Key Laboratory for Structural Chemistry of Unstable and Stable Species, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, P. R. China. E-mail: shengguihe@iccas.ac.cn
cBeijing National Laboratory for Molecular Sciences and CAS Research/Education Centre of Excellence in Molecular Sciences, Beijing 100190, P. R. China
dUniversity of Chinese Academy of Sciences, Beijing 100049, P. R. China
First published on 22nd April 2024
Abstract
Cost-effective and readily accessible 3d transition metals (TMs) have been considered as promising candidates for alkane activation while 3d TMs especially the early TMs are usually not very reactive with light alkanes. In this study, the reactivity of Vn+ and VnO+ (n = 1–9) cluster cations towards ethane under thermal collision conditions has been investigated using mass spectrometry and density functional theory calculations. Among Vn+ (n = 1–9) clusters, only V3–5+ can react with C2H6 to generate dehydrogenation products and the reaction rate constants are below 10−13 cm3 molecule−1 s−1. In contrast, the reaction rate constants for all VnO+ (n = 1–9) with C2H6 significantly increase by about 2–4 orders of magnitude. Theoretical analysis evidences that the addition of ligand O affects the charge distribution of the metal centers, resulting in a significant increase in the cluster reactivity. The analysis of frontier orbitals indicates that the agostic interaction determines the size-dependent reactivity of VnO+ cluster cations. This study provides a novel approach for improving the reactivity of early 3d TMs.
Introduction
Alkanes are highly abundant in nature and constitute the primary components of natural gas and crude oil, serving as essential raw materials for the chemical industry.1 However, due to the robust thermodynamic nature of the C–H bond, its activation presents a considerable challenge.2 Consequently, investigating the mechanisms of C–H bond activation is of great significance in the development of better performing catalysts for alkane transformation.3 The investigation of the reactions between gas-phase atomic clusters with alkane molecules is regarded as a crucial approach to comprehending the mechanisms of C–H activation at the molecular level.Numerous studies have been documented on the activation and conversion of alkanes by gas-phase metal clusters. There has been a predominant focus on the investigation of noble metal clusters. For example, the previous investigations have shown that Ptn+ (n ⩽ 9),4–7 Pdn+ (n = 2 and 3),8 Rhn+ (n = 1–30),9 Os+,10,11 and Ir+12,13 exhibit notable reactivity in dehydrogenation of light alkanes. Additionally, neutral clusters such as Pdn (n ⩽ 23)14 and Ptn (n ⩽ 24),15 and the anionic clusters such as Rhn− (n ⩽ 10),16 RhnC20H10− (n = 4–7),17 and Ptn− (n ⩽ 7)6 have been demonstrated to have highly size-selective patterns in the activation of the C–H bond in methane. In contrast, the studies on alkane C–H activation by base metals are very limited. The reactions of the clusters of 5d base metals Ta18–23 and W24–27 with methane have been reported. Although 3d transition metals (TMs) are more abundant and economically accessible compared to 5d TMs, studies on alkane C–H activation by 3d TMs, especially the early 3d TMs, are very limited. The studies conducted by Armentrout et al. demonstrated that V+ is inactive with CH4.28 In a previously documented study involving the reaction of TaxO+ (x = 4 and 5) with methane,20 it was observed that the incorporation of the ligand O into the metal clusters markedly enhanced the cluster reactivity. In a subsequent investigation of methane activation by tungsten species,24 it was noted that Wn+ (n ![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) 2) exhibited minimal reactivity, while the addition of O significantly promoted CH4 dehydrogenation. These observations prompted us to explore methodologies for improving the reactivity of 3d TM clusters with light alkanes by doping oxygen atoms.
2) exhibited minimal reactivity, while the addition of O significantly promoted CH4 dehydrogenation. These observations prompted us to explore methodologies for improving the reactivity of 3d TM clusters with light alkanes by doping oxygen atoms.
In this study, the reactivity of Vn+ and VnO+ (n = 1–9) with ethane was investigated using a combination of time-of-flight mass spectrometry and quantum chemical calculations. It was observed that the reactivity of vanadium cluster cations toward ethane can be significantly enhanced with the addition of O ligands, affirming the modulating effect of O on the reactivity of early 3d TMs. Insights into improving the catalytic activity of these metals are thus provided. Note that the reaction of Vn+ (n = 1–9) with H2O has been experimentally investigated in the literature.29
Methods
Experimental methods
A laser ablation method was used to generate the Vn+ and VnO+ cations through the irradiation of a focused pulsed laser beam (532 nm, 5–8 mJ, 10 Hz) onto a rotating and translating V disk in the presence of 4 atm He carrier gas. The cluster cations of interest, Vn+ (n = 1–9) and VnO+ (n = 1–9), were mass-selected using a quadrupole mass filter (QMF)30 and then introduced into the linear ion trap (LIT)31 reactor. After thermalization by collisions with a pulse of cooling gas He (3 Pa), the cluster ions reacted with a pulse of C2H6 seeded in He gas for about 2 ms. The temperature of the cooling gas, the reactant gas (C2H6), and the LIT reactor was around 298 K. The masses and abundances of the reactant and product cations were detected using a home-made reflection time-of-flight mass spectrometer (TOF-MS).32Computational methods
Density functional theory (DFT) calculations by using the Gaussian 09 program33 were carried out to investigate the structures of Vn+ and VnO+ (n = 1–9) cations, as well as the reaction mechanisms of Vn+ (n = 2 and 3) and VnO+ (n = 1, 2, and 3) with C2H6. The benchmark calculations showed that the BPBE functional34,35 generally performed best for the bond energy of V–V, V–C, V–O, V–H, C–H, and H–H compared with the experimental values (Table S1, ESI†). Thus, the BPBE functional was adopted in this work. For all the calculations, the TZVP basis sets36 were used for all of the elements (C, H, O, and V). A Fortran code based on a genetic algorithm37 was used to generate initial guess structures of Vn+ (n = 7–9) and VnO+ (n = 5–9) clusters. Reaction mechanism calculations involved the geometric structures of reaction intermediates (IMs) and transition states (TSs) that were optimized and vibrational frequencies were calculated to check that each of the IMs and TSs has zero or only one imaginary frequency. The TSs were optimized using the Berny algorithm method.38 The initial guess structures of the TS species were obtained through relaxed potential energy surface scans using single or multiple internal coordinates. Intrinsic reaction coordinate calculations39 were conducted to make sure that a TS connects two appropriate IMs. The zero-point vibration-corrected energies (ΔH0) in eV are reported in this work. The natural bond orbital (NBO) analysis was performed with the software NBO 5.9.40Results
Experimental results
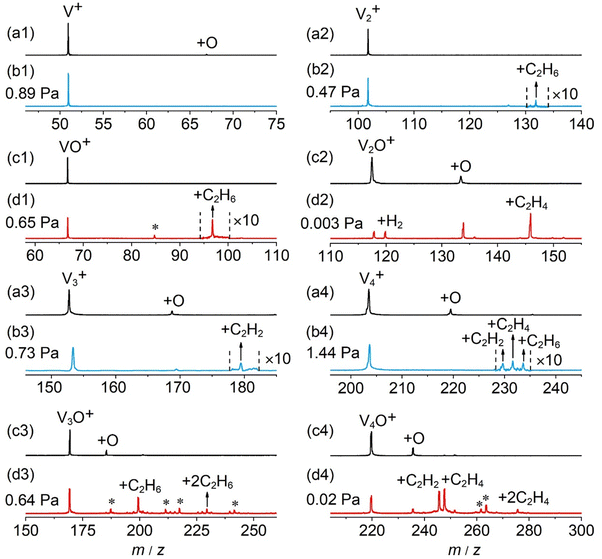
In general, a sharp contrast in reactivity difference of pure vanadium cluster cations versus vanadium oxide cluster cations with ethane was observed (Fig. S1, ESI†): Vn+ with n = 2–5 can lead to the dehydrogenation reaction or adsorption reaction with ethane. However, with the introduction of one oxygen atom, all VnO+ (n = 1–9) can generate adsorption/dehydrogenation product ions with ethane. The typical TOF mass spectra for the reactions of mass-selected Vn+ and VnO+ (n = 1–4) with C2H6 are shown in Fig. 1. When V+ interacts with 0.89 Pa C2H6 for about 2 ms, no new product peaks were observed relative to the background peak generated from the reaction with water impurity. As the cluster size of Vn+ increases, weak cluster reactivity can be observed. Fig. 1(b2) shows that in the reaction between V2+ and 0.47 Pa C2H6 for 2 ms, a very weak product peak (V2C2H6+) for adsorbing a single C2H6 molecule appeared. When the cluster upsizes to V3+ and V4+, the dehydrogenation products of V3C2H2+ and V4C2H2,4+ were observed in Fig. 1(b3) and (b4). In contrast to the case of Vn+, the reactivity of VnO+ with C2H6 was greatly improved. As demonstrated in Fig. 1(d1) and (d3), V1,3O + were able to produce the adsorption products. In the reaction system of V2,4O+, more than half of the initial reactant ions were converted to dehydrogenation product ions at low pressure of C2H6 (⩽0.02 Pa, Fig. 1(d2) and (d4)). In addition, a relatively weak signal that can be assigned to V2OH2+ appears in the reaction of V2O+ with C2H6, corresponding to the loss of a C2H4 molecule (V2O+ + C2H6 → V2OH2+ + C2H4).The rate constants (k1) for the pseudo-first-order reactions of Vn+ and VnO+ (n = 1–9) with C2H6 were estimated using the following equation:
| Cation | k 1, C2H6 | Cation | k 1, C2H6 |
|---|---|---|---|
| V+ | — | VO+ | 3.33 × 10−13 |
| V2+ | 1.13 × 10−13 | V2O+ | 1.49 × 10−9 |
| V3+ | 8.55 × 10−14 | V3O+ | 2.14 × 10−12 |
| V4+ | 1.32 × 10−13 | V4O+ | 2.01 × 10−10 |
| V5+ | 4.04 × 10−12 | V5O+ | 1.50 × 10−10 |
| V6+ | — | V6O+ | 7.28 × 10−11 |
| V7+ | — | V7O+ | 1.49 × 10−11 |
| V8+ | — | V8O+ | 1.85 × 10−12 |
| V9+ | — | V9O+ | 2.94 × 10−13 |
Computational results
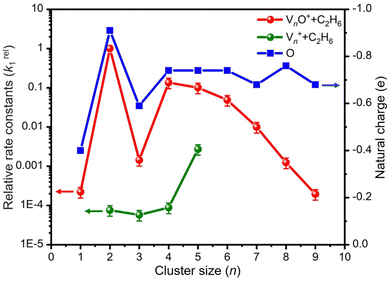
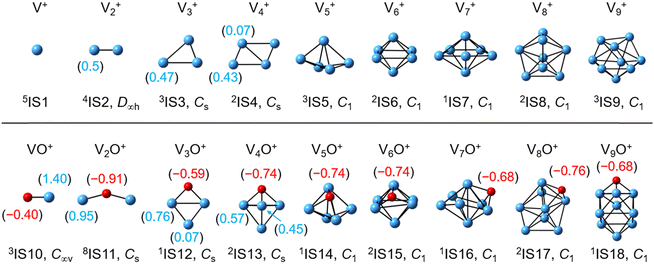
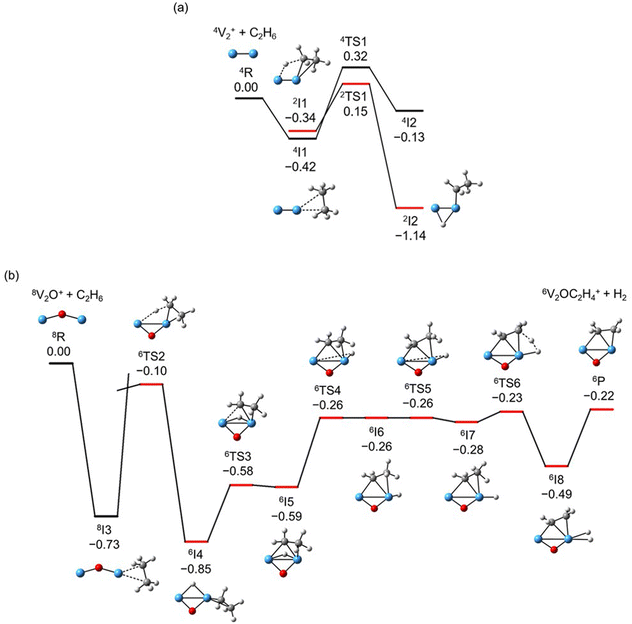
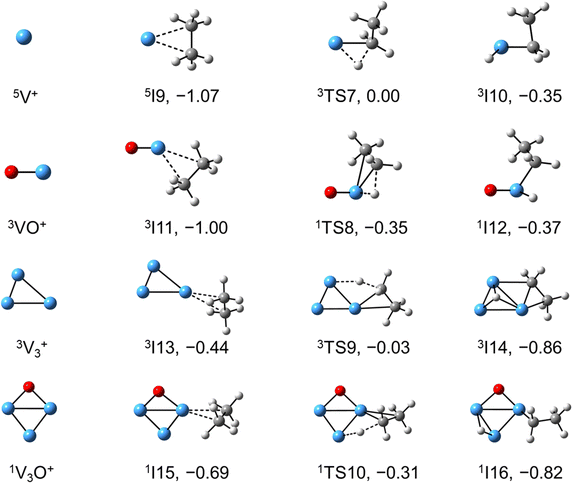
The global minimum structures of Vn+ and VnO+ (n = 1–9) clusters from the DFT calculations are shown in Fig. 3 and Fig. S4–S8 (ESI†). Most of the lowest-lying isomers are consistent with structures calculated with the BP86 method in the literature, except V6+ and V2,9O+.29 For a deeper understanding of the differences in reactivity between Vn+ and VnO+, the reaction pathways of n = 1–3 reaction systems were calculated using the DFT method and the results for V2+ and V2O+ cations with C2H6 are shown in Fig. 4. When a C2H6 molecule approaches the V2+ cation, an encounter complex is formed with a binding energy of 0.42 eV (4I1). The subsequent step for the activation of the first C–H bond involves a spin flip from quartet to doublet states (Fig. S9a, ESI†). Since the energy of 2TS1 is 0.15 eV higher than those of the separated reactants, the process of C–H cleavage initiated by V2+ is kinetically unfavorable under thermal collision conditions. The V2C2H6+ weakly observed in the experiment (Fig. b2) is thus an adsorption product and the C–H bond is not cleaved. In contrast to the inertness of V2+ in cleaving the C–H bond, V2O+ can react with C2H6 to form the dehydrogenation product V2OC2H4+. In V2O+ + C2H6, the V atom captures C2H6 with a binding energy of 0.73 eV to form the complex 8I3. The breaking of the first C–H bond proceeds through a mechanism of synergistic activation by the V–V metal bond involving a spin crossing process (octet → sextet, Fig. S9b, ESI†), resulting in the formation of the lowest energy intermediate 6I4 with a four-membered –V–H–V–O-ring and a three-membered –C–C–V-ring. The transition from 8I3 to 6I4 is kinetically favorable since TS2 has energy lower than that of the isolated reactants by 0.1 eV. Then, the C2H5 moieties in 6I4 moves towards another V atom, resulting in the formation of a new V–C bond in 6I5. After a structural rearrangement to break the V–H bond in 6I5, the second C–H bond can be cleaved. The resulting intermediate 6I8 has enough internal energy to evaporate the H2 unit to produce the experimentally observed V2OC2H4+ product ion.The systems of VnOm+ (n = 1 and 3; m = 0 and 1) involving the first C–H bond cleavage, which is generally viewed as the rate limiting step in alkane conversion, were also considered. As shown in Fig. 5, the oxidative addition of the C–H bond of C2H6 by the cluster systems of V1–3+ encounters the energy barriers in the range of −0.03–0.15 eV. Note that the direct evaporation of the C2H6 from adsorption intermediates (I1, I9, and I13) is an entropically more favorable process, which is in good agreement with the experimental results that only very weak adsorption/dehydrogenation products could be observed. In sharp contrast, the C–H bond cleavage of C2H6 mediated by V1–3O+ experiences a significantly negative energy barrier (⩽−0.1 eV). For the VO+/C2H6 system, the V atom readily traps the C2H6 molecule and releases 1.00 eV energy (3I11). Then, the C–H bond is inserted by the V atom accompanied by a spin flip from triplet to singlet states (3I11 → 1TS8). The energy of the formed intermediate 1I12 (ΔH0 = −0.37 eV) closely approximates that of the transition state 1TS8 (ΔH0 = −0.35 eV), facilitating an almost barrierless transition from I12 back to I11. Although 3I11 can dissociate back to the separated reactants (3I11 → VO+ + C2H6), a small portion of I11 may be stabilized through the collisions with the bath gas, resulting in the observation of the weak adsorption product VOC2H6+ in the experiment (Fig. d1). In contrast, the intermediates (I4–I8) and transition states (TS3–TS6) along the reaction pathway of V2O+/C2H6 are much lower in energy than the TS2 state (Fig. 4). Once intermediate I4 is formed, it has more chance to form I8 that can dissociate into V2OC2H4+ + H2 (6P), which is consistent with the experimental observation that V2O+ reacts much faster than VO+ (Fig. 2). For the system of V3O+/C2H6, considering the low energy barrier of C–H activation (−0.31 eV), I16 shows a higher tendency than I4 to proceed back to the adsorption intermediate (I15) and decompose to the V3O+ + C2H6 under entropy-driven conditions, which rationalizes the lower reaction rate of V3O+ + C2H6 than that of V2O+ + C2H6 in the experiment (Fig. 2).
Discussion
Reactions involving atomic metal ions and the corresponding oxide species with alkanes have been extensively documented,41–52 whereas the oxo-ligand effect of polyatomic metal species has received limited attention. Eckhard et al. performed a comparative study on the reactions of CH4 with Tax+ and TaxO+ (x = 4 and 5) clusters.20 It has been demonstrated that the doped oxygen atom does not directly participate in the reaction. Instead, it modifies the local electronic charge distribution of the tantalum clusters that appears to be favorable for C–H bond activation through a metal insertion mechanism. Given the previous proposals, we conducted a comparison of the charge changes of atoms in the Vn+ and VnO+ systems. In the literature, the C–H cleavage involves electron transfer from the occupied orbitals of alkane to the metal empty orbitals. The amount of positive charges within the cluster will determine its reactivity towards the alkane. According to the NBO analysis shown in Fig. 3, the high electron-withdrawing capability of the O atom significantly increases the positive charge on V atoms in VnO+ systems. Consequently, the VnO+ clusters can have much higher reactivity than the Vn+. For VnO+ cluster systems, the V atom adjacent to the O atom serves as the adsorption site for C2H6 and as reactive sites to bring about C–H activation. The accumulation of large amounts of positive charges in V induced by oxygen is the crucial factor to profoundly affect the cluster reactivity. In other words, a striking correlation between the negative charge on O atom and k1 values emerges as shown in Fig. 2 and 3. V2O+ with the most negative charge (−0.91e) on O among V1–3O+ exhibits the highest reactivity. The oxygen in VO+ carries the least negative charge (−0.40e), resulting in its lowest reactivity. However, the reactivity of V4–9O+ clusters decreases with the increase of the cluster size, while the negative charge on the O atom almost maintains a constant value (−0.68 to −0.74e). This could be attributed to the more crowded steric structure, which hinders the activation of the C–H bond.In transition-metal-catalyzed organic reactions, agostic interaction is commonly defined as the intramolecular interaction between the hydrogen atom of a C–H bond with a nearby metallic center, which plays a crucial role in C–H bond activation.53–56 In such interaction, the σ(C–H) orbital (alkane HOMO) acts as a donor orbital, whereas the acceptor orbitals could be empty molecular orbitals (cluster LUMO) of metal species.57–59 The smaller energy gap helps to form stronger agnostic interaction, enhancing the electron transfer to activate the C–H bond. Therefore, to further explore the effect of the oxygen ligand on the reactivity of metal clusters of different sizes, we analyzed the orbital interactions between VnO+ and C2H6 during the reactions (e.g., V3O+/C2H6 couple in Fig. S10, ESI†) and the HOMO of C2H6 and the LUMO of VnO+ (n = 1–9) cations are shown in Fig. 6. For VnO+ with small cluster sizes (n = 1–3), the energy gap of V2O+ (LUMO) ↔ C2H6 (HOMO) is smaller compared to that of VO+ and V3O+, leading to the strongest agostic interaction and the fastest reaction rate for the V2O+/C2H6 couple (Fig. 2). In contrast, the slowest reaction rate of VO+ with C2H6 can be attributed to the largest energy gap of VO+ (LUMO) ↔ C2H6 (HOMO). For the VnO+ clusters with larger sizes (4 ⩽ n ⩽ 9), the energy gap increases as the cluster is upsized, resulting in weaker and weaker agostic interactions, which is consistent with the rate constant decrease of VnO+ with C2H6 from n = 4 to n = 9 (Fig. 2).
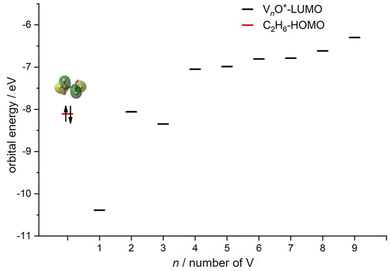 | ||
| Fig. 6 HOMO levels of C2H6 and LUMO levels of VnO+ (n = 1–9) cations. The up and down arrows denote α and β electrons, respectively. | ||
Conclusion
The reactions of ethane with vanadium cluster cations Vn+ (n = 1–9) and their corresponding oxide systems VnO+ (n = 1–9) have been comparatively studied via mass-spectrometry-based experiments. The O atom doped vanadium clusters are much more reactive than the non-doped Vn+ ones. The reactivity of V2O+ is enhanced by four orders of magnitude with respect to that of V2+ and V2O+ is also the most reactive cluster among VnO+ clusters (n = 1–9). The mechanistic studies reveal that the reactivity of VnO+ clusters is enhanced by the modification of charge distribution within the cluster through the introduction of oxygen atoms. The agostic interaction to interpret the size-dependent reactivity of VnO+ has been proposed. This study not only extends our understanding of C–H activation of light alkanes (ethane) by metal systems but also provides insights into doping of O atoms to enhance the reactivity of early 3d transition metals.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 22203078, 92161205, 22121002, and 22322307), the Youth Innovation Promotion Association CAS (No. 2018041), and the China Postdoctoral Science Foundation (No. 2022TQ0289).References
- Y. Wang, P. Hu, J. Yang, Y.-A. Zhu and D. Chen, Chem. Soc. Rev., 2021, 50, 4299–4358 RSC.
- X.-S. Xue, P. Ji, B. Zhou and J.-P. Cheng, Chem. Rev., 2017, 117, 8622–8648 CrossRef CAS PubMed.
- Y. Liu, J.-C. Liu, T.-H. Li, Z.-H. Duan, T.-Y. Zhang, M. Yan, W.-L. Li, H. Xiao, Y.-G. Wang, C.-R. Chang and J. Li, Angew. Chem., Int. Ed., 2020, 59, 18586–18590 CrossRef CAS PubMed.
- G. Kummerlöwe, I. Balteanu, Z. Sun, O. P. Balaj, V. E. Bondybey and M. K. Beyer, Int. J. Mass Spectrom., 2006, 254, 183–188 CrossRef.
- C. Adlhart and E. Uggerud, Chem. Commun., 2006, 2581–2582 RSC.
- U. Achatz, C. Berg, S. Joos, B. S. Fox, M. K. Beyer, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys. Lett., 2000, 320, 53–58 CrossRef CAS.
- C. Adlhart and E. Uggerud, Chem. – Eur. J., 2007, 13, 6883–6890 CrossRef CAS PubMed.
- S. M. Lang, A. Frank and T. M. Bernhardt, J. Phys. Chem. C, 2013, 117, 9791–9800 CrossRef CAS.
- C. A. E. Uggerud, J. Chem. Phys., 2005, 123, 214709 CrossRef PubMed.
- P. B. Armentrout, S. E. J. Kuijpers, O. V. Lushchikova, R. L. Hightower, G. C. Boles and J. M. Bakker, J. Am. Soc. Mass Spectrom., 2018, 29, 1781–1790 CrossRef CAS PubMed.
- P. B. Armentrout, L. Parke, C. Hinton and M. Citir, ChemPlusChem, 2013, 78, 1157–1173 CrossRef CAS PubMed.
- F.-X. Li, X.-G. Zhang and P. B. Armentrout, Int. J. Mass Spectrom., 2006, 255–256, 279–300 CrossRef CAS.
- O. W. Wheeler, M. Salem, A. Gao, J. M. Bakker and P. B. Armentrout, Int. J. Mass Spectrom., 2019, 435, 78–92 CrossRef CAS.
- P. Fayet, A. Kaldor and D. M. Cox, J. Chem. Phys., 1990, 92, 254–261 CrossRef CAS.
- D. M. Cox, D. J. Trevor and A. Kaldor, J. Am. Chem. Soc., 1990, 112, 3742–3749 CrossRef.
- Y. Ren, Y. Yang, Y.-X. Zhao and S.-G. He, J. Phys. Chem. C, 2019, 123, 17035–17042 CrossRef CAS.
- X.-G. Zhao, Z.-P. Zhao, Y.-X. Zhao and S.-G. He, J. Phys. Chem. Lett., 2023, 14, 9192–9199 CrossRef CAS PubMed.
- J. F. Eckhard, T. Masubuchi, M. Tschurl, R. N. Barnett, U. Landman and U. Heiz, J. Phys. Chem. A, 2021, 125, 5289–5302 CrossRef CAS PubMed.
- J. Lengyel, N. Levin, F. J. Wensink, O. V. Lushchikova, R. N. Barnett, U. Landman, U. Heiz, J. M. Bakker and M. Tschurl, Angew. Chem., Int. Ed., 2020, 59, 23631–23635 CrossRef CAS PubMed.
- J. F. Eckhard, T. Masubuchi, M. Tschurl, R. N. Barnett, U. Landman and U. Heiz, J. Phys. Chem. C, 2018, 122, 25628–25637 CrossRef CAS.
- N. Levin, J. Lengyel, J. F. Eckhard, M. Tschurl and U. Heiz, J. Am. Chem. Soc., 2020, 142, 5862–5869 CrossRef CAS PubMed.
- T. J. MacMahon, S. W. Buckner, G. D. Byrd and B. S. Freiser, Inorg. Chem., 1989, 28, 3511–3518 CrossRef.
- C. S. Hinton, L. G. Parke and P. B. Armentrout, J. Phys. Chem. C, 2007, 111, 17773–17787 CrossRef.
- S. Hirabayashi and M. Ichihashi, J. Phys. Chem. A, 2019, 123, 6840–6847 CrossRef CAS PubMed.
- S. Shin, P. B. Armentrout and R. Liyanage, J. Phys. Chem. A, 2006, 110, 1242–1260 CrossRef PubMed.
- A. Simon, J. Lemaire, P. Boissel and P. Maître, J. Chem. Phys., 2001, 115, 2510–2518 CrossRef CAS.
- K. K. Irikura and J. L. Beauchamp, J. Am. Chem. Soc., 1991, 113, 2769–2770 CrossRef CAS.
- N. Aristov and P. B. Armentrout, J. Phys. Chem., 1987, 91, 6178–6188 CrossRef CAS.
- H. Zhang, H. Wu, Y. Jia, B. Yin, L. Geng, Z. Luo and K. Hansen, Commun. Chem., 2020, 3, 148 CrossRef CAS PubMed.
- Z. Yuan, Y.-X. Zhao, X.-N. Li and S.-G. He, Int. J. Mass Spectrom., 2013, 354–355, 105–112 CrossRef CAS.
- Z. Yuan, Z.-Y. Li, Z.-X. Zhou, Q.-Y. Liu, Y.-X. Zhao and S.-G. He, J. Phys. Chem. C, 2014, 118, 14967–14976 CrossRef CAS.
- X.-N. Wu, B. Xu, J.-H. Meng and S.-G. He, Int. J. Mass Spectrom., 2012, 310, 57–64 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev., B Condens. Matter, 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- X.-L. Ding, Z.-Y. Li, J.-H. Meng, Y.-X. Zhao and S.-G. He, J. Chem. Phys., 2012, 137, 214311 CrossRef PubMed.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.9, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2009 Search PubMed.
- J. Roithová and D. Schröder, Chem. Rev., 2010, 110, 1170–1211 CrossRef PubMed.
- R. Wesendrup, C. Heinemann and H. Schwarz, J. Phys. Chem. A, 1995, 239, 75–83 Search PubMed.
- S. Zhou, J. Li, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2016, 55, 10877–10880 CrossRef CAS PubMed.
- K. K. Irikura and J. L. Beauchamp, J. Am. Chem. Soc., 1989, 111, 75–85 CrossRef CAS.
- K. Chen, Z.-C. Wang, M. Schlangen, Y.-D. Wu, X. Zhang and H. Schwarz, Chem. – Eur. J., 2011, 17, 9619–9625 CrossRef CAS PubMed.
- I. Kretzschmar, A. Fiedler, D. Schröder and H. Schwarz, J. Am. Chem. Soc., 1996, 118, 9941–9952 CrossRef.
- A. Fiedler, M. F. Ryan, D. Schroeder and H. Schwarz, J. Am. Chem. Soc., 1995, 117, 2033–2040 CrossRef.
- H. Schwarz, D. Schröder, D. E. Clemmer, Y. Chen, P. B. Armentrout and V. I. Baranov, Int. J. Mass Spectrom. Ion Processes, 1997, 161, 175–191 CrossRef.
- A. Fiedler, M. F. Ryan, D. Schroeder and H. Schwarz, Organometallics, 1994, 13, 4072–4081 CrossRef.
- A. Božović, S. Feil, G. K. Koyanagi, A. A. Viggiano, X. Zhang, M. Schlangen, H. Schwarz and D. K. Bohme, Chem. – Eur. J., 2010, 16, 11605–11610 CrossRef PubMed.
- N. Dietl, C. van der Linde, M. Schlangen, M. K. Beyer and H. Schwarz, Angew. Chem., Int. Ed., 2011, 50, 4966–4969 CrossRef CAS PubMed.
- L. Yue, S. Zhou, X. Sun, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2018, 57, 3251–3255 CrossRef CAS PubMed.
- G. Logothetis and P. L. A. Popelier, J. Organomet. Chem., 1998, 555, 101–111 CrossRef.
- M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914 CrossRef CAS PubMed.
- L. Lin, D. M. Spasyuk, R. A. Lalancette and D. E. Prokopchuk, J. Am. Chem. Soc., 2022, 144, 12632–12637 CrossRef CAS PubMed.
- L. Andrews, H.-G. Cho and X. Wang, Angew. Chem., Int. Ed., 2004, 44, 113–116 CrossRef PubMed.
- M. Lein, Coord. Chem. Rev., 2009, 253, 625–634 CrossRef CAS.
- N. Berkaïne, P. Reinhardt and M. E. Alikhani, Chem. Phys., 2008, 343, 241–249 CrossRef.
- K. M. Altus and J. A. Love, Commun. Chem., 2021, 4, 173 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental and theoretical results (data analysis, DFT calculated structures and reaction mechanisms). See DOI: https://doi.org/10.1039/d4cp00857j |
| This journal is © the Owner Societies 2024 |