Open Access Article
Open Access ArticleO2 activation by subnanometer Re–Pt clusters supported on TiO2(110): exploring adsorption sites†
Andrés
Álvarez-García
 a,
Luis M.
Molina
a,
Luis M.
Molina
 b and
Ignacio L.
Garzón
b and
Ignacio L.
Garzón
 *a
*a
aInstituto de Física, Universidad Nacional Autónoma de México, Apartado Postal 20-364, Ciudad de México 01000, Mexico. E-mail: garzon@fisica.unam.mx
bDepartamento de Física Teórica, Atómica y Optica, Universidad de Valladolid, E-47011 Valladolid, Spain
First published on 16th May 2024
Abstract
Activation of O2 by subnanometer metal clusters is a fundamental step in the reactivity and oxidation processes of single-cluster catalysts. In this work, we examine the adsorption and dissociation of O2 on RenPtm (n + m = 5) clusters supported on rutile TiO2(110) using DFT calculations. The adhesion energies of RenPtm clusters on the support are high, indicating significant stability of the supported clusters. Furthermore, the bimetallic Re–Pt clusters attach to the surface through the Re atoms. The oxygen molecule was adsorbed on three sites of the supported systems: the metal cluster, the surface, and the interface. At the metal cluster site, the O2 molecule binds strongly to RenPtm clusters, especially on the Re-rich clusters. O2 activation occurs by charge transfer from the metal atoms to the molecule. The dissociation of O2 on the RenPtm clusters is an exothermic process with low barriers. As a result, sub-nanometer Re–Pt clusters can be susceptible to oxidation. Similar results are obtained at the metal-support interface, where both the surface and cluster transfer charge to O2. To surface sites, molecular oxygen is adsorbed onto the Ti5c atoms with moderate adsorption energies. The polarons, which are produced by the interaction between the metal cluster and the surface, participate in the activation of the molecule. However, dissociating O2 in these sites is challenging due to the endothermic nature of the process and the high energy barriers involved. Our findings provide novel insights into the reactivity of supported clusters, specifically regarding the O2 activation by Re–Pt clusters on rutile TiO2(110).
1 Introduction
Supported metal clusters (SMCs) represent a category of heterogeneous catalysts comprising metal clusters attached to solid supports, such as metal oxides.1 Re–Pt clusters supported on titania are employed as catalysts for the water–gas shift reaction2 and CO oxidation.3,4 Rhenium has a variety of valence states and higher oxophilicity than other noble metals (Pt, Ir), which may enhance catalytic multifunctionality.5 The utilization of Re–Pt catalysts leads to an economical process because of their extended catalyst lifespan and high yield of desired products.6 The bimetallic system of Re–Pt exhibits unique properties that differ from those of pure Pt and pure Re in catalytic reactions.3 The catalyst containing Re–Pt/TiO2 exhibits higher activity than the pure Pt/TiO2 catalyst for the water gas shift (WGS) reaction.7 The interaction between oxygen and Re–Pt bimetallic clusters is relevant in the aforementioned reactions because PtOx and ReOx can act as promoters or inhibitors.8 The activation of O2 is a pivotal step in oxidation processes, resulting in the creation of more reactive species, such as superoxo, peroxo, and atomic oxygen.9,10 Several factors can influence the activation of O2, including the support type, cluster size, and interface perimeter.11–13 Additionally, metals featuring a low O2 dissociation barrier exhibit a tendency to adsorb O2 and O strongly, rendering them susceptible to oxidation.14Recently, there has been an increasing interest in subnanometer clusters as single-cluster catalysts (SCCs). Small metal clusters, typically composed of fewer than 20 atoms (with a diameter of less than 1 nm), are supported on suitable matrices to form SCCs.15 They are an intermediate size between traditional metal nanoparticles and single-atom catalysts (SACs).16–18 Subnanometer metal clusters exhibit unique physicochemical properties due to quantum confinement effects.19 Controlling the size and arrangement of SCCs with atomic precision is crucial for adjusting the activity and stability of clusters in different catalytic applications.20 Furthermore, the precise control of subnanometer clusters can result in the formation of bimetallic catalysts, such as Au4Pt221 and Rh1Co322 clusters.
The stability of subnanometer clusters is maintained by the metal-support interactions, as well as the low kinetic energy deposition.23 Interactions between highly reactive metals (with incomplete d-shells), such as Re, and reducible oxides, such as titania, can stabilize supported metal clusters composed of only a few atoms.24–26 Ultra-small Re clusters (size = 2–13 atoms) were deposited on graphene and studied by high annular dark-field scanning transmission electron microscopy (HAADF-STEM), where Re clusters presented 3D structures above four-atom size.27 Subnanometer Ptn (n = 4, 7–10, 15) clusters were deposited on the TiO2(110) surface and imaged at atomic resolution using an ultrahigh vacuum scanning tunneling microscope.28 The Pt7 cluster on TiO2(110) exhibits catalytic activity in CO oxidation, where reduction conditions can play a significant role in CO2 production.29 While there are no reports of subnanometer-scale Re–Pt clusters, they have been studied in larger clusters.7 In our previous work, we analyzed the structure of Re–Pt clusters in both the gas phase and supported on the MgO(100) surface. Our findings revealed a transition from a 2D to a 3D configuration at size five.30 In addition, five-atom size clusters allow for the exploration of 3D configurations, with atoms directly interacting with the substrate and others forming a second layer.
The Cu5 cluster has been synthesized with atomic precision and exhibits stability to ultraviolet radiation, temperature, and pH, rendering it an ideal model for the study of polarons in oxide-supported clusters.31 Oxides can serve as inert matrices for dispersing metal nanoparticles or as catalysts themselves. The reducible oxides, such as TiO2, CeO2, and Fe2O3, are capable of exchanging oxygen atoms, making them effective in oxidation reactions.32–34 In particular, the reactivity of rutile TiO2(110) surface for O2 adsorption and dissociation has been studied.35 Oxygen vacancies (Ov) on the TiO2(110) surface act as a source of excess electrons, leading to the dissociation of O2.36,37 This excess of electrons can also be achieved by charge transfer from metal clusters with low resistance to electron donation.38–40 Specifically, Cu5 and Ag5 clusters donate electrons to the support, inducing the formation of one or two polarons.41–43 The excess charge is located in the 3d states of Ti, which causes a reduction of its oxidation state from Ti4+ to Ti3+. Therefore, the study of subnanometer clusters of five-atom size supported on titania is of significant interest due to their computational simplicity, preference for 3D conformations, and the existing background on this topic.
Modeling subnanometer clusters supported on metal oxides is challenging due to their structural intricacies.44 To address this issue, utilizing global optimization algorithms such as Basin-Hopping45 or Genetic Algorithms46 in conjunction with Density Functional Theory (DFT) may be advantageous. In this manuscript, we present an extensive study of the structure of subnanometer RenPtm (n + m = 5) clusters supported on the rutile TiO2(110) surface, evaluating the O2 adsorption and activation on these bimetallic clusters as a function of their relative Re–Pt content. The configuration space of the supported clusters is explored using the Basin-Hopping DFT algorithm. Then, the most stable isomers were selected for a complete study of O2 adsorption at all the possible binding sites: the metal cluster, the TiO2(110) surface away from the supported cluster, and the interfacial region around the cluster. The O–O bond activation is evaluated by various structural (bond length, O–O stretching frequency) and electronic parameters (spin magnetic moment, Bader charges, and density of states). Finally, the dissociation of O2 is also studied using the Nudged Elastic Band (NEB) approach to obtain the activation barriers for this process.
2 Computational details
The structures of the gas-phase PtnRem (n + m = 5) clusters were obtained from our previous study,30 where we performed a global optimization using the Basin-Hopping DFT (BH-DFT) algorithm coupled to VASP (ESI†). The TiO2(110) surface was constructed using a 4 × 2 slab with four trilayers, with the two bottom trilayers fixed to their positions in the bulk during relaxations. The vacuum in the z-direction was 20 Å, and the neighboring images in the horizontal direction were separated by at least 8 Å. A dipole correction perpendicular to the supercell is applied to the total energy. The search for the most stable structures of PtnRem (n + m = 5) clusters supported on TiO2(110) was performed using the BH-DFT algorithm with 50 Monte Carlo steps.DFT calculations were performed in the VASP code47 employing the PBE functional48 and the projector augmented wave (PAW) potentials.49,50 The cutoff energy for the plane-wave basis set was 400 eV. Ti(3s, 3p, 3d, 4s), O(2s, 2p), Pt(5d, 6s), and Re(5d, 6s) electrons were treated explicitly as valence. For titanium, the DFT+U formalism51 was used to describe the highly localized d-electrons,52 with the parameter for the Ti(3d) level set to 4.5 eV. The evaluation of the reducibility of the surface was performed by analyzing the spin magnetic moment and spin density of the system atoms. The convergence criteria of the electronic energy of the self-consistent field (SCF) and the forces of the geometric relaxations were 10−6 eV and 0.01 eV Å−1, respectively. A single Γ point was used for integration of the Brillouin zone, since the large size of the unit cell already results in converged binding energies including only this single point in the calculations.
The adsorption energy for RenPtm clusters (Eads[cluster]) supported on TiO2(110) was calculated as53
| Eads[cluster] = −E[RenPtm/TiO2] + E[TiO2] + E[RenPtm] |
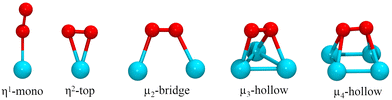
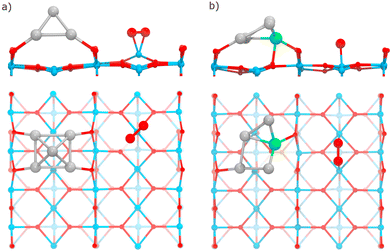
The adsorption of the O2 molecule on the clusters was studied on several binding configurations, depicted in Fig. 1. The adsorption mode η1 is the bonding of an O atom to a metal atom. In the η2, the metal is bonded to the two atoms of the oxygen molecule. The other sites involve O2 bonding on multiple metal atoms (μ2, μ3, μ4). Previous studies have evaluated these types of adsorption sites for oxygen molecule on metal clusters.54,55 On each case, before each structural optimization, the O2 molecule was positioned initially 2.2 Å away from the binding site.
The adsorption energy for O2 to the cluster, either supported or in the gas phase, (Eads[O2]) was calculated as
| Eads[O2] = −EO2/cluster + EO2 + Ecluster |
The charge transfer was studied through a charge density analysis with the Bader approach.56,57 The projected of Density of States (PDOS) over each atom of the system was calculated using VASPKIT code58 with a Gaussian broadening equal to 0.1 eV. The climbing image Nudge-elastic-band (CI-NEB) method was employed to determine the transition states for the reaction pathways of the O2 dissociation reaction.59 Each transition state (TS) presented only one imaginary frequency, which verifies that it is a maximum in the potential energy surface (PES). The stretching frequency of the oxygen molecule was calculated using the harmonic finite difference approximation.60,61 We also studied how temperature affects the oxygen dissociation reaction in gas-phase clusters. We used the harmonic finite difference approximation to calculate the vibrations of the reactants (O2 adsorption on the clusters) and the products (O2 dissociation). The free energy at 300 K and 1 atm was determined using the post-processing code VASPKIT,58 considering rotational, vibrational, translational, and electronic contributions.
3 Results
3.1 Structure and stability of RenPtm (n + m = 5) clusters supported on the TiO2(110)
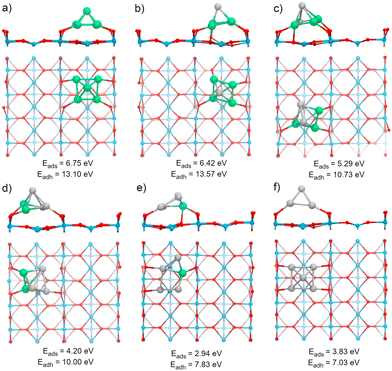
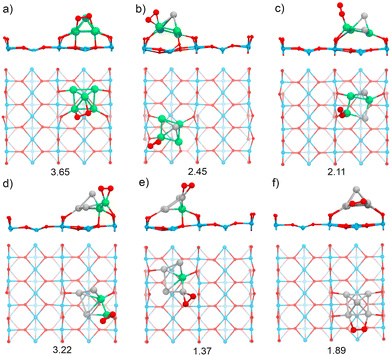
The TiO2(110) surface has three types of sites in its topmost layer: the two-coordinate protruding oxygen (O2c), the three-coordinate oxygen (O3c), and the five-coordinate titanium (Ti5c). The O2c atoms protrude in one dimensional rows above the plane where Ti5c and O3c sites are located. A global optimization of RenPtm (n + m = 5) clusters supported on TiO2(110) was performed using Basin-Hopping DFT. Fig. 2 shows the structure, absorption and adhesion energies of the global minima for each of the RenPtm/TiO2(110) clusters. Although the calculations were performed with four trilayers (12 atomic layers), to improve visualization of the structure only the first trilayer of the surface is displayed. This slab model has been employed in prior investigations studying metal clusters of comparable size.62,63All the clusters, excepting Re1Pt4, have a distorted square pyramidal shape, with its base in contact with the surface. At the global minima found, the clusters try to maximize the number of bonds between the metallic atoms in the bottom layer and the more reactive O2c surface sites. In order to form stronger O–metal bonds by shortening the bond distance, the surface O2c atoms suffer important lateral distortions of around 0.3–0.4 Å. The Re1Pt4 cluster has a very different shape, more planar, and with only three atoms in direct contact with the surface. In the case of Pt5, our results agree with the simulations performed by Jian et al.,64 who obtained the putative global minima for Ptn (n = 4–8) on the rutile TiO2(110) surface, with the Pt5 cluster also having a pyramidal square conformation.
In our previous work,30 gas-phase RenPtm (n + m = 5) clusters were optimized using a similar Basin-Hopping DFT algorithm (ESI,† Fig. S1). Re3Pt2, Re2Pt3, and Pt5 clusters have planar structures, while Re5, Re4Pt1, and Re1Pt4 clusters presented three-dimensional structures. In particular, the Re5 cluster has a square pyramidal configuration, which does not change significantly after adsorption on the TiO2(110) surface. The high internal binding energy of the Re5 cluster is the reason for this behavior, indicating a very strong metal–metal bond. The rest of the clusters, are more fluxional, and the interaction with the substrate results in very important structural changes. For instance, the Pt5 cluster changes from a planar house-shaped configuration to a square pyramid, which was similarly found on the ZrO2(101) surface.65 In the ESI† (Fig. S2 and S3) we compare the global minimum found for each composition, with the first and second isomers (ISO1 and ISO2). For the clusters with a high content of Re, there are no competing isomers with the square pyramidal shape. However, as the Pt content increases, other alternate conformations have similar stabilities to the global minimum shape, as for example the ISO1 conformations for Pt3Re2 and Pt4Re1, less than 0.1 eV apart from the GM one.
Several energetic parameters have been calculated to account for the cluster–surface interaction (Fig. 2). The adsorption energy of the clusters (Eads[cluster]) provides information about the stability of the cluster deposition on the substrate. In general, Eads[cluster] decreases with an increasing amount of Pt in the cluster, with Re1Pt4 being an exception which can be attributed to the high energetic cost of the cluster distortion that takes place during adsorption; indeed, the value of the adhesion energy for this cluster is actually larger than the one for pure Pt5,
The adhesion energy (Eadh), which represents the strength of the interaction between the cluster and the surface, also decreases steadily with a increasing content of Pt. In all cases, the values for Eadh exceed 7 eV (and reach even 13 eV for Re-rich clusters), indicating a high stability of the supported clusters. The relaxed geometries show a marked tendency towards maximizing the number of bonds between Re atoms and surface oxygen atoms; for mixed clusters, Re atoms are always in contact with the substrate, and alternate conformations with Re atoms losing contact with the support are much less stable, as Fig. S2 and S3 (ESI†) show. Comparing the values of Eads or Eadh for Re5 and Pt5 (which both share the same geometric arrangement) it is clear that the intrinsic strength of O–Re bonds is approximately twice as large as the one of O–Pt bonds. The cluster–surface interaction energies for other five atom clusters supported on TiO2(110) reported in the literature are 4.50, 4.53, 5.37, and 6.87 eV for the Cu5,38 Ag5,42 Au5,66 and Pd566 clusters, respectively. Thus, RenPtm (n + m = 5) clusters exhibit a higher affinity for the TiO2(110) surface compared to other clusters of the same size that have been previously reported. Interestingly, the formation of strong bonds between Re and the surface O atoms is affected by the reducible character of the TiO2 oxide; the situation changes for a non-reducible oxide as MgO, where Re-rich clusters do not fit well on the support.30
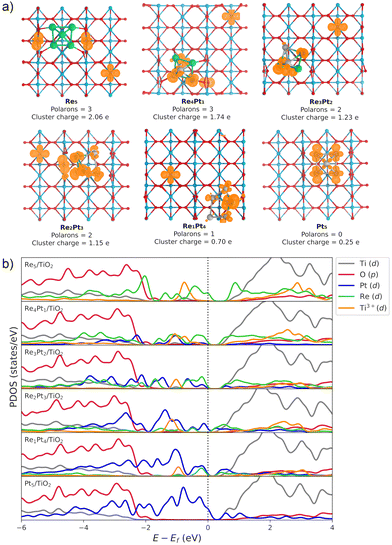
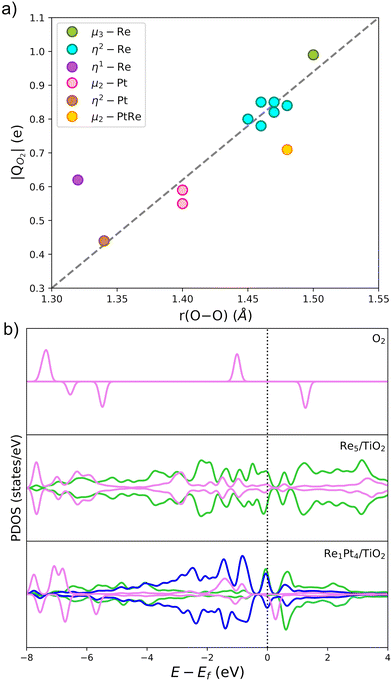
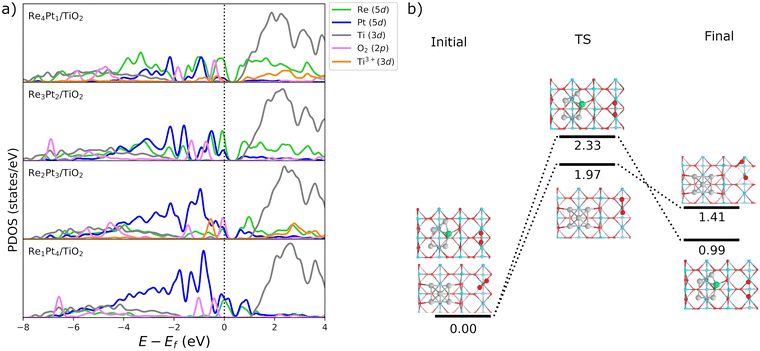
The Bader charge analysis shows that the Re5 cluster donates 2.04 electrons to the surface, while Pt5 transfers only 0.25 electrons (see data in Fig. 3). For bimetallic clusters, the charge transfer to the substrate increases steadily with the Re composition (from 0.70 to 1.74 electrons). Therefore, the stronger interaction between Re and O atoms also results in a larger degree of charge transfer towards the surface. This charge is highly localized on the Ti atoms at the surface, as evidenced by the analysis of the spin magnetic moment. In Fig. 3, we have calculated the spin density distribution and polaron formation for the supported clusters. The charge donation from clusters which contain Re results in polarons appearing on Ti3+ sites. In the case of the Pt5 cluster, the spin density is localized on the metal atoms, so no polarons are formed. In contrast, for the other clusters the spin density and spin magnetic moment are localized on the surface Ti atoms. The polarons are located below or to one side of the cluster. We find that the reducibility of the TiO2(110) surface and the number of polarons formed depends on the composition of the RenPtm (n + m = 5) clusters, ranging from one polaron (Re1Pt4 cluster) to three polarons (Re5 cluster). The reduced Ti atoms exhibit a spin magnetic moment of 0.80–0.85μB, which serve as a parameter to characterize Ti3+ atoms. Interestingly, the Re4Pt1 cluster has one of its polarons in the subsurface, which also happens in titania with oxygen vacancies.67 To conclude, supported RenPtm (n + m = 5) clusters hold polarons to the surface due to the electrostatic attraction, making them more available for chemical reactions than polarons formed through vacancies.68
Fig. 3b shows the projected density of states (PDOS) of RenPtm (n + m = 5) clusters supported on TiO2(110), where the cluster and polaron states have been multiplied by six to ease the observation. Polaron states (3d states of Ti3+) are shown in yellow and are located about 1 eV below the conduction band of TiO2(110). As the number of polarons increases, the intensity of defect states is higher. The Re5 cluster produces three polarons and has a higher intensity of Ti3+ states. In contrast, the supported Pt5 cluster does not have states corresponding to a reduced Ti atom, which is consistent with the fact that they do not form polarons. Finally, the Re4Pt1 cluster has two orange peaks in the gap, corresponding to the surface and subsurface polarons. Furthermore, the Ti3+ 3d1 states are coupled to lattice distortions. To analyze this structural effect without interference from other interactions, we measured lattice distortions for polarons that are not in direct interaction with the cluster. This was done to avoid any interference from the metal-substrate interaction, which also produces a distortion of the surface. We found that for supported Re5, a polaron was identified in close proximity to the cluster, exhibiting an elongation of the Ti–O bond (0.13–0.18 Å) when the oxygens were bound to the Ti cation hosting the polaron. For other clusters, polaron formation was accompanied by a lattice distortion of approximately 0.15 Å known as a phonon cloud. An alternative explanation is that the interaction between the cluster and the surface results in the reduction of Ti atoms in the substrate (from a Ti4+ cation to Ti3+), which causes distortions in the lattice due to the increase in the ionic radius. In a similar vein, Lopez-Caballero et al. reported a distortion of this nature for small polarons induced by the Ag5 cluster supported on TiO2(110).42 Therefore, we can conclude that in the case of Pt–Re mixed clusters, the cluster–surface interaction is responsible for the formation of small polarons.69
3.2 Adsorption and activation of O2 by gas-phase and supported RenPtm clusters
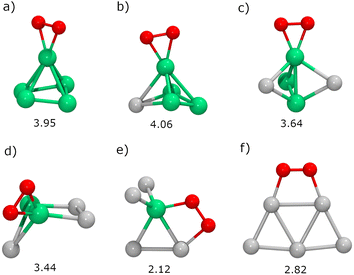
Next, we will study the molecular adsorption and dissociation of O2 on RenPtm (n + m = 5 clusters, both free and supported on TiO2(110). The O2 molecule can adsorb in three different states, as molecular oxygen (O2), superoxo (O2−), or peroxo (O22−). Calculations performed with our DFT model for the gas-phase O2 molecule yielded a bond distance (1.23 Å,), magnetic moment (2.0μB), and stretching vibration (1564 cm−1) consistent with experiments.70 These results support the methodology employed for the O2 activation in the current study. The chemical adsorption of O2 is characterized by a charge transfer from the catalyst to the oxygen molecule, forming superoxo or peroxo species. One possible way of identifying superoxo and peroxo species is to use the stretching frequency of the molecule (below about 900 cm−1 for peroxo and about 900 cm−1 for superoxo), although the boundary is not clear.14 The assignment of a species for adsorbed O2 depends on various electronic and structural parameters. According to experimental reports,10 the superoxide shows an O–O bond elongation (1.35 Å), a decrease in magnetization (1.0μB), and a shift of the stretching frequency (1100 cm−1) with respect to the neutral molecule. Finally, peroxo is a non-magnetic species with more drastic O–O bond stretching (ν = 877 cm−1, r = 1.48 Å).In gas-phase RenPtm clusters with five atoms, the adsorption energy for O2 ranges from 2.12 to 4.06 eV, indicating a strong interaction between the molecule and the RenPtm clusters (Fig. 4). In all cases, the O2 molecule has a strong preference towards binding at the Re sites. The highest adsorption energy was obtained for clusters with significant Re content, such as Re5, Re4Pt1, Re3Pt2, and Re2Pt3, which exhibit their most stable structure in the η2-Re mode. The significant adsorption energies of O2 suggest that desorption is unlikely, particularly in Re-rich clusters. On the other hand, Re1Pt4 and Pt5 clusters prefer bridging-type adsorption (μ2), with much lower O2 binding energies compared to the case of Re-rich clusters. Wang et al. have studied the adsorption of O2 on pure Pt clusters, with Pt4 and Pt6 clusters also showing a bridge-like adsorption mode for molecular O2.71 The O2 molecule adsorbed on RenPtm clusters has a bond length ranging from 1.40 to 1.48 Å, a stretching frequency varying from 644 to 914 cm−1, and a magnetic moment close to zero (Table 1). These values suggest that, for all the gas-phase RenPtm clusters, O2 binds as a peroxo species, indicating a strong activation of the O–O bond upon molecular adsorption.
| Sites | Parameters | Re5 | Re4Pt1 | Re3Pt2 | Re2Pt3 | Re1Pt4 | Pt5 |
|---|---|---|---|---|---|---|---|
| Gas-phase cluster | r O–O | 1.46 | 1.47 | 1.48 | 1.47 | 1.48 | 1.40 |
| ν O–O | 914 | 909 | 898 | 908 | 644 | 758 | |
| M O2 | 0.13 | 0.07 | 0.03 | 0.02 | 0.21 | 0.05 | |
| Supported cluster | r O–O | 1.50 | 1.46 | 1.32 | 1.45 | 1.34 | 1.40 |
| ν O–O | 680 | 925 | 1164 | 938 | 1099 | 831 | |
| M O2 | 0.00 | 0.09 | 0.01 | 0.00 | 0.77 | 0.22 | |
| Surface site | r O–O | 1.45 | 1.45 | 1.41 | 1.45 | 1.41 | 1.45 |
| ν O–O | 951 | 962 | 934 | 957 | 931 | 960 | |
| M O2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | |
| Interface site | r O–O | — | — | 1.41 | 1.39 | 1.41 | 1.40 |
| ν O–O | — | — | 881 | 893 | 843 | 837 | |
| M O2 | — | — | 0.04 | 0.00 | 0.02 | 0.00 | |
In supported RenPtm (n + m = 5) clusters, the adsorption energy for O2 varies from 1.37 to 3.65 eV (Fig. 5). Therefore, in all cases the clusters supported on TiO2(110) exhibit a lower adsorption energy compared to the gas-phase clusters. Several factors contribute to this decrease in reactivity, the most important being the bonding of metal atoms to the surface oxygen atoms. This surface effect is particularly clear in the cases of Re4Pt1 and Re3Pt2; for those clusters the oxygen molecule binds at Re sites which are already forming strong O–Re bonds to the substrate, and this has a high energetic cost of approximately 1.5 eV. Another effect is the transition from 2D geometries (in the unsupported case) to 3D ones for supported clusters; in the case of the Pt5 cluster, we find a decrease of O2 binding energy of almost 1 eV. As it happened for clusters in the gas phase, we find a clear trend for higher O2 adsorption energies in the case of clusters with a high concentration of Re, whereas Pt5 and Re1Pt4 clusters have much lower adsorption energies. The most stable adsorption modes on the supported clusters are: mono (η1-Re), top (η2-Pt, η2-Re), and bridge (μ3-Re, μ2-Pt) types. The high fluxionality of the supported clusters results in important structural changes taking place upon adsorption of the O2 molecule. This effect is particularly strong for the Re3Pt2 and Re2Pt3 clusters, where the Re atom that interacts with O2 experiences a significant displacement, and the square pyramid distorts into a more open conformation. The O2 on supported RenPtm clusters has a bond length from 1.32 to 1.50 Å, a stretching frequency between 680 and 1164 cm−1, and a magnetic moment from 0.00 to 0.77μB (see Table 1, which reports all the parameters for the adsorbing O2 molecule in gas-phase and TiO2 -supported clusters). These parameters can be related to superoxo (for Re3Pt2 and Re1Pt4) and peroxo species (for the rest of clusters), with the highest O–O bond activation taking place on Re5, Re4Pt1, and Re2Pt3 clusters, consistent with the highest adsorption energies.
The Bader charge analysis was performed on the most stable structures to understand the activation of O2 on gas-phase and supported RenPtm clusters. Previous theoretical studies have shown that the charge transfer from the cluster to O2 depends on the adsorption mode.55,72Fig. 6 shows the relationship between the charge received by O2 and the O–O bond length, with the data labeled according to the adsorption mode. There is a linear relationship between the charge and bond length of O2, with only the η1-Re and μ2-RePt modes showing some sizable discrepancies from the linear dependency. The O2 molecule receives a charge ranging from 0.44 to 0.99 e, with the sites which transfer the largest amount of charge being Re atoms (cyan, green), results which are consistent with the larger intrinsic reactivity of these sites. The μ3-Re and η2-Re adsorption modes exhibited a magnetic moment of O2 close to zero, suggesting a full occupation of the π* antibonding orbitals of the molecule. In contrast, when O2 adsorbs on Pt atoms charge transfer decreases and the magnetic moment increases, a fact which correlates with the lower adsorption energies at those sites. Therefore, charge transfer on O2 gives a good measure of the activation of the O–O bond.
An analysis was conducted on the charge of the supported clusters both before and after O2 adsorption, as well as the charge of each atom within the cluster (ESI,† Table S1). After adsorption of O2, the total positive charge on the Re–Pt clusters increases as a result of the charge transfer to the oxygen molecule. Also, we find that the metal atoms directly bonded to O2 are the ones who transfer the majority of the electronic charge to the oxygen molecule. The larger intrinsic reactivity of the Re atoms results in larger charge transfers, compared to Pt.
In Fig. 6b, we have also analyzed the PDOS for O2 adsorption on supported Re5 and Re1Pt4, which are the two clusters with the highest and lowest O2 binding energy, respectively. The first panel shows the PDOS of gas-phase O2, and the two panels below show the PDOS for these two supported clusters. For gas-phase O2, the π* antibonding orbitals split into occupied spin-up and unoccupied spin-down states, resulting in a triplet spin state and a magnetic moment of 2μB. Once the half-occupied π* orbitals are filled, the spin splitting and the magnetic moment disappear.73 When O2 adsorbs at the supported clusters, there are significant differences between the Re-rich and Pt-rich cases. During the adsorption process the 2p-states of the molecule overlap with the 5d-states of the metal atoms, leading to chemisorption of O2. In the case of Re1Pt4, the O2 states of retain spin splitting and have a DOS similar to the superoxo species,74 with antibonding π* orbitals being unoccupied just above the Fermi level. For the Re5 cluster the π* antibonding orbitals are fully occupied, and become symmetric for spin up and spin down, consistent with a peroxo state with the magnetic moment equal to zero. This comparison of the electronic structure for both compositions correlates with the larger cluster-O2 charge transfer and much higher adsorption energy in the case of the Re-rich stoichiometry.
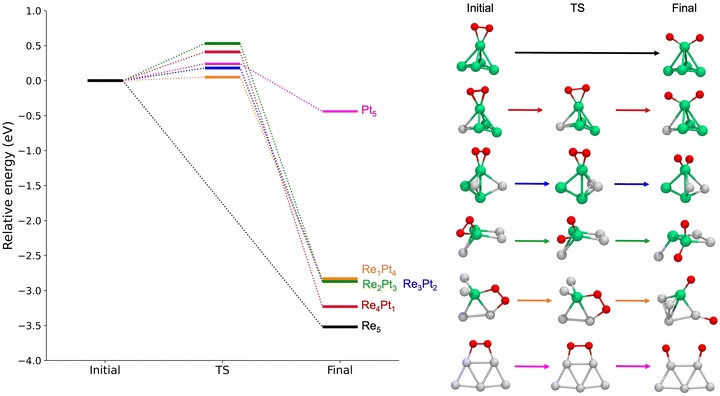
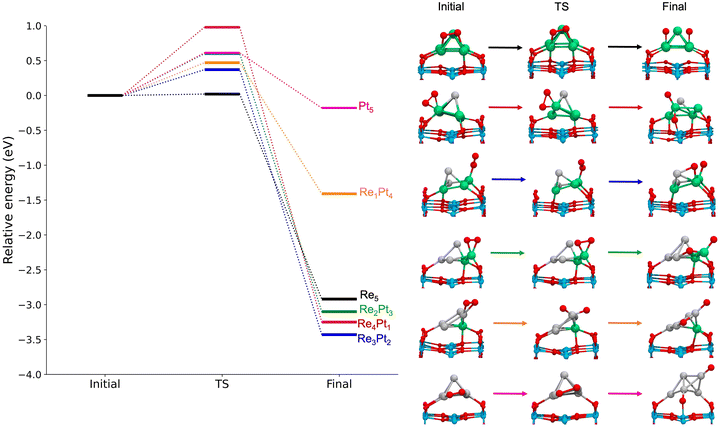
Next, we studied the dissociation of O2 over the metal clusters, comparing the results for both gas-phase clusters, and clusters supported on TiO2(110). In each case, the starting point for the dissociation was taken from the most stable site of molecular O2 adsorption. Table 2 summarizes all the results, showing the values of the activation energies Eact, the reaction energies ΔE and the imaginary frequencies of the transition states, for both gas-phase and supported clusters. The reaction energies ΔE are defined as the energy difference between the initial state (with molecular O2 bonded to the cluster) and the final state (with two separated O adatoms). For unsupported clusters, reaction energies are always large, of the order or 3 eV, with the sole exception of the pure Pt5 cluster. This means that oxygen dissociation is highly exothermic, and dissociative adsorption is strongly favoured whenever there is at least one reactive Re atom in the cluster. In the absence of reactive Re atoms, the reaction energy for Pt5 decreases to only −0.44 eV. Additionally, we calculated the free energy for the dissociation reaction at 300 K and 1 atm on RenPtm (n + m = 5) gas-phase clusters (see data in Table S4 of the ESI†). In most cases, the thermal correction contributes less than 0.1 eV to the reaction energy. Thus, we observed that the trends remain consistent when considering the free energy at 300 K. Thus, this correction has no impact on our analysis.
| Gas-phase clusters | Supported clusters | |||||
|---|---|---|---|---|---|---|
| E act | ΔE | ν i | E act | ΔE | ν i | |
| Re5 | — | −3.52 | — | 0.02 | −2.92 | 415 |
| Re4Pt1 | 0.41 | −3.23 | 561 | 0.98 | −3.25 | 224 |
| Re3Pt2 | 0.18 | −2.87 | 598 | 0.37 | −3.43 | 216 |
| Re2Pt3 | 0.53 | −2.87 | 789 | 0.60 | −3.10 | 579 |
| Re1Pt4 | 0.05 | −2.83 | 347 | 0.47 | −1.41 | 136 |
| Pt5 | 0.24 | −0.44 | 254 | 0.61 | −0.18 | 174 |
For gas-phase clusters, the reaction path for O2 dissociation is shown in Fig. 7. In all cases, activation barriers are low, in the range of 0.0–0.5 eV. The low value of the barrier and the large energy gain for dissociation of O2 causes that, in general, the transition state was found for very small expansions of the O–O bond. In the case of pure Re5, the barrier is extremely small, virtually non existent, and we were not able to properly identify a transition state. The corresponding results for clusters supported on the TiO2(110) surface are shown in Fig. 8. Activation barriers are slightly larger, although they never exceed 1 eV. Again, dissociation of O2 on pure Re5 takes place almost spontaneously, with only a residual barrier of 0.02 eV. The interaction of the surface with the cluster causes some important changes in the mechanisms for O2 dissociation for some compositions; for pure Pt5, the supported cluster undergoes a drastic configuration change after oxygen dissociation and loses bonds at the metal-substrate interface. Reaction energies for supported clusters are, in general, similar to the ones found for gas-phase cluster, with one very important exception, the Re1Pt4 cluster. When this cluster is supported, the reaction energy drops from 2.8 to 1.4 eV. This effect is caused by the binding of the Re atom to the substrate, which serves as an anchoring point. Since this atom is unaccessible to the adsorbed O2 molecule (as there are several Pt atoms on top of it), dissociation must take place at less reactive Pt sites, with an important energetic cost. Overall, the results show that for all compositions dissociation of O2 is an exothermic process with low activation barriers. Nevertheless, there are important quantitative differences between Re-rich clusters, much more reactive, and Pt-rich ones; whenever the reactive Re sites are not available, sizable changes in reactivity will occur.
We have analyzed the charge transfer to O2 when it adsorbs on TiO2-supported clusters (see data in Table S3 of the ESI†). In all the cases, almost all the charge is donated from the 5d-states of the metal clusters, with the change donated from the TiO2 substrate being very small. Finally, we also studied the most stable conformations for the two dissociated oxygen adatoms on both gas-phase and supported clusters. The results are shown in Fig. S4 of the ESI.† In many cases, diffusion of oxygen atoms towards more stable locations is linked to strong conformational changes in the cluster. This happens both for unsupported and for supported clusters. Also, it must be noted that, with respect to the final states reported on Fig. 8, there is a consistent tendency towards separation of the oxygen adatoms; initially, these are bonded to the same atom, but a large energy gain takes place when each one binds at a separate metal site.
3.3 Adsorption of O2 to surface sites of TiO2 substrate
We will now study the adsorption of O2 to surface sites of the TiO2 substrate, separated some distance from RenPtm clusters previously deposited on the surface. First, we have checked that on the pristine TiO2 surface (that is, without metal clusters supported on it) O2 adsorption is very weak (Eads = 0.11 eV), which is in agreement with other theoretical studies.37,75 On the contrary, Sokolovic et al. reported that the reduced TiO2(110) surface can adsorb the oxygen molecule.76 The presence of oxygen vacancies leads to the formation of small polarons located on the next-nearest subsurface Ti6c atoms. These polarons transfer charge to the adsorbed O2 molecule, resulting in the formation of the peroxo species and atomic oxygen.76Similar to the case of reduced TiO2(110) surface with oxygen vacancies, the pristine TiO2 surface with RenPtm clusters supported on it also contains small surface polarons. Previously, our analysis of the electronic structure of the RenPtm/TiO2(110) system has shown that the metal clusters transfer electrons to the surface, leading effectively to the reduction of Ti5c atoms. Consequently, we find that in the presence of supported metal clusters the O2 can adsorb on surface Ti5c with moderately strong adsorption energies, ranging from 0.93 to 1.55 eV (ESI,† Table S2). In general, adsorption of O2 is slightly stronger in the case of Re-rich clusters; the stronger cluster–surface interaction and larger charge transfer also results in stronger O2–TiO2 interactions. In the case of supported Pt5 and Re1Pt4, the adsorption energies of O2 on the surface Ti5c sites are comparable to the ones obtained when O2 adsorbs at these clusters. This means that O2 adsorption on the surface may be significant for these compositions. Also, the process of O2 spillover from the supported cluster to the substrate is feasible, given the similar stability of molecular O2 at both sites. In contrast, for Re-rich compositions, the adsorption energy of O2 is much higher at the metal sites. This fact, together with the very high reaction energy for O2 dissociation at the Re-rich clusters, implies that any O2 molecule that could diffuse from surface sites to the cluster will remain there, being dissociated afterwards.
Depending on the cluster composition, we found two competing adsorption modes: a η2-Ti mode which displaces vertically the Ti5c atom from the surface by about 1 Å, and a μ2-Ti mode where O2 bridges two surface Ti5c sites, with very small vertical displacements for both Ti5c sites. Fig. 9 shows the relaxed structures for these adsorption modes, for the supported Re1Pt4 and Pt5 clusters. The O–O bond lengths for each of these two modes are 1.45 and 1.41 Å, respectively (see Table 1). The stretching frequency for the adsorbed O2 molecule ranges from 931 to 962 cm−1, and its magnetic moment is always equal to zero. These facts indicate that the O2 molecule adsorbs to Ti5c surface sites as a peroxo species.
We have also analyzed the electronic structure of molecular O2 adsorbed at Ti5c surface sites. Table S3 in the ESI† shows the charge transfer to the O2 molecule, for each of the co-adsorbed RenPtm clusters. The values are fairly uniform, ranging from 0.88 to 0.94 electrons. It is interesting to compare the results for O2 adsorption to the metal atoms of the cluster with adsorption of O2 at surface Ti5c sites. When O2 adsorbs at the TiO2 substrate, some part of the charge donated to oxygen is transferred from the substrate, and other part from the cluster. Interestingly, the amount of charge transferred from the surface decreases as the amount of Pt in the cluster increases. We also calculated the PDOS of bimetallic Re–Pt clusters after the O2 adsorption on the surface and analyzed the electronic states of the reduced Ti atoms in the substrate. To enhance the clarity of the plots, we multiplied the Ti3+, the O2 molecule and metal clusters states by ten in the PDOS (Fig. 10). The 5d-states of Pt and Re exhibit minor changes because they do not participate directly on the O2 bonding. The displayed states only show spin up as there is no spin splitting. The 3d states of Ti3+ for Re3Pt2 and Re1Pt4 systems disappear, indicating a charge transfer from Ti3+ atoms to the O2 molecule. Although the other systems retain some polaronic states, there is a significant reduction. This was verified by analyzing the magnetic moment of the Ti atoms, where only one or no polaron remains after adsorption. Thus, Ti3+ atoms facilitate the adsorption of O2 on the surface by transferring electrons to the molecule.
Finally, we have considered the possibility of dissociation of the O2 molecule adsorbed at Ti5c surface sites. The results in Fig. 10b show that this is a very endothermic process. Barriers for O2 dissociation on the surface were calculated in the case of coadsorbed Pt5 and Re1Pt4 systems. In both cases, energy barriers are very high (1.97 and 2.33 eV), leading to final states at least 1 eV higher in energy than the initial state with the O2 molecule intact. This contrasts with the experimental observation of atomic oxygen on the surface with oxygen vacancies.76 Therefore, on surface sites around the Re–Pt supported clusters O2 only experiments a mild activation to a peroxo state, with complete dissociation being unfeasible due to the large barriers involved.
3.4 Adsorption and activation of O2 by the metal-support interface
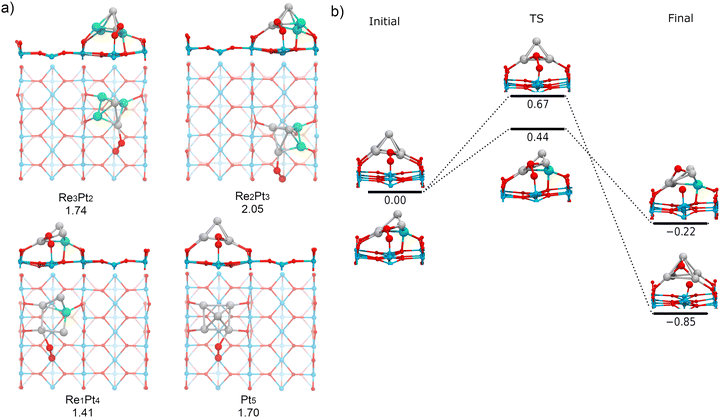
Finally, we have investigated the adsorption and dissociation of O2 at interfacial cluster-TiO2 sites, with the O2 molecule forming bonds with both Ti5c surface atoms and Pt or Re atoms in the supported cluster. These types of catalytic sites are extremely important for a variety of systems and reactions. On one hand, stability of adsorbates at these locations determines if processes of spillover from the cluster to the substrate are feasible (or conversely, reverse spillover from the substrate to the cluster). On the other hand, these sites are the natural meeting place for different reactants which prefer to bind either at the supported cluster, or at the substrate. As a consequence, for many oxidation reactions these sites are believed to be the active sites where the reaction takes place.77,78Fig. 11a shows the most stable conformations found for molecular O2 adsorbed at the cluster-support interface for Re3Pt2, Re2Pt3, Re1Pt4, and Pt5 clusters. For all these compositions, the molecule adsorbs bridging a Ti5c atom in the surface and a Pt atom within the cluster. For Re5 and Re4Pt1, the cluster-support interface is composed exclusively by Re atoms. In these cases, when we relaxed initial starting geometries with O2 bridging Ti and Re sites, we found that the O2 molecule spontaneously dissociates into an oxygen atom bonded to the Re sites in the cluster and another oxygen atom which remains bonded to the Ti5c surface site (see Fig. S5 in the ESI†). It is interesting to compare the binding energies of the final states with one O atom adsorbed at the substrate (4.43 and 5.12 eV for Re5 and Re4Pt1, respectively) with the corresponding values where the two oxygen adatoms remain bonded to the Re-rich clusters (7.74 and 6.65 eV for the most stable conformations on each case). Clearly, there is a high energetic cost against spillover of dissociated oxygen atoms to the substrate, in the case of Re-rich clusters.The adsorption energies at Pt sites vary in a range between 1.41 to 2.05 eV. Such binding strength is similar to the values found for O2 bound at the supported Pt-rich clusters, and it is only slightly larger than the values found at the Ti5c surface sites away from the cluster. The most stable adsorption modes are μ2-TiPt and μ3-TiPt with O–O length ranging from 1.39 to 1.41 Å. At the interface, O2 has a stretching frequency varying between 837 and 893 cm−1, and a magnetic moment equal to zero (see Table 1). Therefore, adsorption of O2 at these sites takes place as a peroxo species. The charge transfer to the O2 molecule if fairly constant, between −0.83 and −0.88 electrons. Part of this extra charge is transferred from the substrate, but the majority is donated by the supported cluster (see Table S3 in the ESI†).
Finally, we have calculated the energy barriers for O2 dissociation at the interface of supported Pt-rich clusters (Pt5 and Re1Pt4, see Fig. 11b). We find that oxygen atom dissociates on the surface and the other on the Pt atoms of the cluster. The process is exothermic, and the energy barriers are similar to those found at the metal cluster site (less than 0.70 eV). Although Re does not directly participate in the dissociation of O2 in this case, it can be observed that the dissociation barrier is lower for the cluster containing a Re impurity. Contrary to the case of Re-rich clusters, the energetic cost for transferring oxygen adatoms from the cluster to the TiO2 substrate is not very high, which means that spillover of dissociated oxygen to the surface can take place for Pt-rich clusters. Overall, our results show that dissociation of O2 at the Pt–Ti interface requires little energy, whereas the Re–Ti interface causes a dissociative adsorption of O2, leading to spontaneous production of atomic oxygen.
4 Conclusions
In this study, the adsorption and activation of O2 on RenPtm (n + m = 5) clusters, both free and supported on TiO2(110), were investigated at the metal cluster, surface, and interfacial sites. The most stable structures for the supported clusters, at various compositions, are characterized by a strong tendency for the Re atoms in the cluster to occupy positions directly in contact with the oxygen surface sites; therefore, in mixed Pt–Re clusters it is expected that Pt atoms will preferentially be displaced towards the top part of the supported cluster, while Re accumulates at the interfacial area, increasing the adhesion of the cluster to the substrate. The composition of RenPtm clusters can tune the formation of surface polarons, increasing the reactivity of the surface towards reactions involving charge transfer. Thus, changes in reactivity may occur due to alterations in the cluster and surface, resulting in the emergence of new active sites, including those found at the interface and on the reduced surface. At the metal cluster sites, the RenPtm clusters have a strong interaction with the O2 molecule, especially on the Re atoms, which are much more reactive than the Pt atoms. The O2 molecule adsorbed on Re–Pt clusters exhibits parameters typical of the peroxo species. This activation of the O–O bond is caused by charge transfer from the cluster atoms to the molecule. Dissociative adsorption can occur on Re atoms due to their significant charge donation to O2. In general, oxidation is expected in RenPtm (n + m = 5) clusters because the energy barriers for dissociation are low (less than 0.7 eV). Finally, the bimetallic Re1Pt4 cluster exhibits a synergistic effect of the metal atoms on its stability and reactivity. The cluster is anchored on the surface by the Re atom, while the Pt atoms activate the O2 molecule.At the surface sites, the composition of RenPtm clusters can tune the formation of surface polarons. Re-rich clusters transfer more electrons to the TiO2(110) surface than Pt-rich clusters, resulting in increased surface reactivity. The oxygen molecule adsorbs onto Ti atoms with moderate adsorption energies (0.93–1.55 eV). The electronic and structural parameters displayed by the O2 on the surface site are analogous to those of peroxo species. Due to the adsorption of oxygen, certain polarons disappear, indicating their involvement in the activation process. However, the activation of O2 can be considered mild on the surface site of Re–Pt supported clusters due to the high energy requirement to break the O–O bond. This finding contrasts with experimental reports for the TiO2(110) surface with oxygen vacancies, where atomic oxygen has been observed.
At the interfacial cluster-support sites, the Re–Ti interface causes the dissociative adsorption of O2, while the Pt–Ti interface activates the O2 molecule with typical structural parameters of a peroxo species. At the Pt–Ti interface, the adsorption energies show a slight increase with respect to the surface sites. Other clusters also exhibit O2 adsorption at the interface, such as Au clusters on the MgO(100)79 and TiO2(101)80 surfaces. Both the metal cluster and Ti surface atoms transfer charge to the O2 molecule. The energy barriers for the dissociation of O2 at the Pt–Ti interface are low, similar to what was found for the cluster sites. Thus, in an oxidizing atmosphere, the interfaces of Pt/TiO2 and Re/TiO2 may become enriched with atomic oxygen. The interface can be an active site for chemical reactions, especially for oxidation reactions that require O2 activation.77
In summary, the RenPtm (n + m = 5) clusters supported on TiO2(110) display three possible sites for O2 adsorption: the metal cluster, the surface, and the interface. All sites transfer charge to the O2 molecule and elongate the O–O bond. In these supported clusters, the metal cluster and interface sites can dissociate the O2 molecule with low energy requirements, while the surface sites requires much more energy. Thus, the sites containing Re and Pt atoms, as well as the Re–Ti and Pt–Ti interfaces, are expected to be oxidized. In Re1Pt4 and Pt5 supported systems, the three active sites compete with each other due to their similar adsorption energies. In terms of the role of metal atoms, Re serves to anchor the cluster to the surface, while Pt is more available to interact with O2. These findings provide new insight into the activation of O2 on Re–Pt clusters supported on TiO2(110) as single-cluster catalysts.
Author contributions
Conceptualisation: AAG, ILG, LMM; formal analysis: AAG, ILG, LMM; funding acquisition: ILG, LMM; supervision: ILG, LMM; visualisation: AAG; writing – original draft: AAG; writing – review & editing: ILG, LMM.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Andrés Álvarez-García gratefully thanks CONACyT-Mexico for the PhD scholarship No. 957475. Calculations were performed at the DGTIC-UNAM Supercomputing Center under Project LANCAD-UNAM-DGTIC-049. This work was supported by DGAPA-UNAM PAPIIT under Project IN106021 and CONACyT-Mexico under Project 285821. Luis M. Molina acknowledges the support from Ministerio de Ciencia e Innovación of Spain (Grant PID2022-138340OB-I00 funded by MCIN/AEI/10.13039/501100011033 and FSE +) and from the University of Valladolid (GIR Nanostructure Physics).Notes and references
- C. Dong, Y. Li, D. Cheng, M. Zhang, J. Liu, Y.-G. Wang, D. Xiao and D. Ma, ACS Catal., 2020, 10, 11011–11045 CrossRef CAS
.
- A. J. Brandt, T. D. Maddumapatabandi, D. M. Shakya, K. Xie, G. S. Seuser, S. Farzandh and D. A. Chen, J. Chem. Phys., 2019, 151, 234714 CrossRef PubMed
.
- R. P. Galhenage, K. Xie, H. Yan, G. S. Seuser and D. A. Chen, J. Phys. Chem. C, 2016, 120, 10866–10878 CrossRef CAS
.
- A. S. Duke, R. P. Galhenage, S. A. Tenney, P. Sutter and D. A. Chen, J. Phys. Chem. C, 2015, 119, 381–391 CrossRef CAS
.
- K. Tomishige, Y. Nakagawa and M. Tamura, Chin. Chem. Lett., 2020, 31, 1071–1077 CrossRef CAS
.
- J. Xiao and R. J. Puddephatt, Coord. Chem. Rev., 1995, 143, 457–500 CrossRef CAS
.
- A. S. Duke, K. Xie, A. J. Brandt, T. D. Maddumapatabandi, S. C. Ammal, A. Heyden, J. R. Monnier and D. A. Chen, ACS Catal., 2017, 7, 2597–2606 CrossRef CAS
.
- A. S. Duke, K. Xie, A. J. Brandt, T. D. Maddumapatabandi, S. C. Ammal, A. Heyden, J. R. Monnier and D. A. Chen, ACS Catal., 2017, 7, 2597–2606 CrossRef CAS
.
- L. Kang, B. Wang, Q. Bing, M. Zalibera, R. Büchel, R. Xu, Q. Wang, Y. Liu, D. Gianolio, C. C. Tang, E. K. Gibson, M. Danaie, C. Allen, K. Wu, S. Marlow, L. D. Sun, Q. He, S. Guan, A. Savitsky, J. J. Velasco-Vélez, J. Callison, C. W. Kay, S. E. Pratsinis, W. Lubitz, J. Y. Liu and F. R. Wang, Nat. Commun., 2020, 11, 17–19 CrossRef PubMed
.
- L. X. Chen, Z. Wen, Z. W. Chen, C. V. Singh and Q. Jiang, J. Mater. Chem. A, 2021, 9, 11726–11733 RSC
.
- C. Vogt and B. M. Weckhuysen, Nat. Rev. Chem., 2022, 6, 89–111 CrossRef PubMed
.
- S. Dai, J. P. Chou, K. W. Wang, Y. Y. Hsu, A. Hu, X. Pan and T. Y. Chen, Nat. Commun., 2019, 10, 1–10 CrossRef CAS PubMed
.
- A. Trinchero, S. Klacar, L. O. Paz-Borbón, A. Hellman and H. Grönbeck, J. Phys. Chem. C, 2015, 119, 10797–10803 CrossRef CAS
.
- M. M. Montemore, M. A. Van Spronsen, R. J. Madix and C. M. Friend, Chem. Rev., 2018, 118, 2816–2862 CrossRef CAS PubMed
.
- X. Li, S. Mitchell, Y. Fang, J. Li, J. Perez-Ramirez and J. Lu, Nat. Rev. Chem., 2023, 754–767 CrossRef PubMed
.
- S. Vajda, M. J. Pellin, J. P. Greeley, C. L. Marshall, L. A. Curtiss, G. A. Ballentine, J. W. Elam, S. Catillon-mucherie, P. C. Redfern, F. Mehmood and P. Zapol, Nat. Mater., 2009, 8, 213–216 CrossRef CAS PubMed
.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed
.
- S. Baskaran, C. Q. Xu, Y. G. Wang, I. L. Garzón and J. Li, Sci. China Mater., 2020, 63, 993–1002 CrossRef CAS
.
- Y. Watanabe, Sci. Technol. Adv. Mater., 2014, 15, 1–12 Search PubMed
.
- B. Ni and X. Wang, Chem. Sci., 2016, 7, 3978–3991 RSC
.
- C. Yao, N. Guo, S. Xi, C. Q. Xu, W. Liu, X. Zhao, J. Li, H. Fang, J. Su, Z. Chen, H. Yan, Z. Qiu, P. Lyu, C. Chen, H. Xu, X. Peng, X. Li, B. Liu, C. Su, S. J. Pennycook, C. J. Sun, J. Li, C. Zhang, Y. Du and J. Lu, Nat. Commun., 2020, 11, 4389 CrossRef CAS PubMed
.
- X. L. Ma, J. C. Liu, H. Xiao and J. Li, J. Am. Chem. Soc., 2018, 140, 46–49 CrossRef CAS PubMed
.
- S. Vajda and M. G. White, ACS Catal., 2015, 5, 7152–7176 CrossRef CAS
.
- P. Kaghazchi and T. Jacob, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 035417 CrossRef
.
- Y.-K. Jeong, Y. M. Lee, J. Yun, T. Mazur, M. Kim, Y. J. Kim, M. Dygas, S. H. Choi, K. S. Kim, O.-H. Kwon, S. M. Yoon and B. A. Grzybowski, J. Am. Chem. Soc., 2017, 139, 15088–15093 CrossRef CAS PubMed
.
- A. S. Chaves, G. G. Rondina, M. J. Piotrowski, P. Tereshchuk and J. L. F. Da Silva, J. Phys. Chem. A, 2014, 118, 10813–10821 CrossRef CAS PubMed
.
- O. Miramontes, F. Bonafé, U. Santiago, E. Larios-Rodriguez, J. J. Velázquez-Salazar, M. M. Mariscal and M. J. Yacaman, Phys. Chem. Chem. Phys., 2015, 17, 7898–7906 RSC
.
- N. Isomura, X. Wu and Y. Watanabe, J. Chem. Phys., 2009, 131, 164707 CrossRef PubMed
.
- S. Bonanni, K. Aït-Mansour, W. Harbich and H. Brune, J. Am. Chem. Soc., 2012, 134, 3445–3450 CrossRef CAS PubMed
.
- A. Álvarez-García, J. C. Luque-Ceballos, L. O. Paz-Borbón and I. L. Garzón, Comput. Mater. Sci., 2022, 214, 111697 CrossRef
.
- S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908 CrossRef CAS
.
- A. R. Puigdollers, P. Schlexer, S. Tosoni and G. Pacchioni, ACS Catal., 2017, 7, 6493–6513 CrossRef
.
- P. G. Moses, A. Janotti, C. Franchini, G. Kresse and C. G. Van De Walle, J. Appl. Phys., 2016, 119, 181503 CrossRef
.
- L. O. Paz-Borbón, A. López-Martínez, I. L. Garzón, A. Posada-Amarillas and H. Grönbeck, Phys. Chem. Chem. Phys., 2017, 19, 17845–17855 RSC
.
- H. F. Wen, H. Sang, Y. Sugawara and Y. J. Li, Phys. Chem. Chem. Phys., 2020, 22, 19795–19801 RSC
.
- H. Xu and S. Y. Tong, Surf. Sci., 2013, 610, 33–41 CrossRef CAS
.
- L. M. Liu, P. Crawford and P. Hu, Prog. Surf. Sci., 2009, 84, 155–176 CrossRef CAS
.
- R. Y. Wang, J. X. Wang, J. Jia and H. S. Wu, Appl. Surf. Sci., 2021, 536, 147793 CrossRef CAS
.
- C. Franchini, M. Reticcioli, M. Setvin and U. Diebold, Nat. Rev. Mater., 2021, 6, 560–586 CrossRef CAS
.
- J. R. D. Lile, A. Bahadoran, S. Zhou and J. Zhang, Adv. Theory Simul., 2022, 5, 2100244 CrossRef
.
- M. Pilar de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500 RSC
.
- P. López-Caballero, S. Miret-Artés, A. O. Mitrushchenkov and M. P. De Lara-Castells, J. Chem. Phys., 2020, 153, 164702 CrossRef PubMed
.
- P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. D. Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853 RSC
.
- F. R. Negreiros, E. Aprà, G. Barcaro, L. Sementa, S. Vajda and A. Fortunelli, Nanoscale, 2012, 4, 1208–1219 RSC
.
- L. O. Paz-Borbón, F. Buendiá, I. L. Garzón, A. Posada-Amarillas, F. Illas and J. Li, Phys. Chem. Chem. Phys., 2019, 21, 15286–15296 RSC
.
- C. J. Heard, S. Heiles, S. Vajda and R. L. Johnston, Nanoscale, 2014, 6, 11777–11788 RSC
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS
.
- V. Ç. Çelik, H. Ünal, E. Mete and Ş. Ellialtıoğlu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205113 CrossRef
.
- L. E. Gálvez-González, J. O. Juárez-Sánchez, R. Pacheco-Contreras, I. L. Garzón, L. O. Paz-Borbón and A. Posada-Amarillas, Phys. Chem. Chem. Phys., 2018, 20, 17071–17080 RSC
.
- E. Davari and D. G. Ivey, Sustainable Energy Fuels, 2018, 2, 39–67 RSC
.
- E. Fernández, M. Boronat and A. Corma, J. Phys. Chem. C, 2015, 119, 19832–19846 CrossRef
.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed
.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed
.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- H. E. Sauceda, F. Salazar, L. A. Pérez and I. L. Garzón, J. Phys. Chem. C, 2013, 117, 25160–25168 CrossRef CAS
.
- A. Posada-Amarillas and I. L. Garzón, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 10362 CrossRef CAS PubMed
.
- J. Zhang and A. N. Alexandrova, J. Phys. Chem. Lett., 2013, 4, 2250–2255 CrossRef CAS
.
- S. V. Ong and S. N. Khanna, J. Phys. Chem. C, 2012, 116, 3105–3111 CrossRef CAS
.
- D. E. Jiang, S. H. Overbury and S. Dai, J. Phys. Chem. C, 2012, 116, 21880–21885 CrossRef CAS
.
- Y. Wang and H. Gao, J. Phys. Chem. B, 2017, 121, 2132–2141 CrossRef CAS PubMed
.
- A. Álvarez-García, J. C. Luque-Ceballos, L. O. Paz-Borbón and I. L. Garzón, Surf. Sci., 2023, 733, 122287 CrossRef
.
- P. M. Kowalski, M. F. Camellone, N. N. Nair, B. Meyer and D. Marx, Phys. Rev. Lett., 2010, 105, 5–8 CrossRef PubMed
.
- T. Shibuya, K. Yasuoka, S. Mirbt and B. Sanyal, J. Phys.: Condens. Matter, 2012, 24, 435504 CrossRef PubMed
.
- Q. Wu, S. Hou, D. Buceta, H. J. Ordoñez, M. Arturo López-Quintela and C. J. Lambert, Appl. Surf. Sci., 2022, 594, 153455 CrossRef CAS
.
-
G. Herzberg, Molecular Spectra and Molecular Structure I: Spectra of Diatomic Molecules, D. Van Nostran Company, 2nd edn, 1963, pp. 1–658 Search PubMed
.
- R. Wang, L. Zhao, J. Jia and H. S. Wu, AIP Adv., 2018, 8, 035307 CrossRef
.
- M. Boronat, A. Pulido, P. Concepción and A. Corma, Phys. Chem. Chem. Phys., 2014, 16, 26600–26612 RSC
.
- P. P. Mkhonto, H. R. Chauke and P. E. Ngoepe, Minerals, 2015, 5, 665–678 CrossRef CAS
.
- M. Alducin, D. Sánchez-Portal, A. Arnau and N. Lorente, Phys. Rev. Lett., 2010, 104, 1–4 CrossRef PubMed
.
- Z. Dohnálek, J. Kim, O. Bondarchuk, J. M. White and B. D. Kay, J. Phys. Chem. B, 2006, 110, 6229–6235 CrossRef PubMed
.
- I. Sokolovic, M. Reticcioli, M. Calkovsky, M. Wagner, M. Schmid, C. Franchini, U. Diebold and M. Setvín, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14827–14837 CrossRef CAS PubMed
.
- L. M. Molina and B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1–22 CrossRef
.
- L. B. Vilhelmsen and B. Hammer, ACS Catal., 2014, 4, 1626–1631 CrossRef CAS
.
- Z. Duan and G. Henkelman, Phys. Chem. Chem. Phys., 2016, 18, 5486–5490 RSC
.
- J. Fabila, D. Romero, L. O. Paz-Borbón and F. Buendía, J. Chem. Phys., 2022, 157, 084309 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1 presents the Bader charge analysis of supported RenPtm clusters on TiO2(110), while Table S3 displays this analysis for O2 activation on the supported clusters. Table S2 shows the structural and energetic parameters for O2 adsorption on the surface site in the presence of supported RenPtm clusters. The most stable structures of gas-phase clusters are displayed in Fig. S1. The lowest energy isomers are displayed in Fig. S2 and S3. The most stable structures for O2 dissociation on RenPtm supported clusters are shown in Fig. S4. Finally, the structures for dissociative adsorption of O2 on the Re–Ti interface are presented in Fig. S5. See DOI: https://doi.org/10.1039/d4cp01118j |
| This journal is © the Owner Societies 2024 |