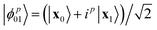Open Access Article
Open Access ArticleSimulation of a Diels–Alder reaction on a quantum computer
Ieva
Liepuoniute
 *a,
Mario
Motta
*a,
Mario
Motta
 ab,
Thaddeus
Pellegrini
ab,
Thaddeus
Pellegrini
 b,
Julia E.
Rice
b,
Julia E.
Rice
 a,
Tanvi P.
Gujarati
a,
Sofia
Gil
c and
Gavin O.
Jones
a,
Tanvi P.
Gujarati
a,
Sofia
Gil
c and
Gavin O.
Jones
 *a
*a
aIBM Quantum, IBM Research – Almaden, 650 Harry Road, San Jose, CA 95120, USA. E-mail: ieva@ibm.com; gojones@us.ibm.com
bIBM Quantum, T. J. Watson Research Center, Yorktown Heights, NY 10598, USA
cCornell University, Ithaca, NY 14850, USA
First published on 24th September 2024
Abstract
The simulation of chemical reactions is an anticipated application of quantum computers. Using a Diels–Alder reaction as a test case, in this study we explore the potential applications of quantum algorithms and hardware in investigating chemical reactions. Our specific goal is to calculate the activation barrier of a reaction between ethylene and cyclopentadiene forming a transition state. To achieve this goal, we use quantum algorithms for near-term quantum hardware (entanglement forging and quantum subspace expansion) and classical post-processing (many-body perturbation theory) in concert. We conduct simulations on IBM quantum hardware using up to 8 qubits, and compute accurate activation barrier in the reaction between cyclopentadiene and ethylene by accounting for both static and dynamic electronic correlation. This work illustrates a hybrid quantum-classical computational workflow to study chemical reactions on near-term quantum devices, showcasing the potential for performing quantum chemistry simulations on quantum hardware to predict activation barriers in agreement with those predicted by CASCI.
1 Introduction
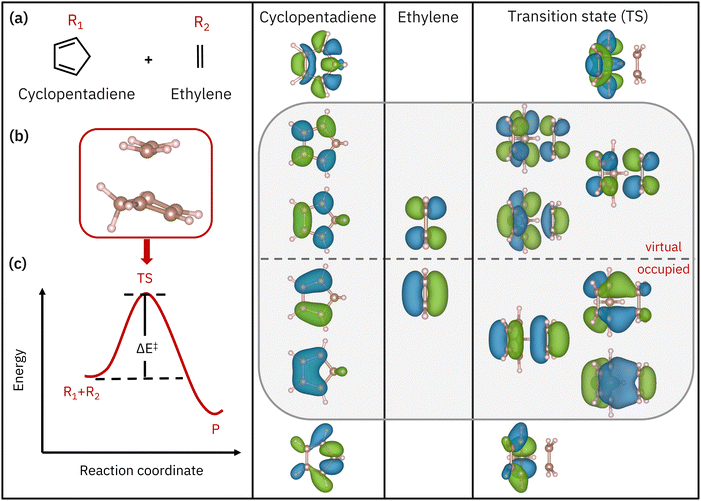
The Diels–Alder reaction, discovered by Otto Diels and Kurt Alder in 1928, remains a fundamental and extensively studied transformation in organic chemistry.1–5 The synthetic versatility of the Diels–Alder reaction is evident in its widespread use for the construction of complex natural products6–8 and the design of novel materials.9–14 This reaction occurs between a conjugated diene and an alkene, referred to as a dienophile, and produces a cyclic compound, typically a six-membered ring. The reaction's efficiency and precise control over stereochemistry have established it as an indispensable tool for organic chemists seeking streamlined routes to elaborate molecular structures.15,16 The extensive applicability of the Diels–Alder reaction in organic synthesis, combined with its intricate mechanistic aspects, positions it as a focal point for ongoing investigation and innovative advancements.17–20The widespread importance and unique challenges of the Diels–Alder reaction make it a valuable testbed for near-term quantum computing algorithms21–25 and hardware. First, breaking and formation of bonds in the course of the reaction may lead to electronic wavefunctions with a multireference character, which can be captured to zeroth order by accurate active-space calculations. The energetics of the reaction then arise from a complex interplay between static and dynamic electronic correlation, the latter resulting from configurations with electrons occupying orbitals outside the active space. Finally, the reactivity and selectivity of the Diels–Alder reactions hinge on the characteristics of their transition states, which are typically more sensitive to approximations in the solution of the Schrödinger equation than reactants and products, due to the presence of partial bonds. Therefore, accurate calculations of the Diels–Alder reaction pose a substantial challenge to quantum computing algorithms, since they require accounting for both static and dynamic electronic correlation in reactants, products, and transition states.
In this work, we study the prototypical example of a Diels–Alder reaction, between cyclopentadiene and ethylene reacting in a synchronous “aromatic type” fashion where the reorganization of π bonds in cyclopentadiene and ethylene (Fig. 1) during bond formation leads to a bridged six-membered ring compound.26 We explore the significance of this Diels–Alder reaction as a compelling testbed for the validation, combination, and refinement of quantum computing algorithms for near-term quantum devices. To that end, we employ hybrid quantum-classical algorithms to solve the Schrödinger equation in an active space on a quantum computer, and then recover dynamical electronic correlation through classical post-processing. For active-space simulations, we use a qubit-reduction technique27–30 called entanglement forging (EF)28,31,32 to define a variational ansatz in the context of the variational quantum eigensolver (VQE) method.33,34 To improve the quality of active-space simulations beyond the level of accuracy afforded by EF, we use a quantum subspace expansion (QSE)35,36 based on single and double electronic excitations from the EF wavefunction. For recovering dynamical electronic correlation, we integrate EF and QSE with second-order perturbation theory (PT2).37,38 We demonstrate the proposed algorithmic workflow (active-space calculations on quantum computers and classical post-processing exemplified by perturbation theory to recover dynamical electronic correlation) on classical simulators and quantum hardware, using up to 8 qubits and error mitigation techniques39–41 to compute the activation energy of the Diels–Alder reaction. To provide accurate results, our framework requires an accurate solution of the Schrödinger equation in the active space, and an accurate description of dynamical correlation. The active-space Schrödinger equation is solved by a combination of EF and QSE, each having approximations (EF in the use of bitstrings and an ansatz,28 and QSE in the use of single and double electronic excitations only).36 Dynamical correlation is captured by second-order perturbation theory, which is also approximate. When these approximations break down, accurate results cannot be expected. The primary goal of this work is to showcase the effectiveness of our approach in capturing the key aspects of electronic structure problems, while also recognizing its inherent approximations and limitations. Our approach seeks to offer a practical framework for quantum computing applications in electronic structure theory, emphasizing the balance between accuracy and computational efficiency, and guiding future advancements.
The structure of this work is as follows: first, we detail the methods employed, emphasizing simulations on quantum hardware, including error mitigation techniques and measurement optimization. We then present and discuss results for predictions of the activation energy of the reaction on quantum simulators and quantum devices. The Appendices includes additional details of the workflow used in this study.
2 Methods
2.1 Active-space selection
In the Diels–Alder reaction, active electrons are defined as those participating in the breaking/formation of bonds as the reaction unfolds. The orbitals involved in the reaction involve two π bonds contributed by the diene reacting with one π bond contributed by the ene counterpart. These undergo conversion into partial π bonds in the transition state, prior to the formation of two σ bonds and one π bond in the product. Overall, this process involves a 6 electron, 6 orbital active space (here denoted AS(6e,6o)). Through the work of Houk and co-workers42 on the retro reaction of norbornene breaking into cyclopentadiene and ethylene, it is known that the breaking/formation of bonds in a Diels–Alder reaction can be studied in an active space of 8 electrons in 8 orbitals, AS(8e,8o). Therefore, in this work, we simulate AS(8e,8o) of MP2 natural orbitals around the highest occupied natural orbital–lowest unoccupied natural orbital (HONO–LUNO) frontier,43 as shown in Fig. 1. We note that most of the active-space orbitals of the transition state have reactant-like character, consistent with the fact that the transition state has an “early” nature. In particular, within the AS(8e,8o) active space shown in Fig. 1, one can recognize an AS(6e,6o) (enclosed in a gray box), spanned by the π and π* orbitals of the reactants and transition state, respectively. In the remainder of this work, we therefore study the AS(6e,6o) alongside the larger AS(8e,8o) active space.2.2 Classical methods
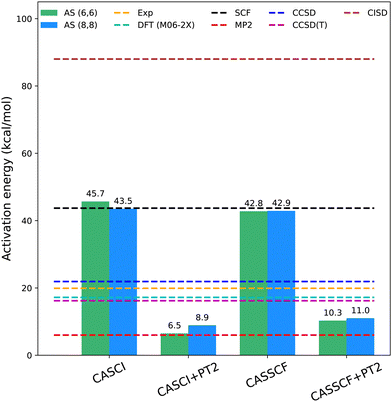
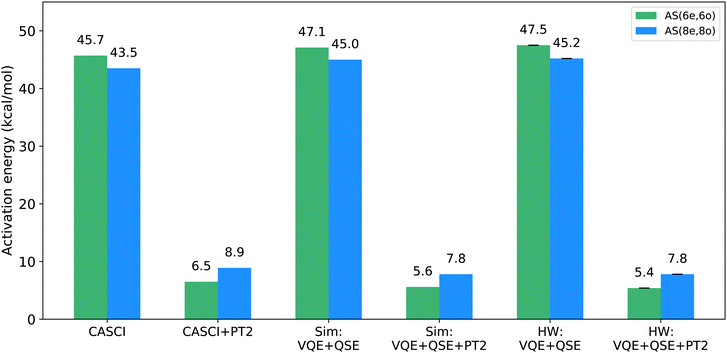
We conducted classical electronic structure simulations using an aug-cc-pVTZ basis set44 with PySCF.45,46 We obtained initial the optimized coordinates for the reactants and transition state from the prior study by Levandowski et al.26 Our CASCI calculations were performed using active spaces comprising MP2 natural orbitals. The CASCI energies for the active spaces of AS(6e,6o) and AS(8e,8o) were 45.7 kcal mol−1 and 43.5 kcal mol−1, respectively (Fig. 2). These values were compared to those obtained in previous computational studies47,48 as well as with data from various studies reporting experimental (Exp) activation barriers derived from the retro-Diels–Alder reaction and the heat of formation for norbornene. Specifically, the reported experimental values span a range of 19.9 to 23.7 ± 1.6 kcal mol−1 in the gas phase (521–570 K)49–53 and the challenges in measuring the forward barrier arise due to competition with the dimerization of cyclopentadiene which possesses an experimental barrier between 14.9 and 16.9 kcal mol−1 in the gas phase.54 A comprehensive study analysis and in-depth discussion can be found in Guner et al.47 The difference between the active-space energies and the experimental values underscores the significance of accounting for dynamical correlation to align the theoretical results with the experimental data. Consequently, we conducted second-order perturbation theory calculations to incorporate dynamical correlation. The activation barriers were found to be 6.5 kcal mol−1 and 8.9 kcal mol−1 for the active spaces of AS(6e,6o) and AS(8e,8o), respectively. CASSCF and CASSCF + PT2 calculations followed a similar trend. These classical electronic structure calculations serve as a reference point for evaluating the accuracy and precision of the quantum-classical algorithms employed in this study. Notably, the method that gets the closest to the experimental values is CCSD which suggests that the system under study is adequately described by a single reference wavefunction with dynamical correlation effects.2.3 Quantum algorithms overview
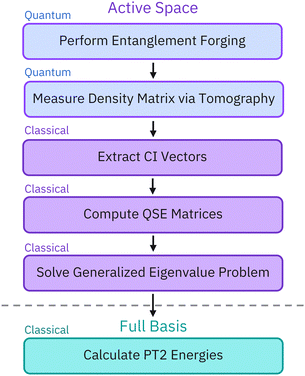
The workflow illustrated in Fig. 3 uses a hybrid quantum-classical approach. First, we carry out active-space calculations using the VQE method, on quantum hardware, using the EF method to formulate a variational ansatz and reduce the number of qubits from 2N to N, where N is the number of active-space orbitals. We then extract the density matrix of our system through tomographic measurements of the ground state on the quantum computer and we project it into the Hilbert space with the correct particle and spin number. The obtained projection (denoted as the CI vector in Fig. 3) is used as a starting point for QSE and PT2. This approach allows us to improve the quality of EF ground-state results and mitigate errors from the quantum device.In the EF algorithm, the active-space Hamiltonian is expressed as a linear combination of tensor products,
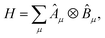 | (1) |
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) μ act on α and β spin-orbitals, respectively. The target wavefunction is represented by a Schmidt decomposition,
μ act on α and β spin-orbitals, respectively. The target wavefunction is represented by a Schmidt decomposition,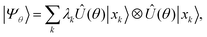 | (2) |
To approximate the ground-state energy of our system, we evaluate the expectation value of Ĥ
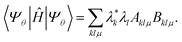 | (3) |
In eqn (3), the matrices Aklμ and Bklμ are defined as
| Aklμ = 〈xk|Û†(θ)ÂμÛ(θ)|xl〉, | (4) |
Bklμ = 〈xk|Û†(θ)![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) μÛ(θ)|xl〉. μÛ(θ)|xl〉. | (5) |
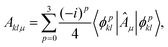 | (6) |
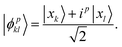 | (7) |
| |Ψ〉 = α|ψEF〉 + βkiâ†kâi|ψEF〉 + γkibjâ†kâ†bâjâi|ψEF〉. | (8) |
In this work, we focused on single and double electronic excitations within the same set of orbitals used to describe the ground state. This flavor of QSE can be regarded as a multi-reference CISD method, where the wavefunction, prepared on a quantum device, is not a single Slater determinant but a correlated electronic state. We classically realize a variational subspace spanned by a set of quantum states {ψI} as |ψI〉 = ÔI|ψEF〉, where ÔI ∈ {I,â†kâi,â†kâ†bâjâi}, which can be generated via additional measurements and post-processing. The Hamiltonian is then diagonalized within the new state space, by solving the generalized eigenvalue problem Hc = ScE and obtaining a variational estimate of the ground state energy. More specifically, obtaining the expansion coefficients c requires computing the matrix elements
Hij = 〈ψEF|Ô†IĤÔJ|ψEF〉 = Tr[Ô†IĤÔJ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ], ], | (9) |
Sij = 〈ψEF|Ô†IÔJ|ψEF〉 = Tr[Ô†IÔJ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ]. ]. | (10) |
We employ a quantum device to compute the matrix elements Hij and Sij by measuring the operators Ô†IĤÔJ and Ô†IÔJ respectively. Following,31 we conduct quantum state tomography on the EF circuits by performing measurements on up to n = 8 qubits in the 3n eigenbases of X, Y, and Z Pauli operators. Through this operation, we obtain a Bloch vector aP = Tr[Pρ], where P is an n-qubit Pauli operator, and use it to calculate the matrix elements Hij and Sij. We then use a classical computer to solve the generalized eigenvalue equation Hc = ScE and obtain approximate eigenpairs. The benefit of this approach is that QSE integrates into the VQE without necessitating any modifications to the quantum circuit, at the cost of additional measurements. Notably, it does not increase the depth of the quantum circuit required for preparing |ψEF〉. This characteristic is beneficial, especially for near-term quantum hardware subject to qubit coherence times and two-qubit gate errors. We remark that quantum state tomography is not required to measure the operators in eqn (9). However, it is necessary to implement the classical post-processing operations described in the forthcoming Section 2.6.
2.4 Hardware calculations
All EF calculations were executed on the 27-qubit ibm_auckland device, using the Qiskit Runtime library to interface the code with quantum devices. Jobs consisting of 300 circuits, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 shots for each circuit, were submitted on quantum hardware. Readout39 and dynamical decoupling40 error mitigation techniques were employed to reduce noise originating from readout and quantum gates, respectively. Particle number was conserved through CI vector projection. Additional details can be found in Appendix.
000 shots for each circuit, were submitted on quantum hardware. Readout39 and dynamical decoupling40 error mitigation techniques were employed to reduce noise originating from readout and quantum gates, respectively. Particle number was conserved through CI vector projection. Additional details can be found in Appendix.
2.5 Error-weighted Pearson correlation analysis
Quantum chemistry experiments on near-term quantum computers demand extensive time and resource utilization, underscoring the importance of achieving optimization in both aspects without compromising result fidelity. To optimize circuit time while maintaining performance, we conducted an in-depth analysis of quantum state tomography experiments on multiple IBM Quantum processors. Our approach involved calculating the Pearson correlation coefficient between quantum hardware results and the ground truth statevector, varying the number of shots, or alternatively, the number of circuit repetitions. Understanding the optimal number of shots required to achieve high-fidelity results enables the optimization of time and resources on near-term quantum computers without compromising result fidelity.To that end, we first simulated tomography circuits for ethylene, cyclopentadiene, and the transition state using Qiskit Aer, representing the resulting statevector as a binary string of zeroes and ones, serving as a ground truth vector. Next, we selected several 27-qubit IBM quantum Falcon processors, including ibm_algiers, ibm_cairo, and ibm_hanoi. The experiments were executed using Qiskit Runtime, employing an optimization level of 3, readout error mitigation, and dynamical decoupling techniques. The variable explored in this study was the number of shots used in each experimental instance. The number of shots was systematically varied, and for each experimental instance, a Bloch vector was computed along with its associated errors. Subsequently, for every shot value, the resulting Bloch vector from the hardware run was correlated using the error-weighted Pearson correlation coefficient rweighted, defined as follows:
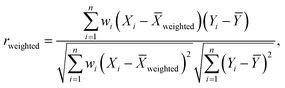 | (11) |
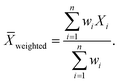
In eqn (11)X and Y represent two sets of data, namely simulator and hardware block vectors, wi are weights, Xi is the i-th data point in X, and Yi is the i-th data point in Y. The mean of Y (Ȳ) and weighted mean of X (Xweighted) are expressed as:
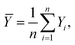 | (12) |
 | (13) |
In eqn (13), the weights are calculated as follows:
| wi = 1 − εi2, | (14) |
2.6 Perturbation theory
An active-space calculation, carried out with an accurate solver and in carefully selected active space, can capture static correlation but not dynamical correlation arising from electronic interactions involving electrons in the inactive orbitals. A way of accounting for dynamical correlation is to combine active-space quantum computation with classical post-processing on the full basis set. An example is complete active-space second-order perturbation theory (CASPT2). Within CASPT2, the Hamiltonian is written as a sum of two terms Ĥ = ĤD +![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , where ĤD is the Dyall Hamiltonian, i.e., the sum between the active-space Born–Oppenheimer Hamiltonian and the restriction of the Fock operator to the non-active space, and
, where ĤD is the Dyall Hamiltonian, i.e., the sum between the active-space Born–Oppenheimer Hamiltonian and the restriction of the Fock operator to the non-active space, and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) = Ĥ − ĤD is treated as a perturbation. The second-order energy contribution is
= Ĥ − ĤD is treated as a perturbation. The second-order energy contribution is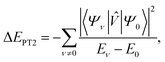 | (15) |
Implementing CASPT2 based on quantum computing data, specifically tomographic measurements, poses two challenges: first, active-space simulations conducted in the Fock space may break particle number conservation and other symmetries due to device noise, with detrimental impact on the accuracy of the ground and excited electronic states; second, statistical uncertainties need to be propagated from active-space quantities to ΔEPT2, leading to imprecise results. In this work, we (i) sample the ground-state density matrix using quantum-state tomography and subsequently extract a configuration interaction (CI) vector by normalizing the density matrix's row/column entries for each sample. The resulting CI vector approximates the QSE wavefunction but has an exact particle number and considerably reduced statistical uncertainties. We then (ii) use each sampled CI vector as the input of a conventional CASPT2 calculation, and finally (iii) average the resulting PT2 energies.
3 Results and discussion
3.1 Active-space quantum calculations
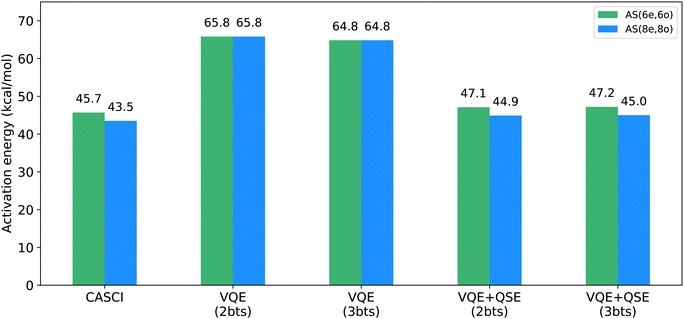
In Fig. 5, we present active-space calculations with EF and EF + QSE, carried out on classical simulators. In EF simulations, two bitstrings were used for the reactants and the transition state, respectively. These bitstrings, derived through a Schmidt decomposition of the FCI wavefunction, corresponded to the Hartree–Fock and HONO–LUNO excitation bitstrings. Given the relatively small size of the problem and the availability of the FCI solution, obtaining the FCI bitstrings and using them in our EF calculations allowed us to assess the effectiveness of the EF method. When analysis of the FCI wavefunction is unavailable, bitstring selection becomes challenging, highlighting an area for improvement in this work. In such instances, bitstring selection can be approached through educated guesswork informed by additional classical calculations (e.g., CCSD, MP2) that provide insights into the system's wavefunction.We further investigated the impact of a third bitstring for simulations of the transition state. Notably, simulated forged-VQE results for the transition state with 3 bitstrings resulted in lower energies, as shown in Fig. 5. This is expected because, as we include more bitstrings, we can achieve a more accurate representation of the electronic wavefunction. However, adding a third bitstring had a modest impact on the EF + QSE energy, which was approximately equal to the CASCI energy for both 2 and 3 bitstrings. Therefore, for computational efficiency, hardware calculations were executed using only two bitstrings for the transition state.
To investigate the multi-reference nature of our EF + QSE method, we performed CISD calculations in the active spaces of (6,6) and (8,8). The activation barriers obtained were 43.7 kcal mol−1 and 43.5 kcal mol−1, respectively. These results are very close to the energy values obtained using CASCI (45.7 and 43.5 kcal mol−1, respectively) and the EF + QSE method (47.1 and 44.9 kcal mol−1, respectively) in the same active spaces. This suggests that the CISD method approximates MR-CISD in this context and that the multi-reference character of the EF method may not significantly impact the accuracy of activation barriers for the chosen active spaces of the Diels–Alder reaction.
Hardware calculations, mitigated with readout and dynamical decoupling error suppression techniques, were further processed to ensure particle number preservation by extracting a CI vector representation as discussed in the previous section. The results obtained in combination with QSE, closely matched the CASCI and statevector simulation results (Fig. 7). The associated statistical uncertainties for the activation barriers were 0.01 kcal mol−1 for both active spaces, with errors increasing with system size, but effectively cancelling out for the activation barriers. For example, when calculating absolute energies for ethylene AS(2e,2o), cyclopentadiene AS(4e,4o), and the transition state AS(6e,6o), respective errors were 0, 3.6 × 10−6, and 1.6 × 10−5 kcal mol−1. Notably, the largest deviations in absolute energies were observed in the transition state, as expected due to its more complex electronic structure, compared to reactants. The primary limitations of our approach stem from the intrinsic design of the EF method, which is optimally suited for simulating systems with low entanglement in the ground state. The EF method exhibits quadratic scaling with the number of bitstrings, fifth power scaling with the number of orbitals/qubits, and linear scaling with the number of parameters. Given this computational cost, it is advantageous to minimize the number of bitstrings and optimize the circuit width (number of qubits) and depth (layers of parametrized gates). Additionally, when based on CI vectors, the implementation of the QSE method incurs a significant measurement cost, impeding scalability. Specifically, it requires 3n measurements, where n is the number of qubits, in the eigenbases of the X, Y, and Z Pauli operators.
3.2 Pearson correlation shot analysis
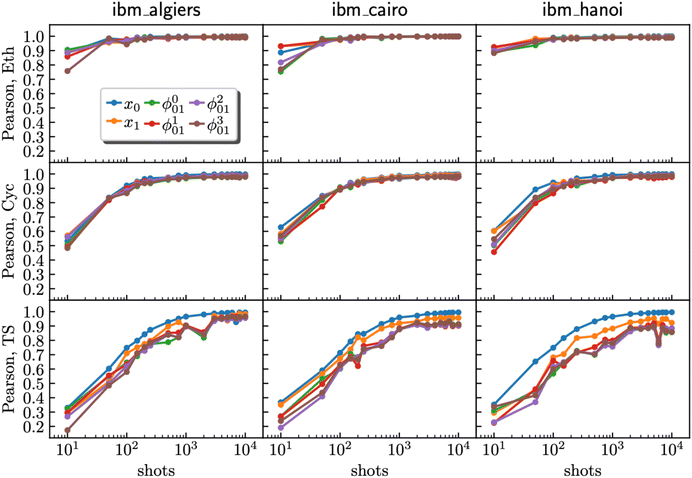
Through additional optimization of hardware experiments and detailed Pearson correlation analysis58 for reactants and the TS, a trend emerged across the three quantum devices (ibm_algiers, ibm_cairo, and ibm_hanoi). The correlation between the hardware results and the ground truth statevector showed a significant improvement as the number of shots increased (Fig. 6). However, our results also reveal a noticeable point of diminishing returns, and this point is contingent upon the circuit complexity inherent in the molecular system under investigation. For the TS, characterized by a high degree of circuit complexity, it became evident that even at the upper limit of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 shots, there existed the potential for further enhancement in the quality of the result by gathering of additional shots. In contrast, for experiments involving cyclopentadiene with a moderate level of circuit complexity, an approximate shot count of 1000 proved to be sufficient to reach a quality plateau. Notably, ethylene, which possesses the least complex circuit, achieved a plateau with only 500 shots.
000 shots, there existed the potential for further enhancement in the quality of the result by gathering of additional shots. In contrast, for experiments involving cyclopentadiene with a moderate level of circuit complexity, an approximate shot count of 1000 proved to be sufficient to reach a quality plateau. Notably, ethylene, which possesses the least complex circuit, achieved a plateau with only 500 shots.
3.3 Perturbation theory
After applying the PT2 correction to the activation barrier energies, the results were found to be consistent with classical CASPT2 energies, as illustrated in Fig. 7. The statistical uncertainties for the activation barriers were 3.7 × 10−3 and 6.7 × 10−3 kcal mol−1 for the AS(6e,6o) and AS(8e,8o), respectively. The low error bars are due to state projection, which reduces statistical fluctuations on the input of the PT2 calculation. Furthermore, the extraction of CI vectors from tomographic measurements yields a pure state (as opposed to a density operator) and ensures the correct number of electrons and spin. A detailed comparison between VQE and QSE, and VQE and QSE with CI vector purification in Table 2 shows that state purification significantly reduces errors.4 Conclusion
In this study, we used the Diels–Alder reaction of cyclopentadiene with ethylene as a testbed for performing near-term simulations of reactions on quantum hardware. We computed the activation barrier of the reaction with an integrated combination of quantum algorithms for active-space calculations (entanglement forging, EF, and quantum subspace expansion, QSE) and classical post-processing to recover dynamical electronic correlation (second-order perturbation theory, PT2). We demonstrated this computational workflow on classical simulators and quantum hardware, using up to 8 qubits and error mitigation. Additionally, insights derived from the Pearson correlation analysis enhanced our understanding of optimal shot selection and its impact on result fidelity in quantum experiments. Economization of hardware experiments is an important research area,59,60 and the obtained insights contribute to a more efficient and accurate implementation of quantum algorithms for chemistry on current quantum hardware.Our results pinpointed drastic approximations in the EF Ansatz, which overestimates the activation barrier by ∼20 kcal mol−1 compared to CASCI. We resolved the discrepancies between active-space quantum computing simulations with the chosen ansatz and CASCI by combining QSE with EF. However, in the systems we have studied, CASCI (and any other active-space calculation) overestimates the activation energy, due to omission of dynamical electronic correlation. To overcome this limitation, we integrated EF and QSE with PT2, obtaining activation energies in agreement with CASPT2 within ∼1 kcal mol−1. These results, however, differ appreciably from experimental data and other classical calculations (CCSD, CCSD(T), DFT) due to the approximation of PT2.
While our findings present compelling evidence of the effective application of the QSE method in refining ground-state approximations and enhancing the accuracy of VQE calculations, several important points should be noted about our methodology. Firstly, tomographic measurements are not scalable to larger system sizes. To address this issue, future work entails employing measurement optimization strategies such as Pauli grouping61–63 and cumulant approximation.64,65 While the development of measurement reduction techniques is a very active area of research, a comprehensive investigation of these methods and their integration with the QSE framework was beyond the scope of this work. Future research could greatly benefit from exploring these avenues, as this would significantly reduce the computational demands associated with current implementations. Second, the classical CI vector sampling approach relies on classical representations of quantum information, thereby limiting its scalability. Additionally, among the methods that can be tested on Diels–Alder reactions in future research are: (i) embedding techniques43,66,67 to define active regions and correlate them with their environment, (ii) variational ansatzes to solve for the Schrödinger equation in the active space seeking a balance between accuracy, computational cost, and hardware compatibility,68–71 (iii) approaches for recovering dynamical correlation, such as transcorrelated,72–74 downfolding,75 similarity transforms,27 and subspace methods,57 and (iv) the sub-space quantum diagonalization (SQD) technique.76 The latter method partially recovers noiseless configuration samples, enhancing the robustness of the quantum-selected CI procedure77 against noise. By leveraging classical distributed computing to process noisy samples from a quantum processor, SQD can produce good approximate solutions for practical problems that exceed the sizes amenable to exact diagonalization.
Our work highlights a Diels–Alder reaction as a compelling testbed for quantum algorithms and hardware, as it allows us to gauge their effectiveness in accounting for static and dynamical electron correlation in non-trivial situations (e.g. transition states), exposing and quantifying algorithmic approximations, and indicating areas and directions of improvement.
Data availability
All data supporting this article are included in the main text and Appendices. The code used in this study is not available for sharing.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: Entanglement forging hardware calculations. Additional details
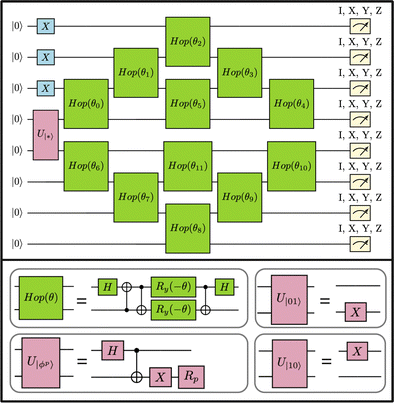
Entanglement forging calculations on quantum hardware were performed for the reactants and transition state in the Diels–Alder reaction. The details on the number of qubits, parameters, gates, circuit depth and the total number of circuits are provided in Table 1. The quantum circuits for the reactants and transition state are shown in Fig. 4 and 8. in Fig. 4), hop-gate, and measurement, there are 4, 4, 2 single-qubit gates and 1, 3, 0 two-qubit gates, respectively. The circuit depth signifies the number of layers of quantum gates executed in parallel for computation completion. Tomography experiments on quantum hardware were run using Qiskit Runtime, which executes quantum circuits in sessions. Each Runtime job session on ibm_auckland contained a maximum of 300 circuits
in Fig. 4), hop-gate, and measurement, there are 4, 4, 2 single-qubit gates and 1, 3, 0 two-qubit gates, respectively. The circuit depth signifies the number of layers of quantum gates executed in parallel for computation completion. Tomography experiments on quantum hardware were run using Qiskit Runtime, which executes quantum circuits in sessions. Each Runtime job session on ibm_auckland contained a maximum of 300 circuits
| System | Qubits | Parameters | Gates | Depth | Circuits |
|---|---|---|---|---|---|
| C2H4(2e,2o) | 2 | 3 | (12,4) | 10 | 54 |
| C5H6(4e,4o) | 4 | 4 | (21,7) | 10 | 486 |
| C5H6(6e,6o) | 6 | 8 | (42,19) | 20 | 4374 |
| TS(6e,6o) | 6 | 8 | (42,19) | 20 | 4374 |
| TS(8e,8o) | 8 | 14 | (72,37) | 30 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 366 366 |
| Method | ΔE‡ (6e,6o) | ΔE‡ (8e,8o) |
|---|---|---|
| SV (VQE + QSE) | 47.10 | 44.95 |
| HW (VQE + QSE) | 46.52 ± 2.10 | 44.49 ± 4.04 |
| HW (VQE + QSE + proj.) | 47.52 ± 0.01 | 45.24 ± 0.01 |
| HW (VQE + QSE + proj. + PT2) | 5.45 ± 0.004 | 7.85 ± 0.007 |
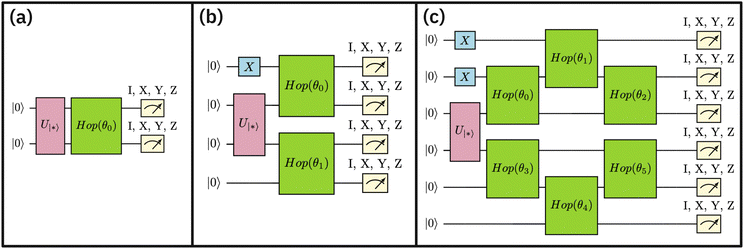 | ||
Fig. 8 Additional quantum circuits run in this study: (a) 2-qubit circuit for active space AS(2e,2o) for ethylene, (b) 4-qubit circuit for an active space AS(4e,4o) for cyclopentadiene, and (c) 6-qubit circuit representing active space AS(6e,6o) for cyclopentadiene and TS. The definitions of the two-qubit unitary  and the “hop-gate” are described in Fig. 4. and the “hop-gate” are described in Fig. 4. | ||
Appendix B: CI vector purification
We employed state projection and CI vector extraction as a noise mitigation/purification technique. The evaluation of noise in states by CI vectors significantly contributes to the reduction of error bars. These CI vectors represent pure states with the correct number of electrons and spin, enhancing the fidelity of our quantum computational analyses.Acknowledgements
The authors express their gratitude to William Kirby (IBM Quantum), Daniel Ess (Brigham Young University), and Ken Houk (UCLA) for their review of this manuscript and valuable feedback.Notes and references
- O. Diels and K. Alder, Justus Liebigs Ann. Chem., 1928, 460, 98–122 CrossRef.
- R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 781–853 CrossRef.
- J. Sauer and R. Sustmann, Angew. Chem., Int. Ed. Engl., 1980, 19, 779–807 CrossRef.
- K. N. Houk, Y. Li and J. D. Evanseck, Angew. Chem., Int. Ed. Engl., 1992, 31, 682–708 CrossRef.
- K. N. Houk, F. Liu, Z. Yang and J. I. Seeman, Angew. Chem., Int. Ed., 2021, 60, 12660–12681 CrossRef CAS PubMed.
- K.-I. Takao, R. Munakata and K.-I. Tadano, Chem. Rev., 2005, 105, 4779–4807 CrossRef CAS.
- M. Juhl and D. Tanner, Chem. Soc. Rev., 2009, 38, 2983–2992 RSC.
- K. C. Nicolaou, S. A. Snyder, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2002, 41, 1668–1698 CrossRef CAS PubMed.
- G. Franc and A. K. Kakkar, Chem. – Eur. J., 2009, 15, 5630–5639 CrossRef CAS PubMed.
- A. Sanyal, Macromol. Chem. Phys., 2010, 211, 1417–1425 CrossRef CAS.
- M. Gregoritza and F. P. Brandl, Eur. J. Pharm. Biopharm., 2015, 97, 438–453 CrossRef CAS PubMed.
- S. Munirasu, J. Albuerne, A. Boschetti-de Fierro and V. Abetz, Macromol. Rapid Commun., 2010, 31, 574–579 CrossRef.
- C. R. Ratwani, A. R. Kamali and A. M. Abdelkader, Prog. Mater. Sci., 2023, 131, 101001 CrossRef.
- M. Vauthier, L. Jierry, J. C. Oliveira, L. Hassouna, V. Roucoules and F. Bally-Le Gall, Adv. Funct. Mater., 2019, 29, 1806765 CrossRef.
- D. McLeod, M. K. Thøgersen, N. I. Jessen, K. A. Jørgensen, C. S. Jamieson, X.-S. Xue, K. Houk, F. Liu and R. Hoffmann, Acc. Chem. Res., 2019, 52, 3488–3501 CrossRef PubMed.
- J. S. Barber, M. M. Yamano, M. Ramirez, E. R. Darzi, R. R. Knapp, F. Liu, K. Houk and N. K. Garg, Nat. Chem., 2018, 10, 953–960 CrossRef PubMed.
- A. N. S. Chauhan, G. Mali and R. D. Erande, Asian J. Org. Chem., 2022, 11, e202100793 CrossRef.
- M.-M. Xu, L. Yang, K. Tan, X. Chen, Q.-T. Lu, K. Houk and Q. Cai, Nat. Catal., 2021, 4, 892–900 CrossRef CAS.
- Y. S. Zholdassov, L. Yuan, S. R. Garcia, R. W. Kwok, A. Boscoboinik, D. J. Valles, M. Marianski, A. Martini, R. W. Carpick and A. B. Braunschweig, Science, 2023, 380, 1053–1058 CrossRef.
- S. Chen, P. Yu and K. Houk, J. Am. Chem. Soc., 2018, 140, 18124–18131 CrossRef.
- I. Kassal, J. D. Whitfield, A. Perdomo-Ortiz, M.-H. Yung and A. Aspuru-Guzik, Annu. Rev. Phys. Chem., 2011, 62, 185–207 CrossRef PubMed.
- M. Motta and J. E. Rice, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1580 Search PubMed.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre and N. P. Sawaya, et al. , Chem. Rev., 2019, 119, 10856–10915 CrossRef.
- B. Bauer, S. Bravyi, M. Motta and G. K.-L. Chan, Chem. Rev., 2020, 120, 12685–12717 CrossRef.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- B. J. Levandowski and K. Houk, J. Org. Chem., 2015, 80, 3530–3537 CrossRef CAS PubMed.
- R. V. Mishmash, T. P. Gujarati, M. Motta, H. Zhai, G. K.-L. Chan and A. Mezzacapo, J. Chem. Theory Comput., 2023, 19, 3194–3208 CrossRef CAS PubMed.
- A. Eddins, M. Motta, T. P. Gujarati, S. Bravyi, A. Mezzacapo, C. Hadfield and S. Sheldon, PRX Quantum, 2022, 3, 010309 CrossRef.
- P. Huembeli, G. Carleo and A. Mezzacapo, arXiv, 2022, preprint, arXiv:2205.00933 DOI:10.48550/arXiv.2205.00933.
- K. Setia, R. Chen, J. E. Rice, A. Mezzacapo, M. Pistoia and J. D. Whitfield, J. Chem. Theory Comput., 2020, 16, 6091–6097 CrossRef PubMed.
- M. Motta, G. O. Jones, J. E. Rice, T. P. Gujarati, R. Sakuma, I. Liepuoniute, J. M. Garcia and Y. Ohnishi, Chem. Sci., 2023, 14, 2915–2927 RSC.
- M. A. Castellanos, M. Motta and J. E. Rice, Mol. Phys., 2023, e2282736 Search PubMed.
- J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger and G. H. Booth, et al. , Phys. Rep., 2022, 986, 1–128 CrossRef.
- D. A. Fedorov, B. Peng, N. Govind and Y. Alexeev, Mater. Theory, 2022, 6, 1–21 CrossRef.
- M. Urbanek, D. Camps, R. Van Beeumen and W. A. de Jong, J. Chem. Theory Comput., 2020, 16, 5425–5431 CrossRef CAS.
- M. Motta, W. Kirby, I. Liepuoniute, K. J. Sung, J. Cohn, A. Mezzacapo, K. Klymko, N. Nguyen, N. Yoshioka and J. E. Rice, Electron. Struct., 2023, 6, 013001 CrossRef.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef.
- A. Tammaro, D. E. Galli, J. E. Rice and M. Motta, J. Phys. Chem. A, 2023, 127, 817–827 CrossRef PubMed.
- P. D. Nation, H. Kang, N. Sundaresan and J. M. Gambetta, PRX Quantum, 2021, 2, 040326 CrossRef.
- B. Pokharel, N. Anand, B. Fortman and D. A. Lidar, Phys. Rev. Lett., 2018, 121, 220502 CrossRef PubMed.
- E. Van Den Berg, Z. K. Minev, A. Kandala and K. Temme, Nat. Phys., 2023, 1–6 Search PubMed.
- S. Wilsey, K. Houk and A. Zewail, J. Am. Chem. Soc., 1999, 121, 5772–5786 CrossRef.
- T. P. Gujarati, M. Motta, T. N. Friedhoff, J. E. Rice, N. Nguyen, P. K. Barkoutsos, R. J. Thompson, T. Smith, M. Kagele and M. Brei, et al. , npj Quantum Inf., 2023, 9, 88 CrossRef.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova and S. Sharma, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen and Z.-H. Cui, et al. , J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- V. Guner, K. S. Khuong, A. G. Leach, P. S. Lee, M. D. Bartberger and K. Houk, J. Phys. Chem. A, 2003, 107, 11445–11459 CrossRef CAS.
- W. L. Jorgensen, D. Lim and J. F. Blake, J. Am. Chem. Soc., 1993, 115, 2936–2942 CrossRef CAS.
- W. C. Herndon, W. B. Cooper Jr and M. J. Chambers, J. Phys. Chem., 1964, 68, 2016–2018 CrossRef CAS.
- B. Roquitte, J. Phys. Chem., 1965, 69, 1351–1354 CrossRef CAS.
- J. Kiefer, S. Kumaran and S. Sundaram, J. Chem. Phys., 1993, 99, 3531–3541 CrossRef CAS.
- N. Balcyoolu and V. Güner, Instrum. Sci. Technol., 2001, 29, 193–200 CrossRef CAS.
- R. Walsh and J. M. Wells, J. Chem. Soc., Perkin Trans. 2, 1976, 52–55 RSC.
- R. D. Froese, M. G. Organ, J. D. Goddard, T. D. P. Stack and B. M. Trost, J. Am. Chem. Soc., 1995, 117, 10931–10938 CrossRef CAS.
- J. I. Colless, V. V. Ramasesh, D. Dahlen, M. S. Blok, M. E. Kimchi-Schwartz, J. R. McClean, J. Carter, W. A. de Jong and I. Siddiqi, Phys. Rev. X, 2018, 8, 011021 CAS.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. De Jong, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Phys. Rev. X, 2020, 10, 011004 CAS.
- H. Yu and A. D. Hutson, J. Appl. Stat., 2022, 1–16 Search PubMed.
- N. C. Rubin, R. Babbush and J. McClean, New J. Phys., 2018, 20, 053020 CrossRef.
- C. Moussa, M. H. Gordon, M. Baczyk, M. Cerezo, L. Cincio and P. J. Coles, Quantum Sci. Technol., 2023, 8, 045019 CrossRef.
- S. Choi and A. F. Izmaylov, J. Chem. Theory Comput., 2023, 19, 3184–3193 CrossRef PubMed.
- T.-C. Yen, V. Verteletskyi and A. F. Izmaylov, J. Chem. Theory Comput., 2020, 16, 2400–2409 CrossRef.
- S. Choi, I. Loaiza and A. F. Izmaylov, Quantum, 2023, 7, 889 CrossRef.
- D. A. Mazziotti, Chem. Phys. Lett., 1998, 289, 419–427 CrossRef CAS.
- D. Zgid, D. Ghosh, E. Neuscamman and G. K. Chan, J. Chem. Phys., 2009, 130, 194107 CrossRef.
- W. Li, Z. Huang, C. Cao, Y. Huang, Z. Shuai, X. Sun, J. Sun, X. Yuan and D. Lv, Chem. Sci., 2022, 13, 8953–8962 RSC.
- M. Rossmannek, P. K. Barkoutsos, P. J. Ollitrault and I. Tavernelli, J. Chem. Phys., 2021, 154, 114105 CrossRef CAS PubMed.
- R. D’Cunha, T. D. Crawford, M. Motta and J. E. Rice, J. Phys. Chem. A, 2023, 127, 3437–3448 CrossRef.
- M. Motta, K. J. Sung, K. B. Whaley, M. Head-Gordon and J. Shee, Chem. Sci., 2023, 14, 11213–11227 RSC.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 3007 CrossRef.
- M. Ostaszewski, L. M. Trenkwalder, W. Masarczyk, E. Scerri and V. Dunjko, Adv. Neural Inf. Process. Syst., 2021, 34, 18182–18194 Search PubMed.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75–107 CrossRef CAS.
- M. Motta, T. P. Gujarati, J. E. Rice, A. Kumar, C. Masteran, J. A. Latone, E. Lee, E. F. Valeev and T. Y. Takeshita, Phys. Chem. Chem. Phys., 2020, 22, 24270–24281 Search PubMed.
- A. Kumar, A. Asthana, C. Masteran, E. F. Valeev, Y. Zhang, L. Cincio, S. Tretiak and P. A. Dub, J. Chem. Theory Comput., 2022, 18, 5312–5324 CrossRef CAS.
- R. Huang, C. Li and F. A. Evangelista, PRX Quantum, 2023, 4, 020313 CrossRef.
- J. Robledo-Moreno, M. Motta, H. Haas, A. Javadi-Abhari, P. Jurcevic, W. Kirby, S. Martiel, K. Sharma, S. Sharma, T. Shirakawa, et al., arXiv, 2024, preprint, arXiv:2405.05068 DOI:10.48550/arXiv.2405.05068.
- K. Kanno, M. Kohda, R. Imai, S. Koh, K. Mitarai, W. Mizukami and Y. O. Nakagawa, arXiv, 2023, preprint, arXiv:2302.11320 DOI:10.48550/arXiv.2302.11320.
| This journal is © the Owner Societies 2024 |