Open Access Article
Open Access ArticleDissociation of HNO3 in water revisited: experiment and theory†
Ipek
Munar‡
 a,
Melike Özkan
Özer‡
a,
Melike Özkan
Özer‡
 b,
Edoardo
Fusco‡
c,
Deniz
Uner
b,
Edoardo
Fusco‡
c,
Deniz
Uner
 *b,
Viktorya
Aviyente
*b,
Viktorya
Aviyente
 *a and
Michael
Bühl
*a and
Michael
Bühl
 *c
*c
aChemistry Department, Bogazici University, 34342 Bebek, Istanbul, Turkey. E-mail: aviye@boun.edu.tr
bMiddle East Technical University, Chemical Engineering, 06800 Ankara, Turkey. E-mail: uner@metu.edu.tr
cEaStCHEM School of Chemistry and Centre of Magnetic Resonance, University of St Andrews, North Haugh, St Andrews KY16 9ST, UK. E-mail: buehl@st-andrews.ac.uk
First published on 14th May 2024
Abstract
Nitric acid dissociation in water is studied as a function of concentration, employing experimental techniques (1H NMR spectroscopy and calorimetry), quantum chemical methods (B3LYP and PBE functionals for molecular clusters) and molecular dynamics simulations (the PBE-D3 functional for solutions under periodic boundary conditions). The extent of dissociation, via proton transfer to a neighboring water molecule, as a function of concentration is studied computationally for molecular nitric acid clusters HNO3(H2O)x (x = 1–8), as well as periodic liquids (HNO3 mole fractions of 0.19 and 0.5, simulated at T = 300 K and 450 K). Despite the simple nature of these structural models, their computed and simulated average 1H chemical shifts compare well with the experimental measurements in this study. Finally, the measured and calculated chemical shifts have shown reasonable relationships with the enthalpy change upon mixing of this binary complex.
Introduction
The investigation of microhydration is key to understanding the behavior of various anions in water solutions and aerosols. The nitrate ion holds a special place among the anions studied since it is one of the most abundant anions on Earth. The nitrate ion participates in a variety of processes ranging from atmospheric chemistry to nuclear waste processing:1 nitric acid is reported to play a role in the formation of the Antarctic stratosphere ozone hole2 and nitrate anion behavior in water solutions may affect further the processes of nuclear waste preparation. Furthermore, nitrate ion pollution in water due to the excessive use of fertilizers is both serious and widespread. The dissociation of strong acids in water is of great importance for a large class of chemical reactions in aqueous solutions.2 Proton transfer (PT) reactions are widely known in chemistry and biochemistry. Among the most familiar of these reactions is the transfer of a proton from strong acids such as nitric acid (HNO3) to a water molecule in an aqueous solution. Theoretical investigation of microhydration is an important task for understanding the behavior of various anions in water solutions and aerosols. Molecular level insight into the dissociation of nitric acid in water has been obtained from DFT calculations and molecular dynamics simulations.3 Xanteas and coworkers have studied the formation of HNO3(H2O)n complexes theoretically (n = 0, 4) and experimentally in the gas phase.4 Calculations (MP2/aug-cc-pVDZ) have predicted the appearance of ion-pair configurations in the gas phase for n = 4 or higher.4 Escribano et al. investigated (B3LYP/aug-cc-pVDZ) the complexes formed by nitric acid with one, two and three water molecules.5 They have found that complexes are stabilized by hydrogen bonds: the acid being the donor with a first water molecule, and further H bonds are formed between successive water molecules. Scott et al. performed MP2/6-311++G(2d,p) and B3LYP/6-311++G(2d,p) calculations to determine the optimum energies and binding energies for HNO3·nH2O systems (n = 1,…, 4). The first stable ion-pair configuration is obtained for a complex with n = 4.6 Leopold and coworkers used Fourier transform microwave spectroscopy to characterize the gas-phase complex HNO3–(H2O)3 in a supersonic jet. The structure was confirmed by MP2/-6-311++G(2df,2pd) calculations and it involved a nearly planar 10-membered ring with the HNO3 proton hydrogen-bonded to the first water.7 Note also that in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mole ratio mixture of HNO3 and H2O at 298 K,8 the percentage of dissociation is 51%, while in a 1
3 mole ratio mixture of HNO3 and H2O at 298 K,8 the percentage of dissociation is 51%, while in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 HNO3/H2O mixture at 278 K, 98% of the acid is dissociated.9 More recently, Leopold summarized the nature of hydrated protons, and a parallel discussion of structural aspects of acid–water complexes was presented.10
20 HNO3/H2O mixture at 278 K, 98% of the acid is dissociated.9 More recently, Leopold summarized the nature of hydrated protons, and a parallel discussion of structural aspects of acid–water complexes was presented.10
In this study, we revisit the work of Lewis et al.,3 where the concentration dependence of the dissociation of nitric acid in water is investigated based on a combination of experiments and theoretical electronic–structure-based molecular dynamics (MD) simulations.
The nitric acid dissociation process steps are shown in Fig. 1, where NP denotes a neutral pair, CIP refers to a contact ion pair, and SSP indicates a solvent-separated ion pair.
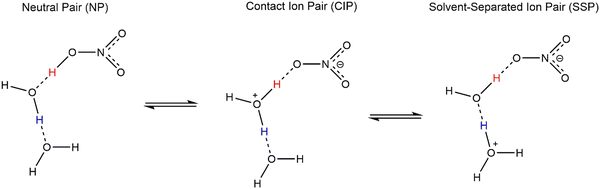 | ||
| Fig. 1 Schematic of consecutive proton transfer NP → CIP → SSP for HNO3 acid dissociation.2 | ||
Lewis et al. studied aqueous nitric acid solutions with concentrations of up to 6 M.3 We now investigate even more concentrated solutions (up to 50 mol%, 20 M), paying special attention to the use of NMR spectroscopy as a diagnostic tool. During these investigations, apparent relationships were revealed between the concentrations of the solutions and both their 1H NMR chemical shifts and the measured heats of mixing. To gain a deeper understanding of the molecular origin of these observations, we performed quantum chemical calculations on small microsolvated HNO3–water clusters with molar ratios covering the concentration range under scrutiny. Without proposing such simple clusters to be faithful representatives of the actual solutions, we now report remarkable similarities in the computed and observed trends for both.
Solvent–solute interactions and their impact on the NMR chemical shifts of the functional groups are well-known in NMR spectroscopy. Routine analyses can comfortably rely on empirical correlations and libraries. The dependence of these chemical shifts on the concentration of the solute can become an important component of the chemical shifts, especially for nuclei with a narrow chemical shift range such as 1H. NMR spectroscopy can be used to extract quantitative information along with molecular structural information. Furthermore, carefully constructed multi-dimensional and/or multi-pulse sequences can reveal the nature and the rate of the local atomic, molecular and spin-exchange interactions. When these factors are combined, NMR spectroscopy becomes an attractive tool for operando methods.11,12 When operando spectroscopy is applied under batch conditions, the solute concentrations are subject to change as a function of time. This change, if expected to occur over a large concentration range, can lead to altering the chemical shifts of other molecules. One of the motivations for this study is to lay the groundwork for demonstrating the effect of the solute concentration on the chemical shifts in 1H NMR spectroscopy, when the nuclear spins are in rapid exchange in the chemical environment such that only a single resonance can be obtained in the NMR timeframe. The second motivation is to look for the reasons through understanding the local structural environment with the help of estimating NMR shifts using first-principles methods. Furthermore, it is important to establish the connection between the NMR chemical shifts and the heats of solvation and heats of dissolution measured through calorimetry.13,14
Methodology
Experimental
1H-NMR measurements were carried out using a Magritek Spinsolve 80 spectrometer. The data were visualized using the software of Magritek Spinsolve 80. For preparing the mixtures, pure water (H2O), heavy water (D2O) and high-purity nitric acid (HNO3, 98%) were used. Mixtures were prepared just before the measurement at constant temperatures (25 °C and 40 °C). Since the mixing of nitric acid and water is significantly exothermic, the mixtures were kept at rest after mixing until they reached the initial temperature. The molar compositions of the mixtures were selected intentionally in order to match the composition of the water–nitric acid complexes with water to nitric acid ratios in the range of 1 to 8. The 1H-NMR chemical shifts of the nitric acid–water mixtures were measured at constant temperatures (25 °C and 40 °C) as a function of composition. Measurements were performed utilizing the proton protocol, and chemical shifts were referenced to the proton chemical shift of tetramethylsilane (TMS). The 1H frequency is 80 MHz in the magnetic field of the benchtop NMR spectrometer. Four scans were sufficient to obtain very good S/N ratios (S/N = signal/noise). A coffee-cup calorimeter was designed and used to determine the adiabatic heat of mixing. A thermally insulated chamber was loaded with the primary component (water or concentrated nitric acid), and its temperature stabilization was monitored with a thermometer with a 0.2 °C sensitivity. The secondary component, equilibrated at the same temperature, was introduced into the chamber. This chamber was carefully sealed and isolated to avoid the evaporative losses of mass and thermal energy. A thermometer was used to measure the generated thermal energy. The maximum temperature was recorded. The heat capacities of the individual components were used to determine excess heat upon mixing. The sensitivity of the mass measurements was within 1 mg, and temperature measurements were within 0.2 °C, resulting in an estimated error of ∼1 mJ of thermal energy.Quantum mechanics (QM)
The equilibrium geometries and vibrational normal modes of hydrated nitric acid clusters and reference molecules were obtained using the PBE functional15 in combination with Pople's 6-311+G(2d,p) basis set. Conformational analysis was performed in order to find the most stable conformer of each cluster (only results for the lowest conformer of each cluster are reported). The geometries were fully optimized, followed by the calculation of the harmonic vibrational frequencies at that level. The vibrational frequencies were used to characterize the minimum nature of the optimized structures and to evaluate thermodynamic corrections to enthalpies (at 1 atm and 323.15 K). Magnetic shielding σ(i) was computed for the most stable structures at the PBE/6-311+G(2d,p) level as well as at the B3LYP/6-311+G(2d,p)//PBE/6-311+G(2d,p) level. To account for the bulk solvation effects, a continuum solvation model based on density (SMD)16 was used for geometry optimization and NMR calculations. The molecular volumes of the nitric acid clusters were obtained using the PBE/6-311+G(2d,p) methodology.Nitric acid clusters and selected water clusters [H2O, (H2O)3, and (H2O)4 as models for pure water], as well as (H3O+)(H2O)3 as a model for a free hydrated proton were calculated. Due to the expected rapid exchange of all protons, all of the protons are taken into account for the average chemical shift calculations of nitric acid clusters.
The 1H chemical shifts δ(i) of the clusters are calculated using eqn (1):
| δ(i) = σ(TMS) − σ(i), | (1) |
The enthalpy of mixing is calculated using eqn (2):
| HNO3 + (x/8)(H2O)8 → HNO3(H2O)x (x = 1, 2, …,8). |
| The enthalpy of mixing = HHNO3(H2O)x − HHNO3 − H(x/8)(H2O)8 | (2) |
Molecular dynamics (MD)
Periodic DFT calculations were performed using version 22.11 of the plane wave CASTEP code,17 which employs the GIPAW18 algorithm to reconstruct the all-electron wave function in the presence of a magnetic field. The generalized gradient approximation (GGA) PBE19 functional was employed with D3-BJ dispersion corrections.20 Wave functions were expanded as plane waves with a kinetic energy smaller than the cutoff energy of 60 Ry (816 eV). Integrals over the first Brillouin zone were performed using a Monkhorst–Pack21 grid with a k-point spacing of 0.1 Å−1. Molecular dynamics trajectories were computed in the NVE and NVT ensemble using the Langevin thermostat,22–24 a time step of 1 fs (0.5 for the x = 0.50 solution at 450 K), and further settings specified in the ESI.† Isotropic magnetic shielding was computed for snapshots taken at regular intervals from the trajectories, using the same level and settings as the MD. 1H shielding was averaged over all H atoms in each frame and over sufficient snapshots to ensure convergence (see ESI†) and converted to chemical shifts according to eqn (1) [where σ(TMS) and σ(i) denote the respective ensemble averages]. The value for TMS was obtained from an MD simulation of a single TMS molecule in an otherwise empty box with the same settings as above; the resulting averaged shielding values were σ(TMS) = 30.84 and 30.81 ppm at 350 K and 450 K, respectively.Results and discussion
Experimental results
| Formula | Mole fraction xHNO3 | Chemical shift, δ, (ppm) | Heat of mixing (kcal mol−1) | |||
|---|---|---|---|---|---|---|
| H2O–HNO3 | D2O–HNO3 | |||||
| 25 °C | 40 °C | 25 °C | 40 °C | |||
| a 1H signal from H2O impurities in D2O. | ||||||
| H2O | 0.00 | 4.77 | 4.77 | 4.77a | 4.77a | n/a |
| HNO3(H2O)8 | 0.11 | 6.47 | 6.28 | 6.68 | 6.77 | −4.20 |
| HNO3(H2O)7 | 0.13 | 6.65 | 6.53 | 6.83 | 6.89 | −4.38 |
| HNO3(H2O)6 | 0.14 | 6.91 | 6.73 | 7.17 | 7.18 | −4.16 |
| HNO3(H2O)5 | 0.17 | 7.16 | 6.99 | 7.44 | 7.41 | −4.18 |
| HNO3(H2O)4 | 0.20 | 7.44 | 7.35 | 7.81 | 7.71 | −4.03 |
| HNO3(H2O)3 | 0.25 | 7.81 | 7.82 | 8.20 | 8.26 | −3.39 |
| HNO3(H2O)2 | 0.33 | 8.27 | 8.16 | 8.55 | 8.58 | −3.02 |
| HNO3(H2O) | 0.50 | 8.84 | 8.85 | 8.99 | 8.95 | −2.17 |
| HNO3 | 1.00 | 11.59 | 11.53 | 11.53 | 11.53 | n/a |
Effect of composition. As can be seen from Table 1, the signals of the nitric acid–water mixtures fall in between those of pure water and nitric acid, and the chemical shift increases with increasing acid concentration.
Effect of temperature. The chemical shifts of the resonance signals in the proton NMR spectrum of many acids and alcohols are slightly temperature dependent, arguably due to changes in vibrational averaging in the R–OH⋯O(H)R moieties with temperature. However, in the nitric acid–water case, there are no long-lived hydrogen bonds like that due to the strong acidity and ionization of the nitric acid, which is expected to afford hydronium ions and rapid diffusion of the protons through the well-known Grotthuss-type mechanism (see the MD results below). Also, the measured chemical shifts were very similar for each mixture composition with the same binary mixture. Therefore, it appears that the temperature increase from 25 to 40 °C had no important effect on the measured chemical shift values among the nitric acid–water mixtures.
Aqueous solutions of nitric acid have a maximum boiling azeotrope at 69% HNO3. Nitric acid undergoes exothermic dilution, which indicates that interactions lead to energy release at the molecular scale. A detailed understanding of the local molecular structure, leading to the energy release upon mixing, is important for both manufacturing and using nitric acid.
The composition-dependent heats of mixing values measured in this work (included in Table 1) compare well with the data reported in the literature.27
Both the measured 1H NMR chemical shifts and the heats of mixing of the solutions show a monotonous trend with the concentrations. To gain more insights into the intermolecular interactions and structural motifs that could underpin these observations, we performed quantum chemical computations for the selected model systems, which are discussed below.
Water clusters: benchmark analysis for 1H-NMR chemical shifts
The calculated average 1H chemical shifts for the small water clusters are reported in Table 2, and the geometries are shown in Fig. S1 in the ESI.†δ(1H) values are higher (more deshielded) at the B3LYP level than at the PBE level. For the trimeric and tetrameric clusters, which are arguably better models for the bulk than a single molecule, the PBE results are in better agreement with the experimental results for the pure liquid (Table 1) than those at the B3LYP level. Therefore, there does not seem to be an advantage of using B3LYP (probably the more widely used functional for NMR computations) over PBE. In the following sections, we will discuss the results obtained with the latter functional.| Formula | δ calc (ppm) PBE/6-311+G(2d,p) | δ calc (ppm) B3LYP/6-311+G(2d,p) |
|---|---|---|
| H2O | 1.39 | 2.05 |
| (H2O)3 | 4.81 | 5.44 |
| (H2O)4 | 5.92 | 6.44 |
| (H2O)8 | 4.92 | 5.48 |
| (H3O+)(H2O)3 | 12.86 | 13.50 |
Nitric acid–water clusters
The initial structures of the microsolvated clusters HNO3(H2O)n (n = 1, 2) and NO3−(H2O)m(H3O)+ (m = 2–3) were taken from the work of Gutberlet and coworkers, which is based on the aggregation-induced dissociation of HCl(H2O)4.28 In this context, we used DFT calculations in order to understand the behavior of nitric acid in water as its mole fraction varies from 0.11 to 0.50. The compositions of modelled nitric acid clusters are given in Table 3, and their electronic and zero-point energies are given in Table S1 (ESI†). We found that microsolvation with a single water molecule maintains a neutral pair (HNO3(H2O)), which ionizes upon the addition of a second water molecule, resulting in a contact ion pair (cf.Fig. 1). Additional water molecules afford solvent-separated ion pairs (NO3−(H2O)m(H3O)+ (m = 2–7)), and the modelled clusters are shown in Fig. 2.2 Spontaneous ionization of strong acids by a small number of solvent molecules is well known, and there is a loose correlation between acid pKa and the number of water molecules required for this ionization.29 The observation that only two water molecules are needed to ionize HNO3 is in line with its very low pKa. Note that these calculations were performed on a polarizable continuum to model bulk solvation in aqueous solutions. For comparison with literature data, which usually does not consider such bulk solvation, we also modeled the same clusters in the gaseous phase and noticed that the ion pair starts to form at n = 4 (see Fig. S2, ESI†). This finding is similar to one of Xanteas and coworkers (MP2/aug-cc-pVDZ), who predicted the appearance of ion-pair configurations in the gas phase for n = 4 or higher.4 Similarly, Scott et al. obtained the first stable ion-pair configuration for a complex with n = 4 (MP2/6-311++G(2d,p) and B3LYP/6-311++G(2d,p)).6 This good agreement provides further validation of our chosen level, PBE/6-311+G(2d,p).| Formula | Mole fraction xHNO3 | Volume (cm3 mol−1) | Molarity (M) | |
|---|---|---|---|---|
| 1 | HNO3(H2O) | 0.50 | 50.0 | 20.0 |
| 2 | NO3−(H2O)(H3O)+ | 0.33 | 66.5 | 15.0 |
| 3 | NO3−(H2O)2(H3O)+ | 0.25 | 80.0 | 12.5 |
| 4 | NO3−(H2O)3(H3O)+ | 0.20 | 103.5 | 9.7 |
| 5 | NO3−(H2O)4(H3O)+ | 0.17 | 125.7 | 8.0 |
| 6 | NO3−(H2O)5(H3O)+ | 0.14 | 121.8 | 8.2 |
| 7 | NO3−(H2O)6(H3O)+ | 0.13 | 148.2 | 6.7 |
| 8 | NO3−(H2O)7(H3O)+ | 0.11 | 144.7 | 6.9 |
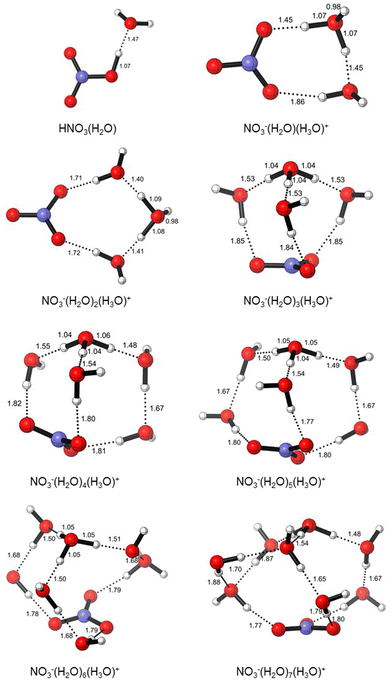 | ||
| Fig. 2 Structures of HNO3(H2O)n (n = 1) and NO3−(H2O)m(H3O)+ (m = 2–7) clusters (PBE/6-311+G(2d,p), SMD = H2O). | ||
When the polarity of the medium is taken into account, in the HNO3(H2O) cluster corresponding to x = 0.50, the acidic proton is on NO3−. As more water is added, the proton moves towards H2O, and H3O+ starts to form. In HNO3(H2O)2, H3O+ is equidistant to NO3−; in HNO3(H2O)3, NO3− is completely separated (1.71 Å) from the protonated water cluster. As the solution becomes more dilute, the proton sticks to H2O and the hydronium ion (H3O+) is surrounded by other H2O molecules, which in turn stabilizes the NO3− anion.
In the following, we will use the results obtained in the continuum (including the SMD-optimized structures) for consistency with the experimental conditions of bulk solutions. The calculated δ values are collected in Table 4. They follow the trend in the observed shifts remarkably well, and the resulting discrepancies Δδ (δexpt − δcalcd) are in the range between −0.61 and 0.38 (−0.61< Δδ < 0.38) ppm. Graphical comparisons between experimental 1H NMR chemical shifts and the estimated values from DFT, as a function of mole fractions, are shown in Fig. S5 (ESI†). Arguably, as the number of water molecules in the clusters increases, the computed trend is to some extent due to the increased weight of the (intact) water sites in the total average.
| Formula | Calculated chemical shifts δ (ppm) | Experimentally measured chemical shifts δ (ppm) | Δδ (ppm) | |
|---|---|---|---|---|
| 1 | HNO3(H2O) | 8.32 | 8.7 | 0.38 |
| 2 | NO3−(H2O)(H3O)+ | 8.74 | 8.13 | −0.61 |
| 3 | NO3−(H2O)2(H3O)+ | 8.12 | 7.72 | −0.40 |
| 4 | NO3−(H2O)3(H3O)+ | 7.74 | 7.45 | −0.29 |
| 5 | NO3−(H2O)4(H3O)+ | 7.18 | 7.12 | −0.06 |
| 6 | NO3−(H2O)5(H3O)+ | 7.07 | 6.83 | −0.24 |
| 7 | NO3−(H2O)6(H3O)+ | 6.75 | 6.64 | −0.11 |
| 8 | NO3−(H2O)7(H3O)+ | 6.62 | 6.45 | −0.17 |
Heat of mixing (experimental and calculated)
We also calculated (PBE/6-311+G(2d,p), 323.15 K, SMD = H2O) the enthalpies of mixing through the enthalpies of formation of our microsolvated clusters from a single HNO3 and a water octamer by using eqn (2) (Table S2, ESI†). These estimations were closer to the measured values at high nitric acid concentrations. At higher water concentrations, the discrepancy between the measured and estimated values increased. A perfect agreement between the experiment and the results for such a microsolvated model cluster was not expected. However, the general trend, i.e. the exothermicity increases with the water content, is well captured qualitatively. Part of this discrepancy can also be attributed to the peculiarities that continue to be discovered about the structure of water, especially at the interfaces.30–33The correlation between the enthalpy of mixing (kcal mol−1) and the average chemical shift (ppm) for the (HNO3)n(H2O) clusters is fair (Fig. S3, R2 = 0.91, ESI†), while the same correlation with the experimental data is also within acceptable limits (Fig. S4, R2 = 0.90, ESI†). With limited data at hand, the relationship between enthalpies of mixing and chemical shifts cannot be generalized at this stage. The NMR chemical shifts reflect the local structures at equilibrium. It is important to conduct further studies to determine whether there is a fundamental basis for the correlation between NMR chemical shift data and the corresponding heats of mixing values.
Simulation of bulk solutions under periodic boundary conditions
To complement the molecular cluster investigation, we performed simulations for bulk solutions under periodic boundary conditions (Fig. S6–S13, ESI†). We explored three different systems, each containing varying amounts of nitric acid. These systems included a pure water solution (x = 0.00), a nitric acid solution with a molecular fraction of x = 0.19, and a nitric acid solution with a molecular fraction of x = 0.50 (see Fig. 3). We specifically chose these solutions to cover the entire range of experimental results, from x = 0.00 to x = 0.50. To limit the computational effort, we started with a small box containing 32 water molecules (akin to that used in early CPMD studies of the properties of liquid water)34,35 and replaced an appropriate number of water molecules with HNO3 molecules to maintain the proper density within the same box dimensions. Because PBE (like the BLYP functional used more commonly) tends to overstructure the pure liquid36 and since this overstructuring is improved by the inclusion of dispersion corrections,37 we used the PBE-D3 variant in all simulations.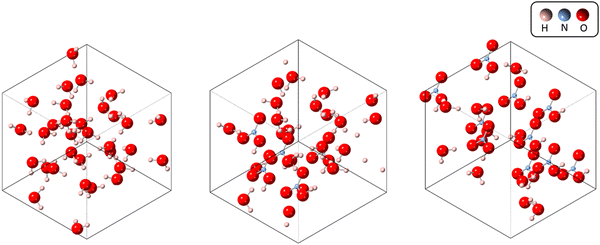 | ||
| Fig. 3 Unit cells for different solutions. From right to left: pure water, molecular fraction of 0.19, 50/50 solution of nitric acid. | ||
We started by simulating pure water and nitric acid solutions at 300 K, which corresponds to one of the experimental temperatures. However, these simulations did not properly describe the liquid-like behaviour of our system. This was validated through the radial distribution functions (RDFs) and the root mean square deviations of atomic positions (RMSDs) (see Fig. 4, and a more detailed description is provided in the ESI†). In our simulations, it appears that the solutions freeze after the first 1.5 ps, which is a physically incorrect representation of a solution.
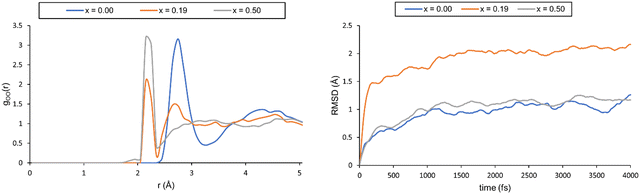 | ||
| Fig. 4 Left: The oxygen–oxygen RDF for different systems computed at 300 K. Right: Plot of the RMSD for the three solutions. | ||
Although frozen, we still computed the chemical shifts for all three solutions. To this end, we extracted 20 snapshots from the MD trajectory and computed the NMR shielding(the computational details for the calculation of the magnetic properties can be found in the ESI†). Magnetic shielding for a single tetramethylsilane (TMS) system computed at the same level of theory provides a reference for chemical shielding. The resulting 1H chemical shifts are collected in Table 5.
| x | δ (CASTEP, 300 K) | δ (Exp., 300 K) | Δδ |
|---|---|---|---|
| 0.00 | 6.1 | 4.8 | 1.3 |
| 0.19 | 8.2 | 7.4 | 0.8 |
| 0.50 | 10.4 | 8.8 | 1.6 |
Overall, the agreement with the experiment is fair, and affords an average error of ∼1.2 ppm. It should be noted that the experimental trend of larger deshielding with increasing acid content is well reproduced and that the error (overestimation of the chemical shift) is rather systematic. Thus, if the reference used is not TMS, but the pure water system the agreement is significantly improved (see Table S6 in the ESI†). This is interesting, as it may suggest that the key interactions arising from the addition of nitric acid in the solution are well captured. Moreover, this sheds light on said interactions, which must be short-ranged as the solution behaves like a solid and the molecules only move about their local position without diffusion through the liquid. Therefore, long-distance interactions arising from the molecules freely moving in solution, which are not accounted for in these simulations, do not seem to be the key factors influencing the chemical shift.
One of the main issues that needs to be addressed is that the simulation does not behave as a solution, but as a solid. In fact, even though the chemical shift can be predicted to a high degree of accuracy when pure water is used as a reference, this is not entirely satisfactory as it only proves that the change introduced by nitric acid is reproduced, but not the behaviour of the solution as a whole. To address this issue, we followed the work of Xantheas and performed MD simulations at a higher temperature (450 K). The oxygen–oxygen RDF at this temperature shows a totally different behaviour, corresponding to a less-structured solution. As reported in ref. 38, a higher temperature allows for a correct description of the second coordination sphere (see the maximum at r ≈ 4.2 Å on the left-hand side of Fig. 5), whereas the probability associated with the first coordination sphere is underestimated (see the maximum at r ≈ 2.9 Å). It should be noted that the shallow well depth between both peaks observed experimentally (indicative of a dynamic exchange between molecules in the first and second solvation spheres) is well reproduced at the higher simulation temperature, whereas the simulation at 300 K has a much deeper well. The RMSD at 450 K also shows a behaviour in line with that of a solution and not with that of a solid. In fact, its value keeps on increasing and does not plateau even after 10 ps (see the right-hand side of Fig. 5).
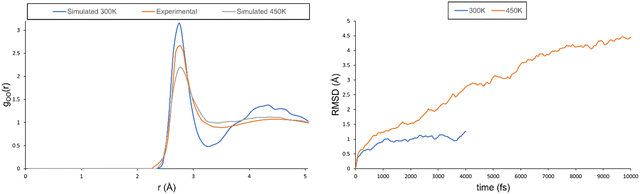 | ||
| Fig. 5 Left: Predicted and experimental oxygen–oxygen RDF for the pure water system (x = 0.00). Right: RMSD plot for the pure water system at 300 and 450 K. | ||
Overall, from the RDF and RMSD analyses, we can conclude that the simulation at 450 K behaves as a proper solution. We have, therefore, repeated the simulations of the two nitric acid solutions at this high temperature. While these systems tend to be more mobile at higher T than at 300 K, they do not attain truly diffusive states (which would probably require much longer simulation times); see the RMSDs in the ESI† (see Fig. S14). Nevertheless, in terms of NMR properties, the increased mobility has a strong beneficial effect. The experimental data (at 300 K) are reproduced almost quantitatively (see Δδ values in Table 6 and Fig. S15, ESI†).
| x | δ (CASTEP, 450 K) | δ (Exp., 300 K) | Δδ |
|---|---|---|---|
| 0.00 | 4.8 | 4.8 | 0.0 |
| 0.19 | 7.4 | 7.4 | 0.0 |
| 0.50 | 8.9 | 8.8 | 0.1 |
This excellent agreement may, to some extent, be fortuitous, given the essentially frozen nature of the solutions in the simulations. With a large proportion of nitrate and hydronium ions, however, diffusion in these concentrated nitric acid solutions may share some characteristics with those in ionic liquids. This is frequently described as a random walk-hopping process between ion cages.39 If the lifetime of such ion cages exceeds the duration of individual hopping events, dynamic averaging of NMR properties over a representative, instantaneous set of such ion cages may indeed capture key features, with further (minor) modulations expected through changes of these properties during hopping. As mentioned, proper modelling of this aspect would require larger boxes and, particularly, much longer simulation times.
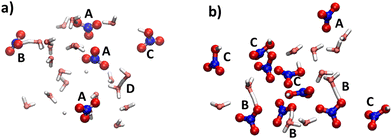
In the dynamic (albeit “frozen”) ensembles of nitric acid solutions, NPs, CIPs and SSPs are encountered to various extents. Fig. 6 shows representative snapshots from the simulations of the two systems (at higher T), where at lower concentrations, SSPs are prevalent (shown as isolated nitrate ions, labeled A), with a smaller population of CIPs and NPs (shown as intact HNO3 moieties, labelled B and C, respectively); see Fig. 6a. At higher concentrations, these populations are reversed as shown in Fig. 6b. There is no indication of the presence of discrete HNO3 dimers (akin to the doubly bridged motif well known for carboxylic acids) in these simulations.
These structural features can be quantified by analysing the relevant RDFs (see ESI† for details). Unfortunately, no energetic quantities could be extracted from these relatively short MD simulations, which could be related to the heats of mixing. Again, much longer simulations (including those for pure HNO3) are required for this purpose.
Conclusions
In this study, insights into the dissociation of nitric acid in water at the molecular level were deduced from 1H NMR, DFT calculations and molecular dynamics simulations. The dependence of 1H NMR chemical shifts on the concentration of the solute has been experimentally measured, and molecular (static) clusters bearing the formula HNO3(H2O)x (x = 1, 2, …, 8) and corresponding to the experimental concentrations have been modeled successfully with PBE/6-311+G(2d,p) in conjunction with the SMD solvation model employing the parameters of H2O. Except for the monohydrated complex (x = 1), all microsolvated clusters have been optimized in a dielectric continuum to contact or solvent-separate ion pairs with discrete NO3− and H3O+ ions. In addition to a pure water reference, MD simulations have been performed for two nitric acid solutions with mole fractions of 0.19 and 0.50 (PBE-D3 functional, T = 300 K and 450 K). Despite using fairly small periodic boxes and short simulation times, the 1H chemical shifts averaged over the trajectories at a higher temperature (T = 450 K) reproduce the observed change in chemical shift in this concentration range very well. As expected, and in line with the molecular cluster models, a much higher degree of dissociation is found at a lower concentration (mole fraction: 0.19) than at a higher one (mole fraction: 0.5), where the majority of nitric acid is present in the form of intact HNO3 molecules.This study has also provided insights into the relationship between the experimentally measured heats of mixing and the chemical shifts of the solutions, as well as between the calculated enthalpies of reaction and the average chemical shifts. Additional data are necessary for a conclusive interpretation of these findings.
Author contributions
The three first authors and the three corresponding authors contributed equally.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MOO and DU extend their appreciation to Dr Ahmet Koç and Dr Hacı Eşiyok for their assistance and Roketsan A. Ş. for access to facilities during the experimental part of this study. MB and EF thank EaStCHEM and the School of Chemistry for their support. Calculations with CASTEP were performed in St Andrews on a local HPC cluster maintained by Dr H. Früchtl. IM and VA thank TUBITAK ULAKBIM, the High Performance and Grid Computing Center (TRUBA resources), for their support: the QM calculations reported in this paper were performed there.References
- N. V. Tkachenko, A. A. Tkachenko, V. A. Kulyukin and A. I. Boldyrev, DFT Study of Microsolvated [NO3(H2O)n]− (N = 1–12) Clusters and Molecular Dynamics Simulation of Nitrate Solution, J. Phys. Chem. A, 2021, 125(40), 8899–8906, DOI:10.1021/acs.jpca.1c07206
.
- S. Wang, R. Bianco and J. T. Hynes, Nitric Acid Dissociation at an Aqueous Surface: Occurrence and Mechanism, Isr. J. Chem., 2009, 49(2), 251–259, DOI:10.1560/ijc.49.2.251
.
- T. Lewis, B. Winter, A. C. Stern, M. D. Baer, C. J. Mundy, D. J. Tobias and J. C. Hemminger, Dissociation of Strong Acid Revisited: X-Ray Photoelectron Spectroscopy and Molecular Dynamics Simulations of HNO3 in Water, J. Phys. Chem. B, 2011, 115(30), 9445–9451, DOI:10.1021/jp205510q
.
- P. R. McCurdy, W. P. Hess and S. S. Xantheas, Nitric Acid–Water Complexes: Theoretical Calculations and Comparison to Experiment, J. Phys. Chem. A, 2002, 106(33), 7628–7635, DOI:10.1021/JP020257E/ASSET/IMAGES/LARGE/JP020257EF00006.JPEG
.
- R. Escribano, M. Couceiro, P. C. Gómez, E. Carrasco, M. A. Moreno and V. J. Herrero, The Nitric Acid Hydrates: Ab Initio Molecular Study, and RAIR Spectra of the Solids, J. Phys. Chem. A, 2003, 107(5), 651–661, DOI:10.1021/JP0262620/ASSET/IMAGES/LARGE/JP0262620F00004.JPEG
.
- J. R. Scott and J. B. Wright, Computational Investigation of the Solvation of Nitric Acid: Formation of the NO3− and H3O+ Ion Pair, J. Phys. Chem. A, 2004, 108(47), 10578–10585, DOI:10.1021/JP047633A/SUPPL_FILE/JP047633ASI20040730_052931.PDF
.
- G. Sedo, J. L. Doran and K. R. Leopold, Partial Proton Transfer in the Nitric Acid Trihydrate Complex, J. Phys. Chem. A, 2009, 113(42), 11301–11310, DOI:10.1021/JP9063033/SUPPL_FILE/JP9063033_SI_001.PDF
.
- H. S. Harned, B. B. Owen and C. V. King, The Physical Chemistry of Electrolytic Solutions, Third Edition, J. Electrochem. Soc., 1959, 106(1), 15C, DOI:10.1149/1.2427250
.
- N. Minogue, E. Riordan and J. R. Sodeau, Raman Spectroscopy as a Probe of Low-Temperature Ionic Speciation in Nitric and Sulfuric Acid Stratospheric Mimic Systems, J. Phys. Chem. A, 2003, 107(22), 4436–4444, DOI:10.1021/JP021746H/ASSET/IMAGES/MEDIUM/JP021746HE00005.GIF
.
- K. R. Leopold, Hydrated Acid Clusters, Annu. Rev. Phys. Chem., 2011, 62, 327–349, DOI:10.1146/annurev-physchem-032210-103409
.
- K. Nakajima, H. Miyaoka, K. Kojima, T. Ichikawa and Y. Kojima, Operando Spectroscopic Analyses for the Ammonia Absorption Process of Sodium Borohydride, Chem. Commun., 2019, 55(15), 2150–2153, 10.1039/C8CC08048H
.
- X. L. Wang, W. Liu, Y. Y. Yu, Y. Song, W. Q. Fang, D. Wei, X. Q. Gong, Y. F. Yao and H. G. Yang, Operando NMR Spectroscopic Analysis of Proton Transfer in Heterogeneous Photocatalytic Reactions, Nat. Commun., 2016, 7(1), 1–7, DOI:10.1038/ncomms11918
.
- G. B. Manelis, G. V. Lagodzinskaya, A. I. Kazakov, A. V. Chernyak, N. G. Yunda and L. S. Kurochkina, Influence of the Supramolecular Structure of the Liquid Reaction Medium on the Kinetics of Acetone Oxidation with Aqueous Solutions of Nitric Acid, Russ. Chem. Bull., 2013, 62(4), 994–1002, DOI:10.1007/S11172-013-0130-1
.
- K. Ramírez-Gualito, R. Alonso-Ríos, B. Quiroz-García, A. Rojas-Aguilar, D. Díaz, J. Jiménez-Barbero and G. Cuevas, Enthalpic Nature of the CH/π Interaction Involved in the Recognition of Carbohydrates by Aromatic Compounds, Confirmed by a Novel Interplay of NMR, Calorimetry, and Theoretical Calculations, J. Am. Chem. Soc., 2009, 131(50), 18129–18138, DOI:10.1021/JA903950T/SUPPL_FILE/JA903950T_SI_002.CIF
.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158–6170, DOI:10.1063/1.478522
.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396, DOI:10.1021/JP810292N/SUPPL_FILE/JP810292N_SI_003.PDF
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First Principles Methods Using CASTEP, Zeitschrift fur Krist, 2005, 220(5–6), 567–570, DOI:10.1524/ZKRI.220.5.567.65075/MACHINEREADABLECITATION/RIS
.
- C. J. Pickard and F. Mauri, All-Electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(24), 245101, DOI:10.1103/PhysRevB.63.245101
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865, DOI:10.1103/PhysRevLett.77.3865
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465, DOI:10.1002/JCC.21759
.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(12), 5188, DOI:10.1103/PhysRevB.13.5188
.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids: Second Edition, Comput. Simul. Liq. Second Ed., 2017, 1–626, DOI:10.1093/oso/9780198803195.001.0001
.
- W. G. Hoover, A. J. C. Ladd and B. Moran, High-Strain-Rate Plastic Flow Studied via Nonequilibrium Molecular Dynamics, Phys. Rev. Lett., 1982, 48(26), 1818, DOI:10.1103/PhysRevLett.48.1818
.
- D. J. Evans, Computer ‘“Experiment”’ for Nonlinear Thermodynamics of Couette Flow, J. Chem. Phys., 1983, 78(6), 3297–3302, DOI:10.1063/1.445195
.
- W. Makulski, M. Wilczek and K. Jackowski,
17O and 1H NMR Spectral Parameters in Isolated Water Molecules, Phys. Chem. Chem. Phys., 2018, 20(35), 22468–22476, 10.1039/C8CP01748D
.
- H. Cho, P. B. Shepson, L. A. Barrie, J. P. Cowin and R. Zaveri, NMR Investigation of the Quasi-Brine Layer in Ice/Brine Mixtures, J. Phys. Chem. B, 2002, 106(43), 11226–11232, DOI:10.1021/jp020449
.
- V. Parker, Thermal properties of aqueous uni-univalent electrolytes, National Institute of Standards and Technology, Gaithersburg, MD, [online] 1965, https://doi.org/10.6028/NBS.NSRDS.2 Search PubMed.
- A. Gutberlet, G. Schwaab, Ö. Birer, M. Masia, A. Kaczmarek, H. Forbert, M. Havenith and D. Marx, Aggregation-Induced Dissociation of HCl(H2O)4 below 1 K: The Smallest Droplet of Acid, Science, 2009, 324(5934), 1545–1548, DOI:10.1126/SCIENCE.1171753
.
- M. Bühl, P. Dabell, D. W. Manley, R. P. McCaughan and J. C. Walton, Bicarbonate and Alkyl Carbonate Radicals: Structural Integrity and Reactions with Lipid Components, J. Am. Chem. Soc., 2015, 137(51), 16153–16162, DOI:10.1021/jacs.5b10693
.
- J. R. Errington and P. G. Debenedetti, Relationship between Structural Order and the Anomalies of Liquid Water, Nat., 2001, 409(6818), 318–321, DOI:10.1038/35053024
.
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, N. Odelius, H. Ogasawara, L. Å. Näslund, T. K. Hirsch, L. Ojamäe, P. Glatzel, L. G. M. Pettersson and A. Nilsson, The Structure of the First Coordination Shell in Liquid Water, Science, 2004, 304(5673), 995–999, DOI:10.1126/SCIENCE.1096205/SUPPL_FILE/WERNET.SOM.PDF
.
- P. Jafari, A. Amritkar and H. Ghasemi, Temperature Discontinuity at an Evaporating Water Interface, J. Phys. Chem. C, 2020, 124(2), 1554–1559, DOI:10.1021/ACS.JPCC.9B10838/ASSET/IMAGES/MEDIUM/JP9B10838_0005.GIF
.
- A. Vittadini, A. Selloni, F. P. Rotzinger and M. Grätzel, Structure and Energetics of Water Adsorbed at TiO2 Anatase101 and 001 Surfaces, Phys. Rev. Lett., 1998, 81(14), 2954, DOI:10.1103/PhysRevLett.81.2954
.
- M. Sprik, J. Hutter and M. Parrinello, Ab Initio Molecular Dynamics Simulation of Liquid Water: Comparison of Three Gradient-corrected Density Functionals, J. Chem. Phys., 1996, 105(3), 1142–1152, DOI:10.1063/1.471957
.
- A. A. Hassanali, J. Cuny, V. Verdolino and M. Parrinello, Aqueous Solutions: State of the Art in Ab Initio Molecular Dynamics, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 2014, 2011, 372, DOI:10.1098/RSTA.2012.0482
.
- J. C. Grossman, E. Schwegler, E. W. Draeger, F. Gygi and G. Galli, Towards an Assessment of the Accuracy of Density Functional Theory for First Principles Simulations of Water, J. Chem. Phys., 2004, 120(1), 300–311, DOI:10.1063/1.1630560
.
- I. C. Lin, A. P. Seitsonen, I. Tavernelli and U. Rothlisberger, Structure and Dynamics of Liquid Water from Ab Initio Molecular Dynamics-Comparison of BLYP, PBE, and RevPBE Density Functionals with and without van der Waals Corrections, J. Chem. Theory Comput., 2012, 8(10), 3902–3910, DOI:10.1021/CT3001848/SUPPL_FILE/CT3001848_SI_001.PDF
.
- S. Yoo, X. C. Zeng and S. S. Xantheas, On the Phase Diagram of Water with Density Functional Theory Potentials: The Melting Temperature of Ice Ih with the Perdew–Burke–Ernzerhof and Becke–Lee–Yang–Parr Functionals, J. Chem. Phys., 2009, 130(22), 221102, DOI:10.1063/1.3153871/938041
.
- M. Sha, X. Ma, N. Li, F. Luo, G. Zhu and M. D. Fayer, Dynamical Properties of a Room Temperature Ionic Liquid: Using Molecular Dynamics Simulations to Implement a Dynamic Ion Cage Model, J. Chem. Phys., 2019, 151(15), 154502, DOI:10.1063/1.5126231/13889142/154502_1_ACCEPTED_MANUSCRIPT.PDF
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01667j |
| ‡ The authors have contributed equally to the manuscript. |
| This journal is © the Owner Societies 2024 |