Open Access Article
Open Access ArticleAnalysis of bonding motifs in unusual molecules I: planar hexacoordinated carbon atoms†
Daniel
Del Angel Cruz
 a,
Katherine N.
Ferreras
a,
Katherine N.
Ferreras
 a,
Taylor
Harville
a,
Taylor
Harville
 a,
George
Schoendorff
a,
George
Schoendorff
 b and
Mark S.
Gordon
b and
Mark S.
Gordon
 *a
*a
aDepartment of Chemistry and Ames National Laboratory, Iowa State University, Ames, Iowa 50011, USA. E-mail: mark@si.msg.chem.iastate.edu
bDepartment of Chemistry, University of South Dakota, Vermillion, South Dakota 57069, USA
First published on 23rd July 2024
Abstract
The bonding structures of CO3Li3+ and CS3Li3+ are studied by means of oriented quasi-atomic orbitals (QUAOs) to assess the possibility of these molecules being planar hexacoordinated carbon (phC) systems. CH3Li and CO32− are employed as reference molecules. It is found that the introduction of Li+ ions into the molecular environment of carbonate has a greater effect on the orbital structure of the O atoms than it does on the C atom. Partial charges computed from QUAO populations imply repulsion between the positively charged C and Li atoms in CO3Li3+. Upon the transition from CO3Li3+ to CS3Li3+, the analysis reveals that the substitution of O atoms by S atoms inverts the polarity of the carbon–chalcogen σ bond. This is linked to the difference in s- and p-fractions of the QUAOs of C and S, as element electronegativities do not explain the observed polarity of the CSσ bond. Partial charges indicate that the larger electron population on the C atom in CS3Li3+ makes C–Li attraction possible. Upon comparison with the C–Li bond in methyllithium, it is found that the C–Li covalent interactions in CO3Li3+ and CS3Li3+ have about 14% and 6% of the strength of the C–Li covalent interaction in CH3Li, respectively. Consequently, it is concluded that only CS3Li3+ may be considered to be a phC system.
1. Introduction
Exceptions to the conventional bonding structures of carbon that are commonly taught in introductory chemistry courses, traditionally characterized by so-called hybridization states, have been of great interest to chemists. The study of such exceptions can provide insight into the nature of the interactions that carbon may establish outside of the well-known bonding patterns observed in most organic molecules. An example of such an exception was proposed in 1970 by Hoffmann and collaborators,1 when they studied a variety of possible planar tetracoordinated carbon (ptC) structures by means of Extended Hückel2–5 (EH), Complete Neglect of Differential Overlap6–10 (CNDO), and ab initio calculations. Their work elucidated a set of strategies to stabilize such ptC geometries. Later, in 1976, Schleyer, Pople and collaborators conducted an extensive analysis of possible ptC systems.11 In their work, they reported 1,1-dilithiocyclopropane and similar three-membered ring systems that contained a C atom that displayed a preference for a ptC structure over a tetrahedral one. Multiple computational studies on ptC systems succeeded the aforementioned works.12,13The interest in unusual carbon bonding motifs has extended beyond tetracoordinate species to planar penta-14 and hexacoordinated15–25 carbon (ppC and phC, respectively) systems. In 2012, Wu and collaborators proposed D3h CO3Li3+ as a viable phC system.23 The D3h geometry was identified as the global minimum on the potential energy surface. Nonetheless, the main argument to consider this molecule as a phC system, and not just a planar carbonate dianion stabilized by three Li+ ions, was the relatively short C–Li distance (2.212 Å at the coupled cluster CCSD(T)/aug-cc-pVTZ level of theory), despite computing significantly low Wiberg Bond Indices26 (WBI) between these atoms. More recently, in 2021, Leyva-Parra and collaborators indicated that the criterion employed by Wu and collaborators to determine hexacoordination was purely geometrical and reported strongly repulsive interactions between the carbon and lithium atoms due to their partial positive charges in the molecule.15 In their work, Leyva-Parra and coauthors suggested a series of alternative molecules in which the oxygen atoms were replaced by heavier, less electronegative chalcogens. It was observed that the central C atom in such systems was covalently bonded to the chalcogens and electrostatically attracted to the alkali metal atoms.
The aim of the present study is to analyze the unusual bonding structures of unique chemical bonds in potentially hexacoordinated carbon species. In order to analyze the bonding structures of these molecules, the quasi-atomic orbital (QUAO) analysis, developed by Ruedenberg and collaborators,27–38 is employed. The bonding interactions in CH3Li are analyzed as well and used as reference for C–Li interactions.
An important aspect of the QUAO analysis is that it is based on the actual molecular wave function, and thus avoids the introduction of inherently biased information based on preconceived notions. Moreover, given the nature of the analysis, QUAOs can be conceptualized as the ab initio counterparts of the early concept of hybrid atomic bond orbitals.29 QUAOs provide a wave function-inherent perspective on the bonding that is consistent with the chemical intuition of the reader.
The details of the QUAO analysis are extensively discussed in ref. 28–31 and thus only the most relevant aspects of the theory are outlined in Section 2 of this work. In Section 3, the computational details of the reported calculations are given. In Section 4, the computed structures and the results of the QUAO analysis are reported and discussed. Finally, the main conclusions of this work are summarized in Section 5.
2. Quasi atomic orbital analysis
In this section an overview of the most relevant aspects and basic concepts of the QUAO analysis is provided. As mentioned in the Introduction, the quasi-atomic orbital analysis, available in the GAMESS electronic structure software,39–42 has been extensively discussed in ref. 28–31. The QUAO analysis reported in this work was done employing RHF wave functions. In general, QUAOs can be conceptualized as minimal basis set orbitals that have been deformed relative to the isolated atom to exhibit the bonding interactions in a molecule. QUAOs can be conceived as the ab initio analogs of the early qualitative concept of “hybrid atomic bond orbitals”.292.1 Conceptual framework
The QUAO analysis is based on the conceptual partitioning of the full molecular orbital (MO) space (for HF wave functions, the HF orbital space) into three distinct subspaces: the chemical core, the valence, and the external space, as shown in Fig. 1. The chemical core and valence spaces are the union of the chemical core and valence spaces of the individual atoms in the molecule, respectively (e.g., in minimal-basis C2, the chemical core space contains the 1s orbitals on each C atom, while the valence space contains the 2s and 2p orbitals on each C atom). The external space is the orthogonal complement to the core and valence spaces. For the study of bonding in molecules, the valence space is the primary interest.29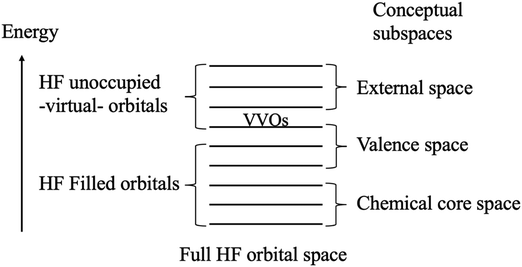 | ||
| Fig. 1 Conceptual partitioning of the full Hartree–Fock (HF) orbital space. The lowest virtual orbitals are replaced by the valence virtual orbitals (VVOs) to fully specify the valence space. | ||
Typically, the Hartree–Fock (HF) self-consistent field (SCF) procedure only yields the bonding and non-bonding combinations of the valence atomic orbitals (AOs). The antibonding combinations are often missing since the virtual (i.e., unoccupied) orbitals are generated as just an orthogonal complement to the occupied set. Thus, in general, the occupied HF space does not span the full valence space. Nonetheless, Ruedenberg and collaborators have shown that the antibonding combinations of the AOs may be extracted from the HF virtual space via a projection onto a set of orthogonal minimal basis set atomic orbitals.43–45 This extraction employs a set of accurate atomic minimal basis set (AAMBS) orbitals, discussed in Section 2.2, and the resulting (antibonding) molecular orbitals are called the valence virtual orbitals (VVOs).46 The VVOs constitute an ab initio analog of the lowest unoccupied molecular orbitals (LUMOs)47–49 and complement the HF filled orbitals to fully specify the valence space in HF SCF calculations, as shown in Fig. 1.
2.2 Accurate atomic minimal basis set
Minimal basis set (MBS) orbitals, i.e., the orbitals obtained from atomic closed- or open-shell HF SCF or multi-configuration self-consistent-field (MCSCF) calculations, are the fundamental basis for the description of the physical nature of the electronic structure of atoms. Concomitantly, MBS orbitals for atoms are the core of a qualitative understanding of chemistry, essentially accounting for the structure of the periodic table.50 Ruedenberg, Gordon and collaborators have shown in previous works27–38,43–46,50–54 the utility of MBS orbitals for the extraction of qualitative and quantitative understanding of the results of molecular electronic structure calculations. This is rooted in the notion that atom-like entities are preserved in molecular electronic wave functions, albeit distorted relative to the free atom wave functions. This notion, although intuitive to chemists, is not usually fundamental to physical theory, in which the conception of molecules is primarily based on the many-electron many-nuclei model.50,55To obtain accurate results from the extractions mentioned above, an accurate representation of the atomic MBS orbitals is important. To this end, a set of AAMBS orbitals has been developed for most atoms in the periodic table.46,56,57 These AAMBS orbitals are embedded in the GAMESS electronic structure program.39–42 The AAMBS orbitals have been chosen to be the HF SCF ground state neutral atom orbitals for the s- and p-blocks. For transition metals, for which multiple low-lying configurations may play a role in molecular interactions, the MBS orbitals of the neutral atoms are obtained from state-averaged (SA) MCSCF calculations involving the two lowest energy atomic configurations.46 In all cases, the core orbitals are included. The AAMBS orbitals are expanded using a large number of primitive Gaussian functions, effectively at the atomic basis set limit, thus providing an effectively exact representation of the (HF or SA-MCSCF) atomic MBS orbitals. For the s- and p-block elements up to Ne, even-tempered Gaussians are used.58 After Ne and up to Xe, well-tempered Gaussians59,60 are employed. A detailed discussion of the AAMBS orbitals can be found in ref. 46 and 57.
2.3 QUAO extraction and orientation
The projection of the AAMBS orbitals onto the valence space is obtained via a singular value decomposition (SVD),29,61,62 of the corresponding orbital overlap matrix. This projection produces the molecular orbitals that are most optimally aligned with the free atom AAMBS orbitals, thus capturing the physical nature of each atom within the molecule. For each atom, the number of projected orbitals is equal to the number of minimal basis valence orbitals of that atom. Once the projection of each atom has been computed independently, the complete set of projected orbitals is orthogonalized. The resulting orthogonal QUAOs represent the set of molecular orbitals that are closest to the free atom AOs.To clearly elucidate the bonding patterns in molecules, the orthogonal QUAOs are adapted to the molecular environment by allowing the QUAOs on each atom to mix with each other, thereby resulting in hybridized orbitals.50,52 In the corresponding one-electron density matrix, the diagonal elements represent orbital populations, while the off-diagonal elements represent bond orders, which are indicative of the covalent bonding interactions in the molecule. To orient the orbitals, the linear combinations of the QUAOs on each atom are taken to be those for which the off-diagonal blocks of the one-electron density matrix have as few elements with large magnitudes as possible.52 The resulting orbitals are called oriented QUAOs, as they capture the covalent interactions in the molecule. The s- and p-characters of the oriented QUAOs are obtained by directly computing their s- and p-fractions. The terms oriented QUAO and QUAO are henceforth used interchangeably.
It is worth noting that, while chemical intuition may allow one to anticipate the bonding patterns in a molecule, the orientation procedure (discussed in detail in ref. 50) makes no prior assumptions about the bonding in any given system, thus providing an unbiased, molecule-inherent picture of bonding. Such an unbiased approach may be of particular relevance in molecules in instances for which intuition/prior assumptions are not good guides.
2.4 Bond orders and kinetic bond orders
For diatomic molecules positive bond orders (BOs) can be associated with bonding interactions, and negative bond orders with antibonding interactions. However, in polyatomic molecules, the signs of the bond orders depend on the phases of the QUAOs. In addition, BOs are not energy quantities. Therefore, Ruedenberg and collaborators introduced kinetic bond orders (KBOs),28,30 which include the kinetic contribution to the interference energy as an approximate energetic measure of the strength of a covalent bonding interaction. This is rooted in the (now widely accepted)63–67 identification of the interference kinetic energy as the fundamental origin of the covalent bond.29–32,68–71 KBOs are then defined by: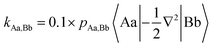 | (1) |
In eqn (1) |Aa〉 represents QUAO a on atom A, and pAa,Bb represents the bond order between QUAO b on atom B and QUAO a on atom A. The scale factor of 0.1 was introduced to compensate for the omission of a potential energy contribution, which is typically antibonding.55,71 Moreover, KBOs have been found to be negative in every situation in which covalent bonding occurs, and have been previously employed to elucidate and compare bonding interactions in various molecules and molecular clusters.27,28,33–36
2.5 Basis set independence
Previous studies by Ruedenberg and collaborators have shown that MOs extracted from electronic wave functions employing atomic minimal basis set (AAMBS) orbitals are consistently basis set independent; i.e., the resulting projections are independent of the working basis used to expand the MOs.43,44 Moreover, it has been observed that, even when large AO bases are employed, the one-electron density matrix is dominated by the terms that involve the minimal basis set orbitals on all atoms.43 Thus, despite the well-known need for extended AO basis sets for the computation of accurate wave functions (and the associated energetics), the AAMBS basis representation has been observed to contain the essential information about bonding in molecules.Given the nature of the AAMBS employed for the extraction of QUAOs, (i.e., the AAMBS AOs represent the exact, basis set-independent, optimal atomic minimal basis set orbitals),46 the overlaps with the working basis remain consistent across different types of extended basis sets, as long as the working basis provides an appropriate description of the electronic structure of the molecule at hand. Such basis set independence has also been observed in the extraction of the valence virtual orbitals29,43 (VVOs) implemented by Schmidt, Hull and Windus,46 which employs the AAMBS orbitals discussed in Section 2.2 as well. An in-depth analysis of the basis set independence of the VVOs obtained employing the AAMBS can be found in ref. 46.
3. Computational details
Previous works have shown that the 2p orbitals in Li may play an important role in the bonding interactions of Li,64,72–74 and that they can be regarded as valence orbitals. Therefore, the version of the AAMBS that includes the 2p orbitals on Li was employed for the extraction of the VVOs and QUAOs in this work.57The geometries of all molecules discussed in this work were optimized at the RHF/6-31G(d), MP2/aug-cc-pVDZ and CCSD(T)/aug-cc-pVTZ levels of theory. For conciseness, the aug-cc-pVDZ and aug-cc-pVTZ basis sets will be referred to as ACCD and ACCT, respectively, throughout this work. The geometry of CH3Li was optimized enforcing C3v symmetry, while the geometries of CO3Li3+ and CS3Li3+ were optimized enforcing D3h symmetry. The corresponding RHF and MP2 hessians were computed to establish the stationary point nature of every geometry. Localized quasi-atomic orbitals were obtained using RHF/6-31G(d) wave functions at the RHF/6-31G(d) and CCSD(T) optimized geometries. The QUAO results are essentially the same at both the RHF and CCSD(T) geometries, thus only the RHF/6-31G(d) results are reported. To compare the results obtained with RHF to those obtained with a higher level of theory, the QUAOs of CH3Li were computed using a full-valence (8,11)-CASSCF/6-311++G(d,p)//RHF/6-311++G(d,p) wave function. It was found that the results did not change significantly when the CASSCF wave function was employed. The comparison of the results obtained at both the RHF and CASSCF levels of theory can be found in Section S4 of the ESI.†
All calculations were done using the GAMESS software39–42 and QUAOs were plotted using the MacMolPlt visualization software75 with contours of 0.1 bohr−3/2 for all QUAOs, except for those centered on Li. For the QUAOs of Li, contours of 0.07 bohr−3/2 were used given their large spatial extent.
4. Hexacoordinated carbon species
4.1 Geometries
The geometries of CH3Li (C3v), CO3Li3+ (D3h) and CS3Li3+ (D3h) optimized at the RHF/6-31G(d) level of theory are shown in Fig. 2. The geometric parameters of all three molecules at the MP2/ACCD and CCSD(T)/ACCT levels of theory can be found Section S1 of the ESI.† A comparison between the RHF, MP2 and CCSD(T) geometries as well as with previously reported results can be found in Section S1 of the ESI† as well.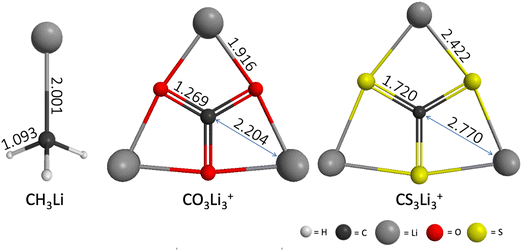 | ||
| Fig. 2 CH3Li (C3v), CO3Li3+ (D3h) and CS3Li3+ (D3h) equilibrium structures computed at the RHF/6-31G(d) level of theory. Interatomic distances shown in Angstroms. | ||
4.2 Quasi-atomic bonding analysis
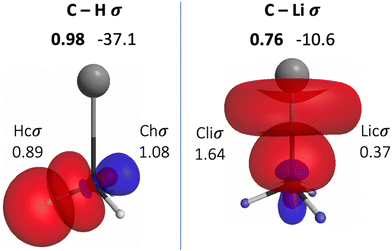
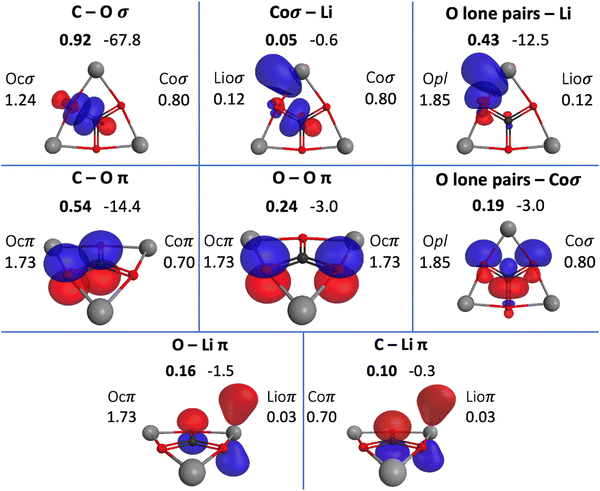
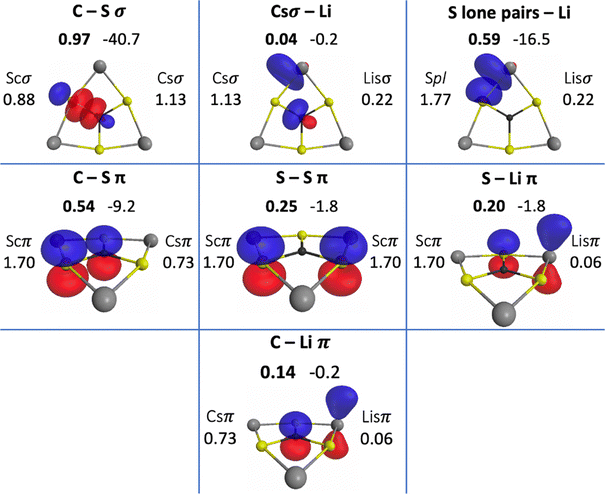
The QUAOs presented in this section are labeled according to their role in their respective molecules. The labeling works as follows: the atomic symbol of the atom on which the orbital is centered is listed first, with the first letter capitalized. If the orbital participates in a (covalent) bonding interaction, the symbol of the complementary atom is listed second in lower case. The third component of the label indicates the kind of bonding in which the orbital participates; e.g., σ or π. Orbitals with occupations close to 2, have the labels sl and pl to denote whether they are primarily an s-type or a p-type lone pair, respectively. For those orbitals with occupations below 0.2, that are not involved in bonding interactions, the label nv is employed to denote that the orbital is nearly vacant. For example, an orbital centered on carbon that participates in a C–O π bonding interaction would be labeled Coπ; an orbital centered on O with a population close to 2 and predominantly p-character would be labeled Opl.The QUAOs obtained for CH3Li are displayed in Fig. 3, those obtained for CO3Li3+ are shown in Fig. 4, and those corresponding to CS3Li3+ are depicted in Fig. 5. For CH3Li, the most relevant bonding interactions are summarized in Table 1; the orbital occupations, as well as s- and p-characters, are presented in Table 2. Partial charges on each atom in every molecule in the present study, computed from QUAO populations, are listed in Table 3. For CO3Li3+, the most relevant bonding interactions are summarized in Table 4; the orbital occupations, as well as their s- and p-characters, are given in Table 5. The results for CS3Li3+ are summarized in Tables 6 and 7, which are analogous to Tables 4 and 5. In general, only interactions with bond orders larger than 0.15 and kinetic bond orders lower than −1.0 kcal mol−1 are reported, with the exception of very weak interactions that may aid in the determination of the coordination number of a C atom.
| Bond | Orbital I | Orbital J | BO | KBO (kcal mol−1) |
|---|---|---|---|---|
| CHσ | Chσ | Hcσ | 0.98 | −37.1 |
| CLiσ | Cliσ | Licσ | 0.76 | −10.6 |
| Orbital | Occupation | Fraction s | Fraction p |
|---|---|---|---|
| Chσ | 1.08 | 0.19 | 0.81 |
| Hcσ | 0.89 | 1 | 0 |
| Cliσ | 1.64 | 0.26 | 0.74 |
| Licσ | 0.37 | 0.81 | 0.19 |
| Linv | 0.02 | 0.09 | 0.91 |
| Molecule | CH3Li | CO32−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 28 |
|||
|---|---|---|---|---|---|
| Atom | C | H | Li | C | O |
| Charge | −0.89 | +0.11 | +0.56 | +0.84 | −0.95 |
| Molecule | CO3Li3+ | CS3Li3+ | ||||
|---|---|---|---|---|---|---|
| Atom | C | O | Li | C | S | Li |
| Charge | +0.90 | −0.68 | +0.72 | −0.12 | −0.12 | +0.49 |
| Bond | Orbital I | Orbital J | CO32−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 28 |
CO3Li3+ | ||
|---|---|---|---|---|---|---|
| BO | KBO | BO | KBO | |||
| COσ | Coσ | Ocσ | 0.93 | −66.0 | 0.92 | −67.8 |
| COπ | Coπ | Ocπ | 0.56 | −16.1 | 0.54 | −14.4 |
| OOπ | Ocπ | Ocπ | 0.24 | −3.4 | 0.24 | −3.0 |
| Opl–Coσ | Opl | Coσ | 0.21 | −5.4 | 0.19 | −3.0 |
| Opl–Lioσ | Opl | Lioσ | 0.43 | −12.5 | ||
| Ocπ–Lioπ | Ocπ | Lioπ | 0.16 | −1.5 | ||
| Lioσ–Coσ | Lioσ | Coσ | 0.05 | −0.6 | ||
| Lioπ–Coπ | Lioσ | Coπ | 0.10 | −0.3 | ||
| Orbital | CO32−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 28 |
CO3Li3+ | ||||
|---|---|---|---|---|---|---|
| Occupation | Fraction s | Fraction p | Occupation | Fraction s | Fraction p | |
| Coσ | 0.81 | 0.32 | 0.68 | 0.80 | 0.29 | 0.71 |
| Coπ | 0.73 | 0.00 | 1.00 | 0.70 | 0.00 | 1.00 |
| Ocσ | 1.27 | 0.38 | 0.62 | 1.24 | 0.28 | 0.72 |
| Ocπ | 1.76 | 0.00 | 1.00 | 1.73 | 0.00 | 1.00 |
| Opl | 1.92 | 0.00 | 1.00 | 1.85 | 0.33 | 0.67 |
| Osl | 2.00 | 0.60 | 0.40 | |||
| Lioσ | 0.12 | 0.28 | 0.72 | |||
| Lioπ | 0.03 | 0.00 | 1.00 | |||
| Linv | 0.01 | 0.36 | 0.64 | |||
| Bond | Orbital I | Orbital J | BO | KBO (kcal mol−1) |
|---|---|---|---|---|
| CSσ | Csσ | Scσ | 0.97 | −40.7 |
| CSπ | Csπ | Scπ | 0.54 | −9.2 |
| Ssπ | Scπ | Scπ | 0.25 | −1.8 |
| Spl–Lisσ | Spl | Lisσ | 0.59 | −16.5 |
| Scπ–Lisπ | Scπ | Lisπ | 0.20 | −1.8 |
| Lisσ–Csσ | Lisσ | Csσ | 0.04 | −0.2 |
| Lisπ–Csπ | Lisπ | Csπ | 0.14 | −0.2 |
| Orbital | Occupation | Fraction s | Fraction p |
|---|---|---|---|
| Csσ | 1.13 | 0.30 | 0.70 |
| Csπ | 0.73 | 0.00 | 1.00 |
| Scσ | 0.88 | 0.11 | 0.89 |
| Scπ | 1.70 | 0.00 | 1.00 |
| Spl | 1.77 | 0.41 | 0.59 |
| Lisσ | 0.22 | 0.31 | 0.69 |
| Lisπ | 0.06 | 0.00 | 1.00 |
| Linv | 0.02 | 0.35 | 0.65 |
The BO of the CLiσ interaction is 0.76 and the KBO is −10.6 kcal mol−1. The occupation numbers of the Cliσ (1.64) and Licσ (0.37) orbitals imply that a transfer of charge, much larger than the one occurring from H to C, occurs from Li to C. This transfer is also consistent with the difference in the electronegativities of Li and C. Moreover, the transfer of charge from H and Li to C lead to the appearance of relatively large opposite partial charges on the Li (+0.56) and C (−0.89) atoms. The presence of these charges is consistent with previous assertions regarding the C–Li interaction in CH3Li as “80–90% ionic”.76,77 Nonetheless, previous studies have also shown that covalent character plays a non-negligible role in the C–Li bond.72,76,78 The covalent nature of the CLiσ interaction is reflected in the corresponding KBO, which suggests a non-trivial degree of covalent character in the interaction. The s- and p-characters of the Cliσ orbital are 0.26 and 0.74, respectively. The Licσ orbital has s- and p-characters of 0.81 and 0.19, respectively, reflecting a small but significant degree of s and p hybridization in Li, consistent with previous observations.64,72–74 The inclusion of the 2p orbitals in the Li AAMBS leads to three Linv orbitals, which are not involved in any bonding interactions in the molecule, and are essentially vacant (Fig. S1, ESI†). Thus, the bonding of Li in CH3Li is dominated by the 2s orbital; the mixing with the 2p functions allows the polarization of the resulting Licσ orbital.
There are three symmetrically equivalent COπ bonds, each with a KBO of −14.4 kcal mol−1 and a BO of 0.54, in which the C atom employs a single Coπ orbital to interact with the three symmetrically equivalent Ocπ orbitals in the molecule. The occupation numbers of the Coπ and Ocπ orbitals are 0.70 and 1.73, respectively, reflecting the polarization of the π-system toward the O atoms. The C–O interactions in the π-system are complemented by bonding interactions between the symmetrically equivalent Ocπ orbitals. This interaction has a BO of 0.24 and a KBO of −3.0 kcal mol−1.
There are several weak interactions in CO3Li3+ that are worth mentioning. There are, for example, two symmetrically equivalent Opl orbitals on each O atom, each with a population of 1.85. The Opl orbitals have s- and p-characters of 0.33 and 0.67, respectively. There are hyperconjugative interactions between the Opl and Coσ orbitals; as shown in Fig. 4, a single Coσ orbital is hyperconjugated with two different Opl orbitals, each located on the two O atoms that the Coσ orbital is not oriented toward. For each Opl–Coσ orbital pair, the hyperconjugative interaction has a BO of 0.19 and KBO of −3.0 kcal mol−1.
Each lithium atom has two symmetrically equivalent Lioσ orbitals that interact with the lone pairs of the two closest O atoms. Each Opl–Lioσ interaction has a BO of 0.43 and a KBO of −12.5 kcal mol−1. The Lioσ orbitals have s and p characters of 0.28 and 0.72, indicating that the mixing of the Li 2s and 2p functions is larger in CO3Li3+ than in CH3Li. Interactions among ligands have been previously suggested to contribute to the stability of planar hypercoordinated species.15,23 Covalent bonding between ligands contributes to the kinetic energy lowering that drives molecule formation; the KBOs indicate that the Opl–Lioσ interactions make non-negligible contributions to that energy lowering.71,79 The Opl–Lioσ interactions are complemented by weak π interactions between O and Li, with a BO and KBO of 0.16 and −1.5 kcal mol−1, respectively. Thus, the six Opl–Lioσ and Ocπ–Lioπ interactions have a total KBO of −84 kcal mol−1, indicating that they make a net contribution to the stabilization of the molecule even larger than that of a single COσ bond.
Wu and collaborators have suggested that CO3Li3+ may be conceptualized as simply a CO32− moiety stabilized by three Li+ ions.23 As shown in Table 4, the BOs and KBOs for the C–O and O–O interactions are similar to the values reported previously by West and collaborators for the carbonate ion.28 The similarity of the KBOs of the COσ and COπ interactions suggests that, as proposed by Wu et al., the bonds between C and O are not significantly affected by the presence of the three lithium ions in CO3Li3+ with respect to CO32−. As shown in Table 5, the main differences between CO32− and CO3Li3+ are observed in the lone pairs of the O atoms, where the introduction of the Li+ ions is observed to increase the mixing of s and p functions.
The C–Li interaction in CO3Li3+ occurs between each Coσ orbital and the two closest Lioσ orbitals (each Lioσ on a different atom), and between the Lioπ and Coπ orbitals. The BO and KBO for the Lioσ–Coσ interaction are 0.05 and −0.6 kcal mol−1, respectively, and the BO and KBO for the Lioπ–Coπ interaction are 0.10 and −0.3 kcal mol−1. The sum of these interactions gives a total C–Li KBO of −1.5 kcal mol−1. This KBO reflects a very weak C–Li covalent interaction. This total KBO of −1.5 kcal mol−1 suggests that the C–Li covalent interaction in CO3Li3+ has about 14% of the strength of the same interaction in CH3Li. So, no significant C–Li covalent bonds exist in CO3Li3+.
Table 3 shows partial positive charges on the C and Li atoms, and partial negative charges on the O atoms. These repelling positive charges on C and Li imply that C–Li ionic attraction is not likely, in agreement with what has been previously observed by Leyva-Parra and collaborators.15 The most significant interactions of each of the three Li atoms are established with the two closest O atoms, via a combination of covalent interactions and ionic attraction.
A possible justification for the slight polarization toward C is based on the orbital s- and p-fractions in C vs. S: the Csσ orbital has an s-character of 0.30 and a p-character of 0.70, while the partner Scσ orbital has an s-character of 0.11 and a p-character of 0.89. The larger s-character of the Csσ orbital with respect to the partner Scσ orbital is not surprising as the 2s and 2p orbitals have a well-known tendency to mix, especially in C. The evident lack of s- and p-orbital mixing in the Scσ orbital can be attributed to the different spatial extents of the 3s and 3p atomic orbitals, as was noted by Kutzelnigg.81,82 Based on previous QUAO analyses of CHσ, COσ and CPσ bonds,28,38 higher s-orbital characters are accompanied by higher orbital populations. For CSσ bonds, given the similarity in the electronegativities of C and S, the difference in the s- and p-characters of the Csσ and Scσ orbitals might determine the polarity of the CSσ bond. This can also be understood in terms of the early concept of orbital electronegativity,83,84 which has been observed to increase as the s-character of an orbital increases.85–87 In the present and previous QUAO analyses,28,38 this effect has been observed to be reflected in orbital populations.
The three CSπ bonds in CS3Li3+ each have a BO of 0.54 and a KBO of −9.2 kcal mol−1. The occupation numbers of the Csπ and Scπ orbitals are 0.73 and 1.70, respectively. All of the QUAOs involved in π bonding have p-characters of 1.00. So, the orbital structure of the C atom resembles sp2 hybridization. The Scπ orbitals are also observed to interact with each other, with a BO of 0.25 and a KBO of −1.8 kcal mol−1.
There are two Spl orbitals on each S atom. Each of these orbitals has an occupation of 1.77 and s- and p-characters of 0.41 and 0.59, respectively. Thus, they represent lone pairs on the S atoms with predominantly p-character and have been labeled as such in the figures and tables.
Each lithium atom employs two symmetrically equivalent Lisσ orbitals to interact with the lone pairs of the two closest S atoms. Each Spl–Lisσ interaction has a BO of 0.59 and a KBO of −16.5 kcal mol−1. The Lisσ orbitals have s- and p-characters of 0.31 and 0.69. A complementary interaction occurs between the Scπ and Lisπ orbitals, with a BO and KBO of 0.20 and −1.8 kcal mol−1, respectively. The six Spl–Lisσ and Scπ–Lisπ interactions have a total KBO of −109.8 kcal mol−1, making the stabilization effect of the covalent interactions between the S and Li atoms comparable to that of the three CSσ bonds (−122.1 kcal mol−1).
The C–Li interaction in CS3Li3+ occurs between each Csσ orbital and the two closest Lisσ orbitals (on two different Li atoms), and between the Csπ and Lisπ orbitals. The Csσ–Lisσ interaction has a BO and KBO of 0.04 and −0.2 kcal mol−1, and the Csπ–Lisπ interaction has a BO and KBO of 0.14 and −0.2 kcal mol−1. Since there are two Csσ–Lisσ and one Csπ–Lisπ interactions between the C atom and each Li atom, there is a total KBO of −0.6 kcal mol−1 for each C–Li interaction. This total KBO suggests that the covalent C–Li interaction in CS3Li3+ has about 6% of the of the strength of the same interaction in CH3Li. Consequently, it is concluded that no significant C–Li covalent bond exists in CS3Li3+.
The computed charges, displayed in Table 3, show that there are small negative charges on the S and C atoms, and a positive charge on the Li atoms. The opposite charges on the C and Li atoms suggest the possibility of ionic attraction between them, consistent with what has been suggested by Leyva-Parra and collaborators.15 The relative charges also imply an ionic attraction between the S and Li atoms.
The occupation numbers of the orbitals involved in the CSσ and COσ interactions show that the substitution of O by S has the effect of inverting the polarity of the carbon–chalcogen sigma bond. The effect of this polarity inversion of the carbon–chalcogen sigma bond is an increase in the negative charge on the C atom. Each CSσ bond increases the electron population on the C atom by about 0.33, relative to CO3Li3+. Consequently, the three CSσ bonds lead to the presence of 0.99 more electrons on the C atom in CS3Li3+ than in CO3Li3+. This extra electron on C is consistent with the ionic attraction between the C and Li atoms in CS3Li3+ that was previously noted by Leyva-Parra and coauthors.15 There is little change in the orbitals involved in π bonding upon transition from CO3Li3+ to CS3Li3+. The C atom has a similar orbital structure in both CO3Li3+ and CS3Li3+, closely resembling sp2 hybridization.
Upon substitution of O by S, the partial charges on the chalcogen atoms become less negative, while the partial charge on the Li atom becomes only slightly less positive. Thus, the ionic attraction between the chalcogens and the Li atoms is expected to be weaker in CS3Li3+ than in CO3Li3+. Moreover, the substitution of O by S decreases the strength of the covalent C–Li interaction from 14% to 6% relative to the C–Li interaction in CH3Li. Therefore, no chemically meaningful covalent C–Li bonds exist in either CO3Li3+ or CS3Li3+. Nonetheless, covalent bonds alone do not determine the coordination number of a given atom. The IUPAC definition for coordination number reads: “the coordination number of a specified atom in a chemical species is the number of other atoms directly linked to that specified atom”.88 While the definition of “linked” can be subject to interpretation, it is reasonable to conclude that it refers to an interaction capable of holding two atoms together. Consequently, the C atom in a given molecule should establish non-negligible interactions with six other atoms to be considered to be hexacoordinated. The present study shows that in the molecules discussed here, this may only occur (marginally) in CS3Li3+, where C–Li ionic attraction is plausible. On the other hand, the lack of C–Li covalent or ionic attractive interactions indicates that CO3Li3+ cannot be considered to be a phC species.
Note that geometry alone is not always a good indicator of the bonding in a molecule. There is a variety of instances in which short interatomic distances do not correlate with favored bonding interactions. One example is the weakened C–C bonds in strained molecules, despite their frequently shorter C–C interatomic distances, relative to their unstrained counterparts.89–91 Despite the useful notions that geometries provide about the interactions that may occur in a molecule, it is evident that electronic structure theory tools, such as the QUAO analysis employed in the present work, enable a more rigorous study of the actual bonding structures in molecules. The importance of such tools is particularly highlighted for unusual molecules.
5. Conclusions
The bonding structures of CO3Li3+ and CS3Li3+ have been analyzed in terms of Quasi Atomic Orbitals. The bonding in CH3Li has been analyzed and used as a reference along with previously reported QUAO results for the carbonate ion. The analysis shows that the bonding interactions between C and O in CO3Li3+ closely resemble those in carbonate. The most notable difference between carbonate and the CO32− moiety in CO3Li3+ is observed to occur in the orbital structure of the lone pairs of the O atoms. These lone pair orbitals have increased s- and p-mixing in CO3Li3+, due to the inclusion of Li+ ions into the molecular environment of CO32−. The main bonding interactions of the Li atoms in CO3Li3+ are with the O atoms, indicating covalent bonding between the “ligands” of the central carbon atom that contributes to the stabilization of the molecule. It is concluded that the introduction of Li+ ions into the molecular environment of CO32− has a greater effect on the O atoms than on the C atom, and that this introduction has little effect on the COσ and COπ bonds.Partial charges computed from QUAO populations indicate that ionic attraction between the C and Li atoms in CO3Li3+ is not plausible, as both the C and Li atoms have positive partial charges.
The QUAO analysis shows that the substitution of the O atoms by S atoms slightly inverts the polarity of the carbon–chalcogen σ bond in the molecule, with respect to CO3Li3+. Similar to CO3Li3+, the main bonding interaction of the Li atoms in CS3Li3+ are established with the S atoms.
The computed partial charges suggest that the ionic attraction between the Li and S atoms in CS3Li3+ is weaker than that between the Li and O atoms in CO3Li3+. The partial charges also indicate the possibility of ionic attraction between the C and Li atoms in CS3Li3+, unlike in CO3Li3+.
There are extremely weak C–Li covalent interactions in both CO3Li3+ and CS3Li3+ that are estimated to have about 14% and 6% of the strength of the C–Li covalent interaction in CH3Li, respectively. It is thus concluded that no chemically meaningful C–Li covalent bonds exist in either CO3Li3+ or CS3Li3+.
It is concluded that because of the possibility of C–Li ionic attraction in CS3Li3+, it can indeed be considered as a planar hexacoordinated carbon species, while CO3Li3+ cannot. This leads to the further conclusion that despite the useful notions provided by molecular geometries, electronic structure theory tools, such as the QUAO analysis employed in this work, are better suited for the study of the bonding in unusual molecules.
The insights presented in this work serve to emphasize the power of the quasi-atomic orbital analysis for providing understanding of the widely varying nature of the chemical bond. This is especially satisfying since these insights are drawn entirely from the wave function, with no implicit or explicit bias.
Data availability
All relevant data is available in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a grant from the Air Force Office of Scientific Research (MSG, KNF), AFOSR FA9550-18-1-0321, and a grant from the Department of Energy Computational Chemical Sciences (CCS) effort (DDAC, TH) from the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biological Sciences, to the Ames National Laboratory. G. S. was supported by a U.S. Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Gas Phase Chemical Physics Program (AL-20-380-066) to the Ames National Laboratory. Ames National Laboratory is operated by Iowa State University under contract no. DE-AC02-07CH11338. The authors are also grateful to Professor Klaus Ruedenberg for providing insights into the QUAO analysis.References
- R. Hoffmann, R. W. Alder and C. F. Wilcox, Planar tetracoordinate carbon, J. Am. Chem. Soc., 1970, 92, 4992–4993 CrossRef CAS.
- R. Hoffmann, Extended Hückel Theory. II. σ Orbitals in the Azines, J. Chem. Phys., 1964, 40, 2745 CrossRef CAS.
- R. Hoffmann, An Extended Hückel Theory. I. Hydrocarbons, J. Chem. Phys., 1963, 39, 1397–1412 CrossRef CAS.
- R. Hoffmann, Extended Hückel Theory. III. Compounds of Boron and Nitrogen, J. Chem. Phys., 1964, 40, 2474–2480 CrossRef CAS.
- R. Hoffmann, Extended hückel theory—v, Tetrahedron, 1966, 22, 521–538 CrossRef CAS.
- J. A. Pople, D. L. Beveridge and P. A. Dobosh, Approximate Self-Consistent Molecular–Orbital Theory. V. Intermediate Neglect of Differential Overlap, J. Chem. Phys., 1967, 47, 2026–2033 CrossRef CAS.
- J. A. Pople, D. P. Santry and G. A. Segal, Approximate Self-Consistent Molecular Orbital Theory. I. Invariant Procedures, J. Chem. Phys., 1965, 43, S129–S135 CrossRef CAS.
- J. A. Pople and G. A. Segal, Approximate Self-Consistent Molecular Orbital Theory. II. Calculations with Complete Neglect of Differential Overlap, J. Chem. Phys., 1965, 43, S136–S151 CrossRef CAS.
- J. A. Pople and G. A. Segal, Approximate Self-Consistent Molecular Orbital Theory. III. CNDO Results for AB2 and AB3 Systems, J. Chem. Phys., 1966, 44, 3289–3296 CrossRef CAS.
- D. P. Santry and G. A. Segal, Approximate Self-Consistent Molecular Orbital Theory. IV. Calculations on Molecules Including the Elements Sodium through Chlorine, J. Chem. Phys., 1967, 47, 158–174 CrossRef CAS.
- J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v R. Schleyer, R. Seeger and J. A. Pople, Stabilization of planar tetracoordinate carbon, J. Am. Chem. Soc., 1976, 98, 5419–5427 CrossRef CAS.
- R. Keese, Carbon Flatland: Planar Tetracoordinate Carbon and Fenestranes, Chem. Rev., 2006, 106, 4787–4808 CrossRef CAS PubMed.
- G. Merino, M. A. Méndez-Rojas, A. Vela and T. Heine, Recent advances in planar tetracoordinate carbon chemistry, J. Comput. Chem., 2007, 28, 362–372 CrossRef CAS PubMed.
- V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Planar pentacoordinate carbons, Nat. Rev. Chem., 2018, 2, 0114 CrossRef CAS.
- L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Planar Hexacoordinate Carbons: Half Covalent, Half Ionic, Angew. Chem., Int. Ed., 2021, 60, 8700–8704 CrossRef CAS PubMed.
- K. Exner and P. von R. Schleyer, Planar Hexacoordinate Carbon: A Viable Possibility, Science, 2000, 290, 1937–1940 CrossRef CAS PubMed.
- K. Ito, Z. Chen, C. Corminboeuf, C. S. Wannere, X. H. Zhang, Q. S. Li and P. v. R. Schleyer, Myriad Planar Hexacoordinate Carbon Molecules Inviting Synthesis, J. Am. Chem. Soc., 2007,(129), 1510–1511 CrossRef CAS PubMed.
- Y. Pei and X. C. Zeng, Probing the Planar Tetra-, Penta-, and Hexacoordinate Carbon in Carbon−Boron Mixed Clusters, J. Am. Chem. Soc., 2008, 130, 2580–2592 CrossRef CAS PubMed.
- R. W. A. Havenith, P. W. Fowler and E. Steiner, Ring Currents in a Proposed System Containing Planar Hexacoordinate Carbon, CB62−, Chem. – Eur. J., 2002, 8, 1068–1073 CrossRef CAS PubMed.
- C.-F. Zhang, S.-J. Han, Y.-B. Wu, H.-G. Lu and G. Lu, Thermodynamic Stability versus Kinetic Stability: Is the Planar Hexacoordinate Carbon Species D3h CN3Mg3+ Viable?, J. Phys. Chem. A, 2014, 118, 3319–3325 CrossRef CAS PubMed.
- Y. Wang, Y. Li and Z. Chen, Planar Hypercoordinate Motifs in Two-Dimensional Materials, Acc. Chem. Res., 2020, 53, 887–895 CrossRef CAS PubMed.
- S.-D. Li, C.-Q. Miao and J.-C. Guo, Tetradecker Transition Metal Complexes Containing Double Planar Hexacoordinate Carbons and Double Planar Heptacoordinate Borons, J. Phys. Chem. A, 2007, 111, 12069–12071 CrossRef CAS PubMed.
- Y.-B. Wu, Y. Duan, G. Lu, H.-G. Lu, P. Yang, P. von, R. Schleyer, G. Merino, R. Islas and Z.-X. Wang, D 3h CN3Be3+ and CO3Li3+: viable planar hexacoordinate carbon prototypes, Phys. Chem. Chem. Phys., 2012, 14, 14760 RSC.
- Q. Luo, X. H. Zhang, K. L. Huang, S. Q. Liu, Z. H. Yu and Q. S. Li, Theoretical Studies on Novel Main Group Metallocene-like Complexes Involving Planar Hexacoordinate Carbon η6-B6C2− Ligand, J. Phys. Chem. A, 2007, 111, 2930–2934 CrossRef CAS PubMed.
- L.-M. Yang, E. Ganz, Z. Chen, Z.-X. Wang and P. von R. Schleyer, Four Decades of the Chemistry of Planar Hypercoordinate Compounds, Angew. Chem., Int. Ed., 2015, 54, 9468–9501 CrossRef CAS PubMed.
- K. B. Wiberg, Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- G. Schoendorff, M. W. Schmidt, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bond Analyses in the Sixth Period: II. Bond Analyses of Cerium Oxides, J. Phys. Chem. A, 2019, 123, 5249–5256 CrossRef CAS PubMed.
- A. C. West, J. J. Duchimaza-Heredia, M. S. Gordon and K. Ruedenberg, Identification and Characterization of Molecular Bonding Structures by ab initio Quasi-Atomic Orbital Analyses, J. Phys. Chem. A, 2017, 121, 8884–8898 CrossRef CAS PubMed.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A comprehensive analysis of molecule-intrinsic quasi-atomic, bonding, and correlating orbitals. I. Hartree-Fock wave functions, J. Chem. Phys., 2013, 139, 234107 CrossRef PubMed.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic, Quasi-Atomic Orbitals. II. Strongly Correlated MCSCF Wave Functions, J. Phys. Chem. A, 2015, 119, 10360–10367 CrossRef CAS PubMed.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic, Quasi-Atomic Orbitals. III. The Covalent Bonding Structure of Urea, J. Phys. Chem. A, 2015, 119, 10368–10375 CrossRef CAS PubMed.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic Quasi-Atomic Orbitals. IV. Bond Breaking and Bond Forming along the Dissociative Reaction Path of Dioxetane, J. Phys. Chem. A, 2015, 119, 10376–10389 CrossRef CAS PubMed.
- J. J. Duchimaza Heredia, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bonding Analysis of Xe-Containing Compounds, J. Phys. Chem. A, 2018, 122, 3442–3454 CrossRef CAS PubMed.
- J. J. Duchimaza Heredia, A. D. Sadow and M. S. Gordon, A Quasi-Atomic Analysis of Three-Center Two-Electron Zr–H–Si Interactions, J. Phys. Chem. A, 2018, 122, 9653–9669 CrossRef CAS PubMed.
- E. B. Guidez, M. S. Gordon and K. Ruedenberg, Why is Si2H2 Not Linear? An Intrinsic Quasi-Atomic Bonding Analysis, J. Am. Chem. Soc., 2020, 142, 13729–13742 CrossRef CAS PubMed.
- J. L. Galvez Vallejo, J. D. Heredia and M. S. Gordon, Bonding analysis of water clusters using quasi-atomic orbitals, Phys. Chem. Chem. Phys., 2021, 23, 18734–18743 RSC.
- T. Harville and M. S. Gordon, Intramolecular hydrogen bonding analysis, J. Chem. Phys., 2022, 156, 174302 CrossRef CAS PubMed.
- D. Del Angel Cruz, J. L. Galvez Vallejo and M. S. Gordon, Analysis of the bonding in tetrahedrane and phosphorus-substituted tetrahedranes, Phys. Chem. Chem. Phys., 2023, 25, 27276–27292 RSC.
- F. Zahariev, P. Xu, B. M. Westheimer, S. Webb, J. Galvez Vallejo, A. Tiwari, V. Sundriyal, M. Sosonkina, J. Shen, G. Schoendorff, M. Schlinsog, T. Sattasathuchana, K. Ruedenberg, L. B. Roskop, A. P. Rendell, D. Poole, P. Piecuch, B. Q. Pham, V. Mironov, J. Mato, S. Leonard, S. S. Leang, J. Ivanic, J. Hayes, T. Harville, K. Gururangan, E. Guidez, I. S. Gerasimov, C. Friedl, K. N. Ferreras, G. Elliott, D. Datta, D. D. A. Cruz, L. Carrington, C. Bertoni, G. M. J. Barca, M. Alkan and M. S. Gordon, The General Atomic and Molecular Electronic Structure System (GAMESS): Novel Methods on Novel Architectures, J. Chem. Theory Comput., 2023, 19, 7031–7055 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- M. S. Gordon and M. W. Schmidt, Theory and Applications of Computational Chemistry, Elsevier, 2005, pp. 1167–1189 Search PubMed.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, Recent developments in the general atomic and molecular electronic structure system, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- W. C. Lu, C. Z. Wang, M. W. Schmidt, L. Bytautas, K. M. Ho and K. Ruedenberg, Molecule intrinsic minimal basis sets. I. Exact resolution of ab initio optimized molecular orbitals in terms of deformed atomic minimal-basis orbitals, J. Chem. Phys., 2004, 120, 2629–2637 CrossRef CAS PubMed.
- W. C. Lu, C. Z. Wang, M. W. Schmidt, L. Bytautas, K. M. Ho and K. Ruedenberg, Molecule intrinsic minimal basis sets. II. Bonding analyses for Si4H6 and Si2 to Si10, J. Chem. Phys., 2004, 120, 2638–2651 CrossRef CAS PubMed.
- W. C. Lu, C. Z. Wang, T. L. Chan, K. Ruedenberg and K. M. Ho, Representation of electronic structures in crystals in terms of highly localized quasiatomic minimal basis orbitals, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 041101 CrossRef.
- M. W. Schmidt, E. A. Hull and T. L. Windus, Valence Virtual Orbitals: An Unambiguous ab Initio Quantification of the LUMO Concept, J. Phys. Chem. A, 2015, 119, 10408–10427 CrossRef CAS PubMed.
- K. Fukui, T. Yonezawa and H. Shingu, A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons, J. Chem. Phys., 1952, 20, 722–725 CrossRef CAS.
- K. Fukui and H. Fujimoto, An MO-theoretical Interpretation of the Nature of Chemical Reactions. I. Partitioning Analysis of the Interaction Energy, Bull. Chem. Soc. Jpn., 1968, 41, 1989–1997 CrossRef CAS.
- K. Fukui and H. Fujimoto, An MO-theoretical Interpretation of the Nature of Chemical Reactions. II. The Governing Principles, Bull. Chem. Soc. Jpn., 1969, 42, 3399–3409 CrossRef CAS.
- J. Ivanic, G. J. Atchity and K. Ruedenberg, Intrinsic local constituents of molecular electronic wave functions. I. Exact representation of the density matrix in terms of chemically deformed and oriented atomic minimal basis set orbitals, Theor. Chem. Acc., 2008, 120, 281–294 Search PubMed.
- E. B. Guidez, Quasi-atomic orbital analysis of halogen bonding interactions, J. Chem. Phys., 2023, 159, 194307 CrossRef CAS PubMed.
- J. Ivanic and K. Ruedenberg, Intrinsic local constituents of molecular electronic wave functions. II. Electronic structure analyses in terms of intrinsic oriented quasi-atomic molecular orbitals for the molecules FOOH, H2BH2BH2, H2CO and the isomerization HNO → NOH, Theor. Chem. Acc., 2008, 120, 295–305 Search PubMed.
- G. Schoendorff, K. Ruedenberg and M. S. Gordon, Multiple Bonding in Rhodium Monoboride. Quasi-atomic Analyses of the Ground and Low-Lying Excited States, J. Phys. Chem. A, 2021, 125, 4836–4846 CrossRef CAS PubMed.
- S. Kim, J. A. Conrad, G. M. Tow, E. J. Maginn, J. A. Boatz and M. S. Gordon, Intermolecular interactions in clusters of ethylammonium nitrate and 1-amino-1,2,3-triazole, Phys. Chem. Chem. Phys., 2023, 25, 30428–30457 RSC.
- K. Ruedenberg, Atoms and interatomic bonding synergism inherent in molecular electronic wave functions, J. Chem. Phys., 2022, 157, 024111 CrossRef CAS PubMed.
- G. Schoendorff, A. C. West, M. W. Schmidt, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bond Analyses in the Sixth Period: I. Relativistic Accurate Atomic Minimal Basis Sets for the Elements Cesium to Radon, J. Phys. Chem. A, 2019, 123, 5242–5248 CrossRef CAS PubMed.
- G. Schoendorff, A. C. West, M. W. Schmidt, K. Ruedenberg, A. K. Wilson and M. S. Gordon, Relativistic ab Initio Accurate Atomic Minimal Basis Sets: Quantitative LUMOs and Oriented Quasi-Atomic Orbitals for the Elements Li–Xe, J. Phys. Chem. A, 2017, 121, 3588–3597 CrossRef CAS PubMed.
- M. W. Schmidt and K. Ruedenberg, Effective convergence to complete orbital bases and to the atomic Hartree–Fock limit through systematic sequences of Gaussian primitives, J. Chem. Phys., 1979, 71, 3951–3962 CrossRef CAS.
- S. Huzinaga and B. Miguel, A comparison of the geometrical sequence formula and the well-tempered formulas for generating GTO basis orbital exponents, Chem. Phys. Lett., 1990, 175, 289–291 CrossRef CAS.
- S. Huzinaga and M. Klobukowski, Well-tempered Gaussian basis sets for the calculation of matrix Hartree–Fock wavefunctions, Chem. Phys. Lett., 1993, 212, 260–264 CrossRef CAS.
- G. W. Stewart, On the Early History of the Singular Value Decomposition, SIAM Rev., 1993, 35, 551–566 CrossRef.
- H. F. King, R. E. Stanton, H. Kim, R. E. Wyatt and R. G. Parr, Corresponding Orbitals and the Nonorthogonality Problem in Molecular Quantum Mechanics, J. Chem. Phys., 1967, 47, 1936–1941 CrossRef CAS.
- W. Kutzelnigg and W. H. E. Schwarz, Formation of the chemical bond and orbital contraction, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2361–2367 CrossRef CAS.
- G. B. Bacskay, Orbital contraction and covalent bonding, J. Chem. Phys., 2022, 156, 204122 CrossRef CAS PubMed.
- G. Frenking, Heretical thoughts about the present understanding and description of the chemical bond, Mol. Phys., 2023, 121, e2110168 CrossRef.
- L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chemical Bonding and Bonding Models of Main-Group Compounds, Chem. Rev., 2019, 119, 8781–8845 CrossRef CAS PubMed.
- W. Kutzelnigg, The Physical Mechanism of the Chemical Bond, Angew. Chem., Int. Ed. Engl., 1973, 12, 546–562 CrossRef.
- K. Ruedenberg, Atoms and bonds in molecules as synergisms of interactions between electrons and nuclei, J. Chem. Phys., 2022, 157, 210901 CrossRef CAS PubMed.
- G. B. Bacskay, S. Nordholm and K. Ruedenberg, The Virial Theorem and Covalent Bonding, J. Phys. Chem. A, 2018, 122, 7880–7893 CrossRef CAS PubMed.
- K. Ruedenberg, The Physical Nature of the Chemical Bond, Rev. Mod. Phys., 1962, 34, 326–376 CrossRef CAS.
- M. W. Schmidt, J. Ivanic and K. Ruedenberg, Covalent bonds are created by the drive of electron waves to lower their kinetic energy through expansion, J. Chem. Phys., 2014, 140, 204104 CrossRef PubMed.
- F. M. Bickelhaupt, N. J. R. Van Eikema Hommes, C. Fonseca Guerra and E. J. Baerends, The Carbon−Lithium Electron Pair Bond in (CH3Li)n (n = 1, 2, 4), Organometallics, 1996, 15, 2923–2931 CrossRef CAS.
- S. Ishikawa, G. Madjarova and T. Yamabe, First-Principles Study of the Lithium Interaction with Polycyclic Aromatic Hydrocarbons, J. Phys. Chem. B, 2001, 105, 11986–11993 CrossRef CAS.
- H. Ago, M. Kato, K. Yahara, K. Yoshizawa, K. Tanaka and T. Yamabe, Ab Initio Study on Interaction and Stability of Lithium-Doped Amorphous Carbons, J. Electrochem. Soc., 1999, 146, 1262–1269 CrossRef CAS.
- B. M. Bode and M. S. Gordon, Macmolplt: a graphical user interface for GAMESS, J. Mol. Graphics Modell., 1998, 16, 133–138 CrossRef CAS PubMed.
- F. M. Bickelhaupt, M. Solà and C. Fonseca Guerra, Covalency in Highly Polar Bonds. Structure and Bonding of Methylalkalimetal Oligomers (CH3M)n (M = Li–Rb; n = 1, 4), J. Chem. Theory Comput., 2006, 2, 965–980 CrossRef CAS PubMed.
- A. Streitwieser, J. E. Williams, S. Alexandratos and J. M. McKelvey, Ab initio SCF-MO calculations of methyllithium and related systems. Absence of covalent character in the carbon–lithium bonds, J. Am. Chem. Soc., 1976, 98, 4778–4784 CrossRef CAS.
- G. D. Graham, D. S. Marynick and W. N. Lipscomb, Effects of basis set and configuration interaction on the electronic structure of methyllithium, with comments on the nature of the carbon–lithium bond, J. Am. Chem. Soc., 1980, 102, 4572–4578 CrossRef CAS.
- M. W. Schmidt, J. Ivanic and K. Ruedenberg, in The Chemical Bond, ed. G. Frenking and S. Shaik, Wiley, 1st edn, 2014, pp. 1–68 Search PubMed.
- W. Gordy and W. J. O. Thomas, Electronegativities of the Elements, J. Chem. Phys., 1956, 24, 439–444 CrossRef CAS.
- W. Kutzelnigg, Chemical Bonding in Higher Main Group Elements, Angew. Chem., Int. Ed. Engl., 1984, 23, 272–295 CrossRef.
- W. Kutzelnigg, Orthogonal and non-orthogonal hybrids, J. Mol. Struct., 1988, 169, 403–419 CrossRef.
- J. Hinze and H. H. Jaffe, Electronegativity. I. Orbital Electronegativity of Neutral Atoms, J. Am. Chem. Soc., 1962, 84, 540–546 CrossRef CAS.
- H. O. Pritchard and H. A. Skinner, The Concept Of Electronegativity, Chem. Rev., 1955, 55, 745–786 CrossRef CAS.
- J. Gasteiger and M. Marsili, Iterative partial equalization of orbital electronegativity—a rapid access to atomic charges, Tetrahedron, 1980, 36, 3219–3228 CrossRef CAS.
- A. D. Walsh, The properties of bonds involving carbon, Discuss. Faraday Soc., 1947, 2, 18 RSC.
- H. A. Bent, An Appraisal of Valence-bond Structures and Hybridization in Compounds of the First-row elements, Chem. Rev., 1961, 61, 275–311 CrossRef CAS.
- P. Muller, Glossary of terms used in physical organic chemistry (IUPAC Recommendations 1994), Pure Appl. Chem., 1994, 66, 1077–1184 CrossRef.
- C. A. Coulson and W. E. Moffitt, I. The properties of certain strained hydrocarbons, London Edinburgh Philos. Mag. J. Sci., 1949, 40, 1–35 CrossRef CAS.
- R. F. W. Bader, T. H. Tang, Y. Tal and F. W. Biegler-Koenig, Properties of atoms and bonds in hydrocarbon molecules, J. Am. Chem. Soc., 1982, 104, 946–952 CrossRef CAS.
- J. A. Boatz and M. S. Gordon, Theoretical studies of three-membered ring compounds Y2H4X (Y = C, Si; X = CH2, NH, O, SiH2, PH, S), J. Phys. Chem., 1989, 93, 3025–3029 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01800a |
| This journal is © the Owner Societies 2024 |