Open Access Article
Open Access ArticleDried hybrid imogolite nanotubes as solids with a changeable surface area: an insight into textural properties based on the correlation between nitrogen gas adsorption, immersion calorimetry into water, and small angle X-ray scattering†
Ali
Dhaini
 a,
Amine
Geneste
a,
Amine
Geneste
 a,
Fadwa
Alfadel Raad
a,
Fadwa
Alfadel Raad
 b,
Pierre
Picot
b,
Gaelle
Martin-Gassin
b,
Pierre
Picot
b,
Gaelle
Martin-Gassin
 a,
Benedicte
Prelot
a,
Benedicte
Prelot
 a,
Pierre-Marie
Gassin
a,
Pierre-Marie
Gassin
 a,
Philippe
Trens
a,
Philippe
Trens
 a,
Antoine
Thill
a,
Antoine
Thill
 *b and
Jerzy
Zajac
*b and
Jerzy
Zajac
 *a
*a
aICGM, UMR 5253, Univ. Montpellier, CNRS, ENSCM, Montpellier, France. E-mail: jerzy.zajac@umontpellier.fr
bUniversité Paris-Saclay, CEA, CNRS, NIMBE, LIONS, 91191 Gif Sur Yvette, France. E-mail: antoine.thill@cea.fr
First published on 4th September 2024
Abstract
Powdered samples of three imogolite materials with an inner surface covered with Si–CH3 groups (hybrid IMO-CH3) were prepared by ambient drying at 323 K, freeze drying, and spray drying. Reliable estimates of the intra-tube (SA), inter-tube (SB), and inter-bundle (SC) specific surface areas of these samples were inferred from a model-guided correlation between the results of measurements by small angle X-ray scattering (SAXS), nitrogen gas adsorption, and immersion calorimetry into water. Since the SAXS studies indicated no significant deformations of IMO-CH3 nanotubes upon drying, further studies by gaseous N2 adsorption at 77 K indicated the intra-tube and inter-bundle specific surface areas as being only accessible to this adsorbate. The outer curved surfaces of IMO nanotubes, including the inter-tube surface areas, were evaluated based on the calorimetric measurements of the enthalpy of immersion into water, using the enthalpy of immersion per unit surface area for a modelled curved surface of gibbsite as the conversion factor. Given the uncertainty in the determination of surface areas, the IMO-CH3 samples were found to possess the limiting values of specific surface areas ranging between 1150 and 1480 m2 g−1. In contrast to the two other materials, ambient-dried IMO-CH3 was characterized by the highest value of SC parameter due to the much smaller bundles formed by the constituent imogolite nanotubes. The accessibility of these surface areas, together with the hydrophobic and hydrophilic surface domains, was demonstrated to depend on the nature of the surrounding medium and the size of the adsorbing species.
1. Introduction
Investigating the textural and surface properties of multifunctional porous materials can be highlighted as a key stage before employing them in industrial applications such as catalysis, liquid effluent treatment, or gas separation. The classical approach focuses on the use of a variety of molecular probes to scan for particular surface properties.1–5Imogolite (IMO) is a nanotubular clay mineral that can be considered as a multifunctional porous material with interesting textural and surface properties.6,7 Each IMO nanotube is composed of a curved gibbsite-like outer surface and an inner surface that is made up of isolated silanol groups in the case of the pristine material referred to as IMO-OH.8 By changing the silicon precursors during the synthesis, it is possible to obtain a hybrid nanotube with an inner surface covered with Si–CH3 groups (a hybrid material denoted as IMO-CH3).9 The structure of imogolite was first proposed by Cradwick et al.10 Recent precise analysis of X-ray diffraction data has enabled further insight into the structure.11,12 It is convenient to use the conventional notation applied to classify carbon nanotubes to describe the imogolite structure. Indeed, Al atoms are positioned on a hexagonal lattice as C atoms in carbon nanotubes. It is thus possible to use the (n,m) coordinates on the hexagonal lattice of a rotation vector which joins the sites that will be gathered upon rolling the structure. Based on the XRD analysis, it is proposed that the synthetic IMO-OH is composed of a mixture of (13,0) and (14,0) zig-zag nanotubes. For the case of IMO-CH3, the structure is proposed to be an armchair with a (8,8) rotation vector.
IMO nanotubes are well dispersed in water and tend to assemble into intertwined bundles with a hexagonal arrangement when dried.10 In a grain composed of IMO bundles, as presented in Fig. 1, three types of pores can exist: intra-tube pores (type A), inter-tube ones (type B), and inter-bundles pores (type C).7 Pores of type A are always present in a dry sample. Type B pores are very small and poorly accessible.13 It has also been observed that nanotube deformation occurs upon drying which can further reduce the accessibility of B pores.14 The pore space of the type C pores depends on the particular drying method and could be totally avoided in perfectly arranged very large bundles. The surface of imogolite is positively charged over a wide range of pH (PZC ∼ 10), and the role of the counter-ion is particularly important in defining the morphology of the dried powder.15
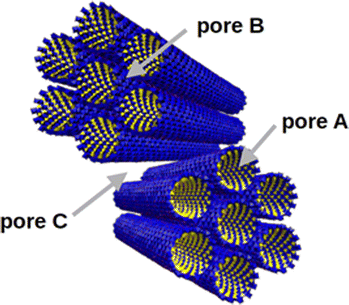 | ||
| Fig. 1 Representation of the three types of porosity present in the structure of a powder composed of IMO bundles: intra-tube (A), inter-tube (B), and inter-bundle (C). | ||
In surface-oriented applications of imogolite, the presence of IMO bundles and the peculiar structure of their porosity should be carefully taken into consideration, ideally with a complete quantitative determination of the various contributions to the total specific surface area. However, to the best of our knowledge, the surface area parameters corresponding separately to each type of porosity have not been reported yet.
As far as the textural properties are concerned, gaseous nitrogen adsorption at 77 K is by far the most widely used characterization tool.16,17 Employed in numerous studies in a routine manner, this method suffers from several shortcomings that limit the generalization of findings. Contrary to the assumption of non-specific and non-localized adsorption, N2 gaseous molecules with a quadrupole moment can undergo specific interactions with some functional surface groups.18 Furthermore, a problem of inaccessible porosity may sometimes arise in relation to the molecular diameter of this adsorbate.19 Estimating correctly the total surface area becomes complicated when nitrogen molecules, due to their geometrical and/or physical properties at very low temperatures, are not capable of penetrating into the intra-granular porosity or the voids between very compactly packed particles. For example, the latter has been reported by Olson et al. for the case of synthetic chrysotile nanotubes forming very compact aggregates.20
It is worth noting that a large range of BET surface areas has been reported for various IMO samples, namely natural, pristine, hybrid, Ge-based, and Fe-doped ones. Table S1 in the ESI† presents some selected examples. In the case of potentially similar samples, the comparison between the values obtained is extremely difficult, because of the lack of precise information on a treatment procedure employed before sorption measurements. Among important physical factors, drying the sample by a specific post-synthesis method21 and the choice of degassing temperature22,23 were shown to highly affect the adsorbate uptake by the solid material. Drying procedures of IMO suspensions (i.e., the outcome of the synthesis routes) applied in the literature included freeze drying24 or ambient drying at 323 K25 or 353 K.26 The IMO samples studied were commonly characterized by N2 adsorption at 77 K, with the degassing temperature varying in a wide range. In some papers, information on the drying treatment or the degassing temperature was omitted.13,26 Some others mentioned somewhat unrealistic degassing temperatures at which the IMO structure could not be stable.7
Calorimetric studies of solid immersion and wetting by small-molecule liquids at room temperature in combination with a modified Harkins and Jura procedure provide an alternative method for determining specific surface areas of powders.27 Nevertheless, the experimental procedures are long and fastidious, and the method fails when the hydrophilic–hydrophobic character of the solid surface is in contrast with that of the immersion liquid. Otherwise, immersion of porous solids into liquids of increasing molecular sizes, as investigated by calorimetry, can be exploited to determine the specific surface area and pore-size distribution.3,28 Again, solvent-induced aggregation between particles can cause significant accessibility issues (e.g., hydrophobic particles dispersed in aqueous solutions29). Besides these conventional characterization techniques, immersion techniques with the use of water as an immersion liquid give rise to the assessment of the hydrophilic character of the solid surface.30 The knowledge of this feature is of high importance whenever a given material is to be used in aqueous media, especially in wastewater treatment.31
Small angle X-ray scattering (SAXS) is sensitive to the repartition of the electronic density in a sample. When the composition of the sample is known and distributed in two distinct phases having different electronic densities, it is possible to extract the specific surface without a priori knowledge of the geometry using general scattering theorems.32 This method is applicable to loosely packed powders and can thus be directly compared to gas adsorption techniques.33 SAXS can also be applied directly to the liquid dispersion of nanoparticles. When the shape of the nanoparticles is known, it is thus possible to determine very precisely their size using scattering models. When a powder is produced from the assembly of such nanoparticles, this technique can thus give very important insight into the shape of the building blocks before drying and eventual artefacts due to packing and/or deformation.34
In light of the above discussion, the main objective of the present work was to investigate the textural properties and the hydrophilic–hydrophobic surface character of hybrid IMO-CH3 samples in regard to the structuration of nanotubes in the form of dry powders. The as-synthesized IMO suspensions were dried by ambient drying (AD), freeze-drying (FD), and spray drying (SD) procedures. An experimental approach based on the SAXS measurements for the nanotubes in water and after drying combined with the use of two probing molecules, gaseous N2 and liquid water, was followed with a view of providing estimates of the intra-tube (SA), inter-tube (SB), and inter-bundle (SC) specific surface areas. The effect of the drying treatment on the textural parameters was quantified. All experiments were carried out with representative samples collected from the same batch obtained upon each drying process. The accessibility of various hydrophobic and hydrophilic surface areas was simultaneously discussed in relation to the nature of the surrounding medium.
2. Experimental
2.1. Materials
The reference gibbsite sample was a kind gift from the laboratory Chimie de la Matière Condensée in Paris (UMR CNRS 7574, Université P. M. Curie, Collège de France). The sample was prepared in line with the synthesis routes described and discussed elsewhere.35 Gibbsite has a layered structure, each layer consisting of octahedrally coordinated Al3+ cations sandwiched between two closed-pack layers of OH− in line with the dioctahedral occupancy pattern. The gibbsite particles are made up by the stacking of octahedral sheets of aluminum hydroxide. The particles of the sample used in the present study represent regularly shaped and fairly monodisperse hexagons with an average diameter of 120 nm and a thickness of 15 nm.2.2. Synthesis and drying of imogolite suspensions
The synthesis protocol of IMO-CH3 adopted and optimised in the present paper was initially proposed by Bottero et al.9 Around 14 g of aluminium-tri-sec-butoxide was added into a Teflon reactor containing 800 mL of an acidic HCl solution to obtain an Al-to-H+ molar ratio of 2. The mixture was left under stirring for around one hour. The Si precursor, trimethoxymethylsilane, was added drop by drop to reach a Si-to-Al molar ratio of 0.6. It is worth noting that the slight excess of Si precursor was previously shown to minimize the formation of aluminium hydroxide particles during synthesis.36 The whole mixture was stirred for a few more hours before being placed in an oven at 373 K for 5 days. The resulting product was dialyzed using 10 kDa dialysis membranes against MilliQ water for several days to reach an external conductivity below 10 μS cm−1.Drying of the IMO suspensions was carried out by following three different methods: ambient drying (AD), freeze drying (FD), and spray drying (SD). Ambient drying was carried out at 323 K and it resulted in small pieces of film. These pieces were subsequently ground into a thin powder. A temperature higher than the ambient one was chosen to accelerate the evaporation of water and thus shorten the process from several days to one night.
In the case of freeze drying (lyophilization), the suspension was first frozen in liquid nitrogen and then dehydrated under vacuum in a Cryonext freeze-drier (CRIOS −80 °C) equipped with an Adixen pump (Pascal 2005 SD). At the end of freeze drying, the solid particles were trapped in loose aggregates representing a cotton-like material. The final thin powder was obtained by gentle manual crushing. A commercial spray dryer (Buchi B-290 Mini Spray Dryer) was utilized in the spray drying procedure. The output particle size of this instrument was in the range of 2 to 25 μm. Compressed air and a two-fluid nozzle (0.7 mm) were used to disperse the liquid. The inlet air temperature was set to 433 K which resulted in an outlet temperature range of 363–383 K. The compressed air flow rate was adjusted to 40 mm (473 L h−1) using the flow meter valve. The liquid feed was introduced into the nozzle using a peristaltic pump set at a 20% pump rate, thus resulting in a liquid flow rate of 7 mL min−1. This procedure led directly to a thin powder.
Additionally, a suspension of pristine IMO-OH and a spray-dried IMO-OH material were used in the SAXS studies for comparison purposes.
The spray dried IMO-CH3 and IMO-OH samples were characterized using X-ray fluorescence spectrometry. A wavelength dispersive X-ray fluorescence (WDXRF) spectrometer (Axios Max, PANalytical, Netherlands) was used to analyse the materials' composition. The Rh-anode X-ray tube was operated at a maximum power of 4 kW with a maximum voltage of 60 kV or a maximum current of 160 mA. To obtain high resolution spectra, eight dispersive LiF200, LiF220, PE002, Ge111, PX1, PX4a, PX5, and PX7 crystals were employed. 14 scans were collected under vacuum, each covering a range of the expected elements, and the peak areas of the characteristic radiations were assessed. Gas scintillation proportional counters and gas flux detectors were used to record the intensity of the characteristic radiations. The quantitative analysis was based on the use of the PANalytical's proven SuperQ software. Both calibration curves and the crystallographic structure were used to estimate the proportion of various elements: IMO-CH3 (O: 53.68 wt%, Al: 25.74 wt%, Si: 12.59 wt%, Cl: 1.83 wt%) and IMO-OH (O: 54.51 wt%, Al: 26.25 wt%, Si: 13.39 wt%, Cl: 1.25 wt%).
2.3. Small angle X-ray scattering
Laboratory SAXS experiments were performed under vacuum using a Xeuss 2.0 apparatus (Xenocs) equipped with a Pilatus 3 R 1 M detector (Dectris). The intensity was plotted against the scattering vector q, with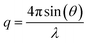 , where λ was the wavelength used (i.e., 0.1542 nm) and 2θ was the scattering angle. The sample-to-detector distance could be adjusted (the distances employed were 42.3, 53.7, and 119.4 cm) and was calibrated with tetradecanol. The detector count was normalized by the direct beam and the calibration was verified with Lupolen and water. Nanotube dispersions in water were analysed directly after dialysis and thus were never dried. They were sealed in leak free glass capillaries (diameter 1.5 mm, wall thickness 0.1 mm, WJM-Glas) or Kapton capillaries (diameter 1.506 mm, wall thickness 41.9 μm, MicroLumen). Dry powders were analysed just after the drying treatment (AD, SD, or FD) and pressed between Kapton sheets. The powder sample holder was not gastight. Therefore, the samples were analysed under a primary vacuum of 0.1 mbar. Standard procedures were applied using the open-source pySAXS software to subtract background scattering and normalize the intensities. Each sample was measured for one hour.
, where λ was the wavelength used (i.e., 0.1542 nm) and 2θ was the scattering angle. The sample-to-detector distance could be adjusted (the distances employed were 42.3, 53.7, and 119.4 cm) and was calibrated with tetradecanol. The detector count was normalized by the direct beam and the calibration was verified with Lupolen and water. Nanotube dispersions in water were analysed directly after dialysis and thus were never dried. They were sealed in leak free glass capillaries (diameter 1.5 mm, wall thickness 0.1 mm, WJM-Glas) or Kapton capillaries (diameter 1.506 mm, wall thickness 41.9 μm, MicroLumen). Dry powders were analysed just after the drying treatment (AD, SD, or FD) and pressed between Kapton sheets. The powder sample holder was not gastight. Therefore, the samples were analysed under a primary vacuum of 0.1 mbar. Standard procedures were applied using the open-source pySAXS software to subtract background scattering and normalize the intensities. Each sample was measured for one hour.
2.4. Nitrogen sorption
Nitrogen adsorption isotherms were determined at 77 K using a Micromeritics 3 flex sorption instrument.Given the thermal stability studies performed based on thermogravimetric, mass-spectrometric (TG-MS), and IR analysis (cf., Section S2 in the ESI†), vacuum treatment (10−5 mbar) of IMO-CH3 samples (around 150 mg) at 473 K carried out overnight was considered to remove practically all water molecules without compromising the structural integrity of the sample. The experimental adsorption–desorption isotherms were subsequently processed to determine the surface area and porosity parameters. The data treatment procedures are detailed in the ESI.†
The N2 adsorption experiment was also conducted at 77 K for a spray-dried IMO-CH3 sample with n-nonane molecules loaded inside its internal cavity. Nonane adsorption was carried out using a home-made adsorption apparatus which is described elsewhere.37 The IMO-CH3 sample was degassed, before measurements, in situ at a temperature of 473 K and a pressure of 10−5 mbar. The experiments were conducted at 298 K. The thermal stability during the measurements was better than 0.10 K. For reaching the appropriate accuracy, two capacitive pressure gauges of 10 Torr and 1000 Torr were used. The adsorption device was driven by the choice of the initial pressure, which was the one before the adsorbate was in contact with the adsorbent (rather than the equilibrium pressure). To avoid any condensation in the apparatus, the maximum relative pressure was chosen at 0.9. After loading the sample with nonane, it was degassed at a temperature of 353 K and a pressure of 10−5 mbar before nitrogen adsorption to remove weakly adsorbed nonane from the external surface of IMO-CH3.
2.5. Immersion calorimetry
The immersion of IMO-CH3 samples in water was carried out at 298 K using a SETARAM C-80 isothermal calorimeter equipped with thermopiles as heat flux sensors. A 30–50 mg sample was placed in a glass ampoule with a fragile tail. The samples were degassed at 473 K overnight. The temperature was raised manually in steps of 293 K every 5 min. The pressure within the glass ampoule was around 10−3 mbar. At the end of the degassing procedure, the bulb of the ampoule was sealed off by a hot flame. The glass bulb was then introduced into a special metallic cylinder containing c.a. 6 mL of ultrapure water. The cylinder was closed with a cap containing a mobile metallic rod to be further used to break the glass bulb. The whole assembly was subsequently introduced into the calorimeter. A reference cell containing 6 mL of ultrapure water was also placed in the calorimeter. After the attainment of thermal equilibrium inside the calorimeter at 303 K, the metallic rod was gently pushed down along the cylinder to break the tail of the glass bulb. A hole was formed in the glass bulb, thus allowing water to enter inside the bulb and wet the powder. The area under the thermal peak obtained in the thermogram, representing the heat flow as a function of the time, was integrated to yield the enthalpy of immersion, ΔimmH, expressed in joules per gram of the solid sample. Each measurement was repeated 2 to 3 times, and the uncertainty in the enthalpy measurement was assessed.The calibration of the calorimetric device was achieved by the Joule effect using built-in platinum resistance to induce a series of precise heat inputs.
3. Results and discussion
3.1. Preliminary considerations
It should be noted that the imogolite surfaces studied in the present paper represent those of powders composed of packed nanotubes in dry grains. It has been argued that the drying procedure can induce the formation of bundles, trapping of counter-ions from the liquid phase, and even nanotube deformation.34 The interactions of the IMO surface with a given probing molecule in the gas (nitrogen) or liquid (water) phase will thus be strongly influenced by the mutual arrangement of nanotubes within the bundles and the bundles between themselves in the grains. The aspect ratio of the particular geometric shape of IMO nanotubes is another factor to consider in this respect since the interactions will also depend on the surface curvature and the macroscopic observables will obviously contain the contributions due to both the lateral (base) surface area of IMO nanotubes, viewed as hollow cylinders, and the curved surfaces of such cylinders. To circumvent this potential difficulty in processing the results of adsorption and immersion experiments, the approach adopted in this paper is based on the use of gibbsite as a reference material having similar surface properties to guide the extraction of textural parameters of IMO powders.Furthermore, the external surface of imogolite bears a positive charge in aqueous suspensions, due to curvature effects and protonation of the surface hydroxyl groups exposed outwardly.15,38 This positive charge is compensated by chloride anions coming from HCl or AlCl3 used in the synthesis. The compensating anions ensure electro-neutrality and screen the electrostatic repulsions between the positively charged nanotubes. In diluted, dialyzed nanotube dispersions, the electrostatic interactions ensure a long-range repulsion and favour the formation of organized liquid crystals. Upon drying of the as-synthesized samples, the counter-ions are likely entrapped within the bundles.39 In contrast to perchlorate anions, Cl− ions are not IR active; they are thus not visible in the IR spectrum. However, analysis of the two spray-dried samples by wavelength dispersive X-ray fluorescence clearly confirms the presence of chloride counter-ions (cf., Section 2.2).
The presence of Cl− ions in the powder has thus to be taken into consideration when analysing the interactions of imogolite surfaces with the probing molecules in a given medium. The dielectric constant of the fluid used is expected to have a strong impact on the accessibility of various imogolite surfaces. Indeed, molecules of high dielectric constant fluids may interact with the compensating ions which consequently results in swelling of bundles and, at least partial, dispersion of IMO nanotubes.
3.2. SAXS studies on IMO nanotubes dispersed in water and dried powders
To shed some light on the possible modification of a nanotube's structure and arrangement, SAXS measurements were carried out on both pristine IMO-OH and hybrid IMO-CH3 nanotubes dispersed in water. The analysis of the pristine nanotube shape is a good starting point for further data processing and interpretation even though the knowledge of the shape of the isolated tubes is clearly not enough to assess the behaviour of the dry powder. The results of SAXS measurements made on IMO-OH and IMO-CH3 nanotubes dispersed in water, as well as the appropriate modelling approach leading to evaluating their dimensions, are discussed in Section S3 in the ESI.† On this basis, a simple geometrical calculation was done to assess the theoretical areas of inner (Sinn) and outer (Sout) surfaces and their ratio. Indeed, it can be easily demonstrated that in the case of a hollow cylindrical geometry, the inner-to-outer surface ratio was equal to the ratio between the radii of the inner and outer curved surfaces. Table 1 shows these values obtained with the radius parameters corresponding to IMO-OH and IMO-CH3 cylinders. Moreover, knowing the molecular structure of IMO-OH and IMO-CH3 nanotubes and their geometrical extension, it was also possible to give estimates of the specific surface area and volume of nanocylinders based only on geometry and composition; the following expressions were applied: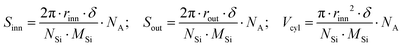 | (1) |
| Parameter | Material sample | |
|---|---|---|
| IMO-OH | IMO-CH3 | |
| Inner cylinder radius, rinn (nm) | 0.7 | 0.9 |
| Outer cylinder radius, rout (nm) | 1.25 | 1.45 |
| Period, δ (Å) | 8.65 | 4.99 |
| Number of SU per period, Nsi | 28 | 18 |
| Number of e− per SU | 100 | 100 |
| External electronic density (e− Å−3) | 0.33 | 0.33 |
| Wall electronic density (e− Å−3) | 0.96 | 0.89 |
| Internal electronic density (e− Å−3) | 0.33 | 0.05 |
| Molar mass of one SU, Msi (g mol−1) | 198 | 196 |
| S out to Sinn ratio | 1.78 | 1.61 |
| Geometrical Sinn (m2 g−1) | 413 | 482 |
| Geometrical Sout (m2 g−1) | 738 | 776 |
| Geometrical Vcyl (cm3 g−1) | 0.14 | 0.22 |
To conclude on the possible modifications of the nanotube conformation or structural deformation of nanotubes in the powdered samples, SAXS measurements were subsequently performed on various IMO-CH3 materials obtained by three different drying procedures after the synthesis stage, and the IMO-OH sample obtained by spray drying. The results are given in Fig. 2.
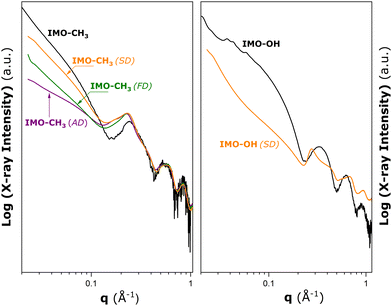 | ||
| Fig. 2 Results of SAXS measurements made on hybrid IMO-CH3 (left panel) and IMO-OH (right panel) materials obtained by different drying procedures after the synthesis stage: ambient drying at 323 K (AD), freeze drying (FD), and spray drying (SD). The black solid lines represent the SAXS patterns for IMO-OH and IMO-CH3 nanotubes dispersed in water added here for comparison purposes (cf., Fig. S3 in the ESI†). | ||
In the case of IMO-CH3, nanotubes in the aqueous phase are already assembled into small bundles containing a few tubes (cf., Section S3 in the ESI†). For the dry powders, the peaks due to the bundle formation in Fig. 2 are increased in intensity, and they are shifted toward lower q values compared to those in the liquid dispersion. This points towards the increased number of nanotubes per bundle. However, the drying procedure does not seem to have a noticeable impact on this parameter. Furthermore, the oscillations at large angles for q > 0.4 Å−1 are approximately the same as the ones measured for dispersion in water. It may be concluded that the nanotubes keep the tubular shape they have in the liquid phase and no significant deformations are observed after drying. The main differences due to various drying procedures are observed in the low angle part of the scattering pattern. This means that the long-range arrangement of the bundles is different depending on the drying method.
For IMO-OH, the curve referring to the aqueous dispersion (black line) corresponds to dispersed nanotubes (no aggregates). A clear deformation of the scattering curve can be seen when the sample is dried (orange line). A correlation peak at q = 0.275 Å−1 is visible in the present case. It is expected that IMO-OH nanotubes adopt 2D hexagonal packing. If the first peak is attributed to q01, then it is possible to estimate the expected positions of q11, q20, and q21 at 0.457, 0.528, and 0.695 Å−1, respectively. It is, however, important to realize that the assignment of the theoretical positions to qhk peaks is strictly valid only in the case of infinitely large bundles. The experimentally determined qhk positions will differ from the theoretical values due to the finite size of the bundles, as argued by Rouzière et al.14 The q11 and q21 peaks are distinguishable on the deformed scattering curve, in contrast to the q20 peak, which coincides with the minimum value of the nanotube form factor making the latter hardly visible. The width of the peaks is also in favour of relatively small or disordered 2D bundles with a hexagonal arrangement of nanotubes.
To reinforce the conclusions drawn from the results of SAXS measurements, which argued against the shape deformation of IMO-CH3 nanotubes, a further study was made on the effect of the drying procedure on the textural properties of such samples. The appropriate textural parameters were inferred progressively from the experimental study of appropriate interfacial phenomena based on the use of two different probing molecules interacting specifically with the walls of various types of pores present in these samples.
3.3. Use of nitrogen adsorption to determine the area of inner curved surfaces of IMO-CH3 nanotubes
Gaseous nitrogen has a low dielectric constant,41 therefore its molecules can interact with chloride anions only through van der Waals forces, especially when it is adsorbed at very low temperatures. No screening effects on the electrostatic interactions among the positively charged IMO nanotubes are therefore expected and the swelling of the bundles cannot be envisaged in this case. Furthermore, taking into account the size of the imogolite nanotubes, as determined by SAXS in the previous section, for non-deformed IMO-CH3 nanotubes touching one another, the diameter of the circle inscribed in the pore B openings is about 0.44 nm. Firstly, note that this size is comparable with those of anhydrous chloride anions which are trapped within pores of type B (e.g., the ionic radius of Cl−1 is 0.181 nm42 or the crystal ionic radius is 0.167 nm43). Secondly, the molecular diameter of N2 is generally estimated to be of a similar size (e.g., the hard-sphere diameter is 0.37 nm and the collision diameter is 0.67 nm,44 the kinetic diameter is 0.36 nm and the van der Waals diameter is 0.47 nm19).In light of the above arguments, the assumption accepted in the present paper is that the surface area viewed by the adsorbing nitrogen molecules does not include the contribution due to the pore walls of type B (i.e., the outer curved surface of imogolite nanotubes located inside the bundles), as the van der Waals diameter of nitrogen is higher compared to the size of the pore B openings. Another piece of information is of importance to validate this assumption. Namely, the adsorption of N2 onto the IMO-CH3 (SD) sample, loaded with n-nonane as a way to block the pores of type A (cf., Section 2.4), is hardly measurable. As n-nonane does not remain adsorbed on a hydrophilic surface (i.e., SB, SC, and Sext) after vacuum degassing treatment, the result of this experiment constitutes a firm argument for inaccessibility of the type B porosity to N2 molecules.
The adsorption of gaseous nitrogen at 77 K can be thus considered an efficient tool to measure the surface area of pore walls of type A, SA, the surface area of pore walls of type C, SC, and the external surface area of the grains, Sext.
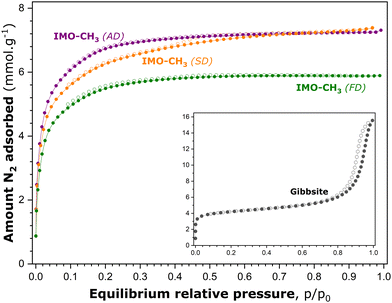
Fig. 3 shows the experimental isotherms of gaseous N2 adsorption–desorption onto various IMO-CH3 samples obtained by the different drying procedures after the synthesis stage. The adsorption–desorption curves measured with the reference gibbsite sample are also added to Fig. 3. Before adsorption measurements, this material underwent the same vacuum treatment (10−5 mbar) overnight at 473 K.
The focus of the analysis is first on the reference gibbsite sample. According to the recent IUPAC classification,17 the experimental isotherm of N2 adsorption–desorption onto this material can be considered as a combination of type Ia, represented by the initial steep portion followed by a pseudo-plateau, and type IVa, possessing an extended hysteresis loop with an onset at around 0.75 p/p0. The most plausible hypothesis to explain this complex shape is that the reference material contains both intra- and inter-particle porosity.45 The latter likely corresponds to the voids among non-rigid aggregates of plate-like particles.
Indeed, the interlayer space of gibbsite is likely responsible for the microporosity probed by the adsorption of gaseous nitrogen. Nanocrystalline gibbsite particles may undergo oriented aggregation in water, depending strongly on the ratio between the basal and edge surfaces of particles, and thus their size.46 Larger gibbsite particles are postulated to aggregate through basal-basal attachment, whereas smaller particles with a low basal-to-edge surface area ratio will preferentially attach through edge surfaces. This oriented aggregation of gibbsite particles certainly leads, after drying of the sample, to the creation of inter-particle porosity which is accessible to the adsorbing nitrogen molecules and, consequently, manifests itself by an extended hysteresis loop on the adsorption–desorption curve at high p/p0 values.
In comparison, the general shape of the adsorption–desorption isotherms obtained with the IMO-CH3 (SD) sample is rather close to type Ib, with a somewhat less-pronounced plateau and a tiny hysteresis loop located between relative pressures of 0.4 and 0.7. This shape might possibly suggest that the material contains, in addition to predominating supermicropores, a small fraction of narrow mesopores.47 The location of the hysteresis loop in the range of moderate p/p0 values excludes the presence of intergranular pores, which constitutes another argument to support the starting assumption that the B porosity is inaccessible to gaseous nitrogen molecules. IMO-CH3 samples obtained by ambient drying and freeze-drying produce reversible adsorption–desorption isotherms of type Ib. In all cases, a very short (and reversible) ascending part at relative pressures close to unity testifies to a very small external surface area.
To provide quantitative estimates of the surface area and porosity parameters on which to base further analysis, the experimental adsorption isotherms shown in Fig. 3 were subsequently processed by following appropriate standard procedures reported in the scientific literature. The data treatment and the corresponding analysis are detailed in the ESI† (Section S4). The most relevant surface area and porosity parameters are listed in Table 2. Following the hypothesis retained at the beginning of this section, the pore surfaces and volumes revealed by gaseous N2 adsorption at 77 K (Table S4 in the ESI†) correspond to the porosity of types A and C.
| Sample | d A (nm) | S A + SC (m2 g−1) | V A + VC (cm3 g−1) |
|---|---|---|---|
| IMO-CH3 (SD) | 1.9 ± 0.2 | 533 ± 8 | 0.25 ± 0.02 |
| IMO-CH3 (AD) | 1.9 ± 0.2 | 583 ± 6 | 0.25 ± 0.03 |
| IMO-CH3 (FD) | 1.9 ± 0.2 | 472 ± 6 | 0.21 ± 0.02 |
The A pores appear to be quite uniformly sized (Fig. S4 in the ESI†). The mean diameter dA is unaffected by the drying procedure and it corresponds well to twice the inner cylinder radius given in Table 1. This provides further evidence against the significant deformation of nanotubes upon drying, in line with the conclusions drawn previously from the SAXS measurements. Additionally, the surface area and pore volume parameters for IMO-CH3 (FD) are equivalent, within experimental error, to the corresponding geometrical parameters Sinn and Vcyl in Table 1. It may be argued that the long-range arrangement of the bundles is such that it produces the smallest surface area and volume contributions due to inter-bundle pores of type C. Further arguments in favour of this hypothesis in relation to the size of the bundles are set out in Section S5 of the ESI.†
The highest deviations from the geometrical model in terms of pore surface and volume are obtained in the case of IMO-CH3 (AD). Simultaneously, the low angle part of the SAXS pattern also shows the greatest difference from that of IMO-CH3 nanotubes dispersed in water (Fig. 2).
In all cases, given the uncertainty in the determination of surface area parameters, it is relevant to neglect the external surface area, i.e., both the lateral (base) surface area of IMO nanotubes as well as the outer curved surfaces of those nanotubes, which are located at the outer periphery of the bundles (see also the discussion in Sections S4 and S5 of the ESI†).
Nevertheless, full quantitative separation between the SA and SC contributions cannot be done on the basis of the results of N2 adsorption alone and this calls for another specific method of characterization.
3.4. Use of immersion calorimetry to determine the area of curved surfaces of IMO nanotubes
In the following analysis, the starting hypothesis is that the dispersing power of water due to its high dielectric constant48 induces hydration of Cl− counter-ions49 and swelling of the bundles. This swelling behaviour is classical for clay minerals containing extra-framework compensating cations in their inter-layer space, in the presence of water vapour or liquid water.50,51 As argued in the previous section (and also in Sections S4 and S5 in the ESI†), the lateral flat surface area of the hybrid imogolite nanotubes is to be neglected. Upon dispersion in water, the pores of type C should disappear to a great extent. Therefore, liquid water can be considered here as a local probe for measuring the total area of the curved surfaces. Again, gibbsite is used as a reference material to quantify the interactions of water molecules with the external surface of IMO nanotubes.In the case of the hybrid IMO-CH3 material, the results of SAXS studies with aqueous dispersions of imogolite nanotubes have already demonstrated the absence of liquid water within the internal cavity of nanotubes. Indeed, the full intrusion of liquid water into the hydrophobic nanopores would probably require high external pressures.52 The absence of liquid water inside IMO-CH3 nanotubes was also demonstrated previously based on IR studies.53 Therefore, for the present IMO-CH3 samples, the wetting by water is certainly limited only to the outer curved surfaces, Sout.
For various IMO materials studied in this paper and the reference gibbsite sample, Table 3 displays the enthalpies of immersion into water, ΔimmH, determined experimentally by immersion calorimetry.
| Sample | ΔimmH (J g−1) | S out (m2 g−1) | S A (m2 g−1) |
|---|---|---|---|
| Gibbsite | −79 ± 4 | — | — |
| IMO-CH3 (SD) | −160 ± 7 | 851 ± 56 | 529 ± 35 |
| IMO-CH3 (AD) | −153 ± 7 | 814 ± 55 | 505 ± 34 |
| IMO-CH3 (FD) | −143 ± 6 | 761 ± 50 | 472 ± 31 |
Similarity in the surface chemistry of gibbsite and outer curved surfaces of IMO-CH3 allows the enthalpy of immersion per unit surface area of gibbsite to be used as a conversion factor to provide an estimate of the Sout parameter. The hypothesis adopted in the present section is that the main difference between the two types of surfaces lies in the areal density of active groups due to the curvature of the imogolite surface.
Indeed, it was demonstrated by using molecular dynamics (MD) simulations and force spectroscopy measurements that the external curved surface of imogolite possessed a surface energy much lower than that of the planar (001) surface of gibbsite.54 The two surfaces were found to exert similar effects on the structure of adsorbed water, but the first water layer was less structured in the case of imogolite. The presence of less structured shells of adsorbed water between the imogolite particles was expected to facilitate their aggregation. In fact, the curvature of imogolite was postulated to impede the formation of in-plane hydrogen bonds between surface hydroxyl groups along the nanotube circumference.54 This likely resulted in less energetically favourable adsorption of water molecules at sub-monolayer coverages and, consequently, in an increased hydrophobicity of the imogolite-water interface in comparison with its planar counterpart.54,55 At high values of surface coverage by adsorbed water, the percentages of surface hydroxyls forming zero, one or two hydrogen bonds with water compensated each other from a quantitative point of view.54
In light of the above discussion, the difference between the surfaces of imogolite and gibbsite is handled through a geometrical correction related to the areal density of OH groups. Based on the geometrical model of gibbsite, the areal density of O is calculated to be 13.4 per nm2.56 The curvature effect will significantly reduce this density. Simple geometric arguments allow the ‘curved’ density to be estimated as the product of the ‘flat’ density and the 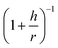 factor, where h is the half-distance between the internal and external layers of oxygen and carbon atoms, and r is the radius of curvature at the middle of the imogolite wall (both parameters taken from Table S2 in the ESI†). For IMO-CH3, one obtains as follows: h = 0.22 nm and r = 1.18 nm. The corresponding OH density is equal to 11.3 per nm2.
factor, where h is the half-distance between the internal and external layers of oxygen and carbon atoms, and r is the radius of curvature at the middle of the imogolite wall (both parameters taken from Table S2 in the ESI†). For IMO-CH3, one obtains as follows: h = 0.22 nm and r = 1.18 nm. The corresponding OH density is equal to 11.3 per nm2.
In the case of gibbsite, liquid water molecules can make contact with the total surface of the sample. In consequence, the normalized enthalpy value can be calculated by dividing the experimental ΔimmH by SBET reported in Table S3 in the ESI.† This gives an enthalpy of −223 mJ m−2. This normalized enthalpy is further considered as the enthalpy reference to quantify the one related to the outer curved surfaces of IMO nanotubes, Sout. Finally, experimental values of Sout have been calculated from the following expressions:
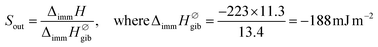 | (2) |
3.5. Validation of the present approach
The question now is to estimate the total surface area, as well as its various contributions, SA, SB, and SC, of the IMO-CH3 powders, which contain imogolite nanotubes organized in either small or large bundles adopting different long-range arrangements. Neither of the three experimental methods alone with the subsequent data processing can provide a reliable evaluation of these important parameters. This is because each method provides only limited information on the different contributions to the total surface area.Since any significant deformation of IMO-CH3 nanotubes upon drying is to be precluded in light of the SAXS experiments, the resulting geometrical parameters and the subsequent modelling of the perfectly dispersed nanotubes, i.e., Sout, Sinn, and Vcyl in Table 1, provide a framework for the calculation of reliable surface area and porosity parameters. The surface area related to the porosity of type A, SA, can be considered as being equal to the experimental parameter obtained from the immersion experiment (Table 3). The contribution due to pores of type C, SC, may be estimated by the difference between the surface areas reported in Tables 2 and 3. The surface area of B pores, SB, will be thus obtained by subtracting from the experimental Sout (Table 3) the SC values. The three types of surface areas obtained on this basis are reported in Table 4, together with the total surface areas.
| Sample | S A (m2 g−1) | S B (m2 g−1) | S C (m2 g−1) | S TOT (m2 g−1) |
|---|---|---|---|---|
| IMO-CH3 (SD) | 529 ± 35 | 840 ± 55 | Small | 1369 ± 103 |
| IMO-CH3 (AD) | 505 ± 34 | 736 ± 50 | 78 ± 10 | 1319 ± 102 |
| IMO-CH3 (FD) | 472 ± 31 | 760 ± 50 | Small | 1232 ± 81 |
It is surprising to notice the differences in the inter-tube surface area among the three samples. Given the heterogeneity, albeit not a large one, of pore sizes revealed by the N2 adsorption (cf., Fig. S4 in the ESI†), this might suggest some deviations from the expected shape or/and size of the IMO nanotubes upon drying. Nevertheless, the uncertainty of SA determination does not allow this hypothesis to be fully validated.
The most relevant differences among the samples are revealed in the inter-bundle surface area, SC. The greatest SC value is obtained in the case of IMO-CH3 (AD). Assuming perfect 2D hexagonal bundles (consistent with the simple geometrical model presented in Section S5 of the ESI†), the SC value of 78 m2 g−1 could correspond to bundles containing a few hundreds of nanotubes (e.g., about 313 nanotubes according to Fig. S8, ESI†). A more disordered long-range organization of bundles could be an alternative explanation. For IMO-CH3 (SD) and (FD), the pores of type C make rather small contributions to the total surface area and pore volume. It is possible to estimate that such a small SC value would correspond to very large bundles (e.g., more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nanotubes as can be inferred from Fig. S8, ESI†). In both cases, these numbers are large enough to be in a range where no size effects on the position of diffraction peaks are observed. This is in line with the similar q01 peaks recorded for the three samples (Fig. 2).
000 nanotubes as can be inferred from Fig. S8, ESI†). In both cases, these numbers are large enough to be in a range where no size effects on the position of diffraction peaks are observed. This is in line with the similar q01 peaks recorded for the three samples (Fig. 2).
It should be realized that the degassing conditions applied before adsorption and immersion measurements, and the degassing temperature in particular, constitute the first factor not to be over-looked with regards to the validity and the reliability of the estimation of SA, SB, and SC. The maximum temperature of 473 K was chosen based on the results of thermogravimetric and mass-spectrometric analysis (Fig. S1 in the ESI†). The corresponding IR spectra of spray dried IMO-CH3 recorded at different temperatures (Fig. S2 in the ESI†) demonstrate the effectiveness of this kind of vacuum heat treatment in removing all adsorbed water from the solid surface and pore volume, provided that it lasts sufficiently long. Additional N2 adsorption and immersion experiments were carried out at lower degassing temperatures: 383 K and 423 K. The effects of degassing treatment on the BET-specific surface area, SBET, and the enthalpy of immersion into water, ΔimmH, for the three IMO-CH3 samples are reported in Table S3, ESI.† It is clear that the results converge to the maximum values obtained for the highest degassing temperature of 473 K.
The accessibility of various surface areas is another important aspect to be considered in view of the potential uses of dried IMO-CH3 powders as solid supports or adsorbents. It follows from the discussion in previous Sections 3.3 and 3.4 that the extent to which the pores of type A and B are accessible to the probing molecules depends both on the size of these molecules and on the nature of the surrounding medium. From this point of view, IMO-CH3 powders cannot be viewed as solids possessing a constant specific surface area with invariant components consistent with the values reported in Table 4. The numbers reported in Table 4 thus represent the limiting values of surface areas.
The inner walls of the nanotubes have a hydrophobic character. Nonetheless, the accessibility of this intra-tube surface area, SA, is restricted by the uniformly sized openings (i.e., 1.9 ± 0.2) at both ends of the nanotubes.
The inter-tube and inter-bundle walls are predominantly hydrophilic. Altogether, the maximum hydrophilic surface area of the dried CH3-IMO nanotubes should be in the order of 800 m2 g−1.
The inter-tube surface area, SB, is not accessible for gaseous N2 molecules and other molecules with comparable or greater sizes. It will undergo an abrupt increase to maximal Sout (Table 3) when the nanotubes are re-dispersed through a swelling effect in a polar solvent such as water. When the dried IMO-CH3 grains are put into contact with water vapor at different equilibrium pressures, the increase in the hydrophilic surface area may be more gradual due to the stepwise opening-up of the inter-tube porosity.
Further studies of water adsorption could explore in depth the possible similarity with the evolution of the specific surface area in Li- and Na-montmorillonites resulting from the increased accessibility of the interlayer space and breaking-up of the clay particles upon the hydration process.57 The inter-bundle surface area is a priori easily accessible, although it will be reduced to zero upon immersion of grains in water or upon extended hydration of grains at high humidity levels.
4. Conclusions
Imogolite is a promising nanotubular material, which has all its constituting atoms very close (i.e., less than 1 nm) to its external and internal interfaces. However, upon drying, the constituent nanotubes inevitably form large bundles through the mechanism of neutralization of positive surface charge due to the trapping of counter-ions. In consequence, the inter-tube voids (i.e., porosity of type B) become inaccessible to gaseous N2 molecules. Therefore, the determination of surface area and porosity parameters based only on the classical (BET model) processing of adsorption–desorption isotherms leads to the underestimated values reported in the literature.The characterization approach adopted in the present work relied on the combination of three experimental methods and appropriate modelling of the resulting data. The results of SAXS measurements for the nanotubes in water and after drying provided a framework for the calculation of reliable estimates of the intra-tube (SA), inter-tube (SB), and inter-bundle (SC) specific surface areas for three hybrid IMO-CH3 samples obtained by ambient drying at 323 K (AD), freeze drying (FD), and spray drying (SD).
It was concluded from SAXS studies that nanotubes did not get deformed upon drying. They appeared to form porous samples and liquid water did not wet the hydrophobic surface of their internal walls. The subsequent SAXS-guided analysis of the adsorption–desorption isotherms for gaseous N2 at 77 K led to the conclusion that the A and C pores accessible to this adsorbate defied the ideal categorization as supermicropores or small mesopores. The αS-plot method proposed to process the adsorption curves yielded the sum of SA and SC areas. The measurements of the enthalpy of immersion in water gave access to the external curved surface area of nanotubes through the dispersion of bundles in this hydrophilic solvent. Finally, the inter-tube surface area was assessed from these results.
Given the uncertainty in the determination of surface areas, the IMO-CH3 samples were found to possess the limiting values of the specific surface areas ranging between 1150 and 1480 m2 g−1. The drying procedure mostly affected the size of the bundles. In contrast to the two other materials, ambient-dried IMO-CH3 was characterized by the highest value of the SC parameter due to the much smaller bundles formed by the constituent imogolite nanotubes. The accessibility of these surface areas, together with the hydrophobic and hydrophilic surface domains, was also demonstrated to depend on the nature of the surrounding medium and the size of the adsorbing species.
Author contributions
Ali Dhaini: investigation, data curation, and writing (original draft). Amine Geneste: investigation and data curation. Fadwa AlFadel Raad: investigation and data curation. Pierre Picot: investigation, data curation, and writing (original draft). Gaëlle Martin Gassin: funding acquisition, resources, and validation. Bénédicte Prelot: methodology, project administration, supervision, and validation. Pierre-Marie Gassin: validation, and writing (original draft). Philippe Trens: investigation, formal analysis, validation, and writing (original draft). Antoine Thill: conceptualization, formal analysis, funding acquisition, project administration, supervision, validation, and writing (original draft, review, editing). Jerzy Zajac: conceptualization, formal analysis, methodology, validation, visualisation, and writing (original draft, review, editing).Data availability
All data generated or analysed in the study are contained within the article and in the related ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors greatly acknowledge the financial support by the French National Agency for Research ANR (BENALOR project, ANR-20-CE09-0029). The authors are also grateful to Dr Nicolas Donzel for his assistance with N2 adsorption measurements and to Julien Fullenwarth for the WDXRF analysis.Notes and references
- K. S. W. Sing and R. T. Williams, Part. Part. Syst. Charact., 2004, 21, 71–79 CrossRef CAS.
- M. Ali Ahmad, B. Prelot, A. Razafitianamaharavo, J. M. Douillard, J. Zajac, F. Dufour, O. Durupthy, C. Chaneac and F. Villiéras, J. Phys. Chem. C, 2012, 116, 24596–24606 CrossRef CAS.
- R. Denoyel, J. Fernandez-Colinas, Y. Grillet and J. Rouquerol, Langmuir, 2002, 9, 515–518 CrossRef.
- B. Prélot, S. Lantenois, Y. Nedellec, M. Lindheimer, J.-M. Douillard and J. Zajac, Colloids Surf., A, 2010, 355, 67–74 CrossRef.
- M. J. Meziani, J. Zajac, J. M. Douillard, D. J. Jones, S. Partyka and J. Roziere, J. Colloid Interface Sci., 2001, 233, 219–226 CrossRef CAS PubMed.
- E. Garrone and B. Bonelli, in Developments in Clay Science, ed. P. Yuan, A. Thill and F. Bergaya, Elsevier, 2016, vol. 7, pp. 672–707 Search PubMed.
- W. C. Ackerman, D. M. Smith, J. C. Huling, Y. W. Kim, J. K. Bailey and C. J. Brinker, Langmuir, 2002, 9, 1051–1057 CrossRef.
- V. C. Farmer, M. J. Adams, A. R. Fraser and F. Palmieri, Clay Miner., 2018, 18, 459–472 CrossRef.
- I. Bottero, B. Bonelli, S. E. Ashbrook, P. A. Wright, W. Zhou, M. Tagliabue, M. Armandi and E. Garrone, Phys. Chem. Chem. Phys., 2011, 13, 744–750 RSC.
- P. D. G. Cradwick, V. C. Farmer, J. D. Russell, C. R. Masson, K. Wada and N. Yoshinaga, Nat. Phys. Sci., 1972, 240, 187–189 CrossRef CAS.
- G. Monet, M. S. Amara, S. Rouzière, E. Paineau, Z. Chai, J. D. Elliott, E. Poli, L.-M. Liu, G. Teobaldi and P. Launois, Nat. Commun., 2018, 9, 2033 CrossRef PubMed.
- A. D'Angelo, E. Paineau, S. Rouzière, É. Elkaim, C. Goldmann, D. Toquer, S. Rols and P. Launois, Appl. Clay Sci., 2023, 242, 107043 CrossRef.
- B. Bonelli, M. Armandi and E. Garrone, Phys. Chem. Chem. Phys., 2013, 15, 13381–13390 RSC.
- S. Rouzière, M. S. Amara, E. Paineau and P. Launois, in Developments in Clay Science, ed. P. Yuan, A. Thill and F. Bergaya, Elsevier, 2016, vol. 7, pp. 254–278 Search PubMed.
- E. Paineau, G. Monet, V. Peyre, C. Goldmann, S. Rouziere and P. Launois, Langmuir, 2019, 35, 12451–12459 CrossRef CAS PubMed.
- K. Sing, Colloids Surf., A, 2001, 187–188, 3–9 CrossRef CAS.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CrossRef CAS.
- C. Hackett and K. D. Hammond, Microporous Mesoporous Mater., 2018, 263, 231–235 CrossRef CAS.
- S. Kunze, R. Groll, B. Besser and J. Thoming, Sci. Rep., 2022, 12, 2057 CrossRef CAS PubMed.
- B. G. Olson, J. J. Decker, S. Nazarenko, V. E. Yudin, J. U. Otaigbe, E. N. Korytkova and V. V. Gusarov, J. Phys. Chem. C, 2008, 112, 12943–12950 CrossRef CAS.
- D. P. Lapham and J. L. Lapham, Int. J. Pharm., 2017, 530, 364–376 CrossRef CAS PubMed.
- G. Sigmund, T. Huffer, T. Hofmann and M. Kah, Sci. Total Environ, 2017, 580, 770–775 CrossRef CAS PubMed.
- K. S. W. Sing, Carbon, 1989, 27, 5–11 CrossRef.
- P. Du, P. Yuan, A. Thill, F. Annabi-Bergaya, D. Liu and S. Wang, Appl. Clay Sci., 2017, 150, 115–124 CrossRef CAS.
- B. Bonelli, I. Bottero, N. Ballarini, S. Passeri, F. Cavani and E. Garrone, J. Catal., 2009, 264, 15–30 CrossRef CAS.
- T. Hongo, J. Sugiyama, A. Yamazaki and A. Yamasaki, Nanopages, 2013, 8, 9–14 CrossRef.
- S. Partyka, F. Rouquerol and J. Rouquerol, J. Colloid Interface Sci., 1979, 68, 21–31 CrossRef CAS.
- S. H. Madani, A. Silvestre-Albero, M. J. Biggs, F. Rodriguez-Reinoso and P. Pendleton, ChemPhysChem, 2015, 16, 3984–3991 CrossRef CAS PubMed.
- R. Zangi and B. J. Berne, J. Phys. Chem. B, 2006, 110, 22736–22741 CrossRef CAS PubMed.
- R. Gulfam and Y. Chen, Research, 2022, 9873075 CAS.
- D. Ahmad, I. van den Boogaert, J. Miller, R. Presswell and H. Jouhara, Energy Sources, Part A, 2018, 40, 2686–2725 CrossRef CAS.
- O. Spalla, S. Lyonnard and F. Testard, J. Appl. Crystallogr., 2003, 36, 338–347 CrossRef CAS.
- C. Cailleteau, F. Angeli, F. Devreux, S. Gin, J. Jestin, P. Jollivet and O. Spalla, Nat. Mater., 2008, 7, 978–983 CrossRef CAS PubMed.
- M. S. Amara, S. Rouzière, E. Paineau, M. Bacia-Verloop, A. Thill and P. Launois, J. Phys. Chem. C, 2014, 118, 9299–9306 CrossRef CAS.
- J.-P. Jolivet, C. Chanéac, D. Chiche, S. Cassaignon, O. Durupthy and J. Hernandez, C. R. Geosci., 2011, 343, 113–122 CrossRef CAS.
- P. Picot, Y. Liao, E. Barruet, F. Gobeaux, T. Coradin and A. Thill, Langmuir, 2018, 34, 13225–13234 CrossRef CAS PubMed.
- N. Tanchoux, P. Trens, D. Maldonado, F. Di Renzo and F. Fajula, Colloids Surf., A, 2004, 246, 1–8 CrossRef CAS.
- J. P. Gustafsson, Clays Clay Miner., 2001, 49, 73–80 CrossRef CAS.
- C. Zanzottera, A. Vicente, E. Celasco, C. Fernandez, E. Garrone and B. Bonelli, J. Phys. Chem. C, 2012, 116, 7499–7506 CrossRef CAS.
- S. Le Caer, M. C. Pignie, Q. Berrod, V. Grzimek, M. Russina, C. Carteret, A. Thill, J. M. Zanotti and J. Teixeira, Nanoscale Adv., 2021, 3, 789–799 RSC.
- A. H. Harvey and E. W. Lemmon, Int. J. Thermophys., 2005, 26, 31–46 CrossRef CAS.
- Y. Marcus, Biophys. Chem., 1994, 51, 111–127 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
-
CRC Handbook of Chemistry and Physics:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Ready-Reference of Chemical and Physical Data, ed. D. R. Lide, CRC Press LLC, 2004, 85th edn Search PubMed.
A Ready-Reference of Chemical and Physical Data, ed. D. R. Lide, CRC Press LLC, 2004, 85th edn Search PubMed. - H. Tao, H. Yang, X. Liu, J. Ren, Y. Wang and G. Lu, Chem. Eng. J., 2013, 225, 686–694 CrossRef CAS.
- T. A. Ho and L. J. Criscenti, J. Colloid Interface Sci., 2021, 600, 310–317 CrossRef CAS PubMed.
- T. Zelenka, Microporous Mesoporous Mater., 2016, 227, 202–209 CrossRef CAS.
- J. D. Stranathan, Phys. Rev., 1935, 48, 538–544 CrossRef CAS.
- M. Boyer, E. Paineau, M. Bacia-Verloop and A. Thill, Appl. Clay Sci., 2014, 96, 45–49 CrossRef CAS.
- F. T. Madsen and M. Müller-Vonmoos, Appl. Clay Sci., 1989, 4, 143–156 CrossRef CAS.
- F. Salles, J.-M. Douillard, O. Bildstein, C. Gaudin, B. Prelot, J. Zajac and H. Van Damme, J. Colloid Interface Sci., 2013, 395, 269–276 CrossRef CAS PubMed.
- A. Tinti, A. Giacomello, Y. Grosu and C. M. Casciola, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E10266–E10273 CrossRef CAS PubMed.
- Y. Liao, P. Picot, M. Lainé, J.-B. Brubach, P. Roy, A. Thill and S. Le Caër, Nano Res., 2018, 11, 4759–4773 CrossRef CAS.
- A. Fernandez-Martinez, J. Tao, A. F. Wallace, I. C. Bourg, M. R. Johnson, J. J. De Yoreo, G. Sposito, G. J. Cuello and L. Charlet, Environ. Sci.: Nano, 2020, 7, 2759–2772 RSC.
- K. Tamura and K. Kawamura, J. Phys. Chem. B, 2001, 106, 271–278 CrossRef.
- E. Balan, M. Lazzeri, G. Morin and F. Mauri, Am. Mineral., 2006, 91, 115–119 CrossRef CAS.
- F. Salles, J.-M. Douillard, R. Denoyel, O. Bildstein, M. Jullien, I. Beurroies and H. Van Damme, J. Colloid Interface Sci., 2009, 333, 510–522 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A literature review of the surface area of imogolite samples, thermal studies of the efficiency of degassing procedures, experimental and modelling SAXS studies on water-dispersed IMO samples, evaluation of textural properties, simple geometrical model of IMO bundles, and the effect of degassing temperature on the results of adsorption and immersion measurements. See DOI: https://doi.org/10.1039/d4cp02396j |
| This journal is © the Owner Societies 2024 |