Intersystem crossing in a dibenzofuran-based room temperature phosphorescent luminophore investigated by non-adiabatic dynamics

Abstract

The use of phosphorescent luminophores is highly beneficial in diverse high-technological and biological applications. Yet, because of the formally forbidden character of intersystem crossing, the use of heavy metals or atoms is usually necessary to achieve high quantum yields. This choice imposes serious constraints in terms of high device cost and inherent toxicity. In this contribution we resort to density functional based surface hopping non-adiabatic dynamics of a potential organic luminophore intended for room-temperature applications. We confirm that intersystem crossing is operative in a ps time-scale without requiring the activation of large-scale movements, thus confirming the suitability of the El Sayed-based strategy for the rational design of fully organic phosphorescent emitters.

---

Introduction

The development of room temperature phosphorescent (RTP) materials has recently attracted considerable interest due to their suitability for applications in electroluminescence, organic lasers, and bioimaging.^1–4 RTP materials are capable of emitting light at room temperature, making them ideal for uses involving organic light-emitting diodes (OLEDs),⁵ bioimaging,^1,6–8 and security ink,^9,10 among others. However, achieving efficient RTP in purely organic compounds is still a formidable scientific challenge.¹¹ Typically, efficient phosphorescent emitters require heavy metals to facilitate intersystem crossing (ISC),^12,13 a process that allows the transition of excited electrons from singlet to triplet states. The use of such heavy metals, while effective, introduces drawbacks such as increased cost and potential toxicity.¹⁴ In this study, we explore an innovative approach to circumvent these limitations by investigating a dibenzofuran-based luminophore through non-adiabatic surface hopping dynamics (SH). By leveraging the principles of density functional theory (DFT), this research aims to demonstrate the feasibility of achieving efficient ISC in organic luminophores without the need of heavy metals.^15,16 This is particularly significant as it opens the door to safer and more cost-effective RTP materials suitable for a broader range of applications.^17,18 To increase ISC, SOC elements should be maximized, since they represent a crucial factor dictating the ISC probability. The presence of heavy metals enhances spin orbit coupling (SOC) in inorganic compounds, conversely in fully organic systems, specific molecular designs and the inclusion of certain functional groups are used to promote efficient SOC. According to the well-known El Sayed rule,¹⁹ SOC will be maximum between singlet and triplet states having a different diabatic nature, since, in this case, the states can be coupled by the magnetic field operator. Thus, SOC and ISC will be maximized when involving transitions between a 1(nπ*) and a 3(ππ*) state. Furthermore, the rigidity of the molecular framework plays a vital role in achieving RTP. Rigid structures minimize non-radiative decay pathways by restricting large-scale molecular vibrations and rotations that can quench the triplet state. Rigidity is efficient in increasing the life-time of the triplet, thereby enhancing phosphorescence.

In this study, we focus on dibenzofuran-based luminophores as potential RTP materials.²⁰ Indeed, dibenzofuran and heterocyclic compounds derivatives are characterized by their aromatic and rigid structures, which lead to efficient phosphorescence.²¹ The design of exploitable luminophores involves optimizing their electronic properties namely to enhance SOC and facilitate ISC. In this respect, the use of conjugated moieties involving carbonyl units is highly favorable, due to the presence of low-lying nπ* states. Yet it has to be pointed out that the states in real molecular systems are rarely of a pure diabatic nature and instead a different degree of mixing between nπ* and ππ* character is observed, slightly complicating the inference of general tendencies. A paradigmatic case involving efficient ISC for organic moieties is the one of benzophenone, which can reach a triplet conversion of up to 100%,^22–24 also due to the extended three states quasi-degeneracy involving S₁ and two lowest triplet states T₁ and T₂, as confirmed by a number of different experimental and computational studies involving non-adiabatic dynamics.^24,25

The benzophenone facile ISC is also at the base of its inherent phototoxicity toward DNA.²⁶

As a matter of fact, different experimental studies on benzophenone ISC and its derivative have been published. An almost unitary phosphorescence, coupled with only a limited delayed fluorescence, which is indicative of a very efficient, yet non ultrafast ISC has been pointed out.^15,27,28

The study of benzophenone materials and the tuning of its phosphorescence by environmental conditions, such as solvent composition and hydrogen bonds have also been performed.^29–31 Interestingly, benzophenone derivative have also been proposed for triplet up-conversion,³² and modified to achieve ultra-long room temperature phosphorescence.³³

Recently an extensive and systematic proposition of molecular rules for the enhancement of ISC in organic emitters has been proposed by Zhao et al.³⁴ based on the consideration of the El Sayed rule and the use of static density functional theory (DFT) calculations. Among the possible compounds, benzophenone and dibenzofuran containing moieties have appeared as the most favorable candidates to enforce high SOC and ISC rates.

As concerns dibenzofuran, its rigid π conjugated scaffold is also optimal to enforce aggregation and crystal formation. Indeed, the reduced vibrational disorder in the condensed phase may be beneficial in slowing non-radiative decay pathways, hence favoring luminescence. Yet, in this case ISC should be achieved without the activation of large amplitude movements, which could be impeded in the solid state.

In this contribution we resort to non-adiabatic dynamics in the surface hopping (SH) formalism to study ISC in the dibenzofuran emitter shown in Fig. 1b, which despite lacking any heavy atoms is displaying optimal luminescence and a phosphorescence quantum yield of about 34%.³⁴ In particular, and going beyond a pure static picture, we will show that the favorable alignment of the involved excited states and their optimal symmetry, in terms of the El Sayed rule, translate into a ps-scale ISC rate, which, thus, should imply the fast population of the triplet manifold. Furthermore, our SH study also confirms that ISC does not involve the activation of any large-scale movement, hence should remain operative also in condensed media, highlighting the optimal characteristic of the chosen dibenzofuran RTP emitter.

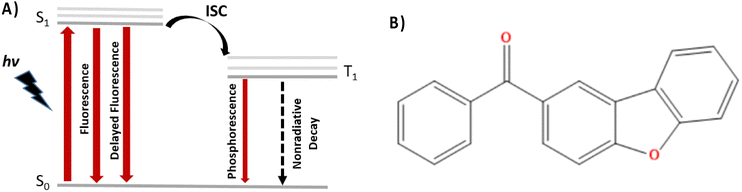Fig. 1 (A) Schematic Jablonski diagram illustrating the relaxation processes operative in phosphorescent luminophores and (B) the dibenzofuran-based compound reported by Zhao et al.³⁴ and studied in the present contribution.

Computational methodology

Prior to the propagation of the non-adiabatic dynamics, the dibenzofuran luminophore's ground state (GS) has been optimized at DFT level using the Gaussian 16 software package.³⁵ The M06-2X³⁶ functional together with the 6-31+G(d,p)³⁷ basis set has been chosen to this aim. The precise geometry optimizations is important since the structural properties and the geometry of the chromophore largely affect its photophysical properties. In our case we are dealing with an aromatic emitter and the choice of M06-2X functional for geometry optimizations is justified by its good performance in reproducing the geometries of similar compounds.³⁸ Integral equation formalism polarizable continuum model (IEF-PCM) is used in DFT calculations, to implicitly model the solvent environment,^39,40 using toluene solvent. Optimized structures were rendered with the CYLview software package.⁴¹

The excited states have been calculated in the framework of time dependent-DFT (TD-DFT) approach, due to its optimal compromise between accuracy and computational cost. More specifically, the Tamm Dancoff approximation (TDA) has been consistently used for the excited states calculations of both singlet and triplet states. This choice is due to the fact that the TDA provides a more balanced description of triplet and singlet excited states, as compared to TD-DFT since it is free from triplet instability issues.⁴² Since some of the excited states presented charge-transfer character their geometry optimization has also been performed using the CAM-B3LYP functional with the 6-31G+(d,p) basis set.

The diabatic nature of the most important excited states has been evaluated using natural transition orbitals (NTOs), which have been obtained post-processing Gaussian output with the Nancy_EX⁴³ code and visualized with the Avogadro⁴⁴ software package. To further characterize the nature of the excited states, the Φs index,^45,46 defining the overlap between the attachment and the detachment density matrices, has been calculated,^43,45 as shown in ESI† (Table S8).

To go beyond this simple static picture, we performed in vacuo SH dynamics using the SHARC code^47,48 coupled with ORCA.⁴⁹ Indeed, SHARC allows taking into account a generalized coupling between the states, such as SOC, and hence may provide the time-scales of ISC, as it is been shown for similar compounds.^24,50–54

As dynamics calculation involve a higher computational cost than statics ones, it is important to find the optimal parameters for electronic structure calculation to maintain good accuracy while minimizing the costs. In order to tune these parameters a benchmark of both basis set and functionals has been performed and results are shown Fig. 2.

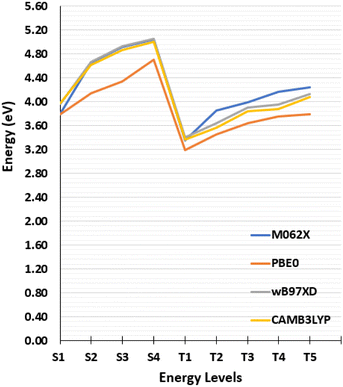Fig. 2 Vertical transitions energies calculated from the Franck–Condon geometry with different exchange correlation functionals.

The singlet and triplet excitation energies have been calculated from the GS, S₁, T₁, T₂ and T₃ equilibrium geometries using different basis sets of increasing size, 6-31G, 6-31G(d), 6-31G(d,p), 6-31+G(d), 6-31+G(d,p), 6-311++G(d,p) (see Tables S3–S7, ESI†) and with different functionals, namely, CAM-B3LYP,⁵⁵ M06-2X, PBE0,⁵⁶ ωB97XD.⁵⁷ As concerns the influence of the exchange–correlation functional on the alignment of the states we report in Fig. 2 the vertical excitation energies for the lowest singlet and triplet states. The effect of basis set appears negligible, as can be appreciated in ESI,† thus justifying the use, in the following, of the smallest double-zeta basis 6-31G for the non-adiabatic dynamics. A slightly more important influence of the functional can be appreciated. Yet, the effects are globally modest and the presence of partially charge-transfer excited states justifies the use of long-range corrected functionals CAM-B3LYP for the following study.

To assure a correct sampling of the ground state equilibrium region, 200 independent structures have been obtained, through a Wigner distribution, using the same level of theory as the one chosen for the SH dynamics. Fifty trajectories, with initial conditions chosen randomly from the initial set of 200, have been propagated in the SH approach. The non-adiabatic dynamics have been performed at TDA level, explicitly calculating the SOC element at each step, and at CAM-B3LYP/6-31G level of theory. A time-step of 0.5 fs has been used for a total time of 2 ps (4000 steps), including the common Persico correlation correction.⁵⁸ Our chosen model has involved explicitly the first excited singlet state, and the lowest four triplet states. An initial total population of the S₁ state was considered, and the time evolution of the states’ population has been fitted with exponential models to obtain the corresponding kinetic model and the global time-scales.

Results and discussion

Geometries optimizations

Upon optimization the ground state geometry of the dibenzofuran-based luminophore presents a non-negligible torsion angle of ∼30° between the two π-conjugated moieties. This geometrical feature is mostly due to the necessity of minimizing the sterical hindrance, as it is the case for the parent benzophenone compound. All the optimized geometries for the different states are explicitly provided in Tables S1 and S2 (ESI†). As reported in Table S2 (ESI†), going from the ground to the first excited singlet state, the torsion angle involving the phenyl ring decreases slightly. On the other hand, the torsion angle in the triplet states remain practically unchanged compared to the ground state. In the case of dibenzofuran, we observe even more modest variations and all states present a torsion of about 25°.

Optical properties

The vertical excitation energies from the Franck–Condon region for the lowest-lying excited states, on either the singlet and triplet manifolds are reported in Table 1.

Table 1 Vertical excitation energies from the Franck–Condon geometry calculated at CAM-B3LYP/6-31G level of theory

State	Excitation energy (eV)	f ^(a)
S1	3.98	0.0014
S2	4.61	0.0303
S3	4.87	0.1810
S4	5.00	0.8612
T1	3.37	—
T2	3.56	—
T3	3.84	—
T4	3.88	—
T5	4.07	—

---

The low energy portion of the absorption spectrum is dominated by two excitations, the lowest one being almost dark and the second one having a much higher oscillator strength. Yet, the S₁ state lies about 0.65 eV lower than the brighter S₂ states. Thus, even if the latter should be populated due to the higher oscillator strength it is reasonable to assume that an ultrafast, fs-based internal conversion, will drive an almost unitary population of the first excited state.

This assumption is also reinforced by the analysis of the topology of the excited state potential energy surfaces. Indeed, when optimizing the S₂ state even if no crossing with S₁ is observed, the gap between the two states is reduced by 0.2 eV. Given the energetic separation between the states, and the modest values of the of the SOC (vide infra), IC appears as much faster than ISC, which should not be competitive. Furthermore, it is also possible to selectively excite S₁ by irradiating on the red tail of this transition even if its cross section is weak. Interestingly, 4 triplet states are found at lower energies than S₁ with T₄ being quasi-degenerate with the lowest excited singlet state.

Electronic nature of states

In Fig. 3 we report the NTOs calculated for the most important low-lying states. The nature of S₁ is, thus, clearly identified as nπ*, while the second excited singlet state has a ππ* nature. The latter shows a partial charge-transfer character even if is mainly localized on the dibenzofuran unit. The same nature of the states is also found in the triplet manifold, with a pronounced nπ* character for T₁ and a local excited nature for T₂. Interestingly, the T₃ states, which will be relevant for the further discussion, can again be described as a ππ* but is mainly localized on the phenyl ring. The values of the SOC elements coupling the lowest triplet and singlet states are reported in Table 2, highlighting small but non negligible coupling of the S₁ states with the triplet manifold.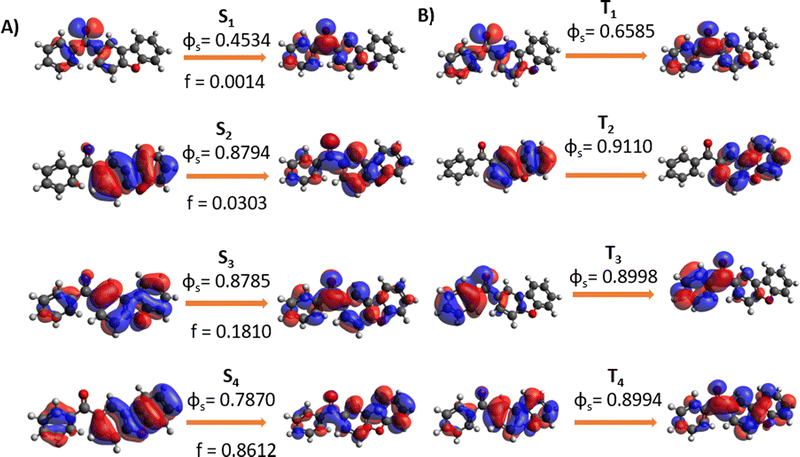

Fig. 3 NTO for singlet (A) and triplet (B) excited states computed at CAM-B3LYP/6-31G level of theory.

Table 2 SOC elements between the different states calculated at CAM-B3LYP/6-31G level of theory and Franck–Condon geometry

	SOC (cm^−1)
S1–T1	7.43
S1–T2	8.48
S1–T3	17.23
S1–T4	7.00
S2–T1	2.13
S2–T2	0.27
S2–T3	0.92
S2–T4	0.17

---

The partial lifting of the El Sayed's rule is most probably due to the partially mixed nature of the states. Furthermore, their partial charge-transfer character, as well as the breaking of the ππ symmetry due to the twisted arrangement, may also be important. Yet, this situation appears as favorable to enforce efficient ISC. Upon geometrical relaxation on the S₁ potential, as indicated on the Jablonski diagram reported in Fig. 4, we may observe that the stabilization of S₁ closes the gap with T₂ and the two states are now separated by only 0.05 eV. This situation is again pointing toward a favorable, albeit non ultrafast ISC, involving those two states, also considering the non-negligible SOC.

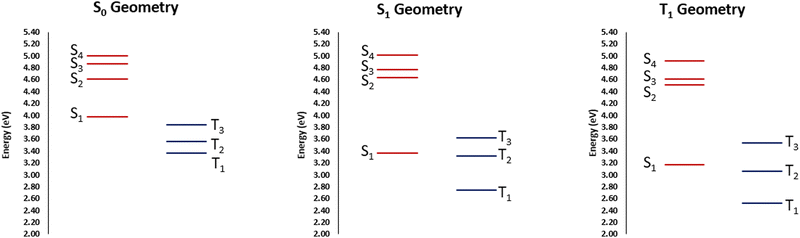Fig. 4 Jablonski diagrams at the most relevant equilibrium geometries obtained at CAM-B3LYP/6-31G level of theory.

Non-adiabatic dynamics

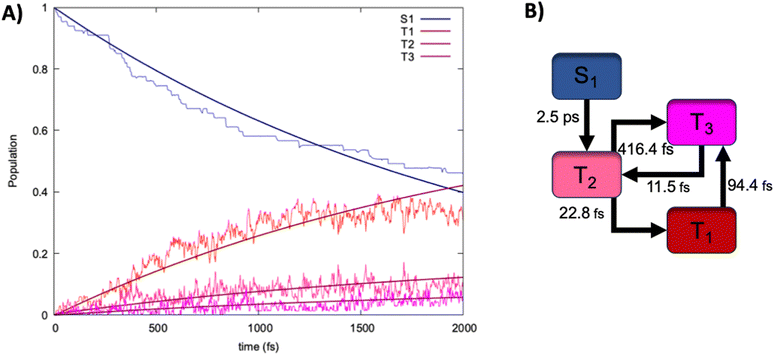
Finally, to assess the mechanisms and the time-scales of ISC we have performed non adubatic dynamics in the SH formalism. The results in terms of time evolution of the population of the different excited states are collected in Fig. 5, together with the ensuing kinetic model inferred from the analysis of the hops between states of different multiplicity, and fitted over a multi exponential model. Indeed, the population of S₁ decays slowly but steadily at the advantage of the triplet manifold, whose population increases. Interestingly, we may observe that after the raise in the population of T₂, T₁ is also readily accessed and becomes the dominant triplet state after about 150 fs. At 2 ps we may observe a perfectly shared population between the singlet and the triplet manifold, with T₁ being the dominant state in the triplet manifold. Yet, we may observe that the population of T₂ is persistent all along the SH dynamics being of about 10% at 2 ps. Furthermore, we may also observe the raising of the population of T₃, which becomes non-negligible at around 500 fs and stays only slightly lower than the one of T₂. Globally, this behavior appears quite surprising since, from the simple analysis of the Jablonski diagram, one could have inferred a straightforward population drift going from S₁ to T₂ and then rapidly towards T₁. Instead, and because of the quasi-degeneracy of the triplet states, a more complicated mechanism (Fig. 5B) takes place. Indeed, the first process leading to S₁ decay can be ascribed as ISC towards T₂, which also represents the time limiting step with a time constant τ of about 2.5 ps. However, the population of this state opens up a complex equilibrium involving T₁ and T₃. If the IC towards the lowest triplet state is clearly the most favorable process having a time constant of only 23 fs, a population transfer towards T₃ is also active, albeit having a much slower characteristic time of about 400 fs. Interestingly, while T₃ readily relaxes back to T₂ (τ of 11 fs) a population drift from T₁ to T₃ is also possible and is relatively fast (τ of 94 fs). Our SH dynamics have thus confirmed that ISC is operative in this dibenzofuran system, thus justifying its efficiency as a metal-free luminophore. The rate limiting step of the ISC, which amounts to 2.5 ps confirms that the process while possible is not ultrafast, probably due to the relatively modest values of the involved SOC.

Fig. 5 (A) Time evolution of the population of the different states following the SH dynamics. (B) Kinetic model used to fit the time evolution of the population; the obtained characteristic time constants are also reported. Note that the population obtained by applying the fitting is also indicated in panel A with darker color shades.

Furthermore, by analyzing the geometrical changes along the SH trajectories we may evidence that no large-scale movement is necessary to trigger ISC. Instead only the activation of small amplitude vibrational movements, mainly related to the carbonyl stretching are necessary. This aspect is mostly favorable for the possible triggering of aggregation induced phosphorescence, which is operative in the present dibenzofuran-based luminophore.

Conclusions

In the present contribution we have studied by extensive TD-DFT modeling, complemented with non-adiabatic SH dynamics the behavior of a dibenzofuran-based chromophore which is a most promising candidate for room temperature phosphorescence. In particular we have confirmed the interplay between nπ* and ππ* states in providing the most favorable conditions for high SOC in full organic compounds, thus favoring the ensuing ISC. While we have confirmed that ISC takes place with a rate limiting step of about 2.5 ps, and involves the transition between S₁ and T₂, we also identify the instauration of a complex equilibrium in the triplet manifold with multiple population transfers between the lowest lying triplet states. In turn this imply that the population of T₂ and T₃ is persisting all along the SH dynamics, thus exceeding the ps time-scale, and should be taken into account. Furthermore, we have shown that ISC does not involve the activation of large amplitude degrees of freedom, and should remain possible also in condensed phase, opening up the possibility of aggregation induced phosphorescence behavior.

Our results, show how SH dynamics may be used to unravel complex and subtle mechanisms which may be important in shaping the photophysical behavior of organic chromophores. They also point out the validity of the exploitation of the El Sayed rule, involving the coupling between states of different diabatic nature in providing efficient organic compounds featuring high ISC rates. In the following we preview to extend this study to the chromophore in condensed phase to take into account the effects of aggregation on its photophysical behavior.

Author contributions

The manuscript was written by contribution of all the authors.

Data availability

Data are available from the authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is partially supported by the LPCT resources, TUBITAK ULAKBIM High Performance and Grid Computing Center (TRUBA resources) and National Center for High Performance Computing of Turkey (UHEM). SC and PU thank TUBITAK (Project Number: 118Z914) and BAP-M (16863) for financial support. PU also thanks TUBITAK for the 2214A International Research Fellowship Programme for PhD Students E.L. Thanks ANR Lymacato and PhotoCT projects for funding her post-doctoral program. A.M. also thanks ANR and CGI (Commissariat à l'Investissement d'Avenir) for their financial support of this work through Labex SEAM (Science and Engineering for Advanced Materials and devices), ANR 11 LABX 086 and ANR 11 IDEX 05 02. The support of the IdEx “Université Paris 2019” ANR-18-IDEX-0001 and of the Platform P3MB is gratefully acknowledged.

References

1. Z. Wu, A. C. Midgley, D. Kong and D. Ding, Organic persistent luminescence imaging for biomedical applications, Mater. Today Bio, 2022, 17, 100481,  DOI:10.1016/j.mtbio.2022.100481.
2. J. Mei, N. L. C. Leung, R. T. K. Kwok, J. W. Y. Lam and B. Z. Tang, Chem. Rev., 2015, 115, 11718–11940,  DOI:10.1021/acs.chemrev.5b00263.
3. X. Xiong, F. Song, J. Wang, Y. Zhang, Y. Xue, L. Sun, N. Jiang, P. Gao, L. Tian and X. Peng, Thermally activated delayed fluorescence of fluorescein derivative for time-resolved and confocal fluorescence imaging, J. Am. Chem. Soc., 2014, 136, 9590–9597,  DOI:10.1021/ja502292p.
4. X. Luo, B. Tian, Y. Zhai, H. Guo, S. Liu, J. Li, S. Li, T. D. James and Z. Chen, Room-temperature phosphorescent materials derived from natural resources, Nat. Rev. Chem., 2023, 7, 800–812,  DOI:10.1038/s41570-023-00536-4.
5. J. H. Kim, J. H. Yun and J. Y. Lee, Adv. Opt. Mater., 2018, 6, 1800255,  DOI:10.1002/adom.201800255.
6. X. Zhen, R. Qu, W. Chen, W. Wu and X. Jiang, The development of phosphorescent probes for: In vitro and in vivo bioimaging, Biomater. Sci., 2021, 9, 285–300,  10.1039/d0bm00819b.
7. A. T. Bui, A. Grichine, A. Duperray, P. Lidon, F. Riobé, C. Andraud and O. Maury, Terbium(III) Luminescent Complexes as Millisecond-Scale Viscosity Probes for Lifetime Imaging, J. Am. Chem. Soc., 2017, 139, 7693–7696,  DOI:10.1021/jacs.7b02951.
8. A. Grichine, A. Haefele, S. Pascal, A. Duperray, R. Michel, C. Andraud and O. Maury, Millisecond lifetime imaging with a europium complex using a commercial confocal microscope under one or two-photon excitation, Chem. Sci., 2014, 5, 3475–3485,  10.1039/c4sc00473f.
9. Y. Lei, W. Dai, J. Guan, S. Guo, F. Ren, Y. Zhou, J. Shi, B. Tong, Z. Cai, J. Zheng and Y. Dong, Wide-Range Color-Tunable Organic Phosphorescence Materials for Printable and Writable Security Inks, Angew. Chem., Int. Ed., 2020, 59, 16054–16060,  DOI:10.1002/anie.202003585.
10. M. M. Abdelhameed, Y. A. Attia, M. S. Abdelrahman and T. A. Khattab, Photochromic and fluorescent ink using photoluminescent strontium aluminate pigment and screen printing towards anticounterfeiting documents, Luminescence, 2021, 36, 865–874,  DOI:10.1002/bio.3987.
11. S. Wang, Z. Cheng, X. Han, H. Shu, X. Wu, H. Tong and L. Wang, Efficient and tunable purely organic room temperature phosphorescence films from selenium-containing emitters achieved by structural isomerism, J. Mater. Chem. C, 2022, 10, 5141–5146,  10.1039/d2tc00337f.
12. J. Jayabharathi, V. Thanikachalam and S. Thilagavathy, Phosphorescent organic light-emitting devices: Iridium based emitter materials – An overview, Coord. Chem. Rev., 2023, 483, 215100,  DOI:10.1016/j.ccr.2023.215100.
13. C. Fan and C. Yang, Yellow/orange emissive heavy-metal complexes as phosphors in monochromatic and white organic light-emitting devices, Chem. Soc. Rev., 2014, 43, 6439–6469,  10.1039/c4cs00110a.
14. M. Li, X. Cai, Z. Chen, K. Liu, W. Qiu, W. Xie, L. Wang and S. J. Su, Boosting purely organic room-temperature phosphorescence performance through a host-guest strategy, Chem. Sci., 2021, 12, 13580–13587,  10.1039/d1sc03420k.
15. C. C. Kenry and B. Liu, Enhancing the performance of pure organic room-temperature phosphorescent luminophores, Nat. Commun., 2019, 10, 2111,  DOI:10.1038/s41467-019-10033-2.
16. Z. Wu, H. Choi and Z. M. Hudson, Achieving White-Light Emission Using Organic Persistent Room Temperature Phosphorescence, Angew. Chem., Int. Ed., 2023, 62, e202301186,  DOI:10.1002/anie.202301186.
17. L. Shi, L. Ding, Y. Zhang and S. Lu, Application of room-temperature phosphorescent carbon dots in information encryption and anti-counterfeiting, Nano Today, 2024, 55, 102200,  DOI:10.1016/j.nantod.2024.102200.
18. M. Ji and X. Ma, Recent progress with the application of organic room-temperature phosphorescent materials, Ind. Chem. Mater., 2023, 1, 582–594,  10.1039/d3im00004d.
19. M. A. El-Sayed, Triplet state. Its radiative and nonradiative properties, Acc. Chem. Res., 1968, 1, 8,  DOI:10.1021/ar50001a002.
20. M. Mońka, D. Grzywacz, E. Hoffman, V. Ievtukhov, K. Kozakiewicz, R. Rogowski, A. Kubicki, B. Liberek, P. Bojarski and I. E. Serdiuk, Decisive role of heavy-atom orientation for efficient enhancement of spin-orbit coupling in organic thermally activated delayed fluorescence emitters, J. Mater. Chem. C, 2022, 10, 11719–11729,  10.1039/d2tc01729f.
21. J. Li, K. Wei, J. Wu, Y. Wang, S. Liu, Y. Ma and Q. Zhao, Simultaneously enhancing organic phosphorescence quantum yields and lifetimes for triphenylphosphine salt doped polymer films, Chem. Sci., 2024, 15, 4881–4889,  10.1039/d4sc00161c.
22. Y. Lee, K. M. Hwang, S. Lee, B. B. Park, T. Kim and W. S. Han, Substituent effect on anthracene-benzophenone triad system: Photophysical properties and application to OLEDs with “hot-exciton” characteristics, Dyes Pigm., 2023, 213, 111171,  DOI:10.1016/j.dyepig.2023.111171.
23. D.-C. Sergentu, R. Maurice, R. W. A. Havenith, R. Broer and D. Roca-Sanjuán, Computational determination of the dominant triplet population mechanism in photoexcited benzophenone, Phys. Chem. Chem. Phys., 2014, 16, 25393–25403,  10.1039/C4CP03277B.
24. M. Marazzi, S. Mai, D. Roca-Sanjuán, M. G. Delcey, R. Lindh, L. González and A. Monari, Benzophenone Ultrafast Triplet Population: Revisiting the Kinetic Model by Surface-Hopping Dynamics, J. Phys. Chem. Lett., 2016, 7, 622–626,  DOI:10.1021/acs.jpclett.5b02792.
25. L. Favero, G. Granucci and M. Persico, Surface hopping investigation of benzophenone excited state dynamics, Phys. Chem. Chem. Phys., 2016, 18, 10499–10506,  10.1039/C6CP00328A.
26. M. C. Cuquerella, V. Lhiaubet-Vallet, J. Cadet and M. A. Miranda, Benzophenone photosensitized DNA damage, Acc. Chem. Res., 2012, 45, 1558–1570,  DOI:10.1021/ar300054e.
27. C. A. Parker and T. A. Joyce, Phosphorescence of benzophenone in fluid solution, Chem. Commun., 1968, 740–750,  10.1039/C19680000749.
28. D. Blazevicius and S. Grigalevicius, A Review of Benzophenone-Based Derivatives for Organic Light-Emitting Diodes, Nanomaterials, 2024, 14, 356,  DOI:10.3390/nano14040356.
29. R. K. Venkatraman, S. Kayal, A. Barak, A. J. Orr-Ewing and S. Umapathy, Intermolecular Hydrogen Bonding Controlled Intersystem Crossing Rates of Benzophenone, J. Phys. Chem. Lett., 2018, 9, 1642–1648,  DOI:10.1021/acs.jpclett.8b00345.
30. İ. Şener, Ç. Şahin, S. Demir, N. Şener and M. Gür, A combined experimental and computational study of electrochemical and photophysical properties of new benzophenone derivatives functionalized with N-substituted-phenyl-1,3,4-thiadiazole-2-amine, J. Mol. Struct., 2020, 1203, 127475,  DOI:10.1016/j.molstruc.2019.127475.
31. R. Gao, Y. Cha, H. Fu and Z. Yu, Excitation-Dependent and Efficient Phosphorescence Based on Benzophenone Derivatives, Adv. Opt. Mater., 2023, 11, 2202095,  DOI:10.1002/adom.202202095.
32. J. Li, X. Li, G. Wang, X. Wang, M. Wu, J. Liu and K. Zhang, A direct observation of up-converted room-temperature phosphorescence in an anti-Kasha dopant-matrix system, Nat. Commun., 2023, 14, 1987,  DOI:10.1038/s41467-023-37662-y.
33. Y. Su, X. Du, B. Fu, G. Wang, X. Piao, G. Wang and K. Zhang, Disrupting n-π* Transition of Benzophenone Derivatives’ T1 States to Achieve Ultralong-Lived Room-Temperature Phosphorescence, ACS Mater. Lett., 2024, 6, 1042–1049,  DOI:10.1021/acsmaterialslett.4c00104.
34. W. Zhao, Z. He, J. W. Y. Lam, Q. Peng, H. Ma, Z. Shuai, G. Bai, J. Hao and B. Z. Tang, Rational Molecular Design for Achieving Persistent and Efficient Pure Organic Room-Temperature Phosphorescence, Chem, 2016, 1, 592–602,  DOI:10.1016/j.chempr.2016.08.010.
35. I. Frisch, M. J. Trucks, G. W. Schlegel, H. B. Scuseria, G. E. Robb, M. A. Cheeseman, J. R. Scalmani, G. Barone, V. Petersson, G. A. Nakatsuji, H. Li, X. Caricato, M. Marenich, A. V. Bloino, J. Janesko, B. G. Gomperts, R. Mennucci and B. Hratch, Gaussian 16, Revision C.01.
36. Y. Zhao and D. G. J. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241,  DOI:10.1063/1.2370993.
37. G. A. Petersson and M. A. Al-Laham, A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms, J. Chem. Phys., 1991, 94, 6081–6090,  DOI:10.1063/1.460447.
38. D. Josa, J. Rodríguez-Otero, E. M. Cabaleiro-Lago and M. Rellán-Piñeiro, Analysis of the performance of DFT-D, M05-2X and M06-2X functionals for studying π⋯π interactions, Chem. Phys. Lett., 2013, 557, 170–175,  DOI:10.1016/j.cplett.2012.12.017.
39. J. Tomasi and M. Persico, Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent, Chem. Rev., 1994, 94, 2027–2094,  DOI:10.1021/cr00031a013.
40. B. Mennucci, Polarizable continuum model, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404,  DOI:10.1002/wcms.1086.
41. C. Y. Legault, CYLview Visualization and analysis software for computational chemistry 1.0b.
42. M. J. G. Peach, M. J. Williamson and D. J. Tozer, Influence of triplet instabilities in TDDFT, J. Chem. Theory Comput., 2011, 7, 3578–3585,  DOI:10.1021/ct200651r.
43. T. Etienne, X. Assfeld and A. Monari, New Insight into the Topology of Excited States through Detachment/Attachment Density Matrices-Based Centroids of Charge, J. Chem. Theory Comput., 2014, 10, 3906–3914,  DOI:10.1021/ct500400s.
44. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeerschd, E. Zurek and G. R. Hutchison, Avogadro: An advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4, 17,  DOI:10.1186/1758-2946-4-17.
45. T. Etienne, X. Assfeld and A. Monari, Toward a quantitative assessment of electronic transitions charge-transfer character, J. Chem. Theory Comput., 2014, 10, 3896–3905,  DOI:10.1021/ct5003994.
46. T. Etienne, X. Assfeld and A. Monari, New insight into the topology of excited states through detachment/attachment density matrices-based centroids of charge, J. Chem. Theory Comput., 2014, 10, 3906–3914,  DOI:10.1021/ct500400s.
47. S. Mai, P. Marquetand and L. González, Nonadiabatic dynamics: The SHARC approach, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370,  DOI:10.1002/wcms.1370.
48. S. Mai, D. Avagliano, M. Heindl, P. Marquetand, M. F. S. J. Menger, M. Oppel, F. Plasser, S. Polonius, M. Ruckenbauer, Y. Shu, D. G. Truhlar, L. Zhang, P. Zobel and L. González, SHARC3.0: Surface Hopping Including Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics, 2023 DOI:10.5281/zenodo.7828641.
49. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327,  DOI:10.1002/wcms.1327.
50. S. Mai, M. F. S. J. Menger, M. Marazzi, D. L. Stolba, A. Monari and L. González, Competing ultrafast photoinduced electron transfer and intersystem crossing of [Re(CO) 3 (Dmp)(His124)(Trp122)] + in Pseudomonas aeruginosa azurin: a nonadiabatic dynamics study, Theor. Chem. Acc., 2020, 139, 1–13,  DOI:10.1007/s00214-020-2555-6.
51. T. Schnappinger, P. Kölle, M. Marazzi, A. Monari, L. González and R. De Vivie-Riedle, Ab initio molecular dynamics of thiophene: The interplay of internal conversion and intersystem crossing, Phys. Chem. Chem. Phys., 2017, 19, 25662–25670,  10.1039/c7cp05061e.
52. M. Nazari, C. D. Bösch, A. Rondi, A. Francés-Monerris, M. Marazzi, E. Lognon, M. Gazzetto, S. M. Langenegger, R. Häner, T. Feurer, A. Monari and A. Cannizzo, Ultrafast dynamics in polycyclic aromatic hydrocarbons: The key case of conical intersections at higher excited states and their role in the photophysics of phenanthrene monomer, Phys. Chem. Chem. Phys., 2019, 21, 16981–16988,  10.1039/c9cp03147b.
53. A. Monari, A. Burger and E. Dumont, Rationalizing the environment-dependent photophysical behavior of a DNA luminescent probe by classical and non-adiabatic molecular dynamics simulations, Photochem. Photobiol. Sci., 2023, 22, 2081–2092,  DOI:10.1007/s43630-023-00431-3.
54. E. Lognon, A. Burger, E. Dumont and A. Monari, Effect of Microhydration in Tuning the Photophysical Behavior of a Luminescent DNA Probe Revealed by Non-Adiabatic Dynamics, ChemPhotoChem, 2024 DOI:10.1002/cptc.202400078.
55. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57,  DOI:10.1016/j.cplett.2004.06.011.
56. M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew-Burke-Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036,  DOI:10.1063/1.478401.
57. J. Da Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620,  10.1039/b810189b.
58. G. Granucci, M. Persico and A. Zoccante, Including quantum decoherence in surface hopping, J. Chem. Phys., 2010, 133, 134111,  DOI:10.1063/1.3489004.

---

Footnote

† Electronic supplementary information (ESI) available: Extended functional and basis sets benchmark topological analysis of the excited states, difference transition matrix from SH dynamics, equilibrium geometries for the different states. See DOI: https://doi.org/10.1039/d4cp02474e

---