Inverse design of ZIFs through artificial intelligence methods

Abstract

We report a tool combining a biologically inspired evolutionary algorithm with machine learning to design fine-tuned zeolitic-imidazolate frameworks (ZIFs), a sub-family of MOFs, for desired sets of diffusivities of species i (D_i) and D_i/D_j of any given mixture of species i and j. We display the efficacy and validitiy of our tool, by designing ZIFs that meet industrial performance criteria of permeability and selectivity, for CO₂/CH₄, O₂/N₂ and C₃H₆/C₃H₈ mixtures.

---

Metal–organic frameworks (MOFs)¹ are multifunctional crystalline nanoporous media, which are studied for several diverse applications among which significant effort has been placed on the development of membranes for gas separations. However, modifying them towards an enhanced selectivity, without lapsing in the so-called permeability-selectivity trade-off is almost impossible in laboratory conditions, due to the complexity of MOF modification-permeability correlation.²

Massive high-throughput MOF screenings in conjunction with artificial intelligence (AI) techniques, such as machine learning (ML), have proved to constitute a very powerful toolset that can extract complex correlations between the structure of a nanoporous solid family and its properties.^3–6 However, even with an accurate MOF-performance correlation, designing materials for specific separations remains a trial-and-error process, though aided by better chemical intuition. In essence, while a predictive model can evaluate existing designs effectively, it falls short in suggesting new ones based on desired performance. Therefore, the design of new materials calls for the inverse direction, which is the target-property -to- MOF-structure prediction.⁷ There is only but a very small number of recent works reporting successful automated design of nanoporous solids driven by a desired target performance and these are limited to sorption properties,^8–17 while diffusivity, which is the governing force of permeability and of overall selectivity in nanoporous membranes,¹⁸ is omitted. There is only one recently published pertinent work, that reports the inverse design of MOFs for kinetic-based separations in MOFs.¹⁹ The scarcity of extended study concerning the inverse problem, combined with the limited focus on sorption, indicate a scientific gap in the domain, since the design of materials with on-demand pre-chosen properties is regarded as a next frontier in materials science.²⁰ In this work we present an inverse design toolkit on zeolitic-imidazolate frameworks (ZIFs), a sub-family of MOFs, that can suggest material designs for requested target diffusivity (D_i, D_i/D_j) values for any i/j mixture. ZIFs were chosen as the focus of this study due to their unique structural characteristics, particularly their tight pore openings, which make them highly suitable for highly challenging kinetic-based separations where the size difference between the mixture species is below 1 Å.^21,22 In contrast, many other MOFs found in existing databases have limited diffusion-based separation capabilities, as their cavities are usually connected by larger openings. Additionally, ZIFs are underrepresented in high-throughput screenings and machine learning applications compared to other MOF sub-families. By focusing on ZIFs in this study, we aim to address this gap in the literature, providing valuable insights and data on a material class that could significantly improve separation performance in challenging gas mixtures.

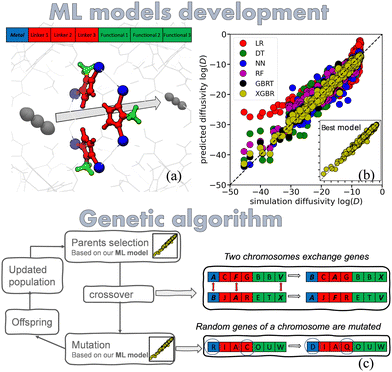
Our method pipeline is as follows: first, we developed and assessed various ML models that can predict the diffusivity of guest molecules, in any ZIF of sodalite (SOD) topology, by using as input readily available information for the ZIF's building-units and the guests, and by taking into consideration the frameworks’ flexibility. Then, based on the best-performing ML model, we developed a genetic algorithm that can suggest new ZIFs for a user-determined separation performance of a gas mixture. Our design approach takes advantage of the ZIF building units, as components that can be replaced to change the aperture size, which – in turn – modulates the kinetics of gas penetrants in the ZIF pores (Fig. 1). We utilized a manually constructed structure database that consists of 69 ZIFs that are of fixed SOD topology, where the building units are varied. Our dataset comprises the diffusivities of 14 gas molecules ranging in size (He: 2.66 Å up to iso-butane: 4.8 Å) in all the ZIFs of our database. The diffusivities have been calculated with dynamically corrected transition state theory (dcTST), that accounted for the flexibility of the framework. The simulations were carried out with in-house developed force fields for the ZIFs and TraPPE force-fields for the gas molecules. Information about the force fields and the dcTST calculations can be found in the (ESI†).

Fig. 1 (a) The aperture bridging the cages used by guest penetrants to propagate from cage to cage and the highlighted ZIF basic building units; (b) performance of the various ML models for the prediction of log D_i, of all gases i considered in all the ZIFs of our database; (c) the genetic algorithm.

The ML regressors examined for the development of efficient ML predictive models were: linear regression (LR), decision tree (DT), random forests (RF), neural networks (NN), as well as Gradient Boosted Tree (GBRT)²³ and extreme gradient boosting regression (XGBR).²⁴ Descriptors were based on readily available information about the linkers, functional groups, and the metal center of each ZIF, as well as information about the guest molecules. Unlike most approaches where building unit descriptors are categorical, our method uses numerical descriptors based on properties such as size and mass. This approach applies not only to the ZIF design space but also to the gases, as we use numerical descriptors for both. As a result, our method has the potential to extrapolate beyond the training set, allowing it to explore unvisited regions of the design space and predict properties for new ZIFs and gases that were not part of the original dataset. The comparison of models (Fig. 1(b)) shows that XGBR followed by GBRT, exhibit a notably better performance. Therefore, XGBR was chosen as the ML model that was employed for this work. Additional information about the dataset, the ML models, the ZIF and gas descriptors, and a table with ML models performance metrics can be found in the ESI.†

Our approach is based on the premise that the trained ML models are functions, the input of which reflect ZIF and diffusant i descriptors/features and the output is an estimate of log D_i of a species i. As such, these functions can guide an optimization process, to find the best descriptors for a desired target value of log D_i. To test our hypothesis, we first tried a conventional optimization algorithm, the L-BFGS-B,²⁵ which is a local search optimization algorithm, that uses the Hessian matrix (second-order derivative). The algorithm worked sufficiently well when used to optimize the value of a simple, linear regression ML model, but fared poorly when more elaborate ML models were considered. For this reason, we used genetic algorithms (GA), which are optimizer algorithms inspired by the Darwinian theory of evolution.²⁶ In GA, each of the structural descriptors (metal, functional group, and organic linker, shown in Fig. 1(a)) are represented as a gene (Fig. 1(c)). A unique set of genes constitutes a chromosome, which corresponds to a unique ZIF. The structure, then, is evolved at each iteration through genetic operations on the chromosome, such as crossover, mutation, replication and selection, and a set of new ZIFs are assembled, with properties that are possibly closer to the requested performance (Fig. 1(c)). Details on the implementation of our GA algorithm can be found in the ESI.†

We combined the ML regressor and the genetic algorithm into a unified tool, which we employed to design optimum ZIFs for the separation of i/j mixtures, that respect target value criteria for D_i and D_i/D_j for three challenging cases: CO₂/CH₄, O₂/N₂ and C₃H₆/C₃H₈. Our goal in all three cases was to design ZIFs that achieve performance beyond the boundaries set by the industry as sufficient permeability, P_i (barrer), and P_i/P_j. These sets of values are (33.7, 35.1),²⁷ (0.83, 8.2)²⁸ and (1.2, 35.6),²⁹ for CO₂/CH₄, O₂/N₂ and C₃H₆/C₃H₈, respectively.

O ₂ /N ₂ is the most studied separation,³⁰ and one of the toughest for membranes, since there are just a few that get close to the industrial standards; there are hardly any membranes that hold a performance level within the region of industrial interest. Our goal was to design ZIFs with D_O2/D_N2–10–50. We set 10⁻¹³ m² s⁻¹ < D_O2 < 5 × 10⁻¹² m² s⁻¹, since according to our findings^31,32P_O2 > 1 barrer corresponds roughly to D_O2 > 10⁻¹³–10⁻¹² m² s⁻¹ in ZIFs. CO₂/CH₄ is the second most investigated mixture in research for membranes separations³⁰ due to the urgency of reducing CO₂ emissions, as well as the need to remove CO₂ from natural gas and biogas streams.³³ According to our findings in our recent works ZIFs^31,32 that exhibit permeabilities beyond the lower industrial limits (∼30 barrer) correspond to D_CO2 > 10⁻¹³ m² s⁻¹. We have thus set the target 10⁻¹⁰ m² s⁻¹ < D_O2 < 5 × 10⁻⁹ m² s⁻¹ and 10⁴ < D_CO2/D_CH4 < 10⁵. Moreover, this time we limited the ZIF generation routine in our GA algorithm, to construct symmetrical ZIFs (linker1 = linker2 = linker3; functional_group_1 = functional_group_2 = functional_group_3), because the search space gets rapidly crowded by proposed optimized structures for the given performance boundaries. Finally, C₃H₆/C₃H₈ reflects a separation of great industrial interest, as it is applied upon two of the most demanded commodity chemicals. Moreover, it is a highly energy intensive process, as, along with C₂H₄/C₂H₆, it accounts for 0.3% of the total energy consumption,³⁴ and no membrane yet has demonstrated promising performance that can replace the existing cryogenic distillation methods. The top performer in this setting is ZIF-67, that has been synthesized and measured for this separation.^29,35 Because ZIF-67 was present in our data, we completely removed any ZIF-67 related data, and we re-trained our XGBR model. We set target values close to ZIF-67 performance, to see whether our tool would design it. This would serve as another level of validation (experiments), besides simulations (like in the first two cases). Thus, the target values set in our design tool were 10⁻¹³ < D_C3H6 < 10⁻¹² m² s⁻¹ and 50 < D_C3H6/D_C3H8 < 200.³⁵

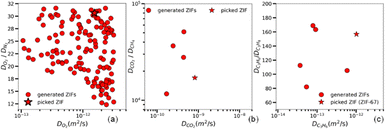
Fig. 2(a)–(c) show the best ZIFs that our GA tool produced on the basis of the given boundary performances for the three separations.

Fig. 2 (a)–(c) Solutions (new ZIFs) for the three desired separation targets.

From the wide collection of new ZIF designs that our tool produced (Fig. 2(a)–(c)), we chose one for each case. Table 1 shows the composition of each of these ZIFs. The third ZIF, as was stated above, is a well-known ZIF in literature, named ZIF-67, but the other two ZIFs are never-seen before, which we named Cd-I-ZIF-7-8 and dFm_Be (more information about the three ZIFs can be found in ESI,† Section 3.4.3). The goal in all three cases was to select a high-performing ZIF, considering both high selectivity and a high diffusion rate for the fast-permeating species. In the case of Fig. 2(a), Cd-I-ZIF-7-8 consistently appeared among the top performers in multiple iterations of the GA procedure. While some other ZIFs occasionally outperformed it, these were almost never the same between iterations, highlighting the randomness inherent in the GA process. We chose Cd-I-ZIF-7-8 due to its reliability in consistently performing well, even though it was not on the efficient frontier in this specific case. We reconstructed these ZIFs, developed the force fields, and equilibrated the structures with MD simulations, in the NPT ensemble (308 K, 1 bar). Then we ran fully flexible TST simulations to validate their performance. Considering the complexity of the systems, the AI tool's predictions match surprisingly well with the simulations. Especially for the case of ZIF-67, our tool is further validated by the additional comparison with the literature's experiments.³⁵

Table 1 Chemical composition, performance predictions and validation (simulations/experiments) of the three selected ZIFs

Formula of generated ZIF	ZIF name	Species (i,j)	Performance		Validation (sims)		Validation (exp.)
			D i (m^2 s^−1)	D i /D j	D i (m^2 s^−1)	D i /D j	D i (m^2 s^−1)	D i /D j
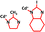
	Cd-I-ZIF-7-8	O2,N2	1.6 × 10^−12	28	1.2 × 10^−12	50
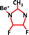
	dFm_Be	CO2, CH4	8.3 × 10^−10	1.7 × 10^4	2.5 × 10^−10	1.0 × 10^4
	ZIFF-67	C3H6,C3H8	1.02 × 10^−12	156	2.0 × 10^−13	200	1.5 × 10^−12	200
							Ref. 35	Ref. 35

---

Moreover, we calculated the solubilities, S_i, of the mixtures’ species in the corresponding ZIFs, at infinite dilution, and we estimated the permeabilities, P_i, through P_i = D_i × S_i, and the resulting ideal selectivities. We plotted the results against data from literature for various membranes (Fig. 3). The Robeson plot of Fig. 3(c) shows that the performance of the new ZIFs is not only within the desired industrial region boundaries for each desired mixture separation but exhibits unprecedented separation performance when compared with competing materials. Also, the third plot serves as an additional validation of our computational approach since the experimental ZIF-67²⁹ performance (P_C3H6 = 11.7; P_C3H6/P_C3H8 = 84.8) is close to our predictions (P_C3H6 =4.9; P_C3H6/P_C3H8 = 172). Information about the permeability estimation computations can be found in the ESI.†

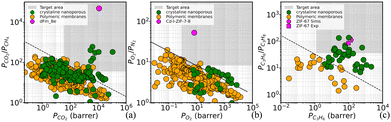Fig. 3 Comparison of the performance of the new designs with literature's membranes, for (a) CO₂/CH₄, (b) O₂/N₂ and (c) C₃H₆/C₃H₈. Blue data were taken from Robeson's seminal work.³⁰ Green data for (a) and (b) were gathered from an extended literature survey and can be found in the SI, while for (c) were taken from Kwon et al.²⁹

Conclusions

We presented an AI-powered software tool that designs nanoporous solids for properties on demand, by combining ML and GAs. Our tool was tested for the design of ZIFs, the assembly of which was driven by a desired set of D_i and D_i/D_j values. More specifically, we set the tool to design various ZIFs that meet industrial performance criteria for separating CO₂/CH₄, O₂/N₂ and C₃H₆/C₃H₈. We chose one ZIF for each case, and we ran simulations to validate that these ZIFs indeed achieve the target separation efficiency that was set initially in our algorithm. The comparison with the simulations, and for one case with available experimental findings, validated our tool's efficacy.

Author contributions

P. K. contributed to conceptualization, formal analysis, investigation, methodology, software, writing, data curation. M. K. contributed to conceptualization, supervision, formal analysis and editing. T. S. contributed to supervision, conceptualization, formal analysis, editing and funding acquisition. G. G. contributed to supervision, conceptualization, software, formal analysis, editing and funding acquisition.

Data availability

The code for the implementation of the genetic algorithm for the inverse design, along with the all the simulation data (training data for the ML models) can be found at: https://github.com/Sileonis/ZIFs_genetic_algorithm. All ZIF variants of this work (SmartDeZIgn database) can be found in the form of.pdb format in our zenodo repository (DOI: https://doi.org/10.5281/zenodo.7799068). The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

References

1. R. Freund, O. Zaremba, G. Arnauts, R. Ameloot, G. Skorupskii, M. Dincă, A. Bavykina, J. Gascon, A. Ejsmont, J. Goscianska, M. Kalmutzki, U. Lächelt, E. Ploetz, C. S. Diercks and S. Wuttke, The Current Status of MOF and COF Applications, Angew. Chem., Int. Ed., 2021, 60, 23975–24001.
2. H. Lyu, Z. Ji, S. Wuttke and O. M. Yaghi, Digital Reticular Chemistry, Chem, 2020, 6, 2219–2241.
3. G. S. Fanourgakis, K. Gkagkas, E. Tylianakis and G. E. Froudakis, A Universal Machine Learning Algorithm for Large-Scale Screening of Materials, J. Am. Chem. Soc., 2020, 142, 3814–3822.
4. P. Krokidas, S. Karozis, S. Moncho, G. Giannakopoulos, E. N. Brothers, M. E. Kainourgiakis, I. G. Economou and T. A. Steriotis, Data mining for predicting gas diffusivity in zeolitic-imidazolate frameworks (ZIFs), J. Mater. Chem. A, 2022, 10, 13697–13703.
5. R. Pétuya, S. Durdy, D. Antypov, M. W. Gaultois, N. G. Berry, G. R. Darling, A. P. Katsoulidis, M. S. Dyer and M. J. Rosseinsky, Machine-Learning Prediction of Metal–Organic Framework Guest Accessibility from Linker and Metal Chemistry, Angew. Chem., Int. Ed., 2022, 61, 1–6.
6. X. Cheng, Y. Liao, Z. Lei, J. Li, X. Fan and X. Xiao, Multi-scale design of MOF-based membrane separation for CO2/CH4 mixture via integration of molecular simulation, machine learning and process modeling and simulation, J. Membr. Sci., 2023, 672, 121430.
7. H. Demir, H. Daglar, H. C. Gulbalkan, G. O. Aksu and S. Keskin, Recent advances in computational modeling of MOFs: From molecular simulations to machine learning, Coord. Chem. Rev., 2023, 484, 215112.
8. Y. G. Chung, D. A. Gómez-Gualdrón, P. Li, K. T. Leperi, P. Deria, H. Zhang, N. A. Vermeulen, J. F. Stoddart, F. You, J. T. Hupp, O. K. Farha and R. Q. Snurr, In silico discovery of metal-organic frameworks for precombustion CO2 capture using a genetic algorithm, Sci. Adv., 2016, 2, e1600909.
9. B. Kim, S. Lee and J. Kim, Inverse design of porous materials using artificial neural networks, Sci. Adv., 2020, 6(1) DOI:10.1126/sciadv.aax9324.
10. Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Inverse design of nanoporous crystalline reticular materials with deep generative models, Nat. Mach. Intell., 2021, 3, 76–86.
11. S. S. Y. Lee, B. Kim, H. Cho, H. Lee, S. S. Y. Lee, E. S. Cho and J. Kim, Computational Screening of Trillions of Metal-Organic Frameworks for High-Performance Methane Storage, ACS Appl. Mater. Interfaces, 2021, 13, 23647–23654.
12. Y. Lim, J. Park, S. Lee and J. Kim, Finely tuned inverse design of metal-organic frameworks with user-desired Xe/Kr selectivity, J. Mater. Chem. A, 2021, 9, 21175–21183.
13. A. Deshwal, C. M. Simon and J. R. Doppa, Bayesian optimization of nanoporous materials, Mol. Syst. Des. Eng., 2021, 6, 1066–1086.
14. J. Park, Y. Lim, S. Lee and J. Kim, Computational Design of Metal-Organic Frameworks with Unprecedented High Hydrogen Working Capacity and High Synthesizability, Chem. Mater., 2023, 35, 9–16.
15. G. O. Aksu and S. Keskin, Advancing CH4/H2 separation with covalent organic frameworks by combining molecular simulations and machine learning, J. Mater. Chem. A, 2023, 11, 14788–14799.
16. J. Wang, J. Liu, H. Wang, M. Zhou, G. Ke, L. Zhang, J. Wu, Z. Gao and D. Lu, A comprehensive transformer-based approach for high-accuracy gas adsorption predictions in metal-organic frameworks, Nat. Commun., 2024, 15, 1–14.
17. H. Park, S. Majumdar, X. Zhang, J. Kim and B. Smit, Inverse design of metal-organic frameworks for direct air capture of CO₂ via deep reinforcement learning, Digit. Discovery, 2024, 3, 728–741.
18. R. Krishna, Methodologies for screening and selection of crystalline microporous materials in mixture separations, Sep. Purif. Technol., 2018, 194, 281–300.
19. M. Zhou and J. Wu, Inverse design of metal–organic frameworks for C₂H₄/C₂H₆ separation, npj Comput. Mater., 2022, 8, 256.
20. J. Noh, G. H. Gu, S. Kim and Y. Jung, Machine-enabled inverse design of inorganic solid materials: promises and challenges, Chem. Sci., 2020, 11, 4871–4881.
21. K. Adil, Y. Belmabkhout, R. S. Pillai, A. Cadiau, P. M. Bhatt, A. H. Assen, G. Maurin and M. Eddaoudi, Gas/vapour separation using ultra-microporous metal–organic frameworks: insights into the structure/separation relationship, Chem. Soc. Rev., 2017, 46, 3402–3430.
22. A. M. O. Mohamed, I. G. Economou and H. K. Jeong, Coarse-grained force field for ZIF-8: A study on adsorption, diffusion, and structural properties, J. Chem. Phys., 2024, 160(20) DOI:10.1063/5.0202961.
23. K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Big-Data Science in Porous Materials: Materials Genomics and Machine Learning, Chem. Rev., 2020, 120, 8066–8129.
24. T. Chen and C. Guestrin, Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, vol. 13, pp. 785–794.
25. R. H. Byrd, P. Lu, J. Nocedal and C. Zhu, A Limited Memory Algorithm for Bound Constrained Optimization, SIAM J. Sci. Comput., 1995, 16, 1190–1208.
26. D. Simon, Evolutionary Optimization Algorithms, John Wiley & Sons, 2013.
27. A. M. W. Hillock, S. J. Miller and W. J. Koros, Crosslinked mixed matrix membranes for the purification of natural gas: Effects of sieve surface modification, J. Memb. Sci., 2008, 314, 193–199.
28. B. Zhang, T. Wang, S. Zhang, J. Qiu and X. Jian, Preparation and characterization of carbon membranes made from poly(phthalazinone ether sulfone ketone), Carbon, 2006, 44, 2764–2769.
29. H. T. Kwon, H. K. Jeong, A. S. Lee, H. S. An and J. S. Lee, Heteroepitaxially Grown Zeolitic Imidazolate Framework Membranes with Unprecedented Propylene/Propane Separation Performances, J. Am. Chem. Soc., 2015, 137, 12304–12311.
30. L. M. Robeson, The upper bound revisited, J. Membr. Sci., 2008, 320, 390–400.
31. P. Krokidas, S. Moncho, E. N. Brothers, M. Castier, H. K. Jeong and I. G. Economou, On the Efficient Separation of Gas Mixtures with the Mixed-Linker Zeolitic-Imidazolate Framework-7-8, ACS Appl. Mater. Interfaces, 2018, 10, 39631–39644.
32. P. Krokidas, M. B. M. Spera, L. G. Boutsika, I. Bratsos, G. Charalambopoulou, I. G. Economou and T. Steriotis Nanoengineered, ZIF fillers for mixed matrix membranes with enhanced CO2/CH4 selectivity, Sep. Purif. Technol., 2023, 307, 122737.
33. B. Shimekit and H. Mukhtar, Natural Gas Purification Technologies - Major Advances for CO2 Separation and Future Directions, Advances in Natural Gas Technology, 2012, ch. 9.
34. D. S. Sholl and R. P. Lively, Seven chemical separations to change the world, Nature, 2016, 532, 435–437.
35. P. Krokidas, M. Castier, S. Moncho, D. N. Sredojevic, E. N. Brothers, H. T. Kwon, H. K. Jeong, J. S. Lee and I. G. Economou, ZIF-67 Framework: A Promising New Candidate for Propylene/Propane Separation. Experimental Data and Molecular Simulations, J. Phys. Chem. C, 2016, 120, 8116–8124.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02488e

---